2.2.1刚体基本运动1
2刚体基本运动

1 r2 n1 i 2 r1 n2
2.齿轮传动
r11= –r22;
1 n1 i12 2 n2
r2 r1 z2 z1
r1
r2
3.齿轮箱传动
1 z2 ; 2 z1
3 z4 ; 4 z3
z1
4
z4
1
z2
上二式相乘,並有:2=3
3
i14
α r ω (ω r )
at an
12
z
例:一矢量 rAB 绕 z轴以角速度定轴转动, drAB 试证: dt ω rAB B z' 证明: r r r
rB rA rAB
k
AB
B
A
x
O' i y x'
A
j y'
drAB drB drA vB v A dt dt dt
l
vA
M
vM
vM v A
B
aM a A
vA l
其中 则
π π 0 cos t 4 4 π π v A l 0 cos t 4 4
16
方向垂直O1A
π π v A l 0 cos t 4 4
O1 φ O2
A点的切向加速度 2
l B
l
n A
a
O
a
A
角速度矢量:
大小:
d dt
表征转角变化
y x
方向: 转动方向,右手螺旋确定指向
ω k
单位:
rad/s
工程中转速n: 一分钟转过的圈数
2 n 60
刚体旋转知识点归纳总结

刚体旋转知识点归纳总结1. 刚体旋转的基本概念刚体是指在一定时间内,其内部各点的相对位置不改变的物体。
刚体旋转是指刚体围绕固定点或固定轴发生的旋转运动。
在刚体旋转中,需要引入一些基本概念:1.1 刚体的转动刚体的旋转可以是定点转动,也可以是定轴转动。
在定点转动中,刚体绕固定点旋转,而在定轴转动中,刚体绕固定轴旋转。
定点转动和定轴转动都是刚体旋转运动的两种基本形式。
1.2 刚体的转动角度和角速度刚体的转动角度是刚体在单位时间内所转过的角度,通常用θ表示。
刚体的角速度是指刚体单位时间内转过的角度,通常用ω表示。
在刚体定点转动中,角速度是刚体绕定点旋转的角度速度;在刚体定轴转动中,角速度是刚体绕定轴旋转的角度速度。
1.3 刚体的转动惯量刚体的转动惯量是衡量刚体抵抗旋转的惯性大小,通常用I表示。
刚体转动惯量的大小取决于刚体形状、质量分布以及旋转轴的位置。
对于质点组成的刚体,其转动惯量可以通过对质点的质量进行积分得到。
1.4 刚体的角动量刚体的角动量是刚体旋转运动的物理量,通常用L表示。
角动量的大小和方向分别由角速度和转动惯量决定。
在定点转动中,如果刚体的角速度和转动惯量都不变,那么刚体的角动量也保持不变;在定轴转动中,如果刚体绕固定轴旋转,那么刚体的角动量也保持不变。
2. 刚体的转动力学刚体的转动力学研究刚体在旋转运动中所受的力和力矩,包括转动定律、角动量定理、动能定理等内容。
2.1 刚体的平衡刚体旋转平衡需要满足一定的条件,包括力矩平衡条件和动量平衡条件。
刚体力矩平衡条件是指刚体所受的合外力矩为零;刚体动量平衡条件是指刚体所受的合外力矩关于某一点的力矩为零。
2.2 刚体的角动量定理刚体的角动量定理描述了刚体在受到外力矩作用下,其角动量的变化规律。
根据角动量定理,刚体所受外力矩产生的角动量变化率等于刚体所受外力矩的矢量和。
2.3 刚体的动能定理刚体的动能定理描述了刚体在旋转运动中,其动能的变化规律。
根据动能定理,刚体所受外力矩产生的功率等于刚体动能的变化率。
机器人操作的数学导论——刚体运动(1——3)

定理2.6 从se(3)到SE(3)的指数变换
三、三维空间中的刚体运动
3.2 刚体运动的指数坐标和运动旋量
描述的不是点在不同坐标系间的变换,而是点 由初始位置p(0)∈R3到经如下刚体转动后的位置坐标间的变换
上式中p(θ),p(0)均在同一坐标系中表示。类似,若gab(0)表示刚 体相对于A系的起始位姿,,那么现对于A系的最终位姿为:
二、三维空间中的旋转运动
2.3 四元数
四元数可用与描述空间旋转运动,它是一个矢量,一般形式为:
简洁表达式为:Q=(q0,q),其中q0∈R,q∈R3
二、三维空间中的旋转运动
2.3 四元数
两四元数内积:
给定Q=(q0,q),其中q0∈R,q∈R3,可获得相应的旋转
描述旋转群还可以使用欧拉角来描述。
对于一运动旋量来说,指数变换反映的是刚体的相对运动, 每一个刚体变换都可写为某个运动旋量的指数。
三、三维空间中的刚体运动
3.2 刚体运动的指数坐标和运动旋量
定理2.7 建立在SE(3)的指数变换是满射变换
3.3 旋量:运动旋量的几何表示
se(3)中的元素 称为运动旋量
三、三维空间中的刚体运动
3.3 旋量:运动旋量的几何表示
将满足这两个性质的3×3矩阵的集合记为SO(3),可 用旋转矩阵表示刚体变换
二、三维空间中的旋转运动
群:对于用算子。构成的二元运算集合G,若满足下面条件则构成一个群。
物体相对于定坐标系的每一次旋转,对应于 一个该形式矩阵 可以证明SO(3)是一个以单位矩阵I作为单位元素、以矩阵乘法作为 群运算的群。 旋转矩阵可通过矩阵相乘来组成新的旋转矩阵: Rac=RabRbc 上式称为旋转的合成法则
刚体运动
第6章.刚体的基本运动.ppt

rA rB BA
(6 -1)
2019/11/5
4
3.速度与加速度分布
当刚体平动时,线段AB的长度和方向都不改变,所以 为一常矢量。
把上式对时间t连续取两次导数,于是得:
vA vB aA aB
(6 - 2) (6 - 3)
4.刚体平移的特点:
刚体平移时,其上各点的轨迹形状相同;在每一瞬时, 各点具有相同的速度和加速度。
θθ a
Oθ
ω
α
α
a
O
ω
题6—5
2019/11/5
13
例6—1 升降机装置由半径为R=50cm的鼓轮
带动,如图6—6所示。被升降的物体的运动方程为x=5t2(t以
秒计,x以米计)。
求鼓轮的转动方程、角速度、
角加速度以及任意瞬时轮缘上一点
R
M的全加速度的大小和方向。
o
解: 鼓轮作定轴转动,重物作
平动,鼓轮的运动和重物的运动 相互之间的联系是通过缆绳来实 现的。
φ
块侧面ab的坐标为x。按题意有 O
x= v0t。
x
由三角形Oab得
tan x v0t
hh
h
b a
图6—7
A v0 x
2019/11/5
16
故杆OA的转动方程为
arctan(v0t )
h
根据(6—5)式,杆的角速度是
v0
d
dt
h 1 (v0t )2
h2
hv0 v02t 2
a 常量
2019/11/5
9
§6—3 转动刚体上各点的速度和加速度
ω O'
A
刚体转动惯量及其计算方法(毕业论文)

本科毕业论文题目:刚体转动惯量及其计算方法目录1、引言 (1)2基本概念 (1)2。
1描述刚体位置的独立变量 (1)2.2 刚体运动的分类 (2)3 刚体力学中的质量和惯性 (2)3.1 刚体力学中的惯性运动 (2)3。
2 惯性运动在刚体力学中的应用 (3)4 刚体的几种基本运动 (3)4。
1 定轴转动 (3)4.2 刚体平面平行运动 (3)4。
3 定点转动 (4)4。
4 一般运动 (4)5 刚体转动惯量的计算方法 (4)5.1 转动惯量的引入 (4)5。
2 转动惯量的计算方法 (6)5.2.1定义法 (6)5.2.2惯量椭球法 (7)5.2.3 惯量主轴法 (8)5.2.4 实验方法测量 (9)5。
2。
5 陀螺运动的描述 (10)6 结论 (13)参考文献: (13)致谢.............................................. 错误!未定义书签。
刚体转动惯量及其计算方法摘要:在刚体动力学中,有大量的篇幅研究刚体的转动问题,无论是定轴转动、平面平行运动,还是绕定点的转动,其动力学方程中均含有转动惯量。
转动惯量在刚体力学中有很重要的的地位,相当于质点在动力学中的质量地位相当,应用较为广泛。
本文对质量各种分布刚体的转动惯量进行浅谈,及对定点转动问题进行定量分析。
关键词:刚体;运动;转动惯量;定点转动.本科毕业生毕业论文1、引言随着科学技术的迅猛发展,转动惯量作为一个重要的工程参数,在越来越多的领域受到重视,如何更方便,快捷,准确的计算转动惯量成为了一个迫切需要解决的问题。
转动惯量等于刚体中每个质元的质量与这一质元到转轴的垂直距离的平方的乘积的和,而与质元的运动速度无关。
与质点的平动动能比较而言,转动惯量相当于平动时的质量。
物体转动时转动惯量是表示物体在转动中惯性大小的量度.关于转动惯量的研究由来已久,现在所取得的成果就是前人一点一滴积累来的。
本文将在此基础上,本着循序渐进的原则,对转动惯量及多种计算方法进行探讨。
2.2 刚体定轴转动定律及其应用
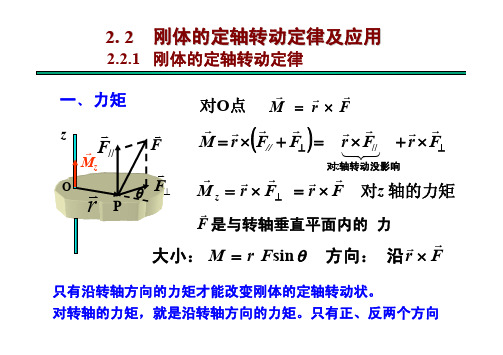
R
dS
r
O
- 2 r kv 2 r d r
0
R
m
- 2 r k r 2 r d r
0
R
4 k r 3dr k R 4
0
R
M 随 变化
M J
M J
4
d J dt
M k R
4
1 2 d k R mR 2 dt
mg
0
d
0
d
0
3g cos d 2L
3g sin L
3) 此时,棒中点C的速度和加速度
L v C rC 6
2
3g sin L
竖直位置?
g acn rC sin 2
g act rC cos 4
例:如图,设滑块A,重物B及滑轮C的质量分别为MA, MB,MC。滑轮C是半径为 r 的均匀圆板。滑块A与桌面之 间,滑轮与轴承之间均无摩擦,轻绳与滑轮之间无滑动。 求:(1)滑块A的加速度a (2)滑块A与滑轮C之间绳的张力T1, (3)滑轮C与重物B之间绳的张力T2。
两边积分
2 k R 2 d dt 0 0 m
0
t
d
0
0
0
2 k R 2 d m
2 k R 2 0 m m0 m 0 N 2 2 2 k R 2 2 4 kR
例. 将一根质量为M,长为L的匀质细杆两端A、B用 等长的线水平地悬挂在天花板上,若突然剪断其中一 根,求此瞬间另一根绳内的张力有多大。 解: 突然剪断B线,棒AB受重力和A线对它的拉力作用 AB绕A点在竖直面内转动。 A线的拉力对A点的力矩为零 重力对A点的力矩为 转动定律
理论力学第5章 点的一般运动与刚体的基本运动

基础部分——运动学第5 章点的一般运动与刚体的基本运动一、运动学的研究对象及任务点刚体zz几何性质z合成分解例1例2例3例4例5例6二、学习运动学的目的三、运动学的分析方法矢量工具数值求解工具四、具体内容第5章点的一般运动与刚体的基本运动点的运动的矢量法点的运动的直角坐标法点的运动的弧坐标法一、运动方程二、轨迹三、点的速度O)(t r )(t t Δ+r vMM ′位矢四、点的加速度点的运动的矢量法一、运动方程点的运动的直角坐标法O rMxy z)(zy,x,xyz二、轨迹方程三、点的速度四、点的加速度AB点的运动的弧坐标法运动轨迹原点O 一、运动方程sMO)(−)(+正方向弧坐标s二、自然轴系主法线n 切线τ,指副法线b思考:共同点不同点)(t r M O三、点的速度⋅lim ⋅st s d d d d r⋅τ⋅=v tsv d d =)(t t Δ+r vM ′sΔO)(−)(+r Δτ四、点的加速度速度大小随时间的变化率方向ττa 22t d d d d tst v ==22t d d d d tst v a ==z切向tas t ΔΔ⋅→Δτ0lim⋅速度方向随时间的变化率z法向n a sΔΔτs ΔΔϕsd d ϕ→方向?n2n2taa +全t 讨论:加速减速[例5-1]纯滚动解:(1)运动方程运动方程=x =y (2)速度22yxv v +t ωcos 22−(3)切向、法向加速度思考:如何求速度投影加速度投影全加速度22a a yx +法向加速度2t2aa −曲率半径(4)运动方程(弧坐标)如何取弧坐标的原点?讨论:Array纯滚动速度为零加速度不为零5-4-1 平行移动(平移)任一直线z形状相同z速度相同z加速度相同5-4-2 定轴转动=矢量表示:=右手规则滑动矢量αωαkz线速度v(弧坐标法)Rv ω=Rna ta αta 方向?z加速度aRa α=t Ra 2n ω=2n2t aa +42ωα+t a α思考:过轴的任一条直线上θαθrωv ×=ααt a rαa ×=t na vωa ×=nr ωr×=td d αααx ′y ′z ′1O i ′j ′k ′rωv ×=[例5-2]解:r ω=+d d r tω−=avtr R +=22ππ[思考题]j i i k ⎜+′⎟⎜′⋅+′⎟′⋅提示:5-5-1 注意区别几组公式5-5-2 描述点的运动的其它方法点的一般运动与刚体基本运动点的一般运动刚体基本运动矢量法直角坐标法弧坐标法其它方法平移定轴转动5-5-3 本章知识结构框图补充:轮系的传动比一、齿轮传动z速度z 切向加速度外啮合内啮合=两齿轮之传动比:21=1 2112R R i ==ωω2112ωω=i 22211±=±=±=正号內啮合负号外啮合11±=外啮合转向推广:二、带轮(链轮)传动二、带轮(链轮)传动z z 皮带与带轮间无相对滑动。
理论力学 第二章 刚体的基本运动

0
nπ 式中n为转速 单位:转/ 分(r/min) 。 山东大学 土建与水利学院工程力学系 THEORETICAL MECHANICS 30
§ 2.2 刚体绕定轴的转动
3.角加速度
描述角速度变化的快慢程度
2
d d lim 2 t 0 t dt dt
单位:弧度/秒2 (rad/s2 ) α与同号,刚体加速转动;
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
§2.4 轮系的传动比
1 n1 r2 Z2 i1,2 2 n2 r1 Z1
此结论对于锥齿轮传动和带 轮传动同样适用。 在一些复杂轮系(如变速器) 中包含有几对齿轮。可将每一对 齿轮的传动算出后,将它们连乘 起来,变为可得总的传动比。
392.8 62.5 转 2π
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
例 题
例2- 3 轮子绕O点作定轴转动,其加速度方向和轮的半径
成60度角,求轮的转动方程,以及角速度和转角之间的关系。
00, 0.
M
O
a
60
THEORETICAL MECHANICS
解 : AB 杆 为 平 移 , O1A 为 定 轴 转 动 。 根 据 平移的特点,在同一瞬 时,M、A两点具有相同 的速度和加速度。
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
例 题
A点作圆周运动,其运动方程为
s O1 A 3π t
ds dv vA 3π (m/s) a A t 0 dt dt
§ 2.1 刚体的平行移动
第七章 刚体的基本运动

第二节 刚体绕定轴转动
一. 转动方程
(1)转角 Ⅰ和Ⅱ夹角 ,单位弧度(rad)
(2)转动方程 =f(t)
(3) 的正、负规定
对着z 轴正向看
逆时针为正 顺时针为负
第二节 刚体绕定轴转动
二、角速度
⑴ 平均角速度
t
⑵ 角速度(瞬时):表示刚
体转动快慢和转动方向的物
理量。
刚体平动→点的运动
第二节 刚体绕定轴转动
1.定义:当刚体运动时 ,刚体内(刚体外)有一 条直线始终保持不动。 2.刚体定轴转动的特点
(1) 始终保持不动的直线称为转轴; (2)其余各点都在垂直于转轴的平面 上以轴上的一点为圆心做圆周运动。
定轴转动实例:电机的转子、机床的主轴、变速箱中 的齿轮、绕固定铰链开关的门窗等!
转动 刚体上任一点的速度分布:
第三节 定轴转动刚体上点的速度和加速度
二.定轴转动刚体上点的加速度
点的加速度包括切向加速度和法向加速度!
⒈ 切向加速度
a
dv dt
d dt
(R)
d
dt
R
R
垂直转动半径,并指向刚体转动的一方。
⒉法向加速度
an
v2 R
(R)2
R
R 2
始终指向转轴O
⒊ 全加速度
⑴ 大小 : a a 2 an2 R 2 4
⑵
方向 :
tg
| a an
|
R| | R 2
| | 2
转动刚体内任一点的切向加速度的大小,等于该点的 转动半径与刚体角加速度的乘积,方向沿轨迹的切线 (垂直于转动半径的方向),指向与ε的转向一致。
2.2 刚体力学基础

Y
M
vC
C mi
yC yi
O
刚体的势能
EP mi gyi
i
mgyc 其中m为刚体的总质量, yc为刚体质心的高度。
质量分布均匀而
有一定几何形状的
X
刚体,质心的位置
为它的几何中心。
例2.22 质量为m ,长为 l 的匀质细杆,可绕杆端的固
定轴在铅直平面内转动。最初杆处于水平位置,放手
后让其自由摆下,试求杆下摆到 角时的角速度和角加
当质点做平面圆周运动时, 由牛顿第二定律:
用矢径叉乘上式两边
rv
v F
rv
d
pv
d
v F
d
pv
dt
(rv pv)
v dt dt
v M
dL
dt
合外力矩
做圆周运动的质点角动量对时间的变化率等于其所受到的 合外力矩。——质点的角动量定理
2. 定轴转动刚体的角动量定理
vv
由转动定理 M J
J
d v
d( J v)
J mjrj2 r2dm j
r2dV V
dm:质量元 dV :体积元
➢ 质量连续分布刚体的转动惯量
J miri2 r2dm dm :质量元
对质量线分布的刚体: dm dl
:质量线密度
对质量面分布的刚体: dm dS
:质量面密度
对质量体分布的刚体:dm dV
:质量体密度
离时两物体的速度和加速度.
解: 以两物体、两滑轮、地球
成为一系统,A外 0,A内非 0 ,
故机械能守恒.以 m1 下降 x 时
的位置为重力势能零点,则有
m1gx
m2
gx
点的一般运动和刚体的基本运动

t 时间间隔内矢径旳变化 量 r(t)= r (t + t )- r(t)
点在 t 瞬时旳速度
v lim r d r r t0 t dt
动点旳速度等于它旳矢径对时间旳一阶导数。
7
v lim r dr t0 t dt
速 度 —— 描述点在 t 时刻运动快慢和运 动方向旳力学量。速度旳方向沿着运动 轨迹旳切线;指向与点旳运动方向一致; 速度大小等于矢量旳模。
❖ 加速度 —— 描述点在 t 时刻速度大小和方 向旳变化率旳力学量。 加速度旳方向为 v旳 极限方向 加速度大小等于矢量a旳模。
10
2、点旳运动旳直角坐标表达法
运动方程 速度 加速度
11
➢运动方程
不受约束旳点在空间有 3个自由度,在直角 坐标系中,点在空间旳位置由3个方程拟定:
x = x(t) y = y(t)
运动方程 速度 加速度
5
运动方程
运动方程 用点在任意瞬时t旳位置矢量r(t)
表达。 r(t)简称为位矢。
z
M
M´
M
r = r (t)
y
x
动点M在空间运动时,矢径r旳末端将描绘出一条
连续曲线,称为矢径端图,它就是动点运动旳轨迹。 6
速 度
t 时刻: 矢径 r(t)
t+ t 时刻: 矢径r (t + t )
2
学习运动学旳意义
➢它为学习动力学,即全方面地分析研 究物体旳机械运动作准备; ➢运动学旳理论能够独立地应用到工程实 际中去。
3
第五章 点旳一般运动和刚体旳基本运动
第一节 点旳运动旳表达法
矢径表达法
直角坐标表达法
弧坐标表达法
第二节 刚体旳基本运动
刚体力学

25
4.定轴转动的动能定理和机械能守恒定律 一. 力矩的功
d A = F d r = FC o s d s = FS i n r d = M Zd
刚体力学
主要内容: 1.刚体定轴转动的描述 2.力矩、刚体定轴转动定律、转动惯量
3.刚体定轴转动的动能定理和机械能守恒定律
*4.刚体定轴转动的角动量定理、角动量守恒定律
1
1. 刚体的平动、转动和定轴转动 一.刚体
1.定义:在任何条件下大小和形状都不发 生变化的物体称为刚体。 2.说明:刚体与质点、理想气体、点电荷等一样是
m
J
2
2
m 2 R d mR 2
2
15
例2.3 试计算质量均匀分布的薄圆盘的垂直于盘面
的中心轴的转动惯量。设圆盘质量为m,半径为R。
解:
J =∫ r d m
2
d m = •2r d r
J= ∫
R 0
2 rd r
3 4
R 1 2 = = mR 2 2
16
例2.4
在质量为 M ,半径为 R 的匀质
例3.3 在倾角为θ 的斜面顶端固定一滑轮,用一根绳子 缠绕数圈后引出与M连接,M与斜面摩擦系数为μ (如图), 设滑轮质量为m,半径为R,轴处无摩擦。试分析M作加速 运动的条件。 N‘
解: 由牛顿第二定律
O mg f
T
N
M g s in θ - T - μ N = M a
第3章_刚体

d dr
F
r
P
1 2
2
A Md
1
2
刚体同时受几个力作用时, 合力或合力矩的功:
A Ai
1
M d
i
2
1
M d
合外力矩的功
M 等于各力矩的功的代数和
dA d 力矩的功率: P M M dt dt
力矩的功率等于力 矩和角速度的乘积
O
u
1 1 2 1 2 2 mu mv J 2 2 2
由系统角动量守恒
mul J mvl
6mu ( M 3m)l
u ( M 3m) v M 3m
z
r
v
P
第二节 刚体对定轴的角动量和转动惯量
刚体是任意两质点间的距离保持不变的特殊质点系 1、刚体对定轴的角动量 这一特殊质点系对该轴上任一O点 的角动量在该轴上的分量或投影 任一质点或质元对O点的角动量为:
z
Li Ri mi vi
在轴上的分量:
vi
1 2 Ek mv 2
z
d dr
F
O
r
P
外力 F 作用于刚体上的P点,时间 dt 内刚 。 体绕定轴转过角度 d ,P点的位移 dr
元功: dA F dr F cos dr
z
O
F cos rd Frsin d Md
z
薄板形刚体对板面内的两条 正交轴的转动惯量之和等于 对过该两轴的交点并垂直于 板面的那条转轴的转动惯量
o
y
ri xi
J z J x J y
刚体基本运动

即:转动刚体内任一点的法向加速度(又称向心加速度)的大小, 等于刚体角速度的平方与该点到轴线的垂直距离的乘积,它的 at 方向与速度垂直并指向轴线。
w
a
M
r a n
j
s
M0
O
2.3 转动刚体内各点的速度和加速度
点的全加速度为:
a
at
j
a at 2 an2 R a 2 w 4 at a tan 2 an w
2.1 刚体的平行移动
如果在物体内任取一直线段,在运动过程 中这条直线段始终与它的最初位置平行,这种 运动称为平行移动,简称平动。
此处有影片播放
2.1刚体的平行移动
C
D
A
摆式输送机的料槽 筛分机构
B
直线行驶的列车车厢
2.1刚体的平行移动
在刚体上任取两点,令A的矢径为rA, B的矢径为rB,两条 矢端曲线是两点的轨迹。
动点的速度矢等于它的矢径对时间的一阶导数。
r dr v lim dt t 0 t
动点的速度矢沿着矢径的矢端曲线的切线,即沿 动点运动轨迹的切线,并与此点运动的方向一致。
1.1 矢量法
3. 加速度 点的速度矢对时间的变化率称为加速度。点的加 速度也是矢量,它表征了速度大小和方向的变化。 点
1.3 自然法
全加速度为at和an的矢量和
a a t an
全加速度的大小和方向由下列二式决定:
v
大小:
at
a a t an
2
2
M
方向:
| at | tan an
an
a
例2:下图为料斗提升机示意图。料斗通过钢丝绳由绕水平轴O 转动的卷筒提升。已知:卷筒的半径为R=16cm,料斗沿铅垂提 升的运动方程为y=2t2,y以cm记,t 以s计。求卷筒边缘一点M在 t=4s时的速度和加速度。
理论力学8刚体的基本运动

前面都为数量表达式,只有大小,而未标明方向; 矢量表达既有大小,又有方向。
一. 角速度和角加速度的矢量表示
按右手定则规定
w , 的方向。
大小:|w ||ddt |
dw dw k k
dt dt
方向如图 w wk
15
二 刚体内任一点的线速度和线加速度的矢积表示
vRw rsin w |w r|wrsin Rw
小于90o , 在同一瞬间的速度和加速度的分布图为:
各点速度分布图
各点加速度分布图
10
§8-4 绕定轴转动刚体的传动问题
传动比:通常称主动轮与从动轮角速度之比
i12
w1 w2
一.齿轮传动
因为是做纯滚动(即没有相对滑动) 1.内啮合
vF vE vF vE
wF rF wE rE
定义齿轮传动比
iEF
aC n Rw02 0.532 4.5m/s 2
aC (aC )2 (aC n )2 12 4.52 4.61 m/s2
tg
aC aC n
1 4.5
0.222,
12.5
⑤ t=3s 时, aC aA 1m/s2,aCn Rw 2 0.592 40.5m/s2
aC
12 40.52 40.51m/s2,
w 2 w02 2
7
§8-3 转动刚体内各点的速度和加速度
一. 线速度V和角速度w之间的关系(即角量与线量的关系)
w , 对整个刚体而言(各点都一样);
v, a 对刚体中某个点而言(各点不一样)。
v
v
lim
t0
R t
wR
v wR
8
二.角加速度 与an ,a 的关系
第六章 刚体的基本运动

z R a M
n
a = α × r + ω× v
aτ = α × r
α × r = α ⋅ r sin θ = α ⋅ R
O
aτ
v
α ω θ r
ω× r
a
n
= ω × v
ω ⋅ v = ω ⋅ ω ⋅ R = ω
dθ = ωo 其中: dt
所以: bcosθ ⋅ ω o = rcos(θ + ϕ ) ⋅ (ω o + ω )
dϕ =ω dt
*
rcos(θ + ϕ ) ω 解得: ω o = bcosθ − rcos(θ + ϕ )
方程*两边对时间取导数,得:
bcosθ ⋅ ω o = rcos(θ + ϕ ) ⋅ (ω o + ω )
一 、角速度的矢量表示
z
ω
k k
ω
z
ω=ω k
右手螺旋规则:右手的四指代表转动的方向,拇指代表角 速度矢量 ω 的方向。
二、角加速度的矢量表示
角加速度矢量定义:
dω α= dt
角加速度矢
α 为角速度矢 ω 对时间的一阶导数
d dω α = ( ωk) = k dt dt
dω d ϕ = 2 α= dt dt
为描述变速的程度,引入传动比的概念。
ω1 R2 z 2 = = 传动比: i12 = ω 2 R1 z1
ω1 n1 α1 R2 z 2 i12 = = = = = ω 2 n2 α 2 R1 z1
二 、皮带轮传动
n1 R1
vB A vA B R2
刚体的定义

刚体的定义引言刚体是力学研究中重要的概念之一。
它在物体的运动以及力的作用等方面都扮演着重要角色。
在本文中,我们将深入探讨刚体的定义以及与之相关的概念。
通过了解刚体的特性和性质,我们可以更好地理解物体的运动和力的作用。
1. 刚体的概念刚体是指在外力作用下形状和大小都不会发生改变的物体。
不同于弹性体或流体,刚体不会因受到外力而发生形变或变形。
刚体的形状和大小是固定的,不受外界因素的影响。
这使得刚体成为力学研究中非常有用的理想模型。
2. 刚体的性质2.1 定义性质刚体的定义性质是指刚体在运动或力作用下,其形状和大小保持不变的性质。
这意味着刚体的各个部分不会相对移动或发生变形。
刚体的定义性质是刚体概念的基础,也是刚体运动和力学性质的重要前提。
2.2 运动性质刚体的运动性质是指刚体在外力作用下的运动规律。
当外力作用于刚体时,刚体将根据力的大小和作用位置发生平动和转动的运动。
平动是指刚体的质心沿直线移动,而转动是指刚体绕着固定轴线旋转。
2.3 力的作用性质刚体在受到外力作用时会产生力矩。
力矩是指力在物体上产生的转动效果。
当外力作用于刚体时,力会对刚体产生力矩,并引起刚体的转动。
力矩的大小由力的大小和作用位置决定。
3. 刚体的模型为了研究刚体的运动和力学性质,我们需要使用刚体的模型。
最简单的刚体模型是质点,质点将整个刚体近似为一个质点,并忽略其形状和大小。
在实际应用中,常用的刚体模型包括刚体的杆、圆盘和球等。
通过合理选择刚体模型,我们可以更好地描述和理解刚体的运动和力学性质。
4. 刚体的应用刚体的概念和性质在生活中和科学研究中有着广泛的应用。
在机械工程领域,刚体的运动和力学性质是设计和优化机械系统的重要基础。
在土木工程中,刚体的概念被用于分析和设计桥梁、建筑和其他结构。
在运动学和动力学研究中,刚体的运动规律和力学性质对于描述和理解物体的运动轨迹和力的作用至关重要。
结论刚体作为力学研究中重要的概念之一,其定义、性质和应用在科学和工程领域起着重要作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
vM = vA
aM = aA
vA = l
=
=
π 4
0
cos
π 4
l 0
cos
π 4
t
方向垂直O1A
7
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
vA
=
π 4
l 0
cos
π 4
t
O1
O2
φl
aAn
aAt
A
aM
n
MaM
t
l
B
O
(+)
A点的切向加速度
aAt
=
dvA dt
=
−
π2 16
l 0
sin
πt 4
A点的法向加速度
aAn
=
vA2 l
=
π2 16
l
2 0
cos
2
πt 4
代入t = 0和t = 2,就可求得这两瞬时A点的速度和加速度, 亦即点M在这两瞬时的速度和加速度。计算结果列表如下:
t (s) φ(rad)
v (m·s-1)
at (m·s-2)
an (m·s-2)
——刚体平行移动 (移动、平动、平移)
图形
滑块
4
物块G
刚体平移
刚体上任取两点的直线在任意时刻都 是平行的。
⚫ 一般地,刚体可沿任意曲线作平移。 ⚫ 刚体平移有可能是空间运动。 问题:平移刚体内各点速度、加速度有何关系?
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
5
刚体的平动
2-各点速度与加速度关系
平移刚体中各点运动的关系
平移刚体任意两点各时刻均满足:
rA = rB + rBA
因为
drBA = 0, 所以 dt
drA = drB dt dt
即 vA = vB, aA = aB
A
A′ A〞
rA
O
B
rB
B′ B〞
结 论:
平移刚体上各点的速度和加速度相同! 平移刚体上各点的运动轨迹相同!
0
0
π 4
(0 水平向右)
0
π2 16
02(l 铅直向上)
2
φ0
0
−
π 16
0l
0
8
例: 荡木用两条等长的钢索平行吊起,如图所示。钢索长
为长l,单位为m。当荡木摆动时钢索的摆动规律
为
= 0 sin
πt 4
,其中 t 为时间,单位为s;转角φ0的单位为
rad,试求当t=0和t=2 s时,荡木的中点M的速度和加速度。
O1
φ l vA
A O
(+)
O2
解: 荡木作平移
vM
M
l B
其中 则
理论力学
刚体基本运动
——刚体平行移动
刚体运动
2
刚体运动学概述 研究内容:
⚫ 刚体宏观运动特点与描述(简单运动-复杂运动) ⚫ 刚体中质点运动与宏观运动的关系 ⚫ 刚体系运动学分析
3
刚体的基本运动:平行移动
1-运动特点
问题:这些刚体的运动有什么共同点?
刚体平行移动的特点
物块G
刚体无转动
刚体上任取两点的 直线在任意时刻都是 平行的。
