含绝对值函数的图像
绝对值函数图像的画法

For personal use only in study and research; not for commercial useFor personal use only in study and research; not for commercial use首先要从简单的绝对值函数画起。
2-=x y :是一条以()0,2为拐点的折线。
或者可以理解为将直线2-=x y 在x 轴下面的部分沿x 轴翻折上去然后再着手于复杂的图像的画法。
221121-++=x x y ,先单独画出两个绝对值的图像,再合到一起。
(叠加后直线的斜率不同) 其中-2和4由两个绝对值为零算的,3为由x=-2和x=4算得的y 值。
最后,最复杂的二次函数中的绝对值的画法。
122--=x x y ,很显然绝对值是将x 变成正数,由前面的图像可知a x y -=的图像总会关于a x =轴对称,故x y 21-=关于y 轴对称,又122-=x y 也关于y 轴对称,所以图像合并起来就容易多了。
仅供个人用于学习、研究;不得用于商业用途。
For personal use only in study and research; not for commercial use.Nur für den persönlichen für Studien, Forschung, zu kommerzie llen Zwecken verwendet werden.Pour l 'étude et la recherche uniquement à des fins personnelles; pas à des fins commerciales.толькодля людей, которые используются для обучения, исследований и не должны использоваться в коммерческих целях.以下无正文仅供个人用于学习、研究;不得用于商业用途。
x-y的绝对值等于零的图像

x-y的绝对值等于零的图像y等于x绝对值的函数图像如下图:y=|x|是分段函数。
x≥0时 y=x。
x《0时 y=-x。
图像是一二象限的角平分线。
扩展资料:绝对值函数的定义域是一切实数,值域是一切非负数。
在计算机语言或计算器中,绝对值函数常记作abs(x) 。
(1)绝对值函数是偶函数,其图形关于y轴对称。
(3)绝对值函数仅在原点不可微,其他点处可微。
(4)与符号函数的关系:∣x∣=sgn(x)·x 或 x=sgn(x)·∣x ∣。
参考资料:百度百科---绝对值函数带有绝对值的函数图像怎么画最根本的方法就是找绝对值的零点,然后消去绝对值,分段画图像。
最简单的比如y=|x|,显然,绝对值内的零点是x=0,那么你就分两段来讨论,x≤0和x>0,可得x≤0时的图像是y=-x,x>0时的图像为y=x,是个V字形。
复杂一点的比如y=|(x-1)(x+5)|+|(x-3)(x+4)|可以看到,这里要去除的绝对值符号有两个,因此需要同时判断两个绝对值符号内代数式的正负。
首先还是找零点,两个绝对值的零点共有四个,分别是x=-5,x=-4,x=1和x=3,那么你就需要将整个数轴分成5段来考虑,分别是(-∞,-5)、(-5,-4)、(-4,1)、(1,3)和(3,+∞),分界点带进去算,是多少就是多少,分段考虑每个绝对值符号内代数式的正负。
比如(-4,1)这个区间,(x-1)(x+5)《0的区间是-5到1,因此,-4到1这个区间内,(x-1)(x+5)《0成立,而(x-3)(x+4)<0可得-4到3,因此,-4到1区间内,(x-3)(x+4)也是小于0的,因此就消去了绝对值符号可得在该区间内的函数表达式为y = -(x-1)(x+5)-(x-3)(x+4) = -2x²-5x+17原来的绝对值函数在-4到1这个区间内的就是函数y = -2x²-5x+17在该区间内的一段。
高考数学微专题4 分段函数(含有绝对值的函数)的图象与性质 课件

实数 m 的最小值为( )
27 A. 8
29 B. 8
13 C. 4
15 D. 4
【思路分析】 根据已知计算出 f(x)=21n[1-|2x-(2n+1)|]≤21n,画出
图象,计算 f(x)=332,解得 x=289,从而求出实数 m 的最小值.
内容索引
【解析】 由题意,得当 x∈[1,2)时,f(x)=12×f(x-1)=12(1-|2x-3|); 当 x∈[2,3)时,f(x)=12f(x-1)=14(1-|2x-5|);…,可得在区间[n,n+1)(n ∈Z)上,f(x)=21n[1-|2x-(2n+1)|]≤21n,所以当 n≥4 时,f(x)≤332.作出函 数 y=f(x)的图象,如图所示,当 x∈72,4时,由 f(x)=18(1-|2x-7|)=332, 解得 x=289,则 m≥289,所以实数 m 的最小值为289.
【答案】 ABD
1234
内容索引
-x2+2, x≤1, 3. (2022 浙江卷)已知函数 f(x)=x+1x-1, x>1,
则 ff12=
________;若当 x∈[a,b]时,1≤f(x)≤3,则 b-a 的最大值是________.
1234
内容索引
【解析】 f12=-122+2=74,f74=74+47-1=3278,所以 ff12=3278.当 x≤1 时,由 1≤f(x)≤3,得 1≤-x2+2≤3,所以-1≤x≤1;当 x>1 时, 由 1≤f(x)≤3 可得 1≤x+1x-1≤3,所以 1<x≤2+ 3.综上,由 1≤f(x)≤3, 得-1≤x≤2+ 3,所以[a,b]⊆[-1,2+ 3],所以 b-a 的最大值为 3+
内容索引
含绝对值的函数

含绝对值的函数知识定位灵活的掌握含有绝对值的函数,主要包括图像画法、函数解析式、与分段函数之间的联系。
本节我们通过一些实例的求解,旨在介绍数学竞赛中与二次函数相关问题的常见题型及其求解方法本讲将通过例题来说明这些方法的运用知识梳理1、用“三点定形法”画单绝对值函数)0()(≠+-=a k h x a x f 的图象:)0()(≠+-=a k h x a x f 与)0()()(2≠+-=a k h x a x g 的图象类似,它们的顶点都是(k h ,),开口方向相同,对称轴相同,单调区间相同。
所不同的是前者的图象是折线,在对称轴两侧是两条射线,而后者的图象是抛物线,在对称轴两侧是两条曲线。
所以可用三点定其型。
三点中,顶点(k h ,)必取,然后在其两侧任意各取一点,分别以顶点为端点,过另一点作出射线,即得)0()(≠+-=a k h x a x f 的图象。
2.用“两点定形法”作双绝对值差式函数b x a x x f ---=)(的图象(1)当a<b 时,⎪⎩⎪⎨⎧>-≤≤-+<-=---=)()(2)()(b x a b b x a ba x a x ba b x a x x f ,可见其图象是由两端为两条平行的射线,中间为连接两射线的端点构成的图形,而图象总是在两个绝对值代数式的零点处转折。
(2)当a>b 时同理。
据此,可以点))(,()),(,(b f b a f a 确定函数b x a x x f ---=)(的图象3.用“多点定形法”作多绝对值函数)()(212211i i i a a a a x m a x m a x m x f <<<-++-+-= 的图象因为⎪⎪⎩⎪⎪⎨⎧≥+++-++++<≤+++-+---+<++++----=)()()()()()()()()()(221121212211211221121i i i i i i i i i i a x a m a m a m x m m m a x a a m a m a m x m m m a x a m a m a m x m m m x f可知其图象是由i 个顶点i A A A 21、、、 决定的折线图,各顶点横坐标由各绝对值代数式的零点决定,中间由1-i 条顺次连接相邻两点的线段组成,两端为两条射线。
衔接点05 含绝对值函数的图象(解析版)

衔接点05 含绝对值函数的图象【基础内容与方法】1.绝对值在自变量上,则去掉函数y 轴左边的图像,再把y 轴右边的图像沿y 轴翻折得到新的图像;2.绝对值在函数解析式上,把x 轴下方的图像沿x 轴翻折得到新的图像;3.同时,函数图像也遵循平移的原则. 类型一:含绝对值的一次函数1.已知函数+2y k x b =+的图象经过点(2-,4)和(6-,2-),完成下面问题: (1)求函数+2y k x b =+的表达式;(2)在给出的平面直角坐标系中,请用适当的方法画出这个函数的图象,并写出这个函数的一条性质; (3)已知函数1+12y x =的图象如图所示,结合你所画出+2y k x b =+的图象,直接写出1+2+12k x b x +>的解集.【答案】(1)3242y x =-++;(2)当2x <-时,y 随x 增大而增大;当2x >-时,y 随x 增大而减少;(3)60x -<<.(1)根据在函数+2y k x b =+中,把点(2-,4)和(6-,2-)代入,可以求得该函数的表达式; (2)根据(1)中的表达式可以画出该函数的图象,根据函数图像增减性几块得出结论; (3)根据图象可以直接写出所求不等式的解集. 解:(1)根据题意,得4622=⎧⎨⋅-++=-⎩b k b解方程组,得324⎧=-⎪⎨⎪=⎩k b所求函数表达式为3242y x =-++. (2)列表如下:描点并连线,函数的图象如图所示, 由图像可知,3242y x =-++性质为:当2x <-时,y 随x 增大而增大;当2x >-时,y 随x 增大而减少.(3)由图象可知:1+2+12k x b x+>的解集是:60x-<<.【点睛】本题考查一次函数和反比例函数的交点、一元一次不等式与一次函数的关系,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.类型二:含绝对值的二次函数(一)绝对值在自变量上2.某班“数学兴趣小组”对函数y=﹣x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:其中,m=.(2)根据上表数据,在如图所示的平面直角坐标系中描点,画出了函数图象的一部分,请画出该函数图象的另一部分.(3)观察函数图象,写出两条函数的性质.(4)进一步探究函数图象发现:①方程﹣x2+2|x|+1=0有个实数根;②关于x的方程﹣x2+2|x|+1=a有4个实数根时,a的取值范围是.【答案】(1)1;(2)详见解析;(3)①函数的最大值是2,没有最小值;②当x>1时,y随x的增大而减小;(4)①2;②1<a<2.【解析】(1)根据对称可得m=1;(2)画出图形;(3)①写函数的最大值和最小值问题;②确定一个范围写增减性问题;(4)①当y=0时,与x轴的交点有两个,则有2个实数根;②当y=a时,有4个实根,就是有4个交点,确定其a的值即可.解:(1)由表格可知:图象的对称轴是y轴,∴m=1,故答案为:1;(2)如图所示;(3)性质:①函数的最大值是2,没有最小值; ②当x >1时,y 随x 的增大而减小; (4)①由图象得:抛物线与x 轴有两个交点 ∴方程﹣x 2+2|x |+1=0有2个实数根; 故答案为2;②由图象可知:﹣x 2+2|x |+1=a 有4个实数根时,即y =a 时,与图象有4个交点,所以a 的取值范围是:1<a <2. 故答案为1<a <2.【点睛】本题考查了抛物线与x 轴的交点,二次函数的性质,结合图像作答是解题的关键. 3.写出函数12)(2+-=x xx f 在什么范围内,y 随x 的增大而增大,. y 随x 的增大而减小?【答案】()f x 的单调递增区间是(1,0]-和(1,)+∞,单调递减区间是(,1]-∞-和(0,1]【解析】由题意转化条件为2221,0()21,0x x x f x x x x ⎧-+≥=⎨++<⎩,作出函数图象,数形结合即可得解.由题意2221,0()21,0x x x f x x x x ⎧-+≥=⎨++<⎩,其图象如图所示:由该函数的图象可得函数2()2||1f x x x =-+的单调递增区间是(1,0]-和(1,)+∞,单调递减区间是(,1]-∞-和(0,1].【点睛】本题考查了分段函数单调区间的确定,考查了二次函数图象与性质及数形结合思想的应用,属于基础题.(二)绝对值在解析式上 4.探究函数22y x x=-的图象与性质.(1)下表是y 与x 的几组对应值.其中m 的值为_______________;(2)根据上表数据,在如图所示的平面直角坐标系中描点,并已画出了函数图象的一部分,请你画出该图象的另一部分;(3)结合函数的图象,写出该函数的一条性质:_____________________________;(4)若关于x 的方程220x x t --=有2个实数根,则t 的取值范围是___________________. 【答案】(1)3;(2)见解析;(3)图象关于直线x=1轴对称.(答案不唯一);(4)t >1或t=0.【解析】(1)把x =3代入解析式计算即可得出m 的值;(2)画出图象即可;(3)根据图象得出性质;(4)观察图象即可得出结论.解:(1)当x =3时,y =2323-⨯=3,∴m =3; (2)如图所示:(3)图象关于直线x =1轴对称.(答案不唯一)(4)观察图象可知:当t >1或t =0时,关于x 的方程220x x t --=有2个实数根. 【点睛】本题考查了函数的图象及性质.解题的关键是画出图象. 5.某班数学兴趣小组对函数6||y x =的图象和性质将进行了探究,探究过程如下,请补充完整. (1)自变量x 的取值范围是除0外的全体实数,x 与y 的几组对应值列表如下:其中,m =_________.(2)根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分.(3)观察函数图象,写出一条函数性质. (4)进一步探究函数图象发现:①函数图象与x 轴交点情况是________,所以对应方程60||x =的实数根的情况是________. ②方程62||x =有_______个实效根; ③关于x 的方程6||a x =有2个实数根,a 的取值范围是________. 【答案】(1)3;(2)见解析;(3)在第一象限内,y 随着x 的增大而减小;(4)①无交点,无实数根;②2;③0a >.【解析】(1)把x=-2代入6||yx=求得y的值,即可得出m的值;(2)根据表格提供的数据描点,连线即可得到函数6||yx=的另一部分图象;(3)观察图象,总结出函数的性质即可;(4)①由于x的值不能为0,故函数值也不能为0,从而可得出函数图象与x轴无交点,因而6||x=无实数根;解:(1)把m=-2代入6||yx=得,63|2|y==-,所以,m=3,故答案为:3(2)如图所示:(3)观察图象可得,在第一象限内,y随着x的增大而减小;(答案不唯一)(4)①∵0x≠,∴y≠0∴函数图象与x轴无交点,∴6||x=无实数根;故答案为:无交点;无实数根;②求方程62||x=的根的个数,可以看成函数6||yx=与直线y=2的交点个数,如图,函数6||yx=与直线y=2有两个交点,故方程62||x=有2个实数根,故答案为:2;③由②的图象可以得出,关于x的方程6||ax=有2个实数根,a的取值范围是0a>,故答案为:0a>.【点睛】本题考查的是反比例函数,主要考查函数图象上点的坐标特征,要求学生非常熟悉函数的性质及函数特征.6.在学习函数时,我们经历了“确定函数的表达式利用函数图象研究其性质——运用函数解决问题“的学习过程,在画函数图象时,我们通过列表、描点、连线的方法画出了所学的函数图象.同时,我们也学习过绝对值的意义(0(0)a a a a a ≥⎧=⎨-<⎩).结合上面经历的学习过程,现在来解决下面的问题: 在函数y=|kx -1|+b 中,当x=0时,y=-2;当x=1时,y=-3. (1)求这个函数的表达式;(2)在给出的平面直角坐标系中,请直接画出此函数的图象并写出这个函数的两条性质; (3)在图中作出函数y=3x -的图象,结合你所画的函数图象,直接写出不等式|kx -1|+b≤3x-的解集. 【答案】(1)y=|x -1|-3.(2)图象见解析.性质:图象关于直线x=1对称,在对称轴左侧,y 随x 的增大而减小,在对称轴右侧,y 随x 增大而增大,函数的最小值为-3. ;(3)1≤x≤3或-3≤x<0.【解析】(1)根据在函数y =|kx−1|+b 中,当x=0时,y=-2;当x=1时,y=-3,可以求得该函数的表达式; (2)由题意根据(1)中的表达式可以画出该函数的图象; (3)由题意直接根据图象可以直接写出所求不等式的解集. 解:(1)在函数y=|kx -1|+b 中,当x=0时,y=-2;当x=1时,y=-3∴2131b k b -=+⎧⎨-=-+⎩,解得:31b k =-⎧⎨=⎩,即函数解析式为:y=|x -1|-3.(2)图象如下:图象关于直线x=1对称,在对称轴左侧,y 随x 的增大而减小,在对称轴右侧,y 随x 增大而增大,函数的最小值为-3. (3)图象如下,观察图像可得不等式|kx -1|+b≤3x-的解集为:1≤x≤3或-3≤x<0. 【点睛】本题考查一次函数和反比例函数的交点、一元一次不等式与一次函数的关系,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.7.若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数.下面我们参照学习函数的过程与方法,探究分段函数⎪⎩⎪⎨⎧>--≤=)1(1)1(2x x x x y 的图象与性质.列表:描点:在平面直角坐标系中,以自变量x 的取值为横坐标,以相应的函数值y 为纵坐标,描出相应的点,如图所示.(1)如图,在平面直角坐标系中,观察描出的这些点的分布,作出函数图象; (2)研究函数并结合图象与表格,回答下列问题: ① 点()15,A y -,27,2B y ⎛⎫- ⎪⎝⎭,15,2C x ⎛⎫⎪⎝⎭,()2,6D x 在函数图象上,1y 2y ,1x 2x ;(填“>”,“=”或“<”)② 当函数值2y =时,求自变量x 的值;③ 在直线1x =-的右侧的函数图象上有两个不同的点()33,P x y ,()44,Q x y ,且34y y =,求34x x +的值;④ 若直线y a =与函数图象有三个不同的交点,求a 的取值范围.【答案】(1)见解析;(2)①<,<;②3x =或1x =-;③342x x +=;④0<<2a . 【解析】 【分析】(1)描点连线即可;(2)①观察函数图象,结合已知条件即可求得答案; ②把y=2代入y=|x -1|进行求解即可;③由图可知1x 3-时,点关于x=1对称,利用轴对称的性质进行求解即可; ④观察图象即可得答案. 【详解】 (1)如图所示: (2)①()1A 5,y -,27B ,y 2⎛⎫- ⎪⎝⎭, A 与B 在1y x=-上,y 随x 的增大而增大,12y y ∴<;15C x ,2⎛⎫⎪⎝⎭,()2D x ,6, C 与D 在y=|x 1|-上,观察图象可得12x <x , 故答案为<,<; ②当y 2=时,12x =-,1x 2∴=-(不符合), 当y 2=时,2x 1=-,x 3∴=或x 1=-; ③()33P x ,y ,()44Q x ,y 在x=1-的右侧,1x 3∴-时,点关于x=1对称,34y y =, 34x x 2∴+=;④由图象可知,0<a<2.【点睛】本题考查反比例函数的图象及性质,一次函数的图象及性质;能够通过描点准确的画出函数图象是解题的关键.。
绝对值函数图像的画法

最先要从简朴的千万于值函数绘起.之阳早格格创做 2-=x y :是一条以()0,2为拐面的合线.
大概者不妨明白为将曲线2-=x y 正在x 轴底下的部分沿x 轴翻合上去 而后再发端于搀纯的图像的绘法.
22
1121-++=x x y ,先单独绘出二个千万于值的图像,再合到所有.(叠加后曲线的斜率分歧)
其中-2战4由二个千万于值为整算的,3为由x=-2战x=4算得的y 值. 末尾,最搀纯的二次函数中的千万于值的绘法.
122--=x x y ,很隐然千万于值是将x 形成正数,由前里的图像可知
a x y -=的图像总会闭于a x =轴对于称,故x y 21-=闭于
y 轴对于称,又122-=x y 也闭于y 轴对于称,所以图像合并起去便简单多了.。
【高中数学】绝对值函数的图像

1.一个绝对值函数图像(“V ”函数)y m a x =-
2.二个绝对值函数()()f x a x m b x n m n =-+-< 其它可以化为这种形式 写成分段形式()()()(),,,a b x am bn x n f x a b x am bn m a b x am bn x x n m +-->⎧⎪=--+⎨⎪-+++<⎩
从图中可以得到一些有用的结论:
当0a b +=时,()f x 有最大值和最小值
当0a b +>时,()f x 有最小值
当0a b +<时,()f x 有最大值
都在分界点取最值!
分三大类0,0,0a b a b a b +=+>+<共8个图
①当0a b +=时有两种情形
【高中数学】绝对值函数的图像
a b+>时有三种情形
②当0
a b+<时有三种情形
③当0
注:对于三个以上的绝对值函数图像,用同样的方法可以得到。
(高考很难见到!)三个以上绝对值配合图像求最值:奇尖偶平,取中间。
三个绝对值相加的函数图像

三个绝对值相加的函数图像
函数图像是数学中最重要的概念之一,函数图像描述了函数的变化趋势。
今天,让我们一起来看看三个绝对值相加的函数图像。
首先,关于三个绝对值相加的函数图像,我们需要了解绝对值函数。
绝对值函数是一种函数,它的定义域和值域都是实数集,作用是取出一个数的绝对值。
当自变量的取值在正数区间时,绝对值函数的图像只有一条直线段,而当自变量的取值在负数区间时,绝对值函数的图像也是一条直线段,只不过两者是相反的。
其次,我们再来看看三个绝对值相加的函数图像。
它由三个绝对值函数叠加而成,其图像是两个凸起的波形拼接而成。
从原点(0, 0)出发,先往右上方,然后往右下方,最后再往右上方,这样形成了一个完整的函数图像。
最后,我们来看看三个绝对值相加的函数图像的一般表达形式。
假设有三个正数u,v,w,那么三个绝对值相加的函数图像可表示为: y=|u|+|v|+|w|
由此可见,三个绝对值相加的函数图像只是对三个绝对值函数做一个叠加而已,其他没有任何变化。
总之,三个绝对值相加的函数图像是三个绝对值函数叠加而成的一个图像,是一种定义域和值域都是实数集的函数,可以使用一般表达式来进行描述。
通过本文的介绍,我们了解了三个绝对值相加的函数图像的结构和特点,希望大家也能掌握这一知识点,提高数学能力。
- 1 -。
中考数学模拟试题函数的绝对值与符号

中考数学模拟试题函数的绝对值与符号函数的绝对值与符号在中考数学中,函数是一个重要的概念,而绝对值函数则是函数中的一个特殊形式。
绝对值函数的图像是一条"V"形曲线,它有很多实际应用。
本文将探讨函数的绝对值与符号的相关内容,从而帮助读者更好地理解和应用这一知识点。
一、绝对值函数的定义绝对值函数是一个以0为对称轴的折线函数,定义如下:当x≥0时,f(x) = x当x<0时,f(x) = -x二、绝对值函数的图像与性质1. 图像:绝对值函数的图像是一条"V"形曲线,开口向上。
2. 性质:(1)非负性:对于任意实数x,有|f(x)| ≥ 0。
(2)对称性:若a为任意实数,则f(a) = f(-a)。
(3)单调性:在x>0的区间上,f(x)为递增函数;在x<0的区间上,f(x)为递减函数。
(4)极值点:绝对值函数的极值点发生在x=0处。
三、绝对值函数与符号的关系1. 正数的绝对值:若x>0,则|f(x)| = x,即正数的绝对值等于其本身。
2. 负数的绝对值:若x<0,则|f(x)| = -x,即负数的绝对值等于其相反数。
3. 非负数的符号:若f(x) ≥ 0,则x ≥ 0,即非负数的符号与其本身一致。
4. 负数的符号:若f(x) < 0,则x < 0,即负数的符号与其相反数一致。
四、绝对值函数的应用举例1. 距离计算:绝对值函数可以用于计算两个点在坐标轴上的距离。
例如,点A的坐标为a,点B的坐标为b,则点A和点B之间的距离为|a-b|。
2. 温度计算:绝对值函数可以用于计算摄氏度和华氏度之间的转换。
例如,将摄氏度C转换为华氏度F的公式为F = 9/5 * C + 32,将华氏度F转换为摄氏度C的公式为C = 5/9 * (F - 32)。
在转换过程中,需要使用绝对值函数来确保转换后的温度是非负的。
3. 判断奇偶性:绝对值函数可以用于判断一个整数的奇偶性。
26.7 含绝对值符号的函数+雷刚

第五节 含绝对值符号的函数26.7 含绝对值符号的函数1.形如)(x f y =的函数试一试 如何作出函数21+=x y 的图像? 根据绝对值的定义,函数21+=x y 可以表示为⎪⎪⎩⎪⎪⎨⎧<+-≥+=021021x x x x y ,, (1)作当x ≥0时,21+=x y 的图像,即图26.7.1中的射线AC ; (2)作当x >0时,21+-=x y 的图像,即图26.7.1的射线AB ; (3)图26.7.1中的折线BAC 即为函数21+=x y 的图像。
由上面我们可以看出,对于函数)(x f y =,当自变量x 取值互为相反数时,所得到的函数值相等,即)()(x f x f -=,因此函数)(x f =图像就是函数)(x f y =(x ≥0)的图像与)0)((<-=x x f y 的图像的全部,并且函数)(x f 的图像关于y 轴对称。
例1 作函数3412--=x x y 的图像解 因为222x x x ==,所以3412--=x x y 是)(x f y =类型的函数 (1)作出当x ≥0时,3412--=x x y 的图像,这是一个开口向上的抛物线在y 轴右边的部分。
由03412=--x x 可以得知,抛物线与x 轴的交点为(2-,0)和(6,0),与y 轴的交点为(0,-3).抛物线的顶点坐标为(2,-4),如图26.7.2所示,曲线ABC 就是当x ≥0时,3412--=x x y 的图像; (2)以y 轴为对称轴,作曲线ABC 的对称图形''C AB ;(3)图中的曲线ABC B C ''即为3412--=x x y 的图像由此,我们可以发现: 画函数)(x f y =的图像的一般步骤:①先作出)0)((>=x x f y 的图像;②将)0)((>=x x f y 的图像沿y 轴翻折到y 轴左侧,就得到了函数)(x f y =的图像例2 已知方程1+=ax x ,有一个负根且无一正根,求a 的取值范围分析 可以把等号两边的式子看作是函数,从函数图像入手比较直观地解决问题 解 原方程即ax x =-1,如图26.7.3,在同一坐标系作函数1-=x y 与ax y =的图像 1-=x y 是尖点(0,-1)的“V ”字形折线,而ax y =是过原点斜率为a 的直线,如图虚线OA 是ax y =的一个极根位置,y 轴是它的另一根限位置,易见当1≥a (即直线OA 的向上的方向与x 轴正方向的夹角不小于︒45)时,OA 与1-=x y 的图像交点位于第三 象限,即方程ax x =-1有一个负根且没有正根。
分析绝对值函数的特点与图像

分析绝对值函数的特点与图像绝对值函数是数学中一类常见的函数,它具有独特的特点和图像。
本文将从多个角度对绝对值函数进行分析,探讨其特点和图像的相关性。
绝对值函数的定义如下:\[ f(x) = |x| = \left\{\begin{array}{ll}x, & \mbox{if } x \geq 0 \\-x, & \mbox{if } x < 0\end{array}\right.\]从定义可以看出,绝对值函数的特点之一是其自变量的值是非负数和负数的情况下的函数值的综合。
下面将分别从函数的解析表达式、特点和图像等方面对绝对值函数进行分析。
1. 解析表达式绝对值函数的解析表达式随着自变量的正负而变化,可以用分段函数的形式表示。
当自变量x大于等于零时,函数值等于x;当自变量x 小于0时,函数值等于-x。
这种定义方式使得绝对值函数具备了两段具有不同特性的解析表达式,进一步反映了绝对值函数的特点。
2. 特点(1)非负性特点:绝对值函数的函数值永远大于等于0,即对于任意的x,有f(x) ≥ 0。
这是由于绝对值函数的定义决定的。
(2)对称性特点:绝对值函数关于y轴对称,即f(-x) = f(x),这可以从绝对值函数的定义中直接得出。
(3)间断性特点:绝对值函数在x = 0处不连续,形成一个特殊的间断点,即左极限和右极限不相等。
因为当x大于0时,函数值是x;而当x小于0时,函数值是-x,使得在x = 0处函数的值发生跳变。
3. 图像绝对值函数的图像是一条以原点(0,0)为顶点,向右打开的V型曲线。
具体地说,当x大于0时,图像上的点位于直线y = x上;当x小于0时,图像上的点位于直线y = -x上。
这样,整体来看,绝对值函数的图像就是由两条直线组成的。
绝对值函数的图像特点可以通过以下几个方面进行进一步分析和理解:(1)切线特点:绝对值函数的图像在x = 0处的切线斜率为0,即在该点处切线是水平的。
绝对值函数图像的画法
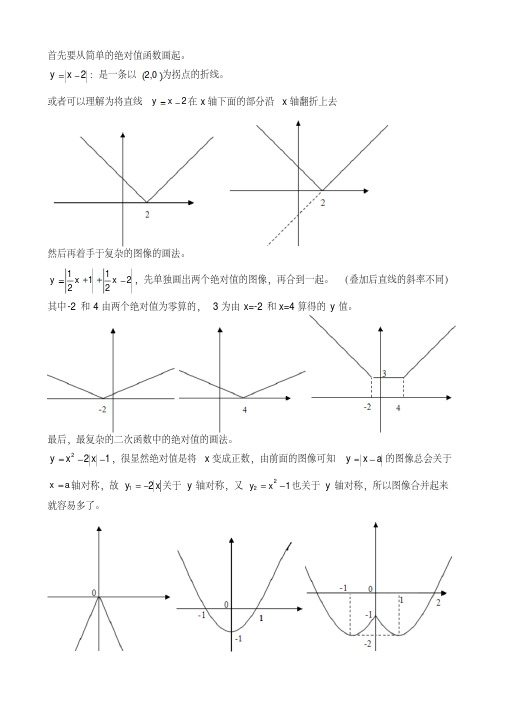
首先要从简单的绝对值函数画起。
2x y :是一条以0,2为拐点的折线。
或者可以理解为将直线
2x y 在x 轴下面的部分沿x 轴翻折上去然后再着手于复杂的图像的画法。
221
121
x x y ,先单独画出两个绝对值的图像,再合到一起。
(叠加后直线的斜率不同)
其中-2和4由两个绝对值为零算的,3为由x=-2和x=4算得的y 值。
最后,最复杂的二次函数中的绝对值的画法。
122x x y
,很显然绝对值是将x 变成正数,由前面的图像可知a x y 的图像总会关于a x 轴对称,故x y 21关于y 轴对称,又122x y 也关于y 轴对称,所以图像合并起来就容易多了。
初二数学绝对值函数知识点详解

初二数学绝对值函数知识点详解绝对值函数是初中数学中常见的一种函数类型,也是大家较早接触到的函数之一。
它在图像上以V形展现,更好地帮助我们理解和应用数学知识。
本文将详细探讨初二数学中的绝对值函数及其应用。
一、绝对值函数定义及性质绝对值函数是一个以自变量x为输入,返回其绝对值| x |为输出的函数。
其数学定义如下:f(x) = | x |绝对值函数的图像为一条从原点出发的V形曲线,关于y轴对称。
它的性质如下:1. f(x) ≥ 0,即绝对值函数的输出值永远大于等于零;2. 当x > 0时,f(x) = x,即在正数区间上,绝对值函数的输出等于自变量的值;3. 当x < 0时,f(x) = -x,即在负数区间上,绝对值函数的输出等于自变量的绝对值的相反数。
二、绝对值函数的图像与性质绝对值函数的图像是一条以原点为顶点的V形曲线。
在图像上,我们可以观察到以下性质:1. 绝对值函数的对称轴为y轴,即图像关于y轴对称;2. 当x > 0时,函数图像为一条直线,斜率为1,倾斜向上;3. 当x < 0时,函数图像为一条直线,斜率为-1,倾斜向下;4. 当x = 0时,函数图像通过原点(0,0)。
三、绝对值函数的运算性质绝对值函数具有一些独特的运算性质,我们来逐一了解:1. | a | = | -a |,即任意实数a的绝对值与其相反数的绝对值相等;2. | a · b | = | a | · | b |,即两个实数的乘积的绝对值等于它们的绝对值的乘积;3. | a ± b | ≤ | a | ± | b |,即两个实数的和或差的绝对值小于等于它们的绝对值之和或差值;4. | a + b | ≥ | a | - | b |,即两个实数的和的绝对值大于等于它们的绝对值之差;5. | 1 | = 1,即任意实数1的绝对值等于1。
四、绝对值函数的应用绝对值函数在实际问题中有许多应用,我们举两个例子来说明:1. 温度变化问题:假设某地初始温度为10摄氏度,随着时间的推移,温度每小时上升2摄氏度。
绝对值函数的象与性质

绝对值函数的象与性质绝对值函数是一种基本的数学函数,它的图像呈现出一种特殊的形状。
本文将探讨绝对值函数的象和性质,帮助读者更好地理解和应用这一函数。
一、绝对值函数的定义绝对值函数通常用符号表示为|y|,表示一个数y的绝对值。
对于实数x,绝对值函数的定义如下:|y| = {y, 当y ≥ 0;{-y, 当y < 0.二、绝对值函数的图像绝对值函数的图像是一条由原点开始的V字形曲线。
根据绝对值函数的定义,当y ≥ 0时,函数的值等于y;当y < 0时,函数的值等于-y。
因此,在y轴的正半轴上,函数的值与y相等,在y轴的负半轴上,函数的值为-y。
三、绝对值函数的性质1. 非负性质:绝对值函数的值总是非负的。
无论y的值是正数、零还是负数,绝对值函数的值都不会小于零。
2. 对称性质:绝对值函数关于y轴对称。
也就是说,当y的值变为-y时,函数的值保持不变。
3. 单调递增性质:当y大于等于0时,绝对值函数是单调递增的;当y小于0时,绝对值函数是单调递减的。
也就是说,随着y值的增加,绝对值函数的值也会增加,反之亦然。
4. 等式性质:对于任意实数x,有|0| = 0和|x| = |-x|。
也就是说,0的绝对值等于0,而任意数x的绝对值等于其相反数的绝对值。
5. 不等式性质:对于任意实数x和实数a,有|x| ≤ a当且仅当-a ≤ x≤ a。
也就是说,对于给定的实数a,绝对值函数的值不会超过a。
综上所述,绝对值函数的象与性质如上所示。
绝对值函数的图像呈现出一种特殊的V字形曲线,具有非负性、对称性、单调递增性、等式性和不等式性等重要性质。
对于需要处理绝对值的数学问题,了解绝对值函数的性质将有助于我们更好地理解和解决这些问题。
通过研究绝对值函数的图像和掌握其性质,我们可以在实际应用中灵活运用绝对值函数。
例如,在数学建模中,绝对值函数常用于表示距离、误差、差值等概念,并常用于处理约束条件、优化问题等。
在物理学中,绝对值函数常用于描述物体的位移、速度、加速度等变化情况。
高二下第8讲 函数遇上绝对值

高二下第8讲 绝对值函数题型一、含绝对值函数的最值,单调性,对称性1、含一个绝对值的一次绝对值函数的最值、单调性、对称性(1)()||f x x =的图像是以原点为顶点的“V ”字形图像;函数在顶点处取得最小值“(0)0f =”,无最大值;在函数(,0],[0,)x ∈−∞↓+∞↑;对称轴为:0x = (2)()||(0)f x kx b k =+≠图像是以(,0)bk−为顶点的“V ”字形图像;在顶点取得最小值:“()0b f k −=”,无最大值;函数在(,],[,)b b x k k ∈−∞−↓−+∞↑;对称轴为:b x k=−(3)函数()||(0)f x k x b k =+≠:0k >时,函数是以(,0)b −为顶点的“V ”字形图像;函数在顶点取得最小值:“()0f b −=”,无最大值;函数在(,],[,)x b b ∈−∞−↓−+∞↑;对称轴为:x b =−0k <时,是以(,0)b −为顶点的倒“V ”字形图像,函数在顶点取得最大值:“()0f b −=”,无最小值;函数在(,],[,)x b b ∈−∞−↑−+∞↓;对称轴为:x b =− 习题1、已知函数()||f x a x b =−在(,1)x ∈−∞↑,求实数,a b 的范围。
2、若函数()2f x a x b =−+在[0,+∞)上为增函数,则实数a 、b 的取值范围是 。
3、(2012届高三一模黄浦区文14) 已知函数()y f x =是R 上的偶函数,当0x ≥时,有2||(),2()sin (0);2x x f x x x ππππ⎧−>⎪⎪=⎨⎪≤≤⎪⎩关于x 的方程()()f x m m R =∈有且仅有四个不同的实数根,若α是四个根中的最大根,则sin()3πα+= .1544、函数与D )A 、 B 、、 D 、5、(2010理)若实数x 、y 、m 满足|x −m |﹥|y −m |,则称x 比y 远离m . (1) 若x 2−1比1远离0,求x 的取值范围;(2) 对任意两个不相等的正数a 、b ,证明:a 3+b 3比a 2b +ab 2远离2; (3) 已知函数f (x )的定义域{|,,}24k D x x k Z x R ππ=≠+∈∈.任取x ∈D ,f (x )等于sin x 和cos x 中远离0的那个值.写出函数f (x )的解析式,并指出它的基本性质(结论不要求证明) 解析:(1) (,( 2.)x ∈−∞+∞;(2) 对任意两个不相等的正数a 、b ,有332a b +>222a b ab +>33222|2|2()()0a b a b ab a b a b +−−+−=+−>,所以3322|2|2a b a b ab +−>+−,即a 3+b 3比a 2b +ab 2远离2;(3) 3sin ,(,)44()cos ,(,)44x x k k f x x x k k ππππππππ⎧∈++⎪⎪=⎨⎪∈−+⎪⎩,性质:1︒f (x )是偶函数,图像关于y 轴对称,2︒f (x )是周期函数,最小正周期2T π=,3︒函数f (x )在区间(,]242k k πππ−单调递增,在区间[,)224k k πππ+单调递减,k ∈Z , 4︒函数f (x )的值域为(2.2、含两个绝对值的一次绝对值函数的最值、单调性、对称性(1)函数()||||()f x x m x n m n =−+−<的图像是以点(,),(,)A m n m B n n m −−为折点的“平底形”图像;在[,]x m n ∈上的每点,函数都取得最小值n m −,无最大值;函数在(,],[,)x m x n ∈−∞↓∈+∞↑ ,在[,]x m n ∈无单调性;对称轴为2m nx +=。
正方形绝对值函数图像画法总结

正方形绝对值函数图像画法总结今天我就来和大家分享一下吧。
正方形绝对值函数有三个解析式:x=-1/(1- sinx), x=1/2, x=3/4。
当且仅当正方形内部对角线互相垂直时,正方形内部各点的横坐标与纵坐标的差都为0,此时它们都可以表示为一个常数 c。
但是正方形不能单独使用函数图像表达其面积,而必须把正方形作为一个整体考虑,通过分割将这些表达在一起,即由点到面积的映射来确定函数的值域,从而得出函数的具体解析式。
首先需要指明的是,正方形绝对值函数的解析式和它所代表的图象都是在平面上描绘出来的,因此它只是研究函数的一种特殊方式,本质还是利用实数系进行运算,而其他类型的函数也可以借鉴这种思想。
例如,直线上的点到直线的距离的两种情况、抛物线中心点的轨迹等。
其次,在一般函数学习的基础上,简化了很多复杂的计算过程。
另外,与直线相交的直线段中垂线的斜率是负值。
最后,还需说明的是:正方形绝对值函数在解题时主要应用了对称性原理。
在求函数值域问题中,往往存在一些特殊位置关系或者具有某种对称性。
通过分别找出函数图像的对称轴及反对称轴,并根据函数对称轴及反对称轴上的点来判断函数值域。
正方形绝对值函数的图像很好地展现了自变量取决于因变量的对称关系,由对称性的引入可使问题易于处理,也有助于突破数列难点,让函数概念更加清晰。
同时,利用正方形绝对值函数的对称性,便于建立变量间的等量关系,将其转化成求函数值域的问题。
还有在多元函数问题中,常会遇到当 n 个变量的乘积仍为常数,然后再对各变量做变号处理,求该常数的几何意义的问题,利用正方形绝对值函数的对称性便于操作,这里就不赘述了。
第一种情况是,若正方形对角线所围成的矩形中,对角线两边长度之比等于1.5:1时,则该函数解析式为 x=-1/(1- sinx);若正方形对角线所围成的矩形中,对角线两边长度之比小于1.5:1时,则该函数解析式为 x=1/2;若正方形对角线所围成的矩形中,对角线两边长度之比大于1.5:1时,则该函数解析式为 x=3/4。
