支持向量机matlab实例及理论_20131201
支持向量机(SVM)、支持向量机回归(SVR):原理简述及其MATLAB实例

支持向量机(SVM)、支持向量机回归(SVR):原理简述及其MATLAB实例一、基础知识1、关于拉格朗日乘子法和KKT条件1)关于拉格朗日乘子法2)关于KKT条件2、范数1)向量的范数2)矩阵的范数3)L0、L1与L2范数、核范数二、SVM概述1、简介2、SVM算法原理1)线性支持向量机2)非线性支持向量机二、SVR:SVM的改进、解决回归拟合问题三、多分类的SVM1. one-against-all2. one-against-one四、QP(二次规划)求解五、SVM的MATLAB实现:Libsvm1、Libsvm工具箱使用说明2、重要函数:3、示例支持向量机(SVM):原理及其MATLAB实例一、基础知识1、关于拉格朗日乘子法和KKT条件1)关于拉格朗日乘子法首先来了解拉格朗日乘子法,为什么需要拉格朗日乘子法呢?记住,有需要拉格朗日乘子法的地方,必然是一个组合优化问题。
那么带约束的优化问题很好说,就比如说下面这个:这是一个带等式约束的优化问题,有目标值,有约束条件。
那么你可以想想,假设没有约束条件这个问题是怎么求解的呢?是不是直接 f 对各个 x 求导等于 0,解 x 就可以了,可以看到没有约束的话,求导为0,那么各个x均为0吧,这样f=0了,最小。
但是x都为0不满足约束条件呀,那么问题就来了。
有了约束不能直接求导,那么如果把约束去掉不就可以了吗?怎么去掉呢?这才需要拉格朗日方法。
既然是等式约束,那么我们把这个约束乘一个系数加到目标函数中去,这样就相当于既考虑了原目标函数,也考虑了约束条件。
现在这个优化目标函数就没有约束条件了吧,既然如此,求法就简单了,分别对x求导等于0,如下:把它在带到约束条件中去,可以看到,2个变量两个等式,可以求解,最终可以得到,这样再带回去求x就可以了。
那么一个带等式约束的优化问题就通过拉格朗日乘子法完美的解决了。
更高一层的,带有不等式的约束问题怎么办?那么就需要用更一般化的拉格朗日乘子法,即KKT条件,来解决这种问题了。
支持向量机介绍课件

支持向量机的应用场景
01
分类问题:支持向量机可以用于 解决二分类或多分类问题,如文 本分类、图像分类等。
03
异常检测:支持向量机可以用于 异常检测,如信用卡欺诈检测、 网络入侵检测等。
02
回归问题:支持向量机可以用于 解决回归问题,如房价预测、股 票价格预测等。
4 支持向量机的优缺点
优点
01
高度泛化:支持向量机具有 很强的泛化能力,能够有效 地处理非线性问题。
02
鲁棒性:支持向量机对异常 值和噪声具有较强的鲁棒性, 能够有效地避免过拟合。
03
计算效率:支持向量机的训 练和预测过程相对较快,能 够有效地处理大规模数据。
04
易于解释:支持向量机的决 策边界直观易懂,便于理解 和解释。
缺点
01
计算复杂度高: 支持向量机的训 练和预测都需要 较高的计算复杂 度
02
容易过拟合:支 持向量机在处理 高维数据时容易 发生过拟合现象
03
模型选择困难:支 持向量机的参数选 择和模型选择较为 困难,需要一定的 经验和技巧
04
不适用于线性不可 分问题:支持向量 机只适用于线性可 分问题,对于非线 性问题需要进行复 杂的特征转换或采 用其他算法
它通过引入松弛变量,允许某些
02
数据点在分类超平面的两侧。 软间隔分类器的目标是最大化间 03 隔,同时最小化松弛变量的数量。 软间隔分类器可以通过求解二次
04
规划问题得到。
3 支持向量机的应用
线性分类
01
支持向量机 可以用于线 性分类问题
02
线性分类器可 以找到最优的
支持向量机(SVM)算法的matlab的实现

⽀持向量机(SVM)算法的matlab的实现⽀持向量机(SVM)的matlab的实现⽀持向量机是⼀种分类算法之中的⼀个,matlab中也有对应的函数来对其进⾏求解;以下贴⼀个⼩例⼦。
这个例⼦来源于我们实际的项⽬。
clc;clear;N=10;%以下的数据是我们实际项⽬中的训练例⼦(例⼦中有8个属性)correctData=[0,0.2,0.8,0,0,0,2,2];errorData_ReversePharse=[1,0.8,0.2,1,0,0,2,2];errorData_CountLoss=[0.2,0.4,0.6,0.2,0,0,1,1];errorData_X=[0.5,0.5,0.5,1,1,0,0,0];errorData_Lower=[0.2,0,1,0.2,0,0,0,0];errorData_Local_X=[0.2,0.2,0.8,0.4,0.4,0,0,0];errorData_Z=[0.53,0.55,0.45,1,0,1,0,0];errorData_High=[0.8,1,0,0.8,0,0,0,0];errorData_CountBefore=[0.4,0.2,0.8,0.4,0,0,2,2];errorData_Local_X1=[0.3,0.3,0.7,0.4,0.2,0,1,0];sampleData=[correctData;errorData_ReversePharse;errorData_CountLoss;errorData_X;errorData_Lower;errorData_Local_X;errorData_Z;errorData_High;errorData_CountBefore;errorData_Local_X1];%训练例⼦type1=1;%正确的波形的类别,即我们的第⼀组波形是正确的波形,类别号⽤ 1 表⽰type2=-ones(1,N-2);%不对的波形的类别,即第2~10组波形都是有故障的波形。
matlab-支持向量机包及用法

matlab-支持向量机包及用法chapter one: matlab高级版本中自带的svm函数我现在使用的matlab版本为matlab 7.6.0(R2008a)这个版本中已经自带svm算法,分别为生物信息工具箱(bioinformatics toolbox)中svmclassify函数和svmtrain函数,为上下级关系。
SVMStruct=svmtrain(Training,Group)%svmtrain的输入为样本点training和样本的分类情况group,输出为一个分类器svmstruct.核函数,核参数,和计算方法等都是可选的,如SVMStruct = svmtrain(…, ‘Kernel_Function’, Kernel_FunctionValue, …)但是切记切记一定要成对出现。
然后,将分类器和testing sample带入svmclassify中,可以得到分类结果和准确度。
举个例子哈svmStruct = svmtrain(data(train,:),groups(train),’Kernel_Function’,'rbf’,'Ke rnel_FunctionValue’,’5′,’showplot’,true);%用了核宽为5的径向基核,且要求作图%这里我觉得原作者的写法有误,应该是svmStruct = svmtrain(data(train,:),groups(train),...'Kernel_Function','rbf','RBF_Sigma',5,'showplot',true);classes = svmclassify(svmStruct,data(test,:),’showplot’,true);%要求输出检测样本点的分类结果,且画图表示。
tip 1: 有归一化scale功能,可以通过调参数实现tip 2: 计算方法可选qp,smo,lstip 3: 有个关于soft margin的盒子条件,我不太明白是干嘛的,谁懂得话,就给我讲讲哈tip 4: 画出来的图很难看to sum up: 挺好的chapter two: 我最早使用的工具箱SVM and Kernel Methods Matlab Toolbox2005年法国人写的,最近的更新为20/02/2008下载的地址为http://asi.insa-rouen.fr/enseignants/~arakotom/toolbox/index.html这是我最早开始用的一个工具箱,我很喜欢,到现在还是,对于svm的初学者是个很好的toolbox.有详细的说明和很多的demo和例子,包含现今几乎所有的有关svm的成熟算法和数据预处理方法(pca及小波等)。
Matlab中的支持向量机与核方法理论与应用

Matlab中的支持向量机与核方法理论与应用引言支持向量机(Support Vector Machine, SVM)是一种强大的机器学习算法,常被用于分类和回归问题的解决。
SVM的核方法是其重要的扩展,通过将输入数据映射到高维特征空间,能够更好地捕获数据的非线性关系。
本文将介绍Matlab中的支持向量机与核方法的理论和应用,探讨其在实际问题中的应用价值。
一、支持向量机的原理支持向量机是一种二分类的监督学习算法。
其基本思想是找到一个超平面,使得两个不同类别的数据样本能够被最大化地分隔开。
这个超平面由支持向量组成,支持向量是离超平面最近的训练样本点。
Matlab中的SVM算法可以通过libsvm或svmtrain函数来实现。
通过选择不同的核函数,如线性核、多项式核、高斯核等,可以实现不同的分类问题的解决。
SVM算法的训练过程是寻找一个最优的超平面,使其能够正确分类训练数据,并保证分类边界的间隔最大化。
二、核方法的原理核方法是SVM的重要扩展,通过将输入数据映射到高维特征空间,能够更好地捕获数据的非线性关系。
核函数的选择非常重要,常用的核函数有线性核、多项式核、高斯核等。
核方法的核心思想是在计算过程中使用核函数代替内积计算,避免了显示地进行特征映射,从而大幅度提高了计算效率。
核方法能够将原始的低维数据映射到高维特征空间,使得原本线性不可分的数据在高维空间中变得线性可分。
Matlab中提供了丰富的核函数,比如线性核函数、多项式核函数、高斯核函数等,用户可以根据实际问题选择适合的核函数,以达到更好的分类效果。
三、支持向量机与核方法的应用支持向量机与核方法在实际问题中有广泛的应用。
以下列举几个典型的应用场景:1. 图像分类支持向量机与核方法在图像分类问题中有很好的应用前景。
通过将图像样本映射到高维特征空间,可以提取出更多的图像特征信息,并将其用于分类任务中。
例如,可以通过SVM和核方法识别人脸、车辆等目标。
支持向量机PPT课件

支持向量机ppt课件
https://
REPORTING
2023
目录
• 支持向量机概述 • 支持向量机的基本原理 • 支持向量机的实现步骤 • 支持向量机的应用案例 • 支持向量机的未来发展与挑战 • 总结与展望
2023
PART 01
支持向量机概述
REPORTING
详细描述
传统的支持向量机通常是针对单个任务进行训练和预测,但在实际应用中,经常需要处理多个相关任务。多任务 学习和迁移学习技术可以通过共享特征或知识,使得支持向量机能够更好地适应多个任务,提高模型的泛化性能。
深度学习与神经网络的结合
总结词
将支持向量机与深度学习或神经网络相结合,可以发挥各自的优势,提高模型的性能和鲁棒性。
模型训练
使用训练集对支持向量机模型进行训练。
参数调整
根据验证集的性能指标,调整模型参数,如惩罚因子C和核函数类 型等。
模型优化
采用交叉验证、网格搜索等技术对模型进行优化,提高模型性能。
模型评估与调整
性能评估
使用测试集对模型进行 评估,计算准确率、召 回率、F1值等指标。
模型对比
将支持向量机与其他分 类器进行对比,评估其 性能优劣。
模型调整
根据评估结果,对模型 进行调整,如更换核函 数、调整参数等,以提 高性能。
2023
PART 04
支持向量机的应用案例
REPORTING
文本分类
总结词
利用支持向量机对文本数据进行分类 ,实现文本信息的有效管理。
详细描述
支持向量机在文本分类中发挥了重要 作用,通过对文本内容的特征提取和 分类,能够实现新闻分类、垃圾邮件 过滤、情感分析等应用。
Matlab中的支持向量机应用

Matlab中的支持向量机应用在机器学习领域中,支持向量机(Support Vector Machine,SVM)是一种非常重要的分类和回归算法。
SVM具有很好的泛化性能和较强的鲁棒性,因此在实际应用中得到了广泛的应用。
在本文中,将重点介绍SVM在Matlab中的应用。
一. SVM算法原理支持向量机是一种基于统计学习理论的二分类模型。
其主要思想是寻找一个超平面,使得离该超平面最近的样本点到该超平面的距离最大化。
这些离超平面最近的样本点被称为支持向量。
SVM的目标是找到一个最优的超平面,使得正负样本点之间的间隔最大化。
如果数据是线性可分的,那么SVM就能找到一个分离超平面。
如果数据是线性不可分的,SVM通过引入松弛变量和核函数来处理。
二. Matlab中的SVM工具箱Matlab是一种非常方便的科学计算软件,它提供了丰富的工具箱和函数用于机器学习和数据分析。
在Matlab中,可以使用统计和机器学习工具箱中的函数来实现支持向量机算法。
使用SVM工具箱可以方便地进行数据预处理、模型选择、模型训练和测试等操作。
三. 数据处理与特征选择在使用SVM算法之前,首先需要对数据进行处理和特征选择。
常见的数据处理包括数据清洗、数据标准化和数据归一化等操作。
特征选择是指从原始数据中选择一些最重要的特征用于训练模型。
常用的特征选择方法有相关系数、卡方检验、互信息等。
Matlab提供了丰富的函数和工具箱可以帮助进行数据处理和特征选择。
四. 模型选择与参数调优在使用SVM算法时,需要选择一个合适的模型和调优相关的参数。
模型选择包括选择合适的核函数、惩罚参数以及其他超参数。
常见的核函数包括线性核函数、多项式核函数和径向基核函数等。
而参数调优可以使用交叉验证等方法选择出最优的参数。
Matlab提供了交叉验证工具和函数来帮助进行模型选择和参数调优。
五. 模型训练与测试在确定了模型和参数后,可以使用支持向量机工具箱中的函数进行模型训练和测试。
支持向量机matlab例题

支持向量机matlab例题当涉及到支持向量机(Support Vector Machine,简称SVM)的例题时,我们可以通过MATLAB来实现和解决。
SVM是一种常用的机器学习算法,用于分类和回归任务。
下面我将给出一个SVM的MATLAB例题,以帮助你更好地理解和应用该算法。
假设我们有一个二维数据集,其中包含两个类别的数据点。
我们的目标是使用SVM对这些数据进行分类。
首先,我们需要创建一个示例数据集。
在MATLAB中,我们可以使用`randn`函数生成随机数据。
假设我们有两个类别,每个类别有100个样本点。
代码如下:matlab.% 生成数据。
rng(1); % 设置随机种子,以确保结果可重现。
n = 100; % 每个类别的样本数量。
X1 = randn(n, 2) + repmat([1, 1], n, 1); % 类别1的数据点。
X2 = randn(n, 2) + repmat([-1, -1], n, 1); % 类别2的数据点。
X = [X1; X2]; % 合并数据。
y = [ones(n, 1); -ones(n, 1)]; % 类别标签。
接下来,我们可以使用`fitcsvm`函数来训练SVM模型,并进行分类。
代码如下:matlab.% 训练SVM模型。
svmModel = fitcsvm(X, y);% 预测分类结果。
y_pred = predict(svmModel, X);现在,我们已经得到了预测的分类结果。
我们可以使用`plot`函数将数据点和决策边界可视化。
代码如下:matlab.% 可视化结果。
figure;gscatter(X(:, 1), X(:, 2), y, 'rb', 'o');hold on;% 绘制决策边界。
h = svmModel.Beta(1);k = svmModel.Beta(2);x1 = linspace(min(X(:, 1)), max(X(:, 1)), 100);x2 = (-svmModel.Bias h x1) / k;plot(x1, x2, 'k--', 'LineWidth', 2);% 设置图形属性。
支持向量机计算例子

支持向量机计算例子支持向量机(Support Vector Machine,SVM)是一种常用的机器学习算法,主要用于分类和回归问题。
它的基本思想是找到一个最优的超平面,将不同类别的样本分开。
在这篇文章中,我将通过列举一些支持向量机的计算例子来介绍它的基本原理和应用。
1. 二分类问题:假设我们有一组二维的数据点,其中一些点属于正类,另一些点属于负类。
通过支持向量机算法,我们可以找到一个最优的超平面,将这两个类别的数据点分开。
具体地,我们可以通过求解一个凸优化问题来找到这个最优超平面。
2. 多分类问题:支持向量机也可以用于多分类问题。
一种常见的方法是通过一对多(One-vs-All)的方式将多分类问题转化为多个二分类问题。
对于每个类别,我们训练一个支持向量机模型,然后根据模型的预测结果来确定样本的类别。
3. 核函数的应用:支持向量机可以通过引入核函数来处理非线性分类问题。
核函数可以将输入空间中的样本映射到一个高维的特征空间,从而使得原本线性不可分的问题变得线性可分。
常用的核函数包括线性核、多项式核和高斯核等。
4. 超参数的选择:在支持向量机算法中,有一些超参数需要我们手动选择,例如正则化参数C和核函数的参数。
为了选择合适的超参数,我们可以使用交叉验证的方法,在训练集上进行多次训练和验证,选择在验证集上表现最好的超参数。
5. 支持向量的概念:在支持向量机中,支持向量是离超平面最近的那些训练样本点。
这些支持向量决定了超平面的位置和形状,它们在分类决策中起到了重要的作用。
支持向量机算法的训练过程就是为了找到这些支持向量。
6. 软间隔分类:如果训练数据中存在一些异常点或噪声,那么我们可能无法找到一个完全分开两个类别的超平面。
此时,我们可以允许一定程度的错误分类,这就是软间隔分类。
通过引入松弛变量,我们可以在最小化分类误差和最大化间隔之间取得一个平衡。
7. 大规模数据集的处理:对于大规模的数据集,直接使用支持向量机算法可能会导致计算复杂度过高的问题。
支持向量机matlab实现(精品文档)_共6页

支持向量机A=load('h:\study.txt'); %加载数据X=A(:,1:2); %特征值的数据label=A(:,3); %标签向量b=0; %待优化的参数[row,col]=size(A); %计算矩阵A的行数和列数iter=0; %迭代次数C=0.4; %最大间隔和分类正确的权重toler=0.001;MAX=40; %最大迭代次数alphas=zeros(row,1);%要求的参数,初始化为0while(iter<MAX)iterchange=0; %判断某一次循环中有没有参数改变for i=1:rowfxi=double((alphas.*label)'*(X*X(i,:)'))+b; %第i个的预测值ei=fxi-double(label(i)); %第i个预测值和真实值之差if (alphas(i)<C&&label(i)*ei<-toler)||(alphas(i)>0&&label(i)*ei>toler)j=i; %产生另外一个值jwhile j==ij=randint(1,1,row)+1;endfxj=double((alphas.*label)'*(X*X(j,:)'))+b; %第j个的预测值ej=fxj-double(label(j)); %第j个预测值和真实值之差alphasoldI=alphas(i); %保留参数的值alphasoldJ=alphas(j);if(label(i)~=label(j)) %限制求导出来的label(j)的值,在L和H之间L=max(0,alphas(j)-alphas(i));H=min(C,C+alphas(j)-alphas(i));elseL=max(0,alphas(j)+alphas(i)-C);H=min(C,alphas(j)+alphas(i));endif L==Hcontinue;endeta=X(i,:)*X(i,:)'+X(j,:)*X(j,:)'-2*X(i,:)*X(j,:)';% 这部分代码是求求导出来的最优值if eta<=0continue;endalphas(j)=alphas(j)+label(j)*(ei-ej)/eta; %求出优化后的alphas(j)值if alphas(j)>H %求出的alphas(j)必须在L和H之间alphas(j)=H;endif alphas(j)<Lalphas(j)=L;endif abs(alphas(j)-alphasoldJ)<0.00001 %若果发生轻微的变化就退出循环continue;endalphas(i)=alphas(i)+label(i)*label(j)*(alphasoldJ-alphas(j));%更新alphas(i)的值b1=b-ei-label(i)*(alphas(i)-alphasoldI)*(X(i,:)*X(i,:)')-label(j)*(alphas(j)-alphasoldJ)*(X(j,:)*X(j,:)');b2=b-ej-label(i)*(alphas(i)-alphasoldI)*(X(i,:)*X(i,:)')-label(j)*(alphas(j)-alphasoldJ)*(X(j,:)*X(j,:)');if alphas(i)>0&&alphas(i)<C %b值得更新b=b1;elseif alphas(j)>0&&alphas(j)<Cb=b2;elseb=(b1+b2)/2;enditerchange=iterchange+1;endendif iterchange==0iter=iter+1;elseiter=0;endend支持向量机主要是寻求一种能够最大间隔的超平面,它与logistic所构造的超平面原理不同的是:它主要是寻求局部点最优(也就是支持向量点),logistic是寻求全局最优。
第五章支持向量机

§5.1 支持向量机的理论基础
由于SVM 的求解最后转化成二次规划问题的求 由于 因此SVM 的解是全局唯一的最优解。 的解是全局唯一的最优解。 解,因此 SVM在解决小样本、非线性及高维模式识别问题 在解决小样本、 在解决小样本 中表现出许多特有的优势, 中表现出许多特有的优势,并能够推广应用到函 数拟合等其他机器学习问题中 。
11
关于支持向量机进一步的理论方法
统计学习理论和有关VC维的理论 统计学习理论和有关 维的理论 核方法的有关理论和方法 SVM求解和最优化的进一步方法 求解和最优化的进一步方法 支持向量回归机的理论和方法
返回
12
§5.4 支持向量机的应用
近年来SVM 方法已经在图像识别、信号处理和 方法已经在图像识别、 近年来 基因图谱识别等方面得到了成功的应用, 基因图谱识别等方面得到了成功的应用,显示 了它的优势。 了它的优势。 SVM 通过核函数实现到高维空间的非线性映射 通过核函数实现到高维空间的非线性映射, 所以适合于解决本质上非线性的分类、 所以适合于解决本质上非线性的分类、回归和 密度函数估计等问题。 密度函数估计等问题。 支持向量方法也为样本分析、因子筛选、 支持向量方法也为样本分析、因子筛选、信息 压缩、知识挖掘和数据修复等提供了新工具。 压缩、知识挖掘和数据修复等提供了新工具。
6
§5.2 支持向量机的特点
SVM 是一种有坚实理论基础的新颖的小样本学习 方法。它基本上不涉及概率测度及大数定律等, 方法。它基本上不涉及概率测度及大数定律等,因 此不同于现有的统计方法。从本质上看, 此不同于现有的统计方法。从本质上看,它避开了 从归纳到演绎的传统过程, 从归纳到演绎的传统过程,实现了高效的从训练样 本到预报样本的“转导推理” 本到预报样本的“转导推理”(transductive inference) ,大大简化了通常的分类和回归等问题。 大大简化了通常的分类和回归等问题。 大大简化了通常的分类和回归等问题 SVM 的最终决策函数只由少数的支持向量所确定 的最终决策函数只由少数的支持向量所确定, 计算的复杂性取决于支持向量的数目, 计算的复杂性取决于支持向量的数目,而不是样本 空间的维数,这在某种意义上避免了“维数灾难” 空间的维数,这在某种意义上避免了“维数灾难”。
Matlab教程课件-SVM支持向量机简介

第一部分 支持向量分类机
1.线性可分问题
代表+1 代表 -1
wT x + b>0
怎样将数据分类?
w Tx + b<0
代表 +1 代表 -1
哪一个“最好”呢?
最大间隔
代表 +1 代表 -1
支持 向量
x
间隔宽度M
x
M (x x )T w 2
w
w
目标1:将所有的点正确分类
wT xi b 1iff yi 1 wT xi b 1iff yi 1
i ,i* 0,i 1,, l
参数由用户给定
第三部分 Libsvm简介
MATLAB自带的svm实现函数是svmtrain和
svmclassify函数,实现C-SVC模型,且仅支持二 分类问题。
LIBSVM是台湾大学林智仁(Lin Chih-Jen)教授等开 发设计的软件。 https://.tw/~cjlin/libsvm/
利用SVM建立分类模型,达到自动分类葡萄酒品 种的目的。
分类问题的数学表示
已知:训练集包含 l 个样本点:
T {( x1, y1 ), , ( xl , yl )}
说明:
xi Rn 是输入向量,其分量称为特征或属性
yi y {1, 2, N} 是输出指标.
问题:对一个新的数据 x ,推断它所对应的输出
b*
yj
l
yii*
(
j
)
jS{ j| j 0}
i1
f (x) (w* )T ( x) b*
l
yii*( xi )T ( x)
yj
l
yii*
(
机器学习作业(六)支持向量机——Matlab实现
机器学习作业(六)⽀持向量机——Matlab实现题⽬下载【】第1题简述:⽀持向量机的实现(1)线性的情况:第1步:读取数据⽂件,可视化数据:% Load from ex6data1:% You will have X, y in your environmentload('ex6data1.mat');% Plot training dataplotData(X, y);第2步:设定不同的C,使⽤线性核函数训练SVM,并画出决策边界:C = 1;model = svmTrain(X, y, C, @linearKernel, 1e-3, 20);visualizeBoundaryLinear(X, y, model);运⾏结果:C = 1时:C = 1000时:其中线性核函数linearKernel:function sim = linearKernel(x1, x2)% Ensure that x1 and x2 are column vectorsx1 = x1(:); x2 = x2(:);% Compute the kernelsim = x1' * x2; % dot productend⾼斯核函数gaussianKernel实现:function sim = gaussianKernel(x1, x2, sigma)% Ensure that x1 and x2 are column vectorsx1 = x1(:); x2 = x2(:);% You need to return the following variables correctly.sim = 0;sim = exp(-norm(x1 - x2) ^ 2 / (2 * (sigma ^ 2)));end训练模型svmTrain函数(实现较为复杂,直接调⽤):function [model] = svmTrain(X, Y, C, kernelFunction, ...tol, max_passes)%SVMTRAIN Trains an SVM classifier using a simplified version of the SMO %algorithm.% [model] = SVMTRAIN(X, Y, C, kernelFunction, tol, max_passes) trains an % SVM classifier and returns trained model. X is the matrix of training% examples. Each row is a training example, and the jth column holds the % jth feature. Y is a column matrix containing 1 for positive examples% and 0 for negative examples. C is the standard SVM regularization% parameter. tol is a tolerance value used for determining equality of% floating point numbers. max_passes controls the number of iterations% over the dataset (without changes to alpha) before the algorithm quits.%% Note: This is a simplified version of the SMO algorithm for training% SVMs. In practice, if you want to train an SVM classifier, we% recommend using an optimized package such as:%% LIBSVM (.tw/~cjlin/libsvm/)% SVMLight (/)%%if ~exist('tol', 'var') || isempty(tol)tol = 1e-3;endif ~exist('max_passes', 'var') || isempty(max_passes)max_passes = 5;end% Data parametersm = size(X, 1);n = size(X, 2);% Map 0 to -1Y(Y==0) = -1;% Variablesalphas = zeros(m, 1);b = 0;E = zeros(m, 1);passes = 0;eta = 0;L = 0;H = 0;% Pre-compute the Kernel Matrix since our dataset is small% (in practice, optimized SVM packages that handle large datasets% gracefully will _not_ do this)%% We have implemented optimized vectorized version of the Kernels here so % that the svm training will run faster.if strcmp(func2str(kernelFunction), 'linearKernel')% Vectorized computation for the Linear Kernel% This is equivalent to computing the kernel on every pair of examplesK = X*X';elseif strfind(func2str(kernelFunction), 'gaussianKernel')% Vectorized RBF Kernel% This is equivalent to computing the kernel on every pair of examplesX2 = sum(X.^2, 2);K = bsxfun(@plus, X2, bsxfun(@plus, X2', - 2 * (X * X')));K = kernelFunction(1, 0) .^ K;else% Pre-compute the Kernel Matrix% The following can be slow due to the lack of vectorizationK = zeros(m);for i = 1:mfor j = i:mK(i,j) = kernelFunction(X(i,:)', X(j,:)');K(j,i) = K(i,j); %the matrix is symmetricendendend% Trainfprintf('\nTraining ...');dots = 12;while passes < max_passes,num_changed_alphas = 0;for i = 1:m,% Calculate Ei = f(x(i)) - y(i) using (2).% E(i) = b + sum (X(i, :) * (repmat(alphas.*Y,1,n).*X)') - Y(i);E(i) = b + sum (alphas.*Y.*K(:,i)) - Y(i);if ((Y(i)*E(i) < -tol && alphas(i) < C) || (Y(i)*E(i) > tol && alphas(i) > 0)), % In practice, there are many heuristics one can use to select% the i and j. In this simplified code, we select them randomly.j = ceil(m * rand());while j == i, % Make sure i \neq jj = ceil(m * rand());end% Calculate Ej = f(x(j)) - y(j) using (2).E(j) = b + sum (alphas.*Y.*K(:,j)) - Y(j);% Save old alphasalpha_i_old = alphas(i);alpha_j_old = alphas(j);% Compute L and H by (10) or (11).if (Y(i) == Y(j)),L = max(0, alphas(j) + alphas(i) - C);H = min(C, alphas(j) + alphas(i));elseL = max(0, alphas(j) - alphas(i));H = min(C, C + alphas(j) - alphas(i));endif (L == H),% continue to next i.continue;end% Compute eta by (14).eta = 2 * K(i,j) - K(i,i) - K(j,j);if (eta >= 0),% continue to next i.continue;end% Compute and clip new value for alpha j using (12) and (15).alphas(j) = alphas(j) - (Y(j) * (E(i) - E(j))) / eta;% Clipalphas(j) = min (H, alphas(j));alphas(j) = max (L, alphas(j));% Check if change in alpha is significantif (abs(alphas(j) - alpha_j_old) < tol),% continue to next i.% replace anywayalphas(j) = alpha_j_old;continue;end% Determine value for alpha i using (16).alphas(i) = alphas(i) + Y(i)*Y(j)*(alpha_j_old - alphas(j));% Compute b1 and b2 using (17) and (18) respectively.b1 = b - E(i) ...- Y(i) * (alphas(i) - alpha_i_old) * K(i,j)' ...- Y(j) * (alphas(j) - alpha_j_old) * K(i,j)';b2 = b - E(j) ...- Y(i) * (alphas(i) - alpha_i_old) * K(i,j)' ...- Y(j) * (alphas(j) - alpha_j_old) * K(j,j)';% Compute b by (19).if (0 < alphas(i) && alphas(i) < C),b = b1;elseif (0 < alphas(j) && alphas(j) < C),b = b2;elseb = (b1+b2)/2;endnum_changed_alphas = num_changed_alphas + 1;endendif (num_changed_alphas == 0),passes = passes + 1;elsepasses = 0;endfprintf('.');dots = dots + 1;if dots > 78dots = 0;fprintf('\n');endif exist('OCTAVE_VERSION')fflush(stdout);endendfprintf(' Done! \n\n');% Save the modelidx = alphas > 0;model.X= X(idx,:);model.y= Y(idx);model.kernelFunction = kernelFunction;model.b= b;model.alphas= alphas(idx);model.w = ((alphas.*Y)'*X)';end(2)⾮线性的情况:第1步:读取数据⽂件,并可视化数据:% Load from ex6data2:% You will have X, y in your environmentload('ex6data2.mat');% Plot training dataplotData(X, y);第2步:使⽤⾼斯核函数进⾏训练:% SVM ParametersC = 1; sigma = 0.1;% We set the tolerance and max_passes lower here so that the code will run % faster. However, in practice, you will want to run the training to% convergence.model= svmTrain(X, y, C, @(x1, x2) gaussianKernel(x1, x2, sigma)); visualizeBoundary(X, y, model);运⾏结果:(3)⾮线性情况2:第1步:读取数据⽂件,并可视化数据:% Load from ex6data3:% You will have X, y in your environmentload('ex6data3.mat');% Plot training dataplotData(X, y);第2步:尝试不同的参数,选取准确率最⾼的:% Try different SVM Parameters here[C, sigma] = dataset3Params(X, y, Xval, yval);% Train the SVMmodel= svmTrain(X, y, C, @(x1, x2) gaussianKernel(x1, x2, sigma)); visualizeBoundary(X, y, model);其中datasetParams函数:function [C, sigma] = dataset3Params(X, y, Xval, yval)% You need to return the following variables correctly.C = 1;sigma = 0.3;C_vec = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30];sigma_vec = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30];m = size(C_vec, 2);error_val = 1;for i = 1:mfor j = 1:mmodel= svmTrain(X, y, C_vec(i), @(x1, x2) gaussianKernel(x1, x2, sigma_vec(j))); pred = svmPredict(model, Xval);error_temp = mean(double(pred ~= yval));if error_temp < error_valC = C_vec(i);sigma = sigma_vec(j);error_val = error_temp;endendendend其中svmPredict函数:function pred = svmPredict(model, X)% Check if we are getting a column vector, if so, then assume that we only% need to do prediction for a single exampleif (size(X, 2) == 1)% Examples should be in rowsX = X';end% Datasetm = size(X, 1);p = zeros(m, 1);pred = zeros(m, 1);if strcmp(func2str(model.kernelFunction), 'linearKernel')% We can use the weights and bias directly if working with the% linear kernelp = X * model.w + model.b;elseif strfind(func2str(model.kernelFunction), 'gaussianKernel')% Vectorized RBF Kernel% This is equivalent to computing the kernel on every pair of examples X1 = sum(X.^2, 2);X2 = sum(model.X.^2, 2)';K = bsxfun(@plus, X1, bsxfun(@plus, X2, - 2 * X * model.X'));K = model.kernelFunction(1, 0) .^ K;K = bsxfun(@times, model.y', K);K = bsxfun(@times, model.alphas', K);p = sum(K, 2);else% Other Non-linear kernelfor i = 1:mprediction = 0;for j = 1:size(model.X, 1)prediction = prediction + ...model.alphas(j) * model.y(j) * ...model.kernelFunction(X(i,:)', model.X(j,:)');endp(i) = prediction + model.b;endend% Convert predictions into 0 / 1pred(p >= 0) = 1;pred(p < 0) = 0;end运⾏结果:第2题概述:实现垃圾邮件的识别第1步:读取数据⽂件,对单词进⾏处理:% Extract Featuresfile_contents = readFile('emailSample1.txt');word_indices = processEmail(file_contents);% Print Statsfprintf('Word Indices: \n');fprintf(' %d', word_indices);fprintf('\n\n');单词处理过程:去除符号、空格、换⾏等;识别出邮箱、价格、超链接、数字,替换为特定单词;在关键词列表中找出出现的关键词,并标记为出单词编号.function word_indices = processEmail(email_contents)% Load VocabularyvocabList = getVocabList();% Init return valueword_indices = [];% ========================== Preprocess Email =========================== % Find the Headers ( \n\n and remove )% Uncomment the following lines if you are working with raw emails with the% full headers% hdrstart = strfind(email_contents, ([char(10) char(10)]));% email_contents = email_contents(hdrstart(1):end);% Lower caseemail_contents = lower(email_contents);% Strip all HTML% Looks for any expression that starts with < and ends with > and replace% and does not have any < or > in the tag it with a spaceemail_contents = regexprep(email_contents, '<[^<>]+>', ' ');% Handle Numbers% Look for one or more characters between 0-9email_contents = regexprep(email_contents, '[0-9]+', 'number');% Handle URLS% Look for strings starting with http:// or https://email_contents = regexprep(email_contents, ...'(http|https)://[^\s]*', 'httpaddr');% Handle Email Addresses% Look for strings with @ in the middleemail_contents = regexprep(email_contents, '[^\s]+@[^\s]+', 'emailaddr');% Handle $ signemail_contents = regexprep(email_contents, '[$]+', 'dollar');% ========================== Tokenize Email =========================== % Output the email to screen as wellfprintf('\n==== Processed Email ====\n\n');% Process filel = 0;while ~isempty(email_contents)% Tokenize and also get rid of any punctuation[str, email_contents] = ...strtok(email_contents, ...[' @$/#.-:&*+=[]?!(){},''">_<;%' char(10) char(13)]);% Remove any non alphanumeric charactersstr = regexprep(str, '[^a-zA-Z0-9]', '');% Stem the word% (the porterStemmer sometimes has issues, so we use a try catch block)try str = porterStemmer(strtrim(str));catch str = ''; continue;end;% Skip the word if it is too shortif length(str) < 1continue;endfor i = 1:size(vocabList),if strcmp(str, vocabList(i)),word_indices = [word_indices i];endend% Print to screen, ensuring that the output lines are not too longif (l + length(str) + 1) > 78fprintf('\n');l = 0;endfprintf('%s ', str);l = l + length(str) + 1;end% Print footerfprintf('\n\n=========================\n');end其中读取关键字列表函数:function vocabList = getVocabList()%% Read the fixed vocabulary listfid = fopen('vocab.txt');% Store all dictionary words in cell array vocab{}n = 1899; % Total number of words in the dictionary% For ease of implementation, we use a struct to map the strings => integers% In practice, you'll want to use some form of hashmapvocabList = cell(n, 1);for i = 1:n% Word Index (can ignore since it will be = i)fscanf(fid, '%d', 1);% Actual WordvocabList{i} = fscanf(fid, '%s', 1);endfclose(fid);end第3步:对关键字进⾏特征值标记,出现的关键词标记为1:% Extract Featuresfeatures = emailFeatures(word_indices);% Print Statsfprintf('Length of feature vector: %d\n', length(features));fprintf('Number of non-zero entries: %d\n', sum(features > 0));其中emailFeatures函数为:function x = emailFeatures(word_indices)% Total number of words in the dictionaryn = 1899;% You need to return the following variables correctly.x = zeros(n, 1);for i = 1:size(word_indices),x(word_indices(i)) = 1;endend第4步:使⽤线性核函数进⾏训练,并分别计算训练集准确率和测试集准确率:% Load the Spam Email dataset% You will have X, y in your environmentload('spamTrain.mat');fprintf('\nTraining Linear SVM (Spam Classification)\n')fprintf('(this may take 1 to 2 minutes) ...\n')C = 0.1;model = svmTrain(X, y, C, @linearKernel);p = svmPredict(model, X);fprintf('Training Accuracy: %f\n', mean(double(p == y)) * 100); % Load the test dataset% You will have Xtest, ytest in your environmentload('spamTest.mat');fprintf('\nEvaluating the trained Linear SVM on a test set ...\n') p = svmPredict(model, Xtest);fprintf('Test Accuracy: %f\n', mean(double(p == ytest)) * 100);运⾏结果:第5步:找出最⾼权重的关键词:% Sort the weights and obtin the vocabulary list [weight, idx] = sort(model.w, 'descend');vocabList = getVocabList();fprintf('\nTop predictors of spam: \n');for i = 1:15fprintf(' %-15s (%f) \n', vocabList{idx(i)}, weight(i));endfprintf('\n\n');fprintf('\nProgram paused. Press enter to continue.\n'); pause;运⾏结果:。
支持向量机原理及matlab实现
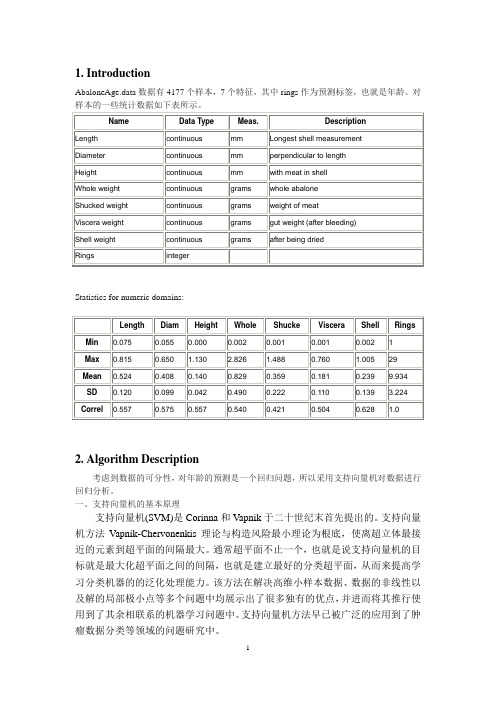
1. IntroductionStatistics for numeric domains:2. Algorithm Description考虑到数据的可分性,对年龄的预测是一个回归问题,所以采用支持向量机对数据进行回归分析。
一、支持向量机的基本原理支持向量机(SVM)是Corinna和Vapnik于二十世纪末首先提出的。
支持向量机方法Vapnik-Chervonenkis理论与构造风险最小理论为根底,使离超立体最接近的元素到超平面的间隔最大。
通常超平面不止一个,也就是说支持向量机的目标就是最大化超平面之间的间隔,也就是建立最好的分类超平面,从而来提高学习分类机器的的泛化处理能力。
该方法在解决高维小样本数据、数据的非线性以及解的局部极小点等多个问题中均展示出了很多独有的优点,并进而将其推行使用到了其余相联系的机器学习问题中。
支持向量机方法早已被广泛的应用到了肿瘤数据分类等领域的问题研究中。
支持向量机的具体求解过程如下: (1) 设已知样本训练集:()(){}()11,,,nn n T x y x y X Y =∈⨯其中,{}(),1,11,2,,n i i x X R y Y i n ∈=∈=-+=,i x 为特征向量。
(2) 选择适当核函数(,)i j K x x 以及参数C ,解决优化问题:()1111,2min n nni i j j i j j i j j y y K x x αααα===-∑∑∑ 1..0,0,1,,ni ii i s t yC i n αα==≤≤=∑得最优解:()***1,...,Tn ααα=。
(3) 选取α*的正分量,计算样本分类阈值:**1(,)li i i i j i b y y K x x α==-∑。
(4) 构造最优判别函数:1()sgn (,)n i i i j i f x y a K x x b **=⎡⎤=+⎢⎥⎣⎦∑。
支持向量机内积核核函数K 的主要种类有: ① 线性内核函数 (,)(,)i j i j K x x x x = ② 多项式核函数 (,)[(,)1]q i j i j K x x x x =+ ③ 高斯径向基核函数 (RBF) 22(,)exp{}i ji j x x K x x σ-=-④ 双曲正切核函数 (Sigmoid 核函数) (,)tanh(())i j i j K x x v x x c =⋅+ 一般地,用SVM 做分类预测时必须调整相关参数(特别是惩罚参数c 和核函数参数g ),这样才可以获得比较满意的预测分类精度,采用Cross Validation 的思想可以获取最优的参数,并且有效防止过学习和欠学习状态的产生,从而能够对于测试集合的预测得到较佳的精度。
支持向量机 多元回归 matlab

文章标题:探讨支持向量机在多元回归中的应用引言支持向量机(Support Vector Machine, SVM)是一种机器学习算法,在数据分类和回归分析中有着广泛的应用。
它通过找到能够对数据进行最佳划分的超平面来解决问题,具有较强的泛化能力和鲁棒性。
在本文中,我们将探讨支持向量机在多元回归中的应用,以及如何在matlab中实现支持向量机的多元回归模型。
一、支持向量机简介支持向量机最初被用于处理线性可分的分类问题,通过找到能够将两个类别分开的最优超平面来实现分类。
随后,支持向量机被扩展到处理非线性分类问题,并在回归分析中也有了广泛的应用。
在支持向量机的训练过程中,选择合适的核函数和正则化参数对模型的性能有着重要的影响。
支持向量机在处理小样本和高维数据时表现出色,具有较强的鲁棒性。
在多元回归问题中,支持向量机可以通过回归分析来预测连续性的输出变量。
与传统的线性回归方法相比,支持向量机在处理非线性关系和存在异常值的数据时更为灵活和稳健。
接下来,我们将介绍支持向量机在多元回归中的具体应用。
二、支持向量机在多元回归中的应用在多元回归分析中,我们常常需要预测多个自变量对因变量的影响。
支持向量机通过构建回归模型来实现这一目标,其核心思想是寻找一个超平面,使得训练数据点到该超平面的距离最小化。
这一过程可以通过求解相应的优化问题来实现,通常可以使用matlab工具进行支持向量机模型的构建和训练。
在matlab中,通过调用相关的支持向量机函数和工具箱,我们可以很方便地构建支持向量机的多元回归模型。
在构建模型之前,需要对数据进行预处理和特征工程,以确保数据的质量和可用性。
接下来,我们可以选择合适的核函数和正则化参数,利用matlab提供的函数来训练支持向量机回归模型。
通过实验和交叉验证,我们可以对模型的性能进行评估和优化,以获得更好的预测效果。
三、个人观点和理解支持向量机在多元回归中的应用具有较强的实用性和灵活性,尤其适用于处理非线性关系和复杂数据结构。
机器学习中支持向量机算法的使用教程及实战案例分析

机器学习中支持向量机算法的使用教程及实战案例分析支持向量机(Support Vector Machine,SVM)是一种重要的机器学习算法,被广泛应用于分类和回归问题。
它在许多实际应用中显示出了出色的性能和鲁棒性。
本文将详细介绍支持向量机算法的原理、使用方法和实战案例分析。
一、支持向量机算法的原理支持向量机算法的基本原理是基于最大间隔分类的思想,通过在特征空间中找到一个最优超平面,将不同类别的数据样本完全分开。
该超平面由支持向量确定,支持向量是距离超平面最近的样本点。
支持向量机算法的目标是最大化间隔。
间隔指的是超平面到最近的样本点的距离,最大化间隔可以提高模型的鲁棒性。
支持向量机算法可以处理线性可分和线性不可分的问题。
对于线性可分问题,可以使用硬间隔支持向量机;对于线性不可分问题,可以使用软间隔支持向量机,通过引入松弛变量来容忍一定的错分类。
二、支持向量机算法的使用方法1. 数据预处理在应用支持向量机算法之前,需要对数据进行预处理。
首先,对数据进行清洗,处理缺失值和异常值。
然后,对数据进行标准化或归一化,以便不同特征之间的数值范围一致。
2. 特征选择选择合适的特征对支持向量机算法的性能至关重要。
可以通过统计方法、相关性分析或专业知识等方式选择最具区分度的特征。
3. 模型训练将数据集分为训练集和测试集,使用训练集对支持向量机模型进行训练。
在模型训练过程中,需要选择合适的核函数和参数,并进行交叉验证来确定最优的模型。
4. 模型评估使用测试集对训练好的支持向量机模型进行评估。
常用的评估指标包括准确率、精确率、召回率和F1值等。
通过评估结果可以判断模型的性能。
三、支持向量机算法的实战案例分析为了更好地理解支持向量机算法的应用,下面将介绍一个实战案例:乳腺癌分类。
乳腺癌是女性常见的恶性肿瘤之一,及早发现和诊断对于治疗和预后非常重要。
在这个案例中,我们将使用支持向量机算法对乳腺癌进行分类。
首先,我们收集了乳腺癌相关的临床特征数据,包括肿块的厚度、大小、形状等。
matlab中最简单的svm例子

在MATLAB中,最简单的SVM(支持向量机)例子可以通过以下步骤实现:1. 导入数据:首先,我们需要导入一些用于训练和测试的数据集。
这里我们使用MATLAB 内置的鸢尾花数据集。
```matlabload fisheriris; % 加载鸢尾花数据集X = meas; % 提取特征矩阵Y = species; % 提取标签向量```2. 划分训练集和测试集:我们将数据集划分为训练集和测试集,以便评估模型的性能。
```matlabcv = cvpartition(size(X,1),'HoldOut',0.5); % 划分训练集和测试集idx = cv.test; % 获取测试集的索引XTrain = X(~idx,:); % 提取训练集的特征矩阵YTrain = Y(~idx,:); % 提取训练集的标签向量XTest = X(idx,:); % 提取测试集的特征矩阵YTest = Y(idx,:); % 提取测试集的标签向量```3. 创建SVM模型:接下来,我们创建一个SVM模型,并设置相应的参数。
```matlabSVMModel = fitcsvm(XTrain,YTrain,'KernelFunction','linear'); % 创建线性核函数的SVM 模型```4. 预测和评估:最后,我们使用训练好的模型对测试集进行预测,并评估模型的性能。
```matlabYPred = predict(SVMModel,XTest); % 对测试集进行预测accuracy = sum(YPred == YTest)/length(YTest) * 100; % 计算准确率fprintf('Accuracy: %.2f%%', accuracy); % 输出准确率```这个例子展示了如何在MATLAB中使用最简单的SVM方法进行分类。
《支持向量机》课件

优化算法
梯度下降法
优化算法使用梯度下降法来迭代更新 超平面的参数,使得分类器的分类效 果不断优化。在每次迭代中,算法计 算当前超平面的梯度并沿着负梯度的 方向更新参数。
核函数参数
对于非线性支持向量机,核函数的参数决定了数据映射到特征空间的复杂度。选择合适的核函数参数可以使分类 器更好地适应数据特性。常见的核函数参数包括多项式核的阶数和RBF核的宽度参数σ。
04
支持向量机的扩展与改进
多分类支持向量机
总结词
多分类支持向量机是支持向量机在多分类问题上的扩展,通过引入不同的策略,将多个分类问题转化 为二分类问题,从而实现对多类别的分类。
金融风控
用于信用评分、风险评估等金融领域。
02
支持向量机的基本原理
线性可分支持向量机
01
线性可分支持向量机是支持向量机的基本形式,用 于解决线性可分问题。
02
它通过找到一个超平面,将不同类别的数据点分隔 开,使得正例和反例之间的间隔最大。
03
线性可分支持向量机适用于二分类问题,且数据集 线性可分的情况。
计算效率高
支持向量机采用核函数技巧,可以在低维空间中 解决高维问题,从而减少计算复杂度。
支持向量机的应用场景
文本分类
利用支持向量机对文本数据进行分类,如垃 圾邮件识别、情感分析等。
生物信息学
支持向量机在基因分类、蛋白质功能预测等 方面具有重要价值。
图像识别
在图像分类、人脸识别等领域,支持向量机 也得到了广泛应用。
03
数字图像处理与机器视觉-基于MATLAB实现 第13章 支持向量机的机器视觉应用

13.3支持向量机的理论基础
本节主要介绍SVM 的理论基础和实现原理,将分别阐述线性可分、非线性可 分以及需要核函数映射这3种情况下的SVM。最后还将学习如何将SVM推广至多类 问题。
13.3.1 线性可分情况下的SVM
如果用一个线性函数(如2维空间中的直线,3维空间中的平面以及更高维数 空间中的超平面)可以将两类样本完全分开,就称这些样本是线性可分(linearly separable)的。反之,如果找不到一个线性函数能够将两类样本分开,则称这些样 本是非线性可分的。
(a)训练样本上的两种分类模型
(b)测试样本上的两种分类模型
图13-1 分类模型的选择
13.2支持向量机的分类思想
13.2.2模型参数的选择
如图13-2所示,2维空间中的两类样本,可以采用(a)图中的任意直线将它们分 开。但哪条直线才是最优的选择?
(a)任意分割超平面
(b)最佳分割超平面
图13-2 分割超平面
第十三章 支持向量机的机器视觉应用
➢ 13.1引言 ➢ 13.2支持向量机的分类思想 ➢ 13.3支持向量机的理论基础 ➢ 13.4 基于MATLAB的SVM的实例
13.1引言
支持向量机 (support vector machine,SVM)是在统计学习理论的基础上发展 起来的新一代学习算法,它在文本分类、手写识别、图像分类、生物信息学等领域中 获得较好的应用。相比于容易过渡拟合训练样本的人工神经网络,支持向量机对于未 见过的测试样本具有更好的推广能力。
图13-2只是在二维情况下的特例——最优分类线,在三维空间中则是具有最大 间隔的平面,更为一般的情况是最优分类超平面。实际上,SVM 正是从线性可分情 况下的最优分类面发展而来的,其主要思想就是寻找能够成功分开两类样本并且具有 最大分类间隔的最优分类超平面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
支持向量机matlab分类实例及理论线性支持向量机可对线性可分的样本群进行分类,此时不需要借助于核函数就可较为理想地解决问题。
非线性支持向量机将低维的非线性分类问题转化为高维的线性分类问题,然后采用线性支持向量机的求解方法求解。
此时需要借助于核函数,避免线性分类问题转化为非线性分类问题时出现的维数爆炸难题,从而避免由于维数太多而无法进行求解。
第O层:Matlab的SVM函数求解分类问题实例0.1 Linear classification%Two Dimension Linear-SVM Problem, Two Class and Separable Situation %Method from Christopher J. C. Burges:%"A Tutorial on Support Vector Machines for Pattern Recognition", page 9%Optimizing ||W|| directly:% Objective: min "f(A)=||W||" , p8/line26% Subject to: yi*(xi*W+b)-1>=0, function (12);clear all;close allclc;sp=[3,7; 6,6; 4,6;5,6.5] % positive sample pointsnsp=size(sp);sn=[1,2; 3,5;7,3;3,4;6,2.7] % negative sample pointsnsn=size(sn)sd=[sp;sn]lsd=[true true true true false false false false false]Y = nominal(lsd)figure(1);subplot(1,2,1)plot(sp(1:nsp,1),sp(1:nsp,2),'m+');hold onplot(sn(1:nsn,1),sn(1:nsn,2),'c*');subplot(1,2,2)svmStruct = svmtrain(sd,Y,'showplot',true);0.2 NonLinear classificationclear all;close allclc;sp=[3,7; 6,6; 4,6; 5,6.5] % positive sample pointsnsp=size(sp);sn=[1,2; 3,5; 7,3; 3,4; 6,2.7; 4,3;2,7] % negative sample points nsn=size(sn)sd=[sp;sn]lsd=[true true true true false false false false false false false] Y = nominal(lsd)figure(1);subplot(1,2,1)plot(sp(1:nsp,1),sp(1:nsp,2),'m+');hold onplot(sn(1:nsn,1),sn(1:nsn,2),'c*');subplot(1,2,2)% svmStruct = svmtrain(sd,Y,'Kernel_Function','linear','showplot',true);svmStruct = svmtrain(sd,Y,'Kernel_Function','quadratic','showplot',true);% use the trained svm (svmStruct) to classify the dataRD=svmclassify(svmStruct,sd,'showplot',true)% RD is the classification result vector0.3 Gaussian Kernal Classificationclear all;close allclc;sp=[5,4.5;3,7; 6,6; 4,6; 5,6.5] % positive sample pointsnsp=size(sp);sn=[1,2; 3,5; 7,3; 3,4; 6,2.7; 4,3;2,7] % negative sample pointsnsn=size(sn)sd=[sp;sn]lsd=[true true true true true false false false false false false false] Y = nominal(lsd)figure(1);subplot(1,2,1)plot(sp(1:nsp,1),sp(1:nsp,2),'m+');hold onplot(sn(1:nsn,1),sn(1:nsn,2),'c*');subplot(1,2,2)svmStruct =svmtrain(sd,Y,'Kernel_Function','rbf','rbf_sigma',0.6,'method','SMO', 'showplot',true);% svmStruct = svmtrain(sd,Y,'Kernel_Function','quadratic','showplot',true);% use the trained svm (svmStruct) to classify the dataRD=svmclassify(svmStruct,sd,'showplot',true)% RD is the classification result vectorsvmtrain(sd,Y,'Kernel_Function','rbf','rbf_sigma',0.2,'method','SM O','showplot',true);0.4 Svmtrain Functionsvmtrain Train a support vector machine classifierSVMSTRUCT = svmtrain(TRAINING, Y) trains a support vector machine (SVM) classifier on data taken from two groups. TRAINING is a numeric matrix of predictor data. Rows of TRAINING correspond to observations; columns correspond to features. Y is a column vector that contains the known class labels for TRAINING. Y is a grouping variable, i.e., it can be acategorical, numeric, or logical vector; a cell vector of strings; or a character matrix with each row representing a class label (see help forgroupingvariable). Each element of Y specifies the group thecorresponding row of TRAINING belongs to. TRAINING and Y must have thesame number of rows. SVMSTRUCT contains information about the trained classifier, including the support vectors, that is used by SVMCLASSIFY for classification. svmtrain treats NaNs, empty strings or 'undefined' values as missing values and ignores the corresponding rows inTRAINING and Y.SVMSTRUCT = svmtrain(TRAINING, Y, 'PARAM1',val1, 'PARAM2',val2, ...) specifies one or more of the following name/value pairs:Name Value'kernel_function' A string or a function handle specifying the kernel function used to represent the dotproduct in a new space. The value can be one of the following:'linear' - Linear kernel or dot product(default). In this case, svmtrainfinds the optimal separating plane in the original space.'quadratic' - Quadratic kernel'polynomial' - Polynomial kernel with defaultorder 3. To specify another order, use the 'polyorder' argument.'rbf' - Gaussian Radial Basis Functionwith default scaling factor 1. Tospecify another scaling factor,use the 'rbf_sigma' argument.'mlp' - Multilayer Perceptron kernel (MLP) with default weight 1 and defaultbias -1. To specify another weight or bias, use the 'mlp_params'argument.function - A kernel function specified using @(for example @KFUN), or ananonymous function. A kernelfunction must be of the formfunction K = KFUN(U, V)The returned value, K, is a matrix of size M-by-N, where M and N arethe number of rows in U and Vrespectively.'rbf_sigma' A positive number specifying the scaling factor in the Gaussian radial basis function kernel.Default is 1.'polyorder' A positive integer specifying the order of the polynomial kernel. Default is 3.'mlp_params' A vector [P1 P2] specifying the parameters of MLP kernel. The MLP kernel takes the form:K = tanh(P1*U*V' + P2),where P1 > 0 and P2 < 0. Default is [1,-1].'method' A string specifying the method used to find the separating hyperplane. Choices are:'SMO' - Sequential Minimal Optimization (SMO)method (default). It implements the L1soft-margin SVM classifier.'QP' - Quadratic programming (requires anOptimization Toolbox license). Itimplements the L2 soft-margin SVMclassifier. Method 'QP' doesn't scalewell for TRAINING with large number ofobservations.'LS' - Least-squares method. It implements the L2 soft-margin SVM classifier.'options' Options structure created using either STATSET or OPTIMSET.* When you set 'method' to 'SMO' (default),create the options structure using STATSET.Applicable options:'Display' Level of display output. Choicesare 'off' (the default), 'iter', and'final'. Value 'iter' reports every500 iterations.'MaxIter' A positive integer specifying themaximum number of iterations allowed. Default is 15000 for method 'SMO'.* When you set method to 'QP', create theoptions structure using OPTIMSET. For details of applicable options choices, see QUADPROGoptions. SVM uses a convex quadratic program,so you can choose the 'interior-point-convex' algorithm in QUADPROG.'tolkkt' A positive scalar that specifies the tolerance with which the Karush-Kuhn-Tucker (KKT) conditions are checked for method 'SMO'. Default is1.0000e-003.'kktviolationlevel' A scalar specifying the fraction of observations that are allowed to violate the KKT conditions for method 'SMO'. Setting this value to be positive helps the algorithm to converge faster if it is fluctuating near a good solution. Default is 0.'kernelcachelimit' A positive scalar S specifying the size of the kernel matrix cache for method 'SMO'. Thealgorithm keeps a matrix with up to S * Sdouble-precision numbers in memory. Default is5000. When the number of points in TRAININGexceeds S, the SMO method slows down. It'srecommended to set S as large as your systempermits.'boxconstraint' The box constraint C for the soft margin. C can bea positive numeric scalar or a vector of positive numbers with the number of elements equal to the number of rows in TRAINING.Default is 1.* If C is a scalar, it is automatically rescaled by N/(2*N1) for the observations of group one, and by N/(2*N2) for the observations of group two, where N1 is the number of observations in group one, N2 is the number of observations in group two. The rescaling is done to take into account unbalanced groups, i.e., when N1 and N2 are different.* If C is a vector, then each element of Cspecifies the box constraint for thecorresponding observation.'autoscale' A logical value specifying whether or not toshift and scale the data points before training. When the value is true, the columns of TRAININGare shifted and scaled to have zero mean unitvariance. Default is true.'showplot' A logical value specifying whether or not to show a plot. When the value is true, svmtrain creates a plot of the grouped data and the separating line for the classifier, when using data with 2features (columns). Default is false.SVMSTRUCT is a structure having the following properties:SupportVectors Matrix of data points with each row corresponding to a support vector.Note: when 'autoscale' is false, this fieldcontains original support vectors in TRAINING.When 'autoscale' is true, this field containsshifted and scaled vectors from TRAINING.Alpha Vector of Lagrange multipliers for the support vectors. The sign is positive for support vectors belonging to the first group and negative forsupport vectors belonging to the second group.Bias Intercept of the hyperplane that separatesthe two groups.Note: when 'autoscale' is false, this fieldcorresponds to the original data points inTRAINING. When 'autoscale' is true, this fieldcorresponds to shifted and scaled data points.KernelFunction The function handle of kernel function used.KernelFunctionArgs Cell array containing the additional arguments for the kernel function.GroupNames A column vector that contains the knownclass labels for TRAINING. Y is a groupingvariable (see help for groupingvariable).SupportVectorIndices A column vector indicating the indices of support vectors.ScaleData This field contains information about auto-scale. When 'autoscale' is false, it is empty. When'autoscale' is set to true, it is a structurecontaining two fields:shift - A row vector containing the negative of the mean across all observations in TRAINING.scaleFactor - A row vector whose value is1./STD(TRAINING).FigureHandles A vector of figure handles created by svmtrain when 'showplot' argument is TRUE.Example:% Load the data and select features for classificationload fisheririsX = [meas(:,1), meas(:,2)];% Extract the Setosa classY = nominal(ismember(species,'setosa'));% Randomly partitions observations into a training set and a test % set using stratified holdoutP = cvpartition(Y,'Holdout',0.20);% Use a linear support vector machine classifiersvmStruct =svmtrain(X(P.training,:),Y(P.training),'showplot',true);C = svmclassify(svmStruct,X(P.test,:),'showplot',true);errRate = sum(Y(P.test)~= C)/P.TestSize %mis-classification rate conMat = confusionmat(Y(P.test),C) % the con第一层、了解SVM1.0、什么是支持向量机SVM要明白什么是SVM,便得从分类说起。
