高等数学 山东科技大学
山东科技大学大一公共课高等数学试卷及答案

山东科技大学期末复习题及参考解答一.填空题1.设点)4,1,1(-A 在曲面),(:y x f z S =上.若3)1,1(=-'x f ,且),(y x f 在其定义域内任意一点),(y x 处满足方程),(),(),(y x f y x f y y x f x y x ='+',则曲面S 在A 点处的切平面方程为 03 =--z y x . 解:由题设有4)1,1(131=-'⋅-⋅y f ,即1)1,1(-=-'y f ,所以 0)4()1()1(3:=--+--z y x ΠT ,即03=--z y x .2.设2e ),,(yz z y x f x =,其中),(y x z z =是由方程0=+++xyz z y x 确定的隐函数,则 1 )1,1,0(=-'x f .解:1d de d )1,1,(d )1,1,0(0==-=-'==x xx x x x x f f . 3.曲线⎩⎨⎧==+-6022x z y x 在点)3,3,6(处的切线与Oz 轴正向的夹角为 6 π.解:曲线方程可写为⎪⎩⎪⎨⎧-===662y z y y x ,6)(,1)(,0)(2-='='='y y y z y y y x ,于是=τ}23,21,0{2}3,1,0{=,23cos =γ,故π6γ=. 4.设n 是曲面632222=++z y x 在点)1,1,1(P 处的外法向量,则函数zy x u 2286+=在点P 处沿方向n 的方向导数 711 =∂∂n u .解:令632),,(222-++=z y x z y x F ,则z F y F x F z y x 2,6,2='='=',于是n }1 ,3 ,2{=,其方向余弦为141cos ,143cos ,142cos ===γβα.又PPux∂==∂ 14886216122=+=∂∂PPy x yz y u, 1486222-=+-=∂∂PPzy x zu ,故711)14(141143148142146=-⋅+⋅+⋅=∂∂Pnu. 5.设22{(,)1}D x y x y =+≤,则235π(2sin 1)d 4Dx x y σ-++=⎰⎰.解: 2323(2sin 1)d d 2sin d d 1d DDDDDx x y x x y σσσσσ-++=-++⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰2π123 00π5πcos d d 00ππ.44θθρρ=+++=+=⎰⎰. 6.交换二次积分的次序:d ),(d d ),(d d ),(d 222222 4 211 11 14 02⎰⎰⎰⎰⎰⎰---+----=+y-y y x x x x y x f y y y x f x y y x f x .7.将直角坐标系下的三次积分化为球坐标系下的三次积分:=⎰⎰⎰-----+----2222221 1 11 11 11d ),,(d d x x y x y x z z y x f y x ⎰⎰⎰2 02cos 022 0d sin )cos ,sin sin ,sin cos (d d πϕπϕϕϕθϕθϕθr r r r r f .8.设有曲线段⎩⎨⎧==ta y ta x L sin cos :(π≤≤t 0),则2 π s a =⎰.解:2 d ππL s a s a a a ==⋅=⎰⎰.9.设C 是圆周)1()1(222>=+-R R y x 的正向,则22 d d π 4C x y y x x y-=+⎰.解:因为当)0,0(),(≠y x 时,xQ y x x y y P ∂∂=+-=∂∂22222)4(4,故可在C 的内部作椭圆周2224:a y x l =+,且l 与C 同向,则⎰=+-C y x x y y x 224d d 222222 4d d 12(11)d ππ2l x y ax y y x a a a a a σ+≤-=+=⋅⋅⋅=⎰⎰⎰. 10.设Ω是光滑闭合曲面∑所围成的空间域,其体积为V ,则沿∑外侧的积分3 d d )(d d )(d d )(V z y z x x z x y y x x z =-+-+-⎰⎰∑.解:V V z y z x x z x y y x x z 3d )111(d d )(d d )(d d )(=++=-+-+-⎰⎰⎰⎰⎰Ω∑.11.若幂级数∑∞=-0)1(n n n x a 在1-=x 处收敛,在3=x 处发散,则其收 )3 ,1[ -=D .解:因为211=--≥R ,213=-≤R ,故2=R ,从而)3 ,1[-=D . 12.设xx x f --=41)(,则 3! )1()(n n n f =.解:因为!)1()(n fa n n =,故n n a n f !)1()(= )(N ∈n . 而∑∑∞=∞=++-=-=---=--=1011)1(31)1(3131113141)(n n nn n n x x x x x x x f , 所以n n n f 3!)1()(= )(N ∈n . 13. ch 2e e )!2(102x x n xx n n =+=-∞=∑.解:易知+∞=R .设=)(x S ∑∞=02)!2(1n n x n ,) ,(∞+-∞∈x ,1)0(=S .=')(x S ∑∞=--112)!12(1n n x n ,) ,(∞+-∞∈x ,0)0(='S . ='')(x S )()!22(1122x S x n n n =-∑∞=-,从而x x C C x S -+=e e )(21.由1)0(=S 及0)0(='S 得⎩⎨⎧=-=+012121C C C C ,解得2121==C C ,故x x S xx ch 2e e )(=+=-. 14.设)(x S 是⎩⎨⎧<≤<≤--=10 ,101 ,)(x x x x f 的以2为周期的Fourier 级数的和函数,则1 )7(, 21 )4(==-S S .解:(1)1011(4)(0),(7)(1)(1)1222S S S S S --++-====-===.15.微分方程0d )(d )1(32=++++y y y x x y 的通解为43 43C y y xy x =+++.解:0d d )d d (d 32=++++y y y y y x x y x , 0)4d()3d()d(d 43=+++y y xy x ,0)43d(43=+++y y xy x ,所以通解为C y y xy x =+++4343.16.用待定系数法求x x y y 2cos 34=+''的特解*y 时,应设]2sin )(2cos )[( x D Cx x B Ax x y +++=*.二.单项选择题1.设函数),(y x f z =在点M 的某邻域内有定义,下列结论正确的是( B )(A)若z 在点M 处沿任意方向l 的方向导数lz ∂∂存在,则z 在点M 处两个偏导数存在.(B)若z 在点M 处可微,则z 在点M 处的梯度存在.(C)若z 在点M 处沿任意方向l 的方向导数lz ∂∂存在,则z 在点M 处连续.(D)若z 在点M 处连续且沿任意方向l 的方向导数lz ∂∂存在,则z 在点M 处可微.2.设曲面224y x z --=上点P 处的切平面平行于平面0122=+++z y x ,则P 点的坐标为( D )(A))2,1,1(-. (B))2,1,1(-. (C))2,1,1(--. (D))2,1,1(.解:因为点P ),,(z y x 处切平面的法向量}1,2,2{y x =n 平行于已知平面的法向量}1,2,2{1=n ,故有112222==y x ,于是得1==y x ,而211422=--=z ,因此P 点的坐标为)2,1,1(. 5.设),(y x f 在域}0,2),{(2>-≤≤=R x Rx y x y x D 上连续,则二重积分=⎰⎰Dy x y x f d d ),(( C )(A)⎰⎰-22 00 d ),(d x Rx Ry y x f x . (B)⎰⎰-22 0 0 d ),(d y R Rx y x f y .(C)⎰⎰--yy R R Rx y x f y 0 22d ),(d . (D)π2in 2π 04d (cos ,sin )d Rs f θθρθρθρρ⎰⎰.8.设有球面:S 1222=++z y x ,1S 是S 的上半部分的上侧,2S 是S 的下半部分的下侧,若=1I ⎰⎰1d d S y x z ,=2I ⎰⎰2d d S y x z ,则( B )(A)21I I <. (B)21I I =. (C)21I I >. (D)021=+I I . 解:=1I ⎰⎰1d d S y x z ⎰⎰≤+--=12222d d 1y x y x y x ,=2I ⎰⎰2d d S y x z ⎰⎰≤+----=12222d )d 1(y x y x y x ⎰⎰≤+--=12222d d 1y x y x y x 1I =.9.以下四式正确的是( B )(A)∑∞=-=+1)1()1ln(n n nn x x (11≤<-x ). (B)20π(1)1(2)!nn n n ∞=-=-∑. (C)x x n x n n n sin )!12()1(02=+-∑∞= (+∞<<∞-x ). (D)211π(1)0(21)!n n n n ∞+=-=+∑. 解:)1ln()1(1x n x n nn+-=-∑∞=, 20π(1)cos π1(2)!nnn n ∞=-==-∑, x xn x n n n sin )!12()1(02=+-∑∞=)0(≠x , 211π(1)sin πππ(21)!n nn n ∞+=-=-=-+∑. 10.设正项级数∑∞=1n n u 收敛,且n n nu ∞→lim 存在,则( A ) (A)n n nu ∞→lim 0=. (B)n n nu ∞→lim 0>. (C)n n nu ∞→lim 0<. (D)不能确定. 解:因为n n nu ∞→lim nu n n 1lim ∞→=存在且∑∞=1n n u 收敛,故必有01lim =∞→n u nn ,否则∑∞=1n n u 发散. 11.将bxa x x f +=)((0≠ab )展为x 的幂级数时,所展幂级数的收敛半径=R ( D )(A)a . (B)b . (C)a b . (D)ba .解:bx a x x f +=)(x ab a x --=11∑∞=-=0)(n n x ab a x ,当1<=-x a b x a b 即b a x <时,级数绝对收敛,当1>-x a b 即b a x >时级数发散,故ba R =. 12.微分方程xy y =' (0<x )满足初始条件e1)2(=-y 的解=y ( C )(A)C x +-22e. (B)22e x . (C)22ex - (D)22Cex -.解:C x +-22e和22Ce x -不是特解,22e x 不满足初始条件,故选(C).(或直接求解.)三.解下列各题1.设),(y x z z =是由方程zz y x e =++确定的隐函数,求22x z ∂∂. 解:将方程两边对x 求导得x z x z z ∂∂=∂∂+e 1,解得1e 1-=∂∂z x z ;两边再对x 求导得22222e )(e x z x z x z z z ∂∂+∂∂=∂∂,解得 22x z ∂∂32)e 1(e e 1)(e z zz z x z -=-∂∂=. 2.设),(y x z z =是由方程0),(2222=--z x x y F 确定的隐函数,且),(v u F 可微,试计算yz x x z y ∂∂+∂∂.解:2122F x F x F x '+'-=', 12F y F y '=',22F z F z '-=',故y z x x z y ∂∂+∂∂zxyF z F y x F z F F x y ='-'-+'-'+'--=21221222][2. 3.求xy y x z ++=222在闭域1:22≤+y x D 上的最大值与最小值.解:令⎩⎨⎧=+='=+='0204x y z y x z yx ,得惟一驻点)0,0(,且0)0,0(=z .在边界122=+y x ,即⎩⎨⎧==ty tx sin cos (π20≤≤t )上,函数化为t t t t t z z cos sin sin cos 2)(22++== 232sin 212cos 21++=t t (π20≤≤t ). 令02cos 2sin )(=+-='t t t z 得81π=t ,832π=t .2232321212121)8(+=++=πz , 2232321212121)83(-=+-+-=πz .经比较得223max +z ,0min =z .4.将44分成三个正数z y x ,,之和,使得函数22232z y x u ++=达到最小值. 解:此问题为:求22232z y x u ++=在044=-++z y x 下的最小值. 作=),,,(λz y x L )44(32222-+++++z y x z y x λ,(0,0,,≠>λz y x ).令⎪⎪⎩⎪⎪⎨⎧=-++='=+='=+='=+='044 06 04 02z y x L z L y L x L z yx λλλλ,解得惟一驻点)8,12,24(.由于u 存在最小值(无最大值),故当8,12,24===z y x 时u 达到最小.5.在椭球面14222=++z y x 的第一卦限部分上求一点,使得椭球面在该点处的切平面在三个轴上的截距的平方和最小.解:设所求点为),,(z y x P .曲面在P 点的法向量}2,2,2{z y x =n ,切平面Π的方程为0)4(4222=++-++z y x Z z yY xX ,即14=++Z z yY xX .化为1411=++zZ y Y x X ,立即可得Π在三个坐标轴上的截距为z y x 4,1,1.于是问题归结为:求=u 2221611z y x ++(0,0,0>>>z y x )在条件14222=++z y x 下的最小值.作),,,(λz y x L λ+++=2221611zy x )14(222-++z y x (0,0,,≠>λz y x ).令⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-++='=+-='=+-='=+-='014 0232 022022222333z y x L z x z L y y L x x L z y x λλλλ⎪⎪⎩⎪⎪⎨⎧=++==⇒14 22 222z y x x z x y ,得惟一解⎪⎪⎩⎪⎪⎨⎧===22121z y x . 由问题的实际意义知,点)2,21,21(即为所求的点.6.设三角形的周长为p 2,问三角形的三边各为多少时,才能使它绕自己的一边旋转所得的旋转体体积最大?解:设ABC ∆三边长分别为z y x ,,,则p z y x 2=++且绕其边AC 旋转(见图). 若记AC 上的高为h ,则ABC ∆的面积))()((21z p y p x p p yh S ---==,从而22))()((4y z p y p x p p h ---=;故旋转体体积=V 21π3y h =4π()()()3p p x p y p z y ---,其中p z y x 2=++ (0,0,0>>>z y x ).为简化计算,我们求函数y z p y p x p u ln )ln()ln()ln(--+-+-=在条件p z y x 2=++下的驻点.为此作辅助函数=),,,(λz y x L y z p y p x p ln )ln()ln()ln(--+-+-)2(p z y x -+++λ.解方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=-++='=+--='=+---='=+--=' 0201011 01p z y x L zp L y y p L xp L z yx λλλλ得惟一驻点)43,21,43(p p p .由问题的实际意义知,)43,21,43(p p p 是V 在p z y x 2=++下的最大值点,即当p BC AB 43==,p AC 21=,且绕AC 旋转时,所得体积最大,3max π12V p =.7.用重积分表示并计算出由曲面222y x z +-=与22y x z +=所围立体的表面积.解:记1S :222y x z +-=,2S :22y x z +=,21S S S +=.在21,S S xOy 平面上的投影域均为1:22≤+y x D .y x S d d 2d 1=,2d d S x y =.故⎰⎰+++=Dy x y x S d )d 4412(22⎰⎰+=Dy x d d2 2πd d θρ⎰⎰1322π12π(14)1)126ρ=++=+.8.一质点在平面力场j i F y xx y )11(1232+-+=的作用下,沿曲线122+-=y y x 由点)0,1(A 运动到点)1,4(-B ,求力场所作的功.解:⎰⎰+-+=⋅=),( 232),( d )11(d 1d B A L B A L y y x x x y W s F . 因为xQx y y P ∂∂==∂∂32,故积分与路径无关,于是⎰⎰⎰--+-+=+-+=1 0 4 1 3)1,4( )0,1( 232d )1611(d 1d )11(d 1y y x x y y x x x y W 16132173215-=-=.9.计算曲线积分⎰-++L y yxy f y x x y xy f y 222d ]1)([d )(1,其中L 是经过)0,0(O , )32,3(A 和)2,1(B 三点的圆周上从A 点到B 点的一段劣弧,f 为可微函数.解: 因为x Q yxy f xy xy f y y P ∂∂=-'+=∂∂2321)()(,故积分与路径无关,于是选择沿⎪⎩⎪⎨⎧==x y x x C B A 2:),((x 从3变到1)积分得 原式=⎰⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--++1 3 2222d 24]1)2(4[2)2(41x x x f x x x f x4d 13-==⎰x x .10.设S 是曲面1222=++z y x (0≥z )的下侧,求⎰⎰++Sy x z x z y z y x d d d d d d 333. 解:记1:22≤+y x σ,σ+=∑S ,∑所围域记为Ω.原式⎰⎰⎰⎰-=∑上内σ=⎰⎰⎰⎰⎰≤+Ω-++-122222d 0d )(3y x V z y x σπ2π12220 0 03d d sin d r r r θϕϕ=-⋅⎰⎰⎰6π5=-.11.计算y x z z f x z y z f z z y x I yy Sd d )e (d d )e (1d d 333⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡++=⎰⎰,其中S 是由曲面22y x z +=,221y x z --=和224y x z --=所围立体的表面外侧,f 具有连续导函数.解:记S 所围立体为Ω,由Gauss 公式得⎰⎰⎰Ω++=V z y x I d )(3222π 2π42240 0 13d d sin d r r r θϕϕ=⋅⎰⎰⎰93(2π5=. 12.计算⎰⎰∑++=y x z x z yz z y xz I d d d d d d 2,其中∑是球面4222=++z y x 介于平面3=z 和2=z 之间的部分,并取法向量与Oz 轴正向成锐角的那一侧.解:记3:=z S ;S ,∑在xOy 平面的投影域:xy D 122≤+y x ;S +∑所围域记为Ω,则 =I ⎰⎰⎰⎰-+∑下下上S S ⎰⎰⎰⎰⎰+++=ΩxyD V z z z σd )3(d )2(22π 10 04d d d 3πz θρρ=+⎰⎰π3π4π=+=.15.判断级数∑∞=-12!)e (n nn n n λλ(0≥λ)的敛散性. 解:因为⎥⎦⎤⎢⎣⎡-++-=++∞→+∞→!)e ()1()!1()e (lim lim 21121n n n n a a n n n n n n n n λλλλ e)11(limλλ=+=∞→n n n, 故当1e<λ,即e <λ时,级数收敛,当e =λ时级数显然收敛; 当1e>λ,即e >λ时,级数发散.16.求幂级数∑∞=+02!21n n n x n n 的收敛域及和函数. 解:因为01!2)!1(21)1(lim lim 2121=⎥⎦⎤⎢⎣⎡++++=+∞→+∞→n n n n a a n n n n n n ,所以) ,(∞+-∞=D . =)(x S ∑∞=+02!21n n n x n n ∑∑∞=∞=+=020)()(2!2!1n n n n x n n x n=+=∑∞=122!e n n x t n n ∑∞=--+112)!1(e n n x t n n t ∑'∞=-+=12][)!1(e n n x n t t ∑'∞=--+=112][)!1(e n n x n tt t 22222e )421(e )(e ]e [e xtx txx x t t t t ++=++='+=,) ,(∞+-∞∈x . 17.将函数231)(2++=x x x f 展为)1(-x 的幂级数.解:231)(2++=x x x f x x x x +-+=++=2111)2)(1(1 )1(31)1(21-+--+=x x 311131211121-+--+=x x∑∑∞=∞=-----=003)1()1(312)1()1(21n nn n n n n n x x , n n n n n x )1)(3121()1(101---=+∞=+∑,)3 ,1(-∈x . 18.将π()2x x ϕ-=(π20<≤x )展为以2π为周期的Fourier 级数,并求级数∑∞=12cos n n nx 的和函数.解: (1)π()2x x ϕ-=在[0, 2π)上满足Dirichlet 条件,且2π0 01()d πa x x ϕ=⎰ 2π 0π1d 0π2x x -==⎰, 2π 0π1cos d π2n x a nx x -==⎰ 2π 2π0 011πcos d cos d 2π2πnx x x nx x -⎰⎰2π2π0 0sin 110sin d 02π[]x nx nx x n n =--=⎰ ( ,2,1=n ), 2π 0π1sin d π2n x b nx x -==⎰ 2π 2π0 011πsin d sin d 2π2πnx x x nx x -⎰⎰2π2π0 0cos 1110cos d 2π[]x nx nx x n n n-=-+=⎰ ( ,2,1=n ); 故∑∞=1sin ~)(n n nx x ϕπ,(0, 2π)20, 0x x -⎧⎪=⎨⎪=⎩. (2)设=)(x f ∑∞=12cos n n nx ,[0, 2π)x ∈,其中=)0(f 221π16n n∞==∑;因为=')(x f 1sin ππ222n nx x x n ∞=--=-=-∑,(0, 2π)x ∈,所以=)(x f ⎰'+xx x f f 0 d )()0(2222ππ2π36π64212x x x x +-=+-=,[0, 2π)x ∈. 19.设有微分方程)(2x y y ϕ=-',其中⎩⎨⎧><=1,01,2)(x x x ϕ.试求在) ,(∞+-∞内的连续函数)(x y y =,使之在)1 ,(-∞和) ,1(∞+内都满足所给方程,且满足条件0)0(=y .解: (1)当1<x 时,方程为22=-'y y ,通解为1e 21-=x C y ,由0)0(=y 得11=C ,所以1e 2-=x y . (2)当1>x 时,方程为02=-'y y ,通解为x C y 22e =.要使)(x y y =在1=x 处连续,必须)1e (lim e lim 21221-=-+→→x x x x C ,即1e e 222-=C ,于是得22e 1--=C ,所以x y 22e )e 1(--=.(3)补充定义=)1(y 1e 2-,则得在) ,(∞+-∞内的连续函数)(x y y =⎩⎨⎧>-≤--1x ,e )e (11,1e 222xx x 满足所给方程及初始条件.20.一质量为m 的汽艇以速度0v 行驶,在0=t 时刻关闭动力继续行驶.假定水对汽艇的阻力与行驶速度v 的n 次方成正比(n 为常数),求v 与关闭动力后行驶距离之间的函数关系.解:设经过t 时间后,行驶的距离为)(t x (0>t ),阻力n kv R -=(0>k ),由Newton 第二定律得 0)]([)(='+''n t x mk t x ,由题设有0)0(,0)0(v x x ='=.因为v t x =')(,所以xv v t x d d )(='',于是方程化为0d d 1=+-n v mk x v ,分离变量得x mk v v n d d 1-=-.(1)当2≠n 时,通解为C x mk n v n+=--22,由0)0()0(v x v ='=得n vC n -=-220,所以x n mk v v nn )2(202--=--,即)()2(220n n v v k n m x ----=; (2)当2=n 时,通解为x mk C v -=e,由0)0()0(v x v ='=得0v C =,故x mk v v -=e0,即vvkm x 0ln =.21.设)(x f 具有二阶连续导数,且积分y x f x y x f x f L x d )(d ])()(2[e '+-'-⎰λ (λ为常数)与路径无关,试求)(x f .解:因为积分与路径无关,故有xQyP ∂∂=∂∂,即)()()(2e x f x f x f x ''=-'-λ,整理得x x f x f x f λe )()(2)(=+'+''.0122=++r r ⇒121-==r r ,所以)(e 21x C C Y x +=-.当1-≠λ时,设x A y λe =*,代入原方程定出2)1(1λ+=A ,即2)1(e λλ+=*xy ,此时通解为=y )(e 21x C C x+-2)1(e λλ++x; 当1-=λ时,设xAx y λe 2=*,代入原方程定出21=A ,即2e 2xx y -*=,此时通解为=y )2(e 221x x C C x ++-.22.设高为)(t h 厘米(t 为时间,单位为小时)的雪堆,在融化过程中其侧面方程为)()(2)(22t h y x t h z +-=,其体积减少的速率与侧面积成正比(比例系数为0.9),问高度为130厘米的雪堆全部融化需要多少小时? 解: 设雪堆的体积为V ,侧面积为S ,则 222 ()()23 0 01[()()]2ππd d d [()()]d ()24h t h t x y h t h t z V z x y h t h t z z h t +≤-==-=⎰⎰⎰⎰, ⎰⎰≤+'+'+=)(2122222d d 1t h y x yx y x z z S ⎰⎰≤+++=)(21222222d d )()(161t h y x y x t h y x2πd ()h t ρ=⎰213π()12h t =. 由题设知S tV 9.0d d -=,即23π()d ()4d h t h t t 213π()91012h t =-,于是 1013d (t)d -=t h , 故C t t h +-=1013)(,由130)0(=h 得130=C ,即 1301013)(+-=t t h .令0)(=t h 得100=t (小时),即高度为130厘米的雪堆全部融化需要100小时.23.求微分方程24d (2)d xy x x y y =- 的通解.解:方程可化为:31d 2d x x y x y y --=-,这是Bernoulli 方程.令1(1)2,z x x --==则方程化为线性方程 3d 42,d z z y y y-=- 44d d 34e2e d (2ln ),y yyy z C y y y C y ---⎡⎤⎰⎰=+-=-⎢⎥⎣⎦⎰ 故通解为24(2ln ).x y C y =-24.求幂级数30(3)!n n x n ∞=∑的和函数. 解:易知收敛半径为+∞,设30(),(, ),(3)!nn x s x x n ∞==∈-∞+∞∑显然(0) 1.s =313211(),(0)0;(),(0)0;(31)!(32)!n n n n x x s x s s x s n n ∞∞--==''''''====--∑∑ 33310()();(33)!(3)!n n n n x x s x s x n n ∞∞-=='''===-∑∑ 故得 ()()0,(0)1,(0)0,(0)0.s x s x s s s '''-=⎧⎨'''===⎩ 或 ()()()e ,(0)1,(0)0. x s x s x s x s s '''⎧++=⎨'==⎩(1)()()0,(0)1,(0)0,(0)0s x s x s s s '''-=⎧⎨'''===⎩的求解过程如下:3212,3123110,1,()e e .2x x r r r s x C C x C x -⎛⎫-===-∴=++ ⎪⎝⎭又21232311()e e ,22x x s x C C x C x -⎡⎤⎛⎫⎛⎫'=+-+-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦21232311()e esin ,22x x s x C C C x -⎡⎤⎛⎫⎫''=+--+-⎢⎥ ⎪⎪⎝⎭⎝⎭⎣⎦于是由初始条件得121231231, 10,210,2C C C C C C ⎧+=⎪⎪⎪-+=⎨⎪⎪--=⎪⎩解得1231, 32,30.C C C ⎧=⎪⎪=⎨⎪=⎪⎩所以和函数212()e e c ,(,).33x x s x x x -=+∈-∞+∞(2)()()()e ,(0)1,(0)0 x s x s x s x s s '''⎧++=⎨'==⎩的求解过程如下:221,212110,()e sin .2x r r r S x C x C x -⎛⎫++==-±∴=+ ⎪⎝⎭因为i 1λω+=不是特征根,故设e x s A =,代入原方程,得1,3A =即1e ,3x s =于是2121()()()e e .3x x s x S x s x C x C x -⎛⎫=+=++ ⎪⎝⎭由(0)1s =得123C =,即2212()e +e .33x x s x C x -⎛⎫=+ ⎪⎝⎭222111()e +e 332x x s x C x -⎡⎤⎫⎫'=-+⎢⎥⎪⎪⎝⎭⎝⎭⎣⎦,由(0)0s '=得20C =,所以和函数212()e e c ,(,).os 33x x s x x x -=+∈-∞+∞四.证明题2.若0lim =∞→n n na ,且∑∞=+-+11])1[(n n n na a n 收敛,试证∑∞=1n n a 收敛. 证:记=n s 1n k k a =∑,=n σ∑=+-+nk k k ka a k 11])1[(, ,2,1=n ,则}{n σ收敛.=n σ )2(21a a -)23(32a a -+)34(43a a -+ +])1[(1+-++n n na a n 13212222+-++++=n n na a a a a 12+-=n n na s ,12121++=∴n n n na s σ.因为}{n σ收敛,所以要证}{n s 收敛,只需证}{1+n na 收敛.事实上,由0lim =∞→n n na 知0)1(lim 1=++∞→n n a n ,于是 =+∞→1lim n n na 0])1(1[lim 1=+++∞→n n a n n n . 因此}{n s 收敛,即∑∞=1n n a 收敛.(且∑∞=1n n a 21=∑∞=+-+11])1[(n n nna an .)3.若幂级数∑∞=0n nn x a 的收敛半径10=R ,则幂级数∑∞=0!n nn x n a 的收敛半径+∞=R . 证:因为10=R ,故对于)1 ,0(0∈x ,级数∑∞=00n n n x a 绝对收敛,从而}{0nn x a 有界,设M x a n n ≤0.于是),(∞+-∞∈∀x ,有nn n n nn n n x x n M x x n x a x n a 000!!!≤≤.而由比值法知,) ,(∞+-∞∈∀x ,∑∞=00!n nn x x n M 收敛,从而∑∞=0!n n n x n a 绝对收敛,故其收敛半径+∞=R .4.设)1(21,211nn n a a a a +==+(N ∈n ),试证:(1) nn a ∞→lim 存在; (2) ∑∞=+-11)(1n n naa收敛.证: (1))1(21,211n n n a a a a +==+1212≥+=nn a a (N ∈n ),即}{n a 有下界;又02121<-=-+nnn n a a a a ,即}{n a 单调递减,故n n a ∞→lim 存在. (2)因为}{n a 单调递减,所以11-+n n a a 0>,即∑∞=+-11)(1n n n a a是正项级数,又因为1≥n a ,所以11-+n n a a =111+++-≤-n n n n n a a a a a (N ∈∀n );而n n a ∞→lim 存在,故∑∞=+-11)(n n n a a 收敛,于是由比较判别法知,∑∞=+-11)(1n n n a a收敛.5.证明: (1)∑∞=+-1)(1ln 1n n n n收敛; (2)1ln 131211lim =++++∞→n n n . 证: (1)因为=+-≤n n n 1ln 10)11ln(1n n +-2211112o n n n n ⎡⎤⎛⎫=--+ ⎪⎢⎥⎝⎭⎣⎦2211,2o n n ⎛⎫=+ ⎪⎝⎭ 而∑∞=121n n收敛,所以∑∞=+-1)(1ln 1n n n n 收敛.(2) ∑∞=+-1)(1ln 1n n n n ∑=∞→++-=nk n k k k1)(ln )1ln(1lim ]ln )1ln(1312ln 3ln 212ln 1[lim n n n n ++-+-++-+-=∞→ )]1ln(131211[lim +-++++=∞→n nn , 因为∑∞=+-1)(1ln 1n n n n收敛,即)]1ln(131211[lim +-++++∞→n n n 存在,故 0ln )1ln(131211lim =+-++++∞→nn n n , 即0ln )1ln(ln 131211lim =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-++++∞→n n n n n ; 易知1ln )1ln(lim =+∞→n n n , 所以 =++++∞→nn n ln 131211lim 1ln )1ln(lim =+∞→n n n . 7. 12111,(2,3,4,).:n n n a a a a a n +-===+=设证明111,,2n n n x a x ∞-=<∑对于收敛().s x 并求其和函数解:111,2n n n x a x ∞-=<∑(1)先证:对于收敛.{}0,,n n a a >由题设知单调增从而112n n n n a a a a +-=+≤,即 2322123222222 (2,3,4,).n n n n n n a a a a a n -----≤≤≤≤≤== 易知2122n n n x∞--=∑的收敛半径为11,,22x ∀<于是2122n n n x ∞--=∑绝对收敛,即1222n n n x∞--=∑收敛;又11122,n n n n n n a xa xx----=≤故2122n n n x ∞--=∑绝对收敛,从而111,2n n n x a x ∞-=<∑对于收敛.(2)再求和函数111() ().2n n n s x a x x ∞-==<∑11111122()11[]n n n n n n n n n n s x a xa xa a x ∞∞∞---+-=====+=+-∑∑∑112112231111n n k m n n k m n n k m a x a xa xa x ∞∞∞∞---+-=====+-=+=+-∑∑∑∑11311111[()1]()k m k m k m a x x a x s x x xs x x x ∞∞--===+-=+---∑∑211(),0.x s x x xx-=-≠解之得21(),(0),1s x x x x=≠--又1(0)1,s a ==所以1,2x ∀<有1211() .1n n n s x a x x x∞-===--∑ 9.设正数列{}n a 单调递减,若级数1(1)nn n a ∞=-∑发散,则111nn n a ∞=⎛⎫ ⎪+⎝⎭∑收敛.证:因为0,n a >且{}n a ,故有极限,设lim ,n n a a →∞=则0.a ≥又因为1(1)n n n a ∞=-∑发散,故由Leibniz 判别法知0a ≠,即lim 0.n n a a →∞=>11lim lim 1,111n n n n a a →∞→∞⎛==<∴ +++⎝111nn n a ∞=⎛⎫ ⎪+⎝⎭∑收敛. 10. 设0,n u ≠且lim 1,n n n u →∞=试证11111(1)n n n n u u ∞-+=⎛⎫-+ ⎪⎝⎭∑条件收敛.证:记1111(1),n n n n a u u -+⎛⎫=-+ ⎪⎝⎭由lim 1,n nn u →∞=知 111lim lim lim 2,11n n n n n n n n a n n n n n u u u u n n →∞→∞→∞++⎛⎫⎛⎫+=+=+= ⎪ ⎪+⎝⎭⎝⎭而11n n ∞=∑发散,故1n n a ∞=∑发散,即原级数不会绝对收敛. 因为11111(1)nk n kk k s u u -+=⎛⎫=-+ ⎪⎝⎭∑ 1122334111111111(1)n nn u u u u u u u u -+⎛⎫⎛⎫⎛⎫⎛⎫=+-+++-+-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ 11111(1),n n u u -+=+-且由1lim lim 1,1n n n n un u n→∞→∞==知1lim 0n nu →∞=,从而111lim(1)0,n n n u -→∞+-=故11lim ,n n s u →∞=即原级数收敛. 因此原级数条件收敛.。
山东科技大学2010-2011学年第2学期期末考试安排

山东科技大学2010-2011学年第2学期期末考试安排数考课程名称监考课程名称监考课程名称监考课程名称监考课程名称监考物流管理08-1 3314-103 李海燕运筹学李堂军企业物流管理辛宝贵供应链管理王炳成仓储管理丁黎黎物流管理08-2 35 王珊运筹学企业物流管理供应链管理仓储管理会计08-1 52 14-105 王静审计学王爱华会计08-2 51 14-107 张玉倩审计学常妍焱会计08-3 51 14-109 向丽丽审计学刘英姿金融08-1 33 14-111 贾慧子管理信息系统周长红税收学陈昕期货与期权周延平金融市场学孟科学金融08-2 3114-113 李冉冉管理信息系统康宏税收学王彩霞期货与期权闻德美金融市场学闻德美金融08-3 30 陈丽英管理信息系统税收学闻德美期货与期权聂国栋金融市场学汪慧芳国贸08-1 3914-121 马风涛国际经济学陈爱萍国际经济合作刘本玲国际货物运输与保险焦习燕国贸08-2 38 孟文强国际经济学陶敏国际经济合作国际货物运输与保险国贸08-3 40 14-203 孙江勇国际经济学于晓燕国际经济合作焦习燕国际货物运输与保险刘本玲工商管理08-1 4114-123 李倩倩市场调查与预测宋平组织理论与设计陈玉和管理信息系统王松经济法王彩霞工商管理08-2 41 任娜市场调查与预测许焕君组织理论与设计许焕君管理信息系统经济法吕君财政08 42 14-205 赵井会纳税检查吕君税务代理理论与实务陈昕国际投资学孙玉红电子商务08-1 3914-221 陈梦国际贸易原理与实务陈爱萍网络安全与认证技术康红Java程序设计语言崔振宇电子商务08-2 37 李瑾国际贸易原理与实务网络安全与认证技术英语08-1 313-404 崔雪红美国文学宋建福英语词汇学翟红华高级英语(2)宋燕翻译(2)翟清永第二外语(3)徐慧英语08-2 27 美国文学英语词汇学高级英语(2) 翻译(2) 第二外语(3)英语08-3 283-504 申佃美美国文学高艳丽英语词汇学彭建武高级英语(2)翟红华翻译(2)向颖博第二外语(3)董莲莲英语08-4 30 美国文学英语词汇学高级英语(2) 翻译(2) 第二外语(3)日语08-1 30 3-215 李颖国际经济法外教2 日语写作外教高级日语外教翻译(2) 孙逢明第二外语(3) 李恒日语08-2 29 3-416 吕晓潇国际经济法隋玉芳日语写作外教高级日语外教3 翻译(2) 李恒第二外语(3) 马力日语08-3 30 3-415 王丽丽国际经济法张学义日语写作外教高级日语外教6 翻译(2) 仇全菊第二外语(3) 李守波环科08 36 1-214 李琳生态学王金凤环境微生物学陆洪省环境监测王金凤环境化学胡术刚环境工程学陈平化工08-1 42 1-208 郭琳化工分离工程高军煤化学乔英云化工设备基础李敏化工08-2 46 1-212 孙玉凤化工分离工程张治山煤化学韩姝娜化工设备基础张治山矿加08-1 40 1-218 孙玉凤选矿学崔广文矿石可选性研究王力矿加08-2 39 1-220 郭琳选矿学邱俊矿石可选性研究邱俊生物08-1 281-124 李慧娟微生物制药韩秋霞发酵工程纪蓓生物工程设备纪蓓生化分离工程纪蓓生物08-2 27 张忠伟微生物制药发酵工程生物工程设备生化分离工程应化08-1 421-228 邱俊高分子物理崔立强应化08-2 42 范海宝高分子物理说明:1、各学院务必将此安排表通知到相关学生班级,未排入该表的课程,由学生班级所在学院负责落实,务必于7月15日前考试(考查)完毕,特殊问题请同教务处教务科联系。
│山东科技大学参考书目│

│⼭东科技⼤学参考书⽬│┌────────────────────────────────────────┐│⼭东科技⼤学参考书⽬│├────────────────────────────────────────┤│030108环境与资源保护法学: 314经济法学:《经济法》潘静成等,中国⼈民⼤学出版││社,1999;444法学综合(含法理和民法):①《法理学》张⽂显,⾼等教育、北京⼤学出││版社,1999②《民法》魏振赢等,⾼等教育、北京⼤学出版社,2000。
环境法学:│学》&zuozhe=&xuanzhe=2 target=_blank>《环境法││学》⾦瑞林,北京⼤学出版社,1999;民事诉讼法:《民事诉讼法》江伟,⾼等教育、北京││⼤学出版社,2000;⾏政法学:《⾏政法与⾏政诉讼法》姜明安,⾼等教育出版社,2000。
││050211外国语⾔学及应⽤语⾔学: 315基础英语(含阅读与写作):①│》&zuozhe=&xuanzhe=2 target=_blank>《英语写作⼿册││》丁往道,外语教学与研究出版社,1994②《⾼级英语(1-2)》张汉熙,外语教学与研究││出版社,1995③《实⽤翻译教程》冯庆华,上海外语教育出版社,2002④《⽂体与翻译》刘││宓庆,中国对外翻译出版公司,2001⑤《英汉对⽐研究》连淑能,⾼等教育出版社,2001;4││45英语综合:①《英国⽂学史及选读(上下册)》吴伟仁,外语教学与研究出版社,2003②││《美国⽂学史及选读(上下册)》吴伟仁,外语教学与研究出版社,2003③《语⾔学教程》││(修)胡壮麟,北京⼤学出版社,2002。
││070101基础数学: 310数学分析:《数学分析》(三版)华东师⼤编,⾼等教育出版社││,2001;401⾼等代数:《⾼等代数》(⼆版)北⼤数学系编,⾼等教育出版社,1988。
高等数学难题解答3(山东科技大学泰山科技学院)

解 若将函数进行奇延拓 则傅里叶系数为 an0(n0 1 2 )
h 2(1cosnh) 2 2 bn f (x)sin nxdx sin nxdx 0 0 n
因此 函数展开成正弦级数为
2 f (x) 1 cosnh sin nx n1 n
n 1 1 )k 2 lim 1 s 0 lim 1 ( 1 k n n n n n k 3 k 1
(2)
1 1 1 1 lim[2 3 4 9 8 27 (2n ) 3n ] n
解
1 1 1 1 23 49 827 (2n) 3n
5 求下列数项级数的和 (1) 解
n2 n 1 n!
n2 n(n 1) n n(n 1) n n ! n ! n ! n1 n1 n1 n1 n!
x
1 xn e 因为 n! n1
两边求导得 e n!xn1 ,再求导得
e e
根据比值审敛法
1 x2 1 当2
即 2 x 2 时
幂级数收敛 当
1 2 x 1 时 2
幂级数发散
又当 x 2 时 幂级数成为 n 是发散的
n 1
所以收敛域为
( 2, 2)
4 求下列幂级数的和函数 (1)
2n 1 x2(n1) n n 1 2
1 (1 1 )n2 n n n 1 3
的前n项部分和
因为
lim n n
级数 因此
1 (1 1 )n2 lim 1 (1 1 )n e 1 所以由根值审敛法 n 3 n n 3 3n 1 (1 1 )n2 收敛 从而部分和数列 { s } 收敛 n n n 3 n 1
高等数学难题解答1(山东科技大学泰山科技学院)

所以ABC的面积为
1 1 S | AC BC | 4 z 2 ( z 1) 2 4 2 2
令
dS 1 8z 2(z 1) 0 dz 4 4z 2 (z 1)2 4
1 z 得 5
所求点为 C(0, 0, 1 )
5
8 画出下列各曲面所围立体的图形
第五章疑难解答
1 已知点A(1, 0, 0)及点B(0, 2, 1) 试在z轴上求一点 C 使ABC的面积最小 解 设所求的点为C(0 0 z) 则 AC (1, 0, z) BC (0, 2, z 1) 因为
i j k 令 AC BC 1 0 z 2zi (z 1) j 2k ,所以ABC的面积为 0 2 z 1
x y z 1 4 2 2
(2)抛物柱面x21z 平面y0 z0及xy1
(3)圆锥面 z x2 y2 及旋转抛物面z2x2y2
7 已知点A(1, 0, 0)及点B(0, 2, 1) 试在z轴上求一点C 使ABC的面积最小
解 设所求的点为C(0 0 z) 则 AC (1, 0, z) BC (0, 2, z 1)
因为
i j k AC BC 1 0 z 2zi (z 1) j 2k 0 2 z 1
s(0 1 1)(1 0 0)(0 1 1)
y z 1 0 设点(1, 1, 1)到直线 的垂线交于点 ( x y z ) x 0 0 0 0 y z 1 0 因为点(x0 y0 z0)在直线 x 0 上
所以(x0 y0 z0)(0 y0 y01) 于是 垂线的方向向量为 s1(1 y01 y0) 显然有ss 10 即
山东科技大学20152016学年第一学期期末考试安排表
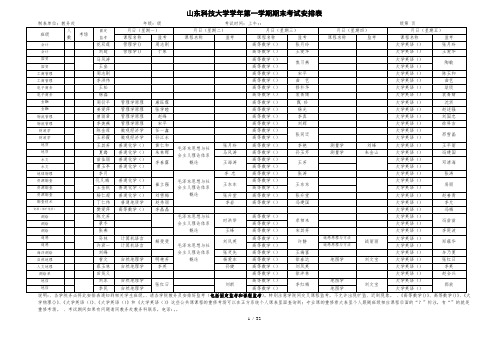
数监考课程名称监考课程名称监考课程名称监考课程名称监考课程名称监考会计花双莲管理学() 周志刚高等数学()张月玲大学英语()张月玲会计刘超管理学() 于泉高等数学()王爱华大学英语()王爱华国贸马风涛高等数学()焦习燕大学英语()陶敏国贸王垒高等数学()大学英语()工商管理周志刚高等数学()宋平大学英语()陈玉和工商管理李洪伟高等数学()曲艺大学英语()曲艺电子商务王松高等数学()修朴华大学英语()耿琰电子商务杨磊高等数学()袁菁婧大学英语()袁菁婧金融周衍平管理学原理康旺霖高等数学()甄珍大学英语()沈圳金融姜爱萍管理学原理张学睦高等数学()杨光大学英语()赵述强物流管理曾丽君管理学原理赵峰高等数学()李真大学英语()刘国忠物流管理李美燕管理学原理宋平高等数学()刘辉大学英语()徐科吉财政学陈金库微观经济学任一鑫高等数学()张同迁大学英语()邢雪晶财政学王彩霞微观经济学孙江永高等数学()大学英语()地质王其芳普通化学()黄仁和毛泽东思想与社会主义理论体系概论张月玲高等数学()李艳测量学刘峰大学英语()王平丽地质夏璐普通化学()朱林晖马风涛高等数学()孙玉芹测量学朱金山大学英语()冯建国水文苗佳丽普通化学()李春露王海涛高等数学()王芳大学英语()邓清海水文曹玉亭普通化学()高等数学()大学英语()地球物理李月毛泽东思想与社会主义理论体系概论李忠高等数学()张涛大学英语()张涛资源勘查孔凡梅普通化学()崔立强王东东高等数学()王东东大学英语()房丽资源勘查王金凯普通化学()高等数学()大学英语()资源勘查杨仁超普通化学()刘雪梅张升堂高等数学()张升堂大学英语()赵善青勘查技术丁仁伟普通地质学赵秀丽李岩高等数学()冯建国大学英语()李允资源(煤矿地质)樊爱萍高等数学()李晶晶大学英语()冯梅测绘陈允芳毛泽东思想与社会主义理论体系概论时洪举高等数学()卓相来大学英语()冯苗苗测绘景冬高等数学()大学英语()测绘张燕王峰高等数学()宋其芳大学英语()李延波遥感孙林计算机语言解斐斐毛泽东思想与社会主义理论体系概论刘凤英高等数学()许静遥感原理与方法战丽丽大学英语()郑蕴华遥感许君一计算机语言高等数学()遥感原理与方法大学英语()海洋测绘刘峰张灵先高等数学()王瑞富大学英语()牟乃夏自然地理曾文自然地理学明艳芳杨爱东高等数学()徐春达地图学刘文宝大学英语()张红日人文地理蔡玉林自然地理学李英孙健高等数学()刘凤英大学英语()李英测绘单田茂义高等数学()徐泮林大学英语()赵会兴地信刘冰自然地理学张红日刘新高等数学()李红梅地图学刘文宝大学英语()郭放地信季民自然地理学高等数学()地图学大学英语()说明:、各学院务必将此安排表通知到相关学生班级。
高等数学 - 山东科技大学泰安校区(泰山科技学院)就业信息网

r 2x x 因为 x 2 x2 y 2 z 2 r
u f (r) r x f (r) x x r
所以
2
r x r u x f (r) x f (r) r r 2 x2 f (r) x2 f (r) r x x2 r2 r3 r2
其在纵轴上的截距为yxy 因此由已知有
1 y 1 y yxyx 即 x
这是一个一阶线性方程 其通解为
ye
x dx
1
[ (1)e
x dx
1
dx C] x( ln x C)
即方程的通解为yx(Cln x) 由于曲线过点(1 1) 所以C1 因此所求曲线的方程为yx(1ln x) 6 已知某车间的容积为30306m3 其中的空气含012%的 CO2(以容积计算) 现以含CO2004%的新鲜空气输入 问每 分钟应输入多少 才能在30min后使车间空气中CO2的含量 不超过006%?(假定输入的新鲜空气与原有空气很快混合均 匀后 以相同的流量排出) 解 设每分钟应输入的空气为a m3 t时刻车间中CO2的浓 度为x(t) 则车间中CO2的含量(以体积计算)在t时刻经过dt min的改变量为
即
(x)tan x(x)sec x
(x) e tan xdx( sec xe tan xdxdx C)
这是一个一阶线性方程 其通解为 cos x(tan xC)sin xCcos x 在已知等式中 令x0得(0)1 代入通解得C1 故
(x)sin xcos x
齐次方程y2yy0的通解为y(C1C2x)ex 因为f(x)cos x ii不是特征方程的根 所以非 齐次方程的特解应设为 y*Acos xBsin x 代入原方程得 2Asin x2Bcos xcos x 比较系数得A0 B
新版山东科技大学数学考研经验考研真题考研参考书

在决定考研的那一刻,我已预料到这一年将是怎样的一年,我做好了全身心地准备和精力来应对这一年枯燥、乏味、重复、单调的机械式生活。
可是虽然如此,我实在是一个有血有肉的人呐,面对诱惑和惰性,甚至几次妥协,妥协之后又陷入对自己深深的自责愧疚当中。
这种情绪反反复复,曾几度崩溃。
所以在此想要跟各位讲,心态方面要调整好,不要像我一样使自己陷入极端的情绪当中,这样无论是对自己正常生活还是考研复习都是非常不利的。
所以我想把这一年的经历写下来,用以告慰我在去年饱受折磨的心脏和躯体。
告诉它们今年我终于拿到了心仪学校的录取通知书,你们的付出和忍耐也终于可以扬眉了。
知道自己成功上岸的那一刻心情是极度开心的,所有心酸泪水,一扫而空,只剩下满心欢喜和对未来的向往。
首先非常想对大家讲的是,大家选择考研的这个决定实在是太正确了。
非常鼓励大家做这个决定,手握通知书,对未来充满着信念的现在的我尤其这样认为。
当然不是说除了考研就没有了别的出路。
只不过个人感觉考研这条路走的比较方便,流程也比较清晰。
没有太大的不稳定性,顶多是考上,考不上的问题。
而考得上考不上这个主观能动性太强了,就是说,自己决定自己的前途。
所以下面便是我这一年来积攒的所有干货,希望可以对大家有一点点小小的帮助。
由于想讲的实在比较多,所以篇幅较长,希望大家可以耐心看完。
文章结尾会附上我自己的学习资料,大家可以自取。
山东科技大学数学的初试科目为:(101)思想政治理论(201)英语一(710)数学分析和(835)高等代数参考书目为:1.《数学分析》(上、下册),华东师范大学数学系,高等教育出版社,2010年(第四版)2.《高等代数》,北京大学数学系,高等教育出版社,2003年(第三版)先说英语,最重要的就是两个环节:单词和真题。
关于单词单词一定要会,不用着急做题,先将单词掌握牢,背单词的方式有很多,我除了用乱序单词,我还偏好使用手机软件,背单词软件有很多,你们挑你们用的最喜欢的就好,我这里就不做分享了。
浅析高等数学课程的“两性一度”——以零点定理为例

山东科技大学2014-2015学年第二学期期末考试安排表

制表单位:教务处年级:2014级考试时间:上午8:00—10:00 2014级第1 页班级人数考场固定监考6月29日(星期一)6月30日(星期二)7月1日(星期三)7月2日(星期四)7月3日(星期五)课程名称监考课程名称监考课程名称监考课程名称监考课程名称监考会计2014-1 3414-121 刘超西方经济学赵友宝高等数学A(2)陈昌柏(外语)中国近现代史纲要周森林大学英语(3-2)宋建福会计2014-2 33 郝敏西方经济学高等数学A(2)中国近现代史纲要大学英语(3-2)国际贸易2014-1 40 14-103 刘本玲高等数学A(2)王君(外语) 中国近现代史纲要刘红英(经管) 大学英语(3-2)东野圣时国际贸易2014-2 36 14-105 焦习燕高等数学A(2)王薇(外语) 中国近现代史纲要王耀东大学英语(3-2)别俊玲金融2014-1 37 14-107 王和平会计学付莉高等数学A(2)王华(外语) 中国近现代史纲要李岩微观经济学+6 任一鑫大学英语(3-2)刘德美金融2014-2 37 14-109 张建刚会计学郭令秀高等数学A(2)曹慧玲(外语) 中国近现代史纲要刘丽威微观经济学张伟大学英语(3-2)陈莹莹财政学2014-1 3014-123 陈金库宏观经济学吴士健高等数学A(2)吕晓潇(外语)中国近现代史纲要杨爱东大学英语(3-2)邵晓燕财政学2014-2 30 陈昕宏观经济学高等数学A(2)中国近现代史纲要大学英语(3-2)工商管理2014-1 43 14-111 高等数学A(2)李庆建(外语)、马恒平中国近现代史纲要吴华眉、马恒平大学英语(3-2)吴桂金、张学睦工商管理2014-2 42 14-113 高等数学A(2)赵峰(经管)、张学睦中国近现代史纲要陶常利 (数学)、吴士健大学英语(3-2)张琳、吴士健物流管理2014-1 45 14-203 张杰高等数学A(2)张福平(经管) 中国近现代史纲要张伟伟 (数学) 运营管理李美燕大学英语(3-2)逄仁山物流管理2014-2 43 14-205 饶卫振高等数学A(2)王松(经管) 中国近现代史纲要李艳艳 (数学) 运营管理王炳成大学英语(3-2)王炳成(经管)电子商务2014-1 42 14-207 侯艳辉高等数学A(2)任艳伟(经管) 中国近现代史纲要邵勇大学英语(3-2)王松(经管)电子商务2014-2 40 14-209 周长红高等数学A(2)董兴林(经管) 中国近现代史纲要王琪大学英语(3-2)李堂军(经管)水文2014-1 40 14-211 谢道雷测量学张燕高等数学A(2)李守春(地质) 大学物理B(2-1)周长红(经管)大学英语(3-2)魏海燕水文2014-2 40 14-213 张伟杰测量学崔先国高等数学A(2)余继峰(地质) 大学物理B(2-1)刘立华(经管)大学英语(3-2)王丽丽资源勘查2014-1 3914-219 王金凯高等数学A(2)常象春(地质)大学物理B(2-1)栾伟娜大学英语(3-2)向颖博资源勘查2014-2 40 王东东高等数学A(2)大学物理B(2-1)大学英语(3-2)资源勘查2014-3 38 14-303 张春荣高等数学A(2)李红梅大学物理B(2-1)王祖和(经管)大学英语(3-2)李颖地质2014-1 3914-221 杨仁超矿物学毛光周高等数学A(2)孟新柱大学物理B(2-1)宋红岩大学英语(3-2)庞燕宁地质2014-2 40 孔凡梅矿物学高等数学A(2)大学物理B(2-1)大学英语(3-2)地球物理2014 34 14-305 王其芳测量学田茂义高等数学A(2)朱鲁(地质) 大学物理A(2-1)杨锋杰(地质)大学英语(3-2)高宗军(地质) 勘查技术2014 40 14-307 李秀芹测量学成枢高等数学A(2)翟培合(地质) 大学物理A(2-1)高宗军(地质)大学英语(3-2)余继峰(地质) 资源(煤矿地质)2014 39 14-309 周振柱高等数学B(2)赵文才大学物理(1)李守春(地质)大学英语(3-2)常象春(地质)测绘2014-1 4014-319 独知行AutoCAD+10徐泮林高等数学A(2)李刚(数)大学物理B(2-1)刘晓蕾大学英语(3-2)李守波测绘2014-2 39 郭金运AutoCAD高等数学A(2)大学物理B(2-1)大学英语(3-2)测绘2014-3 39 14-311 王健AutoCAD+4姜岩高等数学A(2)崔先国(测绘) 大学物理B(2-1)王道岩大学英语(3-2)丁艳霞遥感2014-1 3914-223 江涛C++刘伟科高等数学A(2)李桂玲数字测图原理与方法陈允芳大学物理B(2-1)张晓大学英语(3-2)隋玉芳遥感2014-2 40 朱红春C++ 高等数学A(2)数字测图原理与方法大学物理B(2-1)大学英语(3-2)地信2014-1 4114-321 张蕾C++ +8刘新高等数学A(2)付政庆数据结构与算法+5韩李涛大学物理B(2-1)白培瑞大学英语(3-2)董莲莲地信2014-2 41 刘文宝C++ 高等数学A(2)数据结构与算法大学物理B(2-1)大学英语(3-2)说明:1、各学院务必将此安排表通知到相关学生班级。
2021年山东科技大学专升本科专业

山东科技大学本科专业1、自动化培养目的:本专业培养具备电工技术、电子技术、控制理论、计算机技术与网络技术等领域基本知识和一定专业知识,能在生产过程设计、信息解决等领域从事系统设计、分析及研究等方面工作应用型工程技术人才。
重要课程:电路理论、电子技术、电力拖动、自动控制理论、自动检测技术、信号与系统分析、过程控制系统、软件工程等。
2、计算机科学与技术培养目的:本专业培养具备较夯实计算机科学与技术基本知识和基本技能与办法,可在科研、工程技术、教诲、企事业管理等部门从事计算机应用、信息解决等工作应用型技术人才。
重要课程:高等数学、电路原理、模仿电子技术、计算机网络技术、离散数学、汇编语言、数据构造、操作系统、数据库系统等。
3、采矿工程培养目的:本专业培养具备固体(煤、金属及非金属)矿床开采基本理论和办法,具备采矿工程师基本能力,能在采矿领域从事矿区开发规划、矿山安全技术及工程设计等工作应用型工程技术人才。
重要课程:高等数学、工程力学、电工电子技术、岩体力学、采矿学、矿山压力及控制、矿井通风与安全、矿山机械、矿山供电、技术经济分析等。
4、土木工程培养目的:本专业培养具备从事土木工程项目规划、设计、研究开发、施工和管理能力,能在建筑部门和市政工程等部门从事设计、施工、技术开发和管理工作应用型技术人才。
重要课程:高等数学、材料力学、构造力学、土力学、建筑材料、混凝土构造、钢构造、房屋构造、建筑施工、工程概预算等。
5、测绘工程培养目的:本专业培养具备地面测量、矿山测量、空间测量和照相测量与遥感及地图编制等方面知识,能在国民经济各部门从事基本测绘建设,都市与工程建设等工作应用型工程技术人才。
重要课程:高等数学、英语、工程制图、VF程序设计、数字化测图原理和办法、大地测量学基本、工程测量学、矿山测量学、照相测量、误差理论与测量数据解决基本、GPS原理及应用等。
6、安全工程培养目的:本专业培养适应社会主义当代化经济建设需要、德、智、体全面发展,具备良好素质与基本,能从事安全技术及工程、安全科学与研究、安全监察与管理、安全健康环境检测与监测、安全设计与生产、安全教诲与培训等方面应用型高档工程技术专门人才。
山东科技大学20152016学年第一学期期末考试安排表.doc

感谢你的观看山东科技大学2015-2016学年第一学期期末考试安排表制表单位:教务处年级:2015级考试时间:上午8:00--10:00 2015级第1 页班级人数考场固定监考1月11日(星期一)1月12日(星期二)1月13日(星期三)1月14日(星期四)1月15日(星期五)课程名称监考课程名称监考课程名称监考课程名称监考课程名称监考会计2015-1 49 14-103 花双莲管理学(A) 周志刚高等数学A(2-1)张月玲大学英语(3-1)张月玲会计2015-2 49 14-105 刘超管理学(A) 于泉高等数学A(2-1)王爱华大学英语(3-1)王爱华国贸2015-1 3914-121 马风涛高等数学A(2-1)焦习燕大学英语(3-1)陶敏国贸2015-2 38 王垒高等数学A(2-1)大学英语(3-1)工商管理2015-1 41 14-107 周志刚高等数学A(2-1)宋平大学英语(3-1)陈玉和工商管理2015-2 41 14-109 李洪伟高等数学A(2-1)曲艺大学英语(3-1)曲艺电子商务2015-1 36 14-111 王松高等数学A(2-1)修朴华大学英语(3-1)耿琰电子商务2015-2 36 14-113 杨磊高等数学A(2-1)袁菁婧大学英语(3-1)袁菁婧金融2015-1 44 14-203 周衍平管理学原理+4 康旺霖高等数学A(2-1)甄珍大学英语(3-1)沈圳金融2015-2 45 14-205 姜爱萍管理学原理张学睦高等数学A(2-1)杨光大学英语(3-1)赵述强物流管理2015-1 37 14-207 曾丽君管理学原理赵峰高等数学A(2-1)李真大学英语(3-1)刘国忠物流管理2015-2 38 14-209 李美燕管理学原理宋平高等数学A(2-1)刘辉大学英语(3-1)徐科吉财政学2015-1 3114-123 陈金库微观经济学+2 任一鑫高等数学A(2-1)张同迁大学英语(3-1)邢雪晶财政学2015-2 32 王彩霞微观经济学孙江永高等数学A(2-1)大学英语(3-1)地质2015-1 39 14-211 王其芳普通化学(B)+4 黄仁和毛泽东思想与社会主义理论体系概论张月玲高等数学A(2-1)李艳测量学+10 刘峰大学英语(3-1)王平丽地质2015-2 38 14-213 夏璐普通化学(B)朱林晖马风涛高等数学A(2-1)孙玉芹测量学朱金山大学英语(3-1)冯建国水文2015-1 3514-219 苗佳丽普通化学(B)李春露王海涛高等数学A(2-1)王芳大学英语(3-1)邓清海水文2015-2 34 曹玉亭普通化学(B)高等数学A(2-1)大学英语(3-1)地球物理2015 34 14-303 李月毛泽东思想与社会主义理论体系概论李忠高等数学A(2-1)张涛大学英语(3-1)张涛资源勘查2015-1 3414-221 孔凡梅普通化学(B)崔立强王东东高等数学A(2-1)王东东大学英语(3-1)房丽资源勘查2015-2 36 王金凯普通化学(B)高等数学A(2-1)大学英语(3-1)资源勘查2015-3 34 14-305 杨仁超普通化学(B)+5 刘雪梅张升堂高等数学A(2-1)张升堂大学英语(3-1)赵善青勘查技术2015 39 14-307 丁仁伟普通地质学+8 赵秀丽李岩高等数学A(2-1)冯建国大学英语(3-1)李允资源(煤矿地质)2015 34 14-309 樊爱萍高等数学B(1)李晶晶大学英语(3-1)冯梅测绘2015-1 4014-223 陈允芳毛泽东思想与社会主义理论体系概论时洪举高等数学A(2-1)卓相来大学英语(3-1)冯苗苗测绘2015-2 40 景冬高等数学A(2-1)大学英语(3-1)测绘2015-3 36 14-311 张燕王峰高等数学A(2-1)宋其芳大学英语(3-1)李延波遥感2015-1 3814-319 孙林计算机C语言解斐斐毛泽东思想与社会主义理论体系概论+1刘凤英高等数学A(2-1)许静遥感原理与方法+2战丽丽大学英语(3-1)郑蕴华遥感2015-2 36 许君一计算机C语言高等数学A(2-1)遥感原理与方法大学英语(3-1)海洋测绘2015 39 14-313 刘峰张灵先高等数学A(2-1)王瑞富大学英语(3-1)牟乃夏自然地理2015 38 14-403 曾文自然地理学明艳芳杨爱东高等数学A(2-1)徐春达地图学+1 刘文宝大学英语(3-1)张红日人文地理2015 39 14-405 蔡玉林自然地理学李英孙健高等数学A(2-1)刘凤英大学英语(3-1)李英测绘单2015 38 14-407 田茂义高等数学A(2-1)徐泮林大学英语(3-1)赵会兴地信2015-1 3514-321 刘冰自然地理学张红日C++ +23刘新高等数学A(2-1)李红梅地图学+3刘文宝大学英语(3-1)郭放地信2015-2 34 季民自然地理学C++高等数学A(2-1)地图学大学英语(3-1)说明:1、各学院务必将此安排表通知到相关学生班级。
山东科技大学第一学期高等数学B卷

答题留空不够时 ,可写到纸的背面
注意保持装订完整,试卷拆开无效
密 封 线
系部 专业班级 学号 姓名
密
封
线
内
不 得
答
题
山东科技大学考试试卷
(2020-2021学年度第一学期)
课程名称:高等数学(二) [ B ] 卷 命 题:基础数学教研室 题号 一 二 三 四 五 六 七 总分 得分
三、单项选择题(在每个小题四个备选答案中选出一个正确答案,填在括号中)
(本大题4小题,每小题3分,共12分) 四、填空题(每小题3分,共15分) 一、计算题(每小题7分,共14分)
二、解答下列各题(每小题8分,共16分)
五、解答下列各题(每小题8分,共16分)
答题留空不够时 ,可写到纸的背面
注意保持装订完整,试卷拆开无效
密
封 线 系部 专业班级 学号 姓名
密
封 线 内 不 得 答 题
六、求下列积分(每小题7分,共21分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1 直线的极坐标方程
设一直线离极点O的距离为 ,p 从O到这直线的垂线
与极轴作成的角为θ,从图2.5可以看出,这 直线上的点的特征是
ρ cos(θ- )= p
这就是直线的极坐标方程.
例2 地球卫星和宇宙飞船的运行轨道是圆锥曲线.一宇
宙飞船的运行轨道,近地点高度为175公里,远地点高
满足方程
p =6680(1-e)
p =6553(1+e) 把e和 p解出,得到
e 127 0.0096 13233
=p6680×0.9904=6616公里. 例3 直线的参数方程
x x0 lt -∞<t<+∞ y y0 mt
这式子最初由匀速直线运动得出,但匀速直线运动 只能得出半条直线,t的变化范围是0≤t<+∞,如果把t 的变化范围扩大到-∞<t<+∞,就能得出整条直线.可 见用参数方程时应该注意参数的变化范围.
度为302公里.求这轨道的参数e,p
解 这轨道应是以地心为焦点的椭圆,椭圆上点离焦 点最远的距离是302+6378=6680公里(6378公里是 地球半径),最近的距离是175+6378 =6553公里.
p
从公式(3)看出,最远距离等于 1 e (当 =0),
p最近Βιβλιοθήκη 离等于 1 e(当 =).所以e和 p
