a-1-纯弯曲正应力公式推导
弯曲正应力计算公式推导过程

弯曲正应力计算公式推导过程在我们学习材料力学的时候,有一个非常重要的知识点,那就是弯曲正应力的计算公式推导过程。
这可是个相当关键的内容,就像一把神奇的钥匙,能帮我们打开理解很多结构力学问题的大门。
咱们先来说说弯曲的概念。
想象一下一根长长的木条,你在中间给它施加一个力,这根木条是不是就会弯下去啦?这就是简单的弯曲现象。
那弯曲正应力是怎么回事呢?其实就是在弯曲的时候,材料内部产生的应力。
比如说一根钢梁,它在承受重物的时候会弯曲,这时候钢梁内部各个点就会有不同大小的应力。
咱们来推导这个公式。
先从一个简单的梁的弯曲模型开始。
假设这根梁是等截面的,而且材料是均匀的。
我们考虑梁的一个微小的横截面,就像切蛋糕一样切一小片。
在这一小片上,有一些力在作用着。
想象一下,梁上面的纤维被拉长,下面的纤维被压缩。
而在中间有一个层面,这个层面既不被拉长也不被压缩,我们把它叫做中性层。
中性层就像是梁的“对称轴”。
从中性层到梁的上表面或者下表面的距离,我们叫做 y 。
接下来,咱们得引入一个重要的概念——弯矩 M 。
弯矩就像是让梁弯曲的那个“大力士”。
我们假设梁的横截面上的应力分布是和到中性层的距离y 成正比的。
那应力σ 就可以表示为σ = Ey / ρ ,这里的 E 是材料的弹性模量,ρ 是梁弯曲时的曲率半径。
但是我们更常用的是用弯矩 M 来表示应力。
经过一系列的推导和计算(这里的数学过程就不详细展开啦,不然脑袋都要晕啦),最终我们得到弯曲正应力的计算公式:σ = My / I ,其中 I 是截面的惯性矩。
我还记得有一次,我在工厂里看到工人师傅在安装钢梁。
他们非常小心地计算着钢梁的承载能力,用的就是弯曲正应力的公式。
我在旁边看着,心里就在想,这些看似枯燥的公式,在实际生活中是多么的重要啊!如果计算错了,钢梁可能就承受不住重量,会出大问题的。
总之,弯曲正应力的计算公式虽然推导过程有点复杂,但是只要我们认真理解,掌握其中的关键概念和原理,就能运用它解决很多实际问题。
纯弯曲时的正应力

D=200
D1 d1
解:(1)确定空心轴尺寸
由
max
M W
32
D13 (1
0.64
)
7.9
104
D1 210 mm
(2)比较两种情况下的重量比(面积比):
A空 A实
4
D12 (1 D2
2)
2102 (1 0.62 ) 2002
0.7
4
由此可见,载荷相同、 max要求相等的条件
M z ydA M
A
纯弯曲时的正应力:公式推导
E y
N dA 0
1
A
M y zdA 0 2 M z ydA M 3
A
A
将应力表达式代入(1)式,得
N
A
dA
E
A
ydA
0
Sz ydA 0
A
上式表明中性轴通过横截面形心。
将应力表达式代入(2)式,得
A z
dA
E
yzdA
2. 纯弯曲时的变形特征
(1)各纵向线段弯成弧线,且部分纵向线段伸长, 部分纵向线段缩短。
(2)各横向线相对转过了一个角度,仍保持为直线。 (3)变形后的横向线仍与纵向弧线垂直。
纯弯曲时的正应力:概述
3. 纯弯曲时的基本假设
(1)平截面假设( Plane Assumption )
(a) 变形前为平面的横截面变形后仍为面上无剪应力
(2)纵向纤维间无正应力
纵向纤维无挤压
横截面上只有轴向正应力
纯弯曲时的正应力:公式推导
1. 变形几何关系
M
M
z x
y
中性轴(Neutral Axis)
弯曲杆件正应力计算公式课件

曲杆件的性能。
基于能量方法的正应力计算
01
基于能量方法的正应力计算的扩展
能量方法是分析结构的一种有效方法。通过能量方法,可以更准确地计
算正应力分布。
02
考虑材料弹性的影响
在能量方法中,可以考虑材料的弹性性质,从而更准确地计算应力分布
。
03
基于能量方法的复杂结构分析
对于复杂的结构,基于能量方法可以更有效地进行正应力计算和分析。
03
弯曲杆件正应力计算公式应用
简单弯曲杆件的正应力计算
01
02
03
定义简单弯曲杆件
一个具有均匀截面、承受 沿轴线方向作用的力的直 杆。
推导公式
基于弹性力学和材料力学 的知识,利用能量法或偏 微分方程求解。
公式应用
计算简单弯曲杆件的正应 力分布,包括截面应力和 跨中应力。
复杂弯曲杆件的正应力计算
数值模拟和实验研究
未来研究可以通过数值模拟和实 验研究来进一步验证和改进弯曲 杆件正应力计算公式的准确性和 适用范围。同时,也可以通过这 些方法来研究复杂加载条件下的 正应力分布和结构响应。
多学科交叉和工程应 用
未来的研究可以进一步拓展弯曲 杆件正应力计算公式在其他学科 中的应用,如生物力学、地质力 学等。同时,该公式在工程中的 应用也需要不断改进和创新,以 适应不断发展的工程需求。
3. 变形前各横截面为平面,变形后仍为 平面。
2. 忽略材料加工硬化和蠕变等影响。
弯曲的基本假设 1. 杆件为理想弹性体,无初应力存在。
弯曲的应变与应力
应变
杆件在弯矩作用下,任意截面上 的点沿着与轴线垂直的方向移动 ,导致截面发生翘曲变形。
应力
由于截面翘曲变形,导致截面上 各点存在应力。
弯曲正应力(1)

C截面下端拉应力达到最大值
t ,max 28.8MPa
例2:矩形截面简支梁承受均布载荷作用,如图所示
q=60KN/m A
1m B
180 120
30
K z
C
3m
求:1、C 截面上K点正应力
2、C 截面上最大正应力 3、全梁上最大正应力 4、已知E=200GPa,C 截面的曲率半径ρ
y
1、截面几何性质计算 确定形心的位置
注意
(5)梁在中性轴的两侧分别受拉或受压;
正应力的正 负号(拉或压)可根据弯矩的正负
及梁的变形状态来 确定。 (6)熟记矩形、圆形截面对中性轴的惯性矩的计算式。
实心轴I z =πd 4 / 64
πD 4 d 空心轴I z = (1 4 );α 64 D
矩形I z =bh3 /12
§5-3
2.5 103 88 103 28.8MPa 6 7.64 10
My Iz
A FA
M/KNm
C
1m
B
1m FB
1m
2.5
c,max
4
52 88
2.5 103 52 103 17.0MPa 6 7.64 10
(3)结论 zc
B截面下端压应力达到最大值
c,max 46.1MPa
(1)受力分析,画弯矩图 (2)根据弯矩图确定危险截面
(3)截面为关于中性轴对称 M max 应用计算公式 max Wz (5)计算 M max (6)计算 Wz ,选择工字钢型号
(1)计算简图 F F F
F=F1+F2
F1 6.7kN,
F2 50kN,
(2)绘弯矩图 M FL/4 (3)危险截面
弯曲正应力公式

σ = My Iz
(12.4)
物理条件:材料是线弹性材 料所以可以应用胡克定律, 即σ = Eε。线性变化的应变 必然引起线性变化的应力。 因此,如正应变的变化规律 一样,正应力从在中性轴处 的零应力线性地变化到离 中性轴最远处的最大值。
静力学条件:由横截面上正 应力的合力应为零可以确 定中性轴的位置。
ε = a′b′ − ab = (ρ + y)dθ − ρdθ = y
ab
ρdθ
ρ
(12.1)
注意到中性层上的任 意线不改变长度。根据定 义,沿 a′b′的正应变可表示 为:
47
Stresses in Beams
Physical Condition. The material behaves in a linear-elastic manner so that Hooke’s law applies, that is, σ = Eε. A linear variation of normal strain must then be the consequence of a linear variation in normal stress. Hence, like the normal strain variation, normal stress will vary from zero at the member’s neutral axis to a maximum value, a distance farthest from the neutral axis.
Equation 12.4 is often referred to as the flexure formula. It is used to determine the normal stress in a straight member, having a cross section that is symmetrical with respect to an axis, and the moment is applied perpendicular to this axis.
弯曲正应力计算公式

弯曲正应力计算公式:轻松掌握计算方法
弯曲正应力是弯曲时产生的沿截面垂直于中性轴的应力。
它是构
件在受弯曲载荷时所承受的最大应力之一,对于构件的设计和选型非
常重要。
那么,如何计算弯曲正应力呢?以下是详细的计算公式和步骤。
1. 确定计算截面
在弯曲计算中,首先需要确定计算截面。
计算截面是指在弯曲处
所选取的截面,其位置和大小对于弯曲正应力的计算结果直接影响。
2. 计算截面惯性矩
在确定计算截面后,需要计算截面惯性矩。
惯性矩是表征固体物
理特性的物理量,对于计算弯曲正应力有着关键的作用。
3. 计算截面的模量
截面的模量是指材料在受力下的弹性变形和反应的能力。
根据材
料的弹性模量,可以计算出截面的模量。
4. 计算弯曲正应力
弯曲正应力的计算公式为:σ=b*y/I,其中b为截面宽度,y为截面距离中性轴的距离,I为截面的惯性矩。
通过计算得到的弯曲正应力,就是构件在受到弯曲作用下所承受的应力。
总之,掌握了弯曲正应力的计算公式和步骤,可以快速、准确地
计算出构件的弯曲正应力,从而为构件的设计和选型提供重要的依据。
怎样推导梁的应力公式、变形公式

05、基本知识 怎样推导梁的应力公式、变形公式(供参考) 同学们学习下面内容后,一定要向老师回信(849896803@ ),说出你对本资料的看法(收获、不懂的地方、资料有错的地方),以便考核你的平时成绩和改进我的工作。
回信请注明班级和学号的后面三位数。
1 * 问题的提出 ........................................................................................................................... 12 下面就用统一的步骤,研究梁的应力公式和变形公式。
................................................... 23 1.1梁的纯弯曲(纯弯曲:横截面上无剪力的粱段)应力公式推导 ................................. 24 1.2 梁弯曲的变形公式推导(仅研究纯弯曲) ....................................................................5 5 1.3 弯曲应力公式和变形公式的简要推导 ............................................................................6 6 1.4 梁弯曲的正应力强度条件和刚度条件的建立 ................................................................7 7 2.1 梁剪切的应力公式推导 ....................................................................................................8 8 2.2 梁弯曲的剪应力强度条件的建立 ....................................................................................9 93. 轴向拉压、扭转、梁的弯曲剪切,应力公式和变形公式推导汇总表 (9)1* 问题的提出在材料力学里,分析杆件的强度和刚度是十分重要的,它们是材料力学的核心内容。
12第十二讲(弯曲正应力)

材料力学教案
M z y d A
A
第十二讲:弯曲正应力计算
E
r
A
y dA
2
EI z
r
M
(c)
由式(c)可知,直梁纯弯曲时中性层的曲率为
M r EI z 上式中的EIz称为梁的弯曲刚度。显然,由于纯弯曲时,
梁横截面上的弯矩M 不随截面位置变化。故对于等截面的
1
直梁,包含在中性层内的那根轴线将弯成圆弧。
3、纵向线应变在横截面范围内的变化规律
图c为由相距d x的两横截面取出的梁段在梁弯曲后的情
况,两个原来平行的横截面绕中性轴相对转动了角d。梁的 横截面上距中性轴 z为任意距离 y 处的纵向线应变由图c可知 为
B1B B1 B y d AB1 O1O2 dx
令中性层的曲率半径为r(如图c),则根 1 d 据曲率的定义 有 r dx
材料力学教案
第十二讲:弯曲正应力计算
根据表面变形情况,并设想梁的侧面上的横向线mm和nn是
梁的横截面与侧表面的交线(由表及里),可作出如下推论
(假设):
平面假设
梁在纯弯曲时,其原来的横截面仍保持为平面,
只是绕垂直于弯曲平面(纵向平面)的某一轴转动,转动后 的横截面与梁弯曲后的轴线保持正交。 此假设已为弹性力学的理论分析结果所证实。 三峡大学 工程力学系
将 E 代入,即得弯曲正应力计算公式:
r
y
My Iz
三峡大学 工程力学系
材料力学教案
第十二讲:弯曲正应力计算
二. 纯弯曲理论的推广-横力弯曲中正应力的计算
工程中实际的梁大多发生横力弯曲,此时,对于梁在
纯弯曲时所作的假设不再成立。
弯曲应力—纯弯曲时的正应力(材料力学)

§5-2 正应力计算公式
3、物理关系
σ Eε
M
?
所以 σ E y
z
O
x
应力分布规律:
?
y
直梁纯弯曲时横截面上任意一点的正应力,与它到中性轴的距离成正比。待解决问题中性轴的位置?
中性层的曲率半径
§5-2 正应力计算公式
4、静力关系
横截面上内力系为垂直于横截面的空 间平行力系,这一力系简化得到三个内力分 M 量。
y t max
M
z
y
σtmax
σ cmax My cmax Iz
§5-2 正应力计算公式
二、横力弯曲时梁横截面上的正应力
实际工程中的梁,其横截面上大多同时存在着弯矩和剪力,为横 力弯曲。但根据实验和进一步的理论研究可知,剪力的存在对正应力 分布规律的影响很小。因此对横力弯曲的情况,前面推导的正应力公 式也适用。
(2)最大正应力发生在横截面上离中性轴最远的点处。
σ max M y max Iz
引用记号
Wz
Iz ymax
—抗弯截面系数
则公式改写为
σ max
M Wz
§5-2 正应力计算公式
对于中性轴为对称轴的横截面
矩形截面
Wz
Iz h/2
bh3 / 12 h/2
bh2 6
实心圆截面
Wz
Iz d /2
πd 4 / 64 d /2
推论:必有一层变形前后长度不变的纤维—中性层
⊥ 中性轴 横截面对称轴
中性层
中性轴
横截面对称轴
§5-2 正应力计算公式
2、变形几何关系
d
dx
图(a)
O’
b’ z
第4节 纯弯曲时横截面的正应力
C
Iy Iy b A
2
C
结论
截面对任一轴 z 的惯性矩等于该截面对过形心 而平行于 z 轴的 zC 轴的惯性矩加上两轴之间的距离 的平方与截面面积的乘积。此结论对任一 y 轴也同 样成立。
第七章 直梁弯曲时的内力和应力 二、纯弯曲的概念 纯弯曲:剪力值为零,弯矩值是一常数,内力只 有弯矩,而无剪力的弯曲变形称作纯弯曲。 剪切弯曲:弯曲内力既有弯矩、又有剪力的弯曲 变形称剪切弯曲(或横力弯曲)。 三、纯弯曲时横截面的正应力 1、几何关系 观察梁的变形:取一对 称截面梁,在其表面上画上 横向线m-m和n-n以及纵向线 ab和cd,在梁的纵向对称面 内施加一对等值、反向的力 偶,梁处于纯弯曲状态。
第七章 直梁弯曲时的内力和应力 结论:梁变形后,横向线依然保持直线,且与 梁变形后的轴线垂直。纵向线变为曲线,靠近梁顶 面的纵向线缩短,靠近梁底面的纵向线伸长。
平面假设:梁变形后横截面依然保持平面,且与梁 变形后的轴线垂直,横截面绕自身某轴作了转动。 纵向纤维单向受力假设:梁内各纵向纤维只产生轴 向拉伸或压缩变形。 中性层:梁在弯曲变形时, 一部分纤维伸长,一部分纤 维缩短,必然有一部分纤维 既不伸长也不缩短的层。 中性轴:中性层与横截面的交线。
bh 12
3
抗弯截面模量
3
Iz
,I y
hb 12
Wz
bh 6
2
D Iz 64
4
4
D Wz 32
3
3
D 4 Iz (1 ) 64
d D
D 4 Wz (1 ) 32
d D
第七章 直梁弯曲时的内力和应力 惯性矩的平行移轴公式
Iz Iz a A
第八讲 弯曲正应力

)
/(h0
/
2)
5.8.1 弯曲正应力
7、常见截面的IZ和WZ
IZ = y2dA
A
Wz
=
IZ ymax
Ip =
ρ2dA
A
Wt
=
Ip ρmax
圆截面
IZ
=
d 4
64
Wz
=
d3
32
πd 4 Ip = 32
πd 3 Wt = 16
空心圆截面
IZ
=
D 4
64
(1 −
4)
Wz
=
D3
32
(1− 4 )
yzdA=0
A
y
M
z
My
y z dA
5.8.1 弯曲正应力
惯性矩的定义
y
z
dA
ρ y
O
I y =
z 2 dA
A
Iz =
y2dA
A
I yz =
yzdA
A
z
IP =
2dA
A
5.8.1 弯曲正应力
惯性矩的性质
➢ 惯性矩和惯性积是对一定轴而定义的,而极惯性矩,是 对点定义的。
➢ 任何平面图形对于通过其形心的对称轴和与此对称轴垂 直的轴的惯性积为零。
5.8.1 弯曲正应力
3、几何关系
变形观察
mn aa bb m x n
m´ n a´ a´ b´ b´ m´ n´
(1)平面假设: 变形前为平面的横截面变 形后仍保持为平面,且垂 直于变形后的梁轴线,只 是绕截面内某一轴线偏转 了一个角度。
5.8.1 弯曲正应力
3、几何关系
变形观察
mn aa bb m x n
推导纯弯曲梁正应力公式总结

推导纯弯曲梁正应力公式总结好啦好啦,今天我们来聊一聊纯弯曲梁的正应力公式,说起来这玩意儿,乍一听好像很复杂,但是只要搞清楚一点,就不会觉得它有那么神秘了。
你看,弯曲这事儿,实际上就是梁受力后发生变形,弯曲就像我们蹲下去再站起来,弯了一下再直回来。
梁就像一个大块头,受力的时候会向下或者向上弯,弯的程度跟它的形状、材料和受力方式都有关系。
哦,对了,今天咱们关注的重点就是梁在弯曲的时候,内部会产生正应力,怎么计算这些应力?别急,听我慢慢说。
首先呢,我们要明白一个事实:弯曲是怎样产生的。
比如你想象一下,手拿着一根塑料棒,在中间用力压一下,塑料棒就会开始弯曲。
梁也类似,受力后,它的上下两部分会发生不同的变形。
上面部分可能会被压缩,下面部分则会拉伸。
就像你用力捏面包,中间的面包被压扁,上下两边反而膨胀了。
这时候,梁内部的“应力”就出现了,尤其是正应力,也就是我们要计算的内容。
咱们说到正应力嘛,这个名字听起来好像有点让人摸不着头脑。
正应力其实就是一个简单的东西,指的就是在梁的某一点上,受到的拉伸或者压缩的力量。
想象一下,你弯曲一根木棍,如果你把手放在木棍上,弯曲的地方会感觉到有一种推拉的力,这个力就可以理解为正应力了。
没错,梁的弯曲就是让它的各个点都经历不同程度的拉伸或压缩。
正应力的公式是啥呢?其实挺简单的,公式长得很“高冷”:(sigma = frac{M cdoty{I)。
别担心,公式不难,关键是弄懂每个字母的意思。
(M)是弯矩,顾名思义,就是梁受力后产生的弯曲力矩,换句话说,就是“推着”梁弯曲的那股劲儿。
你可以把它想象成一个小小的旋转力,好像你用手转动一个瓶盖。
(y)是从梁的中性轴到你所关心的点的距离。
这个“中性轴”可以理解为梁在弯曲时的平衡线,任何超过这个中性轴的地方都会被压缩,而低于它的地方则会被拉伸。
(I)是截面惯性矩,别被这个名字吓到,它其实是衡量梁抵抗弯曲能力的一个数字,越大说明梁越“硬”,弯曲得越少。
a-1-纯弯曲正应力公式推导省公开课获奖课件市赛课比赛一等奖课件
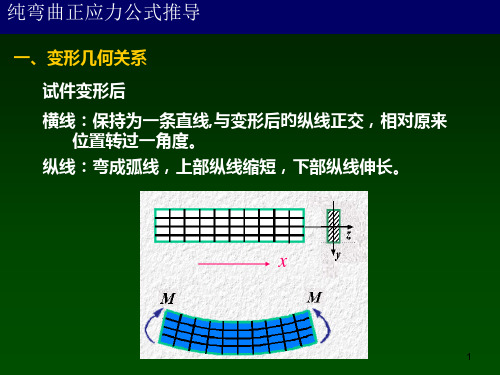
纯弯曲正应力公式推导
正应力性质(正负号))拟定:
σ旳符号可由M与y旳符号拟定,也 可由弯曲变形情况拟定。
s = My
Iz
最大正应力: smax =
令
Wz =
Iz ymax
得 M
smax = Wz
Mymax Iz
抗弯截面系数
7
纯弯曲正应力公式推导
对于剪切弯曲梁,这时两个基本假设并不成立。但试验和理 论分析表白,当l/h(跨高比)较大(>5)时,采用该正应 力公式计算旳误差很小,满足工程旳精度要求(依然可按照 纯弯曲求解)。
2
纯弯曲正应力公式推导
横截面绕中性轴转动
找与横截面上旳正应力有关旳纵向线应变旳变
形规律:
dq
取微段梁dx
1
2
1
2
dx
O1
y
O2
O1'
O2'
ab1Fra bibliotek2a'
b'
dx
1
2
O1O2变形前后长度不变,ρ为中性层旳曲率半径
3
纯弯曲正应力公式推导
xy平面变形特点
变形前 dx= ab=O1O2
变形后 O'1O'2=ρdθ
z
中性轴
5
纯弯曲正应力公式推导
三、静力学关系
FN=∫ AσdA
=
E∫ ρA
ydA
=0
得
M=∫ AσdA·y
M
z
dA y
=
E∫ ρ
A
y2dA
z σdA
y
E =ρ
Iz
∫ A ydA =0
横截面对中性轴 旳面积矩为零, 中性轴过形心。
12弯曲正应力、切应力与强度条件

基本假设2: 纵向纤维无挤压假设
纵向纤维间无正应力。
公式推导
用两个横截面从梁中假想地截取 长为 dx 的一段 。 由平面假设可知,在梁弯曲时, 这两个横截面将相对地旋转一个 角度 d 。
d
横截面的转动将使梁的凹边的纵 向线段缩短,凸边的纵向线段伸 长。由于变形的连续性,中间必 有一层纵向线段 O1O2 无长度改 变。此层称为 中性层 。
横力弯曲时横截面上有切应力(翘曲) 平面假设 不再成立
此外, 横力弯曲时纵向纤维无挤压假设也不成立. 由弹性力学的理论,有结论: 当梁的长度l与横截面的高度h的比值:
l 5 h
则用纯弯曲的正应力公式计算横力弯曲时的正应 力有足够的精度。 l / h > 5 的梁称为细长梁。
4,讨论
My IzmaFra bibliotekna
m
m
m’
n’
b m n
b
m’ n’
(2)变形前垂直于纵向直线的横向线( mm , nn 等)变形后仍 为直线( m’m’ , n’n’ 等) ,但相对转了一个角度,且与 弯曲后的纵向线垂直。
纯弯曲的变形特征 基本假设1: 平面假设 变形前为平面的横截 面变形后仍为平面, 且仍垂直于梁的轴线。
M C 2.5KN .m
M B 3KN .m
最大负弯矩在截面B上
80
RA
P1=8KN
RB
P2=3KN
35
20
A
1m
z c
1m
3
B
1m
D
80
65
20
C
B
+
2.5
B 截面
{
MB t max
纯弯曲梁的正应力实验报告

姓名:班级:学号:实验报告纯弯曲梁的正应力实验一、实验目的:1.测定梁在纯弯曲时横截面上正应力大小和分布规律2.验证纯弯曲梁的正应力公式二、实验设备及工具:1.材料力学多功能试验台中的纯弯曲梁实验装置2.数字测力仪、电阻应变仪三、实验原理及方法:在纯弯曲条件下,根据平面假设和纵向纤维间无挤压的假设,可得到梁横截面上任意一点的正应力,计算公式:σ=My/I z为测量梁横截面上的正应力分布规律,在梁的弯曲段沿梁侧面不同高度,平行于轴线贴有应变片。
贴法:中性层一片,中性层上下1/4梁高处各一片,梁上下两侧各一片,共计五片。
采用增量法加载,每增加等量荷载△P(500N)测出各点的应变增量△ε,求的各点应变增量的平均值△ε实i,从而求出应力增量:σ实i=E△ε实i将实验应力值与理论应力值进行比较,已验证弯曲正应力公式。
四、原始数据:五、实验步骤:1.打开应变仪、测力仪电源开关2.连接应变仪上电桥的连线,确定第一测点到第五测点在电桥通道上的序号。
3. 检查测力仪,选择力值加载单位N或kg,按动按键直至显示N上的红灯亮起。
按清零键,使测力计显示零。
4.应变仪调零。
按下“自动平衡”键,使应变仪显示为零。
5.转动手轮,按铭牌指示加载,加力的学生要缓慢匀速加载,到测力计上显示500N,读数的学生读下5个测点的应变值,(注意记录下正、负号)。
用应变仪右下角的通道切换键来显示第5测点的读数。
以后,加力每次500N,到3000N 为止。
6.读完3000N应变读数后,卸下载荷,关闭电源。
六、实验结果及处理:1.各点实验应力值计算根据上表数据求得应变增量平均值△εPi,带入胡克定律计算各点实验值:σ实i=E△εPi×10-62.各点理论应力值计算载荷增量△P=500N弯矩增量△M=△P/2×a应力理论值计算σ理i=∆M∙YiI z(验证的就是它)3.绘出实验应力值和理论应力值的分布图以横坐标表示各测点的应力σ实和σ理,以纵坐标表示各测点距梁中性层的位置。
弯曲应力的推导 1

b m
b n
m
n
a
o
b m
a
纵向纤维bb:
变形前 变形后
y
dx
o
b n
bb oo d bb ( y)d
所以纵向纤维bb的应变为:
P
d
a a
o o
b n
yd bb ( y )d d y d d bb
b m
My Iz
前提: 细长梁,即梁的跨高比L/h>5时,其误差 不大;
有一模量为E 1 的矩形截面悬臂梁AB , A 端固定, B 端自 由。梁长为L ,截面高度为h1 ,宽度为b 。梁上表面粘着模量 为E2 = 2E1 的增强材料层,该层高度h2 = 0.1h1 ,长度和宽 度与梁AB相同。工作台面D距离B端下表面高度为Δ。在B端作 用垂直向下的载荷 FP 。不考虑各部分的自重。 (1)求组合截面中性轴的位置。 (2)求使梁B 端下表面刚好接触D 台面所需的力 FP 。 (3)求此时粘接面无相对滑动情况下的剪力。 (4)计算梁的剪应力值并画出其沿梁截面高度的分布图。
My Iz 横截面上最大正应力为
max
Mymax M M Iz I z / ymax Wz
抗弯截面模量
Iz ——截面的抗弯截面模量,反映了截面 Wz ymax 的几何形状、尺寸对强度的影响。
矩形、圆形截面对中性轴的惯性矩及抗弯截面模量:
竖放:ห้องสมุดไป่ตู้z h b b
1 3 1 2 I z bh , Wz bh 12 6
1
y
横截面上距中性 轴为y处的轴向变 形规律。
C , y.
弯曲应力-材料力学

max
Mymax Iz
工程力学 Engineering Mechanics
典型例题
例1 图示矩形截面梁,梁上载荷q=100kN/m,梁跨度l=6m,截面尺寸:
b=400mm,h=600mm,材料许用应力[]=100MPa,试判断该梁是否安全。
弹性力学精确分析表明,当跨度l与横截面高度h之比l/h>5(细长梁)时, 纯弯曲正应力公式对于横力弯曲近似成立。
横力弯曲最大正应力
max
M max ymax Iz
弯曲正应力适用范围 细长梁的纯弯曲或横力弯曲 横截面惯性积Iyz=0 弹性变形阶段
工程力学 Engineering Mechanics
YA
2m
2m YB
B 2m
20 b
90
c
z
a
50
解:(3)求解正应力
My Iz
惯性矩
Iz
1 12
50 903
3.0375106 mm4
弯矩
M 10kN.m
典型例题
例1 求图示矩形截面梁指定截面上对应点的正内力。
10kN
1
A
YA
2m
2m YB
B 2m
20 b
90
c
z
a
50
解:(3)求解正应力
M max
1 8
ql 2
1 8
q
62
q
533.3kN/m
练习1
受均布载荷作用的简支梁如图,求 ① 1-1截面上1、2两点的正应力; ② 1-1截面上的最大正应力; ③ 全梁的最大正应力; ④ 已知E=200GPa,求1-1截面的曲率半径。
第五章 弯曲应力

此梁为等截面直梁,故全梁最大弯曲正应力在最大弯矩
所在截面上,其值为
max
M max Wz
6M max bh2
6 7.5106 40 802
175MPa
第五章 弯曲应力
5.2 弯曲切应力简介
5.2.1 矩形截面梁的弯曲切应力 矩形截面梁的任意横截面上,剪力FS皆与横截面的对称
轴y重合(见图5-11(b))。设横截面的高度为h,宽度为b, 现研究弯曲切应力在横截面上的分布规律。
图5-8
第五章 弯曲应力
5.1.4 弯曲正应力公式的适用范围 弯曲正应力公式是在纯弯曲情况下推出的。当梁受到
横向力作用时,一般横截面上既有弯矩又有剪力,这种弯曲 称为横力弯曲。剪力会在横截面上引起切应力τ,从而存在 切应变γ=τ/G。由于切应力沿梁截面高度变化(见下一节), 故切应变γ沿梁截面高度也是非均匀的。因此,横力弯曲时,
第五章 弯曲应力
综上所述,对于各横截面剪力相同的梁和剪力不相同的 细长梁(l>5h),在纯弯曲情况下推导的弯曲正应力公式 (5-2)仍然适用。
第五章 弯曲应力 例5-1 图5-10(a)所示悬臂梁,受集中力F与集中力 偶Me作用,其中F=5kN,Me=7.5kN·m,试求梁上B点左邻 面1-1上的最大弯曲正应力、该截面K点处正应力及全梁的 最大弯曲正应力。
FN 2
dA
A1
式中A1为右侧面pn1的面积,正应力 可按弯曲正应力公式算出,
于是
FN 2
dA
A1
M dM y1 dAM dM
A1
Iz
Iz
A1
y1dAM
dM Iz
S
* z
弯曲杆件正应力计算公式

2.切应力强度条件 2.切应力强度条件
对于等截面直梁,全梁的最大切应力发生在 对于等截面直梁,全梁的最大切应力发生在FQmax 所在截面的中性轴处。 所在截面的中性轴处。
τ max =
FQ ⋅ S z* max Iz ⋅b
≤ [τ ]
当杆件出现以下情况之一时, 当杆件出现以下情况之一时,必须校核切应 力强度,甚至由切应力强度条件来控制: 力强度,甚至由切应力强度条件来控制: 梁的跨度较小或荷载作用在支座附时。 (1)梁的跨度较小或荷载作用在支座附时。 某些组合截面梁( (2)某些组合截面梁(如焊接的工字形钢板 ),当腹板厚度与高度之比小于相应型钢的相 梁),当腹板厚度与高度之比小于相应型钢的相 应比值时。 应比值时。 木梁或玻璃等复合材料梁。 (3)木梁或玻璃等复合材料梁。
M max ≤ [σ ]⋅ Wz
[σ ]
3. 确定许用荷载
=4m
4kN F Q图 4kN
h
下图所示木梁,已知[σ]=10MPa, 例1 下图所示木梁,已知 , [τ]=2MPa,b=140mm,h=210mm,校核梁 , , , 强度。 强度。 q=2kN/m 解 z
b
M图 4kN m ·
作 FQ 和 M图
M A ⋅ y2 8 ×106 × 200 = = = 16MPa 8 Iz 1×10
M B ⋅ y1 12 × 106 ×100 = = = 12MPa 8 Iz 1× 10
100 (y1)
(2).强度条件
产生最大弯矩的截面称为危险截面, 产生最大弯矩的截面称为危险截面,危险 截面上产生最大应力的点称为危险点。 截面上产生最大应力的点称为危险点。 M max ⋅ ymax M max σ max = = ≤ [σ ] IZ Wz 对于脆性材料 + M ⋅ ymax + + σ max = ≤ [σ ] Iz − M ⋅ ymax − − σ max = ≤ [σ ] Iz 式中各量计算均用绝对值。 式中各量计算均用绝对值
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xy平面变形特点
dx= ab=O1O2
变形后 O' O' =ρdθ 1 2
=O1O2
1 2 1
dq
a'1b'2=(ρ+y)dθ
ab的纵向线应变 2 O2'
a'b'-ab (ρ+y)dθ -dx = ε= dx ab = (ρ+y)dθ - ρd θ ρd θ
a
1
b
2
y
O1
O2O1' Nhomakorabeaa'
1
b' dx
My s = Iz
Iz
抗弯截面系数
smax =
M Wz
a7
纯弯曲正应力公式推导
对于剪切弯曲梁,这时两个基本假设并不成立。但实验和理 论分析表明,当l/h(跨高比)较大(>5)时,采用该正应 力公式计算的误差很小,满足工程的精度要求(依然可按照 纯弯曲求解)。 这时
s
=
M(x)y Iz
M(x) 1 = ρ(x) E Iz
纯弯曲正应力公式推导
一、变形几何关系 试件变形后 横线:保持为一条直线,与变形后的纵线正交,相对原来 位置转过一角度。 纵线:弯成弧线,上部纵线缩短,下部纵线伸长。
x
a1
纯弯曲正应力公式推导
假设:
平面假设:变形后的横截面仍为平面,并仍与弯曲后的纵线正交。 单向受力假设:各纵向纤维间无挤压,每根纵向纤维处于单向 受力状态。 中性层:梁中间有一层既不伸长,也不缩短。
2
dx
=
y
ρ
a4
纯弯曲正应力公式推导
二、物理关系 胡克定律
σ=Eε =E
y
ρ
由此可见,横截面上的正应力分布为
z
中性轴
a5
纯弯曲正应力公式推导
三、静力学关系
E ∫ ydA ∫ σ =0 FN= A dA = A ρ M=∫ A dA· σ y
得 ∫ A ydA =0
横截面对中性轴 的面积矩为零, 中性轴过形心。
smax
=
Mmax Wz
公式适用条件: 1. 在线弹性范围; 2. 材料(E)拉压同性; 3. 纯弯曲与横力弯曲; 4. 平面弯曲。
应用于强度校核!
a8
中性轴:中性层与横截面的交线。 中性层
a2
纯弯曲正应力公式推导
横截面绕中性轴转动 找与横截面上的正应力有关的纵向线应变的变 形规律: 取微段梁dx 1 O1 dx 2 1 2 O2' O2 O1'
dq
a
1
b
2
y
a'
1
b'
2
dx
O1O2变形前后长度不变,ρ为中性层的曲率半径
a3
纯弯曲正应力公式推导
M
dA
z
y
z σdA
y 正应力 公式:
My s = Iz
E ∫ y2dA = ρ A E I z = ρ 1 M = EIz 中性层曲率公式 ρ
EIz —— 梁的抗弯刚度
a6
纯弯曲正应力公式推导
正应力性质(正负号))确定: σ的符号可由M与y的符号确定,也 可由弯曲变形情况确定。 最大正应力: smax = 令 得 Iz Wz = ymax Mymax
