(完整版)层次分析法及matlab程序
AHP及matlab程序

层次分析法(AHP)及matlab程序层次分析法是一种新的定性分析与定量分析相结合的系统分析方法,是将人的主观判断用数量形式表达和处理的方法,简称AHP(The Analytic Hierarchy Process)法。
近年来,层次分析法在草地农业生态系统的系统分析、设计与决策中日益受到重视。
1层次分析法的基本方法和步骤层次分析法是把复杂问题分解成各个组成因素,又将这些因素按支配关系分组形成递阶层次结构。
通过两两比较的方式确定各个因素相对重要性,然后综合决策者的判断,确定决策方案相对重要性的总排序。
运用层次分析法进行系统分析、设计、决策时,可分为4个步骤进行;(1)分析系统中各因素之间的关系,建立系统的递阶层次结构;(2)对同一层次的各元素关于上一层中某一准则的重要性进行两两比较,构造两两比较的判断矩阵;(3)由判断矩阵计算被比较元素对于该准则的相对权重;(4)计算各层元素对系统目标的合成权重,并进行排序,2递阶层次结构的建立首先把系统问题条理化、层次化,构造出一个层次分析的结构模型。
在模型中,复杂问题被分解,分解后各组成部分称为元素,这些元素又按属性分成若干组,形成不同层次。
同一层次的元素作为准则对下一层的某些元素起支配作用,同时它又受上面层次元素的支配。
层次可分为三类;(1)最高层:这一层次中只有一个元素,它是问题的预定目标或理想结果,因此也叫目标层;(2)中间层:这一层次包括要实现目标所涉及的中间环节中需要考虑的准则。
该层可由若干层次组成,因而有准则和子准则之分,这一层也叫准则层;(3)最底层:这一层次包括为实现目标可供选择的各种措施、决策方案等,因此也称为措施层或方案层。
上层元素对下层元素的支配关系所形成的层次结构被称为递阶层次结构。
当然,上一层元素可以支配下层的所有元素,但也可只支配其中部分元素。
递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关,可不受限制。
每一层次中各元素所支配的元素一般不要超过9个,因为支配的元素过多会给两两比较判断带来困难。
层次分析法matlab程序及应用
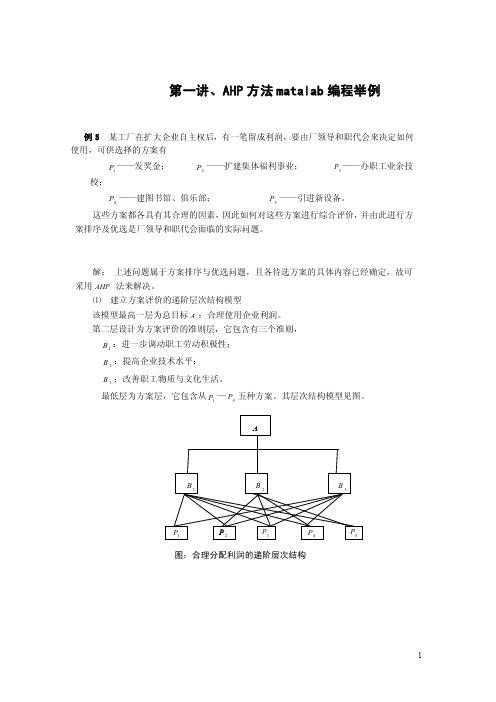
第一讲、AHP 方法matalab 编程举例例5 某工厂在扩大企业自主权后,有一笔留成利润,要由厂领导和职代会来决定如何使用,可供选择的方案有1P ——发奖金; 2P ——扩建集体福利事业; 3P ——办职工业余技校;4P ——建图书馆、俱乐部; 5P ——引进新设备。
这些方案都各具有其合理的因素,因此如何对这些方案进行综合评价,并由此进行方案排序及优选是厂领导和职代会面临的实际问题。
解: 上述问题属于方案排序与优选问题,且各待选方案的具体内容已经确定,故可采用AHP 法来解决。
⑴ 建立方案评价的递阶层次结构模型该模型最高一层为总目标A :合理使用企业利润。
第二层设计为方案评价的准则层,它包含有三个准则,1B :进一步调动职工劳动积极性; 2B :提高企业技术水平; 3B :改善职工物质与文化生活。
最低层为方案层,它包含从1P —5P 五种方案。
其层次结构模型见图。
图:合理分配利润的递阶层次结构⑵ 构造比较判断矩阵设以A 为比较准则,B 层次各因素的两两比较判断矩阵为B A -,类似地以每一个i B 为比较准则,P 层次各因素的两两比较判断矩阵P B i -。
因此得到四个比较判断矩阵如下。
综合各个专家的意见后得到的第三层相对第二层的各个比较判断矩阵⑶ 层次单排序及其一致性检验对于上述各比较判断矩阵,用MATLAB 数学软件求出其最大的特征值及其对应的特征向量,对此特征向量经归一化后,即可得到相应的层次单排序的相对重要性权重向量,一致性指标CI 和一致性比例CR ,列表如下:表 合理使用企业利润的计算结果由此可见,所有四个层次单排序的CR 的值均小于0.1,符合满意一致性要求。
⑷ 层次总排序已知第二层(B 层)相对于总目标A 的排序向量为Tw)2582.0,6370.0,1047.0()2(=,而第二层(P 层)以第二层第i 个因素i B 为准则时的排序向量分别为: T p )0615.0,1465.0,0894.0,2636.0,439.0(31=Tp )2622.0,1175.0,5650.0,0553.0,0(32= Tp )0,125.0,125.0,375.0,375.0(33=则第三层(P 层)相对于总目标的排序向量为Twp p p W )1735.0,1225.0,4015.0,1597.0,1428.0(),,()2(333231=⋅=⑸ 层次总排序的一致性检验由于2CI=()0,0389.0,0198.0(),,232221=CICICI)9.0,9.0,12.1(),,(2322212==RI RI RIRI因此0269.0)258.0,6370.0,1047.0)(0,0389.0,0198.0()2(23==⋅=Tw CI CI9230.0)2582.0,637.0,1047.0)(9.0,9.0,12.1()2(23==⋅=w RI RI3323RICI CRCR+==0624.09230.00269.00332.0=+1.0<(6)结论某工厂合理使用企业留成利润这一总目标,所考虑的五种方案排序的相对优先排序为① 3P (开办职工业务技校),权重为4015.0; ② 5P (引进新技术设备),权重为1735.0; ③ 2P (扩建集体福利事业),权重为1597.0; ④ 1P (发奖金),权重为1428.0;⑤ 4P (建图书馆,俱乐部),权重为1225.0。
(完整版)层次分析法计算权重在matlab中的实现

(完整版)层次分析法计算权重在matlab中的实现信息系统分析与设计作业层次分析法确定绩效评价权重在matlab中的实现小组成员:孙高茹、王靖、李春梅、郭荣1 程序简要概述编写程序一步实现评价指标特征值lam、特征向量w以及一致性比率CR的求解。
具体的操作步骤是:首先构造评价指标,用专家评定法对指标两两打分,构建比较矩阵,继而运用编写程序实现层次分析法在MATLAB中的应用。
通过编写MATLAB程序一步实现问题求解,可以简化权重计算方法与步骤,减少工作量,从而提高人力资源管理中绩效考核的科学化电算化。
2 程序在matlab中实现的具体步骤function [w,lam,CR] = ccfx(A)%A为成对比较矩阵,返回值w为近似特征向量% lam为近似最大特征值λmax,CR为一致性比率n=length(A(:,1));a=sum(A);B=A %用B代替A做计算for j=1:n %将A的列向量归一化B(:,j)=B(:,j)./a(j);ends=B(:,1);for j=2:ns=s+B(:,j);endc=sum(s);%计算近似最大特征值λmaxw=s./c;d=A*wlam=1/n*sum((d./w));CI=(lam-n)/(n-1);%一致性指标RI=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45,1.49,1.51];%RI为随机一致性指标CR=CI/RI(n);%求一致性比率if CR>0.1disp('没有通过一致性检验');else disp('通过一致性检验');endend3 案例应用我们拟构建公司员工绩效评价分析权重,完整操作步骤如下:3.1构建的评价指标体系我们将影响员工绩效评定的指标因素分为:打卡、业绩、创新、态度与品德。
3.2专家打分,构建两两比较矩阵A =1.0000 0.5000 3.0000 4.00002.0000 1.0000 5.00003.00000.3333 0.2000 1.0000 2.00000.2500 0.3333 0.5000 1.00003.3在MATLAB中运用编写好的程序实现直接在MATLAB命令窗口中输入[w,lam,CR]=ccfx(A)继而直接得出d =1.30352.00000.51450.3926w =0.31020.46910.12420.0966lam =4.1687CR =0.0625,通过一致性检验3.4解读程序结果根据程序求解中得出的特征向量,可以得出打卡、业绩、创新以及态度品德在员工绩效评价中所占的权重分别为:0.3102、0.4691、0.1242、0.0966。
层次分析法及matlab程序

层次分析法及Matlab程序一、层次分析法简介层次分析法(Analytic Hierarchy Process,简称AHP)是一种用于决策分析的工具,由美国数学家托马斯·L·萨蒂(Thomas L. Saaty)在1970年代创立。
AHP通过将决策问题划分为多个层次和多个因素,将主要因素和次要因素划分归纳,以定量化的方法分析各因素间优先级的关系,从而对决策方案进行综合评价。
AHP的基本原理是通过构造判断矩阵、计算判断矩阵的特征向量、确定权重,最终得到决策方案的优先级,从而找到最终的最优决策方案。
其主要优点是可定量化、简单易行,适用于大部分决策问题。
二、层次分析法的步骤AHP的具体步骤如下:1.确定决策目标;2.确定影响决策的因素,并将它们分成若干类别,即形成层次结构;3.为每个因素构建判断矩阵,评估每个因素的重要程度(用1~9的数字表示);4.将各判断矩阵进行一致性检验,并计算其权重;5.对计算得到的权重进行优先级排序,选出最优决策方案。
三、Matlab程序实现AHP计算在Matlab中,可以通过编写程序实现AHP的计算。
以下是一份简单的Matlab 程序,用于计算AHP的权重:% 输入判断矩阵A = [1 4 5;1/4 1 2;1/5 1/2 1];% 计算特征向量[V, D] = eig(A);[m, idx] = max(max(D));w = V(:,idx)';w = w/sum(w);% 一致性检验RI = [0 0 0.58 0.9 1.12 1.24 1.32 1.41 1.45 1.49];CR = (max(D) - 3)/2/RI(length(A));CI = sum(CR)/length(A);if CI < 0.1disp('一致性较好,权重为:');disp(w);elsedisp('一致性差,需重新评估判断矩阵!');end该程序用于计算一个3x3的判断矩阵的权重,并输出一致性检验的结果。
层次分析matlab代码(全)

9.0 8.2 8.0 7.8 9.0 9.5 5;
9.6 9.1 8.1 9.9 8.7 9.7 6;
9.5 9.6 8.3 8.1 9.0 9.3 7;
8.6 8.3 8.2 8.1 9.0 9.0 5;
A=[1 2 3 4 5 6 7;
1/2 1 2 3 4 5 6;
1/3 1/2 1 2 3 4 5;
1/4 1/3 1/2 1 2 3 4;
1/5 1/4 1/3 1/2 1 2 3;
1/6 1/5 1/4 1/3 1/2 1 2;
1/7 1/6 1/5 1/4 1/3 1/2 1;];
Evalues4=diag(Eigenvalues4);
Evalues5=diag(Eigenvalues5);
Evalues6=diag(Eigenvalues6);
Evalues7=diag(Eigenvalues7);
%最大特征值lamdaMax,及其一次性指标ci和一次性检验cr
[maxEvalue1,point1]=max(Evalues1);lamdaMax1=maxEvalue1;
for i=1:20
for j=1:20
p6(i,j)=B(i,6)/B(j,6);
end
end
p6;
for i=1:20
for j=1:20
p7(i,j)=B(i,7)/B(j,7);
end
end
p7;
%特征值矩阵Eigenvalues 特征向量Eigenvector
%判断矩阵阶数 n
n=size(A,1)
MATLAB层次分析法

wn
w2
wn
的正互反阵A称一致阵,如
wn
wn
wn
w1
w2
wn
一致阵 • A的秩为1,A的唯一非零特征根为n 性质 • A的任一列向量是对应于n 的特征向量
• A的归一化特征向量可作为权向量
对于不一致(但在允许范围内)的成对
比较阵A,建议用对应于最大特征根
的特征向量作为权向量w ,即
Aw w
• 心理学家认为成对比较的因素不宜超过9个
• 用1~3,1~5,…,1~17,…,1p~9p (p=2,3,4,5),
d+0.1~d+0.9 (d=1,2,3,4)等27种比较尺度对若干实
例构造成对比较阵,算出权向量,与实际对比发现,
1~9尺度较优。
第5页/共27页
一致性检验 对A确定不一致的允许范围
经济效益 B1
过河的效益 A
社会效益 B2
节 收岸 当 建安 交 自
省 入间 地 筑全 往 豪
时 C 商 商 就可 沟 感
间 2 业 业 业 靠 通 C8
C
C C C C6 C7
1
3
4
5
桥梁 D1
隧道 D2
(1)过河效益层次结构
第14页/共27页
环境效益 B3
舒进 美
适出 化
C
方 便
C1
9
C1
1
0
渡船 D3
深入分析实际问题,将有关因素自上而下分层(目标—准则或指标—方案 或对象),上层受下层影响,而层内各因素基本上相对独立。
2)构造成对比较阵
用成对比较法和1~9尺度,构造各层对上一层每一因素的成对比较阵。
3)计算权向量并作一致性检验
层次分析法的MATLAB实现

第八章 层次分析法层次分析法(Analytic Hierarchy Process ,简称AHP )是对一些较为复杂、较为模糊的问题作出决策的简易方法,它特别适用于那些难于完全定量分析的问题。
它是美国运筹学家T. L. Saaty 教授于70年代初期提出的一种简便、灵活而又实用的多准则决策方法。
MATLAB 教程网 §1 层次分析法的基本原理与步骤人们在进行社会的、经济的以及科学管理领域问题的系统分析中,面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。
层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。
运用层次分析法建模,大体上可按下面四个步骤进行:(i )建立递阶层次结构模型;(ii )构造出各层次中的所有判断矩阵;(iii )层次单排序及一致性检验;(iv )层次总排序及一致性检验。
下面分别说明这四个步骤的实现过程。
1.1 递阶层次结构的建立与特点应用AHP 分析决策问题时,首先要把问题条理化、层次化,构造出一个有层次的结构模型。
在这个模型下,复杂问题被分解为元素的组成部分。
这些元素又按其属性及关系形成若干层次。
上一层次的元素作为准则对下一层次有关元素起支配作用。
这些层次可以分为三类:(i )最高层:这一层次中只有一个元素,一般它是分析问题的预定目标或理想结果,因此也称为目标层。
(ii )中间层:这一层次中包含了为实现目标所涉及的中间环节,它可以由若干个层次组成,包括所需考虑的准则、子准则,因此也称为准则层。
(iii )最底层:这一层次包括了为实现目标可供选择的各种措施、决策方案等,因此也称为措施层或方案层。
递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关,一般地层次数不受限制。
每一层次中各元素所支配的元素一般不要超过9个。
这是因为支配的元素过多会给两两比较判断带来困难。
下面结合一个实例来说明递阶层次结构的建立。
例1 假期旅游有1P 、2P 、3P 3个旅游胜地供你选择,试确定一个最佳地点。
Matlab建模教程层次分析法

第八章层次分析法层次分析法(Analytic Hierarchy Process,简称AHP )是对一些较为复杂、较为模糊的问题作出决策的简易方法,它特别适用于那些难于完全定量分析的问题。
它是美国运筹学家T. L. Saaty 教授于70年代初期提出的一种简便、灵活而又实用的多准则决策方法。
§ 1层次分析法的基本原理与步骤人们在进行社会的、经济的以及科学管理领域问题的系统分析中,面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。
层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。
运用层次分析法建模,大体上可按下面四个步骤进行:(i)建立递阶层次结构模型;(ii)构造出各层次中的所有判断矩阵;(iii)层次单排序及一致性检验;(iv)层次总排序及一致性检验。
下面分别说明这四个步骤的实现过程。
1.1递阶层次结构的建立与特点应用AHP分析决策问题时,首先要把问题条理化、层次化,构造出一个有层次的结构模型。
在这个模型下,复杂问题被分解为元素的组成部分。
这些元素又按其属性及关系形成若干层次。
上一层次的元素作为准则对下一层次有关元素起支配作用。
这些层次可以分为三类:(i)最高层:这一层次中只有一个元素,一般它是分析问题的预定目标或理想结果,因此也称为目标层。
(ii )中间层:这一层次中包含了为实现目标所涉及的中间环节,它可以由若干个层次组成,包括所需考虑的准则、子准则,因此也称为准则层。
(iii )最底层:这一层次包括了为实现目标可供选择的各种措施、决策方案等,因此也称为措施层或方案层。
递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关,一般地层次数不受限制。
每一层次中各元素所支配的元素一般不要超过9个。
这是因为支配的元素过多会给两两比较判断带来困难。
下面结合一个实例来说明递阶层次结构的建立。
例1假期旅游有R、F2、F3 3个旅游胜地供你选择,试确定一个最佳地点。
层次分析法及matlab程序

层次分析法建模层次分析法(AHP-Analytic Hierachy process)---- 多目标决策方法70 年代由美国运筹学家T·L·Satty提出的,就是一种定性与定量分析相结合的多目标决策分析方法论。
吸收利用行为科学的特点,就是将决策者的经验判断给予量化,对目标(因素)结构复杂而且缺乏必要的数据情况下,採用此方法较为实用,就是一种系统科学中,常用的一种系统分析方法,因而成为系统分析的数学工具之一。
传统的常用的研究自然科学与社会科学的方法有:机理分析方法:利用经典的数学工具分析观察的因果关系;统计分析方法:利用大量观测数据寻求统计规律,用随机数学方法描述(自然现象、社会现象)现象的规律。
基本内容:(1)多目标决策问题举例AHP建模方法(2)AHP建模方法基本步骤(3)AHP建模方法基本算法(3)AHP建模方法理论算法应用的若干问题。
参考书: 1、姜启源,数学模型(第二版,第9章;第三版,第8章),高等教育出版社2、程理民等, 运筹学模型与方法教程,(第10章),清华大学出版社3、《运筹学》编写组,运筹学(修订版),第11章,第7节,清华大学出版社一、问题举例:A.大学毕业生就业选择问题获得大学毕业学位的毕业生,“双向选择”时,用人单位与毕业生都有各自的选择标准与要求。
就毕业生来说选择单位的标准与要求就是多方面的,例如:①能发挥自己的才干为国家作出较好贡献(即工作岗位适合发挥专长);②工作收入较好(待遇好);③生活环境好(大城市、气候等工作条件等);④单位名声好(声誉-Reputation);⑤工作环境好(人际关系与谐等)⑥发展晋升(promote, promotion)机会多(如新单位或单位发展有后劲)等。
问题:现在有多个用人单位可供她选择,因此,她面临多种选择与决策,问题就是她将如何作出决策与选择?——或者说她将用什么方法将可供选择的工作单位排序?工作选择贡献收入发展声誉工作环境生活环境B、假期旅游地点选择暑假有3个旅游胜地可供选择。
层次分析法MATLAB源程序解析

A=[ 1 2; 1/2 1];[n,n]=size(A;% 计算 A 矩阵的维度,行与列元素个数 ;B=A;%变量分配空间,加快编译速度for i=1:n;B(:,i=A(:,i/sum(A(:,i; %A矩阵各列元素除以各列均值 , 各列归一化 ; endC=ones(n,1;%建立 n 行 ,1列的单位矩阵 ;for i=1:nC(i,:=sum(B(i,:; %B矩阵各行求和 ;endw=ones(n,1;%建立 n 行 ,1列的单位矩阵 ;w=C(:,1/sum(C(:,1; %C矩阵各列元素除以各列均值 , 各列归一化 ; disp('权向量 ';disp(w;% 显示权向量 wD=ones(n,1;%建立 n 行 ,1列的单位矩阵 ;D=A*w;t=sum(D(:,1./w(:,1/n;disp('最大特征值 ';disp(t;% 显示最大特征值 t%一致性检验CI=(t-n/(n-1;% t-维度 n 再除以维度 n-1的值赋给 CIRI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];% 计算的标准 CR=CI/RI(n;% 计算一致性disp(['一致性值 :CR=',num2str(CR]if CR<0.10disp('此矩阵的一致性可以接受 !';disp('CI=';disp(CI;disp('CR=';disp(CR;elsedisp('此矩阵的一致性不可以接受 !';end。
MATLAB层次分析法
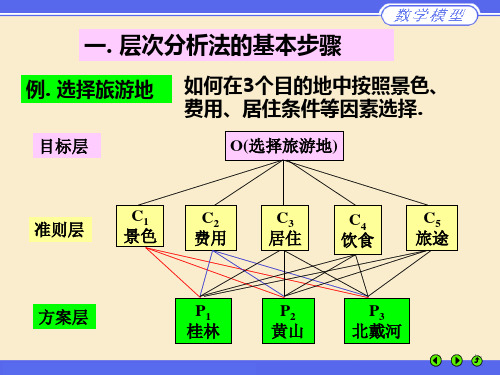
C11
C1
0
桥梁 D1
隧道 D2
渡船 D3
(1)过河效益层次结构
例3 横渡江 河、海峡方 案的抉择
经济代价 B1
过河的代价 A
社会代价 B2
环境代价 B3
投 操 冲冲 交 居 汽 对 对
入 作 击击 通 民 车 水 生
资 维 渡生 拥 搬 排 的 态
金 护 船活 挤 迁 放 污 的
C1 C2 业 方 C5 C6 物 染 破
关
献
入
展
誉
系
对外 贸易
位 置
供选择的岗位
例3 横渡江 河、海峡方 案的抉择
经济效益 B1
过河的效益 A
社会效益 B2
节 收岸 当 建安 交 自
省 入间 地 筑全 往 豪
时 C2 商 商 就 可 沟 感
间
业 业 业 靠 通 C8
C1
C3 C4 C5 C6 C7
环境效益 B3
舒进 美
适出 化
C9
方 便
Ci : C j aij
A
(aij )nn , aij
0,
a ji
1 aij
选 择
1 1/ 2 4 3 3
2
1
7
5
5
A~成对比较阵
旅 A 1/ 4 1/ 7
游 地
1/ 3
1/ 5
1/ 3 1/ 5
1 2
1/ 2 1
1/ 3
1
A是正互反阵
3 1 1
要由A确定C1,…, Cn对O的权向量
2
n
min
wi ( i1,,n ) i1
n j1 ln aij
ln wi wj
Matlab建模教程层次分析法

第八章 层次分析法层次分析法(Analytic Hierarchy Process ,简称AHP )是对一些较为复杂、较为模糊的问题作出决策的简易方法,它特别适用于那些难于完全定量分析的问题。
它是美国运筹学家T. L. Saaty 教授于70年代初期提出的一种简便、灵活而又实用的多准则决策方法。
§1 层次分析法的基本原理与步骤人们在进行社会的、经济的以及科学管理领域问题的系统分析中,面临的常常是一个由相互关联、相互制约的众多因素构成的复杂而往往缺少定量数据的系统。
层次分析法为这类问题的决策和排序提供了一种新的、简洁而实用的建模方法。
运用层次分析法建模,大体上可按下面四个步骤进行:(i )建立递阶层次结构模型;(ii )构造出各层次中的所有判断矩阵;(iii )层次单排序及一致性检验;(iv )层次总排序及一致性检验。
下面分别说明这四个步骤的实现过程。
1.1 递阶层次结构的建立与特点应用AHP 分析决策问题时,首先要把问题条理化、层次化,构造出一个有层次的结构模型。
在这个模型下,复杂问题被分解为元素的组成部分。
这些元素又按其属性及关系形成若干层次。
上一层次的元素作为准则对下一层次有关元素起支配作用。
这些层次可以分为三类:(i )最高层:这一层次中只有一个元素,一般它是分析问题的预定目标或理想结果,因此也称为目标层。
(ii )中间层:这一层次中包含了为实现目标所涉及的中间环节,它可以由若干个层次组成,包括所需考虑的准则、子准则,因此也称为准则层。
(iii )最底层:这一层次包括了为实现目标可供选择的各种措施、决策方案等,因此也称为措施层或方案层。
递阶层次结构中的层次数与问题的复杂程度及需要分析的详尽程度有关,一般地层次数不受限制。
每一层次中各元素所支配的元素一般不要超过9个。
这是因为支配的元素过多会给两两比较判断带来困难。
下面结合一个实例来说明递阶层次结构的建立。
例1 假期旅游有1P 、2P 、3P 3个旅游胜地供你选择,试确定一个最佳地点。
层次分析法matlab程序举例

层次分析法程序举例:A=[1 1/7 1/5 2 4 1/3;7 1 3 5 5 3;5 1/3 1 5 5 3;1/2 1/3 1/5 1 2 1/3;1/4 1/5 1/5 1/2 1 1/5;3 1/3 1/3 3 5 1];[v,d]=eig(A);eigenvalue=diag(d);lamda=max(eigenvalue);cil=(lamda-6)/5;crl=cil/1.26;w1=v(:,1)/sum(v(:,1))挑选合适的工作。
经双方恳谈,已有三个单位表示愿意录用某毕业生。
该生根据已有信息建立了一个层次结构模型,如下图所示。
程序:A=[1 1/7 1/5 2 4 1/3;7 1 3 5 5 3;5 1/3 1 5 5 3;1/2 1/3 1/5 1 2 1/3;1/4 1/5 1/5 1/2 1 1/5;3 1/3 1/3 3 5 1];[v,d]=eig(A);eigenvalue=diag(d);lamda=max(eigenvalue);ci=(lamda-6)/5cr=ci/1.26w1=v(:,1)/sum(v(:,1))B1=[1 1/4 1/2;4 1 3;2 1/3 1]; [v,d]=eig(B1);eigenvalue=diag(d);lamda=max(eigenvalue);cil1=(lamda-3)/2cr1=cil1/0.52b1w=v(:,1)/sum(v(:,1))B2=[1 1/4 1/5;4 1 1/2;5 2 1]; [v,d]=eig(B2);eigenvalue=diag(d);lamda=max(eigenvalue);cil2=(lamda-3)/2cr2=cil2/0.52b2w=v(:,1)/sum(v(:,1))B3=[1 1/2 2; 2 1 3;1/2 1/3 1]; [v,d]=eig(B3);eigenvalue=diag(d);lamda=max(eigenvalue);cil3=(lamda-3)/2cr3=cil3/0.52b3w=v(:,1)/sum(v(:,1))B4=[1 1/3 5; 3 1 7;1/5 1/7 1]; [v,d]=eig(B4);eigenvalue=diag(d);lamda=max(eigenvalue);cil4=(lamda-3)/2cr4=cil4/0.52b4w=v(:,1)/sum(v(:,1))B5=[1 1 7;1 1 7;1/7 1/7 1]; [v,d]=eig(B5);eigenvalue=diag(d);lamda=max(eigenvalue);cil5=(lamda-3)/2cr5=cil5/0.52b5w=v(:,1)/sum(v(:,1))B6=[ 1 7 9;1/7 1 1;1/9 1 1]; [v,d]=eig(B6);eigenvalue=diag(d);lamda=max(eigenvalue);cil6=(lamda-3)/2cr6=cil6/0.52b6w=v(:,1)/sum(v(:,1))q=[0.0091 0.0123 0.0046 0.0324 -6.6613e-016 0.0035 0.0068];r=[cr1 cr2 cr3 cr4 cr5 cr6];pp=w1'.*qqq=w1'.*r欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。
(完整版)层次分析法计算权重在matlab中的实现

信息系统分析与设计作业层次分析法确定绩效评价权重在matlab中的实现小组成员:孙高茹、王靖、李春梅、郭荣1 程序简要概述编写程序一步实现评价指标特征值lam、特征向量w以及一致性比率CR的求解。
具体的操作步骤是:首先构造评价指标,用专家评定法对指标两两打分,构建比较矩阵,继而运用编写程序实现层次分析法在MATLAB中的应用。
通过编写MATLAB程序一步实现问题求解,可以简化权重计算方法与步骤,减少工作量,从而提高人力资源管理中绩效考核的科学化电算化。
2 程序在matlab中实现的具体步骤function [w,lam,CR] = ccfx(A)%A为成对比较矩阵,返回值w为近似特征向量% lam为近似最大特征值λmax,CR为一致性比率n=length(A(:,1));a=sum(A);B=A %用B代替A做计算for j=1:n %将A的列向量归一化B(:,j)=B(:,j)./a(j);ends=B(:,1);for j=2:ns=s+B(:,j);endc=sum(s);%计算近似最大特征值λmaxw=s./c;d=A*wlam=1/n*sum((d./w));CI=(lam-n)/(n-1);%一致性指标RI=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45,1.49,1.51];%RI为随机一致性指标CR=CI/RI(n);%求一致性比率if CR>0.1disp('没有通过一致性检验');else disp('通过一致性检验');endend3 案例应用我们拟构建公司员工绩效评价分析权重,完整操作步骤如下:3.1构建的评价指标体系我们将影响员工绩效评定的指标因素分为:打卡、业绩、创新、态度与品德。
3.2专家打分,构建两两比较矩阵A =1.0000 0.5000 3.0000 4.00002.0000 1.0000 5.00003.00000.3333 0.2000 1.0000 2.00000.2500 0.3333 0.5000 1.00003.3在MATLAB中运用编写好的程序实现直接在MATLAB命令窗口中输入[w,lam,CR]=ccfx(A)继而直接得出d =1.30352.00000.51450.3926w =0.31020.46910.12420.0966lam =4.1687CR =0.0625,通过一致性检验3.4解读程序结果根据程序求解中得出的特征向量,可以得出打卡、业绩、创新以及态度品德在员工绩效评价中所占的权重分别为:0.3102、0.4691、0.1242、0.0966。
层次分析法及matlab程序

层次分析法建模层次分析法(AHP-Analytic Hierachy process)---- 多目标决策方法70 年代由美国运筹学家T·L·Satty提出的,是一种定性与定量分析相结合的多目标决策分析方法论。
吸收利用行为科学的特点,是将决策者的经验判断给予量化,对目标(因素)结构复杂而且缺乏必要的数据情况下,採用此方法较为实用,是一种系统科学中,常用的一种系统分析方法,因而成为系统分析的数学工具之一。
传统的常用的研究自然科学和社会科学的方法有:机理分析方法:利用经典的数学工具分析观察的因果关系;统计分析方法:利用大量观测数据寻求统计规律,用随机数学方法描述(自然现象、社会现象)现象的规律。
基本内容:(1)多目标决策问题举例AHP建模方法(2)AHP建模方法基本步骤(3)AHP建模方法基本算法(3)AHP建模方法理论算法应用的若干问题。
参考书: 1、姜启源,数学模型(第二版,第9章;第三版,第8章),高等教育出版社2、程理民等,运筹学模型与方法教程,(第10章),清华大学出版社3、《运筹学》编写组,运筹学(修订版),第11章,第7节,清华大学出版社一、问题举例:A.大学毕业生就业选择问题获得大学毕业学位的毕业生,“双向选择”时,用人单位与毕业生都有各自的选择标准和要求。
就毕业生来说选择单位的标准和要求是多方面的,例如:①能发挥自己的才干为国家作出较好贡献(即工作岗位适合发挥专长);②工作收入较好(待遇好);③生活环境好(大城市、气候等工作条件等);④单位名声好(声誉-Reputation);⑤工作环境好(人际关系和谐等)⑥发展晋升(promote, promotion)机会多(如新单位或单位发展有后劲)等。
问题:现在有多个用人单位可供他选择,因此,他面临多种选择和决策,问题是他将如何作出决策和选择——或者说他将用什么方法将可供选择的工作单位排序B.假期旅游地点选择暑假有3个旅游胜地可供选择。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
层次分析法建模层次分析法(AHP-Analytic Hierachy process)---- 多目标决策方法70 年代由美国运筹学家T·L·Satty提出的,是一种定性与定量分析相结合的多目标决策分析方法论。
吸收利用行为科学的特点,是将决策者的经验判断给予量化,对目标(因素)结构复杂而且缺乏必要的数据情况下,採用此方法较为实用,是一种系统科学中,常用的一种系统分析方法,因而成为系统分析的数学工具之一。
传统的常用的研究自然科学和社会科学的方法有:机理分析方法:利用经典的数学工具分析观察的因果关系;统计分析方法:利用大量观测数据寻求统计规律,用随机数学方法描述(自然现象、社会现象)现象的规律。
基本内容:(1)多目标决策问题举例AHP建模方法(2)AHP建模方法基本步骤(3)AHP建模方法基本算法(3)AHP建模方法理论算法应用的若干问题。
参考书:1、姜启源,数学模型(第二版,第9章;第三版,第8章),高等教育出版社2、程理民等,运筹学模型与方法教程,(第10章),清华大学出版社3、《运筹学》编写组,运筹学(修订版),第11章,第7节,清华大学出版社一、问题举例:A.大学毕业生就业选择问题获得大学毕业学位的毕业生,“双向选择”时,用人单位与毕业生都有各自的选择标准和要求。
就毕业生来说选择单位的标准和要求是多方面的,例如:①能发挥自己的才干为国家作出较好贡献(即工作岗位适合发挥专长);②工作收入较好(待遇好);③生活环境好(大城市、气候等工作条件等);④单位名声好(声誉-Reputation);⑤工作环境好(人际关系和谐等)⑥发展晋升(promote, promotion)机会多(如新单位或单位发展有后劲)等。
问题:现在有多个用人单位可供他选择,因此,他面临多种选择和决策,问题是他将如何作出决策和选择?——或者说他将用什么方法将可供选择的工作单位排序?工作选择贡献收入发展声誉工作环境生活环境B.假期旅游地点选择暑假有3个旅游胜地可供选择。
例如:1P :苏州杭州,2P 北戴河,3P 桂林,到底到哪个地方去旅游最好?要作出决策和选择。
为此,要把三个旅游地的特点,例如:①景色;②费用;③居住;④环境;⑤旅途条件等作一些比较——建立一个决策的准则,最后综合评判确定出一个可选择的最优方案。
目标层准则层方案层C .资源开发的综合判断7种金属可供开发,开发后对国家贡献可以通过两两比较得到,决定对哪种资源先开发,效用最用。
二、问题分析:例如旅游地选择问题:一般说来,此决策问题可按如下步骤进行:(S1)将决策解分解为三个层次,即:目标层:(选择旅游地) 准则层:(景色、费用、居住、饮食、旅途等5个准则)方案层:(有1P ,2P ,3P 三个选择地点)并用直线连接各层次。
(S2)互相比较各准则对目标的权重,各方案对每一个准则的权重。
这些权限重在人的思维过程中常是定性的。
例如:经济好,身体好的人:会将景色好作为第一选择;中老年人:会将居住、饮食好作为第一选择; 经济不好的人:会把费用低作为第一选择。
而层次分析方法则应给出确定权重的定量分析方法。
(S3)将方案后对准则层的权重,及准则后对目标层的权重进行综合。
(S4)最终得出方案层对目标层的权重,从而作出决策。
以上步骤和方法即是AHP 的决策分析方法。
三、确定各层次互相比较的方法——成对比较矩阵和权向量在确定各层次各因素之间的权重时,如果只是定性的结果,则常常不容易被别人接受,因而Santy 等人提出:一.致矩阵法.... 即:1. 不把所有因素放在一起比较,而是两两相互比较2. 对此时採用相对尺度,以尽可能减少性质不同的诸因素相互比较的困难,提高准确度。
因素比较方法 —— 成对比较矩阵法:目的是,要比较某一层n 个因素n C C C , ,,21 对上一层因素O 的影响(例如:旅游决策解中,比较景色等5个准则在选择旅游地这个目标中的重要性)。
採用的方法是:每次取两个因素i C 和j C 比较其对目标因素O 的影响,并用ij a 表示,全部比较的结果用成对比较矩阵表示,即:)1( 1,0 ,)(=⋅=>=ij ij ijji ij nxn ij a a a a a a A 或 (1) 由于上述成对比较矩阵有特点: jiij ij ij a a a a A 1 ,0 , )(=>= 故可称A 为正互反矩阵:显然,由 jiij a a 1=,即:1=⋅ji ij a a ,故有:1=ji a例如:在旅游决策问题中:2112=a =(费用)(景色)21C C 表示:⎩⎨⎧2O 1O 21的重要性为(费用)对目标的重要性为景色)对目标(C C故:),费用重要性为即景色重要性为21(2112=a14413==a = (居住条件)(景色)31C C 表示:⎩⎨⎧1O C 4O (31的重要性为(居住条件)对目标的重要性为景色)对目标C 即:景色为4,居住为1。
17723==a =(居住条件)(费用)32C C 表示:⎩⎨⎧1O C 7O (32的重要性为(居住条件)对目标的重要性为费用)对目标C即:费用重要性为7,居住重要性为1。
因此有成对比较矩阵:⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=1135131112513131211714155337412121A 问题:稍加分析就发现上述成对比较矩阵的问题: ① 即存在有各元素的不一致性,例如:既然:41114a ;22113313113212112==⇒===⇒==a a C C a C C a 所以应该有:188412131231213223======C C C C a a C C a而不应为矩阵A 中的1723=a②成对比较矩阵比较的次数要求太 ,因:n 个元素比较次数为:!2)1(2-=n n C n 次, 因此,问题是:如何改造成对比较矩阵,使由其能确定诸因素n C C , ,1 对上层因素O 的权重?对此Saoty 提出了:在成对比较出现不一致情况下,计算各因素n C C , ,1 对因素(上层因素)O 的权重方法,并确定了这种不一致的容许误差范围。
为此,先看成对比较矩阵的完全一致性——成对比较完全一致性四:一致性矩阵Def :设有正互反成对比较矩阵:⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=============== 1 a , , 1 , , 1 1nn 221122222212211121121111n n n n n n j iij nn nn W W W W a W W a W W a W W a W W a W W a W W a W W a W W a A(4) 除满足:(i )正互反性:即)1 ( 10=⋅=>ji ij jiij ij a a a a a 或 而且还满足:(ii )一致性:即n 2, 1,j i, ==⋅==ha h a a k a a a a j i kj i j i ij //有点点错误 则称满足上述条件的正互反对称矩阵A 为一致性矩阵,简称一致阵。
一致性矩阵(一致阵)性质:性质1:A 的秩 Rank(A)=1//显然A 的唯一非0的特征根为n性质2:A 的任一列(行)向量都是对应特征根n 的特征向量:即有(特征向量、特征值):⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n n n n n n W W W W W W W W W W WW W W W W W W A212221212111,则向量⎪⎪⎪⎪⎪⎭⎫⎝⎛=321W W W W满足:W n nW nW nW W W W W W W W W W W W W W W W W A n n n nn n n=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=21212112111 即: 0)(=-W nI A我的理解:通过A(变换A 与W 中的元素有关)变换将一致W 矩阵变成权向量W(特征向量),如果正互反矩阵W ’接近一致矩阵,同样的道理变换A 可以将W ’变成权向量(这里的权向量与W ’稍有不同)启发与思考:既然一致矩阵有以上性质,即n 个元素W 1, W 2, W 3 , …W n 构成的向量⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n W W W W 21是一致矩阵A 的特征向量,则可以把向量W 归一化后的向量ω,看成是诸元素W 1, W 2,W 3 , …W n目标的权向量,因此,可以用求A 的特征根和特征向量的办法,求出元素W 1, W 2, W 3 , …W n 相对于目标O 的劝向量。
解释:一致矩阵即:n 件物体n M M M , , ,21 ,它们重量分别为n W W W , , ,21 ,将他们两两比较重量,其比值构成一致矩阵,若用重量向量⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n W W W W 21右乘A ,则:()⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧∑⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛称特征根法,求权向量的方法量权向量,此种用特征向为即对上层因素O的权重,,C ,,C C ,就表示诸因素=W=则归一化后的特征向量,=:重量向量 为特征根的特征向量为以的特征根为n 21 1W W W W ,121 i n W W W n n A 分析:若重量向量⎪⎪⎪⎪⎪⎭⎫⎝⎛=n W W W W 21未知时,则可由决策者对物体n M M M , , ,21 之间两两相比关系,主观作出比值的判断,或用Delphi (调查法)来确定这些比值,使A 矩阵(不一定有一致性)为已知的,并记此主观判断作出的矩阵为(主观)判断矩阵A ,并且此A (不一致)在不一致的容许范围内,再依据:A的特征根或和特征向量W 连续地依赖于矩阵的元素ija ,即当ija 离一致性的要求不太远时,A 的特征根i 和特征值(向量)W 与一致矩阵A 的特征根λ和特征向量W 也相差不大的道理:由特征向量W 求权向量W 的方法即为特征向量法,并由此引出一致性检查的方法。
问题:Remark以上讨论的用求特征根来求权向量W 的方法和思路,在理论上应解决以下问题: 1. 一致阵的性质1是说:一致阵的最大特征根为n (即必要条件),但用特征根来求特征向量时,应回答充分条件:即正互反矩阵是否存在正的最大特征根和正的特征向量?且如果正互反矩阵A 的最大特征根n =max λ时,A 是否为一致阵?2. 用主观判断矩阵A 的特征根λ和特征向量W 连续逼近一致阵A 的特征根λ和特征向量W 时,即: 由λλ=→k kk lim得到:W W k k =∞→lim即: A A k k =∞→lim是否在理论上有依据。
3.一般情况下,主观判断矩阵A 在逼近于一致阵A 的过程中,用与A 接近的*A 来代替A ,即有A A ≈*,这种近似的替代一致性矩阵A 的作法,就导致了产生的偏差估计问题,即一致性检验问题,即要确定一种一致性检验判断指标,由此指标来确定在什么样的允许范围内,主观判断矩阵是可以接受的,否则,要 两两比较构造主观判断矩阵。
