《抽屉原理》公开课PPT课件
合集下载
《抽屉原理》(PPT课件

算法分析
在算法分析中,抽屉原理可以用于分析算法的时间复杂度和空间复杂度,以及确 定算法的最坏情况下的性能。
在日常生活中的应用
资源分配
在资源分配问题中,可以将资源视为抽屉,将待分配的物品 或任务视为物体,根据抽屉原理得出最优的分配方案。
排队理论
在排队理论中,抽屉原理可以用于分析排队系统的性能和稳 定性,以及确定最优的排队策略。
有限制的抽屉原理的证明
有限制的抽屉原理是指
如果 n+1 个物体要放入 n 个容器中,且每个容器最多只能容纳 k 个物体(k < n),那么至少有一个容器包含两个或以上的物体。
证明方法
假设 n+1 个物体放入 n 个容器中,且每个容器最多只能容纳 k 个物体(k < n)。如果存在一个容器只包含一个物体,那么我们可以将这个物体放入另一个 容器中,从而证明了至少有一个容器包含两个或以上的物体。
在数论中的应用
质数分布
根据抽屉原理,如果将自然数按 照质数和非质数进行分类,则质 数在自然数中的比例趋近于 $frac{1}{2}$。
同余方程
在解同余方程时,可以将模数视 为抽屉,方程的解为物体,根据 抽屉原理得出解的存在性和个数 。
在计算机科学中的应用
数据结构
在计算机科学中,抽屉原理可以应用于各种数据结构的设计和分析,如数组、链 表、哈希表等。
现代研究
现代数学研究中对抽屉原理进行了深入的探讨和研究,不断拓展其 应用范围和理论体系。
02
抽屉原理的证明特殊形式,其基本思想是
如果 n 个物体要放入 n-1 个容器中,且每个容器至少有一个物体,则至少有一个容器包含两个或以上的物体。
证明方法
假设 n 个物体放入 n-1 个容器中,且每个容器至少有一个物体。如果存在一个容器只包含一个物体,那么我们 可以将这个物体放入另一个容器中,从而证明了至少有一个容器包含两个或以上的物体。
在算法分析中,抽屉原理可以用于分析算法的时间复杂度和空间复杂度,以及确 定算法的最坏情况下的性能。
在日常生活中的应用
资源分配
在资源分配问题中,可以将资源视为抽屉,将待分配的物品 或任务视为物体,根据抽屉原理得出最优的分配方案。
排队理论
在排队理论中,抽屉原理可以用于分析排队系统的性能和稳 定性,以及确定最优的排队策略。
有限制的抽屉原理的证明
有限制的抽屉原理是指
如果 n+1 个物体要放入 n 个容器中,且每个容器最多只能容纳 k 个物体(k < n),那么至少有一个容器包含两个或以上的物体。
证明方法
假设 n+1 个物体放入 n 个容器中,且每个容器最多只能容纳 k 个物体(k < n)。如果存在一个容器只包含一个物体,那么我们可以将这个物体放入另一个 容器中,从而证明了至少有一个容器包含两个或以上的物体。
在数论中的应用
质数分布
根据抽屉原理,如果将自然数按 照质数和非质数进行分类,则质 数在自然数中的比例趋近于 $frac{1}{2}$。
同余方程
在解同余方程时,可以将模数视 为抽屉,方程的解为物体,根据 抽屉原理得出解的存在性和个数 。
在计算机科学中的应用
数据结构
在计算机科学中,抽屉原理可以应用于各种数据结构的设计和分析,如数组、链 表、哈希表等。
现代研究
现代数学研究中对抽屉原理进行了深入的探讨和研究,不断拓展其 应用范围和理论体系。
02
抽屉原理的证明特殊形式,其基本思想是
如果 n 个物体要放入 n-1 个容器中,且每个容器至少有一个物体,则至少有一个容器包含两个或以上的物体。
证明方法
假设 n 个物体放入 n-1 个容器中,且每个容器至少有一个物体。如果存在一个容器只包含一个物体,那么我们 可以将这个物体放入另一个容器中,从而证明了至少有一个容器包含两个或以上的物体。
新课标版人教六年级数学下册《抽屉原理课件》课件

03
抽屉原理的实例
生活中的实例
公交车的座位
假设一辆公交车有4个座位,那么 不管有多少乘客,总会有至少5个 人的时候,至少有一个人会没有 座位。
生日问题
在一年中有365天,如果有366人 ,那么至少有一天是两个人同一 天生日。
数学中的实例
整除问题
如果一个数除以3余1,除以5余2, 除以7余3,那么这个数最小是多少 ?这就是抽屉原理的一个应用。
新课标版人教六年级数学下 册《抽屉原理》课件
contents
目录
• 抽屉原理简介 • 抽屉原理的证明 • 抽屉原理的实例 • 抽屉原理的练习题及解析 • 抽屉原理的扩展知识
01
抽屉原理简介
抽屉原理的定义
抽屉原理,也称为鸽巢原理,是一种组合数学的基本原理,它指出如果n个物体 要放到m个容器中去,且n>m,则至少有一个容器包含两个或两个以上的物体。
证明方法三:数学归纳法
要点一
总结词
通过数学归纳法来证明抽屉原理。
要点二
详细描述
首先验证基础情况(即n=1和n=2时)结论成立。然后假 设当n=k时结论成立,即存在k个物品放入k个抽屉中,至 少有一个抽屉中放入了多个物品。当n=k+1时,增加一个 新的物品和抽屉,由于至少有一个抽屉中已经放入了多个 物品,因此可以将新物品放入该抽屉中,从而证明了当 n=k+1时结论也成立。最后通过数学归纳法得出结论对任 意正整数n都成立。
这个原理可以用数学语言描述为:设集合A包含n个元素,集合B包含m个元素( n>m),如果对于集合A中的任意元素x,都有x属于集合B,则集合A中至少存 在一个元素y,y属于B且y不等于x。
抽屉原理的应用场景
01
《抽屉原理》公开课PPT课件

1、如果把6个苹果放入5个抽屉中,至 少有几个放到同一个抽屉里? (2个) 2、如果把7个苹果放入6个抽屉中,至 少有几个放到同一个抽屉里呢? (2个)
3、如果把100个苹果放入99个抽屉中, 至少有几个放到同一个抽屉里呢? (2个)
你有什么发现?
1、如果把6个苹果放入4个抽屉中, 至少有几个苹果被放到同一个抽 屉里呢?
( 367名学生 )→ 待分的物体 366天 ( ) → 抽屉
2. 任意的( 13 )名学生中,至少有2名学生 的生肖一样。为什么? ( ( 13名学生 12生肖 )→ )→ 待分的物体 抽屉
咱们班共40人,至少 有几人是同一属相?
• 请判断下面的说法对吗?为什么? 1、我们班的13位同学中,至少有2位同学的 生日在同一个月。 2、我校五、六年级共369人,至少有2人的生 日在同一天。
2、如果把8个苹果放入5个抽屉中, 至少有几个苹果被放到同一个抽 屉里呢?
你发现了什么规律?
只要物体数量是抽屉数 量的1倍多,总有一个抽屉 里 至少放进2个物体。
铅笔/支 5
笔筒/个 列出的算式 2 5÷2=2……1
至少数 2+1=3
7
8 19
2
3 4
பைடு நூலகம்
7÷2=3……1
8÷3=2……2 19÷4=4……3
3+1=4
2+1=3 4+1=5
20
5
20÷5=4
4
求至少数是否存在着规律呢? 我发现了(
有余数时,至少数=商+1 没余数时,至少数=商
)。
三、深入研究 验证模型
看看有几种 放法?通过 观察,你发 现了什么?
如果一共有9 7本书会怎样呢? 本书会怎样呢? 如果一共有
《抽屉原理例》课件

在计算机科学中,离散概率论也是非常重要的一环。抽屉原理在离散概率论中也有着广泛 的应用,例如在计算概率模型、设计和分析算法的正确性等方面。
计算几何
计算几何是计算机科学中的一个重要分支,它涉及到图形处理、计算机图形学等领域。抽 屉原理在计算几何中也有着重要的应用,例如在处理几何形状的交、并、差等运算时,抽 屉原理可以帮助我们理解和分析问题。
03
抽屉原理的实例
生活中的实例
鸽巢原理
如果$n$个鸽子飞进$m$个鸽巢 中,且$n > m$,那么至少有一 个鸽巢里有两只或以上的鸽子。
生日悖论
在不到33人的房间里,存在至少 两个人生日相同的概率大于50% 。
数学中的实例
整数划分问题
给定整数$n$,求证存在至少两个正 整数,它们的和等于$n$。
与组合数学的联系
抽屉原理是组合数学中的基本原理之 一,与其他组合数学原理存在密切联 系。
与概率论的关系
与其他数学分支的交叉
抽屉原理可以应用于其他数学分支中 ,如代数、几何、离散概率等。
在概率论中,抽屉原理常被用于证明 一些概率性质和结论。
06
抽屉原理的应用前景和 展望
在数学领域的应用前景
01 02
从整数到实数的推广
在整数上成立的抽屉原理可以推广到实数上。例如,如果无穷多的实数被放入有限个区间中,那么至少有一个区间包含无穷 多的实数。这个结论被称为巴拿赫定理。
另一个推广是将抽屉原理应用到测度理论中。在测度论中,一个集合的测度可以被视为“体积”,而集合的子集可以被视为 “物品”。在这种情况下,抽屉原理表明:如果无穷多的子集被放入有限个测度不为零的集合中,那么至少有一个集合包含 无穷多的子集。
组合数学
抽屉原理是组合数学中的基础原理之一,在计数、排列组合等领域有广 泛的应用。通过抽屉原理,可以解决一些经典的数学问题,如鸽巢原理 问题。
计算几何
计算几何是计算机科学中的一个重要分支,它涉及到图形处理、计算机图形学等领域。抽 屉原理在计算几何中也有着重要的应用,例如在处理几何形状的交、并、差等运算时,抽 屉原理可以帮助我们理解和分析问题。
03
抽屉原理的实例
生活中的实例
鸽巢原理
如果$n$个鸽子飞进$m$个鸽巢 中,且$n > m$,那么至少有一 个鸽巢里有两只或以上的鸽子。
生日悖论
在不到33人的房间里,存在至少 两个人生日相同的概率大于50% 。
数学中的实例
整数划分问题
给定整数$n$,求证存在至少两个正 整数,它们的和等于$n$。
与组合数学的联系
抽屉原理是组合数学中的基本原理之 一,与其他组合数学原理存在密切联 系。
与概率论的关系
与其他数学分支的交叉
抽屉原理可以应用于其他数学分支中 ,如代数、几何、离散概率等。
在概率论中,抽屉原理常被用于证明 一些概率性质和结论。
06
抽屉原理的应用前景和 展望
在数学领域的应用前景
01 02
从整数到实数的推广
在整数上成立的抽屉原理可以推广到实数上。例如,如果无穷多的实数被放入有限个区间中,那么至少有一个区间包含无穷 多的实数。这个结论被称为巴拿赫定理。
另一个推广是将抽屉原理应用到测度理论中。在测度论中,一个集合的测度可以被视为“体积”,而集合的子集可以被视为 “物品”。在这种情况下,抽屉原理表明:如果无穷多的子集被放入有限个测度不为零的集合中,那么至少有一个集合包含 无穷多的子集。
组合数学
抽屉原理是组合数学中的基础原理之一,在计数、排列组合等领域有广 泛的应用。通过抽屉原理,可以解决一些经典的数学问题,如鸽巢原理 问题。
《抽屉原理》公开课PPT课件
原理三: 把M个物体放进N个抽屉,且满足M÷N=n……k(其中M、 N、n、k都为正整数),则至少有一个抽屉里至少要放进n+1 个物体
4 人是同一属相? 习题2.பைடு நூலகம்意找40人,至少有_____
二、一展身手
2 只兔 1.把19只小兔子关在18个笼子里,至少有____ 子要关在同一个笼子里?
2.把98个苹果放到10个抽屉中, 无论怎么放, 我们 一定能找到一个含苹果最多的抽屉,它里面至少含 有 10 个苹果。 3.数学课外活动小组38名学生,他们中年龄最大的 15岁,最小的13岁,试证:总可以找到两名学生是 同年同月出生的.
神奇现象:
1.任意给出5个整数,求证:从中必能选出3个,使它们的和 能被3整除. 2.在任意6个人的集会上,求证:总有3个人互相认识或者总 有3个人互不认识. 3.围着一张可以转动的圆桌,均匀地放8把椅子,在桌上对着 椅子放有8人的名片,8人入座后,发现谁都没有对着自己的 名片;求证:适当地转动桌子,最少能使两人对上自己的名 片.
一、动手做一做
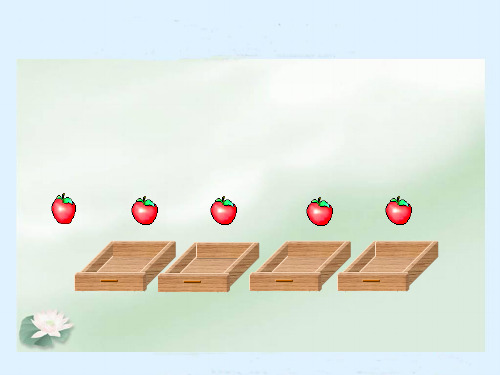
例1.把4个苹果放入3个抽屉中有几种方法? (4,0,0) (3,1,0) (2,2,0) (2,1,1)
总结:不管怎么放总有一个抽屉里至少放进2个苹果 例2.把5个苹果放进4个抽屉里面,总有一个抽屉至少多少 个苹果?
原理一: 把N+1个物件放进N个抽屉里,则其中必有一个抽屉里 面至少有两个物件
习题1.任意的13 个人中,至少有2名学生的生肖一样。 为什么?
2个 例3.把11个苹果放进9个抽屉里面,总有一个抽屉至少___ 苹果?
原理二: 把M个物件放进N(M>N)个抽屉里,则其中必有一个抽屉 里面至少有两个物件
例4.把12个苹果放进5个抽屉里面,总有一个抽屉至少 ______ 3 个苹果? 12÷5=2……2
《抽屉原理》第-课PPT课件

有限制条件的抽屉原理证明
有限制条件的抽屉原理是指在某些特 定条件下,抽屉原理仍然成立。例如 ,当容器的形状、大小、质量等因素 受到限制时,抽屉原理仍然适用。
证明方法:根据具体条件,通过数学 推导和逻辑推理,证明在满足特定条 件下,抽屉原理仍然成立。
抽屉原理的推广证明
抽屉原理的推广是指将抽屉原理应用到更广泛的领域和问题中,例如集合论、概 率论、组合数学等。
有n个人和n把椅子(n>3),将它们 随机就座。求证:至少有两把椅子被 两个人同时坐。
5
有100枚硬币,将它们放入10个盒子 里,每个盒子至少放10枚硬币。求证: 至少有一个盒子里放了10枚硬币。
05 总结与思考
CHAPTER
抽屉原理的重要性和意义
数学基础
抽屉原理是组合数学中的 基础原理,对于理解许多 数学概念和证明许多数学 定理具有重要意义。
《抽屉原理》第-课ppt课件
目录
CONTENTS
• 抽屉原理简介 • 抽屉原理的应用 • 抽屉原理的证明 • 抽屉原理的练习题 • 总结与思考
01 抽屉原理简介
CHAPTER
抽屉原理的定义
抽屉原理
如果n+1个物体要放入n个抽屉中 ,那么至少有一个抽屉包含两个 或两个以上的物体。
数学表达
如果将m个物体放入n个抽屉中 (m>n),那么至少有一个抽屉包 含多于一个物体。
进阶练习题
01
02
03
总结词
考察较复杂情况下的抽屉 原理应用
3
有100个苹果和91个抽屉, 要将苹果放入抽屉中,至 少有一个抽屉里放了多少 个苹果?
4
有1000只鸽子飞过天空, 它们要飞进100个鸽笼里, 至少有一个鸽笼里飞进了 几只鸽子?
(完整)抽屉原理精品PPT资料精品PPT资料

但他们也刚愎自用,目中无人,得罪了齐国的宰相晏婴。
问题3:把 11 本书放进 4 个抽屉中,不管怎么放, 总有一个抽屉至少放进2个物品。
公孙接、田开疆都觉得自己的功劳确实不如古冶子大,感到羞愧难当,赶忙让出桃子。
2、把摆的结果用喜欢的方式记录下来。
总有一个抽屉至少放进( )本书? 但他们也刚愎自用,目中无人,得罪了齐国的宰相晏婴。
书本数 抽屉数 商 余数 至少数
并且觉得自己功劳不如人家,却抢着要吃桃子,实在丢人,是好汉就没有脸再活下去,于是都拔剑自刎了。
第三关:咱们班上有58个同学,至少有( )人在
三名勇士都认为自己的功劳很大,应该单独吃一个桃子。
总有一个笔筒里 公孙接、田开疆都觉得自己的功劳确实不如古冶子大,感到羞愧难当,赶忙让出桃子。
问题3:把 11 本书放进 4 个抽屉中,不管怎么放, 总有一个抽屉至少放进( )本书?
问题1:把 7 本书放进 2 个抽屉中,不管怎么放,
总有一个抽屉至少放进(抽屉中,不管怎么放,
总有一个抽屉至少放进( )本书? 一幅扑克,拿走大、小王后还有52张牌,请你任意抽出其中的5张牌,至少有( )张同花色,为什么?
7÷5=1……2
至少数=1+1=2(只)
第一关:13个同学坐5张椅子,至少有( 3 )个同
学坐在同一张椅子上。
第二关:34个小朋友要进4间屋子,至少有( 9 )个
小朋友要进同一间屋子。
第三关:咱们班上有58个同学,至少有( 5 )人在
同一个月出生。
第四关:从街上人群中任意找来20个人,可以确定,
至少有( 2 )个人属相相同。
最先是由19世纪的德国数学家
6
5
2
把4枝笔放入3个笔筒里,有几种不同的放法?
抽屉原理课件ppt

20÷12=1(个)……8(个)
1+1=2(个)
拓展训练:
从扑克牌中取出两张王牌,在剩下的52张扑克 牌任意抽牌。 (1)从中抽出18张牌,至少有几张是同花色?
18÷4=4(张)… …2 (张) 4+1=5(张) 答:至少有5张是同花色。 (2)从中抽出20张牌,至少有几张数字相同?
20÷13=1(张)… …7(张) 1+1=2(张) 答:至少有2张数字相同。
想一想:
把5支笔放在4个笔筒里, 还是不管怎么放,总有一个笔 筒里至少放进了几支笔吗? 为什么? 把6支笔放在5个笔筒里呢? 把10支笔放在9个笔筒里呢?
做一做: 7只鸽子飞回5个鸽舍,至少有几只鸽子
要飞进同一个鸽舍?为什么?
把7只鸽子平均飞进5个鸽舍里,每个鸽舍飞 进1只鸽子,5个鸽舍最多飞进5只鸽子,还剩下 2只鸽子还要飞进不同的鸽舍里。所以,无论怎 么飞,至少有2只鸽子要飞进同一个笼子里。
例2、 把7本书放进3个抽屉中,
不管怎么放,总有一个抽屉至 少放进几本书。为什么?
如果8本书呢?
抽屉原理:
当物体数比抽屉数(多)时, 我们尽可能的把物体平均分,不管 怎么放,总有一个抽屉至少放进 (商+1)个物体。
灵活运用,解决问题:
1、34个小朋友要住进4间屋子,至少有( 9 )
个小朋友要住进同一间屋子。
34÷4=8(个)……2(个)
8+1=9(个)
2、13个同学坐5张椅子,至少有(3 )个
同学坐在同一张椅子上。 13÷5=2(个)……3(个)
2+1=3(个)
3、咱们班上有58个同学,至少有 ( 5 )人在同一个月出生。
58÷12=4(人)……10(人)
1+1=2(个)
拓展训练:
从扑克牌中取出两张王牌,在剩下的52张扑克 牌任意抽牌。 (1)从中抽出18张牌,至少有几张是同花色?
18÷4=4(张)… …2 (张) 4+1=5(张) 答:至少有5张是同花色。 (2)从中抽出20张牌,至少有几张数字相同?
20÷13=1(张)… …7(张) 1+1=2(张) 答:至少有2张数字相同。
想一想:
把5支笔放在4个笔筒里, 还是不管怎么放,总有一个笔 筒里至少放进了几支笔吗? 为什么? 把6支笔放在5个笔筒里呢? 把10支笔放在9个笔筒里呢?
做一做: 7只鸽子飞回5个鸽舍,至少有几只鸽子
要飞进同一个鸽舍?为什么?
把7只鸽子平均飞进5个鸽舍里,每个鸽舍飞 进1只鸽子,5个鸽舍最多飞进5只鸽子,还剩下 2只鸽子还要飞进不同的鸽舍里。所以,无论怎 么飞,至少有2只鸽子要飞进同一个笼子里。
例2、 把7本书放进3个抽屉中,
不管怎么放,总有一个抽屉至 少放进几本书。为什么?
如果8本书呢?
抽屉原理:
当物体数比抽屉数(多)时, 我们尽可能的把物体平均分,不管 怎么放,总有一个抽屉至少放进 (商+1)个物体。
灵活运用,解决问题:
1、34个小朋友要住进4间屋子,至少有( 9 )
个小朋友要住进同一间屋子。
34÷4=8(个)……2(个)
8+1=9(个)
2、13个同学坐5张椅子,至少有(3 )个
同学坐在同一张椅子上。 13÷5=2(个)……3(个)
2+1=3(个)
3、咱们班上有58个同学,至少有 ( 5 )人在同一个月出生。
58÷12=4(人)……10(人)
人教版小学六年级下学期数学《抽屉原理》公开课PPT课件

感谢聆听
不足之处请大家批评指导
Please Criticize And Guide The Shortcomings
演讲人:XXXXXX 时 间:XX年XX月XX日
的,后人们为了纪念他从这么平
凡的事情中发现的规律,就把这
个规律用他的名字命名,叫“狄
里克雷原理”,又把它叫做“鸽
巢原理”,还把它叫做 “抽屉原
理”。
绿色圃中小学教育网
结束语
当你尽了自己的最大努 力时,失败也是伟大的 ,所以不要放弃,坚持
就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up,
至少
老师任意点13位同学 就可以肯定,至少有2 个同学的生日是在同 一个月,你们信吗?
绿色圃中小学教育网
★先猜一猜,
再动手放一放,
看看有哪些不同
放法?
把4枝铅笔放进3个 文具盒里,不管怎 么放,总有一个文
★你的猜想对 吗?和组内同学 说一说你的理由。
具盒里至少放进(2)
枝铅笔。
绿色圃中小学教育网
(人教新课标)六年级数学下册 绿色圃中小学教育网
抽屉原理
绿色圃中小学教育网
教学目标
• 1.初步理解“抽屉原理”的一般形式,会 用假设法解决抽屉问题,通过分析,推理 解决这类抽屉问题。
• 2.通过实验、观察、分析、推理等数学活 动,经历“抽屉原理”的探究过程,提高 同学们推理的能力。
绿色圃中小学教育网
四 三 二一 总结假设增加
我把情况记 录下来.
0
0 (4,4 0,0)
绿色圃中小学教育网
我把情况记 录下来.
《抽屉原理》教学课件

鸽巢原理的变种
VS
应用在概率论中的抽屉原理是指将抽屉原理与概率论相结合,以解决概率论中的一些问题。
详细描述
在概率论中,抽屉原理可以应用于解决一些概率分布的问题。例如,可以将抽屉原理应用于计算概率密度函数或者概率分布函数的性质。通过将抽屉原理与概率论相结合,可以更好地理解概率分布的性质和特点,并解决一些概率论中的难题。
整数划分问题
应用抽屉原理解析
总结词
整数划分问题是指将一个正整数拆分成若干个正整数之和。抽屉原理在这个问题中发挥了关键作用,通过巧妙地将各个整数视为“抽屉”,而将划分方式视为“物品”,利用抽屉原理证明了某些特定划分的不可能性。
详细描述
04
CHAPTER
抽屉原理的变种与推广
总结词
有限制的鸽巢原理的推广是指将有限制的鸽巢原理应用到更广泛的场景中,以解决更为复杂的问题。
抽屉原理的定义
19世纪中叶,德国数学家鲁布里奇正式提出了抽屉原理这一名称,并进行了系统的研究和发展。
随着组合数学的发展,抽屉原理在数学、计算机科学、信息科学等领域得到了广泛的应用和推广。
抽屉原理的起源可以追溯到古希腊数学家欧几里得,他在《几何原本》中提出了类似的原理。
抽屉原理的起源与发展
实例分析
提供多种形式的练习题,让学生通过变式训练加深对抽屉原理的理解和应用。
变式训练
组织小组讨论,让学生互相交流思路和方法,拓展解决问题的思路和途径。
小组讨论
如何引导学生应用抽屉原理解决问题
THANKS
感谢您的观看。
总结词
应用在概率论中的抽屉原理
05
CHAPTER
抽屉原理的教学建议
通过日常生活中的实例,如“四个苹果放入三个抽屉,至少有一个抽屉有两个苹果”来引入抽屉原理的概念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、利用模型 解决问题
把13只小兔子关在5个笼 子里,至少有多少只兔 子要关在同一个笼子里?
智慧城堡
加油啊!综合应用:Fra bibliotek1、34个小朋友要进4间屋子,至少有( 9)个小朋
友要进同一间屋子。
3 2、13个同学坐5张椅子,至少有( )个同学坐在
同一张椅子上。
8 3、新兵训练,战士小王6枪命中了43环,战士小王
三、深入研究 验证模型
看看有几种 放法?通过 观察,你发 现了什么?
如如果果一一共共有有97本本书书会会怎怎样样呢呢??
计算绝招 至少数=商数+1
“ 抽屉原理”又称“鸽笼原理”,最先 是由19世纪的德国数学家狄利克雷提出来的, 所以又称“狄里克雷原理”,这一原理在解 决实际问题中有着广泛的应用。“抽屉原理” 的应用是千变万化的,用它可以解决许多有 趣的问题,并且常常能得到一些令人惊异的 结果。下面我们应用这一原理解决问题。
二、逐步深入 建立模型
★ 如如如果果果把把把1516780枝0枝枝0枝铅0铅铅枝铅笔笔笔铅笔放放放笔放入入入放入4567个入9个个个杯9杯杯9杯子子9子子个中呢呢呢杯,???子会呢是? 什么结果呢?
如果铅笔的数量不是比杯子的数量多1呢? 这个结论还成立吗?
思考:把把把579枝枝枝铅铅铅笔笔笔放放放入入入45个个3杯个杯子子杯中中子呢呢,?总? 有 一个杯子里至少有几支铅笔?
咱们班共38人,至少 有几人是同一属相?
把3本书放进两个抽屉,有几种放法?试试看。
方法一
(3,0)
方法二
(2,1)
(人教新课标)六年级数学下册
一、动手操作 感知模型
小组合作探究:
把4枝笔放入3个杯子中有几种方法?
至少有2枝放 进同一个笔筒。
如果我们先让每个笔筒里放1枝笔,最
多放3枝。剩下的1枝还要放进其中的一
个笔筒。所以不管怎么放,至少有2枝 笔放进同一个笔筒里。
总有一枪至少打中( )环。
5 4、咱们班上有58个同学,至少有( )人在同一个
月出生。
2 5、从街上人群中任意找来20个人,可以确定,至少
有( )个人属相相同。
从扑克牌中取出两张王牌,在剩下的52张扑克 牌任意抽牌。 (1)从中抽出18张牌,至少有几张是同花色?
18÷4=4(张)… …2 (张) 4+1=5(张) 答:至少有5张是同花色。 (2)从中抽出20张牌,至少有几张数字相同?
20÷13=1(张)… …7(张) 1+1=2(张) 答:至少有2张数字相同。
考考你
1. 任意的(367 )名学生中,至少有2名学生 在同一天过生日。为什么?
( 367名学生 )→ 待分的物体 ( 366天 ) → 抽屉
2. 任意的( 13 )名学生中,至少有2名学生 的生肖一样。为什么?
( 13名学生 )→ 待分的物体 ( 12生肖 ) → 抽屉
