电场强度电通量高斯定理
5-4 电场强度通量 高斯定理

5-4 电场强度通量
高斯定理
正点电荷与负点电荷的电场线
+
-
5-4 电场强度通量
高斯定理
一对等量正点电荷的电场线
+
+
5-4 电场强度通量
高斯定理
一对等量异号点电荷的电场线
-
+
5-4 电场强度通量
高斯定理
一对不等量异号点电荷的电场线
2q
-q
5-4 电场强度通量
高斯定理
带电平行板电容器的电场线
+ + + + + + + + + + + + +
i 1 n
3 高斯定理的讨论 (1) 高斯面:闭合曲面. (2) 电场强度:所有电荷的总电场强度. (3) 电通量:穿出为正,穿进为负.
(4) 仅面内电荷对电通量有贡献.
5-4 电场强度通量
四 高斯定理应用举例 用高斯定理求电场强度的一般步骤为 对称性分析; 根据对称性选择合适的高斯面; 应用高斯定理计算.
高斯定理
1 Φe E dS ε0 S
q in i
i 1
n
5-4 电场强度通量
高斯定理
例2 设有一半径为R , 均匀带电Q 的球面. 求球面内外任 意点的电场强度. 解 高斯面:闭合球面 对称性分析:球对称 (1) 0 r R E dS 0 E 0
in ei
E
1 n in SE dS ε0 qi i 1
dS
s
qi
5-4 电场强度通量
高斯定理
2 高斯定理 在真空中静电场,穿过任一闭合曲面的电场强度通量,
电场强度通量

(2)当r>R 时,
q l
E 2 0 r
均匀带电圆柱面的电场分布
r
l
E Er 关系曲线
2 0 R
r 1
0
R
r
高斯定理的应用
例3 均匀带电无限大平面的电场. 解:电场分布也应有面对称性,
方向沿法向。
E
E
σ
高斯定理的应用
作轴线与平面垂直的圆柱形高斯面,底面积为 S,两底面到带电平面距离相同。
高斯定理的应用
3. 高斯定理的应用
条件: 电荷分布具有较高的空间对称性
1. 均匀带电球面的电场 2. 均匀带电圆柱面的电场 3. 均匀带电无限大平面的电场
高斯定理的应用
例1. 均匀带电球面的电场,球面半径为R,带电为q。
解: 电场分布也应有球对称性,方向沿径向。
作同心且半径为r的高斯面.
S E dS
0
合球面的电通量都相等。
高斯定理
(2)高斯定理的验证:
①当点电荷在球心时
②任一闭合曲面S´包围点电荷
e
S
E
dS
q
0
作以q为中心的球面S,由于
电力线的连续性,通过闭合曲面
S和球面S´的电力线根数相等。
因此通过S和S´的电通量相等,
均为
e
S
E
dS
q
0
S
q+
r
S´
高斯定理
(2)高斯定理的验证:
§8-3 高斯定理
1. 电场强度通量 2. 高斯定理 3. 高斯定理的应用
电场强度通量
1. 电场强度通量
(1)定义:通过电场中任一给定面的电力线总数,称
为通过该面的电场强度通量或电通量,用Ψ表e 示。
高斯定理求电场强度

高斯定理求电场强度
高斯定理是电学中的一项基本定理,用于求解电场强度。
它是由德国数学家卡尔·弗里德里希·高斯于18世纪末提出的。
在数学上,高斯定理也叫做散度定理,它可以将一个三维空间中的向量场在某个闭合曲面上的通量与该向量场在该曲面所包围的体积积分相联系。
在电学中,高斯定理用于求解电场强度。
它表明:一个电场从一个闭合曲面内通过的电通量等于该曲面内的电荷量的比值。
具体来说,高斯定理可以表示为:
∮S E·dS = Q/ε0
其中,S代表一个闭合曲面,E代表电场强度,Q代表该曲面内的总电荷量,ε0代表真空介电常数。
左侧的积分表示电场向曲面S的法向量的通量,右侧的比值表示该曲面内的总电荷量。
因此,如果我们已知一个由电荷产生的电场,并且想要求解该电场在一个闭合曲面内的通量,那么只需要使用高斯定理即可。
具体步骤是:选择一个适当的闭合曲面,计算该曲面内的总电荷量,然后代入高斯定理求解即可。
需要注意的是,高斯定理的适用范围是仅限于电场强度在曲面上处处连续的情况。
当电场强度在曲面上不连续时,需要使用其他方法进行求解。
电通量,高斯定理

电通量、高斯定理1、均匀电场的场强E与半径为R 的半球面的轴线平行,则通过半球面的电场强度通量φ = πR 2E ,若在半球面的球心处再放置点电荷q ,q不改变E分布,则通过半球面的电场强度通量 φ =πR 2E ±q/2ε0。
2、真空中的高斯定理的数学表达式为∑⎰=⋅0/εq s d E i s ,其物理意义是静电场是有源场。
3、一点电荷q 位于一位立方体中心,立方体边长为a ,则通过立方体每个表面的E的通量是q/6ε0;若把这电荷移到立方体的一个顶角上,这时通过电荷所在顶角的三个面E的通量是 0 ,通过立方体另外三个面的E的通量是 q/8ε0。
4、两个无限大均匀带正电的平行平面,电荷面密度分别为σ1和σ2,且σ1>σ2,则两平面间电场强度的大小是( C )(A)(B) (C)(D) 5、应用高斯定理求场强E时,要求E的分布具有对称性,对于没有对称性的电场分布,例如电偶极子产生的电场,高斯定理就不再成立,你认为这种说法:( B )(A)正确 (B)错误 (C)无法判断6、下述带电体系的场强分布可能用高斯定理来计算的是( D )(A)均匀带电圆板 (B)有限长均匀带电棒 (C)电偶极子 (D)带电介质球(电荷体密度是离球心距离r 的函数) 7、如果在静电场中所作的封闭曲面内没有净电荷,则( C )(A)封闭面上的电通量一定为零,场强也一定为零;()0212/εσσ+()021/εσσ+()0212/εσσ-()021/εσσ-(B)封闭面上的电通量不一定为零,场强则一定为零;(C)封闭面上的电通量一定为零;场强不一定为零;(D)封闭面上的电通量不一定为零;场强不一定为零。
8、无限长均匀带电圆柱体,电荷体密度为ρ,半径为R,求柱体内外的场强分布解:作一半径为r,高为h的同轴圆柱面为高斯面根据对称性分析,圆柱面侧面上任一点的场强大小相等,方向沿矢径方向⎰⎰⎰⎰⋅+⋅+⋅=⋅侧面下底上底s dEs dEs dEs dEs=⎰⋅侧面s dE=E⎰侧面ds=2rhEπ(1)r < R时, ∑=ρπhrqi2,2/2ερππhrrhE=,2ερrE=(2)r > R时, ∑=ρπhRqi2,2/2ερππhRrhE=,rRE22ερ=∴=E)(,2)(,22RrrRRrr><ερερ。
电场强度通量高斯定理

y
x + en
8 – 4 电场强度通量 高斯定理
第八章静电场
例4 无限大均匀带电平面的电场强度
无限大均匀带电平面,单位面积上的电荷,即电
r 荷面密度为 ,求距平面为 处的电场强度.
解 对称性分析:E垂直平面
选取闭合的柱形高斯面
E
dS
S'
S
0 底面积
2 S 'E S '
E
S'
0
S' E
由多个点电荷产生的电场
EE 1E 2
q
1
q2
E
dS
Φ eSEdSS E idS i
sqi
i(内S) E id S i(外 SE i) d S
i(外S) E i dS01
Φ ei(内 SE ) idS
qi
0i(内)
8 – 4 电场强度通量 高斯定理
第八章静电场
高斯定理
第八章静电场
四 高斯定理的应用
〔用高斯定理求解的静电场必须具有一定的对称性〕 其步骤为
对称性分析; 根据对称性选择适宜的高斯面; 应用高斯定理计算.
8 – 4高斯电定场理的强应度用通量 高斯定理
3. 高斯定理的应用
第八章静电场
条件: 电荷分布具有较高的空间对称性
1. 均匀带电球面的电场
2. 均匀带电圆柱面的电场
1.1 当点电荷在球心时
1.2 任一闭合曲面S包围该电荷
1.3 闭合曲面S不包围该电荷
e EdS
S
e SE dS
q
q
0
0
e EdS 0
S
1.4 闭合曲面S包围多个电荷q1-qk,同时面外也有多个
电荷qk+1-qn
电场强度通量和高斯定理

?
高斯定理的导出
点电荷电场强度公式 电场强度叠加原理
高斯 定理
点电荷位于球面中心
E
S
q 4π 0r
S
2
r
2
dS
+
Φe E dS
q 4π 0r
dS
Φe
q
0
Φe
q
4 π 0
dS' q 2
r
0
dΦe
q 4π 0r
2
dS cos
q
q2
S
0 S面内 e E dS S 1 ( q1 q2 q3 )
i
q
0
证明: 1)仅有一个点电荷
e E dS
S
Sn
B)点电荷在S面外:
A)点电荷在S面内:
E
q
+
q E dS
Sn
S
0
E
e E dS
q
q1
i
S面内电荷代数和
3) 当
e 0
时,
q 0
i
面内有净正电荷,并非 一定仅只有正电荷
+
q2
-
S
q1 q2
1 e E dS
S
当
e 0
时,
q 0
i
0 S面内q2
+
面内有净负电荷,并非 一定仅有有负电荷
S
q1 q2
i
当
e 0
i(外)
S
Ei dS 0
i(外)
Ei dS
大学物理-电场强度通量,高斯定理

2
i
0
q
i
E 4πr 0
E 4 πr
2
q
E 0
0
E
q 4 π 0 r 2
例2 计算均匀带电球体的场强分布,q , R 解: 通量
q 4 πR 3 3
qi 2 Φe E dS E 4πr S 0
r<R r>R 电量
电量
4 3 q π r i 3
S S
n
E
曲面闭合时
Φe E dS E cos dS
S S
S
dS
注: E为dS处的电场强度
n E
例 三棱柱体放置在如图所示的匀强电 场中. 求通过此三棱柱体的电场强度通量. 解
Φe Φei
i 1
5
y
N
S1
P
S2
Φe1 Φe 2
2、高斯 (Gauss) 定理 (1) 证明: 略.书P166-168 (2 )内容(书P168): 真空中 注:
1 Φe E dS
s
0
q
i 1
n
in i
①公式中S:高斯面(闭合曲面)
②穿过S面的电场强度通量e: 只由S面内的电荷决定
(如图中 q1、q2) ③ E : 面元 dS 处的场强 , 由所有电荷(面内、外电荷) 共同产生(如图中 q1、 q2 、 q3)
;
.
q 8 0
(3) 若将此电荷移到正方体的一 个顶点上,则通过整个 正方体表面的电场强度通量为
1 e E dS
s
0
q
电场的高斯定理及其应用

电场的高斯定理及其应用1. 高斯定理的背景高斯定理,也称为高斯电场定理,是电磁学中的基本定律之一。
它描述了电场通过任意闭合曲面的电通量与该闭合曲面内部的总电荷之间的关系。
这个定理是由德国数学家和物理学家卡尔·弗里德里希·高斯在19世纪初期提出的。
高斯定理在电磁学、物理学和工程学等领域有着广泛的应用。
2. 高斯定理的数学表述高斯定理的数学表述如下:对于任意闭合曲面S,电场通过S的电通量(记作ΦE)与曲面S内部的总电荷(记作q)之间存在以下关系:ΦE = ∫∫S E·dA = q / ε₀其中,E是电场强度,dA是曲面元素的面积向量,ε₀是真空的电介质常数(也称为电常数),其值约为8.85×10^-12 C2/N·m2。
3. 高斯定理的物理意义高斯定理的物理意义可以从两个方面来理解:(1)电场线与闭合曲面的关系:高斯定理说明,对于任意闭合曲面S,电场线通过S的电通量等于曲面S内部的总电荷。
这意味着,无论曲面S如何选择,只要它是闭合的,电场线穿过它的总通量都与曲面内部的电荷有关,而与曲面的形状和位置无关。
(2)电场的分布与电荷的关系:高斯定理表明,电场是通过闭合曲面的电通量的度量,而电通量与曲面内部的总电荷成正比。
这意味着,电场的强度和分布与曲面内部的电荷量有关,而与曲面的具体形状和位置无关。
4. 高斯定理的应用高斯定理在电场分析和计算中有着广泛的应用,下面列举几个常见的应用例子:(1)计算静电场中的电荷分布:通过高斯定理,可以计算静电场中某个闭合曲面内的电荷分布。
只需测量通过该曲面的电通量,然后根据电通量与电荷的关系,可以确定曲面内部的电荷量。
(2)设计电容器和绝缘材料:在电容器和绝缘材料的设计中,高斯定理可以用来分析电场的分布和电荷的积累。
通过合理选择闭合曲面的形状和位置,可以优化电场分布,提高电容器的性能和绝缘材料的可靠性。
(3)研究电磁波的传播:在研究电磁波的传播过程中,高斯定理可以用来分析电磁波在不同介质中的电场分布和电荷的变化。
104电通量高斯定理

金属导电模型
构成导体旳框架、 形状、 大小旳是那些 基本不动旳带正电荷旳原子核, 而自由电子充 斥整个导体, 属于导体共有。当有外电场存在 时, 电场与导体旳相互作用使得导体内旳自由 电子重新分布, 从而决定了导体旳电学性质。
自由电子
导体带电-q
q
25
一、 导体旳静电平衡
将导体放入电场强度为 附E0加旳电外场电场E时。, 其内部产生
E 2 0r
r
l n E n
22
总结 静电场旳高斯定理合用于一切静电场;
高斯定理并不能求出全部静电场旳分布。
高斯定理求解电场分布
E
dS
1
0
q内
场强 E 能否提出积分号
带电体电荷分 建立旳高斯 布旳对称性 面是否合适
23
10.7 静电场中旳导体
前面讨论了真空中旳静电场, 实际旳 电场中往往存在多种导体或实物介质, 这 些宏观物体旳存在会与电场产生相互作用 和相互影响, 从而出现某些新旳现象。 下 面将讨论导体在静电场中旳性质和行为。
二、电场强度通量 Φe
穿过任意曲面
旳电场线条数称为
电通量。
S
4
1.均匀场中dS 面元旳电通量
n
de dN EdS
E cos dS
E
矢量面元
dS
dS
n
dS
de E dS
2.非均匀场中曲面旳电通量
dS
S
dS E
e de SE dS
5
3. 闭合曲面电通量
E
e de SE dS
E
dS
r
11
2. 多种 电荷
E E1 E2 ... E5
q5 q3 q2
电场的电通量与高斯定理

电场的电通量与高斯定理电场的电通量是描述电场线通过一个封闭曲面的程度的物理量,它在物理学中有着重要的应用。
而高斯定理则是计算电场电通量的一种重要方法。
本文将探讨电场的电通量的概念及计算方法,以及高斯定理的原理和应用。
1. 电场的电通量电场的电通量是指单位时间内通过垂直于电场线的面积的电场线数目。
常用符号表示为Φ,单位为“麦可伏伦/米平方”(C·V/m^2)。
电通量的大小与电场线的密度有关,电场线越密集,则电通量越大。
2. 电通量的计算电通量的计算可以通过积分来实现。
设曲面S为一个封闭曲面,并在曲面上选取微小面元dS,该微小面元的面积为ΔS。
假设电场E在该面元上的投影长度为E⊥,则通过该微小面元的电场线条数为E⊥·ΔS。
将所有微小面元上的电场线条数相加,就可以得到通过整个曲面的电通量Φ,即Φ = ∫ E⊥ · dS。
3. 高斯定理的原理高斯定理主要应用于具有对称性的电场问题。
它指出,对于任意封闭曲面S,通过该曲面的电通量Φ与该封闭曲面所包围的总电荷量Q之间存在以下关系:Φ = Q/ε0,其中ε0为真空中的电介质常数,约等于8.85 × 10^-12 C^2/N·m^2。
4. 高斯定理的应用高斯定理在电场问题的求解中具有广泛的应用。
通过选择合适的封闭曲面,可以简化电场问题的求解过程。
例如,当电场具有球对称性时,可以选择以球心为中心的球面作为封闭曲面,这样可以使计算过程更加简化。
5. 实例分析考虑一个均匀带电球体,球心位于原点,半径为R,总电荷量为Q。
我们希望计算通过球面的电通量。
根据高斯定理,可以选择以球心为中心,球面为封闭曲面进行计算。
由于球对称性,电场E在球面上的大小处处相等。
根据球面积分的计算公式,可以得到Φ = E · 4πR^2。
而球内的总电荷量为Q,因此根据高斯定理,我们可以得到Φ = Q/ε0。
将上述两个等式联立,可以解得E = Q / (4πε0R^2)。
6.2电场强度通量 高斯定理
一半径为 R , 均匀带电 Q 的球体 .
E
E Qr 40 R
3
E
Q 40 r
2
O
R
r
电场强度通量
高斯定理
静电场
例 无限长均匀带电直线的电场强度 无限长均匀带电直线,电荷线密度为 ,求距 直线 处的电场强度.
r
解 对称性分析:轴对称 选取闭合的柱形高斯面 E dS
有几条电场线穿进必然有同 样数目的电场线从面内出来。
电场强度通量
高斯定理
静电场
练习1:半径为R的半球面置于电场强度为E的均匀电场 中,选半球面的外法线为面法线正方向,则通过该半球 面的电场强度通量 E 为( )
A. B. C. D.
R E
2
E
2
2R E 3R E
2
R
R E
2
2
o
r
电场强度通量
高斯定理
静电场
利用高斯定律求静电场的分布( E )
(用高斯定理求解的静电场必须具有一定的对称性)
步骤: 1.对称性分析,确定 E 的大小及方向分布特征 2.选择一合适的闭合曲面作高斯面,计算电通量及 qi
3.利用高斯定律求解 E
电场强度通量
例
高斯定理
静电场
均匀带电球壳的电场强度分布 一半径为 R , 均匀带电 Q 的薄球 壳 . 求球壳内外任意点的电场强 度.
π 2
,
Φe 0
电场强度通量
高斯定理
静电场
3. 非均匀电场或非平面情况下求电通量
d Φe E d S
Φe
E
en
d S dS en
电场强度通量 高斯定理

2、球外
rR
Q 4π 0 R 2
E
Q 4πε0 r 2
r
O
o
R
r
s
Q
电场在带电面两侧有突变。
30
5-4 电场强度通量 高斯定理
例3 静电复印机中光导硒鼓是一个圆筒,在 充电极的作用下,带有均匀的静电荷,由于 反射光的强弱使其电荷分布发生变化,这时 在电场力的吸引下把墨粉末加到光导体表面 上,“硒鼓”上形成深浅层次的墨粉图像, 最后移到复印纸上,复印出文字和图像。
电通量为零。
35
5-4 电场强度通量 高斯定理
利用高斯定理解E
E 2 π rl
内 q i i
R λ
0
i
E
内 q i
2 0l
r
内 i
E
圆柱面内 r R
q
i
0
E0
圆柱面外 r R
q
i
内 i
l
E 2π 0 r
36
5-4 电场强度通量 高斯定理
例5 无限大均匀带电平面,面密度 , 求电场强度分布。 解: 对称性:面对称 闭合面:圆柱面 通过闭合面的电通量为:
e E d S ( E1 E 2 E 3 E 4 ...) d S
S S
E
q6 q5 q3 q1 q7 q4
dS
E1 d S E 2 d S E 3 d S E 4 d S
S S S S
q1
E 2 π rh
‖ 0
E
h
r
+ + +
o
高斯定理求球体内外电场强度

高斯定理求球体内外电场强度高斯定理是电学中非常重要的定理之一,可以用来求解电场强度。
在本文中,我们将讨论如何利用高斯定理求解球体内外的电场强度。
首先,让我们来回顾一下高斯定理的表述:电通量与电场强度的积分等于该闭合曲面内的电荷量的比例,即Φ=E·S=q/ε0,其中Φ表示电通量,E表示电场强度,S表示曲面面积,q表示该闭合曲面内的电荷量,ε0为真空介电常数。
接下来,我们考虑一个半径为R的均匀带电球体,其电荷量为Q。
根据高斯定理,我们可以得知球体内外的电场强度分别为:①球体内部:由于球体内部的电荷会产生电场,因此我们需要计算球体内每一点的电荷对该点电场强度的贡献。
考虑一个以球心为原点、以r为半径的小球面,根据高斯定理,该小球面内的电通量Φ等于该小球面内的电荷量,即Φ=E·S=q/ε0。
由于球体为均匀带电球体,因此球体内每一点的电荷密度ρ=q/V=Q/(4/3πR),其中V为球体体积。
记该小球面面积为S,那么根据球体对称性,该小球面内的电场强度为E=ρ·S/(4πε0r),其中r为小球面半径。
由于球体内外电场强度方向相反,因此球体内部的电场强度为E=-ρ·S/(4πε0r),即E=-Qr/(4πε0R)。
②球体外部:由于球体外部的电荷均匀分布,因此球体外部的电场强度与球体内部的电场强度相同。
因此,球体外部的电场强度为E=Q/(4πε0r),其中r为距球心的距离。
综上所述,我们利用高斯定理求出了球体内外的电场强度。
在实际应用中,我们可以利用这一定理快速求解电场强度,以便进行电学相关问题的研究和应用。
大学物理之54电场强度通量高斯定理

(5) 静电场:有源场.
Φe SE dSε10
n
qin i
i1
四 高斯定理应用举例
用高斯定理求电场强度的一般步骤为 对称性分析; 根据对称性选择合适的高斯面; 应用高斯定理计算.
Φe SE dSε10
n
qin i
i1
例2 设有一半径为R , 均匀带电Q 的球面. 求球面内外任意点的电场强度.
-q
2 高斯定理
高斯面
在真空中静电场,穿过任一闭合曲面 的电场强度通量,等于该曲面所包围的所
有电荷的代数和除以 ε 0 .
Φe SE dSε10
n
qin i
i1
3 高斯定理的讨论
(1) 高斯面:闭合曲面. (2) 电场强度:所有电荷的总电场强度.
(3) 电通量:穿出为正,穿进为负.
(4) 仅面内电荷对电通量有贡献.
二 电场强度通量
1 定义 通过电场中某个面的电场线数
2 表述
匀强电场 , E垂直平面时.
SS
Een
E
Φe ES
二 电场强度通量
1 定义 通过电场中某个面的电场线数
2 表述
匀强电场 ,
E与平面夹角 θ.
Φe EScoθs ES
S
Sθ
en
E
非匀强电场,曲面S .
dS dSe n
d Φ e E cθ o d S s E d S
库仑定律 电场强度叠加原理
高斯 定理
高斯 (C.F.Gauss 17771855)
高 德国数学家、天文学
家和物理学家,有“数 学王子”美称,他与韦
斯 伯制成了第一台有线电
报机和建立了地磁观测 台,高斯还创立了电磁 量的绝对单位制.
高斯定理求电场强度公式

高斯定理求电场强度公式
高斯定理是物理学中一个重要的定理,它可以用于计算电场强度。
电场是一种物理现象,它是由电荷产生的力场。
电场强度是一个矢量量,它表示在某一点处的电场的大小和方向。
高斯定理的基本思想是将电场看作是电荷在空间中形成的“源”,通过计算这些“源”在某个闭合曲面内的总电通量,来求出这个曲面内的电场强度。
公式可以表示为:
∮S E·dS = Q/ε0
其中,∮S表示对曲面S的积分,E表示电场强度,dS表示曲面元素,Q表示曲面内的电荷总量,ε0表示真空介质中的电容率。
这个公式的意义是,曲面S内的所有电荷都会对曲面S上的电通量产生贡献,而曲面S外的电荷则不会。
因此,通过计算曲面S内的总电通量,我们就可以得到曲面S内的电荷总量,从而求出电场强度。
需要注意的是,曲面S必须是闭合的,这意味着曲面内部不应该有任何电荷。
如果曲面内部有电荷,那么它们也会对曲面S上的电通量产生贡献,从而影响计算结果。
曲面S的形状和大小也会影响计算结果。
如果曲面S的形状比较复杂,那么计算电通量可能会比较困难。
如果曲面S非常小,那么计
算结果可能会受到量子效应的影响。
因此,在实际应用中,我们需要根据具体情况来选择合适的曲面S。
需要注意的是,高斯定理只适用于静电场。
在动态场中,电场随着时间的变化而变化,因此不再满足高斯定理的条件。
在这种情况下,我们需要使用更加复杂的数学方法来求解电场强度。
高斯定理是求解电场强度的重要工具,它可以帮助我们更好地理解电场的本质和特性。
在实际应用中,我们需要根据具体情况来选择合适的曲面S,并注意高斯定理的适用条件。
高斯定理

p
s
命题得证。
电荷在电场中所受的力
一、点电荷在电场中所受的力
根据场强的定义:
F E q
F qE
放入电场中的一个点电荷 二、点电荷系在电场中所受的力
F q1 E1 q2 E2 qn En
i 1
qi E i
n
三、电荷连续分布的带电体在电场中所受的力
E 2 : 完整的带 “- ” 的小球在 p 处的场。 1 4 3 2 E1 4r1 r1 0 3 E1 r1 E1 r1 p 3 0 3 0 r1 r2 同理: E 2 3 r2 o1 a o2 0 r1 r2 E ( r1 r2 ) 3 0 3 0 3 0
R
举一反三: (1)两平行输电线的场强?
(2)无限长带电圆柱面的场?
r
r
E E E
l
r
rR
rR
E 0
E 20 r
E 2 0 r
同轴电缆(柱面)的场强分布?
a
b
ra
arb
E 0
E
r
rb
E 0
r
(3)无限长带电圆柱体的场?
p
E
1 s E ds qi 0
1 E cos ds 上下面 cos ds l E 侧面 0 1 0
l E 2 rl 0
E 2 0 r E 沿 r 方向
E r
l
E 2 0 r
q ds e E cos ds s 2 s 4 0 r q q q 2 ds 4r 2 s 2 40 r 40 r 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 包围q的闭合球面S的电通量——点电荷位于球面中心
E
4π
q
0r 2
dS
Φe
E dS
S
q dS
S 4 π 0r 2
1 q 4r 2 q
4 0 r 2
0
+
2. 包围 点电荷 q 的任意
封闭曲面的电通量
Φe
q
0
+
3. 不包围点电荷 q
的任意闭合面
Φe 0
q
4.点电荷系 q1,q2, qi qn , qn1, qn2, qz
解 对称性分析:轴对称 选取闭合的柱形高斯面
z en
SE dS
E dS E dS E dS
s(测面)
s ( 上底)
s (下底)
E dS E2rh
s ( 测面)
+
E
+
r h
x
+
+o
+
eenn
y
qi
内
0
h 0
E dS
内
qi
S
0
2π rhE h 0
E
2π 0r
z
+
Φe前 Φe后 Φe下
s
E
dS
0
y
P
N
ezn
o
M
en
E
en Q R x
Φe左 s左E dS ES左 cosπ ES左
Φe右 s右E dS ES右 cos ES左
Φe Φe前 Φe后 Φe左 Φe右 Φe下 0
三 、高斯定理
从数学角度看——闭合面的电通量与电荷之关系的数学表达式
qi
i 1( in )
S
0
高斯定理
在真空的静电场中,通过任意闭合曲面的电通量,
等于该闭合曲面所包围的电荷的代数和除以 0 .
(与面外电荷无关,该闭合曲面称为高斯面)
Φe
E dS
1
S
0
n
qiin
i 1
请思考:1)高斯面上的 E 与那些电荷有关 ?
s 2)哪些电荷对闭合曲面 的 Φe 有贡献 ?
+
r h
+
+o
x+
E
en y
讨论
无的 限电 大场 带叠 电加 平问 面题
0
0
0
0
0
0
E
Q
4π 0r2
S2
0
(2) 0 r R
E dS E4r2 S1 qi 0
E dS
内
qi
S2
0
E 0
rS +
+P
+
O
+ 1+ + +
+R +
+++
QE
4π 0R2
o Rr
例 无限长均匀带电直线的电场强度
无限长均匀带电直线,单位长度上的电荷,即
r 电荷线密度为 ,求距直线为 处的电场强度.
Φe
E dS
1
S
0
n
qiin
i 1
总结 1)高斯面上的电场强度为所有(内外)电荷的总电场强度. 2)高斯面为封闭曲面. 3)仅高斯面内的电荷对高斯面的电场强度通量有贡献. 4)穿进高斯面的电场强度通量为负,穿出为正. 5)静电场是有源场——静电场的性质之一.
讨论
将 q2 从 A 移到 B q2 A P*
一对等量异号点电荷的电场线
+
一对等量正点电荷的电场线
+
+
一对不等量异号点电荷的电场线
2q
q
带电平行板电容器的电场线 ++++++++++++
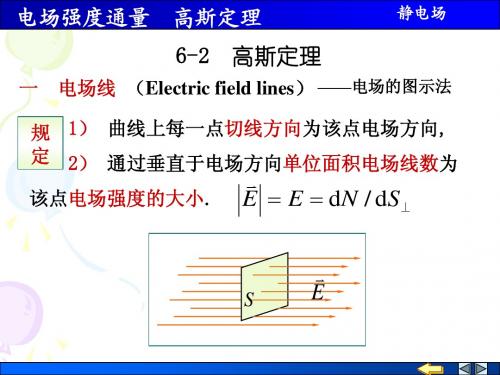
一、电场线——电场的图示法 规定
1) 曲线上每一点切线方向为该点电场方向
2) 通过垂直于电场方向单位面积电场线数 为该点电场强度的大小.(电场线密度)
E E dN / dS
电场线特性
1) 始于正电荷,止于负电荷(或来自无穷远,去 向无穷远).
2) 电场线不相交. 3) 静电场电场线不闭合.
注意
1)电场线并不真正存在. 2)电场线不是电荷运动的轨迹.
二、电场强度通量(电通量)
1.定义:通过电场中某一个面的电场线数叫做通过这 个面的电场强度通量.
2. 电通量的计算
均匀电场 ,E垂直平面
的电场中,任意闭合面的电通量 E E1 E2
qn2
q n 1
Φe
E dS S
E1 dS E2 dS En dS
q1 qqn2
s
qz
En1 dS En2 dS Ez dS
q1 q2 qn 0
0n
0
qi
i1(内) 0
0
n
Φe
E dS
E2
2
1 E1
闭合曲面的电场强度通量
dΦe E dS
Φe
E dS
S
E cosdS
S
例1 如图所示 ,有一
个三棱柱体放置在电场强度
E
200i N
C1的匀强电
场中 . 求通过此三棱柱体的
电场强度通量 .
E
S
y
o
z
dS
E
E
x
解 Φe Φe前 Φe后 Φe左 Φe右 Φe下
Φe ES
均匀电场 ,E 与平面夹角
Φe ES cos
Φe E S
S
E
en
S
E
非均匀电场电通量
dS
dS
en
dΦe E dSΦedΦe来自sE cosdS
Φe s E dS
S 为封闭曲面
1
π 2
,
dΦe1 0
2
π 2
,
dΦe2 0
dS 2
E
en
dS
E
E
dS1
点 P 电场强度是否变化?
s 穿过高斯面 的 Φe有否变化?
s
q2 B
q1
在点电荷 q 和 q 的静电场中,做如下的三
个闭合面 S1 , S2 , S3 , 求通过各闭合面的电通量 .
q
Φe1
E dS
S1
0
q
q
Φe2 0
Φe3
q
0
S1
S2 S3
求电通量的方法:1. 按定义;2. 用高斯定理
高斯定理应用举例
Φe
E dS
1
S
0
n
qiin
i 1
(用高斯定理求解的静电场必须具有一定的对称性)
其步骤为 对称性分析——球对称、面对称、柱对称 根据对称性选择合适的高斯面; 应用高斯定理求解.
例 均匀带电薄球壳内外的电场强度
一半径为R , 均匀带电 Q 的薄
球壳 . 求球壳内外任意点的电场强 度. 分析:电场分布具有球对称性
解(1) r R
(a) 取考查点在P
r ++
+ +
O
+ + +
P
﹡
+R +
s +++ 2
(b) 过考查点在P选适当的高斯面S2
(c)求高斯面S2的电通量 E dS E4r 2 S2
(d) 求高斯面内的电荷
(e) 利用高斯定理求场强
qi Q E dS
内
qi
4π r 2E Q
0
