用Excel计算二项分布概率值的操作步骤
如何使用excel进行概率统计

数理统计实验1Excel基本操作1.1单元格操作1.1.1单元格的选取Excel启动后首先将自动选取第A列第1行的单元格即A1(或a1)作为活动格,我们可以用键盘或鼠标来选取其它单元格.用鼠标选取时,只需将鼠标移至希望选取的单元格上并单击即可.被选取的单元格将以反色显示.1.1.2选取单元格范围(矩形区域)可以按如下两种方式选取单元格范围.(1) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后按住鼠标左键不放,拖动鼠标指针至终点(右下角)位置,然后放开鼠标即可.(2) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后将鼠标指针移到终点(右下角)位置,先按下Shift键不放,而后点击鼠标左键.1.1.3选取特殊单元格在实际中,有时要选取的单元格由若干不相连的单元格范围组成的.此类有两种情况.第一种情况是间断的单元格选取.选取方法是先选取第一个单元格,然后按住[Ctrl]键,再依次选取其它单元格即可.第二种情况是间断的单元格范围选取.选取方法是先选取第一个单元格范围,然后按住[Ctrl]键,用鼠标拖拉的方式选取第二个单元格范围即可.1.1.4公式中的数值计算要输入计算公式,可先单击待输入公式的单元格,而后键入=(等号),并接着键入公式,公式输入完毕后按Enter键即可确认..如果单击了“编辑公式”按钮或“粘贴函数”按钮,Excel将自动插入一个等号.提示:(1) 通过先选定一个区域,再键入公式,然后按CTRL+ENTER 组合键,可以在区域内的所有单元格中输入同一公式.(2) 可以通过另一单元格复制公式,然后在目标区域内输入同一公式.公式是在工作表中对数据进行分析的等式.它可以对工作表数值进行加法、减法和乘法等运算.公式可以引用同一工作表中的其它单元格、同一工作簿不同工作表中的单元格,或者其它工作簿的工作表中的单元格.下面的示例中将单元格B4 中的数值加上25,再除以单元格D5、E5 和F5 中数值的和.=(B4+25)/SUM(D5:F5)1.1.5公式中的语法公式语法也就是公式中元素的结构或顺序.Excel 中的公式遵守一个特定的语法:最前面是等号(=),后面是参与计算的元素(运算数)和运算符.每个运算数可以是不改变的数值(常量数值)、单元格或区域引用、标志、名称,或工作表函数.在默认状态下,Excel 从等号(=)开始,从左到右计算公式.可以通过修改公式语法来控制计算的顺序.例如,公式=5+2*3的结果为11,将2 乘以3(结果是6),然后再加上5.因为Excel 先计算乘法再计算加法;可以使用圆括号来改变语法,圆括号内的内容将首先被计算.公式=(5+2)*3的结果为21,即先用5 加上2,再用其结果乘以3.1.1.6单元格引用一个单元格中的数值或公式可以被另一个单元格引用.含有单元格引用公式的单元格称为从属单元格,它的值依赖于被引用单元格的值.只要被引用单元格做了修改,包含引用公式的单元格也就随之修改.例如,公式“=B15*5”将单元格B15 中的数值乘以5.每当单元格B15 中的值修改时,公式都将重新计算.公式可以引用单元格组或单元格区域,还可以引用代表单元格或单元格区域的名称或标志.在默认状态下,Excel 使用A1 引用类型.这种类型用字母标志列(从A 到IV ,共256 列),用数字标志行(从1 到65536).如果要引用单元格,请顺序输入列字母和行数字.例如,D50 引用了列D 和行50 交叉处的单元格.如果要引用单元格区域,请输入区域左上角单元格的引用、冒号(:)和区域右下角单元格的引用.下面是引用的示例.1.1.7工作表函数Excel 包含许多预定义的,或称内置的公式,它们被叫做函数.函数可以进行简单的或复杂的计算.工作表中常用的函数是“SUM”函数,它被用来对单元格区域进行加法运算.虽然也可以通过创建公式来计算单元格中数值的总和,但是“SUM”工作表函数还可以方便地计算多个单元格区域.函数的语法以函数名称开始,后面是左圆括号、以逗号隔开的参数和右圆括号.如果函数以公式的形式出现,请在函数名称前面键入等号(=).当生成包含函数的公式时,公式选项板将会提供相关的帮助.使用公式的步骤:A. 单击需要输入公式的单元格.B. 如果公式以函数的形式出现,请在编辑栏中单击“编辑公式”按钮.C. 单击“函数”下拉列表框右端的下拉箭头.D. 单击选定需要添加到公式中的函数.如果函数没有出现在列表中,请单击“其它函数”查看其它函数列表.E. 输入参数.F. 完成输入公式后,请按ENTER 键.1.2几种常见的统计函数1.2.1均值Excel计算平均数使用AVERAGE函数,其格式如下:AVERAGE(参数1,参数2,…,参数30)范例:AVERAGE(12.6,13.4,11.9,12.8,13.0)=12.74如果要计算单元格中A1到B20元素的平均数,可用AVERAGE(A1:B20).1.2.2标准差计算标准差可依据样本当作变量或总体当作变量来分别计算,根据样本计算的结果称作样本标准差,而依据总体计算的结果称作总体标准差.(1)样本标准差Excel计算样本标准差采用无偏估计式,STDEV函数格式如下:STDEV(参数1,参数2,…,参数30)范例:STDEV(3,5,6,4,6,7,5)=1.35如果要计算单元格中A1到B20元素的样本标准差,可用STDEV(A1:B20).(2)总体标准差Excel 计算总体标准差采用有偏估计式STDEVP 函数,其格式如下:STDEVP (参数1,参数2,…,参数30)范例:STDEVP (3,5,6,4,6,7,5)=1.251.2.3 方差方差为标准差的平方,在统计上亦分样本方差与总体方差.(1)样本方差S 2=1)(2--∑n x x iExcel 计算样本方差使用VAR 函数,格式如下:VAR (参数1,参数2,…,参数30)如果要计算单元格中A1到B20元素的样本方差,可用 VAR(A1:B20). 范例:VAR (3,5,6,4,6,7,5)=1.81(2)总体方差S 2=n x x i ∑-2)(Excel 计算总体方差使用VARP 函数,格式如下:VARP (参数1,参数2,…,参数30)范例:VAR (3,5,6,4,6,7,5)=1.551.2.4 正态分布函数Excel 计算正态分布时,使用NORMDIST 函数,其格式如下:NORMDIST(变量,均值,标准差,累积)其中:变量(x):为分布要计算的x值;均值(μ):分布的均值;标准差(σ):分布的标准差;累积:若为TRUE,则为分布函数;若为FALSE,则为概率密度函数.范例:已知X服从正态分布,μ=600,σ=100,求P{X≤500}.输入公式=NORMDIST(500,600,100,TRUE)得到的结果为0.158655,即P{X≤500}=0.158655.1.2.5正态分布函数的反函数Excel计算正态分布函数的反函数使用NORMINV函数,格式如下:NORMINV(下侧概率,均值,标准差)范例:已知概率P=0.841345,均值μ=360,标准差σ=40,求NORMINV函数的值.输入公式=NORMINV(0.841345,360,40)得到结果为400,即P{X≤400}=0.841345.注意:(1) NORMDIST函数的反函数NORMINV用于分布函数,而非概率密度函数,请务必注意;(2) Excel 提供了计算标准正态分布函数NORMSDIST(x),及标准正态分布的反函数NORMSINV(概率).Φ=P{X<2}.输入公式范例:已知X~N(0,1), 计算(2)=NORMSDIST(2)Φ=0.97725.得到0.97725,即(2)范例:输入公式=NORMSINV(0.97725) ,得到数值2.若求临界值uα(n),则使用公式=NORMSINV(1-α).1.2.6t分布Excel计算t分布的值(查表值)采用TDIST函数,格式如下:TDIST(变量,自由度,侧数)其中:变量(t):为判断分布的数值;自由度(v):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T服从t(n-1)分布,样本数为25,求P(T>1.711).已知t=1.711,n=25,采用单侧,则T分布的值:=TDIST(1.711,24,1)得到0.05,即P(T>1.711)=0.05.若采用双侧,则T分布的值:=TDIST(1.711,24,2)得到0.1,即()1.7110.1P T >=. 1.2.7 t 分布的反函数Excel 使用TINV 函数得到t 分布的反函数,格式如下:TINV (双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0.05,求t 205.0(10).输入公式=TINV(0.05,10)得到2.2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0.05,求t 0.05 (10).输入公式=TINV(0.1,10)得到1.812462,即t 0.05 (10)= 1.812462.1.2.8 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度;自由度2(2n ):代表第2个样本的自由度.范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2.9)的值.输入公式=FDIST(2.9,5,15)得到值为0.05,相当于临界值α.1.2.9 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0.05,求其上侧0.05分位点F 0.05(9,9).输入公式=FINV(0.05,9,9)得到值为3.178897,即F 0.05(9,9)= 3.178897.若求单侧百分位点F 0.025(9,9),F 0.975(9,9).可使用公式=FINV(0.025,9,9)=FINV(0.975,9,9)得到两个临界值4.025992和0.248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.2.10 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5.226)的值.输入公式=CHIDIST(5.226,12)得到0.95,即1(5.226)F -=0.95或(5.226)F =0.05.1.2.11 卡方分布的反函数Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:CHIINV (上侧概率值α,自由度n )范例:下面的公式计算卡方分布的反函数:=CHIINV(0.95,12)得到值为5.226,即20.95(12)χ=5.226.若求临界值2αχ(n),则使用公式=CHIINV(α, n). 1.2.12 泊松分布计算泊松分布使用POISSON 函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE ,为泊松分布函数值;若FALSE ,则为泊松分布概率分布值.范例:设X服从参数为4的泊松分布,计算P {X =6}及P {X ≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0.104196和0.889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT ,开平方函数SQRT ,和函数SUM ,等等.关于这些函数的具体用法,可以查看Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1 2已知时的置信区间 置信区间为22x u x u n n αα⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m )为:1.14 1.10 1.131.15 1.20 1.12 1.17 1.19 1.15 1.12 1.14 1.20 1.23 1.11 1.141.16.设苗高服从正态分布,求总体均值μ的0.95的置信区间.已知σ =0.01(米). 步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限和置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显著性水平α和标准差σ是具体的数值而不是符号.本例中,=0.05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0.975)*0.01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0.975)*0.01/sqrt(count(b3:g5))计算结果为(1.148225, 1.158025). 2.1.2 2未知时的置信区间置信区间为 22((x t n x t n n n αα⎛⎫--+- ⎝. 例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5)) =average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5)) 计算结果为(1.133695, 1.172555).2.1.3未知时2的置信区间:置信区间为2222122(1)(1),(1)(1)n nn ns sααχχ-⎛⎫ ⎪--⎪--⎪⎝⎭.例3从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间(单位:s)如下:50.7 54.9 54.3 44.8 42.2 69.8 53.4 66.1 48.1 34.5试求总体方差2σ的0.9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0.1.(4)计算样本方差:在单元格C11中输入公式=VAR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0.1/2, count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0.1/2, count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1 当12 =22 =2但未知时1-2的置信区间置信区间为 ()1212211(2)w x y t n n S n n α⎛⎫-±+-+ ⎪ ⎪⎝⎭.例4 在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5和7,分析其蛋白质含量为甲:12.6 13.4 11.9 12.8 13.0乙:13.1 13.4 12.8 13.5 13.3 12.7 12.4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在的范围.(取α=0.05)实验步骤:(1)在A2:A6输入甲组数据,在B2:B8输入乙组数据;(2)在单元格B11输入公式=AVERAGE(A2:A6),在单元格B12中输入公式=AVERAGE(B2:B8),分别计算出甲组和乙组样本均值.(3)分别在单元格C11和C12分别输入公式=VAR(A2:A6),=VAR(B2:B8),计算出两组样本的方差.(4)在单元格D11和D12分别输入公式=COUNT(A2:A6),=COUNT(B2:B8),计算各样本的容量大小.(5)将显著性水平0.05输入到单元格E11中.(6)分别在单元格B13和B14输入=B11-B12-TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)和=B11-B12+TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)计算出置信区间的下限和上限.2.2.21和未知时方差比σ21/σ22的置信区间置信区间为22 112221221212211,(1,1)(1,1)s ss F n n s F n nαα-⎛⎫⎪⎪----⎪⎝⎭.例5有两个化验员A、B,他们独立地对某种聚合物的含氯量用相同的方法各作了10次测定.其测定值的方差分别是SA=0.5419,SB=0.6065.设σ2A和σ2B分别是A、B所测量的数据总体(设为正态分布)的方差.求方差比σ2A/σ2B的0.95置信区间.操作步骤:(1)在单元格B2,B3输入样本数,C2,C3输入样本方差,D2输入置信度.(2)在B4和B5利用公式输入=C2/(C3*FINV(1-D2/2,B2-1,B3-1))和=C2/(C3*FINV(D2/2,B2-1,B3-1))计算出A组和B组的方差比的置信区间上限和下限.2.3练习题1. 已知某树种的树高服从正态分布,随机抽取了该树种的60株林木组成样本.样本中各林木的树高资料如下(单位:m)22.3, 21.2, 19.2, 16.6, 23.1, 23.9, 24.8, 26.4, 26.6, 24.8, 23.9, 23.2, 23.3, 21.4,19.8, 18.3, 20.0, 21.5, 18.7, 22.4, 26.6, 23.9, 24.8, 18.8, 27.1, 20.6, 25.0, 22.5,23.5, 23.9, 25.3, 23.5, 22.6, 21.5, 20.6, 25.8, 24.0, 23.5, 22.6, 21.8, 20.8, 19.5,20.9, 22.1, 22.7, 23.6, 24.5, 23.6, 21.0, 21.3, 22.4,18.7, 21.3, 15.4, 22.9, 17.8,21.7, 19.1, 20.3, 19.8试以0.95的可靠性,对于该林地上全部林木的平均高进行估计.2. 从一批灯泡中随机抽取10个进行测试,测得它们的寿命(单位:100h)为:50.7,54.9,54.3,44.8,42.2,69.8,53.4,66.1,48.1,34.5.试求总体方差的0.9的置信区间(设总体为正态).3. 已知某种玉米的产量服从正态分布,现有种植该玉米的两个实验区,各分为10个小区,各小区的面积相同,在这两个实验区中,除第一实验区施以磷肥外,其它条件相同,两实验区的玉米产量(kg)如下:第一实验区:62 57 65 60 63 58 57 60 60 58第二实验区:56 59 56 57 60 58 57 55 57 55试求出施以磷肥的玉米产量均值和未施以磷肥的玉米产量均值之差的范围(α=0.05)3假设检验实验实验内容:单个总体均值的假设检验;两个总体均值差的假设检验;两个正态总体方差齐性的假设检验;拟合优度检验.实验目的与要求:(1)理解假设检验的统计思想,掌握假设检验的计算步骤;(2)掌握运用Excel进行假设检验的方法和操作步骤;(3)能够利用试验结果的信息,对所关心的事物作出合理的推断.3.1单个正态总体均值μ的检验3.1.12已知时μ的U检验例1 外地一良种作物,其1000m2产量(单位:kg)服从N(800, 502),引入本地试种,收获时任取5块地,其1000m2产量分别是800,850,780,900,820(kg),假定引种后1000m2产量X也服从正态分布,试问:=800kg 有无显著变化.(1)若方差未变,本地平均产量μ与原产地的平均产量μ0(2)本地平均产量μ是否比原产地的平均产量μ=800kg高.0=800kg低.(3)本地平均产量μ是否比原产地的平均产量μ0操作步骤:(1)先建一个如下图所示的工作表:(2)计算样本均值(平均产量),在单元格D5输入公式=AVERAGE(A3:E3);(3)在单元格D6输入样本数5;(4)在单元格D8输入U检验值计算公式=(D5-800)/(50/SQRT(D6);(5)在单元格D9输入U检验的临界值=NORMSINV(0.975);(6)根据算出的数值作出推论.本例中,U的检验值1.341641小于临界值1.959961,故接受原假设,即平均产量与原产地无显著差异.(7)注:在例1中,问题(2)要计算U检验的右侧临界值:在单元格D10输入U检验的上侧临界值=NORMSINV(0.95).问题(3)要计算U检验的下侧临界值,在单元格D11输入U检验下侧的临界值=NORMSINV(0.05).3.1.22未知时的t检验例2某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行驶速度如下:250 238 265 242 248 258 255 236 245 261254 256 246 242 247 256 258 259 262 263该引擎制造商宣称引擎的平均速度高于250 km/h,请问样本数据在显著性水平为0.025时,是否和他的声明抵触?操作步骤:(1)先建如图所示的工作表:(2)计算样本均值:在单元格D8输入公式=AVERAGE(A3:E6);(3)计算标准差:在单元格D9输入公式=STDEV(A3:E6);(4)在单元格D10输入样本数20.(5)在单元格D11输入t检验值计算公式=(D8-250)/(D9/(SQRT(D10)),得到结果1.06087;(6)在单元格D12输入t检验上侧临界值计算公式=TINV(0.05, D10-1).欲检验假设H0:μ=250;H:μ>250.1已知t统计量的自由度为(n-1)=20-1=19,拒绝域为t>t=2.093.由上面计算得025.0到t检验统计量的值1.06087落在接收域内,故接收原假设H0.3.2两个正态总体参数的假设检验3.2.1当12 =22 =2但未知时μ-μ的检验12在此情况下,采用t检验.例试验及观测数据同11.2中的练习题3,试判别磷肥对玉米产量有无显著影响?欲检验假设H0:μ1=μ2;H:μ1>μ2.1操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“t-检验:双样本等方差假设”.(4)选择“确定”.显示一个“t-检验:双样本等方差假设”对话框;(5)在“变量1的区域”输入A2:A11.(6)在“变量2的区域”输入B2:B11.(7)在“输出区域”输入D1,表示输出结果放置于D1向右方的单元格中.(8)在显著水平“α”框,输入0.05.(9)在“假设平均差”窗口输入0.(10)选择“确定”,计算结果如D1:F14显示.得到t值为3.03,“t单尾临界”值为1.734063.由于3.03>1.73,所以拒绝原假设,接收备择假设,即认为使用磷肥对提高玉米产量有显著影响.3.2.2σ21与σ22已知时12μ-μ的U检验例3 某班20人进行了数学测验,第1组和第2组测验结果如下:第1组:91 88 76 98 94 92 90 87 100 69第2组:90 91 80 92 92 94 98 78 86 91已知两组的总体方差分别是57与53,取α =0.05,可否认为两组学生的成绩有差异?操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“z-检验:双样本平均差检验”;(4)选择“确定”,显示一个“z-检验:双样本平均差检验”对话框;(5)在“变量1的区域”输入A2:A11;(6)在“变量2的区域”输入B2:B11;(7)在“输出区域”输入D1;(8)在显著水平“α”框,输入0.05;(9)在“假设平均差”窗口输入0;(10)在“变量1的方差”窗口输入57;(11)在“变量2的方差”窗口输入53;(12)选择“确定”,得到结果如图所示.计算结果得到z=-0.21106(即u统计量的值),其绝对值小于“z双尾临界”值1.959961,故接收原假设,表示无充分证据表明两组学生数学测验成绩有差异.3.2.3两个正态总体的方差齐性的F检验例5羊毛在处理前与后分别抽样分析其含脂率如下:处理前:0.19 0.18 0.21 0.30 0.41 0.12 0.27处理后:0.15 0.13 0.07 0.24 0.19 0.06 0.08 0.12问处理前后含脂率的标准差是否有显著差异?欲检验假设H0:σ21=σ22;H1:σ21≠σ22.操作步骤如下:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”; (3)选定“F-检验 双样本方差”.(4)选择“确定”,显示一个“F-检验:双样本方差”对话框; (5)在“变量1的区域”输入A2:A8. (6)在“变量2的区域”输入B2:B9. (7)在显著水平“α”框,输入0.025. (8)在“输出区域”框输入D1. (9)选择“确定”,得到结果如图所示.计算出F 值2.35049小于“F 单尾临界”值5.118579,且P(F<=f)=0.144119>0.025,故接收原假设,表示无理由怀疑两总体方差相等.4 拟合优度检验拟合优度检验使用统计量221()ki i i i n np np χ=-=∑, (11.1) i i n np k 其中为实测频数,为理论频数,为分组数。
Excel 在推断统计中的应用1
一、二项分布工具(一)简介:在Excel 中想要计算二项分布的概率分布、累积概率,需要利用Excel 的工作表函数BINOMDIST。
函数BINOMDIST 适用于固定次数的独立实验,实验的结果只包含成功或失败二种情况,且每次实验成功的概率固定不变。
例如,已知次品概率的情况下,函数BINOMDIST 可以计算10 个产品中发现2 个次品的概率。
以下例子说明如何在Excel 中计算二项分布的概率,以及如何建立二项分布图表。
(二)操作步骤:例子如下所示,一个推销员打了六个电话,推销成功的概率是0.3,那么可以按以下步骤建立推销成功次数的概率分布图表。
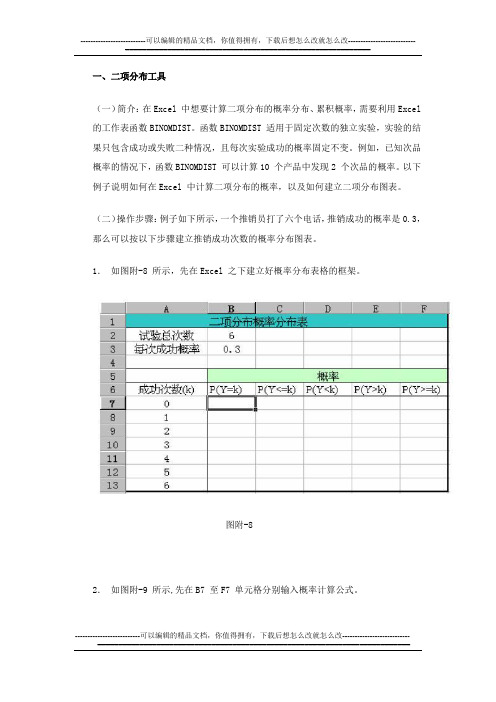
1.如图附-8 所示,先在Excel 之下建立好概率分布表格的框架。
图附-82.如图附-9 所示,先在B7 至F7 单元格分别输入概率计算公式。
图附-93.公式的拷贝。
选取B7 至F7 单元格,拖动“填充柄”至F13 单元格即可完成公式的拷贝操作。
结果图附-10 所示。
图附-104.下面开始创建二项分布图表。
选取B7 至B13 单元格,选取“插入”菜单的“图表”子菜单。
5.选择“柱状图”,然后单击“下一步”。
6. 单击“系列”标签,单击“分类(X)轴标志”框,并用鼠标选取A7至A13 单元格为图表X 轴的轴标,然后单击“下一步”。
7. 分别键入图表名称“二项分布图”,X 轴名称“成功次数”,Y 轴名称“成功概率”,单击“完成”按扭即可生成二项分布图表。
(三)结果说明: 如图附-10 所示,利用Excel 的BINOMDIST 的函数可以计算出二项分布的概率以及累积概率。
BINOMDIST 函数可以带四个参数,各参数的含义分别是:实验成功的次数,实验的总次数,每次实验中成功的概率,是否计算累积概率。
第四个参数是一个逻辑值,如果为TRUE,函数BINOMDIST 返回累积分布函数,如果为FALSE,返回概率密度函数。
二、其它分布的函数(一)函数CRITBINOM:1.说明:函数CRITBINOM 可称为BINOMDIST 的逆向函数,它返回使累积二项式分布概率P(X<=x)大于等于临界概率值的最小值。
用EXCEL作二项分布、产生随机数

7、t分布的计算 、 分布的计算 分布fx=TDIST() ⑴ t分布 分布 分布反函数fx=TINV() ⑵t分布反函数 分布反函数 8、x2分布的计算 、 分布fx=CHIDIST() ⑴ x2分布 分布反函数fx=CHIINV() ⑵ x2分布反函数 9、F分布的计算 、 分布的计算 分布fx=FDIST() ⑴ F分布 分布 分布反函数fx=FINV() ⑵ F分布反函数 分布反函数 请参考中国青年出版社《 函数、 请参考中国青年出版社《Excel2002函数、统计与 函数 分析应用范例》杨世莹编著, 分析应用范例》杨世莹编著,2003第一版本 第一版本
3、二项分布的计算 、 fx=BINOMDIST(x, n, p, FALSE) 4、泊松分布的计算 、 fx=POISSON(x, λ, FALSE) 5、标准正态分布的计算 、 fx=NORMSDIST(数值 数值) 数值 6、标准正态分布反函数的计算 、 fx=NORMSINV(概率值 概率值) 概率值 以上各函数的计算,请见用EXCEL作的“oc曲 作的“ 曲 以上各函数的计算,请见用 作的 线图象”文件,以及用 以及用EXCEL作的“计量抽样附 作的“ 线图象”文件 以及用 作的 件”文件
按Enter键,pa=1.000, 在C2格右下角做成“+ 往下拖移,pa=0.9245, 0.6769, .......0
计算机作OC曲线(图像) OC曲线 三. 计算机作OC曲线(图像) 1.选 1.选p,pa 2.在任务栏找到 图表向导” 2.在任务栏找到 “图表向导” ,击→选 “XY” 散点图→选→“确定” →显出OC曲线. XY 散点图→ 确定” 显出OC曲线. OC曲线
2、样本 、 从总体中抽取部分个体所组成的集合称 总体中抽取部分个体所组成的集合称 所组成的集合 为样本。 为样本。 由于总体的全部数据往往是不能得到的, 由于总体的全部数据往往是不能得到的, 所以总体分布的特征值μ 也是不可知的。 所以总体分布的特征值μ、σ也是不可知的。 也是不可知的 人们从总体中抽取样本是为了认识总 但人们从总体中抽取样本是为了认识总 从样本去推断总体 即搜集的数据中: 推断总体。 体,从样本去推断总体。即搜集的数据中 这个总体的均值为多少? ⑴这个总体的均值为多少 这个总体的标准差是多少? ⑵这个总体的标准差是多少
用EXCEL作二项分布、产生随机数

3.计算:
(1)先在 “B”列,选中B2(此时:计算px=0)
(2)在EXCEL任务栏中找出 “插入”,单击
“插入” →击 “函数” →找到BINOMDIST
(二项分布)→ BINOMDIST(x,n,p,FALSE密
度)
(3)输入数据:x=A2,n=5,p=0.1, FALSE
(4)计算 按 Enter 键,px=0=59.05%
(5)计算:在B2的右下角,显出 “+” ,按 住鼠标往下拖,计算出:px=1=0.354,
px=2=0.134, px=3=0.033, px=4=0.006
px=5=px=6≈0 (6)用上面相似方法,将FALSE换成TRUE,计 算出∑累计.
二.绘制泊松分布图像 1.选x列,p列 2.在任务栏找出 “图表向导” ,击→选 “XY” 散点图→选→“确定” →显出泊松分 布图像.
三. 计算机作OC曲线(图像) 1.选p,pa 2.在任务栏找到 “图表向导” ,击→选 “XY” 散点图→选→“确定” →显出OC曲线.
3.根据需要,调整p轴、pa轴。
四、随机数在计算机中产生
例:已知N=100,要随机n=13的抽取 操作步骤如下: 1.100台产品编号为:1~100 2.打开EXCEL
1、总体与个体
在一个统计问题中,称研究对象的全体为总体,
构成总体的每个成员称为个体。
总体可用一个分布描述,统计学的主要任务是: ⑴研究总体是什么分布? ⑵这个总体(即分布)的均值、方差或标准差是 多少?
2、样本 从总体中抽取部分个体所组成的集合称 为样本。 由于总体的全部数据往往是不能得到的, 所以总体分布的特征值μ 、σ也是不可知的。 但人们从总体中抽取样本是为了认识总 体,从样本去推断总体。即搜集的数据中: ⑴这个总体的均值为多少? ⑵这个总体的标准差是多少?
二项分布资料统计推断的Excel快速实现

收稿日期:2015-01-20通讯作者:王昌富作者简介:周治年(1965-),女,副主任护师,从事血液成分分离工作㊂ *Inte g rated S y stems En g ineerin g ,The Ohio State Universit y ,Columbus ,O H ,USA**华中科技大学同济医学院附属荆州医院检验医学部文章编号:1004-4337(2015)05-0637-04 中图分类号:TP319;R311 文献标识码:A㊃医学数学模型探讨㊃二项分布资料统计推断的Excel 快速实现周治年 彭小娟* 肖秀林** 王昌富**(湖北省荆州市中心血站 荆州434100)摘 要: 目的:探讨对二项分布资料进行统计推断的Excel 实现方法㊂方法:利用Excel 函数BINOMDIST ㊁FINV ㊁NORMS -INV 等,可得到在每次试验中阳性的概率为p 的条件下,n 次独立试验中阳性次数为m 时至多m 次阳性的概率和刚好m 次阳性的概率以及正态分布㊁F 分布的分位数㊂将p ㊁n ㊁m 等原始数据与最终统计分析结论部署在同一界面,将其他中间计算数据隐藏,最终统计分析结论可随原始数据立即呈现㊂结果:建立 二项分布资料统计推断 的Excel 工作表后,进行二项分布资料的统计推断时仅仅录入相关的p ㊁n ㊁m ,不须再录入任何统计公式和命令,就能立即得到统计分析的结果㊂结论:利用Excel 能直观快速进行常见二项分布资料的统计推断㊂关键词: 二项分布; 统计推断; Exceldoi :10.3969/j .issn.1004-4337.2015.05.002 二项分布(Binomial distribution )是离散型随机变量中最常见的分布,常用于描述医学领域中只具有两种互斥结果的离散型随机事件的规律性,如对病人治疗效果的描述 有效与无效;检验结果的描述 阳性与阴性;接触某传染源的描述 暴露与未暴露等㊂参数估计(Parametric estimation )和假设检验(Test of h y -p othesis )是对二项分布资料进行的统计推断(Statistical In -ference )的两种方法[1]㊂参数估计常使用 区间估计 (intervalestimation ),即按一定的概率估计总体均数在哪个范围;假设检验是依据现有的知识建立假设后选用适当的统计量来验证该假设是否成立㊂医学实验室质量和能力认可准则在临床血液学检验领域的应用说明[2](CNAS -L43:2012)的5.6.6条指出医学实验室至少每3个月进行1次形态学检验人员的结果比对㊂每次分析比对结果都要进行二项分布资料的区间估计㊂实际应用时往往要查看采用正态近似法进行简单计算统计用表,或数据不在统计用表所列范围之内,得不到较为严谨的结论㊂为此,我们建立了对二项分布资料快速进行统计推断的Excel 工作表㊂现报道如下㊂1 材料和统计学原理1.1 二项分布总体的区间估计1.1.1 Miettinen 精确概率法[3]例1 某血样按标准方法进行手工白细胞分类计数(总计200个白细胞),其中单核细胞数平均3个,求该血样单核细胞百分数的99%可信区间㊂1970年,Miettinen 根据二项分布与F 分布的关系,导出了总体率的可信限算法㊂设n 个个体中阳性数为m ,样本率为p =m /n ,则总体率的100(1-α)%可信区间为(p L ,p U ):p L =mm +(n -m +1)F α2,2(n -m +1)2m p U =m +1m +1+(n -m )F α22(m +1)2(n -m )当m =0时,p L =0;当m =n 时,p U =1㊂这里,p L 和p U 分别对应两个不同的F 分布,F α/2,2(n -m +1),2m 是自由度为[2(n -m +1),2m ]的左侧概率为α/2的F 分布分位数;F α/2,2(m +1),2(n -m )是自由度为[2(m +1),2(n -m )]的右侧概率为α/2的F 分布分位数㊂1.1.2 正态近似法例2 如果例1中还另计数淋巴细胞平均97个,估计该血样淋巴细胞百分数的99%可信区间㊂当n 较大,p 和1-p 均不太小时,如n p 与n (1-p )均大于5时,样本率p 的抽样分布近似正态分布[1],可按如下正态近似法公式计算总体率的(1-α)可信区间:p ʃu α/2S p ㊂公式中:p 为样本率;S p 为率的标准误,s p =p (1-p )/n ㊂u α/2为标准正态分布α水平的双侧临界值,α=0.01时,u α/2=2.58㊂1.1.3 两总体率之差的区间估计例3 对甲㊁乙两种降压药进行临床疗效评价,将某时段内入院的高血压病人随机分为两组,每组均为100人㊂甲药治疗组80人有效,乙药治疗组50人有效,试估计两种降压药有效率之差的99%可信区间㊂设两个独立样本率分别为p 1和p 2,当n 1与n 2均较大,且p 1㊁1-p 1和p 2㊁1-p 2均不太小,一般认为,当n 1p 1,n 1(1-p 1),n 2p 2,n 2(1-p 2)均大于5时,可按如下正态近似法公式计算两总体率之差的(1-α)可信区间[1]:(p 1-p 2)ʃu a /2S p 1-p 2㊂式中S p 1-p 2为率之差的标准误,S p 1-p 2=p 1(1-p 1)/n 1+p 2(1-p 2)/n 2㊂1.1.4 直接计算法采用Excel 函数BINOMDIST (),计算过程类似1.3.3,可得到率(m /n )的α/2和1-α/2临界值㊂1.2 两个样本率p 1㊁p 2的比较1.2.1 精确概率法例4 按标准方法进行手工白细胞分类计数(总计200个白细胞),其中单核细胞数平均血样A 为2个,血样B 为12个,问A ㊁B 两血样的单核细胞百分数是否不同(α=0.01)?㊃736㊃数理医药学杂志2015年第28卷第5期当n1p1,n1(1-p1),n2p2,n2(1-p2)不是均大于5时,按1.1.1分别计算两总体率的可信区间,当两可信区间无重叠时,可推断两总体均数差异有统计学意义;两可信区间有重叠时,不能推断两总体均数差异有统计学意义㊂1.2.2正态近似法例5试评估例3中的两种降压药有效率是否不同(α= 0.01)?当n较大时(n>50),样本率p的抽样分布近似正态分布,可按照两均数差异的显著性检验的方法分析[3]㊂其统计量为:u=p1-p2/p Cˑ(1-p C)ˑ(1/n1+1/n2)㊂式中p C=(m1+m2)/(n1+n2),p1=m1/n1,p2=m2/n2,自由度d f =n1+n2-2当n较小时(nɱ50),上述推断会产生偏倚,可用如下校正公式:p1=(m1+1)/(n1+2)p2=(m2+1)/(n2+2)u=p1-p2/p1ˑ(1-p1)/(n1+3)+p2ˑ(1-p2)/(n2+3)1.3样本率p与总体(理论)率p0的比较随机抽取容量为n的样本,某事件出现了m次,事件出现的样本率p=m/n,问其所代表的总体率与某个已知的总体率p0是否有差异?1.3.1精确概率法例6某地新生儿染色体异常率平均为1.5%,现该地400名新生儿中只1例染色体异常,问该地新生儿染色体异常率是否低于平均(α=0.01)?当样本例数n较小,特别是当p接近0或1时,不能用正态近似法,应根据Miettinen法计算样本率p所估计的总体率p x的(1-α)%可信区间(p L,p U),当已知的总体率p0在这一区间内时,抽样所代表的总体率p x与这个已知的总体率p0在α水平差异无统计学意义㊂1.3.2正态近似法例7:一般溃疡患者有20%发生胃出血㊂现观察65岁以上溃疡病人304例,有96例发生胃出血症状㊂问65岁以上溃疡患者是否比一般患者易出血(α=0.01)?当m>5且m/n>0.01时,样本率p的抽样分布逼近正态分布,也可用正态近似法计算统计量u后进行假设检验[1],公式如下㊂当n较大,|m-nˑp0|ɤ0.5时:u=m-nˑp0/ nˑp0ˑ(1-p0)=p-p0/p0ˑ(1-p0)/n当n较小,|m-nˑp0|>0.5时,要进行连续性校正:u= (m-nˑp0-0.5)/nˑp0ˑ(1-p0)1.3.3直接计算概率法直接计算概率法[3]:当样本例数n较小,特别是当p接近0或1时(如例6),不能用正态近似法,可采用如下方法计算抽样样本率p x(x/n)与理论率(p0)差异无统计学意义的上㊁下限(p U㊁p L),然后进行推断㊂总体率为p0,含量为n的样本中,某事件发生次数m恰好为x次的概率P(x)=(n x)(1-p0)n-x(p0)x,x=0,1,2, ,n㊂式中(n x)=n!/x!/(n-x)!㊂!为阶乘的符号,如3! =3ˑ2ˑ1,且有0!=1,(p0)0=1㊂事件出现次数不大于m次的概率P(xɤm)=P(0)+P (1)+ +P(m)㊂事件出现次数大于m次的概率P(x>m)=1-P(xɤm)㊂假如n=304,理论率为p0=0.2,α=0.05时,x/n的上下限的Excel计算过程如下:设P T=BINOMDIST(m,n,p,TRUE),则P T是样本容量为n(304),理论率为p0(0.2)时抽样中事件发生次数xɤm的概率,当样本率p x分别是0.13㊁0.14㊁0.15㊁ 逐渐增加时(x 由40㊁43㊁46㊁ 逐渐增加),P T=0.0007㊁0.0032㊁0.0120 逐渐增加㊂设P F=BINOMDIST(m,n,p,FALSE),则P F是样本容量为n(304),理论率为p0(0.2)时抽样中事件发生次数x=m 的概率㊂设P D=1-P T+P F,则P D是样本容量为n(304),理论率为p0(0.2)时抽样中事件发生次数xȡm的概率,当样本率p x 分别是0.13㊁0.14㊁0.15㊁ 逐渐增加时(x由40㊁43㊁46㊁ 逐渐增加),P D=0.9996㊁0.9980㊁0.9921逐渐减小㊂在α(两侧各0.025)水平,样本率p x分别是0.13㊁0.14㊁0.15㊁ 逐渐增加时所有P Tȡα的p x之中最小的p x(0.16)为判断抽样样本率p x(x/n)与理论率(p0)差异无统计学意义的下限(p L);所有P Dȡα的p x之中最大的p x(0.24)为判断抽样样本率p x(x/n)与理论率(p0)差异无统计学意义的上限(p U)㊂如图1所示㊂图1二项分布资料直接计算概率法计算过程示意图2对二项分布资料进行统计推断的Excel快速实现方法Excel有某一单元格可调用另一单元格的数据特点,将原始数据㊁中间计算数据及最终统计分析结论之间进行适当地调用,最终统计分析结论可随原始数据立即呈现㊂按彭小娟等[3]介绍的方法,将二项分布的原始数据与最终统计分析结论部署在同一界面,将其他中间计算数据隐藏,使用时只需在指定单元格录入原始数据后立即可得到统计结论,使统计分析变得直观㊁快速㊂对二项分布资料快速进行统计推断的Ex-cel工作表如图2所示(Excel表中各计算格公式略)㊂3结果对例1~例7采用Excel快速解答如下㊂例1如图2所示,在C3格录入样本量n(200),在C4格录入样本阳性数m(3),在C6格录入显著性水平0.01后,显示在B9格㊁C9格的0.0017㊁0.0538是血样中单核细胞百分数的99%可信区间下限㊁上限㊂例2如图2所示,在C13格录入样本量n(200),在C14格录入样本阳性数m(97),在C16格录入显著性水平0.01后,显示在B19格㊁C19格的0.394㊁0.576是血样中淋巴细胞百分数的99%可信区间下限㊁上限㊂例3如图2所示,在C23㊁D23格录入两组总例数100㊁100,在C24㊁D24格录入两组有效例数80㊁50,在E23格录入显著性水平0.01后,显示在D30㊁E30的0.1368㊁0.4632是两种降压药有效率之差(0.3)的99%可信区间的下限㊁上限㊂例4 如图2所示,在Q3㊁R3格录入两组总例数200㊁200,在Q4㊁R4格录入两组阳性例数2㊁12,在S3格录入显著性水平0.01后,显示在P8和Q8㊁R8和S8的0.00052和0.04553㊁0.0251和0.1171是A㊁B两组总体率的99%可信区间的下限和上限㊂本例两组区间重叠,尚不能推断A㊁B两血样的单核细胞百分数不同㊂本例如果按正态近似法计算,就会得A㊁B两血样的单核细胞百分数差异有统计学意义(u= 2.946,p=0.0032)的错误结论㊂㊃836㊃Journal of Mathematical Medicine Vol.28 No.52015图2对二项分布资料快速进行统计推断的Excel工作表例5如图2所示,在Q12㊁R12格录入两组总例数100㊁100,在Q13㊁R13格录入两组有效例数80㊁50,在S12格录入显著性水平0.01后,P17格显示u值是4.550,P18格是与u 值对应的P值5.358ˑ10-6㊂结论是两种降压药有效率差异有统计学意义㊂例6如图2所示,在W3格录入总例数n(400),在W4格录入阳性例数m(1),在Z3格录入理论率p0(0.015),在Z4格录入显著性水平0.01后,显示在W8格㊁X8格的是样本率0.0025的99%可信区间下限(0.0000251)㊁上限(0.016479)㊂理论率p0(0.015)在这一区间内,统计结论是尚不能推断该地新生儿染色体异常率低于平均水平㊂本例如果按正态近似法计算,就会得与平均百分数1.5%的差异有统计学意义(u= 2.910,P=0.0036)的错误结论㊂本例按直接计算法可得到与精确概率法相同的结论㊂例7如图2所示,在W12格录入总例数n(304),W13格录入阳性例数m(96),Z12格录入理论率p0(0.2),Z13格录入显著性水平0.01,W16格显示u值是4.641,W17格是与u 值对应的P值3.464ˑ10-6㊂结论是两总体率差异有统计学意义,结论是65岁以上溃疡患者是比一般患者易出血㊂本例正态近似法的结论与直接计算法和精确概率法的结论相同㊂以上实例说明二项分布资料的参数估计和假设检验都能利用Excel直观快速地得到统计结论㊂4讨论医学研究中的许多资料如诊断试验结果的阳性率㊁金标准的阳性率㊁样品与试纸条发生反应率㊁FISH分析中有荧光的细胞百分率㊁白细胞分类百分率等都服从二项分布㊂使用Excel对二项分布资料进行统计推断较为简捷:Morten W F[4]等展示了用Excel计算mid-p检验统计量的方法; Weckerle CS[5]等认为Excel函数能简单快速地计算其研究中的二项分布数据;Allison L.C等[6]认为采用二项分布原理确定的FISH分析的临界值是最准确的方法,并可很容易地使用Microsoft Excel中的CRITBINOM函数计算得到;张艳丽等[7]利用Excel软件对住院药房口服抗高血压药物的应用进行了分析;张敏等[8]采用Excel2003软件对271份抗菌药物不良反应进行回顾性分析㊂在实际应用中要注意各统计推断公式的应用条件,二项分布在n足够大时才近似正态分布,但仍与正态分布有不同程度的偏差㊂例如,美国临床实验室标准化协会(CLSI)批准的文件H2O-A2[9]中,涉及到计算总体率的可信区间,在其第一版H2O-A[10]的表1中,p为0~3%的几行,按正态近似公式计算总体率的99%可信区间下限都为负数,而精确概率法则为0~0.8%;p为96%~99%的几行,总体率的99%可信区间上限都大于100,而精确概率法则为99.2%~99.9%㊂因此H2O-A2删除了H2O-A的表1中p小于4%和大于95%的几行,但余下的p为4%~95%的几行的可信区间仍是用正态近似法计算的结果,通过计算可看出这些结果与精确概率法计算的总体率的可信区间是不同的,当p越接近0%或100%时,二者差别越大㊂实际工作中应根据二项分布的原理按精确概率法确定总体率的可信区间(不能用正态近似法,特别是当p%接近0或100时)㊂在计算工具不发达的年代,人们仅能用两个α水平标准正态分布的双侧临界值1.96和2.58,通过简单地计算得出总体率的可信区间(近似值)㊂如今,通过Excel函数FINV 很容易得到F分布的临界值Fα/2,2(n-m+1),2m和Fα/2,2(m+1),2(n-m),从而快速方便地实现Miettinen精确概率法计算总体率的可信区间㊂建议H2O-A再次改版时将表1中的数值以Miettinen精确概率法的计算结果替换正态近似法的结果㊂㊃936㊃数理医药学杂志2015年第28卷第5期参考文献1颜虹.医学统计学.北京:人民卫生出版社,2005,94;104.2 CNAS-CL43:2012医学实验室质量和能力认可准则在临床血液学检验领域的应用说明.3彭小娟,肖秀林,周治年.统计分析的Excel快速实现.武汉:武汉大学出版社,2012,56~57.4 Morten W F,Stian L,Petter L.The McNemar test for binar y matched-p airs data:mid-p and as y m p totic are better than exact conditional.BMC Med Res Methodol,2013,13:91.5 Weckerle CS,Cabras S,Castellanos ME,et al.Quantitative meth-ods in ethnobotan y and ethno p harmacolo gy:considerin g the overall flora-h yp othesis testin g for over andunderused p lant families with the Ba y esian a pp roach.J Ethno p harmacol,2011,137(1):837~843.6 Allison L.C,Mar y E.T,Ron B.Statistical Treatment of Fluores-cence in Situ H y bridization Validation Data to Generate Normal Reference Ran g es Usin g Excel Functions.J Mol Dia g n,2009,11 (4):330~333.7张艳丽,方维军,陈坚.2009~2011年我院住院患者口服抗高血压药应用分析.中国医药导报,2012,9(36):136~138.8 张敏,方勇,徐济萍.271例抗菌药物不良反应分析.中国医药导报,2012,9(3):128~130.9 John A,Onno W,Larr y J,et al.Reference Leukoc y te(WBC) Differential Count(Pro p ortional)and Evaluation of Instrumental Methods;A pp roved Standard-Second Edition.Clinical and Labora-tor y Standards Institute(CLSI)Document H2O-A2,2007.10John A,Stuart A,Robert V,et al.Reference Leukoc y te Differen-tial Count(Pro p ortional)and Evaluation of Instrumental Methods;A pp roved Standard.NCCLS Document H2O-A,1992.An Investi g ation into the Q uick Im p lementation of Statistical Inference forBinomial Distribution in ExcelZhou Zhinian,et al(Central Blood Station o f J in g zhou Cit y,J in g zhou434100)Abstract Ob j ective:To investi g ate the im p lementation method of statistical inference for binomial dis-tribution in Excel.Methods:With the a pp lication of Excel functions,such as BINOMDIST,FINV,NORMS-INV and otherwise,the p robabilit y that the the p ositive times was m,no more than m and j ust m,the q uan-tile of normal distribution and F distribution durin g n times of inde p endent tests can be obtained under the condition that the p ositive p robabilit y was p in each times.De p lo y p,n,m and other ori g inal data and the final conclusion of statistical anal y sis on the same interface,conceal the other intermediate com p utin g data,final conclusion of statistical anal y sis can be p resented immediatel y alon g with the ori g inal data.Results:When im-p lementin g the statistical inference for binomial distribution data,the statistical anal y sis can be obtained onl y throu g h lo gg in g in relevant p,n and m instead of im p utin g an y statistical formal and command if the Excel worksheet has been created.Conclusion:it is p ossible to conduct statistical inference for common binomial dis-tribution data visuall y and q uickl y with the a pp lication of Excel.Ke y words binomial distribution;statistical inference;Excel㊃046㊃Journal of Mathematical Medicine Vol.28 No.52015二项分布资料统计推断的 Excel 快速实现作者:周治年, 彭小娟, 肖秀林, 王昌富作者单位:周治年(湖北省荆州市中心血站 荆州 434100), 彭小娟(Integrated SystemsEngineering,The Ohio State University,Columbus,OH,USA), 肖秀林,王昌富(华中科技大学同济医学院附属荆州医院检验医学部)刊名:数理医药学杂志英文刊名:Journal of Mathematical Medicine年,卷(期):2015(5)引用本文格式:周治年.彭小娟.肖秀林.王昌富二项分布资料统计推断的 Excel 快速实现[期刊论文]-数理医药学杂志 2015(5)。
常用概率函数在EXCEL中的实现

常用概率函数在EXCEL中的实现在Excel中,我们可以使用各种常见的概率函数来解决与概率相关的问题。
以下是一些常见的概率函数及其在Excel中的实现方法:1.累积分布函数(CDF):CDF函数用于计算随机变量小于或等于给定值的概率。
在Excel中,我们可以使用NORM.DIST函数来计算正态分布的累积分布函数。
该函数的语法如下:NORM.DIST(x, mean, standard_dev, cumulative)其中,x是随机变量的值,mean是正态分布的均值,standard_dev 是标准差,cumulative是一个布尔值,如果为TRUE,则计算累积分布函数;如果为FALSE,则计算概率密度函数。
2.概率密度函数(PDF):PDF函数用于计算给定随机变量取一些值的概率。
在Excel中,我们可以使用NORM.DIST函数来计算正态分布的概率密度函数。
该函数的语法与累积分布函数一样。
3.百分位数函数:百分位数函数用于计算给定分布中的一些数值的百分位数。
在Excel 中,我们可以使用PERCENTILE函数来计算一些数据集的一些百分位数。
该函数的语法如下:PERCENTILE(array, k)其中,array是数据集,k是一个介于0和1之间的小数,表示所需的百分位数。
4.期望值(均值):期望值是随机变量的平均值。
在Excel中,我们可以使用AVERAGE函数来计算一个数据集的期望值。
该函数的语法如下:AVERAGE(number1, number2, ...)其中,number1、number2等是数据集中的数值。
5.方差:方差是随机变量的离散程度的度量。
在Excel中,我们可以使用VAR函数来计算一个数据集的方差。
该函数的语法如下:VAR(number1, number2, ...)其中,number1、number2等是数据集中的数值。
6.标准差:标准差是方差的平方根,用于衡量随机变量的离散程度。
概率函数在EXCEL中的使用方法

1.正态分布函数
(1)正态分布函数。 (2)标准正态分布函数。 (3)正态分布函数的反函数。 (4)标准正态分布函数的反函数。
2.绘制正态分布图形
(1)建立正态分布基本数据。 (2)绘制正态分布图形。
图4-7 “序列”对话框
图4-8 结果显示(4~117行隐藏)
图4-9 “坐标轴格式”对话框
1.二项分布函数
二项分布函数适用于固定次数的独立试验,当 试验的结果只包含成功或失败两种情况时,且 当成功的概率在试验期间固定不变,该函数返 回一元二项式分布的概率值,其计算公式为
b(x,
n,
p)
n x
p
x
1
p nx
语法:BINOMDIST(number_s,trials,probability_s,cumulative)
例4-1 抛硬币的结果不是正面就是反面,如果 每次硬币为正面的概率是0.5。则抛硬币10 次 中6次正面的概率为多少?
(1)建立“BINOMDIST函数.xls”工作表,输 入有关数据,如图4-1所示。
(2)在单元格C2中输入公式 “=BINOMDIST(B2,B3,B4,FALSE)”,按回车 键显示结果等于0.205078,如图4-2所示。表示 抛10硬币出现6次的概率为0.205078。
第4章 概率分布与抽样分布
4.1 概率分布 4.2 抽样分布
返回首页
本章学习目标
u Excel离散型随机变量概率分布的工作表函数 u Excel连续型随机变量概率分布的工作表函数 u 利用Excel绘制正态分布图 u Excel抽样分布的工作表函数
4.1 概率分布
4.1.1 概率与概率分布 4.1.2 二项分布 4.1.3 正态分布
用EXCEL计算二项分布概率值的操作步骤

⽤EXCEL计算⼆项分布概率值的操作步骤⽤Excel计算⼆项分布概率值的操作步骤1、进⼊Excel界⾯,单击某⼀单元格。
2、选择【插⼊】——【函数】选项从【选择类别】窗⼝中选择“统计”从【选择函数】窗⼝中选择“BINOMDIST”,单击【确定】3、当【BINOMDIST】对话框出现时:在【Number-s】中输⼊2(成功的次数X)在【trials】中输⼊3(实验的总次数n)在【Probability-s】中输⼊0.05(每次实验成功的概率p)在【Cumulative】中输⼊0(或False),表⽰计算成功次数恰好等于制定数值的概率(输⼊1或True表⽰计算成功次数⼩于或等于制定数值的累计概率值)。
选择【完成】即可得到结果。
计算超⼏何分布概率的步骤与上述过程类似,只不过在第2步【选择函数】窗⼝中选择“HYPGEOMDIST”函数,在第3步中输⼊相应的值即可。
如下在【sample-s】中输⼊成功的次数在【Number-sample】输⼊样本量在【population-s】中输⼊总体中成功的次数在【Number-pop】中输⼊总体中的个体总数单击【确定】即可。
⽤Excel计算泊松分布概率值的操作步骤1、进⼊Excel界⾯,单击某⼀单元格2、选择【插⼊】——【函数】选项从【选择类别】窗⼝中选择“统计”从【选择函数】窗⼝中选择“POISSON”,单击【确定】3、当【POISSON】对话框出现时在【x】中输⼊事件出现的次数在【Mean】中输⼊泊松分布的均值在【Cumulative】中输⼊0或(False),表⽰计算事件出现次数恰好等于指定数值的概率(输⼊1或True表⽰计算成功次数⼩于或等于制定数值的累计概率值)。
只需在【X】选项中,分别填⼊1,2,3即可计算出相应概率。
二项分布资料统计推断的Excel快速实现

例 2 如 果 例 1中 还 另 计 数 淋 巴 细 胞 平 均 9 7个 , 估 计 该 血 样 淋 巴 细胞 百 分 数 的 9 9 可信 区间。 当 较 大 , P和 1 ~ P均 不 太 小 时 , 如 ” p 与 ( 1 一户 ) 均 大 于 5时 , 样 本 率 P的 抽 样 分 布 近 似 正 态 分 布 l 1 j , 可 按 如 下 正 态 近似法公式计算 总体率 的 ( I — ) 可信 区间 : P ± ‰/ 2 S 。公 式 中: P为 样 本 率 ; s 为率 的标准 误 , s 一 户 ( 1 一p ) l n。‰ 为 标准正态分 布 d 水 平 的双 侧 临界 值 , 口 一0 . 0 1 时, ‰l / 2 —2 . 5 8 。 1 . 1 . 3 两 总 体 率 之 差 的 区 间估 计 例 3 对 甲、 乙两种降 压药进行 临床 疗效评 价 , 将 某 时 段 内入 院 的 高血 压 病 人 随 机 分 为 两 组 , 每组 均为 1 o 0人 。 甲 药 治疗组 8 O人 有 效 , 乙药治疗组 5 O人 有 效 , 试 估 计 两 种 降 压 药 有效率之差 的 9 9 可信区间 。 设 两 个 独 立样 本 率 分 别 为 P - 和P z , 当 与 z 均较 大 , 且
二项 分布 资料统计推 断的 E x c e l 快速实现
周治年 彭小娟 肖秀林 一 王昌富 一
( 湖北 省荆 州市 中心血 站
摘
荆州 4 3 4 1 0 0 )
要: 目的 : 探讨 对二项分布资 料进行 统计 推断 的 E x c e l 实 现 方 法 。方 法 : 利用 E x c e l 函数 B I NOMDI S T、 F I NV、 NORMS —
Excel公式和函数 相关概率计算

Excel 公式和函数 相关概率计算通过对函数进行数据的概率分析,即通过研究各种不确定性因素发生的变动,从而对项目可行性和风险性以及方案优劣作出判断的一种不确定性分析。
本节主要学习如何对概率进行计算的方法。
1.BETADIST 函数BETADIST 函数即分布累积函数,通常用于研究样本集合中某些事物的发生和变化情况。
它是返回beta 累积分布的概率密度函数。
beta 累积分布函数通常用于研究样本中一定部分的变化情况。
下面具体介绍BETADIST 函数的用法。
语法:BETADIST(x,alpha,beta,A,B)其中,该函数中各参数功能如下:●X 用来进行函数计算的值,居于可选性上下界(A 和B )之间。
●Alpha 分布参数。
其中,分布参数是用场(一维或多维空间变量的函数)来描述的参数,而不是只用有限个参数。
●Beta 分布参数。
●A 数值x 所属区间的可选下界。
其中,下界是指小于或等于所属区间中所有数据的数值。
●B 数值x 所属区间的可选上界。
其中,上界是指大于或等于所属区间中所有数据的数值。
例如,已知一组数中,计算参数为2,Alpha 分布参数为8,Beta 分布参数为10,上下界分别为3和1,求该组数据中累积函数的函数值。
在工作表中,输入累积分布函数的相关参数,如图8-1所示。
图8-1 输入相关参数 图8-2 选择函数单击【函数库】组中的【插入函数】按钮,弹出【插入函数】对话框。
在【或选择类别】下拉列表中,选择【统计】项,并在【选择函数】列表中,选择BETADIST 项,如图8-2所示。
然后,在【函数参数】对话框中,分别设置函数的参数,如设置参数X 为B2;参数Alpha 为B3;参数Beta 为B4;参数A 为B5;参数B 为B6,如图8-3所示。
提 示 分布累积函数能完整描述一个实数随机变量X 的概率分布情况。
输入数据 选择选择图8-3 设置函数参数其中,在该对话框中,设置的参数,应该注意如下几点:●如果任意参数为非数值型,函数BETADIST 返回错误值#V ALUE!。
excel 二项分布函数估算区间

excel 二项分布函数估算区间二项分布函数是概率论中一种重要的离散概率分布,它描述了在进行一系列独立的是/非试验中,成功的次数的概率分布。
二项分布函数估算区间是用来估计二项分布中成功的次数的置信区间。
在统计学中,置信区间是一种估计统计参数的统计区间,该区间基于样本数据。
本文将介绍二项分布函数估算区间的原理、计算方法以及在实际应用中的一些注意事项。
首先,我们来了解一下二项分布函数的概念和性质。
二项分布是一个离散型的概率分布,它的概率质量函数为:P(X=k) = C(n, k) * p^k * (1-p)^(n-k)其中,n表示试验的总次数,k表示成功的次数,p表示每次试验成功的概率,C(n, k)表示组合数,计算公式为:C(n, k) = n! / (k! * (n-k)!)。
在二项分布中,成功的次数k可以是从0到n的任意整数,因此二项分布的取值范围是0至n。
接下来,我们来介绍二项分布函数估算区间的原理。
估算区间是用来估计总体参数的一个区间,其中包含着参数的真实值。
二项分布函数估算区间的计算方法基于大样本正态分布的近似。
根据中心极限定理,当样本容量足够大时,二项分布可以近似为正态分布。
根据正态分布的性质,我们可以计算出置信区间。
二项分布函数估算区间的计算方法如下:1.首先,根据样本数据和置信水平,计算出样本比例p_hat,即成功的次数k的样本均值。
2.接下来,计算标准误差(standard error),标准误差反映了样本比例的不确定性。
标准误差的计算公式为:SE = sqrt(p_hat *(1 - p_hat) / n),其中n为样本容量。
3.然后,根据置信水平和样本容量,查找标准正态分布的临界值,得到对应的Z值。
4.最后,根据样本比例的标准误差和Z值,计算出二项分布函数估算区间。
估计区间的下限为p_hat - Z * SE,上限为p_hat + Z * SE。
在实际应用中,二项分布函数估算区间有几个需要注意的地方。
Excel在数理统计中的应用

图 2-3 例 2.2.1 福建师范大学数计学院 05 级数本专业成绩数据(具体数据附表 2-1),计算数理 统计成绩的平均值、方差和标准差。 步骤 1 :“插入”=>“函数”=> 选择常用函数下选择函数中的 AVERAGE =>在“函数 参数”窗口参数选择数据区域 S4:S204(或直接输入=AVERAGEZ(S4:S204) ) , 得 68.37 分 步骤 2 :“插入”=>“函数”=> 选择常用函数下选择函数中的 VARP =>在“函数参数” 窗口参数选择数据区域 S4:S204(或直接输入=VARP(S4:S204) ) , 得 237.43 步骤 3 :“插入”=>“函数”=> 选择常用函数下选择函数中的 STDEVP =>在“函数参 数”窗口参数选择数据区域 S4:S204(或直接输入 =STDEVP(S4:S204)) , 得 15.41 数理统计的平均成绩 68.37 分,方差为 237.43,标准差为 15.41
•
一元二项式概率密度函数的计算公式为: b( x, n, p ) = ⎜ ⎟ p (1 − p ) BINOMDIST(x,n,p,0)
n
⎛n⎞ ⎝x⎠
x
n− x
,相当于
•
一元二项式累积分布函数的计算公式为: B ( x, n, p ) = BINOMDIST(n,x,p,1)
∑ b( x, n, p )
x=0
,相当于
CRITBINOM(trials,probability_s,alpha) 返回使累积二项式分布大于等于临界值的最小 值。Trials 伯努利试验次数。Probability_s 每次试验中成功的概率。Alpha 临界值。 NEGBINOMDIST(number_f,number_s,probability_s) 返回负二项式分布。 当成功概率为常 量 probability_s 时,函数 NEGBINOMDIST 返回在到达 number_s 次成功之前,出现 number_f 次失败的概率。Number_f 失败次数。Number_s 成功的极限次数。Probability_s 成功的概率。
xls函数概率
xls函数概率
用excel进行概率计算的操作方法如下:
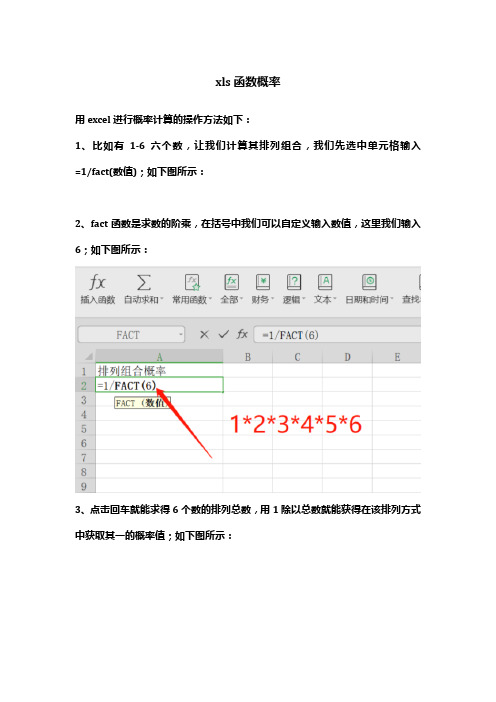
1、比如有1-6六个数,让我们计算其排列组合,我们先选中单元格输入=1/fact(数值);如下图所示:
2、fact函数是求数的阶乘,在括号中我们可以自定义输入数值,这里我们输入6;如下图所示:
3、点击回车就能求得6个数的排列总数,用1除以总数就能获得在该排列方式中获取其一的概率值;如下图所示:
4、返回给定集合中选取若干对象的排列值(最常见的是彩票中的11选5)。
如下图所示:
5、我们在单元格中输入=1/permut()公式;如下图所示:
6、permut()中参数分别为对象总数,每个排列的对象数,比如5选2,我们就输入5和2,点击回车这样就能求得其排列方式总和;用1处以总数就能获得其概率值。
如下图所示:。
自学Excel之37:统计函数(六)

自学Excel之37:统计函数(六)三十一、计算一元二项式分布的概率(BINOM.DIST函数):BINOM.DIST函数用于计算一元二项式分布的概率。
二项(式)分布是在n次独立重复的贝努利试验(只有发生或不发生两种结果的随机试验)中,表示某事件发生次数的随机变量的离散概率分布。
语法是:“=BINOM.DIST(number_s,trials,probability_s,cumulative)”。
参数number_s是试验成功次数;trials是独立试验的总次数;probability_s是每次试验的成功概率;cumulative是决定函数形式的逻辑值。
如果为TRUE,则返回累积分布函数,即最多存在number_s次成功的概率;如果为FALSE,则返回概率密度函数,即存在number_s次成功的概率。
概率密度函数是描述连续型随机变量的输出值,在某个确定的取值点附近的可能性的函数。
随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分,即累积分布函数。
二项式概率密度函数的公式为:(n次试验中有x次成功,成功的概率为p)其中,记作或,是二项式系数。
二项式累积分布函数的公式为:例:抛10次硬币,其中正面向上的为6次,分别用概率密度函数和累积分布函数计算取出A球的二项式分布概率。
1)在D2单元格插入函数:“=BINOM.DIST(B2,A2,C2,TRUE)”,按【Enter】键确认;2)在D4单元格插入函数:“=BINOM.DIST(B2,A2,C2,FALSE)”,按【Enter】键确认。
计算一元二项分布的概率三十二、使用二项式分布计算试验结果的概率(BINOM.DIST.RANGE函数):BINOM.DIST.RANGE函数用于使用二项式分布计算试验结果的概率。
其计算公式如下:语法是:“BINOM.DIST.RANGE(trials,probability_s,number_s,[number_s2] )”。
用EXCEL作二项分布、产生随机数可编辑全文

三. 计算机作OC曲线(图像) 1.选p,pa 2.在任务栏找到 “图表向导” ,击→选 “XY” 散点图→选→“确定” →显出OC曲线.
3.根据需要,调整p轴、pa轴。
四、随机数在计算机中产生 例:已知N=100,要随机n=13的抽取 操作步骤如下: 1.100台产品编号为:1~100 2.打开EXCEL
在EXCEL上选一空格,例如C1 任务栏fx
常用函数
全部 找到
RANDBETWEEN
确定
界 输Bottom(底)1 面:入Top(顶)100
在G1右下角 鼠标 找出 “+” 拖移
n i 1
( xi
x )2
③样本变异系数CV
CV
s x
六、平均值、标准偏差、二项分布、正态分 布等函数在EXCEL中计算
首先,在EXCEL任务栏中找出fx,击 fx→“常用函数”,或击“全部”,找到所 需的计算函数:
1、样本平均值x均 fx=AVERAGE(数值1,2,…n)
或使用:fx=SUM(数值1,2,…n)/n
理,得到了有关总体的丰富信息,这些信息可制 成图与表,或构造成样本的函数。不含未知参数 的样本函数称为统计量。
⑵描述样本集中位置的统计量
①样本均值x均
就是样本的平均数(值)。
x
1 n
n i 1
xi
②样本中位数Me
样本中位数是表示数据集中位置的另一种重要度 量。
在确定Me时,需要将所有样本数据按其数值大 小从小到大重新排列成有序样本:
(4)计算 Enter键,px=0= 0.076
实验三 常用分布概率计算的Excel应用

1.644853627 -1.644853627 1.959963985 -1.959963985
数据演示
正态分布绘图
• 在同一坐标系中画出N(0,1)与N(1.1)的图。
0.45 0.4 0.35 0.3 0.25 0.2 0.15 0.1 0.05 0 -6 -4 -2 0 2 4 6
数据演示
0.00124 0.00928 0.01052
讨论:试通过BINOMDIST函数和
查表两种方式解决该问题。
数据演示
二、泊松分布
• 泊松分布函数POISSON,通常用于预测一段时间内或某一 空间内事件发生的次数。 • 语法: • POISSON(x,mean,cumulative)
• X 事件数。
k012345678910n10p515则pnkcnkpk1pnkbinomdistknp0binomdistk1005150fnkcnkpk1pnkbinomdistknp1binomdistk1005151数据演示?例设某地区流行某种传染病人们受感染的概率为20在该地区某单位共有30人即n30p02?试求?3现对该单位每人都注射一种据称能预防该病的疫苗注射后至多有1人被传染试推断该疫苗是否真的有效
。 其语法结构为:
NORMSINV(probability)
• 其中:Probability为正态分布的概率值。
Z0.95= Z0.05= Z0.975= Z0.025=
NORMSINV(0.95)= NORMSINV(0.05)= NORMSINV(0.975)= NORMSINV(0.025)=
已知
(3) P ( X 1) F (1) P (0) P (1)
0 1 C 30 (0.2) 0 (0.8)30 C 30 (0.2)1 (0.8) 29
Excel在概率论和数理统计应用的举例

Excel在概率论与数理统计中应用的举例理优078 10074399 赵晨一.概率计算1.二项分布概率的计算例2.54(保险业务)今有2500名同一类型的人参加保险公司的人寿保险,参加者每年参保费为1200元,一年中若死亡,保险公司赔偿200000元,据生命表统计这类人员每年死亡率为2‰,试求:⑴保险公司获益的概率α;⑵保险公司获益不少于1000000元的概率β.(P62页)解:现拟用二项分布计算,设ξ~B(2500,0.002),由题意知需解出ξ<15的概率,用Excel 函数计算的步骤如下:操作步骤:①.单击要存放结果的单元格B2②.单击“插入函数”按钮,选择“BINOMDIST”函数,在弹出“函数参数”的对话框中依次输入参数14,2500,0.002,true,如下图所示。
Number_s:求解的试验的成功次数;Trials:独立试验的次数;Probability_s:每次试验的成功概率;Cumulative:如果为“true”,函数BINOMDIST返回P{X≤k(Number_s)}的概率;如果为“false”函数BINOMDIST返回P{X=k(Number_s)}的概率③.单击“确定”按钮,Excel计算的二项分布概率为:0.99982.泊松分布的概率计算例:假设某电话总机交换台每分钟收到的呼唤次数服从参数为3的泊松分布,则在1分钟内恰有2次呼唤的概率是多少?解操作步骤:1.单击要存放结果的单元格B22.单击“插入函数”按钮,选择“POISSON”函数,在弹出“函数参数”的对话框中依次输入参数2,3,false,如下图所示。
X:事件出现的次数Mean:期望值(λ)Cumulative:如果为“true”,函数POISSON返回P{X≤k(X)}的概率;如果为“false”函数POISSON返回P{X=k(X)}的概率3.单击“确定”按钮,Excel计算的泊松分布概率为:0.2243.超几何分布概率的计算例:在52张扑克牌中抽取7张,其中有一张黑桃的概率是多少?解操作步骤:1.单击要存放结果的单元格B22.单击“插入函数”按钮,选择“HYPGEOMDIST”函数,在弹出“函数参数”的对话框中依次输入参数1,13,7,52,如下图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用Excel计算二项分布概率值的操作步骤
1、进入Excel界面,单击某一单元格。
2、选择【插入】——【函数】选项
从【选择类别】窗口中选择“统计”
从【选择函数】窗口中选择“BINOMDIST”,单击【确定】
3、当【BINOMDIST】对话框出现时:
在【Number-s】中输入2(成功的次数X)
在【trials】中输入3(实验的总次数n)
在【Probability-s】中输入0.05(每次实验成功的概率p)
在【Cumulative】中输入0(或False),表示计算成功次数恰好等于制定数值的概率(输入1或True表示计算成功次数小于或等于制定数值的累计概率值)。
选择【完成】即可得到结果。
计算超几何分布概率的步骤与上述过程类似,只不过在第2步【选择函数】窗口中选择“HYPGEOMDIST”函数,在第3步中输入相应的值即可。
如下
在【sample-s】中输入成功的次数
在【Number-sample】输入样本量
在【population-s】中输入总体中成功的次数
在【Number-pop】中输入总体中的个体总数
单击【确定】即可。
用Excel计算泊松分布概率值的操作步骤
1、进入Excel界面,单击某一单元格
2、选择【插入】——【函数】选项
从【选择类别】窗口中选择“统计”
从【选择函数】窗口中选择“POISSON”,单击【确定】
3、当【POISSON】对话框出现时
在【x】中输入事件出现的次数
在【Mean】中输入泊松分布的均值
在【Cumulative】中输入0或(False),表示计算事件出现次数恰好等于指定数值的概率(输入1或True表示计算成功次数小于或等于制定数值的累计概率值)。
只需在【X】选项中,分别填入1,2,3即可计算出相应概率。
