备战2021湖北省各市2019年中考数学圆压轴题真题汇编
2021中考数学压轴题满分训练 – 圆的专题含答案解析

2021中考数学压轴题满分训练–圆的专题1.如图,AB为⊙O直径,C为⊙O上的一点,过点C的切线与AB的延长线相交于点D,CA=CD.(1)连接BC,求证:BC=OB;(2)E是中点,连接CE,BE,若BE=4,求CE的长.2.如图,AB为⊙O的直径,点C在⊙O上,AD与过点C的切线互相垂直,垂足为D.连接BC并延长,交AD的延长线于点E.(1)求证:AE=AB;(2)若AB=20,BC=16,求CD的长.3.如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,过点D作⊙O的切线DE交AB于E.(1)求证:DE⊥AB;(2)如果tan B=,⊙O的直径是5,求AE的长.4.阅读以下材料,并按要求完成相应的任务:莱昂哈德•欧拉(LeonhardEuler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数,公式和定理,下面就是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其中外心和内心,则OI2=R2﹣2Rr.如图1,⊙O和⊙I分别是△ABC的外接圆和内切圆,⊙I与AB相切于点F,设⊙O的半径为E,⊙I的半径为r,外心O(三角形三边垂直平分线的交点)与内心I(三角形三条角平分线的交点)之间的距离OI=d,则有d2=R2﹣2Rr.下面是该定理的证明过程(部分):延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.∵∠D=∠N,∴∠DMI=∠NAI(同弧所对的圆周角相等).∴△MDI∽△ANI.∴=,∴IA•ID=IM•IN,①如图2,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF.∵DE是⊙O的直径,∴∠DBE=90°.∵⊙I与AB相切于点F,∴∠AFI=90°,∴∠DBE=∠IFA.∵∠BAD=∠E(同弧所对的圆周角相等),∴△AIF∽△EDB,∴=.∴IA•BD=DE•IF②任务:(1)观察发现:IM=R+d,IN=(用含R,d的代数式表示);(2)请判断BD和ID的数量关系,并说明理由.(3)请观察式子①和式子②,并利用任务(1),(2)的结论,按照上面的证明思路,完成该定理证明的剩余部分;(4)应用:若△ABC的外接圆的半径为6cm,内切圆的半径为2cm,则△ABC的外心与内心之间的距离为cm.5.【发现】如图(1),AB为⊙O的一条弦,点C在弦AB所对的优弧上,根据圆周角性质,我们知道∠ACB的度数(填“变”或“不变”);若∠AOB=150°,则∠ACB =°.爱动脑筋的小明猜想,如果平面内线段AB的长度已知,∠ACB的大小确定,那么点C是不是在某一个确定的圆上运动呢?【研究】为了解决这个问题,小明先从一个特殊的例子开始研究.如图(2),若AB=2,直线AB上方一点C满足∠ACB=45°,为了画出点C所在的圆,小明以AB为底边构造了一个等腰Rt△AOB,再以O为圆心,OA为半径画圆,则点C在⊙O上.请根据小明的思路在图(2)中完成作图(要求尺规作图,不写作法,保留作图痕迹,并用2B 铅笔或黑色水笔加黑加粗).后来,小明通过逆向思维及合情推理,得出一个一般性的结论,即:若线段AB的长度已知,∠ACB的大小确定,则点C一定在某一个确定的圆上,即定弦定角必定圆,我们把这样的几何模型称之为“定弦定角”模型.【应用】(1)如图(3),AB=2,平面内一点C满足∠ACB=60°,则△ABC面积的最大值为.(2)如图(4),已知正方形ABCD,以AB为腰向正方形内部作等腰△BAE,其中BE =BA,过点E作EF⊥AB于点F,点P是△BEF的内心.①∠BPE=°,∠BPA=°;②连接CP,若正方形ABCD的边长为2,则CP的最小值为.6.如图,BE为⊙O的直径,C为线段BE延长线上一点,CA为⊙O的切线,A为切点,连接AB,AE,AO.∠C=30°.(1)求∠ABC的度数;(2)求证:BO=CE;(3)已知⊙O的半径为6,求图中阴影部分的面积.(结果保留π)7.如图,在△ABC中,点D是AC边上一点,以AD为直径的⊙O与边BC切于点E,且AB=BE.(1)求证:AB是⊙O的切线;(2)若BE=3,BC=7,求⊙O的半径长;(3)求证:CE2=CD•CA.8.如图,AB是⊙O的直径,AC⊥AB,BC交⊙O于点D,点E在劣弧BD上,DE的延长线交AB的延长线于点F,连接AE交BD于点G.(1)求证:∠AED=∠CAD;(2)若点E是劣弧BD的中点,求证:ED2=EG•EA;(3)在(2)的条件下,若BO=BF,DE=1.5,求EF的长.9.定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到这边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连接AD,若AD2=BD•CD,则称点D是△ABC中BC边上的“好点”.(1)如图2,△ABC的顶点是4×4网格图的格点,请仅用直尺画出(或在图中直接描出)AB边上的“好点”;(2)△ABC中,BC=14,tan B=,tan C=1,点D是BC边上的“好点”,求线段BD的长;(3)如图3,△ABC是⊙O的内接三角形,点H在AB上,连接CH并延长交⊙O于点D.若点H是△BCD中CD边上的“好点”.①求证:OH⊥AB;②若OH∥BD,⊙O的半径为r,且r=3OH,求的值.10.如图,DE是△DBC的外角∠FDC的平分线,交BC的延长线于点E,DE的延长线与△DBC的外接圆交于点A.(1)求证:AB=AC;(2)若∠DCB=90°,sin E=,AD=4,求BD的长.11.已知⊙O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D.(1)如图1,求证:BD=ED.(2)如图2,AD为⊙O的直径.若BC=12,sin∠BAC=,求OE的长.12.如图,AB是大半圆O的直径.OA是小半圆O1的直径,点C是大半圆O上的一个动点(不与点A、B重合),AC交小半圆O1于点D,DE⊥OC,垂足为E.(1)求证:AD=DC;(2)求证:DE是半圆O1的切线;(3)如果OE=EC,请判断四边形O1OED是什么四边形,并证明你的结论.13.已知△ABC是⊙O的内接三角形,AB为⊙O的直径.点D是⊙O外一点,连接AD 和OD,OD与AC相交于点E,且OD⊥AC.(1)如图1,若AD是⊙O的切线,tan∠BAC=,证明:AD=AB;(2)如图2,延长DO交⊙O于点F,连接CD,CF,AF.当四边形ADCF为菱形,且∠BAC=30°,BC=1时,求DF的长.14.如图1,在△ABC中,AB=AC,⊙O是△ABC的外接圆,过C作CD∥AB,CD交⊙O于D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.(1)求证:AF是⊙O的切线;(2)求证:AB2﹣BE2=BE•EC;(3)如图2,若点G是△ACD的内心,BC•BE=64,求BG的长.15.已知:△ABC内接于⊙O,连接CO并延长交AB于点E,交⊙O于点D,满足∠BEC =3∠ACD.(1)如图1,求证:AB=AC;(2)如图2,连接BD,点F为弧BD上一点,连接CF,弧CF=弧BD,过点A作AG⊥CD,垂足为点G,求证:CF+DG=CG;(3)如图3,在(2)的条件下,点H为AC上一点,分别连接DH,OH,OH⊥DH,过点C作CP⊥AC,交⊙O于点P,OH:CP=1:,CF=12,连接PF,求PF的长.参考答案1.解:(1)如图,连接OC,AE,过点A作AM⊥CE,垂足为M,∵PC是⊙O的切线,∴∠CAB=∠DCB,又∵CA=CD,∴∠CAB=∠CDB,∴∠DCB=∠CDB,∴BC=BD,又∵AB是⊙O的直径,∴∠ACB=90°,∴∠CAB+∠CBA=90°,∵∠CBA=2∠CDB=2∠CAB,∴∠CBA=90°×=60°,∵OC=OB,∴△OBC是正三角形,∴BC=OB;(2)连接AE,过点A作AM⊥CE,垂足为M,∵E是中点,∴AE=BE=4,∠ACE=∠BCE=∠ACB=×90°=45°,在Rt△AEM中,AE=4,∠AEM=∠CBA=60°,∴EM=AE=2,AM=AE=2,在Rt△ACM中,AM=2,∠ACM=45°,∴CM=AM=2,∴CE=EM+CM=2+2,答:CE的长为2+2.2.(1)证明:连接OC,∵DC切⊙O于C,∴OC⊥CD,∵AE⊥CD,∴AE∥OC,∵AO=BO,∴EC=BC,∴OC=AE,∵OC=OA=OB=AB,∴AE=AB;(2)解:连接AC,∵AB是⊙O的直径,∴∠ACB=90°,∴∠ACE=90°,AC⊥BE,∵由(1)知:AB=AE,∴EC=BC,∵BC=16,∴EC=16,在RtACB中,由勾股定理得:AC===12,在Rt△ACE中,S△ACE==,∵AE=AB=20,∴=CD,解得:CD=9.6.3.(1)证明:连接AD,OD,∵AC为⊙O的直径,∴AD⊥BC,∵AB=AC,∴∠BAD=∠CAD,∵OA=OD,∴∠OAD=∠ODA,∴∠BAD=∠ODA,∴AB∥OD,∵DE是⊙O的切线,∴OD⊥DE,∴DE⊥AB;(2)解:∵tan B==,∴设AD=k,BD=2k,∴AB==k,∵AB=AC=5,∴k=,∴AD=,BD=2,∵S△ABD=AB•DE=AD•BD,∴DE==2,∴AE===1.4.解:(1)∵O、I、N三点共线∴OI+IN=ON∴IN=ON﹣OI=R﹣d故答案为:R﹣d.(2)BD=ID.理由如下:∵点I是△ABC的内心∴∠BAD=∠CAD,∠CBI=∠ABI∵∠DBC=∠CAD,∠BID=∠BAD+∠ABI ∠DBI=∠DBC+∠CBI∴∠BID=∠DBI∴BD=ID.(3)由(2)知BD=ID∴式子②可改写为IA•ID=DE•IF又∵IA•ID=IM•IN∴DE•IF=IM•IN∴2R•r=(R+d)(R﹣d)∴R2﹣d2=2Rr∴d2=R2﹣2Rr.(4)∵d2=R2﹣2Rr=62﹣2×6×2=12∴d=2.故答案为:2.5.解:【发现】根据圆周角性质,∠ACB的度数不变,∵∠AOB=150°,∴∠ACB=∠AOB=75°,故答案为:不变,75°;【研究】补全图形如图1所示,【应用】(1)如图2,记△ABC的外接圆的圆心为O,连接OA,OB,∵∠ACB=60°,∴∠AOB=2∠ACB=120°,∵OA=OB,∴∠OAB=30°,过点O作OH⊥AB于H,∴AH=AB=,在Rt△AHO中,设⊙O的半径为2r,则OH=r,根据勾股定理得,(2r)2﹣r2=3,∴r=1(舍去负数),∴OA=2,OH=1,∵点C到AB的最大距离h为r+OH=2+1=3,∴S△ABC最大=AB•h=×2×3=3,故答案为:3;(2)①∵EF⊥AB,∴∠EFB=90°,∴∠BEF+∠EBF=90°,∵点P是△BEF的内心,∴PE,PB分别是∠BEF和∠EBF的角平分线,∴∠BEP=∠BEF,∠EBP=∠ABP=∠ABE,∴∠BPE=180°﹣(∠BEP+∠EBP)=180°﹣(∠BEF+∠EBF)=180°﹣×90°=135°;在△BPE和△BPA中,,∴△BPE≌△BPA(SAS).∴∠BPA=∠BPE=135°,故答案为:135°,135°;②如图3,作△ABP的外接圆,圆心记作点O,连接OA,OB,在优弧AB上取一点Q,连接AQ,BQ,则四边形APBQ是⊙O的圆内接四边形,∴∠AQB=180°∠BPA=45°,∴∠AOB=2∠AQB=90°,∴OA=OB=AB=,连接OC,与⊙O相交于点P'此时,CP'是CP的最小值,过点O作OM⊥AB于M,ON⊥CB,交CB的延长线于N,则四边形OMBN是正方形,∴ON=BN=BM=AB=1,∴CN=BC+BN=3,在Rt△ONC中,OC==,∴CP 的最小值=CP'=OC﹣OP'=﹣,故答案为:﹣.6.(1)解:∵CA为⊙O的切线,∴∠OAC=90°,∴∠AOC=90°﹣∠C=60°,由圆周角定理得,∠ABC=∠AOC=30°;(2)证明:在Rt△AOC中,∠C=30°,∴OA=OC,∵OA=OB=OE,∴OB=CE;(3)解:在Rt△AOC中,AC==6,∴图中阴影部分的面积=×6×6﹣=18﹣6π.7.(1)证明:连接OB、OE,如图所示:在△ABO和△EBO中,,∴△ABO≌△EBO(SSS),∴∠BAO=∠BEO,∵⊙O与边BC切于点E,∴OE⊥BC,∴∠BEO=∠BAO=90°,即AB⊥AD,∴AB是⊙O的切线;(2)解:∵BE=3,BC=7,∴AB=BE=3,CE=4,∵AB⊥AD,∴AC===2,∵OE⊥BC,∴∠OEC=∠BAC=90°,∠ECO=∠ACB,∴△CEO∽△CAB,∴,即,解得:OE=,∴⊙O的半径长为.(3)证明:连接AE,DE,∵AD是⊙O的直径,∴∠AED=90°,∴∠AEB+∠DEC=90°,∵BA是⊙O的切线,∴∠BAC=90°,∴∠BAE+∠EAD=90°,∵AB=BE,∴∠BAE=∠BEA,∴∠DEC=∠EAD,∴△EDC∽△AEC,∴,∴CE2=CD•CA.8.(1)证明:∵AB是⊙O的直径,∴∠ADB=90°,∵AC⊥AB,∴∠CAB=90°,∴∠ABD=∠CAD,∵=,∴∠AED=∠ABD,∴∠AED=∠CAD;(2)证明:∵点E是劣弧BD的中点,∴=,∴∠EDB=∠DAE,∵∠DEG=∠AED,∴△EDG∽△EAD,∴,∴ED2=EG•EA;(3)解:连接OE,∵点E是劣弧BD的中点,∴∠DAE=∠EAB,∵OA=OE,∴∠OAE=∠AEO,∴∠AEO=∠DAE,∴OE∥AD,∴,∵BO=BF=OA,DE=,∴,∴EF=3.9.解:(1)如图:D即为△ABC边AB上的“好点”;(2)如答图1:过A作AH⊥BC于H,∵tan B=,tan C=1,∴,=1,设AH=3k,则BH=4k,CH=3k,∵BC=14,∴3k+4k=14,解得k=2,∴BH=8,AH=CH=6,设BD=x,则CD=14﹣x,DH=8﹣x,Rt△ADH中,AD2=AH2+DH2=62+(8﹣x)2,而点D是BC边上的“好点”,有AD2=BD•CD=x•(14﹣x),∴62+(8﹣x)2=x•(14﹣x),解得x=5或x=10,∴BD=5或BD=10;(3)①∵∠CAH=∠HDB,∠AHC=∠BHD,∴△ACH∽△DBH,∴,∴AH•BH=CH•DH,∵点H是△BCD中CD边上的“好点”,∴BH2=CH•DH,∴AH=BH,∴OH⊥AB;②如答图2:连接AD,∵OH⊥AB,OH∥BD,∴AB⊥BD,∴AD是直径,∵r=3OH,设OH=m,则OA=3m,BD=2m,Rt△AOH中,AH==2m,∴BH=2m,Rt△BHD中,HD==2m,∵点H是△BCD中CD边上的“好点”,∴BH2=CH•DH,∴CH==m,∴==.10.(1)证明:∵DE是△DBC的外角∠FDC的平分线,∴∠FDE=∠CDE,∵∠ADB=∠ACB=∠FDE,∠ABC=∠CDE,∴∠ABC=∠ACB,∴AB=AC;(2)解:∵∠DCB=90°,∴∠DCE=∠BAD=90°,∴∠E+∠CDE=∠ABD+∠ADB=90°,∵∠ADB=∠FDE=∠CDE,∴∠ABD=∠E,∵sin E=,∴sin∠ABD==,∵AD=4,∴BD=4.11.(1)证明:如图1,连接BE.∵E是△ABC的内心,∴∠ABE=∠CBE,∠BAD=∠CAD,∵∠DBC=∠CAD.∴∠DBC=∠BAD,∵∠BED=∠BAD+∠ABE,∴∠DBE=∠DEB,∴BD=ED;(2)如图2 所示;连接OB.∵AD是直径,AD平分∠BAC,∴AD⊥BC,且BF=FC=6,∵,∴OB=10.在Rt△BOF中,BF=6,OB=10,∴,∴DF=2,在Rt△BDF中,BF2+DF2=BD2,∴,∴,∴.12.证明:(1)连接OD,∵AO为圆O1的直径,则∠ADO=90°.∵AC为⊙O的弦,OD为弦心距,∴AD=DC.(2)证明:∵D为AC的中点,O1为AO的中点,∴O1D∥OC.又DE⊥OC,∴DE⊥O1D∴DE与⊙O1相切.(3)如果OE=EC,又D为AC的中点,∴DE∥O1O,又O1D∥OE,∴四边形O1OED为平行四边形.又∠DEO=90°,O1O=O1D,∴四边形O1OED为正方形.13.解:(1)证明:∵OD⊥AC,∴AE=EC=AC,∠DEA=90°,∵AB为⊙O的直径,∴∠ACB=90°,∵tan∠BAC==,∴BC=AC,∴AE=BC,∵AD是⊙O的切线,∴DA⊥AB,∴∠DAO=∠ACB=90°,∴∠DAE+∠CAB=∠ABC+∠CAB=90°,∴∠DAE=∠ABC,在△DAE和△ABC中,,∴△DAE≌△ABC(ASA),∴AD=AB;(2)在Rt△ABC中,∠BAC=30°,BC=1,∴AB=2,AC=,∵∠ABC=∠AFC=60°,∵四边形ADCF为菱形,∴AC=FC=,∴△AFC是等边三角形,∴∠DFC=AFC=30°,∴CE=FC=,∴EF=CE=,∴DF=2EF=3.14.解:(1)如图1,连接OA,∵AB=AC,∴=,∠ACB=∠B,∴OA⊥BC,∵CA=CF,∴∠CAF=∠CFA,∵CD∥AB,∴∠BCD=∠B,∴∠ACB=∠BCD,∴∠ACD=∠CAF+∠CFA=2∠CAF,∵∠ACB=∠BCD,∴∠ACD=2∠ACB,∴∠CAF=∠ACB,∴AF∥BC,∴OA⊥AF,∴AF为⊙O的切线;(2)∵∠BAD=∠BCD=∠ACB,∠B=∠B,∴△ABE∽△CBA,∴,∴AB2=BC•BE=BE(BE+CE)=BE2+BE•CE,∴AB2﹣BE2=BE•EC;(3)由(2)知:AB2=BC•BE,∵BC•BE=64,∴AB=8,如图2,连接AG,∴∠BAG=∠BAD+∠DAG,∠BGA=∠GAC+∠ACB,∵点G为内心,∴∠DAG=∠GAC,又∵∠BAD+∠DAG=∠GAC+∠ACB,∠BAD=∠ACB,∴∠BAG=∠BGA,∴BG=AB=8.15.(1)证明:如图1中,连接AD.设∠BEC=3α,∠ACD=α.∵∠BEC=∠BAC+∠ACD,∴∠BAC=2α,∵CD是直径,∴∠DAC=90°,∴∠D=90°﹣α,∴∠B=∠D=90°﹣α,∵∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣2α﹣(90°﹣α)=90°﹣α.∴∠ABC=∠ACB,∴AB=AC.(2)证明:如图2中,连接AD,在CD上取一点Z,使得CZ=BD.∵=,∴DB=CF,∵∠DBA=∠DCA,CZ=BD,AB=AC,∴△ADB≌△AZC(SAS),∴AD=AZ,∵AG⊥DZ,∴DG=GZ,∴CG=CZ+GZ=BD+DG=CF+DG.(3)解:连接AD,PA,作OK⊥AC于K,OR⊥PC于R,CT⊥FP交FP的延长线于T.∵CP⊥AC,∴∠ACP=90°,∴PA是直径,∵OR⊥PC,OK⊥AC,∴PR=RC,∠ORC=∠OKC=∠ACP=90°,∴四边形OKCR是矩形,∴RC=OK,∵OH:PC=1:,∴可以假设OH=a,PC=2a,∴PR=RC=a,∴RC=OK=a,sin∠OHK==,∴∠OHK=45°,∵OH⊥DH,∴∠DHO=90°,∴∠DHA=180°﹣90°﹣45°=45°,∵CD是直径,∴∠DAC=90°,∴∠ADH=90°﹣45°=45°,∴∠DHA=∠ADH,∴AD=AH,∵∠COP=∠AOD,∴AD=PC,∴AH=AD=PC=2a,∴AK=AH+HK=2a+a=3a,在Rt△AOK中,tan∠OAK==,OA===a,∴sin∠OAK==,∵∠ADG+∠DAG=90°,∠ACD+∠ADG=90°,∴∠DAG=∠ACD,∵AO=CO,∴∠OAK=∠ACO,∴∠DAG=∠ACO=∠OAK,∴tan∠ACD=tan∠DAG=tan∠OAK=,∴AG=3DG,CG=3AG,∴CG=9DG,由(2)可知,CG=DG+CF,∴DG+12=9DG,∴DG=,AG=3DG=3×=,∴AD===,∴PC=AD=,∵sin∠F=sin∠OAK,∴sin∠F==,∴CT=×FC=×12=,FT===,PT===,∴PF=FT﹣PT=﹣=.。
2019年湖北省中考圆之集萃
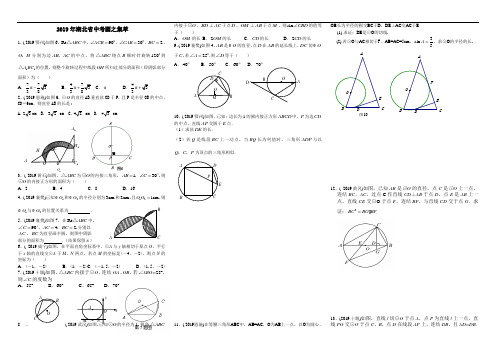
2019年湖北省中考圆之集萃1、( 2019鄂州)如图6,Rt ABC △中,90ACB ∠=,30CAB ∠=,2BC =,O H ,分别为边AB AC ,的中点,将ABC △绕点B 顺时针旋转120到11A BC △的位置,则整个旋转过程中线段OH 所扫过部分的面积(即阴影部分面积)为( )A.7π3B.4π3 C .πD.4π3+2、( 2019恩施)如图6,⊙O 的直径AB 垂直弦CD 于P ,且P 是半径OB 的中点,CD =6cm ,则直径AB 的长是:A.32cmB. 23 cmC.24 cmD. 34 cm3、( 2019黄石)如图,ABC △为O ⊙的内接三角形,130AB C =∠=,°,则O ⊙的内接正方形的面积为( ) A .2 B .4 C .8 D .16 4、( 2019襄樊)已知1O 和2O 的半径分别为3cm 和2cm ,且121cm O O =,则1O 与2O 的位置关系为 .5、(2019襄樊)如图7,在Rt ABC △中,9042C AC BC ===∠°,,,分别以 AC 、BC 为直径画半圆,则图中阴影部分的面积为 .(结果保留π)6、( 2019咸宁)如图,在平面直角坐标系中,⊙A 与y 轴相切于原点O ,平行于x 轴的直线交⊙A 于M 、N 两点,若点M 的坐标是(-4,-2),则点N 的坐标为( )A .(-1,-2)B .(1,-2)C .(-1.5,-2)D .(1.5,-2) 7、( 2019十堰)如图,△ABC 内接于⊙O ,连结OA 、OB ,若∠ABO=25°,则∠C 的度数为 A .55° B .60° C .65° D .70°1,锐角ABC△8、内接于O ⊙,BD AC ⊥于点D ,OM AB ⊥于点M ,则s in C B D ∠的值等于( )A .OM 的长B .2OM 的长C .CD 的长 D .2CD 的长 9、( 2019襄樊)如图4,AB 是O 的直径,点D 在AB 的延长线上,DC 切O 于C ,若25A =∠.则D ∠等于( ) A .40︒ B .50︒ C .60︒10、( 2019鄂州)如图,已知:边长为1的圆内接正方形ABCD中,P 为边CD 的中点,直线AP 交圆于E 点. (1)求弦DE 的长.(2)若Q 是线段BC 上一动点,当BQ 长为何值时,三角形ADP 与以Q C P ,,为顶点的三角形相似.11、( 2019恩施)在等腰三角形ABC 中,AB=AC ,O 为AB 上一点,以O 为圆心、OB 长为半径的圆交BC 于D ,DE ⊥AC 交AC 于E.(1).求证:DE 是⊙O 的切线. (2).若⊙O 与AC 相切于F ,AB=AC=5cm ,53sin =A ,求⊙O 的半径的长.12、( 2019黄冈)如图,已知AB 是⊙O 的直径,点C 是⊙O 上一点,连结BC ,AC ,过点C 作直线CD ⊥AB 于点D ,点E 是AB 上一点,直线CE 交⊙O 于点F ,连结BF ,与直线CD 交于点G .求证:2BC BG BF =13、(2019十堰)如图,直线l 切⊙O 于点A ,点P 为直线l 上一点,直线PO 交⊙O 于点C 、B ,点D 在线段AP 上,连结DB ,且AD=DB .A AH BOOC1H1A1CE图10CACAO CB A D MC ABAO D(2)若AD=1,PB=BO ,求弦AC 的长.14、( 2019武汉)如图,Rt ABC △中,90ABC ∠=°,以AB 为直径作O ⊙交AC 边于点D ,E 是边BC 的中点,连接DE . (1)求证:直线DE 是O ⊙的切线;(2)连接OC 交DE 于点F ,若OF CF =,求tan ACO ∠的值.15、( 2019宜昌)如图12,已知:在O 中,直径4AB =,点E 是OA 上任意一点,过E 作弦CD AB ⊥,点F 是BC 上一点,连接AF 交CE 于H ,连接AC 、(1)求证:ACH AFC △∽△;(2)猜想:AH AF 与AE AB 的数量关系,并说明你的猜想; (3)探究:当点E 位于何处时,14?AEC BOD S S =△△::并加以说明.16、(2019宜昌)已知如图,⊙O 的直径AD =2,BC CD DE ==,∠BAE =90°.(1)求△CAD 的面积;(2)如果在这个圆形区域中,随机确定一个点P ,那么点P 落在四边形ABCD 区域的概率是多少?17、( 2019咸宁)如图,在△ABC 中,∠ABC =90°,以AB 为直径的⊙O 交AC 于点D ,过点D 作切线交BC 于点E .(1)求证:DE = 12BC ;18、(2019咸宁)已知:如图1,把矩形纸片ABCD 折叠,使得顶点A 与边DC 上的动点P 重合(P 不与点D ,C 重合), MN 为折痕,点M ,N 分别在边BC , AD 上,连接AP ,MP ,AM , AP 与MN 相交于点F .⊙O 过点M ,C ,P . (1)请你在图1中作出⊙O (不写作法,保留作图痕迹); (2)AF AN与AP AD是否相等?请你说明理由;(3)随着点P 的运动,若⊙O 与AM 相切于点M 时,⊙O 又与AD 相切于点H . 设AB 为4,请你通过计算,画出..这时的图形.(图2,3供参考)图1图2图3CEBAOFDAB ABCFPMND BCP O DM F FMN DOP CB A。
2021年九年级数学中考一轮复习 圆综合填空压轴题 提升专题训练
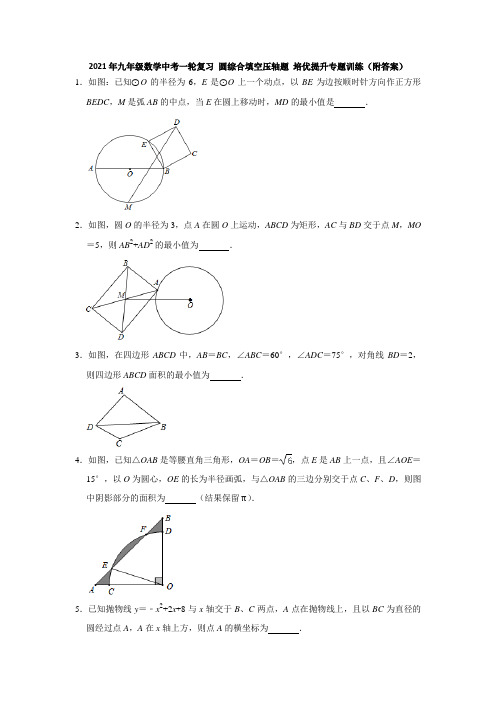
2021年九年级数学中考一轮复习圆综合填空压轴题培优提升专题训练(附答案)1.如图:已知⊙O的半径为6,E是⊙O上一个动点,以BE为边按顺时针方向作正方形BEDC,M是弧AB的中点,当E在圆上移动时,MD的最小值是.2.如图,圆O的半径为3,点A在圆O上运动,ABCD为矩形,AC与BD交于点M,MO =5,则AB2+AD2的最小值为.3.如图,在四边形ABCD中,AB=BC,∠ABC=60°,∠ADC=75°,对角线BD=2,则四边形ABCD面积的最小值为.4.如图,已知△OAB是等腰直角三角形,OA=OB=,点E是AB上一点,且∠AOE=15°,以O为圆心,OE的长为半径画弧,与△OAB的三边分别交于点C、F、D,则图中阴影部分的面积为(结果保留π).5.已知抛物线y=﹣x2+2x+8与x轴交于B、C两点,A点在抛物线上,且以BC为直径的圆经过点A,A在x轴上方,则点A的横坐标为.6.如图,在矩形ABCD中,AB>BC,以点B为圆心,AB的长为半径的圆分别交CD边于点M,交BC边的延长线于点E.若DM=CE,的长为2π,则CE的长.7.如图,过⊙O外一点P作⊙O的两条切线P A,PB,切点分别为A,B,作直线BC,连接AB,AC,若∠P=80°,则∠C=°.8.已知⊙O的直径AB为4cm,点C是⊙O上的动点,点D是BC的中点,AD延长线交⊙O 于点E,则BE的最大值为.9.如图,等腰△ABC中,AC=BC=2.∠ACB=120°,以AB为直径在△ABC另一侧作半圆,圆心为O,点D为半圆上的动点,将半圆沿AD所在直线翻叠,翻折后的弧AD 与直径AB交点为F,当弧AD与BC边相切时,AF的长为.10.如图,△ABC中,∠ACB=90°,BC=3,cos∠B=,将△ABC绕点C顺时针旋转90°得到△AB'C,P为线段AB上的动点,以点P为圆心,P A长为半径作⊙P,当⊙P与△A′B′C的一边所在的直线相切时,⊙P的半径为.11.如图,四边形ABDC内接于半圆O,AB为直径,AD平分∠CAB,AB﹣AC=4,AD=3,作DE⊥AB于点E,则BE的长为,AC的长为.12.已知:如图,四边形ABCD中,AD∥BC,AB=BC=4,∠B=60°,∠C=105°,点E为BC的中点,以CE为弦作圆,设该圆与四边形ABCD的一边的交点为P,若∠CPE =30°,则EP的长为.13.已知x轴上有点A(1,0),点B在y轴上,点C(m,0)为x轴上一动点且m<﹣1,连接AB,BC,tan∠ABO=,以线段BC为直径作⊙M交线段AB于点D,过点B作直线l∥AC,过A,B,C三点的抛物线为y=ax2+bx+e,直线与抛物线和⊙M的另一个交点分别是E,F,当EF=BD时,则m的值为.14.Rt△ABC中,∠ACB=90°,CD为AB边上的高,P为AC的中点,连接PD,BC=6,DP=4.O为边BA上一点,以O为圆心,OB为半径作⊙O,当⊙O与△PDC的一边所在直线相切时,⊙O的半径等于.15.如图,⊙O的直径AB的长12,长度为4的弦DF在半圆上滑动,DE⊥AB于点E,OC ⊥DF于点C,连接CE,AF,则sin∠AEC的值是,当CE的长取得最大值时AF 的长是.16.如图,在平面直角坐标系中,⊙P与x轴相切于原点O,平行于y轴的直线交⊙P于E,F两点,若点E的坐标是(﹣3,﹣1),则点F的坐标是.17.如图,已知在Rt△ABC中,∠ACB=90°,cos B=,BC=3,P是射线AB上的一个动点,以P为圆心,P A为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC 于点E.设线段BE的中点为Q,射线PQ与⊙P相交于点F,点P在运动过程中,当PE ∥CF时,则AP的长为.18.矩形ABCD的边AB=4,边AD上有一点M,连接BM,将MB绕M点逆时针旋转90°得MN,N恰好落在CD上,过M、D、N作⊙O,⊙O与BC相切,Q为⊙O上的动点,连BQ,P为BQ中点,连AP,则AP的最小值为.19.如图,矩形ABCD中,AB=,BC=AB2,E为射线BA上一动点,连接CE交以BE 为直径的圆于点H,则线段DH长度的最小值为.20.如图,抛物线y=x2﹣x﹣1与x轴交于A、B两点,与y轴交于C点,⊙B的圆心为B,半径是1,点P是直线AC上的动点,过点P作⊙B的切线,切点是Q,则切线长PQ的最小值是.21.平面直角坐标系中,⊙O交x轴正负半轴于点A、B,点P为⊙O外y轴正半轴上一点,C为第三象限内⊙O上一点,PH⊥CB交CB延长线于点H,已知∠BPH=2∠BPO,PH =15,CH=24,则tan∠BAC的值为.22.如图,AB是以点O为圆心的圆形纸片的直径,弦CD⊥AB于点E,AB=10,BE=3.将阴影部分沿着弦AC翻折压平,翻折后,弧AC对应的弧为G,则点O与弧G所在圆的位置关系为.23.如图,在平行四边形ABCD中,以对角线AC为直径的圆O分别交BC,CD于点E,F.若AB=13,BC=14,CE=9,则线段EF的长为.24.如图,在扇形OAB中,∠AOB=90°,OA=OB=2,将扇形OAB绕边OB的中点D 顺时针旋转90°得到扇形O'A'B',弧A'B′交OA于点E,则图中阴影部分的面积为.25.如图所示,已知AB=10,点P是线段AB上的动点,以AP为边作正六边形APCDEF,以PB为底作等腰三角形BPN,连接PD,DN,则△PDN的面积的最大值是.26.如图,已知扇形AOB的圆心角为120°,点C是半径OA上一点,点D是弧AB上一点.将扇形AOB沿CD对折,使得折叠后的图形恰好与半径OB相切于点E.若∠OCD =45°,OC=+1,则扇形AOB的半径长是.27.如图,在矩形ABCD中,AB=6,AD=8,点M,N分别为AD,AC上的动点(不含端点),AN=DM,连接点M与矩形的一个顶点,以该线段为直径作⊙O,当点N和矩形的另一个顶点也在⊙O上时,线段DM的长为.参考答案1.解:如图,连接MO,延长MO交⊙O于T,连接BT,OE,BD.∵M是弧AB的中点,AB是直径,∴MT⊥AB,∵OB=OT=6,∴∠OBT=∠OTB=45°,∴BT=OB,∵四边形BCDE是正方形,∴∠EBD=∠OBT=45°,BD=BE,∴∠OBE=∠TBD,==,∴△TBD∽△OBE,∴==,∴TD=OE=6,∵DM≥TM﹣TD,∴DM≥12﹣6,∴DM的最小值为12﹣6.故答案为:12﹣6.2.解:如图,连接OA.∵四边形ABCD是矩形,∴AC=BD,AM=MC=BM=MD,∠BAD=90°,∴AB2+AD2=BD2,∴BD的值最小时,AB2+AD2的值最小,∵AM≥OM﹣OA,OM=5,OA=3,∴AM≥2,∴AM的最小值为2,∴BD的最小值为4,∴AB2+AD2的最小值为16,故答案为16.3.解:如图,连接AC,∵AB=CB,∠ABC=60°,∴△ABC是等边三角形,将△DBC绕点B顺时针旋转60°得△HBA,连接DH,则BD=BH=2,∠HBD=60°,∴△HBD是等边三角形,∴S四边形ABCD=S△ABD+S△BCD=S△BDH﹣S△ADH,∵BD=2,是定值,∴S△BDH是定值,∴当△ADH的面积最大时,四边形ABCD的面积最小,∵∠ADC=75°,∠ABC=60°,∴∠BAD+∠BCD=360°﹣75°﹣60°=225°,∴∠DAH=360°﹣∠BAD﹣∠HAB=360°﹣225°=135°,∵点A在定圆⊙O(△ADH的外接圆)上运动,当O、A、B共线时,△ADH的面积最大,此时,OB⊥DH,设OA交DH于K,则HK=KD=1,∵AH=AD,∴∠AHD=∠ADH=22.5°,在HK上取一点F,使FH=AF,则△AKF是等腰直角三角形,设AK=FK=x,则AF=FH=x,∴1=x+x,∴x=﹣1,∴△ADH面积的最大值=×2×(﹣1)=﹣1,∴四边形ABCD的面积的最小值=×22﹣(2﹣2)=﹣+1.故答案为:﹣+1.4.解:如图,连接OF.作OH⊥EF于H.由题意:∠AOE=∠FOB=15°,∠EOF=90°﹣15°﹣15°=60°,∵∠AOB=90°,OA=OB=,∴AB=2,∵OH⊥AB,OA=OB,∴AH=BH,∴OH=AB=,∠EOH=∠FOH=30°,∴OF==2,∴S阴=(S△AOB﹣2•S扇形EOC﹣S△EOF)+(S扇形OEF﹣S△OEF)=××﹣2×﹣×22+﹣×22=3+﹣2.故答案为3+﹣2.5.解:对于抛物线y=﹣x2+2x+8,令y=0,得到x2﹣2x﹣8=0,解得x=﹣2或4,不妨设B(﹣2,0),C(4,0),A(m,﹣m2+2m+8),由题意(m﹣1)2+(﹣m2+2m+8)2=9,∴(m﹣1)2﹣32+(m+2)2•(m﹣4)2=0,∴(m﹣4)(m+2)+(m+2)2•(m﹣4)2=0,∴(m+2)(m﹣4)[1+(m+2)(m﹣4)]=0,∴(m+2)(m﹣4)(m2﹣2m﹣7)=0,解得m=﹣2或4或1±2,∵点A在x轴的上方,∴点A的横坐标为1±2.6.解:连接BM,则AB=BE=BM,设BM=R,∵四边形ABCD是矩形,∴AB=CD=BE,∠B=∠BCD=90°,∵DM=VE,∴CM=BC,∵的长为2π,∴=2π,解得:R=4,即BM=BE=CD=AB=4,在Rt△BCM中,由勾股定理得:BC2+CM2=BM2,BC=CM=2,∴CE=4﹣2,故答案为:4﹣2.7.解:连接OA,∵过⊙O外一点P作⊙O的两条切线P A,PB,切点分别为A,B,∴∠P AO=∠PBO=90°,∵∠P=80°,∴∠AOB=360°﹣90°﹣90°﹣80°=100°,∴∠C=AOB=50°,故答案为:50.8.解:如图,以OB为直径作⊙K,当直线AE切⊙K于D时,BE的值最大.∵AE是⊙K的切线,∴DK⊥AE,∴∠ADK=90°,∵AB是直径,∴∠AEB=90°,∴∠ADK=∠AEB,∴DK∥BE,∴=,∴=,∴BE=,故答案为.9.解:如图,作点O关于AD的对称点O′,连接O′A,∵AC=BC=2.∠ACB=120°,∴AB=6,∴O′A=OA=3,延长BC交⊙O于点E,∵AB是⊙O的直径,∴∠E=90°,设⊙O′与BC相切于点G,则∠O′GB=90°,∴∠E=∠O′GB,∴AE∥O′G,∵∠ABC=30°,AB=6,∴AE=O′G=3,∴四边形O′AEG为平行四边形,∴AO′∥BE,∴∠O′AB=∠ABC=30°,作O′M⊥AF于M∵O′A=3,∠O′AB=30°,∴AM=MF=,∴AF=2AM=.故答案为:.10.解:①当⊙P与△A′B′C的A′B′边所在的直线相切时,即:⊙P′所在的位置,设切点为H点,圆的半径为R,BC=3,cos∠B=,则sin∠B==sin∠AB′H,则AC=A′C=4,BC=CB′=3,AB′=AC﹣B′C=1,sin∠AB′H===,则R=,②当⊙P与△A′B′C的A′C边所在的直线相切时,即:⊙P′′所在的位置,同理,可得:R=;故:答案为:或.11.解:如图,作DF⊥AC交AC的延长线于F.∵AD平分∠CAB,DF⊥AC,DE⊥AB,∴DE=DF,∵∠DAC=∠DAB,∴=,∴CD=DB,∵∠F=∠DEB=90°,∴Rt△DFC≌Rt△DEB(HL),∴CF=BE,∵∠F=∠AED=90°,AD=AD.DF=DE,∴Rt△ADF≌Rt△ADE(HL),∴AF=AE,∵AB﹣AC=AE+EB﹣(AF﹣CF)=2BE=4,∴BE=2,∵AB是直径,∴∠ADB=90°,∵∠DAE=∠BAD,∠AED=∠ADB=90°,∴△ADE∽△ABD,∴=,∴AD2=AE•AB,设AE=x,则有:63=x(x+2),解得x=7或﹣9(舍弃),∴AE=7,∴AB=AE+BE=9,∵AB﹣AC=4,∴AC=5,故答案为2,5.12.解:如图,连接AC,AE,∵AB=BC=4,∠B=60°,∴△ABC是等边三角形,∵点E为BC的中点,∴BE=CE=2,AE⊥BC,∠EAC=30°,∴AC是以CE为弦的圆的直径,设圆心为O,当⊙O与CD边交于P1,则∠EP1C=30°,∵∠ECP1=105°,∴∠P1EC=45°,过C作CH⊥P1E于H,∴EH=CH=CE=,∴P1H=HC=,∴P1E=+;当⊙O与AD交于P2,A(P3),∵AD∥CE,∴∠ECP2=∠AP2C=90°,∴四边形AECP2是矩形,∴P2E=AC=4,P3E=P2C=2,当⊙O与AB交于P4,∵∠AP4C=90°,∠EP4C=30°,∴∠BP4E=60°,∴△BP4E是等边三角形,∴P4E=BE=2,综上所述,若∠CPE=30°,则EP的长为或4或2或2,故答案为:或4或2或2.13.解:∵tan∠ABO==,且A(1,0),∴OB=2,即:点B的坐标为(0,2).点C(m,0),A(1,0),B(0,2)在抛物线y=ax2+bx+e上,∴,解得:b=﹣,a=,∴x=﹣=.∵EB=﹣(1+m),FB=﹣m,EF=FB﹣EB=1,∴线段EF的长是定值1.∴BD=EF=1.如图所示,连接CD∵BC为直径∴∠CDB=90°∴∠CDA=∠AOB=90°,∠CAD=∠BAO∴△CAD∽△BAO∴=A(1,0),B(0,2),C(m,0),∴AB=,AC=1﹣m,AO=1∵BD=1∴AD=﹣1∴=∴1﹣m=5﹣∴m=故答案为:.14.解:∵∠ADC=90°,P是AC中点,∴AC=2DP=8,又∵BC=6,∴AB=10,则CD===,∴BD==,如图1,若⊙O与CD相切,则⊙O的半径r=BD=;如图2,若⊙O与CP相切,则BO=OE=r,AO=10﹣r,由OE⊥AC知OE∥BC,∴△AOE∽△ABC,∴=,即=,解得r=;如图3,若⊙O与DP所在直线相切,切点F,则OF⊥DP,即∠OFD=∠ACB=90°,OB=OF=r,∴OD=BD﹣BO=﹣r,∵∠ODF=∠ADP=∠A,∴△ODF∽△BAC,∴=,即=,解得r=;综上,当⊙O与△PDC的一边所在直线相切时,⊙O的半径等于或或,故答案为:或或.15.解:如图1,连接OD,∴DO=AB=6,∵OC⊥DF,∴∠OCD=90°,CD=CF=DF=2,在Rt△OCD中,根据勾股定理得,OC==4,∴sin∠ODC===,∵DE⊥AB,∴∠DEO=90°=∠OCD,∴点O,C,D,E是以OD为直径的圆上,∴∠AEC=∠ODC,∴sin∠AEC=sin∠ODC=,如图2,∵CE是以OD为直径的圆中的弦,CE要最大,即:CE是以OD为直径的圆的直径,∴CE=OD=6,∠COE=90°,∵∠OCD=∠OED=90°,∴四边形OCDE是矩形,∴DF∥AB,过点F作FG⊥AB于G,易知,四边形OCFG是矩形,∴OG=CF=2,FG=OC=4,∴AG=OA﹣OG=4连接AF,在Rt△AFG中,根据勾股定理得,AF==4,故答案为,4.16.解:过点P作AP⊥EF交EF于点A,连接PE,设OP=x,∵⊙P与x轴相切于原点O,∴OP⊥OE,∵平行于y轴的直线交⊙P于E,F两点,∴四边形APOB是矩形,∴AB=OP=x,∵点E的坐标是(﹣3,﹣1),∴AP=OB=3,AE=AB﹣BE=x﹣1,在Rt△ABE中,32+(x﹣1)2=x2,解得x=5,∴AE=4,∵AF=AE,∴EF=8,∴BF=EF+BE=9,∴点F的坐标是(﹣3,﹣9).故答案为(﹣3,﹣9).17.解:如图,连接CF,过点P作PG⊥AC于G,设P A=x.在Rt∠ACB中,∵ACB=90°,BC=3,cos B==,∴AB=5,AC===4,∵PG⊥AD,∴AG=DG=P A•cos∠BAC=x,∴AD=x,CD=4﹣x,∵∠ABC+∠A=90°,∠PEC+∠CDE=90°,∵∠A=∠PDA,∴∠ABC=∠PEC,∵∠ABC=∠EBP,∴∠PEC=∠EBP,∴PB=PE,∵点Q为线段BE的中点,∴PQ⊥BC,∴PQ∥AC∴当PE∥CF时,四边形PDCF是平行四边形,∴PF=CD,当点P在边AB的上时,x=4﹣x,x=,当点P在边AB的延长线上时,x=x﹣4,x=,综上所述,当PE∥CF时,AP的长为或.18.解:设⊙O与BC的交点为F,连接OB、OF,如图1所示.∵△MDN为直角三角形,∴MN为⊙O的直径,∵BM与⊙O相切,∴MN⊥BM,∵将MB绕M点逆时针旋转90°得MN,∴MB=MN,∴△BMN为等腰直角三角形,∵∠AMB+∠NMD=180°﹣∠AMN=90°,∠MBA+∠AMB=90°,∴∠NMD=∠MBA,且BM=NP,∠A=∠NMD=90°,∴△ABM≌△DMN(AAS),∴DM=AB=4,DN=AM,设DN=2a,则AM=2a,OF=4﹣a,BM==2,∵BM=MP=2OF,∴2=2×(4﹣a),解得:a=,∴DN=2a=3,OF=4﹣=,∴⊙O半径为,如图2,延长BA,使AH=AB=4,连接HQ,OH,过O作OG⊥AB于G,∵AB=AH,BP=PQ,∴AP=HQ,HQ∥AP,∴当HQ取最小值时,AP有最小值,∴当点Q在HO时,HQ的值最小,∵HG=4+4﹣=,GO=3+4﹣2=5,∴OH===,∴HQ的最小值=﹣=,∴AP的最小值为,故答案为:.19.解:取BC的中点G,连接BH,HG,DG.∵四边形ABCD是矩形,∴AB=CD=,BC=AB2=,∠DCG=90°,∵CG=BG=,∴DG===,∵BE是直径,∴∠BHE=∠BHC=90°,∵BG=GC,∴HG=BC=,∵DH≥DG﹣HG,∴DH≥﹣=,∴DH的最小值为.故答案为.20.解:对于抛物线y=x2﹣x﹣1,令x=0,得到y=﹣1,∴C(0,﹣1),令y=0,x2﹣x﹣1=0,解得x=5或﹣,∴A(﹣,0),B(5,0),∵PQ是切线,∴PQ⊥BQ,∴∠PQB=90°,∴PQ==,∴PB的值最小时,PQ的值最小,根据垂线段最短可知,当BP′⊥AC于P′时,BP′的值最小,∵OA=,OC=1,∴tan∠OAC==,∴∠OAC=30°,∴BP′=AB•sin30°=6×=3,∴PQ的最小值==,故答案为.21.解:设PB交⊙O于点N,连接P A,延长PB、AC交于点M,∵AB是直径,PH⊥CB∴∠ANP=90°=∠ACB=∠H,∴MC∥PH,由圆的对称性可得,P A=PB,∠BPO=∠APO=∠APB,∵∠BPH=2∠BPO,∴∠BPH=∠APB,∴△PHB≌△PNA(AAS),∴PN=PH=15,由MC∥PH得,∠HPB=∠M=∠APM,∴AM=AP=PB,∵AN⊥PM,∴PM=2PN=30,由△PHB∽△MCB,∴==,设MC=a,BC=b,MB=c,则HB=24﹣b,PB=30﹣c,∴==,∴==sin M=sin∠HPB,∴cos∠HPB=在Rt△PHB中,PH=15,∴PB===25,HB=sin∠HPB•PH=20,∴BC=24﹣20=4,MB=30﹣25=5,则MC==3,在Rt△ABC中,BC=4,AC=AM﹣MC=25﹣3=22,∴tan∠BAC===,故答案为:.22.解:过O作OM⊥AC,交⊙O于F,交弧G于H,连接OC,∵AB为⊙O的直径,AB=10,∴OA=OB=OG=OD=5,∵BE=3,∴OE=2,在Rt△OED中,由勾股定理得:CE===,在Rt△AEC中,AC===,∵OF⊥AC,∴AM=AC=,由勾股定理得:OM===,由折叠得:弧G所在圆与圆O是等圆,∴弧G所在圆的半径为5,∴MH=FM=5﹣,∵5﹣<,∴FM<OM,∴O在G所在圆外,故答案为:点在圆外.23.解:如图,连接AE,AF.∵BC=14,CE=9,∴BE=BC﹣EC=14﹣9=5,∵AC是直径,∴∠AEC=∠AEB=90°,∴AE===12,∴AC===15,∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD=13,∴∠DAC=∠ACB,∵∠AFE=∠ACB,∴∠AFE=∠DAC,∵∠AEF=∠ACD,∴△AFE∽△DAC,∴=,∴=,∴EF=,故答案为.24.解:延长EO交O'A'于P,则由∠AOB=90°,OA=OB=2,D为OB中点,可得S阴影OPO′=12﹣=1﹣;∵O′P=OE,∠EPO'=90°,∴cos∠EO'P=,∴∠EO'P=60°,EP=∴S阴影A′PE=S扇形O′A′E﹣S△O′PE=﹣××1=﹣∴S阴影═1﹣+﹣=1﹣+.故答案为1﹣+.25.解:连接AD,作NM⊥PB于M,∵六边形APCDEF是正六边形,∴EF∥AD,DP⊥AB,DP⊥ED,正六边形的每一个内角为120°,∴∠ADE=60°,∴∠ADP=30°∴PD=P A,∵DP⊥AB,NM⊥PB∴PD∥MN,∴PM就是△PDN的PD边的高,设P A=x.则PB=10﹣x,∵在等腰△BPN中,MN⊥PB,∴PM=PB=(10﹣x),∴S△PDN=PD•PM=×x×(10﹣x)=﹣(x﹣5)2+(0<x<10),∴△PDN的面积的最大值为:.故答案为:.26.解:作O关于CD的对称点F,连接CF、EF,如图1所示:则EF为扇形AOB的半径,由折叠的性质得:∠FCD=∠OCD=45°,FC=OC=+1,∴∠OCF=90°,∴△OCF是等腰直角三角形,∴∠COF=45°,OF=OC=+,∴∠EOF=∠AOB﹣∠COF=75°,∵折叠后的图形恰好与半径OB相切于点E,∴∠OEF=90°,∴∠OFE=15°,∵cos∠OFE==cos15°=,如图2所示:∴EF=OF×cos15°=()×=2+;故答案为:2+.27.解:如图1中,当点N在CM为直径的圆上时,设DM=AN=x.∵四边形ABCD是矩形,∴∠ADC=90°,AB=CD=6,BC=AD=8,∴AC===10,∵∠MAN=∠DAC,∠ANM=∠ADC=90°,∴△ANM∽△ADC,∴=,∴=,解得x=,∴DM=如图2中,当点N在BM为直径的圆上时,设BC与圆的交点为H,连接MH,NH.设DM=AN=y.∵BM是直径,∴∠MHB=90°,∴∠MHC=∠D=∠DCH=90°,∴四边形CDMH是矩形,∴CH=DM=y,∵∠NCH=∠BCA,∠CHN=∠CAB,∴△CNH∽△CBA,∴=,∴=,解得y=,∴DM=,故答案为或。
2019年全国各地中考数学压轴题汇编:几何综合(湖北专版)(解析卷)

2019年全国各地中考数学压轴题汇编(湖北专版)几何综合参考答案与试题解析.解答题(共22小题)1 . (2019?天门)请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(1)如图①,四边形ABCD中,AB = AD, / B=Z D,画出四边形ABCD的对称轴m;(2)如图②,四边形ABCD中,AD // BC, Z A=Z D,画出BC边的垂直平分线n.图②解:(1)如图①,直线m即为所求(2)如图②,直线n即为所求2. (2019?武汉)已知AB是。
的直径,AM和BN是。
的两条切线,DC与。
相切于点E,分别交AM、BN于D、C两点.(1)如图1,求证:AB2=4AD?BC;(2)如图2,连接OE并延长交AM于点F,连接CF.若/ADE = 2/OFC, AD = 1 ,求图中阴影部分的面积.(1)证明:连接OC、OD,如图1所示:■「AM和BN是它的两条切线,・•• AMXAB, BNXAB,AM // BN,・./ ADE + / BCE= 180°DC 切。
于E,・./ODE =▲/ADE, /OCE=^/BCE,2 2・./ ODE + ZOCE = 90° ,・./ DOC =90° ,・./AOD + /COB = 90° ,・. /AOD + /ADO = 90° ,・./ AOD =/ OCB,・. / OAD =/ OBC=90° ,.•.△AOD^ABCO,BO BC・•.OA2=AD?BC,』AB) 2=AD?BC,2・•・ AB2=4AD?BC;(2)解:连接OD , OC,如图2所示:・. / ADE = 2/OFC ,/ ADO = / OFC ,・•• / ADO = / BOC , / BOC = / FOC ,・./ OFC =Z FOC,.•.CF = OC,・••CD垂直平分OF,.•.OD=DF,'OCXF 在ACOD 和^CFD 中,・ 0D=DF ,CD=CD.,.△COD^ACFD (SSS),・ ./ CDO =Z CDF ,・ . /ODA + /CDO+/CDF = 180° ,・ ./ ODA = 60° =Z BOC,・ ./ BOE= 120° ,在 RtADAO , AD =运OA, 31 △BOC 中,BC = 73OB ,2 •.AD: BC = 1 : 3,3 •• AD = 1,BC=3, OB = V3,.二图中阴影部分的面积= 2S A OBC - S 扇形 OBE= 2 x ~^x X 3 — 1乂_=3、/^一兀. 二 I图1图12 (2019?天门)如图,E, F 分别是正方形 ABCD 的边CB, DC 延长线上的点,且 BE=CF,过点E 作EG // BF ,交正方形外角的平分线 CG 于点G,连接GF .求证:(1) AEXBF ;(2)四边形BEGF 是平行四边形.证明:(1)二.四边形 ABCD 是正方形,3. A D M AD F M,AB=BC, Z ABC = Z BCD = 90° ,・./ ABE=/ BCF=90° ,'AB 二BC在AABE 和^ BCF 中,,/ABE:NBCF,脚工FABE^A BCF (SAS),AE= BF, / BAE = Z CBF ,・•• EG // BF,・./ CBF = Z CEG,・. / BAE+Z BEA=90° ,・./ CEG + /BEA= 90° ,AE± EG,AE± BF;(2)延长AB至点P,使BP=BE,连接EP,如图所示: 则AP=CE, / EBP =90° ,・./ P = 45° ,・•• CG为正方形ABCD外角的平分线,・./ ECG = 45° ,・./ P = Z ECG,由(1)得/ BAE=Z CEG,'Z P=Z ECG在△ APE 和△ ECG 中,.研二,l ZBAE=ZCEGAPE^A ECG (ASA),AE= EG,••• AE= BF,EG = BF,••• EG // BF,••・四边形BEGF是平行四边形.4. ( 2019?武汉)在△ ABC 中,Z ABC = 90° , —=n, M 是 BC 上一点,连接 AM.BC(1)如图1,若n= 1, N 是AB 延长线上一点, CN 与AM 垂直,求证:BM = BN.(2)过点B 作BPXAM, P 为垂足,连接 CP 并延长交 AB 于点Q.• •• AMXCN,• •.Z AHC = 90° ,• . /ABC=90° ,• ./BAM+/AMB = 90° , Z BCN + Z CMH =90° ,• . / AMB =/ CMH ,/ BAM = / BCN ,• . BA=BC, Z ABM =Z CBN = 90• •.△ABM^ACBN (ASA), BM= BN.①如图2,若n=1,求证:—.PQ BQ②如图3,若M 是BC 的中点,直接写出tan/BPQ 的值.(用含n 的式子表示)AM 交CN 于点H .(1)证明:如图1中,延长(2)①证明:如图2中,作CH//AB交BP的延长线于H .图?BP± AM,・./ BPM =/ ABM =90 ° ,・. /BAM+/AMB = 90° , / CBH+/BMP = 90° ,/ BAM = / CBH ,. CH //AB,・./ HCB+/ABC= 90° ,・. /ABC=90° ,・./ ABM =/ BCH = 90° ,・•• AB= BC,・•.△ABM^ABCH (ASA),BM = CH,. CH // BQ,.PC _ CH _ Bl . = =PQ BQ BQ②解:如图3中,作CH //AB交BP的延长线于H,作CN^BH于N.不妨设BC=2m,则AB = 2mn.A Q~ 邺则BM = CM=m, CH= —, BH =%]+4门2, AM = m/]+4n2,・••—?AM?BP= —?AB?BM ,2 2・-------- PB=7彳,.L?BH?CN= J L?CH?BC ,2 2•. CNXBH, PM ±BH ,MP // CN, ••• CM= BM,・. / BPQ = / CPN,5. (2019?十堰)如图,△ ABC中,AB=AC,以AC为直径的。
2021年中考数学 圆 压轴题 练习

1.如图,放置在直线l上的扇形OAB.由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径OA=2,∠AOB=45°,则点O所经过的运动路径的长是()1)2)3)A.2π+2B.3πC.D.+22.如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为()A.6π﹣B.6π﹣9C.12π﹣D.3.如图是一个几何体的三视图,如果一只蚂蚁从这个几何体的点B出发,沿表面爬到AC的中点D处,则最短路线长为()A.3B.C.3D.34.如图,有一块半径为1m,圆心角为90°的扇形铁皮,要把它做成一个圆锥形容器(接缝忽略不计),那么这个圆锥形容器的高为()(4)(5)(6)(7)A.m B.m C.m D.m5.如图,是一个几何体的三视图,则此几何体的全面积是()A.210πcm2B.175πcm2C.320πcm2D.285πcm26.如图,AB是⊙O的直径,直线DE与⊙O相切于点C,过A,B分别作AD⊥DE,BE⊥DE,垂足为点D,E,连接AC,BC,若AD=,CE=3,则的长为()A.B.πC.πD.π7.如图,四边形ABCD内接于⊙O,AB为直径,AD=CD,过点D作DE⊥AB于点E,连接AC交DE于点F.若sin∠CAB=,DF=5,则AB的长为()A.10B.12C.16D.208.如图,BC是半圆O的直径,D,E是上两点,连接BD,CE并延长交于点A,连接OD,OE.如果∠A=70°,那么∠DOE的度数为()(8)(9)(10)A.35°B.38°C.40°D.42°9.如图,点A、B,C,D在⊙O上,AB=AC,∠A=40°,BD∥AC,若⊙O的半径为2.则图中阴影部分的面积是()A.﹣B.﹣C.﹣D.﹣10.如图,⊙P与x轴交于点A(﹣5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为()A.+B.2+C.4D.2+211.如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=10,AH=8,⊙O的半径为7,则AB=.(11)(12)(13)14 12.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为.13.如图,在正六边形ABCDEF中,分别以C,F为圆心,以边长为半径作弧,图中阴影部分的面积为24π,则正六边形的边长为.14.我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点A(2,1)到以原点为圆心,以1为半径的圆的距离为.15.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为.15 16 1718 16.如图,分别以边长为2的等边三角形ABC的三个顶点为圆心,以边长为半径作弧,三段弧所围成的图形是一个曲边三角形,已知⊙O是△ABC的内切圆,则阴影部分面积为.17.如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得到Rt△FOE,将线段EF绕点E逆时针旋转90°后得到线段ED,分别以O、E为圆心,OA、ED长为半径画弧AF 和弧DF,连接AD,则图中阴影部分的面积是.18.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为.19.如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.(1)求证:AE是⊙O的切线;(2)已知AE=4cm,CD=6cm,求⊙O的半径.20.如图,四边形ADBC内接于⊙O,AD平分∠EDC,AE∥BC交直线BD于E.(1)求证:AE是⊙O的切线;(2)若CD为直径,tan∠ADE=2,求sin∠BDC的值.21.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.(1)求证:直线DF是⊙O的切线;(2)求证:BC2=4CF•AC;(3)若⊙O的半径为2,∠CDF=15°,求阴影部分的面积.22.已知⊙O1的半径为r1,⊙O2的半径为r2.以O1为圆心,以r1+r2的长为半径画弧,再以线段O1O2的中点P为圆心,以O1O2的长为半径画弧,两弧交于点A,连接O1A,O2A,O1A交⊙O1于点B,过点B作O2A 的平行线BC交O1O2于点C.(1)求证:BC是⊙O2的切线;(2)若r1=2,r2=1,O1O2=6,求阴影部分的面积.23.如图,△ABC内接于⊙O,BC=2,AB=AC,点D为上的动点,且cos∠ABC=.(1)求AB的长度;(2)在点D的运动过程中,弦AD的延长线交BC延长线于点E,问AD•AE的值是否变化?若不变,请求出AD•AE的值;若变化,请说明理由;(3)在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.24.如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DF.(1)求证:DF是⊙O的切线;(2)若DB平分∠ADC,AB=5,AD:DE=4:1,求DE的长.25.如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点D,与AC交于点E,延长CD、BA 相交于点F,∠ADF的平分线交AF于点G.(1)求证:DG∥CA;(2)求证:AD=ID;(3)若DE=4,BE=5,求BI的长.26.在▱ABCD中,经过A、B、C三点的⊙O与AD相切于点A,经过点C的切线与AD的延长线相交于点P,连接AC.(1)求证:AB=AC;(2)若AB=4,⊙O的半径为,求PD的长.27.(1)方法选择如图①,四边形ABCD是⊙O的内接四边形,连接AC,BD,AB=BC=AC.求证:BD=AD+CD.小颖认为可用截长法证明:在DB上截取DM=AD,连接AM…小军认为可用补短法证明:延长CD至点N,使得DN=AD…请你选择一种方法证明.(2)类比探究【探究1】如图②,四边形ABCD是⊙O的内接四边形,连接AC,BD,BC是⊙O的直径,AB=AC.试用等式表示线段AD,BD,CD之间的数量关系,并证明你的结论.【探究2】如图③,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,∠ABC=30°,则线段AD,BD,CD之间的等量关系式是.(3)拓展猜想如图④,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,BC:AC:AB=a:b:c,则线段AD,BD,CD之间的等量关系式是.28.如图,⊙O的直径AB垂直于弦CD,垂足为点E,过点C作⊙O的切线,交AB的延长线于点P,连接PD.(1)判断直线PD与⊙O的位置关系,并加以证明;(2)连接CO并延长交⊙O于点F,连接PP交CD于点G,如果CF=10,cos∠APC=,求EG的长.29.如图,在等腰梯形ABCD中,AD∥BC.O是CD边的中点,以O为圆心,OC长为半径作圆,交BC边于点E.过E作EH⊥AB,垂足为H.已知⊙O与AB边相切,切点为F.(1)求证:OE∥AB;(2)求证:EH=AB;(3)若BH=1,EC=,求⊙O的半径.30.如图,AB是⊙O的直径,半径OC⊥AB,垂足为O,直线l为⊙O的切线,A是切点,D是OA上一点,CD 的延长线交直线l于点E,F是OB上一点,CF的延长线交⊙O于点G,连接AC,AG,已知⊙O的半径为3,CE=,5BF﹣5AD=4.(1)求AE的长;(2)求cos∠CAG的值及CG的长.31.如图,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的⊙O 经过点D.(1)求证:①BC是⊙O的切线;②CD2=CE•CA;(2)若点F是劣弧AD的中点,且CE=3,试求阴影部分的面积.32.如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.(1)求证:P A•BD=PB•AE;(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.33.如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O 恰好经过边BC的中点D,并与边AC相交于另一点F.(1)求证:BD是⊙O的切线.(2)若AB=,E是半圆上一动点,连接AE,AD,DE.①当的长度是时,四边形ABDE是菱形;②当的长度是时,△ADE是直角三角形.34.如图,△ABC是等腰直角三角形,且AC=BC,P是△ABC外接圆⊙O上的一动点(点P与点C位于直线AB的异侧)连接AP、BP,延长AP到D,使PD=PB,连接BD.(1)求证:PC∥BD;(2)若⊙O的半径为2,∠ABP=60°,求CP的长;(3)随着点P的运动,的值是否会发生变化,若变化,请说明理由;若不变,请给出证明.35.如图,AB是⊙O的直径,DO⊥AB于点O,连接DA交⊙O于点C,过点C作⊙O的切线交DO于点E,连接BC交DO于点F.(1)求证:CE=EF;(2)连接AF并延长,交⊙O于点G.填空:①当∠D的度数为时,四边形ECFG为菱形;②当∠D的度数为时,四边形ECOG为正方形.36.如图,AB是⊙O的直径,且AB=4,C是⊙O上一点,D是的中点,过点D作⊙O的切线与AB、AC的延长线分别交于点E、F,连接AD.(1)求证:AF⊥EF;(2)填空:①当BE=时,点C是AF的中点;②当∠E=时,四边形OBDC 是菱形.37.如图,在▱ABCD中,AB=3,BC=5,∠B=45°,点E为CD上一动点,经过A、C、E三点的⊙O交BC于点F.【操作与发现】(1)当E运动到AE⊥CD处,利用直尺与规作出点E与点F;(保留作图痕迹)(2)在(1)的条件下,证明:=.【探索与证明】(3)点E运动到任何一个位置时,求证:;【延伸与应用】(4)点E在运动的过程中求EF的最小值.38.如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.(1)求证:△AFG∽△DFC;(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.39.如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D 作BC的平行线与AC的延长线相交于点P.(1)求证:PD是⊙O的切线;(2)求证:AB•CP=BD•CD;(3)若tan∠ABC=2,AB=2,求线段DP 的长.参考答案与试题解析1.如图,放置在直线l上的扇形OAB.由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径OA=2,∠AOB=45°,则点O所经过的运动路径的长是(C)(1)(2)(3)A.2π+2B.3πC .D .+2点O 的运动路径的长=的长+的长+的长=++=,2.如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为(A)A.6π﹣B.6π﹣9C.12π﹣D .解:连接OD,如图,∵扇形纸片折叠,使点A与点O恰好重合,折痕为CD,∴AC=OC,∴OD=2OC=6,∴CD ==3,∴∠CDO=30°,∠COD=60°,∴由弧AD、线段AC和CD所围成的图形的面积=S扇形AOD﹣S△COD =﹣•3•3=6π﹣,∴阴影部分的面积为6π﹣.3.如图是一个几何体的三视图,如果一只蚂蚁从这个几何体的点B出发,沿表面爬到AC的中点D处,则最短路线长为()A.3B .C.3D.3解:如图将圆锥侧面展开,得到扇形ABB′,则线段BF为所求的最短路程.设∠BAB′=n °.∵=4π,∴n=120即∠BAB′=120°.∵E为弧BB′中点,∴∠AFB=90°,∠BAF=60°,∴BF=AB•sin∠BAF=6×=3,∴最短路线长为3.4.如图,有一块半径为1m,圆心角为90°的扇形铁皮,要把它做成一个圆锥形容器(接缝忽略不计),那么这个圆锥形容器的高为(C)(4)(5)(6)A .mB .mC .mD .m解:设底面半径为rm,则2πr =,解得:r =,所以其高为:=(m),5.如图,是一个几何体的三视图,则此几何体的全面积是(A)A.210πcm2B.175πcm2C.320πcm2D.285πcm2解:由已知可得原几何体是一个圆锥和圆柱的组合体,上部分是一个圆锥,下部分是一个圆柱,而且圆锥和圆柱的底面积相等,圆锥的母线长,此几何体的全面积是=π×5×13+π×52+2π×5×12=210πcm2,6.如图,AB是⊙O的直径,直线DE与⊙O相切于点C,过A,B分别作AD⊥DE,BE⊥DE,垂足为点D,E,连接AC,BC,若AD =,CE=3,则的长为(D)A .B .πC .πD .π解:连接OC,∵AB是⊙O的直径,∴∠ACB=90°,∵直线DE与⊙O相切于点C,∴OC⊥DE,∵AD⊥DE,BE⊥DE,∴AD∥OC∥BE,∵OA=OB,∴DC=CE=3,∵AD =,∴tan∠ACD ==,∴∠ACD=30°,∴∠ACO=90°﹣30°=60°,∵OA=OC,∴△AOC是等边三角形,∴OA=AC,∵AC ===2∴⊙O的半径为2,∴的长为:=π,7.如图,四边形ABCD内接于⊙O,AB为直径,AD=CD,过点D作DE⊥AB于点E,连接AC交DE于点F.若sin∠CAB =,DF=5,则AB的长为(D)A.10B.12C.16D.20(7)(8)解:连接BD,如图,∵AB为直径,∴∠ADB=∠ACB=90°,∵AD=CD,∴∠DAC=∠DCA,而∠DCA=∠ABD,∴∠DAC=∠ABD,∵DE⊥AB,∴∠ABD+∠BDE=90°,而∠ADE+∠BDE=90°,∴∠ABD=∠ADE,∴∠ADE=∠DAC,∴FD=F A=5,在Rt△AEF中,∵sin∠CAB =,∴EF=3,∴AE ==4,DE=5+3=8,∵∠ADE=∠DBE,∠AED=∠BED,∴△ADE∽△DBE,∴DE:BE=AE:DE,即8:BE=4:8,∴BE=16,∴AB=4+16=20.8.如图,BC是半圆O的直径,D,E 是上两点,连接BD,CE并延长交于点A,连接OD,OE.如果∠A=70°,那么∠DOE的度数为(C)A.35°B.38°C.40°D.42°解:连接CD,如图:∵BC是半圆O的直径,∴∠BDC=90°,∴∠ADC=90°,∴∠ACD=90°﹣∠A=20°,∴∠DOE=2∠ACD=40°9.如图,点A、B,C,D在⊙O上,AB=AC,∠A=40°,BD∥AC,若⊙O的半径为2.则图中阴影部分的面积是(B)A .﹣B .﹣C .﹣D .﹣解:如图,连接BC、OD、OB、CD,∵∠A=40°,AB=AC,∴∠ACB=70°,∵BD∥AC,∴∠ABD=∠A=40°,∴∠ACD=∠ABD=40°,∴∠BCD=30°,则∠BOD=2∠BCD=60°,又OD=OB,∴△BOD是等边三角形,则图中阴影部分的面积是S扇形BOD﹣S△BOD =﹣×22=π﹣,10.如图,⊙P与x轴交于点A(﹣5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为(B)10 11 12A .+B.2+C.4D.2+2解:连接P A,PB,PC,过P作PD⊥AB于D,PE ⊥OC于E,∵∠ACB=60°,∴∠APB=120°,∵P A=PB,∴∠P AB=∠PBA=30°,∵A(﹣5,0),B(1,0),∴AB=6,∴AD=BD=3,∴PD =,P A=PB=PC=2,∵PD⊥AB,PE⊥OC,∠AOC=90°,∴四边形PEOD是矩形,∴OE=PD =,PE=OD=2,∴CE ===2,∴OC=CE+OE=2+,∴点C的纵坐标为2+,11.如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=10,AH=8,⊙O的半径为7,则AB =.解:作直径AD,连接BD,∵AD为直径,∴∠ABD=90°,又AH⊥BC,∴∠ABD=∠AHC,由圆周角定理得,∠D=∠C,∴△ABD∽△AHC,∴,即,解得,AB=12.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C 恰在弧EF上,则图中阴影部分的面积为﹣.解:连接CD,∵CA=CB,∠ACB=90°,∴∠B=45°,∵点D为AB的中点,∴DC=AB=BD=1,CD⊥AB,∠DCA=45°,∴∠CDH=∠BDG,∠DCH=∠B,,∴△DCH≌△DBG(ASA),∴S四边形DGCH=S△BDC=S△ABC=AB•CD=×2×1=.∴S阴影=S扇形DEF﹣S△BDC=﹣=﹣.13.如图,在正六边形ABCDEF中,分别以C,F为圆心,以边长为半径作弧,图中阴影部分的面积为24π,则正六边形的边长为6.13 14 15∵正六边形的内角是120度,阴影部分的面积为24π,设正六边形的边长为r,∴×2=24π,解得r=6.14.如图,在平面直角坐标系中,点A(2,1)到以原点为圆心,以1为半径的圆的距离为﹣1.解:连接AO交⊙O 于B,则线段AB的长度即为点A(2,1)到以原点为圆心,以1为半径的圆的距离,∵点A(2,1),∴OA==,∵OB=1,∴AB=﹣1,即点A(2,1)到以原点为圆心,以1为半径的圆的距离为﹣1,15.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O 为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为(﹣1,﹣2).解:连接CB,作CB的垂直平分线,如图:在CB的垂直平分线上找到一点D,CD═DB=DA==,所以D是过A,B,C三点的圆的圆心,16.如图,分别以边长为2的等边三角形ABC的三个顶点为圆心,以边长为半径作弧,三段弧所围成的图形是一个曲边三角形,已知⊙O是△ABC的内切圆,则阴影部分面积为π﹣2.解:连接OB,作OH⊥BC于H,如图,∵△ABC为等边三角形,∴AB=BC=AC=2,∠ABC=60°,∵⊙O是△ABC的内切圆,∴OH为⊙O的半径,∠OBH=30°,∵O点为等边三角形的外心,∴BH=CH=1,在Rt△OBH中,OH=BH=,∵S弓形AB=S扇形ACB﹣S△ABC,∴阴影部分面积=3S弓形AB+S△ABC﹣S⊙O=3(S扇形ACB﹣S△ABC)+S△ABC﹣S⊙O=3S扇形ACB﹣2S△ABC﹣S⊙O=3×﹣2××22﹣π×()2=π﹣2.17.如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得到Rt△FOE,将线段EF绕点E逆时针旋转90°后得到线段ED,分别以O、E为圆心,OA、ED长为半径画弧AF 和弧DF,连接AD ,则图中阴影部分的面积是.17 18解:作DH⊥AE于H,∵∠AOB=90°,OA=2,OB=1,∴AB==,由旋转,得△EOF≌△BOA,∴∠OAB=∠EFO ,∵∠FEO+∠EFO=∠FEO +∠HED =90°,∴∠EFO=∠HED ,∴∠HED=∠OAB,∵∠DHE=∠AOB=90°,DE=AB,∴△DHE≌△BOA(AAS),∴DH=OB=1,阴影部分面积=△ADE的面积+△EOF的面积+扇形AOF的面积﹣扇形DEF的面积=×3×1+×1×2+﹣=,18.如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,=,CE=1,AB=6,则弦AF的长度为.解:连接OA、OB,OB交AF于G,如图,∵AB⊥CD,∴AE=BE=AB=3,设⊙O的半径为r,则OE=r﹣1,OA=r,在Rt△OAE中,32+(r﹣1)2=r2,解得r=5,∴OE=5﹣1=4,∵=,∴OB⊥AF,AG=FG,∵AG•OB=OE•AB,∴AG==,∴AF=2AG=.19.如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.(1)求证:AE是⊙O的切线;(2)已知AE=4cm,CD=6cm,求⊙O的半径.19 20(1)证明:连接OA,∵OA=OD,∴∠ODA=∠OAD,∵DA平分∠BDE,∴∠ODA=∠EDA,∴∠OAD=∠EDA,∴EC∥OA,∵AE⊥CD,∴OA⊥AE,∵点A在⊙O上,∴AE是⊙O的切线;(2)过点O作OF⊥CD,垂足为点F,∵∠OAE=∠AED=∠OFD=90°,∴四边形AOFE是矩形,∴OF=AE=4cm,又∵OF⊥CD,∴DF =CD=3cm,在Rt△ODF中,OD ==5cm,即⊙O的半径为5cm.20.如图,四边形ADBC内接于⊙O,AD平分∠EDC,AE∥BC交直线BD于E.(1)求证:AE是⊙O的切线;(2)若CD为直径,tan∠ADE=2,求sin∠BDC的值.(1)证明:连接AB,连接AO并延长交BC于F,如图1:∵ADBC内接于⊙O,AD平分∠EDC,∴∠ADE=∠ACB,∠ADE=∠ADC,∵∠ADC=∠ABC,∴∠ABC=∠ACB,∴AB=AC,∴AF⊥BC∵AE∥BC,∴AE⊥AF,∴AE是⊙O的切线;(2)解:连接AO并延长交BC于G,如图2:∵CD为直径,∴∠DAC=∠CBD=90°,∵AE∥BC,∴∠E+∠CBD=90°,∴∠E=90°,∴四边形AEBG是矩形,∴BG=AE,AG=BE,∵∠ADE=∠ADC=∠ACB,∴tan∠ADE ==tan∠ADC ==tan∠ACB ==2,∴AE=2DE,AC=2AD,AG=2CG=BC=2AE=4DE,∴AD =DE,CD =AD=5DE,∴sin∠BDC ==.21.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为点F.(1)求证:直线DF是⊙O的切线;(2)求证:BC2=4CF•AC;(3)若⊙O的半径为2,∠CDF=15°,求阴影部分的面积.21 22(1)连接OD∵AB=AC ∴∠ABC=∠C,∵OB=OD ∴∠ODB=∠ABC=∠C,∵DF⊥AC ∴∠CDF+∠C=90°,∴∠CDF+∠ODB=90°∴∠ODF=90°,∴直线DF是⊙O的切线;(2)连接AD,则AD⊥BC,则AB=AC,则DB=DC =BC,∵∠CDF+∠C=90°,∠C+∠DAC=90°,∴∠CDF=∠DAC,∵∠DFC=∠ADC=90°∴△CFD∽△CDA,∴CD2=CF•AC,即BC2=4CF•AC;(3)连接OE,∵∠CDF=15°,∠C=75°,∴∠OAE=30°=∠OEA ∴∠AOE=120°,S△OAE =AE×OE sin∠OEA =×2×2×cos30°×2×sin30°=3,S阴影部分=S扇形OAE﹣S△OAE =×π×(2)2﹣3=4π﹣3.22.已知⊙O1的半径为r1,⊙O2的半径为r2.以O1为圆心,以r1+r2的长为半径画弧,再以线段O1O2的中点P 为圆心,以O1O2的长为半径画弧,两弧交于点A,连接O1A,O2A,O1A交⊙O1于点B,过点B作O2A 的平行线BC交O1O2于点C.(1)求:BC是⊙O2的切线;(2)若r1=2,r2=1,O1O2=6,求阴影部分面积.(1)证明:连接AP,∵以线段O1O2的中点P为圆心,以O1O2的长为半径画弧,∴O1P=AP=O2P =∴∠O1AO2=90°,∵BC∥O2A∴∠O1BC=∠O1AO2=90°,过点O2作O2D⊥BC交BC的延长线于点D,∴四边形ABDO2是矩形∴AB=O2D,∵O1A=r1+r2 ∴O2D=r2,∴BC是⊙O2的切线;(2)解:∵r1=2,r2=1,O1O2=6,∴O1A =∴∠AO2C=30°,∵BC∥O2A ∴∠BCE=AO2C=30°,∴O1C=2O1B=4∴BC ===2,∴S阴影===﹣=2﹣π.23.如图,△ABC内接于⊙O,BC=2,AB=AC,点D 为上的动点,且cos∠ABC =.(1)求AB的长度;(2)在点D的运动过程中,弦AD的延长线交BC延长线于点E,问AD•AE的值是否变化?若不变,请求出AD•AE的值;若变化,请说明理由;(3)在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.23 24解:(1)作AM⊥BC,∵AB=AC,AM⊥BC,BC=2BM,∴CM =BC=1∵cos∠ABC ==,BM=1,∴AB ==;(2)连接DC∵AB=AC,∴∠ACB=∠ABC,∵四边形ABCD内接于圆O,∴∠ADC+∠ABC=180°,∵∠ACE+∠ACB=180°,∴∠ADC=∠ACE,∵∠CAE公共角,∴△EAC∽△CAD ∴=,∴AD•AE=AC2=10;(3)在BD上取一点N,使得BN=CD,∴△ABN≌△ACD(SAS),∴AN=AD,∵AN=AD,AH⊥BD,∴NH=HD,∵BN=CD,NH=HD,∴BN+NH=CD+HD=BH.24.如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DF.(1)求证:DF是⊙O的切线;(2)若DB平分∠ADC,AB=5,AD:DE=4:1,求DE的长.(1)证明:连接OD.∵OD=CD,∴∠ODC=∠OCD.∵AC为⊙O的直径∴∠ADC=∠EDC=90°.∵点F为CE的中点∴DF=CF=EF.∴∠FDC=∠FCD.∴∠FDO=∠FCO.又∵AC⊥CE,∴∠FDO=∠FCO=90°.∴DF是⊙O的切线.(2)解:∵AC为⊙O的直径∴∠ADC=∠ABC=90°∵DB平分∠ADC∴∠ADB=∠CDB ∴=∴BC=AB=5,在Rt△ABC中,AC2=AB2+BC2=100,又∵AC⊥CE∴∠ACE=90°.∴△ADC~△ACE ∴=,∴AC2=AD•AE,设DE为x,由AD:DE=4:1,∴AD=4x,AE=5x,∴100=4x•5x,∴x =,∴DE =.25.如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点D,与AC交于点E,延长CD、BA 相交于点F,∠ADF的平分线交AF于点G.(1)求证:DG∥CA;(2)求证:AD=ID;(3)若DE=4,BE=5,求BI的长.25 26(1)证明:∵点I是△ABC的内心,∴∠2=∠7∵DG平分∠ADF∴∠1=∠ADF,∵∠ADF=∠ABC∴∠1=∠2,∵∠3=∠2,∴∠1=∠3,∴DG∥AC;(2)∵点I是△ABC的内心,∴∠5=∠6,∵∠4=∠7+∠5=∠3+∠6,即∠4=∠DAI,∴DA=DI;(3)解:∵∠3=∠7,∠ADE=∠BDA,∴△DAE∽△DBA,∴AD:DB=DE:DA,即AD:9=4:AD,∴AD=6,∴DI=6 ∴BI=BD﹣DI=9﹣6=3.26.在▱ABCD中,经过A、B、C三点的⊙O与AD相切于点A,经过点C的切线与AD的延长线相交于点P,连接AC.(1)求证:AB=AC;(2)若AB=4,⊙O 的半径为,求PD的长.(1)连接AO并延长交BC于点E,交⊙O于点F,∵AP是⊙O的切线,AF是⊙O的直径,∴AF⊥AP∴∠F AP=90°,∵四边形ABCD是平行四边形,∴AD∥BC ∴∠AEB=∠F AP=90°,∴AF⊥BC,∵AF是⊙O的直径,AF⊥BC,∴BE=CE.∵AF⊥BC,BE=CE ∴AB=AC;(2)解:连FC,OC,设OE=x,则EF =﹣x.∵AF是⊙O的直径,∴∠ACF=90°.∵AC=AB=4,AF=2,∴CF ==2.∴CE2=OC2﹣OE2.∵在Rt△FEC中,∠FEC=90°,∴CE2=CF2﹣EF2.∴OC2﹣OE2=CF2﹣EF2,即()2﹣x2=22﹣(﹣x)2.解得,x =∴EC ==,∴BC=2EC =.∵四边形ABCD是平行四边形,∴AD=BC =,∵AD∥BC ∴∠P AC=∠ACB.∵P A,PC是⊙O的切线,∴P A=PC.∴∠P AC=∠PCA.∵AB=AC ∴∠ABC=∠ACB.∴∠P AC=∠ABC,∠PCA=∠ACB,∴△P AC∽△ABC ∴=.∴AP =•AB=2.∴PD=AP﹣AD =.27.(1)如图①,四边形ABCD是⊙O的内接四边形,连接AC,BD,AB=BC=AC.求证:BD=AD+CD.小颖认为可用截长法证明:在DB上截取DM=AD,连接AM…小军认为可用补短法证明:延长CD至点N,使得DN=AD…请你选择一种方法证明.(2)如图②,四边形ABCD是⊙O的内接四边形,连接AC,BD,BC是⊙O的直径,AB=AC.试用等式表示线段AD,BD,CD之间的数量关系,并证明你的结论.【探究2】如图③,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,∠ABC=30°,则线段AD,BD,CD 之间的等量关系式是.(3)如图④,四边形ABCD是⊙O的内接四边形,连接AC,BD.若BC是⊙O的直径,BC:AC:AB=a:b:c,则线段AD,BD,CD之间的等量关系式是BD=BM+DM=.解:∵AB=BC=AC∴∠ACB=∠ABC=60°,如图①,在BD上截取DM=AD,连接AM,∵∠ADB=∠ACB=60°∴△ADM是等边三角形,∴AM=AD,∵∠ABM=∠ACD,∠AMB=∠ADC=120°,∴△ABM≌△ACD(AAS),∴BM=CD,∴BD=BM+DM=CD+AD;(2)如图②,∵BC是⊙O的直径,∴∠BAC=90°,∵AB=AC∴∠ABC=∠ACB=45°,过点A作AM⊥AD交BD于点M,∵∠ADB=∠ACB=45°,∴△ADM是等腰直角三角形,∴AM=AD,∠AMD=45°,∴DM=AD,∴∠AMB=∠ADC=135°,∵∠ABM=∠ACD,∴△ABM≌△ACD(AAS)∴BM=CD,∴BD=BM+DM=CD+AD.如图③,∵若BC是⊙O的直径,∠ABC=30°,∴∠BAC=90°,∠ACB=60°,过点A作AM⊥AD交BD于点M,∵∠ADB=∠ACB=60°∴∠AMD=30°,∴MD=2AD,∵∠ABD=∠ACD,∠AMB=∠ADC=150°,∴△ABM∽△ACD ∴,∴CD ∴;(3)BD=BM+DM=,理由:如图④,∵若BC是⊙O的直径∴∠BAC=90°,过点A作AM⊥AD交BD于点M,∴∠MAD=90°,∴∠BAM=∠DAC,∴△ABM∽△ACD ∴,∴BM =,∵∠ADB=∠ACB,∠BAC=∠NAD=90°,∴△ADM∽△ACB ∴,∴DM =,∴BD=BM+DM =.28.如图,⊙O的直径AB垂直于弦CD,垂足为点E,过点C作⊙O的切线,交AB的延长线于点P,连接PD.(1)判断直线PD与⊙O的位置关系,并加以证明;相切(2)连接CO并延长交⊙O于点F,连接PP交CD于点G,如果CF=10,cos∠APC =,求EG的长.解:(1)连接OD∵在⊙O中,OD=OC,AB⊥CD于点E,∴∠COP=∠DOP.,∴△OCP≌△ODP(SAS).∴∠OCP=∠ODP.又∵PC切⊙O于点C,OC为⊙O半径,∴OC⊥PC,∴∠OCP=90°.∴∠ODP=90°.∴OD⊥PD于点D.∴PD与⊙O相切于点D;(2)作FM⊥AB于点M.∵∠OCP=90°,CE⊥OP于点E,∴∠3+∠4=90°,∠APC+∠4=90°.∴∠3=∠APC.∵cos∠APC =,∴Rt△OCE中,cos∠3==.∵CF=10,∴OF=OC =.∴CE=4,OE=3.又∵FM⊥AB,AB⊥CD,∴∠FMO=∠CEO=90°.在△OFM和△OCE中∴△OFM≌△OCE(AAS).∴FM=CE=4,OM=OE=3.∵在Rt△OCE中,cos∠APC =,设PC=4k,OP=5k,∴OC=3k.∴3k=5,解得:k =.∴OP =,∴PE=OP﹣OE =,PM=OP+OM =,又∵∠FMO=∠GEP=90°,∴FM∥GE.∴△PGE∽△PFM.∴,即.∴GE =.29.如图,在等腰梯形ABCD中,AD∥BC.O是CD边的中点,以O为圆心,OC长为半径作圆,交BC边于点E.过E作EH⊥AB,垂足为H.已知⊙O与AB边相切,切点为F.(1)求证:OE∥AB;(2)求证:EH =AB;(3)若BH=1,EC =,求⊙O的半径.解:(1)证明:在等腰梯形ABCD中,AD∥BC.∴AB=DC,∠B=∠C,∵OE=OC,∴∠OEC=∠C,∴∠B=∠OEC,∴OE∥AB;(2)证明:连接OF,∵⊙O与AB切于点F,∴OF⊥AB,∵EH⊥AB,∴OF∥EH,又∵OE∥AB,∴四边形OEHF为平行四边形,∴EH=OF,连接DF、CF,∵DC是⊙O直径,∴∠DFC=90°,∵DO=OC∴OF =CD =AB,∴EH =AB;(3)解:连接DE,设⊙O的半径为r,∵CD是⊙O的直径,∴∠DEC=90°,则∠DEC=∠EHB,又∵∠B=∠C,∴△EHB∽△DEC,∴,∵BH=1,,∴,在R t△DEC中,DE2+EC2=CD2∴,r>0,解得:,∴⊙O 的半径为.30.如图,AB是⊙O的直径,半径OC⊥AB,垂足为O,直线l为⊙O的切线,A是切点,D是OA上一点,CD 的延长线交直线l于点E,F是OB上一点,CF的延长线交⊙O于点G,连接AC,AG,已知⊙O的半径为3,CE =,5BF﹣5AD=4.(1)求AE的长;(2)求cos∠CAG的值及CG的长.解:(1)延长CO交⊙O于T,过点E作EH⊥CT 于H.∵直线l是⊙O的切线,∴AE⊥OD,∵OC⊥AB,∴∠EAO=∠AOH=∠EHO=90°,∴四边形AEHO是矩形,∴EH=OA=3,AE=OH,∵CH ===5,∴AE=OH=CH﹣CO=5﹣3=2.(2)∵AE∥OC,∴==,∴AD =OA =,∵5BF﹣5AD=4,∴BF=2,∴OF=OB﹣BF=1,AF=AO+OF=4,CF ===,∵∠F AC=∠FGB,∠AFC=∠GFB,∴△AFC∽△GFB,∴=,∴=,∴FG =,∴CG=FG+CF =,∵CT是直径,∴∠CGT=90°,∴GT ===,∴cos∠CTG ===,∵∠CAG=∠CTG,∴cos∠CAG =.31.如图,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的⊙O 经过点D.(1)求证:①BC是⊙O的切线;②CD2=CE•CA;(2)若点F是劣弧AD的中点,且CE=3,试求阴影部分的面积.解:(1)①连接OD,∵AD是∠BAC的平分线,∴∠DAB=∠DAO,∵OD=OA,∴∠DAO=∠ODA,则∠DAB=∠ODA,∴DO∥AB,而∠B=90°,∴∠ODB=90°,∴BC是⊙O的切线;②连接DE,∵BC是⊙O的切线,∴∠CDE=∠DAC,∠C=∠C,∴△CDE∽△CAD,∴CD2=CE•CA;(2)连接DE、OD、DF、OF,设圆的半径为R,∵点F是劣弧AD的中点,∴是OF是DA中垂线,∴DF=AF,∴∠FDA=∠F AD,∵DO∥AB,∴∠ODA=∠DAF,∴∠ADO=∠DAO=∠FDA=∠F AD,∴AF=DF=OA=OD,∴△OFD、△OF A是等边三角形,则DF∥AC,故S阴影=S扇形DFO,∴∠C=30°,∴OD =OC =(OE+EC),而OE=OD,∴CE=OE=R=3,S阴影=S扇形DFO =×π×32=.32.如图,以AB为直径的⊙O外接于△ABC,过A点的切线AP与BC的延长线交于点P,∠APB的平分线分别交AB,AC于点D,E,其中AE,BD(AE<BD)的长是一元二次方程x2﹣5x+6=0的两个实数根.(1)求证:P A•BD=PB•AE;(2)在线段BC上是否存在一点M,使得四边形ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.解:(1)∵DP平分∠APB,∴∠APE=∠BPD,∵AP与⊙O相切,∴∠BAP=∠BAC+∠EAP=90°,∵AB是⊙O的直径,∴∠ACB=∠BAC+∠B=90°,∴∠EAP=∠B,∴△P AE∽△PBD,∴,∴P A•BD=PB•AE;(2)过点D作DF⊥PB于点F,作DG⊥AC于点G,∵DP平分∠APB,AD⊥AP,DF⊥PB,∴AD=DF,∵∠EAP=∠B,∴∠APC=∠BAC,易证:DF∥AC,∴∠BDF=∠BAC,由于AE,BD(AE<BD)的长是x2﹣5x+6=0,解得:AE=2,BD=3,∴由(1)可知:,∴cos∠APC ==,∴cos∠BDF=cos∠APC =,∴,∴DF=2,∴DF=AE,∴四边形ADFE是平行四边形,∵AD=AE,∴四边形ADFE是菱形,此时点F即为M点,∵cos∠BAC=cos∠APC =,∴sin∠BAC =,∴,∴DG =,∴在线段BC上存在一点M,使得四边形ADME是菱形其面积为:DG•AE=2×=33.如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O 恰好经过边BC的中点D,并与边AC相交于另一点F.(1)求证:BD是⊙O的切线.(2)若AB =,E 是半圆上一动点,连接AE,AD,DE.①当的长度是π时,四边形ABDE是菱形;②当的长度是π或π时,△ADE是直角三角形.(1)证明:如图1,连接OD,∵在Rt△ABC中,∠BAC=90°,∠C=30°,∴AB=BC,∵D是BC的中点,∴BD=BC,∴AB=BD,∴∠BAD=∠BDA,∵OA=OD,∴∠OAD=∠ODA,∴∠ODB=∠BAO=90°,即OD⊥BC,∴BD是⊙O的切线.(2)①当DE⊥AC时,四边形ABDE是菱形;如图2,设DE交AC于点M ,连接OE,则DE=2DM,∵∠C=30°,∴CD=2DM,∴DE=CD=AB=BC,∵∠BAC=90°,∴DE∥AB,∴四边形ABDE是平行四边形,∵AB=BD,∴四边形ABDE是菱形;∵AD=BD=AB=CD=BC=,∴△ABD是等边三角形,OD=CD•tan30°=1,∴∠ADB=60°,∵∠CDE=90°﹣∠C=60°,∴∠ADE=180°﹣∠ADB﹣∠CDE=60°,∴∠AOE =2∠ADE=120°,∴的长度为:=π;②若∠ADE=90°,则点E与点F 重合,此时的长度为:=π;若∠DAE=90°,则DE是直径,则∠AOE=2∠ADO=60°,此时的长度为:=π;∵AD不是直径,∴∠AED≠90°;综上可得:当的长度是π或π时,△ADE是直角三角形.34.如图,△ABC是等腰直角三角形,且AC=BC,P是△ABC外接圆⊙O上的一动点(点P与点C位于直线AB的异侧)连接AP、BP,延长AP到D,使PD=PB,连接BD.(1)求证:PC∥BD;(2)若⊙O的半径为2,∠ABP=60°,求CP的长;(3)随着点P的运动,的值是否会发生变化,若变化,请说明理由;若不变,请给出证明.(1)证明:∵△ABC是等腰直角三角形,且AC=BC,∴∠ABC=45°,∠ACB=90°,∴∠APC=∠ABC=45°,∴AB为⊙O的直径,∴∠APB=90°,∵PD=PB,∴∠PBD=∠D=45°,∴∠APC=∠D=45°,∴PC∥BD;(2)解:作BH⊥CP,垂足为H,∵⊙O的半径为2,∠ABP=60°,∴BC=2,∠BCP=∠BAP=30°,∠CPB=∠BAC=45°,在Rt△BCH中,CH=BC•cos∠BCH=,BH=BC•sin∠BCH=,在Rt△BHP中,PH=BH=,∴CP=CH+PH=+;(3)解:的值不变,∵∠BCP=∠BAP,∠CPB=∠D,∴△CBP∽△ABD,∴==,∴=,即=.35.如图,AB是⊙O的直径,DO⊥AB于点O,连接DA交⊙O于点C,过点C作⊙O的切线交DO于点E,连接BC交DO于点F.(1)求证:CE=EF;(2)连接AF并延长,交⊙O于点G.填空:①当∠D的度数为30°时,四边形ECFG为菱形;②当∠D的度数为22.5°时,四边形ECOG为正方形.(1)证明:连接OC,如图,∵CE为切线∴OC⊥CE,∴∠OCE=90°,即∠1+∠4=90°,∵DO⊥AB ∴∠3+∠B=90°,而∠2=∠3,∴∠2+∠B=90°,而OB=OC,∴∠4=∠B,∴∠1=∠2,∴CE=FE;(2)解:①当∠D=30°时,∠DAO=60°,而AB为直径,∴∠ACB=90°,∴∠B=30°,∴∠3=∠2=60°,而CE=FE,∴△CEF为等边三角形,∴CE=CF=EF,同理可得∠GFE=60°,利用对称得FG=FC,∵FG=EF,∴△FEG为等边三角形,∴EG=FG,∴EF=FG=GE=CE,∴四边形ECFG为菱形;②当∠D=22.5°时,∠DAO=67.5°,而OA=OC,∴∠OCA=∠OAC=67.5°,∴∠AOC=180°﹣67.5°﹣67.5°=45°,∴∠AOC=45°,∴∠COE=45°,利用对称得∠EOG=45°,∴∠COG=90°,易得△OEC≌△OEG,∴∠OGE=∠OCE=90°,∴四边形ECOG为矩形,而OC=OG,∴四边形ECOG为正方形.36.如图,AB是⊙O的直径,且AB=4,C是⊙O上一点,D 是的中点,过点D作⊙O的切线与AB、AC的延长线分别交于点E、F,连接AD.(1)求证:AF⊥EF;(2)①当BE=4时,点C是AF的中点;②当∠E=30°时,四边形OBDC是菱形.解:(1)连接OD ,BD,BC,∵ED为⊙O的切线∴OD⊥EF,∵D是的中点∴OD⊥BC,∴EF∥BC∵AB是⊙O的直径,∴∠ACB=90°,∴∠AFE=90°∴AF⊥EF;(2)①当BE=4时,由(1)知,BC∥EF,当AB=BE时,AC=CF,∴当BE=4时,点C是AF的中点,②当∠E=30°时,四边形OBDC是菱形.如图,∵EF是⊙O的切线,∴∠ODE=∠F=90°,∴∠DOE=∠COA=60°,∵OD=OB=OC=OA,∴△ODB,△AOC为等边三角形,∴∠COA=∠DOB=60°,∴∠COD=60°,∴△COD为等边三角形,∴OB=BD=OD=CD=OC,∴四边形OBDC是菱形;37.如图,在▱ABCD中,AB=3,BC=5,∠B=45°,点E为CD上一动点,经过A、C、E三点的⊙O交BC于点F.(1)当E运动到AE⊥CD处,利用直尺与规作出点E与点F;(保留作图痕迹)(2)在(1)的条件下,证明:=.(3)点E 运动到任何一个位置时,求证:;(4)点E在运动的过程中求EF的最小值.解:(1)如图1,(2)如图,易知AC为直径,则AF⊥BC,则S四边形ABCD=BC•AF=CD•AE,∴==(3)如图,作AM⊥BC,AN⊥CD,若E在DN之间由(2)可知,=∵A、F、C、E四点共圆,∴∠AFC+∠AEC=180°,∵∠AFC+∠AFM=180°,∴∠AEN=∠AFM,∵∠AMF=∠ANE∴△AMF∽△ANE∴==若E在CN之间时,同理可证(4)∵A、F、C、E四点共圆,∴∠F AE+∠BCD=180°,∵四边形ABCD为平行四边形,∠B=45°,∴∠BCD=135°,∴∠F AE=45°,∴∠FOE=90°,∴△FOE为等腰直角三角形,∴FE =R∵AN≤AC≤2R,∴E与N重合时,FE最小,此时FE =AC,在△ABC中,AM=BM=3,则CM=2∴由勾股定理可知:AC =此时EF 最小值为38.如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.(1)求证:△AFG∽△DFC;(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.(1)证明:在正方形ABCD中,∠ADC=90°,∴∠CDF+∠ADF=90°,∵AF⊥DE,∴∠AFD=90°,∴∠DAF+∠ADF=90°,∴∠DAF=∠CDF,∵四边形GFCD是⊙O的内接四边形,∴∠FCD+∠DGF=180°,∵∠FGA+∠DGF=180°,∴∠FGA=∠FCD,∴△AFG∽△DFC.(2)解:如图,连接CG.∵∠EAD=∠AFD=90°,∠EDA=∠ADF,∴△EDA∽△ADF,∴=,即=,∵△AFG∽△DFC,∴=,∴=,在正方形ABCD中,∵DA=DC,∴AG=EA=1,DG=DA﹣AG=4﹣1=3,∴CG ==5,∵∠CDG=90°,∴CG是⊙O的直径,∴⊙O 的半径为.39.如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D 作BC的平行线与AC的延长线相交于点P.(1)求证:PD是⊙O的切线;(2)求证:AB•CP=BD•CD;(3)若tan∠ABC=2,AB=2,求线段DP的长.(1)证明:如图1,连接OD.∵AD平分∠BAC,∴∠BAD=∠CAD,∴,∴∠BOD=∠COD=90°,∵BC∥PD,∴∠ODP=∠BOD=90°,∴OD⊥PD,∴PD是⊙O的切线.(2)证明:∵BC∥PD,∴∠PDC=∠BCD.∵∠BCD=∠BAD,∴∠BAD=∠PDC,∵∠ABD+∠ACD=180°,∠ACD+∠PCD=180°,∴∠ABD=∠PCD,∴△BAD∽△CDP,∴,∴AB•CP=BD•CD;(3)解:∵BC是⊙O的直径,∴∠BAC=90°,∵tan∠ABC=2,,∴=2,∴,∴,∴OD=5,如图2,连接OD,过点C作CG⊥DP,垂足为G,则四边形ODGC为正方形,∴DG=CG=OD=5,∵BC∥PD,∴∠CPG=∠ACB,∴tan∠CPG=tan∠ACB,∴,即,解得,GP=10,∴DP=DG+PG=5+10=15.。
2021年中考数学《圆综合压轴题》模拟训练题集(一)

2021年中考数学《圆综合压轴题》模拟训练题集(一)1.如图,在△ABC中,AB=AC,∠A=30°,AB=10,以AB为直径的⊙O交BC于点D,交AC于点E,连接DE,过点B作BP平行于DE,交⊙O于点P,连接CP、OP.(1)求证:点D为BC的中点;(2)求AP的长度;(3)求证:CP是⊙O的切线.2.已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.(1)求证:DE=OE;(2)若CD∥AB,求证:BC是⊙O的切线;(3)在(2)的条件下,求证:四边形ABCD是菱形.3.如图,AB是⊙O的直径,C、G是⊙O上两点,且C是弧AG的中点,过点C的直线CD⊥BG的延长线于点D,交BA的延长线于点E,连接BC,交OD于点F.(1)求证:CD是⊙O的切线;(2)若=,求证:AE=AO;(3)连接AD,在(2)的条件下,若CD=2,求AD的长.4.如图,已知AB是⊙O的切线,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F(1)求证:ED是⊙O的切线;(2)求证:△CFP∽△CPD;(3)如果CF=1,CP=2,sin A=,求O到DC的距离.5.如图1,▱AOBC的顶点A、B、C在⊙O上,点D、E分别在BO、AO的延长线上,且OD=2OB,OE=2OA,连接DE.(1)求∠AOB的度数;(2)求证:DE是⊙O的切线;(3)如图2,设直线DE与⊙O相切于点F,连接AD、BF,判断线段AD与BF的位置关系和数量关系,并证明你的结论.6.如图,AB是⊙O的直径,D是的中点,DE⊥AB于E,交CB于点F.过点D作BC的平行线DM,连接AC 并延长与DM相交于点G.(1)求证:GD是⊙O的切线;(2)求证:GD2=GC•AG;(3)若CD=6,AD=8,求cos∠ABC的值.7.如图1,⊙O是△ABC的外接圆,AB是直径,OD∥AC,OD交⊙O于点E,且∠CBD=∠COD.(1)求证:BD是⊙O的切线;(2)若点E为线段OD的中点,判断以O、A、C、E为顶点的四边形的形状并证明;(3)如图2,作CF⊥AB于点F,连接AD交CF于点G,求的值.8.如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.(1)如图2,当PD∥AB时,求PD的长;(2)如图3,当=时,延长AB至点E,使BE=AB,连接DE.①求证:DE是⊙O的切线;②求PC的长.9.如图,四边形ABCD为矩形,E为BC边中点,以AD为直径的⊙O与AE交于点F.(1)求证:四边形AOCE为平行四边形;(2)求证:CF与⊙O相切;(3)若F为AE的中点,求∠ADF的大小.10.已知AM是⊙O直径,弦BC⊥AM,垂足为点N,弦CD交AM于点E,连按AB和BE.(1)如图1,若CD⊥AB,垂足为点F,求证:∠BED=2∠BAM;(2)如图2,在(1)的条件下,连接BD,若∠ABE=∠BDC,求证:AE=2CN;(3)如图3,AB=CD,BE:CD=4:7,AE=11,求EM的长.11.⊙O是△ABC的外接圆,AB是直径,过的中点P作⊙O的直径PG交弦BC于点D,连接AG、CP、PB.(1)如图1,若D是线段OP的中点,求∠BAC的度数;(2)如图2,在DG上取一点K,使DK=DP,连接CK,求证:四边形AGKC是平行四边形;(3)如图3,取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:PH⊥AB.12.如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.(1)求∠FDE的度数;(2)试判断四边形F ACD的形状,并证明你的结论;(3)当G为线段DC的中点时,①求证:FD=FI;②设AC=2m,BD=2n,求⊙O的面积与菱形ABCD的面积之比.13.如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.(1)求证:AH是⊙O的切线;(2)若OB=4,AC=6,求sin∠ACB的值;(3)若=,求证:CD=DH.14.如图,⊙O与AB,AC分别相切于D,E两点,AB=AC,AO交⊙O于点F,交BC于点G,BC与⊙O交于点P,Q连接EQ(1)求证:AG⊥BC;(2)若DE平分OF,求证:△ADE是等边三角形;(3)在(2)的条件下,若AD=PQ,EQ=2,求BP的长.15.如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接DE.(1)求证:直线DE是⊙O的切线;(2)连接OC交DE于点F,若OF=CF,①判断以O、E、C、D为顶点的四边形的形状,并说明理由;②求tan∠ACO的值.16.如图,在△ABC中,AB=BC,以BC为直径作⊙O交AB于点E、交AC于点F,连结EF、BF、CE,BF与CE相交于点D,点G是EF的中点,连结OG.(1)判断OG与EF的位置关系,直接写出你的结论(不需证明);(2)求证:EF=CF;(3)若BF=2+,OG•FD=8﹣,求⊙O的面积.17.如图,AB、ED是⊙O的直径,点C在ED延长线上,且∠CBD=∠F AB.点F在⊙O上,且AB⊥DF.连接AD并延长交BC于点G.(1)求证:BC是⊙O的切线;(2)求证:BD•BC=BE•CD;(3)若⊙O的半径为r,BC=3r,求tan∠CDG的值.18.如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P 从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t ≤5).以P为圆心,P A长为半径的⊙P与AB、OA的另一个交点分别为C、D,连接CD、QC.(1)求当t为何值时,点Q与点D重合?(2)设△QCD的面积为S,试求S与t之间的函数关系式,并求S的最大值;(3)若⊙P与线段QC只有一个交点,请直接写出t的取值范围.19.如图,四边形ABCD内接于⊙O,已知直径AD=4,∠ABC=120°,∠ACB=45°,连接OB交AC于点E.(1)求AC的长;(2)求CE:AE的值;(3)在CB的延长线上取一点P,使PB=2BC,试判断直线P A和⊙O的位置关系,并证明你的结论.20.如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线AO交BC于点O,以O为圆心,OC长为半径作⊙O,⊙O交AO所在的直线于D、E两点(点D在BC左侧).(1)求证:AB是⊙O的切线;(2)连接CD,若AC=AD,求tan∠D的值;(3)在(2)的条件下,若⊙O的半径为5,求AB的长.21.如图,点C是等边△ABD的边AD上的一点,且∠ACB=75°,⊙O是△ABC的外接圆,连结AO并延长交BD于E、交⊙O于F.(1)求证:∠BAF=∠CBD;(2)过点C作CG∥AE交BD于点G,求证:CG是⊙O的切线;(3)在(2)的条件下,当AF=2时,求的值.22.如图,平行四边形ABCD中,AC=BC,过A、B、C三点的⊙O与AD相交于点E,连接CE.(1)证明:AB=CE;(2)证明:DC与⊙O相切;(3)若⊙O的半径r=5,AB=8,求sin∠ACE的值.23.如图,⊙O是△ABC的外接圆,AB为⊙O的直径,过点C作∠BCD=∠BAC交AB的延长线于点D,过点O 作直径EF∥BC,交AC于点G.(1)求证:CD是⊙O的切线;(2)若⊙O的半径为2,∠BCD=30°;①连接AE、DE,求证:四边形ACDE是菱形;②当点P是线段AD上的一动点时,求PF+PG的最小值.24.如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.(1)求证:△ECF∽△GCE;(2)求证:EG是⊙O的切线;(3)延长AB交GE的延长线于点M,若tan∠G=,AH=3,求EM的值.25.如图,线段AB是⊙O的直径,C、D是半圆的三等分点,过点C的直线与AD的延长线垂直,垂足为点E,与AB的延长线相交于点F,连接OE,交AC于点G.(1)求证:FC是⊙O的切线;(2)连接DC、CO,判断四边形ADCO的形状,并证明;(3)求OG与GE的比值.26.如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.(1)证明:∠E=∠C;(3)设DE交AB于点G,若DF=4,cos B=,E是的中点,求EG•ED的值.27.如图,AB为⊙O的直径,AB=4,P为AB上一点,过点P作⊙O的弦CD,设∠BCD=m∠ACD.(1)已知=,求m的值,及∠BCD、∠ACD的度数各是多少?(2)当=时,是否存在正实数m,使弦CD最短?如果存在,求出m的值,如果不存在,说明理由;(3)在(1)的条件下,且=,求弦CD的长.28.如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.(1)求证:CF是⊙O的切线;(2)求证:△ACM∽△DCN;(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=,求BN的长.29.如图1,AB为⊙O的直径,点C为⊙O上一点,CD平分∠ACB交⊙O于点D,交AB于点E.(1)求证:△ABD为等腰直角三角形;(2)如图2,ED绕点D顺时针旋转90°,得到DE′,连接BE′,证明:BE′为⊙O的切线;(3)如图3,点F为弧BD的中点,连接AF,交BD于点G,若DF=1,求AG的长.30.如图,△BCD内接于⊙O,直径AB经过弦CD的中点M,AE交BC的延长线于点E,连接AC,∠EAC=∠ABD =30°.(1)求证:△BCD是等边三角形;(2)求证:AE是⊙O的切线;(3)若CE=2,求⊙O的半径.31.如图,四边形ABCD为⊙O的内接四边形,且对角线AC为直径,AD=BC,过点D作DG⊥AC,垂足为E,DG分别与AB,⊙O及CB延长线交于点F、G、M.(1)求证:四边形ABCD为矩形;(2)若N为MF中点,求证:NB是⊙O的切线;(3)若F为GE中点,且DE=6,求⊙O的半径.32.如图,AB为⊙O直径,P点为半径OA上异于O点和A点的一个点,过P点作与直径AB垂直的弦CD,连接AD,作BE⊥AB,OE∥AD交BE于E点,连接AE、DE、AE交CD于F点.(1)求证:DE为⊙O切线;(2)若⊙O的半径为3,sin∠ADP=,求AD;(3)请猜想PF与FD的数量关系,并加以证明.33.如图,AB为半圆O的直径,OD⊥AB,与弦BC延长线交于点D,与弦AC交于点E.(1)求证:△AOE∽△DOB;(2)若点F为DE的中点,连接CF,求证:CF为⊙O的切线;(3)在(2)的条件下,若CF=3,tan A=,求AB的长.34.如图,在Rt△ABC中,∠C=90°,BD为∠ABC的平分线,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相交于点M,过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连结FN.(1)求证:AC是⊙O的切线;(2)若AF=4,tan∠N=,求⊙O的半径长;(3)在(2)的条件下,求MN的长.35.如图1,四边形ABCD内接于⊙O,AC为⊙O的直径,AC与BD交于点E,且AE=AB,DA=DB.(1)求证:AB=CB;(2)如图2,△ABC绕点C逆时针旋转30°得到△FGC,点A经过的路径为,若AC=4,求图中阴影部分面积S;(3)在(2)的条件下,连接FB,求证:FB为⊙O的切线.36.如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB点F,连接BE.(1)求证:AC平分∠DAB;(2)求证:PC=PF;(3)若tan∠ABC=,AB=14,求线段PC的长.37.如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连EC,CD (1)试猜想直线AB于⊙O的位置关系,并说明理由;(2)求证:BC2=BD•BE;(3)若tan∠CED=,⊙O的半径为3,求△OAB的面积.38.如图,⊙O中,FG,AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为.(1)分别求出线段AP、CB的长;(2)如果OE=5,求证:DE是⊙O的切线;(3)如果tan∠E=,求DE的长.39.已知:如图,△ABC内接于⊙O,AB为直径,弦CE⊥AB于F,C是的中点,连结BD并延长交EC的延长线于点G,连结AD,分别交CE、BC于点P、Q.(1)求证:AP=CP;(2)若tan∠ABC=,CF=8,求CQ的长;(3)求证:(FP+PQ)2=FP•FG.40.如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.(1)求证:DH是圆O的切线;(2)若A为EH的中点,求的值;(3)若EA=EF=1,求圆O的半径.41.如图,AB是⊙O的直径,点C在⊙O上,点E在线段OA上运动,DE⊥AB,垂足为E,DE交AC于点G,DC是⊙O的切线,交AB的延长线于点F.(1)求证:∠D=2∠A;(2)如图(2),若点E是OA的中点,点H是DE与⊙O的交点,OH∥BC,求证:△DCG是等边三角形;(3)如图(1),若CD=CF,且BF=1,CF=2,求CG的长.42.如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.(1)求证:∠BME=∠MAB;(2)求证:BM2=BE•AB;(3)若BE=,sin∠BAM=,求线段AM的长.43.如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E作直线l∥BC.(1)判断直线l与⊙O的位置关系,并说明理由;(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)在(2)的条件下,若DE=4,DF=3,求AF的长.44.如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为的中点,连接OE交CD于点F,连接BE交CD 于点G.(1)求证:AB=AG;(2)若DG=DE,求证:GB2=GC•GA;(3)在(2)的条件下,若tan D=,EG=,求⊙O的半径.45.如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于点D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.(1)求证:BD=CD;(2)若AE=6,BF=4,求⊙O的半径;(3)在(2)条件下判断△ABC的形状,并说明理由.46.已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.(1)求证:BD是⊙O的切线;(2)求证:CE2=EH•EA;(3)若⊙O的半径为5,sin A=,求BH的长.47.如图,⊙O是△ABC的外接圆,AF平分∠BAC交BC于点E,交⊙O于点F,BD平分∠ABC交AF于点D,过点F作FH∥BC.(1)求证:FH是⊙O的切线;(2)求证:BF=DF;(3)若EF=3,DE=4,求线段AD的长.48.如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F 作射线BC的垂线,垂足为H,连接AC.(1)试判断BE与FH的数量关系,并说明理由;(2)求证:∠ACF=90°;(3)连接AF,过A、E、F三点作圆,如图2,若EC=4,∠CEF=15°,求的长.49.如图,P A为⊙O的切线,A为切点,直线PO交⊙O与点E,F过点A作PO的垂线AB垂足为D,交⊙O与点B,延长BO与⊙O交于点C,连接AC,BF.(1)求证:PB与⊙O相切;(2)试探究线段EF,OD,OP之间的数量关系,并加以证明;(3)若AC=12,tan∠F=,求cos∠ACB的值.50.如图,在△ABC中,∠ACB=90°,D是AB的中点,以DC为直径的⊙O交△ABC的三边,交点分别是G,E,F点.EG与CD交点为M.(1)求证:∠GEF=∠A;(2)求证:△OME∽△EMC;(3)若ME=4,MD:CO=2:5,求⊙O面积.。
2020-2021备战中考数学圆的综合提高练习题压轴题训练含详细答案

2020-2021备战中考数学圆的综合提高练习题压轴题训练含详细答案一、圆的综合1.如图,已知△ABC内接于⊙O,BC交直径AD于点E,过点C作AD的垂线交AB的延长线于点G,垂足为F.连接OC.(1)若∠G=48°,求∠ACB的度数;(2)若AB=AE,求证:∠BAD=∠COF;(3)在(2)的条件下,连接OB,设△AOB的面积为S1,△ACF的面积为S2.若tan∠CAF=12,求12SS的值.【答案】(1)48°(2)证明见解析(3)3 4【解析】【分析】(1)连接CD,根据圆周角定理和垂直的定义可得结论;(2)先根据等腰三角形的性质得:∠ABE=∠AEB,再证明∠BCG=∠DAC,可得»»»CD PB PD==,则所对的圆周角相等,根据同弧所对的圆周角和圆心角的关系可得结论;(3)过O作OG⊥AB于G,证明△COF≌△OAG,则OG=CF=x,AG=OF,设OF=a,则OA=OC=2x-a,根据勾股定理列方程得:(2x-a)2=x2+a2,则a=34x,代入面积公式可得结论.【详解】(1)连接CD,∵AD是⊙O的直径,∴∠ACD=90°,∴∠ACB+∠BCD=90°,∵AD⊥CG,∴∠AFG=∠G+∠BAD=90°,∵∠BAD=∠BCD,∴∠ACB=∠G=48°;(2)∵AB=AE,∴∠ABE=∠AEB,∵∠ABC=∠G+∠BCG,∠AEB=∠ACB+∠DAC,由(1)得:∠G=∠ACB,∴∠BCG=∠DAC,∴»»CD PB=,∵AD是⊙O的直径,AD⊥PC,∴»»CD PD=,∴»»»CD PB PD==,∴∠BAD=2∠DAC,∵∠COF=2∠DAC,∴∠BAD=∠COF;(3)过O作OG⊥AB于G,设CF=x,∵tan∠CAF=12=CF AF,∴AF=2x,∵OC=OA,由(2)得:∠COF=∠OAG,∵∠OFC=∠AGO=90°,∴△COF≌△OAG,∴OG=CF=x,AG=OF,设OF=a,则OA=OC=2x﹣a,Rt△COF中,CO2=CF2+OF2,∴(2x﹣a)2=x2+a2,a=34 x,∴OF=AG=34 x,∵OA=OB,OG⊥AB,∴AB=2AG=32x,∴1213··3 22 1·24·2AB OG x xSS x xCF AF===.【点睛】圆的综合题,考查了三角形的面积、垂径定理、角平分线的性质、三角形全等的性质和判定以及解直角三角形,解题的关键是:(1)根据圆周角定理找出∠ACB+∠BCD=90°;(2)根据外角的性质和圆的性质得:»»»==;(3)利用三角函数设未知数,根CD PB PD据勾股定理列方程解决问题.2.如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.(1)求证:AE=BE;(2)求证:FE是⊙O的切线;(3)若FE=4,FC=2,求⊙O的半径及CG的长.【答案】(1)详见解析;(2)详见解析;(3).【解析】(1)证明:连接CE,如图1所示:∵BC是直径,∴∠BEC=90°,∴CE⊥AB;又∵AC=BC,∴AE=BE.(2)证明:连接OE,如图2所示:∵BE=AE,OB=OC,∴OE是△ABC的中位线,∴OE∥AC,AC=2OE=6.又∵EG⊥AC,∴FE⊥OE,∴FE是⊙O的切线.(3)解:∵EF是⊙O的切线,∴FE2=FC•FB.设FC=x,则有2FB=16,∴FB=8,∴BC=FB﹣FC=8﹣2=6,∴OB=OC=3,即⊙O的半径为3;∴OE=3.∵OE∥AC,∴△FCG∽△FOE,∴,即,解得:CG=.点睛:本题利用了等腰三角形三线合一定理,三角形中位线的判定,切割线定理,以及勾股定理,还有平行线分线段成比例定理,切线的判定等知识.3.如图,AB 为⊙O 的直径,AC 为⊙O 的弦,AD 平分∠BAC ,交⊙O 于点D ,DE ⊥AC ,交AC 的延长线于点E .(1)判断直线DE 与⊙O 的位置关系,并说明理由; (2)若AE =8,⊙O 的半径为5,求DE 的长.【答案】(1)直线DE 与⊙O 相切(2)4 【解析】试题分析:(1)连接OD ,∵AD 平分∠BAC ,∴EAD OAD ∠∠=,∵OA OD =,∴ODA OAD ∠∠=,∴ODA EAD ∠∠=,∴EA ∥OD ,∵DE ⊥EA ,∴DE ⊥OD ,又∵点D 在⊙O 上,∴直线DE 与⊙O 相切 (2)如图1,作DF ⊥AB ,垂足为F ,∴DFA DEA 90∠∠︒==,∵EAD FAD ∠∠=,AD AD =,∴△EAD ≌△FAD ,∴AF AE 8==,DF DE =,∵OA OD 5==,∴OF 3=,在Rt △DOF 中,22DF 4OD OF -==,∴AF AE 8== 考点:切线的证明,弦心距和半径、弦长的关系点评:本题难度不大,第一小题通过内错角相等相等证明两直线平行,再由两直线平行推出同旁内角相等.第二小题通过求出两个三角形全等,从而推出对应边相等,接着用弦心距和弦长、半径的计算公式,求出半弦长.4.四边形 ABCD 的对角线交于点 E ,且 AE =EC ,BE =ED ,以 AD 为直径的半圆过点 E ,圆心 为 O .(1)如图①,求证:四边形 ABCD 为菱形;(2)如图②,若 BC 的延长线与半圆相切于点 F ,且直径 AD =6,求弧AE 的长.【答案】(1)见解析;(2)π2【解析】试题分析:(1)先判断出四边形ABCD 是平行四边形,再判断出AC ⊥BD 即可得出结论; (2)先判断出AD =DC 且DE ⊥AC ,∠ADE =∠CDE ,进而得出∠CDA =30°,最后用弧长公式即可得出结论.试题解析:证明:(1)∵四边形ABCD 的对角线交于点E ,且AE =EC ,BE =ED ,∴四边形ABCD 是平行四边形.∵以AD 为直径的半圆过点E ,∴∠AED =90°,即有AC ⊥BD ,∴四边形ABCD 是菱形;(2)由(1)知,四边形ABCD 是菱形,∴△ADC 为等腰三角形,∴AD =DC 且DE ⊥AC ,∠ADE =∠CDE .如图2,过点C 作CG ⊥AD ,垂足为G ,连接FO .∵BF 切圆O 于点F ,∴OF ⊥AD ,且132OF AD ==,易知,四边形CGOF 为矩形,∴CG =OF =3. 在Rt △CDG 中,CD =AD =6,sin ∠ADC =CG CD =12,∴∠CDA =30°,∴∠ADE =15°. 连接OE ,则∠AOE =2×∠ADE =30°,∴¶3031802AE ππ⋅⨯==.点睛:本题主要考查菱形的判定即矩形的判定与性质、切线的性质,熟练掌握其判定与性质并结合题意加以灵活运用是解题的关键.5.如图,四边形ABCD 内接于⊙O ,对角线AC 为⊙O 的直径,过点C 作AC 的垂线交AD 的延长线于点E ,点F 为CE 的中点,连接DB , DF . (1)求证:DF 是⊙O 的切线;(2)若DB 平分∠ADC ,AB =52AD ,∶DE =4∶1,求DE 的长.【答案】(1)见解析;(2)5【解析】分析:(1)直接利用直角三角形的性质得出DF=CF=EF,再求出∠FDO=∠FCO=90°,得出答案即可;(2)首先得出AB=BC即可得出它们的长,再利用△ADC~△ACE,得出AC2=AD•AE,进而得出答案.详解:(1)连接OD.∵OD=CD,∴∠ODC=∠OCD.∵AC为⊙O的直径,∴∠ADC=∠EDC=90°.∵点F为CE的中点,∴DF=CF=EF,∴∠FDC=∠FCD,∴∠FDO=∠FCO.又∵AC⊥CE,∴∠FDO=∠FCO=90°,∴DF是⊙O的切线.(2)∵AC为⊙O的直径,∴∠ADC=∠ABC=90°.∵DB平分∠ADC,∴∠ADB=∠CDB,∴¶AB=¶BC,∴BC=AB=52.在Rt△ABC中,AC2=AB2+BC2=100.又∵AC⊥CE,∴∠ACE=90°,∴△ADC~△ACE,∴ACAD =AEAC,∴AC2=AD•AE.设DE为x,由AD:DE=4:1,∴AD=4x,AE=5x,∴100=4x•5x,∴x=5,∴DE=5.点睛:本题主要考查了切线的判定以及相似三角形的判定与性质,正确得出AC2=AD•AE是解题的关键.6.如图,已知四边形ABCD是矩形,点P在BC边的延长线上,且PD=BC,⊙A经过点B,与AD边交于点E,连接CE .(1)求证:直线PD是⊙A的切线;(2)若PC=25,sin∠P=23,求图中阴影部份的面积(结果保留无理数).【答案】(1)见解析;(2)20-4π.【解析】分析:(1)过点A作AH⊥PD,垂足为H,只要证明AH为半径即可.(2)分别算出Rt△CED的面积,扇形ABE的面积,矩形ABCD的面积即可.详解:(1)证明:如图,过A作AH⊥PD,垂足为H,∵四边形ABCD是矩形,∴AD=BC,AD∥BC,∠PCD=∠BCD=90°,∴∠ADH=∠P,∠AHD=∠PCD=90°,又PD=BC,∴AD=PD,∴△ADH≌△DPC,∴AH=CD,∵CD=AB,且AB是⊙A的半径,∴AH=AB,即AH是⊙A的半径,∴PD是⊙A的切线.(2)如图,在Rt△PDC中,∵sin∠P=23CDPD,5,令CD=2x,PD=3x,由由勾股定理得:(3x)2-(2x)252,解得:x=2,∴CD=4,PD=6,∴AB=AE=CD=4,AD=BC=PD=6,DE=2,∵矩形ABCD的面积为6×4=24,Rt△CED的面积为12×4×2=4,扇形ABE的面积为12π×42=4π,∴图中阴影部份的面积为24-4-4π=20-4π.点睛:本题考查了全等三角形的判定,圆的切线证明,三角形的面积,扇形的面积,矩形的面积.7.如图,⊙M 与菱形ABCD 在平面直角坐标系中,点M 的坐标为(3,﹣1),点A 的坐标为(﹣2,3),点B 的坐标为(﹣3,0),点C 在x 轴上,且点D 在点A 的左侧. (1)求菱形ABCD 的周长;(2)若⊙M 沿x 轴向右以每秒2个单位长度的速度平移,同时菱形ABCD 沿x 轴向右以每秒3个单位长度的速度平移,设菱形移动的时间为t (秒),当⊙M 与BC 相切,且切点为BC 的中点时,连接BD ,求: ①t 的值; ②∠MBD 的度数;(3)在(2)的条件下,当点M 与BD 所在的直线的距离为1时,求t 的值.【答案】(1)8;(2)①7;②105°;(3)t=636+33. 【解析】分析:(1)根据勾股定理求菱形的边长为2,所以可得周长为8;(2)①如图2,先根据坐标求EF 的长,由EE '﹣FE '=EF =7,列式得:3t ﹣2t =7,可得t 的值;②先求∠EBA =60°,则∠FBA =120°,再得∠MBF =45°,相加可得:∠MBD =∠MBF +∠FBD =45°+60°=105°;(3)分两种情况讨论:作出距离MN 和ME ,第一种情况:如图5由距离为1可知:BD 为⊙M 的切线,由BC 是⊙M 的切线,得∠MBE =30°,列式为3t 3=2t +6,解出即可; 第二种情况:如图6,同理可得t 的值. 详解:(1)如图1,过A 作AE ⊥BC 于E .∵点A 的坐标为(﹣23),点B 的坐标为(﹣3,0),∴AE 3,BE =3﹣2=1,∴AB 22AE BE +2231+()=2. ∵四边形ABCD 是菱形,∴AB =BC =CD =AD =2,∴菱形ABCD 的周长=2×4=8; (2)①如图2,⊙M 与x 轴的切点为F ,BC 的中点为E . ∵M (3,﹣1),∴F (3,0).∵BC =2,且E 为BC 的中点,∴E (﹣4,0),∴EF =7,即EE '﹣FE '=EF ,∴3t ﹣2t =7,t =7;②由(1)可知:BE =1,AE 3 ∴tan ∠EBA =AE BE =33,∴∠EBA =60°,如图4,∴∠FBA =120°.∵四边形ABCD是菱形,∴∠FBD=12∠FBA=11202⨯︒=60°.∵BC是⊙M的切线,∴MF⊥BC.∵F是BC的中点,∴BF=MF=1,∴△BFM是等腰直角三角形,∴∠MBF=45°,∴∠MBD=∠MBF+∠FBD=45°+60°=105°;(3)连接BM,过M作MN⊥BD,垂足为N,作ME⊥BC于E,分两种情况:第一种情况:如图5.∵四边形ABCD是菱形,∠ABC=120°,∴∠CBD=60°,∴∠NBE=60°.∵点M与BD所在的直线的距离为1,∴MN=1,∴BD为⊙M的切线.∵BC是⊙M的切线,∴∠MBE=30°.∵ME=1,∴EB=3,∴3t+3=2t+6,t=6﹣3;第二种情况:如图6.∵四边形ABCD是菱形,∠ABC=120°,∴∠DBC=60°,∴∠NBE=120°.∵点M与BD所在的直线的距离为1,∴MN=1,∴BD为⊙M的切线.∵BC是⊙M的切线,∴∠MBE=60°.∵ME=MN=1,∴Rt△BEM中,tan60°=MEBE,EB=160tan︒=33,∴3t=2t+6+3,t=6+3;综上所述:当点M与BD所在的直线的距离为1时,t=6﹣3或6+3.点睛:本题是四边形和圆的综合题,考查了菱形的性质、圆的切线的性质和判定、特殊的三角函数值、等腰直角三角形的性质、动点运动问题,此类问题比较复杂,弄清动点运动方向、速度、时间和路程的关系,并与方程相结合,找等量关系,求出时间t 的值.8.如图,△ABC 内接于⊙O ,AB 是直径,⊙O 的切线PC 交BA 的延长线于点P ,OF ∥BC 交AC 于点E ,交PC 于点F ,连结AF . (1)判断AF 与⊙O 的位置关系并说明理由; (2)若AC =24,AF =15,求sin B .【答案】(1) AF 与⊙O 相切 理由见解析;(2)35【解析】试题分析:(1)连接OC ,先证∠OCF =90°,再证明△OAF ≌△OCF ,得出∠OAF =∠OCF =90°即可;(2)先求出AE 、EF ,再证明△OAE ∽△AFE ,得出比例式OA AEAF EF=,可求出半径,进而求出直径,由三角函数的定义即可得出结论. 试题解析:解:(1)AF 与⊙O 相切.理由如下:连接OC .如图所示.∵PC 是⊙O 的切线,∴OC ⊥PC ,∴∠OCF =90°.∵OF ∥BC ,∴∠B =∠AOF ,∠OCB =∠COF .∵OB =OC ,∴∠B =∠OCB ,∴∠AOF =∠COF .在△OAF 和△OCF 中,∵OA =OC ,∠AOF =∠COF ,OF =OF ,∴△OAF ≌△OCF (SAS ),∴∠OAF =∠OCF =90°,∴AF 与⊙O 相切;(2)∵△OAF ≌△OCF ,∴∠OAE =∠COE ,∴OE ⊥AC ,AE =12AC =12,∴EF 2215129-=.∵∠OAF =90°,∴△OAE ∽△AFE ,∴OA AE AF EF =,即12159OA =,∴OA =20,∴AB =40,sin B =243405AC AB ==.点睛:本题考查了切线的性质与判定和全等三角形的判定与性质以及相似三角形的判定与性质;熟练掌握切线的证法和三角形相似是解题的关键.9.定义:数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.理解:⑴如图,已知是⊙上两点,请在圆上找出满足条件的点,使为“智慧三角形”(画出点的位置,保留作图痕迹);⑵如图,在正方形中,是的中点,是上一点,且,试判断是否为“智慧三角形”,并说明理由;运用:⑶如图,在平面直角坐标系中,⊙的半径为,点是直线上的一点,若在⊙上存在一点,使得为“智慧三角形”,当其面积取得最小值时,直接写出此时点的坐标.【答案】(1)详见解析;(2)详见解析;(3)P的坐标(223,13),(223,13).【解析】试题分析:(1)连结AO并且延长交圆于C1,连结BO并且延长交圆于C2,即可求解;(2)设正方形的边长为4a,表示出DF=CF以及EC、BE的长,然后根据勾股定理列式表示出AF2、EF2、AE2,再根据勾股定理逆定理判定△AEF是直角三角形,由直角三角形的性质可得△AEF为“智慧三角形”;(3)根据“智慧三角形”的定义可得△OPQ为直角三角形,根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,由垂线段最短可得斜边最短为3,根据勾股定理可求另一条直角边,再根据三角形面积可求斜边的高,即点P的横坐标,再根据勾股定理可求点P的纵坐标,从而求解.试题解析:(1)如图1所示:(2)△AEF是否为“智慧三角形”,理由如下:设正方形的边长为4a,∵E是DC的中点,∴DE=CE=2a,∵BC:FC=4:1,∴FC=a,BF=4a﹣a=3a,在Rt△ADE中,AE2=(4a)2+(2a)2=20a2,在Rt△ECF中,EF2=(2a)2+a2=5a2,在Rt△ABF中,AF2=(4a)2+(3a)2=25a2,∴AE2+EF2=AF2,∴△AEF是直角三角形,∵斜边AF上的中线等于AF的一半,∴△AEF为“智慧三角形”;(3)如图3所示:由“智慧三角形”的定义可得△OPQ为直角三角形,根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,由垂线段最短可得斜边最短为3,由勾股定理可得PQ=,PM=1×2÷3=,由勾股定理可求得OM=,故点P的坐标(﹣,),(,).考点:圆的综合题.10.如图,在直角坐标系中,⊙M经过原点O(0,0),点A(6,0)与点B(0,-2),点D在劣弧»OA上,连结BD交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;(2)求证:BD平分∠ABO;(3)在线段BD的延长线上找一点E,使得直线AE恰为⊙M的切线,求此时点E的坐标.【答案】(1)M的半径r2;(2)证明见解析;(3)点E的坐标为(2632).【解析】试题分析:根据点A和点B的坐标得出OA和OB的长度,根据Rt△AOB的勾股定理得出AB的长度,然后得出半径;根据同弧所对的圆周角得出∠ABD=∠COD,然后结合已知条件得出角平分线;根据角平分线得出△ABE≌△HBE,从而得出2,从而求出OH 的长度,即点E的纵坐标,根据Rt△AOB的三角函数得出∠ABO的度数,从而得出∠CBO 的度数,然后根据Rt△HBE得出HE的长度,即点E的横坐标.试题解析:(1)∵点A6,0),点B为(02)∴62∴根据Rt△AOB的勾股定理可得:2∴e M的半径r=122.(2)根据同弧所对的圆周角相等可得:∠ABD=∠COD ∵∠COD=∠CBO ∴∠ABD=∠CBO ∴BD平分∠ABO(3)如图,由(2)中的角平分线可得△ABE ≌△HBE ∴BH=BA=22∴OH=22-2=2在Rt △AOB 中,3OA OB=∴∠ABO=60° ∴∠CBO=30° 在Rt △HBE 中,HE=2633=∴点E 的坐标为(263,2)考点:勾股定理、角平分线的性质、圆的基本性质、三角函数.11.在平面直角坐标系中,已知点A (2,0),点B (0,),点O (0,0).△AOB 绕着O 顺时针旋转,得△A'OB',点A 、B 旋转后的对应点为A',B',记旋转角为α.(Ⅰ)如图1,A'B'恰好经过点A 时,求此时旋转角α的度数,并求出点B'的坐标; (Ⅱ)如图2,若0°<α<90°,设直线AA'和直线BB'交于点P ,求证:AA'⊥BB'; (Ⅲ)若0°<α<360°,求(Ⅱ)中的点P 纵坐标的最小值(直接写出结果即可).【答案】(Ⅰ)α=60°,B'(3,);(Ⅱ)见解析;(Ⅲ)点P 纵坐标的最小值为﹣2.【解析】【分析】(Ⅰ)作辅助线,先根据点A (2,0),点B (0,),确定∠ABO =30°,证明△AOA'是等边三角形,得旋转角α=60°,证明△COB'是30°的直角三角形,可得B'的坐标;(Ⅱ)依据旋转的性质可得∠BOB'=∠AOA'=α,OB =OB',OA =OA',即可得出∠OBB'=∠OA'A =(180°﹣α),再根据∠BOA'=90°+α,四边形OBPA'的内角和为360°,即可得到∠BPA'=90°,即AA'⊥BB';(Ⅲ)作AB的中点M(1,),连接MP,依据点P的轨迹为以点M为圆心,以MP=AB=2为半径的圆,即可得到当PM∥y轴时,点P纵坐标的最小值为﹣2.【详解】解:(Ⅰ)如图1,过B'作B'C⊥x轴于C,∵OA =2,OB=2,∠AOB=90°,∴∠ABO=30°,∠BAO=60°,由旋转得:OA=OA',∠A'=∠BAO=60°,∴△OAA'是等边三角形,∴α=∠AOA'=60°,∵OB=OB'=2,∠COB'=90°﹣60°=30°,∴B'C=OB’=,∴OC=3,∴B'(3,),(Ⅱ)证明:如图2,∵∠BOB'=∠AOA'=α,OB=OB',OA=OA',∴∠OBB'=∠OA'A=(180°﹣α),∵∠BOA'=90°+α,四边形OBPA'的内角和为360°,∴∠BPA'=360°﹣(180°﹣α)﹣(90°+α)=90°,即AA'⊥BB';(Ⅲ)点P纵坐标的最小值为-2.理由是:如图,作AB的中点M(1,),连接MP,∵∠APB=90°,∴点P的轨迹为以点M为圆心,以MP=AB=2为半径的圆,除去点(2,2),∴当PM⊥x轴时,点P纵坐标的最小值为﹣2.【点睛】本题属于几何变换综合题,主要考查了旋转的性质,含30°角的直角三角形的性质,四边形内角和以及圆周角定理的综合运用,解决问题的关键是判断点P的轨迹为以点M为圆心,以MP 为半径的圆.12.如图,线段BC所在的直线是以AB为直径的圆的切线,点D为圆上一点,满足BD=BC,且点C、D位于直径AB的两侧,连接CD交圆于点E. 点F是BD上一点,连接EF,分别交AB、BD于点G、H,且EF=BD.(1)求证:EF∥BC;(2)若EH=4,HF=2,求»BE的长.【答案】(1)见解析;(2) 233【解析】【分析】(1)根据EF=BD可得»EF=»BD,进而得到»»BE DF=,根据“在同圆或等圆中,同弧或等弧所对的圆周角相等”即可得出角相等进而可证.(2)连接DF,根据切线的性质及垂径定理求出GF、GE的长,根据“在同圆或等圆中,同弧或等弧所对的圆周角相等”及平行线求出相等的角,利用锐角三角函数求出∠BHG,进而求出∠BDE的度数,确定»BE所对的圆心角的度数,根据∠DFH=90°确定DE为直径,代入弧长公式即可求解.【详解】(1)∵EF=BD,∴»EF=»BD∴»»BE DF=∴∠D=∠DEF又BD=BC,∴∠D=∠C,∴∠DEF=∠CEF∥BC(2)∵AB是直径,BC为切线,∴AB⊥BC又EF∥BC,∴AB⊥EF,弧BF=弧BE,GF=GE=12(HF+EH)=3,HG=1DB平分∠EDF,又BF∥CD,∴∠FBD=∠FDB=∠BDE=∠BFH ∴HB=HF=2∴cos∠BHG=HGHB =12,∠BHG=60°.∴∠FDB=∠BDE=30°∴∠DFH=90°,DE为直径,DE=3BE所对圆心角=60°.∴弧BE=163π=233π【点睛】本题是圆的综合题,主要考查圆周角、切线、垂径定理、弧长公式等相关知识,掌握圆周角的有关定理,切线的性质,垂径定理及弧长公式是解题关键.13.已知四边形ABCD 是⊙O 的内接四边形,∠DAB =120°,BC =CD ,AD =4,AC =7,求AB 的长度.【答案】AB =3.【解析】【分析】 作DE ⊥AC ,BF ⊥AC ,根据弦、弧、圆周角、圆心角的关系,求得BC CD =u u u r u u u r ,进而得到∠DAC =∠CAB =60°,在Rt △ADE 中,根据60°锐角三角函数值,可求得DE =23,AE =2,再由Rt △DEC 中,根据勾股定理求出DC 的长,在△BFC 和△ABF 中,利用60°角的锐角三角函数值及勾股定理求出AF 的长,然后根据求出的两个结果,由AB =2AF ,分类讨论求出AB 的长即可.【详解】作DE ⊥AC ,BF ⊥AC ,∵BC =CD ,∴BC CD =u u u r u u u r ,∴∠CAB =∠DAC ,∵∠DAB =120°,∴∠DAC =∠CAB =60°,∵DE ⊥AC ,∴∠DEA =∠DEC =90°,∴sin60°=4DE ,cos60°=4AE , ∴DE =3AE =2,∵AC =7,∴CE =5,∴DC= ∴BC ,∵BF ⊥AC ,∴∠BFA =∠BFC =90°,∴tan60°=BF AF,BF 2+CF 2=BC 2, ∴BF,∴()2227AF +-=, ∴AF =2或AF =32, ∵cos60°=AF AB, ∴AB =2AF ,当AF =2时,AB =2AF =4,∴AB =AD ,∵DC =BC ,AC =AC ,∴△ADC ≌△ABC (SSS ),∴∠ADC =∠ABC ,∵ABCD 是圆内接四边形,∴∠ADC+∠ABC =180°,∴∠ADC =∠ABC =90°,但AC 2=49,2222453AD DC +=+=,AC 2≠AD 2+DC 2,∴AB =4(不合题意,舍去), 当AF =32时,AB =2AF =3, ∴AB =3.【点睛】 此题主要考查了圆的相关性质和直角三角形的性质,解题关键是构造直角三角形模型,利用直角三角形的性质解题.14.如图所示,ABC ∆内接于圆O ,CD AB ⊥于D ;(1)如图1,当AB 为直径,求证:OBC ACD ∠=∠;(2)如图2,当AB 为非直径的弦,连接OB ,则(1)的结论是否成立?若成立请证明,不成立说明由;(3)如图3,在(2)的条件下,作AE BC ⊥于E ,交CD 于点F ,连接ED ,且2AD BD ED =+,若3DE =,5OB =,求CF 的长度.【答案】(1)见解析;(2)成立;(3)145【解析】【分析】 (1)根据圆周角定理求出∠ACB=90°,求出∠ADC=90°,再根据三角形内角和定理求出即可; (2)根据圆周角定理求出∠BOC=2∠A ,求出∠OBC=90°-∠A 和∠ACD=90°-∠A 即可; (3)分别延长AE 、CD 交⊙O 于H 、K ,连接HK 、CH 、AK ,在AD 上取DG=BD ,延长CG 交AK 于M ,延长KO 交⊙O 于N ,连接CN 、AN ,求出关于a 的方程,再求出a 即可.【详解】(1)证明:∵AB 为直径,∴ACB 90∠=︒, ∵CD AB ⊥于D , ∴ADC 90∠=︒,∴OBC A 90∠∠+=︒,A ACD 90∠∠+=︒,∴OBC ACD ∠∠=;(2)成立,证明:连接OC ,由圆周角定理得:BOC 2A ∠∠=,∵OC OB =,∴()()11OBC 180BOC 1802A 90A 22∠∠∠∠=︒-=︒-=︒-, ∵ADC 90∠=︒,∴ACD 90A ∠∠=︒-,∴OBC ACD ∠∠=; (3)分别延长AE 、CD 交⊙O 于H 、K ,连接HK 、CH 、AK ,∵AE BC ⊥,CD BA ⊥,∴AEC ADC 90∠∠==︒,∴BCD CFE 90∠∠+=︒,BAH DFA 90∠∠+=︒,∵CFE DFA ∠∠=,∴BCD BAH ∠∠=,∵根据圆周角定理得:BAH BCH ∠∠=,∴BCD BAH BCH ∠∠∠==,∴由三角形内角和定理得:CHE CFE ∠∠=, ∴CH CF =,∴EH EF =,同理DF DK =,∵DE 3=,∴HK 2DE 6==,在AD 上取DG BD =,延长CG 交AK 于M ,则AG AD BD 2DE 6=-==, BC GC =,∴MCK BCK BAK ∠∠∠==,∴CMK 90∠=︒,延长KO 交⊙O 于N ,连接CN 、AN ,则NAK 90CMK ∠∠=︒=,∴CM //AN ,∵NCK ADK 90∠∠==︒,∴CN //AG ,∴四边形CGAN 是平行四边形,∴AG CN 6==,作OT CK ⊥于T ,则T 为CK 的中点,∵O 为KN 的中点,∴1OT CN 32==, ∵OTC 90∠=︒,OC 5=,∴由勾股定理得:CT 4=,∴CK 2CT 8==,作直径HS ,连接KS ,∵HK 6=,HS 10=,∴由勾股定理得:KS 8=, ∴3tan HSK tan HAK 4∠∠==, ∴1tan EAB tan BCD 3∠∠==, 设BD a =,CD 3a =, ∴AD BD 2ED a 6=+=+,11DK AD a 233==+, ∵CD DK CK +=, ∴13a a 283++=, 解得:9a 5=, ∴113DK a 235=+=, ∴2614CF CK 2DK 855=-=-=. 【点睛】本题考查了垂径定理、解直角三角形、等腰三角形的性质、圆周角定理、勾股定理等知识点,能综合运用知识点进行推理是解此题的关键,综合性比较强,难度偏大.15.对于平面内的⊙C 和⊙C 外一点Q ,给出如下定义:若过点Q 的直线与⊙C 存在公共点,记为点A ,B ,设AQ BQ k CQ+=,则称点A (或点B )是⊙C 的“K 相关依附点”,特别地,当点A 和点B 重合时,规定AQ=BQ ,2AQ k CQ =(或2BQ CQ ). 已知在平面直角坐标系xoy 中,Q(-1,0),C(1,0),⊙C 的半径为r .(1)如图1,当r =①若A 1(0,1)是⊙C 的“k 相关依附点”,求k 的值.②A 2,0)是否为⊙C 的“2相关依附点”.(2)若⊙C 上存在“k 相关依附点”点M ,①当r=1,直线QM 与⊙C 相切时,求k 的值.②当3k =时,求r 的取值范围.(3)若存在r 的值使得直线3y x b =-+与⊙C 有公共点,且公共点时⊙C 的“3相关依附点”,直接写出b 的取值范围.【答案】(1)2.②是;(2)①3k =②r 的取值范围是12r <≤;(3)333b -<. 【解析】【分析】(1)①如图1中,连接AC 、1QA .首先证明1QA 是切线,根据2AQ k CQ =计算即可解决问题;②根据定义求出k 的值即可判断;(2)①如图,当1r =时,不妨设直线QM 与C e 相切的切点M 在x 轴上方(切点M 在x 轴下方时同理),连接CM ,则QM CM ⊥,根据定义计算即可;②如图3中,若直线QM 与C e 不相切,设直线QM 与C e 的另一个交点为N (不妨设QN QM <,点N ,M 在x 轴下方时同理),作CD QM ⊥于点D ,则MD ND =,可得()222MQ NQ MN NQ NQ ND NQ DQ +=++=+=,2CQ =,推出2MQ NQ DQ k DQ CQ CQ +===,可得当3k =3DQ =221CD CQ DQ -=,假设C e 经过点Q ,此时2r =,因为点Q 早C e 外,推出r 的取值范围是12r <…; (3)如图4中,由(2)可知:当3k =12r <….当2r =时,C e 经过点(1,0)Q -或(3,0)E ,当直线3y x b =-+经过点Q 时,3b =3y x b =-+经过点E 时,33b =,即可推出满足条件的b 的取值范围为333b -<<.【详解】(1)①如图1中,连接AC 、1QA .由题意:1OC OQ OA ==,∴△1QA C 是直角三角形,190CA Q ∴∠=︒,即11CA QA ⊥,1QA ∴是C e 的切线,122222QA k QC ∴===. ②Q 2(12,0)A +在C e 上,2212122k -+++∴==,2A ∴是C e 的“2相关依附点”.故答案为:2,是; (2)①如图2,当1r =时,不妨设直线QM 与C e 相切的切点M 在x 轴上方(切点M 在x 轴下方时同理),连接CM ,则QM CM ⊥.(1,0)Q -Q ,(1,0)C ,1r =,2CQ ∴=,1CM =,∴3MQ =,此时23MQ k CQ==; ②如图3中,若直线QM 与C e 不相切,设直线QM 与C e 的另一个交点为N (不妨设QN QM <,点N ,M 在x 轴下方时同理),作CD QM ⊥于点D ,则MD ND =,()222MQ NQ MN NQ NQ ND NQ DQ ∴+=++=+=,2CQ =Q ,∴2MQ NQ DQ k DQ CQ CQ +===,∴当3k =时,3DQ =,此时221CD CQ DQ =-=,假设C e 经过点Q ,此时2r =,Q 点Q 早C e 外,r ∴的取值范围是12r <….(3)如图4中,由(2)可知:当3k =12r <….当2r =时,C e 经过点(1,0)Q -或(3,0)E ,当直线3y x b =+经过点Q 时,3b =3y x b =-+经过点E 时,33b =,∴满足条件的b 的取值范围为333b -<.【点睛】本题考查了一次函数综合题、圆的有关知识、勾股定理、切线的判定和性质、点A (或点)B 是C e 的“k 相关依附点”的定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会考虑特殊位置解决问题,属于中考压轴题.。
2021年全国中考数学真题分类汇编 圆:与圆的有关性质(老师版)
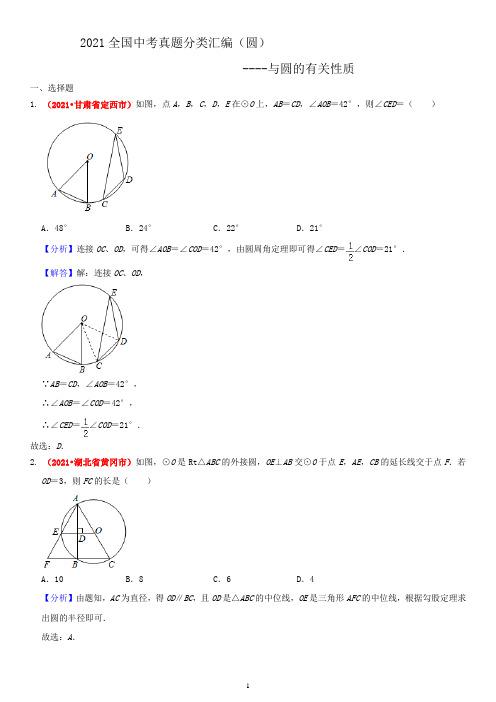
2021全国中考真题分类汇编(圆)----与圆的有关性质一、选择题1.(2021•甘肃省定西市)如图,点A,B,C,D,E在⊙O上,AB=CD,∠AOB=42°,则∠CED=()A.48°B.24°C.22°D.21°【分析】连接OC、OD,可得∠AOB=∠COD=42°,由圆周角定理即可得∠CED=∠COD=21°.【解答】解:连接OC、OD,∵AB=CD,∠AOB=42°,∴∠AOB=∠COD=42°,∴∠CED=∠COD=21°.故选:D.2.(2021•湖北省黄冈市)如图,⊙O是Rt△ABC的外接圆,OE⊥AB交⊙O于点E,AE,CB的延长线交于点F.若OD=3,则FC的长是()A.10 B.8 C.6 D.4【分析】由题知,AC为直径,得OD∥BC,且OD是△ABC的中位线,OE是三角形AFC的中位线,根据勾股定理求出圆的半径即可.3. (2021•湖北省武汉市)如图,AB 是⊙O 的直径,BC 是⊙O 的弦,先将BC 沿BC 翻折交AB 于点D .再将BD 沿AB 翻折交BC 于点E .若BE =DE ,设∠ABC =α,则α所在的范围是( )A .21.9°<α<22.3°B .22.3°<α<22.7°C .22.7°<α<23.1°D .23.1°<α<23.5°故选:B .4. (2021•湖南省邵阳市)如图,点A ,B ,C 是⊙O 上的三点.若∠AOC =90°,∠BAC =30°,则∠AOB 的大小为( )A .25°B .30°C .35°D .40°故选:B .5. (2021•长沙市)如图,点A ,B ,C 在⊙O 上,54BAC ∠=︒,则BOC ∠的度数为( )A. 27︒B. 108︒C. 116︒D. 128︒ 【答案】B6.(2021•江苏省连云港)如图,正方形ABCD内接于O,线段MN在对角线BD上运动,若O的面积为2π,MN ,则AMN周长的最小值是()1A. 3B. 4C. 5D. 6【答案】B7.(2021•山东省聊城市)如图,A,B,C是半径为1的⊙O上的三个点,若AB=2,∠CAB=30°,则∠ABC的度数为()A. 95°B. 100°C. 105°D. 110°【答案】C8.(2021•山东省泰安市)如图,四边形ABCD是⊙O的内接四边形,∠B=90°,∠BCD=120°,AB=2,CD=1,则AD的长为()A.2﹣2 B.3﹣C.4﹣D.2故选:C.9.(2021•湖北省宜昌市)如图,C,D是⊙O上直径AB两侧的两点,设∠ABC=25°,则∠BDC=()A.85°B.75°C.70°D.65°故选:D.10.(2021•广东省)如题7图,AB是O的直径,点C为圆上一点,3CD=,AC=,ABC∠的平分线交AC于点D,1则O的直径为()A.3B.23C.1D.2【答案】B11.(2021•湖北省荆州市)如图,矩形OABC的边OA,OC分别在x轴、y轴的正半轴上,点D在OA的延长线上,若A(2,0),D(4,0),以O为圆心、OD长为半径的弧经过点B,交y轴正半轴于点E,连接DE,BE,则∠BED 的度数是()A.15°B.22.5°C.30°D.45°故选:C.12.(2021•四川省凉山州)点P是O内一点,过点P的最长弦的长为10cm,最短弦的长为6cm,则OP的长为()A. 3cmB. 4cmC. 5cmD. 6cm【答案】B13. (2021•泸州市)在锐角ABC 中,∠A ,∠B ,∠C 所对的边分别为a ,b ,c ,有以下结论:2sinA sinB sinC a c b R ===(其中R 为ABC 的外接圆半径)成立.在ABC 中,若∠A =75°,∠B =45°,c =4,则ABC 的外接圆面积为( )A. 163πB. 643πC. 16πD. 64π【答案】A14. (2021•四川省眉山市)如图,在以AB 为直径的⊙O 中,点C 为圆上的一点,=3,弦CD ⊥AB 于点E ,弦AF 交CE 于点H ,交BC 于点G .若点H 是AG 的中点,则∠CBF 的度数为( )A .18°B .21°C .22.5°D .30°故选:C .15. (2021•四川省南充市)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,CD =2OE ,则∠BCD 的度数为( )A .15°B .22.5°C .30°D .45°故选:B .16. (2021•青海省)如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A ,B 两点,他测得“图上”圆的半径为10厘米,AB =16厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( )17. (2021•四川省自贡市) 如图,AB 为⊙O 的直径,弦CD AB ⊥于点F ,OE AC ⊥于点E ,若3OE =,5OB =,则CD 的长度是( )A. 9.6B. 45C. 53D. 19【答案】A 18. (2021•浙江省金华市)如图,在Rt △ABC 中,∠ACB =90°,以该三角形的三条边为边向形外作正方形,正方形的顶点E ,F ,G ,H ,M ,N 都在同一个圆上.记该圆面积为S 1,△ABC 面积为S 2,则的值是( )A .B .3πC .5πD .故选:C .19. (2021•浙江省丽水市) 如图,AB 是O 的直径,弦CD OA ⊥于点E ,连结,OC OD .若O 的半径为,m AOD α∠=∠,则下列结论一定成立的是( )A. tan OE m α=⋅B. 2sin CD m α=⋅C. cos AE m α=⋅D. 2sin COD S m α=⋅【答案】B20. 2021•浙江省绍兴市)如图,正方形ABCD 内接于⊙O ,点P 在上( )A .30°B .45°C .60°D .90°故选:B .21. 2021•重庆市B )如图,AB 是⊙O 的直径,AC ,BC 是⊙O 的弦,若∠A =20°,则∠B 的度数为( )A .70°B .90°C .40°D .60°故选:A . 22. (2021•重庆市A )如图,四边形ABCD 内接于☉O ,若∠A =80°,则∠C 的度数是( )A. 80°B. 100°C. 110°D. 120°【答案】B 23. (2021•湖北省十堰市)如图,ABC 内接于,120,,O BAC AB AC BD ∠=︒=是O 的直径,若3AD =,则BC =( ) A. 23 B. 33 C. 3 D. 424. (2021•海南省)如图,四边形ABCD 是⊙O 的内接四边形,BE 是⊙O 的直径,连接AE .若∠BCD =2∠BAD ,则∠DAE 的度数是( )A .30°B .35°C .45°D .60°25. (2021•广西玉林市) 学习圆的性质后,小铭与小熹就讨论起来,小铭说:“被直径平分的弦也与直径垂直”,小熹说:“用反例就能说明这是假命题” .下列判断正确的是( )A. 两人说的都对B. 小铭说的对,小燕说的反例不存在C. 两人说的都不对D. 小铭说的不对,小熹说的反例存在【答案】D26.(2021•吉林省)如图,四边形ABCD 内接于⊙O ,点P 为边AD 上任意一点(点P 不与点A ,D 重合)连接CP .若∠B =120°,则∠APC 的度数可能为( )A .30°B .45°C .50°D .65°27. (2021•湖北省黄石市)如图,A 、B 是O 上的两点,60AOB ∠=︒,OF AB ⊥交O 于点F ,则BAF∠等于( )A. 20︒B. 22.5︒C. 15︒D. 12.5︒ 【答案】C二.填空题1.(2021·安徽省) 如图,圆O 的半径为1,ABC 内接于圆O .若60A ∠=︒,75B ∠=︒,则AB =______.【答案】22. (2021•黑龙江省龙东地区)如图,在O 中,AB 是直径,弦AC 的长为5cm ,点D 在圆上,且30ADC ∠=︒,则O 的半径为_____.【答案】5cm3. (2021•湖南省常德市)如图,四边形ABCD 是⊙O 的内接四边形,若∠BOD=80°,则∠BCD 的度数是_____.【答案】140°.4. (2021•长沙市) 如图,在⊙O 中,弦AB 的长为4,圆心O 到弦AB 的距离为2,则AOC ∠的度数为______.【答案】45︒5. (2021•江苏省连云港)如图,OA 、OB 是O 的半径,点C 在O 上,30AOB ∠=︒,40OBC ∠=︒,则OAC ∠=______︒.【答案】256. (2021•江苏省南京市)如图,AB 是O 的弦,C 是AB 的中点,OC 交AB 于点D .若8cm,2cm AB CD ==,则O 的半径为________cm .【答案】57. (2021•湖北省随州市)如图,O 是ABC 的外接圆,连接AO 并延长交O 于点D ,若50C ∠=︒,则BAD ∠的度数为______.8. (2021•四川省成都市)如图,在平面直角坐标系xOy 中,直线y =x +与⊙O 相交于A ,B 两点,且点A在x 轴上,则弦AB 的长为 2 .9. (2021•湖南省娄底市)弧度是表示角度大小的一种单位,圆心角所对的弧长和半径相等时,这个角就是1弧度角,记作1rad .已知1rad,60αβ==︒,则α与β的大小关系是α________β.【答案】<10.(2021•江苏省盐城市)如图,在⊙O 内接四边形ABCD 中,若∠ABC =100°,则∠ADC = 80 °.11. (2021•湖南省张家界市)如图,ABC ∆内接于⊙O ,︒=∠50A ,点D 是BC 的中点,连接OD ,OB ,OC ,则=∠BOD . 5012. (2021•宿迁市) 如图,在Rt△ABC 中,∠ABC =90°,∠A =32°,点B 、C 在O 上,边AB 、AC 分别交O 于D 、E 两点﹐点B 是CD 的中点,则∠ABE =__________.【答案】13︒D O B C三、解答题1.(2021·安徽省)如图,圆O 中两条互相垂直的弦AB ,CD 交于点E .(1)M 是CD 的中点,OM =3,CD =12,求圆O 的半径长;(2)点F 在CD 上,且CE =EF ,求证:AF BD ⊥.【答案】(1)35;(2)见解析.【解析】【分析】(1)根据M 是CD 的中点,OM 与圆O 直径共线可得OM CD ⊥,OM 平分 CD ,则有6M C =,利用勾股定理可求得半径的长;(2)连接AC ,延长AF 交BD 于G ,根据CE EF =,AE FC ⊥,可得AF AC =,12∠=∠,利用圆周角定理可得2D ∠=∠,可得1D ∠=∠,利用直角三角形的两锐角互余,可证得90AGB ∠=︒,即有AF BD ⊥.【详解】(1)解:连接OC ,∵M 是CD 的中点,OM 与圆O 直径共线∴OM CD ⊥,OM 平分CD ,90OMC ∴∠=︒12CD =6MC ∴=.在Rt OMC △中.22OC MC OM +2263=+35=∴圆O 的半径为35(2)证明:连接AC ,延长AF 交BD 于G .CE EF =,AE FC ⊥AF AC ∴=又CE EF =12∠∠∴=BC BC=∴∠=∠2D∴∠=∠1D在Rt BED中90∠+∠=︒D B∴∠+∠=︒190B∴∠=︒AGB90∴⊥AF BD2.(2021•甘肃省定西市)在《阿基米德全集》中的《引理集》中记录了古希腊数学家阿基米德提出的有关圆的一个引理.如图,已知,C是弦AB上一点,请你根据以下步骤完成这个引理的作图过程.(1)尺规作图(保留作图痕迹,不写作法);①作线段AC的垂直平分线DE,分别交于点D,AC于点E,连接AD,CD;②以点D为圆心,DA长为半径作弧,交于点F(F,A两点不重合),连接DF,BD,BF.(2)直接写出引理的结论:线段BC,BF的数量关系.【分析】(1)①根据要求作出图形即可.②根据要求作出图形即可.(2)证明△DFB≌△DCB可得结论.【解答】解:(1)①如图,直线DE,线段AD,线段CD即为所求.②如图,点F,线段CD,BD,BF即为所求作.(2)结论:BF=BC.理由:∵DE 垂直平分线段AC ,∴DA =DC ,∴∠DAC =∠DCA ,∵AD =DF ,∴DF =DC ,=,∴∠DBC =∠DBF ,∵∠DFB +∠DAC =180°.∠DCB +∠DCA =180°,∴∠DFB =∠DCB ,在△DFB 和△DCB 中,,∴△DFB ≌△DCB (AAS ),∴BF =BC .3. (2021•长沙市)如图,点O 为以AB 为直径的半圆的圆心,点M ,N 在直径AB 上,点P ,Q 在AB 上,四边形MNPQ 为正方形,点C 在QP 上运动(点C 与点P ,Q 不重合),连接BC 并延长交MQ 的延长线于点D ,连接AC 交MQ 于点E ,连接OQ .(1)求sin AOQ ∠的值;(2)求AMMN 值;(3)令ME x =,QD y =,直径2AB R =(0R >,R 是常数),求y 关于x 的函数解析式,并指明自变量x 的取值范围.【答案】(125;(251-;(3)242535525()5R y R x x -=<<.4. (2021•江苏省苏州市)如图,四边形ABCD 内接于⊙O ,∠1=∠2,使得CE =AB ,连接ED .(1)求证:BD=ED;(2)若AB=4,BC=6,∠ABC=60°【分析】(1)根据圆内接四边形的性质得到∠A=∠DCE,证明△ABD≌△DCE,根据全等三角形的性质证明结论;(2)过点D作DM⊥BE于M,根据等腰三角形的性质求出BM,进而求出CM,根据正切的定义求出DM,根据正切的定义计算,得到答案.【解答】(1)证明:∵四边形ABCD内接于⊙O,∴∠A=∠DCE,∵∠1=∠2,∴=,∴AD=DC,在△ABD和△DCE中,,∴△ABD≌△DCE(SAS),∴BD=ED;(2)解:过点D作DM⊥BE于M,∵AB=6,BC=6,∴BE=BC+EC=10,∵BD=ED,DM⊥BE,∴BM=ME=BE=5,∴CM=BC﹣BM=1,∵∠ABC=60°,∠8=∠2,∴∠2=30°,∴DM=BM•tan∠7=5×=,∴tan ∠DCB ==.5. (2021•绥化市)如图,在ABC 中,AB AC =,以AB 为直径的O 与BC 相交于点,D DE AC ⊥,垂足为E .(1)求证:DE 是O 的切线;(2)若弦MN 垂直于AB ,垂足为1,,34AG G MN AB ==O 的半径; (3)在(2)的条件下,当36BAC ∠=︒时,求线段CE 的长.【答案】(1)见解析;(2)O 的半径为1;(3)354CE =. 【解析】【分析】(1)连接OD ,由题意可得∠B =∠C ,由半径OB 和OD 可得∠B =∠ODB ,从而∠C =∠ODB ,在Rt △DEC 中可知∠C +∠CDE =90°,则∠OBD +∠CDE =90°,从而得出∠ODE =90°,即可得证DE 是O 的切线;(2)连接OD ,过点D 作DG ⊥AB ,垂足为G ,设AC 与O 交于点H ,连接OH ,分别求解S △OAH ,S 扇形OAH ,S △OBD ,S 扇形O OD ,然后根据S 阴影= S 扇形OAH + S 扇形OBD – S △OAH –S △OBD 求解即可得到阴影部分的面积.【详解】(1)证明:方法一:连接,AD ODAB为直径∴∠=︒ADB90∴⊥AD BCAB AC=,∴为BC中点DO为AB中点OD AC∴∥⊥DE AC∴⊥DE ODOD是O的半径∴是O的切线DE方法二:连接OD=OB OD∴∠=∠OBD ODB⊥DE AC∴∠+∠=︒EDC C90=AB AC∴∠=∠ABC C∴∠=∠ODB C90∴∠+∠=︒EDC ODBODE∴∠=︒.90∴⊥OD DEOD是O的半径∴是O的切线DE方法三:连接ODOB OD =OBD ODB ∴∠=∠AB AC =ABC ACB ∴∠=∠ODB ACB ∴∠=∠OD AC ∴∥DE AC ⊥DE OD ∴⊥ OD 是O 的半径DE ∴是O 的切线(2)解:方法一:连接OM ,MN AB ⊥90OGM ∴∠=︒AB 是直径MN =MG NG =∴= 14AG AB =13AG GB ∴=12AG OG OM ∴== 在Rt MGO 中222222()2OM OG MG OM OM ∴+=+= 1OM ∴=即O 的半径为1方法二:连接AM MB 、 AB 是O 的直径90AMB ∴∠=︒MN AB ⊥90AMG MAG AMG BMG ∴∠+∠=∠+∠=︒ MAG BMG ∴∠=∠AMG MBG ∴∽ MG AG BG MG =∴2MG AG BG =∴⨯:1:4AG AB =:1:3AG BG ∴=12AO BO AB ==G ∴为OA 中点3MN AB MN ⊥=32MG ∴=2MG AG BG =⨯12AG ∴=1AO ∴=即O 的半径为1(3)作ABC ∠的平分线BF 交AC 于F 连接AD 36BAC AB AC ∠=︒=72ABC ACB ∴∠=∠=︒ BF 平分ABC ∠36ABF CBP ∴∠=∠=︒72BFC ∴∠=︒即,BAF ABF BFC ACB ∠=∠∠=∠ BC BF AF ∴==CBF BAC C C ∠=∠∠=∠CBF CAB ∴∽2BC CF AC ∴=⋅设BC x = 则AF x =2CF x ∴=-()222x x ∴=- 解得:51x =±-51BC ∴=-AB ∴是O 的直径90ADB ∴∠=︒AB AC =12CD BD BC ∴== 512CD -∴= DE AC AD BC ⊥⊥90ADC DEC C C ∴∠=∠=︒∠=∠CDE CAD ∴∽△△2CD CE AC ∴=⋅2251()35224CD CE AC --∴=== 6. (2021•山东省临沂市)如图,已知在⊙O 中,==,OC 与AD 相交于点E .求证:(1)AD ∥BC ;(2)四边形BCDE 为菱形.【分析】(1)连接BD ,根据圆周角定理可得∠ADBADB =∠CBDCBD ,根据平行线的判定可得结论;(2)证明△DEFDEF ≌△BCFBCF ,得到DE =BCDE =BC ,证明四边形BCDEBCDE 为平行四边形,再根据得到BCC =CDCD ,从而证明菱形.【解答】解:(1)连接BD ,∵,∴∠ADBADB =∠CBD ,∴ADAD ∥BCBC ;(2)连接CD,∵ADAD∥BBC,∴∠EDFEDF=∠CBFCB,∵,∴BCC=CDCD,∴BFBF=DF,又∠DFE=∠BFBFC,∴△DEFDEF≌△BCF(ASAa),∴DE=BCDE=BC,∴四边形BCDEBCDE是平行四边形,又BCBC=CD,∴四边形BCDEBCDE是菱形.7.(2021•山东省泰安市))如图1,O为半圆的圆心,C、D为半圆上的两点,且=.连接AC并延长,与BD的延长线相交于点E.(1)求证:CD=ED;(2)AD与OC,BC分别交于点F,H.①若CF=CH,如图2,求证:CF•AF=FO•AH;②若圆的半径为2,BD=1,如图3,求AC的值.【分析】(1)如图1中,连接BC.想办法证明∠E=∠DCE即可。
湖北省,2020~2021年中考数学压轴题精选解析

湖北省,2020~2021年中考数学压轴题精选解析湖北省中考数学压轴题精选~~第1题~~(2020潜江.中考模拟) 如图1,已知抛物线C:与x轴的正半轴交于点A,点B为抛物线的顶点,直线l:是一条动直线.(1)求点A、点B的坐标;(2)当直线l经过点A时,求出直线l的解析式,并直接写出此时当时,自变量x的取值范围;(3)如图2,将抛物线C在x轴上方的部分沿x轴翻折,与C在x轴下方的图形组合成一个新的图形C,当直线l与组合图形C有且只有两个交点时,直接写出k的取值范围.~~第2题~~(2020湖北.中考模拟)如图,已知抛物线y=ax+bx+c(a≠0)的对称轴是,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.(1)求抛物线和直线l的解析式;(2)点P是直线AC上方的抛物线上一个动点,过点P作PD⊥x轴于点D,交AC于点E,过点P作PF⊥AC,垂足为F,当△PEF≌△AED时,求出点P的坐标;(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,直接写出所有满足条件的Q点的坐标;若不存在,请说明理由.~~第3题~~(2020天门.中考真卷) 小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟.在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图1表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图2中线段表示小华和商店的距离(米)与时间t(分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题:1112 22(1)填空:妈妈骑车的速度是________米/分钟,妈妈在家装载货物所用时间是________分钟,点M的坐标是____ ____;(2)直接写出妈妈和商店的距离(米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;(3)求t为何值时,两人相距360米.~~第4题~~(2020湖北.中考真卷) 如图,抛物线经过点,顶点为B,对称轴与x轴相交于点A,D为线段的中点.(1)求抛物线的解析式;(2) P为线段上任意一点,M为x轴上一动点,连接,以点M为中心,将逆时针旋转,记点P的对应点为E,点C的对应点为F.当直线与抛物线只有一个交点时,求点M的坐标.~~第5题~~(2019天门.中考模拟) 某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:(1)【操作发现】在等腰△ABC中,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列结论正确的是(填序号即可)①AF=AG= AB;②MD=ME;③整个图形是轴对称图形;④∠DAB=∠DMB.(2)【数学思考】在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD和ME具有怎样的数量和位置关系?请给出证明过程;(3)【类比探索】在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M 是BC的中点,连接MD和ME,试判断△MED的形状.答:~~第6题~~(2019湖北.中考真卷)如图,抛物线的图象经过点C(0,-2),顶点D 的坐标为(1,),与 轴交于A 、B 两点.(1) 求抛物线的解析式.(2) 连接AC ,E 为直线AC 上一点,当△AOC ∽△AEB 时,求点E 的坐标和的值.(3) 点F (0,)是轴上一动点,当为何值时,的值最小.并求出这个最小值.(4) 点C 关于轴的对称点为H ,当 取最小值时,在抛物线的对称轴上是否存在点Q ,使△QHF 是直角三角形?若存在,请求出点Q 的坐标;若不存在,请说明理由.~~第7题~~(2019潜江.中考真卷) 在平面直角坐标系中,已知抛物线C :y =ax +2x -1(a ≠0)和直线l :y =kx +b , 点A (-3,-3),B (1,-1)均在直线l 上.(1) 若抛物线C 与直线l 有交点,求a 的取值范围;(2) 当a =-1,二次函数y =ax +2x -1的自变量x 满足m ≤x ≤m +2时,函数y 的最大值为-4, 求m 的值;(3) 若抛物线C 与线段AB 有两个不同的交点,请直接写出a 的取值范围.~~第8题~~(2018湖北.中考模拟) 已知,抛物线y=ax +ax+b (a≠0)与直线y=2x+m 有一个公共点M (1,0),且a <b .(1) 求b 与a 的关系式和抛物线的顶点D 坐标(用a 的代数式表示);(2) 直线与抛物线的另外一个交点记为N ,求△DMN 的面积与a 的关系式;(3) a=﹣1时,直线y=﹣2x 与抛物线在第二象限交于点G ,点G 、H 关于原点对称,现将线段GH 沿y 轴向上平移t个单位(t >0),若线段GH 与抛物线有两个不同的公共点,试求t 的取值范围.~~第9题~~(2018潜江.中考模拟) 建立模型:(1) 如图 1,已知△ABC ,AC=BC ,∠C=90°,顶点C 在直线 l 上.操作:过点A 作AD ⊥l 于点D ,过点B 作BE ⊥l 于222点E ,求证△CAD ≌△BCE .模型应用:(2) 如图2,在直角坐标系中,直线l :y= x+8与y 轴交于点A ,与x 轴交于点B ,将直线l 绕着点A 顺时针旋转45°得到l . 求l 的函数表达式.(3) 如图3,在直角坐标系中,点B (10,8),作BA ⊥y 轴于点 A ,作BC ⊥x 轴于点C ,P 是线段BC 上的一个动点,点Q (a ,2a ﹣6)位于第一象限内.问点A 、P 、Q 能否构成以点Q 为直角顶点的等腰直角三角形,若能,请求出此时a 的值,若不能,请说明理由.~~第10题~~(2018潜江.中考模拟) 解不等式组,并将它的解集在数轴上表示出来.湖北省中考数学压轴题答案解析~~第1题~~答案:解析:~~第2题~~答案:1122解析:~~第3题~~答案:解析:~~第4题~~答案:解析:答案:解析:答案:解析:答案:解析:~~第8题~~答案:解析:答案:解析:答案:解析:。
2019年湖北省各市中考数学试题汇编(1)(含参考答案与解析)

第Ⅱ卷(非选择题共90分)
二、填空题(本大题共6个小题,每小题3分,共18分)
11.计算 的结果是.
12.武汉市某气象观测点记录了5天的平均气温(单位:℃),分别是25、20、18、23、27,这组数据的中位数是.
13.计算 ﹣ 的结果是.
(1)如图1,过点A画线段AF,使AF∥DC,且AF=DC.
(2)如图1,在边AB上画一点G,使∠AGD=∠BGC.
(3)如图2,过点E画线段EM,使EM∥AB,且EM=AB.
21.(8分)已知AB是⊙O的直径,AM和BN是⊙O的两条切线,DC与⊙O相切于点E,分别交AM、BN于D、C两点.
(1)如图1,求证:AB2=4AD•BC;
(2)如图2,连接OE并延长交AM于点F,连接CF.若∠ADE=2∠OFC,AD=1,求图中阴影部分的面积.
22.(10分)某商店销售一种商品,童威经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如表:
售价x(元/件)
50
60
80
A.0B.1C.2D.3
9.如图,AB是⊙O的直径,M、N是 (异于A、B)上两点,C是 上一动点,∠ACB的角平分线交⊙O于点D,∠BAC的平分线交CD于点E.当点C从点M运动到点N时,则C、E两点的运动路径长的比是( )
A. B. C. D.
10.观察等式:2+22=23﹣2;2+22+23=24﹣2;2+22+23+24=25﹣2…已知按一定规律排列的一组数:250、251、252、…、299、2100.若250=a,用含a的式子表示这组数的和是( )
2021年九级中考数学压轴题满分训练 –几何综合问题(圆的专题)(二)

2021年中考数学压轴题满分训练–几何综合问题(圆的专题)(二)1.如图,以△ABC的边AC为直径的⊙O恰好经过顶点B,∠ABC的平分线交⊙O于点D,过点D作⊙O的切线交BC的延长线于点E.(1)求证:DE∥AC;(2)若AB=8,BC=4,求DE的长.2.如图,⊙O经过Rt△ABC的顶点A,与BC相切于点D,交AC于E,交AB于F,连接AD,DE,DF,EF,∠C=90°.(1)求证:DE=DF.(2)若AE=3,CD=2,求BD的长.3.如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,连接AD,过点D 作⊙O的切线交AC于点E,交AB的延长线于点F.(1)求证:DE⊥AC.(2)如果⊙O的半径为5,cos∠DAB=,求BF的长.4.如图,在Rt△OAB中,∠AOB=90°,OA=OB=4,以点O为圆心、2为半径画圆,过点A作⊙O的切线,切点为P,连接OP.将OP绕点O按逆时针方向旋转到OH时,连接AH,BH.设旋转角为α(0°<α<360°).(1)当α=90°时,求证:BH是⊙O的切线;(2)当BH与⊙O相切时,求旋转角α和点H运动路径的长;(3)当△AHB面积最大时,请直接写出此时点H到AB的距离.5.如图,在⊙O中,AB是直径,AC是弦,AC=AD,连接CD交⊙O于点E,∠ACD =∠DAE.(1)求证:AD是⊙O的切线;(2)过点E作EF⊥AB于F,交AC于G,已知,EG=3.求AG的长;(3)在(2)的条件下,求△ACE的面积.6.如图,在▱ABCD中,AD=8,▱ABCD的面积是72,⊙O与▱ABCD的三条边分别相切于点D、E、F,交AD于点G,DG=3AG.(1)求⊙O的半径的长;(2)求阴影部分的面积(保留π).7.[提出问题]如图1,△ABC是圆O的内接三角形,且AB=AC,D是圆上一点,作AE⊥BD于E.要研究BE,DE,CD之间的关系.[特例分析](1)如图2,当△ABC是等边三角形时,且当D在∠ABC的平分线上时,假设DE=a,则DC=,BE=,BE,DE,CD之间的关系为.[猜想探究](2)在图1中,上述结论是否依然成立,请证明你的猜想.[结论应用](3)如图3,△ABC是等边三角形,∠CBD=15°,AC=,则△BCD的周长为.8.问题发现:(1)如图1,P是半径为2的⊙O上一点,直线m是⊙O外一直线,圆心O到直线m的距离为3,PQ⊥m于点Q,则PQ的最大值为;问题探究:(2)如图2,将两个含有30°角的直角三角板的60°角的顶点重合(其中∠A=∠A'=30°,∠C=∠C'=90°),绕点B旋转△C'A'B,当旋转至CC′=4时,求AA'的长;问题解决:(3)如图3,点O为等腰Rt△ABC的斜边AB的中点,AC=BC=5,OE=2,连接BE,作Rt△BEF,其中∠BEF=90°,tan∠EBF=,连接AF,求四边形ACBF的面积的最大值.9.如图,在△ABC中,AB=AC=2,∠BAC=120°,点D在AB上,AD=2,以点A为圆心,AD长为半径的弧交AC于点E,与BC交于点F,G,P是上一点.将AP绕点A逆时针旋转120°,得到AQ,连接CQ,AF.(1)若BP与所在圆相切,判断CQ与所在圆的位置关系.并加以证明;(2)求BF的长及扇形EAF的面积;(3)若∠PAB=m°,当∠ACQ=30°,直接写出m的值.10.如图,⊙O是△ABC的外接圆,AB=AC,BO的延长线交AC于点D.(1)求证:∠BAC=2∠ABD;(2)若=,求tan∠ABD.11.已知:如图,在△ABC中,点I是△ABC的内心(三角形三条角平分线的交点),延长AI与△ABC的外接圆交于点D,连接BD,DC.求证:(1)DI=DB;(2)若∠BAC=60°,BC=2,求DI的长.12.有一些代数问题,我们也可以通过几何方法进行求解,例如下面的问题:已知:a>b>0,求证:>.经过思考,小明给出了几何方法的证明,如图:①在直线l上依次取AB=a,BC=b;②以AC为直径作半圆,圆心为O;③过B点作直线l的垂线,与半圆交于点D,连接OD.请回答:(1)连接AD,CD,由作图的过程判断,∠ADC=90°,其依据是;(2)根据作图过程,试求线段BD、OD(用a,b的代数式表示),请写出过程;(3)由BD⊥AC,可知BD<OD,其依据是,由此即证明了这个不等式.13.如图,⊙O是△ABC的外接圆,∠ACB=90°.D是⊙O上一点,连接CD,与AB 交于点F,过点A作⊙O的切线交DC延长线于点E,已知AC=EC.(1)求证:AD=AE;(2)若AE=2,EF=2,求⊙O的直径.14.如图,已知扇形AOB的半径OA=4,∠AOB=90°,点C、D分别在半径OA、OB 上(点C不与点A重合),联结CD.点P是弧AB上一点,PC=PD.(1)当cot∠ODC=,以CD为半径的圆D与圆O相切时,求CD的长;(2)当点D与点B重合,点P为弧AB的中点时,求∠OCD的度数;(3)如果OC=2,且四边形ODPC是梯形,求的值.15.如图,已知半圆O的直径AB=4,点P在线段OA上,半圆P与半圆O相切于点A,点C在半圆P上,CO⊥AB,AC的延长线与半圆O相交于点D,OD与BC相交于点E.(1)求证:AD•AP=OD•AC;(2)设半圆P的半径为x,线段CD的长为y,求y与x之间的函数解析式,并写出定义域;(3)当点E在半圆P上时,求半圆P的半径.参考答案1.(1)证明:连接CD,∵AC是⊙O的直径,∴∠ABC=90°,∵BD是∠ABC的平分线,∴∠ABD=∠CBD=∠ABC=45°,又∵DE是⊙O的切线,∴∠CDE=∠CBD=45°,∵∠ABD=∠ACD=45°,∴∠ACD=∠CDE,∴AC∥DE;(2)解:连接OD,过点C作CF⊥DE,垂足为F,则四边形ODFC是正方形,在Rt△ABC中,AC===4,∴DF=FC=OC=OD=2,∵∠E=∠ACB,∠CFE=∠ABC=90°,∴△ABC∽△CFE,∴===,∴EF=CF=,∴DE=DF+EF=2+=3.2.(1)证明:如图,连接OD交EF于G,∵BC是⊙O的切线,∴∠ODB=90°,∵∠C=90°,∴OD∥AC,∴∠ODA=∠EAD,∵OA=OD,∴∠ODA=∠OAD,∴∠OAD=∠EAD,∴=,∴DE=DF;(2)解:∵=,∴OD垂直平分EF,∵∠C=∠CDG=∠DGE=90°,∴四边形CDGE为矩形,∴EG=CD=2,∠AEF=90°,∴EF=2EG=4,在R△AEF中,AF==5,∵O是AF的中点,G是EF的中点,∴OG=AE=,∴CE=DG=OD﹣OG==1,∴AC=AE+CE=4,∵OD∥AC,∴△BOD∽△ABC,∴,∴,∴BD=.3.(1)证明:连接OD,如图,∵AB为⊙O的直径,∴AD⊥BC,∵AB=AC,∴AD平分BC,∴∠CAD=∠BAD,∵OA=OD,∴∠DAO=∠ADO,∴∠EAD=∠ADO,∴AE∥OD,∵EF是⊙O的切线,∴OD⊥EF,∴DE⊥AC;(2)解:∵cos∠DAB=,而AB=10,∴AD=8,在Rt△ADE中,cos∠DAE==,∴AE=,∵OD∥AE,∴△FDO∽△FEA,∴,即=,∴BF=.4.解:(1)证明:∵α=90°,∠AOB=90°,∴∠AOP=∠BOH,又OA=OB=4,OP=OH,在△AOP和△BOH中,,∴△AOP≌△BOH(SAS),∴∠OPA=∠OHB,∵AP是⊙O的切线,∴∠OPA=90°,∠OHB=90°,即OH⊥BH于点H,∴BH是⊙O的切线;(2)如图,过点B作⊙O的切线BC,BD,切点分别为C,D,连接OC,OD,则有OC⊥BC,OD⊥BD,∵OC=2,OB=4,∴,∴∠BOC=60°,同理∠BOD=60°,当点H与点C重合时,由(1)知:α=90°,∴∠OHB=90°.∵圆弧PH的长为;当点H与点D重合时,α=∠POC+∠BOC+∠BOD=90°+2×60°=210°,∴圆弧PH的长为,∴当BH与⊙O相切时,旋转角α=90°或210°,点H运动路径的长为π或;(3)S△AHB=AB•h,h表示点H到直线AB的距离,作ON⊥AB于点N,H在圆O上,在Rt△ONB中,∠OBN=45°,OB=4,∴ON=4cos45°=2,∴h min=ON﹣r=2,h max=2+2,∴当△AHB面积最大时,点H到AB的距离为2.5.(1)证明:如图1,连接BE,则∠B=∠C,∵AB是⊙O的直径,∴∠ACB=90°,∵∠BCE+∠BAE=180°,∴∠ACD+∠DAE=90°,∵∠ACD=∠DAE,∴∠DAE+∠BAE=90°,∴∠BAD=90°,∴BD是⊙O的切线;(2)如图2,延长EF,交⊙O于H,∵EF⊥AB,AB是⊙O的直径,∴=,∴∠ECA=∠AEH,∵∠EAC=∠GAE,∴△EAC∽△GAE,∴=,∵AC=AD,∴∠C=∠D,∵∠C=∠DAE,∴∠D=∠DAE,∴AE=DE=2,∵∠BFE=∠BAD=90°,∴AD∥EF,∴∠D=∠CEF,∴∠C=∠CEF,∴CG=GE=3,∴AC=AG+CG=AG+3,∴=,∴AG=5(负值舍去);(3)如图3,由(2)知,AG=5,CG=3,∵EG∥DA,∴△CEG∽△CDA,∴,∴=,∴CE=,过点E作EM⊥AC于M,设CM=x,在Rt△CME中,根据勾股定理得,EM2=CE2﹣CM2=()2﹣x2,在Rt△AME中,根据勾股定理得,EM2=AE2﹣AM2=(2)2﹣(8﹣x)2,∴()2﹣x2=(2)2﹣(8﹣x)2,∴x=,∴EM2=()2﹣x2,∴EM=(舍去负值),∴S△ACE=AC•EM=×8×=.6.解:(1)连接FO并延长交AD于点H,∵BC与⊙O相切于点F,∴HF⊥BC,∴HF=÷=9,又∵平行四边形ABCD中,AD∥BC,∠HFC=90°,∴∠FHD=90°,∴HF⊥AD,∴DH=DG=3,设⊙O的半径为r,在Rt△DOH中,(3)2+(9﹣r)2=r2,∴r=3;(2)连接OD,OG,在Rt△DOH中,sin∠ODG=,∴∠ODG=30°,又∵OD=OG,∴∠OGD=∠ODG,∴∠GOD=120°,∴阴影部分的面积等于=.7.解:(1)如下图:∵△ABC是等边三角形,∴∠ABC=60°.∵BD是∠ABC的平分线,∵∠DCA=∠ABD,∴∠DCE=30°.∵AE⊥BD,∴CD=2DE=2a.∵BD是圆的直径,∴∠BCD=90°.∵∠DBC=30°∴AB=2CD=4a.∴BE=BD﹣DE=3a.∵DE+CD=3a,∴BE=DE+CD.故答案为:2a;3a;BE=DE+CD.(2)成立.理由:如图,过A作AF⊥CD,交DC延长线于F,连接AD,∵AF⊥CD,AE⊥BD,∴∠AEB=∠AFC=90°.∵同弧所对的圆周角相等,∠ABE=∠ACD.在△ABE和△ACD中,.∴△ABE≌△ACD(AAS).∴AE=AF,BE=CF.在Rt△ADE和Rt△ADF中,.∴Rt△ADE≌Rt△ADF(HL).∴DE=DF.∵CF=CD+DF=CD+DE,∴BE=DE+CD.故结论成立.(3)∵AB=AC,D是圆上一点,AE⊥BD于E,由(2)的结论可得:BE=DE+CD.∵△ABC是等边三角形,∴AB=BC=AC=,∠ABC=60°.∵∠CBD=15°,∴∠ABE=∠ABC﹣∠CBD=45°.∵AE⊥BD,∴AE=BE=AB=×=.∴BE=DE+CD=.∴△BCD的周长为:BC+CD+BD=BC+CD+DE+BE=BC+2BE=+2.故答案为:+2.8.解:(1)如图1,当点P距离直线m最远时,即过点P且垂直于m的直线经过圆心O时,PQ最大,最大值为2+3=5.故答案为:5.(2)如图2,由已知可得:BC=BC′,BA=BA′,∠CBA=∠C′BA′=60°.∴.∵∠CBA=∠C′BA′=60°,∴∠CBA+∠ABC′=∠C′BA′+∠ABC′.即∠CBC′=∠ABA′.∴△CBC′~△ABA′.∴.∵,∴.∴AA′=2CC′=2×4=8.(3)∵四边形ACBF的面积=S△ABC+S△FAB,△ABC的面积为定值,∴△ABF面积最大时,四边形ACBF的面积最大.∵AB=5且位置不变,∴点F距离AB最大时,△ABF面积最大.∵OE=2,∴点E在以O为圆心,半径为2的圆上,如下图所示:∵∠BEF=90°,∴当O,E,F三点在一条直线上,即BE与该圆相切时,△ABF面积最大.过F作FD⊥OB于D,∵AC=BC=5,∴AB=AC=10.∵O为AB的中点,∴BO=5.∵BE⊥OF,∴BE=.∵tan∠EBF=,∴.∴EF=.∴OF=OE+EF=2+.在Rt△BEO中,sin∠EOB=.在Rt△ODF中,sin∠EOB==.∴DF=OF••(2+)=+.∴△ABF面积最大值为×AB×DF=2+.∴四边形ACBF的面积的最大值=S△ABC+S△FAB=×AC×BC+2+=2+.9.解:(1)CQ与所在圆相切;证明:由旋转知,AP=AQ,∠PAQ=120°,∵∠BAC=120°,∴∠PAQ=∠BAC,∴∠PAQ﹣∠PAC=∠BAC﹣∠PAC,∴∠ACQ=∠ABP,∵AC=AB,∴△ACQ≌△ABP(SAS),∴∠AQC=∠APB,∵BP与所在圆相切,∴∠APB=90°,∴∠AQC=90°,∵AQ=AP,∴CQ与所在圆相切;(2)如图,过点A作AN⊥BC于N,∵AB=AC=2,∠BAC=120°,∴∠ABC=30°,∴AN=AB=,∴BN=AN=3,①当点F在点G的左边时,过点F作FM⊥AB于M,设FM=m,在Rt△BMF中,BF=2m,BM=m,∴AM=AB﹣BM=(2﹣m),在Rt△AMF中,根据勾股定理得,FM2+AM2=AF2,∴m2+[(2﹣m)]2=22,∴m=1或m=2,∴BF=2m=2或4(舍),∴BF=AF,∴∠BAF=∠ABC=30°,∴∠EAF=90°,∴S扇形EAF==π;②当点F在点G的右边时,同①的方法得,BF=4,S扇形EAF=﹣=;即当BF=2时,扇形EAF的面积为π,当BF=4时,扇形EAF的面积为;(3)由(1)知,△ACQ≌△ABP,∴∠ABP=∠ACQ=30°,∵∠ABP=30°,∴点P在BC上,即点P与点F或G重合,当点P与点F重合时,∠PAB=∠BAF,由(2)知,∠BAF=30°,∴m=30,当点P与点G重合时,∠PAB=∠BAG=90°,∴m=90,即m的值为30或90.10.解:(1)连接AO,并延长交BC于点H,∵AB=AC,∴.∴AH⊥BC.∴AH平分∠BAC.∴∠BAC=2∠BAH.∵OA=OB,∴∠ABD=∠BAH.∴∠BAC=2∠ABD.(2)过A作AE∥BC,交BD延长线于点E,∴.∵AB=AC,AH⊥BC,∴BH=BC.∴.∵AE∥BC,∴.设OB=OA=4a,则OH=3a.∴BH=.AH=OA+OH=7a.∵∠ABD=∠BAH,∴tan∠ABD=tan∠BAH=.11.(1)证明:连接BI,如图1所示:∵点I是△ABC的内心,∴AD平分∠BAC,∴∠BAD=∠CAD,∠ABI=∠CBI,∵∠BID=∠BAI+∠IBA,∠IBD=∠CBI+∠CBD,∠CBD=∠CAD,∴∠BID=∠IBD,∴DI=DB;(2)解:过点D作DE⊥BC于E,如图2所示:由(1)得:∠BAD=∠CAD,∴,∵DE⊥BC,∴BE=CE=BC=,∵∠BAC=60°,∴∠BAD=∠CAD=30°,∴∠DBC=∠BCD=30°,∴DE=BE=1,BD=2DE=2,∴DI=BD=2.12.解:(1)∵AC为直径,∴∠ADC=90°(直径所对的圆周角是直角).故答案为:直径所对的圆周角是直角;(2)∵BD⊥AC,∴∠ABD=∠CBD=90°.∴∠BAD+∠ADB=90°.∵∠ADC=90°,∴∠CDB+∠ADB=90°.∴∠BAD=∠CDB.∴.∴BD2=AB•BC=ab.∴BD=.∵AB=a,BC=b,∴AC=a+b.∴OD=.(3)∵BD⊥AC,∴BD<OD(直线外一点到直线上各点的所有连线中,垂线段最短).∴>.故答案为:垂线段最短.13.(1)证明:∵∠ACB=90°.∴AB是⊙O的直径,∵EA是⊙O的切线,∴BA⊥EA,∴∠EAC+∠CAB=90°,∵∠B+∠CAB=90°,∴∠EAC=∠B,∵AC=EC,∴∠EAC=∠E,∴∠E=∠B,∵∠B=∠D,∴∠E=∠D,∴AD=AE;(2)解:∵∠EAF=90°,AE=2,EF=2,∴AF==2,由(1)知:AD=AE=2,∵∠B=∠E,∠ACB=∠EAF=90°,∴=,∴AB=AC,如图,过点A作AG⊥CD于点G,设AC=EC=t,则CF=2﹣t,∵tan∠E==,sin∠E===,∴AG=,∴FG==,∴EG=EC+CG,∴CG=CF﹣FG=2﹣t﹣=﹣t,∵AC2=AG2+CG2,∴t2=()2+(﹣t)2,解得t=,∴AB=AC=t=3.∴⊙O的直径是3.14.解:(1)如图1中,∵∠COD=90°,cot∠ODC==,∴可以假设OD=3k,OC=4k,则CD=5k,∵以CD为半径的圆D与圆O相切,∴CD=DB=5k,∴OB=OC=8k,∴AC=OC=4k=2,∴k=,∴CD=.(2)如图2中,连接OP,过点P作PE⊥OA于E,PF⊥OB于F.∵=,∴∠AOP=∠POB,∵PE⊥OA,PF⊥OB,∴PE=PF,∵∠PEC=∠PFB=90°,PD=PC,∴Rt△PEC≌Rt△PFB(HL),∴∠EPC=∠FPB,∵∠PEO=∠EOF=∠OFP=90°,∴∠EPF=90°,∴∠EPF=∠CPB=90°,∴∠PCB=∠PBC=45°,∵OP=OB,∠POB=45°,∴∠OBP=∠OPB=67.5°,∴∠CBO=67.5°﹣45°=22.5°,∴∠OCD=90°﹣22.5°=67.5°.(3)如图3﹣1中,当OC∥PD时,∵OC∥PD,∴∠PDO=∠AOD=90°,∵CE⊥PD,∴∠CED=90°,∴四边形OCED是矩形,∴OC=DE=2,CE=OD,设PC=PD=x,EC=OD=y,则有,可得x=2﹣2(不合题意的已经舍弃),∴PD=2﹣2,∴==﹣1.如图3﹣2中,当PC∥OD时,∴∠COD=∠OCE=∠CED=90°,∴四边形OCED是矩形,∴OC=DE=2,CE=OD,∵OP=4,OC=2,∴PC===2,∴PD=PC=2,∴PE===2,∴EC=OD=2﹣2,∴===3+,综上所述,的值为﹣1或3+.15.解:(1)连接CP,如图:∵AP=CP,AO=DO,∴∠A=∠ACP=∠ADO,∴△ACP∽△ADO,∴,∴AD•CP=OD•AC,∴AD•AP=OD•AC;(2)∵半圆O的直径AB=4,∴AO=2,∵半圆P的半径为x,∴OP=2﹣x,∴∠COP=90°,∴CO2=CP2﹣OP2=x2﹣(2﹣x)2=4x﹣4,Rt△AOC中,AC==2,∵∠A=∠ACP=∠ADO,∴CP∥DO,∴,又线段CD的长为y,∴,变形得:y=,x范围是0<x≤2;(3)设半圆P与AB交于G,连接EG,过E作EH⊥AB于H,如图:设半圆P的半径为x,由(2)知AC=2,∵CO⊥AB,∴BC=AC=2,∵CP∥DO,∴,而OB=2,PB=4﹣x,∴,∴BE=,∵点E在半圆P上,∴∠EGB=∠ACB,且∠B=∠B,∴△CAB∽△GEB,∴=,∴,∴EG=,∵AC=BC,∴EG=BG,而BG=AB﹣AG=4﹣2x,∴=4﹣2x,解得x=或(大于2,舍去),∴半圆P的半径为x=.。
2019年湖北省各市中考压轴题解答题选编(含答案)

2019年湖北省各市中考压轴题解答题选编(2019年宜昌T24)在平面直角坐标系中,正方形AB CD四个顶点的坐标分别为A(-2,4),B(-2,-2),C(4,-2),D(4,4).(1)填空:正方形的面积为:当双曲线y=kx(k≠0)与正方形ABCD有四个交点时,k的取值范围是;(2)已知抛物线L:y=a(x-m)2+n (a>0)顶点P在BC上,与边AB,DC分别交于点E,F,过点B的双曲线y=kx(k≠0)与边DC交于点N.①点Q(m,-m2 -2m +3)是平面内一动点,在抛物线L的运动过程中,点Q随m运动,分别求运动过程中点Q在最高位置和最低位置时的坐标;②当点F在点N下方,AE=NF.点P不与B,C两点重合时,求BE CFBP CP-的值;③求证:抛物线L与直线x=1的交点M始终位于x轴下方.①②第24题图{解析}本题考查了正方形与一次函数、二次函数的综合应用.(1)①先求正方形ABCD 的边长,再求面积;②分k>0和k<0两种情况,分别求出双曲线过界点B与A时k的值,从而求得当双曲线y=kx(k≠0)与正方形ABCD有四个交点时k的取值范围;(2)①先根据“抛物线L:y=a(x-m)2+n (a>0)顶点P在BC上”求得m的范围,再令y Q= -m2-2m+3配方求得此范围内Q在最高位置和最低位置时的坐标;②当双曲线y=kx(k≠0)经过点B(-2.-2)时,先求k与顶点P的纵坐标,用m和a的代数式表示BP、CP、BE、CF,从而表示BE CFBP CP-,最后根据AE =NF求得a与m的关系,得出BE CFBP CP-的值;③用m和a的代数式表示M坐标,根据M纵坐标的最值时m的值,分两种情况,求出点F坐标,用a的代数式表示点E的坐标,根据“点E在边AB上,且此时不与B重合”求得a的范围,从而证得结论.{答案}解:(1)根据题意得正方形ABCD的边长为4-(-2)=6,∴正方形的面积为36.当k>0时,双曲线y=kx(k≠0)与正方形ABCD交于点B(-2,-2)时,k=4,双曲线与正方形有三个交点,∴当双曲线y=kx(k≠0)与正方形ABCD有四个交点时,k的取值范围是0<k<4;当k<0时,双曲线y=kx(k≠0)与正方形ABCD交于点A(-2,4)时,k=-8,此时双曲线也过点C,双曲线与正方形有二个交点,∴当双曲线y=kx(k≠0)与正方形ABCD有四个交点时,k的取值范围是-8<k<0;综上,当双曲线y=kx(k≠0)与正方形ABCD有四个交点时,k的取值范围是0<k<4或-8<k<0.故答案为36;0<k<4或-8<k<0.(2)①由题意,-2≤m≤4.y Q= -m2-2m+3=-(m+1)2+4.当m=-1,y Q最大=4,在运动过程中点Q在最高位置时的坐标为(-1,4).当m<-1时,y Q随m的增大而增大.当m=-2时,y Q最小=3.当m>-1时,y Q随m的增大而减小,当m=4时y Q最小=21.∵3>-21,∴y Q最小=-21.点Q在最低位置时的坐标(4,-21).∴在运动过程中点Q在最高位置时的坐标为(-1,4),最低位置时的坐标(4,-21).②当双曲线y=kx(k≠0)经过点B(-2.-2)时,k=4.∴N(4.1).∵顶点P(m,n)在边BC上,∴n=-2.∴P(m,-2).∴BP=m+2, CP=4-m.∴抛物线:y=a(x-m)2+n (a>0)与边AB,DC分别交于点E,F,∴E(-2,a(-2 -m)2-2).F(4,a(4 -m)2-2).∴BE= a(-2-m)2,CF =a(4-m)2.∴()()222424a m a mBE CFBP CP m m----=-+-= a(m+2)- a(4 - m)= 2am-2a =2a(m-1).∵AE =NF,点F在点N下方,∴6-a(-2-m)2=3-a(4-m)2.∴12a(m -1)=3.a(m -1)= 14.∴BE CFBP CP-=12.③由题意,M(1,a(1 -m)2-2),∴y M= a(1 -m)2-2(-2≤m≤4),即y M= a(m -1)2-2(-2≤m≤4).∵a>0,∴对于每一个a(a>0)值,当m=1时,y M最小=-2.当m= -2或4时,y M最大=9a -2.当m=4时,抛物线L:y=a(x-4)2-2.∴F (4, -2),E(-2,36a-2)。
2021年九年级中考数学第三轮压轴题冲刺专题复习:圆的综合 专项练习题

2021年中考数学第三轮压轴题冲刺专题复习:圆的综合专项练习题1、如图,O是ABC∆的外接圆,其切线AE与直径BD的延长线相交于点E,=.且AE AB(1)求ACB∠的度数;DE=,求O的半径.(2)若22、如图,AB是半圆O的直径,C,D是半圆O上不同于A,B的两点,AD BC=,AC与BD相交于点F.BE是半圆O所在圆的切线,与AC的延长线相交于点E.(1)求证:CBA DAB∆≅∆;(2)若BE BF=,求证:AC平分DAB∠.3、如图,AG是∠HAF的平分线,点E在AF上,以AE为直径的⊙O交AG于点D,过点D作AH的垂线,垂足为点C,交AF于点B.(1)求证:直线BC是⊙O的切线;(2)若AC=2CD,设⊙O的半径为r,求BD的长度.4、如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB 上,⊙O经过A、D两点,交AC于点E,交AB于点F.(1)求证:BC是⊙O的切线;(2)若⊙O的半径是2cm,E是的中点,求阴影部分的面积(结果保留π和根号)5、如图,CE是⊙O的直径,BC切⊙O于点C,连接OB,作ED∥OB交⊙O于点D,BD的延长线与CE的延长线交于点A.(1)求证:AB是⊙O的切线;(2)若⊙O的半径为1,tan∠DEO=,tan∠A=,求AE的长.6、如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB 分别相交于点D,F,且DE=EF.(1)求证:∠C=90°;(2)当BC=3,sinA=时,求AF的长.7、如图,已知A 、B 是⊙O 上两点,△OAB 外角的平分线交⊙O 于另一点C ,CD ⊥AB 交AB 的延长线于D .(1)求证:CD 是⊙O 的切线;(2)E 为的中点,F 为⊙O 上一点,EF 交AB 于G ,若tan ∠AFE=,BE=BG ,EG=3,求⊙O 的半径.8、如图,已知AB 是O 的直径,C 是O 上的一点,D 是AB 上的一点,DE AB ⊥于D ,DE 交BC 于F ,且EF EC =.(1)求证:EC 是O 的切线;(2)若4BD =,8BC =,圆的半径5OB =,求切线EC 的长.9、如图,AB 是⊙O 的直径,点E 为线段OB 上一点(不与O ,B 重合),作EC ⊥OB ,交⊙O 于点C ,作直径CD ,过点C 的切线交DB 的延长线于点P ,作AF ⊥PC 于点F ,连接CB .(1)求证:AC 平分∠FAB ;(2)求证:BC 2=CE•CP ;(3)当AB=4且=时,求劣弧的长度.10、已知⊙O 的直径AB=2,弦AC 与弦BD 交于点E .且OD ⊥AC ,垂足为点F .(1)如图1,如果AC=BD ,求弦AC 的长;(2)如图2,如果E 为弦BD 的中点,求∠ABD 的余切值;(3)联结BC 、CD 、DA ,如果BC 是⊙O 的内接正n 边形的一边,CD 是⊙O 的内接正(n +4)边形的一边,求△ACD 的面积.11、如图,AB 为O 的直径,四边形ABCD 内接于O ,对角线AC ,BD 交于点E ,O 的切线AF 交BD 的延长线于点F ,切点为A ,且CAD ABD ∠=∠.(1)求证:AD CD =;(2)若4AB =,5BF =,求sin BDC ∠的值.12、如图,AB 为⊙O 的直径,C 、D 为⊙O 上的两个点,AĈ=CD ̂=DB ̂,连接AD ,过点D 作DE ⊥AC 交AC 的延长线于点E .(1)求证:DE 是⊙O 的切线.(2)若直径AB =6,求AD 的长.13、如图,在△ABC 中,O 为AC 上一点,以O 为圆心,OC 长为半径作圆,与BC 相切于点C ,过点A 作AD ⊥BO 交BO 的延长线于点D ,且∠AOD =∠BAD .(1)求证:AB 为⊙O 的切线;(2)若BC =6,tan ∠ABC =43 ,求AD 的长.14、如图,⊙O 是△ABC 的外接圆,点O 在BC 边上,∠BAC 的平分线交⊙O 于点D ,连接BD 、CD ,过点D 作BC 的平行线与AC 的延长线相交于点P .(1)求证:PD 是⊙O 的切线;(2)求证:△ABD ∽△DCP ;(3)当AB=5cm ,AC=12cm 时,求线段PC 的长.C B15、如图,AB 为⊙O 的直径,且AB=4,点C 在半圆上,OC ⊥AB ,垂足为点O ,P 为半圆上任意一点,过P 点作PE ⊥OC 于点E ,设△OPE 的内心为M ,连接OM 、PM .(1)求∠OMP 的度数;(2)当点P 在半圆上从点B 运动到点A 时,求内心M 所经过的路径长.16、如图,AB 是半圆O 的直径,C 是AB 延长线上的点,AC 的垂直平分线交半圆于点D ,交AC 于点E ,连接DA ,DC .已知半圆O 的半径为3,BC=2.(1)求AD 的长.(2)点P 是线段AC 上一动点,连接DP ,作∠DPF=∠DAC ,PF 交线段CD 于点F .当△DPF 为等腰三角形时,求AP 的长.17、如图所示:O 与ABC 的边BC 相切于点C ,与AC 、AB 分别交于点D 、E ,//DE OB .DC 是O 的直径.连接OE ,过C 作//CG OE 交O 于G ,连接DG 、EC ,DG 与EC 交于点F .(1)求证:直线AB与O相切;(2)求证:AE ED AC EF⋅=⋅;(3)若13,tan2EF ACE=∠=时,过A作//AN CE交O于M、N两点(M在线段AN上),求AN的长.18、如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I 于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点”,把PQ PH⋅的值称为⊙I关于直线a的“特征数”.(1)如图2,在平面直角坐标系xOy中,点E的坐标为()0,4,半径为1的⊙O 与两坐标轴交于点A、B、C、D.⊙过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点_________(填“A”、“B”、“C”或“D”),⊙O关于直线m的“特征数”为_________;⊙若直线n的函数表达式为4y=+,求O关于直线n的“特征数”;(2)在平面直角坐标系xOy 中,直线l 经过点()1,4M ,点F 是坐标平面内一点,以F ⊙F .若⊙F 与直线l 相离,点()1,0N -是⊙F 关于直线l 的“远点”,且⊙F 关于直线l 的“特征数”是l 的函数表达式.参考答案2021年中考数学第三轮压轴题冲刺专题复习:圆的综合 专项练习题1、如图,O 是ABC ∆的外接圆,其切线AE 与直径BD 的延长线相交于点E ,且AE AB =.(1)求ACB ∠的度数;(2)若2DE =,求O 的半径.解:(1)如图,连接OA .∵AE 是O 的切线,∴90OAE ∠=︒.又∵OB OA =,∴12∠=∠.∵AB AE =,∴1E ∠=∠,∴212AOE E ∠=∠=∠.又∵在Rt AOE ∆中,90AOE E ∠+∠=︒,∴390E ∠=︒.∴30E ∠=︒.∴120AOB ∠=︒.∴1602ACB AOB ∠=∠=︒. (2)设O 的半径为r ,在Rt OAE ∆中,∵30E ∠=︒,∴2OE OA =.∴2OD DE OA +=.∴22r r +=,∴2r =.∴O 的半径是2.2、如图,AB 是半圆O 的直径,C ,D 是半圆O 上不同于A ,B 的两点,AD BC =,AC 与BD 相交于点F .BE 是半圆O 所在圆的切线,与AC 的延长线相交于点E .(1)求证:CBA DAB ∆≅∆;(2)若BE BF =,求证:AC 平分DAB ∠.【解答】(1)证明:AB 是半圆O 的直径,90ACB ADB ∴∠=∠=︒,在Rt CBA ∆与Rt DAB ∆中,BC AD BA AB =⎧⎨=⎩, Rt CBA Rt DAB(HL)∴∆≅∆; (2)解:BE BF =,由(1)知BC EF ⊥,E BFE ∴∠=∠, BE 是半圆O 所在圆的切线,90ABE ∴∠=︒,90∴∠+∠=︒,E BAE由(1)知90∠=︒,D∴∠+∠=︒,DAF AFD90∠=∠,AFD BFE∴∠=∠,AFD E∠=︒-∠,BAF E∴∠=︒-∠,9090DAF AFD∴∠=∠,DAF BAF∴平分DABAC∠.3、如图,AG是∠HAF的平分线,点E在AF上,以AE为直径的⊙O交AG于点D,过点D作AH的垂线,垂足为点C,交AF于点B.(1)求证:直线BC是⊙O的切线;(2)若AC=2CD,设⊙O的半径为r,求BD的长度.【解答】(1)证明:连接OD,∵AG是∠HAF的平分线,∴∠CAD=∠BAD,∵OA=OD,∴∠OAD=∠ODA,∴∠CAD=∠ODA,∴OD∥AC,∵∠ACD=90°,∴∠ODB=∠ACD=90°,即OD⊥CB,∵D在⊙O上,∴直线BC是⊙O的切线;(4分)(2)解:在Rt△ACD中,设CD=a,则AC=2a,AD=a,连接DE,∵AE是⊙O的直径,∴∠ADE=90°,由∠CAD=∠BAD,∠ACD=∠ADE=90°,∴△ACD∽△ADE,∴,即,∴a=,由(1)知:OD∥AC,∴,即,∵a=,解得BD=r.(10分)4、如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB 上,⊙O经过A、D两点,交AC于点E,交AB于点F.(1)求证:BC是⊙O的切线;(2)若⊙O的半径是2cm,E是的中点,求阴影部分的面积(结果保留π和根号)【解答】解:(1)连接OD.、∵OA=OD,∴∠OAD=∠ODA,∵∠OAD=∠DAC,∴∠ODA=∠DAC,∴OD∥AC,∴∠ODB=∠C=90°,∴OD⊥BC,∴BC是⊙O的切线.(2)连接OE,OE交AD于K.∵=,∴OE⊥AD,∵∠OAK=∠EAK,AK=AK,∠AKO=∠AKE=90°,∴△AKO≌△AKE,∴AO=AE=OE,∴△AOE是等边三角形,∴∠AOE=60°,∴S阴=S扇形OAE﹣S△AOE=﹣×22=﹣.5、如图,CE是⊙O的直径,BC切⊙O于点C,连接OB,作ED∥OB交⊙O于点D,BD的延长线与CE的延长线交于点A.(1)求证:AB是⊙O的切线;(2)若⊙O的半径为1,tan∠DEO=,tan∠A=,求AE的长.【解答】解:(1)连接OD,如图.∵ED∥OB,∴∠1=∠4,∠2=∠3,∵OD=OE,∴∠3=∠4,∴∠1=∠2.在△DOB与△COB中,,∴△DOB≌△COB,∴∠ODB=∠OCB,∵BC切⊙O于点C,∴∠OCB=90°,∴∠ODB=90°,∴AB是⊙O的切线;(2)∵∠DEO=∠2,∴tan∠DEO=tan∠2==,∵⊙O的半径为1,OC=1,∴BC=,tan∠A==,∴AC=4BC=4,∴AE=AC﹣CE=4﹣2.6、如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB 分别相交于点D,F,且DE=EF.(1)求证:∠C=90°;(2)当BC=3,sinA=时,求AF的长.【解答】解:(1)连接OE,BE,∵DE=EF,∴∴∠OBE=∠DBE∵OE=OB,∴∠OEB=∠OBE∴∠OEB=∠DBE,∴OE∥BC∵⊙O与边AC相切于点E,∴OE⊥AC∴BC⊥AC∴∠C=90°(2)在△ABC,∠C=90°,BC=3,sinA=∴AB=5,设⊙O的半径为r,则AO=5﹣r,在Rt△AOE中,sinA===∴r=∴AF=5﹣2×=7、如图,已知A、B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD ⊥AB交AB的延长线于D.(1)求证:CD是⊙O的切线;(2)E为的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE=,BE=BG,EG=3,求⊙O的半径.【解答】(1)证明:连接OC,如图,∵BC平分∠OBD,∴∠OBD=∠CBD,∵OB=OC,∴∠OBC=∠OCB,∴∠OCB=∠CBD,∴OC∥AD,而CD⊥AB,∴OC⊥CD,∴CD 是⊙O 的切线;(2)解:连接OE 交AB 于H ,如图,∵E 为的中点,∴OE ⊥AB ,∵∠ABE=∠AFE ,∴tan ∠ABE=tan ∠AFE=,∴在Rt △BEH 中,tan ∠HBE==设EH=3x ,BH=4x ,∴BE=5x ,∵BG=BE=5x ,∴GH=x ,在Rt △EHG 中,x 2+(3x )2=(3)2,解得x=3, ∴EH=9,BH=12,设⊙O 的半径为r ,则OH=r ﹣9,在Rt △OHB 中,(r ﹣9)2+122=r 2,解得r=, 即⊙O 的半径为.8、如图,已知AB 是O 的直径,C 是O 上的一点,D 是AB 上的一点,DE AB ⊥于D ,DE 交BC 于F ,且EF EC =.(1)求证:EC 是O 的切线;(2)若4BD =,8BC =,圆的半径5OB =,求切线EC 的长.【解答】解:(1)连接OC,OC OB=,OBC OCB∴∠=∠,DE AB⊥,90OBC DFB∴∠+∠=︒,EF EC=,ECF EFC DFB∴∠=∠=∠,90OCB ECF∴∠+∠=︒,OC CE∴⊥,EC∴是O的切线;(2)AB是O的直径,90ACB∴∠=︒,5OB=,10AB∴=,6 AC∴==,cosBD BC ABCBF AB∠==,∴8410BF=,5BF∴=,3CF BC BF∴=-=,90ABC A∠+∠=︒,90ABC BFD∠+∠=︒,BFD A∴∠=∠,A BFD ECF EFC∴∠=∠=∠=∠,OA OC=,OCA A BFD ECF EFC∴∠=∠=∠=∠=∠,OAC ECF∴∆∆∽,∴EC CFOA AC=,53562 OA CFECAC⨯∴===.9、如图,AB是⊙O的直径,点E为线段OB上一点(不与O,B重合),作EC ⊥OB,交⊙O于点C,作直径CD,过点C的切线交DB的延长线于点P,作AF ⊥PC于点F,连接CB.(1)求证:AC平分∠FAB;(2)求证:BC2=CE•CP;(3)当AB=4且=时,求劣弧的长度.【解答】(1)证明:∵AB是直径,∴∠ACB=90°,∴∠BCP+∠ACF=90°,∠ACE+∠BCE=90°,∵∠BCP=∠BCE,∴∠ACF=∠ACE,(2)证明:∵OC=OB,∴∠OCB=∠OBC,∵PF是⊙O的切线,CE⊥AB,∴∠OCP=∠CEB=90°,∴∠PCB+∠OCB=90°,∠BCE+∠OBC=90°,∴∠BCE=∠BCP,∵CD是直径,∴∠CBD=∠CBP=90°,∴△CBE∽△CPB,∴=,∴BC2=CE•CP;(3)解:作BM⊥PF于M.则CE=CM=CF,设CE=CM=CF=3a,PC=4a,PM=a,∵∠MCB+∠P=90°,∠P+∠PBM=90°,∴∠MCB=∠PBM,∵CD是直径,BM⊥PC,∴∠CMB=∠BMP=90°,∴△BMC∽△PMB,∴=,∴BM2=CM•PM=3a2,∴BM=a,∴tan∠BCM==,∴∠BCM=30°,∴∠OCB=∠OBC=∠BOC=60°,∠BOD=120°∴的长==π.10、已知⊙O的直径AB=2,弦AC与弦BD交于点E.且OD⊥AC,垂足为点F.(1)如图1,如果AC=BD,求弦AC的长;(2)如图2,如果E为弦BD的中点,求∠ABD的余切值;(3)联结BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,求△ACD的面积.【解答】解:(1)∵OD⊥AC,∴=,∠AFO=90°,又∵AC=BD,∴=,即+=+,∴=,∴==,∴∠AOD=∠DOC=∠BOC=60°,∵AB=2,∴AO=BO=1,∴AF=AOsin∠AOF=1×=,则AC=2AF=;(2)如图1,连接BC,∵AB为直径,OD⊥AC,∴∠AFO=∠C=90°,∴OD∥BC,∴∠D=∠EBC,∵DE=BE、∠DEF=∠BEC,∴△DEF≌△BEC(ASA),∴BC=DF、EC=EF,又∵AO=OB,∴OF是△ABC的中位线,设OF=t,则BC=DF=2t,∵DF=DO﹣OF=1﹣t,∴1﹣t=2t,解得:t=,则DF=BC=、AC===,∴EF=FC=AC=,∵OB=OD,∴∠ABD=∠D,则cot∠ABD=cot∠D===;(3)如图2,∵BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,∴∠BOC=、∠AOD=∠COD=,则+2×=180,解得:n=4,∴∠BOC=90°、∠AOD=∠COD=45°,∴BC=AC=,∵∠AFO=90°,∴OF=AOcos ∠AOF=, 则DF=OD ﹣OF=1﹣, ∴S △ACD =AC•DF=××(1﹣)=.11、如图,AB 为O 的直径,四边形ABCD 内接于O ,对角线AC ,BD 交于点E ,O 的切线AF 交BD 的延长线于点F ,切点为A ,且CAD ABD ∠=∠.(1)求证:AD CD =;(2)若4AB =,5BF =,求sin BDC ∠的值.【解答】解:(1)证明:CAD ABD ∠=∠,又ABD ACD ∠=∠,ACD CAD ∴∠=∠,AD CD ∴=;(2)AF 是O 的切线,90FAB ∴∠=︒, AB 是O 的直径,90ACB ADB ADF ∴∠=∠=∠=︒,90ABD BAD BAD FAD ∴∠+∠=∠+∠=︒,ABD FAD ∴∠=∠,ABD CAD ∠=∠,FAD EAD ∴∠=∠,AD AD =,()ADF ADE ASA ∴∆≅∆,AF AE ∴=,DF DE =,4AB =,5BF =,3AF ∴=,3AE AF ∴==,1122ABF S AB AF BF AD ∆==, ∴431255AB AF AD BF ⨯===,95DE ∴==, 725BE BF DE ∴=-=, AED BEC ∠=∠,90ADE BCE ∠=∠=︒,BEC AED ∴∆∆∽,∴BE BC AE AD =, ∴2825BE AD BC AE ==, ∴7sin 25BC BAC AB ∠==, BDC BAC ∠=∠,∴7sin 25BDC ∠=.12、如图,AB 为⊙O 的直径,C 、D 为⊙O 上的两个点,AĈ=CD ̂=DB ̂,连接AD ,过点D 作DE ⊥AC 交AC 的延长线于点E .(1)求证:DE 是⊙O 的切线.(2)若直径AB =6,求AD 的长.【解答】(1)证明:连接OD,̂=CD̂=DB̂,∵AC×180°=60°,∴∠BOD=13̂=DB̂,∵CD∠BOD=30°,∴∠EAD=∠DAB=12∵OA=OD,∴∠ADO=∠DAB=30°,∵DE⊥AC,∴∠E=90°,∴∠EAD+∠EDA=90°,∴∠EDA=60°,∴∠EDO=∠EDA+∠ADO=90°,∴OD⊥DE,∴DE是⊙O的切线;(2)解:连接BD,∵AB为⊙O的直径,∴∠ADB=90°,∵∠DAB=30°,AB=6,AB=3,∴BD=12∴AD=√62−32=3√3.13、如图,在△ABC中,O为AC上一点,以O为圆心,OC长为半径作圆,与BC相切于点C,过点A作AD⊥BO交BO的延长线于点D,且∠AOD=∠BAD.(1)求证:AB为⊙O的切线;(2)若BC=6,tan∠ABC=43,求AD的长.【解析】(1)作OE⊙AB于点E∵⊙O切BC于点C∴OC⊙BC ⊙ACB=90°∵ AD⊙BD ∴⊙D=90°∴⊙ABD+⊙BAD =90°⊙CBD+⊙BOC=90°∵⊙BOC=⊙AOD ⊙AOD=⊙BAD∴⊙BOC=⊙BAD∴⊙ABD=⊙CBD在⊙OBC和⊙OBE中{∠OEA=∠OCB ∠ABD=∠CBD OB=OB∴△OBC⊙⊙OBE∴OE=OC ∴OE是⊙O的半径. ∵OE⊙AB ∴AB为⊙O的切线.(2)∵tan⊙ABC=ACBC =43,BC=6B⊙AC=8 ⊙AB=√62+82=10∵BE=BC=6 ⊙AE=4∵⊙AOE=⊙ABC ⊙tan⊙AOE=AEEO =43⊙EO=3∴AO=5 OC=3 ⊙BO=√62+32=3√5在△AOD和△BOC中{∠AOD=∠BOC∠ADOE=∠BCO∴△AOD⊙△BOC ∴AOBO =ADBC即3√5=AD6∴AD=2√514、如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.(1)求证:PD是⊙O的切线;(2)求证:△ABD∽△DCP;(3)当AB=5cm,AC=12cm时,求线段PC的长.【解答】解:(1)如图,连接OD,∵BC是⊙O的直径,∴∠BAC=90°,∵AD平分∠BAC,∴∠BAC=2∠BAD,∵∠BOD=2∠BAD,∴∠BOD=∠BAC=90°,∵DP∥BC,∴∠ODP=∠BOD=90°,∴PD⊥OD,∵OD是⊙O半径,∴PD是⊙O的切线;(2)∵PD∥BC,∴∠ACB=∠P,∵∠ACB=∠ADB,∴∠ADB=∠P,∵∠ABD+∠ACD=180°,∠ACD+∠DCP=180°,∴∠DCP=∠ABD,∴△ABD∽△DCP,(3)∵BC是⊙O的直径,∴∠BDC=∠BAC=90°,在Rt△ABC中,BC==13cm,∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠BOD=∠COD,∴BD=CD,在Rt△BCD中,BD2+CD2=BC2,∴BC=CD=BC=,∵△ABD∽△DCP,∴,∴,∴CP=16.9cm.15、如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.(1)求∠OMP的度数;(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.【解答】解:(1)∵△OPE的内心为M,∴∠MOP=∠MOC,∠MPO=∠MPE,∴∠PMO=180°﹣∠MPO﹣∠MOP=180°﹣(∠EOP+∠OPE),∵PE⊥OC,即∠PEO=90°,∴∠PMO=180°﹣(∠EOP+∠OPE)=180°﹣(180°﹣90°)=135°,(2)如图,∵OP=OC,OM=OM,而∠MOP=∠MOC,∴△OPM≌△OCM,∴∠CMO=∠PMO=135°,所以点M在以OC为弦,并且所对的圆周角为135°的两段劣弧上(和);点M在扇形BOC内时,过C、M、O三点作⊙O′,连O′C,O′O,在优弧CO取点D,连DA,DO,∵∠CMO=135°,∴∠CDO=180°﹣135°=45°,∴∠CO′O=90°,而OA=4cm,∴O′O=OC=×4=2,∴弧OMC的长==π(cm),同理:点M在扇形AOC内时,同①的方法得,弧ONC的长为πcm,所以内心M所经过的路径长为2×π=2πcm.16、如图,AB是半圆O的直径,C是AB延长线上的点,AC的垂直平分线交半圆于点D,交AC于点E,连接DA,DC.已知半圆O的半径为3,BC=2.(1)求AD的长.(2)点P是线段AC上一动点,连接DP,作∠DPF=∠DAC,PF交线段CD于点F.当△DPF为等腰三角形时,求AP的长.【解答】解:(1)如图1,连接OD,∵OA=OD=3,BC=2,∴AC=8,∵DE是AC的垂直平分线,∴AE=AC=4,∴OE=AE﹣OA=1,在Rt△ODE中,DE==2;在Rt△ADE中,AD==2;(2)当DP=DF 时,如图2,点P 与A 重合,F 与C 重合,则AP=0;当DP=PF 时,如图4,∴∠CDP=∠PFD ,∵DE 是AC 的垂直平分线,∠DPF=∠DAC ,∴∠DPF=∠C ,∵∠PDF=∠CDP ,∴△PDF ∽△CDP ,∴∠DFP=∠DPC ,∴∠CDP=∠CPD ,∴CP=CD ,∴AP=AC ﹣CP=AC ﹣CD=AC ﹣AD=8﹣2;当PF=DF 时,如图3,∴∠FDP=∠FPD ,∵∠DPF=∠DAC=∠C ,∴△DAC ∽△PDC ,∴, ∴, ∴AP=5,即:当△DPF 是等腰三角形时,AP 的长为0或5或8﹣2.17、如图所示:O 与ABC 的边BC 相切于点C ,与AC 、AB 分别交于点D 、E ,//DE OB .DC 是O 的直径.连接OE ,过C 作//CG OE 交O 于G ,连接DG 、EC,DG与EC交于点F.(1)求证:直线AB与O相切;(2)求证:AE ED AC EF⋅=⋅;(3)若13,tan2EF ACE=∠=时,过A作//AN CE交O于M、N两点(M在线段AN上),求AN的长.【详解】(1)⊙DE//OB,⊙⊙BOC=⊙EDC,⊙CG//OE,⊙⊙DEO=⊙BOE,又⊙⊙DEO=⊙EDC,⊙⊙DEO=⊙BOE,由题意得:EO=CO,BO=BO,⊙⊙BOE⊙⊙BOC(SAS),⊙⊙BEO=⊙BCO=90°,⊙AB是⊙O的切线.(2)如图所示DG与OE交点作为H点,⊙EO//GC,⊙⊙EHD=⊙DGC=90°,又由(1)所知⊙AEO=90°,⊙AE//DF,⊙⊙AEC⊙⊙DFC, ⊙AE DF AC DC=, 由圆周角定理可知⊙EDG=⊙ECG,⊙EOD=2⊙ECD,⊙DO//GC,⊙⊙EOD=⊙GCD=⊙GCE+⊙ECD,⊙⊙ECD=⊙GCE=⊙EDF,又⊙⊙FED=⊙DEC,⊙⊙FED⊙⊙DEC, ⊙DF EF DC ED=, ⊙AE EF AC ED=,即AE ED AC EF ⋅=⋅. (3)⊙13,tan 2EF ACE =∠=,与⊙ACE 相等角的tan 值都相同. ⊙ED=6,则EC=12,根据勾股定理可得CD ===⊙EO=DO=CO=由(2)可得12AE EF AC ED ==, 在Rt⊙AEO 中,可得222AO AE EO =+,即()222AC OC AE EO -=+,⊙((2222AE AE -=+,解得AE=则AC=连接ON,延长BO 交MN 于点I,根据垂径定理可知OI⊙MN,⊙AN//CE,⊙⊙CAN=⊙ACE .在Rt⊙AIO 中,可得222AO AI IO =+,即(()2222OI OI =+, 解得OI=5,则AI=10,在Rt⊙OIN 中, 222ON IN IO =+,即(2225IN =+,解得IN=⊙AN=AI+IN=10+18、如图1,⊙I 与直线a 相离,过圆心I 作直线a 的垂线,垂足为H ,且交⊙I于P 、Q 两点(Q 在P 、H 之间).我们把点P 称为⊙I 关于直线a 的“远点”,把PQ PH ⋅的值称为⊙I 关于直线a 的“特征数”.(1)如图2,在平面直角坐标系xOy 中,点E 的坐标为()0,4,半径为1的⊙O 与两坐标轴交于点A 、B 、C 、D .⊙过点E 画垂直于y 轴的直线m ,则⊙O 关于直线m 的“远点”是点_________(填“A ”、“B ”、“C ”或“D ”),⊙O 关于直线m 的“特征数”为_________;⊙若直线n 的函数表达式为4y =+,求O 关于直线n 的“特征数”;(2)在平面直角坐标系xOy 中,直线l 经过点()1,4M ,点F 是坐标平面内一点,以F ⊙F .若⊙F 与直线l 相离,点()1,0N -是⊙F 关于直线l 的“远点”,且⊙F 关于直线l 的“特征数”是l 的函数表达式.【详解】解:(1)⊙⊙O 关于直线m 的“远点”是点D ,⊙O 关于直线m 的“特征数”为DB·DE=2×5=10;⊙如下图:过圆心O 作OH⊙直线n ,垂足为点H ,交⊙O 于点P 、Q ,⊙直线n 的函数表达式为4y =+,当x=0时,y=4;当y=0时,x=3-,⊙直线n 经过点E (0,4),点F (3-,0),在Rt⊙EOF 中,⊙tan⊙FEO=FO EO =34=3, ⊙⊙FEO=30°,⊙⊙EFO=60°,Rt⊙HOF 中,⊙sin⊙HFO=HO FO, ⊙HO= sin⊙HFO·FO=2,⊙PH=HO+OP=3,⊙PQ·PH=2×3=6,⊙⊙O 关于直线n 的“特征数”为6;(2)如下图,⊙点F 是圆心,点()1,0N -是“远点”,⊙连接NF 并延长,则直线NF⊙直线l ,设NF 与直线l 的交点为点A (m ,n ),设直线l 的解析式为y=kx+b 1(k≠0),将点()1,4M 与A (m ,n )代入y=kx+b 1中,114=k b n mk b +⎧⎨=+⎩①② ⊙-⊙得:n -4=mk -k ,⊙又⊙直线NF⊙直线l ,⊙设直线NF 的解析式为y=1k-x+b 2(k≠0), 将点()1,0N -与A (m ,n )代入y=1k -x+b 2中, 2210=b k m n b k ⎧+⎪⎪⎨⎪=-+⎪⎩④⑤ ⊙-⊙得:-n=1k +m k,⊙ 联立方程⊙与方程⊙,得:41n mk k m n k k -=-⎧⎪⎨-=+⎪⎩解得:222411421k k m k k n k ⎧--=⎪⎪+⎨-⎪=⎪+⎩, ⊙点A 的坐标为(22411k k k --+,2421k k -+); 又⊙⊙F 关于直线l 的“特征数”是⊙F⊙NB·NA=即解得:,⊙[m -(-1)]2+(n -0)2)2, 即(m+1)2+n 2=10, 把222411421k k m k kn k ⎧--=⎪⎪+⎨-⎪=⎪+⎩代入,解得k=-3或k=13; 当k=-3时,m=2,n=1, ⊙点A 的坐标为(2,1),把点A (2,1)与点()1,4M 代入y=kx+b 1中,解得直线l 的解析式为y=-3x+7;当k=13时,m=-2,n=3, ⊙点A 的坐标为(-2,3),把点A (-2,3)与点()1,4M 代入y=kx+b 1中,解得直线l 的解析式为y=13x+113. ⊙直线l 的解析式为y=-3x+7或y=13x+113.。
2021年湖北省中考数学真题分类汇编:图形的性质(附答案解析)
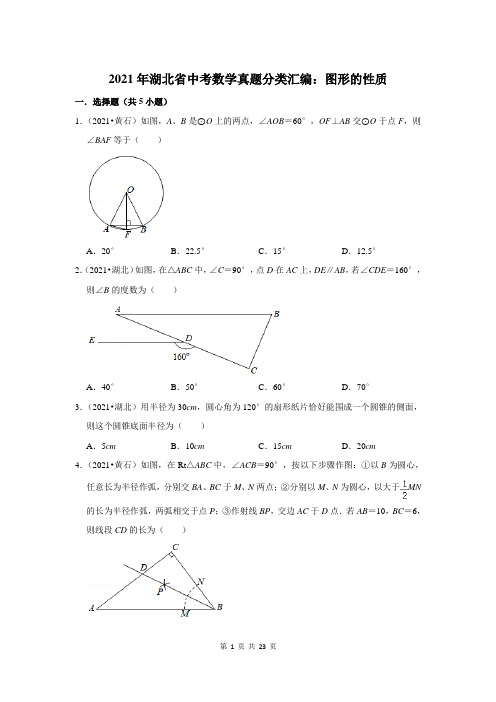
2021年湖北省中考数学真题分类汇编:图形的性质一.选择题(共5小题)1.(2021•黄石)如图,A、B是⊙O上的两点,∠AOB=60°,OF⊥AB交⊙O于点F,则∠BAF等于()A.20°B.22.5°C.15°D.12.5°2.(2021•湖北)如图,在△ABC中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=160°,则∠B的度数为()A.40°B.50°C.60°D.70°3.(2021•湖北)用半径为30cm,圆心角为120°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥底面半径为()A.5cm B.10cm C.15cm D.20cm 4.(2021•黄石)如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN 的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为()A.3B.C.D.5.(2021•鄂州)如图,Rt△ABC中,∠ACB=90°,AC=2,BC=3.点P为△ABC内一点,且满足P A2+PC2=AC2.当PB的长度最小时,△ACP的面积是()A.3B.3C.D.二.填空题(共4小题)6.(2021•随州)如图,⊙O是△ABC的外接圆,连接AO并延长交⊙O于点D,若∠C=50°,则∠BAD的度数为.7.(2021•十堰)如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为.8.(2021•十堰)如图,在边长为4的正方形ABCD中,以AB为直径的半圆交对角线AC 于点E,以C为圆心、BC长为半径画弧交AC于点F,则图中阴影部分的面积是.9.(2021•黄石)如图,在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=45°,AE交BD于M点,AF交BD于N点.(1)若正方形的边长为2,则△CEF的周长是.(2)下列结论:①BM2+DN2=MN2;②若F是CD的中点,则tan∠AEF=2;③连接MF,则△AMF为等腰直角三角形.其中正确结论的序号是(把你认为所有正确的都填上).三.解答题(共4小题)10.(2021•黄石)如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于E点,DE=EF.(1)求证:△ADE≌△CFE;(2)若AB=5,CF=4,求BD的长.11.(2021•黄石)如图,P A、PB是⊙O的切线,A、B是切点,AC是⊙O的直径,连接OP,交⊙O于点D,交AB于点E.(1)求证:BC∥OP;(2)若E恰好是OD的中点,且四边形OAPB的面积是16,求阴影部分的面积;(3)若sin∠BAC=,且AD=2,求切线P A的长.12.(2021•十堰)如图,已知AB是⊙O的直径,C为⊙O上一点,∠OCB的角平分线交⊙O 于点D,F在直线AB上,且DF⊥BC,垂足为E,连接AD、BD.(1)求证:DF是⊙O的切线;(2)若tan∠A=,⊙O的半径为3,求EF的长.13.(2021•湖北)如图1,已知∠RPQ=45°,△ABC中,∠ACB=90°,动点P从点A出发,以2cm/s的速度在线段AC上向点C运动,PQ,PR分别与射线AB交于E,F两点,且PE⊥AB,当点P与点C重合时停止运动,如图2,设点P的运动时间为xs,∠RPQ与△ABC的重叠部分面积为ycm2,y与x的函数关系由C1(0<x≤5)和C2(5<x ≤n)两段不同的图象组成.(1)填空:①当x=5s时,EF=cm;②sin A=;(2)求y与x的函数关系式,并写出x的取值范围;(3)当y≥36cm2时,请直接写出x的取值范围.2021年湖北省中考数学真题分类汇编:图形的性质参考答案与试题解析一.选择题(共5小题)1.(2021•黄石)如图,A、B是⊙O上的两点,∠AOB=60°,OF⊥AB交⊙O于点F,则∠BAF等于()A.20°B.22.5°C.15°D.12.5°【考点】圆心角、弧、弦的关系;圆周角定理.【专题】圆的有关概念及性质;推理能力.【分析】先根据垂径定理得到=,则∠AOF=∠BOF=30°,然后根据圆周角定理得到∠BAF的度数.【解答】解:∵OF⊥AB,∴=,∴∠AOF=∠BOF=∠AOB=×60°=30°,∴∠BAF=∠BOF=×30°=15°.故选:C.【点评】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理和圆心角、弧、弦的关系.2.(2021•湖北)如图,在△ABC中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=160°,则∠B的度数为()A.40°B.50°C.60°D.70°【考点】平行线的性质;三角形内角和定理.【专题】三角形;运算能力.【分析】利用平角的定义可得∠ADE=20°,再根据平行线的性质知∠A=∠ADE=20°,再由内角和定理可得答案.【解答】解:∵∠CDE=160°,∴∠ADE=20°,∵DE∥AB,∴∠A=∠ADE=20°,∴∠B=180°﹣∠A﹣∠C=180°﹣20°﹣90°=70°.故选:D.【点评】本题考查的是等腰三角形的性质,平行线的性质以及三角形内角和定理的运用,解题时注意:两直线平行,内错角相等.3.(2021•湖北)用半径为30cm,圆心角为120°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥底面半径为()A.5cm B.10cm C.15cm D.20cm【考点】圆锥的计算.【专题】与圆有关的计算;运算能力.【分析】圆锥的底面圆半径为rcm,根据圆锥的底面圆周长=扇形的弧长,列方程求解.【解答】解:设圆锥的底面圆半径为rcm,依题意,得2πr=,解得r=10.故选:B.【点评】本题考查了圆锥的计算.圆锥的侧面展开图为扇形,计算要体现两个转化:1、圆锥的母线长为扇形的半径,2、圆锥的底面圆周长为扇形的弧长.4.(2021•黄石)如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN 的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为()A.3B.C.D.【考点】角平分线的性质;勾股定理;作图—基本作图.【专题】作图题;几何直观.【分析】利用基本作图得BD平分∠ABC,过D点作DE⊥AB于E,如图,根据角平分线的性质得到则DE=DC,再利用勾股定理计算出AC=8,然后利用面积法得到•DE ×10+•CD×6=×6×8,最后解方程即可.【解答】解:由作法得BD平分∠ABC,过D点作DE⊥AB于E,如图,则DE=DC,在Rt△ABC中,AC===8,∵S△ABD+S△BCD=S△ABC,∴•DE×10+•CD×6=×6×8,即5CD+3CD=24,∴CD=3.故选:A.【点评】本题考查了作图﹣基本作图:熟练掌握基本作图(作已知角的角平分线).也考查了角平分线的性质.5.(2021•鄂州)如图,Rt△ABC中,∠ACB=90°,AC=2,BC=3.点P为△ABC内一点,且满足P A2+PC2=AC2.当PB的长度最小时,△ACP的面积是()A.3B.3C.D.【考点】三角形三边关系;直角三角形斜边上的中线;勾股定理;勾股定理的逆定理;圆周角定理;点与圆的位置关系.【专题】等腰三角形与直角三角形;圆的有关概念及性质;解直角三角形及其应用;推理能力.【分析】取AC中点O,连接OP,BO,由勾股定理的逆定理可求∠APC=90°,可得点P在以AC为直径的圆上运动,由三角形的三边关系可得BP≥BO﹣OP,当点P在线段BO上时,BP有最小值,由锐角三角函数可求∠BOC=60°,即可求解.【解答】解:取AC中点O,连接OP,BO,∵P A2+PC2=AC2,∴∠APC=90°,∴点P在以AC为直径的圆上运动,在△BPO中,BP≥BO﹣OP,∴当点P在线段BO上时,BP有最小值,∵点O是AC的中点,∠APC=90°,∴PO=AO=CO=,∵tan∠BOC==,∴∠BOC=60°,∴△COP是等边三角形,∴S△COP=OC2=×3=,∵OA=OC,∴△ACP的面积=2S△COP=,故选:D.【点评】本题考查了点与圆的位置关系,直角三角形的性质,锐角三角函数,勾股定理的逆定理等知识,找到BP最小值时,点P的位置是解题的关键.二.填空题(共4小题)6.(2021•随州)如图,⊙O是△ABC的外接圆,连接AO并延长交⊙O于点D,若∠C=50°,则∠BAD的度数为40°.【考点】圆周角定理;三角形的外接圆与外心.【专题】圆的有关概念及性质;运算能力;应用意识.【分析】连接BD,由圆周角定理的推论可知∠ABD=90°,因为∠C与∠ADB所对的弧为,所以∠ADB=∠C=50°.所以∠BAD=90°﹣∠ADB=90°﹣50°=40°.【解答】解:连接BD,如图.∵AD为直径,∴∠ABD=90°,∵∠C与∠ADB所对的弧为,∴∠ADB=∠C=50°.∴∠BAD=90°﹣∠ADB=90°﹣50°=40°.故答案为:40°.【点评】本题主要考查了圆周角定理的推论,直径所对的圆周角为直角,同弧所对的圆周角相等.掌握这些性质是及作出合适的辅助线是解题的关键.7.(2021•十堰)如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为20.【考点】三角形中位线定理;矩形的性质.【专题】几何图形问题.【分析】根据题意可知OM是△ADC的中位线,所以OM的长可求;根据勾股定理可求出AC的长,利用直角三角形斜边上的中线等于斜边的一半可求出BO的长,进而求出四边形ABOM的周长.【解答】解:∵O是矩形ABCD的对角线AC的中点,M是AD的中点,∴OM=CD=AB=2.5,∵AB=5,AD=12,∴AC==13,∵O是矩形ABCD的对角线AC的中点,∴BO=AC=6.5,∴四边形ABOM的周长为AB+AM+BO+OM=5+6+6.5+2.5=20,故答案为:20.【点评】本题考查了矩形的性质、三角形的中位线的性质以及直角三角形斜边上的中线等于斜边的一半这一性质,题目的综合性很好,难度不大.8.(2021•十堰)如图,在边长为4的正方形ABCD中,以AB为直径的半圆交对角线AC 于点E,以C为圆心、BC长为半径画弧交AC于点F,则图中阴影部分的面积是3π﹣6.【考点】正方形的性质;圆周角定理;扇形面积的计算.【专题】矩形菱形正方形;圆的有关概念及性质;运算能力.【分析】根据扇形的面积公式和三角形面积公式即可得到结论.【解答】解:连接BE,∵AB为直径,∴BE⊥AC,∵AB=BC=4,∠ABC=90°,∴BE=AE=CE,∴S弓形AE=S弓形BE,∴图中阴影部分的面积=S半圆﹣(S半圆﹣S△ABE)﹣(S△ABC﹣S扇形CBF)=π×22﹣(﹣)﹣(﹣)=3π﹣6,故答案为3π﹣6.【点评】本题考查了扇形面积的计算,正方形的性质,正确的识别图形是解题的关键.9.(2021•黄石)如图,在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=45°,AE交BD于M点,AF交BD于N点.(1)若正方形的边长为2,则△CEF的周长是4.(2)下列结论:①BM2+DN2=MN2;②若F是CD的中点,则tan∠AEF=2;③连接MF,则△AMF为等腰直角三角形.其中正确结论的序号是①③(把你认为所有正确的都填上).【考点】全等三角形的判定与性质;勾股定理;等腰直角三角形;正方形的性质;解直角三角形.【专题】图形的全等;等腰三角形与直角三角形;矩形菱形正方形;图形的相似;几何直观;推理能力;应用意识.【分析】(1)过A作AG⊥AE,交CD延长线于G,证明△ABE≌△ADG,得BE=DG,AG=AE,由∠EAF=45°,证明△EAF≌△GAF,得EF=GF,故△CEF的周长:EF+EC+CF=GF+EC+CF=CD+BC,即可得答案;(2)①将△ABM绕点A逆时针旋转90°得到△ADH,连接NH,证明△AMN≌△AHN,可得MN=HN,Rt△HDN中,有HN2=DH2+DN2,即得MN2=BM2+DN2,故①正确;②过A作AG⊥AE,交CD延长线于G,设DF=x,BE=DG=y,Rt△EFC中,(2x﹣y)2+x2=(x+y)2,解得x=y,即=,设x=3m,则y=2m,Rt△ADG中,tan G===3,即得tan∠AEF=3,故②不正确;③由∠MAN=∠NDF=45°,∠ANM=∠DNF,得△AMN∽△DFN,有=,可得△ADN∽△MFN,从而∠MFN=∠ADN=45°,△AMF为等腰直角三角形,故③正确.【解答】解:(1)过A作AG⊥AE,交CD延长线于G,如图:∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠ABC=∠ADC=90°,∴∠BAE=90°﹣∠EAD=∠DAG,∠ABE=∠ADG=90°,在△ABE和△ADG中,,∴△ABE≌△ADG(ASA),∴BE=DG,AG=AE,∵∠EAF=45°,∴∠EAF=∠GAF=45°,在△EAF和△GAF中,,∴△EAF≌△GAF(SAS),∴EF=GF,∴△CEF的周长:EF+EC+CF=GF+EC+CF=(DG+DF)+EC+CF=DG+(DF+EC)+CF=BE+CD+CF=CD+BC,∵正方形的边长为2,∴△CEF的周长为4;故答案为:4;(2)①将△ABM绕点A逆时针旋转90°得到△ADH,连接NH,∵∠EAF=45°,∴∠EAF=∠HAF=45°,∵△ABM绕点A逆时针旋转90°得到△ADH,∴AH=AM,BM=DH,∠ABM=∠ADH=45°,又AN=AN,∴△AMN≌△AHN(SAS),∴MN=HN,而∠NDH=∠ABM+∠ADH=45°+45°=90°,Rt△HDN中,HN2=DH2+DN2,∴MN2=BM2+DN2,故①正确;②过A作AG⊥AE,交CD延长线于G,如图:由(1)知:EF=GF=DF+DG=DF+BE,∠AEF=∠G,设DF=x,BE=DG=y,则CF=x,CD=BC=AD=2x,EF=x+y,CE=BC﹣BE=2x﹣y,Rt△EFC中,CE2+CF2=EF2,∴(2x﹣y)2+x2=(x+y)2,解得x=y,即=,设x=3m,则y=2m,∴AD=2x=6m,DG=2m,Rt△ADG中,tan G===3,∴tan∠AEF=3,故②不正确;③∵∠MAN=∠NDF=45°,∠ANM=∠DNF,∴△AMN∽△DFN,∴=,即=,又∠AND=∠FNM,∴△ADN∽△MFN,∴∠MFN=∠ADN=45°,∴∠MAF=∠MF A=45°,∴△AMF为等腰直角三角形,故③正确,故答案为:①③.【点评】本题考查正方形性质及应用,涉及全等三角形的判定与性质、旋转变换、相似三角形的判定及性质、勾股定理等知识,综合性较强,解题的关键是根据题意作出辅助线,构造全等三角形.三.解答题(共4小题)10.(2021•黄石)如图,D是△ABC的边AB上一点,CF∥AB,DF交AC于E点,DE=EF.(1)求证:△ADE≌△CFE;(2)若AB=5,CF=4,求BD的长.【考点】全等三角形的判定与性质.【专题】证明题;推理能力.【分析】(1)利用角角边定理判定即可;(2)利用全等三角形对应边相等可得AD的长,用AB﹣AD即可得出结论.【解答】(1)证明:∵CF∥AB,∴∠ADF=∠F,∠A=∠ECF.在△ADE和△CFE中,,∴△ADE≌△CFE(AAS).(2)∵△ADE≌△CFE,∴AD=CF=4.∴BD=AB﹣AD=5﹣4=1.【点评】本题主要考查了全等三角形的判定与性质.选择合适的判定方法是解题的关键.11.(2021•黄石)如图,P A、PB是⊙O的切线,A、B是切点,AC是⊙O的直径,连接OP,交⊙O于点D,交AB于点E.(1)求证:BC∥OP;(2)若E恰好是OD的中点,且四边形OAPB的面积是16,求阴影部分的面积;(3)若sin∠BAC=,且AD=2,求切线P A的长.【考点】圆的综合题.【专题】几何综合题;推理能力.【分析】(1)证明OP⊥AB,BC⊥AB,可得结论.(2)设OE=m,用m的代数式表示AB,OP,构建方程求出m,求出OA,AB,OE,再根据S阴=S扇形OAB﹣S△AOB,求解即可.(3)在Rt△AOE中,sin∠CAB==,可以假设OE=x,则OA=OD=3x,DE=2x,AE===2x,在Rt△ADE中,根据AD2=AE2+DE2,构建方程求出x,再证明sin∠APE=sin∠CAB==,可得结论.【解答】(1)证明:∵P A,PB是⊙O的切线,∴P A=PB,∵OA=OB,∴OP⊥AB,∵AC是直径,∴∠ABC=90°,∴BC⊥AB,∴BC∥OP.(2)解:∵OE=DE,AB⊥OD,∴AO=AD,∵OA=OD,∴AD=OA=OD,∴△AOD是等边三角形,∴∠AOD=60°,设OE=m,则AE=BE=m,OA=2m,OP=4m,∵四边形OAPB的面积是16,∴•OP•AB=16,∴×4m×2m=16,∴m=2或﹣2(舍弃),∴OE=2,AB=4,OA=2m=4,∵OD⊥AB,∴=,∴∠AOD=∠BOD=60°,∴∠AOB=2∠AOD=120°,∴S阴=S扇形OAB﹣S△AOB=﹣×4×2=﹣4.(3)解:在Rt△AOE中,sin∠CAB==,∴可以假设OE=x,则OA=OD=3x,DE=2x,AE===2x,在Rt△ADE中,AD2=AE2+DE2,∴(2)2=(2x)2+(2x)2,∴x=1或﹣1(舍弃),∴OE=1,OA=3,AE=2,∵P A是切线,∴P A⊥OA,∴∠OAP=90°,∴∠CAB+∠BAD=90°,∠APO+∠P AE=90°,∴∠CAB=∠APO,∴sin∠APE=sin∠CAB==,∴P A=3AE=6.【点评】本题属于圆综合题,考查了切线长定理,垂径定理,解直角三角形,等边三角形的判定和性质,四边形的面积等知识,解题的关键是学会利用参数构建方程解决问题,属于中考压轴题.12.(2021•十堰)如图,已知AB是⊙O的直径,C为⊙O上一点,∠OCB的角平分线交⊙O 于点D,F在直线AB上,且DF⊥BC,垂足为E,连接AD、BD.(1)求证:DF是⊙O的切线;(2)若tan∠A=,⊙O的半径为3,求EF的长.【考点】勾股定理;切线的判定与性质;平行线分线段成比例;锐角三角函数的定义;解直角三角形.【专题】圆的有关概念及性质;推理能力.【分析】(1)连接OD,则∠ODC=∠OCD,CD平分∠OCB,则∠OCD=∠BCD=∠ODC,所以OD∥CE,又CE⊥DF,则OD⊥DF,所以DF是⊙O的切线;(2)在Rt△ABD中,tan∠A==,则AD=2BD,由勾股定理可得,BD2+AD2=AB2,即BD2+(2BD)2=62,解得BD=,在Rt△BDE中,BD=,由勾股定理可得,BE2+DE2=BD2,即BE2+(2BE)2=()2,解得BE=,则DE=,由(1)知BE∥OD,=,即=,解得EF=.【解答】解:(1)如图,连接OD,∵OC=OD,∴∠ODC=∠OCD,∵CD平分∠OCB,∴∠OCD=∠BCD,∴∠ODC=∠BCD,∴OD∥CE,∴∠CEF=∠ODE,∵CE⊥DF,∴∠CEF=90°,∴∠ODE=90°,即OD⊥DF,∴DF是⊙O的切线;(2)∵AB是⊙O的直径,∴∠ADB=90°,∴tan∠A==,则AD=2BD,在Rt△ABD中,∠ADB=90°,AB=2r=6,∴BD2+AD2=AB2,即BD2+(2BD)2=62,解得BD=,由(1)知DF是⊙O的切线,∴∠BDF=∠A,∵BE⊥DF,∴∠BEF=90°,∴tan∠BDF==,则DE=2BE,在Rt△BDE中,BD=,由勾股定理可得,BE2+DE2=BD2,即BE2+(2BE)2=()2,解得BE=,则DE=,由(1)知BE∥OD,∴=,即=,解得EF=.【点评】本题主要考查切线的性质和判定,三角函数,勾股定理,平行线分线段成比例等内容,要判定切线需证明垂直,作出正确的辅助线是解题关键.13.(2021•湖北)如图1,已知∠RPQ=45°,△ABC中,∠ACB=90°,动点P从点A出发,以2cm/s的速度在线段AC上向点C运动,PQ,PR分别与射线AB交于E,F两点,且PE⊥AB,当点P与点C重合时停止运动,如图2,设点P的运动时间为xs,∠RPQ与△ABC的重叠部分面积为ycm2,y与x的函数关系由C1(0<x≤5)和C2(5<x ≤n)两段不同的图象组成.(1)填空:①当x=5s时,EF=10cm;②sin A=;(2)求y与x的函数关系式,并写出x的取值范围;(3)当y≥36cm2时,请直接写出x的取值范围.【考点】三角形综合题.【专题】几何综合题;推理能力.【分析】(1)当x=5时,如图3中,点F与B重合.利用三角形的面积公式求出EF,PE,可得结论.(2)分两种情形:当0<x≤5时,重叠部分是△PEF,当5<x≤6时,如图4中,重叠部分是四边形PTBE,分别利用三角形面积公式求解即可.(3)求出y=36时,对应的x的值,可得结论.【解答】解:(1)当x=5时,如图3中,点F与B重合.∵∠RPQ=45°,PE⊥AB,∴∠PEF=90°,∴∠EPF=∠PFE=45°,∴EF=EP,由题意•EF•PE=50,∴EF=PE=10(cm),∵AP=5×2=10(cm),∴sin A===.故答案为:10,.(2)当0<x≤5时,重叠部分是△PEF,y=×(×2x)2=2x2.如图3中,在Rt△APE中,AE===20(cm),∴AB=EF+AE=30(cm),∴BC=AB=6(cm),∴AC===12,∴点P从A运动到C的时间x==6,当5<x≤6时,如图4中,重叠部分是四边形PTBE,作BL∥PF交AC于L,过点L作LJ⊥AB于J,LK⊥AC交AB于K,过点B作BH⊥PF于H.∵BL∥PF,∴∠LBJ=∠PFE=45°,∴△BLJ是等腰直角三角形,∴BJ=LJ=10(cm),BL=10(cm),∵tan A==,∴LK=5,AK=25,∴BK=AB﹣AK=30﹣25=5,∵BC∥KL,∴∠FBT=∠BKL,∴△FBT∽△BKL,∴=,∴=,∴FT=(12x﹣60)(cm),∵BH=BF=(6x﹣30)=3x﹣15,∴y=S△PEF﹣S△BTF=×2x×2x﹣×(12x﹣60)•(3x﹣15)=﹣34x2+360x ﹣900.综上所述,y=.(3)当y=36时,2x2=36,x=3,﹣34x2+360x﹣900=36,解得x=6或,∵<5,∴x=不符合题意舍弃,观察图象可知,满足条件的x的值为3≤x≤6.【点评】本题属于三角形综合题,考查了解直角三角形,三角形的面积,相似三角形的判定和性质等知识,解题的关键是读懂图象信息,学会添加常用辅助线,构造相似三角形解决问题.。
专题16 几何类压轴题-湖北省2019-2021年3年中考真题数学分项汇编(解析版)

专题16 几何类压轴题一、单选题1.(2021·湖北中考真题)如图,在正方形ABCD 中,4AB =,E 为对角线AC 上与A ,C 不重合的一个动点,过点E 作EF AB ⊥于点F ,EG BC ⊥于点G ,连接,DE FG .下列结论:①DE FG =;②DE FG ;③BFG ADE ∠=∠;④FG 的最小值为3.其中正确结论的个数有( ) A .1个B .2个C .3个D .4个 【答案】C【分析】延长DE ,交FG 于点N ,交AB 于点M ,连接BE ,交FG 于点O ,先根据正方形的性质、三角形全等的判定定理与性质得出DE BE =,再根据矩形的判定与性质可得BE FG =,由此可判断①;先根据三角形全等的性质可得ABE ADE ∠=∠,再根据矩形的性质可得OB OF =,然后根据等腰三角形的性质可得BFG ABE ∠=∠,由此可判断③;根据直角三角形的性质可得90ADE AMD ∠+∠=︒,从而可得90BFG AMD ∠+∠=︒,由此可判断②;先根据垂线段最短可得当DE AC ⊥时,DE 取得最小值,再解直角三角形可得DE 的最小值,从而可得FG 的最小值,由此可判断④.【详解】解:如图,延长DE ,交FG 于点N ,交AB 于点M ,连接BE ,交FG 于点O ,四边形ABCD 是正方形,4AB =,4,90,45AD AB ABC BAD BAE DAE ∴==∠=∠=︒∠=∠=︒,在ABE △和ADE 中,AB AD BAE DAE AE AE =⎧⎪∠=∠⎨⎪=⎩,()ABE ADE SAS ∴≅,,BE DE ABE ADE ∴=∠=∠,90,,ABC EF AB EG BC ∠=︒⊥⊥,∴四边形BFEG 是矩形,,BE FG OB OF ∴==,DE FG ∴=,即结论①正确;OB OF =,BFG ABE ∴∠=∠,BFG ADE ∴∠=∠,即结论③正确;90BAD ∠=︒,90ADE AMD ∴∠+∠=︒,90BFG AMD ∴∠+∠=︒,90FNM ∴∠=︒,即DE FG ,结论②正确;由垂线段最短可知,当DE AC ⊥时,DE 取得最小值,此时在Rt ADE △中,sin 42DE AD DAE =⋅∠=⨯= 又DE FG =,FG ∴的最小值与DE 的最小值相等,即为④错误;综上,正确的结论为①②③,共有3个,故选:C .【点睛】本题考查了正方形的性质、三角形全等的判定定理与性质、解直角三角形等知识点,通过作辅助线,构造全等三角形和直角三角形是解题关键.2.(2020·湖北省直辖县级行政单位·中考真题)如图,已知ABC 和ADE 都是等腰三角形,90BAC DAE ∠=∠=︒,,BD CE 交于点F ,连接AF ,下列结论:①BD CE =;②BF CF ⊥;③AF 平分CAD ∠;④45AFE ∠=︒.其中正确结论的个数有( )A .1个B .2个C .3个D .4个【答案】C【分析】 ①证明△BAD△△CAE,再利用全等三角形的性质即可判断;②由△BAD△△CAE 可得△ABF=△ACF ,再由△ABF+△BGA=90°、△BGA=△CGF 证得△BFC=90°即可判定;③分别过A 作AM△BD 、AN△CE,根据全等三角形面积相等和BD=CE ,证得AM=AN,即AF 平分△BFE,即可判定;④由AF 平分△BFE 结合BF CF ⊥即可判定.【详解】解:△△BAC=△EAD△△BAC+△CAD=△EAD+△CAD,即△BAD=△CAE在△BAD 和△CAE 中AB=AC, △BAD=△CAE,AD=AE△△BAD△△CAE△BD=CE故①正确;△△BAD△△CAE△△ABF=△ACF△△ABF+△BGA=90°、△BGA=△CGF△△ACF+△BGA=90°,△△BFC=90°故②正确;分别过A作AM△BD、AN△CE垂足分别为M、N △△BAD△△CAE△S△BAD=S△CAE,△1122BD AM CE AN ⋅=⋅△BD=CE△AM=AN△AF平分△BFE,无法证明AF平分△CAD.故③错误;△AF 平分△BFE ,BF CF ⊥△45AFE ∠=︒故④正确.故答案为C .【点睛】本题考查了全等三角形的判定与性质、角平分线的判定与性质以及角的和差等知识,其中正确应用角平分线定理是解答本题的关键.3.(2020·湖北荆门市·中考真题)在平面直角坐标系中,长为2的线段CD (点D 在点C 右侧)在x 轴上移动()0,2A ,()0,4B ,连接AC 、BD ,则AC BD +的最小值为( )A .B .C .D .【答案】B【分析】 作A (0,2)关于x 轴的对称点A’(0,-2),再过A’作A’E△x 轴且A’E=CD=2,连接BE 交x 轴与D 点,过A’作A’C△DE 交x 轴于点C ,得到四边形CDEA’为平行四边形,故可知AC+BD 最短等于BE 的长,再利用勾股定理即可求解.【详解】作A (0,2)关于x 轴的对称点A’(0,-2)过A’作A’E△x 轴且A’E=CD=2,故E (2,-2)连接BE 交x 轴与D 点过A’作A’C△DE 交x 轴于点C ,△四边形CDEA’为平行四边形,此时AC+BD 最短等于BE 的长,即故选B .【点睛】此题主要考查最短路径的求解,解题的关键是熟知直角坐标系、平行四边形的性质.4.(2019·湖北黄石市·中考真题)如图,矩形ABCD 中,AC 与BD 相交于点E ,:AD AB =,将ABD △沿BD 折叠,点A 的对应点为F ,连接AF 交BC 于点G ,且2BG =,在AD 边上有一点H ,使得BH EH +的值最小,此时BH CF=( )A B C D .32【答案】B【分析】设BD 与AF 交于点M .设AB=a ,,根据矩形的性质可得△ABE 、△CDE 都是等边三角形,利用折叠的性质得到BM 垂直平分AF ,BF=AB=a ,.解直角△BGM ,求出BM ,再表示DM ,由△ADM△△GBM ,求出B 点关于AD 的对称点B′,连接B′E ,设B′E 与AD 交于点H ,则此时BH+EH=B′E ,值最小.建立平面直角坐标系,得出B (3,,B′(3,-,E (0,利用待定系数法求出直线B′E 的解析式,得到H (1,0),然后利用两点间的距离公式求出BH=4,进而求出BH CF =【详解】如图,设BD 与AF 交于点M .设AB=a ,,△四边形ABCD 是矩形,△△DAB=90°,tan△ABD=1AD AB =,,△ABD=60°,△△ABE 、△CDE 都是等边三角形,△BE=DE=AE=CE=AB=CD=a ,△将△ABD 沿BD 折叠,点A 的对应点为F ,△BM 垂直平分AF ,BF=AB=a ,,在△BGM 中,△△BMG=90°,△GBM=30°,BG=2,△GM=12BG=1,△DM=BD -BM=2a△矩形ABCD 中,BC△AD ,△△ADM△△GBM ,△AD DM BG BM ==,AD=BC=6,易证△BAF=△FAC=△CAD=△ADB=△BDF=△CDF=30°,△△ADF 是等边三角形,△AC 平分△DAF ,△AC 垂直平分DF ,作B 点关于AD 的对称点B′,连接B′E ,设B′E 与AD 交于点H ,则此时BH+EH=B′E ,值最小.如图,建立平面直角坐标系,则A (3,0),B (3,,B′(3,-,E (0,易求直线B′E 的解析式为y=△H (1,0),,△BH CF ==3. 故选B .本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质,解直角三角形,等边三角形、垂直平分线、相似三角形的判定与性质,待定系数法求直线的解析式,轴对称-最短路线问题,两点间的距离公式等知识.综合性较强,有一定难度.分别求出BH 、CF 的长是解题的关键.二、填空题5.(2021·湖北黄冈市·中考真题)如图,正方形ABCD 中,1AB =,连接AC ,ACD ∠的平分线交AD 于点E ,在AB 上截取AF DE =,连接DF ,分别交CE ,AC 于点G ,H ,点P 是线段GC 上的动点,PQ AC ⊥于点Q ,连接PH .下列结论:①CE DF ⊥;②DE DC AC +=;③EA =;④PH PQ +的_____.【答案】①②④【分析】先根据SAS 定理证出ADF DCE ≅,从而可得ADF DCE ∠=∠,再根据角的和差即可判断结论①;根据等腰三角形的性质可得,DC CH AF AH ==,然后根据线段的和差、等量代换即可判断结论②;先根据正方形的性质可得AC 1DC CH ==可得1DE AF AH ===,从而可得2EA =③;过点P 作PM CD ⊥于点M ,连接HM ,先根据角平分线的性质可得PM PQ =,再根据两点之间线段最短、垂线段最短可得当HM CD ⊥时,PH PQ +取得最小值,然后解直角三角形即可得判断结论④.解:四边形ABCD 是正方形,1AB =,1,90,45,//CD AD AC ADC DAF ACD AB CD ∴==∠=∠=︒∠=︒,在ADF 和DCE 中,90AD DC DAF CDE AF DE =⎧⎪∠=∠=︒⎨⎪=⎩,()ADF DCE SAS ∴≅,ADF DCE ∴∠=∠,18090DCE DEG CDE ∠+∠=︒-∠=︒,90ADF DEG ∴∠+∠=︒,90DGE ∴∠=︒,即CE DF ⊥,结论①正确; CE 平分ACD ∠,CE DF ⊥,1CH DC ∴==,CDH CHD AHF ∴∠=∠=∠,//AB CD ,CDH AFH ∴∠=∠,AFH AHF ∴∠=∠,AF AH ∴=,AF DE =DE DC AF CH AH CH AC ∴+=+=+=,结论②正确;1,CH AC =1DE AF AH AC CH ∴===-=,)112EA AD DE ∴=-=-=EA AH ∴==即EA =,结论③错误;如图,过点P 作PM CD ⊥于点M ,连接HM ,CE 平分ACD ∠,PM CD ⊥,PQ AC ⊥,PM PQ ∴=,PH PQ PH PM +=+∴,由两点之间线段最短得:当点,,H P M 共线时,PH PM +取得最小值HM ,由垂线段最短得:当HM CD ⊥时,HM 取得最小值,此时在Rt CHM 中,sin sin 452HM CH ACD =⋅∠=︒=,即PH PQ +④正确; 综上,所有正确结论的序号是①②④,故答案为:①②④.【点睛】本题考查了正方形的性质、等腰三角形的性质、解直角三角形等知识点,较难的是④,利用两点之间线段最短、垂线段最短得出当HM CD ⊥时,HM 取最小值是解题关键.6.(2020·湖北随州市·中考真题)如图,已知矩形ABCD 中,3AB =,4BC =,点M ,N 分别在边AD ,BC 上,沿着MN 折叠矩形ABCD ,使点A ,B 分别落在E ,F 处,且点F 在线段CD 上(不与两端点重合),过点M 作MH BC ⊥于点H ,连接BF ,给出下列判断:①MHN BCF ∽;②折痕MN 的长度的取值范围为1534MN <<;③当四边形CDMH 为正方形时,N 为HC 的中点;④若13DF DC =,则折叠后重叠部分的面积为5512.其中正确的是_____.(写出所有正确判断的序号).【答案】①②③④【分析】由题意,逐一判定,①由折叠的性质以及等腰三角形三线合一的性质即可判定;②根据题意点F在线段CD上(不与两端点重合),假设F分别在C、D两点,即可得出其取值范围;③由相似三角形、正方形的性质以及勾股定理构建方程,即可判定;④由相似三角形以及勾股定理,得出梯形MEFN的面积和△MEO 的面积,即可得解;【详解】由折叠性质,得,BG=FG,BN=FN△BF△MN△△BIH=△MIG,MH BC⊥△△HBI=△GMI△△MHN=△BCF=90°△MHN BCF∽故①结论正确;假设F与C重合时,MN取得最小值,即为3;假设F与D重合时,MN取得最大值,△MHN BCF∽△MH BC MN BF=△MH=3,BC=4,5BF==△154 MN=△点F 在线段CD 上(不与两端点重合)△折痕MN 的长度的取值范围为1534MN <<故②结论正确;△四边形CDMH 为正方形△MH=HC=3△BH=1△MHN BCF ∽ △MH BC HN CF= 令HN x =,则3CN x =-,1FN BN x ==+△CF ==△3x =△132x =,23x =(不符合题意,舍去) △12HN HC =,即N 为HC 的中点 故③结论正确;④△13DF DC =,AB=CD=3 △DF=1,CF=2△BF ===△MHN BCF ∽ △MH BC HN CF= △HN=32 △△FGN△△MHN△52FN ===△32CN === △BH=BC -HN -NC=4-32-32=1 △△EMO=△CNF ,△MEO=△NCF=90°△△MEO△△NCF△ME NC EO CF= △EO=43 △折叠后重叠部分的面积为: ()1115145513122222312MEO MEFN S S ME FN EF ME EO ⎛⎫-=+⨯-⨯=+⨯-⨯⨯= ⎪⎝⎭△梯形 故④结论正确; 故答案为:①②③④.【点睛】此题主要考查矩形的折叠性质以及相似三角形的综合运用,熟练掌握,即可解题.7.(2020·湖北武汉市·中考真题)如图,折叠矩形纸片ABCD ,使点D 落在AB 边的点M 处,EF 为折痕,1AB =,2AD =.设AM 的长为t ,用含有t 的式子表示四边形CDEF 的面积是________.【答案】211144t t -+ 【分析】 首先根据题意可以设DE =EM =x ,在三角形AEM 中用勾股定理进一步可以用t 表示出x ,再可以设CF =y ,连接MF ,所以BF =2−y ,在三角形MFN 与三角形MFB 中利用共用斜边,根据勾股定理可求出用t 表示出y ,进而根据四边形的面积公式可以求出答案.【详解】设DE =EM =x ,△222(2)x x t =-+,△x =244t + , 设CF =y ,连接FM ,△BF =2−y ,又△FN = y ,NM =1,△22221(2)(1)y y t +=-+-,△y =2244t t -+, △四边形CDEF 的面积为:1()2x y CD +=221424()244t t t +-++∙1, 故答案为:211144t t -+. 【点睛】本题主要考查了勾股定理的综合运用,熟练掌握技巧性就可得出答案.8.(2021·湖北襄阳市·中考真题)如图,正方形ABCD 的对角线相交于点O ,点E 在边BC 上,点F 在CB 的延长线上,45EAF ∠=︒,AE 交BD 于点G ,1tan 2BAE ∠=,2BF =,则FG =______.【答案】【分析】作出如图所示的辅助线,利用SAS 证明△ADH ≅△ABF 以及△EAF ≅△EAH ,在Rt △ABE 中,利用勾股定理求得正方形的边长,再证明△BAF ~△OAG ,即可求解.【详解】解:如图,在CD 上取点H ,使DH =BF =2,连接EH 、AH ,△四边形ABCD 是正方形,△△ADH =△ABC =△ABF =90°,AD =AB ,△BAC =△DAC =45°,△△ADH ≅△ABF (SAS ),△△DAH =△BAF ,AH =AF ,△△EAF =45°,即△BAF +△EAB =45°,△△DAH +△EAB =45°,则△EAH =45°,△△EAF =△EAH =45°,△△EAF ≅△EAH (SAS ),△EF =EH , △1tan 2BE BAE AB ∠==, 设BE =a ,则AB =2a ,EC =a ,CH =2a -2,EF =EH =a +2,在Rt △CEH 中,222EC CH EH +=,即()()222222a a a +-=+, 解得:3a =,则AB =AD =6,BE =EC =3,在Rt △ABE 中,222AB BE AE +=,△AE同理AF ,AO =AB sin 45︒△BE △AD , △12EG BE AG AD ==,△AG△AO AG ==AB AF ==, △AO AB AG AF =, △△EAF =△BAC =45°,△△BAF =△OAG ,△△BAF ~△OAG ,△::AG AF AO AB ==△△GAF =△OAB =45°,△△GAF 是等腰直角三角形,△FG = AG故答案为:【点睛】本题主要考查了四边形综合题,熟练掌握正方形的性质,全等三角形的判定及性质,相似三角形的判定和性质,锐角三角函数是解题的关键.9.(2020·湖北恩施土家族苗族自治州·中考真题)如图,在平面直角坐标系中,ABC 的顶点坐标分别为:()2,0A -,()1,2B ,()1,2C -.已知()1,0N -,作点N 关于点A 的对称点1N ,点1N 关于点B 的对称点2N ,点2N 关于点C 的对称点3N ,点3N 关于点A 的对称点4N ,点4N 关于点B 的对称点5N ,…,依此类推,则点2020N 的坐标为______.【答案】(-1,8)【分析】先求出N1至N6点的坐标,找出其循环的规律为每6个点循环一次即可求解.【详解】解:由题意得,作出如下图形:N点坐标为(-1,0),N点关于A点对称的N1点的坐标为(-3,0),N1点关于B点对称的N2点的坐标为(5,4),N2点关于C点对称的N3点的坐标为(-3,8),N3点关于A点对称的N4点的坐标为(-1,8),N4点关于B点对称的N5点的坐标为(3,-4),N 5点关于C 点对称的N 6点的坐标为(-1,0),此时刚好回到最开始的点N 处,△其每6个点循环一次,△20206=3364÷,即循环了336次后余下4,故2020N 的坐标与N 4点的坐标相同,其坐标为(-1,8) .故答案为:(-1,8) .【点睛】本题考查了平面直角坐标系内点的对称规律问题,本题需要先去验算前面一部分点的坐标,进而找到其循环的规律后即可求解.10.(2019·湖北武汉市·中考真题)问题背景:如图,将ABC ∆绕点A 逆时针旋转60°得到ADE ∆,DE 与BC 交于点P ,可推出结论:PA PC PE +=问题解决:如图,在MNG ∆中,6MN =,75M ∠=︒,MG =O 是MNG ∆内一点,则点O 到MNG ∆三个顶点的距离和的最小值是___________【答案】【分析】如图,将△MOG 绕点M 逆时针旋转60°,得到△MPQ ,易知△MOP 为等边三角形,继而得到点O 到三顶点的距离为:ON +OM +OG =ON +OP +PQ ,由此可以发现当点N 、O 、P 、Q 在同一条直线上时,有ON +OM +OG 最小,此时,△NMQ =75°+60°=135°,过Q 作QA△NM 交NM 的延长线于A ,利用勾股定理进行求解即可得.【详解】如图,将△MOG 绕点M 逆时针旋转60°,得到△MPQ ,显然△MOP 为等边三角形,△,OM +OG =OP +PQ ,△点O 到三顶点的距离为:ON +OM +OG =ON +OP +PQ ,△当点N 、O 、P 、Q 在同一条直线上时,有ON +OM +OG 最小,此时,△NMQ =75°+60°=135°,过Q 作QA△NM 交NM 的延长线于A ,则△MAQ=90°,△△AMQ =180°-△NMQ=45°,△MQ =MG =△AQ =AM =MQ•cos45°=4,△NQ ==故答案为【点睛】本题考查了旋转的性质,最短路径问题,勾股定理,解直角三角形等知识,综合性较强,有一定的难度,正确添加辅助线是解题的关键.三、解答题11.(2021·湖北襄阳市·中考真题)在ABC 中,90ACB ∠=︒,AC m BC =,D 是边BC 上一点,将ABD △沿AD 折叠得到AED ,连接BE .(1)特例发现:如图1,当1m =,AE 落在直线AC 上时,①求证:DAC EBC ∠=∠;②填空:CD CE的值为______; (2)类比探究:如图2,当1m ≠,AE 与边BC 相交时,在AD 上取一点G ,使ACG BCE ∠=∠,CG 交AE 于点H .探究CG CE 的值(用含m 的式子表示),并写出探究过程;(3)拓展运用:在(2)的条件下,当2m =,D 是BC 的中点时,若6EB EH ⋅=,求CG 的长.【答案】(1)①见解析;②1;(2)CGm CE=,见解析;(3)CG = 【分析】(1)①根据折叠性质证明即可;②当1m =,证明ACD ≌BCE ,即可得出CDCE的值; (2)延长AD 交BE 于点F ,根据折叠性质证明ACG BCE △∽△,即可得出结论;(3)由(2)可知2AG CG AC m BE CE BC ====,设CG x =,则AG =,CE =,2BE x =,可得AGH ECH ≌△△,再由勾股定理列方程求解即可. 【详解】解:(1)①证明:延长AD 交BE 于点F .由折叠得90AFB ACB ∠=︒=∠.△90DAC ADC BDF EBC ∠+∠=∠+∠=︒. △ADC BDF ∠=∠, △DAC EBC ∠=∠. ②当1m =,即1ACBC=时,可知AC =BC ,在ACD △和BCE 中,90DAC EBC ACD BCE AC BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩, △ACD ≌BCE (AAS ), △CD CE =, △1CDCE=. 故答案为:1; (2)解:CGm CE=. 理由:延长AD 交BE 于点F ,由折叠得90AFB ACB ∠=︒=∠.△90ADC DAC BDF CBE ∠+∠=∠+∠=︒, △ADC BDF ∠=∠, △DAC CBE ∠=∠, △ACG BCE ∠=∠, △ACG BCE △∽△, △CG ACm CE BC==. (3)解:由折叠得90AFB ∠=︒,BF FE =, △D 是BC 的中点, △//DF CE ,△90BEC BFD ∠=∠=︒,AGC ECG ∠=∠,GAH CEA ∠=∠,由(2)知ACG BCE △∽△, △90AGC BEC ∠=∠=︒,AG CG AC m BE CE BC ====, D 是BC 的中点,2,BC CD ∴=△ACCD=, △tanCG DC GAC AG AC =∠==,设CG x =,则AG =,CE =,2BE x =,△AG CE =,,,GAH HEC AHG CHE ∠=∠∠=∠△AGH ECH ≌△△, △AH EH =,GH CH =, △12GH x =,在Rt AGH 中,由勾股定理得32AH x EH ===, △6EB EH ⋅=, △3262x x ⋅=,解得x =,△CG =. 【点睛】本题为三角形综合题,考查折叠的性质,全等三角形判定与性质,相似三角形的判定及性质,勾股定理等知识点,根据折叠性质找到角度之间的关系是解题的关键.12.(2021·湖北宜昌市·中考真题)如图,在矩形ABCD 中,E 是边AB 上一点,BE BC =,EF CD ⊥,垂足为F .将四边形CBEF 绕点C 顺时针旋转()090αα︒<<︒,得到四边形CB E F '''.B E ''所在的直线分别交直线BC 于点G ,交直线AD 于点P ,交CD 于点K .E F ''所在的直线分别交直线BC 于点H ,交直线AD 于点Q ,连接B F ''交CD 于点O .(1)如图1,求证:四边形BEFC 是正方形; (2)如图2,当点Q 和点D 重合时. ①求证:GC DC =;②若1OK =,2CO =,求线段GP 的长;(3)如图3,若//BM F B ''交GP 于点M ,1tan 2G ∠=,求'GMB CF H S S △△的值.【答案】(1)见解析;(2)①见解析;②(3)125- 【分析】(1)先利用三个角是直角的四边形是矩形证明,再根据BE BC =证得结论; (2)①证明''CGB CDF ≅即可得到结论;②方法一:设正方形边长为a ,根据'~'B KO F CO ,求出11''22B K BC a ==,利用勾股定理得到222''B K B C CK +=,求出a,得到B C '=B K '=,根据B KC '△△CKG ,求出KG ,再根据PKD GKC ≅,求出答案;方法二:过点P 作PM GH ⊥于点M ,根据CG CD =,2CD CK =求出6CG =,由26PM CK ==,12GM =,再利用勾股定理求得结果;(3)方法一:延长''B F 与BH 的延长线交于点R ,证明~'GBM CRF ,求出'1'2F H CF =,设'F H x =,'2CF x =,则CH =,证明'~'RB C RF H ,求得2'''22CF R CF HSSx ==,由'~'GB C GE H ,求出)21GB x =,利用~'GBM CRF,求出'65GMB CF R SS -=,即可得到答案;方法二,过点B 作BN PG ⊥,垂足为点N .设FH x =,则'''''2CF B E E F BC x ====,'4GB x =,求得(2'465GBN CHF S GB S CH -⎛⎫== ⎪⎝⎭,证明~'GBN GCB ,求出GB GC =,再证明~''MBN B F C ,求出答案;方法三:设AB 与PQ 交于N 点,设FH x =,则'''''2CF CB B E E F BC x =====,'4GB x =,证明~'MBN F OC ,得到(2'9620MBN F OC S BN S CO -⎛⎫==⎪⎝⎭,根据12GBNS BG BN =⨯⨯,求出答案. 【详解】(1)在矩形ABCD 中,90B BCD ∠=∠=︒, △EF AB ⊥,则90EFB ∠=︒, △四边形BEFC 是矩形. △BE BC =,△矩形BEFC 是正方形. (2)①如图1,△90GCK DCH ∠=∠=︒,△'90CDF H ∠+∠=︒,90KGC H ∠+∠=︒, △'KGC CDF ∠=∠,又△''B C CF =,''GB C CF D ∠=∠, △''CGB CDF≅, △CG CD =.②方法一:设正方形边长为a ,△PG △CF ',△'~'B KO F CO ,△'1'2B K OK CF CO ==, △11''22B K BC a ==,△在'Rt B KC 中,222''B K B C CK +=,△222132a a ⎛⎫+= ⎪⎝⎭,△a =.△B C '=,B K '= △90,CB K GCK B KC GKC ''∠=∠=︒∠=∠, △B KC '△△CKG , △2CK B K KG '=⋅,△KG = △1,,2B K a KE DKE B KC DE K KB C ''''''==∠=∠∠=∠, △△B ’CK △△E ’KD , △DK =KC ,又△△DKP =△GKC ,△P =△G , △PKD GKC ≅, △PG=KG ,△PG =方法二:如图2,过点P 作PM GH ⊥于点M , 由''CGB CDF ≅, 可得:CG CD =,由方法一,可知2CD CK =, △6CG =,由方法一,可知K 为GP 中点,从而26PM CK ==,12GM =,从而由勾股定理得PG =(3)方法一:如图3,延长''B F 与BH 的延长线交于点R , 由题意可知,'//CF GP ,'//RB BM , △~'GBM CRF ,'G F CR ∠=∠, △'1tan tan ''2F HG F CH CF ∠=∠==,设'F H x =,'2CF x =,则CH =, △''''''2CB CF E F B E BC x =====, △'//'CB HE , △'~'RB C RF H , △''1''2F H RH RF B C RC RB ===, △CH RH =,'''B F RF =,△2CR CH ==,2'''22CF R CF HS Sx ==,△'//'CB HE , △'~'GB C GE H , △'22'33GC B C x GH E H x ===, '2'3B C E H ==,△)21GB x =,△~'GBM CRF ,△22'21GMB CF Rx S GB S CR ⎡⎤⎛⎫=== ⎪⎝⎭△'''2CF R CF HS S=,△'125GMB CF H S S -=.方法二,如图4,过点B 作BN PG ⊥,垂足为点N . 由题意可知,'//CF GP ,'//HE BN , △~'GBN CHF ,△2'GBN CHF S GB S CH ⎛⎫= ⎪⎝⎭, △'//CF GP , △'NGB F CH ∠=∠, △'1tan tan ''2CB FH G F CH GB CF ∠=∠===, 设FH x =,则'''''2CF B E E FBC x ====,'4GB x =, △CH =,CG =,则)21GB x =,△(22'21465GBN CHF x S GB S CH ⎛⎫-⎛⎫=== ⎪⎝⎭, △2'1'2CF HSCF FH x =⋅=,△(2465GBNSx-=,△'//HE BN , △~'GBN GCB ,△'GB GC CB BN === △'//CB BN ,//''BM B F ,'//'CF GB , △~''MBN B F C ,△22'''MBN B F C S BN S CB ⎛⎫=== ⎪⎝⎭⎝⎭ △(2''266255MBNB F CSSx --==,△(((222462626555MBG NBG MBNSSSxxx---=-=-=,△'125GMB CF H S S -=.方法三:如图5,设AB 与PQ 交于N 点,设FH x =,则'''''2CF CB B E E F BC x =====,'4GB x =, 由题意可知,'//CF GP ,//''BM B F ,//BN CO , △~'MBN F OC ,△2'MBN F OCS BN SCO ⎛⎫=⎪⎝⎭, 由方法(2)可知,)21GB x =,所以)1BN x =,又△23CO CK ==, △(2'9620MBN F OC S BN S CO -⎛⎫==⎪⎝⎭, △((22963642035BMNSxx --=⨯=,△)(2221162GBNSBG BNx x =⨯⨯==-,△(((2223626655GBMGBNNBMS S Sx xx--=-=--=,△2'1''2CF HSCF FH x =⨯⨯=, △'GMB CF H S S =.【点睛】此题考查正方形的判定定理及性质定理,旋转的性质,全等三角形的判定及性质,相似三角形的判定及性质,锐角三角函数,综合掌握各知识点并熟练应用解决问题是解题的关键.13.(2021·湖北武汉市·中考真题)问题提出 如图(1),在ABC 和DEC 中,90ACB DCE ∠=∠=︒,BC AC =,EC DC =,点E 在ABC 内部,直线AD 与BE 交于点F ,线段AF ,BF ,CF 之间存在怎样的数量关系?问题探究 (1)先将问题特殊化.如图(2),当点D ,F 重合时,直接写出一个等式,表示AF ,BF ,CF 之间的数量关系;(2)再探究一般情形.如图(1),当点D ,F 不重合时,证明(1)中的结论仍然成立.问题拓展 如图(3),在ABC 和DEC 中,90ACB DCE ∠=∠=︒,BC kAC =,EC kDC =(k 是常数),点E 在ABC 内部,直线AD 与BE 交于点F ,直接写出一个等式,表示线段AF ,BF ,CF 之间的数量关系.【答案】(1)BF AF -.(2)见解析;问题拓展:BF k AF -⋅=.【分析】(1)先证明△BCE △△ACD ,得到AF =BE ,BF -BE =BF -AF =EF ;(2)过点C 作CG CF ⊥交BE 于点G ,证明ACD BCE ≅△△,ACF BCG ≅△△,CGF △是等腰直角三角形即可;利用前面的方法变全等为相似证明即可.【详解】问题探究 (1)BF AF -=.理由如下:如图(2),△△BCA =△ECF =90°,△△BCE =△ACF ,△BC =AC ,EC =CF ,△BCE △△ACF ,△BE =AF ,△BF -BE =BF -AF =EF ;(2)证明:过点C 作CG CF ⊥交BE 于点G ,则90FCG ACB ∠=∠=︒,△BCG ACF ∠=∠.△90ACB DCE ∠=∠=︒,△BCE ACD ∠=∠.又△AC BC =,DC EC =,△ACD BCE ≅△△,△CAF CBG ∠=∠.△ACF BCG ≅△△.△AF BG =,CF CG =,△CGF △是等腰直角三角形.△GF =.△BF AF BF BG GF -=-==.问题拓展 BF k AF -⋅=.理由如下:△△BCA =△ECD =90°,△△BCE =△ACD ,△BC =kAC ,EC =kCD ,△△BCE △△ACD ,△△EBC =△FAC ,过点C 作CM CF ⊥交BE 于点M ,则90FCM ACB ∠=∠=︒,△BCM ACF ∠=∠.△△BCM △△ACF ,△BM :AF =BC :AC =MC :CF =k ,△BM =kAF ,MC =kCF ,△BF -BM =MF ,MF =△BF - kAF .【点睛】本题考查了等腰直角三角形的性质,三角形全等的判定和性质,三角形相似的判定和性质,勾股定理,熟练掌握三角形全等的判定,三角形相似的判定,勾股定理是解题的关键.14.(2020·湖北省直辖县级行政单位·中考真题)实践操作:第一步:如图1,将矩形纸片ABCD 沿过点D 的直线折叠,使点A 落在CD 上的点A '处,得到折痕DE ,然后把纸片展平.第二步:如图2,将图1中的矩形纸片ABCD 沿过点E 的直线折叠,点C 恰好落在AD 上的点C '处,点B 落在点B '处,得到折痕EF ,B C ''交AB 于点M ,C F '交DE 于点N ,再把纸片展平.问题解决:(1)如图1,填空:四边形AEA D '的形状是_____________________;(2)如图2,线段MC '与ME 是否相等?若相等,请给出证明;若不等,请说明理由;(3)如图2,若2cm,'4cm AC DC '==,求:DN EN 的值.【答案】(1)正方形;(2)MC ME '=,见解析;(3)25【分析】(1)有一组邻边相等且一个角为直角的平行四边形是正方形;(2)连接EC ',由(1)问的结论可知,90AD BC EAC B '=∠=∠=︒,,又因为矩形纸片ABCD 沿过点E 的直线折叠,可知折叠前后对应角以及对应边相等,有B B '∠=∠,B C BC ''=,90AE B C EAC B ''''=∠=∠=︒,,可以证明Rt EC A '和Rt C EB ''全等,得到C EA EC B '''∠=∠,从而有MC ME '=;(3)由Rt EC A Rt C EB '''≌,有AC B E ''=;由折叠知,AC BE '=,可以计算出()8cm AB =;用勾股定理计算出DF 的长度,再证明DNF ENG ∽得出等量关系,从而得到:DN EN 的值.【详解】(1)解:△ABCD 是平行四边形,△'////AD BC EA ,'//AE DA△四边形'AEA D 是平行四边形△矩形纸片ABCD 沿过点D 的直线折叠,使点A 落在CD 上的点A '处△'AED A ED ≌△'AE A E =△90A ∠=△四边形AEA D '的形状是正方形故最后答案为:四边形AEA D '的形状是正方形;(2)MC ME '=理由如下:如图,连接EC ',由(1)知:AD AE =△四边形ABCD 是矩形,△90AD BC EAC B '=∠=∠=︒,由折叠知:B C BC B B '''=∠=∠,△90AE B C EAC B ''''=∠=∠=︒,又EC C E ''=,△Rt EC A Rt C EB '''≌△C EA EC B '''∠=∠△MC ME '=(3)△Rt EC A Rt C EB '''≌,△AC B E ''=由折叠知:B E BE '=,△AC BE '=△2(cm)4(cm)AC DC ''==,△()2428cm AB CD ==++=设cm DF x =,则()8cm FC FC x '==-在Rt DC F '中,由勾股定理得:2224(8)x x +=-解得:3x =,即()3cm DF =如图,延长BA FC ',交于点G ,则AC G DC F ''∠=∠ △3tan tan 4AG DF AC G DC F AC DC ''∠=∠==='' △3(cm)2AG =△3156(cm)22EG =+= △//DF EG ,△DNF ENG ∽ △152::3:25DN EN DF EG === 【点睛】(1)本问主要考查了正方形的定义,即有一组邻边相等且一个角为直角的平行四边形是正方形,其中明确折叠前后对应边、对应角相等是解题的关键;(2)本问利用了正方形的性质以及折叠前后对应边、对应角相等来证明三角形全等,再根据角相等则边相等即可做题,其中知道角相等则边相等的思想是解题的关键;(3)本问考查了全等三角形、相似三角形的性质、角相等则正切值相等以及勾股定理的应用,其中知道三角形相似则对应边成比例是解题的关键.15.(2020·湖北中考真题)如图1,已知ABC EBD △≌△,90ACB EDB ∠=∠=︒,点D 在AB 上,连接CD 并延长交AE 于点F ,(1)猜想:线段AF 与EF 的数量关系为_____;(2)探究:若将图1的EBD △绕点B 顺时针方向旋转,当CBE ∠小于180︒时,得到图2,连接CD 并延长交AE 于点F ,则(1)中的结论是否还成立?若成立,请证明;若不成立,请说明理由;(3)拓展:图1中,过点E 作EG CB ⊥,垂足为点G .当ABC ∠的大小发生变化,其它条件不变时,若EBG BAE ∠=∠,6BC =,直接写出AB 的长.【答案】(1)AF=EF ;(2)成立,理由见解析;(3)12【分析】(1) 延长DF 到G 点,并使FG=DC ,连接GE ,证明△ACF ≌△EDG ,进而得到△GEF 为等腰三角形,即可证明AF=GE=EF ;(2)证明原理同(1),延长DF 到G 点,并使FG=DC ,连接GE ,证明△ACF ≌△EDG ,进而得到△GEF 为等腰三角形,即可证明AF=GE=EF ;(3)补充完整图后证明四边形AEGC 为矩形,进而得到△ABC=△ABE=△EBG=60°即可求解.【详解】解:(1)延长DF 到G 点,并使FG=DC ,连接GE ,如下图所示△ABC EBD △≌△,△DE=AC ,BD=BC ,△△CDB=△DCB ,且△CDB=△ADF ,△△ADF=△DCB ,△△ACB=90°,△△ACD+△DCB=90°,△△EDB=90°,△△ADF+△FDE=90°,△△ACD=△FDE ,又延长DF 使得FG=DC ,△FG+DF=DC+DF ,△DG=CF ,在△ACF 和△EDG 中,AC ED ACF EDG CF DG =⎧⎪∠=∠⎨⎪=⎩,△△ACF ≌△EDG(SAS),△GE=AF ,△G=△AFC ,又△AFC=△GFE ,△△G=△GFE△GE=EF△AF=EF ,故AF 与EF 的数量关系为:AF=EF.故答案为:AF=EF ;(2)仍旧成立,理由如下:延长DF 到G 点,并使FG=DC ,连接GE ,如下图所示设BD 延长线DM 交AE 于M 点,△ABC EBD △≌△,△DE=AC ,BD=BC ,△△CDB=△DCB ,且△CDB=△MDF ,△△MDF=△DCB ,△△ACB=90°,△△ACD+△DCB=90°,△△EDB=90°,△△MDF+△FDE=90°,△△ACD=△FDE ,又延长DF 使得FG=DC ,△FG+DF=DC+DF ,△DG=CF ,在△ACF 和△EDG 中,AC ED ACF EDG CF DG =⎧⎪∠=∠⎨⎪=⎩,△△ACF ≌△EDG(SAS),△GE=AF ,△G=△AFC ,又△AFC=△GFE ,△△G=△GFE△GE=EF ,△AF=EF,故AF与EF的数量关系为:AF=EF.故答案为:AF=EF;(3)如下图所示:△BA=BE,△△BAE=△BEA,△△BAE=△EBG,△△BEA=△EBG,△AE//CG,△△AEG+△G=180°,△△AEG=90°,△△ACG=△G=△AEG=90°,△四边形AEGC为矩形,△AC=EG,且AB=BE,△Rt△ACB≌Rt△EGB(HL),△BG=BC=6,△ABC=△EBG,又△ED=AC=EG,且EB=EB,△Rt△EDB≌Rt△EGB(HL),△DB=GB=6,△EBG=△ABE,△△ABC=△ABE=△EBG=60°,△△BAC=30°,△在Rt△ABC中由30°所对的直角边等于斜边的一半可知:==.AB BC212故答案为:12.【点睛】本题属于四边形的综合题,考查了三角形全等的性质和判定,矩形的性质和判定,本题的关键是延长DF 到G 点并使FG=DC ,进而构造全等,本题难度稍大,需要作出合适的辅助线.16.(2020·湖北咸宁市·中考真题)定义:有一组对角互余的四边形叫做对余四边形.理解:(1)若四边形ABCD 是对余四边形,则A ∠与C ∠的度数之和为______;证明:(2)如图1,MN 是O 的直径,点,,A B C 在O 上,AM ,CN 相交于点D .求证:四边形ABCD 是对余四边形;探究:(3)如图2,在对余四边形ABCD 中,AB BC =,60ABC ︒∠=,探究线段AD ,CD 和BD 之间有怎样的数量关系?写出猜想,并说明理由.【答案】(1)90°或270°;(2)见解析;(3)222CD AD BD +=,理由见解析【分析】(1)分当△A 和△C 互余时,当△B 和△D 互余时,两种情况求解;(2)连接BO ,得到△BON+△BOM=180°,再利用圆周角定理证明△C+△A=90°即可;(3)作△ABD 的外接圆O ,分别延长AC ,BC ,DC ,交圆O 于E ,F ,G ,连接DF ,DE ,EF ,先证明GF 是圆O 的直径,得到222GE EF GF +=,再证明△ABC△△FEC ,△ACD△△GCE ,△BCD△△GCF ,可得22222222AB CF AD GC AC EF AC GE +=+,BC BD CD k GC GF CF===,从而得出222222AB CD AD BC AC BD +=,根据△ABC 为等边三角形可得AB=AC=BC ,从而得到222CD AD BD +=.【详解】解:(1)△四边形ABCD 是对余四边形,当△A 和△C 互余时,△A+△C=90°,当△B 与△D 互余时,△B+△D=90°,则△A+△C=360°-90°=270°,故答案为:90°或270°;(2)如图,连接BO ,可得:△BON=2△C ,△BOM=2△A ,而△BON+△BOM=180°,△2△C+2△A=180°,△△C+△A=90°,△四边形ABCD 是对余四边形;(3)△四边形ABCD 为对于四边形,△ABC=60°,△△ADC=30°,如图,作△ABD 的外接圆O ,分别延长AC ,BC ,DC ,交圆O 于E ,F ,G ,连接DF ,DE ,EF ,则△AEF=△ABC=60°,△AEG=△ADG=30°,△△AEF+△AEG=90°,即△FEG=90°,△GF 是圆O 的直径,△AB=BC ,△△ABC 为等边三角形,△△ABC=△AEF ,△ACB=△ECF ,△△ABC△△FEC ,得:AB AC BC EF FC EC==,则2222AB CF AC EF =, 同理,△ACD△△GCE ,得:AC AD CD GC GE CE==,则2222AC GE AD GC =, △BCD△△GCF ,得:BC BD CD k GC GF CF ===, 可得:22222222AB CF AD GC AC EF AC GE +=+,而222GE EF GF+=,△222222 AB CF AD GC AC GF+=,△222 222222CD BC BD AB AD ACk k k+=,△222222AB CD AD BC AC BD+=,△AB=BC=AC,△222CD AD BD+=.【点睛】本题考查了相似三角形的判定和性质,四边形的新定义问题,圆周角定理,等边三角形的判定和性质,多边形内角和,解题的关键是理解对余四边形的概念,结合所学知识求证.17.(2020·湖北随州市·中考真题)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1)后人称之为“赵爽弦图”,流传至今.(1)①请叙述勾股定理;②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)(2)①如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足123S S S +=的有_______个;②如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为1S ,2S ,直角三角形面积为3S ,请判断1S ,2S ,3S 的关系并证明;(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图8所示的“勾股树”.在如图9所示的“勾股树”的某部分图形中,设大正方形M 的边长为定值m ,四个小正方形A ,B ,C ,D 的边长分别为a ,b ,c ,d ,已知123α∠=∠=∠=∠,则当α∠变化时,回答下列问题:(结果可用含m 的式子表示)①2222a b c d +++=_______;②b 与c 的关系为_______,a 与d 的关系为_______.【答案】(1)①如果直角三角形的两条直角边分别为,a b ,斜边为c ,那么222+=a b c ,(或者:在直角。
2021年九级中考数学压轴题 –几何综合问题(圆的专题)(三)

2021年九级中考数学压轴题满分训练–几何综合问题(圆的专题)(三)1.如图所示,AC与⊙O相切于点C,线段AO交⊙O于点B.过点B作BD∥AC交⊙O 于点D,连接CD、OC,且OC交DB于点E.若∠CDB=30°,DB=4cm.(1)求⊙O的半径长;(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)2.如图,△ABC内接于⊙O,且AB为⊙O的直径,OE⊥AB交AC于点E,在OE的延长线上取点D,使得DE=DC.(1)求证:CD是⊙O的切线;(2)若AC=2,BC=,求CD的长.3.如图,四边形ABCD内接于⊙O,BC为⊙O的直径,⊙O的切线AP与CB的延长线交于点P.(1)求证:∠PAB=∠ACB;(2)若AB=12,cos∠ADB=,求PB的长.4.如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC =13,过点O作OD⊥AC于点D.(1)求证:∠B=∠COD;(2)求AB的长.5.如图,AB是⊙O的直径,AE是弦,C是弧AE的中点,过点C作⊙O的切线交BA 的延长线于点G,过点C作CD⊥AB于点D,交AE于点F.(1)求证:GC∥AE;(2)若sin∠EAB=,OD=3,求AE的长.6.如图,AD与⊙O相切于点D,点A在直径CB的延长线上.(1)求证:∠DCB=∠ADB;(2)若∠DCB=30°,AC=3,求AD的长.7.如图1,在⊙O中,弦AB⊥弦CD,垂足为点E,连接AD、BC、AO,AD=AB.(1)求证:∠CAO=2∠CDB;(2)如图2,过点O作OH⊥AD,垂足为点H,求证:2OH+CE=DE;(3)如图3,在(2)的条件下,延长DB、AC交于点F,过点D作DM⊥AC,垂足为M交AB于N,若BC=12,AF=3BF,求MN的长.8.如图,在△ABC中,∠ABC=90°,AB=8,BC=6.以BC为直径的⊙O交AC于D,E是AB的中点,连接ED并延长交BC的延长线于点F.(1)求证:DE是⊙O的切线;(2)求DB的长.9.如图,在Rt△ABC中,∠ACB=90°,AB=10,AC=6,点D为BC边上的一个动点,以CD为直径的⊙O交AD于点E,过点C作CF∥AB,交⊙O于点F,连接CE、CF、EF.(1)当∠CFE=45°时,求CD的长;(2)求证:∠BAC=∠CEF;(3)是否存在点D,使得△CFE是以EF为腰的等腰三角形,若存在,求出此时CD 的长;若不存在,试说明理由.10.直线l与⊙O相离,OB⊥l于点B,且OB=5,OB与⊙O交于点P,A为圆上一点,AP的延长线交直线l于点C,且AB=BC.(1)求证:AB是⊙O的切线;(2)若⊙O的半径为3,求线段AP的长.11.如图,已知直线l与⊙O无公共点,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长交直线l于点C,使得AB=AC.(1)求证:AB是⊙O的切线;(2)若BP=2,sin∠ACB=,求AB的长.12.如图,在△ABC中,AB=AC.以AB为直径的⊙O分别与BC、AC相交于点D、E,连接AD.过点D作DF⊥AC,垂足为点F,(1)求证:DF是⊙O的切线;(2)若⊙O的半径为4,∠CDF=22.5°,求图中阴影部分的面积.13.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC,垂足为点H,连接DE,交AB于点F.(1)求证:DH是⊙O的切线;(2)若⊙O的半径为4,①当AE=FE时,求的长(结果保留π);②当时,求线段AF的长.14.如图,AB是⊙O的直径,点C和点D分别在AB和⊙O上,且AC=AD,DC的延长线交⊙O于点E,过E作AC的平行线交⊙O于点F,连接AF,DF.(1)求证:四边形ACEF是平行四边形;(2)当sin∠EDF=,BC=4时,求⊙O的半径.15.如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D 作DE⊥AC,分别交AC、AB的延长线于点E,F.(1)求证:EF是⊙O的切线;(2)若AC=6,CE=2,求CB的长.参考答案1.解:(1)∵AC与⊙O相切于点C,∴∠ACO=90°.∵BD∥AC,∴∠BEO=∠ACO=90°,∴DE=EB=BD==2(cm)∵∠D=30°,∴∠O=2∠D=60°,在Rt△BEO中,sin60°=,=.∴OB=5,即⊙O的半径长为5cm.(2)由(1)可知,∠O=60°,∠BEO=90°,∴∠EBO=∠D=30°.在△CDE与△OBE中,.∴△CDE≌△OBE(AAS).∴S阴影=S扇OBC=π•42=(cm2),答:阴影部分的面积为cm2.2.(1)证明:连接OC,如图1,∵DC=DE,∴∠DCE=∠DEC,∵∠DEC=∠AEO,∴∠DCE=∠AEO,∵OA⊥OE,∴∠A+∠AEO=90°,∴∠DCE+∠A=90°,∵OA=OC,∴∠A=∠ACO,∴∠DCE+∠ACO=90°,∴OC⊥DC,∴CD是⊙O的切线;(2)如图2,过点D作DF⊥CE于点F,∵AC=2,BC=,∴AB===5,∵AB为⊙O的直径,∴∠ACB=90°,∴∠ACB=∠AOE,又∵∠A=∠A,∴△AOE∽△ACB,∴,∴,∴AE=,∴CE=AC﹣AE=2﹣=,∵CD=DE,∴CF=CE=,∠DEC=∠DCE,∵∠DEC=∠AEO,∠AEO=∠B,∴∠DCE=∠B,又∵∠DFC=∠ACB,∴△DFC∽△ACB,∴,∴,∴DC=.3.解:(1)证明:如图,连接OA,∵AP为⊙O的切线,∴OA⊥AP,∴∠OAP=90°,∴∠OAB+∠PAB=90°,∵OA=OB,∴∠OAB=∠OBA,∴∠OBA+∠PAB=90°,∵BC为⊙O的直径,∴∠ACB+∠OBA=90°,∴∠PAB=∠ACB;(2)由(1)知∵∠PAB=∠ACB,且∠ADB=∠ACB,∴∠PAB=∠ACB=∠ADB,∴,∵AB=12,∴AC=16,∴,∴OB=10,过B作BF⊥AP于F,∵∠ADB=∠FAB,,∴,∴,∴在Rt△ABF中,,∵OA⊥AP,BF⊥AP,∴BF∥OA,∴△PBF∽△POA,∴,∴,∴.答:PB的长为.4.解:(1)作直径AE,连接CE,∴∠ACE=90°,∴∠CAE+∠E=90°,∵OA=OC,∴∠CAE=∠OCD,∴∠OCD+∠E=90°,∵OD⊥AC,∴∠OCD+∠COD=90°,∴∠COD=∠E,∵∠B=∠E,∴∠B=∠COD;(2)∵AH⊥BC,∴∠AHB=90°,∴∠ACE=∠AHB,∵∠B=∠E,∴△ABH∽△AEC,∴=,∴AB=,∵AC=24,AH=18,AE=2OC=26,∴AB==.5.(1)证明:连接OC,交AE于点H.∵C是弧AE的中点,∴OC⊥AE.∵GC是⊙O的切线,∴OC⊥GC,∴∠OHA=∠OCG=90°,∴GC∥AE;(2)解:∵OC⊥GC,GC∥AE,∴OC⊥AE,∵CD⊥AB,∴∠CHF=∠FDA=90°,∵∠CFH=∠AFD,∴∠OCD=∠EAB.∴.在Rt△CDO中,OD=3,∴OC=5,∴AB=10,连接BE,∵AB是⊙O的直径,∴∠AEB=90°.在Rt△AEB中,∵,∴BE=6,∴AE=8.6.(1)证明:如图,连接OD,∵AD与⊙O相切于点D,∴OD⊥AD,∴∠ODB+∠ADB=90°,∵CB是直径,∴∠CDB=90°,∴∠ODB+∠ODC=90°,∴∠ODC=∠ADB,∵OD=OC,∴∠ODC=∠OCD,∴∠C=∠ADB;(2)解:∵∠DCB=∠ADB,∠DAC=∠CAD,∴△ADB∽△ACD,∴=,∵CB是直径,∴∠CDB=90°,∠DCB=30°,∴tan∠DCB==,∴=,∵AC=3,∴AD=3.7.解:(1)如图,连接AO、DO,∵AB=AD,∴,∴∠AOB=∠AOD,∴AO=OB,AO=OD,∴△AOB≌△AOD,∴∠BAO=∠DAO,延长AO交BD于点H,∵AB=AD,∴AH⊥BD,∴∠AHB=∠AHD=90°,∵,∴∠ACD=∠ABD,∴∠CAB=∠BAO=∠OAD,∴∠CAO=2∠CDB.(2)过点O作OT⊥CD,则CT=DT,∵CD⊥AB,CD⊥OT,OQ⊥AB,∴∠OQB=∠OTE=∠AED=90°,∴四边形OTEQ为矩形,∴OQ=ET,∵TD=CT=ET+CE,∵AB=AD,∴OQ=OH,∴2OH+CE=DE.(3)如图,∵∠ACB+∠ADB=180°,∠FCB+∠ACB=180°,∴∠ADB=∠FCB,∵∠F=∠F,∴△FCB∽△FDA,∵CB=12,∴AB=AD=36,∵∠BCD=∠BAD,∠AEB=∠AED,∴△CEB∽△AED,∴,设BE=x,则AE=36﹣x,ED=3x,∵AB⊥CD,∴∠AED=90°,则在Rt△AED中,AE2+ED2=AD2,(36﹣x)2+(3x)2=362,解得:,∴BD=∵CD⊥AB,∴∠BED=90°,∠NMA=90°,∠ANM=∠END,∴∠NED=∠MAN,∴∠BDE=∠EDN,∵ED=ED,∴△BED≌△NED,∴,∵∠CDB=∠CAB,∠NMA=∠BED,∴△AMN∽△DEB,∴,∴,8.(1)证明:连接BD,DO,∵BC是⊙O的直径,∴∠ADB=90°.∴∠CDB=90°,又∵E为AB的中点,∴DE=EB=EA,∴∠EDB=∠EBD.∵OD=OB,∴∠ODB=∠OBD.∵∠ABC=90°,∴∠EDB+∠OBD=90°.即OD⊥DE.∴DE是⊙O的切线.(2)解:在Rt△ABC中,AB=8,BC=6,∴AC===10,∵,∴.9.解:(1)∵∠CFE=90°,∠CFE=∠CDE,∴∠CDE=45°,∵∠ACB=90°,∴∠DAC=45°,∴∠DAC=∠ADC,∴AC=CD=6;(2)证明:∵∠ACB=90°,∴∠BAC+∠B=90°,∵CF∥AB,∴∠B=∠FCB,又∵∠FCB=∠DEF,∴∠BAC+∠DEF=90°,∵CD为⊙O的直径,∴∠CED=90°,∴∠DEF+∠CEF=90°,∴∠BAC=∠CEF;(3)①如图1,当EF=CE时,则∠EFC=∠ECF,∵四边形CEDF为圆内接四边形,∴∠ADG=∠ECF,又∵∠CDE=∠CFE,∴∠ADG=∠CDE,∵CD为⊙O的直径,∴∠DFC=90°,∵FC∥AB,∴∠FGA=90°,∴∠FGA=∠ACD,∵AD=AD,∴△AGD≌△ACD(AAS),∴DG=CD,在Rt△BDG中,设CD=x,∵BG2+DG2=BD2,∴42+x2=(8﹣x)2,∴x=3,即CD=3;②如图2,当EF=CF时,则∠CEF=∠ECF,∵四边形CEDF为圆内接四边形,∴∠ADG=∠ECF,又∵∠CEF=∠CDF=∠BDG,∴∠ADG=∠BDG,∵FC∥AB,∠DFC=90°,∴∠FGA=90°,∴∠FGA=∠ACD,∵GD=GD,∴△BGD≌△AGD(ASA),∴BD=AD,在Rt△ACD中,设CD=x,∵CD2+AC2=AD2,∴x2+62=(8﹣x)2,∴x=,即CD=;综合以上可得CD的长为3或.10.证明:(1)连接OA,∵OA=OP,∴∠OPA=∠OAP=∠BPC,∵AB=BC,∴∠BAC=∠ACB,∵OB⊥l,∴∠ACB+∠BPC=90°,∴∠BAC+∠OAP=90°,即OA⊥AB,∴AB与⊙O相切;(2)解:如图,连接AO并延长交⊙O于D,连接PD,则∠APD=90°,∵OB=5,OP=3,∴PB=2,∴BC=AB==4,在Rt△PBC中,PC==2,∵∠DAP=∠CPB,∠APD=∠PBC=90°,∴△DAP∽△CPB,∴,即,解得,AP=.11.(1)证明:连接OB,如图1,∵AB=AC,∴∠ABC=∠ACB,∵OA⊥l,∴∠ACB+∠APC=90°,∵OB=OP,∴∠OBP=∠OPB,∵∠OPB=∠APC,∴∠OBP+∠ACB=90°,∴∠OBP+∠ABC=90°,即∠OBA=90°,∴OB⊥AB,∴AB是⊙O的切线;(2)解:作直径BD,连接PD,则∠BPD=90°,如图2,∵AB是⊙O的切线,∴∠ABC=∠D,∵∠ABC=∠ACB,∴∠D=∠ABC=∠ACB,∵sin∠ACB=,∴sin∠D==,∵BP=2,∴BD=10,∴OB=OP=5,∵sin∠ACB=,∴=,∴=,设PA=x,则AB=AC=2x,在Rt△AOB中,AB=2x,OB=5,OA=5+x,∴(2x)2+52=(5+x)2,解得x=,∴AB=2x=.12.(1)证明:连接AD.∵AB是⊙O的直径,∴∠ADB=90°,∴AD⊥BC.又AB=AC=13,BC=10,D是BC的中点,∴BD=5.连接OD;由中位线定理,知DO∥AC,又DF⊥AC,∴DF⊥OD.∴DF是⊙O的切线;(2)连接OE,∵DF⊥AC,∠CDF=22.5°,∴∠ABC=∠ACB=67.5°,∴∠BAC=45°,∵OA=OE,∴∠AOE=90°,∵⊙O的半径为4,∴S扇形AOE=4π,S△AOE=8∴S阴影=S扇形AOE﹣S△AOE=4π﹣8.13.证明:(1)连接OD,如图1,∵OB=OD,∴△ODB是等腰三角形,∠OBD=∠ODB①,在△ABC中,∵AB=AC,∴∠ABC=∠ACB②,由①②得:∠ODB=∠OBD=∠ACB,∴OD∥AC,∵DH⊥AC,∴DH⊥OD,∴DH是圆O的切线;(2)①∵AE=EF,∴∠EAF=∠EAF,设∠B=∠C=α,∴∠EAF=∠EFA=2α,∵∠E=∠B=α,∴α+2α+2α=180°,∴α=36°,∴∠B=36°,∴∠AOD=72°,∴的长==;②连接AD,∵AB为⊙O的直径,∴∠ADB=∠ADC=90°,∵⊙O的半径为4,∴AB=AC=8,∵,∴=,∴AD=2,∵AD⊥BC,DH⊥AC,∴△ADH∽△ACD,∴=,∴=,∴AH=3,∴CH=5,∵∠B=∠C,∠E=∠B,∴∠E=∠C,∴DE=DC,∵DH⊥AC,∴EH=CH=5,∴AE=2,∵OD∥AC,∴∠EAF=∠FOD,∠E=∠FDO,∴△AEF∽△ODF,∴=,∴=,∴AF=.14.(1)证明:∵AC=AD,∴∠ADC=∠ACD,∵AC∥EF,∴∠ACD=∠E,∴∠ADC=∠E,∴=,∴=,∴AD=EF,∵AD=AC,∴AC=EF,∵AC∥EF,∴四边形ACEF是平行四边形;(2)解:连接BD,∵四边形ACEF是平行四边形,∴AF∥CE,∴∠EDF=∠AFD,∵所对圆周角∠B和∠AFD,∴∠AFD=∠B,∴∠B=∠EDF,∵AB是⊙O的直径,∴∠ADB=90°,∵sin∠EDF=,∴sin B=sin∠EDF==,∴设AD=2x,AB=3x,∵AC=AD,BC=4,∴3x﹣2x=4,解得:x=4,即AB=3x=3×4=12,∵AB为⊙O的直径,∴⊙O的半径是6.15.(1)证明:连接OD交BC于H,如图所示:∵OA=OD,∴∠OAD=∠ODA,∵AD平分∠BAC,∴∠OAD=∠DAC,∴∠ODA=∠DAC,∴OD∥AE,∵DE⊥AC,∴OD⊥EF,∵OD是⊙O的半径,∴EF是⊙O的切线;(2)解:∵AB为⊙O的直径,∴∠ACB=90°,∴∠HCE=90°,又∵DE⊥AC,∴∠E=90°,由(1)得:OD⊥EF,∴∠HDE=90°,∴四边形CEDH是矩形,∴HD=CE=2,∴∠CHD=90°,∴∠OHB=90°,∴OD⊥BC,∴OH平分BC,∴OH是△ABC的中位线,∴OH=AC=3,∴OB=OD=OH+HD=5,∴AB=2OB=10,∴CB===8.。
2019年湖北省各市中考数学真题汇编压轴题综合练:《二次函数》

如果别人思考数学的真理像我一样深入持久,他也会找到我的发现。
——高斯2019年湖北省各市中考数学真题汇编压轴题综合练:《二次函数》1.(2019•恩施州)如图,抛物线y=ax2﹣2ax+c的图象经过点C(0,﹣2),顶点D的坐标为(1,﹣),与x轴交于A、B两点.(1)求抛物线的解析式.(2)连接AC,E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和的值.(3)点F(0,y)是y轴上一动点,当y为何值时,FC+BF的值最小.并求出这个最小值.(4)点C关于x轴的对称点为H,当FC+BF取最小值时,在抛物线的对称轴上是否存在点Q,使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.2.(2019•襄阳)如图,在直角坐标系中,直线y=﹣x+3与x轴,y轴分别交于点B,点C,对称轴为x=1的抛物线过B,C两点,且交x轴于另一点A,连接AC.(1)直接写出点A,点B,点C的坐标和抛物线的解析式;(2)已知点P为第一象限内抛物线上一点,当点P到直线BC的距离最大时,求点P的坐标;(3)抛物线上是否存在一点Q(点C除外),使以点Q,A,B为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由.3.(2019•随州)如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c与y轴交于点A(0,6),与x轴交于点B(﹣2,0),C(6,0).(1)直接写出抛物线的解析式及其对称轴;(2)如图2,连接AB,AC,设点P(m,n)是抛物线上位于第一象限内的一动点,且在对称轴右侧,过点P作PD⊥AC于点E,交x轴于点D,过点P作PG∥AB交AC于点F,交x轴于点G.设线段DG的长为d,求d与m的函数关系式,并注明m的取值范围;(3)在(2)的条件下,若△PDG的面积为,①求点P的坐标;②设M为直线AP上一动点,连接OM,直线OM交直线AC于点S,则点M在运动过程中,在抛物线上是否存在点R,使得△ARS为等腰直角三角形?若存在,请直接写出点M及其对应的点R的坐标;若不存在,请说明理由.4.(2019•随州)某食品厂生产一种半成品食材,成本为2元/千克,每天的产量p(百千克)与销售价格x(元/千克)满足函数关系式p=x+8,从市场反馈的信息发现,该半成品食材每天的市场需求量q(百千克)与销售价格x(元/千克)满足一次函数关系,部分数据如表:2 4 (10)销售价格x(元/千克)市场需求量q(百12 10 (4)千克)已知按物价部门规定销售价格x不低于2元/千克且不高于10元/千克.(1)直接写出q与x的函数关系式,并注明自变量x的取值范围;(2)当每天的产量小于或等于市场需求量时,这种半成品食材能全部售出,而当每天的产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃.①当每天的半成品食材能全部售出时,求x的取值范围;②求厂家每天获得的利润y(百元)与销售价格x的函数关系式;(3)在(2)的条件下,当x为元/千克时,利润y有最大值;若要使每天的利润不低于24(百元),并尽可能地减少半成品食材的浪费,则x应定为元/千克.5.(2019•荆州)如图,在平面直角坐标系中,平行四边形OABC的顶点A,C的坐标分别为(6,0),(4,3),经过B,C两点的抛物线与x轴的一个交点D的坐标为(1,0).(1)求该抛物线的解析式;(2)若∠AOC的平分线交BC于点E,交抛物线的对称轴于点F,点P是x轴上一动点,当PE+PF的值最小时,求点P的坐标;(3)在(2)的条件下,过点A作OE的垂线交BC于点H,点M,N分别为抛物线及其对称轴上的动点,是否存在这样的点M,N,使得以点M,N,H,E为顶点的四边形为平行四边形?若存在,直接写出点M的坐标,若不存在,说明理由.6.(2019•湖北)在平面直角坐标系中,已知抛物线C:y=ax2+2x﹣1(a≠0)和直线l:y =kx+b,点A(﹣3,﹣3),B(1,﹣1)均在直线l上.(1)若抛物线C与直线l有交点,求a的取值范围;(2)当a=﹣1,二次函数y=ax2+2x﹣1的自变量x满足m≤x≤m+2时,函数y的最大值为﹣4,求m的值;(3)若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围.7.(2019•黄冈)如图①,在平面直角坐标系xOy中,已知A(﹣2,2),B(﹣2,0),C (0,2),D(2,0)四点,动点M以每秒个单位长度的速度沿B→C→D运动(M不与点B、点D重合),设运动时间为t(秒).(1)求经过A、C、D三点的抛物线的解析式;(2)点P在(1)中的抛物线上,当M为BC的中点时,若△PAM≌△PBM,求点P的坐标;(3)当M在CD上运动时,如图②.过点M作MF⊥x轴,垂足为F,ME⊥AB,垂足为E.设矩形MEBF与△BCD重叠部分的面积为S,求S与t的函数关系式,并求出S的最大值;(4)点Q为x轴上一点,直线AQ与直线BC交于点H,与y轴交于点K.是否存在点Q,使得△HOK为等腰三角形?若存在,直接写出符合条件的所有Q点的坐标;若不存在,请说明理由.8.(2019•荆州)若二次函数y=ax2+bx+c(a≠0)图象的顶点在一次函数y=kx+t(k≠0)的图象上,则称y=ax2+bx+c(a≠0)为y=kx+t(k≠0)的伴随函数,如:y=x2+1是y =x+1的伴随函数.(1)若y=x2﹣4是y=﹣x+p的伴随函数,求直线y=﹣x+p与两坐标轴围成的三角形的面积;(2)若函数y=mx﹣3(m≠0)的伴随函数y=x2+2x+n与x轴两个交点间的距离为4,求m,n的值.9.(2019•黄石)如图,已知抛物线y=x2+bx+c经过点A(﹣1,0)、B(5,0).(1)求抛物线的解析式,并写出顶点M的坐标;(2)若点C在抛物线上,且点C的横坐标为8,求四边形AMBC的面积;(3)定点D(0,m)在y轴上,若将抛物线的图象向左平移2个单位,再向上平移3个单位得到一条新的抛物线,点P在新的抛物线上运动,求定点D与动点P之间距离的最小值d(用含m的代数式表示)10.(2019•十堰)已知抛物线y=a(x﹣2)2+c经过点A(﹣2,0)和C(0,),与x 轴交于另一点B,顶点为D.(1)求抛物线的解析式,并写出D点的坐标;(2)如图,点E,F分别在线段AB,BD上(E点不与A,B重合),且∠DEF=∠A,则△DEF能否为等腰三角形?若能,求出BE的长;若不能,请说明理由;(3)若点P在抛物线上,且=m,试确定满足条件的点P的个数.11.(2019•荆门)为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据场调查,在草莓上市销售的30天中,其销售价格m(元/公斤)与第x 天之间满足m=(x为正整数),销售量n(公斤)与第x天之间的函数关系如图所示:如果李大爷的草莓在上市销售期间每天的维护费用为80元.(1)求销售量n与第x天之间的函数关系式;(2)求在草莓上市销售的30天中,每天的销售利润y与第x天之间的函数关系式;(日销售利润=日销售额﹣日维护费)(3)求日销售利润y的最大值及相应的x.12.(2019•十堰)某超市拟于中秋节前50天里销售某品牌月饼,其进价为18元/kg.设第x天的销售价格为y(元/kg),销售量为m(kg).该超市根据以往的销售经验得出以下的销售规律:①当1≤x≤30时,y=40;当31≤x≤50时,y与x满足一次函数关系,且当x=36时,y=37;x=44时,y=33.②m与x的关系为m=5x+50.(1)当31≤x≤50时,y与x的关系式为;(2)x为多少时,当天的销售利润W(元)最大?最大利润为多少?(3)若超市希望第31天到第35天的日销售利润W(元)随x的增大而增大,则需要在当天销售价格的基础上涨a元/kg,求a的取值范围.13.(2019•孝感)如图1,在平面直角坐标系xOy中,已知抛物线y=ax2﹣2ax﹣8a与x 轴相交于A、B两点(点A在点B的左侧),与y轴交于点C(0,﹣4).(1)点A的坐标为,点B的坐标为,线段AC的长为,抛物线的解析式为.(2)点P是线段BC下方抛物线上的一个动点.①如果在x轴上存在点Q,使得以点B、C、P、Q为顶点的四边形是平行四边形.求点Q的坐标.②如图2,过点P作PE∥CA交线段BC于点E,过点P作直线x=t交BC于点F,交x轴于点G,记PE=f,求f关于t的函数解析式;当t取m和4﹣m(0<m<2)时,试比较f的对应函数值f1和f2的大小.14.(2019•咸宁)某工厂用50天时间生产一款新型节能产品,每天生产的该产品被某网店以每件80元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第x天的生产成本y(元/件)与x(天)之间的关系如图所示,第x天该产品的生产量z(件)与x (天)满足关系式z=﹣2x+120.(1)第40天,该厂生产该产品的利润是元;(2)设第x天该厂生产该产品的利润为w元.①求w与x之间的函数关系式,并指出第几天的利润最大,最大利润是多少?②在生产该产品的过程中,当天利润不低于2400元的共有多少天?15.(2019•鄂州)“互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)直接写出y与x的函数关系式;(2)设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?16.(2019•咸宁)如图,在平面直角坐标系中,直线y=﹣x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点且与x轴的负半轴交于点C.(1)求该抛物线的解析式;(2)若点D为直线AB上方抛物线上的一个动点,当∠ABD=2∠BAC时,求点D的坐标;(3)已知E,F分别是直线AB和抛物线上的动点,当以B,O,E,F为顶点的四边形是平行四边形时,直接写出所有符合条件的E点的坐标.17.(2019•宜昌)在平面直角坐标系中,正方形ABCD的四个顶点坐标分别为A(﹣2,4),B(﹣2,﹣2),C(4,﹣2),D(4,4).(1)填空:正方形的面积为 ;当双曲线y =(k ≠0)与正方形ABCD 有四个交点时,k 的取值范围是: ;(2)已知抛物线L :y =a (x ﹣m )2+n (a >0)顶点P 在边BC 上,与边AB ,DC 分别相交于点E ,F ,过点B 的双曲线y =(k ≠0)与边DC 交于点N .①点Q (m ,﹣m 2﹣2m +3)是平面内一动点,在抛物线L 的运动过程中,点Q 随m 运动,分别求运动过程中点Q 在最高位置和最低位置时的坐标;②当点F 在点N 下方,AE =NF ,点P 不与B ,C 两点重合时,求﹣的值;③求证:抛物线L 与直线x =1的交点M 始终位于x 轴下方.18.(2019•荆门)已知抛物线y =ax 2+bx +c 顶点(2,﹣1),经过点(0,3),且与直线y=x ﹣1交于A ,B 两点.(1)求抛物线的解析式;(2)若在抛物线上恰好存在三点Q ,M ,N ,满足S △QAB =S △MAB =S △NAB =S ,求S 的值;(3)在A ,B 之间的抛物线弧上是否存在点P 满足∠APB =90°?若存在,求点P 的横坐标;若不存在,请说明理由.(坐标平面内两点M (x 1,y 1),N (x 2,y 2)之间的距离MN =)19.(2019•鄂州)如图,已知抛物线y =﹣x 2+bx +c 与x 轴交于A 、B 两点,AB =4,交y 轴于点C ,对称轴是直线x =1.(1)求抛物线的解析式及点C 的坐标;(2)连接BC ,E 是线段OC 上一点,E 关于直线x =1的对称点F 正好落在BC 上,求点F 的坐标;(3)动点M 从点O 出发,以每秒2个单位长度的速度向点B 运动,过M 作x 轴的垂线交抛物线于点N ,交线段BC 于点Q .设运动时间为t (t >0)秒. ①若△AOC 与△BMN 相似,请直接写出t 的值;②△BOQ 能否为等腰三角形?若能,求出t 的值;若不能,请说明理由.20.(2019•武汉)已知抛物线C 1:y =(x ﹣1)2﹣4和C 2:y =x 2 (1)如何将抛物线C 1平移得到抛物线C 2?(2)如图1,抛物线C 1与x 轴正半轴交于点A ,直线y =﹣x +b 经过点A ,交抛物线C 1于另一点B .请你在线段AB 上取点P ,过点P 作直线PQ ∥y 轴交抛物线C 1于点Q ,连接AQ .①若AP =AQ ,求点P 的横坐标; ②若PA =PQ ,直接写出点P 的横坐标.(3)如图2,△MNE 的顶点M 、N 在抛物线C 2上,点M 在点N 右边,两条直线ME 、NE 与抛物线C 2均有唯一公共点,ME 、NE 均与y 轴不平行.若△MNE 的面积为2,设M 、N 两点的横坐标分别为m 、n ,求m 与n 的数量关系.21.(2019•武汉)某商店销售一种商品,经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如表:售价x(元/件)50 60 80周销售量y(件)100 80 40周销售利润w(元)1000 1600 1600 注:周销售利润=周销售量×(售价﹣进价)(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);②该商品进价是元/件;当售价是元/件时,周销售利润最大,最大利润是元.(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值.参考答案1.解:(1)由题可列方程组:,解得:∴抛物线解析式为:y=x2﹣x﹣2;(2)如图1,∠AOC=90°,AC=,AB=4,设直线AC的解析式为:y=kx+b,则,解得:,∴直线AC的解析式为:y=﹣2x﹣2;当△AOC∽△AEB时=()2=()2=,∵S△AOC =1,∴S△AEB=,∴AB×|y E|=,AB=4,则y E=﹣,则点E(﹣,﹣);由△AOC∽△AEB得:∴;(3)如图2,连接BF,过点F作FG⊥AC于G,则FG=CF sin∠FCG=CF,∴CF+BF=GF+BF≥BE,当折线段BFG与BE重合时,取得最小值,由(2)可知∠ABE=∠ACO∴BE=AB cos∠ABE=AB cos∠ACO=4×=,|y|=OB tan∠ABE=OB tan∠ACO=3×=,∴当y=﹣时,即点F(0,﹣),CF+BF有最小值为;(4)①当点Q为直角顶点时(如图3):由(3)易得F(0,﹣),∵C(0,﹣2)∴H(0,2)设Q(1,m),过点Q作QM⊥y轴于点M.则Rt△QHM∽Rt△FQM∴QM2=HM•FM,∴12=(2﹣m)(m+),解得:m=,则点Q(1,)或(1,)当点H为直角顶点时:点H(0,2),则点Q(1,2);当点F为直角顶点时:同理可得:点Q(1,﹣);综上,点Q的坐标为:(1,)或(1,)或Q(1,2)或Q(1,﹣).2.解:(1)y=﹣x+3,令x=0,则y=3,令y=0,则x=6,故点B、C的坐标分别为(6,0)、(0,3),抛物线的对称轴为x=1,则点A(﹣4,0),则抛物线的表达式为:y=a(x﹣6)(x+4)=a(x2﹣2x﹣24),即﹣24a=3,解得:a=﹣,故抛物线的表达式为:y=﹣x2+x+3…①;(2)过点P作y轴的平行线交BC于点G,作PH⊥BC于点H,则∠HPG=∠CBA=α,tan∠CBA===tanα,则cosα=,设点P(x,﹣x2+x+3),则点G(x,﹣x+3),则PH=PG cosα=(﹣x2+x+3+x﹣3)=﹣x2+x,∵<0,故PH有最大值,此时x=3,则点P(3,);(3)①当点Q在x轴上方时,则点Q,A,B为顶点的三角形与△ABC全等,此时点Q与点C关于函数对称轴对称,则点Q(2,3);②当点Q在x轴下方时,(Ⅰ)当∠BAQ=∠CAB时,,△QAB∽△BAC,由勾股定理得:AC=5,AQ==20,过点Q作QH⊥x轴于点H,由△QHA∽△COA得:==,∵OC=3,∴QH=12,则AH=16,OH=16﹣4=12,∴Q(12,﹣12);根据点的对称性,当点Q在第三象限时,符合条件的点Q(﹣10,﹣12);当x=12时,y=﹣x2+x+3=﹣12;当x=﹣10时,y=﹣x2+x+3=﹣12;故点Q的坐标为:(12,﹣12)或(﹣10,﹣12);(Ⅱ)当∠BAQ=∠CBA时,则直线AQ∥BC,直线BC表达式中的k为:﹣,则直线AQ的表达式为:y=﹣x﹣2…②,联立①②并解得:x=10或﹣4(舍去﹣4),故点Q(10,﹣7),=,而=≠,即Q,A,B为顶点的三角形与△ABC不相似,故舍去,Q的对称点(﹣8,﹣7)同样也舍去,即点Q的为:(﹣8,﹣7)、(10,﹣7)均不符合题意,都舍去;综上,点Q的坐标为:(2,3)或(12,﹣12)或(﹣10,﹣12).3.解:(1)∵抛物线与x轴交于点B(﹣2,0),C(6,0)∴设交点式y=a(x+2)(x﹣6)∵抛物线过点A(0,6)∴﹣12a=6∴a=﹣∴抛物线解析式为y=﹣(x+2)(x﹣6)=﹣x2+2x+6=﹣(x﹣2)2+8 ∴抛物线对称轴为直线x=2.(2)过点P作PH⊥x轴于点H,如图1∴∠PHD=90°∵点P(m,n)是抛物线上位于第一象限内的一动点且在对称轴右侧∴2<m<6,PH=n=﹣m2+2m+6,n>0∵OA=OC=6,∠AOC=90°∴∠ACO=45°∵PD⊥AC于点E∴∠CED=90°∴∠CDE=90°﹣∠ACO=45°∴DH=PH=n∵PG∥AB∴∠PGH=∠ABO∴△PGH∽△ABO∴∴GH=n∴d=DH﹣GH=n﹣n=n=(﹣m2+2m+6)=﹣m2+m+4(2<m<6)(3)①∵S=DG•PH=△PDG∴n•n=解得:n1=,n2=﹣(舍去)∴﹣m2+2m+6=解得:m1=﹣1(舍去),m2=5∴点P坐标为(5,)②在抛物线上存在点R,使得△ARS为等腰直角三角形.设直线AP解析式为y=kx+6把点P代入得:5k+6=∴k=﹣∴直线AP:y=﹣x+6i)若∠RAS=90°,且S在线段AC上,如图2∵直线AC解析式为y=﹣x+6∴直线AR解析式为y=x+6解得:(即点A)∴R(2,8)∵∠ASR=∠OAC=45°∴RS∥y轴∴x S=x R=2∴S(2,4)∴直线OM:y=2x∵解得:∴M(,),ii)若∠ASR=90°,如图4∴∠SAR=∠ACO=45°∴AR∥x轴∴R(4,6)∵S在AR的垂直平分线上∴S(2,4)∴M(,)iii)若∠ARS=90°,如图5∴∠SAR=∠ACO=45°,RS∥y轴∴AR∥x轴∴R(4,6)∴S(4,2)∴直线OM:y=x∵解得:∴M(6,3)ix)点M在点A的左侧时,∠SAR=90°,如图6,∴∠SRA=45°,R和S关于y轴对称,∴R(2,8),S(﹣2,8),∴OM:y=﹣4x,∵解得:,∴M(,)综上所述,M1(,),R1(2,8);M2(,),R2(4,6);M3(6,3),R 3(4,6);M4(,),R4(2,8).4.解:(1)由表格的数据,设q与x的函数关系式为:q=kx+b根据表格的数据得,解得故q与x的函数关系式为:q=﹣x+14,其中2≤x≤10(2)①当每天的半成品食材能全部售出时,有p≤q即x+8≤﹣x+14,解得x≤4又2≤x≤10,所以此时2≤x≤4②由①可知,当2≤x≤4时,y=(x﹣2)p=(x﹣2)(x+8)=x2+7x﹣16当4<x≤10时,y=(x﹣2)q﹣2(p﹣q)=(x﹣2)(﹣x+14)﹣2[x+8﹣(﹣x+14)]=﹣x2+13x﹣16即有y=(3)当2≤x≤4时,y=x2+7x﹣16的对称轴为x===﹣7∴当2≤x≤4时,除x的增大而增大∴x=4时有最大值,y==20当4<x≤10时y=﹣x2+13x﹣16=﹣(x﹣)2+,∵﹣1<0,>4∴x=时取最大值即此时y有最大利润要使每天的利润不低于24百元,则当2≤x≤4时,显然不符合故y=﹣(x﹣)2+≥24,解得5≤x≤8故当x=5时,能保证不低于24百元,并尽可能地减少半成品食材的浪费,故答案为:,55.解:(1)∵平行四边形OABC中,A(6,0),C(4,3)∴BC=OA=6,BC∥x轴∴x B=x C+6=10,y B=y C=3,即B(10,3)设抛物线y=ax2+bx+c经过点B、C、D(1,0)∴解得:∴抛物线解析式为y=﹣x2+x﹣(2)如图1,作点E关于x轴的对称点E',连接E'F交x轴于点P∵C(4,3)∴OC=∵BC∥OA∴∠OEC=∠AOE∵OE平分∠AOC∴∠AOE=∠COE∴∠OEC=∠COE∴CE=OC=5∴x E=x C+5=9,即E(9,3)∴直线OE解析式为y=x∵直线OE交抛物线对称轴于点F,对称轴为直线:x=﹣=7∴F(7,)∵点E与点E'关于x轴对称,点P在x轴上∴E'(9,﹣3),PE=PE'∴当点F 、P 、E '在同一直线上时,PE +PF =PE '+PF =FE '最小 设直线E 'F 解析式为y =kx +h ∴解得:∴直线E 'F :y =﹣x +21 当﹣x +21=0时,解得:x =∴当PE +PF 的值最小时,点P 坐标为(,0).(3)存在满足条件的点M ,N ,使得以点M ,N ,H ,E 为顶点的四边形为平行四边形. 设AH 与OE 相交于点G (t ,t ),如图2 ∵AH ⊥OE 于点G ,A (6,0) ∴∠AGO =90° ∴AG 2+OG 2=OA 2∴(6﹣t )2+(t )2+t 2+(t )2=62 ∴解得:t 1=0(舍去),t 2=∴G (,)设直线AG 解析式为y =dx +e ∴解得:∴直线AG :y =﹣3x +18当y =3时,﹣3x +18=3,解得:x =5 ∴H (5,3)∴HE =9﹣5=4,点H 、E 关于直线x =7对称①当HE 为以点M ,N ,H ,E 为顶点的平行四边形的边时,如图2 则HE ∥MN ,MN =HE =4∵点N 在抛物线对称轴:直线x =7上 ∴x M =7+4或7﹣4,即x M =11或3当x=3时,y M=﹣×9+×3﹣=∴M(3,)或(11,)②当HE为以点M,N,H,E为顶点的平行四边形的对角线时,如图3则HE、MN互相平分∵直线x=7平分HE,点F在直线x=7上∴点M在直线x=7上,即M为抛物线顶点∴y M=﹣×49+×7﹣=4∴M(7,4)综上所述,点M坐标为(3,)、(11,)或(7,4).6.解:(1)点A(﹣3,﹣3),B(1,﹣1)代入y=kx+b,∴,∴,∴y=x﹣;联立y=ax2+2x﹣1与y=x﹣,则有2ax2+3x+1=0,∵抛物线C与直线l有交点,∴△=9﹣8a≥0,∴a≤且a≠0;(2)根据题意可得,y=﹣x2+2x﹣1,∵a<0,∴抛物线开口向下,对称轴x=1,∵m≤x≤m+2时,y有最大值﹣4,∴当y=﹣4时,有﹣x2+2x﹣1=﹣4,∴x=﹣1或x=3,①在x=1左侧,y随x的增大而增大,∴x=m+2=﹣1时,y有最大值﹣4,∴m=﹣3;②在对称轴x=1右侧,y随x增大而减小,∴x=m=3时,y有最大值﹣4;综上所述:m=﹣3或m=3;(3)①a<0时,x=1时,y≤﹣1,即a≤﹣2;②a>0时,x=﹣3时,y≥﹣3,即a≥,直线AB的解析式为y=x﹣,抛物线与直线联立:ax2+2x﹣1=x﹣,∴ax2+x+=0,△=﹣2a>0,∴a<,∴a的取值范围为≤a<或a≤﹣2;7.解:(1)设函数解析式为y=ax2+bx+c,将点A(﹣2,2),C(0,2),D(2,0)代入解析式可得,∴,∴y=﹣﹣x+2;(2)∵△PAM≌△PBM,∴PA=PB,MA=MB,∴点P为AB的垂直平分线与抛物线的交点,∵AB=2,∴点P的纵坐标是1,∴1=﹣﹣x+2,∴x=﹣1+或x=﹣1﹣,∴P(﹣1﹣,1)或P(﹣1+,1);(3)CM=t﹣2,MG=CM=2t﹣4,MD=4﹣(BC+CM)=4﹣(2+t﹣2)=4﹣t,MF=MD=4﹣t,∴BF=4﹣4+t=t,∴S=(GM+BF)×MF=(2t﹣4+t)×(4﹣t)=﹣+8t﹣8=﹣(t﹣)2+;当t=时,S最大值为;(4)设点Q(m,0),直线BC的解析式y=x+2,直线AQ的解析式y=﹣(x+2)+2,∴K(0,),H(﹣,),∴OK2=,OH2=+,HK2=+,①当OK=OH时,=+,∴3m2+12m+8=0,∴m=﹣2+或m=﹣2﹣;②当OH=HK时,+=+,∴m2+4m+8=0,∴m无解;③当OK=HK时,=+,∴m2+4m﹣8=0,∴m=﹣2+2或m=﹣2﹣2;综上所述:Q(﹣2+2,0)或Q(﹣2﹣2,0)或Q(﹣2+,0)或Q(﹣2﹣,0)8.解:∵y=x2﹣4,∴其顶点坐标为(0,﹣4),∵y=x2﹣4是y=﹣x+p的伴随函数,∴(0,﹣4)在一次函数y=﹣x+p的图象上,∴﹣4=0+p.∴p=﹣4,∴一次函数为:y=﹣x﹣4,∴一次函数与坐标轴的交点分别为(0,﹣4),(﹣4,0),∴直线y=﹣x+p与两坐标轴围成的三角形的两直角边都为|﹣4|=4,∴直线y=﹣x+p与两坐标轴围成的三角形的面积为:.(2)设函数y =x 2+2x +n 与x 轴两个交点的横坐标分别为x 1,x 2,则x 1+x 2=﹣2,x 1x 2=n , ∴,∵函数y =x 2+2x +n 与x 轴两个交点间的距离为4, ∴,解得,n =﹣3,∴函数y =x 2+2x +n 为:y =x 2+2x ﹣3=(x +1)2﹣4, ∴其顶点坐标为(﹣1,﹣4),∵y =x 2+2x +n 是y =mx ﹣3(m ≠0)的伴随函数, ∴﹣4=﹣m ﹣3, ∴m =1.9.解:(1)函数的表达式为:y =(x +1)(x ﹣5)=(x 2﹣4x ﹣5)=x 2﹣x ﹣, 点M 坐标为(2,﹣3);(2)当x =8时,y =(x +1)(x ﹣5)=9,即点C (8,9),S 四边形AMBC =AB (y C ﹣y M )=×6×(9+3)=36;(3)y =(x +1)(x ﹣5)=(x 2﹣4x ﹣5)=(x ﹣2)2﹣3,抛物线的图象向左平移2个单位,再向上平移3个单位得到一条新的抛物线, 则新抛物线表达式为:y =x 2, 则定点D 与动点P 之间距离PD ==,令t =,则x 2=3t ,可得PD =,当t =﹣=﹣时,PD 有最小值,∵t ≥0, ∴3﹣2m ≤0,即m ≥时,PD 的最小值d =;当m <时,3﹣2m >0,t ≥0,∴t2+(3﹣2m)t+m2≥0,故当PD最小时,t=0,即x=0,∴当点P与点O重合时,PD最小,即PD的最小值d=|m|∴d=.10.解:(1)由题意:,解得,∴抛物线的解析式为y=﹣(x﹣2)2+3,∴顶点D坐标(2,3).(2)可能.如图1,∵A(﹣2,0),D(2,3),B(6,0),∴AB=8,AD=BD=5,①当DE=DF时,∠DFE=∠DEF=∠ABD,∴EF∥AB,此时E与B重合,与条件矛盾,不成立.②当DE=EF时,又∵△BEF∽△AED,∴△BEF≌△AED,∴BE=AD=5③当DF=EF时,∠EDF=∠DEF=∠DAB=∠DBA,△FDE∽△DAB,∴=,∴==,∵△BEF∽△ADE∴==,∴EB=AD=,答:当BE的长为5或时,△CFE为等腰三角形.(3)如图2中,连接BD,当点P在线段BD的右侧时,作DH⊥AB于H,连接PD,PH,PB.设P[n,﹣(n﹣2)2+3],则S△PBD =S△PBH+S△PDH﹣S△BDH=×4×[﹣(n﹣2)2+3]+×3×(n﹣2)﹣×4×3=﹣(n﹣4)2+,∵﹣<0,∴n=4时,△PBD的面积的最大值为,∵=m,∴当点P在BD的右侧时,m的最大值==,观察图象可知:当0<m<时,满足条件的点P的个数有4个,当m=时,满足条件的点P的个数有3个,当m>时,满足条件的点P的个数有2个(此时点P在BD的左侧).11.解:(1)当1≤x≤10时,设n=kx+b,由图知可知,解得∴n=2x+10同理得,当10<x≤30时,n=﹣1.4x+44∴销售量n与第x天之间的函数关系式:n=(2)∵y=mn﹣80∴y=整理得,y=(3)当1≤x≤10时,∵y=6x2+60x+70的对称轴x===﹣5∴此时,在对称轴的右侧y随x的增大而增大=1270∴x=10时,y取最大值,则y10当10<x<15时∵y=﹣4.2x2+111x+580的对称轴是x=﹣==≈13.2<13.5 ∴x=13时,y取得最大值,此时y=1313.2当15≤x≤30时∵y=1.4x2﹣149x+3220的对称轴为x==>30∴此时,在对称轴的左侧y随x的增大而减小∴x=15时,y取最大值,y的最大值是y=130015综上,草莓销售第13天时,日销售利润y最大,最大值是1313.2元12.解:(1)依题意,当x=36时,y=37;x=44时,y=33,当31≤x≤50时,设y=kx+b,则有,解得∴y与x的关系式为:y=x+55(2)依题意,∵W=(y﹣18)•m∴整理得,当1≤x≤30时,∵W随x增大而增大∴x=30时,取最大值W=30×110+1100=4400当31≤x≤50时,W=x2+160x+1850=∵<0∴x=32时,W取得最大值,此时W=4410综上所述,x为32时,当天的销售利润W(元)最大,最大利润为4410元(3)依题意,W=(y+a﹣18)•m=∵第31天到第35天的日销售利润W(元)随x的增大而增大∴对称轴x==>34.5,得a>2.5故a的的取值范围为a>2.5.13.解:(1)由题意得:﹣8a=﹣4,故a=,故抛物线的表达式为:y=x2﹣x﹣4,令y=0,则x=4或﹣2,即点A、B的坐标分别为(﹣2,0)、(4,0),则AC=2,故答案为:(﹣2,0)、(4,0)、2、y=x2﹣x﹣4;(2)①当BC是平行四边形的一条边时,如图所示,点C向右平移4个单位、向上平移4个单位得到点B,设:点P(n,n2﹣n﹣4),点Q(m,0),则点P向右平移4个单位、向上平移4个单位得到点Q,即:n+4=m,n2﹣n﹣4+4=0,解得:m=4或6(舍去4),即点Q(6,0);当BC是平行四边形的对角线时,设点P(m,n)、点Q(s,0),其中n=m2﹣m﹣4,由中点公式可得:m+s=4,n+0=﹣4,解得:s=2或4(舍去4),故点Q(2,0);故点Q的坐标为(2,0)或(6,0);②如图2,针对于抛物线y=x2﹣x﹣4,令x=0,则y=﹣4,∴C(0,﹣4)∵B(4,0),∴直线BC的解析式为y=x﹣4,过点P作PH∥x轴交BC于点H,∵PE∥AC轴,∴∠HEP=∠ACB,∵PH∥x轴,∴∠PHE=∠ABC=45°,∴△EPH∽△CAB,∴,即:,则EP=PH,设点P(t,y P),∵点P在抛物线y=x2﹣x﹣4上,∴y P=t2﹣t﹣4设点H(x H,y P),∵点H在直线y=x﹣4上,∴y P=x H﹣4则t2﹣t﹣4=x H﹣4,则x H=t2﹣t,f=PH=[t﹣(t2﹣t)]=﹣(t2﹣4t),=﹣(m2﹣4m),当t=m时,f1=﹣(m2﹣2m),当t=4﹣m时,f2则f 1﹣f 2=﹣m (m ﹣),则0<m <2, ∴f 1﹣f 2>0,f 1>f 2.14.解:(1)由图象可知,第40天时的成本为40元,此时的产量为z =﹣2×40+120=40 则第40天的利润为:(80﹣40)×40=1600元 故答案为1600 (2)①设直线AB 的解析式为y =kx +b (k ≠0),把(0,70)(30,40)代入得,解得∴直线AB 的解析式为y =﹣x +70 (Ⅰ)当0<x <30时w =[80﹣(﹣x +70)](﹣2x +120)=﹣2x 2+100x +1200 =﹣2(x ﹣25)2+2450 ∴当x =25时,w 最大值=2450 (Ⅱ)当30≤x ≤50时,w =(80﹣40)×(﹣2x +120)=﹣80x +4800∵w 随x 的增大而减小 ∴当x =30时,w 最大值=2400 ∴w =,第25天的利润最大,最大利润为2450元②(Ⅰ)当0<x ≤30时,令﹣2(x ﹣25)2+2450=2400, 解得x 1=20,x 2=30∵抛物线w =﹣2(x ﹣25)2+2450开口向下 由其图象可知,当20≤x ≤30时,w ≥2400此时,当天利润不低于2400元的天数为:30﹣20+1=11天(Ⅱ)当30<x≤50时,由①可知当天利润均低于2400元综上所述,当天利润不低于2400元的共有11天.15.解:(1)由题意可得:y=100+5(80﹣x)整理得y=﹣5x+500;(2)由题意,得:w=(x﹣40)(﹣5x+500)=﹣5x2+700x﹣20000=﹣5(x﹣70)2+4500∵a=﹣5<0∴w有最大值即当x=70时,w最大值=4500∴应降价80﹣70=10(元)答:当降价10元时,每月获得最大利润为4500元;(3)由题意,得:﹣5(x﹣70)2+4500=4220+200解之,得:x1=66,x2=74,∵抛物线开口向下,对称轴为直线x=70,∴当66≤x≤74时,符合该网店要求而为了让顾客得到最大实惠,故x=66∴当销售单价定为66元时,既符合网店要求,又能让顾客得到最大实惠.16.解:(1)在中,令y=0,得x=4,令x=0,得y=2 ∴A(4,0),B(0,2)把A(4,0),B(0,2),代入,得,解得∴抛物线得解析式为(2)如图,过点B作x轴得平行线交抛物线于点E,过点D作BE的垂线,垂足为F∵BE ∥x 轴,∴∠BAC =∠ABE ∵∠ABD =2∠BAC ,∴∠ABD =2∠ABE 即∠DBE +∠ABE =2∠ABE ∴∠DBE =∠ABE ∴∠DBE =∠BAC 设D 点的坐标为(x ,),则BF =x ,DF =∵tan ∠DBE =,tan ∠BAC =∴=,即解得x 1=0(舍去),x 2=2 当x =2时,=3∴点D 的坐标为(2,3) (3)当BO 为边时,OB ∥EF ,OB =EF 设E (m ,),F (m ,)EF=|()﹣()|=2解得m=2,,1当BO为对角线时,OB与EF互相平分过点O作OF∥AB,直线OF交抛物线于点F()和()求得直线EF解析式为或直线EF与AB的交点为E,点E的横坐标为或∴E点的坐标为(2,1)或(,)或()或()或()17.解:(1)由点A(﹣2,4),B(﹣2,﹣2)可知正方形的边长为6,∴正方形面积为36;有四个交点时0<k<4或﹣8<k<0;故答案为36,0<k<4或﹣8<k<0;(2)①由题意可知,﹣2≤m≤4,y Q=﹣m2﹣2m+3=﹣(m+1)2+4,当m=﹣1,y Q最大=4,在运动过程中点Q在最高位置时的坐标为(﹣1,4),当m<﹣1时,y Q随m的增大而增大,当m=﹣2时,y Q最小=3,当m>﹣1时,y Q随m的增大而减小,当m=4时,y Q最小=﹣21,∴3>﹣21,∴y Q最小=﹣21,点Q在最低位置时的坐标(4,﹣21),∴在运动过程中点Q在最高位置时的坐标为(﹣1,4),最低位置时的坐标为(4,﹣21);②当双曲线y=经过点B(﹣2,﹣2)时,k=4,∴N(4,1),∵顶点P(m,n)在边BC上,∴n=﹣2,∴BP=m+2,CP=4﹣m,∵抛物线y=a(x﹣m)2﹣2(a>0)与边AB、DC分别交于点E、F,∴E(﹣2,a(﹣2﹣m)2﹣2),F(4,a(4﹣m)2﹣2),∴BE=a(﹣2﹣m)2,CF=a(4﹣m)2,∴=﹣=a(m+2)﹣a(4﹣m)=2am﹣2a=2a(m﹣1),∵AE=NF,点F在点N下方,∴6﹣a(﹣2﹣m)2=3﹣a(4﹣m)2,∴12a(m﹣1)=3,∴a(m﹣1)=,∴=;③由题意得,M(1,a(1﹣m)2﹣2),∴y M=a(1﹣m)2﹣2(﹣2≤m≤4),y=a(m﹣1)2﹣2(﹣2≤m≤4),M∵a>0,∴对应每一个a(a>0)值,当m=1时,y M最小=﹣2,当m=﹣2或4时,y M最大=9a﹣2,当m=4时,y=a(x﹣4)2﹣2,∴F(4,﹣2),E(﹣2,36a﹣2),∵点E在边AB上,且此时不与B重合,∴﹣2<36a﹣2≤4,∴0<a≤,∴﹣2<9a﹣2≤﹣,∴y M≤﹣,同理m=﹣2时,y=y=a(x+2)2﹣2,∴E(﹣2,﹣2),F(4,36a﹣2),∵点F 在边CD 上,且此时不与C 重合, ∴﹣2<36a ﹣2≤4, 解得0<a ≤, ∴﹣2<9a ﹣2≤﹣, ∴y M ≤﹣,综上所述,抛物线L 与直线x =1的交点M 始终位于x 轴下方; 18.解:(1)∵抛物线的顶点为(2,﹣1) ∴顶点式为y =a (x ﹣2)2﹣1 ∵抛物线经过点C (0,3) ∴4a ﹣1=3 解得:a =1∴抛物线的解析式为y =(x ﹣2)2﹣1=x 2﹣4x +3 (2)解得:,∴A (1,0),B (4,3) ∴AB =设直线y =x ﹣1与y 轴交于点E ,则E (0,﹣1) ∴OA =OE =1 ∴∠AEO =45° ∵S △QAB =S △MAB =S △NAB =S∴点Q 、M 、N 到直线AB 的距离相等如图,假设点M 、N 在直线AB 上方,点Q 在直线AB 下方 ∴MN ∥AB 时,总有S △MAB =S △NAB =S要使只有一个点Q 在直线AB 下方满足S △QAB =S ,则Q 到AB 距离必须最大 过点Q 作QC ∥y 轴交AB 于点C ,QD ⊥AB 于点D ∴∠CDQ =90°,∠DCQ =∠AEO =45° ∴△CDQ 是等腰直角三角形∴DQ=CQ设Q(t,t2﹣4t+3)(1<t<4),则C(t,t﹣1)∴CQ=t﹣1﹣(t2﹣4t+3)=﹣t2+5t﹣4=﹣(t﹣)2+∴t=时,CQ最大值为∴DQ最大值为=AB•DQ=∴S=S△QAB(3)存在点P满足∠APB=90°.∵∠APB=90°,AB=3∴AP2+BP2=AB2设P(p,p2﹣4p+3)(1<p<4)∴AP2=(p﹣1)2+(p2﹣4p+3)2=p4﹣8p3+23p2﹣26p+10,BP2=(p﹣4)2+(p2﹣4p+3﹣3)2=p4﹣8p3+17p2﹣8p+16∴p4﹣8p3+23p2﹣26p+10+p4﹣8p3+17p2﹣8p+16=(3)2整理得:p4﹣8p3+20p2﹣17p+4=0p2(p2﹣8p+16)+4p2﹣17p+4=0p2(p﹣4)2+(4p﹣1)(p﹣4)=0(p﹣4)[p2(p﹣4)+(4p﹣1)]=0∵p<4∴p﹣4≠0∴p2(p﹣4)+(4p﹣1)=0展开得:p3﹣4p2+4p﹣1=0(p3﹣1)﹣(4p2﹣4p)=0(p﹣1)(p2+p+1)﹣4p(p﹣1)=0(p﹣1)(p2+p+1﹣4p)=0∵p>1∴p﹣1≠0∴p2+p+1﹣4p=0解得:p1=,p2=(舍去)∴点P横坐标为时,满足∠APB=90°.19.解:(1))∵点A、B关于直线x=1对称,AB=4,∴A(﹣1,0),B(3,0),代入y=﹣x2+bx+c中,得:,解得,∴抛物线的解析式为y=﹣x2+2x+3,∴C点坐标为(0,3);(2)设直线BC的解析式为y=mx+n,则有:,解得,∴直线BC的解析式为y=﹣x+3,∵点E、F关于直线x=1对称,又E到对称轴的距离为1,∴EF=2,∴F点的横坐标为2,将x=2代入y=﹣x+3中,得:y=﹣2+3=1,∴F(2,1);(3)①如下图,连接BC交MN于Q,MN=﹣4t2+4t+3,MB=3﹣2t,△AOC与△BMN相似,则,即:,解得:t=或﹣或1(舍去、﹣),故:t=1;②∵M(2t,0),MN⊥x轴,∴Q(2t,3﹣2t),∵△BOQ为等腰三角形,∴分三种情况讨论,第一种,当OQ=BQ时,∵QM⊥OB∴OM=MB∴2t=3﹣2t∴t=;第二种,当BO=BQ时,在Rt△BMQ中∵∠OBQ=45°,∴BQ=,∴BO=,即3=,∴t=;第三种,当OQ=OB时,则点Q、C重合,此时t=0而t>0,故不符合题意综上述,当t=或秒时,△BOQ为等腰三角形.20.解:(1)y=(x﹣1)2﹣4向左平移1个单位长度,再向上平移4个单位长度即可得到y=x2;(2)如图1,①设抛物线C与y轴交于C点,直线AB与y轴交于D点,1:y=(x﹣1)2﹣4,∵C1∴A(3,0),C(0,﹣3),∵直线y=﹣x+b经过点A,∴b=4,∴D(0,4),∵AP=AQ,PQ∥y轴,∴P、Q两点关于x轴对称,设D(0,4)关于x轴的对称点为D',则D'(0,﹣4),∴直线AD'的解析式为y=x﹣4,由,得x1=3,x2=,∴x Q=,∴x P=x Q=,∴P点横坐标为;②设P(m,4﹣m),Q(m,m2﹣2m﹣3),∵PA=PQ,∴(m2﹣m﹣7)2=(m﹣3)2+(4﹣m)2,∴|m2﹣m﹣7|=|m﹣3|,∵﹣1<m<3,∴﹣m2+m+7=(3﹣m),∴m=﹣或m=3(舍),∴P点横坐标为﹣;(3)设经过M与E的直线解析式为y=k(x﹣m)+m2,∴,则有x2﹣kx+km﹣m2=0,△=k2﹣4km+4m2=(k﹣2m)2=0,∴k=2m,∴直线ME的解析式为y=2mx﹣m2,同理:直线NE的解析式为y=2nx﹣n2,∴E(,mn),∴[(n2﹣mn)+(m2﹣mn)]×(m﹣n)﹣(n2﹣mn)×(﹣n)﹣(m2﹣mn)×(m﹣)=2,∴(m﹣n)3﹣=4,∴(m﹣n)3=8,∴m﹣n=2.21.解:(1)①依题意设y=kx+b,则有解得:所以y关于x的函数解析式为y=﹣2x+200;②该商品进价是50﹣1000÷100=40,设每周获得利润w=ax2+bx+c:则有,解得:,∴w=﹣2x2+280x﹣8000=﹣2(x﹣70)2+1800,∴当售价是70元/件时,周销售利润最大,最大利润是1800元;故答案为:40,70,1800;(2)根据题意得,w=(x﹣40﹣m)(﹣2x+200)=﹣2x2+(280+2m)x﹣8000﹣200m=﹣2(x﹣)2+m2﹣60m+1800,∵m>0,∴对称轴x=>70,∵﹣2<0,∴抛物线的开口向下,∵x≤65,∴w随x的增大而增大,当x=65时,w=1400,最大即1400=﹣2×652+(280+2m)×65﹣8000﹣200m,解得:m=5.一天,毕达哥拉斯应邀到朋友家做客。
2020-2021备战中考数学压轴题专题复习——圆与相似的综合附答案

2020-2021备战中考数学压轴题专题复习——圆与相似的综合附答案一、相似1.如图,在⊙O中,直径AB经过弦CD的中点E,点M在OD上,AM的延长线交⊙O于点G,交过D的直线于F,且∠BDF=∠CDB,BD与CG交于点N.(1)求证:DF是⊙O的切线;(2)连结MN,猜想MN与AB的位置有关系,并给出证明.【答案】(1)证明:∵直径AB经过弦CD的中点E,, = ,即是的切线(2)解:猜想:MN∥AB.证明:连结CB.∵直径AB经过弦CD的中点E,∴ = , = ,∴∵∴∴∵∴∵∵∴∴∴MN∥AB.【解析】【分析】(1)要证DF是⊙O的切线,由切线的判定知,只须证∠ODF=即可。
由垂径定理可得AB⊥CD,则∠BOD+∠ODE=,而∠ODF=∠CDF+∠ODE,由已知易得∠BOD=∠CDF,则结论可得证;(2)猜想:MN∥AB.理由:连结CB,由已知易证△CBN∽△AOM,可得比例式,于是由已知条件可转化为,∠ODB是公共角,所以可得△MDN∽△ODB,则∠DMN=∠DOB,根据平行线的判定可得MN∥AB。
2.如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.(1)求抛物线对应的二次函数的表达式;(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.【答案】(1)解:∴代入,得解得∴抛物线对应二次函数的表达式为:(2)解:如图,设直线CD切⊙P于点E.连结PE、PA,作点.由得对称轴为直线x=1,∴∴∴为等腰直角三角形.∴∴∴∴为等腰三角形.设∴在中,∴∴整理,得解得,∴点P的坐标为或(3)解:存在点M,使得∽.如图,连结∵∴为等腰直角三角形,∴由(2)可知,∴∴分两种情况.当时,∴,解得.∴∴当时,∴,解得∴∴综上,点M的坐标为或【解析】【分析】(1)用待定系数法即可求解;(2)由(1)中的解析式易求得抛物线的对称轴为直线x=1,顶点D(1,4),点C(0,3),由题意可设点P(1,m),计算易得△DCF为等腰直角三角形,△DEP为等腰三角形,在直角三角形PED和APQ中,用勾股定理可将PE、PA用含m的代数式表示出来,根据PA=PE可列方程求解;(3)由△DCM∽△BQC所得比例式分两种情况:或,根据所得比例式即可求解。
2021年九年级中考数学复习《中考压轴题:圆的综合应用》经典题型提升练习(四)

2021年中考数学复习《中考压轴题:圆的综合应用》经典题型提升练习(四)1.如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE 平分∠BAC交边BC与点E,经过A、D、E三点的即的圆心F恰好在y轴上,⊙F与y轴交于另一点G.(1)求证:BC是⊙F的切线;(2)试探究线段AG、AD、CD之间的关系,并证明;(3)若点A(O,﹣1)、D(2,0),求AB的长.2.如图,在Rt△ABC中,∠ABC=90°,⊙O(圆心O在△ABC内部)经过B,C两点,交线段AC于点D,直径BH交AC于点E,点A关于直线BD的对称点F落在⊙O上.连结BF.(1)求证:∠C=45°;(2)在圆心O的运动过程中;①若tan∠EDF=,AB=6,求CE的长;②若点F关于AC的对称点落在△BFE边上时,求点的值.(直接写出答案);(3)令⊙O与边AB的另一个交点为P,连结PC,交BD于点Q,若PC⊥BF,垂足为点G,求证:BD=AD+CE.3.如图①,△ABC和△CDE都是等腰直角三角形,∠ACB=∠DCE=90°,且点A在ED的延长线上,以DE为直径的⊙O与AB交于G、H两点,连接BE.(1)求证:BE是⊙O的切线;(2)如图②,连接OB、OC,若tan∠CAD=,试判断四边形BECO的形状,请说明理由;(3)在(2)的条件下,若BF=,请你求出HG的长.4.如图1,AB为半圆O的直径,半径OP⊥AB,过劣弧AP上一点D作DC⊥AB于点C.连接DB,交OP于点E,∠DBA=22.5°.(1)若OC=2,则AC的长为;(2)试写出AC与PE之间的数量关系,并说明理由;(3)连接AD并延长,交OP的延长线于点G,设DC=x,GP=y,请求出x与y之间的等量关系式.(请先补全图形,再解答).5.如图,在△ABC中,AB=AC=4,以AB为直径的⊙O交BC于点D,交AC于点E,点P是AB的延长线上一点,且∠PDB=∠A,连接DE、OE.(1)求证:PD是⊙O的切线;(2)填空:①当∠P的度数为时,四边形OBDE是菱形;②当∠BAC=45°时,△CDE的面积为.6.如图,△OAB中,OA=OB=5cm,AB长为8cm,以点O为圆心6cm为直径的⊙O交线段OA 于点C,交直线OB于点E、D,连接CD,EC.(1)求证:△OCD∽△OAB;(2)求证:AB为⊙O的切线;(3)在(2)的结论下,连接点E和切点,交OA于点F求证:OF•CE=OD•CF.7.已知:在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中点,以CD为直径的⊙Q分别交BC、BA于点F、E,点E位于点D下方,连接EF交CD于点G.(1)如图1,如果BC=2,求DE的长;(2)如图2,设BC=x,=y,求y关于x的函数关系式及其定义域;(3)如图3,连接CE,如果CG=CE,求BC的长.8.已知:在矩形ABCD中,AB=a(a为定值),连接AC,点O是AC上的一个动点,以AO 为半径的⊙O与AD交于点P.(1)如图(a),当∠DCP=∠DAC时,求证:PC是⊙O的切线;(2)在(1)的条件下,若△APC是等腰三角形,①请你判断⊙O与BC的位置关系,并说明理由;②求⊙O的半径(用含a的代数式表示);(3)如图(b),若BC=AB=a,且点O运动到AC与BD的交点处,在弧CD上任取一点Q,连接AQ、BQ分别交BD、AC于M,N.求证:四边形ABNM的面积为定值.9.如图,△ABC内接于⊙O,AB=BC,AO⊥BC于D.(1)求证:△ABC是等边三角形;(2)若AB=1,P是劣弧上一个动点,∠APC=60°(点P与B、C不重合),PA交BC于点E,设AE=x,EP=y,求y与x之间的函数关系式,并写出自变量x的取值范围;(3)在(2)的前提下,令∠PAC=α,∠APC=β,当y取何值时,sin2α+sin2β=1.10.如图①,已知A、B是⊙O1上的两点,直线l与⊙O1相交于B、C两点,过A点作⊙O1的切线AO,AO⊥l交于点O,已知BC=8,⊙O1的半径为5.(1)证明:∠ABO1=∠ABO.(2)求AB的长.(3)如图②,以AO所在直线为x轴,以直线l为y轴,建立如图所示的直角坐标系,过A、B两点作⊙O2与y轴的正半轴交于点M,与O1B的延长线交于点N,当⊙O2的大小变化时,BM﹣BN的值是否改变?若改变,请说明理由.若不变,请求出该值.参考答案1.(1)证明:连接EF,如图1所示:∵AE平分∠BAC,∴∠FAE=∠CAE,∵FA=FE,∴∠FAE=∠FEA,∴∠FEA=∠EAC,∴FE∥AC,∴∠FEB=∠C=90°,即BC是⊙F的切线;(2)解:AG=AD+2CD;理由如下:作FR⊥AD于R,连接DF,如图2所示:则∠FRC=90°,又∠FEC=∠C=90°,∴四边形RCEF是矩形,∴EF=RC=RD+CD,∠EFR=90°,∵FR⊥AD,∴AR=RD=AD,∴EF=RD+CD=AD+CD,∵AF=EF,∴AF=AD+CD,∴AG=2AF=AD+2CD;(3)解:设⊙F的半径为r,则r2=(r﹣1)2+22,解得,r=,∴FA=FG=FE=,∵点A(O,﹣1)、D(2,0),∴AD==,∴AR=,∵∠EFR=90°,∴∠BFE+∠AFR=90°,∵∠BFE+∠EBF=90°,∴∠EBF=∠AFR,∵∠BEF=∠FRA=90°,∴△BEF∽△FRA,∴=,即=,解得:BF=,∴AB=AF+BF=+=.2.(1)证明:∵点A,F关于直线BD对称,∵∠BFD=∠C,∴∠A=∠C,∵∠ABC=90°,∴∠C=45°;(2)①解:∵点A,F关于直线BD对称,∴AD=DF,AB=FB,∵∠A=∠C=45°,∴AB=BC=FB=6,∴,∵BH是直径,∴由圆的对称性可知,△BFE≌△BCE,∴∠BFE=∠C=∠BFD=45°,FE=CE,∴∠DFE=90°,∵tan∠EDF=,AB=6,∴设DF=AD=3a,则EF=CE=4a,DE=5a,∵AC==6,∴AC=3a+4a+5a=6,解得,a=,∴CE=4a=2;②如图1,当点F关于AC的对称点落在BF边上时,连接DO,设FF'交AC于点M,则AC垂直平分FF',由(1)知,∠A=∠C=45°,∠ABC=90°,∴BA=BC,∠ABM=∠CBM=×90°=45°,∵点A,F关于直线BD对称,∴AD=DF,AB=FB,∴△ABD≌△FBD(SSS),∴∠ABD=∠FBD,由(2)知,△BFE≌△BCE,∴∠FBE=∠CBE,∴∠ABD=∠FBD=∠FBE=∠CBE=22.5°,∴∠DBE=∠DBF+∠EBF=45°,∵OD=OB,∴∠OBD=∠ODB=45°,∴∠DOB=90°,在△BDM与△BEM中,∠BDM=∠BEM=90°﹣22.5°=67.5°,∴BD=BE,在等腰Rt△BOD中,设OB=OD=r,则BD=r,∴BE=r,OE=(﹣1)r,∴==﹣1;如图2,当点F关于AC的对称点落在BE边上时,∵∠DF'E=∠DOE=90°,∴点F'与点O重合,连接OF,则OD=OF=DF,∴△DOF为等边三角形,∴∠ODF=60°,由对称性知,∠ODE=∠FDE=30°,在Rt△DOE中,tan∠ODE==tan30°=,∴=;综上所述,的值为﹣1或;(3)如图3,连接PD,FC,FC交BH于点M,∵∠ABC=90°,∴PC⊥BF,∴CF=BC=BF,∴△FBC是等边三角形,∴BG=CM=BF,∠QGB=∠CME=90°,∠DBF=∠DCF,∴△QBG≌△ECM(ASA),∴BQ=CE,∵∠PDA=90°,∠A=45°,∴DP=DA=DF,∴,∵∠DPC=(),∠DQP=∠QDC+∠QCP=(),∴∠DPC=∠DQP,∴DQ=DP=AD,∴BD=AD+CE.3.(1)证明:∵△ABC和△CDE都是等腰直角三角形,∴BC=AC,EC=DC,∴∠DCE=∠ACB=90°,∴∠DCE﹣∠FCD=∠ACB﹣∠FCD,∴∠BCE=∠ACD,∴△BCE≌△ACD(SAS),∴∠CBE=∠CAD,∴∠ABE+∠BAE=90°,∴∠AEB=90°,∴BE⊥OE,又∵OE是⊙O的半径,∴BE是⊙O的切线;(2)四边形BECO是平行四边形,理由如下:∵点O是ED的中点,∴CO是DE边上的中线,∵△CDE是等腰三角形,∴CO是DE边上的高线,∴CO⊥DE,∴∠COE=∠AOC=90°,∵∠AEB=90°,∴∠AEB=COE,∴CO∥BE,∵在Rt△AOC中,tan∠CAD=,∴=,∴AO=2CO,∴DO=CO,∴AD=CO,∵△BCE≌△ACD,∴BE=AD,∴BE=CO,∴四边形BECO是平行四边形;(3)∵四边形BECO是平行四边形,∴CF=BF=,∴BC=2,∴AC=BC=2,∴AB==2,设OC=x,则AO=2x,∵在Rt△AOC中,OC2+AO2=AC2,∴x2+(2x)2=(2)2,解得,x=2(取正值),∴OC=BE=2,AO=4,如图3,过点O作OM⊥AB于点M,连接OG,∴∠AMO=90°,HG=2MG,∴∠AMO=∠AEB=90°,∵∠MAO=∠BAE,∴△MAO∽△BAE,∴=,∴=,∴OM=,在Rt△MOG中,OM2+MG2=OG2,∴()2+MG2=22,∴MG=(取正值),∴HG=2MG=.4.解:(1).∵∠DBA=22.5°∴∠DOC=45°∵OC=2∴OD=∴AC=OA﹣OC=(2)连接AD,DP,OD,过点D作DF⊥OP,垂足为点F.∵∠DCA=∠DFP=90°,AD=DP,CD=DF∴Rt△ACD≌Rt△DFP(HL)∴AC=PF∵∠A=∠CDB=∠OEB=∠DEF,∠ACD=∠DFE=90°,CD=DF ∴Rt△ACD≌Rt△DEF(HL)∴AC=EF∴PE=2AC(3)如图所示,由∠DCO=90°,∠DOC=45°得OD==∵∠ADB=90°,点O是AB中点∴AB=2OD=∵∠A=∠GED,∠GDE=∠ADB,AD=DE∴△DGE≌△DBA(ASA)∴GE=AB=x∵PE=2AC∴PE=2()∴GP=GE﹣PE=即:y=2x5.解:(1)如图,连接OD∵OB=OD,∠PDB=∠A∴∠ODB=∠ABD=90°﹣∠A=90°﹣∠PDB ∴∠ODB+∠PDB=90°∴∠ODP=90°又∵OD是⊙O的半径∴PD是⊙O的切线(2)①30°若四边形OBDE为菱形,则OB=BD=DE=EO=OD ∴△OBD为等边三角形∴∠ABD=∠A=60°∴∠PDB=30°∴∠P=30°即当∠P为30°时,四边形OBDE为菱形②如图所示∵AO=OE=2,∠AOE=90°∴AE=∴EC=4﹣∵∠BAC=45°∴∠EDB=135°∴∠EDC=45°设DF=EF=b,FC=a∵△EFC∽△ADC∴∴∵a2+b2=(4﹣)2解得a=()b,b2=4﹣2S===b2=△CDE6.证明:(1)∵OC=OD,OA=OB,∴=,又∵∠COD=∠AOB,∴△OCD∽△OAB;(2)过点O作OG⊥AB,垂足为G,∴∠OGA=∠OGB=90,∵OA=OB,∴AG=BG=4,在Rt△AOG中,OA=5,AG=4,∴OG==3,∵⊙O的直径为6,∴半径r为3,∴OG=r=3,又OG⊥AB,∴AB为⊙O的切线;(3)∵OA=OB,AG=BG,∴∠AOG=∠BOG,∵OE=OC,∴∠OEC=∠OCE,∵∠AOB=∠OEC+∠OCE,∴∠AOG=∠OCE,∴OG∥EC,∴△FOG∽△FCE,∴=,∴OF•CE=OD•CF,∵OG=OD,∴OF•CE=OD•CF.7.解:(1)如图1中,连接CE.在Rt△ACB中,∵∠ACB=90°,AC=1,BC=2,∴AB==,∵CD是⊙Q的直径,∴∠CED=90°,∴CE⊥AB,∵BD=AD,∴CD=AB=,∵•AB•CE=•BC•AC,∴CE=,在Rt△CDE中,DE===.(2)如图2中,连接CE,设AC交⊙Q于K,连接FK,DF,DK.∵∠FCK=90°,∴FK是⊙Q的直径,∴直线FK经过点Q,∵CD是⊙Q的直径,∴∠CFD=∠CKD=90°,∴DF⊥BC,DK⊥AC,∵DC=DB=DA,∴BF=CF,CK=AK,∴FK∥AB,∴=,∵BC=x,AC=1,∴AB=,∴DC=DB=DA=,∵△ACE∽△ABC,∴可得AE=,∴DE=AD﹣AE=﹣,∴=,∴=,∴y=(x>1).(3)如图3中,连接FK.∵CE=CG,∴∠CEG=∠CGE,∵∠FKC=∠CEG,∵FK∥AB,∴∠FKC=∠A,∵DC=DA,∴∠A=∠DCA,∴∠A=∠DCA=∠CEG=∠CGE,∴∠CDA=∠ECG,∴EC=DE,由(2)可知:=﹣,整理得:x2﹣2x﹣1=0,∴x=1+或1﹣(舍弃),∴BC=1+.8.解:(1)证明:连接OP,如图a,∵OA=OP,∴∠DAC=∠APO,∵∠DCP=∠DAC,∴∠DCP=∠APO,∵四边形ABCD是矩形,∴∠D=90°,CD=AB=a,∴∠DCP+∠DPC=90°,∴∠OPC=180°﹣∠DPC﹣∠APO=180°﹣∠DPC﹣∠DCP=90°,∴OP⊥PC,∴PC是⊙O的切线;(2)①BC是⊙O的切线,理由如下:如图a﹣1,过点O作OE⊥BC于E,∵△APC是等腰三角形,∴AP=PC,∴∠PAC=∠PCA,∵AD∥BC,∴∠PAC=∠ACE=∠PCA,又∵∠OPC=∠OEC=90°,OC=OC,∴△OPC≌△OEC(AAS),∴OP=OE,又∵OE⊥BC,∴BC是⊙O的切线;②∵AP=PC,∴∠DAC=∠ACP,∵∠DAC+∠ACD=∠DAC+∠ACP+∠DCP=90°,∴∠DAC=∠DCP=∠ACP=30°,∵在Rt△CDP中,cos∠DCP==,∴PC==a,∵Rt△OPC中,tan∠OCP==,∴OP=PC=,∴⊙O半径为;(3)连接DQ、CQ,如图b,∵矩形ABCD中,BC=AB=a,∴矩形ABCD是正方形,∴AB=AD=BC=a,∠AOB=∠AOM=∠BON=90°,∠ADM=∠BCN=45°,∴AC=BD=a,OA=OB=a,AC、BD为⊙O直径,∵Q在弧CD上运动,∴∠AQB=∠AOB=45°,∵∠ADM=∠AQB=45°,∠DAM=∠QBM,∴△ADM∽△BQM,∴,∴BM=,∵∠BCN=∠AQB=45°,∠CBN=∠QAN,∴△BCN∽△AQN,∴,∴AN=,∵AC、BD为⊙O直径,∴∠AQC=∠BQD=90°,∵∠AOM=∠AQC=90°,∠OAM=∠QAC,∴△AOM∽△AQC,∴,∴AM•AQ=AO•AC=a2,∵∠BON=∠BQD=90°,∠OBN=∠QBD,∴△BON∽△BQD,∴,∴BN•BQ=BO•BD=a2,∴S四边形AMNB =S△AMB+S△NMB=MB•OA+MB•ON=MB(OA+ON)=MB•AN=••=•=•=a2,∴四边形AMNB的面积为定值.9.(1)证明:∵△ABC内接于⊙O,AO⊥BC,∴BD=CD=BC,∴AB=AC,∵AB=BC,∴AB=BC=AC,∴△ABC是等边三角形;(2)解:由(1)得:△ABC是等边三角形,∴AC=AB=BC=1,∠ABC=∠ACB=60°,∴BD=CD=,AD=BD=,∵∠APC=∠ABC,∴∠ACB=∠APC,又∵∠CAE=∠PAC,∴△ACE∽△APC,∴=,∴AE×AP=AC2=1,即x(x+y)=1,∴y=又∵AD<AE<AB,∴<x<1;(3)解:∵∠APC=∠B=60°,∠PAC=α,∠APC=β,∴sin2α=sin2∠APC=()2=,∵sin2α+sin2β=1.∴sin2β=1﹣=,∴sinβ=,∴∠PAC=30°,∴点E与D重合,如图所示:连接OB,则OB平分∠ABC,∴∠OBD=30°,∵AD⊥BC,∴OD=BD=,OP=OA=OB=2OD=,∴PD=PE=OP﹣OD=﹣=;即y取时,sin2α+sin2β=1.10.解:(1)连接O1A,过O1作EO1⊥BC于E,∵EO1⊥BC,∴BE=BC=4,∵O1B=5,∴O1E===3,∵过A点作⊙O1的切线AO,∴AO1⊥AO,且AO⊥l,EO1⊥BC,∴四边形OEO1A是矩形,∴AO=O1E=3,AO1∥OE,AO1=EO=5,∴∠O1AB=∠ABO,∵O1A=O1B,∴∠O1AB=∠O1BA,∴∠ABO1=∠ABO;(2)∵OB=OE﹣BE=5﹣4=1,∴AB===;(3)在MB上截取MG=NB,连接AM,AN,AG,MN,∵四边形ABNM是圆内接四边形,=∠NMA,∴∠ABO1=∠ABO,∠ABO=∠ANM∵∠ABO1∴∠AMN=∠ANM,∴AM=AN,∵=,∴∠AMG=∠ANB,且AM=AN,MG=NB,∴△AMG≌△ANB(SAS)∴AG=AB,且AO⊥BC,∴BO=GO=1,∴BG=2,∴BM﹣BN=BM﹣MG=BG=2,∴BM﹣BN的值不变.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
备战2021湖北省各市2019年中考数学圆压轴题真题汇编数学试题1.(2019•孝感)如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆⊙O 交于点D,与AC交于点E,延长CD、BA相交于点F,∠ADF的平分线交AF于点G.(1)求证:DG∥CA;(2)求证:AD=ID;(3)若DE=4,BE=5,求BI的长.2.(2019•襄阳)如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O 相交于点D,过D作直线DG∥BC.(1)求证:DG是⊙O的切线;(2)若DE=6,BC=6,求优弧的长.3.(2019•黄石)如图,AB是⊙O的直径,点D在AB的延长线上,C、E是⊙O 上的两点,CE=CB,∠BCD=∠CAE,延长AE交BC的延长线于点F.(1)求证:CD是⊙O的切线;(2)求证:CE=CF;(3)若BD=1,CD=,求弦AC的长.4.(2019•荆门)已知锐角△ABC的外接圆圆心为O,半径为R.(1)求证:=2R;(2)若△ABC中∠A=45°,∠B=60°,AC=,求BC的长及sin C的值.5.(2019•荆州)如图,AB是⊙O的直径,点C为⊙O上一点,点P是半径OB 上一动点(不与O,B重合),过点P作射线l⊥AB,分别交弦BC,于D,E两点,在射线l上取点F,使FC=FD.(1)求证:FC是⊙O的切线;(2)当点E是的中点时,①若∠BAC=60°,判断以O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;②若tan∠ABC=,且AB=20,求DE的长.6.(2019•咸宁)如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD 为直径的⊙O分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G.(1)试判断FG与⊙O的位置关系,并说明理由.(2)若AC=3,CD=2.5,求FG的长.7.(2019•宜昌)已知:在矩形ABCD中,E,F分别是边AB,AD上的点,过点F 作EF的垂线交DC于点H,以EF为直径作半圆O.(1)填空:点A(填“在”或“不在”)⊙O上;当=时,tan ∠AEF的值是;(2)如图1,在△EFH中,当FE=FH时,求证:AD=AE+DH;(3)如图2,当△EFH的顶点F是边AD的中点时,求证:EH=AE+DH;(4)如图3,点M在线段FH的延长线上,若FM=FE,连接EM交DC于点N,连接FN,当AE=AD时,FN=4,HN=3,求tan∠AEF的值.8.(2019•十堰)如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,点E为AC延长线上一点,且∠CDE=∠BAC.(1)求证:DE是⊙O的切线;(2)若AB=3BD,CE=2,求⊙O的半径.9.(2019•随州)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且∠BAC=2∠CBF.(1)求证:BF是⊙O的切线;(2)若⊙O的直径为3,sin∠CBF=,求BC和BF的长.10.(2019•湖北)已知△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,连接DB,DC.(1)如图①,当∠BAC=120°时,请直接写出线段AB,AC,AD之间满足的等量关系式:;(2)如图②,当∠BAC=90°时,试探究线段AB,AC,AD之间满足的等量关系,并证明你的结论;(3)如图③,若BC=5,BD=4,求的值.11.(2019•宜昌)如图,点O是线段AH上一点,AH=3,以点O为圆心,OA的长为半径作⊙O,过点H作AH的垂线交⊙O于C,N两点,点B在线段CN的延长线上,连接AB交⊙O于点M,以AB,BC为边作▱ABCD.(1)求证:AD是⊙O的切线;(2)若OH=AH,求四边形AHCD与⊙O重叠部分的面积;(3)若NH=AH,BN=,连接MN,求OH和MN的长.12.(2019•咸宁)定义:有一组邻边相等且对角互补的四边形叫做等补四边形.理解:(1)如图1,点A,B,C在⊙O上,∠ABC的平分线交⊙O于点D,连接AD,CD.求证:四边形ABCD是等补四边形;探究:(2)如图2,在等补四边形ABCD中,AB=AD,连接AC,AC是否平分∠BCD?请说明理由.运用:(3)如图3,在等补四边形ABCD中,AB=AD,其外角∠EAD的平分线交CD 的延长线于点F,CD=10,AF=5,求DF的长.13.(2019•鄂州)如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,PB.(1)求证:PB是⊙O的切线;(2)求证:E为△PAB的内心;(3)若cos∠PAB=,BC=1,求PO的长.参考答案1.(1)证明:∵点I是△ABC的内心,∴∠2=∠7,∵DG平分∠ADF,∴∠1=∠ADF,∵∠ADF=∠ABC,∴∠1=∠2,∵∠3=∠2,∴∠1=∠3,∴DG∥AC;(2)证明:∵点I是△ABC的内心,∴∠5=∠6,∵∠4=∠7+∠5=∠3+∠6,即∠4=∠DAI,∴DA=DI;(3)解:∵∠3=∠7,∠ADE=∠BDA,∴△DAE∽△DBA,∴AD:DB=DE:DA,即AD:9=4:AD,∴AD=6,∴DI=6,∴BI=BD﹣DI=9﹣6=3.2.(1)证明:连接OD交BC于H,连接OB、OC,如图,∵点E是△ABC的内心,∴AD平分∠BAC,∴∠BOD=∠COD,∴=,∴OD⊥BC,BH=CH,∵DG∥BC,∴OD⊥DG,∴DG是⊙O的切线;(2)解:连接BD、OB,如图,∵点E是△ABC的内心,∴∠ABE=∠CBE,∵∠DBC=∠BAD,∴∠DEB=∠BAD+∠ABE=∠DBC+∠CBE=∠DBE,∴DB=DE=6,∵BH=BC=3,在Rt△BDH中,sin∠BDH===,∴∠BDH=60°,而OB=OD,∴△OBD为等边三角形,∴∠BOD=60°,OB=BD=6,∴∠BOC=120°,∴优弧的长==8π.3.解:(1)连接OC,如右图所示,∵AB是⊙O的直径,∴∠CAD+∠ABC=90°,∵CE=CB,∴∠CAE=∠CAB,∵∠BCD=∠CAE,∴∠CAB=∠BCD,∵OB=OC,∴∠OBC=∠OCB,∴∠OCB+∠BCD=90°,∴∠OCD=90°,∴CD是⊙O的切线;(2)∵∠BAC=∠CAE,∠ACB=∠ACF=90°,AC=AC,∴△ABC≌△AFC(ASA),∴CB=CF,又∵CB=CE,∴CE=CF;(3)∵∠BCD=∠CAD,∠ADC=∠CDB,∴△DCB∽△DAC,∴,∴,∴DA=2,∴AB=AD﹣BD=2﹣1=1,设BC=a,AC=a,由勾股定理可得:,解得:a=,∴.4.解:(1)如图1,连接AO并延长交⊙O于D,连接CD,则∠ACD=90°,∠ABC=∠ADC,∵sin∠ABC=sin∠ADC=,∴=2R;(2)∵=2R,同理可得:==2R,∴2R==2,∴BC=2R•sin A=2sin45°=,如图2,过C作CE⊥AB于E,∴BE=BC•cos B=cos60°=,AE=AC•cos45°=,∴AB=AE+BE=,∵AB=2R•sin C,∴sin C==.5.解:(1)证明:连接OC,∵OB=OC,∴∠OBC=∠OCB,∵PF⊥AB,∴∠BPD=90°,∴∠OBC+∠BDP=90°,∵FC=FD∴∠FCD=∠FDC∵∠FDC=∠BDP∴∠OCB+∠FCD=90°∴OC⊥FC∴FC是⊙O的切线.(2)如图2,连接OC,OE,BE,CE,①以O,B,E,C为顶点的四边形是菱形.理由如下:∵AB是直径,∴∠ACB=90°,∵∠BAC=60°,∴∠BOC=120°,∵点E是的中点,∴∠BOE=∠COE=60°,∵OB=OE=OC∴△BOE,△OCE均为等边三角形,∴OB=BE=CE=OC∴四边形BOCE是菱形;②若tan∠ABC=,且AB=20,求DE的长.∵=tan∠ABC=,设AC=3k,BC=4k(k>0),由勾股定理得AC2+BC2=AB2,即(3k)2+(4k)2=202,解得k=4,∴AC=12,BC=16,∵点E是的中点,∴OE⊥BC,BH=CH=8,∴OE×BH=OB×PE,即10×8=10PE,解得:PE=8,由勾股定理得OP===6,∴BP=OB﹣OP=10﹣6=4,∵=tan∠ABC=,即DP=BP==3∴DE=PE﹣DP=8﹣3=5.6.解:(1)FG与⊙O相切,理由:如图,连接OF,∵∠ACB=90°,D为AB的中点,∴CD=BD,∴∠DBC=∠DCB,∵OF=OC,∴∠OFC=∠OCF,∴∠OFC=∠DBC,∴OF∥DB,∴∠OFG+∠DGF=180°,∵FG⊥AB,∴∠DGF=90°,∴∠OFG=90°,∴FG与⊙O相切;(2)连接DF,∵CD=2.5,∴AB=2CD=5,∴BC==4,∵CD为⊙O的直径,∴∠DFC=90°,∴FD⊥BC,∵DB=DC,∴BF=BC=2,∵sin∠ABC=,即=,∴FG=.7.解:(1)连接AO,∵∠EAF=90°,O为EF中点,∴AO=EF,∴点A在⊙O上,当=时,∠AEF=45°,∴tan∠AEF=tan45°=1,故答案为:在,1;(2)∵EF⊥FH,∴∠EFH=90°,在矩形ABCD中,∠A=∠D=90°,∴∠AEF+∠AFE=90°,∠AFE+∠DFH=90°,∴∠AEF=∠DFH,又FE=FH,∴△AEF≌△DFH(AAS),∴AF=DH,AE=DF,∴AD=AF+DF=AE+DH;(3)延长EF交HD的延长线于点G,∵F分别是边AD上的中点,∴AF=DF,∵∠A=∠FDG=90°,∠AFE=∠DFG,∴△AEF≌△DGF(ASA),∴AE=DG,EF=FG,∵EF⊥FH,∴EH=GH,∴GH=DH+DG=DH+AE,∴EH=AE+DH;(4)过点M作MQ⊥AD于点Q.设AF=x,AE=a,∵FM=FEEF⊥FH,∴△EFM为等腰直角三角形,∴∠FEM=∠FMN=45°,∵FM=FE,∠A=∠MQF=90°,∠AEF=∠MFQ,∴△AEF≌△QFM(ASA),∴AE=FQ=a,AF=QM,∵AE=AD,∴AF=DQ=QM=x,∵DC∥QM,∴,∵DC∥AB∥QM,∴,∴,∵FE=FM,∴,∠FEM=∠FMN=45°,∴△FEN~△HMN,∴,∴.8.解:(1)如图,连接OD,AD,∵AC是直径,∴∠ADC=90°,∴AD⊥BC,∵AB=AC,∴∠CAD=∠BAD=∠BAC,∵∠CDE=∠BAC.∴∠CDE=∠CAD,∵OA=OD,∴∠CAD=∠ADO,∵∠ADO+∠ODC=90°,∴∠ODC+∠CDE=90°∴∠ODE=90°又∵OD是⊙O的半径∴DE是⊙O的切线;(2)解:∵AB=AC,AD⊥BC,∴BD=CD,∵AB=3BD,∴AC=3DC,设DC=x,则AC=3x,∴AD==2x,∵∠CDE=∠CAD,∠DEC=∠AED,∴△CDE∽△DAE,∴=,即==∴DE=4,x=,∴AC=3x=14,∴⊙O的半径为7.9.(1)证明:连接AE,∵AB是⊙O的直径,∴∠AEB=90°,∴∠1+∠2=90°.∵AB=AC,∴2∠1=∠CAB.∵∠BAC=2∠CBF,∴∠1=∠CBF∴∠CBF+∠2=90°即∠ABF=90°∵AB是⊙O的直径,∴直线BF是⊙O的切线;(2)解:过点C作CH⊥BF于H.∵sin∠CBF=,∠1=∠CBF,∴sin∠1=,∵在Rt△AEB中,∠AEB=90°,AB=3,∴BE=AB•sin∠1=3×=,∵AB=AC,∠AEB=90°,∴BC=2BE=2,∵sin∠CBF==,∴CH=2,∵CH∥AB,∴=,即=,∴CF=6,∴AF=AC+CF=9,∴BF==6.10.解:(1)如图①在AD上截取AE=AB,连接BE,∵∠BAC=120°,∠BAC的平分线交⊙O于点D,∴∠DBC=∠DAC=60°,∠DCB=∠BAD=60°,∴△ABE和△BCD都是等边三角形,∴∠DBE=∠ABC,AB=BE,BC=BD,∴△BED≌△BAC(SAS),∴DE=AC,∴AD=AE+DE=AB+AC;故答案为:AB+AC=AD.(2)AB+AC=AD.理由如下:如图②,延长AB至点M,使BM=AC,连接DM,∵四边形ABDC内接于⊙O,∴∠MBD=∠ACD,∵∠BAD=∠CAD=45°,∴BD=CD,∴△MBD≌△ACD(SAS),∴MD=AD,∠M=∠CAD=45°,∴MD⊥AD.∴AM=,即AB+BM=,∴AB+AC=;(3)如图③,延长AB至点N,使BN=AC,连接DN,∵四边形ABDC内接于⊙O,∴∠NBD=∠ACD,∵∠BAD=∠CAD,∴BD=CD,∴△NBD≌△ACD(SAS),∴ND=AD,∠N=∠CAD,∴∠N=∠NAD=∠DBC=∠DCB,∴△NAD∽△CBD,∴,∴,又AN=AB+BN=AB+AC,BC=5,BD=4,∴=.11.解:(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,∵∠AHC=90°,∴∠HAD=90°,即OA⊥AD,又∵OA为半径,∴AD是⊙O的切线;(2)解:如右图,连接OC,∵OH=OA,AH=3,∴OH=1,OA=2,∵在Rt△OHC中,∠OHC=90°,OH=OC,∴∠OCH=30°,∴∠AOC=∠OHC+∠OCH=120°,∴S扇形OAC==,∵CH==,∴S△OHC=×1×=,∴四边形ABCD与⊙O重叠部分的面积=S扇形OAC+S△OHC=+;(3)设⊙O半径OA=r=OC,OH=3﹣r,在Rt△OHC中,OH2+HC2=OC2,∴(3﹣r)2+12=r2,∴r=,则OH=,在Rt△ABH中,AH=3,BH=+1=,则AB=,在Rt△ACH中,AH=3,CH=NH=1,得AC=,在△BMN和△BCA中,∠B=∠B,∠BMN=∠BCA,∴△BMN∽△BCA,∴=即==,∴MN=,∴OH=,MN=.12.解:(1)证明:∵四边形ABCD为圆内接四边形,∴∠A+∠C=180°,∠ABC+∠ADC=180°,∵BD平分∠ABC,∴∠ABD=∠CBD,∴,∴AD=CD,∴四边形ABCD是等补四边形;(2)AC平分∠BCD,理由如下:如图2,过点A分别作AE⊥BC于点E,AF垂直CD的延长线于点F,则∠AEB=∠AFD=90°,∵四边形ABCD是等补四边形,∴∠B+∠ADC=180°,又∠ADC+∠ADF=180°,∴∠B=∠ADF,∵AB=AD,∴△ABE≌△ADF(AAS),∴AE=AF,∴AC是∠BCF的平分线,即AC平分∠BCD;(3)如图3,连接AC,∵四边形ABCD是等补四边形,∴∠BAD+∠BCD=180°,又∠BAD+∠EAD=180°,∴∠EAD=∠BCD,∵AF平分∠EAD,∴∠FAD=∠EAD,由(2)知,AC平分∠BCD,∴∠FCA=∠BCD,∴∠FCA=∠FAD,又∠AFC=∠DFA,∴△ACF∽△DAF,∴,即,∴DF=5﹣5.13.(1)证明:连结OB,∵AC为⊙O的直径,∴∠ABC=90°,∵AB⊥PO,∴PO∥BC∴∠AOP=∠C,∠POB=∠OBC,OB=OC,∴∠OBC=∠C,∴∠AOP=∠POB,在△AOP和△BOP中,,∴△AOP≌△BOP(SAS),∴∠OBP=∠OAP,∵PA为⊙O的切线,∴∠OAP=90°,∴∠OBP=90°,∴PB是⊙O的切线;(2)证明:连结AE,∵PA为⊙O的切线,∴∠PAE+∠OAE=90°,∵AD⊥ED,∴∠EAD+∠AED=90°,∵OE=OA,∴∠OAE=∠AED,∴∠PAE=∠DAE,即EA平分∠PAD,∵PA、PB为⊙O的切线,∴PD平分∠APB∴E为△PAB的内心;(3)解:∵∠PAB+∠BAC=90°,∠C+∠BAC=90°,∴∠PAB=∠C,∴cos∠C=cos∠PAB=,在Rt△ABC中,cos∠C===,∴AC=,AO=,∵△PAO∽△ABC,∴,∴PO===5.。
