第三章 n维向量组 PPT课件
线性代数课件6第三章向量空间

线性代数课件6第三章向量空间第三章向量空间3.13.23.33.4n维向量概念及其线性运算线性相关与线性无关向量组的秩向量空间3.1n维向量概念及其线性运算3.1.1n维向量及其线性运算3.1.2向量的线性组合3.1.1n维向量及其线性运算定义3.1.1由n个数a1,a2,……,an组成的有序数组(a1,a2,……,an)称为一个n维向量,数ai称为该向量的第i个分量i=1,2,…,n向量的维数指的是向量中分量的个数.向量写成一行(a1,a2,……,an)列向量写成一行(a1,a2,……,an)T列向量写成一列a1a2.an行向量用小写的黑体字母:α,β,某,y,…表示向量用带下标的白体字母:ai,bi,某i,yi,…表示向量1行、列不同不等:1,22次序不同不等:1,22,1n维向量——矩阵定义一个n维行向量a1,a2,,an.可以定义为一个1n的矩阵b1b2一个n维列向量bn.可以定义为一个n1的矩阵既然向量是一个特殊的矩阵则:1.向量相等=矩阵相等2.零向量=零矩阵3.负向量=负矩阵4.向量运算=矩阵运算a1,a2,,ana1,a2,,an几个定义(1)定义3.1.2所有分量都是0的n维向量称为n维0向量记作:0=(0,0,…,0).向量α=(a1,a2,…,an)的所有分量都取相反数组成的向量,称为α负向量-α=(-a1,-a2,…,-an)如果n维向量α=(a1,a2,…,an)与n维向量β=(b1,b2,…,bn)的对应分量都相等,即ai=bi,(i=1,2,…,n)则称向量α与β相等,记作α=β定义3.1.3几个定义(2)定义3.1.4(向量的加法)设n维向量α=(a1,a2,…,an),β=(b1,b2,…,bn),则α与β的和是向量α+βα+β=(a1+b1,a2+b2,…,an+bn);α与β的差是向量α-βα-β=α+(-β)=(a1-b1,a2-b2,…,an-bn)定义3.1.5(数与向量的乘法)设α=(a1,a2,…,an)是n维向量,k为一个数,则数k与α的乘积称为数乘向量,简称数乘,记作kα,并且kα=(ka1,ka2,…,kan).约定:kα=αk.线性运算律设α,β,γ都是n维向量,k,l是数,则(1)α+β=β+α;(加法交换律)(2)(α+β)+γ=α+(β+γ);(加法结合律)(3)α+0=α;(4)α+(-α)=0;(5)1某α=α;(6)k(α+β)=kα+kβ;(数乘分配律)(7)(k+l)α=kα+lα;(数乘分配律)(8)(kl)α=k(lα).(数乘向量结合律)例1设α=(2,1,3),β=(-1,3,6),γ=(2,-1,4).求向量2α+3β-γ.解2α+3β-γ=2(2,1,3)+3(-1,3,6)-(2,-1,4)=(4,2,6)+(-3,9,18)-(2,-1,4)=(-1,12,20).例2设α=(1,0,-2,3),β=(4,-1,-2,3),求满足2α+3β+3γ=0向量γ.解γ=-1/3(2α+β)=-1/3[2(1,0,-2,3)+(4,-1,-2,3)]=-1/3[(2,0,-4,6)+(4,-1,-2,3)]=-1/3(6,-1,-6,9)=(-2,1/3,2,-3).练习习题3.1P862.(2)答案P184解某=3α-β=3(2,0,1)-(3,1,-1)=(6,0,3)-(3,1,-1)=(3,-1,4).3.1.2向量的线性组合1.向量的线性组合2.向量的线性表出关系的几何解释3.线性组合的——矩阵表示法4.表出系数的求法1.向量的线性组合定义3.1.6设α1,α2,…,αm是一组n维向量,k1,k2,…,km是一组常数,则称k1α1+k2α2+…+kmαm为的一个线性组合.常数k1,k2,…,km称为该线性组合的组合系数.若一个n维向量β可以表示成β=k1α1+k2α2+…+kmαm,则称β是α1,α2,…,αm的线性组合,或称β可用α1,α2,…,αm线性表出(线性表示).仍称k1,k2,…,km为该线性组合的组合系数,或表出系数显然,零向量可以用任意一组α1,α2,…,αm(同维向量)线性表出:0=0α1+0α2+…+0αm(k1=0,k2=0,…,km=0)零向量的平凡表出式表出系数全为0——必是0向量向量组若干同维数的向量组成的集合——向量组m个向量α1,α2,…,αm组成的向量组——记为R:α1,α2,…,αm或R={α1,α2,…,αm}例3:矩阵——向量组表示法Aaija11a21ai1am1a12a22ai2am2a1ja2jaijamjmna1na11,a12,,a1na2na21,a22,,a2nA的行向量组量m个n维行向ainai1,ai2,,ain(i1,2,,m)amnam1,am2,,amnAaijmna11a21ai1am1a12a22ai2am2a1ja2jaijamja1na2nainamnA的列向量组a1ja11a12a1na2ja21a22a2naijai1ai2ainaaaam1m2mnmjn个m维列向量(j1,2,,n)n维标准单位向量组Eaij100010nn01,0,01第i个分量为其余01,分量为00,1,,02i0,,0,1,0,,00i1,2,,n10,0,,1n。
第三章 n维向量组 PPT课件

显然
A
1T
,
T 2
,
T 3
,所以
2 0 3
5 1 0
线性412无 关。
0 0 0
解:(1)设
5 2 7 5 2 7
A
1T
,
T 2
,
T 3
2
1
1 2
1
1
因为该向量组是由3个3维9向量1组成8的,即9满足推1 论81,所以,我
们只需计算
A 527
A 2 1 1 40 18 14 63 32 5 0 9 1 8
所以 1, 2 ,3 线性相关。 (2)作初等行变换
1 2 3 1 2 3
4 1 1 0 A 0 1 1 2
2 1 0 1 2 1 0 2
要 能被向量组 1,2 ,3 线性表出,即要求非齐次线性方程组
4x1 x2 x3 0
x2 x3 2 2x1 x2 1
2x1 x2 2
有解,而由定理4.1.1知,该方程组有解的充要条件是 r(A) r(A)
命题3.2.2:对 m 维向量组1,2, ,n,记 A 1,2 , ,n
下列三结论等价
(1)1,2, ,n 线性相关;
(2)AX O有非零解; (3)r(A) n 或者也可以换个角度,下列三结论等价
(1)1,2, ,n 线性无关;
(2)AX O只有零解; (3)r(A) n
推论1:当m n 时,对 n 个 n 维向量1,2, ,n ,记A
n
把原始向量的序号 1,2 , ,n , 标注在矩阵右侧;
第二步:对矩阵 A 作初等行变换,化为行阶梯形矩阵,且
将每次变换的过程标注在右侧;
第三步:若最后的行阶梯形矩阵中,标注有 的行不是零行, 则向量 不能被向量组1,2, ,n 线性表出;若标注有 的行
(完整版)2.3n维向量的概念

1 n维向量的概念 2 n维向量空间 3 线性相关性
回顾
解析几何 既有大小又有方向的量
几何形象: 可随意 平行移动的有向线段
向量
(n 3)
线性代数
坐 有次序的实数组成的数组
标 代数形象:向量的坐标表示式
(x, y) (x, y, z)
系
一、 n维向量的概念
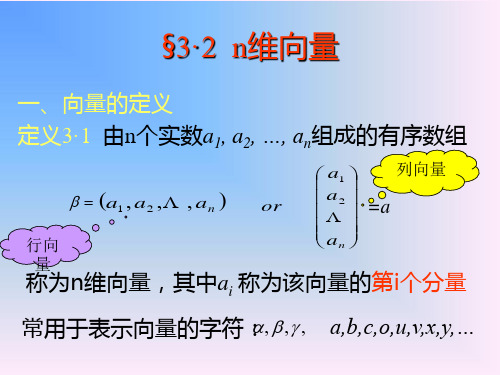
定义1 n个有次序的数 a1, a2 , , an 所组成的数组称为 n维向量,这n个 数称为该向量的n个分量,第 i 个数称为第 i 个分量。
式 11 2,2 称为向m量m
的线性1 ,组合2 ,。 ,m
若 11 22 mm,则称 能由向量组 1,2, ,m 线性表示。
向量1,2 ,L
,m的所有线性组合11 22 L
m
所组成的
m
集合V是一个向量空间.我们称这个空间为由向量1,2 ,L
,
生成的
m
向量空间,记为 L(1,2 ,L ,m )
解 因为对于V1的任意两个元素 0, a2 ,L , an , 0,b2 ,L ,bn V1, 所以有 0, a2 b2 ,L , an bn V1 且 0, a2 ,L , an V1.
所以 V1是向量空间 . V2不是向量空间 .
因为若 1, a2 ,L , an V2 , 则2 2, 2a2 ,L , 2an V2 ,所以V2 不是向量空间.
三、 线性相关性
若干个同维数的列向量(或同维数的行向量)所组成的集合叫做向量组.
定义6 给定向量组A : 1,2 ,L ,m ,如果存在不全为零的数k1, k2 ,L , km 使k11 k22 L kmm 0
则称向量组A是线性相关的,否则称它线性无关.
线代课件-向量组

,
3
0 1
线性表示。
但3不可由向量组B线性表示,故向量组 A不可由
向量组B线性表示,进而向量组 A与向量组B不等价。
1 0 1
(2)向量组B :
1
0 0
,
2
2 0
,
3
1 0
1 0
与向量组
A
: 1
0 0
,
2
10 等价。
§3.2 向量組的線性相關性
一、定義
【定义 4】 设有向量组1,2 , ,m ,
若存在一组不全为零的数 x1, x2 , , xm,使得
x11 x22 xmm 0, 则称向量组1,2 , ,m 线性相关。
否则,称1,2 , ,m 线性无关。即
当且仅当 x1, x2 , , xm全为零时,才有
x11 x22 xmm 0, 则称1,2 , ,m 线性无关。
例 1 1 1,2,3T ,2 2,3,4T ,3 0,0,0T ; 相關
0
b
b3
b1
0
b2
0
b3
1
bn 0 0 0
0
0
bn
0
1
b1 1 0 0
b2
0
1
0
b
b3
b1
0
b2
0
b3
1
bn 0 0 0
0
0
bn
0
1
1 0 0
0
0
1
0
0
En
0
0
1
0
【注 1】若 AB C ,则 C 的列向量组可由 A的列向量组线性表示,( AB C ) C 的行向量组可由B的行向量组线性表示。( AB C )
n维向量空间与线性相关性.ppt

(1)
(加法交换律)
(2) ( ) ( ) (加法结合律)
(3) O O
(4) ( ) O
(5)1
(6) kl kl
(数乘结合律)
(7) k k k (数对向量的分配律)
(8) k l k l (向量对数的分配律)
其中 , , F n ,1,k,l F , O 为 F n 中的零向量。
即
a1,a 2 , ,a n 。
设 (a1,a 2 , ,a n ) , b1,b2 , ,bn 都是 n 维向量,则 当且 仅当 ai bi i 1,2, , n
3.1.2 n 维向量的运算 既然向量可看成矩阵,那么,由矩阵运算的定义就可得向
量的运算。
定义 2 设 (a1, a 2 , , a n ) , b1, b2 , , bn Fn , k F ,
在数学中,把具有上述八条规律的运算称为线性运算。 故向量的加法运算和数乘向量的运算统称为向量的线性运 算
定义 3 数域 F(一般为实数域 R 或复数域C )上全体 n 维
向量的集合,连同定义在其上的线性运算,称为数域 F 上的
n 维向量空间,仍记为 F n 。当 F 为 R 时,称为 n 维实向量空
间,记为 Rn 。
3.2 向量组的线性相关性
本节将利用 n 维向量空间中向量的线性运算来研究向量
之间的线性关系,着重讨论有关向量的三个基本概念: 线性组合,线性相关与线性无关。
以下总是在一个固定的数域 F 上的 n 维向量空间中进行
讨论,不再每次说明。
3.2.1 线性组合与线性表示
定义 1 设有 n 维向量1, 2 , , m 及 ,如果存在一组数
第 3 章 n 维向量及向量组的线性相关性 3.1 n 维向量
线性代数第3章 n维向量与线性方程组

29
例3.3.3判定向量组α1=(1,0,3,2),α2=(0, 1,4,3)的线性相关性. 定理3.3.6 如果向量组α1,α2,…,αs线性无 关,而β,α1,α2,…,αs线性相关,则β可 由α1,α2,…,αs线性表示,且表示式是惟一 的.
30
31
32
3.4 在实际问题中,一个向量组有时含有很多个 向量.对于一个线性相关的向量组,只要所含的向 量不全是零向量,就一定存在一部分向量,它们 是线性无关的.本节主要介绍向量组的最大线性无 关组和向量组的秩.
2
由n维向量加法与数乘运算的定义,不难证明, n维向量的线性运算满足下列运算规律:
3
例3.1.1 设
解
4
例3.1.2 将线性方程组
写成向量方程的形式.
5
解
令
6
即
7
3.2 3.2.1 向量的线性组合 定义3.2.1 例3.2.1 设有向量0=(0,0,0),α1=(1,-1, 2),α2=(3,5,6),α3=(-2,4,3),问: 向量0能否表为向量α1,α2,α3的线性组合?
8
例3.2.2 求证:任何一个n维向量 α=(a1,a2,…,an)都可由向量组
线性表示.
9
证明 因为
10
例3.2.3设β=(1,1,1),α1=(0,1,-1),α2= (1,1,0),α3=(1,0,2),问β能否由α1, α2,α3线性表示?若能,写出线性表示式. 解 设
11
12
3.2.2 向量组的线性相关性 定义3.2.2 例3.2.4 已知α1=(1,1,1),α2=(0,2,5), α3=(2,4,7),试判定向量组α1,α2,α3的 线性相关性.
33
大学线性代数课件3.4节N维向量

1
1
0
2
, 2
1 0
0 0
2
,
3
1 1
0
2 2
,
4
0
1 1
2 2
.
由于 i , j
0, 1,
i j且i, j 1,2,3,4. i j且i, j 1,2,3,4.
所以1,2 ,3 ,4为一标准正交向量组.
同理可知
1 0 0 0
e1
000,
e2
b2
R
n
bn
a1
,
a1b1
a2b2
anbn
b1, b2 ,, bn
a2
b1
T
a1, a2 ,, an
b2
T
an
bn
即 , T T
向量内积的性质: 设 , 均, 为n维向量, 为实数,则
1 , , 2 , , ,
100,
e3
100,
e4
100.
也 为 一 个 标 准 正 交 向 量组 .
(标准正交向量组不唯一)
注意:正交向量组可作为向量空间的一组基。
正交基与标准正交基 正交向量组为基----正交基 标准正交向量组为基----标准正交基。
欧式空间R n中, 若一组基1 , 2 ,
满足标准正交向量组的条件,
§3.4 内积与向量组的正交化
一、内积的定义及性质 二、向量的长度(模)及性质 三、正交向量组的概念及求法
前面主要介绍了向量的线性运算,向量组的线性 相关与线性无关性,并讨论了向量空间中的基、维 数以及向量的坐标等概念。
但在向量空间中还没有涉及度量性质,即还没有 考虑向量空间中的向量的大小、向量间的夹角等问 题。
n维向量及其运算向量组的线性相关性教学课件

空间向量具有三个分量,可以通过三个空间向量的线性组合来表示出任意一个空间向量,从而可以解决空间几何中的角度、距离、垂直和平行等问题。
空间向量的线性相关性
在几何中的应用
通过建立一元线性方程组,可以用向量表示未知数,利用向量的线性相关性求解方程组。
通过对向量空间的定义和性质的研究,可以建立向量空间的运算和结构,进而研究更为复杂的代数问题。
向量组线性相关性的判定定理
03
向量组的线性表示与矩阵
向量组的线性表示的定义:对于给定向量组A和向量b。存在一组系数$\lambda_1,\ldots,\lambda_n$
向量组的线性表示的概念与性质
线性表示的性质
唯一性:当且仅当$\mathbf{b}=0$时。存在一组非零系数$\lambda_1,\ldots,\lambda_n$
数乘运算示例:假设有一个实数k,则k×a=[k×1,k×2,k×3]=[k,2k,3k]。
减法运算示例:假设有一个3维向量c=[7,8,9],则c-a=[7-1,8-2,9-3]=[6,6,6],即c-a=[6,6,6]。
n维向量的运算实例
02
向量组的线性相关性
向量组的定义
有限个向量组成的集合称为一个向量组
非零向量组 $\mathbf{a_1,a_2,...,a_n}$ 与 $\mathbf{b_1,b_2,...,b_n}$ 线性相关
向量组 $\mathbf{a_1,a_2,...,a_n}$ 线性无关的充分必要条件是其中任意不等于零的向量的个数小于等于 $n$
向量组的线性相关性的定义与性质
01
02
在物理中的应用
05
总结与展望
向量组的秩
从定义、性质、计算方法等方面,系统地介绍了向量组的秩的基本概念和基本理论。
线性代数PPT

T
叫做 n 维向量空间.
x ( x1 , x 2 ,, x n ) a1 x1 a 2 x 2 a n x n b
T
n维向量空间 Rn中的 n 1 维超平面. 叫做
n 维向量的实际意义
确定飞机的状态,需 要以下6个参数: 机身的仰角
机翼的转角
机身的水平转角
第三章 向量组的线性相关性
• • • •
n维向量及其运算 向量组的线性相关性 向量组的秩 向量空间简介
第三章 向量组的线性相关性
3.1 n维向量及其运算
3.1.1 n维向量的概念
定义1
n 个有次序的数 a1 , a2 , , an 所组成的数
组称为n维向量,这n个数称为该向量的n个分量, 第i个数ai 称为第i个分量 .
系
代数形象: 向量空 间 中 的 平 面
( x, y, z ) ax by cz d r ( x , y, z )
P ( x, y, z )
一 一 对 应
T
ax by cz d
T
r ( x, y, z )
n n 3时, 维向量没有直观的几何形象.
R x ( x1 , x 2 ,, x n ) x1 , x 2 ,, x n R
b j k1 j 1 k 2 j 2
k11 k12 k 21 k 22 ( b1 , b2 ,, bs ) 1 , 2 ,, m ) ( k m1 k m 2 矩阵K m s ( k ij )称为这一线性表示的系
k1 s k2s k ms 数矩阵 .
v1 0.
例5. 向量组
第3章 n维向量

第三章 n 维向量一、n 维向量的概念与运算 (一)n 维向量的概念n 个数n a a a ,...,,21构成的有序数组称为n 维向量,记作()n a a a ,...,,21或()Tn a a a ,...,,21分别称为n 维行向量或n维列向量,也就是n ⨯1或1⨯n 的矩阵,数i a 称为向量的第i 个分量(二)n 维向量的运算如果,),...,,(21T n a a a =αT n b b b ),...,,(21=β 1.加法 T n n b a b a b a ),...,,(2211+++=+βα 2.数乘 T n ka ka ka k ),...,,(21=α3.内积 αββαβαT T n n b a b a b a ==+++=...),(22114.若0),(=βα,则βα,正交 ★22221...),(n T a a a +++==αααα★22221...n a a a +++=α 00),(=⇔==αααααT二、线性组合与线性表出1.线性组合若干个同维数的列向量(或同维数的行向量)所组成的集合叫做向量组由s 个n 维向量s ααα,...,,21及s 个常数s k k k ,...,,21所构成的向量s s k k k ααα+++...2211称为向量组s ααα,...,,21的一个线性组合,其中s k k k ,...,,21称为组合系数2.线性表出如n 维向量β能表示成向量s ααα,...,,21的线性组合βααα=+++s s k k k ...2211则称β可由s ααα,...,,21线性表出,或说β是s ααα,...,,21的线性组合3.向量组等价如果向量组(1)s ααα,...,,21的每个向量都可以有向量组(2)t βββ,...,,21线性表出,则称向量组(1)可由向量组(2)线性表出; 如果两个向量组可以互相线性表出,则称两个向量等价①等价向量组具有传递性、对称性及反身性,但向量个数可以不一样,线性相关也可以不一样 ②任一向量组和它的极大无关组等价 ③向量组的任意两个极大相关组等价④两个等价的线性无关的向量组所含向量的个数相同⑤等价的向量组具有相同的秩,★但秩相同的向量组不一定等价★⑥如果向量组(1)可由向量组(2)线性表出,⇒=)2()1(r r 向量组(1)(2)等价★单向线性表出+秩相同三、向量组的线性相关与线性无关 (一)线性相关与线性无关的概念1.线性相关对于n 维向量s ααα,...,,21,如存在一组不全为0的数s k k k ,...,,21,使得0...2211=+++s s k k k ααα,则称此向量组s ααα,...,,21线性相关2.线性无关对于n 维向量s ααα,...,,21,如果0...2211=+++s s k k k ααα必有0...21====s k k k ,则称此向量组s ααα,...,,21线性无关;或者说如存在一组数s k k k ,...,,21不全为0,必有0...2211≠+++s s k k k ααα,称此向量组s ααα,...,,21线性无关(二)线性相关与线性无关的充分必要条件1.线性相关的充分必要条件向量组s ααα,...,,21线性相关★⇔齐次方程组0...),...,,(2121=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡s s x x x ααα有非零解★s r s ),...,,(21ααα⇔(秩小于向量个数)★⇔存在某i α可由其他1-s 个向量线性表出★n n 个维向量线性相关0,...,,21=⇔s ααα ★n n 个1+维向量一定线性相关★2.线性无关的充分必要条件 向量组s ααα,...,,21线性无关★⇔齐次方程组0...),...,,(2121=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡s s x x x ααα只有零解★s r s =⇔),...,,(21ααα(秩等于向量个数)★★⇔每一个向量i α都不能用其他1-s 个向量线性表出★3.几个重要结论(1)阶梯形向量组一定线性无关(2)★若向量组s ααα,...,,21线性无关,则它的任一个部分分组ti i i ααα,...,,21必然线性无关★(3)★若向量组s ααα,...,,21线性无关,则它的任一个延伸组⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡s s βαβαβα,,,...2211必然线性无关★ (4)★两两正交、非零的向量组必然线性无关★四、线性相关性与线性表出的关系(1)向量组s ααα,...,,21线性相关的充要条件是s α可以用其余1-s 个向量组表示,存在即可,不需要全部 (2)若向量组s ααα,...,,21线性无关,而向量组βααα,s ,...,,21线性相关,则β可由s ααα,...,,21线性表出,且表示法唯一★(3)若向量组s ααα,...,,21可由向量组t βββ,...,,21线性表出,且t s 大于 s ααα,...,,21⇒线性相关★ ★(4)若向量组s ααα,...,,21可由向量组t βββ,...,,21线性表出,且s ααα,...,,21线性无关t s ≤⇒★五、向量组的秩与矩阵的秩(一)向量组的秩与矩阵的秩的概念1.极大线性无关组在向量组s ααα,...,,21中,如存在一个部分组ti i i ααα,...,,21线性无关,且在添加进组任一向量jα(如果还有的话),向量组j i i i tαααα,,...,,21一定线性相关,则称ti i i ααα,...,,21是向量组s ααα,...,,21的一个极大线性无关组①只由一个零向量构成的向量组不存在极大的线性无关组,规定它的秩为0,一个线性无关组的极大线性无关组就是该向量自身②一般来说,向量组的极大线性无关组不是唯一的;但这些极大线性无关组是等价的,从而每个极大线性无关组中所含向量的个数都是r ,即个数r 是由原向量唯一确定的2.向量组的秩(引入了向量组的秩)(第二章通过等价的矩阵引入矩阵的秩)向量组s ααα,...,,21的极大线性无关组中所含向量的个数r ,称为该该向量的秩,记为r r s =),...,,(21ααα3.矩阵的秩矩阵A 中非零子式的最高阶数称为矩阵A 的秩,记作)(A r矩阵A 中的秩r A r =)(⇔A 中有r 阶子式不为0,r +1阶子式(若还有)全为0 矩阵A 中的秩r A r ≥)(⇔A 中有r 阶子式不为0 矩阵A 中的秩r A r )(⇔A 中有r 阶子式全为0(二)向量组的秩与矩阵的秩的关系①A A r =)(的行秩(矩阵A 的行向量的秩)=A 的列秩(矩阵A 的列向量的秩);求向量的极大线性无关组和向量组的秩时,可通过对矩阵的初等变换化成阶梯形矩阵来实现(行列变换可混用) ②经初等变换矩阵,向量组的秩均不变;③若向量组(1)可由向量组(2)线性表出,则)2()1(r r ≤;特别地,等价的向量组有相同的秩;但秩相同不一定等价六、矩阵秩的重要公式)()(.1T A r A r = ★)()()(.2B r A r B A r +≤+ ★0),()(.3≠=k A r kA r★))(),(min()(.4B r A r AB r = ))()()()(B r AB r A r AB r ≤≤,A 如.5可逆,)()(B r AB r =;如B 可逆,)()(A r AB r =★A .6是n m ⨯矩阵,B 是p n ⨯矩阵,如0=AB ,则n B r A r ≤+)()(★B 每列都是方程解,方程解的个数为)(A r n -七、施密特正交化(前提条件是线性无关)若s ααα,...,,21线性无关,则可构造s βββ,...,,21使其两两正交,且i β是s ααα,...,,21的线性组合,再把i β单位化。
线性代数课件-3.2 n维向量
定义36 对于给定的向量组 β , α 1 , α 2 , , α n 定义 若存在一组数
k 1 , k 2 , , k n ,使得
β = k1α 1 + k 2α 2 + + k nα n
线性表示. 则称向量 β 可由向量组α 1 ,α 2 ,,α n 线性表示. 或向量 β 是向量组 α 1 ,α 2 ,,α n 的线性组合. 的线性组合.
线性表示. 线性表示.
证明: 证明:
1 0 0 0 a1 a1 0 0 a 0 a 0 1 0 2 2 = + + ∵要证:存在一组数 +, k = …,k +,使 + + a n α = 要证:存在一组数k12, a1 n a 2 使 0 0 1 a a 0 0 ε n n α = k + k ε + + k ε
α + β = β +α α + ( β + γ ) = (α + β ) + γ α +0 =α α + ( α ) = 0
( k + t )α = k α + t α k (α + β ) = k α + k β ( kt )α = k ( t α ) 1α = α
改书P 改书 100
【例2】 已知四维向量 α 1 , α 2 , β 满足关系 】
=β
线性方程组的向量表达式: 线性方程组的向量表达式: x 1α 1 + x 2 α 2 + + x n α n = β 或
α 1 x1 + α 2 x 2 + + α n x n = β
三,向量间的线性关系
n 维向量空间.ppt

ax
(ax ,a y ,az )
az
axi a y j azk. x ax
o
ay
a y
ay y
一、n 维向量的概念
1.定义
由数域P上的n个数组成的有序数组 (a1,a2 ,L ,an ) 称为数域P上的一个n维向量; ai 称为该向量的第i个分量.
注:① 向量常用小写希腊字母, , ,L 来表示; ② 向量通常写成一行 (a1,a2 ,L ,an ) ,
• 与向量大小相等,方向相反的向量称为的 负向量,即 OA.
向量的线性运算
向量相等 当平面向量 OA, OB 的终点重合时,称这两个向量相等.
向量加法
设, 为平面向量 , 称+为这两个向量的和,
- = +(-)为两个向量的差.
数乘向量
设为平面向量 ,k为一实数,称k为数k与向量的数乘.
k是这样的向量,其大小(模)为的k倍,
当k0时,k方向与相同;
当k0时,k方向与相反; 向量加法和数乘运算统称
当k=0时,k=0.
线性运算.
平面向量及线性运算示意
和的运算
α α+β β
αβ
α
β
数乘向量运算(k>0)
α kα
α
kα
N a
M
平面向量(2维)
2维(平面)向量的坐标表示
平面解析几何中,引进了坐标(或分量)的概念, 即在平面直角坐标系中,一个平面向量惟一对应着一个 2维有序数组 (a1,a2),称a1,a2为该向量的坐标。
B
AA
空间向量(3维)示意
3维向量及线性运算的坐标表示
向量的坐标表示
(ax ,a y ,az ),ax ,a y ,az称作的坐标.
线性代数课件PPT 第3章.线性方程组

2) (α β) γ α ( β γ() 加法结合律)
3) 存在任意一个向量α,有α 0n α 4)存在任意一个向量α,存在负向量-α,使α (α) 0n
5) 1α α
6) k(lα) (kl)α(数乘结合律)
7) k(α β) kα kβ(数乘分配律)
m
kiai k1α1 k2α2 L kmαm
i 1
称为向量组α1, α2,L , αm在数域F上的一个线性组合。如果记
m
β kiαi,就说β可由α1, α2,L , αm线性表示。 i 1
10
3.1 n维向量及其线性相关性
线性相关性 定义:如果对m个向量α1, α2, α3, ... , αm∈Fn,有m个不全 为0的数k1,k2,...,km∈F,使
α=(a1 a2 an) 其中ai 称为α的第i个分量。
向量写成行的形式称为行向量,向量写作列的形式称为 列向量(也可记作行向量的转置)。
a1
αT
a2
M
an
3
3.1 n维向量及其线性相关性
向量的定义 数域F上全体n元向量组成的集合,记作Fn。
4
3.1 n维向量及其线性相关性
向量的运算
定义:设α=(a1, a2, ... , an),β=(b1, b2, ... , bn)∈Fn,k∈F,
定义:
1)α=β,当且仅当ai=bi (i=1,...,n); 2)向量加法(或α与β之和)为
α β (a1 b1, a2 b2 , ... , an bn )
k1α1 k2α2 L kmαm 0n
成立,则称α1, α2, α3, ... ,αm线性相关;否则,称α1, α2, α3, ... ,αm线性无关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
组成的向量组称为 n 维单位向量组,且任意 n 维向量都可以被该
向量组线性表出。(有的书上用1 (1,0, ,0),2 (0,1, ,0), , n (0,0, ,1) 表示单位向量组。) (4)向量组1,2 , ,m 中任意向量都可以用这个向量组线性 表出,即 i 0 1 0 2 0 i1 1i 0 i1 0 m
则向量 (b1, b2 , , bm ) 可由向量组 1,2 , ,n 线性表出的充
分必要条件是线性方程组
a11k1 a21k2 an1kn b1
a12k1
a22k2
an2kn
b2
a1mk1 a2mk2 anmkn bm
有解。
【注】定理3.2.1和命题1的区别是,定理3.2.1中向量组是 1, 2 ,
(2)分量都是零的向量称为零向量,记作 O,即O (0,0, ,0)
(3)向量(a1,a2 , ,an ) 称为向量 (a1, a2 , , an ) 的负
向量,记作
2. 向量的线性运算 (1)向量的加法
定义3.1.2:设 (a1, a2 , , an ), (b1,b2 , ,bn ) ,那么向 量 (a1 b1, a2 b2 , , an bn ) 称为 与 的和,记为 ,即
n
把原始向量的序号 1,2 , ,n , 标注在矩阵右侧;
第二步:对矩阵 A 作初等行变换,化为行阶梯形矩阵,且
将每次变换的过程标注在右侧;
第三步:若最后的行阶梯形矩阵中,标注有 的行不是零行, 则向量 不能被向量组1,2, ,n 线性表出;若标注有 的行
是零行,则令标注的表达式为零,通过移项化简,则能用向量组
3
1 1 0
0
2
1
0 2
3
1 1 1 1 2
ቤተ መጻሕፍቲ ባይዱ
1 1 1 1 2
4 r1 r2 r1r3
0
4
2
2
4
2
1
1 2r2
0
2 1 1 22 1/ 21
0
0
2 2
1 1
1
2
2
3
0
0
2 1 1
2
1
2
2 3
1 1 1 1
2
r2 r3 r2 r4
0
2 1 1
22 1/ 21
a1 b1, a2 b2 , , an bn
【注】由此可知向量的减法
( ) a1 b1, a2 b2 , , an bn
(2)向量的数乘
定义3.1.3:设 (a1, a2 , , an ) 为 n 维向量, R ,向量 (a1, a2 , , an ) 称为数 与向量 的乘积,记作
令
1
A
2
n
若 A 0,则向量 (b1, b2 , , bn ) 可由向量组 1,2 , ,n 线性
表出。
命题1:设 m 维向量组为
1 (a11, a12, , a1m ),2 (a21, a22, , a2m ), , n (an1, an2, , anm ), (b1,b2, ,bm )
r3 r4
0
0
0 0
0 0
0 1
2 2 2
3 1/ 21 1/ 21
1 1 1 1
2
0
2 1 1
22 1/ 21
0
0
0 0
0 0
1 0
2 2 2
1/ 21 3 1/ 21
所以,向量 不能由向量组 1,2 ,3 线性表出。
同样的题目,我们利用4.1的方法该如何做呢?
解:以 1,2 ,3, 为列向量构造矩阵 A,则有
显然
A
1T
,
T 2
,
T 3
,所以
2 0 3
5 1 0
线性412无 关。
0 0 0
8
则矩阵 A 可由列向量组 1, 2 , 3, 4 表示成 A 1, 2 , 3, 4
二. 向量组的线性组合
1. 定义3.2.2:设 ,1,2 , ,s 都是 n 维向量,如果存在 一组数 k1, k2 , , ks,使得关系式 k11 k22 kss 成立, 则称向量 是向量组 1,2 , , s 的线性组合,并称向量 可由 向量组 1,2 , , s 线性表示(或线性表出)。
向量的加法和数乘统称为向量的线性运算。
(3)向量的线性运算满足的运算规律
( ) ( ) O ( ) O 1 () () ( ) ( )
例:设1 (1,1,0),2 (0,1,1),3 (3,4,1),求1 2 和 31 2 2 3
例:设有四个三维向量
(0,4,2),1 (1,2,3),2 (2,3,1),3 (3,1,2) 试将向量 表示为1,2 ,3 的线性组合。
解:设存在一组数 k1, k2, k3,使得关系式 k11 k22 k33
成立,则有(0,4,2) k1(1,2,3) k2 (2,3,1) k3(3,1,2),即
,n,共有 n 个向量,且每个向量都是 n 维,而命题1中向量
组是1,2, ,n ,共有 n 个向量,但每个向量都是 m 维。其实, 当m n 时,命题1就是定理3.2.1,所以命题1的使用范围更广。
定理3.2.2:若向量 可由 m 维向量组线性表出,则矩阵
1
2
A 的 行经初等行变换可将其化为零行。
命题3.2.2:对 m 维向量组1,2, ,n,记 A 1,2 , ,n
下列三结论等价
(1)1,2, ,n 线性相关;
(2)AX O有非零解; (3)r(A) n 或者也可以换个角度,下列三结论等价
(1)1,2, ,n 线性无关;
(2)AX O只有零解; (3)r(A) n
推论1:当m n 时,对 n 个 n 维向量1,2, ,n ,记A
根据上述定义,线性无关可定义为:
设有 n 维向量组1,2 , ,m,若只有当 k1 k2 km 0 时,才有 k11 k22 kmm O 成立,则称向量组1,2 , ,
m 线性无关。
2. 几点说明 (1)只含一个向量的向量组线性相关的充分必要条件是该 向量是零向量;只含一个向量的向量组线性无关的充分必要条件
2k1k123kk2 23kk33
0 4
3k1 k2 2k3 2
由克莱姆法则得 k1 1,k2 1,k3 1,所以向量 可以表示为
向量组 1,2 ,3 的线性组合,且 1 2 3
2. 如何判断一个向量可由一个向量组线性表出 定理3.2.1:设 n 维向量组为
1 (a11, a12, , a1n ),2 (a21, a22, , a2n ), , n (an1, an2, , ann ), (b1,b2, ,bn )
即 V1 对于向量的加法和数乘运算封闭,所以是一个向量空间。
3.2 向量组及其线性组合
知识点 向量组的概念 向量组的线性组合(即线性表出)
一. 向量组的概念
定义3.2.1:若干个 n 维行向量(列向量)所组成的集合称 为 n 维行(列)向量组。
例如向量组
1 (1,2,1),2 (3,4,7),3 (2,1,5),4 (4,6,1)
解: 1 2 (1,1,0) (0,1,1) (1,0,1) 31 22 3 3(1,1,0) 2(0,1,1) (3,4,1) (0,1,1)
三. 向量空间
定义3.1.4:设 V 为 n 维向量的集合,如果 V 非空,且 V 对 于向量的加法及数乘运算封闭,则集合 V 为向量空间。
4 1 1 0 A 0 1 1 2
2 1 0 1 2 1 0 2
要 能被向量组 1,2 ,3 线性表出,即要求非齐次线性方程组
4x1 x2 x3 0
x2 x3 2 2x1 x2 1
2x1 x2 2
有解,而由定理4.1.1知,该方程组有解的充要条件是 r(A) r(A)
【注】(1)向量 是向量组 1,2 , , s 的线性组合,和向量 可由向量组 1,2 , , s 线性表出是一个意思。
(2)O 向量是任意向量组的线性组合,或者说 O 向量可由任意 向量组线性表出。 (3)设有 n 个 n 维单位向量:
e1 (1,0, ,0),e2 (0,1, ,0), ,en (0,0, ,1)
解:(1)设
5 2 7 5 2 7
A
1T
,
T 2
,
T 3
2
1
1 2
1
1
因为该向量组是由3个3维9向量1组成8的,即9满足推1 论81,所以,我
们只需计算
A 527
A 2 1 1 40 18 14 63 32 5 0 9 1 8
所以 1, 2 ,3 线性相关。 (2)作初等行变换
1 2 3 1 2 3
行向量: a1, a2 , , an
列向量:
也叫行矩阵
b1
b1, b2 ,
, bn T
b2 bn
也叫列矩阵
二. 向量的线性运算
1. 几个常用知识点
(1)若 n 维向量 (a1, a2 , , an ), (b1,b2 , ,bn ) 的对应
分量都相等,即 ai bi (i 1,2, , n) 时,称 与 相等,记作
1,2 , ,n ,下列三结论等价
(1)1,2, ,n 线性相关(无关);
(2)
有非零解(只有零解);
AX 0
(3)
推论2A:当0 0 时,则 n 个 m 维向量
性
nm
1,2, ,n
一定线
相关。
例3:讨论下列向量组的线性相关性
(1)1 5,2,9,2 2,1,1,3 7,1,8
(2)1 1,2,0,3,2 2,5,1,0,3 3,4,1,2
