理论力学第十五章资料
合集下载
第十五章碰撞_理论力学
应选
，即小锤大砧。
打桩也属于这种情况。不过我们希望碰撞结束后，桩应获得最大的动能，以使桩克服土
壤的阻力前进，即碰撞过程中系统的动能损失应尽可能地小。为此，应选 大锤小桩。
，即
4. 两球的斜碰撞
当球心速度不在连心线上时，两球发生斜碰撞，这
时两球球心均作二维平面运动（球是光滑的，因而碰撞后不发生转动）。建立坐标系 Oxy 将
在理想情况下，可以有 ，即材料变形完全不能恢复，称为塑性碰撞（例如粘土）。 这时，两球相撞后粘在一起运动。
在理想情况下，也可以有 ，即材料变形可以完全恢复，称为完全弹性碰撞。这时， 可由式（15-7）求得两球碰撞后的速度。
将式（15-7）的最后两式相减，可得
或
（15-8）
此式常称为碰撞的牛顿公式，它有明确的物理意义，恢复系数等于碰撞后两球相分离的速度
与碰撞前两球相接近的速度之比。可以证明，在物体间是单点碰撞的情况下，式（15-6）与 （15-8）是等价的。因此，也可以用式（15-8）作为恢复系数的定义。
对球与固定面相碰撞的情况，可令式（15-7）中
，
的速度为
，求得球在碰后
或 由此可导出一种恢复系数的实验测定法。小球由 h1 的高度处由静止开始自由下落，碰到固 定面后弹回，弹回的高度是 h2，则
为作用于质点 i 上的质系的
外力。文字表述是：质系在 t2 及 t1 时刻的动量的变化，等于在同一时间间隔内作用于质系 的外碰撞冲量的主矢，可写成质心运动定理形式
★ 质系动量矩定理的积分形式（冲量矩定理）
（15-2）
（15-3）
或
式中 与 分别为 t2 及 t1 时刻质系对 O 点的动量矩， 为质点 i 的矢径，根据前面 的假设，在碰撞过程中它是不变的。文字表述是：质系在 t2 及 t1 时刻对 O 点动量矩的变化， 等于在同一时间间隔内作用于质系的外碰撞冲量对同一点的主矩。矩心可以取在固定点 O ， 也可以取在质系的质心 C 。即：
长沙理工大学理论力学A课件第15章
2. 若
I
vC
K
x
Ix 0 vCy ) I y m(vCy
则轴承反碰撞冲量等于零。
15-5 碰撞冲量对定轴转动刚体的作用· 撞击中心 设质心C到轴承的距离为d,则
I Oy
m
C
25
I Ox
O
I y md ( 0) I
y
0
M z (I )
(e) i
d
Jz
x
15-5 碰撞冲量对定轴转动刚体的作用· 撞击中心 由冲量定理:
24
mv'Cx mvCx I x I Ox mv'Cy mvCy I y I Oy
I Oy
m
I Ox
O
y
d
C
0 若轴承没有撞坏，则 vCx vCx
I Ox I x I Oy m(v'Cy vCy ) I y
(b)
15-5 碰撞冲量对定轴转动刚体的作用· 撞击中心
O O
28
m
l
d
m
m
d
(a)
(b)
(a)
(b)
1 2 ml JO 3 2 OK l l md 3 m 2 1 1 d 3d 2 md 2 m ( )2 m ( ) 65 3 2 2 2 OK d 2 md 48
15-6 碰撞问题举例
26
(2) 用锄头，挥大锤，击棒球，若打击点与撞击中心接近， 则手感轻松，否则手会疼痛。
15-5 碰撞冲量对定轴转动刚体的作用· 撞击中心 问题 1 何时不可避免约束冲量? 当
27
d 0 ，转轴过质心， h
。
I
vC
K
x
Ix 0 vCy ) I y m(vCy
则轴承反碰撞冲量等于零。
15-5 碰撞冲量对定轴转动刚体的作用· 撞击中心 设质心C到轴承的距离为d,则
I Oy
m
C
25
I Ox
O
I y md ( 0) I
y
0
M z (I )
(e) i
d
Jz
x
15-5 碰撞冲量对定轴转动刚体的作用· 撞击中心 由冲量定理:
24
mv'Cx mvCx I x I Ox mv'Cy mvCy I y I Oy
I Oy
m
I Ox
O
y
d
C
0 若轴承没有撞坏，则 vCx vCx
I Ox I x I Oy m(v'Cy vCy ) I y
(b)
15-5 碰撞冲量对定轴转动刚体的作用· 撞击中心
O O
28
m
l
d
m
m
d
(a)
(b)
(a)
(b)
1 2 ml JO 3 2 OK l l md 3 m 2 1 1 d 3d 2 md 2 m ( )2 m ( ) 65 3 2 2 2 OK d 2 md 48
15-6 碰撞问题举例
26
(2) 用锄头，挥大锤，击棒球，若打击点与撞击中心接近， 则手感轻松，否则手会疼痛。
15-5 碰撞冲量对定轴转动刚体的作用· 撞击中心 问题 1 何时不可避免约束冲量? 当
27
d 0 ，转轴过质心， h
。
高中物理理论力学知识点总结
（2）若在连接电路时，有A （10Ω 1A）和B （20Ω 1A）两 个滑动变阻器可供选择，则应该选择变阻器 B（填 “A”或“B”）连入电路，才能保证实验顺利进行．
（3）小明合理地连接好电路，闭合开关，发现无论怎 样调节滑动变阻器灯泡都不亮．小明分析后发现是 灯泡的故障．请你依据表一中电流表、电压表示数 出现的几种情况，帮小明判断故障原因，并将其填 写在表一对应的空格中． 表一：
（4）当小灯泡正常发光时，电流表的示数如图 乙所示，则小灯泡的额定功率是 0.6 W．
【练习3】在测2.5V小灯泡（电阻大约为10Ω左右）额 定功率的实验时，小明连接了如图甲所示的电路， 其中电源电压为6V．
（1）在连接电路时，开关必须 断开．请将实物电路连接 完整（要求：滑动变阻器的滑片向右移动时小灯变 亮）． 如图所示
B．连接电路时，开关要断开，闭合开关前，要把 滑动变阻器置于最大阻值处.
C．在调节滑动变阻器的滑片时，要一边调节，一 边注意观察电压表的示数，以免烧坏灯泡.
【例2】实验室购买了一批规格为“2.5V 0.75W”的 小灯泡，小明利用其中一只灯泡做测量小灯泡电 功率的实验．
（1）用笔画线代替导线把如图所示的实物电路补 充完整．
①分析这组数据，你认为该小灯泡是否合格： ，其原因是： ．
②假如生产这种小灯泡钨丝的粗细是一定的，则这 个小灯泡内钨丝的长度与合格产品相比是长了还 是短了？答： ．
【例3】图1是小红同学在“测量小灯泡的电功 率”实验中连接的实验电路，小灯泡的额定 电压为3.8V，电源电压为6V． （1）当开关闭合，滑动变阻器的滑片向左滑 动时，电流表示数 ，电压表示 数 ．（填“变大”“变小”或“不变”）
②灯泡实际功率随着灯泡两端的电压的增加而变大；
（3）小明合理地连接好电路，闭合开关，发现无论怎 样调节滑动变阻器灯泡都不亮．小明分析后发现是 灯泡的故障．请你依据表一中电流表、电压表示数 出现的几种情况，帮小明判断故障原因，并将其填 写在表一对应的空格中． 表一：
（4）当小灯泡正常发光时，电流表的示数如图 乙所示，则小灯泡的额定功率是 0.6 W．
【练习3】在测2.5V小灯泡（电阻大约为10Ω左右）额 定功率的实验时，小明连接了如图甲所示的电路， 其中电源电压为6V．
（1）在连接电路时，开关必须 断开．请将实物电路连接 完整（要求：滑动变阻器的滑片向右移动时小灯变 亮）． 如图所示
B．连接电路时，开关要断开，闭合开关前，要把 滑动变阻器置于最大阻值处.
C．在调节滑动变阻器的滑片时，要一边调节，一 边注意观察电压表的示数，以免烧坏灯泡.
【例2】实验室购买了一批规格为“2.5V 0.75W”的 小灯泡，小明利用其中一只灯泡做测量小灯泡电 功率的实验．
（1）用笔画线代替导线把如图所示的实物电路补 充完整．
①分析这组数据，你认为该小灯泡是否合格： ，其原因是： ．
②假如生产这种小灯泡钨丝的粗细是一定的，则这 个小灯泡内钨丝的长度与合格产品相比是长了还 是短了？答： ．
【例3】图1是小红同学在“测量小灯泡的电功 率”实验中连接的实验电路，小灯泡的额定 电压为3.8V，电源电压为6V． （1）当开关闭合，滑动变阻器的滑片向左滑 动时，电流表示数 ，电压表示 数 ．（填“变大”“变小”或“不变”）
②灯泡实际功率随着灯泡两端的电压的增加而变大；
《理论力学》考试知识点.
《理论力学》考试知识点静力学第一章静力学基础1、掌握平衡、刚体、力的概念以及等效力系和平衡力系，静力学公理。
2、掌握柔性体约束、光滑接触面约束、光滑铰链约束、固定端约束和球铰链的性质。
3、熟练掌握如何计算力的投影和平面力对点的矩，掌握空间力对点的矩和力对轴之矩的计算方法，以及力对轴的矩与对该轴上任一点的矩之间的关系。
4、对简单的物体系统，熟练掌握取分离体并画出受力图。
第二章力系的简化1、掌握力偶和力偶矩矢的概念以及力偶的性质。
2、掌握汇交力系、平行力系、力偶系的简化方法和简化结果。
3、熟练掌握如何计算主矢和主矩；掌握力的平移定理和空间一般力系和平面力系的简化方法和简化结果。
4、掌握合力投影定理和合力矩定理。
5、掌握计算平行力系中心的方法以及利用分割法和负面积法计算物体重心。
第三章力系的平衡条件1、了解运用空间力系（包括空间汇交力系、空间平行力系和空间力偶系）的平衡条件求解单个物体和简单物体系的平衡问题。
2、熟练掌握平面力系（包括平面汇交力系、平面平行力系和平面力偶系）的平衡条件及其平面力系平衡方程的各种形式；熟练掌握利用平面力系平衡条件求解单个物体和物体系的平衡问题。
3、了解静定和静不定问题的概念。
4、掌握平面静定桁架计算内力的节点法和截面法，掌握判断零力杆的方法。
第四章摩擦1、掌握运用平衡条件求解平面物体系的考虑滑动摩擦的平衡问题。
2、了解极限摩擦定律、滑动摩擦系数、摩擦角、自锁现象、摩阻的概念。
运动学第五章点的运动1、掌握描述点的运动的矢量法、直角坐标法和弧坐标法，能求点的运动方程。
2、熟练掌握如何计算点的速度、加速度及其有关问题。
第六章刚体的基本运动1、掌握刚体平动和定轴转动的特征；掌握刚体定轴转动的转动方程、角速度和角加速度；掌握定轴转动刚体角速度矢量和角加速度矢量的概念以及刚体内各点的速度和加速度的矢积表达式。
2、熟练掌握如何计算定轴转动刚体的角速度和角加速度、刚体内各点的速度和加速度。
第15章 分析力学基础-哈
Qk
( Fx i
xi qk
Fyi
yi qk
Fzi
zi ) qk
( V xi V yi V zi ) xi qk yi qk zi qk
V (k 1,2,3, , N ) qk
（15-13）
则由广义坐标表示的平衡条件可写成下面形式
Qk
V qk
0
(k 1,2,3, , N )
令Qk
n i 1
( Fx i
xi qk
Fyi
yi qk
Fzi
zi ) qk
(k 1,2,3, , N )（15-7）
N
则（15-6）可以写成 WF Qk qk 0 k 1
（15-8）
上式中 Qk qk具有功的量纲，所以Qk成为与广义坐标qk相对应 的广义力。
由于广义坐标的独立性，q可以任意选取，则若（15-8）成立 ，必须有
V V (x1, y1, z1, , xn , yn , zn )
（15-11）
则虚功方程（15-6）中各力的投影可以表达为
Fxi
V xi
, Fyi
V yi
, Fzi
V zi
WF (Fxixi Fyiyi Fzi zi )
于是有
( Vi xi
xi
Vi yi
yi
Vi zi
zi )
V
理论力学电子教程
第十五章 分析力学基础
本章针对矢量力学所遇到的困难，采用分析数学的方 法来求解动力学问题，它利用能量和功来描述物体运 动与相互作用之间的关系，在达朗伯原理和虚位移原 理的基础上，导出动力学普遍方程和拉格朗日第二类 方程（简称拉格朗日方程）。成为研究动力学问题的 有力手段，在解决非自由质点系的动力学问题时，显 得十分简捷、规范。
理论力学---第十五章 单自由度系的振动 [同济大学]
![理论力学---第十五章 单自由度系的振动 [同济大学]](https://img.taocdn.com/s3/m/f12734254b73f242336c5f62.png)
d2x k x 0, dt 2 m
d2x 2 n x 0, dt 2
n2
k , m
F
δs mg k
k
xO
n
v0
s
x mg x
y
A xo (
2π
2
n
v0
)2 ,
ωx α arctan n 0 v0
解 : x c1 cos nt c2 sin nt
第十五章 单自由度系统的振动 §15-1 有阻尼自由振动
1.弹簧力 2.静伸长 3.阻尼力 4. 4 方程
m
Fk k ( s x ),
δs mg k
c Fc
k F
s
x
y
Fc cv
d2 x dx k(x δs ) c mg kx c dx dt 2 dt dt 2 k c x dx 2 2 n , 2n , d 2 2n ωn x0 m m dt dt
m1 m
d T 0, dt d T , m x dt x
V k 2b 2 k1 ( x a )(a )
x0=0 (碰撞时位移、重力不计)
2 ωn
(m1 m) kx 0, x
x A sin(n t )
Ae nTn Ai 1
4 π 2 A2c 2 P 2 4 π 2 2 , T2 g2 Td
c
2 πP 2 2 Td T 2 gATTd
如:=0.05, 10次后振幅仅原4.3%。
Td T
d 2 x 2 Ac dx 2 ωn x0 dt 2 m dt
1
1. 无阻尼的自由振动
理论力学课本及习题集答案
理论力学课本及习题集答案
西北工业大学理论力学教研室
2009年7月
第一章:静力学的基本概念
第二章:平面基本力系
第三章:平面任意力系
第五章:空间基本力系
第六章:空间任意力系
第七章:重 心
第八章:点的运动
第九章:刚体的基本运动
第十章:点的复合运动
日
啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
第十一章:刚体的平面运动
第十二章:刚体的转动合成
第十四章:质点动力学基础
第十五章:质点的振动
第七章:动能定理
第十八章:动量定理
第十九章:动量矩定理
第二十章:碰撞理论
第二十一章:达朗伯原理
第二十二章:虚位移原理
西北工业大学理论力学教研室
2009年7月
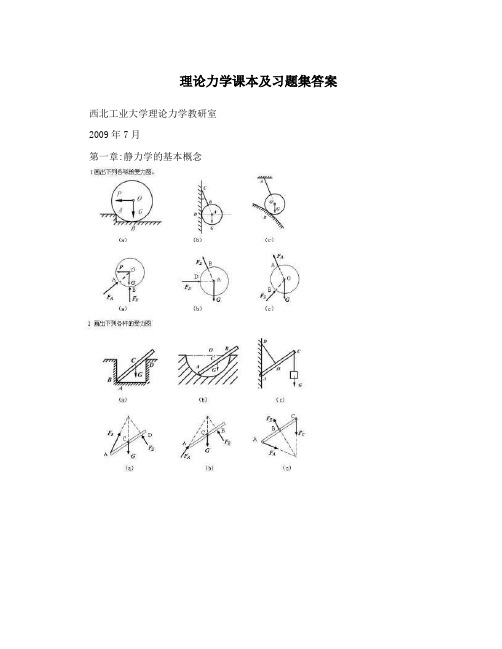
第一章:静力学的基本概念
第二章:平面基本力系
第三章:平面任意力系
第五章:空间基本力系
第六章:空间任意力系
第七章:重 心
第八章:点的运动
第九章:刚体的基本运动
第十章:点的复合运动
日
啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊
第十一章:刚体的平面运动
第十二章:刚体的转动合成
第十四章:质点动力学基础
第十五章:质点的振动
第七章:动能定理
第十八章:动量定理
第十九章:动量矩定理
第二十章:碰撞理论
第二十一章:达朗伯原理
第二十二章:虚位移原理
理论力学电子教案(经典完整版)
A
O
D
B
连接 .不计各杆的自重 ,各
接触面都是光滑的.试分别
C
画出管道O,水平杆AB,斜杆
BC及整体的受力图.
18
解:(1)取管道O为研究对象.
P
O
ND´
A
XA YA
D
RB´ P
B
(4)取整体为研究对象.
ND
(2)取斜杆BC为研究对象.
RB
B A XA YA C
O
D
B
RC
C
(3)取水平杆AB为研究对象.
40
(2)力对点的矩的解析表示
i mo(F) = r×F = x Fx j y Fy k z Fz
若各力的作用线均在 xy 平面内.则Fz = 0, 即任一力的坐标 z = 0 则有
x mo(F) = x Fx - y Fy = Fx
y Fy
41
例题3-1.如图所示,力 F 作用在边长为 a 的正立 方体的对角线上.设 oxy 平面与立方体的底面 ABCD平行,两者之间的
35
第三章 力偶理论
36
内容提要
3-1.力对点的矩 3-2.两平行力的合成 3-3.力偶与力偶矩 3-4.力偶的等效条件 3-5.力偶系的合成与平衡
37
重 点
1.力偶的基本性质
2.力偶系的合成方法
3.力偶系的平衡条件
难 点
1.力偶的基本性质
2.力偶矩矢量的方向
38
3-1.力对点的矩
z
B F A r
理 论 力 学
1
目录
• • • • • • • • • • • • • • • • • • • • • 绪 论 第一章 静力学基本概念与公理 第二章 汇交力系 第三章 力偶理论 第四章 平面任意力系 第五章 桁架 第六章 摩擦 第七章 空间力系 第八章 点的运动 第九章 刚体的基本运动 第十章 点的合成运动 第十一章 刚体的平面运动 第十二章 动力学基本定律 第十三章 动量定理 第十四章 动量矩定理 第十五章 动能定理 第十六章 碰撞 第十七章 达朗伯原理 第十八章 虚位移原理 第十九章 动力学普遍方程和拉格朗日方程 附 录
O
D
B
连接 .不计各杆的自重 ,各
接触面都是光滑的.试分别
C
画出管道O,水平杆AB,斜杆
BC及整体的受力图.
18
解:(1)取管道O为研究对象.
P
O
ND´
A
XA YA
D
RB´ P
B
(4)取整体为研究对象.
ND
(2)取斜杆BC为研究对象.
RB
B A XA YA C
O
D
B
RC
C
(3)取水平杆AB为研究对象.
40
(2)力对点的矩的解析表示
i mo(F) = r×F = x Fx j y Fy k z Fz
若各力的作用线均在 xy 平面内.则Fz = 0, 即任一力的坐标 z = 0 则有
x mo(F) = x Fx - y Fy = Fx
y Fy
41
例题3-1.如图所示,力 F 作用在边长为 a 的正立 方体的对角线上.设 oxy 平面与立方体的底面 ABCD平行,两者之间的
35
第三章 力偶理论
36
内容提要
3-1.力对点的矩 3-2.两平行力的合成 3-3.力偶与力偶矩 3-4.力偶的等效条件 3-5.力偶系的合成与平衡
37
重 点
1.力偶的基本性质
2.力偶系的合成方法
3.力偶系的平衡条件
难 点
1.力偶的基本性质
2.力偶矩矢量的方向
38
3-1.力对点的矩
z
B F A r
理 论 力 学
1
目录
• • • • • • • • • • • • • • • • • • • • • 绪 论 第一章 静力学基本概念与公理 第二章 汇交力系 第三章 力偶理论 第四章 平面任意力系 第五章 桁架 第六章 摩擦 第七章 空间力系 第八章 点的运动 第九章 刚体的基本运动 第十章 点的合成运动 第十一章 刚体的平面运动 第十二章 动力学基本定律 第十三章 动量定理 第十四章 动量矩定理 第十五章 动能定理 第十六章 碰撞 第十七章 达朗伯原理 第十八章 虚位移原理 第十九章 动力学普遍方程和拉格朗日方程 附 录
理论力学达朗贝尔原理(动静法)
miri cosi zi (miri 2 sin i zi )
由
cos
i
xi ri
,
sin i
yi ri
有 MI x mix iz i2 m i y iz i
记 Jyz m i y iz i, Jxz m i x iz i
称对 y、z 轴的惯性积， 对x、z 轴的惯性积。
M Ix J xz J yz 2
已知: P, R, J , a, m.
求：支座A，B受到的附加约束力。
解 ： FI ma
MI0
J
J
a R
M B 0 mgl2 FIl2 Pl3 M IO FAl1 l2 0
Fy 0 FA FB mg P FI 0
解得：FA
l1
1
l2
mgl2
Pl3
a
ml2
J R
第十五章 达朗贝尔原理(动静法)
§15-1 惯性力·质点的达朗贝尔原理
一、惯性力的概念
人用手推车 F ' F ma
力 F '是由于小车具有惯性，力图保持其原
有的运动状态，对于施力物体(人手)产生 的反抗力。称为小车的惯性力。
定义：质点惯性力
FI m a
质点惯性力的大小等于质点的质量与加速度的乘积，方
Fz 0 FBz FRz 0
M x 0 FB yOB FAyOA M x M I x 0
M y 0 FAxOA FBxOB M y M I y 0
解得
FAx
1 AB
M y FRxOB M Iy FIxOB
FAy
1 AB
M x FRyOB M Ix FIyOB
由 miar mi ar mar
由
cos
i
xi ri
,
sin i
yi ri
有 MI x mix iz i2 m i y iz i
记 Jyz m i y iz i, Jxz m i x iz i
称对 y、z 轴的惯性积， 对x、z 轴的惯性积。
M Ix J xz J yz 2
已知: P, R, J , a, m.
求：支座A，B受到的附加约束力。
解 ： FI ma
MI0
J
J
a R
M B 0 mgl2 FIl2 Pl3 M IO FAl1 l2 0
Fy 0 FA FB mg P FI 0
解得：FA
l1
1
l2
mgl2
Pl3
a
ml2
J R
第十五章 达朗贝尔原理(动静法)
§15-1 惯性力·质点的达朗贝尔原理
一、惯性力的概念
人用手推车 F ' F ma
力 F '是由于小车具有惯性，力图保持其原
有的运动状态，对于施力物体(人手)产生 的反抗力。称为小车的惯性力。
定义：质点惯性力
FI m a
质点惯性力的大小等于质点的质量与加速度的乘积，方
Fz 0 FBz FRz 0
M x 0 FB yOB FAyOA M x M I x 0
M y 0 FAxOA FBxOB M y M I y 0
解得
FAx
1 AB
M y FRxOB M Iy FIxOB
FAy
1 AB
M x FRyOB M Ix FIyOB
由 miar mi ar mar
理论力学分析静力学
2021年8月8日 35
理论力学CAI
2021年8月8日 36
理论力学CAI
2021年8月8日 37
理论力学CAI
2021年8月8日 38
理论力学CAI
求平衡结构的约束力
2021年8月8日 39
理论力学CAI
例 多跨静定梁，求支座A处反力。
2021年8月8日 40
理论力学CAI
解：将支座A除去，代入相应的约束反力F A 。
FEx
m L
46
理论力学CAI
图示平面平衡系统 ，已知AB＝ 1.5L，BD＝DE＝L，AB、DE 处 于 水平位置。F作用在DE中点，q为均
匀载荷，滑块E与接触面的摩擦系数
为0.7，不计所有刚体的重量。 求： 固定端A处的约束力。
2021年8月8日 47
理论力学CAI
1. 解除水平约束， 代之水平约束力。
fk (xi ) 0, i 1,2,,3n；k 1,2,, r(约束数) fk (xi，t) 0, i 1,2,,3n；k 1,2,, r (约束数)
2021年8月8日 8
理论力学CAI
双侧约束与单侧约束
y
x
O
B
yB 0(双侧约束)
y
O
B
x
yB 0(单侧约束)
只能限制质点或质点系单一方向运动的约束称为单侧约束。
对于完整约束系统，唯一地确定系统在空间位形 的独立坐标的数目，也就是广义坐标的数目，称为系 统的自由度数。
对于非完整约束系统，广义坐标的数目大于自由度 数。这时，系统的自由度等于独立的虚位移数目。
在虚位移这章中我们只讨论质点或质点系受定常、 双侧、完整约束的情况。
2021年8月8日 15
第十五章位移法
1
A
B
1
M1图
L
A
B
L
M2图
X2=1
X1
2EI L
A
，X
2
6EI L2
A
M BA
2EI L
A
，F
QBA
6EI L2
A
M AB
4EI L
A
，
F
QAB
6EI L2
A
10
等截面单跨超静定梁的杆端内力
【4】内力图
2EI L
A
A
B
4EI L
A
M图
A
B
6EI L2
A
FQ图
第十五章
BA
FP B
X2=1
（e）MP图
第十五章
图（2）
5
等截面单跨超静定梁的杆端内力
δ1 1
1 EI
1
L
1
L EI
δ2 2
1 EI
1 2
L
L
2L 3
L3 3EI
Δ1 P
1 EI
FP a2 2
1
FP a2 2EI
δ1 2
δ2 1
1 EI
1 2
L
L 1
L2 2EI
0
第十五章
故得： Z1
3FP L2 112EI
17
第一节 位移法的基本概念
M AB
理论力学题库参考资料
2014级理论力学期末考试试题题库理论力学试题第一章物系受力分析画图题1、2、3、4、5、第二章平面汇交力系计算题1、2、3、4、5、6、7、第三章平面任意力系计算题1、2、4、5、6、7、8、第四章空间力系计算题1、2、3、4、5、6、第五章静力学综合填空题1、作用在刚体上某点的力，可以沿着其作用线移动到刚体上任意一点，并不改变它对刚体的作用效果。
2、光滑面约束反力方向沿接触面公法线指向被约束物体。
3、光滑铰链、中间铰链有1个方向无法确定的约束反力,通常简化为方向确定的 2 个反力。
4、只受两个力作用而处于平衡的刚体，叫二力构件,反力方向沿二力作用点连线。
5、约束力的方向与该约束所能阻碍的位移方向相反 .6、柔软绳索约束反力方向沿绳索 ,指向背离被约束物体.7、在平面内只要保持力偶矩和转动方向不变，可以同时改变力偶中力的大小和力臂的长短，则力偶对刚体的作用效果不变。
8、力偶的两个力在任一坐标轴上投影的代数和等于零，它对平面内的任一点的矩等于力偶矩，力偶矩与矩心的位置无关。
9、同一平面内的两个力偶,只要力偶矩相等,则两力偶彼此等效.10、平面汇交力系可简化为一合力 ,其大小和方向等于各个力的矢量和,作用线通过汇交点.11、平面汇交力系是指力作用线在同一平面内 ,且汇交与一点的力系.12、空间平行力系共有 3 个独立的平衡方程.13、空间力偶对刚体的作用效果决定于力偶矩大小、力偶作用面方位、力偶的转向三个因素。
14、空间任意力系有 6 个独立的平衡方程.15、空间汇交力系的合力等于各分力的矢量和,合力的作用线通过汇交点 .第五章静力学综合摩擦填空题1、当作用在物体上的全部主动力的合力作用线与接触面法线间的夹角小于摩擦角时，不论该合力大小如何，物体总是处于平衡状态，这种现象称为自锁现象.2、答案：50N3、答案：φm/24、静摩擦力Fs的方向与接触面间相对滑动趋势的方向相反，其值满足__0<=F S<=F MAX摩擦现象分为滑动摩擦和__滚动摩阻__两类。
ch15理论力学课程
(15.2)
式中 FX 、 FY 、 FZ 为作用于质点上的力 F 在直角坐标轴上的投影， δ x 、 δ y 、 δ z 为
虚位移 δ r 在直角坐标轴上的投影。
由于虚功是在假想的虚位移中所作的功，因而虚功是假想的，是虚的。在图 15.5 中， 按图示虚位移，力 F 作的虚功为 δW = −F ⋅δ rB ，力偶 M 作的虚功为 δW = M ⋅δϕ 。图示机
∑ ∑ Fi
⋅δ
r i
+
FNi
⋅δ r i
=
0
∑ 由于质点系具有理想约束，则约束反力在虚位移中所作的虚功为零，即
FNi
⋅δ r i
=
0
，
代入上式得
∑ Fi
⋅δ r i
=
0
于是得
∑ ∑ δWFi = Fi ⋅δ ri = 0
这就是质点系平衡条件必要性的证明。
2. 充分性的证明
设作用于质点系的所有主动力在虚位移中所作虚功的和为零，即
力 FNi ，在这些力的作用下质点处于平衡，因此有：
Fi + FNi = 0 任给质点系以某种虚位移时，质点 Mi 的虚位移为 δ ri ，则作用在质点 Mi 上的力 Fi 和 FNi
虚功的和为
Fi ⋅ δ ri + FNi ⋅ δ ri = 0
对于质点系内所有质点，都可以得到与上式相同的式子。将所有等式两边分别相加，得
xC = rϕ + C 所以轮子受到的约束是完整约束。 如果约束方程中包含坐标对时间的导数，而且约束方程不可能积分为有限形式，这种 约束称为非完整约束。非完整约束总是微分方程的形式。 本章只讨论受定常的双面几何约束的质点系的平衡问题。
15.1.2 自由度和广义坐标
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
r
i
ri
0
FNi
ri
0
或记为
WFi 0
此方程称虚功方程,其表达的原理称虚位移原理或虚功原理:
对于具有理想约束的质点系,其平衡的充分必要条件是:
作用于质点系的所有主动力在任何虚位移中所作的虚功的和
等于零.
解析式为
Fxi xi Fyi yi Fzi zi 0
§ 15-2 虚位移原理
解得
FBx
3 2
F
cot
k 0
cot
§ 15-2 虚位移原理
例15-3 图所示椭圆规机构中,连杆AB长为L,滑块Ａ, Ｂ与杆重均不计,忽略各处摩擦,机构在图示位置平衡.
求：主动力 FA与 FB之间的关系。
已知: l,,略自重和摩擦,求 : 平衡时FA与FB关系。
解:
(1) 几何法： 给虚位移
在弹簧处也代之以 力,如图,其中：
FC FG k 0 WF 0 FBx xB FC yC FG yG F yG 0
xB 2l cos , yC l sin , yG 3l sin xB 2l sin , yC l cos, yG 3l cos
FBx (2l sin ) k 0l cos k 0 3l cos F 3l cos 0
例15-1 如图所示,在螺旋压榨机的手柄AB上作用一在
水平面内的力偶(
F,
F
),其力矩
M
2Fl ,螺杆的螺
距为 h.
求:机构平衡时加在被压物体上的力.
已知: M 2Fl,螺距为h,求 : 平衡时加在物体上的力
解:给虚位移 , s,
W F
FN s 2Fl
0
与 s 满足如下关系：
s h 2
,
va
vC
h sin 2
代入到
M FvC 0 中,亦得
M
Fh
sin 2
用建立坐标,取变分的方法,有
M F xC 0
xC h cot BC
xC
h sin2
解得
M
Fh
sin 2
例15-5 求图所示无重组合梁支座Ａ的约束力.
约束条件随时间变化的称
非定常约束,否则称定常约束.
x2 y2 l0 vt 2
§15-1 约束 ·虚位移·虚功 （3） 其它分类
约束方程中包含坐标对时间的导数,且不可能积分为有
限形式的约束称非完整约束,否则为完整约束.
约束方程是等式的，称双侧约束（或称固执约束）， 约束方程为不等式的，称单侧约束（或称非固执单侧约束）。
解:解除B端水平约束,以力FBX 代替：
wF FBxxB FyG 0 xB 2l cos , yG 3l sin xB 2l sin , yG 3l cos
代入虚功方程:
FBx 2l sin F 3l cos 0
FBx
3 2
F
cot
如图在CG 间加一弹簧,刚度K,且已有伸长量δ0 ,仍求 FBX .
本章只讨论定常的双侧、完整、几何约束；
fi x1, y1, z1, , xn , yn , zn 0 i 1,2, , s
n为质点系数，S 为约束方程数
§15-1 约束 ·虚位移·虚功
2 虚位移
在某瞬时,质点系在约束允许的条件下,可能实现的任何
无限小的位移称为虚位移 .
虚位移 r, x, 等
,
vB
rB
dt
代入到
Fi
ri
0
中, 得
为虚速度
FBvB FAvA 0
由速度投影定理,有
vB cos vA sin ,
代入上式
得 FA FB tan
§ 15-2 虚位移原理
例15-4 如图所示机构,不计各构件自重与各处摩
擦,求机构在图示位置平衡时,主动力偶矩Ｍ与主动力 Ｆ之间的关系.
如
x2 y2 l2
§15-1 约束 ·虚位移·虚功
f x, y, z 0
§15-1 约束 ·虚位移·虚功
x
2 A
y
2 A
r2
xB x A yB yA 2 l 2
yB 0 限制质点系运动情况的运动学条件称运动约束.
vA r 0
xA r 0
§15-1 约束 ·虚位移·虚功
2 定常约束和非定常约束
理论力学（Ⅰ）
第十五章 虚位移原理
东北大学 应用力学研究所 李永强
第十五章 虚位移原理
§1·虚位移·虚功
1 约束及其分类
限制质点或质点系运动的条件称为约束，
限制条件的数学方程称为约束方程.
（1）几何约束和运动约束
限制质点或质点系在空间的几何位置的条件称为几何约束.
rA
,
rB
,
Fi
ri
0
FA rA FB rB 0
由
rB cos rA sin
(
rA
,
rB
在
A
,B
连线上投影相等)
代入虚功方程,有
FA cosr BFB rB 0
即 FA FB tan
已知: l,,略自重和摩擦,求 : 平衡时FA与FB关系。
(2) 用解析法.建立 坐标系,由：
Fxi xi Fyi yi Fzi zi 0
有 FB xB FA yA 0
xB l cos, yA l sin
xB l sin , yA l cos
得 FA FB tan
已知: l,,略自重和摩擦,求 : 平衡时FA与FB关系。
(3) 定义:
虚速vA度法drtA
实位移 dr , dx, d 等
3 虚功
力在虚位移W中作F的功 r称 虚功.
4 理想约束
如果在质点系的任何虚位移中,所有约束力所作虚功的和
等于零，称这种约束为理想约束.
WN
WNi
FNi
ri
0
§ 15-2 虚位移原理
设质点系处于平衡,有
Fi Fi
FriNiF0Ni
ri
0
即
Fi
F i
WF
2Fl
FN h 2
0
因 是任意的 ，故
2Fl FN h 0
2
FN
4 l
h
F
§ 15-2 虚位移原理
例15-2 图中所示结构,各杆自重不计,在Ｇ点作用一铅直 向上的力Ｆ, AC CE CD CB DG GE l
求:支座Ｂ的水平约束力.
已知: F, AC CE CD CB DG GE l,求 : B处水平反力
已知: 略自重和摩擦,求 : 平衡时M与F关系。
解: 给虚位移 , rc
wF M F rc 0
由图中关系有
ra
re sin
re
OB
h
sin
,
rC
ra
h sin 2
代入虚功方程得
M
Fh
sin 2
已知: 略自重和摩擦,求 : 平衡时M与F关系。
用虚速度法:
ve
OB
h
sin