勾股定理的逆定理课件
合集下载
勾股定理的逆定理-完整版课件
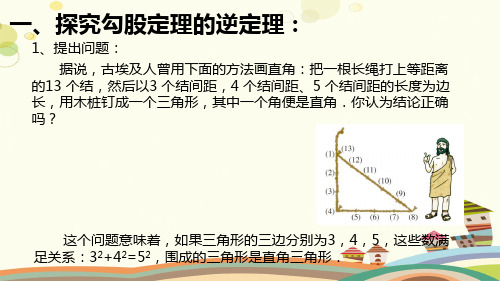
一、探究勾股定理的逆定理:
2、实验探究: (1)画一画:下列各组数中的两数平方和等于第三数的平方,分别以这些数 为边长画出三角形(单位:cm),它们是直角三角形吗? ① 2.5,6,6.5; ② 6,8,10. (2)量一量:用量角器分别测量上述各三角形的最大角的度数. (3)想一想:请判断这些三角形的形状,并提出猜想.
PQ=16×1.5=24,PR=12×1.5=18,QR=30. ∵24²+18²=30², 即PQ²+PR²=QR², ∴△PQR为直角三角形,即∠QPR=90°. ∵∠1=45°, ∴∠2=45°,即“海天”号沿西北方向航行.
练习4、如图,如图,南北向MN为我国领域,即MN以西为我国领海,以东 为公海.上午9时50分,我反走私A艇发现正东方向有一走私艇C以13海里/时的 速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇B.已知 A、C两艇的距离是13海里,A、B两艇的距离是5海里;反走私艇B测得离C艇 的距离是12海里.若走私艇C的速度不变,最早会在什么时间进入我国领海?
2
2
∴BE= AB•BC60.
B
AC 13
.
在Rt△BCE中,由勾股定理得,
N
∴CE= BC 2BE 2 12 2(60 )2144
13 13
∴最早进入时间≈0.85小时=51分钟.
.
9时50分+51分=10时41分.
答:走私艇最早在10时41分进入我国领海.
五、课堂小结:
1、利用勾股定理的逆定理判定是否为直角三角形的一般步骤: ①确定最大边长c; ②计算a2+b2和c2的值, 若a2+b2=c2,则此三角形是直角三角形; 若a2+b2<c2,则此三角形是钝角三角形; 若a2+b2>c2,则此三角形是锐角三角形. 2、互逆命题表明两个命题在形式上的关系,将一个命题的题设和结论互换 即可得到它的逆命题,当原命题成立时,它的逆命题不一定成立,即互逆 的两个命题不一定同真或同假. 3、已知一三角形的三边的长度时,首先应对该三角形进行判断,判断最长 边的平方是否等于其余两边的平方和,如何满足这一条件则此三角形为直 角三角形.
勾股定理的逆定理ppt课件

数学 八年级上册 SK
第
勾股定理
3
章
3.2 勾股定理的逆定理
-
3.2 勾股定理的逆定理
探究与应用
探 活动1 探索并应用勾股定理的逆定理,体会“数”与
究
“形”的内在联系
与
应 [思考探究]
用 1.写出“直角三角形两条直角边的平方和等于斜边的平方”
的逆命题.
解:如果一个三角形的两条边的平方和等于第三边的平方,那么
是钝角三角形;如果a2+b2>c2,那么这个三角形是锐角三角形.
探 究
[概括新知]
与 勾股定理的逆定理:如果三角形的三边长分别为a,b,c,且a2+
应
用 b2=c2,那么这个三角形是直角三角形.
探 归纳 勾股定理与勾股定理的逆定理的联系与区别
究
与
勾股定理
勾股定理的逆定理
应 用
在Rt△ABC中,∠C=90°, 在△ABC中,BC=a,AC=b, 条件
例2 C [解析] A项,82+52≠172,不能构成直角三角形,故不 是勾股数,不符合题意; B项,1.5,2,2.5不都是正整数,故不是勾股数,不符合题意; C项,52+122=132,且5,12,13都是正整数,故是勾股数,符合题 意; D项,32+42≠62,不能构成直角三角形,故不是勾股数,不符合 题意. 故选C.
根据勾股定理,可得A'B'2=a2+b2.
因为AB2=a2+b2,
所以A'B'2=AB2,所以A'B'=AB.
根据“SSS”,可证△ABC≌△A'B'C'.
于是,∠C=∠C'=90°,
第
勾股定理
3
章
3.2 勾股定理的逆定理
-
3.2 勾股定理的逆定理
探究与应用
探 活动1 探索并应用勾股定理的逆定理,体会“数”与
究
“形”的内在联系
与
应 [思考探究]
用 1.写出“直角三角形两条直角边的平方和等于斜边的平方”
的逆命题.
解:如果一个三角形的两条边的平方和等于第三边的平方,那么
是钝角三角形;如果a2+b2>c2,那么这个三角形是锐角三角形.
探 究
[概括新知]
与 勾股定理的逆定理:如果三角形的三边长分别为a,b,c,且a2+
应
用 b2=c2,那么这个三角形是直角三角形.
探 归纳 勾股定理与勾股定理的逆定理的联系与区别
究
与
勾股定理
勾股定理的逆定理
应 用
在Rt△ABC中,∠C=90°, 在△ABC中,BC=a,AC=b, 条件
例2 C [解析] A项,82+52≠172,不能构成直角三角形,故不 是勾股数,不符合题意; B项,1.5,2,2.5不都是正整数,故不是勾股数,不符合题意; C项,52+122=132,且5,12,13都是正整数,故是勾股数,符合题 意; D项,32+42≠62,不能构成直角三角形,故不是勾股数,不符合 题意. 故选C.
根据勾股定理,可得A'B'2=a2+b2.
因为AB2=a2+b2,
所以A'B'2=AB2,所以A'B'=AB.
根据“SSS”,可证△ABC≌△A'B'C'.
于是,∠C=∠C'=90°,
《勾股定理的逆定理》勾股定理PPT精品课件

问题3 古埃及人用来画直角的三边满足这个等式吗?
∵32+42=52,∴满足.
猜想:
命题2:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直
角三角形。
这个命题和前面学的命题1(勾股定理)之间有什么关系吗?
1.题设和结论正好相反的两个命题,叫做互逆命题。
2.如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
勾股定理的逆定理
1、理解勾股定理的逆定理。
2、了解逆命题的概念,知道原命题为真命题,它的逆命题不一
定为真命题。
3、应用勾股定理的逆定理解决实际问题。
学习目标
学习目标
1.理解勾股定理的逆定理及证明过程。
2.能简单的运用勾股定理的逆定理判定直角三角形。
3.利用勾股定理逆定理解决实际问题
重点
运用勾股定理的逆定理判定直角三角形。
命题2是正确的吗?你能试着证明吗?
利用勾股定理逆定理判断直角三角形
下面以a,b,c为边长的三角形是不是直角三角形?
1)a=15 ,b=8 ,c=17
2)a=13 ,b=14 ,c=15
解:∵152+82=289,172=289,
∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形。
∴∠QPR=90°。
P
由“远航”号沿东北方向航行可知,∠QPS=45°。 ∴∠RPS=45°,
即“海天”号沿西北方向航行。
E
利用勾股定理逆定理判断直角三角形
满足下列条件的△ABC不是直角三角形的是(
A.BC=1,AC=2,AB=
C.BC:AC:AB=3:4:5
)
B.BC=1,AC=2,AB=
∵32+42=52,∴满足.
猜想:
命题2:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直
角三角形。
这个命题和前面学的命题1(勾股定理)之间有什么关系吗?
1.题设和结论正好相反的两个命题,叫做互逆命题。
2.如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题。
勾股定理的逆定理
1、理解勾股定理的逆定理。
2、了解逆命题的概念,知道原命题为真命题,它的逆命题不一
定为真命题。
3、应用勾股定理的逆定理解决实际问题。
学习目标
学习目标
1.理解勾股定理的逆定理及证明过程。
2.能简单的运用勾股定理的逆定理判定直角三角形。
3.利用勾股定理逆定理解决实际问题
重点
运用勾股定理的逆定理判定直角三角形。
命题2是正确的吗?你能试着证明吗?
利用勾股定理逆定理判断直角三角形
下面以a,b,c为边长的三角形是不是直角三角形?
1)a=15 ,b=8 ,c=17
2)a=13 ,b=14 ,c=15
解:∵152+82=289,172=289,
∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形。
∴∠QPR=90°。
P
由“远航”号沿东北方向航行可知,∠QPS=45°。 ∴∠RPS=45°,
即“海天”号沿西北方向航行。
E
利用勾股定理逆定理判断直角三角形
满足下列条件的△ABC不是直角三角形的是(
A.BC=1,AC=2,AB=
C.BC:AC:AB=3:4:5
)
B.BC=1,AC=2,AB=
勾股定理的逆定理课件

详细描述
在勾股定理的逆定理的证明中,反证 法是通过假设三角形不是直角三角形 ,然后利用勾股定理的逆定理推导出 矛盾的结论,从而证明三角形一定是 直角三角形。
证明方法二:直接证明法
总结词
直接证明法是一种直接根据已知 条件和定理,通过逻辑推理得到 结论的证明方法。
详细描述
在勾股定理的逆定理的证明中, 直接证明法是通过直接利用勾股 定理的条件和结论,推导出三角 形一定是直角三角形。
对于任意的整数a、b、c,都存在无穷多 个整数x、y、z,满足x²+y²=z²,且x、y 、z互质。
勾股定理的逆定理与欧几里得公设的关系
勾股定理的逆定理是 欧几里得公设的一个 推论。
勾股定理的逆定理证 明了欧几里得公设的 正确性。
欧几里得公设是勾股 定理逆定理的基础。
05 勾股定理的逆定理的挑战 和问题
勾股数的性质
唯一性
对于任何一个正整数n,都存在唯 一的一组整数a、b、c,满足 n=a²+b²=c²。
自然数性
勾股数的三边长可以都是自然数。
无穷多性
对于任意正整数n,都存在无穷多个 勾股数。
勾股数的扩展
广义勾股数
如果三个整数的平方和等于另一个整数 的平方,则这三个数被称为广义勾股数 。
VS
勾股数的组合
勾股定理的逆定理课件
目录
• 勾股定理的逆定理的概述 • 勾股定理的逆定理的证明 • 勾股定理的逆定理的应用 • 勾股定理的逆定理的扩展 • 勾股定理的逆定理的挑战和问题 • 勾股定理的逆定理的案例分析
01 勾股定理的逆定理的概述
什么是勾股定理的逆定理
勾股定理的逆定理定义
如果一个三角形的三条边满足两边的平方和等于第三边的平方,那么这个三角形 是直角三角形。
在勾股定理的逆定理的证明中,反证 法是通过假设三角形不是直角三角形 ,然后利用勾股定理的逆定理推导出 矛盾的结论,从而证明三角形一定是 直角三角形。
证明方法二:直接证明法
总结词
直接证明法是一种直接根据已知 条件和定理,通过逻辑推理得到 结论的证明方法。
详细描述
在勾股定理的逆定理的证明中, 直接证明法是通过直接利用勾股 定理的条件和结论,推导出三角 形一定是直角三角形。
对于任意的整数a、b、c,都存在无穷多 个整数x、y、z,满足x²+y²=z²,且x、y 、z互质。
勾股定理的逆定理与欧几里得公设的关系
勾股定理的逆定理是 欧几里得公设的一个 推论。
勾股定理的逆定理证 明了欧几里得公设的 正确性。
欧几里得公设是勾股 定理逆定理的基础。
05 勾股定理的逆定理的挑战 和问题
勾股数的性质
唯一性
对于任何一个正整数n,都存在唯 一的一组整数a、b、c,满足 n=a²+b²=c²。
自然数性
勾股数的三边长可以都是自然数。
无穷多性
对于任意正整数n,都存在无穷多个 勾股数。
勾股数的扩展
广义勾股数
如果三个整数的平方和等于另一个整数 的平方,则这三个数被称为广义勾股数 。
VS
勾股数的组合
勾股定理的逆定理课件
目录
• 勾股定理的逆定理的概述 • 勾股定理的逆定理的证明 • 勾股定理的逆定理的应用 • 勾股定理的逆定理的扩展 • 勾股定理的逆定理的挑战和问题 • 勾股定理的逆定理的案例分析
01 勾股定理的逆定理的概述
什么是勾股定理的逆定理
勾股定理的逆定理定义
如果一个三角形的三条边满足两边的平方和等于第三边的平方,那么这个三角形 是直角三角形。
八年级数学下册教学课件《勾股定理的逆定理的应用》

(2)a = 41 ,b = 4,c = 5;
∵b2 + c2 = 42 + 52 = 16 + 24 = 41,a2 = ( 41 )2 = 41, ∴b2 + c2 = a2.
由勾股定理的逆定理知这个三角形是直角三角形.
(3)a = 5 ,b = 1,c = 3 ;
4
4
∵b2 + c2 = 12 + ( 3 )2 = 1 + 9 = 25,a2 = ( 5 )2 = 25 ,
由勾股定理得:EF2 = EC2 + FC2 = 5x2,
B
E
C
AE2 = AB2 + BE2 = 20x2,AF2 = AD2 + DF2 = 25x2 = 25x2,
∴EF2 + AE2 = 25x2 = AF2.
由勾股定理的逆定理知,∠AEF = 90°.
拓广探索 【选自教材 P34】
7. 我们知道 3,4,5 是一组勾股数,那么 3k,4k,5k (k 是正整数)也是一组勾股数吗?一般地,如果 a,b, c 是一组勾股数,那么 ak,bk,ck(k 是正整数)也是 一组勾股数吗?
课堂小结
勾股理的 逆定理
判断一个三角形是不是直角三角形 判断航行方向 计算不规则四边形面积
综合运用 【选自教材 P34】
4. 在△ABC 中,AB =13,BC = 10,BC 边上的中线
AD =12. 求 AC.
解:在△ABD中,BD =
1 2
BC
=
5.
AD
=
12,AB
=
13.
∵BD2 + AD2 = 52 + 122 = 25 + 144 =169,
【教学课件】《勾股定理的逆定理+第1课时》精品教学课件

(1) a=7,b=24,c=25; (2) a=7,b=8,c=11.
解: (1) ∵最大边是c=25, c²=625,a²+b²=7²+24²=625, ∴a²+b²=c². ∴ △ABC是直角三角形,最大边c所对的角是直角.
(2) ∵最大边是c=11, c²=121,a²+b²=7²+8²=113, ∴a²+b²≠c². ∴ △ABC不是直角三角形.
证明猜想 已知:如图,在△ABC中,AB=c,BC=a,AC=b,a2+b2=c2. 求证:△ABC是直角三角形.
△ABC是直角三角形
∠C是直角
构造两直角边分别为 a,b的Rt△A′B′C′
△ABC ≌ △A′B′C′
∠C=∠C ′=90°
A
c
b
B
a
C
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
∴ △ABC是直角三角形.
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
勾股定理的逆定理
如果三角形两边的平方和等于第三边的平方,那么这个三
勾
角形是直角三角形.
股
定
勾股定理与其逆定理的关系
A
理
勾股定理与其逆定理是互逆定理.
c
b
的
勾股定理
逆
直角三角形
a²+b²=c² B a C
勾股定理的逆定理
操作 请你动手画一画吧.用圆规、直尺作△ABC,使得AB=5,AC=4, BC=3,如图,量一量∠C,它是90°吗?
(1)画射线AM,然后以点A为圆心,AB长为半径画弧,交射线AM于点B; (2)分别以点A,B为圆心,线段AC、BC长为半径画弧,两弧相交于点C;
解: (1) ∵最大边是c=25, c²=625,a²+b²=7²+24²=625, ∴a²+b²=c². ∴ △ABC是直角三角形,最大边c所对的角是直角.
(2) ∵最大边是c=11, c²=121,a²+b²=7²+8²=113, ∴a²+b²≠c². ∴ △ABC不是直角三角形.
证明猜想 已知:如图,在△ABC中,AB=c,BC=a,AC=b,a2+b2=c2. 求证:△ABC是直角三角形.
△ABC是直角三角形
∠C是直角
构造两直角边分别为 a,b的Rt△A′B′C′
△ABC ≌ △A′B′C′
∠C=∠C ′=90°
A
c
b
B
a
C
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
∴ △ABC是直角三角形.
创设情境 探究新知 应用新知 巩固新知 课堂小结 布置作业
勾股定理的逆定理
如果三角形两边的平方和等于第三边的平方,那么这个三
勾
角形是直角三角形.
股
定
勾股定理与其逆定理的关系
A
理
勾股定理与其逆定理是互逆定理.
c
b
的
勾股定理
逆
直角三角形
a²+b²=c² B a C
勾股定理的逆定理
操作 请你动手画一画吧.用圆规、直尺作△ABC,使得AB=5,AC=4, BC=3,如图,量一量∠C,它是90°吗?
(1)画射线AM,然后以点A为圆心,AB长为半径画弧,交射线AM于点B; (2)分别以点A,B为圆心,线段AC、BC长为半径画弧,两弧相交于点C;
《勾股定理的逆定理》数学教学PPT课件(5篇)

求证:△ ABC是直角三角形
证明:画一个△A′B′C′,
使∠
C′=900,
B′C′= a,
A'
A
B
b
b
a
C
B'
a
C'
在△ ABC和△ A′B′C′中
BC = a = B′C′,
CA = b = C′A′,
AB = c = A ′B′
C′A′=b
∵ ∠ C′=900
∴ A′B′ 2= a2+b2
∵ a2+b2=c2
c
b
C
作用:已知三角形的三边长,判断
这个三角形是否为直角三角形。
a
B
,
自主学习
例1:注意归纳例题的解题步骤和解题技巧!
已知三角形三条边的长度分别是:(1)1,
,
(2)2,3,4;
(3)3n,4n,5n(n > 0), 它们是否分别构成直角三角形?
解
(1)在 1, ,,
中,
)2 ,所以,边长为1,
(
∴S四边形ABCD=S△ABD+S△BCD
B
1
= -AB×AD+
2
1
= -×3×4+
2
1
-BD×CD
2
1
-×5×12
2
= 36
所以四边形ABCD的面积
为36.
C
知识升华
满足
a b的三个正整数,
c
2
称为勾股数组.
2
2
自主检测
1、满足________
勾股数组。
的三个____
__
正整数
如:
证明:画一个△A′B′C′,
使∠
C′=900,
B′C′= a,
A'
A
B
b
b
a
C
B'
a
C'
在△ ABC和△ A′B′C′中
BC = a = B′C′,
CA = b = C′A′,
AB = c = A ′B′
C′A′=b
∵ ∠ C′=900
∴ A′B′ 2= a2+b2
∵ a2+b2=c2
c
b
C
作用:已知三角形的三边长,判断
这个三角形是否为直角三角形。
a
B
,
自主学习
例1:注意归纳例题的解题步骤和解题技巧!
已知三角形三条边的长度分别是:(1)1,
,
(2)2,3,4;
(3)3n,4n,5n(n > 0), 它们是否分别构成直角三角形?
解
(1)在 1, ,,
中,
)2 ,所以,边长为1,
(
∴S四边形ABCD=S△ABD+S△BCD
B
1
= -AB×AD+
2
1
= -×3×4+
2
1
-BD×CD
2
1
-×5×12
2
= 36
所以四边形ABCD的面积
为36.
C
知识升华
满足
a b的三个正整数,
c
2
称为勾股数组.
2
2
自主检测
1、满足________
勾股数组。
的三个____
__
正整数
如:
新人教版初中数学八年级下册17.2.1 勾股定理的逆定理

8.(2018·南通)下列长度的三条线段能组成直角三角形的是( A )
A.3,4,5
B.2,3,4
C.4,6,7
D.5,11,12
9.(2019·益阳)已知 M,N 是线段 AB 上的两点,AM=MN=2, NB=1,以点 A 为圆心,AN 长为半径画弧;再以点 B 为圆 心,BM 长为半径画弧,两弧交于点 C,连接 AC,BC,则△ABC 一定是( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
答案显示
1.如果两个命题的题设和结论刚好相反,那么这样的两个命题 叫做__互__逆___命__题___,如果把其中一个命题叫做原命题,那么 另一个叫做它的__逆__命__题____.
2.一般地,如果一个定理的逆命题经过证明是正确的,那么它 也是一个定理,称这两个定理互为_逆__定___理__.
3.下列命题的逆命题正确的是( A ) A.两条直线平行,内错角相等 B.若两个实数相等,则它们的绝对值相等 C.全等三角形的对应角相等 D.若两个实数相等,则它们的平方也相等
17.(2019·河北)已知:整式 A=(n2-1)2+(2n)2,整式 B>0. 尝试 化简整式 A. 解:A=(n2-1)2+(2n)2=n4-2n2+1+4n2=n4+2n2+1 =(n2+1)2.
发现 A=B2,求整式 B. 解:∵A=B2,B>0,∴B=n2+1.
联想 由上可知,B2=(n2-1)2+(2n)2,当 n>1 时,n2-1,2n,
(30°,60°,45°)的和的形式; (2)用旋转法将△CPB 绕点 C 顺时针旋转 90°到△CP′A 的位置.
解:如图,将△CPB 绕点 C 顺时针旋转 90°得△CP′A,则 P′C =PC=2,P′A=PB=1,∠BPC=∠AP′C,连接 PP′. 因为∠PCP′=90°,所以 PP′2=22+22=8. 又因为 P′A=1,PA=3, 所以 PP′2+P′A2=8+1=9,PA2=9. 所以 PP′2+P′A2=PA2. 所以∠AP′P=90°. 易知∠CP′P=45°, 所以∠BPC=∠AP′C=∠AP′P+∠CP′P=90°+45°=135°.
勾股定理的逆定理 展示课说课课件

4
1
实验
3
证明
1 设置情境,提出问题
通过回忆勾股定理的内容,以及勾股定理的数学符号语言如何表 受到勾股定理揭示了直角三角形可以由“形”的特殊性得到其“三 —即由“形→数”,使学生在已体会到由“形→数”的情况下,有 的置疑,完成提问“如果三角形的三边长a,b,c,且满足a²+b²=c², 三角形吗?”培养学生的逆向思维,以及发现和提出问题的能力.
(2)了解原命题、逆命题的 进一步加(1)要求经历勾股定 的探究过程,了解证明几何命题 法,同时体会“构造法”证明数 基本思想,并能应用勾股定理的 判断一个三角形是不是直角三角形
教第学一章 目标解析
目标(2)要求知道互逆命题 点,能根据原命题写出它的逆命题 命题为真命题时,逆命题不一定为 理解用“举反例”来判断逆命题为 方法.
02
03
“全等”
根据学生的几何 知识基础和学习经验, 启发他们想到可以利 用“三角形”中的 “全等三角形”.
“构造”
根据问题中已 知条件,通过尺规 作图构造一个直角 三角形.
这是本节课的难点.教师一定要给足时 生充分讨论,提出解决问题的方法.如果学生 和解决办法,可适时点拔以下关键点:
(1)从已知条件不能直接证明△ABC是直角 办?
(2)我们至今学过哪些几何知识?有哪些 题的方法和经验?
由此启发学生想到可以利用“三角形” 三角形”,而至少要有两个三角形才能考虑 能顺理成章地想到可先构造一个直角三角 △ABC与这个直角三角形全等即可,从而突破 学难点.
5 运用定理
通过练习把陈述性的定理转化为认知操作,学会用 理判断一个三角形是不是为直角三角形,规范地示范解 勾股数的概念.
作第一业章 布置 教科书第33页练习第1,2; 习题17.2第4,5题.
《勾股定理的逆定理》勾股定理PPT课件(第2课时)

13
4
12
┐
3
探究新知
解:连接BD 在Rt△ABD中
∵AB=3,AD=4 ∴BD= AB 2 AD 2 =5
在△BCD中 ∵CD=13 , BC=12
∴CD2=BC2+BD2
13
45
12
┐
3
∴△BCD是直角三角形 ∴∠DBC=90°
∴S四边形ABCD=S△ABD+S△BCD = 1×3×4+ 1×5×12=36
此时四边形ABCD 的面积是多少?
5、 已知a、b、c为△ABC的三边,且 满足 a2+b2+c2+338=10a+24b+26c. 试判断△ABC的形状.
思维训练
6、△ABC三边a,b,c为边向外作 正方形,正三角形,以三边为 直则径作是半直圆角,三若角S形1+吗S2=?S3成立,
C
S2
A
b
ca
能替工人师傅想办法完成任务吗?
9.三个半圆的面积分别为S1=3π, S2=4π,S3=7π,把三个半圆拼成如 右图所示的图形,则△ABC一定是
直角三角形吗?
B
C
D
B'
A'
A
B
勾股定理:
如果直角三角形的两直角边为a,b, 斜边长为c ,那么a2+b2=c2.
B
反过来,如果一个 a
c
三角形的三边长a、b、
(C)1:2:4; (D)1:3:5.
3. 三角形的三边分别是a、b、c, 且满足
(a+b)2-c2=2ab, 则此三角形是:( )
A. 直角三角形;
B. 是锐角三角形;
八年级数学勾股定理的逆定理课件-应用

人教版
第2课时勾股定理的逆定 理(二) —— 应用
(2)在图2中,画一个三边长分别为3,2, 13的三角形,一共可以画 16 个这样的三角形. 解析:如图2,一共可以画16个这样的三角形.
图2
数学
八年级 下册
人教版
第2课时勾股定理的逆定 理(二) —— 应用
10.在某小区在社区工作人员及社区居民的共同努力之下,
数学
八年级 下册
人教版
第2课时勾股定理的逆定 理(二) —— 应用
8.如图,明明在距离水面高度为5 m的岸边C处,用绳子拉船 靠岸,开始时绳子BC的长为13 m.若明明收绳6 m后,船到 达D处,则船向岸边A处移动了多少米?
数学
八年级 下册
人教版
第2课时勾股定理的逆定 理(二) —— 应用
解:∵开始时绳子BC的长为13 m,明明收绳6 m后,船到达D处,
数学
八年级 下册
人教版
第2课时勾股定理的逆定 理(二) —— 应用
知识点 勾股定理逆定理的应用 【例题】如图,甲船以5海里/时的速度离开港口O沿南偏东 30°方向航行,乙船同时同地沿某方向以12海里/时的速度 航行.已知它们离开港口2小时后分别到达B,A两点,且AB =26海里.你知道乙船是沿哪个方向航行的吗?
数学 人教版 八年级 下册
目 录
CONTENTS
数学
八年级 下册
人教版
第2课时勾股定理的逆定 理(二) —— 应用
第十七章 勾股定理
17.2 勾股定理的逆定理 第2课时勾股定理的逆定理(二) —— 应用
01 课标要求
02 基础梳理
03 典例探究
04 课时训练
数学
八年级 下册
八年级数学下册教学课件《勾股定理的逆定理》

勾股定理的逆定理
活动一:引用故事,导入新课
【故事导入】
据说,古埃及人用右图的方法画直 角:把一根长绳打上等距离的 13 个结, 然后以 3 个结间距、4 个结间距、5 个 结间距的长度为边长,用木桩钉成一个 三角形,其中一个角便是直角.
你知道为什么吗?今天我们就来学习其中的原因.
活动二:问题引入,自主探究
B
C a
① A′
c b
直角三角形吗?
B′
C′
a
②
根据勾股定理,A′B′2 = B′C′2 + A′C′2 = a2 + b2 = c2. ∴ A′B′ = c .在△ABC 和△A′B′C′ 中,
A c
b
BC = a = B′C′,AC = b = A′C′, AB = c = A′B′, ∴△ABC ≌△ A′B′C′(SSS). ∴∠C=∠C′=90°,
探究点 1 勾股定理的逆定理
类似古埃及人画直角的故事,我们准备三根绳子来模仿 操作,看看能否得到和古埃及人相同的结果.
(1)让一根绳子的一端与 0 刻度线重合,分别在 3 cm,
7 cm,12 cm 处做标记,得到长度分别为 3 cm,4 cm,5 cm
的三段,然后以这三段为边围成一个三角形,量量看是不是
求四边形 ABCD 的面积.
解:∵AD = 8,AB = 6,BD = 10,CD = 26,BC = 24,
∴ AB2 +AD2 = BD2, BD2 +BC2 = CD2 .
∴△ABD 和△BDC 都是直角三角形,
且∠A = 90°,∠DBC = 90°.
∴ S四边形ABCD = S△ABD + S△BDC =
活动一:引用故事,导入新课
【故事导入】
据说,古埃及人用右图的方法画直 角:把一根长绳打上等距离的 13 个结, 然后以 3 个结间距、4 个结间距、5 个 结间距的长度为边长,用木桩钉成一个 三角形,其中一个角便是直角.
你知道为什么吗?今天我们就来学习其中的原因.
活动二:问题引入,自主探究
B
C a
① A′
c b
直角三角形吗?
B′
C′
a
②
根据勾股定理,A′B′2 = B′C′2 + A′C′2 = a2 + b2 = c2. ∴ A′B′ = c .在△ABC 和△A′B′C′ 中,
A c
b
BC = a = B′C′,AC = b = A′C′, AB = c = A′B′, ∴△ABC ≌△ A′B′C′(SSS). ∴∠C=∠C′=90°,
探究点 1 勾股定理的逆定理
类似古埃及人画直角的故事,我们准备三根绳子来模仿 操作,看看能否得到和古埃及人相同的结果.
(1)让一根绳子的一端与 0 刻度线重合,分别在 3 cm,
7 cm,12 cm 处做标记,得到长度分别为 3 cm,4 cm,5 cm
的三段,然后以这三段为边围成一个三角形,量量看是不是
求四边形 ABCD 的面积.
解:∵AD = 8,AB = 6,BD = 10,CD = 26,BC = 24,
∴ AB2 +AD2 = BD2, BD2 +BC2 = CD2 .
∴△ABD 和△BDC 都是直角三角形,
且∠A = 90°,∠DBC = 90°.
∴ S四边形ABCD = S△ABD + S△BDC =
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
说出下列命题的逆命题,并判断它们是否正确. • • • • • 1.原命题:猫有四只脚.( ) 逆命题:有四只脚的是猫.( ) 2.原命题:对顶角相等.( ) 逆命题:相等的角是对顶角.( ) 3.原命题:线段垂直平分线上的点,到这条 线段两端距离相等.( ) • 逆命题:到线段两端距离相等的点,在这条线 段的垂直平分线上.( ) • 4.原命题:角平分线上的点,到这个角的两 边距离相等.( ) • 逆命题:到角两边距离相等的点,在这个角的 平分线上.( )
猜想
• 命题2 如果三角形的三边长a,b,c满足 a2+b2=c2, 那么这个三角形是直角三角形. 命题1 如果直角三角形的两直角边长分别为 a,b,斜边长为c,那么a2+b2=c2, 互逆命题 在一对命题中,第一个命题的题设 恰为第二个命题的结论,而第一个命题的结 论恰为第二个命题的题设,像这样的两个命 题叫做互逆命题.如果把其中一个叫做原命 题,那么另一个叫做它的逆命题.
3.如图,在正方形ABCD中,F是CD的 1 中点,E为BC上一点且EC= 4 BC,求 证:∠EFA=90°
A
D
F
B
C
E
中考链接
已知:如图,四边形ABCD 中,∠B=900,AB=3,BC=4, CD = 12 , AD = 13, 求 四 边 形 ABCD的面积?
C 准备好了吗? B D A
2 a
+
2 b
=
2 c
那么这个三角形是直角三角形。
勾股定理
互逆命题
如果直角三角形两直角边分别为a,b, 斜边为c,那么 a2 + b2 = c2
勾股定理的逆命题
已知:在△ABC中,AB=c BC=a CA=b 且a2+b2=c2 求证:△ ABC是直角三角形
勾股定理的逆命题 逆定理 如果三角形的三边长a、b、c满足
开启
智慧
定理与逆定理
如果一个定理的逆命题经过证明是真命题,那么它 是一个定理,这两个定理称为互逆定理,其中一个 定理称另一个定理的逆定理. 我们已经学习了一些互逆的定理,如:
两直线平行,内错角相等;内错角相等,两直线平行.
想一想:
互逆命题与互逆定理有何关系?
驶向胜利 的彼岸
勾股定理的逆命题 如果三角形的三边长a、b、c满足
(2)最大边为15
解:(1)最大边为17
∵152+82=225+64 =289
172 =289
∵132+142=169+196=365
152 =225
∴152+82 =172
∴以15, 8, 17为边长的
三角形是直角三角形
∴132+ 142 ≠ 152 ∴以13, 15, 14为边长的
三角形不是直角三角形
解152 82 172 a c b
2 2 2
∴△ABC为直角三角形,且∠B=90° 1 1 ∴ △ABC的面积为 a c 15 8 60. 2 2
15
17
B
8
A
例 一个零件的形状如图所示,按规定这个零 件中∠A和∠DBC都应为直角。工人师傅量得 这个零件各边尺寸,这个零件符合要求吗?
S四边形ABCD=36
课堂小结
• • • • 1.勾股定理的逆定理及其作用; 2.什么是互逆命题; 3.什么是互逆定理; 4.什么是勾股数.
作业:84页, 习题18.2第1题、第4题
当第一个数是偶数(大于2)时,则第二个数 是第一个数除以2再平方后减1,第三个数 是第一个数除以2平方后加1
• .古希腊的哲学家柏拉图曾指出,如果m表 示大于1的整数,a=2m,b=m2-1,c=m2+1, 那么a,b,c为勾股数.你认为对吗?如果 对,你能利用这个结论得出一些勾股数吗?
练一练.在△ABC中,a=15, b=17, c=8, C 求此三角形的面积。
下面以a,b,c为边长的三角形是不是直角 三角形?如果是那么哪一个角是直角?
(1) a=25 b=20 c=15 (2) a=13 b=14 c=15 (3) a=1 b=2 c= 3 (4) a:b: c=3:4:5
是 ∠_____ ; A=900 ____
不是 ____ _____ ; 是 ∠ _____0; ____ B=90 0 ∠ C=90; 是 _____ _____
• 在数学的天地里,重要的不是我们 知道什么,而是我们怎么知道什 么。——毕达哥拉斯
一:复习与巩固
1,勾股定理的内容是什么? 如果直角三角形两直角边长分别为a,b
斜边长为c,那么a +b =c,在Rt ABC中,A, B, C, 所对的边分别
为a, b, c, C 90 , 求下列式中未知边的长度。
例1:判断由线段a,b,c组成的三角形是不是直角
三角形? (1) a=15,b=17,c=8; (2) a=13,b=15,c=14 是直角三角形, 只要看两条较小边长的平方和是否等于 长的三个正整数,称为勾股数组. 最大边长的平方.
分析:根据勾股定理的逆定理, 判断一个三角形是不 像15,17,8,能够成为直角三角形三条边
42 32 32 A:______
52 32 42 C:______2 D:______ 82 102 62 62 32 4 B:_______
5.猜想:让我们猜想一下,一个三角形各边长数量应满足怎样 的关系时,这个三角形才可能是直角三角形呢? 你的猜想是 两较短边长度的平方和等于最长边长度的平方 。
a =3,b =4,c= 5 a 5, c 13, b 12
你知道吗?
• 据说古埃及人用下图的方法画直角:把一 根长绳打上等距离的13个结,然后以3个结、 4个结、5个结的长度为边长,用木桩钉成 一个三角形,其中一个角便是直角.你知 道为什么吗?
探究
1.画图:画出边长分别是下列各组数的三角形(单位:厘米) A:3、4、3 ;B:3、4、5;C:3、4、6;D:6、8、10 2.测量:用你的量角器分别测量一下上述各三角形的最大角的 度数,并记录如下: A:_______ B:_______ C:______ D:_______ 3.判断:请判断一下上述你所画的三角形的形状. 锐角三角形 B:_______ C:______ D:______ 直角三角形 钝角三角形 直角三角形 A:______ 4.找规律:根据上述每个三角形所给的各组边长请你找出最长边 的平方与其他两边的平方和之间的关系。
C
13
D
答案:符合 A
2 2 2
4
5
12
又 BD2 +BC2 =52 +122 169
B
AB AD 3 4 25 BD2 52 25
3 2
BD2 +BC2 DC2
DC2 132 169
AB2 AD2 BD2
BDC 900
A 900
(2)如果两个实数相等,那么它们的平方相等.
逆命题:如果两个实数的平方相等,那么这两个实数相等. 不成立
(3)如果两个实数相等,那么它们的绝对值相等.
逆命题:如果两个实数的绝对值相等,那么这两个实数相等. 不成立
(4)全等三角形的对应角相等.
逆命题:对应角相等的两个三角形是全等三角形. 不成立
感悟: 一个命题是真命题,它逆命题却不一定是真命题. 原命题成立时, 逆命题有时成立, 有时不成立
明确下面问题
• (1)任何一个命题都有逆命题; • (2)原命题是正确,逆命题不一定正确, 原命题不正确,逆命题可能正确; • (3)原命题与逆命题的关系就是,命题中 题设与结论相互转换的关系.
试一试
说出下列命题的逆命题.这些命题的逆命题成立吗?
(1)两条直线平行,内错角相等.
逆命题: 内错角相等,两条直线平行. 成立
2 a
+
2 b
=
2 c
那么这个三角形是直角三角形。且边 C所对的角为直角。
勾股定理
互逆命题 定理
如果直角三角形两直角边分别为a,b, 斜边为c,那么 a2 + b2 = c2
• 勾股定理的逆定理 • 如果三角形的三边长a,b,c满足 a2+b2=c2, 那么这个三角形是直角三角形.
说明:(1)一般地,如果一个定理的逆命题经过证明 是正确的,它也是一个定理,称这两个定理为互逆定 理; (2)勾股定理主要反映了直角三角形三边之间的数量 关系,它是解决直角三角形中有关计算与证明的主要 依据; (3)勾股定理的逆定理主要的应用是把数转化为形, 通过计算三角形三边之间的关系来判断一个三角形是 否是直角三角形,它可作为直角三角形的判定依据.
像25,20,15,能够成为直角三角形
三条边长的三个正整数,称为勾股数.
到
请你找出一些勾股数组
3,4,5;5,12,13, 6,8,10; 7,24,25;8,15,17; 9,40,41 10,24,26;11,60,61;12,35,37…… 当第一个数是奇数(大于1)时,则第二个 数是第一个数的平方减1再除以2,第三 个数是第一个数的平方加1再除以2
