几何证明选讲解三角形排列组合(教师版)
专题:解三角形之平面几何问题

专题:解三角形题之平面几何问题一、知识要点考试说明:1、掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题。
2、能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何有关的实际问题。
高频考点:1、边角的求解;2、判断三角形的形状;求与面积、范围有关的问题;3、解决平面几何图形问题;4、解决实际问题。
高考中,利用正弦、余弦定理解三角形问题是必考的,题型较多,有基础题,比如直接利用定理解三角形,也有难题,比如求范围的问题,出题比较灵活,一些同学总是掌握的不是很好,下面就近几年高考题,给大家分类整理各种题型,希望对大家有所帮助。
二、典型例题【例1】(2016•新课标Ⅲ)在ABC ∆中,4B π=,BC 边上的高等于13BC ,则cos A 等于( ) A .31010B .1010C .1010-D .31010- 分析:作出图形,令DAC θ∠=,依题意,可求得2253cos 512()()33a ADACa a θ===,25sin 5θ=,利用两角和的余弦即可求得答案.解答:解:设ABC ∆中角A 、B 、C 、对应的边分别为a 、b 、c ,AD BC ⊥于D ,令DAC θ∠=,在ABC ∆中,4B π=,BC 边上的高1133AD h BC a ===, 13BD AD a ∴==,23CD a =,在Rt ADC ∆中,cos a ADACθ===sin θ=cos cos()coscos sinsin 444A πππθθθ∴=+=-=-=. 故选:C .【例2】(2017•浙江)已知ABC ∆,4AB AC ==,2BC =,点D 为AB 延长线上一点,2BD =,连结CD ,则BDC ∆的面积是 ,cos BDC ∠= .分析:如图,取BC 得中点E ,根据勾股定理求出AE ,再求出ABC S ∆,再根据12BDC ABC S S ∆∆=即可求出,根据等腰三角形的性质和二倍角公式即可求出 解答:解:如图,取BC 得中点E ,4AB AC ==,2BC =,112BE BC ∴==,AE BC ⊥,AE ∴==11222ABC S BC AE ∆∴=⋅=⨯ 2BD =,12BDC ABC S S ∆∆∴==, 2BC BD ==, BDC BCD ∴∠=∠, 2ABE BDC ∴∠=∠在Rt ABE ∆中, 1cos 4BE ABE AB ∠==, 21cos 2cos 14ABE BDC ∴∠=∠-=,cos BDC ∴∠=点评:本题考查了解三角形的有关知识,关键是转化,属于基础题【例3】记ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c .已知2b ac =,点D 在边AC 上,sin sin BD ABC a C ∠=.(1)证明:BD b =;(2)若2AD DC =,求cos ABC ∠. 分析:(1)利用正弦定理求解;(2)要能找到隐含条件:BDA ∠和BDC ∠互补,从而列出等式关系求解. 解答:解:(1)证明:由正弦定理知,2sin sin b cR ABC ACB==∠∠,2sin b R ABC ∴=∠,2sin c R ACB =∠,2b ac =,2sin 2sin b R ABC a R ACB ∴⋅∠=⋅∠,即sin sin b ABC a C ∠=,sin sin BD ABC a C ∠=, BD b ∴=;(2)法一:由(1)知BD b =,2AD DC =,23AD b ∴=,13DC b =, 在ABD ∆中,由余弦定理知,2222222222()1393cos 221223b b c BD AD AB b c BDA BD AD b b b +-+--∠===⋅⋅, 在CBD ∆中,由余弦定理知,2222222221()1093cos 12623b b a BD CD BC b a BDC BD CD b b b +-+--∠===⋅⋅, BDA BDC π∠+∠=, cos cos 0BDA BDC ∴∠+∠=,即2222221391090126b c b a b b--+=,得2221136b c a=+,2b ac=,22 31160c ac a∴-+=,3c a ∴=或23c a =,在ABC∆中,由余弦定理知,22222cos22a cb ac acABCac ac+-+-∠==,当3c a=时,7cos16ABC∠=>(舍);当23c a=时,7cos12ABC∠=;综上所述,7 cos12ABC∠=.法二:点D在边AC上且2AD DC=,∴1233BD BA BC=+,∴212 33BD BA BD BC BD=⋅+⋅,而由(1)知BD b=,∴212cos cos 33b bc ABD ab CBD=⋅∠+⋅∠,即3cos2cosb c ABD a CBD=⋅∠+⋅∠,由余弦定理知:22222241993222b c b a b bb c abc ab+-+-=⋅+⋅,222 1136b c a∴=+,2b ac=,22 31160c ac a∴-+=,3c a ∴=或23c a =,在ABC∆中,由余弦定理知,22222cos22a cb ac acABCac ac+-+-∠==,当3c a=时,7cos16ABC∠=>(舍);当23c a=时,7cos12ABC∠=;综上所述,7 cos12ABC∠=.点评:本题考查正弦定理及余弦定理的内容,是一道好题.【例4】(2020•江苏)在ABC∆中,角A、B、C的对边分别为a、b、c.已知3a=,c=45B=︒.(1)求sin C的值;(2)在边BC 上取一点D ,使得4cos 5ADC ∠=-,求tan DAC ∠的值.分析:(1)由题意及余弦定理求出b 边,再由正弦定理求出sin C 的值;(2)三角形的内角和为180︒,4cos 5ADC ∠=-,可得ADC ∠为钝角,可得DAC ∠与ADC C ∠+∠互为补角,所以sin sin()DAC ADC C ∠=∠+∠展开可得sin DAC ∠及cos DAC ∠,进而求出tan DAC ∠的值. 解答:解:(1)因为3a =,2c =,45B =︒.,由余弦定理可得:2222cos 9223252b ac ac B =+-=+-⨯⨯⨯=, 由正弦定理可得sin sin c bC B =,所以225sin sin 45255c C b =︒==, 所以5sin 5C =; (2)因为4cos 5ADC ∠=-,所以23sin 15ADC cos ADC ∠=-∠=,在三角形ADC 中,易知C 为锐角,由(1)可得225cos 15C sin C =-=, 所以在三角形ADC 中,25sin sin()sin cos cos sin 25DAC ADC C ADC C ADC C ∠=∠+∠=∠∠+∠∠=, 因为(0,)2DAC π∠∈,所以2115cos 125DAC sin DAC ∠=-∠=,所以sin 2tan cos 11DAC DAC DAC ∠∠==∠.点评:本题考查三角形的正弦定理及余弦定理的应用,及两角和的正弦公式的应用,属于中档题.三、提高训练1、在平面四边形ABCD 中,75A B C ∠=∠=∠=︒.2BC =,则AB 的取值范围是 (62,62) . 分析:如图所示,延长BA ,CD 交于点E ,设12AD x =,2AE x =,62DE +=,CD m =,求出62624x m ++=+,即可求出AB 的取值范围. 解答:解:方法一:如图所示,延长BA ,CD 交于点E ,则在ADE ∆中,105DAE ∠=︒,45ADE ∠=︒,30E ∠=︒, ∴设12AD x =,22AE x =,624DE x +=,CD m =, 2BC =,62()sin1514x m +∴+︒=, ∴62624x m ++=+, 04x ∴<<,而622262422AB x m x x +=+-=+-, AB ∴的取值范围是(62-,62)+.故答案为:(62-,62)+. 方法二:如下图,作出底边2BC =的等腰三角形EBC ,75B C ==︒,倾斜角为150︒的直线在平面内移动,分别交EB 、EC 于A 、D ,则四边形ABCD 即为满足题意的四边形; 当直线移动时,运用极限思想,①直线接近点C 时,AB 62; ②直线接近点E 时,AB 62 故答案为:(6262).点评:本题考查求AB 的取值范围,考查三角形中的几何计算,考查学生的计算能力,属于中档题. 2、ABC ∆中,D 是BC 上的点,AD 平分BAC ∠,2BD DC =. (Ⅰ)求sin sin BC∠∠.(Ⅱ)若60BAC ∠=︒,求B ∠. 解:(Ⅰ)如图, 由正弦定理得:,sin sin sin sin AD BD AD DCB BADC CAD==∠∠∠∠, AD 平分BAC ∠,2BD DC =,∴sin 1sin 2B DC C BD ∠==∠;(Ⅱ)180()C BAC B ∠=︒-∠+∠,60BAC ∠=︒, ∴31sin sin()cos sin 22C BAC B B B ∠=∠+∠=∠+∠, 由(Ⅰ)知2sin sin B C ∠=∠, 3tan 3B ∴∠=,即30B ∠=︒.3、在ABC ∆中,34A π∠=,6AB =,32AC =D 在BC 边上,AD BD =,求AD 的长. 解:34A π∠=,6AB =,32AC = ∴在ABC ∆中,由余弦定理可得:2222cos 90BC AB AC AB AC BAC =+-∠=. 3104BC ∴=⋯分在ABC ∆中,由正弦定理可得:sin sin AC BCB BAC=∠, 10sin 10B ∴=, 310cos 810B ∴=⋯分 过点D 作AB 的垂线DE ,垂足为E ,由AD BD =得:cos cos DAE B ∠=,Rt ADE ∴∆中,31012cos cos AE AD DAE B===⋯∠分四、课后作业1、(2021•浙江)在ABC ∆中,60B ∠=︒,2AB =,M 是BC 的中点,23AM =,则AC = ;cos MAC ∠= .2、(2017•全国)在ABC ∆中,D 为BC 的中点,8AB =,6AC =,5AD =,则BC = .3、(2013•福建)如图,在ABC ∆中,已知点D 在BC 边上,AD AC ⊥,22sin 3BAC ∠=,32AB =,3AD =,则BD 的长为 .4、(2013•广东)(几何证明选讲选做题)如图,在矩形ABCD 中,3AB =,3BC =,BE AC ⊥,垂足为E ,则ED = .5、(2017•新课标Ⅲ)ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin 30A A =,27a =,2b =.(1)求c ;(2)设D 为BC 边上一点,且AD AC ⊥,求ABD ∆的面积.课后作业答案:1.解:在ABM ∆中:2222cos60AM BA BM BA BM =+-⋅︒,22212222BM BM ∴=+-⨯⋅⋅,2280BM BM ∴--=,解得:4BM =或2-(舍去).点M 是BC 中点,4MC ∴=,8BC =,在ABC ∆中:22228228cos6052AC =+-⨯⨯︒=,AC ∴=在AMC ∆中:cos MAC ∠==.故答案为: 2.解:在ABC ∆中,D 为BC 的中点,8AB =,6AC =,5AD =, 可得1()2AD AB AC =+,平方可得2221(2)4AD AB AC AB AC =++,即为2546436286cos BAC ⨯=++⨯⨯∠, 可得cos 0BAC ∠=,可得ABC ∆为直角三角形,且90BAC ∠=︒,则10BC =, 故答案为:10. 3.解:AD AC ⊥,90DAC ∴∠=︒,90BAC BAD DAC BAD ∴∠=∠+∠=∠+︒,sin sin(90)cos BAC BAD BAD ∴∠=∠+︒=∠=,在ABD ∆中,AB =3AD =,根据余弦定理得:2222cos 189243BD AB AD AB AD BAD =+-∠=+-=,则BD4.解:矩形ABCD ,90ABC ∴∠=︒,∴在Rt ABC ∆中,AB 3BC =,根据勾股定理得:AC =12AB AC ∴=,即30ACB ∠=︒,2332BC EC AC ==, 60ECD ∴∠=︒,在ECD ∆中,3CD AB ==,332EC =, 根据余弦定理得:222279212cos 3424ED EC CD EC CD ECD =+-∠=+-=, 则212ED =. 故答案为:2125.解:(1)sin 3cos 0A A +=, tan 3A ∴=-,0A π<<,23A π∴=, 由余弦定理可得2222cos a b c bc A =+-, 即2128422()2c c =+-⨯⨯-,即22240c c +-=,解得6c =-(舍去)或4c =, 故4c =.(2)2222cos c b a ab C =+-, 162842272cos C ∴=+-⨯⨯⨯,2cos 7C ∴=,272cos 7AC CD C∴=== 12CD BC ∴=113sin 4223222ABC S AB AC BAC ∆=⋅⋅∠=⨯⨯⨯=, 132ABD ABC S S ∆∆∴==。
高中数学几何证明选讲详解

【命题立意】本题考查几何证明选做题的解法,属送分题
【思路点拨】条件
【规范解答】因为以AC为直径的圆与AB交于点D,所以
A. B. C. D.
【解析】设半径为 ,则 ,由 得 ,从而 ,故 ,选A.
7.在 中, 分别为 上的点,且 , 的面积是 ,梯形 的面积为 ,则 的值为( )
A. B. C. D.
【解析】 ,利用面积比等于相似比的平方可得答案B.
8.半径分别为1和2的两圆外切,作半径为3的圆与这两圆均相切,一共可作( )个.
5. (2010·天津高考理科·T14)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P,若 ,则 的值为
【命题立意】考查三角形的相似性质的应用。
【思路点拨】利用相似三角形的性质进行转化。
【规范解答】由题意可知 ∽ 相似,
所以 ,由 及已知条件
可得 ,又 , 。
【答案】
6.(2010·广东高考文科·T14)如图3,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD= ,点E,F分别为线段AB,CD的中点,则EF=.
【答案】
7.(2010·广东高考理科·T14)如图3,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD= ,∠OAP=30°,则CP=______.
【命题立意】本题考察垂径定理及相交弦定理.
【思路点拨】由垂径定理得 ,算出 ,再由相交弦定理求出
【规范解答】因为 为 的中点,由垂径定理得 ,在 中, ,由相交弦定理得: ,即 ,
2016年-2017年普通高等学校招生全国统一考试数学文试题(全国卷2,参考版解析)

高考衣食住用行衣:高考前这段时间,提醒同学们出门一定要看天气,否则淋雨感冒,就会影响考场发挥。
穿着自己习惯的衣服,可以让人在紧张时产生亲切感和安全感,并能有效防止不良情绪产生。
食:清淡的饮食最适合考试,切忌吃太油腻或者刺激性强的食物。
如果可能的话,每天吃一两个水果,补充维生素。
另外,进考场前一定要少喝水!住:考前休息很重要。
好好休息并不意味着很早就要上床睡觉,根据以往考生的经验,太早上床反而容易失眠。
考前按照你平时习惯的时间上床休息就可以了,但最迟不要超过十点半。
用:出门考试之前,一定要检查文具包。
看看答题的工具是否准备齐全,应该带的证件是否都在,不要到了考场才想起来有什么工具没带,或者什么工具用着不顺手。
行:看考场的时候同学们要多留心,要仔细了解自己住的地方到考场可以坐哪些路线的公交车?有几种方式可以到达?大概要花多长时间?去考场的路上有没有修路堵车的情况?考试当天,应该保证至少提前20分钟到达考场。
2016年高考新课标Ⅱ卷文数试题参考解析一、 选择题:本大题共12小题。
每小题5分,在每个小题给出的四个选项中,只有一项是符合要求的。
1. 已知集合{123}A =,,,2{|9}B x x =<,则A B =I (A ){210123}--,,,,, (B ){21012}--,,,, (C ){123},, (D ){12},【答案】D【解析】由29x <得,33x -<<,所以{|33}B x x =-<<,所以{1,2}A B =I ,故选D. 2. 设复数z 满足i 3i z +=-,则z =(A )12i -+ (B )12i - (C )32i + (D )32i - 【答案】C【解析】由3z i i +=-得,32z i =-,故选C. 3. 函数=sin()y A x ωϕ+ 的部分图像如图所示,则(A )2sin(2)6y x π=-(B )2sin(2)3y x π=-(C )2sin(2+)6y x π=(D )2sin(2+)3y x π=【答案】A4. 体积为8的正方体的顶点都在同一球面上,则该球面的表面积为 (A )12π (B )323π (C )8π (D )4π 【答案】A【解析】因为正方体的体积为8,所以正方体的体对角线长为233,所以球面的表面积为243)12ππ⋅=,故选A.5. 设F 为抛物线C :y 2=4x 的焦点,曲线y =kx(k >0)与C 交于点P ,PF ⊥x 轴,则k = (A )12 (B )1 (C )32(D )2【答案】D【解析】(1,0)F ,又因为曲线(0)ky k x=>与C 交于点P ,PF x ⊥轴,所以21k =,所以2k =,选D.6. 圆x 2+y 2−2x −8y +13=0的圆心到直线ax +y −1=0的距离为1,则a =(A )−43 (B )−34(C )3 (D )2 【答案】A【解析】圆心为(1,4),半径2r =,所以2211a =+,解得43a =-,故选A.7. 如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π (B )24π (C )28π (D )32π 【答案】C【解析】因为原几何体由同底面一个圆柱和一个圆锥构成,所以其表面积为28S π=,故选C.8. 某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯 ,则至少需要等待15秒才出现绿灯的概率为 (A )710 (B )58 (C )38 (D )310【答案】B【解析】至少需要等待15秒才出现绿灯的概率为40155408-=,故选B. 9. 中国古代有计算多项式值得秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的a 为2,2,5,则输出的s = (A )7 (B )12 (C )17 (D )34【答案】C【解析】第一次运算,a=2,s=2,n=2,k=1,不满足k>n; 第二次运算,a=2,s=2226⨯+=,k=2,不满足k>n; 第三次运算,a=5,s=62517⨯+=,k=3,满足k>n , 输出s=17,故选C .10. 下列函数中,其定义域和值域分别与函数y=10lg x的定义域和值域相同的是 (A )y =x (B )y =lg x (C )y =2x(D )y x=【答案】D 【解析】lg 10xy x ==,定义域与值域均为()0,+∞,只有D 满足,故选D .11. 函数π()cos 26cos()2f x x x =+-的最大值为 (A )4 (B )5(C )6(D )7【答案】B【解析】因为2311()2(sin )22f x x =--+,而sin [1,1]x ∈-,所以当sin 1x =时,取最大值5,选B.12. 已知函数f (x )(x ∈R )满足f (x )=f (2-x ),若函数 y =|x 2-2x -3| 与 y =f (x ) 图像的交点为(x 1,y 1),(x 2,y 2),…,(x m ,y m ),则1=mi i x =∑(A)0 (B)m (C) 2m (D) 4m 【答案】B【解析】因为2(),y |23|y f x x x ==--都关于1x =对称,所以它们交点也关于1x =对称,当m 为偶数时,其和为22m m ⨯=,当m 为奇数时,其和为1212m m -⨯+=,因此选B. 二.填空题:共4小题,每小题5分.13. 已知向量a =(m ,4),b =(3,-2),且a ∥b ,则m =___________. 【答案】6-【解析】因为a ∥b ,所以2430m --⨯=,解得6m =-.14. 若x ,y 满足约束条件103030x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩,则z =x -2y 的最小值为__________.【答案】5-15. △ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若4cos 5A =,5cos 13C =,a =1,则b =____________. 【答案】2113【解析】因为45cos ,cos 513A C ==,且,A C 为三角形内角,所以312sin ,sin 513A C ==,13sin sin(C)sin cos cos sin 65B A AC A C =+=+=,又因为sin sin a b A B =,所以sin 21sin 13a Bb A ==.16. 有三张卡片,分别写有1和2,1和3,2和3. 甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________________. 【答案】1和3【解析】由题意分析可知甲的卡片上数字为1和3,乙的卡片上数字为2和3,丙卡片上数字为1和2. 三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)等差数列{n a }中,34574,6a a a a +=+= (I )求{n a }的通项公式;(II)设nb =[na ],求数列{nb }的前10项和,其中[x]表示不超过x 的最大整数,如[0.9]=0,[2.6]=2【试题分析】(I )先设{}n a 的首项和公差,再利用已知条件可得1a 和d ,进而可得{}n a 的通项公式;(II )根据{}n b 的通项公式的特点,采用分组求和法,即可得数列{}n b 的前10项和.18. (本小题满分12分)某险种的基本保费为a (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:(I )记A 为事件:“一续保人本年度的保费不高于基本保费”。
专题14图形中的等腰三角形分类讨论(解析版)

专题14图形中的等腰三⾓形分类讨论(解析版)专题14 图形中的等腰三⾓形分类讨论教学重难点1.理解等腰三⾓形的性质和判定定理;2.能⽤等腰三⾓形的判定定理进⾏相关计算和证明;3.初步体会等腰三⾓形中的分类讨论思想;4.体会在函数动点中寻找某些特殊的点形成的等腰三⾓形;5.培养学⽣进⾏独⽴思考,提⾼独⽴解决问题的能⼒。
【备注】:1.此部分知识点梳理,根据第1个图先提问引导学⽣回顾学过的等腰三⾓形的性质,可以在⿊板上举例让学⽣画图;2再根据第2个图引导学⽣总结出题⽬中经常出现的⼀些等腰三⾓形的题型;3.和学⽣⼀起分析⼆次函数背景下等腰三⾓形的基本考点,为后⾯的例题讲解做好铺垫。
建议时间5分钟左右。
等腰三⾓形的性质:等腰三⾓形常见题型分类:函数背景下的等腰三⾓形的考点分析:1.求解相应函数的解析式;2.根据函数解析式求解某些特殊点的坐标;3.根据点的位置进⾏等腰三⾓形的讨论:分“指定腰长”和“不指定腰长”两⼤类;4.根据点的位置和形成的等腰三⾓形⽴等式求解。
【备注】:1.以下每题教法建议,请⽼师根据学⽣实际情况参考;2.在讲解时:不宜采⽤灌输的⽅法,应采⽤启发、诱导的策略,并在读题时引导学⽣发现⼀些题⽬中的条件(相等的量、不变的量、隐藏的量等等),使学⽣在复杂的背景下⾃⼰发现、领悟题⽬的意思;3.可以根据各题的“参考教法”引导学⽣逐步解题,并采⽤讲练结合;注意边讲解边让学⽣计算,加强师⽣之间的互动性,让学⽣参与到例题的分析中来;4.例题讲解,可以根据“教法指导”中的问题引导学⽣分析题⽬,边讲边让学⽣书写,每个问题后⾯有答案提⽰;5.引导的技巧:直接提醒,问题式引导,类⽐式引导等等;6.部分例题可以先让学⽣⾃⼰试⼀试,之后再结合学⽣做的情况讲评;7.每个题⽬的讲解时间根据实际情况处理,建议每题7分钟,选讲例题在时间⾜够的情况下讲解。
1.(2019青浦⼆模)如图1,已知扇形MON的半径为,∠MON=90°,点B在弧MN上移动,联结BM,作OD⊥BM,垂⾜为点D,C为线段OD上⼀点,且OC=BM,联结BC并延长交半径OM于点A,设OA=x,∠COM的正切值为y.(1)如图2,当AB⊥OM时,求证:AM=AC;(2)求y关于x的函数关系式,并写出定义域;(3)当△OAC为等腰三⾓形时,求x的值.整体分析:(1)先判断出∠ABM=∠DOM,进⽽判断出△OAC≌△BAM,即可得出结论;(2)先判断出BD=DM,进⽽得出,进⽽得出AE=,再判断出,即可得出结论;(3)分三种情况利⽤勾股定理或判断出不存在,即可得出结论.详解:(1)∵OD⊥BM,AB⊥OM,∴∠ODM=∠BAM=90°.∵∠ABM+∠M=∠DOM+∠M,∴∠ABM=∠DOM.∵∠OAC=∠BAM,OC=BM,∴△OAC≌△BAM,∴AC=AM.(2)如图2,过点D作DE∥AB,交OM于点E.∵OB=OM,OD⊥BM,∴BD=DM.∵DE∥AB,∴,∴AE=EM.∵OM=,∴AE=.∵DE∥AB,∴,∴.()(3)(i)当OA=OC时.∵.在Rt△ODM中,.∵.解得,或(舍).(ii)当AO=AC时,则∠AOC=∠ACO.∵∠ACO>∠COB,∠COB=∠AOC,∴∠ACO>∠AOC,∴此种情况不存在.(ⅲ)当CO=CA时,则∠COA=∠CAO=α.∵∠CAO>∠M,∠M=90°﹣α,∴α>90°﹣α,∴α>45°,∴∠BOA=2α>90°.∵∠BOA≤90°,∴此种情况不存在.即:当△OAC为等腰三⾓形时,x的值为.点睛:本题是圆的综合题,主要考查了相似三⾓形的判定和性质,圆的有关性质,勾股定理,等腰三⾓形的性质,建⽴y关于x 的函数关系式是解答本题的关键.图形背景下等腰三⾓形分类讨论的解题⽅法和策略:1.先寻找题⽬中的条件:相等的⾓、相等的边、相似的三⾓形等;2.根据题⽬中的条件求解相关线段的长度;3.等腰三⾓形讨论中,分三步⾛:分类、画图、计算;4.等腰讨论中,当不能直接利⽤边长相等求解时,⼀般情况下通过“画底边上的⾼”辅助线结合三⾓⽐计算求解;5.注意点的位置取舍答案;6.根据题⽬条件,注意快速、正确画图,⽤好数形结合思想;7.利⽤⼏何定理和性质或者代数⽅法建⽴⽅程求解都是常⽤⽅法。
几何证明选讲解三角形排列组合(教师版)
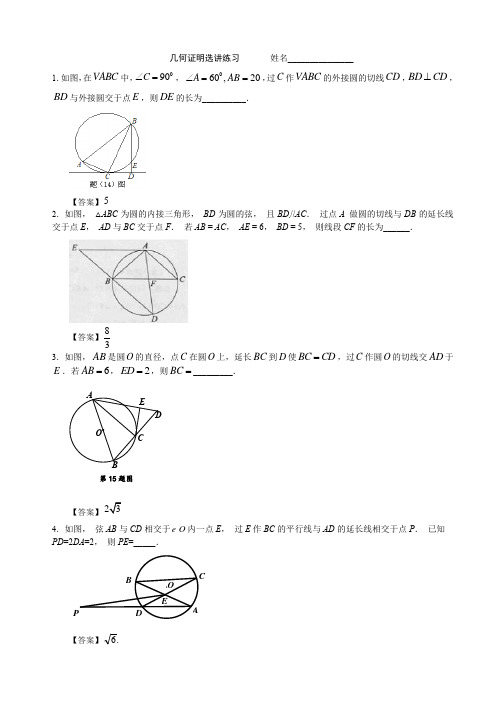
几何证明选讲练习 姓名_______________1.如图,在中,,,过作的外接圆的切线,,与外接圆交于点,则的长为__________.【答案】2.如图, △ABC 为圆的内接三角形, BD 为圆的弦, 且BD //AC . 过点A 做圆的切线与DB 的延长线交于点E , AD 与BC 交于点F . 若AB = AC , AE = 6, BD = 5, 则线段CF 的长为______.【答案】833.如图,AB 是圆O 的直径,点C 在圆O 上,延长BC 到D 使BC CD =,过C 作圆O 的切线交AD 于E .若6AB =,2ED =,则BC =_________.【答案】4.如图, 弦AB 与CD 相交于O 内一点E , 过E 作BC 的平行线与AD 的延长线相交于点P . 已知PD =2DA =2, 则PE =_____.【答案】.6 ABC 090C ∠=060,20A AB ∠==C ABC CD BD CD ⊥BD EDE5.A ED CB O 第15题图5.如图2,O 中,弦,AB CD 相交于点,2P PA PB ==,1PD =,则圆心O 到弦CD 的距离为____________.【答案】23 6.如图,圆O 上一点C 在直线AB 上的射影为D ,点D 在半径OC 上的射影为E .若3AB AD =,则CEEO的值为___________.【答案】8 7.如图,AB 为圆O 的直径,P A 为圆O 的切线,PB 与圆O 相交于D .若PA=3,916PD DB =::,则PD=_________;AB=___________.【答案】95;4 解三角形练习1.如图,△ABC 中,AB=AC=2,BC=点D在BC 边上,∠ADC=45°,则AD 的长度等于______.【命题意图】本题考查运用正余弦定理解三角形,是中档题.【解析】(法1)过A 作AE ⊥BC,垂足为E ,∵AB=AC=2,BC=∴E 是BC 的中点,且EC=O D EBACRt AEC ∆中,AE=又∵∠ADE=45°,∴DE=1,∴AD=(法2) ∵AB=AC=2,BC=由余弦定理知,cos C =2222AC BC AB AC BC +-⨯∴C=30°, 在△ADC 中,∠ADE=45°,由正弦定理得,sin sin AD AC C ADC=∠, ∴AD=sin sin AD C ADC ∠=12⨯2.如图,在△ABC 中,D 是边AC 上的点,且AB AD =,2AB =,2BC BD =,则sin C 的值为( )A.3 B.6 C3 D6【答案】D【解析】设BD a =,则由题意可得:2,BC a =2AB AD a ==,在ABD ∆中,由余弦定理得: 222cos 2AB AD BD A AB AD +-==⋅2232a a ⨯-=13,所以sin A=,在△ABC 中,由正弦定理得,sin sin AB BC C A =,所以2sin C =,解得sin CD . 3.,EF 是等腰直角ABC ∆斜边AB 上的三等分点,则tan ECF ∠=( )A .1627B .23 CD .34【答案】D4.在△ABC 中, 4ABC π∠=,AB 3BC =,则sin BAC ∠ =( ) (A )(B )(C )(D )【答案】C5.ABC ∆中,90C ∠=,M 是BC 的中点,若31sin =∠BAM ,则=∠BAC sin ________.【答案】36.在△ABC 中,已知AB=4,AC=7,BC 边的中线27=AD ,求边BC 的长.7.如图,在四边形ABCD 中,AC 平分∠DAB ,∠ABC=60°,AC=7,AD=6,S △ADC =2315,求AB 的长.排列组合练习题1.有6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品,已知6位同学之间共进行了13次交换,则收到份纪念品的同学人数为( ) 或 或 或 或【解析】选①设仅有甲与乙,丙没交换纪念品,则收到份纪念品的同学人数为人②设仅有甲与乙,丙与丁没交换纪念品,则收到份纪念品的同学人数为人.2.将字母排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有A .12种B .18种C .24种D .36种答案A【命题意图】本试题考查了排列组合的用用.4()A 13()B 14()C 23()D 24D 261315132C -=-=4244,,,,,a a b b c c【解析】利用分步计数原理,先填写最左上角的数,有3种,再填写右上角的数为2种,在填写第二行第一列的数有2种,一共有.3.现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这些卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为(A )232 (B)252 (C)472 (D)484解析:,答案应选C . 另解:. 4. 两人进行乒乓球比赛,先赢三局着获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有( )A .10种B .15种C .20种D .30种【解析】甲赢和乙赢的可能情况是一样的,所以假设甲赢的情况如下:若两人进行3场比赛,则情况只有是甲全赢1种情况;若两人进行4场比赛,第4场比赛必为甲赢前3场任选一场乙赢为种情况;若两人进行5场比赛,第5场比赛必为甲赢前4场任选一场乙赢为种情况;综上,甲赢有10种情况,同理,乙赢有10种情况,则所有可能出现的情况共20种,故选C .5.若从1,2,2,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有A .60种B .63种C .65种D .66种【解析】1,2,2,…,9这9个整数中有5个奇数,4个偶数.要想同时取4个不同的数其和为偶数,则取法有:4个都是偶数:1种;2个偶数,2个奇数:种; 4个都是奇数:种.∴不同的取法共有66种.【答案】D6.某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课个1节,则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 (用数字作答).【解析】概率为 语文、数学、英语三门文化课间隔一节艺术课,排列有种排法,语文、数学、英语三门文化课相邻有种排法,语文、数学、英语三门文化课两门相邻有种排法. 32212⨯⨯=472885607216614151641122434316=-=--⨯⨯=--C C C C 472122642202111241261011123212143431204=-+=⨯⨯+-⨯⨯=+-C C C C C 313=C 624=C 225460C C =455C =3____53344A A 3312122223A C C A C3故所有的排法种数有在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为5。
第18讲 阿基米德三角形(解析几何)(解析版)

第18讲阿基米德三角形知识与方法阿基米德(约公元前287年一前212年),是伟大的古希腊哲学家、百科式科学家、数学家、物理学家,并且享有“力学之父”的美称.他在求体积或面积时采用的“平衡法”一档杆原理,被后人命名为“阿基米德方法”.正是由于他对当时数学作出的突出贡献以及对后世数学发展的深邃影响,他又被后人誉为“数学之神”.本节主要探讨的阿基米德三角形指的是圆锥曲线(椭圆、双曲线、拋物线)的弦与过弦的端点的两条切线所围成的三角形.阿基米德三角形得名于阿基米德在研究与拋物线有关的面积问题时得出的一个结论:抛物线的弦与拋物线所围成的封闭图形的面积,等于抛物线的弦与过弦的端点的两条切线所围成的三角形面积的三分之二.(结论的证明利用了“平衡法”)该结论的变式叙述可见于《普通高中课程标准实验教科书·数学选修3-1(A版):数学史选讲》(人民教育出版社2007年1月第2版).接下来,我们就去探讨一下阿基米德三角形中蕴藏的一些重要性质:条件:已知抛物线C:x2=2py(p>0),如图所示,D为某一直线l上的动点,过D作C的两条切线,切点分别为A,B,F为直线AB与y轴的交点,则有以下结论成立:结论1.1直线AB的方程为(x1+x2)x−2py−x1x2=0.证明:设A(x1,y1),则x12=2py1.由于y′=xp ,所以切线DA的斜率为x1p,故切线DA的方程为x1x=p(y+y1)(1)设B(x2,y2),同理可得DB的方程为x2x=p(y+y2)(2) (1)÷(2)化简后,可得y=x1x22p(3)将(3)代入(1),可得x=x1+x22,所以点D的坐标为(x1+x22,x1x22p)故直线AB的方程为(x1+x2)x−2py−x1x2=0说明:特别的,当D为直线y=−p2上的动点时,直线AB的方程为(x1+x2)x−2py+p2=0且该直线过拋物线的焦点F.第二部分中的典例第(1)问考查的就是该性质的具体运用.结论1.2k DF⋅k AB=k DA⋅k DB=x1x2p2证明:由结论1.1的证明可知点F的坐标为(0,−x1x22p)又k DF=2x1x2p(x1+x2),k AB=x1+x22p,k DA=x1p,k DB=x2p,所以结论1.2得证.说明:特别的,当D为直线y=−p2上的动点时,有DF⊥AB,DA⊥DB;且此时△DAB面积的达到最小,其最小值为p2.第三部分中的第2题、第3题考查的均是该条性质及推论的运用,如若我们对上述性质比较熟悉,则审题结束时【答案】或许已了然于心.结论1.3在阿基米德△DAB中,有∠DFA=∠DFB.证明:如图,过点A,B分别作抛物线准线的垂线AA1,BB1,垂足为A1,B1.连接A1D,B1D,DF,AF,BF,A1F,则k A1F =−px1,k AD=x1p.易知,AD⊥A1F.又AA1=AF,所以AD垂直且平分A1F,故A1D=DF,∠DA1A=∠DFA.同理可得B1D=DF,∠DB1B=∠DFB,所以A1D=B1D=DF,∠DA1B1=∠DB1A1.进而∠DA1A=∠DB1B,即∠DFA=∠DFB.说明:第三部分中的第4题的第(2)问恰恰就考查了这一结论.结论1.4DA,AB,DB的斜率成等差数列、A,D,B三点的横坐标成等差数列.证明:结合结论1.2的证明过程以及点D坐标(x1+x22,x1x22p),稍作运算,便可证得该结论.说明:第三部分中的第5题的第(1)问中就涉及到了这一结论.结论1.5线段FA,FD,FB的长度之间的关系为FD2=x12x22p2+p2|x1x2|⋅FA⋅FB−p2.证明:经过简单计算即可得到上述结果.说明:特别的,当D为直线y=−p2上的动点时,有线段FA,FD,FB的长度成等比数列.结论1.6若以E(0,−5x1x22p)为圆心的圆与直线AB相切于点T,则四边形ADBE的面积为|x1−x2|38p −x1x2⋅|x1−x2|p证明:易知DA ⃗⃗⃗⃗⃗ =(x 1−x 22,x 1(x 1−x 2)2p ),DB ⃗⃗⃗⃗⃗⃗ =(x 2−x 12,x 2(x 2−x 1)2p). 利用面积公式S ΔDAB =12√DA ⃗⃗⃗⃗⃗ 2⋅DB ⃗⃗⃗⃗⃗⃗ 2−(DA ⃗⃗⃗⃗⃗ ⋅DB⃗⃗⃗⃗⃗⃗ )2,可得 S △DAB=12|x 1−x 22⋅x 2(x 2−x 1)2p −x 2−x 12⋅x 1(x 1−x 2)2p |=|x 1−x 2|38p又S △EAB =12|EF|⋅|x 1−x 2|=12(−5x 1x 22p +x 1x 22p )⋅|x 1−x 2|=−x 1x 2⋅|x 1−x 2|p所以S 四边形 ADBE =S Δ+S ΔA =|x 1−x 2|38p−x 1x 2⋅|x 1−x 2|p.说明:当D 为直线y =−p2上的动点,且E (0,5p2)时,则四边形ADBE 的面积为|x 1−x 2|38p+p |x 1−x 2|.结论1.7△DAB 的重心G 满足的方程为4x 2−6py −x 1x 2=0. 证明:过程从略,感兴趣的读者可自行尝试证明.说明:当D 为直线y =−p2上的动点时,△DAB 的重心G 的轨迹方程为4x 2−6py +p 2=0结论1.8 若P 为拋物线弧AB 上一点,拋物线在点P 处的切线与直线..分别交与M,N 两点,则S △DMN :S △PAB =1:2证明:设P (x 3,y 3),则有x M =x 1+x 32,x N =x 2+x 32,所以AM MD =MP PN =DNNB =|x 1−x 3||x 2−x 3|.设AMMD =MP PN=DNNB =a,S △PMD =b ,因为S ΔPMA S ΔPMD=AMMD =a ,所以S ΔPMA =ab同理S △PND =b a ,S ΔPNB =b a 2,所以S △DMN =b (1+1a ). 又S ΔNMD S △BAD=MD⋅DN AD⋅BD=a(a+1)2,所以S ΔBAD =b ⋅(a+1)3a 2.所以S ΔPBA =S ΔDAB −S △DMN −S ΔPAM −S ΔPBN =b ⋅2(a+1)a所以S ΔDMN :S △PAB =1:2.值得注意的是抛物线的性质远也不止这些,上述所列诸条,大多数是在区域模拟考试及高考中经常出现的.众所周知,以阿基米德三角形为背景的直线的定点、三角形的面积、轨迹、最值等相关问题是高考和模拟考考查的热点也是难点.纸上得来终觉浅,接下来我们不妨从多个视角去赏析一道高考题,以进一步体会阿基米德三角形的相关性质.典型例题【例1】已知曲线C:y =12x 2,D 为直线y =−12上的动点,过D 作C 的两条切线,切点分别为A,B . (1)证明:直线AB 过定点;(2)若以E (0,52)为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积.【答案】(1)见解析;(2)3或4√2.【分析】分析题目可知,直线AB 是切点所在的直线,只需找到㔹点的共同属性即可.故可采用“设而不求”的思想就将该问题解决. 【解析】解法1:设而不求设D (t,−12),A (x 1,y 1),则x 12=2y 1.由于y ′=x ,所以切线DA 的斜率为x 1,故y 1+12x1−t=x 1即DA 的方程为2tx 1−2y 1+1=0.设B (x 2,y 2),同理可得DB 的方程为2tx 2−2y 2+1=0. 故直线AB 的方程为2tx −2y +1=0,所以直线AB 过定点(0,12).(2)由(1)得直线AB 的方程为y =wx +12.由{y =tx +12y =x 22,可得x 2−2tx −1=0 于是x 1+x 2=2t,x 1x 2=−1,y 1+y 2=t (x 1+x 2)+1=2t 2+1,|AB|=√1+t 2|x 1−x 2|=√1+t 2×√(x 1+x 2)2−4x 1x 2=2(t 2+1)设d 1,d 2分别为点D,E 到直线AB 的距离,则d 1=√t 2+1,d 2=√t 2+1.因此,四边形ADBE 的面积S =12|AB|(d 1+d 2)=(t 2+3)√t 2+1. 设M 为线段AB 的中点,则M (t,t 2+12).由于EM⃗⃗⃗⃗⃗⃗ ⊥AB ⃗⃗⃗⃗⃗ ,而EM ⃗⃗⃗⃗⃗⃗ =(t,t 2−2),AB⃗⃗⃗⃗⃗ 与向量(1,t)平行,所以t +(t 2−2)t =0.解得t =0或t =±1. 当t =0时,S =3;当t =±1时,S =4√2.因此,四边形ADBE 的面积为3或4√2.分析:本题还可从寻找切点A,B 定直线入手,将直线AB 用参数表示,借助海伦秦九韶公式将面积问题解决. 解法2:求切点定直线(1)设D (t,−12),过D 点与C 相切的直线方程设为y +12=k(x −t),切线AD,BD 的斜率分别为k 1,k 2.由{y +12=k(x −t)y =x 22,可得x 2−2kx +2kt +1=0(1) 由Δ=0,可得k 2−2kt −1=0(2)于是k 1+k 2=2t,k 1k 2=−1 将@代入(1),可得A (k 1,k 122),B (k 2,k 222),所以k AB =k 1+k 22=t.故直线AB 的方程为y =k 1+k 22x +12,即直线AB 过定点(0,12).(2)设线段AB 的中点坐标为T (x 0,y 0),则有 x 0=k 1+k 22=t,y 0=k 12+k 224=t 2+12,所以k ET =t 2−2t又k AB ⋅k ET =−1,解得t =0或t =±1 又DA ⃗⃗⃗⃗⃗ =(k 1−k 22,k 12+12),DB⃗⃗⃗⃗⃗⃗ =(k 2−k 12,k 22+12) 利用面积公式S =12√AB ⃗⃗⃗⃗⃗ 2⋅AC ⃗⃗⃗⃗⃗ 2−(AB ⃗⃗⃗⃗⃗ ⋅AC ̅̅̅̅)2=12|x 1y 2−x 2y 1|可得 S △DAB=12|k 1−k 22⋅k 22+12−k 2−k 12⋅k 12+12|=18|k 1−k 2|3 同理可得 S △EAB =|k 1−k 2|当t =0时,|k 1−k 2|=2,此时S 冏边形 ADBE =18|k 1−k 2|3+|k 1−k 2|=3 当t =±1时,|k 1−k 2|=2√2,此时S 㐰边形 ADBE =18|k 1−k 2|3+|k 1−k 2|=4√2注:此处给出的这种方法是解决此类问题的通性通法,但注意不要漏掉斜率为0的情形. 解法3:设直线定“待参”设直线AB 的方程设为y =kx +m,A (x 1,y 1),B (x 2,y 2)由{y =kx +my =x 22,可得x 2−2kx −2m =0.于是x 1+x 2=2k,x 1x 2=−2m由于y ′=x ,所以切线DA,BD 的斜率分别为x 1,x 2 所以切线DA,BD 的方程分别为x 1x =y +y 1,x 2x =y +y 2联立可得D 点的纵坐标y D =12x 1x 2=−m ,又D 为直线y =−12上的动点,所以m =12 故直线AB 过定点(0,12) (2)由(1)知x D =y D +y 1x 1=12x 1x 2+12x 12x 1=x 1+x 22=k设线段AB 的中点坐标为T (x 0,y 0),则有x 0=x 1+x 22=k所以TD 垂直于直线y =−12过A,B 分别作直线y =−12的垂线,垂足分别为A 1,B 1,如图所示,所以点D 为A 1B 1的中点.记AB 过的定点为F ,则有AA 1=AF,BB 1=BF 由(1)知k AD ⋅k BD =x 1x 2=−1,所以DA ⊥DB 易得S △DAB =12S 梯形AA 1B 1B =(y 1+12+y 2+12)|x 1−x 2|2=|x 1−x 2|38又S △EAB =12|EF|⋅|x 1−x 2|=12(52−12)⋅|x 1−x 2|=|x 1−x 2| 以下计算同方法二. 解法四:设切点定截距设A (x 1,x 122),B (x 2,x 222),D (m,−12),直线AB:y =kx +b . 联立{y =12x 2y =kx +b⇒x 2−2kx −2b =0,由韦达定理得{x 1+x 2=2kx 1⋅x 2=−2b又y ′=x ,从而直线DA,DB 的方程分别为y =x 1x −12x 12,y =x 2x −12x 22.因为切线过点D (m,−12),所以有{mx 1−12x 12=−12mx 2−12x 22=−12即x 1,x 2为方程x 2−2mx −1=0的两根,即x 1⋅x 2=−1=−2b ⇒b =12,所以直线AB 过定点(0,12).(2)由(1)知,x 1+x 2=2k ,则y 1+y 2=k (x 1+x 2)+1=2k 2+1,所以,AB 的中点T (k,k 2+12). 当k =0时,M (0,12),此时,四边形ADBE 的面积S =3.当k ≠0时,由k TE ⋅k AB =−1得k 2−2k=−1k ,解得k 2=1.所以,|AB|=√1+k 2⋅√(x 1+x 2)2−4x 1x 2=2(k 2+1)=4. 又点E 到直线AB 的距离d 1=√1+k 2=√2,点D 到直线AB 的距离d 2=√1+k 2=√2所以四边形ADBE 的面积S =12×|AB|×(d 1+d 2)=4√2.综上,四边形ADBE 的面积为3或4√2.强化训练以阿基米德三角形为背景考查的高考题主要还有以下几种类型.(一)轨迹问题1.如图,抛物线C 1:x 2=4y,C 2:x 2=−2py(p >0).点M (x 0,y 0)在拋物线C 2上,过M 作C 1的切线,切点为A,B(M为原点O 时,A,B 重合于O).当x 0=1−√2时,切线MA 的斜率为−12. (1)求p 的值;(2)当M 在C 2上运动时,求线段AB 中点N 的轨迹方程(A,B 重合于O 时,中点为O ).【答案】(1)p =2;(2)见解析 【解析】(1)p =2过程从略; (2)设N(x,y),A (x 1,x 124),B (x 2,x 224),x 1≠x 2由N 为线段AB 中点知x =x 1+x 22(1),所以y =x 12+x 228(2).所以,切线MA,MB 的方程分别为y =x 12(x −x 1)+x 124,(3)y =x 22(x −x 2)+x 224.(4)由(3)(4)得,MA,MB 的交点M (x 0,y 0)的坐标为x 0=x 1+x 22,y 0=x 1x 24.因为点M (x 0,y 0)在C 2上,即x 02=4y 0,所以x 1x 2=−x 12+x 226.(5)由(1)(2)(5)得x 2=43y,x ≠0.当x 1=x 2时,A,B 重合于O 时,中点N 为O ,坐标满足x 2=43y .因此AB 中点N 的轨迹方程为x 2=43y .2.已知抛物线x 2=4y 的焦点为F,A,B 是抛物线上的两动点,且AF ⃗⃗⃗⃗⃗ =λFB ⃗⃗⃗⃗⃗ (λ>0)过A,B 两点分别作扡物线的切线,设其交点为M .(1)证明FM̅̅̅̅̅⋅AB ⃗⃗⃗⃗⃗ 为定值; (2)设△ABM 的面积为S ,写出S =f(λ)的表达式,并求S 的最小值.【答案】(1)见解析;(2)4.【解析】(1)由已知条件,得F(0,1),λ>0. 设A (x 1,y 1),B (x 2,y 2).由AF⃗⃗⃗⃗⃗ =λFB ⃗⃗⃗⃗⃗ (λ>0) 即(−x 1,1−y )=λ(x 2,y 2−1),也即{−x 1=λx 2①1−y 1=λ(y 2−1)②将①式两边平方并把x 12=4y 1,x 22=4y 2代入得y 1=λ2y 2③解②、③式得y 1=λ,y 2=1λ,且有x 1x 2=−4, 拋物线方程为y =14x 2,求导得y ′=12x .所以过抛物线上A,B 两点的切线方程分别是y =12x 1(x −x 1)+y 1,y =12x 2(x −x 2)+y 2易得M 的坐标为(x 1+x 22,−1).所以FM ⃗⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ =(x 1+x 22,−2)⋅(x 2−x 1,y 2−y 1)=0 (II)由(I )知在△ABM 中,FM ⊥AB ,因而S =12|AB|⋅|FM|.又|FM⃗⃗⃗⃗⃗⃗ |=√(x 1+x 22)2+(−2)2=√λ+1λ+2=√λ√λ|AB⃗⃗⃗⃗⃗ |=λ+1λ+2=(√λ+√λ)2于是S =12|AB|⋅|FM|=12(√λ√λ)3,由√λ+√λ⩾2知S ⩾2,且当λ=1时,S 取得最小值4.3.如图,等边三角形OAB 的边长为8√3,且其三个顶点均在拋物线E:x 2=2py(p >0)上.(1)求抛物线E 的方程;(2)设动直线l 与抛物线E 相切于点P ,与直线y =−1相交于点Q .证明以PQ 为直径的圆恒过y 轴上某定点.【答案】(1)x 2=4y ; (2)见解析.【解析】(1)抛物线E 的方程为x 2=4y ,过程略.(2)设P (x 0,y 0),x 0≠0,由y =14x 2,得y ′=12x ,直线l 的方程为y −y 0=12x 0(x −x 0),即y =12x 0x −14x 02.联立20011241y x x x y ⎧=-⎪⎨⎪=-⎩,即200421x x x y ⎧-=⎪⎨⎪=-⎩,所以2004,12x Q x ⎛⎫-- ⎪⎝⎭ 设M (0,y 1),所以MP⃗⃗⃗⃗⃗⃗ =(x 0,y 0−y 1),MQ ⃗⃗⃗⃗⃗⃗ =(x 02−42x 0,−1−y 1) 因为MP ⃗⃗⃗⃗⃗⃗ ⋅MQ ⃗⃗⃗⃗⃗⃗ =0,所以x 02−42x 0−y 0−y 0y 1+y 1+y 12=0.又y 0=14x 02(x 0≠0),所以y 1=1 故以PQ 为直径的圆恒过M(0,1).4.如图,设抛物线C:y =x 2的焦点为F ,动点P 在直线l:x −y −2=0上运动,过P 作拋物线C 的两条切线PA,PB ,且与抛物线C 分别相切于A,B 两点. (1)求△APB 的重心G 的轨迹方程; (2)证明∠PFA =∠PFB .【答案】(1)y =13(4x 2−x +2); (2)见解析.【解析】(1)设切点A,B 坐标分别为(x,x 02)和(x 1,x 12)((x 1≠x 0), 所以切线AP 的方程为:2x 0x −y −x 02=0; 切线BP 的方程为:2x 1x −y −x 12=0;解得P 点的坐标为:x P =x 0+x 12,y P =x 0x 1所以△APB 的重心G 的坐标为x G =x 0+x 1+x P3=x P ,y G =y 0+y 1+y P 3=x 02+x 12+x 0x 13=(x 0+x 1)2−x 0x 13=4x P2−y p 3所以y p =−3y G +4x G 2,由点P 在直线l 上运动.从而得到重心G 的轨迹方程为: x −(−3y +4x 2)−2=0,y =13(4x 2−x +2).(2)因为FA ⃗⃗⃗⃗⃗ =(x 0,x 02−14),FP ⃗⃗⃗⃗⃗ =(x 0+x 12,x 0x 1−14),FB ⃗⃗⃗⃗⃗ =(x 1,x 12−14). 由于P 点在拋物线外,则|FP⃗⃗⃗⃗⃗ |≠0.所以cos∠AFP =FP ⃗⃗⃗⃗⃗ ⋅FA ⃗⃗⃗⃗⃗ |FP⃗⃗⃗⃗⃗ ||FA ⃗⃗⃗⃗⃗ |=x 0+x 12⋅x +(x x −14)(x 2−14)|FP ̅̅̅̅|√x 02+(x 02−14)2=x 0x 1+14|FP⃗⃗⃗⃗⃗ |同理有cos∠BFP =FP ⃗⃗⃗⃗⃗ ⋅FB ⃗⃗⃗⃗⃗ |FP⃗⃗⃗⃗⃗ ||FB ⃗⃗⃗⃗⃗ |=x 0+x 12⋅x +(x x −14)(x 2−14)|FP ⃗⃗⃗⃗⃗ |√x 12+(x 12−14)2=x 0x 1+14|FP⃗⃗⃗⃗⃗ |所以∠PFA =∠PFB .5.如图,设抛物线方程为 x 2=2py(p >0),M 为直线y =−2p 上任意一点,过M 引抛物线的切线,切点分别为A,B .(1)求证:A,M,B 三点的横坐标成等差数列;(2)已知当M 点的坐标为(2,−2p)时,|AB|=4√10,求此时抛物线的方程;(3)是否存在点M ,使得点C 关于直线AB 的对称点D 在拋物线x 2=2py(p >0)上,其中点C 满足 OC⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +OB⃗⃗⃗⃗⃗ (O 为坐标原点).若存在,求出所有适合题意的点的坐标;若不存在,请说明理由.【解析】(1)证明:由题意设A (x 1,x 122p ),B (x 2,x 222p),x 1<x 2,M (x 0,−2p ). 由x 2=2py 得y =x 22p,得y ′=xp,所以k MA =x 1p,k MB =x 2p.因此直线MA 的方程为y +2p =x 1p(x −x 0),直线MB 的方程为y +2p =x 2p(x −x 0).所以x 122p+2p =x 1p(x 1−x 0),(1)x 222p+2p =x 2p(x 2−x 0).(2)由(1)、(2)得x 1+x 22=x 1+x 2−x 0,因此x 0=x 1+x 22,即2x 0=x 1+x 2.所以A,M,B 三点的横坐标成等差数列.(2) 由(1)知,当x 0=2时,将其代入(1)、(2)并整理得:x 12−4x 1−4p 2=0,x 22−4x 2−4p 2=0所以x 1,x 2是方程x 2−4x −4p 2=0的两根,因此x 1+x 2=4,x 1x 2=−4p 2, 又k AB =x 222p −x 122p x2−x 1=x 1+x 22p=x 0p,所以k AB =2p由弦长公式得|AB|=√1+k2√(x1+x2)2−4x1x2=√1+4p2√16+16p2.又|AB|=4√10,所以p=1或p=2,因此所求抛物线方程为x2=2y或x2=4y.(3)设D(x3,y3),由题意得C(x1+x2,y1+y2),则CD的中点坐标为Q(x1+x2+x32,y1+y2+y32).设直线AB的方程为y−y1=x0p(x−x1),由点Q在直线AB上,并注意到点(x1+x22,y1+y22)也在直线AB上,代入得y3=x0px3.若D(x3,y3)在拋物线上,则x32=2py3=2x0x3.因此x3=0或x3=2x0.即D(0,0)或D(2x0,2x02p).(1)当x0=0时,则x1+x2=2x0=0,此时,点M(0,−2p)适合题意.(2)当x0≠0,对于D(0,0), 此时C(2x0,x12+x222p ),k CD=x12+x222p2x0=x12+x224px0,又k AB=x0p,AB⊥CD所以k AB⋅k CD=x0p ⋅x12+x224px0=x12+x224p2=−1,即x12+x22=−4p2,矛盾.对于D(2x0,2x02p ),因为C(2x0,x12+x222p),此时直线CD平行于y轴,又k AB=x0p≠0,所以直线AB与直线CD不垂直,与题设矛盾,所以x0≠0时,不存在符合题意的M点.综上所述,仅存在一点M(0,−2p)适合题意.。
高三数学模拟试卷(八)文(含解析)-人教版高三全册数学试题

2016年某某省某某市东北育才学校高考数学模拟试卷(文科)(八)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.为了解某高级中学学生的体重状况,打算抽取一个容量为n的样本,已知该校高一、高二、高三学生的数量之比依次为4:3:2,现用分层抽样的方法抽出的样本中高三学生有10人,那么样本容量n为()A.50 B.45 C.40 D.202.若命题p:∃x0∈R,x02+1>3x0,则¬p是()A.∃x0∈R,x02+1≤3x0B.∀x∈R,x2+1≤3xC.∀x∈R,x2+1<3x D.∀x∈R,x2+1>3x3.设z=1+i(是虚数单位),则+=()A.1 B.﹣1 C.i D.﹣i4.已知集合A={﹣2,﹣1,0,1,2},B={x|x=(﹣1)n+n,n∈N},则A∩B=()A.{0,2} B.{0,1,2} C.{﹣2,0,1,2} D.{﹣2,﹣1,0,1,2}5.《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺.问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”.这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一.”就是说:圆堡瑽(圆柱体)的体积为:V=×(底面的圆周长的平方×高).则由此可推得圆周率π的取值为()A.3 B.3.14 C.3.2 D.3.36.执行如图所示的程序框图,如果输出S=3,那么判断框内应填入的条件是()A.k≤6 B.k≤7 C.k≤8 D.k≤97.已知函数f(x)=,则下列结论正确的是()A.f(x)是偶函数B.f(x)是增函数C.f(x)是周期函数 D.f(x)的值域为[﹣1,+∞)8.如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置的可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为()A.4πB.5πC.6πD.7π9.已知不等式组的解集记为D,则对∀(x,y)∈D使得2x﹣y取最大值时的最优解是()A.(2,1)B.(2,2)C.3 D.410.若等比数列的各项均为正数,前4项的和为9,积为,则前4项倒数的和为()A.B.C.1 D.211.tan20°+4sin20°的值为()A.B.C.D.12.已知A,B分别为椭圆的左、右顶点,不同两点P,Q在椭圆C上,且关于x轴对称,设直线AP,BQ的斜率分别为m,n,则当取最小值时,椭圆C的离心率为()A.B.C.D.二.填空题:本大题共4小题,每小题5分.13.过原点作曲线y=e x的切线,则切线方程为.14.某一简单几何体的三视图如图,则该几何体的外接球的表面积为.15.在△ABC中,内角A、B、C的对边分别为a、b、c,且a=4,b=3,c=2,若点D为线段BC上靠近B的一个三等分点,则AD=.16.已知函数F(x)=e x满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,若∀x∈(0,2]使得不等式g(2x)﹣ah(x)≥0恒成立,则实数a的取值X 围是.三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程和演算步骤17.设数列{a n}的前n项和为S n,且2a n=S n+2.(Ⅰ)求{a n}的通项公式;(Ⅱ)设数列b n=,其前n项和为T n,求T n.18.在某学校一次考试的语文与历史成绩中,随机抽取了25位考生的成绩进行分析,25位考生的语文成绩已经统计在茎叶图中,历史成绩如下:(Ⅰ)请根据数据在茎叶图中完成历史成绩统计;(Ⅱ)请根据数据完成语文成绩的频数分布表及语文成绩的频率分布直方图;语文成绩的频数分布表:语文成绩分组[50,60)[60,70)[70,80)[80,90)[90,100)[100,110)[110,120]频数(Ⅲ)设上述样本中第i位考生的语文、历史成绩分别为x i,y i(i=1,2,…,25).通过对样本数据进行初步处理发现:语文、历史成绩具有线性相关关系,得到:=x i=86, =y i =64,(x i﹣)(y i ﹣)=4698,(x i﹣)2=5524,≈0.85.①求y关于x的线性回归方程;②并据此预测,当某考生的语文成绩为100分时,该生历史成绩.(精确到0.1分)附:回归直线方程的斜率和截距的最小二乘法估计公式分别为:==, =﹣.19.如图,在四棱锥P ﹣ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点.已知PD=,CD=4,AD=.(Ⅰ)若∠ADE=,求证:CE⊥平面PDE;(Ⅱ)当点A到平面PDE的距离为时,求三棱锥A﹣PDE的侧面积.20.已知椭圆C: =1(a>b>0)的两焦点与短轴的一个端点的连线构成等边三角形,直线x+y+2﹣1=0与以椭圆C的右焦点为圆心,椭圆的长半轴为半径的圆相切.(1)求椭圆C的方程;(2)设点B,C,D是椭圆上不同于椭圆顶点的三点,点B与点D关于原点O对称,设直线CD,CB,OB,OC的斜率分别为k1,k2,k3,k4,且k1k2=k3k4.(i)求k1k2的值;(ii)求OB2+OC2的值.21.设函数f(x)=lnx+,m∈R.(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;(Ⅱ)讨论函数g(x)=f′(x)﹣零点的个数;(Ⅲ)若对任意b>a>0,<1恒成立,求m的取值X围.请从下面所给的22、23、24三题中选定一题作答,并用2B铅笔在答题卡上将所选题目对应的题号方框涂黑,按所涂题号进行评分;不涂、多涂均按所答第一题评分;多答按所答第一题评分.[选修4-1:几何证明选讲]22.如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.(1)求△ABP的面积;(2)求弦AC的长.[选修4-4:坐标系与参数方程]23.在直角坐标系xOy中,圆C的参数方程(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.(Ⅰ)求圆C的极坐标方程;(Ⅱ)直线l的极坐标方程是ρ(sinθ+)=3,射线OM:θ=与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.[选修4-5:不等式选讲]24.已知函数f(x)=|x+2|﹣|x﹣1|.(Ⅰ)试求f(x)的值域;(Ⅱ)设若对∀s∈(0,+∞),∀t∈(﹣∞,+∞),恒有g(s)≥f(t)成立,试某某数a的取值X围.2016年某某省某某市东北育才学校高考数学模拟试卷(文科)(八)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.为了解某高级中学学生的体重状况,打算抽取一个容量为n的样本,已知该校高一、高二、高三学生的数量之比依次为4:3:2,现用分层抽样的方法抽出的样本中高三学生有10人,那么样本容量n为()A.50 B.45 C.40 D.20【考点】分层抽样方法.【分析】利用分层抽样性质求解.【解答】解:∵高一、高二、高三学生的数量之比依次为4:3:2,现用分层抽样的方法抽出的样本中高三学生有10人,∴由分层抽样性质,得:,解得n=45.故选:B.2.若命题p:∃x0∈R,x02+1>3x0,则¬p是()A.∃x0∈R,x02+1≤3x0B.∀x∈R,x2+1≤3xC.∀x∈R,x2+1<3x D.∀x∈R,x2+1>3x【考点】命题的否定.【分析】直接利用特称命题的否定是全称命题写出结果即可.【解答】解:因为特称命题的否定是全称命题.所以,命题p:∃x0∈R,x02+1>3x0,则¬p 是∀x∈R,x2+1≤3x,故选B.3.设z=1+i(是虚数单位),则+=()A.1 B.﹣1 C.i D.﹣i【考点】复数代数形式的乘除运算.【分析】利用复数的除法运算法则化简复数为a+bi的形式即可.【解答】解:z=1+i(是虚数单位),则+===1.故选:A.4.已知集合A={﹣2,﹣1,0,1,2},B={x|x=(﹣1)n+n,n∈N},则A∩B=()A.{0,2} B.{0,1,2} C.{﹣2,0,1,2} D.{﹣2,﹣1,0,1,2}【考点】交集及其运算.【分析】求出B中x的值确定出B,找出A与B的交集即可.【解答】解:∵A={﹣2,﹣1,0,1,2},B={x|x=(﹣1)n+n,n∈N}={0,1,2,…},∴A∩B={0,1,2},故选:B.5.《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺.问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”.这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一.”就是说:圆堡瑽(圆柱体)的体积为:V=×(底面的圆周长的平方×高).则由此可推得圆周率π的取值为()A.3 B.3.14 C.3.2 D.3.3【考点】排序问题与算法的多样性.【分析】由题意,圆柱体底面的圆周长20尺,高4尺,利用圆堡瑽(圆柱体)的体积V=×(底面的圆周长的平方×高),求出V,再建立方程组,即可求出圆周率π的取值.【解答】解:由题意,圆柱体底面的圆周长20尺,高4尺,∵圆堡瑽(圆柱体)的体积V=×(底面的圆周长的平方×高),∴V=×=,∴∴π=3,R=,故选:A.6.执行如图所示的程序框图,如果输出S=3,那么判断框内应填入的条件是()A.k≤6 B.k≤7 C.k≤8 D.k≤9【考点】程序框图.【分析】根据程序框图,写出运行结果,根据程序输出的结果是S=3,可得判断框内应填入的条件.【解答】解:根据程序框图,运行结果如下:S k第一次循环 log23 3第二次循环 log23•log34 4第三次循环 log23•log34•log45 5第四次循环 log23•log34•log45•log56 6第五次循环 log23•log34•log45•log56•log67 7第六次循环 log23•log34•log45•log56•log67•log78=log28=3 8故如果输出S=3,那么只能进行六次循环,故判断框内应填入的条件是k≤7.故选B.7.已知函数f(x)=,则下列结论正确的是()A.f(x)是偶函数B.f(x)是增函数C.f(x)是周期函数 D.f(x)的值域为[﹣1,+∞)【考点】函数的值域;函数单调性的判断与证明;函数奇偶性的判断.【分析】根据函数的性质分别进行判断即可.【解答】解:当x≤0时,f(x)=cos2x不是单调函数,此时﹣1≤cos2x≤1,当x>0时,f(x)=x4+1>1,综上f(x)≥﹣1,即函数的值域为[﹣1,+∞),故选:D8.如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置的可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为()A.4πB.5πC.6πD.7π【考点】几何概型.【分析】由几何概型概率计算公式,以面积为测度,可求该阴影部分的面积.【解答】解:设该多边形的面积为S,则,∴S=5π,故选B.9.已知不等式组的解集记为D,则对∀(x,y)∈D使得2x﹣y取最大值时的最优解是()A.(2,1)B.(2,2)C.3 D.4【考点】简单线性规划.【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定z的最大值.【解答】解:作出不等式组对应的平面区域如图:(阴影部分ABC).设z=2x﹣y,则y=2x﹣z,平移直线y=2x﹣z,由图象可知当直线y=2x﹣z经过点C时,直线y=2x﹣z的截距最小,此时z最大.即,即C(2,1),故使得2x﹣y取最大值时的最优解是(2,1),故选:A.10.若等比数列的各项均为正数,前4项的和为9,积为,则前4项倒数的和为()A.B.C.1 D.2【考点】等比数列的前n项和.【分析】设此等比数列的首项为a1,公比为q,前4项之和为S,前4项之积为P,前4项倒数之和为M,由等比数列性质推导出P2=()4,由此能求出前4项倒数的和.【解答】解:∵等比数列的各项均为正数,前4项的和为9,积为,∴设此等比数列的首项为a1,公比为q前4项之和为S,前4项之积为P,前4项倒数之和为M,若q=1,则,无解;若q≠1,则S=,M==,P=a14q6,∴()4=(a12q3)4=a18q12,P2=a18q12,∴P2=()4,∵,∴前4项倒数的和M===2.故选:D.11.tan20°+4sin20°的值为()A.B.C.D.【考点】三角函数的化简求值.【分析】首先利用弦切互化公式及正弦的倍角公式对原式进行变形,再两次运用和差化积公式,同时结合正余弦互化公式,转化为特殊角的三角函数值,则问题解决.【解答】解:tan20°+4sin20°========2sin60°=.故选B.12.已知A,B分别为椭圆的左、右顶点,不同两点P,Q在椭圆C上,且关于x轴对称,设直线AP,BQ的斜率分别为m,n,则当取最小值时,椭圆C的离心率为()A.B.C.D.【考点】椭圆的简单性质.【分析】设P(x0,y0),则Q(x0,﹣y0),=.A(﹣a,0),B(a,0),利用斜率计算公式肯定:mn=,=++=,令=t>1,则f(t)=+﹣2lnt.利用导数研究其单调性即可得出.【解答】解:设P(x0,y0),则Q(x0,﹣y0),=.A(﹣a,0),B(a,0),则m=,n=,∴mn==,∴=++=,令=t>1,则f(t)=+﹣2lnt.f′(t)=+1+t﹣=,可知:当t=时,函数f(t)取得最小值=++﹣2ln=2+1﹣ln2.∴=.∴=.故选:D.二.填空题:本大题共4小题,每小题5分.13.过原点作曲线y=e x的切线,则切线方程为y=ex .【考点】利用导数研究曲线上某点切线方程.【分析】欲求切点的坐标,先设切点的坐标为( x0,e x0),再求出在点切点( x0,e x0)处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=x0处的导函数值,再结合导数的几何意义即可求出切线的斜率.最后利用切线过原点即可解决问题.【解答】解:y′=e x设切点的坐标为(x0,e x0),切线的斜率为k,则k=e x0,故切线方程为y﹣e x0=e x0(x﹣x0)又切线过原点,∴﹣e x0=e x0(﹣x0),∴x0=1,y0=e,k=e.则切线方程为y=ex故答案为y=ex.14.某一简单几何体的三视图如图,则该几何体的外接球的表面积为25π.【考点】由三视图求面积、体积.【分析】几何体为底面为正方形的长方体,底面对角线为4,高为3.则长方体的对角线为外接球的直径.【解答】解:几何体为底面为正方形的长方体,底面对角线为4,高为3,∴长方体底面边长为2.则长方体外接球半径为r,则2r==5.∴r=.∴长方体外接球的表面积S=4πr2=25π.故答案为:25π.15.在△ABC中,内角A、B、C的对边分别为a、b、c,且a=4,b=3,c=2,若点D为线段BC上靠近B的一个三等分点,则AD=.【考点】解三角形.【分析】利用余弦定理求出cosB,再利用余弦定理解出AD.【解答】解:在△ABC中,由余弦定理得cosB==.在△ABD中,BD==.由余弦定理得:AD2=BD2+AB2﹣2BD•AB•cosB=.∴AD=.故答案为:.16.已知函数F(x)=e x满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,若∀x∈(0,2]使得不等式g(2x)﹣ah(x)≥0恒成立,则实数a的取值X 围是.【考点】函数奇偶性的性质.【分析】根据函数的奇偶性求出g(x),h(x)的表达式,然后将不等式恒成立进行参数分离,利用基本不等式进行求解即可得到结论.【解答】解:∵函数F(x)=e x满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,∴e x=g(x)+h(x),e﹣x=g(x)﹣h(x),∴g(x)=,h(x)=.∵∀x∈(0,2]使得不等式g(2x)﹣ah(x)≥0恒成立,即﹣a•≥0恒成立,∴a≤==(e x﹣e﹣x)+,设t=e x﹣e﹣x,则函数t=e x﹣e﹣x在(0,2]上单调递增,∴0<t≤e2﹣e﹣2,此时不等式t+≥2,当且仅当t=,即t=时,取等号,∴a≤2,故答案为:.三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程和演算步骤17.设数列{a n}的前n项和为S n,且2a n=S n+2.(Ⅰ)求{a n}的通项公式;(Ⅱ)设数列b n=,其前n项和为T n,求T n.【考点】数列的求和;数列递推式.【分析】(Ⅰ)运用n=1时,a1=S1,当n≥2时,a n=S n﹣S n﹣1,结合等比数列的通项公式,计算即可得到所求;(Ⅱ)求得b n=﹣,运用数列的求和方法:裂项相消求和,化简整理即可得到所求和.【解答】解:(Ⅰ)当n=1时,由2a1=S1+2=a1+2,得a1=2.当n≥2时,由,以及a n=S n﹣S n﹣1,两式相减可得,则数列{a n}是首项为2,公比为2的等比数列,故;(Ⅱ)由(Ⅰ)可得,故其前n项和化简可得T n =﹣.18.在某学校一次考试的语文与历史成绩中,随机抽取了25位考生的成绩进行分析,25位考生的语文成绩已经统计在茎叶图中,历史成绩如下:(Ⅰ)请根据数据在茎叶图中完成历史成绩统计;(Ⅱ)请根据数据完成语文成绩的频数分布表及语文成绩的频率分布直方图;语文成绩的频数分布表:语文成绩分组[50,60)[60,70)[70,80)[80,90)[90,100)[100,110)[110,120]频数(Ⅲ)设上述样本中第i位考生的语文、历史成绩分别为x i,y i(i=1,2,…,25).通过对样本数据进行初步处理发现:语文、历史成绩具有线性相关关系,得到:=x i=86, =y i=64,(x i ﹣)(y i ﹣)=4698,(x i ﹣)2=5524,≈0.85.①求y关于x的线性回归方程;②并据此预测,当某考生的语文成绩为100分时,该生历史成绩.(精确到0.1分)附:回归直线方程的斜率和截距的最小二乘法估计公式分别为:==, =﹣.【考点】线性回归方程;茎叶图.【分析】(Ⅰ)根据所给数据,可得历史成绩的茎叶图;(Ⅱ)根据所给数据,可得语文成绩的频数分布表及语文成绩的频率分布直方图;(Ⅲ)求出a,b,可得y关于x的线性回归方程,并据此预测当某考生的语文成绩为100分时,该考生的历史成绩.【解答】解:(Ⅰ)根据题意,在茎叶图中完成历史成绩统计,如图所示;(Ⅱ)语文成绩的频数分布表;语文成绩分组[50,60﹚[60,70﹚[70,80﹚[80,90﹚[90,100﹚[100,110﹚[110,120]频数 1 2 3 7 6 5 1 语文成绩的频率分布直方图:;(Ⅲ)由已知得b=0.85,a=64﹣0.85×86=﹣9.1,∴y=0.85x﹣9.1,∴x=100时,y=75.9≈76,预测当某考生的语文成绩为100分时,该考生的历史成绩为76分.19.如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点.已知PD=,CD=4,AD=.(Ⅰ)若∠ADE=,求证:CE⊥平面PDE;(Ⅱ)当点A到平面PDE的距离为时,求三棱锥A﹣PDE的侧面积.【考点】直线与平面垂直的判定;棱柱、棱锥、棱台的体积.【分析】(Ⅰ)在Rt△DAE中,求出BE=3.在Rt△EBC中,求出∠CEB=.证明CE⊥DE.PD ⊥CE.即可证明CE⊥平面PDE.(Ⅱ)证明平面PDE⊥平面ABCD.过A作AF⊥DE于F,求出AF.证明BA⊥平面PAD,BA⊥PA.然后求出三棱锥A﹣PDE的侧面积S侧=++.【解答】(本小题满分12分)解:(Ⅰ)在Rt△DAE中,AD=,∠ADE=,∴AE=AD•tan∠ADE=•=1.又AB=CD=4,∴BE=3.在Rt△EBC中,BC=AD=,∴tan∠CEB==,∴∠CEB=.又∠AED=,∴∠DEC=,即CE⊥DE.∵PD⊥底面ABCD,CE⊂底面ABCD,∴PD⊥CE.∴CE⊥平面PDE.…(Ⅱ)∵PD⊥底面ABCD,PD⊂平面PDE,∴平面PDE⊥平面ABCD.如图,过A作AF⊥DE于F,∴AF⊥平面PDE,∴AF就是点A到平面PDE的距离,即AF=.在Rt△DAE中,由AD•AE=AF•DE,得AE=•,解得AE=2.∴S△APD=PD•AD=××=,S△ADE=AD•AE=××2=,∵BA⊥AD,BA⊥PD,∴BA⊥平面PAD,∵PA⊂平面PAD,∴BA⊥PA.在Rt△PAE中,AE=2,PA===,∴S△APE=PA•AE=××2=.∴三棱锥A﹣PDE的侧面积S侧=++.…20.已知椭圆C: =1(a>b>0)的两焦点与短轴的一个端点的连线构成等边三角形,直线x+y+2﹣1=0与以椭圆C的右焦点为圆心,椭圆的长半轴为半径的圆相切.(1)求椭圆C的方程;(2)设点B,C,D是椭圆上不同于椭圆顶点的三点,点B与点D关于原点O对称,设直线CD,CB,OB,OC的斜率分别为k1,k2,k3,k4,且k1k2=k3k4.(i)求k1k2的值;(ii)求OB2+OC2的值.【考点】直线与圆锥曲线的综合问题.【分析】(1)设出椭圆右焦点坐标,由题意可知,椭圆右焦点F2到直线x+y+2﹣1=0的距离为a,再由椭圆C的两焦点与短轴的一个端点的连线构成等边三角形得到a,b,c的关系,结合焦点F2到直线x+y+2﹣1=0的距离为a可解得a,b,c的值,则椭圆方程可求;(2)(i)由题意设B(x1,y1),C(x2,y2),则D(﹣x1,﹣y1),由两点求斜率公式可得是,把纵坐标用横坐标替换可得答案;(ii)由k1k2=k3k4.得到.两边平方后用x替换y可得.结合点B,C在椭圆上得到.则OB2+OC2的值可求.【解答】解:(1)设椭圆C的右焦点F2(c,0),则c2=a2﹣b2(c>0),由题意,以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆的方程为(x﹣c)2+y2=a2,∴圆心到直线x+y+2﹣1=0的距离①,∵椭圆C的两焦点与短轴的一个端点的连线构成等边三角形,∴,a=2c,代入①式得,,故所求椭圆方程为;(2)(i)设B(x1,y1),C(x2,y2),则D(﹣x1,﹣y1),于是=;(ii)由(i)知,,故.∴,即,∴.又=,故.∴OB2+OC2=.21.设函数f(x)=lnx+,m∈R.(Ⅰ)当m=e(e为自然对数的底数)时,求f(x)的极小值;(Ⅱ)讨论函数g(x)=f′(x)﹣零点的个数;(Ⅲ)若对任意b>a>0,<1恒成立,求m的取值X围.【考点】利用导数研究函数的极值;函数恒成立问题;函数的零点.【分析】(Ⅰ)m=e时,f(x)=lnx+,利用f′(x)判定f(x)的增减性并求出f(x)的极小值;(Ⅱ)由函数g(x)=f′(x)﹣,令g(x)=0,求出m;设φ(x)=m,求出φ(x)的值域,讨论m的取值,对应g(x)的零点情况;(Ⅲ)由b>a>0,<1恒成立,等价于f(b)﹣b<f(a)﹣a恒成立;即h (x)=f(x)﹣x在(0,+∞)上单调递减;h′(x)≤0,求出m的取值X围.【解答】解:(Ⅰ)当m=e时,f(x)=lnx+,∴f′(x)=;∴当x∈(0,e)时,f′(x)<0,f(x)在(0,e)上是减函数;当x∈(e,+∞)时,f′(x)>0,f(x)在(e,+∞)上是增函数;∴x=e时,f(x)取得极小值为f(e)=lne+=2;(Ⅱ)∵函数g(x)=f′(x)﹣=﹣﹣(x>0),令g(x)=0,得m=﹣x3+x(x>0);设φ(x)=﹣x3+x(x>0),∴φ′(x)=﹣x2+1=﹣(x﹣1)(x+1);当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上是增函数,当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上是减函数;∴x=1是φ(x)的极值点,且是极大值点,∴x=1是φ(x)的最大值点,∴φ(x)的最大值为φ(1)=;又φ(0)=0,结合y=φ(x)的图象,如图;可知:①当m>时,函数g(x)无零点;②当m=时,函数g(x)有且只有一个零点;③当0<m<时,函数g(x)有两个零点;④当m≤0时,函数g(x)有且只有一个零点;综上,当m>时,函数g(x)无零点;当m=或m≤0时,函数g(x)有且只有一个零点;当0<m<时,函数g(x)有两个零点;(Ⅲ)对任意b>a>0,<1恒成立,等价于f(b)﹣b<f(a)﹣a恒成立;设h(x)=f(x)﹣x=lnx+﹣x(x>0),则h(b)<h(a).∴h(x)在(0,+∞)上单调递减;∵h′(x)=﹣﹣1≤0在(0,+∞)上恒成立,∴m≥﹣x2+x=﹣+(x>0),∴m≥;对于m=,h′(x)=0仅在x=时成立;∴m的取值X围是[,+∞).请从下面所给的22、23、24三题中选定一题作答,并用2B铅笔在答题卡上将所选题目对应的题号方框涂黑,按所涂题号进行评分;不涂、多涂均按所答第一题评分;多答按所答第一题评分.[选修4-1:几何证明选讲]22.如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,切点为A,PB交AC于点E,交⊙O于点D,PA=PE,∠ABC=45°,PD=1,DB=8.(1)求△ABP的面积;(2)求弦AC的长.【考点】与圆有关的比例线段.【分析】(1)利用圆的切线的性质,结合切割线定理,求出PA,即可求△ABP的面积;(2)由勾股定理得AE,由相交弦定理得EC,即可求弦AC的长.【解答】解:(1)因为PA是⊙O的切线,切点为A,所以∠PAE=∠ABC=45°,…又PA=PE,所以∠PEA=45°,∠APE=90°…因为PD=1,DB=8,所以由切割线定理有PA2=PD•PB=9,所以EP=PA=3,…所以△ABP的面积为BP•PA=…(2)在Rt△APE中,由勾股定理得AE=3…又ED=EP﹣PD=2,EB=DB﹣DE=8﹣2=6,所以由相交弦定理得EC•EA=EB•ED=12 …所以EC==2,故AC=5…[选修4-4:坐标系与参数方程]23.在直角坐标系xOy中,圆C的参数方程(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.(Ⅰ)求圆C的极坐标方程;(Ⅱ)直线l的极坐标方程是ρ(sinθ+)=3,射线OM:θ=与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.【考点】简单曲线的极坐标方程;直线与圆的位置关系.【分析】(I)圆C的参数方程(φ为参数).消去参数可得:(x﹣1)2+y2=1.把x=ρcosθ,y=ρsinθ代入化简即可得到此圆的极坐标方程.(II)由直线l的极坐标方程是ρ(sinθ+)=3,射线OM:θ=.可得普通方程:直线l,射线OM.分别与圆的方程联立解得交点,再利用两点间的距离公式即可得出.【解答】解:(I)圆C的参数方程(φ为参数).消去参数可得:(x﹣1)2+y2=1.把x=ρcosθ,y=ρsinθ代入化简得:ρ=2cosθ,即为此圆的极坐标方程.(II)如图所示,由直线l的极坐标方程是ρ(sinθ+)=3,射线OM:θ=.可得普通方程:直线l,射线OM.联立,解得,即Q.联立,解得或.∴P.∴|PQ|==2.[选修4-5:不等式选讲]24.已知函数f(x)=|x+2|﹣|x﹣1|.(Ⅰ)试求f(x)的值域;(Ⅱ)设若对∀s∈(0,+∞),∀t∈(﹣∞,+∞),恒有g(s)≥f(t)成立,试某某数a的取值X围.【考点】函数恒成立问题;函数的值域.【分析】(1)将含有绝对值的函数转化为分段函数,再求分段函数的值域;(2)恒成立问题转化成最小值最大值问题,即g(x)min≥f(x)max.【解答】解:(Ⅰ)函数可化为,∴f(x)∈[﹣3,3](Ⅱ)若x>0,则,即当ax2=3时,,又由(Ⅰ)知∴f(x)max=3若对∀s∈(0,+∞),∀t∈(﹣∞,+∞),恒有g(s)≥f(t)成立,即g(x)min≥f(x)max,∴,∴a≥3,即a的取值X围是[3,+∞).。
最新2021-2022年高考数学(理)教学案: 几何证明选讲 Word版含解析

第十六章几何证明选讲考纲展示命题探究考点一平行线截割定理与相似三角形1平行线等分线段定理定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.推论1经过三角形一边的中点与另一边平行的直线必平分第三边.推论2经过梯形一腰的中点,且与底边平行的直线平分另一腰.2平行线分线段成比例定理定理三条平行线截两条直线,所得的对应线段成比例.推论平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.3相似三角形的判定及性质(1)定义:对应角相等,对应边成比例的两个三角形叫做相似三角形.相似三角形对应边的比值叫做相似比.(2)一般三角形相似的判定定理预备定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.判定定理1两角对应相等,两三角形相似.判定定理2两边对应成比例且夹角相等,两三角形相似.引理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.判定定理3三边对应成比例,两三角形相似.(3)直角三角形相似的判定定理定理①如果两个直角三角形有一个锐角对应相等,那么它们相似.②如果两个直角三角形的两条直角边对应成比例,那么它们相似.定理如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.(4)相似三角形的性质定理①相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.②相似三角形周长的比等于相似比.③相似三角形面积的比等于相似比的平方.结论:相似三角形外接圆的直径比、周长比等于相似比,外接圆的面积比等于相似比的平方.4直角三角形的射影定理直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上的射影与斜边的比例中项.如图所示,在Rt△ABC中,AC⊥BC,CD⊥AB,则CD2=AD·BD,AC2=AD·AB,BC2=BD·AB.注意点相似三角形性质的作用(1)可用来证明线段成比例、角相等.(2)可间接证明线段相等.(3)为计算线段的长度及角的大小创造条件.(4)可计算周长、特征线段长等.1.思维辨析(1)如果两个三角形的三个内角分别相等,则它们相似.()(2)在△ABC 和△A ′B ′C ′中,若有AB A ′B ′=AC A ′C ′,则△ABC ∽△A ′B ′C ′.( )(3)直角三角形ABC 中,∠C =90°,CD ⊥AB ,则有△ABC ∽△ACD ,△ABC ∽△CBD .( )答案 (1)√ (2)× (3)√2.如图,在△ABC 中,∠AED =∠B ,DE =6,AB =10,AE =8,则BC 的长为( )A.154 B .7C.152D.245答案 C解析 由已知条件∠AED =∠B ,∠A 为公共角,所以△ADE ∽△ACB ,则有DE BC =AE AB ,从而BC =6×108=152.3.在Rt △ABC 中,∠C =90°,CD ⊥AB 于D ,若BD ∶AD =1∶3,则∠BCD =________.答案 π6解析 由射影定理得,CD 2=AD ·BD , 又∵BD ∶AD =1∶3,令BD =x ,AD =3x ,∴CD 2=AD ·BD =3x 2,∴CD =3x ,在Rt △CDB 中,tan ∠BCD =BD CD =x 3x =33,∴∠BCD=π6.[考法综述]考查三角形相似,利用平行线等分线段定理,三角形相似的性质,直角三角形射影定理证明两个三角形相似,通常与圆交错考查.命题法1平行线分线段成比例定理典例1如图,在△ABC中,点D是AC的中点,点E是BD的中点,AE交BC于点F,则BFFC的值为________.[解析]如图,过点D作DM∥AF交BC于点M.∵点E 是BD 的中点,∴在△BDM 中,BF =FM .又点D 是AC 的中点,∴在△CAF 中,CM =MF ,∴BF FC =BF FM +MC=12.[答案] 12【解题法】 平行线分线段成比例定理的应用以相似三角形为载体,通过三角形相似构建相应线段比,解题时要充分利用中点作辅助线,从而有效利用定理.命题法2 三角形相似的判定与性质典例2 (1)如图,在△ABC 中,AB =AC ,过点A 的直线与其外接圆交于点P ,交BC 的延长线于点D .①求证:PC AC =PD BD ;②若AC =3,求AP ·AD 的值.(2)如图,梯形ABCD 内接于⊙O ,AD ∥BC ,过点C 作⊙O 的切线,交BD 的延长线于点P ,交AD 的延长线于点E .①求证:AB 2=DE ·BC ;②若BD =9,AB =6,BC =9,求切线PC 的长.[解] (1)①证明:因为∠CPD =∠ABC ,∠PDC =∠PDC ,所以△DPC ∽△DBA ,所以PC AB =PD BD .又AB =AC ,所以PC AC =PD BD .②因为∠ABC +∠APC =180°,∠ACB +∠ACD =180°, ∠ABC =∠ACB ,所以∠ACD =∠APC .又∠CAP =∠DAC ,所以△APC ∽△ACD ,所以AP AC =AC AD .所以AP ·AD =AC 2=9.(2)①证明:∵AD ∥BC ,∴AB =CD ,∠EDC =∠BCD . 又PC 与⊙O 相切,∴∠ECD =∠DBC .∴△CDE ∽△BCD .∴DC BC =DE DC .∴CD 2=DE ·BC ,即AB 2=DE ·BC .②由①知,DE =AB 2BC =629=4,∵AD ∥BC ,∴△PDE ∽△PBC ,∴PD PB =DE BC =49.又∵PB -PD =9,∴PD =365,PB =815.∴PC 2=PD ·PB =365×815=54252.∴PC =545.【解题法】 相似三角形的判定定理的选择(1)已知有一角相等时,可选择判定定理一与判定定理二.(2)已知有两边对应成比例时,可选择判定定理二与判定定理三.(3)判定两个直角三角形相似时,首先看是否可以用判定直角三角形相似的方法来判定,如不能,再考虑用判定一般三角形相似的方法来判定.1.如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于点E,过点B的圆的切线与AD的延长线交于点F.在上述条件下,给出下列四个结论:①BD平分∠CBF;②FB2=FD·F A;③AE·CE =BE·DE;④AF·BD=AB·BF.则所有正确结论的序号是() A.①② B.③④C.①②③D.①②④答案 D解析由弦切角定理知∠FBD=∠BAD,∵AD 平分∠BAC ,∠CBD =∠CAD ,∴∠BAD =∠DBC .∴∠FBD =∠CBD ,即BD 平分∠CBF ,∴①正确;由切割线定理知,②正确;由相交弦定理知,AE ·ED =BE ·EC ,∴③不正确;∵△ABF ∽△BDF ,∴AB BD =AF BF ,∴AF ·BD =AB ·BF ,∴④正确.故选D.2.如图,在平行四边形ABCD 中,点E 在AB 上且EB =2AE ,AC 与DE 交于点F ,则△CDF 的面积△AEF 的面积=________.答案 9解析 ∵EB =2AE ,∴AB =3AE ,又△DFC ∽△EF A ,∴S △CDF S △AEF=DC 2AE 2=AB 2AE 2=9.3.如图,在△ABC 中,AB =AC ,△ABC 的外接圆⊙O 的弦AE 交BC 于点D .求证:△ABD ∽△AEB .证明因为AB=AC,所以∠ABD=∠C.又因为∠C=∠E,所以∠ABD=∠E,又∠BAE为公共角,可知△ABD∽△AEB.4.如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=23,求四边形EBCF 的面积.解(1)证明:由于△ABC是等腰三角形,AD⊥BC,所以AD是∠CAB的平分线.又因为⊙O分别与AB,AC相切于点E,F,所以AE=AF,故AD⊥EF.从而EF∥BC.(2)由(1)知,AE=AF,AD⊥EF,故AD是EF的垂直平分线.又EF为⊙O的弦,所以O在AD上.连接OE,OM,则OE⊥AE.由AG等于⊙O的半径得AO=2OE,所以∠OAE=30°.因此△ABC和△AEF 都是等边三角形.因为AE =23,所以AO =4,OE =2.因为OM =OE =2,DM =12MN =3,所以OD =1.于是AD =5,AB =1033.所以四边形EBCF 的面积为12×⎝ ⎛⎭⎪⎫10332×32-12×(23)2×32=1633.5.如图,AB 为⊙O 的直径,直线CD 与⊙O 相切于E ,AD 垂直CD 于D ,BC 垂直CD 于C ,EF 垂直AB 于F ,连接AE ,BE .证明:(1)∠FEB =∠CEB ;(2)EF2=AD·BC.证明(1)由直线CD与⊙O相切,得∠CEB=∠EAB.由AB为⊙O的直径,得AE⊥EB,从而∠EAB+∠EBF=π2.,又EF⊥AB,得∠FEB+∠EBF=π2从而∠FEB=∠EAB.故∠FEB=∠CEB.(2)由BC⊥CE,EF⊥AB,∠FEB=∠CEB,BE是公共边,得Rt △BCE≌Rt△BFE,所以BC=BF.类似可证:Rt△ADE≌Rt△AFE,得AD=AF.又在Rt△AEB中,EF⊥AB,故EF2=AF·BF,所以EF2=AD·BC.考点二圆的初步1圆周角定理圆上一条弧所对的圆周角等于它所对的圆心角的一半.2圆心角定理圆心角的度数等于它所对弧的度数.推论1同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.推论2半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.3圆内接四边形的性质与判定定理性质定理1圆的内接四边形的对角互补.性质定理2圆内接四边形的外角等于它的内角的对角.判定定理如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.判定定理的推论如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.4圆的切线的性质及判定定理性质定理圆的切线垂直于经过切点的半径.推论1经过圆心且垂直于切线的直线必经过切点.推论2经过切点且垂直于切线的直线必经过圆心.判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线.5弦切角定理弦切角等于它所夹的弧所对的圆周角.6与圆有关的比例线段相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等.割线定理从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.注意点圆中的有关定理可以解决的问题类型相交弦定理、切割线定理主要用于与圆有关的比例线段的计算与证明,解决问题时要注意相似三角形的知识及相关圆的性质的综合应用.圆周角定理与弦切角定理多用于证明角的关系,从而证明三角形全等或相似,也可用于求线段的长或角的大小及与圆的切线有关的问题.1.思维辨析(1)相同长度的弧所对的圆心角相等.()(2)任何四边形都有外接圆.( )(3)同一段弧所对的圆周角是圆心角的12.( )(4)圆的切线长是割线与圆交点的两条线段长的比例中项.( ) 答案 (1)× (2)× (3)√ (4)×2.如图,过点P 的直线与⊙O 相交于A ,B 两点.若P A =1,AB =2,PO =3,则⊙O 的半径等于________.答案6解析 设圆的半径为r ,则(3-r )(3+r )=1×3,即r 2=6,解得r= 6.3.如图,过点D 作圆的切线切于B 点,作割线交圆于A ,C 两点,其中BD =3,AD =4,AB =2,则BC =________.答案 32解析 由切割线定理,得BD 2=CD ·AD ,得CD =94.又∵∠A =∠DBC ,∠D =∠D ,∴△ABD ∽△BCD ,BD CD =AB BC ,解得BC =32.[考法综述] 利用圆的切线的性质、切割线定理、相交弦定理确定圆中有关线段之间的关系,解题中一般应用弦切角定理,圆周角定理等确定角之间的关系,结合三角形相似的判定与性质或三角形的其他定理确定边角之间的关系,证明有关线段的等式或者求线段的长.命题法圆中的有关定理及其应用典例如图所示,⊙O1与⊙O2相交于A,B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC相交于点P.(1)求证:AD∥EC;(2)若AD是⊙O2的切线,且P A=6,PC=2,BD=9,求AD的长.[解](1)证明:如图所示,连接AB,CE.∵AC是⊙O1的切线,∴∠BAC=∠ADB.又∠BAC=∠CEP,∴∠ADB=∠CEP,∴AD∥EC.(2)解法一:∵P A是⊙O1的切线,PD是⊙O1的割线,∴P A2=PB·PD,即62=PB·(PB+9).∴PB=3或PB=-12(舍去).在⊙O2中由相交弦定理,得P A·PC=BP·PE,∴PE =4.∴DE =BD +PB +PE =9+3+4=16.∵AD 是⊙O 2的切线,DE 是⊙O 2的割线,∴AD 2=DB ·DE =9×16=144.∴AD =12.解法二:设BP =x ,PE =y .∵P A =6,PC =2,∴由相交弦定理得P A ·PC =BP ·PE ,即xy =12 ①∵AD ∥EC ,∴DP PE =APPC ,∴9+x y =62 ②联立①②,解得⎩⎨⎧x =3y =4或⎩⎨⎧x =-12y =-1(舍去),∴DE =9+x +y =16.∵AD 是⊙O 2的切线,DE 是⊙O 2的割线,∴AD2=DB·DE=9×16=144,∴AD=12.【解题法】应用圆中的有关定理的解题思路圆中的有关定理为圆中证明等积式和有关计算提供了有力的方法和工具,应用时一方面要熟记定理的等积式的结构特征,另一方面,在与定理相关的图形不完整时,要借助辅助线补齐相应部分.处理与圆有关的比例线段的常见思路:(1)利用相似三角形.(2)利用圆的有关定理.(3)利用平行线分线段成比例定理及推论.(4)利用面积关系.1.如图,在圆O 中,M ,N 是弦AB 的三等分点,弦CD ,CE分别经过点M ,N .若CM =2,MD =4,CN =3,则线段NE 的长为( )A.83 B .3 C.103 D.52 答案 A解析 由题意可得CM ·MD =AM ·MB ,则2×4=2AM 2,AM =2.因为M 、N 是弦AB 的三等分点,所以AM =NB ,AN =MB ,又CN ·NE=AN ·NB ,即3NE =4×2,解得NE =83.2.如图所示,已知AB 是圆O 的直径,AB =4,EC 是圆O 的切线,切点为C ,BC =1.过圆心O 作BC 的平行线,分别交EC 和AC 于点D 和点P ,则OD =________.答案 8解析 由题意得OP =12BC =12,OA =2,于是P A =CP =22-⎝ ⎛⎭⎪⎫122=152.因为∠DCP =∠B =∠POA ,又∠DPC =∠APO ,所以△DCP ∽△AOP ,故PD P A =PC PO ,即PD =15212×152=152,所以OD =152+12=8.3.如图,圆O 的弦AB ,CD 相交于点E ,过点A 作圆O 的切线与DC的延长线交于点P,若P A=6,AE=9,PC=3,CE∶ED=2∶1,则BE=________.答案 2解析由切割线定理得P A2=PC·PD,得PD=P A2PC =623=12,∴CD=PD-PC=12-3=9,即CE+ED=9,∵CE∶ED=2∶1,∴CE=6,ED=3.由相交弦定理得AE·EB=CE·ED,即9EB=6×3,得EB=2.4.如图,△ABC 中,BC =6,以BC 为直径的半圆分别交AB ,AC 于点E ,F ,若AC =2AE ,则EF =________.答案 3解析 ∵四边形BCFE 是圆内接四边形,∴∠C +∠BEF =180°,∴∠C =∠AEF ,∴△AEF ∽△ACB ,∴AE AC =EF BC =12,∴EF =3.5.如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.(1)若D为AC的中点,证明:DE是⊙O的切线;(2)若OA=3CE,求∠ACB的大小.解(1)证明:连接AE,由已知得,AE⊥BC,AC⊥AB.在Rt△AEC中,由已知得,DE=DC,故∠DEC=∠DCE.连接OE,则∠OBE=∠OEB.又∠ACB+∠ABC=90°,所以∠DEC+∠OEB=90°,故∠OED=90°,DE是⊙O的切线.(2)设CE=1,AE=x,由已知得AB=23,BE=12-x2.由射影定理可得,AE2=CE·BE,所以x2=12-x2,即x4+x2-12=0.可得x=3,所以∠ACB=60°.6.如图所示,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F.证明:(1)∠MEN+∠NOM=180°;(2)FE·FN=FM·FO.证明(1)如图所示.因为M,N分别是弦AB,CD的中点,所以OM⊥AB,ON⊥CD,即∠OME=90°,∠ENO=90°,因此∠OME +∠ENO=180°.又四边形的内角和等于360°,故∠MEN+∠NOM=180°.(2)由(1)知,O,M,E,N四点共圆,故由割线定理即得FE·FN =FM·FO.7.如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE ,垂足为C .(1)证明:∠CBD =∠DBA ;(2)若AD =3DC ,BC =2,求⊙O 的直径.解 (1)证明:因为DE 为⊙O 的直径,则∠BED +∠EDB =90°,又BC ⊥DE ,所以∠CBD +∠EDB =90°,从而∠CBD =∠BED .又AB 切⊙O 于点B ,得∠DBA =∠BED ,所以∠CBD =∠DBA .(2)由(1)知BD 平分∠CBA ,则BA BC =AD CD =3,又BC =2,从而AB =3 2.所以AC=AB2-BC2=4,所以AD=3.由切割线定理得AB2=AD·AE,即AE=AB2=6,AD故DE=AE-AD=3,即⊙O的直径为3.8.如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.(1)证明:∠D=∠E;(2)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.证明(1)由题设知A,B,C,D四点共圆,∴∠D=∠CBE,又BC=EC,∴∠CBE=∠E,∴∠D=∠E.(2)设BC的中点为N,连接MN,则由MB=MC,知MN⊥BC,故O在直线MN上.又AD不是⊙O的直径,M为AD的中点,故OM⊥AD,即MN⊥AD.∴AD∥BC,∴∠A=∠CBE.又∠CBE=∠E,故∠A=∠E,由(1)知,∠D=∠E,∴△ADE为等边三角形.9.如图,P是⊙O外一点,P A是切线,A为切点,割线PBC与⊙O 相交于点B,C,PC=2P A,D为PC的中点,AD的延长线交⊙O于点E.证明:(1)BE=EC;(2)AD·DE=2PB2.证明(1)连接AB,AC,由题设知P A=PD,故∠P AD=∠PDA.因为∠PDA=∠DAC+∠DCA,∠P AD=∠BAD+∠P AB,∠DCA=∠P AB,所以∠DAC =∠BAD ,从而BE ︵=EC ︵.因此BE =EC .(2)由切割线定理得P A 2=PB ·PC .因为P A =PD =DC ,所以DC =2PB ,BD =PB ,由相交弦定理得AD ·DE =BD ·DC ,所以AD ·DE =2PB 2.10.如图,EP 交圆于E ,C 两点,PD 切圆于D ,G 为CE 上一点且PG =PD ,连接DG 并延长交圆于点A ,作弦AB 垂直EP ,垂足为F .(1)求证:AB为圆的直径;(2)若AC=BD,求证:AB=ED.证明(1)∵PD=PG,∴∠PDG=∠PGD,由于PD为切线,故∠PDA=∠DBA,又∠PGD=∠EGA,∴∠DBA =∠EGA.∴∠DBA+∠BAD=∠EGA+∠BAD,从而∠BDA=∠PF A.由AF⊥EP,得∠PF A=90°,∴∠BDA=90°,故AB是直径.(2)连接BC,DC.∵AB是直径,∴∠BDA=∠ACB=90°,在Rt△BDA与Rt△ACB中,AB=BA,AC=BD.∴Rt△BDA≌Rt△ACB,∴∠DAB=∠CBA.又∠DCB=∠DAB.∴∠DCB=∠CBA,∴DC∥AB.∵AB⊥EP,∴DC⊥EP,∠DCE为直角.∴ED为直径,由(1)得ED=AB.如图,在△ABC中,D为BC的中点,E在CA上,且AE=2CE,AD,BE交于F,求AF FD.[错解][错因分析]错误得出三角形相似,比例关系混乱.[正解]取BE的中点G,连接DG在△BCE中,∵D,G是BC、BE的中点,∴DG∥EC,且DG=12EC,又∵AE=2CE,且DG=12EC,∴△DFG∽△AFE,∴AFFD =EFFG=AEDG=AE12EC=4.[心得体会]………………………………………………………………………………………………时间:90分钟基础组1.[2021·枣强中学期末]如图,等边三角形DEF内接于△ABC,且DE∥BC,已知AH⊥BC于点H,BC=4,AH=3,则△DEF的边长为________.答案 43解析 设DE =x ,AH 交DE 于点M ,显然MH 的长度与等边三角形DEF 的高相等,又DE ∥BC ,则DE BC =AM AH =AH -MH AH ,∴x 4=3-32x 3=2-x2,解得x =43.2.[2021·衡水二中仿真]如图,在△ABC 中,DE ∥BC ,EF ∥AB ,AD =5,DB =3,FC =2,则BF =________.答案 103解析 由平行线的性质可得BF FC =AE EC =AD BD =53,所以BF =53FC =103.3.[2021·枣强中学期中]如图所示,圆的内接三角形ABC 的角平分线BD 与AC 交于点D ,与圆交于点E ,连接AE ,已知ED =3,BD =6,则线段AE 的长为________.答案 3 3解析 易知∠CBE =∠CAE =∠ABE ,又∠E =∠E ,所以△EAD ∽△EBA ,所以AE EB =EDAE ,所以AE 2=EB ·ED =27,所以AE =3 3.4.[2021·冀州中学猜题]如图,AB 与CD 相交于点E ,过E 作BC 的平行线与AD 的延长线交于点P ,已知∠A =∠C ,PD =2DA =2,则PE =________.答案 6解析因为PE∥BC,所以∠C=∠PED,所以∠A=∠PED,又∠P 是公共角,所以△PED∽△P AE.则PD PE =PEP A,即PE2=P A·PD.由PD=2DA=2,可得PE2=6.∴PE= 6.5.[2021·武邑中学仿真]如图,过圆O外一点P作圆O的割线PBA与切线PE,E为切点,连接AE、BE,∠APE的平分线分别与AE、BE相交于点C、D,若∠AEB=40°,则∠PCE=________.答案70°解析由PE为切线可得∠PEB=∠P AE,由PC为角平分线可得∠EPC=∠APC.由△P AE的内角和为180°,得2(∠APC+∠BAE)+40°=180°,所以∠APC+∠BAE=70°,故∠PCE=∠APC+∠BAE=70°.6.[2021·衡水中学模拟]如图,已知四边形PQRS是圆内接四边形,∠PSR=90°,过点Q作PR,PS的垂线,垂足分别为H,K,HK 与QS交于点T,QK交PR于点M.求证:(1)QM HM =MP MK ; (2)QT =TS .证明 (1)因为∠QHP =∠QKP ,所以Q ,H ,K ,P 都在以QP 为直径的圆上,即Q ,H ,K ,P 四点共圆,由相交弦定理得QM ·MK =HM ·MP ,所以QM HM =MP MK .(2)因为Q ,H ,K ,P 四点共圆,所以∠HKS =∠HQP .因为∠PSR=90°,所以PR 为圆的直径,所以∠PQR =90°,∠QRH =∠HQP .而∠QSP =∠QRH ,综上可得∠QSP =∠HKS ,所以TS =TK .又∠SKQ =90°,所以∠SQK =∠TKQ ,所以QT =TK ,所以QT =TS .7.[2021·冀州中学期中]如图,在等腰梯形ABCD中,AD∥BC,过D点作AC的平行线DE,交BA的延长线于点E,求证:(1)△ABC≌△DCB;(2)DE·DC=AE·BD.证明(1)因为四边形ABCD为等腰梯形,所以AB=DC,∠ABC =∠DCB,又BC=BC,所以△ABC≌△DCB.(2)因为AD∥BC,DE∥AC,所以∠EDA=∠ACB.又由△ABC≌△DCB 知∠ACB=∠DBC,所以∠EDA=∠DBC.由AD∥BC得∠EAD=∠ABC,=又∠ABC=∠DCB,所以∠EAD=∠DCB.所以△AED∽△CDB,所以DEBDAE,所以DE·DC=AE·BD.DC8.[2021·衡水中学仿真]由⊙O外一点P引⊙O的切线P A,PB,过P引割线PCD交⊙O于点C,D,OP与AB交于点E.求证:∠CEO+∠CDO=180°.证明如图,连接AO,则AO⊥P A,又AE⊥OP,则P A2=PE·PO.因为P A2=PC·PD,所以PE·PO=PC·PD,从而C,D,O,E四点共。
【世纪金榜】人教版第一轮复习理科数学教师用书配套课件选修全等与相似

.
【加固训练】如图所示,在△ABC中,∠CAB=90°,AD⊥BC于D,BE是∠ABC
的平分线,交AD于F,求证:
DF=AE . AF EC
【证明】由三角形的内角平分线定理得,
在△ABD中, DF=BD .①
AF AB
在△ABC中, AE=AB,②
EC BC
在Rt△ABC中,由射影定理知,AB2=BD·BC,
系列4部分 选修4-1 几何证明选讲 第一节 全等与相似
【知识梳理】 1.图形变化的不变性与平移、旋转、反射 (1)图形变化的不变性: ①图形在变化过程中,有些性质改变了,有些性质仍然保持_不__变__. ②常见的图形变化,如平移、_旋__转__、_轴__对__称__、相似(包括位似).
(2)平移、旋转、反射: ①平移变换:图形的_平__移__过程称为平移变换. ②旋转变换:图形的_旋__转__过程称为旋转变换. ③反射变换:一个图形F绕一条直线l翻转__1_8_0_°_得到另外一个图形 F′,则F与F′关于l_对__称__,这种图形的变化过程称为反射变换,直线 l称为反射轴.
4.直角三角形的射影定理 直角三角形的每一条直角边是它在斜边上的射影与斜边的_比__例__中__项__, 斜边上的高是两条直角边在斜边上射影的_比__例__中__项__.
【小题快练】(本部分为教师用书独具)
1.(2015·天津模拟)如图所示,在平行四边形ABCD中,AE∶EB=1∶2,
若S△AEF=6cm2,则S△ADF为 (
【变式训练】如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边 上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为F,G.
(1)求证: AF =CG .
教师版高中数学必修+选修知识点全归纳

x ,都有 f x f x ,那么就称函数 f x 为
偶函数.偶函数图象关于 y 轴对称. 2、 一般地,如果对于函数 f x 的定义域内任意一个
x ,都有 f x f x ,那么就称函数 f x 为
奇函数.奇函数图象关于原点对称. 知识链接:函数与导数 1、函数 y f ( x) 在点 x0 处的导数的几何意义: 函数 y f ( x) 在点 x0 处的导数是曲线 y f ( x) 在
当 n 为偶数时, a a .
n n
3、 我们规定:
n m n ⑴am a
a 0, m, n N
⑵a
n
*
, m 1;
M log a M log a N ; N
n
⑶ log a M
n log a M .
1 n 0 ; an
r s
4、 运算性质: ⑴a a a
r s
5、换底公式: log a b
log c b log c a
a 0, r, s Q ;
a 0, a 1, c 0, c 1, b 0 .
3
教师版高中数学必修+选修知识点全归纳 |
6、重要公式: log an b m 7、 倒数关系:log a b
必修 1 数学知识点
第一章:集合与函数概念 § 1.1.1、集合 1、 把研究的对象统称为元素,把一些元素组成的总 体叫做集合。集合三要素: 确定性、互异性、无 序性。 2、 只要构成两个集合的元素是一样的,就称这两个 集合相等。 3、 常见集合:正整数集合: N * 或 N ,整数集合:
f ( x1 ) f ( x2 ) 0 f ( x)在[a, b] 上是增函数; f ( x1 ) f ( x2 ) 0 f ( x)在[a, b] 上是减函数.
高二数学几何选讲试题答案及解析

高二数学几何选讲试题答案及解析于点,过点作两1.如图,已知⊙与⊙相交于、两点,过点A作⊙的切线交⊙O2圆的割线,分别交⊙、⊙于点、,与相交于点.(1)求证:;(2)若是⊙的切线,且,,求的长.【答案】(1)证明见解析;(2)【解析】(1)圆的切线的性质定理圆的切线垂直于过切点的半径,推论1经过圆心且垂直于切线的直线必过切点,推论2经过切点且垂直于切线的直线必过圆心;(2)圆的切线的性质定理经过半径的外端并且垂直于这条半径的直径是圆的切线;若已知条件中直线与圆的公共点不明确,则应过圆心作直线的垂线,得到垂线段,设法证明这条垂线段的长等于圆的半径;(3)掌握与圆有关的比例线段,如相交弦定理,割线定理,切割线定理,切线长定理.试题解析:解:(I)∵AC是⊙O的切线,∴∠BAC=∠D,1又∵∠BAC=∠E,∴∠D=∠E,∴AD∥EC. 5分(II)设BP=x,PE=y,∵PA=6,PC=2,∴=12 ①∵AD∥EC,∴,∴②由①、②解得(∵x>0,y>0)∴DE=9+x+y=16,∵AD是⊙O的切线,∴AD2=DB·DE=9×16,∴AD=12. 11分2【考点】(1)证明直线与直线平行;(2)求切线长.2.如图,在△ABC中,AB=8,AC=7,BC=6,D是AB的中点,∠ADE=∠ACB,则DE=_________.【答案】.【解析】首先由知,∽,所以.然后因为AB=8,D是AB的中点,所以.又AC=7,BC=6,所以,即.【考点】相似三角形的性质.3.如图,AC为⊙O的直径,OB⊥AC,弦BN交AC于点M.若OC=,OM=1,则MN=_________.【答案】1.【解析】因为AC为⊙O的直径,OB⊥AC,且OC=,OM=1,所以,. 设,由相交弦定理知,即,所以,即.【考点】与圆有关的比例线段.4.如图,四边形是圆的内接四边形,延长和相交于点,若,,则的值为()A.B.C.D.【答案】B【解析】四边形是圆的内接四边形,它的两对对角互补,进而得到∽,因而有,故选择B.【考点】平面几何中的圆与四边形.5.如图在△中,∥,,交于点,则图中相似三角形的对数为( ).A.1B.2C.3D.4【答案】B【解析】,;又,,故选B.【考点】相似三角形.6.如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.(1)求证:△ABE≌△ACD;(2)若AB=6 cm,BC=4 cm,求AE的长.【答案】(1)见解析;(2).【解析】(1)欲证三角形全等,需牢牢掌握这种证明方法和所需要的条件.本小题,(已知),下寻找另外的边和角,考虑到这里有圆,所以运用同弧所对应的圆周角相等可得(弧所对),接着证明(其他角和边不好证,同时这里有弦切角可以利用).(2)欲求,因,则可转化为求,考虑到,需将联系起来就得考虑三角形相似.注意到,.试题解析:(1)证明因为XY是⊙O的切线,所以.因为,所以,∴. 2分因为,所以. 4分因为,又因为,所以. 5分(2)解因为,,所以, 7分所以,即 8分因为,,所以.所以AE. 10分【考点】(1)三角形全等的证明;(2)三角形相似的证明与应用;(3)圆性质的应用.7.如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=,AF∶FB∶BE=4∶2∶1,若CE与圆相切,求线段CE的长.【答案】【解析】利用相交弦定理可得到的等量关系,并结合已知条件可计算出,利用切割线定理可得到的等量关系,并结合前面所得可得结果.试题解析:由相交弦定理得,由于,可解得,所以.由切割线定理得,即.【考点】相交弦定理,切割线定理.8.若一个直角三角形的一条直角边为3 cm,斜边上的高为2.4 cm,则这个直角三角形的面积为A.7.2 cm2B.6 cm2C.12 cm2D.24 cm2【答案】B【解析】长为3 cm的直角边在斜边上的射影为=1.8 (cm),故由射影定理知斜边长为=5 (cm),∴三角形的面积为×5×2.4=6 (cm2).9.如图,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD=,点E,F分别为线段AB,AD的中点,则EF=________.【答案】【解析】连接BD、DE,由题意可知DE⊥AB,DE=a,即BC=DE=a,∴BD==a,∴EF=BD=.10.如图所示,圆内的两条弦AB、CD相交于圆内一点P,已知PA=PB=4,PC=PD.求CD 的长.【答案】10【解析】解设CD=x,则PD=x,PC=x.由相交弦定理,得PA·PB=PC·PD,∴4×4=x·x,x=10.∴CD=10.11.如图所示,PA是⊙O的切线,切点为A,PA=2.AC是⊙O的直径,PC与⊙O交于点B,PB=1,则⊙O的半径r=________.【答案】【解析】依题意,△PBA∽△ABC,所以=,即r===.12.如图所示,P、Q分别在BC和AC上,BP∶CP=2∶5,CQ∶QA=3∶4,则等于A.3∶14B.14∶3C.17∶3D.17∶14【答案】B【解析】过Q点作QM∥AP交BC于M,则==,又∵=,∴=.又==,==,∴=,∴=.13.如图所示,点D、E分别在AB、AC上,下列条件能判定△ADE与△ACB相似的有①∠AED=∠B②=③=④DE∥BCA.1个 B.2个 C.3个 D.4个【答案】C【解析】由判定定理1知①正确,由判定定理2知②正确,由预备定理1知④正确,③不符合相似三角形的判定定理,故不正确,从而选C.14.如图所示,在直角梯形ABCD中,AB=7,AD=2,BC=3.设边AB上的一点P,使得以P、A、D为顶点的三角形和以P、B、C为顶点的三角形相似,那么这样的点P有A.1个 B.2个C.3个 D.4个【答案】C【解析】设AP=x,则PB=7-x.(1)若△PAD∽△PBC,则=,即=,得x=<7,符合条件.(2)若△PAD∽△CBP,即=,x2-7x+6=0,解得x1=1,x2=6也符合条件,故满足条件的点P 有3个.15. 在四边形ABCD 中,∠A =135°,∠B =∠D =90°,BC =2,AD =2,则四边形ABCD 的面积是______. 【答案】4【解析】因∠B =∠D =90°,于是设想构造直角三角形,延长BA 与CD 的延长线交于E ,则得到Rt △BCE 和Rt △ADE ,由题目条件知,△ADE 为等腰直角三角形,所以DE =AD =2,所以S △ADE =×2×2=2. 又可证Rt △EBC ∽Rt △EDA , 所以=2=2=3.∴S △EBC =3S △EDA ,∴S 四边形ABCD =S △EBC -S △ADE =4.16. 如图所示,D 为△ABC 中BC 边上的一点,∠CAD =∠B ,若AD =6,AB =8,BD =7,求DC 的长.【答案】9【解析】解 ∵∠CAD =∠B ,∠C =∠C , ∴△CAD ∽△CBA.∴==.∴AC =,AC =.∴=.设CD =x , 则=,解得x =9.故DC =9.17. 如图所示,已知⊙O 的两条弦AB 、CD 相交于AB 的中点E ,且AB =4,DE =CE +3,则CD 的长为________.【答案】5【解析】由相交弦定理知 EA·EB =EC·ED. (*)又∵E 为AB 中点,AB =4,DE =CE +3, ∴(*)式可化为22=EC(CE +3)=CE 2+3CE , ∴CE =-4(舍去)或CE =1.∴CD =DE +CE =2CE +3=2+3=5.18. 如图所示,已知BC 是⊙O 的弦,P 是BC 延长线上一点,PA 与⊙O 相切于点A ,∠ABC =25°,∠ACB=80°,求∠P的度数.【答案】55°【解析】解因为PA与⊙O相切于点A,所以∠PAC=∠ABP=25°.又因为∠ACB=80°,所以∠ACP=100°.又因为∠PAC+∠PCA+∠P=180°,所以∠P=180°-100°-25°=55°.19.(拓展深化)如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.(1)求证:△ABE≌△ACD;(2)若AB=6 cm,BC=4 cm,求AE的长.【答案】(1)见解析 (2)cm【解析】(1)证明因为XY是⊙O的切线,所以∠1=∠2.因为BD∥XY,所以∠1=∠3,∴∠2=∠3.因为∠3=∠4,所以∠2=∠4.因为∠ABD=∠ACD,又因为AB=AC,所以△ABE≌△ACD.(2)解因为∠3=∠2,∠ABC=∠ACB,所以△BCE∽△ACB,=,AC·CE=BC2.因为AB=AC=6 cm,BC=4 cm,所以6·(6-AE)=16.所以AE=cm.20.如图所示,在Rt△ABC中,∠C=90°,AC=4,BC=3,以BC上一点O为圆心作⊙O与AB相切于E,与AC相切于C,又⊙O与BC的另一个交点为D,则线段BD的长为A.1B.C.D.【答案】C【解析】⊙O与AC相切于C,则∠ACB=90°,又AC=4,BC=3,∴AB=5,连接OE,且设⊙O的半径为R,则由△OEB∽△ACB,∴OB==R,∴BC=OC+OB=R+R=R=3,∴R=,∴BD=BC-2R=3-=.21.若两条直线(a+2)x+(1-a)y-3=0,(a-1)x+(2a+3)y+2=0与两坐标轴围成的四边形有一个外接圆,则实数a=________.【答案】1或-1【解析】由圆内接四边形的性质,知(a+2)(a-1)+(1-a)·(2a+3)=0,整理得a2=1,∴a=±1. 22.(拓展深化)如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.(1)证明:B、D、H、E四点共圆;(2)证明:CE平分∠DEF.【答案】见解析【解析】证明(1)在△ABC中,因为∠B=60°,所以∠BAC+∠BCA=120°.因为AD,CE是角平分线,所以∠HAC+∠HCA=60°,故∠AHC=120°.于是∠EHD=∠AHC=120°.因为∠EBD+∠EHD=180°,所以B、D、H、E四点共圆.(2)连接BH,则BH为∠ABC的平分线,得∠HBD=30°.由(1)知B、D、H、E四点共圆.所以∠CED=∠HBD=30°.又∵∠AHE=∠EBD=60°,由已知可得EF⊥AD,可得∠CEF=30°,所以CE平分∠DEF.23.如图,点A、B、C是圆O上的点,且AB=4,∠ACB=30°,则圆O的面积等于A.4π B.8πC.12π D.16π【答案】D【解析】连接OA、OB,∵∠ACB=30°,∴∠AOB=60°,又∵OA=OB,∴△AOB为等边三角形,又AB=4,∴OA=OB=4,∴S=π·42=16π.⊙O24.在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D.若BC=m,∠B=α,则AD的长为A.m sin2α B.m cos2αC.m sin αcos α D.m sin αtan α【答案】C【解析】由射影定理,得AB2=BD·BC,AC2=CD·BC,即m2cos2α=BD·m,m2sin2α=CD·m,即BD=mcos2α,CD=msin2α.又∵AD2=BD·DC=m2cos2αsin2α,∴AD=mcos αsin α.故选C.25.如图,在正方形ABCD中,E为AB的中点,AF⊥DE于点O,则等于________.【答案】【解析】在Rt△DAO及Rt△DEA中,∠ADO为公共角,∴Rt△DAO∽Rt△DEA,∴=,即=.∵E为AB的中点,∴==,∴=.26. (拓展深化)如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α.且DM交AC于F,ME交BC于G,(1)写出图中三对相似三角形,并证明其中的一对;(2)连接FG,如果α=45°,AB=4,AF=3,求FG的长.【答案】(1)△AMF∽△BGM,△DMG∽△DBM,△EMF∽EAM,证明见解析 (2)【解析】解(1)△AMF∽△BGM,△DMG∽△DBM,△EMF∽EAM.以下证明:△AMF∽△BGM.∵∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B,∴△AMF∽△BGM.(2)当α=45°时,可得AC⊥BC且AC=BC.∵M为AB的中点,∴AM=BM=2.又∵△AMF∽△BGM,∴=∴BG===.又AC=BC=4×sin 45°=4,∴CG=4-=.∵CF=4-3=1,∴FG===.27.如图所示,已知DE∥BC,BF∶EF=3∶2,则AC∶AE=________,AD∶DB=________.【答案】3∶22∶1【解析】∵DE∥BC,∴==.∵BF∶EF=3∶2,∴==.∴AC∶AE=3∶2.又DE∥BC,得AB∶AD=3∶2,即=.∴=.即==2,即=2.∴AD∶BD=2∶1.28.如图,以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED,DC的延长线交BE于点F,求证:EF=BF.【答案】见解析【解析】证明如图所示,连接AE交DC于O.∵四边形ACED是平行四边形.∴O是AE的中点.∵在梯形ABCD中,DC∥AB,在△EAB中,OF∥AB,又∵O是AE的中点,∴F是EB的中点,∴EF=BF.29.如图甲,四边形是等腰梯形,.由4个这样的等腰梯形可以拼出图乙所示的平行四边形,则四边形中度数为 ( )A.B.C.D.【答案】C【解析】由于上底和两腰长已知,故要求梯形面积,关键是要找出底边上和高,由于图形中无法再分析出边与边的关系,所以我们可以从角的方向入手,求梯形的内角。
高中数学第十一章 几何证明选讲(选修4-1)

第十一章⎪⎪⎪几何证明选讲(选修4-1)第一节 相似三角形的判定及有关性质1.平行线的截割定理 (1)平行线等分线段定理定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.推论1:经过三角形一边的中点与另一边平行的直线必平分第三边. 推论2:经过梯形一腰的中点,且与底边平行的直线平分另一腰. (2)平行线分线段成比例定理定理:三条平行线截两条直线,所得的对应线段成比例.推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例. 2.相似三角形的判定定理(1)判定定理1:两角对应相等,两三角形相似.(2)判定定理2:两边对应成比例且夹角相等,两三角形相似. (3)判定定理3:三边对应成比例,两三角形相似. 3.相似三角形的性质定理(1)性质定理:相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.(2)推论:相似三角形外接圆的直径比、周长比等于相似比,外接圆的面积比等于相似比的平方.4.直角三角形相似的判定定理(1)判定定理1:如果两个直角三角形有一个锐角对应相等,那么它们相似. (2)判定定理2:如果两个直角三角形的两条直角边对应成比例,那么它们相似. (3)判定定理3:如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.5.直角三角形射影定理直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.[小题体验]1.(教材习题改编)如图,AB ∥EM ∥DC ,AE =ED ,EF ∥BC ,EF=12 cm ,则BC 的长为________ cm.解析:由⎭⎪⎬⎪⎫AB ∥EM ∥DC AE =ED ⇒E 为AD 中点,M 为BC 的中点, 又EF ∥BC ⇒EF =MC =12 cm. ∴BC =2MC =24 cm. 答案:242.(教材习题改编)如图,D ,E 分别是△ABC 的边AB ,AC 上的点,DE ∥BC 且ADDB=2,那么△ADE 与四边形DBCE 的面积比是________.解析:∵DE ∥BC ,∴△ADE ∽△ABC , ∴S △ADE S △ABC =AD 2AB 2. ∵AD DB =2,∴AD AB =23,∴S △ADE S △ABC =49,故S △ADE S 四边形DBCE =45. 答案:451.在使用平行线截割定理时易出现对应边的对应顺序混乱,导致错误. 2.在解决相似三角形的判定或应用时易出现对应边和对应角的对应失误.3.射影定理是直角三角形中的一个重要结论,其实质就是三角形的相似.但要注意满足直角三角形射影定理结论的三角形不一定是直角三角形,所以要搞清楚定理中的条件和结论之间的关系,不能乱用.[小题纠偏]1.(2016·鞍山模拟)如图,在▱ABCD 中,E 是BC 上一点,BE ∶EC =2∶3,AE 交BD 于点F ,则BF ∶FD 的值为________.解析:因为AD =BC ,BE ∶EC =2∶3, 所以BE ∶AD =2∶5,因为AD ∥BC , 所以BF ∶FD =BE ∶AD =2∶5, 所以BF ∶FD 的值为25.答案:252.如图,在Rt △ABC 中 ,∠BAC =90°,AD 是斜边BC 上的高,若AB ∶AC =2∶1,则AD ∶BC 为________.解析:设AC =k ,则AB =2k ,BC =5k , ∵∠BAC =90°,AD ⊥BC , ∴AC 2=CD ·BC , ∴k 2=CD ·5k ,∴CD =55k , 又BD =BC -CD =455k , ∴AD 2=CD ·BD =55k ·455k =45k 2, ∴AD =255k ,∴AD ∶BC =2∶5. 答案:2∶5考点一 平行线分线段成比例定理的应用(基础送分型考点——自主练透)[题组练透]1.如图,在梯形ABCD 中,AD ∥BC ,BD 与AC 相交于点O ,过点O 的直线分别交AB ,CD 于E ,F ,且EF ∥BC ,若AD =12,BC =20,求EF 的值.解:∵AD ∥BC , ∴OB OD =BC AD =2012=53, ∴OB BD =58.∵OE ∥AD ,∴OE AD =OB BD =58.∴OE =58AD =58×12=152,同理可求得OF =38BC =38×20=152,∴EF =OE +OF =15.2.如图,在△ABC 中,点D 是AC 的中点,点E 是BD 的中点,AE 交BC 于点F ,求BFFC 的值.解:如图,过点D 作DM ∥AF 交BC 于点M . ∵点E 是BD 的中点,∴在△BDM 中,BF =FM . 又点D 是AC 的中点, ∴在△CAF 中,CM =MF , ∴BF FC =BF FM +MC =12.[谨记通法]平行线分线段成比例定理及推论的应用的一个注意点及一种转化(1)一个注意点:利用平行线分线段成比例定理来计算或证明,首先要观察平行线组,再确定所截直线,进而确定比例线段及比例式,同时注意合比性质、等比性质的运用.(2)一种转化:解决此类问题往往需要作辅助的平行线,要结合条件构造平行线组,再应用平行线分线段成比例定理及其推论转化比例式解题.考点二 相似三角形的判定及性质 (重点保分型考点——师生共研)[典例引领]如图,在△ABC 中,AB =AC ,∠BAC =90°,D ,E ,F 分别在AB ,AC ,BC 上,AE =13AC ,BD =13AB ,且CF =13BC .求证:(1)EF ⊥BC ; (2)∠ADE =∠EBC . 证明:设AB =AC =3a , 则AE =BD =a ,CF =2a . (1)CE CB =2a 32a =23,CF CA =2a 3a =23. 又∠C 为公共角, 故△BAC ∽△EFC ,由∠BAC =90°,得∠EFC =90°, 故EF ⊥BC .(2)由(1)得EF =FC AC ·AB =2a , 故AE EF =a 2a =22,AD BF =2a 22a =22,∴AE EF =AD BF, ∴△ADE ∽△FBE , 所以∠ADE =∠EBC .[由题悟法]证明相似三角形的一般思路(1)先找两对内角对应相等.(2)若只有一个角对应相等,再判定这个角的两邻边是否对应成比例. (3)若无角对应相等,就要证明三边对应成比例.[即时应用]如图,已知在△ABC 中,D 是BC 边的中点,且AD =AC ,DE ⊥BC ,DE 与AB 相交于点E ,EC 与AD 相交于点F .(1)求证:△ABC ∽△FCD ;(2)若S △FCD =5,BC =10,求DE 的长.解:(1)证明:因为DE ⊥BC ,D 是BC 的中点,所以EB =EC ,所以∠B =∠BCE .又因为AD =AC ,所以∠ADC =∠ACB.所以△ABC ∽△FCD.(2)如图,过点A 作AM ⊥BC , 垂足为点M .因为△ABC ∽△FCD ,BC =2CD , 所以S △ABC S △FCD =⎝⎛⎭⎫BC CD 2=4.又因为S △FCD =5,所以S △ABC =20. 因为S △ABC =12BC ·AM ,BC =10,所以20=12×10×AM ,所以AM =4.因为DE ∥AM ,所以DE AM =BDBM . 因为DM =12DC =52,BM =BD +DM ,所以DE 4=55+52,解得DE =83.考点三 直角三角形中的射影定理 (重点保分型考点——师生共研)[典例引领]如图所示,CD 垂直平分AB ,点E 在CD 上,DF ⊥AC ,DG ⊥BE ,F ,G 分别为垂足.求证:AF ·AC =BG ·BE . 证明:因为CD 垂直平分AB , 所以∠ADC =∠BDC =90°,AD =D B.在Rt △ADC 中,因为DF ⊥AC , 所以AD 2=AF ·AC . 同理BD 2=BG ·BE . 所以AF ·AC =BG ·BE .[由题悟法]对射影定理的理解和应用(1)利用直角三角形的射影定理解决问题首先确定直角边与其射影.(2)要善于将有关比例式进行适当的变形转化,有时还要将等积式转化为比例式或将比例式转化为等积式,并且注意射影定理的其他变式.(3)注意射影定理与勾股定理的结合应用.[即时应用]在Rt △ACB 中,∠C =90°,CD ⊥AB 于D ,若BD ∶AD =1∶9,求tan ∠BCD 的值. 解:由射影定理得CD 2=AD ·BD , 又BD ∶AD =1∶9, 令BD =x ,则AD =9x (x >0). ∴CD 2=9x 2, ∴CD =3x .Rt △CDB 中,tan ∠BCD =BD CD =x 3x =13.1.如图,在四边形ABCD 中,EF ∥BC ,FG ∥AD ,求EF BC +FGAD 的值.解:由平行线分线段成比例定理得 EF BC =AF AC ,FG AD =FC AC ,故EF BC +FG AD =AF AC +FC AC =AC AC =1.2.如图,等边三角形DEF 内接于△ABC ,且DE ∥BC ,已知AH ⊥BC 于点H ,BC =4,AH =3,求△DEF 的边长.解:设DE =x ,AH 交DE 于点M ,显然MH 的长度与等边三角形DEF 的高相等,又DE ∥BC ,则DE BC =AM AH =AH -MH AH , 所以x4=3-32x 3=2-x 2,解得x =43.故△DEF 的边长为43.3.如图,M 是平行四边形ABCD 的边AB 的中点,直线l 过点M 分别交AD ,AC 于点E ,F ,交CB 的延长线于点N .若AE =2,AD =6,求AFAC的值. 解:∵AD ∥BC , ∴△AEF ∽△CNF , ∴AF CF =AE CN , ∴AF AF +CF =AEAE +CN.∵M 为AB 的中点,∴AE BN =AMBM =1,∴AE =BN , ∴AF AC =AF AF +CF =AE AE +BN +BC =AE 2AE +BC. ∵AE =2,BC =AD =6, ∴AF AC =22×2+6=15.4.如图,AD ,BE 是△ABC 的两条高,DF ⊥AB ,垂足为F ,交BE 于点G ,交AC 的延长线于H ,求证:DF 2=GF ·HF .证明:在△AFH 与△GFB 中, 因为∠H +∠BAC =90°, ∠GBF +∠BAC =90°,所以∠H =∠GBF .因为∠AFH =∠BFG =90°, 所以△AFH ∽△GFB , 所以HF BF =AF GF , 所以AF ·BF =GF ·HF .因为在Rt △ABD 中,FD ⊥AB , 所以DF 2=AF ·BF . 所以DF 2=GF ·HF .5.(2016·大连模拟)如图,已知D 为△ABC 中AC 边的中点,AE ∥BC ,ED 交AB 于G ,交BC 延长线于F ,若BG ∶GA =3∶1,BC =8,求AE 的长.解:因为AE ∥BC ,D 为AC 的中点, 所以AE =CF ,AE BF =AG BG =13.设AE =x ,又BC =8, 所以x x +8=13,所以x =4. 所以AE =4.6.(2016·大连模拟)如图,在△ABC 中,D 是AC 的中点,E 是BD 的中点,AE 的延长线交BC 于F .(1)求BFFC 的值;(2)若△BEF 的面积为S 1,四边形CDEF 的面积为S 2,求S 1∶S 2的值. 解:(1)过点D 作DG ∥BC ,并交AF 于点G ,因为E 是BD 的中点,所以BE =DE . 又因为∠EBF =∠EDG ,∠BEF =∠DEG , 所以△BEF ≌△DEG ,则BF =DG , 所以BF ∶FC =DG ∶FC .又因为D 是AC 的中点,则DG ∶FC =1∶2, 则BF ∶FC =1∶2,即BF FC =12.(2)若△BEF 以BF 为底,△BDC 以BC 为底, 则由(1)知BF ∶BC =1∶3,又由BE ∶BD =1∶2,可知h 1∶h 2=1∶2, 其中h 1,h 2分别为△BEF 和△BDC 的高, 则S △BEF S △BDC =13×12=16, 则S 1∶S 2=1∶5. 故S 1∶S 2的值为15.7.如图,在△ABC 中,AB =AC ,过点A 的直线与其外接圆交于点P ,交BC 的延长线于点D.(1)求证:PC AC =PDBD ;(2)若AC =3,求AP ·AD 的值.解:(1)证明:因为∠CPD =∠ABC ,∠PDC =∠PDC , 所以△DPC ∽△DBA ,所以PC AB =PD BD . 又AB =AC ,所以PC AC =PD BD. (2)因为∠ABC +∠APC =180°,∠ACB +∠ACD =180°, ∠ABC =∠ACB , 所以∠ACD =∠APC .又∠CAP =∠DAC ,所以△APC ∽△ACD , 所以AP AC =AC AD. 所以AP ·AD =AC 2=9.8.△ABC 中,D ,E ,F 分别是BC ,AB ,AC 上的点,AD ,EF 交于点P ,若BD =DC ,AE =AF .求证:AB AC =PF PE .证明:过F 作MN ∥AD 交BA 的延长线及DC 于M ,N .对△MEF ,有PF PE =AMAE ,因为AE =AF ,所以PF PE =AM AF. 对△MBN ,有AB AM =BDDN , 因为BD =DC ,所以AB AM =DCDN . 对△ADC ,有AC AF =DC DN ,所以AB AM =ACAF . 所以AB AC =AM AF ,所以AB AC =PF PE .第二节 直线与圆的位置关系1.圆周角(1)定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半. (2)推论1:①同弧或等弧所对的圆周角相等; ②同圆或等圆中,相等的圆周角所对的弧也相等. (3)推论2:①半圆(或直径)所对的圆周角是直角; ②90°的圆周角所对的弦是直径. 2.圆的切线(1)判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. (2)性质定理:圆的切线垂直于经过切点的半径.(3)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.3.弦切角定理及其推论(1)定理:弦切角等于它所夹的弧所对的圆周角. (2)推论:弦切角的度数等于它所夹的弧的度数的一半. 4.圆中的比例线段(1)相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等.(2)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.[小题体验]1.(教材习题改编)如图,已知AB ,BC 是⊙O 的两条弦,AO ⊥BC ,AB =3,BC =22,则⊙O 的半径等于________.解析:设垂足为D ,⊙O 的半径等于R , ∵AB ,BC 是⊙O 的两条弦, AO ⊥BC ,AB =3,BC =22, ∴AD =1,∴R 2=2+(R -1)2, ∴R =1.5.故⊙O 的半径为1.5. 答案:1.52.如图,AC 为⊙O 的直径,OB ⊥AC ,弦BN 交AC 于点M .若OC =3,OM =1,则MN 的长为________.解析:由题意得: CM =CO +OM =3+1, AM =AO -OM =3-1, BM 2=OB 2+OM 2=4,BM =2, 根据相交弦定理有CM ·AM =BM ·MN ,代入数值可解得MN =CM ·AM BM =(3+1)(3-1)2=1.答案:13.如图,⊙O 的直径AB =6 cm ,P 是AB 延长线上的一点,过P 点作⊙O 的切线,切点为C ,连接AC ,若∠CPA =30°,PC =________ cm.解析:连接OC ,则OC ⊥PC .又OC =3,∠CPA =30°, ∴CP =OCtan 30°=3 3.答案:3 31.解决圆周角、圆心角及弦切角问题时,角之间关系易于混淆导致错误.2.使用相交弦定理与切割线定理时,注意对应线段成比例及相似三角形知识的应用.[小题纠偏]1.如图所示,CD 是圆O 的切线,切点为C ,点B 在圆O 上,BC =2,∠BCD =30°,则圆O 的面积为________.解析:设圆O的半径为r,过B作⊙O的直径BA,连接AC,则∠ACB=90°.又由弦切角定理得∠CAB=∠BCD=30°,∴AB=2BC=4.∴r=2,∴S=πr2=4π.答案:4π2.如图所示,已知⊙O的割线PAB交⊙O于A,B两点,割线PCD经过圆心,若PA=3,AB=4,PO=5,则⊙O的半径为________.解析:设⊙O的半径为r.由割线定理得PA·PB=PC·PD,3×7=(PO-r)(PO+r),即21=25-r2,∴r2=4,∴r=2.答案:2考点一圆周角、弦切角和圆的切线问题(基础送分型考点——自主练透)[题组练透]1.(2016·黄冈模拟)已知点C在圆O的直径BE的延长线上,直线CA与圆O相切于A,∠ACB的平分线分别交AB,AE于D,F两点,求∠AFD的大小.解:因为AC为圆O的切线,由弦切角定理,得∠B=∠EAC.又因为CD平分∠ACB,则∠ACD=∠BCD,所以∠B+∠BCD=∠EAC+∠ACD.根据三角形外角定理,∠ADF=∠AFD.因为BE是圆O的直径,则∠BAE=90°,所以△ADF是等腰直角三角形.所以∠ADF=∠AFD=45°.2.(2015·广东高考改编)如图,已知AB是圆O的直径,AB=4,EC是圆O的切线,切点为C,BC=1.过圆心O作BC的平行线,分别交EC和AC于点D和点P,求OD的长.解:由题意得OP =12BC =12,OA =2,于是PA =CP =22-⎝⎛⎭⎫122=152. 因为∠DCP =∠B =∠POA ,又∠DPC =∠APO ,所以△DCP ∽△AOP , 故PD PA =PCPO, 即PD =15212×152=152,所以OD =152+12=8.[谨记通法]1.圆周角定理及其推论与弦切角定理及其推论多用于推出角的关系,从而证明三角形全等或相似,可求线段或角的大小.2.涉及圆的切线问题时要注意弦切角的转化;关于圆周上的点,常作直径(或半径)或向弦(弧)两端作圆周角或弦切角.考点二 圆内接四边形的性质及判定 (重点保分型考点——师生共研)[典例引领](2016·昆明模拟)如图所示,已知D 为△ABC 的BC 边上一点,⊙O 1经过点B ,D ,交AB 于另一点E ,⊙O 2经过点C ,D ,交AC 于另一点F ,⊙O 1与⊙O 2的另一交点为G .(1)求证:A ,E ,G ,F 四点共圆;(2)若AG 切⊙O 2于G ,求证:∠AEF =∠ACG . 证明:(1)如图,连接GD ,四边形BDGE ,四边形CDGF 分别内接于⊙O 1,⊙O 2, ∴∠AEG =∠BDG , ∠AFG =∠CDG ,又∠BDG +∠CDG =180°, ∴∠AEG +∠AFG =180°,∴A,E,G,F四点共圆.(2)∵A,E,G,F四点共圆,∴∠AEF=∠AGF,∵AG与⊙O2相切于点G,∴∠AGF=∠ACG,∴∠AEF=∠ACG.[由题悟法]证明四点共圆的常用方法(1)若四个点到一定点等距离,则这四个点共圆.(2)若一个四边形的一组对角的和等于180°,则这个四边形的四个顶点共圆.(3)若一个四边形的一个外角等于它的内对角,则这个四边形的四个顶点共圆.(4)若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线段的两个端点共圆.[即时应用](2016·吉林实验中学)如图,圆周角∠BAC的平分线与圆交于点D,过点D的切线与弦AC的延长线交于点E,AD交BC于点F.(1)求证:BC∥DE;(2)若D,E,C,F四点共圆,且AC=BC,求∠BAC.解:(1)证明:因为DE为圆的切线,所以∠EDC=∠DAC.又因为∠DAC=∠DAB,∠DAB=∠DCB,所以∠EDC=∠DCB,所以BC∥DE.(2)因为D,E,C,F四点共圆,所以∠CFA=∠CED,由(1)知∠ACF=∠CED,所以∠CFA=∠ACF.设∠DAC=∠DAB=x,因为AC=BC,所以∠CBA=∠BAC=2x,所以∠CFA=∠FBA+∠FAB=3x,在等腰△ACF中,180°=∠CFA+∠ACF+∠CAF=7x,则x≈25.7°,所以∠BAC=2x≈51.4°.考点三 与圆有关的比例线段 (重点保分型考点——师生共研)[典例引领](2015·陕西高考)如图,AB 切⊙O 于点B ,直线AO 交⊙O 于D ,E 两点,BC ⊥DE ,垂足为C .(1)证明:∠CBD =∠DBA;(2)若AD =3DC ,BC =2,求⊙O 的直径. 解:(1)证明:因为DE 为⊙O 的直径, 所以∠BED +∠EDB =90°.又BC ⊥DE ,所以∠CBD +∠EDB =90°, 从而∠CBD =∠BED.又AB 切⊙O 于点B ,得∠DBA =∠BED , 所以∠CBD =∠DBA . (2)由(1)知BD 平分∠CBA , 则BA BC =ADCD=3. 又BC =2,从而AB =3 2. 所以AC =AB 2-BC 2=4, 所以AD =3.由切割线定理得AB 2=AD ·AE , 即AE =AB 2AD =6,故DE =AE -AD =3, 即⊙O 的直径为3.[由题悟法]与圆有关的比例线段解题思路(1)见到圆的两条相交弦就要想到相交弦定理. (2)见到圆的两条割线就要想到割线定理. (3)见到圆的切线和割线就要想到切割线定理.[即时应用]1.(2015·天津高考改编)如图,在圆O 中,M ,N 是弦AB 的三等分点,弦CD ,CE 分别经过点M ,N ,若CM =2,MD =4,CN =3,求线段NE 的长.解:由题意可得CM ·MD =AM ·MB , 则2×4=2AM 2,AM =2. 又CN ·NE =AN ·NB , 即3NE =4×2,解得NE =83.2.(2015·湖北高考改编)如图,PA 是圆的切线,A 为切点,PBC 是圆的割线,且BC =3PB ,求ABAC的值. 解:因为PA 是圆的切线, A 为切点,PBC 是圆的割线,由切割线定理,知PA 2=PB ·PC =PB (PB +BC ), 因为BC =3PB ,所以PA 2=4PB 2,即PA =2PB. 由弦切角定理,得∠PAB =∠PCA , 又∠APB =∠CPA ,故△PAB ∽△PCA , 所以AB AC =PB PA =12.1.(2015·重庆高考改编)如图,圆O 的弦AB ,CD 相交于点E ,过点A 作圆O 的切线与DC 的延长线交于点P ,若PA =6,AE =9,PC =3,CE ∶ED =2∶1,求BE 的长.解:由切割线定理,知PA 2=PC ·PD , 即62=3PD , 解得PD =12,所以CD =PD -PC =9, 所以CE =6,ED =3.由相交弦定理,知AE ·EB =CE ·ED ,即9BE =6×3,解得BE =2.2.(2016·兰州双基测试)如图,在正△ABC 中,点D ,E 分别在BC ,AC 上,且BD =13BC ,CE =13CA ,AD ,BE 相交于点P .求证:(1)P ,D ,C ,E 四点共圆; (2)AP ⊥CP .证明:(1)在正△ABC 中,由BD =13BC ,CE =13CA ,知:△ABD ≌△BCE ,∴∠ADB =∠BEC ,即∠ADC +∠BEC =180°, ∴P ,D ,C ,E 四点共圆.(2)连接DE ,在△CDE 中,CD =2CE ,∠ACD =60°, 由正弦定理知∠CED =90°,由P ,D ,C ,E 四点共圆知,∠DPC =∠DEC , ∴AP ⊥CP .3.(2016·陕西一检)如图,设AB 为⊙O 的任一条不与直线l 垂直的直径,P 是⊙O 与l 的公共点,AC ⊥l ,BD ⊥l ,垂足分别为C ,D ,且PC =PD.(1)求证:l 是⊙O 的切线;(2)若⊙O 的半径OA =5,AC =4,求CD 的长.解:(1)证明:连接OP , ∵AC ⊥l ,BD ⊥l , ∴AC ∥BD.又OA =OB ,PC =PD , ∴OP ∥BD ,从而OP ⊥l .∵点P 在⊙O 上,∴l 是⊙O 的切线. (2)由(1)可得OP =12(AC +BD ),∴BD =2OP -AC =10-4=6. 过点A 作AE ⊥BD ,垂足为E , 则BE =BD -AC =6-4=2. ∴在Rt △ABE 中,AE =AB 2-BE 2=102-22=4 6. ∴CD =4 6.4.(2015·全国卷Ⅰ)如图,AB 是⊙O 的直径,AC 是⊙O 的切线,BC交⊙O 于点E .(1)若D 为AC 的中点,证明:DE 是⊙O 的切线; (2)若OA =3CE ,求∠ACB 的大小. 解:(1)证明:如图,连接AE ,由已知得AE ⊥BC ,AC ⊥AB. 在Rt △AEC 中,由已知得DE =DC ,故∠DEC =∠DCE . 连接OE ,则∠OBE =∠OEB. 又∠ACB +∠ABC =90°, 所以∠DEC +∠OEB =90°,故∠OED =90°,即DE 是⊙O 的切线. (2)设CE =1,AE =x .由已知得AB =23,BE =12-x 2. 由射影定理可得AE 2=CE ·BE , 所以x 2=12-x 2,即x 4+x 2-12=0. 解得x =3,所以∠ACB =60°.5.(2015·沈阳一模)如图所示,已知AB 为圆O 的直径,C ,D 是圆O 上的两个点,CE ⊥AB 于E ,BD 交AC 于G ,交CE 于F ,CF =FG .(1)求证:C 是劣弧BD 的中点; (2)求证:BF =FG .证明:(1)∵CF =FG ,∴∠CGF =∠FCG . ∵AB 是圆O 的直径,∴∠ACB =∠ADB =π2.∵CE ⊥AB ,∴∠CEA =π2.∵∠CBA =π2-∠CAB ,∠ACE =π2-∠CAB ,∴∠CBA =∠ACE .∵∠CGF =∠DGA ,∠DGA =∠ABC , ∴π2-∠DGA =π2-∠ABC , ∴∠CAB =∠DAC , ∴C 为劣弧BD 的中点.(2)∵∠GBC =π2-∠CGB ,∠FCB =π2-∠GCF ,∴∠GBC =∠FCB ,∴CF =FB ,∴BF =FG .6.(2016·贵州七校联考)如图,⊙O 1和⊙O 2的公切线AD 和BC 相交于点D ,A ,B ,C 为切点,直线DO 1交⊙O 1于E ,G 两点,直线DO 2交⊙O 2于F ,H 两点.(1)求证:△DEF ∽△DHG ;(2)若⊙O 1和⊙O 2的半径之比为9∶16,求DEDF 的值. 解:(1)证明:∵AD 是两圆的公切线, ∴AD 2=DE ·DG ,AD 2=DF ·DH , ∴DE ·DG =DF ·DH ,∴DE DH =DF DG , 又∵∠EDF =∠HDG , ∴△DEF ∽△DHG .(2)连接O 1A ,O 2A , ∵AD 是两圆的公切线, ∴O 1A ⊥AD ,O 2A ⊥AD , ∴O 1,A ,O 2共线,∵AD 和BC 是⊙O 1和⊙O 2的公切线, DG 平分∠ADB ,DH 平分∠ADC , ∴DG ⊥DH ,∴AD 2=O 1A ·O 2A .设⊙O 1和⊙O 2的半径分别为9x 和16x ,则AD =12x , ∵AD 2=DE ·DG ,AD 2=DF ·DH ,∴144x 2=DE (DE +18x ),144x 2=DF (DF +32x ), ∴DE =6x ,DF =4x , ∴DE DF =32.7.(2016·沈阳模拟)如图,已知圆O 1与圆O 2外切于点P ,直线AB 是两圆的外公切线,分别与两圆相切于A ,B 两点,AC 是圆O 1的直径,过C 作圆O 2的切线,切点为D.(1)求证:C ,P ,B 三点共线; (2)求证:CD =CA .证明:(1)连接PC ,PA ,PB ,BO 2,∵AC是圆O1的直径,∴∠APC=90°.连接O1O2必过点P,∵AB是两圆的外公切线,A,B为切点,∴设∠BAP=∠ACP=α,∴∠AO1P=2α.由于O1A⊥AB,O2B⊥AB,∴∠BO2P=π-2α,∴∠O2BP=α.又∠ABP+∠O2BP=90°,∴∠ABP+∠BAP=90°,∴C,P,B三点共线.(2)∵CD切圆O2于点D,∴CD2=CP·CB.在△ABC中,∠CAB=90°,又∵AP⊥BC,∴CA2=CP·CB,故CD=CA.8.(2015·全国卷Ⅱ)如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.(1)证明:EF∥BC;(2)若AG等于⊙O的半径,且AE=MN=23,求四边形EBCF的面积.解:(1)证明:由于△ABC是等腰三角形,AD⊥BC,所以AD是∠CAB的平分线.又因为⊙O分别与AB,AC相切于点E,F,所以AE=AF,故AD⊥EF,从而EF∥BC.(2)由(1)知,AE=AF,AD⊥EF,故AD是EF的垂直平分线.又EF为⊙O的弦,所以O在AD上.连接OE,OM,则OE⊥AE.由AG等于⊙O的半径得AO=2OE,所以∠OAE =30°.因此△ABC 和△AEF 都是等边三角形. 因为AE =23,所以AO =4,OE =2.因为OM =OE =2,DM =12MN =3, 所以OD =1.于是AD =5,AB =1033. 所以四边形EBCF 的面积为12×⎝⎛⎭⎫10332×32-12×(23)2×32=1633.。
高中数学 正余弦定理解三角形 教师版

【教师备案】在初中的时候,我们就学过解直角三角形,解直角三角形是怎么回事呢?在直角三角形中,除了告诉我们直角外,还有5个要素,我们发现,如果解这个三角形,把要素都求出来,必须要知道至少2个要素,当然不能为2个角,换言之,解直角三角形就是知二求三的过程.当然,在我们学习了任意角的三角函数之后,我们的视野不能这么小,如果给我们一个一般的三角形,那我们应该如何解这个三角形呢?我们应该至少要知道几个量?我们先来回顾一下初中边和角相关的东西,我们在初中学过尺规作图,而且学过三角形全等的证明(SSS SAS ASA AAS ,,,),只要给出上述条件我们就能把三角形确定,也就是全等. 那么,为什么我们知道2条边1个夹角就能求出其他要素呢?而知道两条边和一边的对角就无法证明三角形全等呢?三角形的边和角之间存在什么关系呢?尺规作图毕竟是定性的感受,在高中阶段,我们可以给出一个严格的证明,就是今天我们要讲的正余弦定理.正余弦定理的本质就是构造边与角之间的关系,由角就可以求出边,由边就可以求出角.下面我们就先来介绍正弦定理.知识切片我会解三角形你会么?在ABC △中的三个内角A ,B ,C 的对边分别用a b c ,,表示: 1.正弦定理:在三角形中,各边的长和它所对的角的正弦的比相等,即sin sin sin a b cA B C==. 【教师备案】 正弦定理的推导由三角形中的线段关系或者由三角形的外接圆可以直接得到,且2sin sin sin a b cR A B C ===,其中R 为ABC △的外接圆的半径.建议老师用三角形的外接圆给学生证明,因为板块1.4中讲三角形面积的时候还会用到三角形的外接圆,所以不如这时给学生讲了.利用三角形中的线段关系证明正弦定理:①在R t ABC △中(如图),有sin sin a bA B c c==,,因此sin sin a b c A B ==,又因为sin 1C =,所以sin sin sin a b cA B C== ②在锐角ABC △中(如图),作CD AB ⊥于点D ,有sin CDA b =,即sin CD b A =;sin CDB a=,即sin CD a B =,因此 sin sin b A a B =,即sin sin a b A B =,同理可证sin sin a c A C=,因此sin sin sin a b cA B C== ③在钝角ABC △中(如图),作CD AB ⊥,交AB 的延长线于点D ,则sin CDA b =,即sin CD b A =;()sin 180sin CDB B a =-=,即sin CD a B =,因此sin sin b A a B =,即sin sin a b A B =,同理可证sin sin a cA C=,因此sin sin sin a b cA B C== 利用平面几何知识证明正弦定理:如图所示,设O 为ABC △的外接圆的圆心,连BO 并延长交O 于A ',连A C ',则A A '= 或πA A '=-,∴sin sin 2BC a A A A B R '===',即2sin aR A =,同理可证2sin sin b c R B C ==,故有2sin sin sin a b cR A B C=== 当ABC △是钝角三角形时,类似地得出上述结论. 利用向量知识证明正弦定理:①当ABC △是锐角三角形时,过A 点作单位向量i 垂直于AB , 如图,∵AC AB BC =+, ∴()i AC i AB BC i AB i BC i BC ⋅=⋅+=⋅+⋅=⋅, ∴()()cos 90cos 90b A a B -=-,得sin sin b A a B =,1.1正弦定理与其在解三角形中的应用知识点睛iCAc b a DCB A c b aDCB AC B Ac bOA 'C A得sin sin a bA B= ②当ABC △为钝角三角形时,类似地得出上述结论2.利用正弦定理解三角形⑴解三角形:三角形的三个内角和它们的对边分别叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形.⑵利用正弦定理可解下列两类型的三角形:①已知三角形的任意两个角与一边,求其它两边和另一角;【教师备案】有了正弦定理之后,我们可以简单的看出,任意的两个角与一边相当于AAS 和ASA 的条件,可以确定所有的角,然后可以确定所有的边,因此,三角形也随之确定.②已知三角形的两边与其中一边的对角,计算另一边的对角,进而计算出其它的边与角.【教师备案】1.已知三角形的两边和一边的对角,由正弦定理可以求得另一边的对角的正弦值,但是解三角形时,因为在(0,π)内,互补的角的正弦值相等,所以求得另一边所对的角的正弦值之后,可能对应有一个角或两个角,因此无法确定三角形的形状,这就是为什么SSA 无法证明三角形全等的原因.2.利用正弦定理证明三角形中“大边对大角”的结论:①当ABC △为锐角三角形时,若a b >,则sin sin A B >,又π02A B ⎛⎫∈ ⎪⎝⎭,,,正弦函数在此区间内单调递增,故A B >;②当ABC △为钝角三角形时,若A 为钝角,则由πA B +<得,πB A <-,又ππ02A B ⎛⎫-∈ ⎪⎝⎭,,,故由正弦函数的单调性知:()sin sin πsin B A A <-=,从而由正弦定理知:b a <.对直角三角形,此结论显然成立,故综上知,在任意三角形中,均有大边对大角.3.此时,到底取一个角还是取两个角,关键保持一个原则“大边对大角”.具体讨论如下:已知,a b 和角A ,若B 为钝角或直角,则C 至多有一个解; 若B 为锐角,得分情况讨论,如图:无解的情况例如:3460b c B ===︒,,,求C . 由sin sin b c B C=sin 4sin 60sin 13c B C b ︒⇒==>, ∴C 无解,从而满足此条件的三角形不存在.这就是sin c B b >的情况.【教师备案】在讲利用正弦定理解三角形时,对于边角互化和利用边角互化判断三角形形状的题型建议放到同步去讲,本板块只讲利用正弦定理解两种类型三角形,在讲完“已知两角和任一边解三角形”后就可以让学生做例1;在讲“已知两边和其中一边的对角解三角形”时一定要注意三角形的多解问题,具体的多解见考点2的【教师备案】,讲完多解问题后就可以让学生做例2的铺垫以及例2.b sin A<a<b , 两解一解考点1:已知两角和任一边解三角形【例1】 已知两角和任一边解三角形⑴ 已知ABC △中,a b c ,,分别是A B C 、、的对边,3c =,60A =︒,45C =︒, 则a =_______.⑵在ABC △中,30B =︒,45C =︒,1c =,则b =_______;三角形的外接圆半径R =_______. ⑶在ABC △中,已知8a =,60B =,75C =,则b =_______. 【解析】⑴322 ⑵22;22已知30B =,45C =,1c =,由正弦定理得:2sin sin b cR B C==, 所以sin 1sin 302sin sin 452c B b C ⋅===,1122sin sin 4522c R C ====,22R =⑶46由60B =,75C =,知45A =,再由正弦定理有846sin 45sin 60bb =⇒=考点2:已知两边和其中一边的对角解三角形【铺垫】根据下列条件解三角形:①6031A a b ===,,;②3012A a b ===,,;③30610A a c ===,,; ④150105A a c ===,,,其中有唯一解的个数为( ) A .1 B .2 C .3 D .4 【解析】C ①3sin 32b A =<,又31>∵,∴有唯一解;②sin 2sin301b A ==,∴有唯一解;③sin 10sin305610c A ==<<,∴有两解;④有唯一解.【例2】 已知两边和一边对角解三角形⑴在ABC △中,已知4522A a b ===,,,则B =_______.⑵已知ABC △中,a b c ,,分别是A B C 、、的对边,222345a b A ===︒,,, 则B =_______.⑶已知ABC △,三个内角A B C ,,的对边分别记为a b c ,,,若245c x b B ===︒,,,且这个 三角形有两解,求x 的取值范围. ⑷(目标班专用)(2010山东卷理数)在ABC △中,角A B C 、、所对的边分别为a b c 、、,若2a =,2b =,sin cos 2B B +=,则角A 的大小为 .【解析】⑴30 根据正弦定理得:sin sin a b A B =,∴sin 2sin 451sin 22b A B a ⋅===,b a <∵,B A <∴, B ∴为锐角,即30B = ⑵60或120经典精讲由正弦定理得,sin 23sin 453sin 222b A B a ===,∵sin b A a b <<,∴这个三角形有两组解,即60B =或120. ⑶ 由正弦定理可得:sin sin c b C B =,解得:2sin 4xC =,由于三角形有两解,又45B =︒, 则45135C <<︒且90C ≠,则2sin 12C <<,即22124x<<,解得222x <<.【点评】 本题的⑶也可用以下方法解,当sin c B b c <<,即sin 2x B x <<时,对应两个C 的值,方程有两组解,解得222x <<.⑷ π6由sin cos 2B B +=平方得12sin cos 2B B +=,即sin 21B =,因为0πB <<,所以π4B =.又因为22a b ==,,所以在ABC △中,由正弦定理得:22sin sin A B =,解得1sin 2A =. 又a b <∵,所以AB <,所以π6A =.【点评】 易错点:忽略a b <A B ⇒<的隐藏条件.多解.【教师备案】在正弦定理中,我们还有两种类型的全等没有讨论,SAS 和SSS 型,正弦定理处理的是对边对角的情形,仅仅用正弦定理是很难把三角形求解出来的,因此,我们需要一个新的工具,能够把边的条件化成角,就是下面所介绍的余弦定理.1.余弦定理:三角形任何一边的平方等于其它两边的平方和减去这两边与它们夹角的余弦的积的两倍,即:2222222222cos ,2cos ,2cos .c a b ab C b a c ac B a b c bc A ⎧=+-⎪=+-⎨⎪=+-⎩ 它的变形为:222222222cos ,2cos ,2cos .2a b c C ab a c b B ac b c a A bc ⎧+-=⎪⎪⎪+-=⎨⎪⎪+-=⎪⎩<教师备案> 余弦定理的推导可以由三角形的向量运算直接得到,比如:2222()()2a BC BA AC BA AC BA BA AC AC ==+⋅+=+⋅+()22222cos π2cos c bc A b c bc A b =+-+=-+.也可以通过坐标法及两点距离公式得到.建立合适的坐标系,如图,得()()()cos sin 000A b C b C B a C ,,,,,, 从而有22(cos )(sin )AB c b C a b C ==-+,整理得:2222cos c a b ab C =+-.也可以通过三角形中的线段关系证明:在ABC △中,已知边a b ,及C ∠(为了方便起见,假设C ∠为最大的角),求边c 的长证明:当90C ∠=时,那么222c a b =+1.2余弦定理及其在解三角形中的应用知识点睛bxyB C A (b cosC , b sinC)当90C ∠≠时,如图,无论C ∠为锐角还是为钝角,都过A 点做边BC 的高,交BC (或延长线)于点D ,这时高AD 把ABC △分成两个直角三角形ADB 和ADC , 则sin AD b C =,cos BD a b C =-,在Rt ADB △中,运用勾股定理,得 ()222222sin cos c AD BD b C a b C =+=+-222cos a b ab C =+-2.余弦定理及其变形常用来解决这样两类解三角形的问题: ①已知两边和任意一个内角解三角形; ②已知三角形的三边解三角形.【教师备案】老师在讲完余弦定理后,可以就SSS 和SAS 型的全等证明做个简单讲解,这样子整个讲义的主线就串在一起.然后,可以让学生做【铺垫】,【铺垫】是直接套公式的,做完【铺垫】就可以做例3,例3是灵活的运用余弦定理解三角形,在解题过程中需要转化的;学生在能够灵活运用余弦定理后,就可以讲考点4,用余弦定理判断三角形形状,在三角形中,因为每个角都在()0π,内,所以一个角的正弦不能判断这个角是锐角还是钝角,但是余弦就能很快的判定是锐角还是钝角,在三角形中,当cos 0α>时,α为锐角;当cos 0α<时,α为钝角;当cos 0α=时,α为直角;考点4的【铺垫】是直接根据三角形的三条边判断三角形形状的,老师可以让学生先体会一下怎么样用余弦判定三角形形状,例4是已知三角形形状,求边的取值范围的,在解题过程中要注意用余弦定理和构成三角形的条件.考点3:用余弦定理解三角形【铺垫】⑴在ABC △中,5a =,8b =,60C =︒,则c =_______.⑵在ABC △中,222a b c bc =++,则A 等于( ).A . 60B . 45C .120 D . 30 【解析】⑴ 7 由余弦定理2222cos 25644049c a b ab C =+-=+-=,∴7c =. ⑵C∵2222222()1cos 222b c a b c b c bc A bc bc +-+-++===-∵0180A <<,∴120A =.【例3】 余弦定理解三角形⑴在ABC △中,5a =,8b =,7c =,则sin C =_______.⑵在ABC △中,已知3sin 5A =,sin cos 0A A +<,35a =,5b =,则c =______.⑶在ABC △中,若1378cos 14a b C ===,,,则最大角的余弦是( ). A .15- B .16- C .17- D .18-【解析】⑴32经典精讲abcABCDD cbaCBA由余弦定理2222cos c a b ab C =+-,∴1cos 2C =,3sin 2C =. ⑵∵sin cos 0A A +<,且3sin 5A =,24cos 1sin 5A A =--=-∴,又∵35a =,5b =,2222cos a b c bc A =+-,∴()2224355255c c ⎛⎫=+-⨯⨯⨯- ⎪⎝⎭,即28200c c +-=,解得2c =或10c =-(舍),∴2c = ⑶ C由2222cos c a b ab C =+-,∴3c =,则b a c >>,∴最大角为B ,∴2221cos 27a cb B ac +-==-考点4:用余弦定理判断三角形形状【教师备案】最大角定三角形的形状,由余弦定理易得,较小两边的平方和与最大边的平方的差可以定最大角是锐角、直角或钝角.注意:三角形三边关系应满足的为:较小两边的和大于 第三边.【铺垫】在ABC △中,已知5a =,6b =,7c =,则此三角形是一个 三角形.【解析】锐角三角形 c b a >>∵,∴角C 为最大角,2221cos 025a b c C ab +-==>∴,∴角C 为锐角,∴三角形为锐角三角形 【例4】 判断三角形形状⑴ 若以34x ,,为三边组成一个直角三角形,则x 的值为 . ⑵ 若以34x ,,为三边组成一个锐角三角形,则x 的取值范围为 . ⑶ 若以34x ,,为三边组成一个钝角三角形,则x 的取值范围为 . 【追问】我们还可以考虑,当我们知道三角形两边的情况下,求某一个角的取值范围,例如下面这个问题:已知ABC △中,12AB BC ==,,则C ∠的取值范围是________________⑷ (目标班专用)已知三角形的三边长为三个连续自然数, 且最大角是钝角.求这个三角形三边的长. 【解析】 ⑴ 5722234x +=或22234x +=.⑵)75依题意有:22217434x x x ⎧<<⎪>⎨⎪+>⎩或22217434x x x ⎧<<⎪⎨⎪+>⎩≤75x <.⑶ (()1757,∪, 解法一:依题意有:22217434x x x⎧<<⎪>⎨⎪+<⎩或22217434x x x ⎧<<⎪⎨⎪+<⎩≤解得57x <<或17x <<.解法二:本题也可以由函数的图象来解决,如图,设圆的半径3OA =, 4OB =,圆上任取一点与O B ,两点构成三角形,从图形上看 出,当圆上的点在点D 和点E 上时,构成直角三角形;当点 在DE 上时,构成锐角三角形;当点在AD 和EG 上时,构成 钝角三角形.由此可以很快得出答案.【追问】π06⎛⎤ ⎥⎝⎦,⑷设三角形三边的长为:()12n n n n *++∈N ,,最大角为α,∴222(1)(2)cos 2(1)n n n n n α++-+=+,∵α是钝角,∴cos 0α<,∴222(1)(2)02(1)n n n n n ++-+<+,2(1)0n n +>∵,∴222(1)(2)0n n n ++-+<∴2230n n --<,∴13n n *-<<∈N ,∵,1n =∴或2. 当1n =时,123,,不能构成三角形的三边,故舍去. 当2n =时,234,,即为所求三边的长.【拓展】⑴钝角三角形的三边分别是12a a a ++,,,其最大角不超过120,求a 的取值范围. ⑵在ABC △中,若三条边是三条连续的正整数,且最大角是最小角的2倍,求ABC △的三条边长.【解析】 ⑴∵钝角三角形的三边分别是12a a a ++,,,∴显然有210a a a +>+>>,设钝角三角形 的最大的(内)角为α,依题意,得90120α<≤,由()()()()()()22212313cos 21212a a a a a a a a a a a α++-+-+-===++,可得13022a a--<≤, 解得332a ⎡⎫∈⎪⎢⎣⎭,⑵设最小内角为θ,三边长为11n n n -+,,,根据正弦定理得:11sin sin 2n n θθ-+=, 112cos n n θ+-=∴,()1cos 21n n θ+=-∴,根据余弦定理得:()()()22211cos 21n n n n n θ++--=+,()()()()2221112121n n n n n n n ++--+=-+∴,解得5n =,从而得ABC △的三条边分别为456,,GFEDCBAO1.正弦定理灵活应用:①2sin a R A =,2sin b R B =,2sin c R C = (其中R 为ABC △的外接圆的半径);②sin2a A R =,sin 2b B R =,sin 2cC R=;③::sin :sin :sin a b c A B C =. 2.正余弦定理的综合应用已知条件 应用定理 一般解法一边和两角(如a B C ,,) 正弦定理 由πA B C ++=,求角A ;由正弦定理求出b 与c .两边和夹角 (如a b C ,,) 余弦定理 正弦定理 由余弦定理求第三边c ;由正弦定理求出小边所对的角(此角一定是锐角);再由πA B C ++=,求剩下的角.三边(a b c ,,) 余弦定理正弦定理由余弦定理求出最大角,然后正弦计算剩余两角. 两边和其中一边的对角 (如a b A ,,) 正弦定理余弦定理 由正弦定理求出角B ;由πA B C ++=,求出角C ;再利用正弦定理或余弦定理求c .【教师备案】本板块主要讲正余弦定理在解三角形中的灵活应用,尤其是正弦定理的灵活运用,根据正弦定理可以得到三角形的边与角之间的关系,可以把角全部换成边,也可以把边全部换成角,【铺垫】就是根据正弦定理把边用角表示,例5是先要根据正弦定理把边角化掉再根据余弦定理解三角形,此类题型不属于边角互化题型,是正弦定理的灵活运用,边角互化的题型是比如“2sin a b A =”类型的,对于这类题我们放到同步去讲;在讲完正余弦定理的灵活运用后就可以让学生体会一下正余弦定理在平面几何中的应用,因为在同步的时候不会讲此类题型,所以在预习的时候可以给学生介绍一下,具体见例6和目标班学案2,而对于三角形中()sin sin A B C +=的应用建议放到同步去讲.【铺垫】在ABC △中,若::1:2:3A B C =,则::a b c =______.【解析】 由已知得306090A B C ===,,,::sin :sin :sin 1:3:2a b c A B C ==∴【例5】 正余弦定理的综合运用⑴在ABC △中,若sin :sin :sin 3:2:4A B C =,则cos C 的值为( )A .14-B .14C .23-D .23⑵在ABC △中,若222sin sin sin A B C +<,则角C 为( )A .锐角B .钝角C .直角D .不确定【追问】在ABC △中,若cos cos cos a b cA B C==,则ABC △是( ) A .直角三角形 B .等边三角形C .钝角三角形D .等腰直角三角形 ⑶(2010天津理7)在ABC △中,内角A B C ,,的对边分别为a b c ,,,若223a b bc -=,sin 23sin C B =,则A =( )A .30B .60C .120D .1501.3正余弦定理在解三角形中的灵活应用经典精讲知识点睛【解析】⑴A 根据正弦定理sin 2a A R =,sin 2b B R =,sin 2cC R=,sin :sin :sin ::3:2:4A B C a b c ==∴,2223241cos 2324C +-==-⨯⨯∴⑵B222sin sin sin A B C +<∵,∴根据正弦定理得222a b c +<,222cos 02a b c C ab+-=<∴,∴角C 为钝角 【追问】B ⑶A由sin 23sin C B =,根据正弦定理,得23c b =.所以22236a b bc b -==,即227a b =.由余弦定理得2223cos 22b c a A bc +-==.所以30A =︒.【例6】 正余弦定理在平面几何中的应用⑴ 在平行四边形ABCD 中,3AB =,5BC =,6AC =,求BD⑵ 在ABC △中,已知4AB =,7AC =,BC 边上的中线7AD =,那么BC = .⑶ (目标班专用)在ABC △中,已知46AB =6cos ABC ∠=,AC 边上的中线5BD ,求sin A 的值【解析】 ⑴如图,在ABC △中,2222cos AC AB BC AB BC B =+-⋅,即222635235cos B =+-⋅⋅ ①在ABD △中,2222cos BD AB AD AB AD A =+-⋅,即22235235cos BD A =+-⋅⋅ ② ①+②得:()22226235BD +=+,即42BD =【点评】由本题可以得出平行四边形定理:平行四边形的对角线平方之和等于四条边长平方之和⑵ 解法一:如图:设BD x =,则2BC x =,DC x =,∵πADB ADC ∠=-∠,cos cos ADB ADC ∠=-∠∴,由余弦定理,得222222774722772222x x x x ⎛⎫⎛⎫+-+- ⎪ ⎪⎝⎭⎝⎭=-⋅⋅⋅⋅,解得92x =,9BC =∴ 解法二:由平行四边形定理得:()2222247781BC =+-=,9BC =∴⑶ 如图:设E 为BC 的中点,连接DE ,则DE AB ∥,且1262DE AB ==BE x =,在BDE △中利用余弦定理可得: 2222cos BD BE ED BE ED BED =+-⋅∠,()()6cos cos πcos πcos BED DEC ABC ABC ∠=-∠=-∠=-∠=∵28266523x =++∴,解得1x =或73x =-(舍),故2BC =,从而222282cos 3AC AB BC AB BC ABC =+-⋅∠=,即DA 72xx745463DCADCB A2213AC =, 又30sin 6ABC ∠=∵,故22123sin 306A =,70sin 14A =∴【教师备案】因为三角形的面积和正余弦定理关系不是特别紧密,而且到本讲结束,三角形的面积公式已经全部讲完,所以把三角形的面积单独做一个板块,老师可以把所有的三角形面积公式给学生讲一下. 面积公式:()11111sin sin sin 222224a abcS ah a b c r ab C bc A ac B R ==++====.其中r 为ABC △内切圆半径,R 为外接圆半径.【教师备案】在求三角形的面积时,学生印象最深的就是12a ah ,那这个时候老师就可以根据12a ah 推导其它公式,并且老师可以在这里把三角形的面积公式全部给学生整理一下,但是本讲重点是介绍1sin 2S ab C =类型的三角形面积公式,如果学生的程度很好,老师可以介绍一下“海伦公式”和圆内接四边形面积公式.【选讲】海伦公式:()()()S p p a p b p c =---,其中2a b cp ++=. 【推导】 ()2222222111sin 1cos 12224a b c S ab C ab C ab a b+-==-=- ()()()2222222222221142244a b a b c ab a b c ab a b c =-+-=++---+()()()()()()22221144a b c c a b a b c a b c a c b b c a ⎡⎤⎡⎤=+---=+++-+-+-⎣⎦⎣⎦ 令()12p a b c =++,则()()()S p p a p b p c =---圆内接四边形面积:()()()()S p a p b p c p d =----,其中2a b c dp +++=. 【推导】由()22222cos 2cos πa b ab c d cd θθ+-=+--,可得2222cos 22a b c d ab cdθ+--=+()()222222222sin 1cos 22ab cd a b c d ab cdθθ+-+--=-=+()()()()=22b c d a a c d b a b d c a b c d ab cd++-++-++-++-+1.4三角形的面积知识点睛CB A c b aDC BAπ-θθd cba(){}()11sin sin πsin 22S ab cd ab cd θθθ=+-=+ ()()()()()()()()1=42222b c d a a c d b a b d c a b c d a b c d a b c d a b c d a b c d a b c d p a p b p c p d ++-++-++-++-++++++++++++⎛⎫⎛⎫⎛⎫⎛⎫=---- ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭=----【教师备案】老师在讲完三角形的面积后就可以让学生做【铺垫】,【铺垫】是直接利用公式求三角形面积的,例7不能够直接利用公式求三角形面积,需要先看在面积公式中缺少哪些变量,然后再根据题中的已知条件利用正余弦定理求出所需要的变量,最后再利用面积公式就可以了.第三题放了一道关于圆内接四边形面积的题目,供老师选择使用;例8是已知三角形面积解三角形,在解题过程中会用到正余弦定理,对于求面积的最大值的问题建议放到同步,因为在求最大值的问题时大多数要用到均值定理,学生这时候还没学,所以建议以后再讲.【铺垫】 在ABC △中,若5AB =,7BC =,33sin 14B =,求ABC △的面积. 【解析】 ∵5AB =,7BC =,33sin 14B =, 1133153sin 5722144ABCS AB BC B =⋅⋅=⨯⨯⨯=△∴【例7】求面积⑴ 已知ABC △,三个内角,,A B C 的对边分别记为a b c ,,,43460b c B ===︒,,,求ABC S △. ⑵ 已知ABC △,三个内角,,A B C 的对边分别记为a b c ,,,若234a b c ===,,,求ABC S △. ⑶(目标班专用)已知:四边形ABCD 内接于圆O ,四边长依次为2,7,6,9,求圆直径. 【解析】⑴ 分析:三角形的已知条件为常见的SSA 型.根据条件有两种思路求三角形的面积: 11sin sin 22ABC S bc A ac B ∆=⋅=⋅.所以欲求三角形面积需要先求A 或先求a .方法一:由正弦定理知sin sin b cB C =,sin 4sin 601sin 243c B C b ︒===, 因为C 是三角形的一个内角,故30C ︒=或150︒, 又60B ︒=,故30C ︒=.180603090A ︒︒︒︒=--=,从而1832ABC S bc ∆==.方法二:由余弦定理得222cos 2a c bB ac +-=,即24320a a --=.()()480a a +-=.因为0a >,所以8a =.1sin 832ABC S ac B ∆=⋅=.⑵ 要求面积,先求一个角,已知三边,可以用余弦定理求一角:222416911cos 21616a cb B ac +-+-===,经典精讲∴2315sin 1cos 16B B =-=, ∴113153sin 241522164ABC S ac B ∆==⋅⋅⋅=. ⑶85.【铺垫】已知ABC △的三边长分别为a b c ,,,且面积()22214ABC S b c a =+-△,则A 等于( ) A .45 B .30 C .120 D .15【解析】 A()2221112cos cos 442ABC S b c a bc A bc A =+-=⨯=△,又1sin 2ABC S bc A =△∵,sin cos A A =∴,45A =∴【例8】 已知三角形面积解三角形ABC △中,角A B C ,,的对边分别为a b c ,,,22sin 3cos C C =,7c =,又ABC △的面积为332, 求⑴角C 的大小;⑵a b +的值【解析】⑴由已知得()221cos 3cos C C -=,1cos 2C =∴或cos 2C =-(舍), ∴在ABC △中,60C =⑵133sin 22ABC S ab C ==△∵,133sin 6022ab =∴,6ab =∴,又2222cos c a b ab C =+-∵,()22272cos a b ab C =+-∴,227a b ab +-=∴,2213a b +=∴,222255a b a b ab +=++==∴【演练1】 (2010北京卷文理10)在ABC △中,若2π133b c C ==∠=,,,则________a = 【解析】1 方法一: 由余弦定理222cos 2a b c C ab+-=得, 220a a +-=.∵0a >,∴1a =.方法二: 由正弦定理sin sin b c B C =得,1sin 2B =,π6B =或5π6,又因为b c <,即B C <, 所以π6B =,∴2ππππ366A =--=.∴1a b ==.【演练2】 在ABC △中,角A B C ,,的对边分别为a b c ,,,若()222tan 3a c b B ac +-=,则角B 的值为( ).实战演练A .π6 B . π3 C .π6或5π6 D . π3或2π3【解析】D由余弦定理2222cos a c b ac B +-=及()222tan a c b B +-得, sin B =. 所以π3B =或2π3.【演练3】 在ABC △中,已知222sin sin sin sin B C A A C --=,则角B 的大小为( )A .150︒B .30︒C .120︒D .60︒ 【解析】A由222sin sin sin sin B C A A C --及正弦定理可得222b c a --=即得222cos 2a c b B ac +-==,∴150B =︒.【演练4】 在ABC △中,角A B C ,,所对的边分别是a b c ,,,1tan 2A =,cos B = 若ABC △最长的边为1,则最短边的长为( ).A B C D 【解析】D由cos B =B 为锐角,∴1tan 3B =,故()()tan tan πtan C A B A B =--=-+tan tan 11tan tan A BA B+=-=--⋅①, 由①知135C ∠=︒,故c 边最长,即1c =,又tan tan A B >,故b 边最短,∵sin B =,sin C =sin sin b c B C =,∴sin sin c B b C ==【演练5】(2011西城一模文15) 设ABC △的内角A ,B ,C 所对的边长分别为a ,b ,c ,且4cos 5B =,2b =. ⑴ 当30A =︒时,求a 的值;⑵ 当ABC △的面积为3时,求a c +的值.【解析】 ⑴ 因为4cos 5B =,所以3sin 5B =,由正弦定理sin sin a b A B =,可得10sin303a =︒,所以53a =.⑵ 因为ABC △的面积1sin 2S ac B =,3sin 5B =,所以3310ac =,10ac =.由余弦定理2222cos b a c ac B =+-,得222284165a c ac a c =+-=+-,即2220a c +=.所以2()220a c ac +-=,2()40a c +=,所以,a c +=概念要点回顾1.正弦定理公式;余弦定理公式22a b+-= .2.三角形面积公式S=.盲人数学家——欧拉1783年9月18日,法国人蒙高尔费兄弟举行了第二次热气球升空试验。
高考数学一轮复习 几何证明选讲 第1课时 相似三角形的判定及有关性质课件 理(选修41)

另一腰.
平分
• 2.平行线分线段成比例定理 • 三条平行线截两条直线,所得的___对__应线段成比例. • 推论:平行于三角形一边的直线截其他两边(或两边的延长
线)所得的对应线段成_______. • 3.相似三角形的判定 比例 • 判定定理1:两角对应_____,两三角形相似. • 判定定理2:两边对应___相__等___且夹角______,两三角形相 • 似判.定定理3:三边对应___成__比__例_,两三角形相相等似.
【解析】 (1)证明:∵OE∥BC, ∴AAEB=AAOC.又∠BAC=∠CAB,∴△EAO∽△BAC. ∴OBCE=AAEB,同理OBCF=DDCF. ∵AD∥EF∥BC,∴AABE=DDCF,∴OBCE=OBCF. ∴OE=OF.
(2)∵OE∥AD,∴BBOD=BBEA,∴△EBO∽△ABD. ∴OADE=BBOD,同理OBCE=AAOC. 又 AD∥BC,∴BBOD=CAOC,∴OADE+OBCE=CAOC+AAOC=1. • 【答案】 (1)略 (2)1
• 答案 6
解析 由直角三角形射影定理,得 AC2=AD·AB. ∴AB=AACD2=422=8,∴BD=AB-AD=8-2=6.
授人以渔
题型一 平行线分线成比例
例1 如图,在梯形 ABCD 中,AD∥BC,EF 经过梯形对角线 的交点 O,且 EF∥AD. (1)求证:OE=OF; (2)求OADE+OBCE的值.
即6-3x=3
x
,所以 3
x2-6x+9=0,解得
x=3.
(2)若△ADP∽△BCP,则ABDC=BAPP,
即 3
33=6-x x,解得 x=23.
几何证明选讲知识点汇总与练习(内含答案)

⼏何证明选讲知识点汇总与练习(内含答案)《⼏何证明选讲》知识点归纳与练习(含答案)⼀、相似三⾓形的判定及有关性质平⾏线等分线段定理平⾏线等分线段定理:如果⼀组平⾏线在⼀条直线上截得的线段相等,那么在其他直线上截得的线段也相等。
推理1:经过三⾓形⼀边的中点与另⼀边平⾏的直线必平分第三边。
推理2:经过梯形⼀腰的中点,且与底边平⾏的直线平分另⼀腰。
平分线分线段成⽐例定理平分线分线段成⽐例定理:三条平⾏线截两条直线,所得的对应线段成⽐例。
推论:平⾏于三⾓形⼀边的直线截其他两边(或两边的延长线)所得的对应线段成⽐例。
相似三⾓形的判定及性质相似三⾓形的判定:定义:对应⾓相等,对应边成⽐例的两个三⾓形叫做相似三⾓形。
相似三⾓形对应边的⽐值叫做相似⽐(或相似系数)。
由于从定义出发判断两个三⾓形是否相似,需考虑6个元素,即三组对应⾓是否分别相等,三组对应边是否分别成⽐例,显然⽐较⿇烦。
所以我们曾经给出过如下⼏个判定两个三⾓形相似的简单⽅法:(1)两⾓对应相等,两三⾓形相似;(2)两边对应成⽐例且夹⾓相等,两三⾓形相似;(3)三边对应成⽐例,两三⾓形相似。
预备定理:平⾏于三⾓形⼀边的直线和其他两边(或两边的延长线)相交,所构成的三⾓形与三⾓形相似。
判定定理1:对于任意两个三⾓形,如果⼀个三⾓形的两个⾓与另⼀个三⾓形的两个⾓对应相等,那么这两个三⾓形相似。
简述为:两⾓对应相等,两三⾓形相似。
判定定理2:对于任意两个三⾓形,如果⼀个三⾓形的两边和另⼀个三⾓形的两边对应成⽐例,并且夹⾓相等,那么这两个三⾓形相似。
简述为:两边对应成⽐例且夹⾓相等,两三⾓形相似。
判定定理3:对于任意两个三⾓形,如果⼀个三⾓形的三条边和另⼀个三⾓形的三条边对应成⽐例,那么这两个三⾓形相似。
简述为:三边对应成⽐例,两三⾓形相似。
引理:如果⼀条直线截三⾓形的两边(或两边的延长线)所得的对应线段成⽐例,那么这条直线平⾏于三⾓形的第三边。
定理:(1)如果两个直⾓三⾓形有⼀个锐⾓对应相等,那么它们相似;(2)如果两个直⾓三⾓形的两条直⾓边对应成⽐例,那么它们相似。
备战高考数学(精讲+精练+精析)专题13.1几何证明选讲试题文(含解析)

专题1 几何证明选讲(文科)【三年高考】1. 【2016高考天津】如图,AB是圆的直径,弦CD与AB相交于点E,BE=2AE=2,BD=ED,则线段CE的长为__________.【答案】2.【2016高考新课标1卷】如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,OA为半径作圆.(I)证明:直线AB与O相切;(II)点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.【解析】(Ⅰ)设是的中点,连结,因为,所以,.在中,,即到直线的距离等于圆的半径,所以直线与⊙相切.(Ⅱ)因为,所以不是四点所在圆的圆心,设是四点所在圆的圆心,作直线.由已知得在线段的垂直平分线上,又在线段的垂直平分线上,所以.同理可证,.所以.3.【2016高考新课标2】如图,在正方形中,分别在边上(不与端点重合),且,过点作,垂足为.(Ⅰ) 证明:四点共圆;(Ⅱ)若,为的中点,求四边形的面积.4.【2016高考新课标3】如图,中的中点为,弦分别交于两点.(I)若,求的大小;(II)若的垂直平分线与的垂直平分线交于点,证明.【解析】(Ⅰ)连结,则.因为,所以,又,所以.又,所以,因此.(Ⅱ)因为,所以,由此知四点共圆,其圆心既在的垂直平分线上,又在的垂直平分线上,故就是过四点的圆的圆心,所以在的垂直平分线上,又也在的垂直平分线上,因此.5.【2015高考新课标2,】如图,为等腰三角形内一点,圆与的底边交于、两点与底边上的高交于点,与、分别相切于、两点.(Ⅰ)证明:;(Ⅱ)若等于的半径,且,求四边形的面积.【解析】(Ⅰ)由于是等腰三角形,,所以是的平分线.又因为分别与、相切于、两点,所以,故.从而.(Ⅱ)由(Ⅰ)知,,,故是的垂直平分线,又是的弦,所以在上.连接,,则.由等于的半径得,所以.所以和都是等边三角形.因为,所以,.因为,,所以.于是,.所以四边形的面积.6.【2015高考陕西,】如图,切于点,直线交于,两点,,垂足为.(I )证明:;(II )若,,求的直径.7.【2015高考新课标1】如图,AB是O的直径,AC是O的切线,BC交O于E.(Ⅰ)若D为AC的中点,证明:DE是O的切线;(Ⅱ)若,求∠ACB的大小.【解析】(Ⅰ)连结AE,由已知得,AE⊥BC,AC⊥AB,在Rt△AEC中,由已知得DE=DC,∴∠DEC=∠DCE,连结OE,∠OBE=∠OEB,∵∠ACB+∠ABC=90°,∴∠DEC+∠OEB=90°,∴∠OED=90°,∴DE是圆O的切线. (Ⅱ)设CE=1,AE=,由已知得AB=,,由射影定理可得,,∴,解得=,∴∠ACB=60°.8.【2015高考湖南】如图,在圆中,相交于点的两弦,的中点分别是,,直线与直线相交于点,证明:(1);(2)【解析】(1)如图所示,∵,分别是弦,的中点,∴,,即,,,又四边形的内角和等于,故;(2)由(I)知,,,,四点共圆,故由割线定理即得9. 【2014高考辽宁第22题】如图,EP交圆于E、C两点,PD切圆于D,G为CE上一点且,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.(Ⅰ)求证:AB为圆的直径;(Ⅱ)若AC=BD,求证:AB=ED.【解析】(Ⅰ)因为PD=PG,所以∠PDG=∠PGD. 由于PD为切线,故∠PDA=∠DBA, 又由于∠PGD=∠EGA,故∠DBA=∠EGA,所以∠DBA+∠BAD=∠EGA+∠BAD,从而∠BDA=∠PFA.由于AF垂直EP,所以∠PFA=90°,于是∠BDA=90°,故AB是直径.(Ⅱ)连接BC,DC.由于AB是直径,故∠BDA=∠ACB=90°,在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,从而Rt△BDA≌Rt△ACB,于是Rt△BDA与∠DAB=∠CBA.又因为∠DCB=∠DAB,所以∠DCB=∠CBA,故DC∥AB. 由于ED是直径,由(Ⅰ)得ED=AB.10. 【2014高考全国2第22题】如图,P是O外一点,PA是切线,A为切点,割线PBC与O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交O于点E.证明:(Ⅰ)BE=EC;(Ⅱ)AD DE=2【解析】(Ⅰ)连结AB,AC,由题意知PA=PD,故,因为,,,所以,从而,因此BE=EC. (Ⅱ)由切割线定理得:,因为,所以,,由相交弦定理得:===,所以等式成立.11. 【2014高考全国1第22题】如图,四边形是的内接四边形,的延长线与的延长线交于点,且.(Ⅰ)证明:;(Ⅱ)设不是的直径,的中点为,且,证明:为等边三角形.【三年高考命题回顾】纵观前三年各地高考试题, 高考对几何证明的考查,主要考查有关三角形相似、全等、面积、线段长度及角相等的求解及证明,以平行线等分线段定理,平行线截割定理,相似三角形的判定与性质定理,直角三角形射影定理,圆心角、圆周角定理,圆内接四边形的性质定理及判定定理,圆的割线定理,切割线定理,弦切角定理,相交弦定理等为主要考查内容,题目难度一般为中、低档,备考中应严格控制训练题的难度.【2017年高考复习建议与高考命题预测】由前三年的高考命题形式可以看出, 高考对这部分要求不是太高,要求会以圆为几何背景,利用直角三角形射影定理,圆周角定理、圆的切线的判定定理及性质定理,相交弦定理、圆内接四边形的性质定理与判定定理、切割线定理证明三角形相似,全等,求线段长等,预测2017年高考还会以圆为几何背景,考查相交线定理,切割线定理,以及圆内接四边形的性质定理与判定定理,考查学生的数形结合的能力.“几何证明选讲”是选修系列4的一个专题,该专题在高考中只考查“相似三角形”和“圆”这两部分平面几何内容,且与另三个选修4的专题一起命题,供考生选择作答.其核心内容为:线段成比例与相似三角形,圆的切线及其性质,与圆有关的相似三角形等.对同学们来说,“几何证明选讲”是初中所学知识的深化,因而倍感亲切.试题题型为解答题,且难度不大.题型以比例问题为主,平行线分线段成比例定理、相似形、角平分线定理、直角三角形中的射影定理、圆中的割线定理、切割线定理和相交弦定理等,都涉及线段成比例,因此比例问题是本专题中所占比重最大的题型.解决这类问题,主要方法就是设法利用上述定理,并灵活变形.复习建议:圆内接四边形的重要结论:内接于圆的平行四边形是矩形;内接于圆的菱形是正方形;内接于圆的梯形是等腰梯形.应用这些性质可以大大简化证明有关几何题的推证过程.与圆有关的比例线段的证明要诀:相交弦、切割线定理是法宝,相似三角形中找诀窍,联想射影定理分角线,辅助线来搭桥,第三比作介绍,代数方法不可少,分析综合要记牢,十有八九能见效.【2017年高考考点定位】几何证明选讲的内容涉及的考点可归纳为:①相似三角形的定义与性质;②平行线截割定理;③直角三角形射影定理;④圆周角与圆心角定理;⑤圆的切线的判定定理及性质定理;⑥弦切角的性质;⑦相交弦定理;⑧圆内接四边形的性质定理和判定定理;⑨切割线定理.【考点1】相似三角形的判定与性质【备考知识梳理】1.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.推论1:经过三角形一边的中点与另一边平行的直线必平分第三边.推论2:经过梯形一腰的中点,且与底边平行的直线平分另一腰.2.平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例.推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.3.相似三角形的判定与性质(1)判定定理:结论相似三角形外接圆的直径比、周长比等于相似比,外接圆的面积比等于相似比的平方射影定理直角三角形中,每一条直角边是这条直角边在斜边上的射影和斜边的比例中项;斜边上的高是两条直角边在斜边上的射影的比例中项【规律方法技巧】1.判定两个三角形相似的常规思路(1)先找两对对应角相等;(2)若只能找到一对对应角相等,则判断相等的角的两夹边是否对应成比例;(3)若找不到角相等,就判断三边是否对应成比例,否则考虑平行线分线段成比例定理及相似三角形的“传递性”.2.借助图形判断三角形相似的方法(1)有平行线的可围绕平行线找相似;(2)有公共角或相等角的可围绕角做文章,再找其他相等的角或对应边成比例;(3)有公共边的可将图形旋转,观察其特征,找出相等的角或成比例的对应边.3.比例线段常用平行线产生,利用平行线转移比例是常用的证题技巧,当题中没有平行线条件而有必要转移比例时,也常添加辅助平行线,从而达到转移比例的目的.4.判定两个三角形相似要注意结合图形特征灵活选择判定定理,特别要注意对应角和对应边.在一个题目中,相似三角形的判定定理和性质定理可能多次用到.相似三角形的性质可用来证明线段成比例、角相等;也可间接证明线段相等.5..在使用直角三角形射影定理时,要学会将“乘积式”转化为相似三角形中的“比例式”.证题时,要注意作垂线构造直角三角形是解直角三角形时常用的方法.6.相似关系的证明中,经常要应用比例的性质:若,则①;②;③;④;⑤;⑥.7.辅助线作法:几何证明题的一个重要问题就是作出恰当的辅助线,相似关系的基础就是平行截割定理,故作辅助线的主要方法就是作平行线,见中点取中点连线利用中位线定理,见比例点取等比的分点构造平行关系,截取等长线段构造全等关系,立体几何中通过作平行线或连结异面直线上的点化异为共等等都是常用的作辅助线方法.【考点针对训练】1.【2016届河南省郑州一中高三考前冲刺四】如图所示,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N作割线NAB,交圆O于A,B两点,连接PA并延长,交圆O于点C,连接PB交圆O于点D,若MC=BC.(1)求证:△APM△ABP;(2)求证:四边形PMCD是平行四边形.2.【2016年山西省右玉一中高考冲刺压轴卷三】如图,已知⊙和⊙相交于两点,为⊙的直径,直线交⊙于点,点为弧中点,连结分别交⊙、于点,连结.(Ⅰ)求证:;(Ⅱ)求证:.【解析】(Ⅰ)连结,∵为⊙的直径,∴,∵为⊙的直径,∴,∵,∴,∵为弧中点,∴,∵,∴,∴,∴,∴.(Ⅱ)由(Ⅰ)知,,∴,∴,由(Ⅰ)知,∴.【考点2】圆的有关问题【备考知识梳理】1.圆周角定理(1)圆周角:顶点在圆周上且两边都与圆相交的角.(2)圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半.(3)圆心角定理:圆心角的度数等于它所对弧的度数.推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.2.圆内接四边形的性质与判定定理(1)性质:定理1:圆内接四边形的对角互补.定理2:圆内接四边形的外角等于它的内角的对角.(2)判定:判定定理:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.推论:如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.另外:若两点在一条线段同侧且对该线段张角相等,则此两点与线段两个端点共圆,特别的,对定线段张角为直角的点共圆.3.圆的切线(1)直线与圆的位置关系直线与圆交点的个数直线到圆心的距离d与圆的半径r的关系相交两个d<r相切一个d=r相离无d>r性质定理:圆的切线垂直于经过切点的半径.推论1:经过圆心且垂直于切线的直线必经过切点.推论2:经过切点且垂直于切线的直线必经过圆心.判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.(3)切线长定理:从圆外一点引圆的两条切线长相等.3.弦切角(1)弦切角:顶点在圆上,一边与圆相切,另一边与圆相交的角.(2)弦切角定理及推论①定理:弦切角的度数等于所夹弧的度数的一半.②推论:同弧(或等弧)上的弦切角相等,同弧(或等弧)上的弦切角等于它所夹的弧所对的圆周角. 4.与圆有关的比例线段定理名称基本图形条件结论应用相交弦定理弦AB、CD相交于圆内点P(1)PA·PB=PC·PD;(2)△ACP∽△DBP(1)在PA、PB、PC、PD四线段中知三求一;(2)求弦长及角切割线定理PA切⊙O于A,PBC是⊙O的割线(1)PA2=PB·PC;(2)△PAB∽△PCA(1)已知PA、PB、PC知二可求一;(2)求解AB、AC割线定理PAB、PCD是⊙O的割线(1)PA·PB=PC·PD;(2)△PAC∽△PDB(1)求线段PA、PB、PC、PD及AB、CD;(2)应用相似求AC、BD(1)(2)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.(4)切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.【规律方法技巧】1. 与圆有关的比例线段: (1)应用相交弦定理、切割线定理要抓住几个关键内容:如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等.(2)相交弦定理、切割线定理主要是用于与圆有关的比例线段的计算与证明.解决问题时要注意相似三角形知识及圆周角、弦切角、圆的切线等相关知识的综合应用.(3)相交弦定理、切割线定理、割线定理、切线长定理统称为圆幂定理:圆的两条弦或其延长线若相交,各弦被交点分成的两条线段长的积相等.当两交点在圆内时为相交弦定理,当两交点在圆外时为割线定理,两交点重合时为切线,一条上两点重合时为切割线定理,两条都重合时为切线长定理,应用此定理一定要分清两条线段是指哪两条.2. 弦切角定理及推论的应用(1)圆周角定理及其推论与弦切角定理及其推论多用于推出角的关系,从而证明三角形全等或相似,可求线段或角的大小.(2)涉及圆的切线问题时要注意弦切角的转化;关于圆周上的点,常作直线(或半径)或向弦(弧)两端画圆周角或作弦切角.3. 证明多点共圆,当两点在一条线段同侧时,可证它们对此线段张角相等,也可以证明它们与某一定点距离相等;如两点在一条线段异侧,则证明它们与线段两端点连成的凸四边形对角互补.4.涉及圆的切线问题时要注意弦切角的转化;关于圆周上的点,常作直径(或半径)或向弦(弧)两端画圆周角或作弦切角.5.一般地,涉及圆内两条相交弦时首先要考虑相交弦定理,涉及两条割线时要想到割线定理,涉及切线和割线时要注意应用切割线定理,要注意相交弦定理中线段之间的关系与切割线定理线段关系之间的区别.6.在平面几何的有关计算中往往要使用比例线段,产生比例线段的一个主要根据是两三角形相似.在涉及两圆的公共弦时,通常是作出两圆的公共弦.如果有过公共点的切线就可以使用弦切角定理.在两个圆内实现角的等量代换,这是解决两个圆相交且在交点处有圆的切线问题的基本思考方向.【考点针对训练】1.【2016届湖北七市教研协作体高三4月联考】已知中,,是外接圆劣弧上的点(不与点重合),延长至,延长至.(1)求证:;(2)若,中边上的高为,求外接圆的面积.2.【2016届陕西省高三下学期教学质检二】如图,已知圆与相交于两点,过点作圆的切线交圆于点,过点作两圆的割线,分别交圆、圆于点、,与相交于点. (Ⅰ)求证:;(Ⅱ)若是圆的切线,且,求的长.【解析】(Ⅰ)连接.∵是圆的切线,∴.又∵,∴,∴.(Ⅱ)证明:设,∵,∴.又∵,∴,∴.又∵,联立上述方程得到,∴.∵是圆的切线,∴.∴.【应试技巧点拨】1.辅助线作法:几何证明题的一个重要问题就是作出恰当的辅助线,相似关系的基础就是平行截割定理,故作辅助线的主要方法就是作平行线,见中点取中点连线利用中位线定理,见比例点取等比的分点构造平行关系,截取等长线段构造全等关系,立体几何中通过作平行线或连结异面直线上的点化异为共等等都是常用的作辅助线方法.2.比例的性质的应用相似关系的证明中,经常要应用比例的性质:若,则①;②;③;④;⑤;⑥.3.同一法:先作出一个满足命题结论的图形,然后证明图形符合命题已知条件,确定所作图形与题设条件所指的图形相同,从而证明命题成立.4.证明多点共圆,当两点在一条线段同侧时,可证它们对此线段张角相等,也可以证明它们与某一定点距离相等;如两点在一条线段异侧,则证明它们与线段两端点连成的凸四边形对角互补.5.与圆有关的比例线段(1)应用相交弦定理、切割线定理要抓住几个关键内容:如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等.(2)相交弦定理、切割线定理主要是用于与圆有关的比例线段的计算与证明.解决问题时要注意相似三角形知识及圆周角、弦切角、圆的切线等相关知识的综合应用.二年模拟1. 【2016年山西榆林高三二次模考】如图所示,在中,是的平分线,的外接圆交于点,.(1)求证:;(2)当时,求的长.2. 【2016年湖北八校高三四次联考】如图,在锐角三角形中,,以为直径的圆与边另外的交点分别为,且于.(Ⅰ)求证:是的切线;(Ⅱ)若,,求的长.【解析】(Ⅰ)连结则又,∴为的中点,而为中点,∴,又,∴,而是半径,∴是的切线.(Ⅱ)连,则,则,∴,设,则,由切割线定理得:,即,解得:(舍),∴EFDOC BA3. 【2016年安徽安庆二模】如图,以的边为直径作圆,圆与边的交点恰为边的中点,过点作于点.(I )求证:是圆的切线;(II )若,求的值.【解析】(Ⅰ)如图,连接.因为是的中点,是的中点,所以//.因为,所以,所以是⊙的切线. (Ⅱ)因为是⊙的直径,点在⊙上,所以. 又是的中点,所以. 故.因为,所以. 在直角三角形中,;在直角三角形中,. 于是.4.【2016年江西高三九校联考】如图所示,为的直径,为的中点,为的中点.(1)求证:;(2)求证:.5. 【2016年安徽淮北一中高三模考】如图,是圆上的两点,为圆外一点,连结分别交圆于点,且,连结并延长至,使.(1)求证:;(2)若,且,求.【解析】(1)连结,因为,又因为,所以,所以,由已知,所以,且,所以,所以.(2)因为,所以,则,所以,又因为,所以,所以,所以.6. 【2016年江西南昌高三一模】如图,圆M与圆N交于A, B两点,以A为切点作两圆的切线分别交圆M和圆N于C、D两点,延长DB交圆M于点E,延长CB交圆N于点F.已知BC=5, DB=10. (I)求AB的长;(II)求.【解析】(Ⅰ)根据弦切角定理,知,,∴△∽△,则,故.(Ⅱ)根据切割线定理,知,,两式相除,得(*).由△∽△,得,,又,由(*)得.7. 【2016年河南八市高三三模】已知,内接于圆,延长到点,使得交圆于点.(1)求证:;(2)若,求证:.【解析】(1)如图,连结..又(2)8.【2016届河北省石家庄市高三二模】如图,内接于⊙,,弦交线段于,为的中点,在点处作圆的切线与线段的延长线交于,连接.(I)求证:;(II)若,⊙的半径为,求切线的长.【解析】(I)证明:在中,弦相交于E,,又E为AC的中点,所以,又因为,,根据射影定理可得,;(II)因为为直径,所以,又因为,所以为等腰直角三角形.,根据勾股定理得,解得,所以,由(I)得所以,所以.9.【2016届陕西省高三高考全真模拟四】如下图,是圆的两条互相垂直的直径,是圆上的点,过点作圆的切线交的延长线于.连结交于点.(1)求证:;(2)若圆的半径为,求的长.【解析】(1)证明:连接,由弦切角定理知,又,即.由切割线定理得,所以.(2)由知,.在中,由得,.在中,由得,于是.10.【2016届山西右玉一中高三下学期模拟】已知如图,四边形是圆的内接四边形,对角线交于点,直线是圆的切线,切点为,.(1)若,求的长;(2)在上取一点,若,求的大小.11. 【2015届陕西西安西北工大附中高三下学期5月模拟】如图,和相交于A,B两点,过A 作两圆的切线分别交两圆于两点,连结并延长交于点.证明:(Ⅰ);(Ⅱ).【解析】(1)由与相切于,得,同理,所以从而,即(2)由与相切于,得,又,得从而,即,综合(1)的结论,12.【2015届陕西省西工大附中高三下学期模拟考试一】如图,⊙的直径的延长线与弦的延长线相交于点,为⊙上一点,AE=AC ,交于点,且,(Ⅰ)求的长度.(Ⅱ)若圆F 与圆内切,直线PT与圆F切于点T,求线段PT的长度【解析】(Ⅰ)连结,由同弧对应的圆周角与圆心角之间的关系结合题中条件弧长等于弧长可得,又,,从而,故∽,∴, 由割线定理知,故.(Ⅱ)若圆F 与圆内切,设圆的半径为,因为即,所以是圆的直径,且过点圆的切线为,则,即.13.【2015届吉林省吉林市高三第三次模拟考试】如图,在△ABC 中,,以为直径的⊙O 交于,过点作⊙O 的切线交于,交⊙O 于点.(Ⅰ)证明:是的中点;(Ⅱ)证明:.【解析】(Ⅰ)证明:连接,因为为⊙O 的直径,所以,又,所以CB切⊙O于点B ,且ED 切于⊙O 于点E ,因此,,所以,得,因此,即是的中点(Ⅱ)证明:连接BF ,可知BF 是△ABE 斜边上的高,可得△ABE ∽△AFB ,于是有,即,同理可证,所以.14.【2015届辽宁省师大附中高三模拟考试】如图,圆周角的平分线与圆交于点,过点的切线与弦的延长线交于点,交于点.(1)求证:;(2)若四点共圆,且弧与弧相等,求【解析】(1)因为与圆相切,,平方,所以,,所以(2)弧与弧相等,设,,,.15.【2015届陕西省西安市第一中学高三下学期自主命题二】如图,在中,是的角平分线,的外接圆交于点,.EDCA B(Ⅰ)求证:; (Ⅱ)当,时,求的长.【解析】(Ⅰ)连接,因为是圆内接四边形,所以又∽,即有,又因为,可得因为是的平分线,所以,从而(Ⅱ)由条件知,设,则,根据割线定理得,即即,解得或(舍去),则.EDCA B拓展试题以及解析 1. 如图,内接于⊙,弦AE 交BC 于点D ,已知,,OD =1,. (Ⅰ)求;(Ⅱ)求中BC 边上的高.【入选理由】本题主要考查平面几何的相关知识,同时考查考生的逻辑推理能力.高考对平面几何的考查主要是通过三角形全等或三角形相似进行边角转化,并综合运用圆的切割线定理、相交弦定理等 进行证明计算.以圆为背景是基本不变的,因而灵活应用圆的几何性质,找准有关的对应三角形、对应边和对应角是解题的关键.本题构思巧妙,难度不大,故选此题.2.如图,过圆外一点作圆的切线,切点为,割线、割线分别交圆于与、与.已知的垂直平分线与圆相切.(1)求证:;(2)若,,求的长.【解析】(1)证明:连结,∵与圆相切,∴.又为的垂直平分线,∴,∴,∴.(2)由(1)知且为的中点,∴为的中点,且,∴.∵为圆的切线,∴,∴,∴,∴.【入选理由】本题考查圆的切割线定理,弦切角定理等基础知识,意在考查逻辑思维能力和推理论证能力. 切割线定理、三角形相似、四点共圆的性质,是高考重点考查知识点,本题难度不大,故选此题.3.如图,直线AB过圆心O,交圆O于A、B,直线AF交圆O于F(不与B重合),直线与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.求证:(Ⅰ);(Ⅱ).【证明】(Ⅰ)连接,是直径,,.切圆于,..(Ⅱ)连接,切圆于,.又∽..【入选理由】本题考查圆的弦切角定理、三角形相似等基础知识,意在考查逻辑思维能力和推理论证能力.本题由弦切角定理入手,得出三角形相似,从而可证,本题难度不大,故选此题.4.如图,是⊙的直径,是圆上两点,交于点,若,.(Ⅰ)求证:;(Ⅱ)求线段的长度.【入选理由】本题考查平面几何的证明,具体涉及圆的性质,四点共圆,割线定理等基础知识,意在考察学生推理证明和逻辑思维能力.本题考查知识基础,综合性强,是高考出题方向,故选此题.5.如图,圆内接四边形满足∥,在的延长线上,且. 若,.(Ⅰ)证明:;(Ⅱ)求的长.【解析】(Ⅰ)由知是圆的切线. ∴由弦切线角定理得,又,∴,∴;(Ⅱ)由(Ⅰ)知,又,∴∽,∴,又,,∴,∵,∴. 【入选理由】本题考查圆的切线的性质,圆內接四边形的性质,三角形相似等基础知识,意在考察学生推理证明和逻辑思维能力.本题考查知识基础,难度不大,故选此题.6.如图,点P是△ABC的外接圆O在C点的切线与直线AB的交点.(Ⅰ)若∠ACB=∠APC,证明:BC⊥PC;(Ⅱ)若D是圆O上一点,∠BPC=∠DAC,AC=,AB=,PC=4,求CD的长.【证明】(Ⅰ)由弦切角定理知,∠ABC=∠ACP,∵∠ACB=∠APC,∴△ACB∽△APC,∴∠BAC=∠CAP,∵∠BAC+∠CAP=,∴∠BAC=∠CAP=90°,∴BC是圆O的直径,又PC是圆O的切线,∴BC⊥PC. (Ⅱ)由切割线定理知,,即,即,解得(负值舍去),由弦切角定理及同弧所对的圆周角相等知,∠ACP=∠ABC=∠CDA,∵∠BPC=∠DAC,∴△CAD∽△APC,∴,∴=.【入选理由】本题考查三角形相似的判定与性质、弦切角定理、切割线定理等基础知识,意在考查学生推理证明和逻辑思维能力.本题第一问由弦切角入手,得三角形相似,从而得结论,第二问由切割线定理入手,结合弦切角定理及同弧所对的圆周角相等,得三角形相似,像这种题型考查知识基础,综合性强,是高考出题方向,故选此题.7.如图所示,在四边形中,交于点,.(Ⅰ)求证:、、、四点共圆;(Ⅱ)过作四边形外接圆的切线交的延长线于,,求证:平分.【证明】(Ⅰ)∵,∴,,∵,, ∴,,∴=,=,=,=,∴=+++=+++==,∴、、、四点共圆;(Ⅱ)由弦切角定理可知:∠=∠,∵,∴∽,∴=,∵,∴=,∴=,∴=,∴=,∴=∠,∴平分.。
高三数学解析几何试题答案及解析

高三数学解析几何试题答案及解析1.(本小题满分10分)选修4-1:几何证明选讲如图,是圆的直径,是半径的中点,是延长线上一点,且,直线与圆相交于点、(不与、重合),与圆相切于点,连结,,.(Ⅰ)求证:;(Ⅱ)若,求.【答案】(Ⅰ)详见解析(Ⅱ)【解析】(Ⅰ)证明目标可看做线段成比例,即证明思路确定为证明三角形相似:利用切割线定理得:,又由与相似,得;所以(Ⅱ)由(1)知,,与相似,则,所以试题解析:(1)连接,,,为等边三角形,则,可证与相似,得;又,则(2)由(1)知,,与相似,则因为,所以【考点】三角形相似,切割线定理2.(本小题满分10分)选修4—4:坐标系与参数方程在直角坐标系中,直线的参数方程为为参数),以该直角坐标系的原点为极点,轴的正半轴为极轴的极坐标系下,圆的方程为.(Ⅰ)求直线的普通方程和圆的圆心的极坐标;(Ⅱ)设直线和圆的交点为、,求弦的长.【答案】(Ⅰ)的普通方程为,圆心;(Ⅱ).【解析】(Ⅰ)消去参数即可将的参数方程化为普通方程,在直角坐标系下求出圆心的坐标,化为极坐标即可;(Ⅱ)求出圆心到直线的距离,由勾股定理求弦长即可.试题解析:(Ⅰ)由的参数方程消去参数得普通方程为 2分圆的直角坐标方程, 4分所以圆心的直角坐标为,因此圆心的一个极坐标为. 6分(答案不唯一,只要符合要求就给分)(Ⅱ)由(Ⅰ)知圆心到直线的距离, 8分所以. 10分【考点】1.参数方程与普通方程的互化;2.极坐标与直角坐标的互化.:的焦点,且抛物线3.(本题满分12分)如图,O为坐标原点,点F为抛物线C1C1上点P处的切线与圆C2:相切于点Q.(Ⅰ)当直线PQ的方程为时,求抛物线C1的方程;(Ⅱ)当正数变化时,记S1,S2分别为△FPQ,△FOQ的面积,求的最小值.【答案】(Ⅰ);(Ⅱ).【解析】第一问要求抛物线的方程,任务就是求的值,根据导数的几何意义,设出切点坐标,从而求得,再根据切点在切线上,得,从而求得,进而得到抛物线的方程,第二问根据三角形的面积公式,利用题中的条件,将两个三角形的面积转化为关于和切点横坐标的关系式,从而有,利用基本不等式求得最值.试题解析:(Ⅰ)设点,由得,,求导,……2分因为直线PQ的斜率为1,所以且,解得,所以抛物线C1的方程为.(Ⅱ)因为点P处的切线方程为:,即,根据切线又与圆相切,得,即,化简得,由,得,由方程组,解得,所以,点到切线PQ的距离是,所以,,所以,当且仅当时取“=”号,即,此时,,所以的最小值为.【考点】导数的几何意义,三角形的面积,基本不等式.4.(本小题满分12分)已知椭圆的左、右焦点分别为F1(-3,0),F2(3,0),直线y=kx与椭圆交于A、B两点.(Ⅰ)若三角形AF1F2的周长为,求椭圆的标准方程;(Ⅱ)若,且以AB为直径的圆过椭圆的右焦点,求椭圆离心率e的取值范围.【答案】(Ⅰ);(Ⅱ).【解析】(Ⅰ)直接由题意和椭圆的概念可列出方程组,进而可求出椭圆的标准方程即可;(Ⅱ)首先设出点,然后联立直线与椭圆的方程并整理可得一元二次方程,进而由韦达定理可得,再结合可列出等式并化简即可得到等式,最后结合已知,即可求出参数的取值范围,进而得出椭圆离心率e的取值范围即可.试题解析:(Ⅰ)由题意得,得.结合,解得,.所以,椭圆的方程为.(Ⅱ)由得.设.所以,易知,,因为,,所以.即,将其整理为.因为,所以,即,所以离心率.【考点】1、椭圆的标准方程;2、直线与椭圆的相交综合问题;5.(本小题满分12分)椭圆()的上顶点为,是上的一点,以为直径的圆经过椭圆的右焦点.(1)求椭圆的方程;(2)动直线与椭圆有且只有一个公共点,问:在轴上是否存在两个定点,它们到直线的距离之积等于?如果存在,求出这两个定点的坐标;如果不存在,说明理由.【答案】(1);(2)存在两个定点,.【解析】(1)由题设可得①,又点P在椭圆C上,可得②,又③,由①③联立解得c,b2,即可得解.(2)设动直线l的方程为y=kx+m,代入椭圆方程消去y,整理得(﹡),由△=0,得,假设存在,满足题设,则由对任意的实数k恒成立.由即可求出这两个定点的坐标.试题解析:(1),,由题设可知,得①又点在椭圆上,,②③①③联立解得,,故所求椭圆的方程为(2)当直线的斜率存在时,设其方程为,代入椭圆方程,消去,整理得()方程()有且只有一个实根,又,所以,得假设存在,满足题设,则由对任意的实数恒成立,所以,解得,或当直线的斜率不存在时,经检验符合题意.总上,存在两个定点,,使它们到直线的距离之积等于.……12分【考点】1、直线与圆锥曲线的关系;2、椭圆的标准方程.【方法点晴】本题主要考查了椭圆的标准方程的解法,考查了直线与圆锥曲线的关系,综合性较强,属于中档题.处理直线与圆锥曲线的关系问题时,注意韦达定理的应用,同时还得特别注意直线斜率不存在时的情况的验证.6.直线被圆截得的弦长为()A.1B.2C.4D.【答案】C【解析】圆心,圆心到直线的距离,半径,所以最后弦长为.故选C.【考点】点到直线的距离.7.(本小题12分)己知、、是椭圆:()上的三点,其中点的坐标为,过椭圆的中心,且,。
2013年高考数学全国各地名校重组卷01 文(教师版)课标版

2013年高考全国各地名校重组卷之数学文(课标版)01(教师版)【组卷说明】本卷以各地名校2013届高三入学、月考、期中试题为主题、以课标卷为模板、以“高考考试大纲”为指导进行组卷,是高考复习必备的优秀试卷。
本卷针对高考考点,难易程度重新组合试题。
重组角度:结合高考考点、重点、热点,内容覆盖各个章节各个知识点,从不同角度,不同方式考查知识点;考查目的:选用在知识交汇点处命题的题目,在考查考生的基础知识的同时,又考查数形结合、转化与化归、分类讨论、函数与方程等数学思想的应用,提高考生综合应用所学知识解题的能力。
希望本卷对大家有所帮助。
一、选择题:(共10小题,每小题5分,共50分)1.(某某省某某一中,检测题)设全集U=R ,集合A= {x|x 2-2x<0},B={x|x>l ),则集合U A C B =( )A .{x|0<x<l}B .{x|0<x ≤1)C .{x|0<x<2}D .{x-|x ≤1}2.(某某某某一中,期中试题)已知椭圆的中心在原点,离心率e =12,且它的一个焦点与抛物线y 2=-4x 的焦点重合,则此椭圆方程为( )A.22143x y +=B. 22186x y +=C. 2212x y += D. 2214x y += 3.(某某师大附中,期中试题)命题“,xx R e x ∃∈<”的否定是( ) A.,xx R e x ∃∈>B.,xx R e x ∀∈≥C.,xx R e x ∃∈≥D.,xx R e x ∀∈>4. 已知()[]21=cos 112,,f x x x x -∈-,则导函数()'f x 是( )A .仅有最小值的奇函数B .既有最大值,又有最小值的偶函数C .仅有最大值的偶函数D .既有最大值,又有最小值的奇函数几何性质,函数的基本性质是高考考查的重要内容,常以选择、填空的形式考查,属 中低档题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何证明选讲练习 姓名_______________
1.如图,在中,,
,过作的外接圆的切线,,与外接圆交于点,则的长为__________.
【答案】
2.如图, △ABC 为圆的内接三角形, BD 为圆的弦, 且BD //AC . 过点A 做圆的切线与DB 的延长线交于点E , AD 与BC 交于点F . 若AB = AC , AE = 6, BD = 5, 则线段CF 的长为______.
【答案】83 3.如图,AB 是圆O 的直径,点C 在圆O 上,延长BC 到D 使BC CD =,过C 作圆O 的切线交AD 于E .若6AB =,2ED =,则BC =_________.
【答案】23
4.如图, 弦AB 与CD 相交于O 内一点E , 过E 作BC 的平行线与AD 的延长线相交于点P . 已知PD =2DA =2, 则PE =_____.
【答案】.6
ABC 090C ∠=060,20A AB ∠==C ABC CD BD CD ⊥BD E DE 5E
D O
P
A B C
.
A E
D C
B O 第15题图
5.如图2
,在半径为7的O中,弦,
AB
CD
相交于点,2
P
PA PB
=
=,1
PD=,则圆心O到弦CD 的距离为____________.
【答案】
2
3
6.如图,圆O上一点C在直线AB上的射影为D,点D在半径OC上的射影为E.若3
AB AD
=,则CE
EO 的值为___________.
【答案】8
7.如图,AB为圆O的直径,P A为圆O的切线,PB与圆O相交于D.若PA=3,916
PD DB=
::,则PD=_________;AB=___________.
【答案】
9
5
;4
解三角形练习
1.如图,△ABC中,AB=AC=2,BC=,点D 在BC边上,∠ADC=45°,则AD的长度等于
______.
【命题意图】本题考查运用正余弦定理解三角形,是中档题.
【答案】2
23
【解析】(法1)过A 作AE ⊥BC,垂足为E ,∵AB=AC=2,BC=
23,∴E 是BC 的中点,且EC=3,在Rt AEC ∆中,AE=22AC EC -=1,又∵∠ADE=45°,∴DE=1,∴AD=
2;
(法2) ∵AB=AC=2,BC=23,由余弦定理知, cos C =2222AC BC AB AC BC +-⨯=2222(23)22223
+-⨯⨯=32, ∴C=30°, 在△ADC 中,∠ADE=45°,由正弦定理得,sin sin AD AC C ADC
=∠, ∴AD=sin sin AD C ADC ∠=1
222
⨯
=2. 2.如图,在△ABC 中,D 是边AC 上的点,且AB AD =,23AB BD =
,2BC BD =,则sin C 的值为( )
A .33
B .36
C .63
D .66
【答案】D
【解析】设BD a =,则由题意可得:2,BC a = 3AB AD a ==
,在ABD ∆中,由余弦定理得: 222cos 2AB AD BD A AB AD +-==⋅22232432()a a a ⨯-⨯=13,所以sin A =21cos A -=223,在△ABC 中,由正弦定理得,sin sin AB BC C A =,所以32sin 22a C a =,解得sin C =6,故选D . 3.,E F 是等腰直角ABC ∆斜边AB 上的三等分点,则tan ECF ∠=( )
A .1627
B .23
C .3
D .34
【答案】D
4.在△ABC 中, 4ABC π∠=
,AB 3BC =,则sin BAC ∠ =( ) (A )
(B )
(C )
(D )
【答案】C
5.ABC ∆中,90C ∠=,M 是BC 的中点,若3
1sin =∠BAM ,则=∠BAC sin ________.
6.在△ABC 中,已知AB=4,AC=7,BC 边的中线2
7=
AD ,求边BC 的长.
7.如图,在四边形ABCD 中,AC 平分∠DAB ,∠ABC=60°,AC=7,AD=6,S △ADC =
2
315,求AB 的长.
排列组合练习题
1.有6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品,已知6位同学之间共进行了13次交换,则收到份纪念品的同学人数为( ) 或 或 或 或
【解析】选
①设仅有甲与乙,丙没交换纪念品,则收到份纪念品的同学人数为人
②设仅有甲与乙,丙与丁没交换纪念品,则收到份纪念品的同学人数为人.
2.将字母排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有
A .12种
B .18种
C .24种
D .36种
4()A 13()B 14()C 23()D 24D 261315132C -=-=4244,,,,,a a b b c c
答案A
【命题意图】本试题考查了排列组合的用用.
【解析】利用分步计数原理,先填写最左上角的数,有3种,再填写右上角的数为2种,在填写第二行第一列的数有2种,一共有.
3.现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这些卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为
(A )232 (B)252 (C)472 (D)484
解析:,答案应选C . 另解:. 4. 两人进行乒乓球比赛,先赢三局着获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有( )
A .10种
B .15种
C .20种
D .30种
【解析】甲赢和乙赢的可能情况是一样的,所以假设甲赢的情况如下:
若两人进行3场比赛,则情况只有是甲全赢1种情况;
若两人进行4场比赛,第4场比赛必为甲赢前3场任选一场乙赢为种情况;
若两人进行5场比赛,第5场比赛必为甲赢前4场任选一场乙赢为种情况;
综上,甲赢有10种情况,同理,乙赢有10种情况,
则所有可能出现的情况共20种,故选C .
5.若从1,2,2,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有
A .60种
B .63种
C .65种
D .66种
【解析】1,2,2,…,9这9个整数中有5个奇数,4个偶数.要想同时取4个不同的数其和为偶数,则取法有:
4个都是偶数:1种;
2个偶数,2个奇数:种;
4个都是奇数:种.
∴不同的取法共有66种.
【答案】D
6.某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课个1节,则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 (用数字作答).
【解析】概率为 语文、数学、英语三门文化课间隔一节艺术课,排列有种排法,语文、数学、英语三门文化课相邻有32212⨯⨯=4728856072166
14151641122434316=-=--⨯⨯=--C C C C 4721226422021112412610111232
12143431204=-+=⨯⨯+-⨯⨯=+-C C C C C 313=C 624=C 225460C C =455C =3____5
33
44A A
种排法,语文、数学、英语三门文化课两门相邻有种排法. 故所有的排法种数有在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 3
312122223A C C A C 35。
