第十五章欧拉图与哈密顿图
合集下载
离散数学课件15欧拉图与哈密顿图
证明 若G是平凡图,结论显然成立。
下面设G为非平凡图,设G是m条边的n阶无 向图,
并设G的顶点集V={v1,v2,…,vn}。 必要性。因为G为欧拉图,所以G中存在欧 拉回路,
设C为G中任意一条欧拉回路,vi,vj∈V, v2i0,2v0/7j/都23 在C上,
定理15.1的证明
充分性。由于G为非平凡的连通图可知,G中边数 m≥1。
2020/7/23
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的 ,且G中恰有两个奇度顶点。
证明 充分性。设G的两个奇度顶点分别为u0和v0, 对G加新边(u0,v0),得G =G∪(u0,v0), 则G 是连通且无奇度顶点的图, 由定理15.1可知,G 为欧拉图, 因而存在欧拉回路C ,而C=C -(u0,v0)为G中一 条欧拉通路, 所以G为半欧拉图。
并2行从020/7遍/C23 上G 的i中某的顶欧点拉vr回开路始C行遍i,,i=每1遇,2,到…v,s*j,i,最就后
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的 ,且G中恰有两个奇度顶点。
证明 必要性。设G是m条边的n阶无向图,因为G为 半欧拉图, 因而G中存在欧拉通路(但不存在欧拉回路), 设Г=vi0ej1vi1…vim-1ejmvim为G中一条欧拉通路, vi0≠vim。 v∈V(G),若v不在Г的端点出现,显然d(v)为偶 数, 若v在端点出现过,则d(v)为奇数,
欧拉对物理力学、天文学、弹道学、航海学、建筑学、音 乐都有研究!有许多公式、定理、解法、函数、方程、常数等 是以欧拉名字命名的。欧拉写的数学教材在当时一直被当作标 准教程。19世纪伟大的数学家高斯曾说过“研究欧拉的著作永 远是了解数学的好方法”。欧拉还是数学符号发明者,他创设 的许多数学符号,例如π,i,e,sin,cos,tg,Σ,f (x)等等, 至今202沿0/7/2用3 。
下面设G为非平凡图,设G是m条边的n阶无 向图,
并设G的顶点集V={v1,v2,…,vn}。 必要性。因为G为欧拉图,所以G中存在欧 拉回路,
设C为G中任意一条欧拉回路,vi,vj∈V, v2i0,2v0/7j/都23 在C上,
定理15.1的证明
充分性。由于G为非平凡的连通图可知,G中边数 m≥1。
2020/7/23
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的 ,且G中恰有两个奇度顶点。
证明 充分性。设G的两个奇度顶点分别为u0和v0, 对G加新边(u0,v0),得G =G∪(u0,v0), 则G 是连通且无奇度顶点的图, 由定理15.1可知,G 为欧拉图, 因而存在欧拉回路C ,而C=C -(u0,v0)为G中一 条欧拉通路, 所以G为半欧拉图。
并2行从020/7遍/C23 上G 的i中某的顶欧点拉vr回开路始C行遍i,,i=每1遇,2,到…v,s*j,i,最就后
半欧拉图的判定定理
定理15.2 无向图G是半欧拉图当且仅当G是连通的 ,且G中恰有两个奇度顶点。
证明 必要性。设G是m条边的n阶无向图,因为G为 半欧拉图, 因而G中存在欧拉通路(但不存在欧拉回路), 设Г=vi0ej1vi1…vim-1ejmvim为G中一条欧拉通路, vi0≠vim。 v∈V(G),若v不在Г的端点出现,显然d(v)为偶 数, 若v在端点出现过,则d(v)为奇数,
欧拉对物理力学、天文学、弹道学、航海学、建筑学、音 乐都有研究!有许多公式、定理、解法、函数、方程、常数等 是以欧拉名字命名的。欧拉写的数学教材在当时一直被当作标 准教程。19世纪伟大的数学家高斯曾说过“研究欧拉的著作永 远是了解数学的好方法”。欧拉还是数学符号发明者,他创设 的许多数学符号,例如π,i,e,sin,cos,tg,Σ,f (x)等等, 至今202沿0/7/2用3 。
欧拉图与哈密顿图

例15.3 在图15.6中给出的三个图都是 二部图。它们中的那些是哈密顿图?哪些 是半哈密顿图?为什么? 解 在(1)中,易知互补顶点子集 V1={a,f},V2={b,c,d,e}。设此二部图为G1, 则G1=<V1,V2,E>. p(G1-V1)=4>|V1|=2,由 定理15.6及其推论可知,G1不是哈密顿 图,也不是半哈密顿图。
是在G'中存在u到v的路径Г2,显然Г1 与Г2边不重,这说明u,v处于Г1∪Г2 形成的简单回路上。
三、求欧拉图中欧拉回路的算法
设G为欧拉图,一般来说G中存 在若干条欧拉回路,下面介绍两种求 欧拉回路的算法。
1.Fleury算法,能不走桥就不走桥: (1)任取v0∈V(G),令P0=v0. (2)设Pi=v0e1v1e2…eivi已经行遍, 按下面方法来从E(G)-{e1,e2,…,ei}中选 取ei+1: (a)ei+1与vi相关联; (b)除非无别的边可供行遍, 否则ei+1不应该为Gi=G-{e1,e2,…,ei}中的 桥。 (3)当(2)不能再进行时,算法停止。
p(C-V1)达到最大值|V1|,而当V1中顶点在C 上有彼此相邻的情况时,均有p(C-V1)<|V1|, 所以有p(C-V1)≤|V1|.而C是G的生成子图, 所以,有p(G-V1)≤p(C-V1)≤|V1|. 本定理的条件是哈密顿图的必要条件, 但不是充分条件。可以验证彼得松图(图 14.3中(1)所示)满足定理中的条件,但 它不是哈密顿图。当然,若一个图不满足 定理中的条件,它一定不是哈密顿图。
2.逐步插入回路法 设G为n阶无向欧拉图,V(G)={v1,v2,…,vn}, 求G中欧拉回路的逐步插入回路法的算法如下: 开始 i←0,v*=v1,v=v1,P0=v1, G0=G. 1.在Gi中任取一条与V关联的边 e=(v,v'),将e及v’加入到Pi中得到Pi+1. 2.若v '=v*,转3,否则i←i+1,v=v' , 转1.
第十五章欧拉图与哈密顿图

具有哈密顿回路的图称为半哈密顿图。平 凡图是哈密顿图。
图中所示的三个无向图都有哈密顿回路, 所以都是哈密顿图。有向图中,()具有哈 密顿回路,因而它是哈密顿图。()只有哈 密顿通路,但无哈密顿回路,因而它是半哈 密顿图,而()中既无哈密顿回路,也没有 哈密顿通路,因而不是哈密顿图,也不是半 哈密顿图。
∈(),若不在Г的端点出现,显然 ()为偶数,若在端点出现过,则()为 奇数,因为Г只有两个端点且不同,因而 中只有两个奇数顶点。另外,的连通 性是显然的。
充分性: 设的两个奇度顶点分别 为 和,对加新边(),
得' ∪(),则'是连通且无奇度 顶点 的图,由定理可知,‘为欧拉 图,因而存在欧拉回路',而' () 为中一条欧拉通路,所以为半欧拉图。
图
由定理立即可知,图()图 为欧拉图,本图既可以看成圈, ,,之并(为 清晰起见,将个圈画在()中),也 可看成圈与圈 之并(两个圈画在()中)。将() 分解成若干个边不重的圈的并不是() 图特有的性质,任何欧拉图都有这个性 质。
定理 是非平凡的欧拉图当且仅 当是连通的且为若干个边不重的圈的并。
证 读者用定理证明。
下面给出一些哈密顿图和半哈密顿图 的充分条件。
定理 设是阶无向简单图,若对
于中任意不相邻的顶点,均有
()()≥
()
则中存在哈密顿通路。
证: 首先证明是连通图。否则至少 有两个连通分支,设是阶数为 的两个连通分支,设∈(),∈(), 因为是简单图,所以 ()()
()()≤≤
这与()矛盾所以必为连通图。
可以证明,当算法停止时所得简单回路 …()为中一条欧拉回路。
例 图()是给定的欧拉图。某人用算法 求中的欧拉回路时, 走了简单回路 之 后(观看他的错误走法),无法行遍了,试 分析在哪步他犯了错误?
《离散数学》课件-第15章欧拉图与哈密顿图

例如
彼得松图 彼得松图满足定理15.6,但不是哈密顿图。
例15.3 下图中三个图都是二部图,判断它们 哪些是哈密顿图,哪些是半哈密顿图?
G1
G2
G3
二部图与哈密顿图的关系
设二部图G=<V1,V2,E>,
|V2||V1|。若|V2||V1|+2,则
G即不是哈密顿图,又不是半哈
G1
密顿图
(1)G1=<V1,V2,E>, 互补顶点子集为V1={a,f},V2={b,c,d,e}。 则p(G1-V1)=|V2|=4,|V1|=2, p(G1-V1)>|V1|且p(G1-V1)>|V1|+1。 所以G1即不是哈密顿图,又不是半哈密顿图。
亚瑟王和他的骑士们
◼ 亚瑟王一次召见他的p个骑士,已知每一个 骑士在骑士中的仇人不超过p/2-1个。证明:能让 这些骑士围坐在圆桌旁,使每个人都不与他的仇 人相邻。
其它重要的定理
◼ 定理1 如果G是一个n(n3)阶简单图, 且n/2,则G是哈密顿图。
◼ 定理2 如果G是一个n(n3)阶完全图, 且n为奇数,则G是哈密顿图且图中有(n-1)/2个 边不相交的哈密顿回路。
穿过每一道门,通过所有房间?
15.2 哈密顿图
1859年,爱尔兰数学家威廉·哈密尔顿发明 了一个旅游世界的游戏。将一个正十二面体的 20个顶点分别标上世界上大城市的名字,要求 玩游戏的人从某城市出发沿12面体的棱,通过 每个城市恰一次,最后回到出发的那个城市。
哈密尔顿游戏是在左图中如何 找出一个包含全部顶点的圈。
点的回路称为欧拉回路 定义(欧拉图和半欧拉图)
具有欧拉回路的图称为欧拉图 具有欧拉通路无欧拉回路的图称为半欧拉图 规定平凡图是欧拉图
欧拉图于哈密顿图
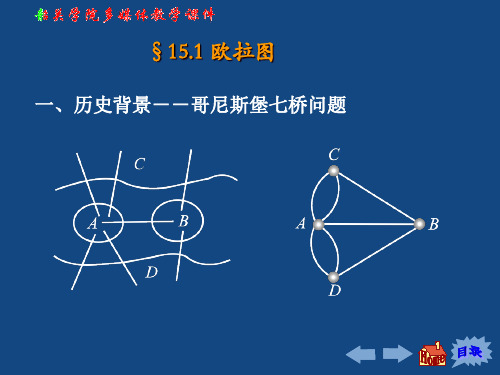
§15.1 欧拉图
一、历史背景--哥尼斯堡七桥问题
}
1
二、定义 欧拉通路 (欧拉迹) ——通过图中每条边一次 且仅一次,并且过每一顶点的通路。 欧拉回路 (欧拉闭迹) ——通过图中每条边一次 且仅一次,并且过每一顶点的回路。 欧拉图 ——存在欧拉回路的图。
}
2
三、无向图是否具有欧拉通路或回路的判定
(3) 具有哈密尔顿回路而没有欧拉回路,
解:
(4) 既没有欧拉回路,也没有哈密尔顿回路。
解:
}
14
作业
习题十五 2、11、14、15、20
}
15
余顶点的入度均等于出度, 这两个特殊的顶点中,一个 顶点的入度比出度大1,另一 个顶点的入度比出度小1。
D 有欧拉回路( D为欧拉图) D 连通, D 中所有
顶点的入度等于出度。
}
6
例3、判断以下有向图是否欧拉图。
}
7
§15.2 哈密尔顿图
一、问题的提出
1859年,英国数学家哈密尔顿,周游世界游戏。
(2)
解:是哈密尔顿图,
存在哈密尔顿回路和通路。
}
11
例1、判断下图是否具有哈密尔顿回路,通路。
(3)
解:不存在哈密尔顿回路,
也不存在哈密尔顿通路。
}
12
例2、画一个无向图,使它
(1) 具有欧拉回路和哈密尔顿回路,
解:
(2) 具有欧拉回路而没有哈密尔顿回路, 解:
}
13
例2、画一个无向图,使它
G 中只有两个奇度 G 有欧拉通路 G 连通,
顶点(它们分别是欧拉通路的
两个端点)。
G有欧拉回路( G为欧拉图) G 连通, G 中均
一、历史背景--哥尼斯堡七桥问题
}
1
二、定义 欧拉通路 (欧拉迹) ——通过图中每条边一次 且仅一次,并且过每一顶点的通路。 欧拉回路 (欧拉闭迹) ——通过图中每条边一次 且仅一次,并且过每一顶点的回路。 欧拉图 ——存在欧拉回路的图。
}
2
三、无向图是否具有欧拉通路或回路的判定
(3) 具有哈密尔顿回路而没有欧拉回路,
解:
(4) 既没有欧拉回路,也没有哈密尔顿回路。
解:
}
14
作业
习题十五 2、11、14、15、20
}
15
余顶点的入度均等于出度, 这两个特殊的顶点中,一个 顶点的入度比出度大1,另一 个顶点的入度比出度小1。
D 有欧拉回路( D为欧拉图) D 连通, D 中所有
顶点的入度等于出度。
}
6
例3、判断以下有向图是否欧拉图。
}
7
§15.2 哈密尔顿图
一、问题的提出
1859年,英国数学家哈密尔顿,周游世界游戏。
(2)
解:是哈密尔顿图,
存在哈密尔顿回路和通路。
}
11
例1、判断下图是否具有哈密尔顿回路,通路。
(3)
解:不存在哈密尔顿回路,
也不存在哈密尔顿通路。
}
12
例2、画一个无向图,使它
(1) 具有欧拉回路和哈密尔顿回路,
解:
(2) 具有欧拉回路而没有哈密尔顿回路, 解:
}
13
例2、画一个无向图,使它
G 中只有两个奇度 G 有欧拉通路 G 连通,
顶点(它们分别是欧拉通路的
两个端点)。
G有欧拉回路( G为欧拉图) G 连通, G 中均
第十五章 欧拉图与哈密顿图

长度大于或等于3的圈,设C为G中一个圈,
删除C上的全部边,得G的生成子图G',
, G2 , 设G'有s个连通分支 G1
公共顶点为,i=1, 2, … , s.
, 每个连通分支 , Gs
至多有k条边,且无奇度顶点,并且设G'i与C的
, G2 , 由归纳假设可知, G1
, 都是欧拉图, , Gs
并设G的顶点集 V={v1, v2, … , vn }.
必要性. 因为G为欧拉图,所以G中存在欧拉回路, 设C为G中任意一条欧拉回路, vi , vj ∈V,
vi, vj都在C上,因而vi , vj 连通,所以G为 连通图.
又vi∈V,vi在C上每出现一次获得2度,
若出现k次就获得2k 度,即d(vi)=2k .
点的入度都等于出度.
Байду номын сангаас
由定理15.3和15.4立即可知,图15.1中所示3个
有向图中只有(4)是欧拉图,没有半欧拉图.
图15.1
由定理15.1立即可知,图15.3(1)图为欧拉图.
图15.3
本图既可以看成圈
v1v2v8v1 , v2v3v4v2 , v4v5v6v4 , v6v7v8v6 之并(为清晰起见,
vim -1e jm vim为G中一条欧拉
vi 0 vim . v V (G ), 若v不在Г的端点出现, 通路,
显然d(v)为偶数,若v在端点出现过,则d(v)为奇数,
因为Г只有两个端点且不同,因而G中只有两个
奇数顶点. 另外,G的连通性是显然的.
充分性. 设G的两个奇度顶点分别为u0和v0,对G加 新边(u0, v0),得G ' =G∪(u0,v0),则G '是 连通且无奇度顶点的图,由定理15.1可知,G ' 为欧拉图,因而存在欧拉回路C ' ,而
欧拉图与哈密顿图

求欧拉图中欧拉回路的算法
Fleury算法;能不走桥就不走桥
1 任取v0∈VG;令P0=v0; 2 设Pi=v0e1v1e2…eivi已经行遍;按下面方法来从
EGe1;e2;…;ei中选取ei+1: a ei+1与vi相关联; b 除非无别的边可供行遍;否则ei+1不应该为
Gi=Ge1;e2;…;ei中的桥; 3当2不能再进行时;算法停止;
例15 1
例15 1 设G是非平凡的且非环的欧拉图;证明: 1λG≥2; 2对于G中任意两个不同顶点u;v;都存在简单回路C含u和v;
证明 1由定理15 5可知;e∈EG;存在圈C;e在C中; 因而pGe=pG;故e不是桥; 由e的任意性λG≥2;即G是2边连通图;
例15 1
例15 1 设G是非平凡的且非环的欧拉图;证明: 1λG≥2; 2对于G中任意两个不同顶点u;v;都存在简单回路C含u和v;
可以验证彼得松图满足定理中的条件;但不是哈密顿图;
若一个图不满足定理中的条件;它一定不是哈密顿图;
推论
推论 设无向图G=<V;E>是半哈密顿图;对于任意的V1V且 V1≠;均有 pGV1≤|V1|+1
证明 设P是G中起于u终于v的哈密顿通路; 令G =G∪u;v在G的顶点u;v之间加新边; 易知G 为哈密顿图; 由定理15 6可知;pG V1≤|V1|; 因此;pGV1 = pG V1u;v ≤ pG V1+1 ≤ |V1|+1
若vi与vj有哈共密同语顿言图;就是在v能i;vj将之间图连中无向所边有vi;v顶j; 由此组成点边都集合能E;安则G排为8在阶无某向个简单初图级; 回路 vi∈V;上dvi为的与图vi有;共同语言的人数;
欧拉图和哈密尔顿图ppt课件

有欧拉通路
全部结点为偶结点, 有欧拉回路
有欧拉通路
。a
a、b、c、e
。a
全部结点为
b。 。c 都为奇结点, 。 。 。 无欧拉通路
b。
。c
d
e
f 与欧拉回路 。 。 。
偶结点, 有欧拉回路
d e f 有欧拉通路
ppt课件
8
例7-8 如图街道,是否存在一条投递线路使 邮递员从邮局a出发通过所有街到一次在回 到邮局a?
可达的:在图G中,结点u和结点v之间存在一
条路,则称结点u到结点v是可达的。
ppt课件
2
无向图的连通性
连通:在无向图G中,结点u和结点v之间存在一 条路,则称结点u与结点v是连通的。约定:任一 结点与自身总是连通的。 连通图:若图G中,任意两个结点均连通,则称G 是连通图,否则称非连通图。对非连通图可分成几
个无公共结点的连通分支。无向图中结点间的连通
关系是等价关系。 图是连通的判定法则:从图中任意一结点出发,
通过某些边一定能到达其它任意一结点,则称
图是连通的。
ppt课件
3
练习1:连通图的判定
指出下列各图是否连通
(1)
(2)
(3)
(4)
(5)
(6)
ppt课件 (7)
(8)
4
欧拉图
设G=<V,E>是连通无向图 欧拉通路:在图G中存在一条通路,经过图G 中每条边一次且仅一次。
第二节 图的连通性
通路和回路 无向图的连通性 有向图的连通性 欧拉图 哈密顿图
ppt课件
1
通路和回路 给定图G V , E
通路: G中前后相互关联的点边交替序列 w=v0e1v1e2…envn称为连接v0到vn的通路。 W中边的数目K称为通路W的长。
全部结点为偶结点, 有欧拉回路
有欧拉通路
。a
a、b、c、e
。a
全部结点为
b。 。c 都为奇结点, 。 。 。 无欧拉通路
b。
。c
d
e
f 与欧拉回路 。 。 。
偶结点, 有欧拉回路
d e f 有欧拉通路
ppt课件
8
例7-8 如图街道,是否存在一条投递线路使 邮递员从邮局a出发通过所有街到一次在回 到邮局a?
可达的:在图G中,结点u和结点v之间存在一
条路,则称结点u到结点v是可达的。
ppt课件
2
无向图的连通性
连通:在无向图G中,结点u和结点v之间存在一 条路,则称结点u与结点v是连通的。约定:任一 结点与自身总是连通的。 连通图:若图G中,任意两个结点均连通,则称G 是连通图,否则称非连通图。对非连通图可分成几
个无公共结点的连通分支。无向图中结点间的连通
关系是等价关系。 图是连通的判定法则:从图中任意一结点出发,
通过某些边一定能到达其它任意一结点,则称
图是连通的。
ppt课件
3
练习1:连通图的判定
指出下列各图是否连通
(1)
(2)
(3)
(4)
(5)
(6)
ppt课件 (7)
(8)
4
欧拉图
设G=<V,E>是连通无向图 欧拉通路:在图G中存在一条通路,经过图G 中每条边一次且仅一次。
第二节 图的连通性
通路和回路 无向图的连通性 有向图的连通性 欧拉图 哈密顿图
ppt课件
1
通路和回路 给定图G V , E
通路: G中前后相互关联的点边交替序列 w=v0e1v1e2…envn称为连接v0到vn的通路。 W中边的数目K称为通路W的长。
第十五章欧拉图与哈密顿图

定理15.5 G是非平凡的欧拉图当且仅当G是 连通的且为若干个边不重的圈的并.
本定理的证明可用归纳法. 例15.1 设G是非平凡的且非环的欧拉图,证明:
(1)λ(G)≥2. (2)对于G中任意两个不同顶点u, v,都存在 简单回路C含 u 和 v.
证 (1)由定理15.5可知,e E(G), 存在圈C, e 在C中,因而 p(G - e) p(G), 故 e 不是桥。 由 e 的任意性λ(G)≥2,即G是2边-连通图。
在这里做个规定: 平凡图是欧拉图.
例1 下列各图中 是否有欧拉回路、欧位通路? 图15.1
解:e1 e2 e3 e4 e5 为(1)中的欧拉回路,所以(1)图为欧拉图. e1 e2 e3 e4 e5 为(2)中的一条欧拉通路,但图中不存在 欧拉回路(为什么?),所以(2)为半欧拉图。
(3)中既没有欧拉回路也没有欧拉通路(为什么?), 所以(3)不是欧拉图,也不是半欧拉图。
设(2)中图为G2,则 G2 V1,V2 , E , 其中 V1 {a, g,h,i,c},V2 {b,e, f , j,k,d }, 易知, p(G2 -V1) |V2 | 6 |V1 | 5,由定理15.6可知, G2不是哈密顿图,但G2是半哈密顿图,其实, baegjckhfid 为G2中一条哈密顿通路.
图示:
(a)
“周游世界” 智力题
(b)
哈密顿图
一、哈密顿通路、哈密顿回路、 哈密顿图、 半哈密顿图的定义
定义15.2 经过图(有向图或无向图)中所有 顶点一次且仅一次的通路称为哈密顿通路;
经过图中所有顶点一次且仅一次的回路称为哈密 顿回路;
具有哈密顿回路的图称为哈密顿图; 具有哈密顿通路但不具有哈密顿回路的图称为半哈 密顿图.
离散数学课件15欧拉图与哈密顿图

04
欧拉图与哈密顿图的应用 场景
欧拉图的应用场景
路径规划
欧拉图可以用于表示从一 个点到另一个点的路径, 常用于物流、交通和旅行 等领域。
网络流问题
欧拉图可以用于解决最大 流和最小割等问题,在网 络优化、资源分配和计划 制定等方面有广泛应用。
组合优化
欧拉图可以用于表示组合 优化问题,如旅行商问题、 排班问题等,是求解这些 问题的常用工具。
一个图存在哈密顿回路当且仅当其所有顶点的度都大于等于2 。
哈密顿图的性质
哈密顿图中的所有顶点的度都 大于等于2。
一个图存在哈密顿回路当且仅 当其所有顶点的度都大于等于2。回 路。
哈密顿图的构造方法
添加边法
在所有顶点的度都大于等于2的图 中,不断添加边,直到所有顶点的 度都大于等于2,最后得到的图就 是哈密顿图。
哈密顿图的应用场景
社交网络分析
哈密顿图可以用于表示社交网络 中的路径,分析人际关系和信息
传播路径。
生物信息学
哈密顿图可以用于表示基因组、蛋 白质组等生物信息数据,进行基因 序列比对、蛋白质相互作用分析等。
推荐系统
哈密顿图可以用于表示用户和物品 之间的关系,进行个性化推荐和智 能推荐。
欧拉图与哈密顿图在计算机科学中的应用
欧拉图的构造方法
欧拉图的构造方法1
总结词
通过添加一条边将所有顶点连接起来, 从而形成一个欧拉图。
详细描述了两种构造欧拉图的方法, 为实际应用中构造欧拉图提供了思路。
欧拉图的构造方法2
通过将两个欧拉图合并,并连接它们 的所有顶点,从而形成一个新的欧拉 图。
02
哈密顿图
哈密顿图的定义
哈密顿图(Hamiltonian Graph)是指一个图存在一个遍历其 所有边且每条边只遍历一次的路径,这个路径称为哈密顿路径, 如果该路径的起点和终点是同一点,则称这个路径为哈密顿回 路。
欧拉图与哈密顿图s

说明:该推论是充分条件但不是必要的。 例如:
该五边形是哈密顿图,但任意两个不相邻的顶点度 数之和为4,图形阶数为5。
座位问题
例 在某次国际会议的预备会中,共有8人参加,他 们来自不同的国家。如果他们中任两个无共同语言的人 与其余有共同语言的人数之和大于或等于8,问能否将这 8个人排在圆桌旁,使其任何人都能与两边的人交谈。
例15.2(P296) v2e2v3e3v4e14v9e10v2e1v1e8v8e9v2
例15.2(P296)
利用欧拉图可以解决哥尼斯堡七桥问题: 从某地出发,对每座跨河桥只走一次,而在遍历 了七座桥之后,却又能回到原地。
由定理15.1(无向欧拉图的判定定理)可知该问题无解。
思考 如下图所示,从一房间出发,问能否不重复地
(1)
(2)
(3)
(4)
(5)
(6)
(1)(2)(3)(4)为哈密顿图 (5)为半哈密顿图 (6)既不是哈密顿图,又不是半哈密顿图。
到目前为止,还没有找到判断哈密顿图简单的充分必 要条件。
下面介绍哈密顿图和半哈密顿图的必要条件
定理15.6 设无向图G=<V,E>是哈密顿图,V1是V的任意 非空子集,则有p(G-V1)≤|V1|,其中p(G-V1)为G-V1的连 通分支数。
定义(哈密顿通路和哈密顿回路) 经过图(有向图或无向图)每个顶点一次
且仅一次的通路称为哈密顿通路。 经过图每个结点一次且仅一次的回路(初
级回路)称为哈密顿回路。 定义(哈密顿图和半哈密顿图)
存在哈密顿回路的图称为哈密顿图。 存在哈密顿通路但不存在哈密顿回路的图 称为半哈密顿图。 平凡图是哈密顿图。
由两判定定理,立即可知 (4)为欧拉图, (5)、(6)即不是欧拉图,也不是半欧拉图。
该五边形是哈密顿图,但任意两个不相邻的顶点度 数之和为4,图形阶数为5。
座位问题
例 在某次国际会议的预备会中,共有8人参加,他 们来自不同的国家。如果他们中任两个无共同语言的人 与其余有共同语言的人数之和大于或等于8,问能否将这 8个人排在圆桌旁,使其任何人都能与两边的人交谈。
例15.2(P296) v2e2v3e3v4e14v9e10v2e1v1e8v8e9v2
例15.2(P296)
利用欧拉图可以解决哥尼斯堡七桥问题: 从某地出发,对每座跨河桥只走一次,而在遍历 了七座桥之后,却又能回到原地。
由定理15.1(无向欧拉图的判定定理)可知该问题无解。
思考 如下图所示,从一房间出发,问能否不重复地
(1)
(2)
(3)
(4)
(5)
(6)
(1)(2)(3)(4)为哈密顿图 (5)为半哈密顿图 (6)既不是哈密顿图,又不是半哈密顿图。
到目前为止,还没有找到判断哈密顿图简单的充分必 要条件。
下面介绍哈密顿图和半哈密顿图的必要条件
定理15.6 设无向图G=<V,E>是哈密顿图,V1是V的任意 非空子集,则有p(G-V1)≤|V1|,其中p(G-V1)为G-V1的连 通分支数。
定义(哈密顿通路和哈密顿回路) 经过图(有向图或无向图)每个顶点一次
且仅一次的通路称为哈密顿通路。 经过图每个结点一次且仅一次的回路(初
级回路)称为哈密顿回路。 定义(哈密顿图和半哈密顿图)
存在哈密顿回路的图称为哈密顿图。 存在哈密顿通路但不存在哈密顿回路的图 称为半哈密顿图。 平凡图是哈密顿图。
由两判定定理,立即可知 (4)为欧拉图, (5)、(6)即不是欧拉图,也不是半欧拉图。
欧拉图与哈密顿图

*
例6 求图中(1) 所示带权图K4中最短哈密顿回路.
(1) (2)
*
解 C1= a b c d a, W(C1)=10 C2= a b d c a, W(C2)=11 C3= a c b d a, W(C3)=9 可见C3 (见图中(2)) 是最短的,其权为9.
算法: (1) 任取v0V(G),令P0=v0. (2) 设Pi = v0e1v1e2…eivi 已经行遍,按下面方法从 E(G){e1,e2,…,ei }中选取ei+1: (a) ei+1与vi 相关联; (b) 除非无别的边可供行遍,否则ei+1不应该为 Gi = G{e1,e2,…,ei }中的桥. (3) 当 (2)不能再进行时,算法停止. 可以证明算法停止时所得简单通路 Pm = v0e1v1e2…emvm (vm=v0)为G 中一条欧拉回路. 用Fleury算法走出上一页图(1),(2)从A出发(其实从任何一点 出发都可以)的欧拉回路各一条.
欧拉图的判别法
#2022
*
定理15.3 有向图D是欧拉图当且仅当D是强连通的且每个顶 点的入度都等于出度. 本定理的证明类似于定理15.1. 定理15.4 有向图D是半欧拉图当且仅当D是单向连通的,且 D中恰有两个奇度顶点,其中一个的入度比出度大1,另一个 的出度比入度大1,而其余顶点的入度都等于出度. 本定理的证明类似于定理15.1. 定理15.5 G是非平凡的欧拉图当且仅当G是连通的且为若干 个边不重的圈之并. 可用归纳法证定理15.5.
证明
证(着重关键步骤) (1) 由()及简单图的性质,用反证法证明G连通. (2) = v1v2…vl 为极大路径,l n, 若l = n(结束). 下面讨论l<n的情况,即要证G中存在过上所有顶点的圈. ① 若(v1,vl)在G中,则(u,v)为G中圈
欧拉图和哈密而顿图

15.1 欧拉图 欧拉(1707-1783):瑞士著名的数学家。13岁进入 欧拉 :瑞士著名的数学家。 岁进入 巴塞尔大学, 岁取得哲学硕士学位 岁取得哲学硕士学位。 巴塞尔大学,16岁取得哲学硕士学位。1736年, 年 他证明了欧拉定理, 他证明了欧拉定理,并解决了哥尼斯堡桥的问 从而成为图论的创始人。 题,从而成为图论的创始人。 定义15.1 通过图(无向图或有向图)中每一条边 通过图(无向图或有向图) 定义 一次且仅一次行遍图中所有顶点的通路称为欧 拉通路。通过图(无向图或有向图) 拉通路。通过图(无向图或有向图)中每一条 边一次且仅一次行遍图中所有顶点的回路称为 欧拉回路。具有欧拉回路的图称为欧拉图, 欧拉回路。具有欧拉回路的图称为欧拉图,具 有欧拉通路而无欧拉回路的图称为半欧拉图。 有欧拉通路而无欧拉回路的图称为半欧拉图。
16
15.欧拉图与哈密顿图 欧拉图与哈密顿图
15.2 哈密顿图
到目前为止, 到目前为止,还没有找到哈密尔顿通路存在的充 分必要条件。下面介绍一个必要定理。 分必要条件。下面介绍一个必要定理。 定理15.6:设无向图 G=<V , E> 是哈密尔顿 G=<V, 定理 : 设无向图G=<V E>是哈密尔顿 图,则对V的每个非空真子集 均成立: 则对 的每个非空真子集S均成立: 的每个非空真子集 均成立 w(G-S) ≤|S| 其中, 中的顶点数, 表示G删去 其中, |S| 是S中的顶点数, w(G-S)表示 删去 中的顶点数 表示 删去S 顶点集后得到的图的连通分图的个数。 顶点集后得到的图的连通分图的个数。
9
15.欧拉图与哈密顿图 欧拉图与哈密顿图
例:用定理解决哥尼斯堡桥的问题
15.1 欧拉图
个结点为奇次数, 有4个结点为奇次数, ∴不存在欧拉回路,也不存在欧拉路径。 不存在欧拉回路,也不存在欧拉路径。 故要从一点出发经过桥一次且仅一次的路径, 故要从一点出发经过桥一次且仅一次的路径 , 再回到出发点是不可能的。 再回到出发点是不可能的。
16
15.欧拉图与哈密顿图 欧拉图与哈密顿图
15.2 哈密顿图
到目前为止, 到目前为止,还没有找到哈密尔顿通路存在的充 分必要条件。下面介绍一个必要定理。 分必要条件。下面介绍一个必要定理。 定理15.6:设无向图 G=<V , E> 是哈密尔顿 G=<V, 定理 : 设无向图G=<V E>是哈密尔顿 图,则对V的每个非空真子集 均成立: 则对 的每个非空真子集S均成立: 的每个非空真子集 均成立 w(G-S) ≤|S| 其中, 中的顶点数, 表示G删去 其中, |S| 是S中的顶点数, w(G-S)表示 删去 中的顶点数 表示 删去S 顶点集后得到的图的连通分图的个数。 顶点集后得到的图的连通分图的个数。
9
15.欧拉图与哈密顿图 欧拉图与哈密顿图
例:用定理解决哥尼斯堡桥的问题
15.1 欧拉图
个结点为奇次数, 有4个结点为奇次数, ∴不存在欧拉回路,也不存在欧拉路径。 不存在欧拉回路,也不存在欧拉路径。 故要从一点出发经过桥一次且仅一次的路径, 故要从一点出发经过桥一次且仅一次的路径 , 再回到出发点是不可能的。 再回到出发点是不可能的。
150 欧拉图与哈密顿图

于是在G'中存在 u 到 v 的路径Г2,显然Г1与Г2边
不重,这说明 u, v 处于Г1∪Г2形成的简单回路上
第2节 哈密顿图
一、哈密顿通路、哈密顿回路、 哈密顿图、 半哈密顿图的定义 二、哈密顿图与半哈密顿图的 一些必要与充分条件
一、哈密顿通路、哈密顿回路、 哈密顿图、 半哈密顿图的定义
定义15.2 经过图(有向图或无向图)中所有 顶点一次且仅一次的通路称为哈密顿通路. 经过 图中所有顶点一次且仅一次的回路称为哈密顿回路.
为G中一条欧拉
vi 0 vim . v V (G ), 通路,
若v不在Г的端点出现,
显然d(v)为偶数,若v在端点出现过,则d(v)为奇数,
因为Г只有两个端点且不同,因而G中只有两个
奇数顶点. 另外,G的连通性是显然的.
充分性. 设G的两个奇度顶点分别为u0和v0,对G加 新边(u0, v0),得G ' =G∪(u0,v0),则G '是 连通且无奇度顶点的图,由定理15.1可知,G ' 为欧拉图,因而存在欧拉回路C ' ,而
所有顶点的回路称为欧拉回路;具有欧拉回路的
图称为欧拉图,具有欧拉通路而无欧拉回路的图 称为半欧拉图.
从定义不难看出:
欧拉通路是图中经过所有边的简单的生成通路
(经过所有顶点的通路称为生成通路), 欧拉回路是经过所有边的简单的生成回路。 在这里做个规定,即平凡图是欧拉图.
例1 下列各图中 是否有欧拉回路、欧位通路?
大值|V1|,而当V1中顶点在C上有彼此相邻的情
况时,均有 p(C - V1 ) | V1 |, 所以有 p(C - V1 ) | V1 | .
(2)设m≤k (k≥1)时结论成立, 要证明m=k+1时,结论也成立。
22 欧拉图与哈密顿图
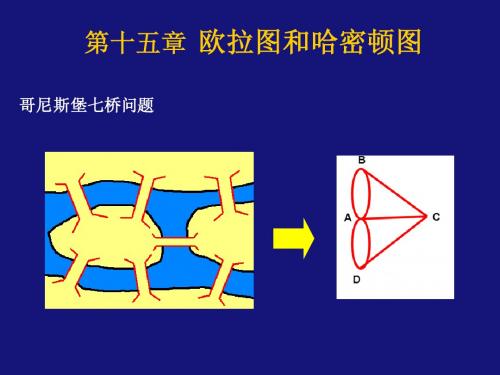
2.若h1=G,则G是欧拉图,否则转下一步。 3.记H=G-h1,因为G是连通图,所以H与h1至少有一个节点重 合,不妨记为vi,又因为h1中d(vi)是偶数,故在H中d(vi)仍 是偶数,从而从图H的节点vi出发,重复步骤1的做法,又 可得简单回路h2: (vi,e’1,v1,e’2,…,vi)这里ei’≠ ej’(i≠j),那么h1∪ h2所对应的简单回路是:(v0,e1,v1,e2,…,vi, e1’,v1,e2’,…,vi, ei+1,…,ek+1,v0)。不妨将h1∪ h2仍记为h2,转步骤2。 对于有限图G,我们总可以在有限步骤中构造出简单回路 h1,使得h1=G,故G是欧拉图。
②现在我们来证明:若G中对于每一对不相邻的节点u,v, 有d(u)+d(v)≧n,则G是哈密顿图。因为若在G中每一对不 相邻节点u,v之间连一条无向边,得到图H,则H是n阶无 向完全图,从而H是哈密顿图,由引理,可知G是哈密顿 图。 ③由2,我们可直接推出若任一节点v满足d(v)≥n/2,则G是 哈密顿图。 例8 格雷码及其应用:构造长度为n的2进制编码的序列, 使相邻的码仅相差1位 用Qn来建模 (接下页)
例6 证明图7-35中的图没有哈密顿回路。
证明: 证明: G中没有哈密顿回路,因为G有1度顶点,即e。现 在考虑H。因为顶点a, b,d 和e 的度都为2,所以这些顶 点关联的每一条边都必然属于任意一条哈密顿回路。现在 容易看出H中不存在哈密顿回路,因为任何这样的哈密顿 回路都不得不包含4条关联c的边,这是不可能的。
解: 图G1具有欧拉回路,例如a, e, c, d, e, b, a。G2和G3都没 有欧拉回路。但是G3具有欧拉通路,即a, c, d, e, b, d, a, b。 G2没有欧拉通路。 图H2具有欧拉回路,例如a, g, c, b, g, e, d, f, a。H1和 H3都没有欧拉回路。H3具有欧拉通路,即c, a, b, c, d, b,但 是H1没有欧拉通路。
第十五章 欧拉图与哈密顿图

例:图中给出的二部图,哪些是哈密顿图, a 哪些是半哈密顿图? a e f
b
c f G1
d
e
b
g
h j k
i
d
c G2 (1)V1={a,f},V2={b,c,d,e},p(G1-V1)=4>|V1|,都不是 (2)V1={a,g,h,i,c},V2={b,e,f,j,k,d},
p(G2-V1)=|V2|=6>|V1|=5,半哈密顿图
a b g i h j
c
d
(3)V1={a,c,g,h,e},V2={b, f d,i,j,f},|V1|=|V2|, G3存在哈密顿回路: abcdgihjefa
G3 e 一般情况下,设二部图G=<V1,V2,E>,|V1||V2|,且 |V1|2, |V2|2,由定理15.6及其推论,可以得到以 下结论: (1)若G是哈密顿图,则|V1|=|V2|。 (2)若G是半哈密顿图,则|V2|=|V1|+1。 (3) |V2||V1|+2,则G不是(半)哈密顿图。
第十五章 欧拉图与哈密顿图
本章的内容 欧拉图 哈密顿图
本章的先行知识是第十四章
15.1 欧拉图
一、哥尼斯堡七桥问题
图论之父
瑞士数学家:列昂德· 欧拉(Leonhard Euler)
二、无向欧拉图
1.定义: 经过图中每条边一次且仅 一次行遍所有结点的通路
(1)欧拉通路 (2)欧拉回路
(3)欧拉图 (4)半欧拉图
充分性:
设G的两个奇度结点分别为u0和v0,令 G’=G(u0,v0),则G’连通且无奇度结点的图, 因此G’为欧拉图,因而存在欧拉回路C’,而 C=C’- (u0,v0)为G中一条欧拉通路,所以G为半 欧拉图。
离散数学15 欧拉图与哈密顿图

穿过每一道门,通过所有房间?
15.2 哈密顿图
1859年,爱尔兰数学家威廉·哈密尔顿发明 了一个旅游世界的游戏。将一个正十二面体的 20个顶点分别标上世界上大城市的名字,要求 玩游戏的人从某城市出发沿12面体的棱,通过 每个城市恰一次,最后回到出发的那个城市。
哈密尔顿游戏是在左图中如何 找出一个包含全部顶点的圈。
定义(哈密顿通路和哈密顿回路) 经过图(有向图或无向图)每个顶点一次
且仅一次的通路称为哈密顿通路。 经过图每个结点一次且仅一次的回路(初
级回路)称为哈密顿回路。 定义(哈密顿图和半哈密顿图)
存在哈密顿回路的图称为哈密顿图。 存在哈密顿通路但不存在哈密顿回路的图 称为半哈密顿图。 平凡图是哈密顿图。
由两判定定理,立即可知 (4)为欧拉图, (5)、(6)即不是欧拉图,也不是半欧拉图。
例15.2(P296) v2e2v3e3v4e14v9e10v2e1v1e8v8e9v2
◼ Fleury算法
◼ (1)任取v0V(G),令P0=v0。 ◼ (2)设Pi=v0e1v1e2…..eivi已经行遍,则按下面
判断所示两图是否为欧拉图、半欧拉图?
无向欧拉图与无向半欧拉图的判断方法
定理15.1(无向欧拉图的判定)无向图G是欧拉图当 且仅当G是连通图,且G中没有奇度顶点。
定理15.2(无向半欧拉图的判定)无向图G是半欧拉 图当且仅当G是连通图,且G中恰有两个奇度顶点。
(1)
(2)
(3)
有向欧拉图与有向半欧拉图的判断方法
(1)
(2)
(3)
(4)
(5)
(6)
(1)(2)(3)(4)为哈密顿图 (5)为半哈密顿图 (6)既不是哈密顿图,又不是半哈密顿图。
15.2 哈密顿图
1859年,爱尔兰数学家威廉·哈密尔顿发明 了一个旅游世界的游戏。将一个正十二面体的 20个顶点分别标上世界上大城市的名字,要求 玩游戏的人从某城市出发沿12面体的棱,通过 每个城市恰一次,最后回到出发的那个城市。
哈密尔顿游戏是在左图中如何 找出一个包含全部顶点的圈。
定义(哈密顿通路和哈密顿回路) 经过图(有向图或无向图)每个顶点一次
且仅一次的通路称为哈密顿通路。 经过图每个结点一次且仅一次的回路(初
级回路)称为哈密顿回路。 定义(哈密顿图和半哈密顿图)
存在哈密顿回路的图称为哈密顿图。 存在哈密顿通路但不存在哈密顿回路的图 称为半哈密顿图。 平凡图是哈密顿图。
由两判定定理,立即可知 (4)为欧拉图, (5)、(6)即不是欧拉图,也不是半欧拉图。
例15.2(P296) v2e2v3e3v4e14v9e10v2e1v1e8v8e9v2
◼ Fleury算法
◼ (1)任取v0V(G),令P0=v0。 ◼ (2)设Pi=v0e1v1e2…..eivi已经行遍,则按下面
判断所示两图是否为欧拉图、半欧拉图?
无向欧拉图与无向半欧拉图的判断方法
定理15.1(无向欧拉图的判定)无向图G是欧拉图当 且仅当G是连通图,且G中没有奇度顶点。
定理15.2(无向半欧拉图的判定)无向图G是半欧拉 图当且仅当G是连通图,且G中恰有两个奇度顶点。
(1)
(2)
(3)
有向欧拉图与有向半欧拉图的判断方法
(1)
(2)
(3)
(4)
(5)
(6)
(1)(2)(3)(4)为哈密顿图 (5)为半哈密顿图 (6)既不是哈密顿图,又不是半哈密顿图。
15欧拉图与哈密顿图

中国地质大学本科生课程
离散数学
第15章 欧拉图与哈密顿图
数学家欧拉
欧拉,瑞士数学家, 欧拉,瑞士数学家,欧拉是科学 史上最多产的一位杰出的数学家, 史上最多产的一位杰出的数学家,他从 19岁开始发表论文,直到 岁,他一生 岁开始发表论文, 岁开始发表论文 直到76岁 共写下了886本书籍和论文,其中在世 本书籍和论文, 共写下了 本书籍和论文 多篇论文。 时发表了700多篇论文。彼得堡科学院 时发表了 多篇论文 为了整理他的著作,整整用了47年 为了整理他的著作,整整用了 年。在 他双目失明后的17年间 年间, 他双目失明后的 年间,也没有停止对 数学的研究,口述了好几本书和400余 数学的研究,口述了好几本书和 余 篇的论文。 篇的论文。 欧拉对物理力学、天文学、弹道学、航海学、建筑学、 欧拉对物理力学、天文学、弹道学、航海学、建筑学、音 乐都有研究!有许多公式、定理、解法、函数、方程、常数等 乐都有研究!有许多公式、定理、解法、函数、方程、 是以欧拉名字命名的。 是以欧拉名字命名的。欧拉写的数学教材在当时一直被当作标 准教程。 世纪伟大的数学家高斯曾说过 世纪伟大的数学家高斯曾说过“ 准教程。19世纪伟大的数学家高斯曾说过“研究欧拉的著作永 远是了解数学的好方法” 欧拉还是数学符号发明者, 远是了解数学的好方法”。欧拉还是数学符号发明者,他创设 的许多数学符号,例如π, , , , 等等, 的许多数学符号,例如 ,i,e,sin,cos,tg,Σ,f (x)等等, , , , 等等 至今沿用。 至今沿用。
匈牙利数学家厄多斯
保罗‧厄多斯(1913-1996)是一位匈牙利的数学家。 保罗‧厄多斯(1913-1996)是一位匈牙利的数学家。 (1913 是一位匈牙利的数学家 其父母都是匈牙利的高中数学教师。 其父母都是匈牙利的高中数学教师。 1983年以色列政府颁给十万美元 沃尔夫奖金” 政府颁给十万美元“ 1983年以色列政府颁给十万美元“沃尔夫奖金”(WolfPrize 就是由他和华裔美籍的陈省身教授平分。 )就是由他和华裔美籍的陈省身教授平分。 厄多斯是当代发表最多数学论文的数学家, 厄多斯是当代发表最多数学论文的数学家,也是全世界和各种 各样不同国籍的数学家合作发表论文最多的人。 各样不同国籍的数学家合作发表论文最多的人。他发表了 1000多篇的论文 平均一年要写和回答1500 多篇的论文, 1500多封有关于 近1000多篇的论文,平均一年要写和回答1500多封有关于 数学问题的信。他可以和任何大学的数学家合作研究, 数学问题的信。他可以和任何大学的数学家合作研究,他 每到一处演讲就能和该处的一两个数学家合作写论文, 每到一处演讲就能和该处的一两个数学家合作写论文,据 说多数的情形是人们把一些本身长期解决不了的问题和他 讨论,他可以很快就给出了问题的解决方法或答案, 讨论,他可以很快就给出了问题的解决方法或答案,于是 人们赶快把结果写下来,然后发表的时候放上他的名字, 人们赶快把结果写下来,然后发表的时候放上他的名字, 厄多斯的新的一篇论文就这样诞生了。 厄多斯的新的一篇论文就这样诞生了。
离散数学
第15章 欧拉图与哈密顿图
数学家欧拉
欧拉,瑞士数学家, 欧拉,瑞士数学家,欧拉是科学 史上最多产的一位杰出的数学家, 史上最多产的一位杰出的数学家,他从 19岁开始发表论文,直到 岁,他一生 岁开始发表论文, 岁开始发表论文 直到76岁 共写下了886本书籍和论文,其中在世 本书籍和论文, 共写下了 本书籍和论文 多篇论文。 时发表了700多篇论文。彼得堡科学院 时发表了 多篇论文 为了整理他的著作,整整用了47年 为了整理他的著作,整整用了 年。在 他双目失明后的17年间 年间, 他双目失明后的 年间,也没有停止对 数学的研究,口述了好几本书和400余 数学的研究,口述了好几本书和 余 篇的论文。 篇的论文。 欧拉对物理力学、天文学、弹道学、航海学、建筑学、 欧拉对物理力学、天文学、弹道学、航海学、建筑学、音 乐都有研究!有许多公式、定理、解法、函数、方程、常数等 乐都有研究!有许多公式、定理、解法、函数、方程、 是以欧拉名字命名的。 是以欧拉名字命名的。欧拉写的数学教材在当时一直被当作标 准教程。 世纪伟大的数学家高斯曾说过 世纪伟大的数学家高斯曾说过“ 准教程。19世纪伟大的数学家高斯曾说过“研究欧拉的著作永 远是了解数学的好方法” 欧拉还是数学符号发明者, 远是了解数学的好方法”。欧拉还是数学符号发明者,他创设 的许多数学符号,例如π, , , , 等等, 的许多数学符号,例如 ,i,e,sin,cos,tg,Σ,f (x)等等, , , , 等等 至今沿用。 至今沿用。
匈牙利数学家厄多斯
保罗‧厄多斯(1913-1996)是一位匈牙利的数学家。 保罗‧厄多斯(1913-1996)是一位匈牙利的数学家。 (1913 是一位匈牙利的数学家 其父母都是匈牙利的高中数学教师。 其父母都是匈牙利的高中数学教师。 1983年以色列政府颁给十万美元 沃尔夫奖金” 政府颁给十万美元“ 1983年以色列政府颁给十万美元“沃尔夫奖金”(WolfPrize 就是由他和华裔美籍的陈省身教授平分。 )就是由他和华裔美籍的陈省身教授平分。 厄多斯是当代发表最多数学论文的数学家, 厄多斯是当代发表最多数学论文的数学家,也是全世界和各种 各样不同国籍的数学家合作发表论文最多的人。 各样不同国籍的数学家合作发表论文最多的人。他发表了 1000多篇的论文 平均一年要写和回答1500 多篇的论文, 1500多封有关于 近1000多篇的论文,平均一年要写和回答1500多封有关于 数学问题的信。他可以和任何大学的数学家合作研究, 数学问题的信。他可以和任何大学的数学家合作研究,他 每到一处演讲就能和该处的一两个数学家合作写论文, 每到一处演讲就能和该处的一两个数学家合作写论文,据 说多数的情形是人们把一些本身长期解决不了的问题和他 讨论,他可以很快就给出了问题的解决方法或答案, 讨论,他可以很快就给出了问题的解决方法或答案,于是 人们赶快把结果写下来,然后发表的时候放上他的名字, 人们赶快把结果写下来,然后发表的时候放上他的名字, 厄多斯的新的一篇论文就这样诞生了。 厄多斯的新的一篇论文就这样诞生了。
大学离散数学欧拉图和哈密尔顿图

(a)
(b)
推论1:哈密尔顿图无割点.
2020/9/28
24
计算机科学学院 刘芳
15.2.3 Hamilton图的判定方法
例3:
▪ 证明下述各图不是哈密顿图。
2020/9/28
25
计算机科学学院 刘芳
15.2.3 Hamilton图的判定方法
推论2:
▪ 对二部图G=< V1,V2,E>
若| V1 |≠| V2 |,则一定不是H图。 证明:
2020/9/28
14
计算机科学学院 刘芳
15.1.4 中国邮路问题
例如:
2020/9/28
15
计算机科学学院 刘芳
15.1.4 中国邮路问题
判断条件
▪ 定理:
▪ 设L是图G的包含所有边的回路,则L具有最小长 度的充分必要条件是: ▪ 每条边最多重复一次; ▪ G的每个回路上,所有重复边的长度之和,不 超过该回路长度的一半。
2020/9/28
16
计算机科学学院 刘芳
15.2 Hamilton 图
15.2.1 问题引入 15.2.2 Hamilton图的定义 15.2.3 Hamilton图的判定方法 15.2.4 应用举例
2020/9/28
17
计算机科学学院 刘芳
15.2.1 问题引入
周游世界问题(W.Hamilton, 1859年)
▪ 可以用结点表示城市,城市间的交通路线用边表示,而 城市间的交通线路距离可用附加于边的权表示。
▪ 这样,上述问题可以归结为寻找一条权的总和为最短的 哈密尔顿回路的问题。
2020/9/28
30
计算机科学学院 刘芳
分析
▪ 穷举法 ▪ 近似算法 ▪ …………
15欧拉图与哈密顿图

问题转化为在图中找一条哈密顿回路. ABDFGECA即可.
哈密顿图的判定 定理1(必要条件): 设无向图G=<V, E>是哈密顿 图, V1是V的任意非空子集, 则p(G-V1)≤V1. 推论: 设无向图G=<V, E>是半哈密顿图, V1是V 的任意非空子集, 则p(G-V1)≤V1+1.
在Peterson图中, 虽然对任意顶 点集V1, 都满足p(G-V1)|V1|,但 它不是哈密顿图.
基本思想:能不走桥就不走桥
15.2 哈密顿图 定义1. 经过无向(有向)图中所有顶点恰好一次 的路(圈)称为哈密顿路(圈). 定义2. 具有哈密顿圈的图称为哈密顿图. 定义3. 具有哈密顿路但不具有哈密顿圈的图 称为半哈密顿图. 例1. 判断下列图形是否哈密顿图或半哈密顿图.
半哈密顿图 哈密顿图
都不是
例4. 判断下列有向图是否欧拉图或半欧拉图.
都不是 半欧拉图
欧拉图
一笔画问题:从某点出发,不间断地画完整个图. 即在图中找出欧拉通路(回路).
Fleury算法: (1) 任取v0∊V(G), (2) 设Pi=v0e1v1e2eivi,
若E(G)-{e1,e2,ei}中没有与vi关联的边, 则计 算停止; 否则在vi关联的边中优先选择非桥的边 添加. (3) 令i=i+1, 返回(2).
定理2(充分条件): 设G=<V, E>是无向简单图. 若对任意两个不相邻顶点u,vV, 均有 d(u)+d(v)|V|-1, 则G中存在哈密顿路; 若对任意两个不相邻顶点u,vV, 均有 d(u)+d(v)|V|, 则G是哈密顿图.
推论: n阶无向简单图G中, n>2, (G)n/2, 则G是
哈密顿图的判定 定理1(必要条件): 设无向图G=<V, E>是哈密顿 图, V1是V的任意非空子集, 则p(G-V1)≤V1. 推论: 设无向图G=<V, E>是半哈密顿图, V1是V 的任意非空子集, 则p(G-V1)≤V1+1.
在Peterson图中, 虽然对任意顶 点集V1, 都满足p(G-V1)|V1|,但 它不是哈密顿图.
基本思想:能不走桥就不走桥
15.2 哈密顿图 定义1. 经过无向(有向)图中所有顶点恰好一次 的路(圈)称为哈密顿路(圈). 定义2. 具有哈密顿圈的图称为哈密顿图. 定义3. 具有哈密顿路但不具有哈密顿圈的图 称为半哈密顿图. 例1. 判断下列图形是否哈密顿图或半哈密顿图.
半哈密顿图 哈密顿图
都不是
例4. 判断下列有向图是否欧拉图或半欧拉图.
都不是 半欧拉图
欧拉图
一笔画问题:从某点出发,不间断地画完整个图. 即在图中找出欧拉通路(回路).
Fleury算法: (1) 任取v0∊V(G), (2) 设Pi=v0e1v1e2eivi,
若E(G)-{e1,e2,ei}中没有与vi关联的边, 则计 算停止; 否则在vi关联的边中优先选择非桥的边 添加. (3) 令i=i+1, 返回(2).
定理2(充分条件): 设G=<V, E>是无向简单图. 若对任意两个不相邻顶点u,vV, 均有 d(u)+d(v)|V|-1, 则G中存在哈密顿路; 若对任意两个不相邻顶点u,vV, 均有 d(u)+d(v)|V|, 则G是哈密顿图.
推论: n阶无向简单图G中, n>2, (G)n/2, 则G是
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由定理立刻可知,图中的三 个无向图中,只有()中无奇度顶点, 因而()是欧拉图,而()、()都 有奇度顶点,因而它们都不是欧拉图。
定理 : 无向图是半欧拉图当且仅 当是连通的,且中恰有两个奇度顶点。
证: 必要性 设是条边的阶无向图, 因为为半欧拉图,因而中存在欧拉通路
(但不存在欧拉回路),设 Г… 为中一条欧拉通路, ≠ .
二、判别定理
定理 无向图是欧拉图当且仅当是连 通图,且中没有奇度顶点。
证: 若是平凡图,结论显然成立, 下面设为非平凡图,设是条边的阶 无向图。并设的顶点集{,…}. 必要性: 因为为欧拉图,所以中存
在欧拉回路,设为中任意一条欧拉回路,
∈,都在上,因而连通 所以为连通图。又 ∈,在上每 出现一次获得度,若出现次就获得 度,即(),所以中无奇度顶点。
由定理立即可知,图中() 是半欧拉图,但()不是半欧拉图。
定理 有向图是欧拉图当且仅当 是强连通的且每个顶点的入度都等于出度。 本定理的证明类似于定理 .
定理 有向图是半欧拉图当且仅 当是单向连通的,且中恰有两个奇度 顶点,其中一个的入度比出度大,另一 个的出度比入度大,而其余顶点的入度 都等于出度。
,,…,由归纳假设可知,', ',…'都是欧拉图,因而都存在欧拉 回路‘,,….最后将还原(即将
删除的边重新加上),并从上的某顶点
开始行遍,每遇到 ,就行遍’ 中的 欧拉回路’ ,,…,最后回到,得 回路
… … … … … … …,
此回路经过中每条边一次且仅一次并行 遍中所有顶点,因而它是中的欧拉回 路 ,故为欧拉图。
可以证明,当算法停止时所得简单回路 …()为中一条欧拉回路。
例 图()是给定的欧拉图。某人用算法 求中的欧拉回路时, 走了简单回路 之 后(观看他的错误走法),无法行遍了,试 分析在哪步他犯了错误?
图
解: 此人行遍时犯了能不走桥就不 走桥的错误,因而他没行遍出欧拉回路。 当他走到时,{}为 图()所示。此时为该图中的桥, 而均不是桥,他不应该走,而应 该走或,他没有走,所以犯了错误。 注意,此人在行遍中,在遇到过桥, 处遇到过桥,但当时除桥外他无别的 边可走,所以当时均走了桥,这是不会犯 错误的。
本定理的证明可用归纳法。
例 设是非平凡的且非环的欧拉图, 证明:
λ()≥. ()对于中任意两个不同顶点, 都存在简单回路含和.
证 ()由定理可知, ∈(), 存在圈,在中,因而()(),故 不是桥。由的任意性λ()≥,即是 边连通图。
() ∈(),≠,由的连通 性可知,之间必存在路径Г,设 ' (Г),则在 '中与还必连通,否则, 与必处于 '的不同的连通分支中,这说明 在Г上存在中的桥,这与()矛盾。于
欧拉图与哈密顿图
欧拉图
一.欧拉通路、欧拉回路、欧拉图、半 欧拉图的定义
定义 通过图(无向图或有向图)中所 有边一次且仅一次行遍图中所有顶点 的通路称为欧拉通路,通过图中所有 边一次并且仅一次行遍所有顶点的回 路称为欧拉回路。具有欧拉回路的图 称为欧拉图,具有欧拉通路而无 欧拉回路的图称为半欧拉图。
图
由定理立即可知,图()图 为欧拉图,本图既可以看成圈, ,,之并(为 清晰起见,将个圈画在()中),也 可看成圈与圈 之并(两个圈画在()中)。将() 分解成若干个边不重的圈的并不是() 图特有的性质,任何欧拉图都有这个性 质。
定理 是非平凡的欧拉图当且仅 当是连通的且为若干个边不重的圈的并。
从定义不难看出,欧拉通路是图中经 过所有边的简单的生成通路(经过所有顶 点的通路称为生成通路),类似地,欧拉 回路是经过所有边的简单的生成回路。
在这里做个规定,即平凡图是欧拉图。
图
在图所示各图中,为 ()中的欧拉回路,所以()图为欧拉 图。为()中的一条欧拉通路, 但图中不存在欧拉回路,所以()为半欧 拉图。()中既没有欧拉回路,也没有欧 拉通路,所以()不是欧拉图,也不是半 欧拉图。为()图中的欧拉回路, 所以()图为欧拉图。(),()图中 都既没有欧拉回路,也没有欧拉通路
.逐步插入回路法
设为阶无向欧拉图,(){,…}, 求中欧拉回路的逐步插入回路法的算法如下:
←,*,,, .
.在中任取一条与关联的边 ('),将及’加入到中得到.
.若 '*,转,否则←' , 转.
.若()(),结束,否则,令 (),在中任取一条与 中某顶点关联的边,先将改 写成起点(终点)为的简单回路,再 置*, ←,转.
∈(),若不在Г的端点出现,显然 ()为偶数,若在端点出现过,则()为 奇数,因为Г只有两个端点且不同,因而 中只有两个奇数顶点。另外,的连通 性是显然的。
充分性: 设的两个奇度顶点分别 为 和,对加新边(),
得' ∪(),则'是连通且无奇度 顶点 的图,由定理可知,‘为欧拉 图,因而存在欧拉回路',而' () 为中一条欧拉通路,所以为半欧拉图。
现在再考虑例中图中图 (),用逐步插入回路法可以走出多 条欧拉回路。现在走出一条来:
开始时,置*,,,
,经过步得 ,
是长度为的简单回路,见演示中红边பைடு நூலகம்所示。
在中有条边与上的顶点相关联, 比如取与,先将改写成以为起点 (终点)的简单回路:
', 然后置*,,再经过步得
充分性: 由于为非平凡的连通图可 知,中边数≥.对作归纳法。
()时,由的连通性及无奇度顶 点可知,只能是一个环,因而为欧拉图。
()设≤(≥)时结论成立,要证明 时,结论也成立。由的连通性及
无奇度顶点可知,δ()≥.类似于例 ,用扩大路径法可以证明中存在 长度大于或等于的圈,设为中一个 圈,删除上的全部边,得的生成子 图’ ,设’有个连通分支’’,…, ‘,每个连通分支至多有条边,且无 奇度顶点,并且设‘与的公共顶点为
是在'中存在到的路径Г,显然Г 与Г边不重,这说明处于Г∪Г 形成的简单回路上。
三、求欧拉图中欧拉回路的算法
设为欧拉图,一般来说中存 在若干条欧拉回路,下面介绍两种求 欧拉回路的算法。
.算法,能不走桥就不走桥:
()任取∈(),令. ()设…已经行遍, 按下面方法来从(){,…}中选 取:
否则不应该为{,…}中的 桥。
