第三章 第3节 三角函数的图象和性质
三角函数图像及性质的总结
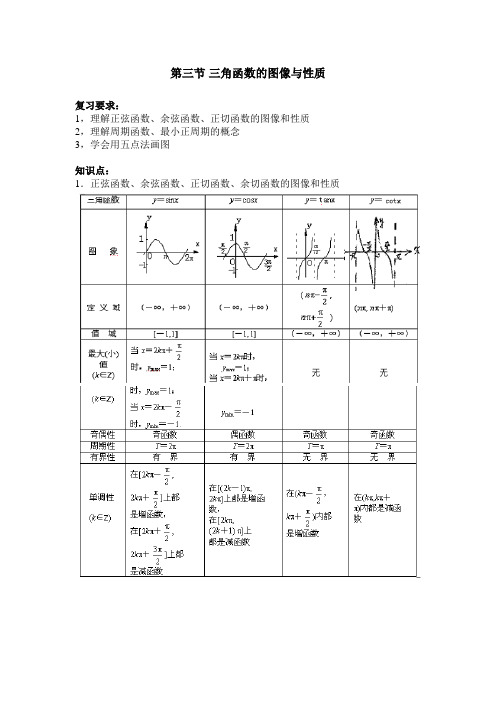
第三节三角函数的图像与性质复习要求：1，理解正弦函数、余弦函数、正切函数的图像和性质2，理解周期函数、最小正周期的概念3，学会用五点法画图知识点：1．正弦函数、余弦函数、正切函数、余切函数的图像和性质3．函数B x A y ++=)sin(ϕω），（其中00>>ωA最大值是B A +，最小值是A B -，周期是ωπ2=T ，频率是πω2=f ，相位是ϕω+x ，初相是ϕ；其图象的对称轴是直线)(2Z k k x ∈+=+ππϕω，凡是该图象与直线B y =的交点都是该图象的对称中心。
4．由y ＝sin x 的图象变换出y ＝sin(ωx ＋ϕ)的图象一般有两个途径，只有区别开这两个途径，才能灵活进行图象变换。
利用图象的变换作图象时，提倡先平移后伸缩，但先伸缩后平移也经常出现无论哪种变形，请切记每一个变换总是对字母x 而言，即图象变换要看“变量”起多大变化，而不是“角变化”多少。
途径一：先平移变换再周期变换(伸缩变换)先将y ＝sin x 的图象向左(ϕ＞0)或向右(ϕ＜0＝平移｜ϕ｜个单位，再将图象上各点的横坐标变为原来的ω1倍(ω＞0)，便得y ＝sin(ωx ＋ϕ)的图象。
途径二：先周期变换(伸缩变换)再平移变换。
先将y ＝sin x 的图象上各点的横坐标变为原来的ω1倍(ω＞0)，再沿x 轴向左(ϕ＞0)或向右(ϕ＜0＝平移ωϕ||个单位，便得y ＝sin(ωx ＋ϕ)的图象。
5．由y ＝A sin(ωx ＋ϕ)的图象求其函数式：给出图象确定解析式y =A sin （ωx +ϕ）的题型，有时从寻找“五点”中的第一零点（－ωϕ，0）作为突破口，要从图象的升降情况找准．．第一个零点的位置。
6．对称轴与对称中心： sin y x =的对称轴为2x k ππ=+，对称中心为(,0) k k Z π∈； cos y x =的对称轴为x k π=，对称中心为2(,0)k ππ+； 对于sin()y A x ωφ=+和cos()y A x ωφ=+来说，对称中心与零点相联系，对称轴与最值点联系。
三角函数的图象与性质 (共44张PPT)
(
)
3 3 A.－2，2 3 3 3 3 C. － ， 2 2
解析： 当 故
π π 1 π π 5π x∈0，2 时， 2x－ ∈－ 6， 6 ， sin2x－6 ∈－2，1， 6
上是减函数 － π ， 0 C．在[0，π]上是增函数，在
)
π π π π D．在2，π和－π，－2上是增函数，在－2，2 上是减函数
3．(2015· 皖南八校模拟)函数 f(x)＝cos 2x＋2sin x 的最大值与最小值 的和是 A．－2 3 C．－ 2
4．求函数 y＝cos x＋sin
2
π x|x|≤4 的最大值与最小值．
π 2 2 解：令 t＝sin x，∵|x|≤ ，∴t∈－ ， . 4 2 2
∴y＝－t
2
1 2 5 ＋t＋1＝－t－2 ＋ ， 4
1－ 2 1 5 2 ∴当 t＝ 时，ymax＝ ，当 t＝－ 时，ymin＝ . 2 4 2 2 ∴函数 y＝cos x＋sin
sin 2x＞0， 解析：由 2 9－x ≥0，
π kπ＜x＜kπ＋ ，k∈Z， 2 得 －3≤x≤3.
π π ∴－3≤x＜－ 或 0＜x＜ . 2 2 ∴函数 y＝lg(sin 2x)＋ 9－x
2
π π 的定义域为－3，2 ∪0，2 .
2
π 1－ 5 x通法]
1．三角函数定义域的求法 求三角函数定义域实际上是构造简单的三角不等式(组)，常借 助三角函数线或三角函数图象来求解．
2．三角函数值域的不同求法 (1)利用 sin x 和 cos x 的值域直接求；
【金版教程】届高考数学总复习 第3章 第3讲 三角函数的图象与性质课件 理 新人教A版
求形如y＝Asin(ωx＋φ)(A>0，ω>0)的函数的单调区间，基
本思路是把ωx＋φ看作一个整体，由－
π 2
＋2kπ≤ωx＋φ≤
π 2
＋
2kπ(k∈Z)求得函数的增区间，由
π 2
＋2kπ≤ωx＋φ≤
3π 2
＋2kπ(k
∈Z)求得函数的减区间．若在y＝Asin(ωx＋φ)中，ω<0，则应
先利用诱导公式将解析式转化，使x的系数变为正数，再进行
(1)y＝cos(x＋π3)(x∈[0，π])的值域________． (2)y＝tan(4π－x)的单调递减区间__________.
1.f(x＋T)＝f(x) 最小 最小正周期
想一想：提示：f[(x＋2)＋2]＝－f(x＋2)＝f(x)，即f(x＋4)
＝f(x)，所以f(x)是周期为4的函数．
____
________
________
____
y＝tanx
无最值
____ ________ 无对称轴
____
判断以下命题的正误． ①y＝sinx在第一象限是增函数．( ) ②y＝cosx在[0，π]上是减函数．( ) ③y＝tanx在定义域上为增函数．( ) ④y＝|sinx|的周期为2π.( ) ⑤y＝ksinx＋1，x∈R则y的最大值为k＋1.( )
Z)
π＋2kπ(k∈Z)
奇
偶
奇
(kπ，0)，k∈Z
(kπ＋
π 2
，
0)，k∈Z
(
kπ 2
，0)，k∈Z
x＝kπ＋
π 2
，k∈Z
x＝kπ，k∈Z
2π 2π π
判一判：①× ②√ ③× ④× ⑤×
第3章《三角函数、解三角形》(第3节)ppt 省级一等奖课件
第三章 三角函数、解三角形
5．(教材习题改编)y＝2－3cosx＋π4 的最大值为________．此时 x
＝________．
解析 当 cosx＋π4 ＝－1 时，函数 y＝2－3cosx＋π4 取得最大
值
5，此时
π x＋ 4 ＝π＋2kπ，从而
x＝34π＋2kπ，k∈Z.
2．最小正周期： 如果在周期函数f(x)的所有周期中存在一个 最小的正数 ， 那么这个 最小正数 就叫做f(x)的最小正周期．
第三章 三角函数、解三角形
二、正弦函数、余弦函数、正切函数的图象和性质
函数
y＝sin x
y＝cos x
y＝tan x
图象
第三章 三角函数、解三角形
定 义 域 值域
R [－1，1]
[规律方法] 1．三角函数的奇偶性的判断技巧 首先要对函数的解析式进行恒等变换，再根据定义、诱导公 式去判断所求三角函数的奇偶性；也可以根据图象做判断．
第三章 三角函数、解三角形
2．求三角函数周期的方法 (1)利用周期函数的定义； (2)利用公式：y＝Asin(ωx＋φ)和 y＝Acos(ωx＋φ)的最小正周期为
(kπ －π2 ，π2 ＋k π ) (k∈Z)上递增
减
第三章 三角函数、解三角形
x＝
π 2
＋2kπ
(k∈Z)
x＝ 2kπ
(k∈Z)
最 时，ymax＝1；x＝
时，ymax＝1；x＝
值
－π2 ＋2kπ (k∈Z)
π ＋2kπ (k∈Z) 时，ymin＝－1
时，ymin＝－1
奇偶性
奇函数
偶函数
奇函数
第三章 三角函数、解三角形
(2)下列函数中，周期为π ，且在[π4 ，π2 ]上为减函数的是(
三角函数的图象与性质
-
;
-1
y=cosx
2 3
4 5 4 5
6 x 6 x
五.定义域 、值域及取到最值时相应的x的集合:
-6 -5
-4 -3
复习回顾
-2 -
y y=sinx
1 o
-1
2 3
y
si-n6x的对称-5轴：x
k -4
2-,3对 称点-：2(k
,0);
-
y cosx的对称轴：x k , 对称点：(k ,0);
1.4.1正弦、余弦函数的图象
复习
回顾 三角函数
三角函数线
正弦函数 余弦函数 正切函数
sin=MP
正弦线MP cos=OM 余弦线OM tan=AT 正切线AT
y PT
-1
O
M A(1,0) x
正弦、余弦函数的图象
问题：如何作出正弦、余弦函数的图象？
途径：利用单位圆中正弦、余弦线来解决。
描图：用光滑曲线
复习回顾
一.正弦余弦函数的作图： 几何描点法（利用三角函数线） 五点法作简图
二.周期性：
函数y Asin(x )和y Acos(x )，x R的周期T 2 | |
三.奇偶性：
y sin x为奇函数，图像关于原点对称； y cosx为偶函数图像关于y轴对称。
-6 -5
-4 -3
复习回顾 y y=sinx
(0,11)
3
( 2 ,1)
-
(-o12 ,0)
( 2 ,0)
2
( ,-1)
3
线
4
5 6 x
正弦、余弦函数的图象
y
五点画图法
1
(
2
,1)
三角函数的图像和性质PPT课件
2021/6/7
1
一、三角函数图像的作法 二、三角函数图像的性质 三、f(x)= Asin(x+) 的性质
几何法 五点法 图像变换法
2021/6/7
2
一、三角函数图象的作法
1.几何法 y=sinx 作图步骤:
y
(1)等分单位圆作出特殊角的三角函数线;
(2)平移三角函数线; (3)用光滑的曲线连结各点.
得 到 y = s i n ( ω x + ) 在 某 周 期 内 的 简 图
步骤4
各点纵的坐纵标坐标变为伸原长来或的缩A倍短(横坐标不变)；
得 到 y = A s i n ( ω x + ) 在 某 周 期 内 的 简 图
沿x轴
扩展
步骤5
得 到 y = A s i n ( ω x + ) 在 R 上 的 图 象
3
x
11
返回目录
二、三角函数图象的性质
函数 y sin x
ycosx
y tanx
图象
y 1
0
1
2 x
y
1
0
1
2
x
y
2
3 2
2
0
3 2
x
单调性
[2k， 32k](kz)
2
2
递减
[ 2 k， 2 2 k](k 递z)增
[2k， 2k](kz) 递增 [2 k,2 k](k z)
22
递减
纵向伸长3倍
y=3sinx
左移 π 3π
y=3横si向n(缩x+短31) y=3sin(2x+ 2π) 方法2： y=sinx 3
第三节 三角函数的图象与性质
题点(一) 求单调区间
[逐点例析]
[例 1] (1)函数 y＝log12cos32π－2x的单调递增区间是 A．kπ－π4，kπ＋π4 (k∈Z )
()
B．kπ－π4，kπ (k∈Z )
C．kπ－kπ＋π4，kπ＋34π (k∈Z )
D．kπ＋π4，kπ＋34π (k∈Z )
(2)函数 y＝|tan x|的单调递增区间为________，单调递减区间为_______．
2．三角函数值域或最值的3种求法 形如y＝asin x＋k或y＝acos x＋k的三角函数，直接利用sin
直接法 x，cos x的值域求出 形如y＝asin x＋bcos x＋k的三角函数，化为y＝Asin(ωx＋φ)＋
化一法 k的形式，确定ωx＋φ的范围，根据正弦函数单调性写出函数 的值域(最值) 形如y＝asin2x＋bsin x＋k的三角函数，可先设sin x＝t，化为 关于t的二次函数求值域(最值)；形如y＝asin xcos x＋b(sin
[解析]
(1)y＝log
1 2
cosπ3－2x＝log
1 2
(－sin 2x)，
由－sin 2x>0 得 sin 2x<0，即 2kπ－π<2x<2kπ，k∈Z ，
即 kπ－π2<x<kπ，k∈Z ，
设 t＝－sin 2x，则 y＝log 1 t 为减函数， 2
要求
y＝log
1 2
cosπ3－2x的递增区间，
二、“基本技能”运用好 1．y＝|tan x|·cos x0≤x<32π，x≠π2的图象是
答案：D
()
2．已知函数 f(x)＝cosωx＋π4 (ω>0)的最小正周期为 π，则 ω＝________. 答案：2
第三章 第三节 正弦、余弦、正切函数的图像与性质
最 ymax＝1(k∈Z)； 2kπ 时， 值 x＝ymin＝－1(k∈Z)
x＝2kπ 时 ， ymax＝1(k∈Z)； π＋2kπ 时， X＝ ymin＝－1(k∈Z)
无最值
函数 奇偶 性
y＝sinx
y＝cosx
y＝tanx 奇 对称中心 ( ，0)， k∈Z
奇
偶
对称中心
对称中心 (kπ＋ ,0) k∈Z
图 象
函 数 定 义 域
y＝sinx
y＝cosx
y＝tanx
R
R
{x|x≠
＋2kπ，k∈Z}
值 {y|－1 ≤ y ≤ 1} 域
{y|－1≤ y ≤ 1}
R
函 数
[－
y＝sinx
＋2kπ，
y＝cosx [(2k－1)π，2kπ]
y＝tanx
(－ Kπ， Kπ) 上递增 k∈Z ＋ +
上递增，∈Z； ＋ 2kπ] 单 上递增，k∈Z； [2kπ，(2k＋1)π] 调 [ ＋2kπ， ＋2kπ] 性 上递减，k∈Z 上递减，k∈Z
＋2kπ≤ωx－ φ ≤
3.对于y＝Atan(ωx＋φ)(A、ω、 φ为常数)，其周期T＝
单调区间利用ωx＋ φ ∈(kπ－ 的取值范围，即为其单调区间. ，kπ＋
，
)(k∈Z)，解出x
[特别警示] 求三角函数的单调区间时，一定要注意A和ω 的符号.
已知函数f(x)＝log2[ (1)求函数的定义域；
在[0,2π]内，满足sinx＝cosx的x为
再结合正弦、余弦函数的周期是2π，所以定义域为{x|
＋2kπ＜x＜
＋2kπ，k∈Z}.
1.形如y＝Asin(ωx＋φ)(A＞0，ω＞0)的函数的单调区间， 基本思路是把ωx＋ φ 看作一个整体，由－ ＋2kπ≤ωx
高考数学第3章三角函数、解三角形第3讲三角函数的图象与性质创高三全册数学
第四页，共七十六页。
2.正弦函数、余弦函数、正切函数的图象和性质
函数 y＝sinx
y＝cosx
y＝tanx
图象
定义 域 值域
xx∈R，且 x≠
R
R
kπ＋π2，k∈Z
01 _[－___1_,1__] 02 _[－___1_,1_]_ 03 _R_
12/12/2021
第五页，共七十六页。
续表
函数
y＝sinx
y＝cosx
y＝tanx
最值
当 x＝π2＋2kπ
当 x＝2kπ(k∈Z)时，ymax
x∈
(k∈Z)时，ymax＝1；
＝1；
－π2＋kπ， π2＋kπ
当 x＝32π＋2kπ (k∈Z)时，ymin＝－1
当 x＝π＋2kπ (k∈Z)时，ymin＝－1
，k∈Z，无最大值， 也无最小值
12/12/2021
第二十四页，共七十六页。
解析
2．已知π3为函数 f(x)＝sin(2x＋φ)0<φ<π2的零点，则函数 f(x)的单调递 增区间是( )
A.2kπ－152π，2kπ＋1π2(k∈Z) B.2kπ＋1π2，2kπ＋71π2(k∈Z) C.kπ－51π2，kπ＋1π2(k∈Z) D.kπ＋1π2，kπ＋71π2(k∈Z)
第二十页，共七十六页。
1．函数 y＝ tanx＋ －cosx的定义域为｛__x_2_k_π_＋__π_≤__x_＜__2_kπ_＋__3_2π_，__k_∈__Z_．
解析
tanx≥0， 由
－cosx≥0，
得
tanx≥0，
cosx≤0.
所以 2kπ＋π≤x<2kπ＋32π，k∈
高二数学课件：第三章 第三节 三角函数的图象与性质
1 1 1 【解析】(1)由log2 sinx -1≥0,log2 sinx ≥1, sinx ≥2, 1 0＜sinx≤ 2 得2kπ＜x≤2kπ+ 6 或 5 2kπ+ 6 ≤x＜2kπ+π,k∈Z. 5 答案：(2kπ,2kπ+ 6 ]∪[2kπ+ 6 ,2kπ+π)(k∈Z) 2 1 (2)由2kπ- 6 ≤x≤2kπ+ 3 (k∈Z),得- 2 ≤cosx≤1,所以函 1 数y=f(x)的定义域为[- 2 ,1]. 1 答案：[- 2 ,1]
函数的单调区间，这就要求同学们熟练掌握基本三角函数的单
调区间.
(2)图象法
函数的单调性表现在图象上是：从左到右，图象上升趋势的区
间为单调递增区间，图象下降趋势的区间为单调递减区间，如
果能画出三角函数的图象，那它的单调区间就直观明了了 .
【变式训练】求下列函数的单调递增区间： (1)y＝cos(2x＋ )；(2)y＝3sin( － x ).
2 2
( (
) )
③y=tanx在定义域上是增函数.
④y=sin|x|是偶函数.
(
(
)
)
⑤y=sin2x的周期为2π .
⑥y=cos2x的对称中心为(kπ +
,0)，k∈Z. 2
(
(
)
)
(2)若直线y=a与函数y=sinx,x∈［-2π ,2π )的图象有4个交点, 则a的取值范围是_______.
6 3 2
【解析】(1)设ｕ＝2x＋ ，则y＝cosｕ
6
当2kπ－π≤ｕ≤2kπ(k∈Z)时，y＝cosu随u的增大而增大.
又∵ｕ＝2x＋ 随x的增大而增大(x∈R),
第三章 第三节 三角函数的图象和性质1
π x＋ . 4
答案： A
返回
4．(2012· 宁德质检)函数y＝tan 为________．
解析：把函数y＝tan
π －x的单调递减区间 3
π π －x变为y＝－tan x－ . 3 3
π π π 由kπ－2<x－3<kπ＋2，k∈Z， π 5 得kπ－6<x<kπ＋6π，k∈Z.
返回
函数
对称
y＝sinx
(k，0)，
y＝cosx
π (kπ＋2，0)， k∈Z
y＝tanx
kπ ( 2 ，0)， k∈Z
对
称 性
中心 对称 轴l：
k∈Z
π x＝kπ＋2， k∈Z
x＝kπ， k∈Z 2π π
无
周期性
2π
返回
返回
1．函数y＝tan
π －x的定义域是 4
(
)
π A.x|x≠4，x∈R π B.x|x≠－4，x∈R π x|x≠kπ＋ ，k∈Z，x∈R C. 4 3π x|x≠kπ＋ ，k∈Z，x∈R D. 4
[巧练模拟]———————(课堂突破保分题，分分必保！)
π 3．(2012· 桂林模拟)若函数f(x)＝(1＋tan x)cos x,0≤x＜2， 则f(x)的最大、最小值分别为 A. 2和1 C．2和 2 B．2和1 D．2和 3 ( )
返回
解析：f(x)＝(1＋tan x)cos x＝cos x＋sin x＝ 2sin π π π 3π ∵0≤x＜2，∴4≤x＋4＜ 4 . ∴1≤f(x)≤ 2.
返回
[精析考题] [例4] (2010· 湖北高考)函数f(x)＝ 3sin
三角函数的图像与性质课件PPT
正解：因为 x∈π6，π，所以借助函数 y＝sin x 的图象可知， 此时 0≤sin x≤1.于是由 sin x＝2m－1，得 0≤2m－1≤1，解得 m 的取值范围12≤m≤1.
纠错心得：三角函数的取值范围与定义域有关，因此，在求解 有关范围问题时，一定要先看清定义域，再由定义域推得三角函数 的取值范围，最后求出正确答案．
思路点拨：要使函数有意义，则 sin x＞0 且 25－x2≥0，即 sin x＞0 且－5＜x＜5，结合图象求出在区间(－5,5)上满足 sin x＞0 的 x 的取值范围，即原函数的定义域．
解： 使函数有意义的条件是s2i5n－x＞x2≥0，0， 记 sin x＞0 的 x 取值为 集合 A,25－x2≥0 的 x 取值为集合 B，则 A＝(2kπ，2kπ＋π)，k∈Z， B＝[－5,5]．用图象表示如下：
小结 为了突出函数的这个特性，我们把函数f(x)＝sin x称为周 期函数，2kπ为这个函数的周期 (其中k∈Z且k≠0).
思考3 正弦函数y＝sin x的周期是否唯一？正弦函数y＝sin x 的周期有哪些？ 答 正弦函数y＝sin x的周期不止一个. ±2π，±4π，±6π，… 都 是 正 弦 函 数 的 周 期 ， 事 实 上 ， 任 何 一 个 常 数 2kπ(k∈Z 且 k≠0)都是它的周期.
探究点一 周期函数的定义
思考1 观察正弦函数图象知，正弦曲线每相隔2π个单位重复出现 其理论依据是什么？ 答 诱导公式sin(x＋2kπ)＝sin x(k∈Z)当自变量x的值增加2π的整 数倍时，函数值重复出现.数学上，用周期性这个概念来定量地刻 画这种“周而复始”的变化规律.
思考2 设f(x)＝sin x，则sin(x＋2kπ)＝sin x可以怎样表示？把函数 f(x)＝sin x称为周期函数，那么，一般地，如何定义周期函数呢？ 答 f(x＋2kπ)＝f(x)(k∈Z)这就是说：当自变量x的值增加到x＋2kπ 时，函数值重复出现. 一般地，对于函数y＝f(x)，如果存在一个不为零的常数T，使得当x 取定义域内的每一个值时，f(x＋T)＝f(x)都成立，那么就把函数y＝ f(x)叫做周期函数，不为零的常数T叫做这个函数的周期.
三角函数的图象和性质
在区间 [0,
2
]
上是单调函数,
必有
2
≤
,
即 0<≤2.
∴0<
4k+2 3
≤2(kZ).
解得 k=0 或 1.
∴=2
或
2 3
.
综上所述,
=
2
,
=2 或
2 3
.
6.如果函数 的值.
y=sin2x+acos2x
的图象关于直线
x=-
8
对称,
求a
解: y=sin2x+acos2x= a2+1 sin(2x+), 其中, tan=a.
3.周期性: ①y=sinx、y=cosx 的最小正周期都是
Asin(x+) 和 f(x)=Acos(x+)的最小正周期都是
2;
T=
2|②| .f(x)=
4.奇偶性与对称性: 正弦函数y=sinx(xR)是奇函数, 对称中心
是 (x(kR),是0)偶(k函Z数),,对对称称轴中是心直是线(kx=+k2,+02)((kkZZ)),;对余称弦轴函是数直y=线coxs=x k (kZ) (正(余)弦型函数的对称轴为过最高点或最低点且垂
性, 如果是周期函数, 求出它的一个周期.
解:
(1)由∴∵∴2kfsfs((iixnx+n))xx=的4--lcoc<定oogxss<21xx义(2s=>ik域n0,x2+为-s即ic5n4o{(xsx,x2|-k)s2≥ik4nlZ)(o≤x+g-21424<2,)x>=<0-2得k12:.+
5
4
三角函数的图象和性质
三角函数定义域、值域的求解策略 (1)求与三角函数有关的定义域问题实际上是解简单的三角不等式，也可借助三角函数线或三角函数图 象来求解． (2)求解三角函数的值域(最值)，首先把三角函数化为 y＝Asin(ωx＋φ)＋k 的形式，再求最值(值域)，或 用换元法(令 t＝sinx，或 t＝sinx±cosx)化为关于 t 的二次函数求值域(最值)． (3)换元法的应用：把 sinx 或 cosx 看作一个整体，转化为二次函数，求给定区间上的值域(最值)问题．此 时注意所换元的取值范围.
第3讲 三角函数的图象和性质
1.能画出 y＝sinx，y＝cosx，y＝tanx 的图象，了解三角函数的周期性． 2．理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值，图象 与 x 轴的交点等)，理解正切函数在区间－π2，2π内的单调性.
板块一 知识梳理·自主学习
考点 1 周期函数和最小正周期
递增；π 在 2
＋2kπ，32π＋2kπ]
，k∈Z 上 ，k∈Z 上
在 [(2k－1)π，2kπ] k∈Z 上递增；
，在－π2
＋kπ，
在 [2kπ，(2k＋1)π]，k∈Z 上递增
π2＋kπ，
递减
k∈Z 上递减
－xπ2＝＋π22＋kπ2(kkπ∈Z(k)∈时Z)，时y，miny＝max－＝11；x＝
[必备知识]
考点 2 正弦函数、余弦函数、正切函数的图象和性质
函数
y＝sinx
y＝cosx
y＝tanx
图象
定义 域
值域
x∈R [－1,1]
x∈R [－1,1]
{ x|x∈R 且 x≠π2＋kπ，k∈Z } R
续表 函数
单调性
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 第三节 三角函数的图象和性质1.函数y ＝tan 4x π(-)的定义域是 ( ) A ．{x |x ≠π4，x ∈R}B ．{x |x ≠－π4，x ∈R}C ．{x |x ≠kπ＋π4，k ∈Z ，x ∈R}D ．{x |x ≠kπ＋3π4，k ∈Z ，x ∈R}解析：∵x －π4≠kπ＋π2，∴x ≠kπ＋34π，k ∈Z.答案：D2．求下列函数的定义域：(1)y ＝cos x ＋tan x ；(2)y ＝lg(2sin x －1)＋－tan x －1cos(x 2＋π8).解：(1)要使函数有意义，则⎩⎪⎨⎪⎧ cos x ≥0，tan x ≥0，即⎩⎨⎧ 2kπ－π2≤x ≤2kπ＋π2，kπ≤x ＜kπ＋π2，(k∈Z)， 所以2kπ≤x ＜2kπ＋π2(k ∈Z)．所以函数y ＝cos x ＋tan x 的定义域是{x |2kπ≤x ＜2kπ＋π2，k ∈Z}．(2)由函数式有意义得⎩⎪⎨⎪⎧2sin x －1＞0，－tan x －1≥0，cos(x 2＋π8)≠0，得⎩⎪⎨⎪⎧ sin x ＞12，tan x ≤－1，x 2＋π8≠kπ＋π2，(k ∈Z)．即⎩⎪⎨⎪⎧ 2kπ＋π6＜x ＜2kπ＋5π6，kπ－π2＜x ≤kπ－π4，x ≠2kπ＋3π4，(k ∈Z)．求交集得2kπ＋π2＜x ＜2kπ＋3π4(k ∈Z)． 所以函数的定义域是{x |2kπ＋π2＜x ＜2kπ＋3π4，k ∈Z}． 3.若函数y ＝sin x ＋f (x )在[－π4，3π4]内单调递增，则f (x )可以是 ( ) A ．1 B ．cos x C ．sin x D ．－cos x解析：y ＝sin x －cos x ＝2sin(x －π4)，－π2≤x －π4≤π2，满足题意，所以f (x )可以是－cos x . 答案：D4．求y ＝3tan(π6－x 4)的周期及单调区间． 解：y ＝3tan(π6－x 4)＝－3tan(x 4－π6)， ∴T ＝π|ω|＝4π， ∴y ＝3tan(π6－x 4)的周期为4π. 由kπ－π2＜x 4－π6＜kπ＋π2，得4kπ－4π3＜x ＜4kπ＋8π3(k ∈Z)， y ＝3tan(x 4－π6)在(4kπ－4π3，4kπ＋8π3)(k ∈Z)内单调递增． ∴y ＝3tan(π6－x 4)在(4kπ－4π3，4kπ＋8π3)(k ∈Z)内单调递减．5.已知函数y ＝sin x 的定义域为[a ，b ]，值域为[－1，12]，则b －a 的值不可能是 ( )A.π3B.2π3 C ．π D.4π3解析：画出函数y ＝sin x 的草图分析知b －a 的取值范围为[2π3，4π3]． 答案：A6．已知函数f (x )＝2sin ωx (ω＞0)在区间[－π3，π4]上的最小值是－2，则ω的最小值等于( ) A.23 B.32C ．2D ．3 解析：由题意知⎩⎨⎧ T 4≤π3，T ＝2πω，解得ω≥32. 答案：B 7．设函数f (x )＝2cos 2x ＋3sin2x ＋a (a 为实常数)在区间[0，π2]上的最小值为－4，那么a 的值等于 ( )A ．4B ．－6C ．－4D ．－3解析：y ＝cos2x ＋3sin2x ＋a ＋1＝2sin(2x ＋π6)＋a ＋1， ∵x ∈[0，π2]，∴2x ＋π6∈[π6，7π6]， ∴y min ＝2×(－12)＋a ＋1＝a ＝－4. 答案：C8．(2010·诸城模拟)设函数f (x )＝2cos 2x ＋23sin x ·cos x ＋m (m ，x ∈R)(1)化简函数f (x )的表达式，并求函数f (x )的最小正周期；(2)当x ∈[0，π2]时，求实数m 的值，使函数f (x )的值域恰为[12，72]． 解：(1)f (x )＝2cos x ＋23sin x cos x ＋m＝1＋cos2x ＋3sin2x ＋m＝2sin(2x ＋π6)＋m ＋1， ∴函数f (x )的最小正周期T ＝π.(2)∵0≤x ≤π2， ∴π6≤2x ＋π6≤7π6， ∴－12≤sin(2x ＋π6)≤1，m ≤f (x )≤m ＋3.又12≤f (x )≤72，故m ＝12.9.(2009·江西高考) ( )A ．2π B.3π2 C ．π D.π2解析：f (x )＝(1＋3tan x )cos x ＝cos x ＋3sin x＝2sin(x ＋π6)，T ＝2π|ω|＝2π. 答案：A10．(2009·福建四地六校联考)若函数f (x )同时满足下列三个性质：①最小正周期为π；②图象关于直线x ＝π3对称；③在区间[－π6，π3]上是增函数．则y ＝f (x )的解析式可以是 ( )A ．y ＝sin(2x －π6)B ．y ＝sin(x 2＋π6) C ．y ＝cos(2x －π6) D ．y ＝cos(2x ＋π3) 解析：逐一验证，由函数f (x ) 的周期为π，故排除B ；又∵cos(2×π3－π6)＝cos π2＝0，故y ＝cos(2x －π6)的图象不关于直线x ＝π3对称； 令－π2＋2kπ≤2x －π6≤π2＋2kπ，得－π6＋kπ≤x ≤π3＋kπ，k ∈Z ， ∴函数y ＝sin(2x －π6)在[－π6，π3]上是增函数． 答案：A11．已知f (x )＝sin(ωx ＋π3)(ω＞0)，f (π6)＝f (π3)，且f (x )在区间(π6，π3)有最小值，无最大值，则ω＝________. 解析：由f (π6)＝f (π3)， 知f (x )的图像关于x ＝π4对称．且在x ＝π4处有最小值， ∴π4ω＋π3＝2kπ－π2， 有ω＝8k －103(k ∈Z)． 又∵12T ＝πω＞π3－π6＝π6，∴ω＜6，故k ＝1，ω＝143. 答案：14312．(文)若a ＝(3cos ωx ，sin ωx )，b ＝(sin ωx,0)，其中ω＞0，记函数f (x )＝(a ＋b )·b ＋k .(1)若函数f (x )的图象中相邻两条对称轴间的距离不小于π2，求ω的取值范围； (2)若函数f (x )的最小正周期为π，且当x ∈[－π6，π6]时，函数f (x )的最大值是12，求函数f (x )的解析式，并说明如何由函数y ＝sin x 的图象变换得到函数y ＝f (x )的图象． 解：∵a ＝(3cos ωx ，sin ωx )，b ＝(sin ωx,0)，∴a ＋b ＝(3cos ωx ＋sin ωx ，sin ωx )．故f (x )＝(a ＋b )·b ＋k ＝3sin ωx cos ωx ＋sin 2ωx ＋k ＝32sin2ωx ＋1－cos2ωx 2＋k ＝32sin2ωx －12cos2ωx ＋12＋k ＝sin(2ωx －π6)＋k ＋12. (1)由题意可知T 2＝π2ω≥π2，∴ω≤1. 又ω＞0，∴0＜ω≤1.(2)∵T ＝2π2ω＝π，∴ω＝1. ∴f (x )＝sin(2x －π6)＋k ＋12. ∵x ∈[－π6，π6]，∴2x －π6∈[－π2，π6]． 从而当2x －π6＝π6，即x ＝π6时，f (x )max ＝f (π6)＝sin π6＋k ＋12＝k ＋1＝12， ∴k ＝－12.故f (x )＝sin(2x －π6)． 由函数y ＝sin x 的图象向右平移π6个单位长度，得到函数y ＝sin(x －π6)的图象，再将得到的函数图象上所有点的横坐标变为原来的12倍(纵坐标不变)，得到函数y ＝sin(2x －π6)的图象． (理)(2009·重庆高考)设函数f (x )＝sin(π4x －π6)－2cos 2π8x ＋1. (1)求f (x )的最小正周期；(2)若函数y ＝g (x )与y ＝f (x )的图象关于直线x ＝1对称，求当x ∈[0，43]时，y ＝g (x )的最大值．解：(1)f (x )＝sin π4x cos π6－cos π4x sin π6－cos π4x ＝32sin π4x －32cos π4x ＝3sin(π4x －π3)， 故f (x )的最小正周期为T ＝2ππ4＝8. (2)法一：在y ＝g (x )的图象上任取一点(x ，g (x ))，它关于x ＝1的对称点为(2－x ，g (x ))． 由题设条件，点(2－x ，g (x ))在y ＝f (x )的图象上，从而g (x )＝f (2－x )＝3sin[π4(2－x )－π3] ＝3sin(π2－π4x －π3) ＝3cos(π4x ＋π3)． 当0≤x ≤43时，π3≤π4x ＋π3≤2π3，因此y ＝g (x )在区间[0，43]上的最大值为g max ＝3cos π3＝32. 法二：因区间[0，43]关于x ＝1的对称区间为[23，2]，且y ＝g (x )与y ＝f (x )的图象关于x ＝1对称，故y ＝g (x )在[0，43]上的最大值即为y ＝f (x )在[23，2]上的最大值． 由(1)知f (x )＝3sin(π4x －π3)， 当23≤x ≤2时，－π6≤π4x －π3≤π6. 因此y ＝g (x )在[0，43]上的最大值为 g max ＝3sin π6＝32.。