2018级高中数学教材过渡调整——当不分文理的新高考遇上分文理的旧教材
新高考背景下的高中数学课堂构建策略分析

新高考背景下的高中数学课堂构建策略分析随着我国教育改革的不断深入,高中教育也迎来了新的变革。
新高考制度的实施,使得高中数学课堂面临着新的挑战和机遇。
在这一背景下,如何构建适应新高考需求的高中数学课堂,成为每一位数学教师所面临的重要课题。
本文将就新高考背景下的高中数学课堂构建进行分析,并提出相应的策略。
一、新高考的背景与特点1. 新高考背景新高考是指我国自2014年起开始实施的“3+3”新高考制度,即“3年高中+3年高校”的教育模式。
新高考制度采取了综合素质评价、多元录取的原则,旨在培养学生的创新能力、实践能力和综合素质,突出个性发展和多元评价,强调学生的发展为本。
2. 新高考特点新高考制度下,高中数学课堂的特点主要表现在以下几个方面:(1)课程内容重新调整。
新高考要求学生具备更为全面的素质,因此数学课堂的内容不仅仅局限于知识的传授,还需要培养学生的创新思维和实践能力。
(2)考试形式发生改变。
新高考取消了传统的高考,采取了多样化的考试形式,如高校自主招生、综合素质评价等,对学生的综合评价更加全面和多元化。
二、高中数学课堂的构建策略在新高考背景下,高中数学课堂的构建需要根据新的教育理念和考试形式,灵活调整教学策略,培养学生的创新思维和实践能力,使其更好地适应新高考的要求。
具体而言,高中数学课堂的构建策略应包括以下几个方面:1. 强化基础知识的教学基础知识是数学学习的重要基础,也是新高考的考试内容。
在构建高中数学课堂时,要注重对基础知识的深入讲解和梳理,帮助学生掌握数学的基本概念和定理,打好数学学习的基础。
要结合实际教学,引导学生运用所学知识解决实际问题,增强他们的数学应用能力。
2. 注重培养学生的创新思维新高考强调培养学生的创新能力,因此在高中数学课堂的构建中,要注重培养学生的创新思维。
可以通过设计开放性的数学问题,引导学生在实际情境中思考和解决问题,培养他们的数学建模能力和创新意识。
要鼓励学生勇于提出自己的观点和思考,培养他们的独立思考能力。
普通高中新课程新教材实施方案解读

基础教育课程改革历程回顾
2017年 2018年 2019年
2020年
国家教材委员会成立 北京、天津、山东、海南第二批进入新高考(3+3) 教育部印发《普通高中课程方案和语文等学科课程标准(2017年版) 教育部印发《关于做好普通高中新课程新教材实施工作的指导意见》 辽宁、广东、河北、湖北、湖南、江苏、福建、重庆第三批进入新高考(3+1+2) 《国务院办公厅关于新时代推进普通高中育人方式改革的指导意见》发布 《 中共中央国务院关于深化教育教学改革全面提高义务教育质量的意见》发布 教育部关于在部分高校开展基础学科招生改革试点工作的意见 北京、天津、上海、辽宁、山东、海南6个省份率先使用普通高中新课程新教材 <<中国高考评价体系>由教育部考试中心发布(高考“为什么考”“考什么”“怎么考”) 《中共中央 国务院关于全面加强新时代大中小学劳动教育的意见》颁布 《教育部办公厅关于遴选建立普通高中新课程新教材实施国家级示范区和示范校的通知》 《 教育部关于印发普通高中课程方案和语文等学科课程标准( 2020 年修订)的通知》 《教育部关于做好普通高中新课程新教材实施国家级示范区和示范校建设工作的通知》
六、探索学分互认转换制度,构建人才成长“立交桥” 探索建立多种形式学习成果的认定转换制度,打通普通高校、高职院校、成人高校之间的联系 通道,构建人才成长“立交桥”。
高考遵循了三个价值取向: 第一是促进公平,包括招生计划分配、清理各种加分项目、农村专项、东西部省份协作计划; 第二是以人为本,分类招生、等级性考试、多次考试、合并录取批次、专业+学校志愿填报; 第三是科学选才,“两依据一参考”、自主招生、综合评价招生是在破除唯分数论上下功夫 (南方科技大学, 深莫斯科大学)。
基础教育课程改革进入全面深化阶段
“三新”背景下高中数学高效课堂的构建策略

“三新”背景下高中数学高效课堂的构建策略作者:冷承然来源:《天津教育·下》2024年第05期高中教育是学生教育生涯中重要的成长阶段,是我国教育体系的重要组成部分,也是升入高等院校的主要途径。
新课标、新教材、新高考(简称“三新”)的落实,为高中数学教学带来了新的发展契机,为广大高中生的数学学习带来了巨大的挑战。
在这样的教育背景下,高中数学教师应该积极改变教育观念和教学方法,真正地从学生的实际学情和最近发展区出发,以新教材的编制内容和新高考的考核重点为教学引导,结合新课程标准的具体要求创新设计教学活动,从而构建高效数学课堂,培养学生的数学核心素养。
本文从新课标、新教材、新高考的具体内容出发,结合人教A版高中数学教材中的具体教学案例,从聚焦核心素养、加强师生互动、构建教学情境、开展单元教学四个维度,对高中数学课堂教学进行深入研究,以期找到提高课堂教学效果和质量的有效途径,推动高中数学教学改革的稳步发展。
一、当下高中数学课堂的教学实施现状(一)学生个体的差异延缓了教学进程高中阶段的学科教学难度呈几何趋势递增,尤其是数学,对很多学生来说似乎是难以逾越的大山,成为他们学习上岸过程中一个巨大阻碍。
高中阶段,每个班级大概有五十个人,这五十名学生因为自身的学习能力和学科基础不同,造成学习数学知识时理解程度不同、掌握速度不同、认知深度不同,学习进度差距较大,最终直接影响教师的教学进度。
要想更好地提高每个学生的学习质量,差异化教学是一种行之有效的方法。
但是,教学时间有限且宝贵,高中数学教师往往会选择班级中水平中高段的学生作为教学活动设计的主要对象,然后采用统一的教学内容和方法开展具体的教学活动。
这种统一的教学内容,包括课堂上的教学活动、课后的作业布置、后续的作业和测试批改等,既影响着学生的学习过程,又衡量着学生的学习成果。
这样的教学模式忽视了学生个体差异的这个客观因素,影响了高中数学教学的进程,降低了数学课堂的质量和效率。
高考试题(卷)分析与反思

析18数学高考,思19复习策略渭南高级中学李华工作坊成员第一篇:2018年高考课标全国卷II数学试题分析试题分析2018年高考课标全国卷II理科数学遵循《课程标准》的基本理念,严格贯彻《2018年全国(新课标卷)考试说明》的基本要求,依纲守标,能力立意,贴近社会生活,富含时代气息,突出理性思维和应用能力的考查,注重知识的综合运用。
从题目上看考察内容注重基础,重视培养能力;从风格上看,考卷既考察了数学知识方法在学科内的应用,也有解决实际问题的题目,同时也有对数学文化方面进行的考查。
所以面对基础性、综合性、应用性、创新性、开放性更高要求的题目,2019届及往后各届同学应该在审题、读题方面多下功夫,细细揣摩出题人考查意图。
一、突出数学思维价值充分考查理性思维数学是理性思维的典范,2018年数学试题注重基础知识和基本数学思想方法的考查,特别减少了需要大量、繁琐运算的题目。
小题中低档题多,选择、填空的压轴题难度也不大。
解析几何文理同题(文20,理19),虽然以抛物线为载体,但运算量降低,随之难度下降,理科试题中位置也前移。
二、密切结合社会实践注重考查应用能力2018年数学试题适应高考改革和数学发展的趋势,密切结合社会实践,贴近生活,贴近考生,强化数学应用能力的考查,例如,理科第5题结合社区服务活动,考查了古典概型;理科第13题以产品质量为背景考查了二项分布的应用;文、理的第18题在这个以环境基础设施投资为背景的统计题中,完全不需概率知识,也不要求学生计算回归方程,但需要学生用所学知识分析两个方程的可靠性。
考查很灵活,不能套作,需要学生实际分析和解决问题的能力。
比如理科第1、4、5、6、13、14、17题,这些题目都考察了学生的基础知识和基本技能,同时试卷中数学知识体系的主干内容占有较高比例如对函数与导数、三角函数与解三角形、立体几何、解析几何、数列、概率统计等内容有非常高比重的考查,充分体现了高考对主干知识的重视程度。
分享阅读屈原涉江视频

阅读屈原涉江视频A4打印/ 可编辑关于调整普通高中2018级学生课程方案和课程内容的通知各设区市、县(市、区)教育局,各普通高中学校:为解决现行普通高中各学科教材与《普通高中课程方案(2017版)》不匹配的问题,决定对2018年秋季入学的普通高中学生的课程方案和部分学科课程内容进行调整,调整后的方案见附件1和附件2。
全省2018级普通高中学生执行调整后的方案。
原方案中未做调整的部分,仍按原方案及“省教育厅关于印发江苏省普通高中各学科课程标准教学要求(修订稿)的通知”(苏教教科[2009]2号)执行。
2017、2016级学生按原方案组织课程教学。
各级教育行政部门和学校要抓紧做好各项准备工作,严格落实调整方案,保证课程教学秩序的稳定。
因方案和内容调整,2018级学生部分学科教材的征订时间须做相应调整,具体为:语文必修5教材与必修3、必修4教材同时征订;历史必修2、必修3教材与必修1教材在高一年级同时征订;思想政治必修1、必修2、必修3教材均需在高一年级征订。
附件1:江苏省普通高中2018级学生课程学分结构表附件2:江苏省普通高中2018级学生部分学科课程内容调整说明2018年月日江苏省普通高中2018级学生课程学分结构表说明:本表中的“必修”课程,根据学生全面发展需要设置,全修全考;“选择性必修”课程根据学生个性发展和升学考试需要设置,选修选考;“选修”课程由学校根据实际情况统筹规划开设,学生自主选择修习,学而不考或学而备考。
江苏省普通高中2018级学生部分学科课程内容调整说明语文注:1.本次调整是根据新课程方案在现有教材基础上的调整。
调整原则是:根据新课程方案中的学分要求,对现有必修教材作适当增删,增加部分是新课标中有明确要求而现有教材没有的诗文。
选修教材的使用仍然由各学校自己决定。
教材读本建议使用江苏教育出版社的教材配套读本,学校可以根据自己的实际情况选择其他版本的读本,但要注意读本与教材配套的科学性。
多源流理论视域下的中国高考科目设置政策变迁研究

2023年12月Vol.39,No.4Dec.2023青岛科技大学学报(社会科学版)Journal of Qingdao University of Science and Technology (Social Sciences)第39卷第4期[收稿日期]2023-09-28[作者简介]徐祥运(1963-),男,辽宁丹东人,辽宁理工职业大学马克思主义学院教授,博士。
多源流理论视域下的中国高考科目设置政策变迁研究[摘 要]恢复高考以来,我国高考科目设置政策变迁大体上可以概括成三个主要阶段:“文六理七”和会考基础上的“3+2”模式阶段;以“3+理综(文综)”为主流的“3+X”模式阶段;新一轮高考改革中的“3+3”和“3+1+2”模式阶段。
这些科目设置政策的变迁,涉及和影响了不同的利益群体。
在多源流理论视域下,我国高考科目设置的变革都是问题源流、政策源流和政治源流共同推动的结果。
其中,政治源流发挥着更为重要的作用,能够单独地促成政策之窗的开启。
基于此,为了教育更加契合立德树人的本质要求,未来高考科目设置政策变革既要聚焦高考科目设置的现实问题、重视政策源流的“软化”作用,又要重视国家重要战略的引领作用。
[关键词]多源流理论;高考科目设置;政策变迁[中图分类号]G640 [文献标识码]A [文章编号]1671-8372(2023)04-0098-08A study on the policy changes of subject setting in college entrance examination in China from theperspective of multi-source theoryXU Xiang-yun 1,GAO Hai-xin 2,XU Bo-chang 3(1. School of Marxism ,Liaoning Vocational University of Technology ,Jinzhou 121007,China ;2. School of Public Administration ,Dongbei University of Finance and Economics ,Dalian 116025,China ;3. College of Education ,BeijingNormal University ,Beijing 100875,China )Abstract:Since the resumption of the college entrance examination in China ,the changes of the subject setting policy of the examination can be summarized into three main stages : the mode of “six subjects for liberal arts ,and seven subjects for sciences ”and “3+2”based on the pre-college entrance examination ;the mode of “3+X ”with “3+1 comprehensive subject of science courses (or 1 comprehensive subject of liberal arts courses )”as the mainstream ;and the mode of “3+3”and the mode of “3+1+2”in the new round of college entrance examination reform. These changes in subject setting policies involve and aff ect diff erent interest groups. From the perspective of multi-source theory ,the reform of the subject setting of college entrance examination in China is the result of the problem source ,the policy source and the political source. Among them ,political source plays a more important role ,which can independently facilitate the opening of the policy window. Based on this ,in order to better meet the essential requirements of moral education ,the future reform of college entrance examination subject setting policy should not only focus on the practical problems of examination subject setting ,pay attention to the “softening ”role of policy sources ,but also pay attention to the leading role of important national strategies.Key words:multi-source theory ;subject setting of college entrance examination ;policy change○ 徐祥运1,高海鑫2,徐博昌3 (1.辽宁理工职业大学 马克思主义学院,辽宁 锦州 121007;2.东北财经大学 公共管理学院,辽宁 大连 116025;3.北京师范大学 教育学院, 北京 100875)● 社会治理研究·99·第4期一、引言高等学校招生考试(简称高考)制度的改革内容包括招生录取方式的改革、高考内容的改革、高考形式的改革以及高考科目设置改革四个部分[1],其中高考科目设置改革一直是高考改革最为重要的部分。
天津高考改革方案天津高考改革方案:取消文理分科英语一年两次考试

天津高考改革方案:取消文理分科英语一年两次考试取消文理分科。
这个举措可是个大动作,以前的高考,文科和理科就像两条平行线,互不相交。
但现在的学生,谁不想全面发展呢?取消文理分科,意味着学生们可以自由选择自己喜欢的科目,不再被固定在某个领域。
这样一来,学生们可以根据自己的兴趣和特长,有针对性地进行学习,更有利于培养出个性化的人才。
然后,英语考试一年两次。
这个改革可谓是与时俱进,以前的高考英语考试只有一次机会,如果发挥不佳,那就只能硬着头皮去面对。
现在好了,一年两次考试,给了学生们更多的机会。
这样一来,学生们可以更加从容地面对英语考试,提高自己的英语水平。
详细说一说这个方案的亮点。
一、取消文理分科,让学生自由选择科目1.学生可以根据自己的兴趣和特长选择科目,有利于培养个性化人才。
2.打破传统教育观念,提高学生综合素质。
3.增加学生自主选择权,提高教育公平性。
二、英语考试一年两次,提高学生英语水平1.给学生更多机会,提高英语成绩。
2.增强学生英语学习兴趣,提高英语应用能力。
3.促进英语教育改革,提高教育质量。
当然,这个方案的实施也需要克服一些困难。
1.教育资源分配问题。
取消文理分科,意味着教育资源需要重新分配,如何确保每个学生都能享受到优质教育资源,是个挑战。
2.教师队伍建设。
取消文理分科,教师队伍也需要进行相应调整,如何提高教师综合素质,是个问题。
3.学生心理适应。
取消文理分科,学生需要适应新的教育模式,如何帮助学生顺利过渡,是个关键。
那么,如何解决这些问题呢?1.加大教育资源投入,提高教育公平性。
政府需要加大对教育的投入,确保每个学生都能享受到优质教育资源。
2.加强教师队伍建设,提高教师综合素质。
通过培训、选拔等方式,提高教师队伍的整体素质。
3.做好学生心理辅导,帮助学生顺利过渡。
学校和家长要共同关注学生心理健康,帮助学生适应新的教育模式。
天津高考改革方案:取消文理分科英语一年两次考试,是一个具有前瞻性的改革举措。
“三新”背景下高中数学课堂教学创新路径探究

三新背景下高中数学课堂教学创新路径探究三新 背景下高中数学课堂教学创新路径探究万佩君(江苏省海安市南莫中学,江苏㊀南通㊀226600)ʌ摘要ɔ随着我国教育改革的深入推进,新课标㊁新教材㊁新高考( 三新 )的变化对高中数学教育教学提出了更高的要求.在此背景下,数学教师需要着重创新课堂教学模式与策略方法,以满足学生在新课改环境下对知识掌握㊁能力提升以及核心素养发展的多元需求.基于此,文章深入探讨了高中数学课堂教学的具体创新路径,主张在新教材使用上采用单元整体教学法;在新课程实施上倡导自主㊁合作㊁探究式学习,融入生活情境与信息技术,以提升学生的核心素养;为应对新高考考核,提倡强化四基四能培养,实行分层个性化教学,以期有效推动高中数学课堂教学模式的创新实践,切实提升教学质量与育人效果.ʌ关键词ɔ 三新 ;高中数学;课堂教学;创新路径三新 即新课标㊁新教材㊁新高考,这三方面的改革发展对教育教学提出了更高的要求.新课标强调以核心素养培养为导向,创新教学内容㊁教学方式与教学评价;新教材设计强调数学知识的整体性和应用性,倡导单元整体教学;新高考制度明确了由单纯考试到立德树人㊁从知识能力到综合考查㊁从解答问题到多维命题的考核要求.面对 三新 的迫切呼唤,高中数学课堂教学亟待一场深刻的转型与重构,从而全面提升学生数学素养,促使他们更好地应对新时代教育的挑战.一㊁整合新教材,实施单元整体教学新教材以其鲜明的系统性与关联性特点,要求教师在教学过程中打破传统章节分割,积极整合教材内容,推行单元整体教学法,以促进学生对数学知识的深度理解,提升学生的综合运用能力.因此,教师应系统梳理教材知识点,深入解读教材内涵,将不同章节内容有效衔接,打破知识壁垒,构建起层次分明㊁逻辑严谨的知识网络体系.在教学实施中,教师可以设计主题式的教学单元,将分散的知识点串联起来,形成有关联的学习链;同时,注重搭建单元情境,引导学生在解决实际问题的过程中发现并理解单元学习大概念,再运用所学知识解决更为复杂的问题,从而促进知识的迁移与融会贯通.以人教A版数学 指数函数与对数函数 单元教学为例,教师可以针对指数与对数的概念㊁性质㊁运算规则及函数图像等基础知识,借助思维导图工具进行整体知识的建构,引导学生宏观把握指数与对数知识体系及它们的联系.在教学活动中,教师应积极倡导小组互动学习方式,鼓励学生对比㊁探讨 当底数相同时,指数函数y=ax与其反函数对数函数y=logax在图像上的对应特性 ,然后进一步探索不同底数下函数变化的规律特征,动手绘制图像并建立数学模型,直观呈现指数函数与对数函数之间的一一对应关系,从而提高对两者本质联系的深层次认识.然后,教师要注重引导学生提炼出单元学习大概念,如 指数与对数存在互逆性,指数函数与对数函数互为反函数,且两者图像关于直线y=x对称 .此外,教师可以设计综合性任务活动,要求学生运用所学的指数与对数知识解决实际增长率计算㊁放射性物质衰减分析等实际问题.通过这样的实践活动,抽象的数学原理在具体情境中得到验证和应用,从而助力学生加强对指数与对数知识的理解与掌握.二㊁研究新课标,发展学生核心素养(一)坚持以生为本,引导自主学习新课标高度重视学生自主学习能力的培养,特别是在高中阶段学科众多的情况下,养成良好的自主学习习惯与能力对学生学习来说至关重要.因此,在课前,教师可以设计多样化的预习任务,如布置开放性问题㊁提供微课资源等,引导学生自行构建知识框架,自主发现问题㊁思考问题.例如,在教授 集合的基本运算 这一内容时,教师可以精心制作或搜集优秀的微课视频资源,借助生动形象的动画讲解交集㊁并集㊁全集及补集等核心概念,展示它们的具体运算过程,引导学生在视觉化的学习环境中独立领悟和牢固掌2握原本较为抽象的集合知识内容.同时,学生可以记录自己的预习问题,将其作为课上学习的重点,以提高学习效率.与此同时,教师应鼓励学生在课后持续探索,设置专题研究㊁拓展阅读㊁习题精练等多元化的学习任务,使学生利用数字化教育资源进行自我检测和深度学习.此外,教师应提倡学生制订个人学习计划,定期进行反思总结㊁自我评估,调整学习策略,逐步提高自己的独立思考㊁解决问题等能力,让自主学习成为日常学习的重要组成部分,真正实现从被动接受知识到主动探索求知的角色转变.(二)联系生活情境,强化互动理解新课标倡导基于学生现实经验来构建真实情境,以增强学生对数学知识的直观理解和深度体验.对此,教师应精心设计与日常生活㊁社会热点密切相关的数学案例,引导学生观察生活中的数学现象,分析其中蕴含的数学原理.在情境中,教师可以巧妙设计层层递进的问题链,引导学生进行深度思考㊁分析与探索,使他们在解决问题的过程中逐步掌握数学知识与技能,实现深度学习的学习目标.以人教A版数学教材中 指数函数 的教学为例,教师可以精心创设一个与学生的生活紧密相关且具有时代感的情境案例:假设小杰同学的父母为其设立了一个教育储蓄账户,并存入首笔资金2000元,银行提供的年复利率为1.5%.教师向全班提出挑战性问题: 如果按照复利计算,要多少年,小杰的教育储蓄账户存款能增长到本金的三倍呢? 这样的生活化情境导入瞬间拉近了数学与学生的距离,引发了他们对日常生活中指数增长现象的关注.接着,教师可以提出互动问题,引导学生深入思考: 一年后,存款会增加多少? 对此,学生可以进行简单计算并回答.随后,教师可以继续提问: 两年后,账户中的金额变成多少了呢? 通过此问题深化学生对复利计算内涵与运算逻辑的思考.教师还可以提问: 是否有一个通用的公式可以描述这种持续增长的情况? 这个问题能引导学生思考复利增长模型与指数函数的本质.之后,教师可以组织实践活动,要求学生使用电子软件(如Excel)建立数学模型,实时观测存款随时间推移的变化情况,并最终找出存款增长到本金的三倍的确切年数.在互动环节中,各小组成员互相讨论㊁交流观点,共同解决问题对指数函数表达式y=C(1+r)t进行实际应用.最后,通过对该生活案例的深入剖析,学生不仅能深入理解并熟练掌握指数函数的基本性质和运算规则,还将在解决实际问题的过程中提升自己的逻辑推理能力和数学思维水平,切实提高数学素养.(三)鼓励合作探究,提升实践能力新课标鼓励学生进行合作探究式学习,以促进学生核心素养的发展.在课堂教学中,教师应精心设计多样化的合作探究项目,指导学生小组围绕复杂的数学综合问题展开团队协作,通过共同研讨㊁思维碰撞来深化对知识的理解.需要注意的是,教师要适时介入学生的小组学习活动,提供必要的方法指导,引导学生搭建数学模型㊁验证假设㊁攻克难题,确保学生顺利推进项目学习,在互助互鉴的过程中不断提升数学实践能力.以人教A版数学教材 指数函数 的教学为例,教师可以设计一个名为 揭示指数函数特性 的团队研究任务,要求学生分组合作,深入了解当底数a的取值范围不同时(0<a<1和a>1),指数函数y=ax的增长模式及图像的形状.教师为学生提供交互式绘图工具,如Matlab㊁几何画板等,让学生亲手绘制底数a的取值范围不同时指数函数的图像.教师可以将学生分为若干小组,让每组选定两个底数(如0.5和3),并绘制这两个底数对应的指数函数的图像,然后以1为单位逐渐增加自变量x的值,并仔细观察x的值增大时函数值的变化规律,记录具有代表性的函数值.接下来,各小组可以进行同底数指数函数图像的变化模拟,以强化实验的客观性与普适性.对于实验结果,小组内部需要对所绘图像进行深入分析,构建数学模型,阐述为什么在0<a<1时指数函数呈递减趋势,而在a>1时函数呈递增趋势.最后,各小组需准备一份动态展示报告,汇总他们的发现和论证过程,并在班级全体同学面前进行分享㊁交流和互评.比如有的小组从几何直观(如曲线走势)解释函数特性,有的小组则利用代数解析(如导数概念)阐释这一现象.学生从不同的角度审视问题㊁发展思维,这种方式的学习不仅能让学生扎实地掌握指数函数的核心性质,而且提升了他们的数学核心素养.(四)运用信息技术,提升课堂实效新课标明确强调要加强信息技术与数学课程的融合,促进教学方式变革.在此背景下,教师应充分利用现代信息技术手段丰富课堂模式,引入在线学习平台,利用智能化教学软件辅助讲解难点,实现直观化教学,激发学生自主学习的兴趣与积极性.例如,在学习 立体图形 时,教师可以借助3D建模软件创建立体图形的三维模型,使学生能够在交互式环境中亲自旋转㊁缩放模型,从不同角度观察立方体㊁圆柱㊁棱柱等各种立体图形的结构特征及其直投影,增强空间观念和几何直觉.同时,教师可以利用智能白板或类似的教学工具展示斜二测画法的具体步骤,通过动画演示帮助学生理解平面图与实物图之间的关系,加深学生对立体图形的理解.3另外,教师要善用信息技术收集并分析学生的学习数据,如作业完成情况㊁在线测试成绩等,以此为基础及时调整教学内容与教学节奏,精准定位学生的知识盲点,有针对性地进行辅导,不断提高课堂教学效率,将信息技术与数学教学深度融合,打造高效㊁智能㊁互动性强的新型数学课堂.三㊁对接新高考,实现精准个性教学(一)高考考查导向,强化 四基 四能中国高考评价体系从高考的核心功能㊁考查内容㊁考查要求三个方面回答 为什么考㊁考什么㊁怎么考 的考试本源性问题,从而给出 培养什么人㊁怎样培养人㊁为谁培养人 这一教育根本问题在高考领域的答案.在此背景下,教师应适时开展真题解析与模拟演练,使学生了解高考对能力素养的要求,根据考查内容有针对性地设计课堂教学活动,将高考要求的关键知识点与能力培养贯穿于每一堂课中,确保教学内容紧密贴合高考要求,逐层递进地强化 四基 与四能 ,提升学生迎战新高考的综合能力.例如,针对2023年高考数学新课标Ⅰ卷第12题中几何体能否放入正方体容器内的问题,教师在教学相关立体几何内容时,首先要引导学生掌握立体几何的基本概念和公式,如几何体表面积㊁体积的计算方法及空间几何体的性质和关系,这是解决此类问题的基础.其次,结合该题型,教师可以设计一系列将不同几何体放入容器的问题,要求学生综合运用几何直观㊁逻辑推理和数学运算能力,分析几何体与容器的尺寸关系,判断几何体能否放进去.此外,教师要引入实际生活中的案例或情境(如家具包装㊁仓库储存等),让学生体会几何体与容器容纳问题在现实生活中的应用,从而增强他们应用所学的数学知识解决实际问题的能力;最后,教师要鼓励学生从不同角度思考问题,如尝试变换几何体形状或容器大小,探究更多的可能性,并在解题过程中发展创新性思维.教师通过实施这样高效㊁精准㊁匹配高考的教学,使学生在提高高考应对技巧的同时全面发展核心素养,从而更加从容㊁自信地应对新高考.(二)实施分层教学,满足差异性需求针对学生的个体差异,教师可以采用分层教学模式,将教学内容㊁教学活动等分为不同层次,确保每名学生都能在其原有水平基础上得到有效提升.在日常教学中,教师可根据学生对数学知识的掌握程度和学习能力,设计多层次的学习任务与活动,如为基础较弱的学生布置巩固基础知识的习题,为中等水平的学生设置提升技能的习题,为学有余力的学生布置具有拓展性㊁挑战性的任务,从而最大限度地满足各层次学生的差异性学习需求,实现教学效果的最大化.以人教A版高中数学 复数的四则运算 教学为例,基础较弱的学生的首要任务是扎实掌握复数的基础知识,包括复数的定义㊁实部和虚部的概念及复数的标准形式表示.教师可以设计一系列基础习题(如简单的复数加减运算),通过练习使学生熟练掌握复数的常规计算方法,并确保他们能正确理解和识别复数的各种表达形式;对于中等水平的学生,除了巩固他们的基础知识外,教师可增设一些提升技能的练习(如涉及多项复数的加减混合运算㊁带有系数的复数乘法运算等),引导学生归纳复数运算法则,培养他们解决中等难度复数问题的能力.对于学有余力的学生,教师可以设计一些有拓展性㊁挑战性的任务,如复数除法运算㊁复数幂运算㊁复数在解决实际问题,电路分析㊁信号处理等领域中的应用等.此外,教师可以引导他们探索复数运算的几何意义,通过复平面上的图形变换理解复数运算的内在逻辑.在整个教学过程中,教师需保持敏锐的教学观察,及时调整教学难度和教学内容,对不同层次的学生给予个性化的指导与反馈,确保每名学生都能在自身的基础上得到提升,从而达到提高整体教学效果的目标.结 语综上所述, 三新 背景下的高中数学课堂教学创新是一项系统性工程,要求教师紧跟教育改革的步伐,深研新课标内涵,活用新教材内容,对接新高考要求.教师要整合教学内容,实施单元教学,同时开展情境教学㊁小组合作探究,以信息技术辅助教学,全力激发学生自主探究与深度学习的积极性,促进其全面发展.只有如此,才能真正实现高中数学课堂教学的高质量转型,为国家培养更多具有高水平数学素养和创新能力的人才.ʌ参考文献ɔ[1]段吉俊. 三新 背景下的高中数学教学改革探究[J].中学课程辅导,2023(16):93-95.[2]赵红宁. 三新 背景下高中数学教学策略分析[J].高考,2023(34):51-53.[3]黄彪. 三新 背景下的高中数学课堂教学策略研究[J].天天爱科学(教育前沿),2023(11):61-63.[4]杜小利. 三新 改革下高中数学高效课堂构建策略研究[J].考试周刊,2024(3):70-74.[5]董凤娇. 三新 背景下高中数学支架式教学策略研究:以 概率统计 为例[J].理科爱好者,2023(6):82-84.[6]王千方. 三新 背景下高中数学课堂教学策略探究[J].成才之路,2024(2):85-88.[7]王海莉. 三新 背景下的高中数学课堂构建策略分析[J].试题与研究,2022(18):101-103.4。
课程标准视域下的高中数学新旧教材比较分析——以“三角函数”章节为例

课程标准视域下的高中数学新旧教材比较分析——以“三角函数”章节为例广西南宁市第二中学(530000)刘存华岑盛锋广西师范大学数学与统计学院(541004)周莹党的十九大明确提出“立德树人”的目标,基础教育课程在其中发挥了至关重要的作用.2003年教育部发布《普通高中数学课程标准(实验版)》(以下简称为旧课标),并据此编写了2007版普通高中课程标准实验教科书,但是随着时代和社会的发展,旧课标和教材显现出不足之处.因此,2013年教育部开启了普通高中课程修订工作,2018年发布《普通高中数学课程标准(2017版)》(以下简称为新课标)并编写出版了2019年版普通高中数学教科书.十余年来,一线教育工作者已经习惯了旧教材的旧教材的内容和教学模式,新教材的发布与实施会产生一定的不适应性.只有认识新旧教材的共性与差异,才能掌握新教材、用好新教材,为落实“立德树人”目标助力.那么,新旧教材有何区别?新教材有何改进与特色?改进有何依据?为探讨以上问题,本文以2007版普通高中课程标准实验数学教科书(以下简称为旧教材)⑴和2019年版普通高中数学教科书(以下简称为新教材)为研究对象,从开章引言、正文内容、例习题、章末小结五个方面对“三角函数”内容进行比较分析,为教师理解教材和实施教学提供些许参考.一、结构编排比较表1结构编排比较旧教材(必修4)新教材(必修第一册)第一章三角函数1.1任意角和弧度制5.1任意角和弧度制5.2三角函数的概念5.3诱导公式5.4三角函数的图象与性质5.5三角恒等变换5.6函数y=Asin(a)x+(/))5.7二角函数的应用(包含振幅、周期、频率、和相位)1.2任意角的三角函数1.3三角函数的诱导公式1.4三角函数的图象与性质1.5函数y=Asin(ft;%+0)1.6三角函数模型的简单应用第三章三角恒等变换3.1两角和与差的正弦、余弦和正切公式3.2简单的三角恒等变换变化一:将旧教材1.5节中的振幅、周期、频率以及相位等改编至三角函数的应用中,借助与物理学中的“简谐运动”结合引出,有助于学生体会利用三角函数构造刻画周期变化的数学模型⑶.变化二:旧教材在旧课标的指导下——用向量的数量积推导两角差余弦公式,因此在“三角函数”和“三角恒等变换”中间穿插了“平面向量”,此做法割裂了“三角函数”与“三角恒等变换”的联系.新教材将“三角恒等变换”合并至“三角函数”中,考虑因素有二:其一,沿用单位圆性质推导两角差余弦公式,体现研究方法的连续性,达到“减负”效果;其二,注意“函数”主线内容的逻辑关系,体现同一主线内容之间的有机衔接.建议在必修第二册的向量学习中增加“向量积推导两角差余弦公式”的教学,拓展向量应用的同时复习旧知,将不同主线内容联系起来构建知识体系.*本文系2019年度广西高等教育本科教学改革工程重点项目“系统性思维能力导向的数学有效教学研究与实践”(2019JGZ110);广西壮族自治区研究生教育创新计划项目(XYCSZ2019084)的阶段性研究成果.周莹为本文通讯作者.二、开章引入比较人教版数学教材的每一章开头都会有章导言和一幅与文章内容相关的章头图等素材,由此来进行开篇引入学习•开章引入在课堂导入、内容教学、联系巩固等多方面有着广泛的应用.因此,有必要对开章引言进行比较研究.旧教材的开章引入占用2页篇幅,内容包括:章标题、目录、大小章头图、引言四部分.章头图以宇宙天体的运行为大背景,辅以质点运动小图,进行说明周期性现象无处不在.章引言中第一段举例叙述了周期性现象,第二段由函数是一种模型指出本章要学习的另一种函数模型,第三段呈现问题串引入本章学习.新教材的开章引入仅用了1页篇幅,内容包括章标题、章头图以及章引言.章头大图不变,删减了小图举例.章前言第一段和第三段相较旧版而言内容并无太多变化,第二段引导学生类比指数函数的研究过程和方法来学习三角函数.表2新旧教材引言对比旧教材新教材1.月亮圆缺变化的周期性,即朔一上弦一望一下弦一朔;潮汐变化的周期性,即海水在月球和太阳引力作用下发生的周期性涨落现象……2.我们知道,函数是刻画客观世界变化规律的数学模型.在数学1中,我们学习了指数函数、对数函数等,指导这些函数可以用来刻画现实问题中某些类型的变化规律.那么,在数学中又如何刻画客观世界中的周期性变化规律呢?本章要学习的三角函数就是刻画这种变化规律的数学模型.3.三角函数到底是一种怎样的函数?它具有哪些特有的性质?在解决具有周期性变化规律的问题中到底发挥哪些作用?下面我们就来研究这些问题.1.月亮圆缺、潮汐变化、……2.前面我们学习了函数的一般概念,并研究了指数函数、对数函数等,知道了函数的研究内容、过程和方法,以及如何用某类函数刻画相应现实问题的变化规律.本章我们将利用这些经验,学习刻画周期性变化规律的三角函数.3.三角函数是怎样的函数?它具有哪些特性?如何利用三角函数模型刻画各种周期性变化现象?本章我们就来研究这些问题.从上面的对比我们可以看出,新教材删减了“目录”,因为主要内容已经在书本目录中已经有所体现,就不用再次赘述•“章小图”的作用是为了表达“周期性无处不在”,但是引言第一段的若干例子已经达成了这个目的,因此将其改编至第244页的习题不失为一个好办法.删除“目录”、调整“章小图”、精炼引言的词句表达,体现数学简洁美的同时降低学生的阅读负荷量.另一个变化在于引言第二段,既继承了旧教材的“由旧知导新知”,还引导学生用已有的知识经验、研究方法去学习新知,增强教材可读性和指导性.三、正文内容比较(―)主体内容比较概念引入的不同.比如在“诱导公式”一节,旧教材在课前探究环节提出6个问题让学生思考77-a、”+a、-a、号-a与a的终边、三角函数有何关系,紧接着在同一个图中给出所有角度终边关系•看似是以问题串的形式引导学生思考,数形结合地顺利引入到诱导公式,但实质上在课堂伊始就拋给学生一系列的问题,并给出一个复杂的图解,无疑给大部分学生造成心理负担,打击学习自信心.同样是利用圆的对称性进行研究三角函数的对称性,但不同的是,新教材先探究了”+a与a的关系,然后再引导学生各个击破.此举遵循“最近发展区间”理念进行引入,将“集中剿灭”改为“各个击破”,遵循学生的认知规律,有利于提升学生的学习成就感和积累活动经验.概念深化的不同.同样以“诱导公式”一节为例,旧教材在讲解公式二的推导过程中,对于公式三、四等都是在“同理,我们有”之后直接给出结论.这种“重结果轻过程”式地直接给出结论,十分不利于学生学习知识和理解结论.新教材在展现每一个结论之前,都会给出一定的提示语来帮助学生自证结论,如“如图,作P,关于%轴的对称点匕,则以OP3为终边的角为-a”,抑或是以设置探究问题和旁白的形式引导学生.这种通过问题解决的方式驱动学生去学习,学生可以在这样的过程中主动探究,从而获得知识,发展能力.细节处理的不同.新教材较旧教材更加严谨细致,譬如在“诱导公式”一节中,旧教材的多个图形均用“Pi'PJ标示不同的点.但是新教材在此节中不同的图和不同的点依次以“P1,P2,P3、巴、代”来标示,这不仅是体现了教材的科学性,更是给学生展示数学的严谨性.又如第178页中,给三角函数下定义时将教材中“正弦、余弦”更改为“正弦函数、余弦函数”,新教材在概念、符号等方面都更注重规范性⑸.(二)信息技术整合比较“互联网+”时代,数学教育也需响应时代要求,利用信息技术来促进自身发展•在旧课标已经明确提议将信息技术与课程进行整合,新课标教材编写建议也指出可通过信息技术融入课程实现教材内容呈现方式多样化,那么新教材在信息技术融入方面有何突破?主要体现在以下情形:与正文内容整合,第197页利用信息技术描绘足够多的点,从而连成精确正弦函数图象,克服常态教学的不足;与例题整合,第173页的例4和例5中演示了如何利用计算器进行角度制与弧度制的互化;与练习题整合,第203页随堂练习中指出可借助技术画出函数图象检验题目所求函数的周期,提升学生的实操能力;值得注意的是,新教材将旧教材中“利用正切线画正切函数图象”的信息技术应用一栏删去,这是因为在课堂教学已经讲解了正切函数图象的画法,此处有“多此一举”之嫌.新教材的处理方法,是将其改编为第214页的一道复习题,真正实现“用”信息技术,而不是“看”信息技术.(三)数学文化融入比较新课标指出教材应当把数学文化融入到学习内容中,新教材在这方面表现在:第一,利用数学文化进行导入.譬如,通过探究“筒车”的盛水筒距离水面的相对高度与时间的关系,从而得出三角函数模型•利用中国传统文化中的数学元素进行导入,一来可以增强学生的文化自信,二来可以使得引入自然不强硬.第二,与例题进行结合•在第238页的例题2中,以学生熟悉感兴趣的“摩天轮”进行设题,提升学生的学习兴趣,也能让学生体会数学与人类生活的密切关系.从新课标可知,将数学文化融入教材已经形成意识,但是融入方式、融入程度还有待加强.因此建议参考湘教版、北师版教材,在三角函数一章设置“阅读材料”栏目来展现数学文化材料,比如“数学与音乐”、“数学家傅里叶”.抑或是与习题结合设题,这样可以改善练习题“无背景”占比过高的现状同,在学生做题时无形的渗入数学文化.(四)例习题比较分析1.例习题数量比较表3新旧教材例习题数量对比各小节名称例习题对比例题习题旧教材新教材旧教材新教材任意角和弧度制762423三角函数的概念/任意角的三角函数763332三角函数诱导公式/诱导公式4(10.2%)5(13.5%)13(6%)17(9%)三角函数的图像与性质6(15%)7(19%)31(14%)37(19%)三角恒等变换101070(32%)43(21.5%)函数y二4sin((y%+</))的图像/函数y=Asin((w%+</))221211三角函数模型的简单应用/三角函数的应用4299章末复习2727总计4037219199由表3可得知,总体数量上新旧教材的习题相差20道题,例题相差无几.这是由于旧教材中将“三角恒等变换”独立作为一章,因此在习题的数量上比新教材更多一些•认真研究各小节的习题对比,新教材将其合并到“三角函数”当中,是因为考虑到同一主线内不同知识点之间的逻辑关系,习题虽然相对减少,但是足以达到训练和评价效果.另外,可以看出在“诱导公式”和“三角函数的图像与性质”两个部分,新教材的例题、习题占比均高于旧教材.因此较之以前,教师在“诱导公式”、“三角函数的图像与性质”应该着重教学与训练.2.习题调整变化在例题上有两处改变:其一,在例题更具示范性.例如“三角函数的概念”的例2,旧教材给出了角a终边上固定一点P(-3,-4),求角的三角函数值,基本达到巩固知识的效果.新教材将终边上的点一般化为P(%,y),求证三角函数.一般化的例题更具备上更注重内在思维的训练,做到每一道例题都更具典型性与示范性.其二,例题更注重引导性.新教材在某些较为复杂的例题比旧教材多了一个环节——“分析”,分析主要是给予思路和方法上的提示,这有利于学生自主学习,降低例题难度.在习题上有三处变化:第一,随堂练习更具有针对性.新教材通过衡量知识点容量和难度设置随堂“练习”,其做法是将旧教材中的习题拆解成为多处训练,“一讲一练”式的设计有利于学生及时巩固知识点,亦有利于教师的教学设计.第二,小节习题更具层次性.新教材改变了旧教材中“A组”、组”混乱设置,将习题重新按照难度分类为“复习巩固”、“综合运用”、“拓广探索”.不同层次的习题可供不同水平的学生选用,由浅入深,帮助学生巩固知识、理解应用、培养创新能力.第三,复习题更具有效性.新教材的复习题全盘考虑整章内容,通过“筛选”、“删减”、“合并”、“增加”,最后形成的题目既能保证全面评价有效性,又能避免题海战术,从而提高复习有效性.五、小结比较分析新旧教材的小结均包括"本章知识结构"和"回顾与反思”,新教材在这两部分均有所改进:(一)本章知识结构比较知识结构框图主要是根据知识的发展和研究路径,用流程图(或结构图)的形式串联主要知识点,从而形成的思维导图.新教材的知识结构框图有机的整合了旧教材中的“三角函数”与“简单的三角恒等变换”两章的主要内容,并且在“三角函数的图像和性质”进行了扩展•总体而言,新教材的思维导图更加完整•建议在以知识为主的思维导图的基础上,适当补充所学到的数学思想和方法,培养学生的“四基”.在实际教学当中,教师可以结合教材知识结构框图,运用思维导图软件带领学生进行章末复习,或可达到事半功倍之效.(二)回顾与反思比较“回顾”是以“先”、“然后”、“接着”等关联词串讲了本章的主要内容,然后分知识块进行详细的阐述•在阐述的过程中阐述了本章内容与其他内容之间、本章内容内部之间的关系,揭示了数学思想和研究方法,从而发展学生的数学学科核心素养.“反思”给出若干个问题,以问题驱动学生回忆和复习全章核心知识.问题涉及的内容十分广泛,例如:“概括引入弧度制的必要性”、“归纳一下研究三角函数的图像与性质的过程与方法”、“画一张公式逻辑图,并指出数学思想方法”、“搜集数据并建立函数模型”•这种“问题引领”的反思形式极大程度上调动学生学习数学的积极性,发展学生自主学习和归纳的能力•相对旧教材零散的“回顾与反思”,新教材更加系统和全面,所提出的问题更具有引导性,给学生“鱼”的同时授之以“渔”,更进一步提升其“欲”.总之,新教材充分地体现了新课标中的基本理念和目标要求,依据教材编写建议,将“立德树人”理念渗入教材•较之旧教材,在结构、内容、例习题、小结等方面均有较大的改进.希望教育工作者关注变化,在继承旧教材的基础上把握好新教材,顺利进行新旧教材的过渡,落实“立德树人”目标•同参考文献[1]课程教材研究所,中学数学课程教材研发中心.普通高中课程标准实验教科书A版数学(必修4)[M],北京:人民教育出版社,2007.[2]中华人民共和国教育部.普通高中数学课程标准(实验)[M],北京:人民教育出版社,2003.[3]中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].北京:人民教育出版社,2018.[4]王佩,赵思林.对人教A版高中数学教材中几个问题的商榷[J].教学与管理,2018(04):42-44,[5]严家丽,孔凡哲,李清.中美高中数学教材难度特征的比较研究一以《核心数学课程》和人教A版教材为例[J].上海教育科研,2014(03)=72-75.[6]侯学萍,武锡环.高中数学新旧教材中函数内容的比较研究[J].数学通报,2009,48(10):11-14.。
高中数学课改前后教材版本及使用地区

理科选修2—1, 2—2, 2—3
其余选修教材(选修三系列有6本,选修四系列有十本)
共计26本
人教A版:
河南、山西、河北、内蒙古、天津、湖南、黑龙江、福建、浙江、吉林、宁夏、
山东(青岛、淄博、枣庄、烟台、济宁、泰安、临沂、莱芜、聊城、滨州、荷泽)、
安徽(合肥、芜湖、淮南、马鞍山、铜陵、安庆、黄山、滁州、巢湖、六安、池州、宣城)、
广西湖北青海甘肃四川云南贵州西藏重庆陕西新疆江西安徽蚌埠淮北阜阳宿州亳州广东广州河源海南文昌琼海儋州三亚其余大部分地区用人教版本广东梅州深圳江苏福建小部分地区选修部分待定人教版人教a版人教b版北师大版必修155个模块选修有4个系列其中系列1系列2由若干模块组成系列3系列4由若干专题组成文科选修1112理科选修212223其余选修教材选修三系列有6本选修四系列有十本共计26本苏教版湘教版鄂教版
教材版本
教材系列
使用地区
大纲版
人教版
第一册高一(上∕下)
第二册高二(上)
第二册高二(下A)
第二册高二(下B)
第三册Ⅰ高三文科
第三册Ⅱ高三理科
高三:
湖北、河北、内蒙古、云南(4个)
高二、高三:
广西、青海、甘肃、四川、贵州、西藏、重庆(7个)
课标版
人教A版
必修1—5(5个模块)
选修有4个系列,其中系列1、系列2由若干模块组成,系列3、系列4由若干专题组成
人教B版
北师大版
陕西、新疆、江西
安徽(蚌埠、淮北、阜阳、宿州、亳州)
广东(广州、河源、)
海南(文昌、琼海、儋州、三亚,其余大部分地区用人教版本)
苏教版
广东(梅州、深圳)、江苏
湘教版
山东省高考数学考试大纲2022

山东省高考数学考试大纲2022第一部分新高考全国卷1.1 新高考全国卷的分类及教材使用情况1.新高考全国卷分为新高考一卷和新高考二卷两套试卷,其中使用新高考一卷的省份有:山东、湖南、湖北、河北、广东、江苏、福建共7省使用新高考二卷的省份有:海南、辽宁、重庆共3省2.以上10个省份中,使用新教材的省份有:山东、海南、辽宁共3省使用旧教材的省份有:湖南、湖北、河北、广东、江苏、福建、重庆共10省尽管使用教材有所不同,但高考所考察的范围为新、旧教材的交集。
3.新高考不分文理。
1.2 新高考全国卷的试卷结构选择题(单选,每小题5分,共8小题,满分40分);选择题(多选,每小题5分,漏选得2分,错选不得分,共4小题,满分20分);填空题(每小题5分,共4小题,满分20分);解答题(第17小题10分,第18~22小题每题12分,共70分)。
1.3 新高考全国卷的内容调整1.3.1 相对于旧教材的内容调整1.(必修1)删除映射2.(必修2)删除三视图、中心投影和平行投影3.(必修3)删除算法4.(必修3)删除系统抽样5.(必修3)删除几何概型6.(必修5)删除二元一次不等式组与简单线性规划问题7.(选修2-1)删除基本逻辑联结词中的“且”与“或”、命题的四种形式8.(选修2-2)删除推理与证明(数学归纳法保留,但高考不作要求)9.(选修2-2)删除定积分与微积分基本定理10.(选修4-4)删除“坐标系与参数方程”整本书11.(选修4-5)删除“不等式选讲”整本书1.3.2 相对于新教材的内容调整1.(必修第二册)平面向量投影的概念以及投影向量的意义不作要求2.(人教A版必修第二册/人教B版必修第四册)复数的三角形式不作要求3.(必修第二册)有限样本空间的含义不作要求4.(必修第二册)分层随机抽样的样本均值和样本方差不作要求5.(必修第二册)用样本估计百分位数,及百分位数的统计含义不作要求6.(选择性必修第一册)空间向量投影的概念以及投影向量的意义不作要求7.(选择性必修第一册)用向量方法解决空间中的距离问题不作要求8.(人教A版选择性必修第二册/人教B版选择性必修第三册)数学归纳法不作要求9.(人教A版选择性必修第三册/人教B版选择性必修第二册)利用全概率公式计算概率不作要求第二部分旧高考全国卷2.1 旧高考全国卷的分类及教材使用情况1.旧高考全国卷分为甲卷和乙卷两套试卷,其中使用甲卷的省份有:广西、云南、贵州、四川、西藏共5省使用乙卷的省份有:黑龙江、吉林、新疆、青海、宁夏、甘肃、山西、内蒙古、河南、陕西、安徽、江西共12省2.以上17个省份均使用旧教材。
探索“半文半理”组合上课
探索“半文半理”组合上课作者:陈焕伟车凤莉郑德友来源:《教育周报·教研版》2019年第40期摘要:2014年9月,国务院印发了《关于深化考试招生制度改革的实施意见》,对推进考试招生制度改革作出了全面部署。
山东省教育厅于2016年发布了《山东省深化考试招生制度改革实施方案》,自2017年秋季入学的高中新生开始全面实施新高考改革,实行“6选3”。
新高考改革的核心是打破“唯分数论”,实施“两依据一参考”的多元评价机制,激励学校深化课程改革,落实国家课程方案,认真开展选课走班教学,提升教育质量。
关键字:高中 ;选课走班 ;半文半理 ;组合上课 ;模式推进新高考改革,选课走班是高中学校育人变革的核心。
山东省新高考改革落地实施一年多以来,我校在选课走班方面大胆开拓,2017级“定二走一,两次组合”的走班方案在全省推广。
2018级在2017级选课走班方案的基础上,进一步完善和创新,形成了新的、具有开创性的选课走班模式。
一、选课前的准备工作(1)选课走班首要的问题是“怎样选”。
学生选择了最适合的三门选考学科,才能既满足其的个性发展需求,又能实现学校教学效益的最优化。
为提高选课的针对性和精准性,2018级做了以下准备工作。
高一下学期开学之前,2018级学生通过我校选科云平台进行了正式选课。
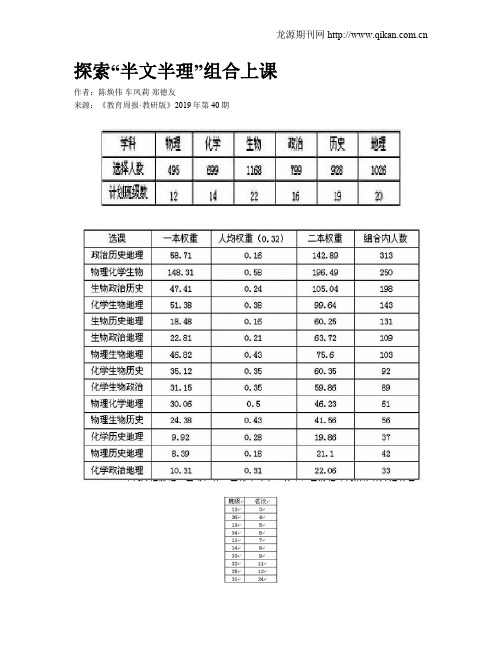
各学科选课人数统计如下:(2)走班最大的问题:如何在最大化尊重学生选择的前提下,均衡分班,使得各班教师能够在一个平台上竞争。
我们把全年级学生根据成绩排序,划定了优秀生,给优秀生加了一个小数,也就是继续保持优秀的可能性,作为该生的优秀权重。
各组合选课人数及权重信息如下:(3)分析选课数据,寻求规律,寻找突破点。
结合权重数据分析学生的选课结果后,我们发现:纯文组合“政史地”的人均权重只有0.16,而纯理组合“物化生”的人均权重高达0.58。
如果直接按组合分班,班级间权重差别将过大,导致后期班级管理、教师评价方面的一系列隐患和难题。
新高考背景下高中数学教学模式的改革探析

新高考背景下高中数学教学模式的改革探析新高考的背景下,高中数学课程教学的改革趋势越发显著,根据新时期高中数学课程教学的目标和方向,通过创新课程教学的方法和思路,强化对高中数学课程体系的设计,来适应新高考的教学环境,提升高中数学的教学能力和水准,也能有效的落实素质教育以及现代化人才培养的目标。
基于此,本文主要探讨了新高考背景下高中数学教学模式的改革探析。
标签:新高考;高中数学;改革对策引言中学数学教学改革一定要落实好素质教育的要求,本着为学生终身发展的目的,既要让学生掌握数学知识提高学习成绩,又要注重锻炼和提高学生的学习能力和个人素质。
只有这样,我们才能真正落实素质教育,真正开展适合学生的、促进学生全面发展的课堂教学。
1高中数学课程的教学现状1.1教學模式过于传统就目前数学教学模式的发展而言,虽然中国的新课程改革取得了可喜的成绩,但其强度也在不断增加。
但在具体的教学实践当中,高中数学课堂仍存在一些根本上的问题并没有得到有效解决。
大部分的高中课堂还在利用传统的教学模式,即“满堂灌”的形式。
具体来说,就是教师在讲台上传授知识,学生被动、机械地接受。
这一模式不仅导致学生的思维被固定,与教学原始初衷背道而驰,还使得人文精神的教学严重受到制约。
长此以往利用这种模式教学,会使得本就枯燥的数学课堂了无生机,呆板的课堂气氛的无法带动学生进行高中数学的学习[1] 。
1.2高考压力的客观因素随着新课程改革的不断深入,理想的教学模式一直是创新教育所追求的目标。
然而,高中生面临高考,具有巨大的学习压力,因此高中数学的有效开展,也是教育部门的重点关注内容。
目前,我国对于高中数学教学方式的优化已经取得了一定的成绩,但是我国每个地区的发展情况不同。
针对不同的学生、不同的学校所要制定的教学目标也不同。
在新课程改革的大背景下,创新教育作为其重要内容。
在不断的实践当中,教学模式也得到了很大程度的改变。
高中教师应当立足于自身的教学实际,深入到时代的变化中,从而对教学模式进行全面的改革,使数学课堂效果可以达到理想目标[2] 。
文理不分科什么时候实行为什么取消文理分科

文理不分科什么时候实行为什么取消文理分科
其实,从2014年开始,上海市和浙江省两地就作为高考改革试点,取消了文理分科。
但是真正全面推广文理不分科还是在2017年,甚至有一些省市是在2018年9月以后才开始施行不分文理的新高考政策的。
也就是说。
具体从什么时候开始实行文理不分科还是要看考生所在的省份,不同的省份,实行时间是不同的。
扩展资料
高考取消文理分科的原因:
高考取消文理分科是目前社会中普遍关注的重要话题,目前高中阶段有很多的学生都有偏科的现象,所以为了高中生可以全面发展,近些年,各省市开始逐步推进高考文理分科。
我国目前高中生接受的往往都是应试教育,但是教育的目的`并不应该单单是为了应对高考,而应该是全面提高素质。
所以,取消文理分科最大的原因就是希望可以改变应试教育,让高中生可以全面发展。
但是对于文理不分科,各方意见不一。
赞成文理不分科的人认为,文理分科是畸形教育,剥夺了学生全面发展的机会和权利。
但是反对者认为,文理不分科,是在为高中生学习增加负担。
由此可见,高考改革取消文理分科只是第一步,对于教学方法、教学内容、学习资源等等整个教育体系都需要作出调整,只有这样才能从根本上解决教育问题。
新高考改革的实际困境及其应对

新高考改革的实际困境及其应对目录一、新高考改革概述 (2)1. 新高考改革背景 (3)2. 新高考改革目标 (4)二、新高考改革的实际困境 (4)1. 教育资源分配不均 (6)2. 考试科目设置与高中课程衔接问题 (7)3. 高考评价体系不完善 (9)4. 考生心理健康与学业压力问题 (10)5. 政策执行力度与教师培训问题 (11)三、应对新高考改革的策略 (12)1. 加强教育资源整合与优化配置 (14)2. 完善考试科目设置与高中课程的衔接 (15)3. 构建科学的高考评价体系 (16)4. 关注学生心理健康与学业压力问题 (17)5. 提高政策执行力度与加强教师培训 (18)四、案例分析 (19)1. 成功实施新高考改革的地区或学校案例 (21)2. 新高考改革过程中的挑战与应对经验教训 (21)五、结论与展望 (23)1. 新高考改革的成效与影响 (24)2. 对未来新高考改革的建议与展望 (25)一、新高考改革概述新高考改革是我国教育改革的重要组成部分,旨在更好地适应社会发展需求,提高学生综合素质,推动教育公平。
该改革以新课程改革为基础,对高考制度进行全面调整和优化,主要涉及考试科目的设置、考试内容的改革、考试方式的创新以及招生录取机制的完善等方面。
新高考改革旨在更好地反映学生的综合素质和创新能力,促进学生全面发展,同时也为高校选拔优秀人才提供更加科学、公正的机制。
在实际推行过程中,新高考改革也面临一些实际困境,需要采取相应的应对措施。
新高考改革的内容丰富多样,包括调整考试科目的设置以更好地适应多元化人才培养的需求,改革考试内容以更加注重考察学生的综合素质和创新能力,创新考试方式以更加科学、公正地评价学生水平,以及完善招生录取机制以更好地实现教育公平等。
这些改革措施的实施,旨在为学生提供更多的选择和发展空间,促进教育公平和人才培养质量的提升。
在实际推行过程中,由于各种因素的影响,新高考改革也面临诸多挑战和困境。
新高考背景下开展高中数学有效教学

新高考背景下开展高中数学有效教学的实践研究杨㊀卫(江苏省沭阳高级中学㊀223600)摘㊀要:面对新时期教育所面临的各种挑战和发展机遇ꎬ高考随之也迎来了新的改变ꎬ大部分地区为了适应新高考进行了有针对性的调整和转变ꎬ从而更好地适应如今教育体制的改革.在高中阶段ꎬ数学作为一门重要的基础性课程ꎬ面对新高考政策的变化ꎬ教师应该摒弃传统教学当中的不足ꎬ紧跟新时代的步伐ꎬ本文笔者结合教学实际ꎬ探索了新高考模式下的高中数学有效教学.关键词:新高考ꎻ高中数学ꎻ有效教学中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2022)36-0044-03收稿日期:2022-09-25作者简介:杨卫(1989.10-)ꎬ男ꎬ江苏省沭阳人ꎬ本科ꎬ中学一级教师ꎬ从事高中数学教学研究.㊀㊀随着社会和时代的发展ꎬ人们对于教学质量的要求也逐渐提高ꎬ非常重视学生综合能力的培养ꎬ高中阶段对于学生的成长而言是一个非常重要且关键的时期.新高考下教学策略地全面转变ꎬ高中数学教学也进行了一定的变革和发展.为了更好地寻找适合学生学习的教学方式ꎬ在高中数学的教学过程中ꎬ教师要积极地研究传统教学的一些不足之处ꎬ并根据这些不足进行改进和发展.在为高中学生进行教学中ꎬ教师需要不断对新政策进行研究ꎬ依据学生的变化来调整教师的教学方法ꎬ只有这样才能够让学生的学习更加符合实际教学需要ꎬ帮助学生更好的去适应社会发展.因此本文根据教学实际探索了基于新高考下的高中数学教学策略ꎬ希望能对数学教育工作者有所启示.1当前高中数学教学存在的问题1.1教师教学模式单一数学本身的学科特点就是带有一定复杂性和抽象性ꎬ尤其是高中阶段数学学科ꎬ需要学生掌握的数学知识变得更加复杂ꎬ更加困难.如果教师没有使用恰当的教学策略ꎬ很容易让学生对数学产生厌烦情绪ꎬ有时会使学生失去学习的自信心.在传统的教学模式下ꎬ教师一味地迎合应试教育的要求ꎬ让学生在题海战术的学习模式下进行数学知识的学习ꎬ不仅会让学生的内心产生巨大的心理负担ꎬ也没有办法让学生体会到数学这门学科所带来的乐趣.因此随着新高考制度的推行ꎬ不管是对于学生的学习ꎬ还是对于教师所开展的教学活动ꎬ都是一个新的契机ꎬ我们的最终目标是使学生能够在繁重的学业压力下轻松的学习.1.2课堂练习容量大高中数学的练习题比较大ꎬ且存在着许多偏离新课程标准的比较难的题目.考虑到数学作为基础学科来说ꎬ涉及到大量的练习量ꎬ而习题量很大造成部分学生有一定的畏难心里.高中数学练习存在着内容宽泛㊁数量多且具有一定难度的情况ꎬ占据很大一部分课余时间.高中数学的练习题设计方面ꎬ主要存在着单一化的重复性题目较多ꎬ且大部分题目偏离学生实际以及教学大纲ꎬ应用范围较为狭窄ꎬ背44离新课标的要求ꎬ会造成浪费学生的学习时间.另外ꎬ单一化的练习形式ꎬ并不能使学生完整掌握各类题型.在应试教育的影响下ꎬ高中学生往往有很大的升学压力.在实际的教学实践中ꎬ部分练习设计过分重视数量而忽视质量ꎬ存在着严重的同质性㊁单一化的问题ꎬ并没有重视如何提升学生的数学实际应用ꎬ很多练习题目设计缺乏必要的规范性ꎬ也会造成学生的学习负担进一步加重ꎬ导致数学练习题完成效率偏低.1.3知识点讲解不够深入高中所开展的数学课程是帮助学生促进自身思维能力和运用能力的关键课程ꎬ但是如今所开设的数学学科当中ꎬ很多教师在进行教学活动的时候ꎬ并没有对其中的学习内容进行深入的挖掘ꎬ也没有重点进行强化训练ꎬ学生在课堂上的参与度较低ꎬ导致整节课堂依旧是以教师作为主体.2新高考模式下高中数学教学的有效策略2.1加强基础知识教学ꎬ帮助学生巩固和理解只有帮助学生建立稳固的基础ꎬ才能够促使学生去学习接下来的数学知识ꎻ只有学生掌握好牢固的基础知识ꎬ才能够更有信心地去面对接下来更为困难的数学学习ꎬ并进行创新.在给学生进行教学活动时ꎬ教师应该重视学生基础知识的学习和掌握ꎬ使学生能够在面对不同数学问题的时候ꎬ灵活地运用所学习到的知识ꎬ这样才能更好地激发学生对数学这门学科的喜爱和热情.为了实现这一点ꎬ首先ꎬ教师可以在每节课上课的时候ꎬ为学生留出一定的时间来巩固基础知识ꎬ由于教材当中很多概念都是由文字来呈现给学生的ꎬ因此学生在这部分的学习过程中很容易出现囫囵吞枣ꎬ只记住一个大概的意思ꎬ教师应该针对这种情况帮助学生巩固基础的概念和公式.其次ꎬ教材中有非常多的课后习题ꎬ大部分课后习题都是依据这节课的内容来进行设计的ꎬ这就需要教师能够重视起这部分练习题来让学生进行训练ꎬ使其对于知识进行巩固和理解.2.2运用合作探究ꎬ突出学生在课堂上的主体地位立足于新高考教学理念当中的高中数学教学ꎬ教师应该努力的改变传统的学习方式.传统教学中往往是通过教师讲授ꎬ学生被动听讲ꎬ或者教师一味地给学生分析知识内容ꎬ让学生来进行笔记的记录ꎬ但是这种学习方式会压制学生的思维能力.在新的教育理念下ꎬ教师应该摒弃传统教学的不足之处ꎬ积极运用探究式合作学习模式ꎬ教师和学生一起进行合作学习ꎬ将课堂的主导权归还给学生ꎬ并引导学生在与教师㊁同伴的合作过程当中发挥自身的智慧ꎬ促进团体的凝聚力ꎬ使每一位学生都能够在学习的过程当中达到教师提出的目标要求.在学习数学知识的同时ꎬ还能够更好地培养学生的责任心㊁合作意识以及道德素养ꎬ让学生能够在合作探究的过程中获得自尊和自信ꎬ从而提升高中课堂教学的效率ꎬ真正实现教师主导性和学生主体性的统一.2.3运用信息化教学ꎬ拓展数学课程资源通过互联网平台可以整合多种信息化教学资源ꎬ对于高中阶段的数学课程教学发展具有重要作用.一般情况下ꎬ数学教师展示课程内容的方式主要以示范讲解为主ꎬ对于数学教学内容的拓展引入和展示还缺乏较好的运用.而在信息化的数学课程教学模式中ꎬ教师可通过互联网途径引入多种数学课程知识ꎬ还可通过多种影音资料展示以及通过线上课程教学途径等ꎬ使学生在当前的数学课程学习中ꎬ可以从多个角度进行深度㊁拓展性学习.因此ꎬ在信息化教学的发展背景下ꎬ教师应重视该种教学方法㊁教学技术手段的应用ꎬ对教学观念进行全面创新.在信息化教学模式中ꎬ教师可通过整合互联网教学资源的方式ꎬ将数学课程的内容进一步拓展和优化.互联网背景主张教学资源之间的整合㊁传播与高效化应用ꎬ满足当前素质教育与全人教育的发展需求.教师在后续的数学课程内容制定与资源拓展中ꎬ应重视信息化教学资源开发与教学模式的有效创设ꎬ使学生可以在当前的信息化数学课程中得到较好的综合素养的培育.例如ꎬ在几何部分的内容教学中ꎬ教师可结合互联网资源引入拓展性几何题型ꎬ或者引入近几年高考高频考查的几何题型ꎬ使学生从数学课程的拓展性题型资源中ꎬ深入当前的数学课程学习.另外ꎬ教54师在引入拓展性数学课程资源的过程中ꎬ还应在教学模式上进行相应的创新ꎬ使学生从不同的数学课程项目和实践活动中ꎬ锻炼自身的数学解题能力以及拓展自身的数学学科知识视野.2.4运用情境教学ꎬ提高学生整体学习效率在传统教学的开展过程中ꎬ如果仅仅是通过教师在课堂上利用一些基本的教具来进行演示和提高学生对于知识的学习ꎬ那么这种方式很难让每一位学生都能够清晰明了地去理解这个数学知识ꎬ降低教学的效果.新时代高中数学教师为学生开展的课堂教学ꎬ教师应该重视起学生手脑并用ꎬ为学生设计一些可以进行实际操作的教学场景ꎬ运用多元化的教学活动来将教学和活动内容相结合ꎬ使学生在一个真实的情境当中运用数学知识ꎬ从而感受数学知识的乐趣ꎬ提高学习的效率.高中数学练习设计还应结合实际来进行情境创设ꎬ符合学生的生活实际的数学题目能更好激发学生的学习兴趣ꎬ并能积极联系学生已经具备的知识体系内容ꎬ更好地通过教学将知识融入到情境过程中ꎬ体现出生活中的数学的重要性ꎬ帮助学生感悟到数学的魅力ꎬ并全面激发学生学习的积极性.比如ꎬ在进行 立体几何 的教学实践中ꎬ教师可以选择生活中的几何实物图ꎬ这样可帮助学生更快地掌握所涉及到的几何知识ꎬ从点线面三位一体到柱锥台球等知识ꎬ实现学生整体的数学学习效率的提升.2.5增加数学练习的趣味性ꎬ鼓励学生自主探究在新课标理念下ꎬ结合高中数学的特点ꎬ落实相应的知识能力㊁情感态度以及价值观的三维目标的统一ꎬ能更好地发挥出高中数学练习设计的目标ꎬ改变传统模式下不重视情感态度价值观的情况.在实际的数学练习环节ꎬ应重视加强情感表达的内容ꎬ发挥出数学练习的作用ꎬ更好地促进师生交流和沟通ꎬ并能进一步重视开展高质量的数学练习的多样化发展ꎬ实现学生的数学学习积极性全面提升.在实际教学实践中ꎬ应落实题目符合实际ꎬ情况多样化的题型ꎬ贴近学生的生活ꎬ并能融入相应的趣味性的内容ꎬ重视实现思维方式和思维结果的融合发展ꎬ更好地帮助学生来进行教学情境的创设ꎬ鼓励他们勇于探索数学学习的魅力.在实际教学实践中ꎬ高中数学练习设计应发挥答案多元化㊁一题多解等方面的作用ꎬ尽可能鼓励学生进行自主探究ꎬ为学生提供独立思维的锻炼ꎬ鼓励学生有效实现良好的自我发现㊁自主学习㊁自主探究ꎬ鼓励并更好地激发学生的思考ꎬ不断提升学生的交流和沟通能力.在培养数学思维的实践中ꎬ可以选择特定范围的题目ꎬ鼓励学生从自身出发来量身定做部分题目ꎬ重视培养学生发现问题并解决问题的能力ꎬ提升学生的综合实践能力ꎬ通过必要的交流及汇报工作ꎬ大大增强了学生的数学实践应用能力.在新高考背景下ꎬ高考数学不再出现文理的分卷ꎬ而是以统一的标准来进行考试ꎬ这对于传统教学来说是一个较大的冲击.作为高中数学老师ꎬ要能积极地将新高考的政策贯穿到学生的日常学习当中ꎬ注重学生综合能力的培养.随着新的教学理念的深入推进ꎬ在高中的数学课堂上ꎬ教师应该积极地运用恰当的教学模式来培养学生的综合能力ꎬ提高学生的学习水平ꎬ为未来的学习和发展奠定竖实的基础.参考文献:[1]张林.新高考背景下高中数学课堂如何培养学生的核心素养[J].数理化解题研究ꎬ2021ꎬ505(12):42-43.[2]谭桂香.高考内容改革背景下的高中数学教学策略探究[J].考试周刊ꎬ2021(06):76-77.[3]张起洋.新高考模式下高中数学的有效课堂教学方法研究[J].学苑教育ꎬ2021(11):45-46.[4]吴春强.新高考背景下的高中数学课堂有效教学[J].数学大世界(上旬版)ꎬ2021ꎬ452(04):61.[5]李英刚.培养学生核心素养ꎬ构建高中数学高效课堂[J].数学教学通讯ꎬ2021ꎬ748(03):71-72.[6]张园萍ꎬ孙亮萍.高中数学课堂教学发展学生数学核心素养的研究[J].学周刊ꎬ2021ꎬ465(09):21-22.[责任编辑:李㊀璟]64。
新课标视角下新旧版高中数学教材对比分析

新课标视角下新旧版高中数学教材对比分析作者:项海圆来源:《科教导刊》2021年第04期摘要人民教育出版社依据2017年版普通高中数学课程标准出版了2020版高中数学新教材,对数列内容进行了删减和补充,本文通过文本内容、组织结构、例题和习题难度三个方面对新、旧教材进行对比分析,揭示数列内容变化的差异,希望为教科书的改革提供参照。
以古为镜,经世致用。
关键词数列教材比较研究中图分类号:G423.3 文献标识码:A DOI:10.16400/ki.kjdks.2021.02.070A Comparative Analysis of the New and Old Versions of High School Mathematics Textbooks from the Perspective of the New Curriculum Standards——Take the humanist series as an exampleXIANG Haiyuan(College of Mathematics, Yunnan Normal University, Kunming, Yunnan 650500)Abstract The People's Education Press published the 2020 edition of the New High School Math Textbook, which is based on the 2017 edition of the General High School math curriculum standards, this paper makes a comparative analysis of the new and old textbooks from three aspects: text content, organization structure, examples and difficulty of exercises, so as to reveal the differences in the changes of the contents of the sequence of numbers and to provide reference for the reform of textbooks. Take the ancient times as a mirror and apply it to the real world.Keywords number series; textbooks; comparative research0 引言数列作为一种特殊的函数——离散函数,是一种重要的数学模型。
教师如何应对新高考的变化

教师如何应对新高考的变化新高考改革带来了诸多变化,对于教师而言,这是新的挑战也是新的机遇。
为了更好地帮助学生应对新高考,教师需要积极调整教学策略和方法,提升自身的专业素养。
首先,教师要深入理解新高考的政策和要求。
新高考在考试形式、科目设置、评价方式等方面都有了较大的变革。
例如,不再单纯分文理科,而是采用“3+1+2”或“3+3”的选科模式,这就要求教师了解不同选科组合的特点和优势,以及对应的高校招生政策。
同时,新高考更加注重对学生综合素质的评价,教师需要熟悉综合素质评价的内容和标准,引导学生在日常学习和生活中注重自身综合素质的培养。
其次,教师需要更新教育观念。
新高考强调学生的自主选择和个性化发展,教师要从传统的“以教为主”转变为“以学为主”,尊重学生的兴趣和特长,激发学生的学习主动性和积极性。
在教学过程中,要注重培养学生的创新思维和实践能力,鼓励学生提出问题、解决问题,而不是简单地传授知识。
再者,教师要优化教学方法。
新高考对学生的学科素养和综合能力提出了更高的要求,教师需要采用多样化的教学方法来满足学生的需求。
例如,运用项目式学习、探究式学习等方法,让学生在实践中掌握知识和技能。
同时,利用现代信息技术手段,如在线课程、虚拟实验室等,丰富教学资源,提高教学效果。
教师还应加强对学生的生涯规划指导。
新高考选科与学生未来的职业发展密切相关,教师要帮助学生了解自己的兴趣、能力和职业倾向,指导学生合理选科和规划未来。
可以通过开设生涯规划课程、组织职业体验活动等方式,让学生对不同职业有更直观的认识,从而做出更适合自己的选择。
在课程设计方面,教师要根据新高考的要求进行调整。
对于必修课程,要注重基础知识的讲解和核心素养的培养;对于选修课程,要结合学校实际和学生需求,开设丰富多样的课程,满足学生个性化发展的需要。
同时,要注意不同课程之间的衔接和融合,避免知识的割裂。
新高考改革也对教师的跨学科教学能力提出了要求。
很多现实问题的解决需要综合运用多学科知识,教师要打破学科界限,加强与其他学科教师的交流与合作,开展跨学科教学活动。
文理科数学教材的区别有哪些

文理科数学教材的区分有哪些【导语】有很多的同学是非常的想知道,文理科数学有什么区分的,作者整理了相干信息,期望会对大家有所帮助!文科和理科数学教材有区分吗必修部分的考察要求是完全一样的如果有选修4系列,那么也是一样的理科必选选修2系列3本文科必选选修1系列2本这两个选修系列是有差别的地方,主要在于理科多的内容(中等题):计数原理及其相干的概率统计,积分,数学归纳法,空间向量文科理科数学差很多吗文科函数部分:定积分、复合函数的导数、导数的几何意义不考;函数次数不能超过三次;立体几何部分:空间向量、向量方法都不考;角度只要求直线与平面的,不要求异面直线和二面角;圆锥曲线部分:直线与圆锥曲线、曲线方程都不考;浙江文科考核直线与抛物线关系概率部分:计数原理、二项式、离散型、正态散布、几何概率都不考;数学归纳法不考;(1)理科:知道两条异面直线所成角、直线与平面所成角、二面角的概念文科:了解两条异面直线所成角及二面角的概念,知道并会求直线与平面所成角。
(2)理科:能用坐标法解决简单的直线与椭圆、抛物线的位置关系等问题。
文科:能用坐标法解决简单的直线与抛物线的位置关系等问题。
(3)理科:了解方程的曲线与曲线的方程的对应关系。
文科:无(4)理科:空间向量与立体几何(整大块)文科:无(5)理科:导数概念及其几何意义1.了解导数概念的实际背景。
2.知道导数的几何意义。
文科:无(6)理科:无特别提示的限制文科:1.了解函数单调性和导数的关系;能利用导数研究函数的单调性,会求函数的单调区间(对多项式函数不超过三次)。
2.了解函数在某点获得极值的必要条件和充分条件;会用导数求函数的极大值、极小值(对多项式函数不超过三次);会求闭区间上函数的值、最小值(对多项式函数不超过三次)。
(7)理科:数学归纳法:了解数学学归纳法的原理,能用数学归纳法证明一些简单的数学命题。
文科:无(8)理科:计数原理。
文科:框图(9)理科:能求简单的复合函数(仅限于形如f(ax+b))的导数。
