椭圆焦半径公式及应用
证明焦半径公式

证明焦半径公式一、椭圆焦半径公式的证明。
(一)椭圆的标准方程。
设椭圆方程为frac{x^2}{a^2}+frac{y^2}{b^2} = 1(a>b>0),其左、右焦点分别为F_1(-c,0),F_2(c,0)(其中c^2=a^2-b^2)。
(二)设点P(x_0,y_0)在椭圆上。
1. 求PF_1(左焦半径)- 根据两点间距离公式,PF_1=√((x_0)+c)^2+y_{0^2}。
- 因为点P(x_0,y_0)在椭圆frac{x^2}{a^2}+frac{y^2}{b^2} = 1上,所以y_0^2=b^2(1-frac{x_0^2}{a^2})。
- 将y_0^2=b^2(1 - frac{x_0^2}{a^2})代入PF_1=√((x_0)+c)^2+y_{0^2}中,得到:PF_1=√((x_0)+c)^2+b^2(1-frac{x_{0^2}{a^2})} =√(x_0)^2+2cx_{0+c^2+b^2-frac{b^2x_0^2}{a^2}} =√(frac{a^2)x_0^2+2a^2cx_{0+a^2c^2+a^2b^2-b^2x_0^2}{a^2}} =√(frac{(a^2)-b^{2)x_0^2+2a^2cx_0+a^2(b^2+c^2)}{a^2}}- 又因为c^2=a^2-b^2,所以:PF_1=√(frac{c^2)x_0^2+2a^2cx_{0+a^4}{a^2}} =√(frac{(cx_0)+a^2)^2{a^2}} =<=ft frac{cx_0+a^2}{a}right- 因为-a≤slant x_0≤slant a且a > 0,c>0,所以cx_0+a^2>0,则PF_1 = a +ex_0(其中e=(c)/(a)为椭圆的离心率)。
2. 求PF_2(右焦半径)- 同样根据两点间距离公式,PF_2=√((x_0)-c)^2+y_{0^2}。
焦半径公式推导及应用

焦半径公式推导及应用在我们学习圆锥曲线的过程中,焦半径公式可是个相当重要的“小伙伴”。
今天咱们就一起来好好琢磨琢磨这个焦半径公式的推导以及它在解题中的神奇应用。
先来说说啥是焦半径。
简单来讲,焦半径就是圆锥曲线上的一点到焦点的距离。
那对于椭圆来说,设椭圆方程为$\frac{x^2}{a^2} +\frac{y^2}{b^2} = 1$($a>b>0$),焦点在$x$轴上,焦点坐标为$F_1(-c,0)$,$F_2(c,0)$,点$P(x_0,y_0)$是椭圆上的任意一点。
那焦半径$|PF_1|$和$|PF_2|$咋算呢?咱们一步步来。
根据椭圆的定义,椭圆上任意一点到两焦点的距离之和等于长轴$2a$,所以有$|PF_1| + |PF_2| = 2a$。
再根据两点间的距离公式,$|PF_1| = \sqrt{(x_0 + c)^2 + y_0^2}$,$|PF_2| = \sqrt{(x_0 - c)^2 + y_0^2}$。
把这俩式子相加得到:$\sqrt{(x_0 + c)^2 + y_0^2} + \sqrt{(x_0 - c)^2 + y_0^2} = 2a$。
经过一番整理和化简(这过程可有点复杂,就不详细展开啦),最终就能得到焦半径公式:$|PF_1| = a + ex_0$,$|PF_2| = a - ex_0$。
这里的$e$是椭圆的离心率,$e = \frac{c}{a}$。
咱再来说说双曲线。
设双曲线方程为$\frac{x^2}{a^2} -\frac{y^2}{b^2} = 1$($a>0$,$b>0$),焦点在$x$轴上,焦点坐标为$F_1(-c,0)$,$F_2(c,0)$,点$P(x_0,y_0)$是双曲线上的任意一点。
同样根据双曲线的定义,双曲线上任意一点到两焦点的距离之差的绝对值等于实轴长$2a$,所以有$||PF_1| - |PF_2|| = 2a$。
椭圆的焦半径

椭圆的焦半径是什么?
椭圆的焦半径:MF1=a+ex0,MF2=a-ex0,X0为M的横坐标。
焦半径公式的推导:利用双曲线的第二定义,设双曲线其左右焦点,则由第二定义:同理即有焦点在x轴上的双曲线的焦半径公式,同理有焦点在y轴上的双曲线的焦半径公式。
其中分别是双曲线的下上焦点。
注意:双曲线焦半径公式与椭圆的焦半径公式的区别在于其带绝对值符号,如果要去绝对值,需要对点的位置进行讨论。
相关结论
A(x1,y1),B(x2,y2),A,B在抛物线y1=2px上,则有:
①直线AB过焦点时,x1x2 = p²/4 ,y1y2 = -p²。
(当A,B在抛物线x ²=2py上时,则有x1x2 = -p²,y1y2 = p²/4 ,要在直线过焦点时才能成立)。
②焦点弦长:|AB| = x1+x2+P = 2P/[(sinθ)1]=(x1+x2)/2+P。
③(1/|FA|)+(1/|FB|)= 2/P;(其中长的一条长度为P/(1-cosθ),短的一条长度为P/(1+cosθ))。
④若OA垂直OB则AB过定点M(2P,0)。
椭圆焦半径公式的证明和应用共7页文档
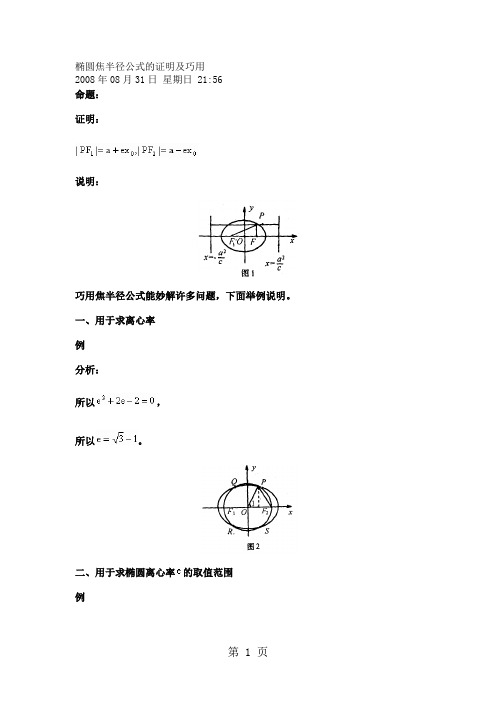
椭圆焦半径公式的证明及巧用2008年08月31日星期日 21:56命题:证明:说明:巧用焦半径公式能妙解许多问题,下面举例说明。
一、用于求离心率例分析:所以,所以。
二、用于求椭圆离心率的取值范围例分析:由得故,即,又。
所以。
三、用于求焦半径的取值范围例分析:所以。
四、用于求两焦半径之积例分析:由知,所以的最小值为,最大值为。
五、用于求三角形的面积例分析:。
由余弦定理得。
解得所以六、用于求点的坐标例分析:及得,解得所以。
七、用于证明定值问题例分析:化简得所以为定值。
八、用于求角的大小例分析:所以所以。
九、用于求线段的比。
例分析:由两式相减并化简得。
所以。
所以。
令,则,故所以,所以。
如图设的坐标为,椭圆与双曲线的离心率分别为,则,,消去得,。
不妨设,由成等差数列得,即。
易知易知的最值不妨设为椭圆的左焦点,而,则。
故。
设的坐标为,则如图,连,则,由焦半径公式得,即。
若椭圆的焦点在轴上,则有。
我们把椭圆上的点到两焦点的距离称为焦半径,而(或)、(或)称为焦半径公式。
如图1,椭圆的准线方程为和。
由椭圆的第二定义得,化简即得1如图为椭圆的两个焦点,以线段为直径的圆交椭圆于四点,顺次连结这四点和两个焦点,恰好围成一个正六边形,则离心率。
2已知为椭圆的焦点,若椭圆上恒存在点,使,求离心率的取值范围。
3若是椭圆上的点,为椭圆的焦点,求的取值范围。
4若为椭圆的左、右焦点,为椭圆上任意一点,求的最值。
5 若是椭圆上一点,为椭圆的左、右焦点,且,求的面积S。
6 若为椭圆上的点,为椭圆的焦点,且,则的横坐标为_________。
由,,7已知为椭圆上两点,为椭圆的顶点,F为焦点,若成等差数列,求证:为定值。
,8 如图3,设椭圆与双曲线有公共焦点,为其交点,求。
9过椭圆的左焦点作与长轴不垂直的弦的垂直平分线交轴于,则。
4,设的坐标分别为,AB的中点为,则。
AB的垂直平行线方程为N的坐标为若椭圆的焦点为。
椭圆焦半径公式的证明及巧用

椭圆焦半径公式的证明及巧用
一、椭圆焦半径公式的证明
设椭圆的两个焦点分别为F1(-c,0)和F2(c,0),中心点为
O(0,0),则椭圆的参数方程为:
x=a*cosθ
y=b*sinθ
其中,θ为椭圆上任意一点P的极角,a和b分别为椭圆的长轴和短轴长度。
将P的坐标代入椭圆焦半径的定义式,得到:c=(F1P+F2P)/2
c=[(-c-x)²+y²+(c-x)²+y²]½/2
c=[2a²-2x²]½/2
将x=a*cosθ代入上式,得到:
c=[2a²-2a²cos²θ]½/2
c=a(1-cos²θ)½
c=a*sinθ
因此,椭圆焦半径的公式为c=a*sinθ。
二、椭圆焦半径公式的巧用
1.焦距的计算
在光学中,焦距是指光线从远处垂直射入透镜后汇聚到的点与透镜的距离。
对于一个椭圆形的反射器或折射器,其焦距可以通过椭圆焦半径公式计算得到。
2.卫星轨道的计算
卫星轨道是指卫星绕地球或其他天体运行的路径。
对于一个地球同步轨道,其轨道形状为椭圆,可以通过椭圆焦半径公式计算出卫星与地球的距离。
3.椭圆的绘制
在计算机图形学中,椭圆的绘制是一个常见的问题。
通过椭圆焦半径公式,可以计算出椭圆上每个点的坐标,并将其绘制出来。
坐标表示的焦半径公式

一.坐标表示的焦半径公式1、椭圆(一类)由代入整理得,同理,可以假想点P在y轴右边,且x>0 帮助,显然总有符合椭圆定义。
公式常见应用:(1)椭圆上点到焦点最远距离a+c,最近距离a—c(2)椭圆上三点A,B,C,若成等差数列,则到同一个焦点的焦半径也成等差数列.(3)定义直线为椭圆的左右准线。
由焦半径公式,椭圆上任意一点P(x,y)到对应焦点和对应准线的距离之比总等于离心率e.2。
双曲线由代入整理得,由双曲线上点,若点P在右支上,同理,。
总有.若点P在左支上,同理,.总有.公示的应用:(1)若双曲线上同一支上的三点A,B,C,有成等差数列,则它们到同一个焦点的焦半径也成等差数列.(2)定义直线为双曲线的左右准线.由焦半径公式,双曲线上任意一点P(x,y)到对应焦点和对应准线的距离之比总等于离心率e.3。
抛物线公式的应用:抛物线上三点A,B,C,若,则.二.圆锥曲线统一定义及方向角表示的焦半径公式1、统一定义:平面上到定点F与定直线l 距离之比等于常数e的点轨迹。
若0〈e〈1,轨迹为椭圆。
若e=1,则轨迹为抛物线.若e〉1,则轨迹为双曲线.2.方向角焦半径公式(1)方向角定义如图:将Fx当始边,FM当终边所成角定义为点M的方向角.方向角范围将焦准距离统一表示为P。
对于椭圆,双曲线(要求记忆)(2)公式:e:离心率,对于椭圆,双曲线,.(3)公式的应用:焦点弦长公式说明:(1)焦点弦长公式中,方向角以平方形式出现,不影响计算,可将方向角改为焦点弦和对称轴夹角:.(2)有对称性改为夹角,公式对椭圆,双曲线的左右焦点弦都成立.(3)对于双曲线当所决定的焦点弦与渐近线平行,在实际上不存在。
若较小,使时,此时公式应表为,此时焦点弦的两个端点分在两支上.(4)对于抛物线,∵e=1 ,。
为焦点弦与对称轴夹角.(5)通径:垂直对称轴的焦点弦称通径,在,令得通径的统一表示2eP。
对于椭圆,双曲线:;对于抛物线:2eP=2P。
椭圆焦半径公式及应用

椭圆焦半径公式及应用
椭圆焦半径是椭圆所具有的重要特性之一,它影响并决定了椭圆的形状及大小。
椭圆焦半径公式是椭圆圆周长关于圆心角的函数,可由数学的角度上描述,通常用
L表示圆周长,用2a表示椭圆的长轴,用2b表示椭圆的短轴,用θ表示圆心角,当θ=π时,椭圆周长L即椭圆的长轴2a,而当θ=2π时,椭圆周长L即椭圆的
短轴2b,综上所述,解得椭圆焦半径公式可用下式表示:
$f=\frac{2b^2+2a^2\theta}{4a\theta}$
椭圆焦半径具有重要的工程应用。
例如在电波无线系统中,对于传播衰减,若
能够将天线的辐射模式准确推导,即可准确计算传播衰减误差。
实际中,一般考虑一个圆柱上海具有椭圆形状的发射电子,椭圆焦半径与其发射电子的空间定位有关,也就是说,把椭圆焦半径计算准确,就可以精确推导出发射电子的空间定位,从而推导出从发射端到接收端的信号衰减。
同时,椭圆焦半径还有其他的计算用途,例如在求解受力问题时,当定义椭圆
轴的方向与弯矩(梁的轴向)方向准一致时,椭圆梁的应力通常可以由非定常元素法直接求解,而其中也需要用到椭圆焦半径公式。
此外,研究特殊有限元分析时,椭圆焦半径公式也多次被采用,从而便于精确的求解出有关问题的结果。
综而言之,椭圆焦半径公式求解计算椭圆的形状及大小,具有重要的工程应用,受力分析、有限元分析等多个应用领域都会充分使用到它的方便之处。
椭圆的焦半径公式倾斜角

椭圆的焦半径公式倾斜角椭圆是高中数学中一个非常重要的图形,而其中的焦半径公式和倾斜角更是有着不少有趣的知识点。
咱先来说说椭圆的焦半径公式。
这玩意儿看起来有点复杂,其实搞懂了就会发现也没那么难。
焦半径就是椭圆上一点到焦点的距离。
对于椭圆方程,如果焦点在 x 轴上,那焦半径公式就是 |PF₁| = a + ex₀,|PF₂| = a - ex₀;要是焦点在 y 轴上,公式就变成 |PF₁| = a + ey₀,|PF₂| = a - ey₀。
这里面的 a 是椭圆的长半轴,e 是离心率,x₀、y₀是椭圆上点的坐标。
我记得之前给学生讲这个知识点的时候,有个学生就一脸懵,完全不理解。
我就跟他说,你就把这个公式想象成一个寻宝的密码。
a 就像是你出发的基地,e 是你前进的速度,x₀或者 y₀就是你走的步数。
你按照这个密码去走,就能找到宝藏,也就是算出焦半径的长度。
这孩子听了之后,眼睛一下子亮了,好像突然就开窍了。
再来说说椭圆的倾斜角。
倾斜角可是个很神奇的东西,它能让椭圆变得更加生动有趣。
倾斜角就是椭圆的对称轴和 x 轴正方向的夹角。
通过倾斜角,我们可以更好地理解椭圆的位置和方向。
有一次我在课堂上做演示,拿了一个椭圆的模型,不断地改变它的倾斜角,让学生们观察椭圆的变化。
他们都特别好奇,眼睛紧紧地盯着模型,生怕错过任何一个细节。
在做练习题的时候,很多同学容易把焦半径公式和倾斜角的相关题目搞混。
这时候就得让他们静下心来,好好回忆公式的推导过程,以及倾斜角的定义。
其实数学就是这样,只要多琢磨,多练习,就没有攻克不了的难题。
总之,椭圆的焦半径公式和倾斜角虽然有点复杂,但只要我们用心去学,多思考,多动手,就一定能掌握它们。
就像我们在生活中遇到困难一样,只要不放弃,总会找到解决的办法。
希望同学们在学习数学的道路上,能够勇往直前,不断探索,发现更多的数学之美!。
焦半径的推导公式

1.焦半径公式,P为椭圆上任意一点,则│PF1│= a + eXo
│PF2│= a - eXo
(F1 F2分别为其左,右焦点)
2.通径长= 2b²/a
3.焦点三角形面积公式
S⊿PF1F2 = b²tan(θ/2)(θ为∠F1PF2)
(这个可能有点难理解,不过结合第一定义可以较快的推,双曲线的也是同样方法)
4.(左)准点Q (自己取的名字方便叙述,准线与X轴的焦点)
过左焦点F1的任意一条线与椭圆交与A ,B 那么一定有:X轴平分∠AQB
(在右边也是一样)
二.双曲线
1.通径就不说了
2.焦半径公式(有8个,很难打符号的,不过可以根据极坐标方程来直接解答,比焦半径公式还快一些)
3.焦点三角形面积公式
S⊿PF1F2 =b²cot(θ/2)(左右支都是它)
三.抛物线
y²=2px (p>0)过焦点的直线交它于A(X1,Y1),B(X2,Y2)两点
1.│AB│=X1 + X2 + p =2p/sin²θ(θ为直线AB的倾斜角)
2. Y1*Y2 = -p²,X1*X2 = p²/4
3.1/│FA│+ 1/│FB│= 2/p
4.结论:以AB 为直径的圆与抛物线的准线线切
5.焦半径公式:│FA│= X1 + p/2 = p/(1-cosθ)
四. 通性直线与圆锥曲线y= F(x)相交于A ,B,则
│AB│=√(1+k²)* [√Δ/│a│]。
椭圆焦半径公式及应用

椭圆焦半径公式及应用椭圆焦半径公式是指椭圆的焦半径与椭圆的长半轴、短半轴以及离心率之间的关系。
在数学中,椭圆通常由两个焦点和一个常数和直线之间的距离之和等于该常数的所有点组成。
椭圆在很多领域都有广泛的应用,如工程、天文学和天体力学等。
首先,椭圆焦半径公式可以由椭圆的离心率和长短半轴表示。
对于一个椭圆,焦半径是指从焦点到椭圆上任意一点的距离。
椭圆的离心率e定义为焦距与长半轴之比。
则椭圆的焦半径r与长半轴a、离心率e和椭圆上一点到焦点的距离d的关系可以用以下公式表示:r = a(1 - e^2) / (1 - e cosθ)其中,θ是椭圆上一点与焦点和长轴之间的夹角。
1.天文学和天体力学:椭圆是描述行星和卫星轨道的基本几何形状之一、在天文学中,椭圆焦半径公式被用来计算行星和卫星的轨道参数,如半长轴和离心率。
2.工程学:椭圆的焦半径公式在光学工程、雷达系统和卫星通信等领域中有广泛的应用。
例如,在光学镜头设计中,椭圆形镜头可以用来纠正成像系统的畸变。
椭圆焦半径公式可以帮助工程师计算并优化这些镜头的参数。
3.生物医学:椭圆形病灶在医学图像处理和治疗中有重要的应用。
通过计算病灶的焦半径,医生可以确定其位置和大小,从而辅助临床诊断和治疗。
4.地理学和测绘学:在地理信息系统(GIS)和测量领域,椭圆形地球模型常用于地球表面的测量和分析。
椭圆焦半径公式可以用来计算地球上不同点之间的距离和方位。
总之,椭圆焦半径公式是椭圆几何性质的重要描述之一、它在不同领域的应用可以帮助我们理解和解决各种实际问题。
无论是天体轨道计算、工程设计、医学诊断还是地理测量,椭圆焦半径公式都具有重要的地位和实用性。
在今后的研究和实践中,我们可以继续挖掘和应用椭圆焦半径公式的潜力,为人类的进步和发展做出更多的贡献。
椭圆的另一个焦半径公式及其应用_王健

=
2
4 -
槡2 cos2
θ
.
[ ( 3) 不妨设直线 AB 的倾斜角为 α ∈ 0,
)π
2
. 因 AB ⊥ DE,则直线 CD 的倾斜角为 α +
π 2
.
由椭圆焦点弦公式,知
AB
=
a2
2ab2 - c2 cos2
, α
( ) DE =
2ab2
a2 - c2 cos2
α
+
π 2
=
a2
2 -
ab2 c2 sin2
对第 ② 问,由平面几何知识相似比可知,
用 AF1 、BF2 分别把 PF1 、PF 2 表示出来,从而 只要引入变量 AF1 倾斜角,运用椭圆焦半径公
式,即可迅速求证.
解
( 1)
x2 2
+ y2
= 1. ( 过程略)
( 2) ① 设直线 AF1 的倾斜角为 α,因 BF2
∥ AF1 故直线 BF2 的倾斜角也为 α,由椭圆焦
; θ
( 3) 过点 F 1 ( - 2,0) 作两条互相垂直的 直线分别交椭圆 C 于 A,B 和 D,E,求 AB + DE
的最小值.
·14·
分析 本题常见思路是设直线斜率为 k,
把直线方程 与 椭 圆 方 程 联 立,用 韦 达 定 理 和
弦长公式,求出 AB、DE 的长,构建关于 k 函数,
[ ) 的倾斜角为 α ∈ 0,π2 ,则直线 PQ 的倾斜
角为 α
+
π 2
.
由推论
2,知
MN
=
a2
2 -
ab2 c2 si
n2
高中数学:焦半径公式及其应用

高中数学:焦半径公式及其应用从圆锥曲线(特指椭圆、双曲线、抛物线)的定义与标准方程出发,如何去推导与焦点相关的焦半径公式、焦点弦长公式及其相关的结论,进而加以应用.本文不作特别说明,椭圆、双曲线、抛物线都是针对焦点在轴上标准方程(其中抛物线考虑标准方程),分别为椭圆或双曲线的左、右焦点,是抛物线的焦点,是相应圆锥曲线上的一点.所有的公式推导均以椭圆方程为例,且优先考虑左焦点对应的相关公式.双曲线可以完全类比椭圆的推导过程得到,特殊情况会另外说明.焦半径是指圆锥曲线上任意一点与焦点的连线段.对于椭圆与双曲线上的任意一点,都对应两条焦半径;对于抛物线上的任意一点,焦半径唯一存在.设是椭圆上任意一点,则有从而焦半径而,所以其中为椭圆的离心率.事实上,在由椭圆的定义推导椭圆方程的过程中,就已经产生了这个式子,设满足即分子有理化得于是有(1)(2)两式相加得即为椭圆上一点到椭圆左焦点的距离.于是我们得到椭圆的焦半径公式(I):同理有双曲线的焦半径公式(I):当点在双曲线上的不同支上时,绝对值里面式子的正负大家可以自行讨论.抛物线的焦半径公式可以直接由抛物线的定义得到,即例1椭圆的右焦点为,直线与轴的交点为,在椭圆上存在点满足线段的垂直平分线过点,则椭圆离心率的取值范围是____.正确答案是.解设,则有,即解得又因为,所以有两边同除可解得由椭圆的焦半径公式(I)知,已知椭圆上一点的横坐标,就很容易求出椭圆的焦半径长,但有时,我们知道的不是横坐标的值,而是焦半径与轴形成的角度,我们可以从上面的焦半径公式(I)出发去推导由焦半径与轴正半轴所成的角对应的焦半径公式.设与轴正半轴形成的角度为,则有整理得,于是有解得同理可以推得右焦点对应的焦半径公式其中,是焦半径与轴正半轴所成的角,注意,同一个点与左焦点与右焦点连线形成的焦半径与轴正半轴所成的角不是同一个角,这是与焦半径公式(I)很不相同的地方,如图:于是我们得到椭圆的焦半径公式(II):其中为焦半径与轴正半轴所成的角.对于双曲线来说,与椭圆类似可以得到双曲线的焦半径公式(II),需要注意的是,当双曲线上的点在双曲线的不同支上时,焦半径公式(I)中绝对值的正负不同,所以需要分别讨论.双曲线的焦半径公式(II):当在双曲线的左支时,有当在双曲线的右支时,有其中为焦半径与轴正半轴所成的角.抛物线的焦半径公式为:其中为焦半径与轴正半轴所成的角.椭圆的焦半径公式(II)有两个常用的推论:推论1 椭圆的焦点弦长公式:其中为椭圆的焦点弦,的倾斜角为.圆锥曲线的焦点弦是指过某一焦点的直线与该圆锥曲线相交得到的两个交点之间的线段.当该弦与轴(椭圆的长轴,双曲线的实轴)垂直时,得到的弦我们称为通径.因为焦半径公式(II)是与角度相关的公式,所以我们很容易从它得到椭圆的焦点弦长公式.证明设是过椭圆左焦点的焦点弦,的倾斜角为,不妨设点在轴上方,如图:由焦半径公式(II)知于是这就是椭圆的焦点弦长公式,容易知道,对于经过椭圆右焦点的弦,此公式同样适用.事实上,对于双曲线,同样有推论1,即双曲线的焦点弦长公式:其中为双曲线的焦点弦,的倾斜角为.不论两点在双曲线的同支还是异支上,都有这个公式成立,只是绝对值中的式子正负有所不同.抛物线的焦点弦长公式更为简单,即其中是抛物线的焦点弦,的倾斜角为.例2椭圆,为椭圆上四个不同的点,都不和轴垂直,且分别过,,求证:为定值.解设的倾斜角为,则的倾斜角为,则由焦点弦长公式知所以为定值.推论2 椭圆的焦点弦被焦点所分成的两段线段长的调和平均数为定值(即焦半径的倒数和为定值).证明由焦半径公式(I)知于是我们知道与的调和平均数为定值,即这个定值就是半通径长,由均值不等式易知椭圆的所有焦点弦中,通径长最短.几道练习:练习1椭圆的焦点为和,点在椭圆上,如果线段的中点在轴上,求的值.练习2椭圆的左右焦点分别为,过的直线交椭圆于两点,过的直线交椭圆于两点,,求四边形面积的取值范围.答案练习1 .提示设,则,于是于是.练习2 .提示设的倾斜角为,则的倾斜角为,于是四边形的面积练习3备注1椭圆的焦半径公式(I)是从椭圆的第一定义向第二定义过渡的重要桥梁,可以通过椭圆的焦半径公式(I)去发掘椭圆的第二定义.由焦半径公式(I)知设直线:,称为椭圆的左准线,记点到的距离为,则有即椭圆上任一点到椭圆左焦点的距离与到左准线的距离的比为定值,这个值为椭圆的离心率.同样地有椭圆的右准线于是有,椭圆上的任意点到椭圆的焦点与对应准线的距离的比值为定值.对于双曲线也有类似的结论,双曲线的准线方程为双曲线上任意点到焦点的距离与到对应准线的距离的比也为定值,即为双曲线的离心率.同时,平面上到定点与到定直线(其中)的距离比为定值(其中)的轨迹为椭圆、双曲线或抛物线,取决于的大小.当时为椭圆,当时为抛物线,当时为双曲线.从而有圆锥曲线的统一定义:平面上到一个定点的距离与到一条定直线(其中定点不在直线上)的距离的比为定值的点的轨迹为圆锥曲线,时这个定义就是抛物线的定义,当的范围在与上时,对应的定义被称为椭圆与双曲线的第二定义.备注2由椭圆的焦半径公式(II)很容易得到椭圆的极坐标方程:以椭圆的一个焦点为极点,以轴正半轴方向为极轴方向建立极坐标系,则椭圆上任意一点的坐标满足:这就是椭圆的极坐标方程,注意如果以椭圆的右焦点为极点,轴正方向为极轴建立极坐标系,得到的极坐标方程为▍▍ ▍▍。
(完整版)椭圆焦半径公式及应用

椭圆焦半径公式及应用.椭圆上的任意一点到焦点F的长称为此曲线上该点的焦半径,根据椭圆的定义,很容易推导出椭圆的焦半径公式。
在涉及到焦半径或焦点弦的一些问题时,用焦半径公式解题可以简化运算过程。
一、公式的推导设P(,)是椭圆上的任意一点,分别是椭圆的左、右焦点,椭圆,求证,。
证法1:。
因为,所以∴又因为,所以∴,证法2:设P到左、右准线的距离分别为,由椭圆的第二定义知,又,所以,而。
∴,。
二、公式的应用例1 椭圆上三个不同的点A()、B()、C()到焦点F(4,0)的距离成等差数列,求的值。
解:在已知椭圆中,右准线方程为,设A、B、C到右准线的距离为,则、、。
∵,,,而|AF|、|BF|、|CF|成等差数列。
∴,即,。
评析:涉及椭圆上点到焦点的距离问题,一般采用焦半径公式求解,即利用焦半径公式可求出A、B、C三点到焦点的距离,再利用等差数列的性质即可求出的值。
例2 设为椭圆的两个焦点,点P在椭圆上。
已知P、、是一个直角三角形的三个顶点,且,求的值。
解:由椭圆方程可知a=3,b=2,并求得,离心率。
由椭圆的对称性,不妨设P(,)()是椭圆上的一点,则由题意知应为左焦半径,应为右焦半径。
由焦半径公式,得,。
(1)若∠为直角,则,即,解得,故。
(2)若∠为直角,则,即=,解得,故。
评析:当题目中出现椭圆上的点与焦点的距离时,常利用焦半径公式把问题转化,此例就利用焦半径公式成功地求出值。
例3 已知椭圆C:,为其两个焦点,问能否在椭圆C 上找一点M,使点M到左准线的距离|MN|是与的等比中项。
若存在,求出点M的坐标;若不存在,请说明理由。
解:设存在点M(),使,由已知得a=2,,c=1,左准线为x=-4,则,即+48=0,解得,或。
因此,点M不存在。
评析:在涉及到椭圆上的点与其焦点的距离时,如果直接用两点间距离公式,运算将非常复杂,而选用焦半径公式可使运算简。
椭圆的焦半径公式及其拓展

1椭圆的焦半径公式及其拓展1. 焦半径:连结椭圆上一点与对应焦点的线段的长度,叫做椭圆的焦半径。
2. 焦半径公式:(1)),(00y x P 是椭圆)0(12222>>=+b a by a x 上一点,)0,(),0,(21c F c F -是左、右焦点,e 是椭圆的离心率,则0201,ex a PF ex a PF -=+=.(2)),(00y x P 是椭圆)0(12222>>=+b a bx a y 上一点,),0(),,0(21c F c F -是上、下焦点,e 是椭圆的离心率,则0201,-ey a PF ey a PF +==.推导过程:(以x 型椭圆方程为例进行推导)方法一:利用椭圆的标准方程推导 由两点间距离公式,可知20201)(y c x PF ++=, 根据椭圆方程)0(12222>>=+b a b y a x ,解得)(22222x a ab y -= 故)(2022220x a a b y -= 将上式代入20201)(y c x PF ++= 可得:)(0001a x a ex a x ac a PF ≤≤-+=+= 同理可得:)(--0002a x a ex a x a c a PF ≤≤-== 方法二:利用椭圆的第二定义2椭圆的左准线方程为:ca x 2-=,设点),(00y x P 到左准线的距离为PD 由椭圆的第二定义:)(002011a x a ex a c a x e PD e PF e PD PF ≤≤-+=⎪⎪⎭⎫ ⎝⎛+==⇒= 同理可得:)(-002a x a ex a PF ≤≤-=五、典型例题例1:在椭圆18422=+y x 上有一个点P ,满足P 到一个焦点的距离是到另一个焦点距离的3倍,则点P 的坐标为________.【推荐理由】可以直观对比出运用焦半径公式的优越性,且同时考查了椭圆的对称性,学生容易漏情况,是易错题.解法一:根据椭圆方程:18422=+y x 可知,椭圆焦点为)2,0()2,0(-和 设),(n m P ,则有18422=+n m 且2222)2(3)2(n m n m ++=+-或2222)2-(3)2(n m n m +=++ 解两次二次方程可得:)2,2()2,2(±-±P P 或解法二:设椭圆度上下焦点分别为21,F F ,点),(n m P 由椭圆方程可知:22,2,22===e c a3利用焦半径公式:,2222,22-2221n PF n PF +== 由题意可得:212133PF PF PF PF ==或解一元一次方程可得:2±=n 所以)2,2()2,2(±-±P P 或【思路点拨】1.椭圆上的点到焦点的距离即是焦半径的概念,很直接联系到焦半径公式;2.本题明确到P 上、下焦点的距离哪个大,故要分类讨论,或者根据椭圆的对称性直接得到结果,需要考虑全面,否则容易漏解,这是本题的易错点.【点评】本题的两种解法对比可以看出,对比利用距离公式,利用焦半径达到了降次的作用,大大化简了计算过程,可以让学生简洁高效地求解。
谈谈椭圆焦半径公式及其应用

知识导航椭圆是历年高考的必考内容,也是圆锥曲线的核心内容.与椭圆有关的问题一般难度和运算量都较大.而在解题时灵活运用椭圆的焦半径公式,能有效地简化运算,提升解题的效率.一、椭圆的焦半径公式我们把连接椭圆上一点与对应焦点的线段的长度,叫做椭圆的焦半径.椭圆的焦半径公式有两种形式:坐标式和三角式.设椭圆x 2a 2+y 2b2=1的左焦点为F 1()-c ,0、右焦点为F 1()-c ,0,在椭圆上任取的一点P ()x 0,y 0,则椭圆的坐标式焦半径公式为|PF 1|=a +ex 0,|PF 2|=a -ex 0.这里e 为离心率.若在椭圆x 2a 2+y 2b2=1()a >b >0中,过左焦点F 1的直线l 与椭圆交于A ,B 两点(A 位于x 轴上方,B 位于x 轴下方),直线的倾斜角为θ,且椭圆的离心率为e ,则椭圆的角度式焦半径公式为||AF 1=b 2a -c cos θ=b 2a 1-e cos θ;||BF 1=b 2a +c cos θ=b 2a1+e cos θ.二、椭圆焦半径公式的应用1.椭圆的坐标式焦半径公式的应用根据椭圆的坐标式焦半径公式的特点,我们可以利用椭圆的坐标式焦半径公式解答“已知椭圆方程和椭圆上点的坐标,求椭圆的焦半径”的问题.例1.设F 1,F 2是椭圆C :x 236+y 220=1的两个焦点,M 为C 上一点且在第一象限,若ΔMF 1F 2为等腰三角形,则M 的坐标为_______.解:由题意得a =6,b =25,c =4,e =c a =23,因为点M 为椭圆C 上一点且在第一象限,所以当||MF 1=||F 1F 2时,ΔMF 1F 2为等腰三角形设M ()x 0,y 0,则||MF 1=a +ex 0,||F 1F 2=2c =8,所以6+23x 0=8,解得x 0=3,将x 0=3代入椭圆C 方程可得y 0=15,所以M ()3,15.本题若利用两点间距离公式求解,计算过程较为复杂.这里利用椭圆的坐标式焦半径公式表示出||MF 1,根据||MF 1=||F 1F 2求出M 点的坐标.该过程简单,运算量小.例2.如图,ΔABC 为椭圆x 24+y 23=1的内接三角形,且右焦点F 为ΔABC 的重心,则||FA +||FB +||FC =_______.分析:因为ΔABC 为椭圆的内接三角形,F 为椭圆右焦点,所以||FA ,||FB ,||FC 即为椭圆焦半径,可设出A ,B ,C 三点的坐标,用椭圆的坐标式焦半径公式表示出||FA ,||FB ,||FC ,根据右焦点F 为ΔABC 的重心列出关系式,化简即可求出结果.解:根据椭圆的方程可得a =2,b =3,c =1,F ()1,0,e =c a =12,设A ()x 1,y 1,B ()x 2,y 2,C ()x 3,y 3,则||FA =a -ex 1=2-12x 1,||FB =a -ex 2=2-12x2,||FC =a -ex 3=2-12x 3,因为F 为ΔABC 的重心,所以x 1+x 2+x33=1,即x 1+x 2+x 3=3,所以||FA +||FB +||FC =2-12x 1+2-12x 2+2-12x 3=6-x 1+x 2+x32=92.2.椭圆的角度式焦半径公式的应用根据椭圆的角度式焦半径公式的特点,我们可以利用椭圆的角度式焦半径公式解答以下问题:(1)已知椭圆方程和过椭圆焦点的直线的倾斜角角度,求椭圆的焦半径;(2)已知椭圆的方程和椭圆的焦半径关系式,求过椭圆焦点的直线的斜率.例3.过椭圆x 24+y 23=1的左焦点F 作倾斜角为60°的直线l ,l 与椭圆交于A 、B 两点,则1||AF +1||BF =_______.分析:已知椭圆的方程和过椭圆焦点的直线方程的倾斜角角度,可利用椭圆角度式焦半径公式表示出38解题宝典||AF ,||BF ,这样便可快速求出1||AF +1||BF 的值.解:由题意得a =2,b =3,||AF =b 2a -c cos 60°,||BF =b 2a +c cos 60°,所以1||AF +1||BF =a -c cos 60°b 2+a +c cos 60°b 2=2a b 2=2×23=43.例4.已知椭圆C :x 22+y 2=1的左右焦点分别为F 1,F 2,点A ,B 是椭圆C 上位于x 轴上方的两点,并且AF 1//BF 2.如果||AF 1-||BF 2=,求直线||AF 1的斜率k .分析:先设∠AF 1F 2=θ,用椭圆角度式焦半径公式表示出||AF 1,||DF 1,然后由椭圆对称性可表示出BF ,根据已知条件列出关系式,即可求出cos θ,再通过三角恒等变换求得tan θ,就能得到所求的斜率.解:由题意得a =2,b =1,c =1,设∠AF 1F 2=θ,由椭圆角度式焦半径公式可得||AF 1=||DF 1=12+cos θ,因为AF 1//BF 2,所以由椭圆对称性可得||BF 2=||DF 1=12+cos θ,又||AF 1-||BF 2=,所以,化简得6cos 2θ+4cos θ-26=0,解得cos θ=由sin θ2+cos θ2=1得sin θ,所以k =tan θ=sin θcos θ.总之,椭圆的焦半径公式的两种形式有着各自的特点和适用范围,在解答与椭圆有关的问题中应用非常广泛.在解题时,我们常常需要将椭圆的焦半径公式与椭圆的方程、定义、性质等结合起来应用.这就要求同学们不仅要加深对概念、公式、性质的理解,强化训练,同时也要培养灵活处理问题的能力.(作者单位:湖南人文科技学院数学系)含参问题的类型有很多,如求参数的取值范围、证明不等式恒成立、判断函数的单调性等.解答含参问题的途径也有很多,如利用方程思想、利用导数法、借助待定系数、利用函数思想等.本文重点探讨一下解答含参问题的三种途径:利用方程思想、利用函数的性质、借助待定系数,以帮助同学们拓宽解题的思路.一、利用方程思想方程思想是解答高中数学问题的常用思想,是指通过建立方程或者方程组使问题获解的数学思想.在解答含参问题时,我们可以根据代数式的特点建立方程或者方程组,然后利用方程的判别式△=b 2-4ac 、根与系数的关系来解答问题.例1.已知函数f ()x =x 2-()m +5x +2()m +5在定义域内恒为非负数,求方程2x m +1=||m +2+1的根的取值范围.解:因为f ()x 恒为非负数,所以方程f (x )=0的判别式△=()m +52-8()m +5≤0,解得-5≤m ≤3.方程2xm +1=|m +2|+1可化为2x=()m +1()|m -2|+1,当-5≤m ≤2时,2x =()m +1()2-m +1,所以2x =-m 2+2m +3=-()m -12+4,则2x ≤4,x ≤2,当2<m ≤3时,2x =()m +1()m -1=m 2-1,3<m 2-1≤8,所以log 23<x ≤3.39。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
椭圆焦半径公式及应用 TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-
椭圆焦半径公式及应用
.
椭圆上的任意一点到焦点F的长称为此曲线上该点的焦半径,根据椭圆的定义,很容易推导出椭圆的焦半径公式。
在涉及到焦半径或焦点弦的一些问题时,用焦半径公式解题可以简化运算过程。
一、公式的推导
设P(,)是椭圆上的任意一点,分别是椭圆的左、右焦点,椭圆,求证,。
证法1:。
因为,所以
∴
又因为,所以
∴,
证法2:设P到左、右准线的距离分别为,由椭圆的第二定义知
,又,所以,而。
∴,。
二、公式的应用
例1 椭圆上三个不同的点A()、B()、C()到焦点F(4,0)的距离成等差数列,求的值。
解:在已知椭圆中,右准线方程为,设A、B、C到右准线的距离为,则、、。
∵,,,而|AF|、|BF|、|CF|成等差数列。
∴,即,。
评析:涉及椭圆上点到焦点的距离问题,一般采用焦半径公式求解,即利用焦半径公式可求出A、B、C三点到焦点的距离,再利用等差数列的性质即可求出的值。
例2 设为椭圆的两个焦点,点P在椭圆上。
已知P、、
是一个直角三角形的三个顶点,且,求的值。
解:由椭圆方程可知a=3,b=2,并求得,离心率。
由椭圆的对称性,不妨设P(,)()是椭圆上的一点,则由题意知应为左焦半径,应为右焦半径。
由焦半径公式,得,。
(1)若∠为直角,则,即
,解得,故。
(2)若∠为直角,则,即
=
,解得,故。
评析:当题目中出现椭圆上的点与焦点的距离时,常利用焦半径公式把问题转化,此例就利用焦半径公式成功地求出值。
例3 已知椭圆C:,为其两个焦点,问能否在椭圆C上找一点M,使点M到左准线的距离|MN|是与的等比中项。
若存在,求出点M的坐标;若不存在,请说明理由。
解:设存在点M(),使,由已知得a=2,,c=1,左准线为x=-4,则,即+48=0,解得,或。
因此,点M不存在。
评析:在涉及到椭圆上的点与其焦点的距离时,如果直接用两点间距离公式,运算将非常复杂,而选用焦半径公式可使运算简。
