两点式和截距式PPT演示文稿(1)

合集下载

7.2(2)直线的方程-两点式,截距式.ppt

直线 l 的斜率为 k
由点斜式方程 y y1 y 2 y1 x 2 x1
y 2 y1 x 2 x1
p2
( x x 1 ).
( y1 y 2 )
化简为
y y1 y2 y1

x x1 x2 x1
——直线方程的两点式
例1 、已知直线l于x轴交于点A(a,0), 于y轴交于B(0, b), (a 0, b 0)，求直线l的方程。
直线 l过点 P ( 4 ,1) 4 1 1 4 b a ab a b
2 4 ab 4 ab ab 16

P(4,1)
A

0
x
S
S min
1
ab 8 （当 a 4 b 即 a 8 , b 2时取等号）
2 x y 8 , 直线 l 方程为 1 x 4y 8 0 8 2
解：
(1)
y 1 3 1 y5 05 y 50

x2 02 x0 50
y 2 x 3.
(2)

y x 5.
5 4
(3)

x 42
y
x.
y y0 k ( x x0 )
应用范围
k存在 k存在
k存在且k 0
k存在且 0 且不过原点
y kx b
y y1 y2 y1 x x1 x2 x1
x a

y b
1.
课堂练习
1 .求过下列两点的直线的（1） P1 ( 2 ,1)、 P2 ( 0 , 3 ); ( 2 ) A ( 0 , 5 )、 B ( 5 , 0 ); ( 3 ) C ( 4 , 5 )、 D ( 0 , 0 ). 两点式方程，再化成斜截式方程：

高二数学时直线方程的两点式与截距式PPT课件

第13页/共38页
【解】法一：依题意，直线 l 的斜率存在且不为 0，设其斜率为 k，则可得直线的方程为：y＋2＝k(x－3)．令 x＝0，得 y＝－2－3k；令 y＝0，得 x＝2k＋3. 由题意得：－2－3k＝3＋2k，解得 k＝－1 或 k＝－23.
第14页/共38页
∴l 的方程为：y＋2＝－(x－3)或 y ＋2＝－23(x－3)．即为：x＋y－1＝0 或 2x＋3y＝0. 法二：设直线 l 在两坐标轴上的截距均为 a. (1)若 a＝0，则直线 l 过原点，此时 l 的方程为：2x＋3y＝0；
本部分内容讲解结束
按ESC键退出全屏播放
第37页/共38页
第15页/共38页
(2)若 a≠0，则 l 的方程可设为：xa＋ay＝1. 由 l 过点(3，－2)，知3a＋－a2＝1，即 a＝1. ∴直线 l 的方程为 x＋y＝1，即 x＋y－1＝0. 综合(1)、(2)可知：直线 l 的方程为 2x＋3y ＝0 或 x＋y－1＝0.
第16页/共38页
【点评】本题主要理解截距的概念．法一绕开截距，待定斜率(存在) 没有失根；法二直接待定截距，有失根，注意讨论特殊情形．
第2页/共38页
三基能力强化
1．若直线 l 在 x 轴上的截距为 2，在 y
轴上的截距为 3，则 l 的方程为( )
A．y＝32x＋3
B．y＝32x－3
C．3x＋2y－6＝0 D．3x＋2y＋6＝0
答案：C
第3页/共38页
2．下列四个命题中，假命题是( ) A．经过定点P(x0，y0)的直线不一定都可以用方程y－y0＝k(x－x0)表示 B ．经过两个不同点 P1(x1 ， y1) ， P2(x2 ， y2) 的直线都可以用方程 (y － y1)(x2－x1)＝(x－x1)(y2－y1)表示

高一数学两点式截距式(PPT)5-1

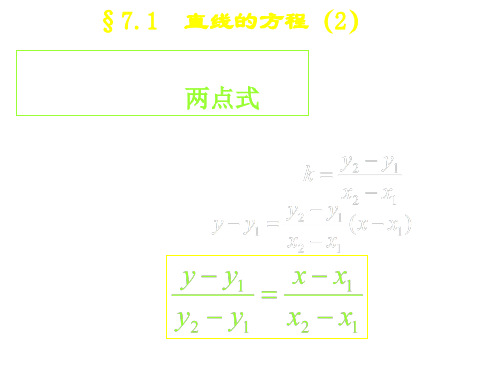
§7.1 直线的方程（2）
注：截距式适用于与两坐标轴不垂直且不过原点的直线。
练习2：课本第41页 2
例1、三角形的顶点是 A(-5, 0), B(3,-3), C(0, 2), 求、新课 1、直线方程的两点式
若直线L经过点P1(x1,y1)、P2(x2,y2)，并且x1≠x2，则它的斜率
代入点斜式，得
当y1≠y2时
石头：界～｜墓～｜里程～｜纪念～｜立了一块～。【碑额】’名碑的上端。也叫碑首或碑头。【碑记】名刻在碑上的记事文章。【碑碣】〈书〉名碑：墓前立有～。【碑刻】名刻在碑上的文字或图画：拓印～。【碑林】名石碑林立的地方，如陕西西安碑林。【碑铭】名碑文。【碑首】名碑额。【碑拓】名碑刻的拓本。【碑帖】名；大语文加盟阅读班加盟快速阅读加盟语文辅导班加盟；石刻、木刻法书的拓本或印本，多做习字时临摹的范本。【碑头】名碑额。【碑文】名刻在碑上的文字；准备刻在碑上的或从碑上抄录、拓印的文字。【碑阴】ī名碑的背面。【碑志】名碑记。【碑座】（～儿）名碑下边的底座。【鹎】（鵯）名鸟，羽毛大部为黑褐色，腿短而细。吃果实和昆虫。种类很多，常见的有白头鹎等。【箄】〈书〉捕鱼的小竹笼。【北】①名方位词。四个主要方向之一，清晨面对太阳时左手的一边：～头儿｜～面｜～风｜～房｜城～｜往～去｜坐～朝南。②北部地区，在我国通常指黄河流域及其以北的地区：～味｜～货。③（）名姓。【北】〈书〉打败仗：败～｜连战皆～｜追奔逐～（追击败逃的敌军）。【北半球】名地球赤道以北的部分。【北边】?ɑ名①（～儿）方位词。北。②〈口〉北方?。【北朝】名北魏（后分裂为东魏、西魏）、北齐、北周的合称。参看页〖南北朝〗。【北辰】名古书上指北极星：众星环～。【北斗星】ī名大熊星座的七颗明亮的星，分布成勺形。用直线把勺形边上两颗星连接起来向勺口方向延长约五倍的距离，就遇到小熊座α星，即现在的北极星。【北豆腐】?名食品，豆浆煮开后加入盐卤，使凝结成块，压去一部分水分而成，比南豆腐水分少而硬（区别于 “南豆腐”）。【北伐战争】第一次国内战争时期，以中国国民党和中国合作的统一战线为基础，组织国民军进行的一次反对帝国主义和封建军阀统治的战争（—）。因这次战争从广东出师北伐，所以叫北伐战争。参看页〖第一次国内战争〗。【北方】名①方位词。北。②北部地区，在我国一般指黄河流域及其以北的地区。【北方话】名长江以北的汉语方言。广义的北方话还包括四川、重庆、云南、贵州和广西北部的方言。北方话是普通话的基础方言。【北非】名非洲北部，通常包括埃及、苏丹、利比亚、突尼斯、阿尔及利亚、摩洛哥、西撒哈拉等。【北瓜】?〈方〉名南瓜。【北国】〈书〉名指我国的北部：～风光。【北寒带】名北半球的寒带，在北极圈与北极之间。参看页〖寒带〗。【北回归线】ī名北纬°′的纬线。参看页〖回归线〗。【北货】名北方所产的食品，如

高中数学必修二《直线的两点式方程》PPT (1)

示意图
方程
使用范围
x
a≠0,
b≠0
a
y
+ =1
b
谢谢！
解答有关问题.
思维脉络
1.直线方程的两点式
名称
两
点
式
已知条件
P1(x1,y1),
P2(x2,y2),
其中 x1≠x2,
y1≠y2
示意图
方程
y-y 1
=
x-x1
x2 -x1
y 2 -y 1
使用范围
斜率存在
且不为 0
2.直线方程的截距式
名称
已知条件
截
距
式
在 x,y 轴上
的截距为 a,
b 且 ab≠0
P1(x1,y1 ),P2(x2 ,y 2 )的点的直线
都可以用方程 (yyபைடு நூலகம் )(x2 x1 ) (x x1 )(y2 y1 )表示 ;
x y
C.不经过原点的直线
都可以用方程 1表示 ;
a b
D.经过定点的直线都
可以用 y kx b表示 .
M(
,
),即M( , )
2
2
2 2
3 1
y0
x5
过A（－5，
0），M( , )的直线方程为

1
3
2 2
0
5
2
2
整理得：x+13y+5=0
这就是BC边上中线所在的直线的方程。
练习1：求过下列两点的直线方程
(1)M(-1,4),N(1,10)
(2)P1(2,1),P2(0,-3)

02教学课件_2.2.2 直线的两点式方程(共25张PPT)

可以确定一条直线。
这样，在直角坐标系中，给定一个点p0(x0,y0)和斜率k,可得出直线方程。
若给定直线上两点p1(x1,y1)p2(x2,y2),你能否得出直线的方程呢?
探究新知
1．直线的两点式方程
(1)直线的两点式方程的定义
y－y1 x－x1
＝
y
－y
x2－x1
2
1
__________________就是经过两点
点的坐标还有限制条件吗?
答案:这个方程对两点的坐标没有限制,即它可以表示过任意两点的直线方程.
2.已知直线l过点A(3,1),B(2,0),则直线l的方程为
y-1
x-3
解析:由两点式,得0-1 = 2-3,化简得 x-y-2=0.
答案:x-y-2=0
.
二、直线的截距式方程
点睛：直线的截距式方程是直线的两点式方程的特殊情况,由直线的截距式方程
2
S 取最大值为-3×152+20×15+54 000=54 150(m2).
因此点 P 距 AE 15 m,距 BC 50 m 时所开发的面积最大,
最大面积为 54 150 m2.
归纳总结二次函数最值问题,一方面要看顶点位置,另一方面还要看定义域的范围.结
合图形求解,有时并非在顶点处取得最值.
当堂检测

不垂直于x、y轴的直线
点P1 ( x1，y1 )和点P2 ( x2，y2 )
y1 y2 x1 x2
在x轴上的截距 a
在y轴上的截距 b
x y
1
a b
不垂直于x、y轴的直线
不过原点的直线
课堂小结
课堂小结：
－3
)

直线的方程-2两点式、截距式)PPT课件

THANKS FOR WATCHING
感谢您的观看
在交通领域，例如在道路规划中，可以使用这两种方程形式来表示道路的走向和交点。
在物理学中，例如在电场分析中，可以使用这两种方程形式来描述电场线的分布和方向。
04 练习与巩固
基础练习题
01
02
03
题目1
已知两点$P_1(x_1, y_1)$ 和$P_2(x_2, y_2)$，求直线方程的两点式。
直线的方程。
截距式方程
截距式方程是另一种形式的直线方程，它表示直线在x轴和y轴上的截距。
直线方程的应用
了解直线方程在实际问题中的应用，如几何、物理和工程问题。
学习心得体会
通过学习本章，我掌握了直线方程的两种形式，即两点式和截距式，并了解了它们在实际问题中的应用。
学习过程中，我遇到了一些困难，如理解截距式方程的推导过程和如何应用直线方程解决实际问题。但通过反复阅读教材和与同学讨论，我逐
在实际生活中，例如道路修建、桥梁设计等工程领域，常常需要使用到截距式直线方程来描述道路或桥梁的走向。
在解析几何中，截距式直线方程也是一种重要的直线方程形式，用于解决一些特定的问题。
03 两种直线方程的比较
异同点比较
相同点
两点式和截距式都是用来表示直线方程的方法，它们都可以表示直线上的点。
渐克服了这些困难。
学习本章后，我意识到数学在实际问题中的重要性，并计划在未来的学习中更加注重数学知识的应用。
下一步学习计划
深入学习直线的其他方程形式，如点斜式和斜截式。
学习如何利用直线方程解决更复杂的实际问题，如解析几何和物
理问题。
复习和巩固已学过的直线方程知识，确保自己能够熟练掌握和应

两点式和截距式PPT教学课件

cij() =1 cij≥ ∨(aik∧bkj)≥
k, (aik∧bkj)≥ k, aik ≥ , bkj≥
k, aik() =bkj() =1 ∨(aik()∧bkj())=1
cij() =0 cij＜ ∨(aik∧bkj)＜ k, (aik∧bkj)＜ k, aik＜或 bkj＜
k, aik() =0或bkj() =0 ∨(aik()∧bkj())=0
(2) 这些性质在有限论域情况下,就是模糊矩阵合成运算的性质.
§2.3 模糊等价矩阵
模糊等价关系
若模糊关系R是X上各元素之间的模糊关系，且满足：
(1)自反性：R(x, x) =1； I ≤R ( rii =1 )
(2)对称性：R(x, y) =R(y, x)；RT=R( rij= rji)
(3)传递性：R2R,
160 0.2 0.8 1 0.8 0.2
170 0.1 0.2 0.8 1 0.8
180 0 0.1 0.2 0.8 1
模糊关系的合成
设 R1 是 X 到 Y 的关系, R2 是 Y 到 Z 的关系, 则R1与 R2的合成 R1 ° R2是 X 到 Z 上的一个关系.
(R1°R2) (x, z) = ∨{[R1 (x, y)∧R2 (y, z)]| y∈Y } 当论域为有限时，模糊关系的合成化为模糊
0 1 1
1
1 1
对任意的∈[0, 1]，有
性质1：A≤B A ≤B；性质2：(A∪B) = A∪B，(A∩B) = A∩B；性质3：( A ° B ) = A ° B；性质4：( AT ) = ( A )T.
下面证明性质1： A≤B A ≤B 和性质3.
性质1的证明： A≤B aij≤bij；

2.2.2直线的两点式方程课件(共20张PPT)

所以所求直线方程为： + − 3 = 0或 = 2.
(，0)
Байду номын сангаас

例2 ⑴ 过点(1,2)并且在两个坐标轴上的截距相等的直线有几条?并求其方程．
(2) 过(1,2)并且在两个坐标轴上的截距的绝对值相等的直线有几条? 并求其方程．
解：三条
①当直线的两截距相等过原点时， = 2
②当直线的两截距相等不过原点时， + − 3 = 0

典例剖析
例3 三角形的顶点分别是(−5,0), (3, −3), (0,2)，求边所在直线的方程，以及该边上
中线所在直线的方程.

变式1 求边上的垂直平分线所在直线的方程.
：5 + 3 − 6 = 0 = −

=

1
3
M ,
2
2
+

（1）在轴上的截距为2，在轴上的截距是3；
由截距式得：
x y
1
2 3
整理得：3x 2 y 6
0
（2）在轴上的截距为-5，在轴上的截距是6；
由截距式得：
x
y
1
5 6
整理得： 6 x 5 y 30 0
典例剖析
例2 ⑴ 过点(1,2)并且在两个坐标轴上的截距相等的直线有几条?并求其方程．
斜截式
斜率, 在轴上的纵截距
y kx b
斜
率
必
须
存
在
斜率不存在时，
直线方程为：x x0
思考：已知直线上两点1(1, 1), 2(2, 2)（其中1 ≠ 2, 1 ≠ 2 ），如何求出通过这两点的

必修二2.1.2直线的方程(2)两点式和截距式课件

栏目导航
例3：已知：直线 l 过 A(0, 5)
B(5, 0) 求直线 l 的方程
截距式：x y 1 5 5
在x轴上截
距
在y轴上截距
栏目导航
练习2：写出下列直线的截距式方程 (1)x轴上的截距是2，y轴上的截距是3； (2)x轴上的截距是4，y轴上的截距是6；
(3)x轴上的截距是 1 ，y轴上的截距是 1
2
2
(1) x y 1 23
(2) x y 1 46
(3)
x 1
y 1
1
22
例4： ABC中A(5, 0), B(3, 3),C(0, 2)
求三角形各边的直线的方程
解：由两点式求直线AB
y C
3x+8y+15=0
A
由斜截式求直线BC
O
x 5x+3y-6=0
B
由截距式求直线AC
2x-5y+10=0
栏目导航
学习目标 1．了解直线方程的两点式的推导
核心素养
过程．(难点)
2 ．会利用两点式求直线的方通过学习本节内容来提升学生的
程．(重点)
数学运算核心素养.
3．掌握直线方程的截距式，并会
应用．(易错点)
栏目导航
1、点斜式直线方程
点：P1(x1, y1)
y y1 k(x x1)
（7）斜率为-2，在y轴上的截距为-5
(1) y 2x 3 2 1
(2) y 3 x 6 2 33
(3) y 3
(4) y 3x 4 3 2 (5) y 3x 5 (6)x 2 (7) y 2x 5
第2章平面解析几何初步
2.1 直线与方程 2.1.2 直线的方程第2课时两点式和截距式

人教版数学2《直线的两点式与截距式方程》上课(共18张PPT)教育课件

学习重要还是人脉重要?现在是一个双赢的社会，你的价值可能更多的决定了你的人脉，我们所要做的可能更多的是专心打造自己，把自己打造成一个优秀的人、有用的人、有价值的人，当你真正成为一个优秀有价值的人的时候，你会惊喜地发现搞笑人脉会破门而入。从如下方面改进：1、专心做可以提升自己的事情； 2、学习并拥有更多的技能；3、成为一个值得交往的人；4学会独善其身，尽量少给周围的人制造麻烦，用你的独立赢得尊重。理财的时候需要做的一方面提高收入，令一方面是节省开支。这就是所谓的开源节流。时间管理也是如此，一方面要提高效率，另一方面是要节省时间。主要做法有：1、同时做两件事情（备注：请认真选择哪些事情可以同时做），比如跑步的时候边听有声书；2、压缩休息时间提升睡眠效率，比如晚睡半小时早起半小时（6~7个小时即可）；3、充分利用零碎时间学习，比如做公交车、等车、上厕所等。
化简：
yy1 xx1 y2 y1 x2 x1
一、直线的两点式方程
两点式适用范围：与坐标轴不垂直的直线
思考：当x1 x2时，当 y1 y2 时，直线方程怎么表示？ 1、当x1 x2时，直线与X轴垂直，方程为
xx10(或 xx1)
2、当 y1 y2 时，直线与Y轴垂直，方程为 yy10(或 yy1)
3
k= 2 ；直线的方程为 3x2y10 。
讨论：如何用点斜式的方法推导两点式方程. 还有其他的方法吗？
一、直线的两点式方程
已知直线经过两点， P 1(x1,y1)P ,2(x2,y2) (x1x2,y1y2)

直线的两点式和截距式的方程及一般式方程PPT课件

参数法求解
参数法是一种将变量用参数表示出来的方法，适用于已知一个点
坐标和斜率的情况。
步骤：首先根据已知条件设定参数方程，然后根据参数方程解出
变量的值。
例如，已知点A(1,2)和斜率m=1，代入参数方程得：{x=t*cosα,
y=t*sinα}，将点A的坐标代入得： {t*cosα=1, t*sinα=2}，解得：
力的合成与分解
在分析力的作用时，直线方程可以用来表示力的方向和大小。
电路分析
在电路分析中，直线方程可以用来描述电流、电压和电阻之间的关系。
实际生活问题
交通规划
在城市交通规划中，直线方程可以用来描述道路的走向和长度。
建筑结构设计
在建筑设计时，直线方程可以用来确定建筑物的位置、高度和方向。
直线的两点式和截距式的方程及一般式方程ppt课件
contents
目录
• 直线的两点式方程 • 直线的截距式方程 • 直线的一般式方程 • 直线方程的求解方法 • 直线方程在实际问题中的应用
01 直线的两点式方程
定义
两点式方程
给定直线上的两个点$(x_1, y_1)$ 和$(x_2, y_2)$，通过这两点可以确定一条直线的方程。
经济数据分析
在经济数据分析中，直线方程可以用来描述经济增长、消费和收入之间的关系。
THANKS FOR WATCHING
感谢您的观看
推导过程
通过两点确定一条直线的原理，设直线上的两点为 (P_1(x_1, y_1)) 和 (P_2(x_2, y_2))，斜率 (m = frac{y_2 - y_1}{x_2 - x_1})，截距 (b = y_1 - m cdot x_1)。

2.2.2直线的两点式方程课件(人教版)(1)

概念学习
例3：如图，已知直线与x轴的交点为A(a, 0)，与y轴的交点为B(0, b)，
其中a ≠ 0，b ≠ 0.求直线的方程.
解：将两点A(a, 0)，B(0, b)的坐标代入两点式，得
y−0
b−0
=
x−a
，
0−a
即
x
a
y
b
+ = 1.
概念学习
例3：如图，已知直线与x轴的交点为A(a, 0)，与y轴的交点为B(0, b)，
3
1
,
)，即( , − ).
2
2
2
2
由中点坐标公式，可得点M的坐标为(
3
1
y−0
过A(−5,0)，M( , − )两点的直线方程为 1
2
2
− −0
2
x+5
=3 ，
2
+5
整理可得x + 13y + 5 = 0.这就是BC边上中线AM所在直线的方程.
变式引申
例4：已知∆ABC的三个顶点A(−5,0)，B(3, −3)，C(0,2).
y−y1
把
y2 −y1
=
x−x1
叫做直线的两点式方程，简称两点式.
x2 −x1
思考：
两点式方程中，分母不能为0，故有x1 ≠ x2 ，y1 ≠ y2 ，据此
我们可以得到两点式方程的适用条件是什么？
思辨
两点式方程的运用条件：
问题3：当 x1 = x2 ，y1 ≠ y2 时，直线方程是什么？ = 1 或 = 2
∴直线的方程是： = 2 + 2（待定系数法）
概念学习
问题2：已知直线经过P1 x1 ，y1 和P2 x2 ，y2 (x1 ≠ x2 , y1 ≠ y2 )两点，

选择必修第二章 2.2.2 直线的两点式方程课件(共18张PPT)

∴边AB所在直线的方程为 = 2.
−1
∵(2, −1)，(4,1)，由直线方程的两点式可得
−1−1
=
−4
，
2−4
∴边所在直线的方程为x-y-3=0.
−2
同理可由直线方程的两点式得直线的方程为
1−2
=
−2
，
4−2
即x+2y-6=0.
∴三边AB，AC，BC所在的直线方程分别为x=2,x-y-3=0,x+2y-6=0.
养.
温故知新
1.直线的点斜式方程
若直线过定点(x0，y0)且斜率为k，则直线方程为
y-y0=k(x-x0)
2.直线的斜截式方程
若直线的斜率为k且它在y轴上的截距为b，则直线方程为
y=kx+b
若直线过定点(x0，y0)且斜率不存在（与x轴垂直），则直线方程为
x-x0=0 ，即 x=x0.
新知探究
已知直线l经过两点P1(x1,y1)，P2(x2,y2) (其中x1≠x2，y1≠y2)，因为两点确定一条
新知探究
【例4】求过点(5,2)，且在坐标轴上截距互为相反数的直线的方程．
解：当直线l在坐标轴上截距都不为零时，设其方程为 +
−3

将A(－3,4)代入上式，有
+
4
−

−
= 1，
= 1，
解得a＝－7.
∴直线l的方程为x－y＋7＝0.
当直线l在坐标轴上的截距都为零时，设其方程为y＝kx.
不同但本质一致，都是对直线的定量刻画.在对直线的定量刻画中，斜率处于核
心地位.点斜式方程是其他所有形式的方程的基础，其他所有形式的方程都是点

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例2.已经直线l过A(1，－3)B(2，1)两点，求直线l的的两点式方程，并把它转化为直线的斜截式、截距式和点斜式．
例3.求过点M（3，-4），且在两坐标轴上截距相等的直线方程
y
注意：截距相等与截得的距离相等不一样! 0 x 当直线过原点，横纵截距相等都为0
直线的方程
7.2.2两点式和截距式
2014年9月21日星期日Biblioteka 对直线的两点式方程公式的理解：
(1)方程中的x，y代表直线l上动点的坐标，x1，y1，x2， y2代表两个已知点的坐标．
(2)直线的两点式方程中，要求x1≠x2，y1≠y2 ．当x1=x2时，直线平行于y轴，直线的方程为x=x1，当y1=y2时，直线平行于x轴，直线的方程为y=y1． (3)直线的两点式方程比较复杂，要注意它的特征．
(4)如果把两点式进行一下变形为
x2 x1 y y1 y2 y1 x x1 就可表示任意的直线。
4、回答下列问题:
（1）两条直线有相同的斜率，但在x轴上的截距不同，那么它们在y轴上的截距可能相同吗? （2）两条直线在y轴上的截距相同，但是斜率不同，那么他们在x轴上的截距可能相同吗? （3）任一条直线都可以用截距式方程表示吗?