字典序 排列
python 字符串排序规则

在Python 中,字符串排序的规则是根据字符的Unicode 编码值来确定的。
具体来说,字符串的排序规则如下:1. 字典序排序:Python 中的字符串是按照字典序进行排序的。
这意味着字符串的字符将按照它们在Unicode 编码中的顺序进行排列。
例如,字母"a" 的Unicode 编码值比字母"b" 的Unicode 编码值小,因此在排序时"a" 将排在"b" 之前。
2. 区分大小写:在默认情况下,Python 中的字符串排序是区分大小写的。
这意味着大写字母将排在小写字母之前。
例如,字母"A" 的Unicode 编码值比字母"a" 的Unicode 编码值小,因此在排序时"A" 将排在"a" 之前。
3. 可选忽略大小写:如果你希望在排序时忽略字符串的大小写,可以使用`lower()` 或`upper()` 方法将所有字符串转换为小写或大写形式,然后再进行排序。
例如:```pythonstrings = ['Apple', 'banana', 'orange', 'grape']sorted_strings = sorted(strings, key=str.lower)print(sorted_strings) # 输出['Apple', 'banana', 'grape', 'orange']```在这个例子中,我们使用`lower()` 方法将所有字符串转换为小写形式,然后按照字典序进行排序。
总的来说,Python 中的字符串排序规则是基于Unicode 编码值的字典序排序,并可选择忽略大小写。
C++实现数字按照字典序排序

break;
if(i==0)return 1;
}
for(j=n-1;j>i;j--){
if(A[i]<A[j])break;
}
swap(i,j);
antsort(i+1,n-1);
}
}
main(){
int i,n=4;
NextNum(n);
}
其运行结果为:
求四个数中两个数的组合
if(NextNum()==1)
break;
}
}
程序运行结果为:
程序2:对于有6个数的数组,保持其中两个数不动
#include "stdio.h"
#include "stdlib.h"
int n=5;
int AA[5]={0,0,0,0,0};
int flag[5]={0,1,0,1,0};//当i=1时,第n-i个数不动
else{
AA[i+2]++;
AA[i]=0;
i++;
}
}
else {
AA[i+1]++;
AA[i]=0;
}
}
else
break;
}
return(0);
}
main(){
long i;
for( ; ; ){
for(i=n-1;i>=0;i--)
printf("%2d",AA[i]);
printf("\n");
if(NextNum()==1)
break;
c语言哈希表字典序排序

c语言哈希表字典序排序C语言哈希表字典序排序哈希表是一种以键值对(key-value)方式存储数据的数据结构,通过将键值映射成数组下标,从而快速地查找对应的值。
哈希表的查找效率非常高,可以达到O(1),而不受数据量变化的影响。
然而,哈希表在显示其优越性时,也面临着排序的问题。
排序是数据处理中一个非常重要的问题,常见的排序方法有冒泡排序、插入排序、选择排序、快速排序、归并排序等。
这些排序方法,可以对于数组和链表这样的线性数据结构排序。
对于哈希表这样的非线性数据结构,如何进行排序呢?下面,我们将介绍如何使用哈希表来实现字典序排序。
1.哈希表实现字典序排序哈希表实现字典序排序,主要有两种方法:一种是使用桶排的思想,另一种是使用STL库函数。
下面,我们将依次讲解。
1.1.桶排思想桶排思想是对数据分治,将数据划分为若干个桶,每个桶存储一定范围的数据。
通常,划分的依据有多种,比如元素的大小、元素的个位数、十位数等。
对于实现字典序排序,我们可以使用元素的首字母作为桶排的依据。
具体实现过程如下:(1)初始化一个哈希表,键是元素的首字母,值是指向一个存储该首字母的所有元素的列表的指针。
(2)遍历待排序的元素列表,将每个元素根据其首字母分别存储在对应的哈希表中。
(3)遍历哈希表,对于每个键值对,将其对应的元素列表按照字典序排序。
(4)遍历哈希表,按照键的字典序输出元素。
下面是代码实现:```struct node {char *s;node *next;};int hash(char *s) {return s[0] - 'a';node *bucket[26];void sort() {for (int i = 0; i < 26; i++) {node *p = bucket[i];while (p) {node *q = p->next;while (q) {if (strcmp(p->s, q->s) > 0) { char *t = p->s;p->s = q->s;q->s = t;}q = q->next;}p = p->next;}}}void output() {for (int i = 0; i < 26; i++) {node *p = bucket[i];while (p) {printf("%s ", p->s);p = p->next;}}printf("\n");}int main() {int n;scanf("%d", &n);for (int i = 0; i < n; i++) {char *s = (char *) malloc(101);scanf("%s", s);int h = hash(s);node *p = (node *) malloc(sizeof(node)); p->s = s;p->next = bucket[h];bucket[h] = p;}sort();output();return 0;}```1.2.STL库函数使用STL库函数是一种更加简单的方法,只需要使用哈希表和vector 即可。
全排列生成算法

全排列的生成算法对于给左的字符集,用有效的方法将所有可能的全排列无重复无遗漏地枚举出来。
字典序法按照字典序求下一个排列的算法广例字符集{1,2,3},较小的数字较先,这样按字典序生成的全排列是:123,132,213,231,312,321o注意一个全排列可看做一个字符串,字符串可有前缀、后缀/生成给泄全排列的下一个排列所谓一个全排列的下一个排列就是这一个排列与下一个排列之间没有其他的排列。
这就要求这一个排列与下一个排列有尽可能长的共同前缀,也即变化限制在尽可能短的后缀上。
广例839647521是1—9的排列。
1—9的排列最前而的是123456789,最后而的是987654321,从右向左扫描若都是增的,就到了987654321,也就没有下一个了。
否则找出第一次出现下降的位置。
算法:由P1P2...Pn生成的下一个排列的算法如下:1求j=max{j| Pj-I<pj}2.求|=max{k| Pi-1<Pk }3.交换Pi-1与PI得到P1P2...PI-1 (P i....Pn ),将红色部分顺序逆转,得到结果.例求839647521的下一个排列1.确定i,从左到右两两比较找出后一个数比前一个大的组合,在这里有39 47,然后i 取这些组中最到的位宜号(不是最大的数)在这两组数中7的位置号最大为6,所以i=62.确立I.找岀在i (包括i)后面的所有比i前面那一位大的数的最大的位置号,在此例中7, 5都满足要求,则选5, 5的位置号为7,所以1=73.先将4和5交换,然后将5后的四位数倒转得到结果8396574213 839651247以上算法是在数论课上老师给岀的关于字典序全排列的生成算法,以前也经常要用到全排列生成算法来生成一个全排列对所有的情况进行测试,每次都是现到网上找一个算法,然后直接copy代码,修改一下和自己的程序兼容就行了,也不看是怎么来的,不是我不想看,实在是说的很抽象,那一大堆公式来吓人,一个实例都不给,更有甚者连算法都没有,只是在那里说,想看都看不懂,也没那个耐心取理解那些人写出来的那种让人无法忍受的解释。
字典序排序规则

字典序排序规则字典序,也称为英文字母顺序,是一种使用字母表进行顺序排列的方式。
它也被称为字母表排序法,其有效性已经被大量应用于信息管理、文件组织和文本处理等领域。
字典序是一种以字母表为基础的排序方式,它可以比较任何一个特定的字符串,并以正确的顺序进行排序。
字典序排序,从简单的角度来说,就是把所有出现的字符按照字母表的顺序排列,并以此排序来确定字母表中字符出现的次序。
字典序排序将字母表按照字母顺序依次排列,由a开始,最后以z结束,顺序如下:a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z。
字典序排序按照字母顺序来排列,字母表中可有大写字母、小写字母、数字以及其他特殊符号。
由于大写字母的键位在小写字母的键位之前,因此大写字母会被首先显示出来,比如“A-Za-z”,这样先被显示出来的字母就是A,而且,比如“0-9A-Za-z”,这样先被显示出来的字母就是0。
字典序排序可以对英文字母及多种字符进行排列,但是只有当所有字符都处于统一的字符集中才能有效地实施这种排序。
比如,如果所有字符都是中文的话,就不能使用字典序排序法。
字典序排序比较的的是字符的拼写顺序,而不是字符的语义意义。
这种排序方式一般使用于一些信息类或文件文本的参考目录,因为这样可以使用字典序比较查找的效率更高,它广泛地应用在数据库和文件管理领域。
字典序排序与其他排序方式所不同的是,它不会重复叠加排序,即便是在一些特定场景下,字典序在短时间内也能达到排序的效果,它也不消耗多余的时间。
字典序排序是利用字母表对字符进行排序的一种方式,它可以有效的节省时间和空间,提高查找效率,被广泛应用于信息管理、文件组织和文本处理等领域。
字典序排序比较简便,相比其他排序方式,它具有较高的效率,应用范围广泛,因此得到了广大用户的认可。
字典序排序规则

字典序排序规则字典序排序规则,也称为字母表排序规则,是指将语文中所有书写单节字(包括汉字和英文字母)按照一定的规则进行排序的一种排序方式。
其中,英文字母按照其所代表的音节从A到Z的顺序进行排列,而汉字按照其在《现代汉语常用字表》中的编号从1到11,035的顺序来排序。
字典序排序规则的由来字典序排序规则也有一定的历史背景:第一个汉字字典,即《说文解字》是由著名汉学家、篆书研究家白求恩在古代经典里发现的,它是中国最早的汉字字典,最早的汉字字典排序规则的基础就是在《说文解字》的基础上进行构建的,当时,按照《说文解字》的排序规则,汉字按照构音节→部首→字形来排列,在实践的过程中受到了很多限制,所以,在20世纪初,英文字典序排序规则出现了。
字典序排序规则的应用字典序排序规则也有广泛应用:例如,在新闻报刊和文学类书籍出版中,经常会用字典序排列文章,不同文章之间的先后顺序便可以很快速、简单地按照字典序列出来;又如,词典、书目及文献的索引等,都会采用字典序排序规则来进行索引查询,以便用户容易、快速地查找某个词条;此外,在编程语言的程序开发中,字典序排序规则也有着广泛的应用,例如,通过字典序排序规则,可以实现文件的快速查找。
字典序排序规则的优点字典序排序规则具有一定的优势:首先,可以满足大多数索引查询的需求;其次,字母表中英文字母的排列是有规律的,而汉字在《现代汉语常用字表》中的编号也是有序的,能够有效地避免汉字书写时的混乱;再次,排序的过程简单易行,可以大大节省排序的时间;最后,字典序排序规则也具有良好的可读性,它能在有限的空间里产生多种排序效果,节约人力和财力。
总结总而言之,字典序排序规则是一种非常有用的排序方式,它受到英文字典序排序规则的启发,通过字母表中英文字母和《现代汉语常用字表》中汉字排列的有序序号,能够有效地缩小排序的范围,满足不同排序需求,具有很强的可读性和可操作性,能够大大节省人力和时间。
排列的字典序问题

int k; for(j=length-2;j>0;) if (list[j-1]>list[j]) j--; else break; k=j-1; //交换位置 for(xb=length-1;xb<=j;xb--) if (list[xb]>list[k]) break;//最小较大数 temp=list[k];list[k]=list[xb];list[xb]=temp;//交换 }
问题描述
❖ n个元素{1,2,…,n}有n!个不同的排 列。将这n!个排列按字典序排列, 并编号为0,1,…,n!-1。每个排列的 编号为其字典序值。当n=3时,6 个不同排列的字典序值如下:
字典序值 0
1
2
3
4
5
排列
123 132 213 231 312 321
编程任务
❖ 给定n以及n个元素{1,2,…,n}的一个排列,计 算出这个排列的字典序值,以及按字典序排 列的下一个排列。
时间复杂性
❖ 本题对某排列的字典序值的时间复杂性为: O(n*(n-1)/2);求下一个排列的时间复杂性 最好情况为O(1),一般情况为:O(nlogn)。
字典序排列
9
7
3. 将a[i]与a[k]互换位置
void exchange(int a[],int i,int k) { int temp; temp=a[i]; a[i]=a[k]; a[k]=temp; a); len = sizeof(a)/sizeof(int); for(m=i+1,n=len-1;m<n;m++,n--) { temp=a[m]; a[m]=a[n]; a[n]=temp; }
1
图1.11是一棵高度为4的树,按从根节点到叶子节点依次向下搜索并 读出边的标号顺序,自左向右,依次为1234,1243,1324,134…,即 1,2,3,4的全排列。
问题:已知一个排列,如何得出下一个排列
2
字典序法算法
求(p)= p1…pj-1 pjpj+1pk-1 pkpk+1…pn的下一个排列:
5
字典序算法实现
1. 找出从右到左第一个小于它右边数的数,返回其数组下标 i1 int search1(int a[]) { int i; for(i=len-1;i>=1;i--) { if(a[i-1]<a[i]) //数组下标从0开始 return i-1; } return -1; }
6
2. 找到 a[i]右边比a[i]大的下标最大的数,返回其数组下标k int search2(int a[],int n) { int k; for(k=len-1;k>n;k--){ if(a[k]>a[n]) return k; } return -1; }
字典树
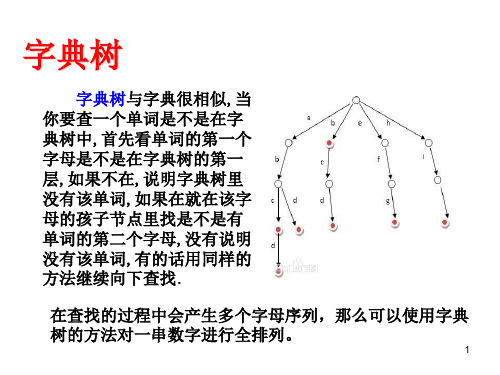
字典树与字典很相似,当 你要查一个单词是不是在字 典树中,首先看单词的第一个 字母是不是在字典树的第一 层,如果不在,说明字典树里 没有该单词,如果在就在该字 母的孩子节点里找是不是有 单词的第二个字母,没有说明 没有该单词,有的话用同样的 方法继续向下查找. 在查找的过程中会产生多个字母序列,那么可以使用字典 树的方法对一串数字进行全排列。
字符串的全排列(字典序排列)

字符串的全排列(字典序排列)题⽬描述输⼊⼀个字符串,打印出该字符串中字符的所有排列。
例如输⼊字符串abc,则输出由字符a、b、c 所能排列出来的所有字符串abc, acb, bac, bca, cab, cba。
题⽬分析穷举与递归⼜是⼀个经典问题,最容易想到的解决⽅法仍然是穷举(我实在是太爱穷举法了,每当被问到算法问题不知道如何解决的时候,总可以祭出穷举⼤旗,从⽽多争取3分钟的思考时间)。
穷举虽好,但它⼤多数情况下都不是被需要的那个答案,是因为看起来代码太Low不够⾼⼤上吗?在这种情况下,穷举法裹着貂⽪⼤⾐的亲戚——递归就出现了。
虽然空间复杂度和时间复杂度没有任何改进,⽽且还增加了系统开销(关于递归法的系统开销不在这⾥讨论,之后再找专门的时间阐述),但是就是因为长得好看(代码看起来精炼),递归的B格⼉就⾼了很多。
递归法对于这个题⽬同样⾮常适⽤,基本思路就是固定⼀个字符,然后对剩余的字符做全排列……不赘述,请⾃⼰想。
如果你也跟我⼀样永远想不明⽩递归,那就画画图,写写代码,debug⼀下,每天花3-4个⼩时,静下⼼来仔细捉摸,总(ye)会(bu)想(hui)明⽩的。
贴⼀段July和他伙伴们在《程序员编程艺术:⾯试和算法⼼得》中的代码实现,供做噩梦时使⽤。
p.s. 我已加了注释/** Permute full array of input string by general recusion* @ char* perm [in/out] The string need to do permutation* @ int from [in] The start position of the string* @ int to [in] The end position of the string*/void CalcAllPermutation(char* perm, int from, int to){if (to <= 1){return;}if (from == to){//all characters has been permutedfor (int i = 0; i <= to; i++)cout << perm[i];cout << endl;}else{// always select one character, then full array the left ones.for (int j = from; j <= to; j++){swap(perm[j], perm[from]); //swap the selected character to the beginning of stringCalcAllPermutation(perm, from + 1, to); // Permute left characters in full array.swap(perm[j], perm[from]); //recovery the string to original one (swap the selected character back to its position.)}}}字典序这是⼀个⽐递归更有趣的答案,不知道算不算经典解法,起码开拓了思路,跟每⼀次接触新鲜的算法⼀样,仍然想了半天的时间,因此照例把思考过程更细致的记录下来(虽然July和他伙伴们在《程序员编程艺术:⾯试和算法⼼得》中已经说了很多),再加上⼀些⼩修改。
字典顺序0比1小

字典顺序0比1小
字典排序是一种对于随机变量形成序列的排序方法。
即按照字母顺序,或者数字小大顺序,由小到大的形成序列。
以问题中提到的序列为例,“ilove”的第一个字母是“i”,“baray”的第一个字母是“b",在字母表中,”i“是排到”b“前面的,所以”ilove“就应该排到”baray“前面。
字母表序列:
A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z。
字典序:在数学中,字典或词典顺序(也称为词汇顺序,字典顺序,字母顺序或词典顺序)是基于字母顺序排列的单词按字母顺序排列的方法。
这种泛化主要在于定义有序完全有序集合(通常称为字母表)的元素的序列(通常称为计算机科学中的单词)的总顺序。
字典序的形式定义:
给定两个偏序集A和B,(a,b)和(a′,b′)属于笛卡尔积A×B,则字典序定义为:(a,b) ≤ (a′,b′) 当且仅当a<a′ 或(a=a′ 且b≤b′)。
结果是偏序。
如果A和B是全序, 那么结果也是全序。
字典序的定义-概述说明以及解释

字典序的定义-概述说明以及解释1.引言1.1 概述字典序是一种排序方法,它基于字母或数字的顺序,按照从左到右的顺序逐个比较字符或数字的大小。
在字典序中,首先比较第一个字符或数字,如果相同,则继续比较第二个字符或数字,以此类推,直到找到不同的字符或数字为止。
根据比较结果来确定其在序列中的位置。
字典序在日常生活中非常常见,我们在查看字典、电话簿、学生名单等时经常会遇到。
它不仅在实际应用中具有很大的作用,而且在计算机科学中也是一个重要的概念。
字典序的应用非常广泛,如字符串排序、搜索引擎排序算法、数据库索引等。
在字符串排序中,我们可以使用字典序将字符串按照字母顺序进行排序,这对于进行字符串的查找和比较非常有帮助。
在搜索引擎中,字典序能够根据搜索关键词的字母顺序将搜索结果进行排序,提高搜索效率。
而数据库索引则可以使用字典序对数据库中的数据进行排序和查找。
本文将重点介绍字典序的定义和应用,通过对字典序的深入了解,可以更好地理解其在实际生活和计算机科学中的重要性和应用价值。
同时,本文还将展望字典序在未来的发展趋势,探讨其在更多领域中的应用前景。
1.2文章结构1.2 文章结构本文将按照以下结构进行叙述:第一部分是引言。
引言主要包括三个部分:概述、文章结构和目的。
在概述中,将简要介绍字典序的概念和重要性。
文章结构部分将对整篇文章的组织结构进行说明,提供读者整体了解文章脉络的导引。
目的部分说明本文撰写的目的,明确了解字典序定义和应用的重要性。
第二部分是正文。
正文包括两个部分:字典序的定义和字典序的应用。
其中,字典序的定义部分将详细解释字典序的含义、定义和特点。
此部分将探讨字典序如何根据字母表的排列顺序进行排序,以及如何应用于不同的情境中。
字典序的应用部分将探讨字典序在实际生活中的各种应用,如字符串排序、排列组合问题等。
将通过实例和案例来说明字典序在不同领域中的实际应用,并探讨其优势和局限性。
第三部分是结论。
结论部分将总结全文的主要观点和观点。
字典序排序规则

字典序排序规则字典序是一种常用的文本排序方法,也叫作字母排序、字符排序或词典顺序,它是指按照字符串中第一个字母的字母表顺序来排序。
它是一种通用的方法,可以用于排序不同语言中的字符串。
字典序排序规则可以分为三个基本概念:字母表顺序,比较原则和大小写规则。
字母表顺序是指排序时按照英文字母的出现次序来排列,如A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z,以及分隔符。
比较原则是按照字符串中每个字符的字母表顺序来比较,比较的结果可以是相等、小于或者大于,这取决于字符串中比较字符的出现次序。
如果比较字符之间出现相等,就比较下一个字符。
这样就能确定字典序排序的位置。
大小写规则是指对于有些排序系统,小写字母比大写字母优先,反之大写字母比小写字母优先。
字典序排序规则可以用于排序各种字符串,包括单词表、英文文章、文件名、文件路径、网址和编程语言中的符号标识符。
它也可以用于查找文本中的某个字符串,例如使用搜索引擎搜索某个关键字时。
字典序排序规则也可以用于排序多种数据类型,如整数、日期和浮点数。
由于字符串和数字可以转换为一个字符串,因此可以将这些数据类型排序成字母序。
这样就可以利用字典序排序规则来比较多种数据类型。
字典序排序规则对于数据库、文件系统和其他应用有很多用处,它可以极大地提高检索准确性,也可以减少搜索所需的时间。
另外,字典序排序规则可以用于排序不可见的数据,这也有助于检索文本中的信息。
字典序排序是一种有用的排序算法,它可以应用于多种情境中,并帮助解决检索的效率问题。
它的好处是简单,易于理解,易于实现,可以应用于排序不同语言的字符串,以及各种数据类型,这些都使它成为一种非常流行的文本排序算法。
排列问题中的字典排序法

字典排序法详解
排列问题中,有一种字典排序法,字典排序法的的规律就是:最右边的数,从右往左,遇到第一个比其小的数时,排列到这个数的前面,原来的数则排在此数后面。
然后最右边的数再从右往左,遇到第一个比其小的数时排列到这个数的前面,剩下的数排列顺序不变。
按此循环,最右边的数遇到第一个比其小的数时,就排列到其前面,剩下的数排列顺序不变,依此类推。
例:如何将排列1 2 3 4 5变成5 4 3 2 1 ?
排列1 2 3 4 5 ,最右边的一个数是5,然后从右往左数,遇到的第一个比5小的数是4,则把5排到4的前面,排列变成了1 2 3 5 4。
此时最右边的数变成了4,从右往左,遇到的第一个比4小的数是3,则把4排到3的前面,剩下的数排列次序不变,于是排列变成了1 2 4 3 5。
如此循环下去,将排列1 2 3 4 5变成5 4 3 2 1则需要进行一下步骤:
12345
12354
12435
12453
13245
13254
13425 13452 21345 21354 21435 21453 23145 23154 23415 23451 23541 24351 24531 32451 32541 34251 34521 35421 43521 45321 54321。
什么是字典序

什么是字典序
字典序:对于数字1、2、3......n的排列,不同排列的先后关系是从左到右逐个比较对应的数字的先后来决定的。
例如对于5个数字的排列 12354和12345,排列12345在前,排列12354在后。
按照这样的规定,5个数字的所有的排列中最前面的是12345,最后面的是54321。
算法说明:
设置了中介数的字典序全排列生成算法,与递归直接模拟法和循环直接模拟法的最大不同是,不需要模拟有序全排列的生成过程,也就不需要逐一地生成各个全排列,只要知道初始全排列,就能根据序号(m-1),直接得到第m个全排列,因此速度非常快。
它的缺点是在生成序号(m-1)的递增进进制数时,需要事先创建一个用来存储n的阶乘数n! 的数组p[],所以n的值不能太大,否则就会溢出,根据我的测试结果,当1<=n<=20时不会溢出,当21<=n 时会溢出。
设置了中介数的字典序全排列生成算法需要设置中介数,在实际应用中比较繁琐,不如由前一个排列直接推得下一个排列方便。
汉字字典的编排方式

汉字字典的编排方式汉字字典有三种方法排列汉字:汉语拼音查字法,部首查字法,难检字查字法。
一、按音序排列汉字《字典》序言之后,就是《汉语拼音字母索引》,拼音按英文字母歌编排,以大写字母断开,依次为ABCDEFG,HlJKLMN,OPQRST,UWXYZ,而大Ⅴ不能单列。
每个大写字母下方,按占位先后排序,每一位仍遵循字母歌先后次序的规律,全部以小写字母写成音节,空些格在该行右方显示一个例字。
每个音节,又按四声顺序在正文处把字目依次排列。
例:以“B”开头的音节表ba bai ban bang bao bei ben beng bi bianBiang biao bie bin bing bobu以上共17个以b开头的音节,音节再从轻声,阴平,阳平,上声到去声排列汉字。
汉字音节与声调相同,又以横竖撇点折的顺序依次排字目。
随手辑十七个例字代表各音节,八白班邦包,北笨绷笔边,()标别濒冰,波不。
又以音节ba为例,罢八拔把霸依次排列。
而粑巴八扒叭五字同音,按笔顺排列为粑扒叭八巴。
二、按部首排列汉字部首先按笔画多少分类,从一画的排列完了,再排列二画的,依次往后推。
而每个部首下方,去掉偏旁部首后,也按笔画从少到多顺序排列,相同笔画按笔顺规则“横竖撇点折”理顺次序。
以“扌”为例,一画扎,二画打扔,三画扛扣扪,……有序编排。
《汉字偏旁部首检字表》里,检测到的汉字这一栏右边页码,则是字典正文页码,与拼音检字表的页码相吻合。
也就是说,字典正文,还是以字母歌为序,依次编排汉字的,音节轻声打头再从一声到四声,同音字遵循笔顺规则编排。
三、难检字有《难检字笔画索引》排列汉字难检字,只提供笔画数即可,笔画数相同,又要按横竖撇点折先后次序查字。
例凹凸,均为6画,凸在前,首笔肩部一横,凹在后,首笔左边一竖。
查到所需捡测字的页码,字典正文规则,同音序查字编排法一致。
排列的字典序问题

排列的字典序问题Problem Descriptionn个元素{1,2,...,n}有n!个不同的排列。
将这n!个排列按字典序排列并编号为0,1,...,n!-1。
每个排列的编号为其字典序值。
例如,当n=3时,6个不同排列的字典序值如下:字典序值012345排列123132213231312321给定n,以及n个元素{1,2,...,n}的⼀个排列,计算出这个排列的字典序值,以及按字典序排列的下⼀个排列。
Input输⼊包括多组数据。
每组数据的第⼀⾏是元素个数n(1<=n<=13),接下来1⾏是n个元素{1,2,...,n}的⼀个排列。
Output对于每组数据,输出两⾏,第⼀⾏是字典序值,第2⾏是字典序排列的下⼀个排列。
Sample Input8 2 6 4 5 8 1 7 3Sample Output82272 6 4 5 83 1 7-----------------------------------------------------------------此处为⽐较,可以掠过不看,直接下拉----------------------------------------------------------------------------------------------------------------------------排列的字典序,此题似乎与之前说过的类似,但是输⼊顺序有区别的。
输⼊123全排列输出:123132213231321312字典序输出:123132213231312321区别在于最后的两⾏,为什么会出现这样的情况呢?是因为在全排列问题时,利⽤的是对原数组进⾏替换。
初始:1 2 3交换[1] [3] ,则变成 3 2 1,再接下来的替换中,就按照 2 1进⾏的。
若想按照字典序输⼊,需要利⽤头尾数组算法。
建⽴两个数组 head,tail初始化head为空,tail 为n个顺序元素。
算法之字典排序法

算法之字典排序法2. 字典序法字典序法就是按照字典排序的思想逐一产生所有排列.设想要得到由1,2,3,4以各种可能次序产生出4!个“单词”. 肯定先排1234, 再排1243, 下来是1324, 1342, …., 4321.分析这种过程, 看如何由一个排列得到下一个排列, 并给出严格的数学描述.例2.3 设有排列(p) =2763541, 按照字典式排序, 它的下一个排列是?(q) =2764135.(1) 2763541 [找最后一个正序35](2) 2763541 [找3后面比3大的最后一个数](3) 2764531 [交换3,4的位置](4) 2764135 [把4后面的531反序排列为135即得到最后的排列(q)]求(p)=p1⋯p i-1p i…p n的下一个排列(q):(1) 求i=max{j⎪ p j-1<p j}(找最后一个正序)(2) 求j=max{k⎪ p i-1<p k}(找最后大于p i-1者)(3) 互换p i-1与p j得p1…p i-2 p j p i p i+1⋯p j-1 p i-1 p j+1…p n(4) 反排p j后面的数得到(q):p1…p i-2 p j p n⋯p j+1p i-1p j-1 ….p i+1 p i例2.4 设S={1,2,3,4}, 用字典序法求出S的全部排列. 解1234, 1243, 1324, 1342, 1423, 1432,2134, 2143, 2314, 2341, 2413, 2431,3124, 3142, 3214, 3241, 3412, 3421,4123, 4132, 4213, 4231, 4312, 4321.字典排序法C++代码:#include<iostream.h>void repailie(int *a,int n,int dp){int *bb=new int[n-dp];int *cc=new int[n-dp];int ti=0;for(int i=dp+1;i<n;i++){bb[ti++]=a[i];}for(int j=0;j<ti;j++){a[j+dp+1]=bb[ti-j-1];}//cout<<a[dp+1]<<" ";//cout<<endl;}int main(void){int n;cout<<"请输入1至无穷大的数"<<endl;cin>>n;int *a=new int[n];int p=1;//n的阶层int q=1;//循环记录int b,c;//最后一对正序int bi,ci;//记录b和c的位置int d;//最后大于b者int di;//记录d的位置for (int o=1;o<=n;o++){p=p*o;//cout<<p<<" ";}for (int i=0;i<n;i++){a[i]=i+1;cout<<a[i]<<" ";}cout<<endl;while(q<p){for(int j=n-1;j>=0;j--){if(a[j-1]<a[j]){b=a[j-1];bi=j-1;c=a[j];ci=j;break;}}//cout<<bi<<" "<<ci<<" "<<endl;for(int k=n-1;k>=0;k--)if (a[k]>b){d=a[k];di=k;break;}}//cout<<di<<endl;for(int l=0;l<n;l++){if(l==di){a[l]=b;//cout<<a[l]<<endl;}if(l==bi){a[l]=d;//cout<<a[l]<<endl;}repailie(a,n,bi);for (int m=0;m<n;m++){cout<<a[m]<<" ";}cout<<endl;++q;}}运行结果图:。
字典序排序规则

字典序排序规则
字典序排序规则是一个重要的技术概念,它广泛应用于计算机程序设计和其他数据处理领域。
字典序排序是一种排序算法,它将字符串按照字母表顺序进行排列。
它通常被用来给字符串、数字或其他类型的数据按字母顺序排序,这是实现简单比较的一种方法。
字典序排序规则的实现主要基于字母表的序列排序,字母表的顺序通常以下面几大条例为基础:
1、按字母的字母表顺序排列:从小写到大写,从A到Z;
2、小写的字母在大写的字母之前;
3、同样的字母,根据拼音或其他支配方法来排列,例如同样是“a”,小写字母a”排在大写字母A”之前;
4、如果字符串中出现相同的字母,根据下一个字母来排序,并且比较它们的字典序。
举例来说,根据字典序排序规则,字符串“abc”、“abd”、“aag”、“aaz”应该按照下面的顺序来排列:
“abc”、“aag”、“abd”、“aaz”。
字典序排序规则的优点在于它的实现简便快捷。
它可以在常数时间复杂度内完成排序,因此可以用来排序大量数据,而且在拼写错误和其他不同分类方法中效果都非常好。
字典序排序也可以用于不同字符串的比较,因此在字符串比较方面效果也很好。
字典序排序是一种常用的字符串排序方法,它已经被广泛应用于排序数据和文件的名称,让查找和访问变得更方便,也可以用于不同
字符串的比较,提高效率。
它的实现简便快捷,而且效率较高,在某些情况下可以节省时间和空间,比如排序大量数据时。
因此,字典序排序规则在计算机程序设计和其他数据处理领域应用非常广泛,是一种重要的技术概念。
字典序排序是什么意思

字典序排序是什么意思
今天老师在课堂上给我们讲了“字典序排序是什么意思”。
哎呀,听起来好像很难懂,老师一开始说得我有点糊里糊涂的。
后来,老师拿出了一个大大的字典,指着上面的词给我们讲解。
老师说,字典序排序其实就是按照字母在字典里出现的顺序来排的。
就像我们翻字典的时候,先看“a”的词,再看“b”的词,接着是“c”的词,依次类推。
哇,原来是这么简单!
我和小伙伴们一起试着把一些词排排看。
比如,“苹果”“香蕉”“西瓜”,我们先把它们写出来,然后就开始按字母顺序排列。
“香蕉”排在前面,因为“b”比“x”小,“西瓜”排在因为“x”排得最靠后。
我觉得这个字典序排序就像玩游戏一样,好玩又有趣!嘿嘿,我现在知道了字典序排序是什么意思啦!下次我自己也能把词语排得整整齐齐的啦!
—— 1 —1 —。
字典序排序规则

字典序排序规则
字典序排序是一种常用的排序方法,它可以用来给一组文字或数字按照英语字母顺序进行排列,以便使读者更容易找到想要的文字或数字。
字典序排序按照字母的编码排序,即A-Z的顺序,排序时,先比较字母的大小,如果字母一样则把字母后面的数字比较,如果数字也一样,则该序列最大。
按照字典序排序规则,所有字母数字按照A-Z的顺序排列,将所有的A放在第一位,Z放在最后一位,如果两个字母一样,则比较字母后面的数字,数字小的放在前面。
另外,如果字符串中混合了汉字和数字,汉字要按照拼音的拼写顺序排列,而数字要按照十进制的顺序排列。
规则中还有特殊符号的处理方法,不同的符号按照符号的Unicode编码大小排序,最后再按照字母的字典序排序规则。
字典序排序规则具有简单易懂、比较方便等特点,得到了广泛的应用,它可以用在文件索引、文件名称、搜索引擎中对字符串排序、书籍目录等场景中,减少不必要的查找时间,提高工作效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目描述:
大家知道,给出正整数n,则1到n这n个数可以构成n!种排列,把这些排列按照从小到大的顺序(字典顺序)列出,如n=3时,列出1 2 3,1 3 2,2 1 3,2 3 1,3 1 2,3 2 1六个排列。
任务描述:
给出某个排列,求出这个排列的下k个排列,如果遇到最后一个排列,则下1排列为第1个排列,即排列1 2 3…n。
比如:n = 3,k=2 给出排列2 3 1,则它的下1个排列为3 1 2,下2个排列为3 2 1,因此答案为3 2 1。
Input
第一行是一个正整数m,表示测试数据的个数,下面是m组测试数据,每组测试数据第一行是2个正整数n( 1 <= n < 1024 )和k(1<=k<=64),第二行有n个正整数,是1,2 … n的一个排列。
Output
对于每组输入数据,输出一行,n个数,中间用空格隔开,表示输入排列的下k个排列。
Sample Input
3
3 1
2 3 1
3 1
3 2 1
10 2
1 2 3 4 5 6 7 8 9 10
Sample Output
3 1 2
1 2 3
1 2 3 4 5 6 7 9 8 10
题意:有一个已知的排列,求这个排列之后的第k个排列。
如果遇到最后一个排列,则下1排列为第1个排列,即排列1 2 3…n。
需要注意的两点:
1,如果用next_permutation()提交,C++过,而G++TLE;
2,即使使用C++提交,scanf(),printf()过,cin,cout TLE。
[cpp]view plaincopy
1.#include <iostream>
2.#include <algorithm>
ing namespace std;
4.
5.int main()
6.{
7.int num[1111];
8.int m,n,k;
9. scanf("%d",&m);
10.while(m--)
11. {
12. scanf("%d%d",&n,&k);
13.for(int i=0;i<n;i++)
14. scanf("%d",&num[i]);
15.while(k--)
16. next_permutation(num,num+n);
17.for(int i=0;i<n;i++)
18. printf("%d ",num[i]);
19. printf("\n");
20. }
21.return 0;
22.}。
