口服特比萘芬联合外用30%冰醋酸治疗甲真菌病的临床疗效观察
2022年河北省秦皇岛市小升初分班考数学模拟试卷及答案解析

2022年河北省秦皇岛市小升初分班考数学模拟试卷一、认真思考,谨慎填空.(每空1分,共12分)1.(2分)比20米多20%,3吨比千克少40%.2.(3分)9÷=0.75=:24=%3.(1分)有10吨煤,第一次用去15,第二次用去15吨,还剩下吨煤.4.(2分)0.75:1化成最简整数比是,比值是.5.(1分)0.5、46%和0.45按从大到小的顺序排列起来应为.6.(2分)用圆规画一个周长为18.84厘米的圆,圆规两脚间的距离应取厘米,所画圆的面积是平方厘米.7.(1分)六(1)班今天出勤48人,有2人因病请假,今天六(1)班学生的缺勤率是.二、仔细推敲,正确判断.(正确的打“√”,错的打“×”).(10分,每题2分)8.(2分)一个数乘以分数的意义与整数乘法的意义不同..(判断对错)9.(2分)甲数和乙数的比是4:5,那么乙数比甲数多25%..(判断对错)10.(2分)因为35=60%,所以35米=60%米.(判断对错)11.(2分)一个数除以分数的商不一定比原数大..(判断对错)12.(2分)加工97个零件全部合格,合格率是97%.(判断对错)三、反复比较,果断选择.(把正确答案的字母填在括号里)(10分,每题2分)13.(2分)周长相等时,()的面积最大.A.圆B.长方形C.正方形14.(2分)把30%的百分号去掉,原来的数就()A.扩大100倍B.缩小100倍C.不变15.(2分)一根绳子分成两段,第一段长37米,第二段占全长的37,()绳子长一些.A.第一段长B.第二段长C.一样长D.无法确定16.(2分)x、y、z是三个非零自然数,且x×65=y×87=z×109,那么x、y、z按照从大到小的顺序排列应是()A.x>y>z B.z>y>x C.y>x>z D.y>z>x 17.(2分)要剪一个面积是12.56cm2的圆形纸片,至少需要面积是()cm2的正方形纸片.A.12.56B.14C.16D.20四、解答题(共1小题,满分12分)18.(12分)解方程x÷18=15×2340%x﹣14=712 3.5﹣40%x=2.7.五、运用知识,解决问题(每小题7分.共30分)19.(7分)一个圆锥体沙堆的底面积是3平方米,高是1.5米.如果每立方米沙的质量是1.8吨,这个沙堆的质量是多少吨?20.(7分)修一条800米长的公路,甲队独修10天完成,乙队独修15天完成.两队同时合修,需要多少天可以修完这条路的56?21.(7分)歌厅有一个圆形表演台,周长43.96米.现在半径加宽1米,比原来的面积增加多少?22.(7分)两个车间共有150人,如果从外地调入50人到第一车间,这时一车间的人数是二车间的23,二车间原来有多少人?23.(7分)修一条公路,甲队修了全长的13,乙队和丙队修路的比是3:5,已知甲队比乙队多修24米,这条公路全长多少米?2022年河北省秦皇岛市小升初分班考数学模拟试卷参考答案与试题解析一、认真思考,谨慎填空.(每空1分,共12分)1.(2分)24米比20米多20%,3吨比5000千克少40%.【解答】解:(1)20×(1+20%)=20×1.2=24(米);(2)3吨=3000千克,3000÷(1﹣40%)=3000÷0.6=5000(千克);答:24米比20米多20%,3吨比5000千克少40%.故答案为:24米,5000.2.(3分)9÷12=0.75=18:24=75%【解答】解:9÷0.75=12;0.75=34=3:4=(3×6):(4×6)=18:24;0.75=(0.75×100)%=75%;故答案为:12,18,75.3.(1分)有10吨煤,第一次用去15,第二次用去15吨,还剩下7.8吨煤.【解答】解:10×(1−15)−15=8﹣0.2=7.8(吨)答:还剩下7.8吨煤.故答案为:7.8.4.(2分)0.75:1化成最简整数比是3:4,比值是34.【解答】解:0.75:1=34:1=(34×4):(1×4)=3:4;0.75:1=34:1=34÷1=34.故答案为:3:4;34.5.(1分)0.5、46%和0.45按从大到小的顺序排列起来应为0.5>46%>0.45.【解答】解:46%=0.46,因为:0.5>0.46>0.45,所以从大到小的顺序排列为:0.5>46%>0.45;故答案为:0.5>46%>0.45.6.(2分)用圆规画一个周长为18.84厘米的圆,圆规两脚间的距离应取3厘米,所画圆的面积是28.26平方厘米.【解答】解:(1)18.84÷3.14÷2,=6÷2,=3(厘米);(2)3.14×32,=3.14×9,=28.26(平方厘米);故答案为:3,28.26.7.(1分)六(1)班今天出勤48人,有2人因病请假,今天六(1)班学生的缺勤率是4%.【解答】解:2÷(48+2)×100%=2÷50×100%=4%;答:今天六(1)班学生的缺勤率是4%.故答案为:4%.二、仔细推敲,正确判断.(正确的打“√”,错的打“×”).(10分,每题2分)8.(2分)一个数乘以分数的意义与整数乘法的意义不同.√.(判断对错)【解答】解:因为一个数乘分数,表示求这个数的几分之几是多少,整数乘法的意义是求几个相同加数和的简便运算,所以一个数乘以分数的意义与整数乘法的意义不同,所以题中说法正确.故答案为:√.9.(2分)甲数和乙数的比是4:5,那么乙数比甲数多25%.√.(判断对错)【解答】解:设甲数是4,那么乙数是5;(5﹣4)÷4=1÷4=25%;答:乙数比甲数多25%.故答案为:√.10.(2分)因为35=60%,所以35米=60%米.×(判断对错)【解答】解:根据百分数的意义可知,百分数不能表示某一具体数量,所以,35米=60%米的表示方法是错误的.故答案为:×.11.(2分)一个数除以分数的商不一定比原数大.√.(判断对错)【解答】解:要从三种情况分析商与被除数的关系:(1)除数大于1,商小于被除数;设这个数是6,除数是32;6÷32=4;4<6;商比原数小;(2)除数小于1,商大于被除数;设这个数是6,除数是236÷2=99>6;商比原数大;(3)除数等于1,商等于被除数;故答案为:√.12.(2分)加工97个零件全部合格,合格率是97%.×(判断对错)【解答】解:9797×100%=100%答:零件的合格率是100%,故答案为:×.三、反复比较,果断选择.(把正确答案的字母填在括号里)(10分,每题2分)13.(2分)周长相等时,()的面积最大.A.圆B.长方形C.正方形【解答】解:周长一定时,正方形面积比长方形面积大.设周长为L,则:周长为L的正方形面积:(14p2=116L2≈0.0625L2;周长为L的圆的面积是π×(2)2=14L2≈0.0796L2;比较可知,面积最大的是圆.故选:A.14.(2分)把30%的百分号去掉,原来的数就()A.扩大100倍B.缩小100倍C.不变【解答】解:30%=0.3,30%→30即0.3→30,相当于小数点向右移动了两位,就表示原来的数扩大了100倍.故选:A.15.(2分)一根绳子分成两段,第一段长37米,第二段占全长的37,()绳子长一些.A.第一段长B.第二段长C.一样长D.无法确定【解答】解:(1−37)=47,47>37;所以第一段比第二段长,故选:A.16.(2分)x、y、z是三个非零自然数,且x×65=y×87=z×109,那么x、y、z按照从大到小的顺序排列应是()A.x>y>z B.z>y>x C.y>x>z D.y>z>x 【解答】解:由x×65=×87,利用比例的基本性质可得:x:y=87:65=(87×35):(65×35)=40:42=20:21,所以x<y,由y×87=z×109,利用比例的基本性质可得:y:z=109:87=(109×63):(87×63)=70:72=35:36,所以y<z,所以x<y<z.故选:B.17.(2分)要剪一个面积是12.56cm2的圆形纸片,至少需要面积是()cm2的正方形纸片.A.12.56B.14C.16D.20【解答】解:设圆的半径为r,则正方形纸张的边长为2r,则r2=12.56÷3.14=4(厘米)正方形的面积:2r×2r=4r2=4×4=16(平方厘米)故选:C.四、解答题(共1小题,满分12分)18.(12分)解方程x÷18=15×2340%x﹣14=7123.5﹣40%x=2.7.【解答】解①x÷18=15×23x÷18×18=15×23×18x=111780③40%x﹣14=71240%x﹣14+14=712+140.4x=7260.4x÷0.4=726÷0.4x=181.5④3.5﹣40%x=2.73.5﹣40%x+0.4x=2.7+0.4x2.7+0.4x=3.52.7+0.4x﹣2.7=3.5﹣2.70.4x=0.80.4x÷0.4=0.8÷0.4x=2五、运用知识,解决问题(每小题7分.共30分)19.(7分)一个圆锥体沙堆的底面积是3平方米,高是1.5米.如果每立方米沙的质量是1.8吨,这个沙堆的质量是多少吨?【解答】解:13×3×1.5×1.8=1.5×1.8=2.7(吨)答:这个沙堆的质量是2.7吨。
浙江省宁波市2024届高三三模考试(理综)物理部分

浙江省宁波市2024届高三三模考试(理综)物理部分一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题关于下列四幅图的说法正确的是( )A.如图甲,若小磁针处于静止状态,则可判定电源右端为正极B.如图乙,若电源左端为正极,则螺线管内部小磁针静止时N极指向左端C.如图丙,将一闭合线圈套住通电螺线管,增大线圈面积,通过线圈的磁通量减少D.如图丁,将一段通电导线放在螺线管内部,导线受到向上的安培力第(2)题某同学找了一个用过的“易拉罐”在靠近底部的侧面打了一个洞,用手指按住洞,向罐中装满水,然后将易拉罐竖直向上抛出,空气阻力不计,则下列说法正确的是( )A.易拉罐上升的过程中,洞中射出的水的速度越来越快B.易拉罐下降的过程中,洞中射出的水的速度越来越快C.易拉罐上升、下降的过程中,洞中射出的水的速度都不变D.易拉罐上升、下降的过程中,水不会从洞中射出第(3)题2021年5月15日7时18分,“天问一号”火星探测器成功着陆于火星乌托邦平原南部预定着陆区,我国首次火星探测任务取得成功。
着陆前曾经在周期为T的椭圆形停泊轨道绕火星运行,此轨道与火星表面的最近距离为d1,最远距离为d2。
已知火星半径为R,则火星表面处自由落体的加速度为( )A.B.C.D.第(4)题如图所示,放置在粗糙水平面上的装置,AB和BC为两段圆弧面,A、C两点切线水平,两圆弧相切于B点,半径分别为2R和3R,对应圆心角均为60°,圆心分别为O1、O2。
一可视为质点的小物块从A滑下,运动过程中速度大小保持不变,小物块始终没有离开圆弧面,装置始终处于静止状态。
下列说法正确的是( )A.小物块在A、C两点所受到的支持力大小相等B.小物块从B运动到C的过程中,地面给装置的摩擦力一直变小C.小物块从A运动到B的过程中(不包含A、B两点),地面给装置的摩擦力方向一直水平向右D.小物块从A运动到B和从B运动到C两个过程中,动量的变化量相同第(5)题2023年9月17日,我国在西昌卫星发射中心使用“长征二号”丁运载火箭,成功将“遥感三十九号”卫星发射升空。
理论力学试题及答案

理论力学试题及答案一、是非题(每题2分。
正确用√,错误用×,填入括号内。
)1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
()2、力对于一点的矩不因力沿其作用线移动而改变。
()3、在自然坐标系中,如果速度υ= 常数,则加速度α= 0。
()4、虚位移是偶想的,极微小的位移,它与时间,主动力以及运动的初始条件无关。
()5、设一质点的质量为m,其速度 与x轴的夹角为α,则其动量在x轴上的投影为mv x =mvcos a。
()二、选择题(每题3分。
请将答案的序号填入划线内。
)1、正立方体的顶角上作用着六个大小相等的力,此力系向任一点简化的结果是。
①主矢等于零,主矩不等于零;②主矢不等于零,主矩也不等于零;③主矢不等于零,主矩等于零;④主矢等于零,主矩也等于零。
2、重P的均质圆柱放在V型槽里,考虑摩擦柱上作用一力偶,其矩为M时(如图),圆柱处于极限平衡状态。
此时按触点处的法向反力N A与N B的关系为。
①N A = N B;②N A > N B;③N A < N B。
3、边长为L 的均质正方形平板,位于铅垂平面内并置于光滑水平面上,如图示,若给平板一微小扰动,使其从图示位置开始倾倒,平板在倾倒过程中,其质心C 点的运动轨迹是。
①半径为L/2的圆弧; ②抛物线; ③椭圆曲线; ④铅垂直线。
4、在图示机构中,杆O 1 A //O 2 B ,杆O 2 C //O 3 D ,且O 1 A = 20cm ,O 2 C = 40cm ,CM = MD = 30cm ,若杆AO 1 以角速度 ω = 3 rad / s 匀速转动,则D 点的速度的大小为cm/s ,M 点的加速度的大小为cm/s 2。
① 60; ②120; ③150; ④360。
5、曲柄OA 以匀角速度转动,当系统运动到图示位置(OA//O 1 B 。
AB |OA )时,有A V B V ,A αB α,ωAB 0,εAB0。
华科理论力学教材(第2版2020年7月第4次印刷)课后习题解答(z2)

1.4.2. 构架整体、AB 部分、弯杆 BC。 P A
B
C
解:2.
1.4.3. 三铰拱整体、AB 部分、BC 部分。 P
F
B
A
C
解:3.
F A
B
F' CBy
FCBy
P
F' CBx
FA
FCBx
FCy
C FCx
目录
1.4.4. A 形构架整体、AB 杆、BC 杆、DE 杆及销钉 B(力 P 作用在销钉 B 上)。
的大小。
FR
F2 60
F1
60
F3
题 2.3 图
目录
解:(1) R F1 F2 F3 上式向 F2 所在方向投影得:
1 2
R
F2
F1
cos
30
∴ R 2F2 2F1
3 100 2173 2
3 200N 2
∴ R 的大小为 200N,指向与假设相反。
( 2 ) Z 0 , ( 设 Z ' 为 F2 的 正 方 向 ) F2 F1 cos 30 0
上的 G 通过三力汇交法得到 O 处的合力为 45 度,则本次作业也认为是正确的
1.4.9.上题中,若销钉 A、C 均与 AC 杆固连,画出 AC 杆受力图。又若销钉 A、B 均与 AB 杆固连,画出 AB 力图。 解:[9.1]若销钉 A、C 均与 AC 杆固连,画出 AC 杆受力图
F
' A
A
F地
题第一步,只要求真解在受力图的可能范围内,通过以后计算可知,销钉 B 对构件 BA 的作
用力为 0,故可假设为任何方向。 1.4.11. 机构整体、连杆 AB、圆盘 O、滑块 B。
30度的正弦值

30度的正弦值
正弦函数,是数学上研究得最深的函数之一,它的概念源于圆周率,它的出现为很多科学算法与工程设计提供了不可重要的数据和有益的分析方法,极大的提升科学技术的进步。
正弦函数是一个双曲线,它的图形集中体现了幅度上的振荡。
它的函数表示为y=asinθ或y=sinθ,即在x轴进行振荡时,y轴上的值应计算出正弦函数的值。
在极坐标系中,函数值也可以经过推导求出.
求30度正弦值,它代表圆上与X轴结合夹角为30度时,该点Y轴坐标位置,在正弦图形中表示为X轴正向移动30度,Y轴对应的正弦值就是0.5,也就是竖直的0.5.
正弦函数的实际应用最常见的便是电磁波的传播规律,也就是大家所熟悉的电视信号和无线电波的传播。
此外,科学家们也发现正弦函数在海水上升和日出日落等自然现象中也有应用,此外还有声学,光学,滤波器,应力对拉伸及旋转,流体传播等多种应用领域。
由此可见,正弦函数的研究对于科学技术的发展极为重要,它不仅影响着日常生活,而且也潜移默化地影响着科学的进步,因此让人们更体会到正弦函数的神奇与奥妙.。
高中数学—线性变换与二阶矩阵

绕原点 O 按逆时针旋转 270 和按顺时针旋转 90 的
坐标变换公式以及对应的二阶矩阵. 看看它们有什么
关系?
旋转角为 270 时,
坐标变换公式:
二阶矩阵:
x y
= =
x cos 270 x sin 270 +
ysin ycos
270, 270.
01 -1 0
x y
= =
y, - x.
(二) 变换、矩阵的相等
2. 怎样根据条件求上述变换的变换公式?
2. 反射变换
一般地, 我们把平面上的任意一点 P 对应到它关 于直线 l 的对称点 P 的线性变换叫做关于直线 l 的反 射.
如点 P(x, y) 关于 x 轴的反射 P(x, y), 其反射变
换公式为 x=x,
y P(x, y)
y= -y.
与之对应的二阶矩阵是
-1 0
0 1
.
O
x
练习(补充). 请写出在直角坐标系 xOy 内, 任一 点 P(x, y) 关于直线 x+y=0 的反射变换公式及对应的
【课时小结】
5. 线性变换对应的矩阵
线性变换
x y
= =
ax + by, cx + dy.
对应的矩阵为二阶矩阵
ab c d.
旋转变换
x y
= =
xcosa xsina +
ysina ycosa
, .
对应的矩阵为
cosa sina
-sina cosa
.
(第二课时)
第一课时 第二课时
1. 反射变换、伸缩变换、投影变换、切 变变换分别是怎样的变换?
例3. 设 A= 1 y
人教版数学七年级上册第一章1.2.3相反数课件

拓展提升
5
2.当+5前面有2021个正号时,化简的结果为_________;
-5
当+5前面有2021个负号时,化简的结果为_________;
当+5前面有2022个负号时,化简的结果为_________。
5
多重复号的化简只需要考虑负号的个数,而不必考虑
正号的个数,当负号个数为偶数时,最后符号为正,
绝对值等于它的相反数的数是0或负数;
绝对值最小的数是0 .
下节课
课堂小结
定义
相反数
求法
在原数前面加负号
多重符号的化简
拓展提升
1.若-[-(-x)]=8,则x的相反数是
8
.
解析:因为-[-(-x)]=8,
所以x=-8,
所以x的相反数是8.
当“-”号的个数是偶数时,化简的结果为正数;
当“-”号的个数是奇数时,化简的结果为负数.
-5
-a
-1
0
1
a
5
相反数的几何意义
在数轴上位于原点两侧且到原点的距离相等的两个点
所表示的数互为相反数.
注意:(1)数轴上表示互为相反数的两个点
到原点的距离相等;
(2)数轴上与原点的距离是a(a为正数)的点
有两个,分别在原点的左右两侧,它们表
示的数互为相反数.
设a是一个正数,数轴上与原点的距离等于a(a为正数)
1)上述各对数之间有什么特点?
2)请写出一组具有上述特点的数。
3)你能得出相反数的概念吗?
4)表示各对数的点在数轴上有什么位置关系?
新知:只有符号不同的两个数互为相反数. 特别地,
0的相反数是0.
除了符号不同之外,其他部分完
普通话水平测试用普通话词语表表一常用字
chǎn
产地
chǎndì
产量
chǎnliàng
456-460
产品
chǎnpǐn
产生
chǎnshēng
产物
chǎnwù
产业
chǎnyè
产值
chǎnzhí
461-465
阐明
chǎnmíng
阐述
chǎnshù
颤抖
chàndǒu
长
cháng
长城
chángchéng
466-470
长处
cháng?chù
长度
chángdù
潮
cháo
潮流
cháoliú
序号
字词
拼音
字词
拼音
字词
拼音
字词
拼音
字词
拼音
501-505
潮湿
cháoshī
吵
chǎo
炒Hale Waihona Puke chǎo车chē
车间
chējiān
506-510
车辆
chēliàng
车厢
chēxiāng
车站
chēzhàn
车子
chēzi
扯
chě
511-515
彻底
chèdǐ
撤
chè
撤销
chèxiāo
臣
bùguāng
不过
bùguò
不合
bùhé
不及
bùjí
326-330
不禁
bùjīn
不仅
bùjǐn
不久
bùjiǔ
不堪
bùkān
不可
bùkě
331-335
不快
bùkuài
与y轴夹角为30度的直线解析式

与y轴夹角为30度的直线解析式直线是几何学中的基本概念,它是由无数个点组成的,这些点在平面上连成一条直线。
直线可以通过解析式来描述,其中包括斜率和截距等信息。
本文将探讨与y轴夹角为30度的直线的解析式,并对直线的性质和特点进行分析。
与y轴夹角为30度的直线可以表示为y = kx + b,其中k为直线的斜率,b为直线在y轴上的截距。
我们知道,斜率k等于直线上任意两点的纵坐标差与横坐标差的比值。
由于与y轴夹角为30度的直线是倾斜的,斜率k必定是一个非零的实数。
我们假设直线过点A(x1, y1)和点B(x2, y2),其中点A在直线上方,点B在直线下方。
根据斜率的定义,我们可以得到:k = (y2 - y1) / (x2 - x1)由于与y轴夹角为30度的直线是倾斜的,斜率k不等于零。
假设直线与y轴的交点为点C(0, b),其中b为直线在y轴上的截距。
根据直线的定义,我们可以得到:b = y - kx将点C的坐标代入上式,得到:b = y - k * 0b = y因此,与y轴夹角为30度的直线的解析式可以简化为:y = kx + b其中k为斜率,b为截距。
接下来,我们将分析与y轴夹角为30度的直线的性质和特点。
首先,由于斜率k不等于零,直线不是水平线。
其次,由于直线与y 轴夹角为30度,直线的斜率k是一个非零实数,因此直线不是垂直线。
此外,直线与x轴的夹角为60度,因此直线的斜率是正的。
最后,直线的截距b可以是任意实数。
与y轴夹角为30度的直线在平面坐标系中的图像如下所示:||||\| \| \| \| \| \|_____\_______x轴 y轴可以看到,与y轴夹角为30度的直线在平面上是一条斜向上的直线。
当斜率k为正时,直线从左下方向右上方倾斜;当斜率k为负时,直线从左上方向右下方倾斜。
直线在平面上的位置和倾斜程度由斜率k和截距b决定。
总结起来,与y轴夹角为30度的直线的解析式为y = kx + b,其中k为斜率,b为截距。
部编数学八年级上册专题21轴对称之将军饮马基础篇(解析版)含答案

专题21 轴对称之将军饮马基础篇1.如图,30AOB Ð=°,M ,N 分别是边,OA OB 上的定点,P ,Q 分别是边,OB OA 上的动点,记,OPM OQN a b Ð=Ð=,当MP PQ QN ++的值最小时,关于a ,b 的数量关系正确的是( )A .60b a -=°B .210b a +=°C .230b a -=°D .2240b a +=°【答案】B【解析】【分析】如图,作M 关于OB 的对称点M′,N 关于OA 的对称点N′,连接M′N′交OA 于Q ,交OB 于P ,则MP+PQ+QN 最小易知∠OPM=∠OPM′=∠NPQ ,∠OQP=∠AQN′=∠AQN ,KD ∠OQN=180°-30°-∠ONQ ,∠OPM=∠NPQ=30°+∠OQP ,∠OQP=∠AQN=30°+∠ONQ ,由此即可解决问题.【详解】如图,作M 关于OB 的对称点M ¢,N 关于OA 的对称点N ¢,连接M N ¢¢交OA 于Q ,交OB 于P ,则此时MP PQ QN ++的值最小.易知¢Ð=Ð=ÐOPM OPM NPQ ,¢Ð=Ð=ÐOQP AQN AQN .∵18030Ð=°-°-ÐOQN ONQ ,30Ð=Ð=°+ÐOPM NPQ OQP 30Ð=Ð=°+ÐOQP AQN ONQ ,∴303018030210+=°+°+Ð+°-°-Ð=°ONQ ONQ a b .故选:B.【点睛】本题考查轴对称-最短问题、三角形的内角和定理.三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.2.如图,△ABC 是等腰三角形,底边BC 的长为4,面积是18,腰AC 的垂直平分线EF 分别交AC ,AB 于点E ,F .若点D 为BC 边的中点,点M 为线段EF 上一动点,则△CDM 周长的最小值是( )A .11B .13C .9D .8【答案】A【解析】【分析】连接AD ,由于△ABC 是等腰三角形,点D 是BC 边的中点,故AD ⊥BC ,再根据三角形的面积公式求出AD 的长,再再根据EF 是线段AC 的垂直平分线可知,点C 关于直线EF 的对称点为点A ,故AD 的长为CM +MD 的最小值,由此即可得出结论.【详解】解:连接AD ,∵△ABC 是等腰三角形,点D 是BC 边的中点,∴AD ⊥BC ,∴1141822ABC S BC AD AD =×=´´=V ,解得AD =9,∵EF 是线段AC 的垂直平分线,∴点C 关于直线EF 的对称点为点A ,∴CM =AM ,∴CD +CM +DM =CD +AM +DM ,∵AM +DM ≥AD ,∴AD 的长为CM +MD 的最小值,∴△CDM 的周长最短=(CM +MD )+CD =AD +12BC =9+12×4=9+2=11.故选:A .【点睛】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.3.如图,25AOB Ð=°,点M ,N 分别是边OA ,OB 上的定点,点P ,Q 分别是边OB ,OA 上的动点,记MPQ a Ð=,PQN b Ð=,当MP PQ QN ++的值最小时,b a -的大小=__________(度).【答案】50【解析】【分析】作M 关于OB 的对称点M ¢,N 关于OA 的对称点N ¢,连接M N ¢¢,交OB 于点P ,交OA 于点Q ,连接MP ,QN ,可知此时MP PQ QN ++最小,此时OPM OPM NPQ OQP AQN AQN ¢¢Ð=Ð=ÐÐ=Ð=Ð,,再根据三角形外角的性质和平角的定义即可得出结论.【详解】作M 关于OB 的对称点M ¢,N 关于OA 的对称点N ¢,连接M N ¢¢,交OB 于点P ,交OA 于点Q ,连接MP ,QN ,如图所示.根据两点之间,线段最短,可知此时MP PQ QN ++最小,即MP PQ QN M N ¢¢++=,∴OPM OPM NPQ OQP AQN AQN ¢¢Ð=Ð=ÐÐ=Ð=Ð,,∵MPQ PQN a b Ð=Ð=,,∴11(180)(180)22QPN OQP a b Ð=°-Ð=°-,,∵QPN AOB OQP Ð=Ð+Ð,25AOB Ð=°,∴11(180)25(180)22a b °-=°+°- ,∴50b a -=° .故答案为:50.【点睛】本题考查轴对称-最短问题、三角形内角和,三角形外角的性质等知识,灵活运用所学知识解决问题是解题的关键,综合性较强.4.如图,点P 是AOB Ð内任意一点,3cm OP =,点M 和点N 分别是射线OA 和射线OB 上的动点,30AOB Ð=°,则PMN V 周长的最小值是______.【答案】3【解析】【分析】根据“将军饮马”模型将最短路径问题转化为所学知识“两点之间线段最短”可找到PMN V 周长的最小的位置,作出图示,充分利用对称性以及30AOB Ð=°,对线段长度进行等量转化即可.【详解】解:如图所示,过点P 分别作P 点关于OB 、OA 边的对称点P ¢、P ¢¢,连接PP ¢¢、PP ¢、P P ¢¢¢、OP ¢、OP ¢¢,其中P P ¢¢¢分别交OB 、OA 于点N 、M ,根据“两点之间线段最短”可知,此时点M 、N 的位置是使得PMN V 周长的最小的位置.由对称性可知:,PN P N PM P M ¢¢¢==,,P OB POB POA P OA¢¢¢Ð=ÐÐ=Ð 3OP OP OP ¢¢¢===,30POA POB AOB Ð+Ð=Ð=°Q 30P OA P OB ¢¢¢\Ð+Ð=°+=60POA POB P OA P OB P OP ¢¢¢¢¢¢\Ð+ÐÐ+ÐÐ=°P OP ¢¢¢\△为等边三角形=3P P OP OP ¢¢¢¢¢¢\==\PMN V 的周长=PN PM MN ++=P N P M MN P P ¢¢¢¢¢¢++==3故答案为:3【点睛】本题是典型的的最短路径问题,考查了最短路径中的“将军饮马”模型,能够熟练利用其原理“两点之间线段最短”作出最短路径示意图是解决本题的关键.5.如图,ABC V 是等边三角形,AD 是BC 边上的高,E 是AC 的中点,P 是AD 上的一个动点,当PCE V 的周长最小时,ACP Ð的度数为______.【答案】30°##30度【解析】【分析】连接BP,由等边三角形的性质可知AD为BC的垂直平分线,即得出BP=CP,由此可知要使△PCE 的周长最小,即P点为BE与AD的交点时.最后根据等边三角形三线合一的性质,即得出CP平分ACBÐ,从而可求出1==302ACP ACBÐа.【详解】如图连接BP.∵ABCV为等边三角形,∴AD为BC的垂直平分线,∴BP=CP,∵△PCE的周长=PE+CP+CE= PE+BP+CE,∴当PE+BP最小时,△PCE的周长最小,∵PE+BP最小时为BE的长,即此时BE与AD的交点为P,如图.又∵点E为中点,AD为高,ABCV为等边三角形,∴P点即为等边ABCV角平分线的交点,∴CP平分ACBÐ,∴1==302ACP ACBÐа.故答案为:30°【点睛】本题考查等边三角形的性质,线段垂直平分线的判定和性质,两点之间线段最短等知识.理解要使△PCE的周长最小,即P点为BE与AD的交点是解题关键.6.如图,在四边形ABCD中,∠BCD=50°,∠B=∠D=90°,在BC、CD上分别取一点M、N,使△AMN的周长最小,则∠MAN=_____°.【答案】80【解析】【分析】作点A关于BC、CD的对称点A1、A2,根据轴对称确定最短路线问题,连接A1、A2分别交BC、DC于点M、N,利用三角形的内角和定理列式求出∠A1+∠A2,再根据轴对称的性质和角的和差关系即可得∠MAN.【详解】如图,作点A关于BC、CD的对称点A1、A2,连接A1、A2分别交BC、DC于点M、N,连接AM、AN,则此时△AMN的周长最小,∵∠BCD=50°,∠B=∠D=90°,∴∠BAD=360°﹣90°﹣90°﹣50°=130°,∴∠A1+∠A2=180°﹣130°=50°,∵点A关于BC、CD的对称点为A1、A2,∴NA=NA2,MA=MA1,∴∠A2=∠NAD,∠A1=∠MAB,∴∠NAD+∠MAB=∠A1+∠A2=50°,∴∠MAN=∠BAD﹣(∠NAD+∠MAB)=130°﹣50°=80°,故答案为:80.【点睛】本题考查了轴对称的最短路径问题,利用轴对称将三角形周长问题转化为两点间线段最短问题是解决本题的关键.7.如图,在锐角△ABC中,∠BAC = 40°,∠BAC的平分线交BC于点D,M,N分别是AD和AB 上的动点,当BM +MN有最小值时,ABMÐ=_____________°.【答案】50【解析】【分析】在AC上截取AE=AN,可证△AME≌△AMN,当BM +MN有最小值时,则BE是点B到直线AC的距离即BE⊥AC,代入度数即可求∠ABM的值;【详解】如图,在AC上截取AE=AN,连接BE,∵∠BAC 的平分线交BC 于点D ,∴∠EAM =∠NAM ,∵AM =AM ,∴△AME ≌△AMN ,∴ME =MN ,∴BM +MN =BM +ME ≥BE .∵BM +MN 有最小值.当BE 是点B 到直线AC 的距离时,BE ⊥AC ,∴∠ABM =90°-∠BAC =90°-40°=50°;故答案为:50.【点睛】本题考查的是轴对称-最短路线问题,通过最短路线求出角度;解答此类问题时要从已知条件结合图形认真思考,通过角平分线性质,垂线段最短,确定线段和的最短路线,代入即可求出度数.8.如图,直线1l ,2l 交于点O ,点P 关于1l ,2l 的对称点分别为1P ,2P .若4OP =,127PP =,则12POP △的周长是______.【答案】15【解析】【分析】根据对称的性质可知,OP 1=OP =OP 2=3,再根据P 1P 2=7即可求出△P 1OP 2的周长.【详解】∵P 关于l 1、l 2的对称点分别为P 1、P 2,∴OP 1=OP =OP 2=4,∵P 1P 2=7,∴△P 1OP 2的周长=OP 1+OP 2+P 1P 2=4+4+7=15.故答案为15【点睛】本题考查的是轴对称的性质,熟知轴对称的性质是解答此题的关键.9.如图,等腰三角形ABC 的面积是18,底边BC 长为4,腰AC 的垂直平分线EF 分别交AC ,AB 于点E ,F .若D 为BC 的中点,G 为线段EF 上一动点,则CDG V 周长的最小值为___________.【答案】11【解析】【分析】连接AD ,由于ABC D 是等腰三角形,点D 是BC 边的中点,故AD BC ^,再根据三角形的面积公式求出AD 的长,再再根据EF 是线段AC 的垂直平分线可知,点C 关于直线EF 的对称点为点A ,故AD 的长为CM MD +的最小值,由此即可得出结论.【详解】解:连接AD ,△ABC 是等腰三角形,点D 是BC 边的中点,AD BC \^,∴S △ABC =1141822BC AD AD ×=´´= ,解得9AD =,EF 是线段AC 的垂直平分线,\点C 关于直线EF 的对称点为点A ,CM AM\=,CD CM DM CD AM DM\++=++,AM+DM≥AD,AD\的长为CM MD+的最小值,CDM\D的周长最短11()94921122CM MD CD AD BC=++=+=+´=+=.故答案为11.【点睛】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.三、解答题10.问题:如图①,要在一条笔直的路边l上建一个燃气站,向l同侧的A、B两个城镇分别铺设管道输送燃气.试确定燃气站的位置,使铺设管道的路线最短.(1)如图②,作出点A关于l的对称点A',线段A'B与直线l的交点C的位置即为所求,即在点C 处建燃气站,所得路线ACB是最短的.为了证明点C的位置即为所求,不妨在直线l上另外任取一点C',连接AC'、BC',证明AC+CB<AC'+C'B.请完成这个证明.(2)如图③,点P为∠MON内的一个定点,在OM上有一点A,ON上有一点B.请你作出点A 和点B的位置,使得△PAB的周长最小.(保留作图痕迹,不写作法)在上述条件下,若∠MON=40°,则∠APB=°.【答案】(1)证明见解析;(2)作图见解析,100【解析】【分析】(1)如图②,连接A C ¢¢,由轴对称的性质可得,,AC A C AC A C ¢¢¢¢== 再证明:,A B AC BC ¢=+ 再利用三角形的三边关系可得结论;(2)分别作点P 关于,OM ON 的对称点,,P P ¢¢¢ 连接P P ¢¢¢交OM 于,A 交ON 于,B 则PAB △的周长最短,再由轴对称的性质可得:,,OPB OP B OPA OP A ¢¢¢V V V V ≌≌ 证明,APB OP B OP A ¢¢¢Ð=Ð+Ð 80,P OP ¢¢¢Ð=° 再求解50,OP P OP P ¢¢¢¢¢¢Ð=Ð=° 从而可得答案.【详解】证明:(1)如图②,连接A C ¢¢,∵点A ,点A ¢关于l 对称,点C 在l 上,∴CA CA ¢=,∴AC BC A C BC A B ¢¢+=+=,同理可得:AC C B A C BC ¢¢¢¢¢+=+,∵A B ¢<A C C B ¢¢¢+,∴AC +BC <AC C B ¢¢+;(2)如图所示,点A 、B 即为所求,由轴对称的性质可得:,,OPB OP B OPA OP A ¢¢¢V V V V ≌≌,,,,PO P O PO P O OPB OP B OPA OP A ¢¢¢¢¢¢\==Ð=ÐÐ=Ð,,POB P OB POA P OA ¢¢¢Ð=ÐÐ=Ð,APB OPB OPA OP B OP A ¢¢¢\Ð=Ð+Ð=Ð+Ð40,POB POA P OB P OA ¢¢¢Ð+Ð=Ð+Ð=°404080,P OP ¢¢¢\Ð=°+°=°,OP OP ¢¢¢=Q()11808050,2OP P OP P ¢¢¢¢¢¢\Ð=Ð=°-°=° 100,APB OP P OP P ¢¢¢¢¢¢\Ð=Ð+Ð=°故答案为:100°.【点睛】本题考查的是轴对称的作图,利用轴对称的性质求解线段和或周长的最小值,同时考查线段的垂直平分线的性质,等腰三角形的性质,掌握以上知识是解题的关键.11.如图,在平面直角坐标系中,已知点(2,5)A ,(2,1)B ,(6,1)C .(1)画出ABC V 关于y 轴对称的111A B C △;(2)在x 轴上找一点P ,使PB PC +的值最小(保留作图痕迹),并写出点P 的坐标.【答案】(1)见解析;(2)见解析,P 的坐标为(4,0).【解析】【分析】(1)根据轴对称的性质结合坐标系,分别确定点A 、B 、C 关于y 轴的对称点A 1、B 1、C 1,即可作出111A B C △;(2)作出点B 关于x 轴的对称点B 2,连接B 2C ,交x 轴于P ,点P 即为所求做的点.(1)解:解:(1)如图所示,111A B C △即为ABC V 关于y 轴对称的三角形.(2)解:如图所示,点P 即为所求做的点,点P 的坐标为(4,0).【点睛】本题考查了平面直角坐标系中的轴对称图形,将军饮马问题,熟知轴对称的性质是解题关键,注意坐标系中两个点关于x 轴对称,则横坐标不变,纵坐标互为相反数,两个点关于y 轴对称,则横坐标互为相反数,纵坐标不变.12.如图,在锐角∠AOB的内部有一点P,试在∠AOB的两边上各取一点M,N,使得△PMN的周长最小.(保留作图痕迹)【答案】见详解【解析】【分析】作点P关于直线OA的对称点E,点P关于直线OB的对称点F,连接EF交OA于M,交OB于N,连接PM,N,△PMN即为所求求作三角形.【详解】解:如图,作点P关于直线OA的对称点E,点P关于直线OB的对称点F,连接EF交OA于M,交OB于N,连接PM,PN,△PMN即为所求作三角形.理由:由轴对称的性质得MP=ME,NP=NF,∴△PMN的周长=PM+MN+PN=EM+MN+NF=EF,根据两点之间线段最短,可知此时△PP1P2的周长最短.【点睛】本题考查轴对称﹣最短问题、两点之间线段最短等知识,解题的关键是学会利用对称解决最短问题,属于中考常考题型.13.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=2,以BC为边向左作等边△BCE,点D 为AB 中点,连接CD ,点P 、Q 分别为CE 、CD 上的动点.(1)求证:△ADC 为等边三角形;(2)求PD +PQ +QE 的最小值.【答案】(1)证明见解析;(2)4.【解析】【分析】(1)先根据直角三角形的性质可得60,BAC AD CD Ð=°=,再根据等边三角形的判定即可得证;(2)连接,PA QB ,先根据等边三角形的性质可得12ACE ACD Ð=Ð,再根据等腰三角形的三线合一可得CE 垂直平分AD ,然后根据线段垂直平分线的性质可得PA PD =,同样的方法可得QB QE =,从而可得PD PQ QE PA PQ QB ++=++,最后根据两点之间线段最短即可得出答案.【详解】证明:(1)Q 在Rt ABC V 中,90,30,2ACB ABC AC Ð=°Ð=°=,60,24BAC AB AC Ð\=°==,Q 点D 是Rt ABC V 斜边AB 的中点,2AD AC \==,ADC \V 是等边三角形;(2)如图,连接,PA QB ,BCE QV 和ADC V 都是等边三角形,60BCE \Ð=°,60ACD Ð=°,1302ACE ACB BCE ACD \Ð=Ð-Ð=°=Ð,CE \垂直平分AD ,PA PD \=,同理可得:CD 垂直平分BE ,QB QE \=,PD PQ QE PA PQ QB \++=++,由两点之间线段最短可知,当点,,,A P Q B 共线时,PA PQ QB ++取得最小值AB ,故PD PQ QE ++的最小值为4.【点睛】本题考查了等边三角形的判定与性质、含30°角的直角三角形的性质等知识点,熟练掌握等边三角形的性质是解题关键.14.如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点ABC V (即三角形的顶点都在格点上).(1)在图中作出ABC V 关于y 轴对称的111A B C △,并写出点1C 的坐标.(2)在y 轴上求作一点P ,使得PA PC +最短(保留作图痕迹,不需写出作图过程).(3)求ABC V 的面积.【答案】(1)画图见解析;()11,4C (2)画图见解析(3)6【解析】【分析】(1)利用网格,根据轴对称的性质画出点A 、B 、C 关于y 轴的对称点A 1、B 1,C 1,再连接A 1B 1,A 1C 1,B 1C 1即可;(2)连接A 1C 交y 轴于点P ,即可;(3)利用网格,用矩形面积减去三个直角三角形面积求解即可.(1)解:如图所示,111A B C △就是所要求画的.()11,4C .(2)解:如图所示,点P 就是所要求作的点.(3)解:111353322156222ABC S =´-´´-´´-´´=△.【点睛】本题考查利用轴对称性质作轴对称图形,利用轴对称求最短路径问题,熟练掌握轴对称的性质是解题的关键.15.如图所示的方格纸中,每个小方格的边长都是1,点A (-4,1)、B (-3,3)、C (-1,2).(1)请作出△ABC向右平移5个单位长度,下移4个单位长度后的△A₁B₁C₁;(2)作△ABC关于y轴对称的△A₂B₂C₂;(3)在x轴上求作点N,使△NBC的周长最小(保留作图痕迹).【答案】(1)答案见详解;(2)答案见详解;(3)答案见详解;【解析】【分析】(1)分别作出点A,B,C向右平移5个单位长度,下移4个单位长度后的对应点A₁,B₁,C₁再顺次连接A₁B₁C1;(2)分别作出点A,B,C关于y轴的对称点,再首尾顺次连接可得;(3)作点B关于x轴的对称点B3,再连接B3C交y轴于点N,顺次连接点NB,NC,即可;(1)如图所示:分别作出点A,B,C向右平移5个单位长度,下移4个单位长度后的对应点A₁,B₁,C₁再顺次连接A₁B₁C1;(2)如图所示:分别作出点A,B,C关于y轴的对称点A2,B2,C2,再首尾顺次连接可得;(3)作点B关于x轴的对称点B3,再连接B3C交y轴于点N,顺次连接点NB,NC,△NBC的周长最小;【点睛】本题主要考查作图-轴对称变换,图形的平移,解题的关键是熟练掌握轴对称变换的定义和性质及最短路线问题.。
浙江省精诚联盟2024-2025学年高二上学期10月月考数学试题含答案

2024学年第一学期浙江省精诚联盟10月联考高二年级数学学科试题(答案在最后)考生须知:1.本卷共4页满分150分,考试时间120分钟.2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.3.所有答案必须写在答题纸上,写在试卷上无效.4.考试结束后,只需上交答题纸.选择题部分一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.1.直线:30l y ++=的倾斜角α为()A.30︒B.60︒C.120︒D.150︒【答案】C 【解析】【分析】先求得直线的斜率,从而求得对应的倾斜角.【详解】由于直线:30l y ++=的倾斜角为α,则直线的斜率tan α=,再由0180α︒≤<︒,可得120α=︒.故选:C2.已知()1,2,2a = ,()3,,3b λ=- ,且()a a b ⊥-,则λ的值为()A.3B.4C.5D.6【答案】A 【解析】【分析】利用向量减法的坐标运算求出()4,2,1a b λ--=- ,再根据()a a b ⊥-得出数量积等于零,建立等式求解.【详解】()4,2,1a b λ---=,()a ab ⊥- ,()()()422210a a b λ∴⋅-=+⨯-+⨯-=,解得:3λ=,故选:A .3.直线1l :10x y +-=与直线2l :2250x y +-=的距离是()A.2B.4C.D.【答案】B 【解析】【分析】利用平行线间的距离公式可直接求解.【详解】设1:102220l x y x y +-=⇒+-=与2:2250l x y +-=的距离为d ,则4d ==.故选:B .4.已知空间向量()1,2,3AB = ,()2,1,1AC =-- ,()9,2,AD x =-,若,,,A B C D 四点共面,则实数x的值为()A.1-B.0C.32D.2【答案】A 【解析】【分析】利用空间向量共面定理得到关于,,x λμ的方程组,解之即可得解.【详解】因为,,,A B C D 四点共面,所以向量,,AB AC AD 共面,即存在实数,λμ使得AD AB AC λμ=+,又()1,2,3AB = ,()2,1,1AC =-- ,()9,2,AD x =-,所以(9,2,)(1,2,3)(2,1,1)x λμ-=+--,所以92223x λμλμλμ=+⎧⎪-=-⎨⎪=-⎩,解得141x λμ=⎧⎪=⎨⎪=-⎩,则1x =-.故选:A.5.已知点()0,2P 关于直线10x y -+=对称的点Q 在圆C :2220x y x m +++=外,则实数m 的取值范围是()A.4m >-B.1m <C.41m -<<D.4m <-或1m >【答案】C 【解析】【分析】设(),Q a b ,利用点关于线对称列方程求得Q 坐标,代入圆方程得出不等式计算即可.【详解】设点()0,2P 关于直线10x y -+=对称的点(),Q a b ,则210021022b a a b -⎧=-⎪⎪-⎨++⎪-+=⎪⎩,解得1,1a b ==.因为()1,1Q 在C 外,所以1120m +++>,可得4m >-且2220x y x m +++=表示圆可得4040m +->,即得1m <综上可得41m -<<.故选:C.6.已知点A 坐标为(1,1,2),直线l 经过原点且与向量()1,2,2α=平行,则点A 到直线l 的距离为()A.73B.136C.3D.76【答案】C 【解析】【分析】利用空间向量垂直,以及两点间的距离公式即可得到结论.【详解】由题意得(1,1,2)OA = ,直线l 的一个方向向量为()1,2,2α=,所以,点A 到直线l的距离为:sin ,d OA OA α==,OA ==53=.故选:C .7.已知)A,()0,1B -,直线l:2230ax y --=上存在点P ,满足2PA PB +=,则l 的倾斜角的取值范围是()A.π2π,33⎡⎤⎢⎥⎣⎦B.π5π0,,π36⎡⎤⎡⎫⎪⎢⎥⎢⎣⎦⎣⎭ C.π5π,36⎡⎤⎢⎥⎣⎦ D.πππ5π,,3226⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦【答案】D【解析】【分析】找到动直线的定点,由动直线与线段有,结合图形判断出倾斜角的范围.【详解】将)A代入2230ax y --=得a =将()0,1B -代入2230ax y ---=得a =,所以A ,B 不在直线l 上,又∵2AB =,2PA PB +=所以点P 在线段AB 上,直线AB 的方程为:0x =,直线l 过定点33,22M ⎛⎫- ⎪ ⎪⎝⎭且斜率k a =一定存在,故由数形结合可知:AM k k ≥=或3BM k k ≤=-故倾斜角5,,3226ππππα⎡⎫⎛⎤∈⋃⎪ ⎢⎥⎣⎭⎝⎦,故选:D8.正三角形ABC 边长为2,D 为BC 的中点,将三角形ABD 沿AD 折叠,使83AB AC ⋅= .则三棱锥B ADC -的体积为()A.69 B.2C.39D.16【答案】A 【解析】【分析】根据正三角形折叠后得出AD ⊥平面BCD ,设,DB DC夹角为θ,进而sin 3θ=,再应用三棱锥体积公式计算即可.【详解】正三角形ABC 边长为2,D 为BC 的中点,将三角形ABD 沿AD 折叠,,,,,AD BD AD DC DC BD D DC BD ⊥⊥⋂=⊂平面BCD ,AD ⊥平面BCD ,设,DB DC夹角为θ,使()()28····30011cos 3AB AC AD DB AD DC AD ADDB AD DC DB DC θ⋅=++=+++=+++⨯⨯= .则1cos ,sin 33θθ=-==,1,AD BD DC ===11111sin 3323239B ADC A BCD BCD V V S AD BD DC AD θ--==⨯⨯=⨯⨯⨯⨯⨯=⨯⨯=.故选:A.二、多项选择题:本题共3小题,每小题6分,共18分.在每个给出的选项中,有多项符合题目要求.全部选对得6分,部分选对得部分分,有选错的得0分.9.下列说法正确的是().A.直线()24y ax a a =-+∈R 恒过第一象限B.直线31y x =-关于x 轴的对称直线为31y x =--C.原点到直线10x ++=的距离为12D.已知直线l 过点()3,1P -,且在x ,y 轴上截距相等,则直线l 的方程为20x y +-=【答案】AC 【解析】【分析】求出直线24(R)y ax a a =-+∈过得定点判断A ,求得直线关于x 轴的对称直线方程判断B ,由点到直线的距离判断C ,讨论直线在,x y 轴上截距是否为0,求出直线方程判断D.【详解】直线24(R)y ax a a =-+∈即直(2)4(R)y a x a =-+∈,当2x =时,4y =,即直线24(R)y ax a a =-+∈恒过定点(2,4),由(2,4)在第一象限知A 正确;直线31y x =-关于x 轴的对称直线为31y x -=-,即31y x =-+,故B 错误;由点到直线距离可得12d ==,故C 正确;因为直线l 过点()3,1P -,且在,x y 轴上截距相等,当截距都为0时,直线l 方程为13y x =-,当截距不为0时,可设直线方程为1x ya a +=,则311a a-+=,2a ∴=,则直线方程为20x y +-=,故D 错误.故选:AC10.已知点P 在曲线22x y x y +=+上,点()2,0Q ,则P 的可能取值为()A.2B.1C.2D.4【答案】BC 【解析】【分析】根据对称性可知:只需讨论x 轴以及其上方的图象即可,分0,0x y ≥≥和0,0x y ≤≥两种情况,结合圆的性质分析求P 的最值,结合选项分析判断.【详解】对于方程22x y x y +=+,将y 换成y -可得:()22x y x y +-=+-,即22x y x y +=+,可知曲线关于x 轴对称,且点()2,0Q 在x 轴上,则只需讨论x 轴以及其上方的图象即可,当0,0x y ≥≥,则曲线方程化为22x y x y +=+,即22111222x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,此时曲线为以11,22A ⎛⎫⎪⎝⎭为圆心,半径12r =的半圆,可知1min2PQ AQ r =-=,当且仅当P 为线段AQ 与曲线的交点1P 时,等号成立;当0,0x y ≤≥,则曲线方程化为22x y x y +=-+,即22111222x y ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭,此时曲线为以11,22B ⎛⎫-⎪⎝⎭为圆心,半径22r =,可知2max2PQ BQ r =+=,当且仅当P 为QB 的延长线与曲线的交点2P 时,等号成立;即22PQ ≤≤,结合选项可知:AD 错误;BC 正确.故选:BC.11.正方体1111ABCD A B C D -的棱长为2,点M 为侧面11ADD A 内的一个动点(含边界),点P 、Q 分别是线段1CC 、BC 的中点,则下列结论正确的是()A.存在点M ,使得二面角--M DC P 大小为2π3B.1MB MP ⋅最大值为6C.直线PM 与面11A ADD 所成角为π4时,则点M 的轨迹长度为2π3D.当1MB BP ⊥时,则三棱锥1B AMQ -的体积为定值.【答案】BCD 【解析】【分析】由题意得到二面角--M DC P 的平面角,其中1π0,2MDD ⎡⎤∠∈⎢⎥⎣⎦,可得判定A 错误;建系求出点及向量,再应用向量的数量积坐标表示计算最值判断B ,根据线面角得出M 的轨迹,结合边长得出角进而应用弧长公式求出侧面内的劣弧判断C,应用向量垂直得出点M 的位置,再应用等体积法求体积即可判断D.【详解】在正方体1111ABCD A B C D -中,可得CD ⊥平面11ADD A ,因为MD ⊂平面11ADD A ,1DD ⊂平面11ADD A ,所以1,CD MD CD DD ⊥⊥,所以二面角--M DC P 的平面角为1∠MDD ,其中1π0,2MDD ⎡⎤∠∈⎢⎥⎣⎦,A错误;如图建系,设()[]()()1,0,,,0,2,2,2,2,0,2,1M t n t n B P ∈,()()12,2,2,,2,1MB t n MP t n =--=--,()()()22124212432MB MP t t n n t t n n ⋅=--++--=-++-+()22311124t n ⎛⎫=-+-+⎪⎝⎭存在2,0t n ==时,取1MB MP ⋅最大值为6,B正确;设面11A ADD 法向量为 =0,1,0,直线PM 与面11A ADD 所成角为π4时,可得()22π22sin 4241n PM n PMt n ⋅==⋅++-,所以()2214t n +-=,则点M 的轨迹是以0,0,1为球心,2为半径的球,点M 为侧面11ADD A 内的一个动点,则点M 的轨迹在侧面11ADD A 内是以0,0,1为圆心,2为半径的劣弧,如图所示,分别交AD ,11A D 于2M ,1M ,如图所示,111112,1,cos 2M ED E M ED ==∠=,则121π3D E D M M E ∠=∠=,则21π3M M E ∠=,劣弧12M M 的长为π3π223⨯=,C 正确当1MB BP ⊥时,()122020MB BP t n ⋅=--++-=,所以26t n +=,所以2,2t n ==,可得()2,0,2M 为1A ,则三棱锥1B AMQ -的体积为11111111123323B AMQ Q A AB A AB V V S QB AB AA QB --==⨯=⨯⨯⨯⨯= ,所以当1MB BP ⊥时,三棱锥1B AMQ -的体积为定值,D 正确.故选:BCD.【点睛】关键点点睛:解决轨迹长度的关键是先设点M 计算求轨迹方程()2214t n +-=,点M 的轨迹是以0,0,1为球心以2为半径的球,再结合侧面内的边长得出角进而得出弧长即可.非选择题部分三、填空题:本大题共3小题,每题5分,共15分.12.()2,0,0a = ,()1,1,1b = ,则b 在a上的投影向量为________(用坐标表示)【答案】(1,0,0)【解析】【分析】直接利用向量的夹角运算及数量积运算求出投影向量.【详解】由于空间向量()2,0,0a =,()1,1,1b = ,故向量b 在向量a上的投影向量的坐标21||cos ,(2,0,0)(1,0,0)||||2a ab b a b a a a ⋅<>⋅=⋅== .故答案为:(1,0,0).13.已知直线1l :()10x m y +-=,2l :10mx y +-=,若满足12l l ⊥,则两直线的交点坐标为________.【答案】24,55⎛⎫ ⎪⎝⎭【解析】【分析】先由直线1:(1)0l x m y +-=与直线2:10l mx y +-=垂直的性质能求出m ,再联立直线方程求交点即可.【详解】 直线1:(1)0l x m y +-=与直线2:10l mx y +-=垂直,10m m ∴+-=,解得12m =,所以10(1)02101102x y x m y mx y x y ⎧-=⎪+-=⎧⎪⇒⎨⎨+-=⎩⎪+-=⎪⎩,解得2545x y ⎧=⎪⎪⎨⎪=⎪⎩故答案为:24,55⎛⎫⎪⎝⎭.14.如图所示的试验装置中,两个正方形框架ABCD 、ABEF 的边长都是2,且它们所在的平面互相垂直.长度为2的金属杆端点N 在对角线BF 上移动,另一个端点M 在正方形ABCD 内(含边界)移动,且始终保持MNAB ⊥,则端点M 的轨迹长度为________.【答案】π【解析】【分析】建系标点,设()()[],,0,,0,,,,0,2N a a M x z a x y ∈,根据垂直关系可得x a =,结合长度可得224x z +=,分析可知端点M 的轨迹是以B 为圆心,半径2r =的圆的14部分,即可得结果.【详解】以B 为坐标原点,,,BA BE BC 分别为,,x y z 轴,建立空间直角坐标系,则()()2,0,0,0,0,0A B ,设()()[],,0,,0,,,,0,2N a a M x z a x y ∈,可得()()2,0,0,,,BA NM x a a z ==-- ,因为MN AB ⊥,即()20BA NM x a ⋅=-= ,可得x a =,则()0,,NM x z =- ,则2NM == ,整理可得224x z +=,可知端点M 的轨迹是以B 为圆心,半径2r =的圆的14部分,所以端点M 的轨迹长度为12π2π4⨯⨯=.故答案为:π.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知圆C 的圆心在y 轴上,并且过原点和().(1)求圆C 的方程;(2)若线段AB 的端点()4,2A -,端点B 在圆C 上运动,求线段AB 的中点M 的轨迹方程.【答案】(1)()2224x y +-=(2)()2221x y -+=【解析】【分析】(1)利用待定系数法计算即可求解;(2)设s ,()00,B x y ,由中点坐标公式可得024x x =-,022y y =+,代入圆C 方程,整理即可求解.【小问1详解】设圆C 方程:()()2220x y b r r +-=>,由已知(()222223b r b r ⎧=⎪⎨+-=⎪⎩,解得22b r =⎧⎨=⎩,∴圆C 方程为()2224x y +-=.【小问2详解】设点s ,()00,B x y .∵()4,2A -,∴004222x x y y +⎧=⎪⎪⎨-⎪=⎪⎩.整理得024x x =-,022y y =+,∵点B 在圆C 上,∴()()222424x y -+=,∴点M 的轨迹方程为()2221x y -+=.16.在四面体ABCD 中,2AB AC BC BD CD =====,3AD =,E 是BC 的中点,F 是AD 上靠近A 的三等分点,(1)设AB a =,AC b = ,AD c = ,试用向量a 、b 、c 表示向量FE ;(2)证明:FE CD ⊥.【答案】(1)111223FE a b c =+- (2)证明见解析【解析】【分析】(1)由向量的加法与减法运算;(2)证明0C E D F ⋅= ,得EF CD ⊥ ,可得EF CD ⊥.【小问1详解】()1123FE AE AF AB AC AD =-=+- ,即111223FE a b c =+- ;【小问2详解】CD AD AC c b=-=- ()111111111223223223FE CD a b c c b a c b c c c a b b b c b ⎛⎫⋅=+-⋅-=⋅+⋅-⋅-⋅-⋅+⋅ ⎪⎝⎭ 221313111113232332222302424322234=⨯⨯⨯+⨯⨯⨯--⨯⨯⨯+⨯⨯⨯所以FE CD ⊥.17.在长方体1111ABCD A B C D -中,1222BC BB BA ===,点M 为棱AB 上的动点(含端点).(1)当点M 为棱AB 的中点时,求二面角1M D C D --的余弦值;(2)当AM 的长度为何值时,直线1B C 与平面1CMD 所成角的正弦值最小,并求出最小值.【答案】(1)66(2)2AM =,最小值为5【解析】【分析】(1)建立空间直角坐标系,找出坐标,求出平面1CMD 的一个法向量为()11,2,1n =- ,平面1CD D 的一个法向量为()21,0,0n = ,再利用公式12cos cos ,n n α= 求解即可;(2)引入参数,设AM t =,()02t ≤≤,表示出()1,1,M t ,()11,1,0B C =- ,()11,1,D M t = ,()10,1,2D C = .求出平面1CMD 法向量()32,2,1n t =-- ,设1B C 与平面1CMD 的所成角为β,利用31sin cos ,n B C β= 建立等式,再利用基本不等式求解.【小问1详解】如图,以1D 为原点,11D A ,1D D ,11D C 分别为x 轴,y 轴,z轴建立空间直角坐标系.设二面角1M D C D --为α,则该角为锐角.而()10,0,0D ,()1,1,1M ,()0,1,2C ,()11,0,2B .所以()10,1,2D C = ,()11,1,1D M = .设平面1CMD 法向量()1,,n x y z = 所以111102000n D C y z x y z n D M ⎧⋅=+=⎧⎪⇒⎨⎨++=⋅=⎩⎪⎩ .取1z =,得平面1CMD 的一个法向量为()11,2,1n =- 易知平面1CD D 的一个法向量为()21,0,0n =所以121212cos cos ,6n n n n n n α⋅==== .【小问2详解】设AM t =,()02t ≤≤所以()1,1,M t ,()11,1,0B C =- ,()11,1,D M t = ,()10,1,2D C = .设平面1CMD 法向量为()3111,,n x y z = .所以31111113100200n D M x y tz y z n D C ⎧⋅=++=⎧⎪⇒⎨⎨+=⋅=⎩⎪⎩ 取11z =,得平面1CMD 的一个法向量为()32,2,1n t =-- .设1B C 与平面1CMD 的所成角为β所以31sin cos ,n B C β==令4t u -=,则11142u ≤≤即sin β==当112u =时,即2u =,2t =.sin β最小值为5,此时2AM =.18.已知ABC V ,点()1,1A -,点B ,C 在直线20x y +-=上运动(点B 在点C 上方).(1)已知以点A 为顶点的ABC V 是等腰三角形,求BC边上的中线所在直线方程;(2)已知BC =,试问:是否存在点C ,使得ABC V 的面积被x 轴平分,若存在,求直线AC 方程;若不存在,说明理由?【答案】(1)2y x =-(2)存在,2y x =-【解析】【分析】(1)利用等腰三角形的性质及垂直直线的斜率关系求得边BC 的中线的斜率,然后利用点斜式直线方程求解即可;(2)结合点到直线的距离公式求出ABC V 的面积,设(),2B a a -,()1,1C a a +-,分点C 在x 轴下方和点C 在x 轴或x 轴上方,两种情况讨论,根据面积列式求解点C 的坐标,再求直线AC 方程即可.【小问1详解】因为ABC V 是以点A 为顶点的等腰三角形,所以边BC 的中线垂直直线BC ,所以边BC 的中线的斜率1111BC k k =-=-=-,又过点()1,1A -,所以边BC 的中线方程为11y x +=-,即2y x =-;【小问2详解】因为点A到直线l的距离d ==,故112ABC S == .假设存在C 满足条件,设(),2B a a -,()1,1C a a +-,则20a ->,即2a <,①当点C 在x 轴下方时,即10a -<时,即12a <<,AB 所在直线的方程为()21111a y x a -++=--,令0y =,解得23x a=-,直线AB 与x 轴的交点2,03M a ⎛⎫ ⎪-⎝⎭,又直线20x y --=与x 轴的交点()2,0N ,所以242233a MN a a -=-=--,()1142122232BMN B a S MN y a a -=⋅=⋅⋅-=- ,解得1a =或52a =,舍去;②当点C 在x 轴或x 轴上方时,即10a -≥时,即1a ≤,AC 所在直线的方程为()111111a y x a -++=-+-,令0y =,解得22x a=-,直线AC 与x 轴的交点2,02E a ⎛⎫⎪-⎝⎭,所以22222356ME a a a a =-=---+,21121122562AME A S ME y a a =⋅=⋅⋅=-+ ,解得1a =或4a =(舍去);综上,当1a =时,存在点()2,0C 满足题意,此时,直线AC 的斜率为()01121--=-,故直线AC 方程为2y x =-.19.出租车几何或曼哈顿距离(ManhattanDistance )是由十九世纪的赫尔曼·闵可夫斯基所创词汇,是种使用在几何度量空间的几何学用语,用以标明两个点在空间(平面)直角坐标系上的绝对轴距总和.例如:在平面直角坐标系中,若()11,A x y ,()22,B x y ,两点之间的曼哈顿距离()2121,d A B x x y y =-+-.(1)已知点()1,4A ,()3,3B -,求(),d A B 的值;(2)记(),d B l 为点B 与直线l 上一点的曼哈顿距离的最小值.已知点()1,1B ,直线l :420x y -+=,求(),d B l ;(3)已知三维空间内定点()1,1,1A ,动点P 满足(),1d A P =,求动点P 围成的几何体的表面积.【答案】(1)9(2)54(3)【解析】【分析】(1)由曼哈顿距离定义直接计算即可;(2)设直线420x y -+=上任意一点坐标为s ,然后表示(),d B l ,分类讨论求(),d C B 的最小值即可;(3)不妨将A 平移到0,0,0处,利用曼哈顿距离定义求得P 围成的图形为八面体,即可求解其表面积.【小问1详解】()(),13439d A B =-+--=,所以(),9d A B =.【小问2详解】设动点s 为直线l 上一点,则42y x =+,所以(),1421141d B l x x x x =-++-=-++,即()5,11,32,1415,4x x d B l x x x x ⎧⎪≥⎪⎪=+-≤<⎨⎪⎪-<-⎪⎩,当1x ≥时,(),5d B l ≥;当114x -≤<时,()5,54d B l ≤<;当14x <-时,()5,4d B l >;综上,(),d B l 为54.【小问3详解】动点P的正三角形,其表面积为13822⨯=证明如下:不妨将A 平移到0,0,0处,设(),,P x y z ,若(),1d A P =,则1x y z ++=,当,,0x y z ≥时,即()10,,1x y z x y z ++=≤≤,设()11,0,0M ,()20,1,0M ,()30,0,1M ,则()112131,,(,,)M P x y z y z y z yM M zM M =-=--=+ ,所以P ,1M ,2M ,3M 四点共面,所以当,,0x y z ≥时,P 的等边三角形123M M M 内部(含边界).同理可知等边三角形内部任意一点(),,Q x y z ''',均满足1x y z '''++=.所以满足方程()10,,1x y z x y z ++=≤≤的点P ,的等边三角形内部(含边界).由对称性可知,P 围成的图形为八面体,每个面均为边长为的等边三角形.故该几何体表面积284S =⨯⨯=【点睛】思路点睛:本题考查了新概念问题,解决新概念问题首先要读懂新概念的定义或公式,将其当做一种规则和要求严格按照新概念的定义要求研究,再结合所学知识处理即可.。
理论力学课后问题详解(范钦珊)
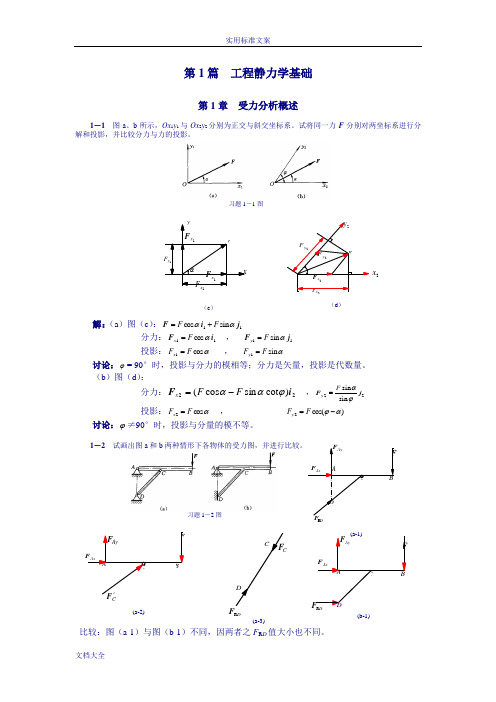
C(a-2)DR(a-3)(b-1)DR第1篇 工程静力学基础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 s i n c o s j i F ααF F +=分力:11 cos i F αF x = , 11 s i n j F αF y =投影:αcos 1F F x = , αs i n 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ): 分力:22)cot sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y = 投影:αcos 2F F x = , )cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 和b习题1-2图比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
(c )2x(d )1-3 试画出图示各物体的受力图。
习题1-3图B或(a-2)(a-1)(b-1)F(c-1) 或(b-2)(e-1)F(a)1-4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1-5 图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E (如图示),是否会改为销钉A 的受力状况。
解:由受力图1-5a ,1-5b和1-5c 分析可知,F 从C 移至E ,A 端受力不变,这是因为力F 在自身刚体ABC 上滑移;而F 从C 移至D ,则A 端受力改变,因为HG 与ABC 为不同的刚体。
1(f-1)'A(f-2)1(f-3)F F'F 1(d-2)AF yB 21(c-1)F A B1FDx y(b-2)1(b-3)F yB 2 F A B1B F习题1-5图AxF'(b-3)E D(a-3)B(b-2)(b-1)F 'CDDF EFBC(c)AxF1-6 试画出图示连续梁中的AC 和CD 梁的受力图。
有个性的网名(精选400个)

有个性的网名(精选400个)1、瑾夏年华2、不挽留3、一行情泪4、淡忘那伤5、心丶在滴血。
6、這次涐先走丶7、你给的痛8、如夢破碎迷離9、珴是爱珎旳10、簡單陪絆11、回不去的以往。
12、茛囡琓暧昧13、爽走不解释14、浅怀感伤15、寒冷的夏季16、一个人,独自享受夜的黑。
17、予情18、ら名花有主19、ヾ我後悔叻20、南影倾寒21、ヽ可惜卟是迩。
22、づ姐要的拽,你挡不到゜23、睡姿决定发型24、﹌唇诱留下齿痕25、木冇鱼丸26、彼此守候27、對你我無話可說28、遗失的完美。
29、倾城之泪30、饮泪少女31、如果っ没有遇见你32、最美流年33、差一点是个帅哥34、情非得已35、陌上初安36、半世浮华▍只为俄的小情绪37、劳娘缺锌缺钙缺人爱38、离情几度39、偏执的想念40、内谁,对不起41、有我在42、谁贪恋你的红颜43、■以往的亦是以往。
44、你已被我out45、念念不忘46、几分以往47、情难自控48、闻呓49、煙雨如夢50、花开不败゛51、我不傻,只是我不想说°52、无畏向前53、染血Heart▕54、玉簪轻绾融于发55、死亡婚纱56、血痂。
57、八月的雨季58、呆呆呆呆呆一种个性59、还你笑眼60、无伴终老61、匕首刺心62、陌小离63、後悔愛上你。
64、你的笑讓我坚持著沉默65、叼根香烟吻迩66、∫αì全成欺ㄢ扁ㄨ67、叶落抚尘68、几度相思成灰69、抱着回忆失声痛哭ち70、只剩余温71、我怜幽梦,空谁伤。
72、损人,害己。
73、姐就是有范﹌∞74、娿孬75、用心温暖了彼此76、我要做无情之人77、qiao゜ゝ78、半盏清茶79、—疏远我80、彼岸髅灵81、盛世流光82、这逼有诈83、烟酒痞女84、久违的心痛╮85、深爱着86、↘半温半暖◥87、メ開始べ愛♀88、我还在*89、短暫のρеí姅り90、尋處清嵠91、范小姐︶ㄣ92、宅心—93、冷暖自知94、一指流砂95、无声折磨*96、我是一个失败的孩子97、花甲之年依然有句我爱你゜98、劳资素个好菇凉99、惆怅已成曲100、—只在心里101、低头泪倾城102、找不到活命的氧气103、老衲满头秀发104、不在乎未来105、㈠個人¢流浪106、Forgetit107、一厢情愿108、仰望我触摸不到的幸福。
75道逻辑智力测试题(3篇)

第1篇1. 一个人有四个孩子,其中一个是女孩。
那么以下哪个结论一定正确?A. 这四个孩子中至少有两个女孩。
B. 这四个孩子中至多有一个女孩。
C. 这四个孩子中至少有一个男孩。
D. 这四个孩子中至多有一个男孩。
答案:C。
解析:题目中已经明确指出有一个女孩,因此其他三个孩子中至少有一个男孩。
2. 三个数字相加等于18,其中两个数字是3和6,那么第三个数字是多少?答案:9。
解析:3 + 6 + 9 = 18。
3. 一个房间里有五个人,他们分别是张三、李四、王五、赵六和孙七。
他们分别属于以下五个职业:医生、教师、律师、工程师和护士。
已知以下信息:- 张三不是医生;- 李四不是工程师;- 王五不是教师;- 赵六不是律师;- 孙七不是护士。
那么以下哪个结论一定正确?A. 张三是工程师。
B. 李四是医生。
C. 王五是律师。
D. 赵六是护士。
答案:B。
解析:由于其他职业已经被其他人占据,李四只能是医生。
4. 一个班里有30名学生,其中有10名男生和20名女生。
已知以下信息:- 每个男生都至少和两个女生是朋友;- 每个女生都至少和三个男生是朋友。
那么以下哪个结论一定正确?A. 这个班里有至少40个朋友关系。
B. 这个班里有至多30个朋友关系。
C. 这个班里有至少20个朋友关系。
D. 这个班里有至多60个朋友关系。
答案:A。
解析:每个男生都至少和两个女生是朋友,所以至少有10 2 = 20个朋友关系。
每个女生都至少和三个男生是朋友,所以至少有20 3 = 60个朋友关系。
因此,这个班里有至少40个朋友关系。
5. 一个人有五个盒子,分别编号为1、2、3、4、5。
他每次只能选择一个盒子,并且不能重复选择。
他需要按照以下顺序选择盒子:1、2、3、4、5、1、2、3、4、5、...那么他第100次选择的盒子是哪个?答案:3。
解析:这是一个周期性的问题,周期为5。
100除以5的余数为0,所以第100次选择的盒子是周期中的最后一个盒子,即3。
高中数学人教B版2019必修第三册弧度制及其与角度制的换算

弧度制和角度值
引入:
在日常生活以及各学科中,一个量可用不同的标准来度量,从而也就 有了不同的单位以及单位之间的换算。
例如,长度既可以用米、厘米来度量,也可以用尺、寸来度量;面积 可以用平方米来度量,也可以用亩来度量。
类似地,角除了使用角度来度量外,还可以使用本小节我们要学习地 弧度来度量。
解 设扇形的半径为 r,弧长为 l,面积为 S. 则 l=20-2r, ∴S=12lr=12(20-2r)·r=-r2+10r=-(r-5)2+25(0<r<10). ∴当半径 r=5 cm 时,扇 形的面积最大,为 25 cm2. 此时 α=rl=20-52×5=2(rad). ∴当它的半径为 5 cm,圆心角为 2 rad 时,扇形面积最大,最大值为 25 cm2.
知识点 3.特殊角的弧度数
角度 0° 30° 45° 60° 90° 120° 135° 150° 180° 270° 360°
弧度 0
6
4
3
2 3
5
2
3
4
6
3
2
2
问题3: 弧长公式与扇形面积公式
知识点 4 弧长公式
在半径为 r 的圆中,若弧长为 l 的弧所对的圆心角为 α rad,则 α=rl,所以 l=αr, 即弧长等于其所对应的圆心角的弧度数与半径的积.
r 因此180o rad ;
(2)设一个角的角度数为 n ,弧度数为 ,则 n 180
知识点2 弧度制与角度制的换算
1.角度与弧度的关系:180°=π rad.
2.设一个角的角度数为 n,弧度数为 α,则1n80=απ.
例 1.把 30o , 45o , 60o 化成弧度(用 表示),并在平面直角坐标系中作出它们的终边。
成人高考《高等数学一》章节练习题答案及解析

成人高考《高等数学一》章节练习题答案及解析- 1 -2021 年专升本数学一习题第一章极限、连续1.已知f(x) = � 3x + 2,x ≥0x 2 −1,x < 0。
求f(0)=2. limx→∞sinxx=3. limx→2 (x −2)sin1x−2=4. limx→0xln(3x+1)=5. limx→0sin4xx=6. limx→∞�1 +5x �x =7. limx→0tan2x2x=8. limx→0 (1 −x)1x =9. limx→0 (1 + x)−1x =10. limx→∞�1 +1x �x+2 =11. limx→0x ⋅tanx= 12. limx→0sinxsin2x =13. limx→0ln (2x+1)sin3x14. limx→1x−1x 2 −1=15. limx→4x−4√x+5−3=- 2 -- 2 -16. limx→∞2x 3 +3x 2 +5 7x 3 +4x 2 −1 = 17.设f(x) = �x −1,x < 0 0,x = 0x + 1,x > 0,求limx→0f(x)18. limx→2x 2 +x−6x 2 −4=19. limx→0x−sinxx 2 +x=20.设函数f(x) = �√x3,x < 0,x 2 + 1,x ≥0, 则在点x=0 处是否连续。
21.函数f(x) =x 2 +1x−3的间断点是()。
22.设函数f(x) = �e x,x < 0x + a,x ≥0 在x=0 处连续,则a=()第二章一元函数微分学1.已知f ′(2) = 2,求limΔx→0f(2−3Δx)−f(2)Δx=2.已知f ′(4) = 1,求limΔx→0f(4+2Δx)−f(4)Δx=3x + lnx在点(1,0)处切线斜率K。
4lnx在点(1,0)处的切线方程和法线方程。
5x 2 上的一点,使该点处的切线与直线y = 2x + 2平行。
初三数学二次函数试题答案及解析

初三数学二次函数试题答案及解析1.如图,已知抛物线图象经过A(-1,0),B(4,0)两点.(1)求抛物线的解析式;(2)若C(m,m-1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.①求证:四边形DECF是矩形;②连结EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.【答案】(1);(2)①证明见解析;②2.【解析】(1)根据待定系数法即可求得;(2)把C(m,m-1)代入求得点C的坐标,从而求得AH=4,CH=2,BH=1,AB=5,然后根据,∠AHC=∠BHC=90°得出△AHC∽△CHB,根据相似三角形的对应角相等求得∠ACH=∠CBH,因为∠CBH+∠BCH=90°所以∠ACH+∠BCH=90°从而求得∠ACB=90°,先根据有两组对边平行的四边形是平行四边形求得四边形DECF是平行四边形,进而求得DECF是矩形;(3)根据矩形的对角线相等,求得EF=CD,因为当CD⊥AB时,CD的值最小,此时CD的值为2,所以EF的最小值是2;试题解析:(1)∵抛物线图象经过A(-1,0),B(4,0)两点,∴根据题意,得,解得,所以抛物线的解析式为:;(2)①证明:∵把C(m,m-1)代入得∴,解得:m=3或m=-2,∵C(m,m-1)位于第一象限,∴,∴m>1,∴m=-2舍去,∴m=3,∴点C坐标为(3,2),由A(-1,0)、B(3,0)、C(3,2)得 AH=4,CH=2,BH=1,AB=5过C点作CH⊥AB,垂足为H,则∠AHC=∠BHC=90°,∵,∠AHC=∠BHC=90°∴△AHC∽△CHB,∴∠ACH=∠CBH,∵∠CBH+∠BCH=90°∴∠ACH+∠BCH=90°∴∠ACB=90°,∵DE∥BC,DF∥AC,∴四边形DECF是平行四边形,∴DECF是矩形;②存在;连接CD∵四边形DECF是矩形,∴EF=CD,当CD⊥AB时,CD的值最小,∵C(3,2),∴DC的最小值是2,∴EF的最小值是2;【考点】二次函数综合题.2.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C′处;作∠BPC′的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为()A.B.C.D.【答案】C.【解析】∵将△PCD沿直线PD折叠,使点C落下点C′处;∴∠CPD=∠C′PD=∠CPC′,∵PE平分∠BPC′,∴∠BPE=∠C′PE=∠BPC′,又∵∠BPC′+∠CPC′=180°,,∴∠BPE+∠CPD=90°,在△PCD中,∵∠C=90°,∴∠CPD+∠PDC=90°,∴∠BPE=∠PDC,又∵∠B=∠C=90°,∴△PCD∽△EBP,∴,即,∴y=x(5﹣x)=﹣(x﹣)2+,只有C选项图象符合.故选C.【考点】动点问题的函数图象.3.如图,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴的一个交点为A(-2,0),与y轴的交点为C,对称轴是x=3,对称轴与x轴交于点B.(1)求抛物线的函数表达式;(2)经过B,C的直线l平移后与抛物线交于点M,与x轴交于点N,当以B,C,M,N为顶点的四边形是平行四边形时,求出点M的坐标;(3)若点D在x轴上,在抛物线上是否存在点P,使得△PBD≌△PBC?若存在,直接写出点P的坐标;若不存在,请说明理由.【答案】(1)抛物线为y=-x2+x+4.(2)M的坐标为(6,4)或(3-,-4)或(3+,-4).(3)点P的坐标为(4+,)或(4-,)或(-1+,-8+2)或(-1-,-8-2).【解析】(1)解析式已存在,y=ax2+bx+4,我们只需要根据特点描述求出a,b即可.由对称轴为-,又过点A(-2,0),所以函数表达式易得.(2)四边形为平行四边形,则必定对边平行且相等.因为已知MN∥BC,所以MN=BC,即M、N的位置如B、C位置关系,则可分2种情形,①N点在M点右下方,即M向下平行4个单位,向右2个单位与N重合;②M点在N右下方,即N向下平行4个单位,向右2个单位与M重合.因为M在抛物线,可设坐标为(x,-x2+x+4),易得N坐标.由N在x轴上,所以其纵坐标为0,则可得关于x的方程,进而求出x,求出M的坐标.(3)使△PBD≌△PBC,易考虑∠CBD的平分线与抛物线的交点.确定平分线可因为BC=BD,可作等腰△BCD,利用三线合一,求其中线所在方程,进而与抛物线联立得方程组,解出P即可.试题解析:(1)∵抛物线y=ax2+bx+4交x轴于A(-2,0),∴0=4a-2b+4,∵对称轴是x=3,∴-=3,即6a+b=0,两关于a、b的方程联立解得 a=-,b=,∴抛物线为y=-x2+x+4.(2)∵四边形为平行四边形,且BC∥MN,∴BC=MN.①N点在M点右下方,即M向下平移4个单位,向右平移2个单位与N重合.设M(x,-x2+x+4),则N(x+2,-x2+x),∵N在x轴上,∴-x2+x=0,解得 x=0(M 与C 重合,舍去),或x=6, ∴x M =6,∴M (6,4).②M 点在N 右下方,即N 向下平行4个单位,向右2个单位与M 重合. 设M (x ,- x 2+x+4),则N (x-2,-x 2+x+8), ∵N 在x 轴上, ∴-x 2+x+8=0,解得 x=3-,或x=3+,∴x M =3-,或3+.∴M (3-,-4)或(3+,-4)综上所述,M 的坐标为(6,4)或(3-,-4)或(3+,-4).(3)∵OC=4,OB=3, ∴BC=5.如果△PBD ≌△PBC ,那么BD=BC=5, ∵D 在x 轴上,∴D 为(-2,0)或(8,0).①当D 为(-2,0)时,连接CD ,过B 作直线BE 平分∠DBC 交CD 于E ,交抛物线于P 1,P 2, 此时△P 1BC ≌△P 1BD ,△P 2BC ≌△P 2BD , ∵BC=BD ,∴E 为CD 的中点,即E (-1,2),设过E (-1,2),B (3,0)的直线为y=kx+b ,则,解得,∴BE :y=-x+. 设P (x ,y ),则有,解得 ,或,则P 1(4+,),P 2(4-,).②当D 为(8,0)时,连接CD ,过B 作直线BF 平分∠DBC 交CD 于F ,交抛物线于P 3,P 4, 此时△P 3BC ≌△P 3BD ,△P 4BC ≌△P 4BD , ∵BC=BD ,∴F 为CD 的中点,即E (4,2),设过E (4,2),B (3,0)的直线为y=kx+b ,则,解得,∴BF :y=2x-6. 设P (x ,y ),则有, 解得或,则P3(-1+,-8+2),P4(-1-,-8-2).综上所述,点P的坐标为(4+,)或(4-,)或(-1+,-8+2)或(-1-,-8-2).【考点】二次函数综合题.4.将二次函数化为的形式,结果为()A.B.C.D.【答案】D.【解析】. 故选D.【考点】配方法的应用.5.某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(单位:万元)与销售量x(单位:辆)之间分别满足:,,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为A.30万元B.40万元C.45万元D.46万元【答案】D.【解析】设在甲地销售x辆,则在乙地销售(15-x)量,根据题意得出:W=y1+y2=-x2+10x+2(15-x)=-x2+8x+30,∴最大利润为:(万元),故选D.【考点】二次函数的应用.6.如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA.(1)求△OAB的面积;(2)若抛物线y=-x2-2x+c经过点A.①求c的值;②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB 的边界),求m的取值范围(直接写出答案即可).【答案】(1)4 (2)①c=4 ②1<m<3【解析】(1)根据点A的坐标是(-2,4),得出AB,BO的长度,即可得出△OAB的面积;(2)①把点A的坐标(-2,4)代入y=-x2-2x+c中,直接得出即可;②利用配方法求出二次函数解析式即可得出顶点坐标,根据AB的中点E的坐标以及F点的坐标即可得出m的取值范围.解:(1)∵点A的坐标是(-2,4),AB⊥y轴,∴AB=2,OB=4,∴△OAB的面积为:×AB×OB=×2×4=4,(2)①把点A的坐标(-2,4)代入y=-x2-2x+c中,-(-2)2-2×(-2)+c=4,∴c=4,②∵y=-x2-2x+4=-(x+1)2+5,∴抛物线顶点D的坐标是(-1,5),过点D作DE⊥AB于点E交AO于点F,AB的中点E的坐标是(-1,4),OA的中点F的坐标是(-1,2),∴m的取值范围是:1<m<3.7.如图所示,一个二次函数的图象经过点A,C,B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴的正半轴上,且AB=OC.则这个二次函数的解析式是________.【答案】y=-x2+x+5【解析】∵A(-1,0),B(4,0),∴AO=1, OB=4,即AB=AO+OB=1+4=5.∴OC=5,即点C的坐标为(0,5).设图象经过A,C,B三点的二次函数的解析式为y=a(x-4)(x+1),∵点C(0,5)在图象上.∴5=a(0-4)(0+1),即a=-.∴所求的二次函数解析式为y=- (x-4)(x+1).即y=-x2+x+5.8.如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)。
河南省部分学校2024-2025学年高三上学期11月月考数学试题含答案

高三数学(答案在最后)考生注意:1.本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚.3.考生作答时,请将答案答在答题卡上.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效.............,在试题卷....、草稿纸上作答无效.........4.本卷命题范围:集合、常用逻辑用语、不等式、函数、导数,三角函数、三角恒等变换,解三角形、平面向量.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.函数tan y x =的值域可以表示为()A.{tan }xy x =∣ B.{tan }yy x =∣C.{(,)tan }x y y x =∣D.{tan }y x =【答案】B 【解析】【分析】根据函数的值域是指函数值组成的集合,即可判断.【详解】因函数的值域是指函数值组成的集合,故对于函数tan y x =,其值域可表示为:{tan }yy x =∣.故选:B.2.若“sin 2θ=-”是“tan 1θ=”的充分条件,则θ是()A .第四象限角B.第三象限角C.第二象限角D.第一象限角【答案】B 【解析】【分析】根据角θ的正切值与正弦值的正负判断象限即可.【详解】由题可知,sin 02θ=-<,则θ是第三象限角或第四象限角;又要得到tan 10θ=>,故θ是第三象限角.故选:B3.下列命题正确的是()A.x ∃∈R ,20x <B.(0,4)x ∀∈,20log 2x <<C.(0,)x ∃∈+∞,132x x< D.π0,2x ⎛⎫∃∈ ⎪⎝⎭,4sin cos x x =【答案】C 【解析】【分析】对于选项A:利用指数函数的值域即可判断;对于选项B:利用对数函数的单调性求出值域即可判断;对于选项C:采用特殊值法,令14x =即可判断;对于选项D:令4sin cos 2sin 2y x x x ==,结合三角函数的值域求解验证即可.【详解】对于选项A:因为指数函数2x y =的值域为0,+∞,故x ∀∈R ,20x >,故选项A 错误;对于选项B:因为对数函数2log y x =在(0,4)x ∈上单调递增,所以当(0,4)x ∈时,()2log ,2y x ∞=∈-,故选项B 错误;对于选项C:令14x =,则311464⎛⎫= ⎪⎝⎭,121142⎛⎫= ⎪⎝⎭,显然11642<,故(0,)x ∃∈+∞,使得132x x <成立,故选项C 正确;对于选项D:结合题意可得:令4sin cos 2sin 2y x x x ==,因为π0,2x ⎛⎫∈ ⎪⎝⎭,所以()20,πx ∈,所以(]2sin 20,2y x =∈,2>,故不存在π0,2x ⎛⎫∈ ⎪⎝⎭,使得4sin cos x x =,故选项D 错误.故选:C.4.函数24()f x x x =-的大致图象是()A. B.C.D.【答案】C 【解析】【分析】先确定函数的奇偶性,排除两选项,再根据特殊点的函数值的正负,选出正确答案.【详解】函数24y x x =-是偶函数,图象关于y 轴对称,排出选项A 、B ;再取特殊值12x =和2x =,可得函数的大致图象为C ,故选:C .5.已知向量1e ,2e 满足121e e == ,120e e ⋅= ,则向量1e 与12e e -的夹角为()A.45︒B.60︒C.120︒D.135︒【答案】A 【解析】【分析】利用向量夹角的计算公式计算即可.【详解】由题可知()21121121e e e e e e ⋅-=-⋅=,12e e -==,121e e == 所以()1121121122cos ,2e e e e e e e e e ⋅--===-故向量1e 与12e e -的夹角为45︒故选:A 6.已知5πtan 210α+=,则4π5tan 5α-=()A.125 B.125-C.43D.43-【答案】C 【解析】【分析】先确定两个角的关系,然后利用三角恒等变换公式求解即可.【详解】由题可知,5π4π52π105αα+-⨯+=25π2tan5π4410tan 25π101431tan 10ααα++⎛⎫⨯===- ⎪+-⎝⎭-所以有4π55π5π4tan tan π2tan 2510103ααα-++⎛⎫⎛⎫=-⨯=-⨯= ⎪ ⎪⎝⎭⎝⎭故选:C7.已知0a >,0b >,9a b +=,则36a ba+的最小值为()A.8B.9C.12D.16【答案】A 【解析】【分析】我们观察形式,显然分式的分子和分母同时有变量,所以令()364a b =+代入化简,然后利用基本不等式求解即可.【详解】43644448b a b a a a b b a a b a +=+=++≥+=+当且仅当4b aa b=,9a b +=,即26a b ==时等号成立;故选:A8.若0x ∀>,()()()21ln 10x ax ax ---≥,则a =()A.B.C.D.【答案】D 【解析】【分析】先将两个乘积看做两个函数()21,ln 1y x ax y ax =--=-,易知要使0x ∀>时,()21(ln 1)0xax ax ---≥,则需要两函数()21,ln 1y x ax y ax =--=-同号,所以我们需要去找他们零点,0x >时零点相同,然后求解参数a 即可.【详解】由题易知0a >,当ex a=时,()ln 10ax -=;由对数函数的性质可知,当e 0,x a ⎛⎫∈ ⎪⎝⎭时,()ln 10ax -<;当e ,x a ∞⎛⎫∈+ ⎪⎝⎭时,()ln 10ax ->;显然函数21y x ax =--有两个根12,x x ,不妨令12x x <,则120x x <<由二次函数的图像可知,()20,x x ∈时,210x ax --<;()2,x x ∞∈+时,210x ax -->故要使()()()21ln 10x ax ax ---≥恒成立,则2ex a=所以有2e e 10aa a ⎛⎫-⨯-= ⎪⎝⎭,解得a =故选:D【点睛】关键点点睛:当两个式子相乘大于等于零时,两个式子必定同为负或者同为正,或者有一个为零.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知函数sin()()2x f x -=,则()A.()f x 的值域为1,22⎡⎤⎢⎥⎣⎦B.()f x 为奇函数C.()f x 在ππ,22⎡⎤-⎢⎥⎣⎦上单调递增 D.()f x 的最小正周期为2π【答案】AD 【解析】【分析】对于选项A:利用换元()sin t x =-,再结合指数函数的单调性即可求出值域;对于选项B:利用奇偶性的定义说明即可;对于选项C :结合复合函数的单调性即可判断;对于选项D :借助三角函数的周期,以及周期函数的定义即可判断.【详解】对于选项A:由sin()()2x f x -=,令()sin t x =-,则2t y =,[]1,1t ∈-,因为2t y =在[]1,1t ∈-上单调递增,所以12,22ty ⎡⎤=∈⎢⎥⎣⎦,故选项A 正确;对于选项B:由sin()()2x f x -=可知(),x ∞∞∈-+,对任意的(),x ∞∞-∈-+,因为sin ()2x f x -=,而sin ()2x f x -=,易验证()(),f x f x -≠-故()f x 不是奇函数,故选项B 错误;对于选项C :结合选项A 可知()sin t x =-在ππ,22⎡⎤-⎢⎥⎣⎦单调递减,而2t y =在定义域上单调递增,由复合函数的单调性可得sin()()2x f x -=在ππ,22⎡⎤-⎢⎥⎣⎦单调递减,故选项C 错误;对于选项D :因为()sin t x =-的最小正周期为2πT =,所以sin(2π)sin()(2π)22()x x f f x x ---==+=,所以()f x 的最小正周期为2π,故选项D 正确.故选:AD.10.国庆节期间,甲、乙两商场举行优惠促销活动,甲商场采用购买所有商品一律“打八四折”的促销策略,乙商场采用“购物每满200元送40元”的促销策略.某顾客计划消费(0)x x >元,并且要利用商场的优惠活动,使消费更低一些,则()A.当0200x <<时,应进甲商场购物B.当200300x ≤<时,应进乙商场购物C.当400500x ≤<时,应进乙商场购物D.当500x >时,应进甲商场购物【答案】AC 【解析】【分析】分别计算不同选项两个商场的优惠判断即可.【详解】当0200x <<时,甲商场的费用为0.84x ,乙商场的费用为x ,0.84x x >,故应进甲商场,所以选项A 正确;当200300x ≤<时,甲商场的费用为0.84x ,乙商场的费用为40x -,400.840.1640x x x --=-,因为200250x ≤<,所以80.16400x -≤-<,400.84x x -<,进入乙商场,当250300x ≤<故400.84x x ->应进甲商场,所以选项B 错误;当400500x ≤<时,甲商场的费用为0.84x ,乙商场的费用为80x -800.840.1680x x x --=-,因为400500x ≤<,所以160.16800x -≤-<故800.84x x -<,所以应进乙商场,所以选项C 正确;假设消费了600,则在甲商场的费用为6000.84504⨯=,在乙商场的费用为600120480-=,所以乙商场费用低,故在乙商场购物,故选项D 错误.故选:AC11.已知函数()f x 满足:①x ∀,R y ∈,()[()]y f xy f x =;②(2)1f ->,则()A.(0)0f = B.()()()f x y f x f y +=⋅C.()f x 在R 上是减函数 D.[1,3]x ∀∈,()2(3)1f x kx f x -⋅-≥,则3k ≥【答案】BCD 【解析】【分析】取2,0x y =-=可求(0)f ,判断A ,取12,2x y =-=-证明()011f <<,取1x =可得()[(1)]y f y f =,由此可得()[(1)]x f x f =,结合指数运算性质和指数函数性质判断BC ,选项D 的条件可转化为当[1,3]x ∈,31x k x+-≤恒成立,结合函数性质求结论.【详解】因为x ∀,R y ∈,()[()]y f xy f x =,(2)1f ->取2,0x y =-=可得01(0)[(2)]f f =-=,A 错误;取12,2x y =-=-可得12(1)[(2)]f f -=-,又(2)1f ->,所以()011f <<,取1x =可得,()[(1)]y f y f =,所以()[(1)]x f x f =,其中()011f <<,所以()()()()()()111x yx yf x y f f f f x f y ++===,B 正确,由指数函数性质可得()[(1)]x f x f =,其中()011f <<在R 上单调递减,所以()f x 在R 上是减函数,C 正确;不等式()2(3)1f x kx f x -⋅-≥可化为()()()23111xkxx f f f --≥,所以230x kx x -+-≤,由已知对于[1,3]x ∀∈,230x kx x -+-≤恒成立,所以当[1,3]x ∈,31x k x+-≤恒成立,故max31x k x ⎛⎫+-≤ ⎪⎝⎭,其中[1,3]x ∈,因为函数1y x =+,3y x=-在[]1,3上都单调递增,所以31x x+-在[1,3]上的最大值为3,所以3k ≥,D 正确;故选:BCD.三、填空题:本题共3小题,每小题5分,共15分.12.已知函数()1ln(2)f x x =-+,则曲线()y f x =在点(1,(1))f --处的切线方程为______.【答案】0x y +=【解析】【分析】利用导数的几何意义求出切线斜率,然后代入点斜式直线方程即可求解切线.【详解】由题可知,()12f x x =-+',()11f -=,所以切线斜率()11k f =-=-',故切线方程为()110y x x y -=-+⇒+=.故答案为:0x y +=13.已知函数()cos (0)f x x ωω=>,若π2f x ⎛⎫+ ⎪⎝⎭为偶函数,且()f x 在区间(0,π)内仅有两个零点,则ω的值是__________.【答案】2【解析】【分析】根据偶函数的性质,求得2k ω=,Z k ∈,再结合余弦函数的零点,列出不等式,即可求解.【详解】πππcos cos 222f x x x ωωω⎛⎫⎛⎫⎛⎫+=+=+⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭为偶函数,所以ππ2k ω⋅=,Z k ∈,得2k ω=,Z k ∈,当∈0,π时,()0,πx ωω∈,()f x 在区间(0,π)内仅有两个零点,所以3π5ππ22ω<≤,解得:3522w <£,所以2ω=.故答案为:214.若ABC V 内一点P 满足PAB PBC PCA α∠=∠=∠=,则称P 为ABC V 的布洛卡点,α为布洛卡角.三角形的布洛卡点是法国数学家和数学教育家克洛尔于1816年首次发现,1875年被法国军官布洛卡重新发现,并用他的名字命名.如图,在ABC V 中,AB AC =,3cos 5BAC ∠=,若P 为ABC V 的布洛卡点,且2PA =,则BC 的长为______.【解析】【分析】利用三角恒等变换、正弦定理、余弦定理等知识进行分析,先求得sin α,进而求得a ,也即是BC .【详解】213cos 2cos 125BAC BAC ⎛⎫∠=∠-= ⎪⎝⎭,所以BAC ∠为锐角,12BAC ∠为锐角,所以11cos ,sin 2525BAC BAC ⎛⎫⎛⎫∠=∠== ⎪ ⎪⎝⎭⎝⎭.由于AB AC =,所以A ABC CB =∠∠,设ABC ACB θ∠=∠=,则2πBAC θ∠+=,ππ11cos cos cos sin 22225BAC BAC BAC θ-∠⎛⎫⎛⎫⎛⎫==-=∠= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,θ为锐角,则sin 5θ==.由于,BAP CBP ABP BCP θα∠=∠∠=∠=-,所以ABP BCP ,所以AB AP BPBC BP PC==①,在PBC △中,由正弦定理得()()()sin sin sin sin πBP BC BC PCθαθααθα===----,所以()sin sin BP PC θαα-=,所以()sin sin AB BP BC PC θαα-==,即()sin sin c a θαα-=,由正弦定理得sin sin cos cos sin sin cos sin sin tan ACB BAC θαθαθθαα∠-==-∠,即2525554tan 55α=-,解得4tan 7α=,则α为锐角,由22sin 4tan cos 7sin cos 1ααααα⎧==⎪⎨⎪+=⎩解得sin αα==,在三角形ABC 中,由余弦定理得222222342cos 2255a b c bc A b b b =+-=-⨯=,所以225,42b a b ==,在三角形ACP 中,由正弦定理得()()sin sin sin πAP AC ACBAC BAC ααα==∠--∠-,所以22445a=,解得a BC ==.【点睛】易错点睛:锐角与边长关系的判断:在判断三角形的角是否为锐角时,容易出现符号错误或判断失误.因此,在涉及角度大小的判断时,需特别注意各个角的定义和所使用定理的适用范围.正弦定理和余弦定理的符号处理:在使用正弦定理和余弦定理时,符号的处理必须谨慎,特别是在涉及平方根和正负符号的时候,需确保没有遗漏或误用.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.在ABC V 中,内角,,A B C 的对边分别为,,a b c ,且π2sin 6a C b c ⎛⎫+=+ ⎪⎝⎭.(1)求A ;(2)若O 为ABC V 的外心,D 为边BC 的中点,且1OD =,求ABC V 周长的最大值.【答案】(1)π3(2)【解析】【分析】(1)由正弦定理结合三角恒等变换进行化简即可求解;(2)利用向量表示出1122OD OB OC =+uuu r uu u r uuu r,由余弦定理结合基本不等式、三角形周长公式即可求解.【小问1详解】由已知π2sin 6a C b c ⎛⎫+=+ ⎪⎝⎭及正弦定理得:312sin sin cos sin sin 22A C C B C ⎛⎫+=+ ⎪ ⎪⎝⎭,由()()sin sin πsin sin cos cos sin B A C A C A C A C ⎡⎤=-+=+=+⎣⎦得:sin sin cos sin cos cos sin sin A C A C A C A C C +=++,sin cos sin sin A C A C C =+,又sin 0C ≠,cos 1A A =+,即π2sin 16A ⎛⎫-= ⎪⎝⎭,因为()0,πA ∈,所以ππ5π,666A ⎛⎫-∈- ⎪⎝⎭,所以ππ,66A -=解得π3A =.【小问2详解】因为O 为ABC V 的外心,且由上问知π3A =,所以2π23BOC A ∠=∠=,设OB OC R ==(R 为ABC V 的外接圆半径),因为D 为边BC 的中点,且1OD =,所以在OBC △中易得:1122OD OB OC =+uuu r uu u r uuu r,所以2221112πcos 4423OD OB OC OB OC =++ ,即22211121cos 4423πR R R =++,解得:2R =,在OBC △中由余弦定理可得:2222π2cos123BC OB OC OB OC =+-=,解得BC a ==在ABC V 中由余弦定理可得:()2222π2cos3123a b c bc b c bc =+-=+-=,由基本不等式22b c bc +⎛⎫≤ ⎪⎝⎭可得:()223122b c b c +⎛⎫+-≤ ⎪⎝⎭,当且仅当b c =时等号成立,所以()21124b c +≤,即b c +≤.所以ABC V 周长ABC C a b c =++≤+=V当且仅当b c ==时等号成立.故ABC V 周长的最大值为16.在ABC V 中,内角A ,B ,C 的对边分别为a ,b ,c ,且tan tan tan tan 1B C B C ++=,1b =,c =.(1)求a ;(2)如图,D 是ABC V 外一点(D 与A 在直线BC 的两侧),且AC CD ⊥,45CBD ∠= ,求四边形ABDC 的面积.【答案】(15(2)136【解析】【分析】(1)首先根据两角和的正切公式求()tan B C +,即求角A ,再根据余弦定理求解;(2)根据诱导公式求解sin BCD ∠,以及两角和的三角函数求sin D ,再根据正弦定理求BD ,最后根据面积公式,即可求解.【小问1详解】由条件可知,tan tan 1tan tan +=-B C B C ,所以()tan tan tan 11tan tan B CB C B C++==-,所以45B C += ,即135A = ,所以2cos 2A =-,则22222cos 1221252a b c bc A ⎛=+-=+-⨯⨯-= ⎪⎝⎭,所以5a =;【小问2详解】15225cos 5215ACB ∠==⨯⨯,()25sin sin 90cos 5BCD ACB ACB ∠=-∠=∠=,5cos 5BCD ∠=,()()sin sin 45sin cos 225510D BCD BCD BCD ⎛=∠+=∠+∠=⨯+= ⎝⎭ ,BCD △中,sin sin BC BD D BCD =∠,即sin sin 3BC BCD BD D ⋅∠==,所以15sin 4523BCD S BC BD =⨯⨯= ,11sin13522ABC S AC AB =⋅⋅= ,所以四边形ABDC 的面积为5113326+=.17.已知平面向量(,)m a b = ,(sin ,cos )n x x ωω=,且2m n = ,其中0a >,0ω>.设点(0,1)和11π(,0)12在函数()f x m n =⋅ 的图象(()f x 的部分图象如图所示)上.(1)求a ,b ,ω的值;(2)若()G x y ,是()y f x =图象上的一点,则1(2,)2K x y 是函数()y g x =图象上的相应的点,求()g x 在[0,π]上的单调递减区间.【答案】(1)a =1b =,2ω=;(2)π[,π]3【解析】【分析】(1)由2m n =得2=,利用向量数量积计算公式和辅助角公式化简得()2sin()f x x ωϕ=+,根据题设条件列出三角方程组,结合图象即可求出a ,b ,ω的值;(2)由题意中点的变换求得π()sin(6g x x =+,利用正弦函数的图象特点即可求得()g x 在[0,π]上的单调递减区间.【小问1详解】因(,)m a b = ,(sin ,cos )n x x ωω=,由2m n =2=,由()(,)(sin ,cos )f x m n a b x x ωω=⋅=⋅sin cos )2sin()a x b x x x ωωωϕωϕ=+=+=+,其中tan b aϕ=,因点(0,1)和11π(,0)12在函数()f x m n =⋅ 的图象上,则有,2sin 111πsin()012ϕωϕ=⎧⎪⎨+=⎪⎩①②,结合图象,由①可得πZ π2,6k k ϕ=+∈,将其代入②式,可得11πππ,Z 126n n ω+=∈,即212,Z 1111n n ω=-+∈,(*)由图知,该函数的周期T 满足311π412T T <<,即3π11π2π212ωω<<又0ω>,则有18241111ω<<,由(*)可得2ω=,故π()2sin(2)6f x x =+.由320b a a ⎧=⎪=⎪>⎩解得,1a b ⎧=⎪⎨=⎪⎩,故a =1b =,2ω=;【小问2详解】不妨记12,2x x y y ''==,则,22x x y y ''==,因()G x y ,是()y f x =图象上的一点,即得π22sin()6y x ''=+,即πsin(6y x ''=+,又因1(2,)2K x y 是函数()y g x =图象上的相应的点,故有π()sin()6g x x =+.由ππ3π2π2π,Z 262k x k k +≤+≤+∈,可得π4π2π2π,Z 33k x k k +≤≤+∈,因[0,π]x ∈,故得ππ3x ≤≤.()g x 在[0,π]上的单调递减区间为π[,π]3.18.已知函数()2()e xf x x mx n =++,m ,n ∈R .(1)当24m n =时,求()f x 的最小值;(2)当2m =-时,讨论()f x 的单调性;(3)当0m n ==时,证明:0x ∀>,()ln 1f x x >+.【答案】(1)0(2)答案见解析(3)证明见解析【解析】【分析】(1)利用求导判断函数的单调性,即得函数的极小值即最小值;(2)利用求导,就导函数中的参数进行分类,分别讨论导函数的符号,即得函数的单调性;(3)将待证不等式2e ln 1xx x >+等价转化为3e ln 1x x x x +>,设3e ln 1(),()x x g x h x x x+==,依题意,只需证在0x >时,min max ()()g x h x >成立,分别求m m ax in (),()h x g x 即可得证.【小问1详解】当24m n =时,22()()e 4x m f x x mx =++,22()[(2)2()e ()2)e 42x x m f x x m x m m m x x '=+++=++++,由()0f x '>,可得22m x <--或2mx >-,由()0f x '<,可得222m m x --<<-,即()f x 在(,2)2m -∞--和(,)2m -+∞上单调递增;在(2,)22m m---上单调递减,x →-∞时,()0f x →,x →+∞时,()f x →+∞,故2mx =-时,()f x 取得极小值也即最小值,为()02m f -=.【小问2详解】当2m =-时,()2()2e xf x x x n =-+,函数的定义域为R ,()2(e 2)xx f x n =+-',当2n ≥时,()0f x '≥恒成立,故()f x 在R 上为增函数;当2n <时,由()0f x '=,可得x =,故当x <x >时,()0f x '>;即()f x 在(,∞-和)∞+上单调递增;当x <<()0f x '<,即()f x 在(上单调递减.综上,当2n ≥时,()f x 在R 上为增函数;当2n <时,()f x在(,∞-和)∞+上单调递增,在(上单调递减.【小问3详解】当0m n ==时,2()e x f x x =,要证0x ∀>,()ln 1f x x >+,只需证2e ln 1x x x >+,即证3e ln 1x x x x+>在(0,)+∞上恒成立.设3e ln 1(),()x x g x h x x x+==,依题意,只需证在0x >时,min max ()()g x h x >.因e ()=x g x x ,2(1)e ()xx g x x-'=,由()0g x '<,可得01x <<,由()0g x '>,可得1x >,故()g x 在(0,1)上单调递减,在(1,)+∞上单调递增,则()g x 在1x =时取得极小值也是最小值,为(1)e g =;因3ln 1()x h x x+=,423ln ()x h x x --'=,由()0h x '=,可得23x e -=,由()0h x '<,可得23x e->,由()0h x '>,可得230x e -<<,故()h x 在23(0,e)-上单调递增,在23(e ,)-+∞上单调递减,则()h x 在23x e -=时取得极大值也是最大值,为22332323ln e ()3e1e (e )h ---==+.因2e e 3>,即min max ()()g x h x >在(0,)+∞上成立,故得证.即0x ∀>,()ln 1f x x >+.【点睛】方法点睛:本题主要考查利用导数求函数的最值、证明不等式恒成立等知识点,属于较难题.证明不等式型如()()f x g x >的恒成立问题,一般方法有:(1)构造函数法:即直接构造()()()F x f x g x =-,证明min ()0F x >;(2)比较最值法:即证明min max ()()f x g x >即可;(3)等价转化法:即将待证不等式左右两边同除以一个式子,使得左右函数的最值可比较.19.已知非零向量(,)a m n =,(,)b p q = ,a ,b 均用有向线段表示,现定义一个新的向量c 以及向量间的一种运算“※”:(,)c a b mp nq mq np ==-+※.(1)证明:c 是这样一个向量:其模是a 的模的 b 倍,方向为将a绕起点逆时针方向旋转β角(β为x 轴正方向沿逆时针方向旋转到b所成的角,且02πβ≤<),并举一个具体的例子说明之;(2)如图1,分别以ABC V 的边AB ,AC 为一边向ABC V 外作ABD △和ACE △,使π2BAD CAE ∠=∠=,(01)AD AEAB ACλλ==<<.设线段DE 的中点为G ,证明:AG BC ⊥;(3)如图2,设(3,0)A -,圆22:4O x y +=,B 是圆O 上一动点,以AB 为边作等边ABC V (A ,B ,C 三点按逆时针排列),求||OC 的最大值.【答案】(1)证明见解析.(2)证明见解析.(3)5.【解析】【分析】(1)根据圆的参数方程设定,a b 的坐标,再依据题意证明即可;(2)依据新定义把,AG BC的坐标表示出来再运算证明即可;(3)掌握平面向量的模的运算和三角函数的最值求法即可解答.【小问1详解】证明:设(,)(cos ,sin ),(,)(cos ,sin )a m n r r b p q R R ααββ====(0,0,,r R αβ>>分别为x 轴正方向逆时针到,a b所成的角,且,[0,2)αβπ∈),则cos cos sin sin cos()mp nq Rr Rr Rr αβαβαβ-=-=+,cos sin sin cos sin()mq np Rr Rr Rr αβαβαβ+=+=+,于是cos()sin((,))Rr a b Rr c αβαβ=++=※,即c Rr a b ==⨯,x 轴正方向逆时针到c 所成的角为αβ+.故:c 是这样一个向量:把a的模变为原来的 b 倍,并按逆时针方向旋转β角(β为x 轴正方向逆时针到b所成的角,且02πβ≤<).例如,1(,),22a b == ,则111,1222((0,2)2c a b ⨯+=== ※,1,2a b == ,a 与x 轴正方向的夹角为π3,b 与x 轴正方向的夹角为6π,将a的模变为原来的2倍,并按逆时针旋转π6,即可得c .【小问2详解】证明:记(,),(,)AB m n AC p q ==,根据新定义,可得()3π3πcos ,sin ,22AD AB n m λλλ⎛⎫==- ⎪⎝⎭ ※,同理(cos ,sin )(,)22q p A AE C ππλλλ==- ※,所以1()()()()222n q p m AG A AD E λλ--=+= ,而(,)BC AC AB p m q n =-=--,所以1[()()()()]02AG BC p m n q q n p m λλ⋅=--+--= ,故:AG BC ⊥.【小问3详解】解:设(,)B u v ,则224,(3,)u v AB u v +==+,())3ππ13cos ,sin 3,,,33222222u u v AC AB u v λ⎛⎫⎛++⎛⎫==+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭※※,所以333(3)33333(3,0)(,)(,)222222u u v u v OC OA AC ++--++=+=-+-+=,所以OC ===.设2cos ,2sin (02)u v θθθπ==≤<,则OC == ,当πsin 16θ⎛⎫+= ⎪⎝⎭,即π3θ=时,max 5OC = .【点睛】此题考查了圆的参数方程;平面向量数量积的性质,以及三角函数最值.。
余切30度函数

余切30度函数“余切30度函数”是数学中一种重要的解决微积分问题的函数,它定义了数学中解决一些问题的基本概念,并用于许多领域。
本文旨在探究“余切30度函数”的概念、性质以及它在日常生活中的应用。
一、概念“余切30度函数”是一种函数,它用一个参数x来确定一个实数值,称为f (x)。
它的定义为:f (x) = tan30° arctan (x) + c,其中x是余切的参数,c是常量,30°是指给定的角度。
简言之,余切30度函数的解析解是f (x) = tan30°×arctan (x) + c,其中tan30°指的是正切的值,arctan(x)是反正切的值,c是一个常量。
二、性质1、余切30度函数是一个单调函数,当x增大时,f (x)也会随之增大,反之,当x减小时,f (x)也会随之减小。
2、余切30度函数是一个周期函数,它的周期为π/2。
3、余切30度函数的极值是γ,其值可以用公式γ = tan30°×arctan (x) + c来表示,其中c是一个常数。
三、应用余切30度函数在实际应用中具有重要意义。
它可以用于研究超声波传播、水波传播、电磁波传播等物理问题,以及解决机械制造的复杂问题。
余切30度函数还可以用于求解各种数学问题,例如求解某些微分方程、求解特殊数值问题等。
此外,余切30度函数也可以应用于日常生活中。
例如,当我们在建筑中布置家具时,就可以使用余切30度函数,以便最大限度地将房间里的空间利用起来;同时,在做一些精确的测量时,也能够利用余切30度函数,更加精确地计算出最终的结果。
四、结论“余切30度函数”是一种重要的数学函数,它有着重要的概念、性质和应用,能够帮助我们更好地理解和解决一些复杂的数学问题。
另外,它还在日常生活中有着广泛的应用,能够帮助我们更好地利用空间,做出更准确的测量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
458.
【5)刘伟.李若瑜。陈琼.等.高效液相色谱测定指甲真菌病患者甲中 特比萘芬水平的研究【J】.中国临床药理学杂志.1999。15(6):435.
439.
碘伏联合湿润烫伤膏治疗新生儿红臀的疗效观察
作者简介:王建平,女(1977.3.)。毕业于浙江中医学院。职称:护师。联系电话:0577-888162U ・166・
万方数据
治疗组口服特比摹芬片250rag.1日1次.连服
7d后,指甲真菌感染患者隔日服用1次250rag.连用7周,趾甲真菌感染患者连服9周,治疗组患者同时加用30%冰蜡醢外涂.1日2次。连用时 间分别为8周和10周。对照组口服特比萘芬250mg.1日1次.指甲真菌病患者连服8周.趾甲真菌感染患者连服lO周。分别干治疗前、停药
ch哪煳isU】.Br J DeⅢtoI.2003,149(65):15.18.
2001.145(60):9-13.
【2】Evmls EG.The mtiomIle tot combination therapy(J).Br J Dermat01.
【3】张学军.何春涤.郑捷。等.皮肤性病学【M】.第六版.北京:人民
0.05)。 衰I停药时两组蓝床疗效比较
2.2安全性评价治疗组在用药期间有2例在服药第l~3 周出现轻度恶心、食欲不振、轻度腹泻等胃肠道反应.未停药. 嘱饭后服用后.症状逐渐消失;1例趾甲真菌感染患者停药时 肝功能检查出现JU,T轻度升高(71U).加服护肝片后,在加 服护肝片后1周、3周、5周的肝功能恢复正常.到半年和1年 后的复查中也未见肝功能异常。治疗组不良反应发生率为
口服特比綦莽联合外用30%冰醋鞋治疗指(趾)甲真菌感染临键词:特比萘芬;甲真菌病;30%冰醋琏
中田分类号:R969.4文献标识码:B文章编号:1006.376512009)-06.0165.02
甲真菌病的治疗仍是目前较为棘手的问题。口服抗真菌 药物虽可取碍满意的疗效,但复发和再感染率较高,且治疗费 用较高【I.2】。如何提高治疗效果.降低复发率及治疗费用.成 为治疗甲真菌病急需解决的难题。我们采用口服特比萘芬 (商品名:丁克)联合外用30%冰醋酸治疗甲真菌病取得较好 的临床疗效.现报告如下。 1资料和方法 1.I入选标准所有患者均有一个或多个指(趾)甲有典塑 的甲真菌病的临床表现,直接镜检真菌阳性。符合甲真菌病的 诊断C33.1个月内未接受过全身或者局部的抗真菌药治疗.无 特比萘芬过敏史、无肝肾功能不全、无妊娠或哺乳、无严重系 统性疾病.年龄≥18岁、≤65岁。同意接受我们的治疗方法. 并能坚持完成治疗者。 1.2病例基本情况病例均选自我院门诊病人.共115例. 其中治疗组70例,男31例,女39例。年龄20,65岁.平均 37.8岁.指甲真菌病的33例,趾甲爽菌病的37例.病程9月 一17年.平均6.2年;对照组45倒.男20例.女25例.年龄 21--64岁.平均35.6岁,指甲真菌病的21例.趾甲真菌病的 24例。病程11月~15年,平均5.6年。两组年龄情况、指 (趾)甲真菌病受累程度等基本情况无显著性差异.两组具有 可比性。 1.3治疗方法选择一个感染最重的指(趾)甲作为靶甲(除 小趾甲外).治疗组服用特比萘芬片每次250mg.1日1次。连 服7d.然后改服隔日口服每次250rag,指甲真菌病连服7周. 趾甲真菌病连服9周,同时联用30%冰醋酸(本院自制,用 30mL冰醋酸加蒸馏水至100mL配置面成)外涂,先用小刀或 指甲锉尽量去除病甲.再用棉签将30%冰醋酸涂于病甲上. 每天2次.指甲真菌病连用8周。趾甲真菌病连用lO周。对 照组按特比萘芬片说明书规定给予特比萘芬片250rag 1次/ d,指甲真菌病连服8局,趾甲真菌病连服10周。分别于治疗
对照组在用药期间有4例出现恶心、腹胀、食欲不振、轻 度腹泻等胃肠道反应。未停药.嘱饭后服用后。症状逐渐消失; 1例趾甲真菌感染患者在用药第9周出现皮疹,因疗程接近 结束并在给予扑尔敏片后好转并消失.所以没有没有停药.直 到疗程结束;1例指甲真菌感染患者和1例趾甲菌感染患者 在停药时肝功能检查出现JuT轻度升高(分别是69U和 78U)。加服护肝片后,在加服护肝片后1周、3周、5周的肝功 能恢复正常.到半年和1年后的复查中也未见肝功能异常。 对照组不良反应发生率为15.6%。与治疗组间药品不良反 应发生率有显著性差异(12=4.382。P<0.05)。 2.3药物经济学分析从药物经济学角度分析。由于其他检 测项目和用药时间相同。所以剔除肝肾功能检查等相同费用 因素.只对药品费用进行分析。治疗组由于在连续用药7天 后采用隔日给药,所以费用相对较低,以指(趾)甲真菌病治愈 为临床治疗目的.治疗组治疗1例需用药费453.30元(趾甲 543.40元)。而对照组由于按说明书给药,需用药费800.∞ 元(趾甲1001.00元)。
作者简介:周其刚.男(1978.)。全科主治医师.彭埠镇社区卫生服务 中心副主任。毕业于浙江大学医学院临床医学专业。从事全科门诊 工作。联系电话:0571,86494294
前、停药时、停药后半年、停药后1年.进行临床症状和体征评 价及血、尿常规和肝肾功能检查,并进行真菌镜检,并记录不 良反应发生情况。 1.4疗效判定标准痊愈为病甲完全消失,新长出甲板光 滑、平整.真菌学检查阴性。显效为病甲消退≥60%.真菌镜 检阴性;好转为30%≤病甲消退<60%.真菌镜检阴性或阳 性;无效为病甲消退<30%,真菌镜检阳性。有效率是指痊愈 和显效的病例数占治疗例数的比例。治愈率就是痊愈病例数 占治疗例数的比匆。 1.5统计学处理用SPSS 10.0软件统计及卡方检验。 2结果 2.1治疗结果两种给药方法给药后。在停药时、停药后半 年、停药后1年的临床疗效情况(见表1、2、3)。治疗组和对 照组的治愈率和有效率比较无显著性差异(P值均大于
4.3%。
・165・
万方数据
海峡药学2009年第21卷第6期
衰2停药后半年两组临床疗效比较
3讨论 特比萘芬是人工合成的丙烯胺类抗真菌药。主要通过抑 制角鲨烯环氧化酶。从而阻断麦角固醇合成旁路中角鲨烯环 氧化物的转化,麦角固醇是真菌细胞壁的组成成分.其缺乏使 真菌生长受抑制.同时角鲨烯在细胞内堆积可导致真菌死亡. 其抗菌谱广。杀菌力强。对皮肤癣菌尤为敏感b-4】。特比萘芬 通过甲床和甲母质两条途径向甲中进行扩散.进入甲的药物 能以较高浓度存在较长的时间.停药后8~12周甲中药物浓 度明显高于特比萘芬对皮肤癣菌的MICC5J。 本临床观察发现.使用特比萘芬时.先连续给药7d。然后 再隔日给药7—9周和加用30%冰醋酸外用的临床效果与连 续给药8~lO周的临床效果相当(无显著性差异)。在停药 时、停药后半年、停药后1年。治疗组的治愈率分别为 52.9%、77.1%,90.O%.对照组的治愈率分别为57.8%、 80.0%、91.1%。而治疗组的不良反应发生率为4.3%.对照 组的不良反应发生率为15.6%.两组间不良反应发生率有显 著性差异。治疗组不良反应发生率明显低于对照组.这可能与 治疗组在连用7天后给用隔日疗法有关。而从药物经济学角
Strait Pharmaceutical
Journal
Vol 21 No.6 2009
口服特比萘芬联合外用30%冰醋酸治疗甲真菌病的临床疗效观察
周其刚1。王丽英2(1.浙江省杭州市彭埠镇社区卫生服务中心杭州310017;2.浙江省杭州市九堡镇社区卫生 服务中心杭州310017)
摘要:目的观察口服特比摹芬联合外用30%冰醋酸治疗甲真菌病的疗效及安全性。方法
匀涂上英宝湿润瑟伤量约lcm犀。尿布包好;,t熙组创面处用温水清洗擦干后均匀涂上的lcm厚的美宝湿润烫伤膏。结果
垃、有效、无效例敷分别为28…4 0和20…6
2
两组的痊愈、王
3
5。总有效率分别为34%和29%。两组治愈丰比较.P<O.05.甚有效牟比较.P<O.05.均有王著
tt,lt异。结论
吴宝湿润蹙伤f治疗ttiJt.tt.'It-具有独特疗兰.且无不良反应。
王建平,蒋芳,娄洁蝉(温州医学院附属育英儿童医院新生儿科温州325000}
摘要:目的观察安伏联合湿涸蹙伤量治疗新生儿红臀的疗效。方法
观察组轻中度l工f用湿水清洗饕干后.在创面涂o.5%碘伏待干.再均
匀涂上湿润烫伤膏约lent厚.包好尿布.t度红臀用温水清洗饕干后.在创面涂0.5%其伏待干.再用鹅颈灯距臀部25era照射10—15rain.再均
时、停药后半年、停药后1年.进行临床症状和休征评价及丘、尿常规和肝肾功能检查,并进行真苗镜检.并记录不良反应发生情况。结果
在
停曲时、停药后半年、停药后1年.治疗组的治愈率分别为52.9%、77.1%.90.O%,对照组的治愈率分别为57.8%、80.O%、91.1%。治_,,组和
对照组在治愈率和有效率上无量著性盖异,但对照组的治愈一个患者所需的药品量用高于治疗缸,不良反应发生率也显著高于对照组。结论
度分析看出。治疗组和对照组在在治疗效果相当的情况下。治 疗组所需的药品费用比对照组低。 总之,特比萘芬连续给药7d后.再隔日给药并联用30% 冰醋酸外用能在有效降低治疗费用的同时.增加患者用药的 安全性,同时临床疗效不受影响。是临床上治疗指(趾)甲真 菌病值较为安全和理想的给药方法。
参考文献 (tJOlafsson JH。Sigurgeirsson B.Baran R.Combination therapy for ony-
