电路 第8章习题 相量法
chapter08相量法电路原理

3. 旋转因子
复数 ejy = cos y + jsin பைடு நூலகம் = 1∠y
Aejy
A逆时针旋转一个角度y ,模不变
j
e2 cosjsinj
ej( 2)c 2 o 2 s) 2 (js i 2 n) (j
j I
Im
I
Im A (t)[ ] 2Isiw n t (y)
wy i2 I sit n) ( A ( t)2 I e jw t ( y )
A(t)还可以写成
A(t) 2Iejyejwt 2 I ejwt
复常数
称
I Iy
为正弦量 i(t) 对应的相量。
i(t)2Isiw n t (y) II y
旋转相量在纵轴上的投影就是正弦函数
请看演示
三. 相量图
ωy y i(t)2 I sitn i() I I i
wy y u (t)2 U sitn u ( ) U U u
U
I
yu yi
四. 相量运算
(1) 同频率正弦量相加减
u1(t) 2U1s iw nt (y1)Im2(U 1ejwt)
(2) 角频率(angular frequency) w
(3) 初相位(initial phase angle) y
i i(t)=Imsin(w t+y)
Im
wt
y
波形图
ii
000 0 0
t
yy y =0y =/2 y =-/2
一般 |y |
二、同频率正弦量的相位差 (phase difference)。
电路原理 第八章_相量法

复数 复数
—
孙惠英 shy@
上页
下页
返回
第8章
4、正弦量的相量表示法(续)
—
已知正弦量 220√ 2 cos ( ω t-35° ) 有效值相量 最大值相量 220/ -35° — 220√ 2 /-35°
已知 相量 10/45° and 正弦量的角频率ω 相应的正弦量 — 10 √ 2 cos( ωt + 45° )
0 ωt1
ωt2
ωt
φ
图8-5 用旋转矢量表示的正弦量
孙惠英 shy@
上页
下页
返回
第8章
4、正弦量的相量表示法 F = ⎪F⎪e j(ω t + ϕ )
ejθ = cosθ + jsinθ
设:有一复数
欧拉公式
F = ⎪F⎪ej(ωt + ϕ ) = ⎪F⎪cos(ωt + ϕ) + j⎪F⎪sin(ωt +ϕ) Re [F] = ⎪F⎪cos(ωt + ϕ ) Im [F] = ⎪F⎪sin(ωt + ϕ )
返回
第8章
三、旋转因子
/ϕ 旋转因子: e jϕ = 1 — A = ⎪A⎪ejα Aejϕ = ⎪A⎪ejαejϕ = ⎪A⎪ej(α+ϕ ) ejπ/2 = j1 e-jπ/2 = − j1
+j
Aejϕ
ϕ α
0
A
+1
e-jπ = − 1
孙惠英 shy@
上页
下页
返回
第8章
ϕ 12 = ϕ 1- ϕ 2 —— u1 超前于 u2 的相角 ϕ 21 = ϕ 2- ϕ 1 —— u2 超前于 u1 的相角
《 电路》第8章 相量法

0
1 UC 5. j C I C jC
3. I m j CUm Um
6. U L j LI L
di L 7. u C dt
UL Um 4. X L IL I m
返 回
上 页
下 页
例5
A
已知 UAB 50V, UAC 78V, 问:UBC ?
1
i2 (t ) 3 cos(100 π t 300 )
返 回 上 页 下 页
同样可以建立正弦电压与相量的对应关系:
u(t ) 2U cos( t θ ) U Uθ
例1
i 141.4 cos(314t 30o )A 已知 u 311.1cos(3 14t 60o )V
试用相量表示i, u . 解
I 10030 A,
o
U 220 60o V
例2
解
已知 I 5015 A, f 50Hz .
试写出电流的瞬时值表达式。
i 50 2cos( 314t 15 ) A
返 回
上 页
下 页
例1 试判断下列q
F Re
返 回
上 页
下 页
例
解
已知正弦电流波形如图,=103rad/s,
1.写出 i(t) 表达式;2.求最大值发生的时间t1
i(t ) 100 cos( t ) 10 t 0 50 100 cos
3
100 50 o
i
π 3
π 3
3
t t1
由于最大值发生在计时起点右侧
I +
邱关源《电路》第八章相量法2

17
例1: 已知: R1 1000 , R2 10 , L 500mH , C 10F , BUCT
U 100V , 314rad / s , 求:各支路电流。
i2 R1 i1
i3 C
+
R2
_u
L
I1
I2 R1
I3
j 1 C
+
R2
_ U
Z1
Z2
jL
解:画出电路的相量模型
0.5770
A
瞬时值表达式为:
i1 0.6 2 sin(314 t 52.3 ) A i2 0.181 2 sin(314t 20 ) A i3 0.57 2 sin(314 t 70 ) A
解毕!
20
9. 2 阻抗(导纳)的串联和并联
一. RLC串联电路
用相量法分析R、L、C串联电路的阻抗。
2I R
.
.
1 UR UC
24
BUCT
练习:P188 8—11 12
25
作业
BUCT
习题:8-16 9-1 (b)、(f) 9-5 预习:第9章
26
j
G 导纳三角形
(二) R、L、C 元件的阻抗和导纳
(1)R:ZR R , YR 1 R G
(2)L:Z L jL jX L ,
1
1
YL
j
jL
L
jBL
(3)C:ZC
j 1
C
jX C ,
YC jC jBC
15
(三)阻抗和导纳的等效互换
º R
Z
18
I1
I2 R1
邱关源《电路》第五版 第八章 相量法
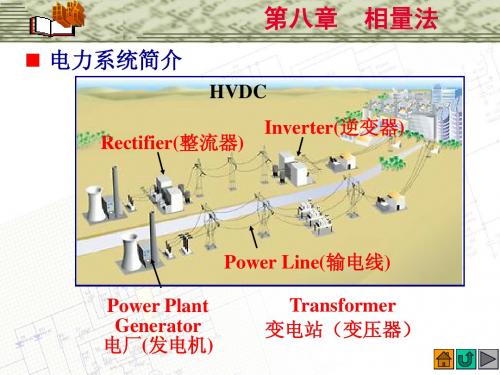
电力系统简介
HVDC Rectifier(整流器)
相量法
Inverter(逆变器)
Power Line(输电线) Power Plant Generator 电厂(发电机) Transformer 变电站(变压器)
第八章 复数(自学) 正弦量 相量法的基础 电路定律的相量形式
相量法
§8-1 复数(自学)
Charles Proteus Steinmetz
(1865~1923)
§8-3 相量法的基础
一、正弦量的相量
i 2I cos(t i )
设有一个复指数函数
2 Ie j( t i )
2 Ie j( t i ) 2 I cos( t i ) j 2 I sin( t i ) Re[ 2 Ie j( t i ) ] 2 I cos( t i ) i
1 I T
T
0
1 i dt T
2
T
0
2 I m cos2 ( t i )dt
Im 0.707 I m 2
I m 2I
i I m cos( t i ) 2I cos(t i )
§8-2 正弦量
四、同频正弦量的相位差 同频正弦量相角之差称为相位差。用 表示。
i
u
反 相
t
u
正 交 0
i t 0
1 2
i
t
电 压 超 前 电 流
§8-3 相量法的基础
The notion of solving ac circuits using phasors
was first introduced by Charles Proteus Steinmetz
第08章 相量法

2 , e
j
复
数
Im
ɺ + jI
π
2 =+j
ɺ I
π
2
= cos
j−
π
2
+ j sin
0
Re
ɺ − jI
α =−
π
2
π
2
, e
= cos(− ) + j sin(− ) = − j 2 2
π
π
ɺ −I
2>、反向因子-1 、反向因子
α = ±π , e j ±π = cos(±π ) + j sin(±π ) = −1
def
T
0
有效值也称均方根值 有效值也称均方根值(root-meen-square,简 也称均方根值 , 记为 rms。) 。
8. 1 正弦量的基本概念
电流有效值的物理意义: 电流有效值的物理意义: 周期性电流 i 流过电阻 R,在一周期 内吸收的 ,在一周期T 电能,等于一直流电流I 流过R 在时间T 电能,等于一直流电流 流过 , 在时间 内吸收的电 的有效值。 能,则称电流 I 为周期性电流 i 的有效值。 i(t) 如图: 如图: T 2
m
8. 2
一、复数A表示形式 复数 表示形式
复
数
Im b A
在平面上, 在平面上,由O指向A的有向 指向 线段(向量), ),表示复数 线段(向量),表示复数A。 1、直角坐标表示 、 代数形式: 代数形式:
O Im b
a A |A|
Re
A=a+jb
Re[A]=a Im[A]=b
1 j = =−j j j⋅ j
8. 1 正弦量的基本概念
电路分析相量法

量的相量乘以 jω ,即表示di/dt 的相量为
j I I( i 90o )
该相量的模为ωI ,辐角则超前原相量π/2 。
对 i 的高阶导数 dni/dtn ,其相量为 ( j )。n I
3)正弦量的积分
设 i 2I cos( t i ),则
idt Re[ 2Ie j t ] dt Re[ (
F1F2 | F1 | 1 | F2 | 2 | F1 || F2 | (1 2 )
可见复数的乘法运算使用指数形式或极坐标形式较为简便。
3)除法运算
a)代数形式
F1 F2
a1 a2
jb1 jb2
(a1 (a2
jb1 )(a2 jb2 )(a2
jb2 ) jb2 )
(a1a2
b1b2 ) j(a2b1 a22 b22
设 F1 a1 jb1 , F2 a2 jb2 ,则
F1 F2 (a1 jb1 ) (a2 jb2 ) (a1 a2 ) j(b1 b2 )
平行四边形法则:
+j F1 +F2 F1
F2 o
+1
+j F1
F2 o
F1-F2 +1
2)乘法运算 a)代数形式
F1F2 (a1 jb1 )(a2 jb2 ) (a1a2 b1b2 ) j(a1b2 a2b1 )
di d Re[ 2Ie j t ] Re[ d ( 2Ie j t )] Re[ 2( j I)e j t ]
dt dt
dt
Re[ 2 Ie ] j( ti 90o ) 2 I cos( t i 90o )
上式表明:
复指数函数实部的导数等于复指数函数导数的实部;
第8章-相量法-习题库

第八章相量法一、填空题1、正弦电压()cos()u u t t ωθ=+,对应的相量表示为 。
2、若()10cos(31430)i t t =- ()5sin(31430)u t t =-,则i u 与的相位差为 。
3、已知正弦交流电压010cos(31430)V u t =+,该电压有效值U = 。
4、在纯电感交流电路中,电压与电流的相位关系是电压_____电流900,感抗X L =_____,单位是____。
5、在纯电感正弦交流电路中,若电源频率提高一倍,而其他条件不变,则电路中的电流将变______。
6、在纯电容正弦交流电路中,已知I=5A,电压cos(314)V U t =,电容量C=_____。
7、在纯电容正弦交流电路中,增大电源频率时,其他条件不变,电容中电流I 将____。
8、一个感抗20Ω的纯电感两端电压是10c o s (30)V ,u t ω=+则通过它的电流瞬时值为__ _A 。
二、选择题1、两个同频率正弦交流电的相位差等于1800时,则它们相位关系是____。
A 、同相B 、反相C 、相等 2、正弦交流电的最大值等于有效值的___倍。
A 、2 B 、 2 C 、 1/2 3、在纯电容正弦交流电路中,复容抗为____。
A 、c j ω- B 、 c j ω/- C 、 c j ω/ 4、在纯电容正弦交流电路中,下列各式正确的是_____。
A 、C i U C ω=B 、I UC ω∙∙= C 、I U C ω= D 、/i U C = 5、若某元件的端电压为05cos(31435)V u t =+,电流02cos(314125)A i t =+,i u 、 为关联方向, 则该元件是___。
A 、电阻B 、电感C 、电容 6、任意一个相量乘以j 相当于该相量 。
A 逆时针旋转90o B 顺时针旋转90o C 逆时针旋转60oD 逆时针旋转60o 三、判断题1、正弦量的初相角与起始时间的选择有关,而相位差则与起始时间无关。
电路(第八章)相量法

或
a | A | cosθ b | A | sinθ
Im A2
图解法
(1)加减运算——采用代数形式 若 则
A1=a1+jb1, A2=a2+jb2 A1±A2=(a1±a2)+j(b1±b2)
A1
0 Re
(2) 乘除运算——采用指数形式或极坐标形式
若 则:
A1=|A1| 1 ,A2=|A2| 2
Im 2I
i ( t ) I m cos(w t Ψ ) 2 I cos(w t Ψ )
同理,可得正弦电压有效值与最大值的关系:
U
1 2
Um
或
U m 2U
若一交流电压有效值为U=220V,则其最大值为Um311V; U=380V, Um537V。
注 (1)工程上说的正弦电压、电流一般指有效值,如设
j >0, u超前ij 角,或i 落后u j 角(u 比i先到达最大值); u, i u i
yu yi j j <0, i 超前 uj 角,或u 滞后 i j 角,i 比 u 先到达最大值。
O
wt
特殊相位关系:
j = (180o ) ,反相:
u, i u u i 0 iw t
j = 0, 同相:
直流I
物 理 意 义
R
交流i
R
W RI T
2
W Ri ( t )dt
T 2 0
电流有效 值定义为
1 T 2 I 0 i (t )dt T
def
有效值也称均方根值 (root-meen-square)
同样,可定义电压有效值:
正弦电流、电压的有效值 设 i(t)=Imcos(w t+ )
电路第五版第8章相量法(xs)

o
∴
i(t ) u(t )
I 100 30
o
U 220 60
o
2. 相量运算 (1) 同频率正弦量相加减
u 1 ( t ) U m1 cos( w t + Ψ u 2 ( t ) U m2 cos( w t + Ψ ) Re( 1 ) Re( 2
jw t
182.5 + j132.5 225.5 36o
(4) 旋转因子: 复数 ejq =cosq +jsinq =1∠q A• ejq 相当于A逆时针旋转一个角度q ,而模不变。故 把 ejq 称为旋转因子。 A• ejq Im
A• ejq =|A| qA + q
0
q
A Re
特殊旋转因子:
ejp/2 = j 也是旋转因子,逆时针转了90。 e-jp/2 = - j, 顺时针转了90 。
jθ 1 |
e
j( θ 1 θ 2 )
| A1 | | A2 |
θ1 θ
2
乘法:模相乘,角相加; 除法:模相除,角相减。
例1.
5 47 + 10-25 = (3.41+j3.657) + (9.063-j4.226) =12.47 - j0.567 = 12.48 -2.61
+
1 jω C
U
1 jω C
I C jX C I C
U
U
-
IC=w CU
i=u+90°
IC
相量模型 B C = w C, 称为容纳,单位为 S
u
第8章 相量法

] Re(Ume e
jθ jωt
)
Um Umej θ Umθ - - - U(t)振幅 量 相
根据正弦量和相量的表示可以画出其波形图和相量图 (下页)
21
电压U正弦波形图和 相量图:
1、根据u(t) Umcos(ωtθ)
U(t) Um θ ωt +j
Um
θ
2、根据 量Um Umθ 相
第八章 相量法(173) ——线性正弦稳态电路分析方法
$8-1 复数(复习) 一、复数的多种表示形式 1、复数F的直角坐标形式(代数形式):F=a+jb a 、 b 均为实数, a实部, b虚部。 ( j 1)
1
2、复数F在复平面上的向量表示: F=a+jb
F a 2 b 2 ...模
O
2、F2 1.2152
3、F3 5180
实部(a):shift 虚部(b):RCL
O
1.06 j0.56 5
利用计算器转换功能: POL( r,θ)= tan
三、复数的四则运算: 1、复数加减运算(代数形式) 若F1= a1+jb1 F2=a2+jb2
6
F1+F2= (a1+jb1)+(a2+jb2) = (a1 + a2)+ j(b1 +b2) F1-F2= (a1+jb1) -(a2+jb2) = (a1 - a2)+ j(b1 -b2)
14
u
t
t
i
u i 0 , u 与 i 同相
u i
u i 0 , u 超前 i
u
t
i
第8章_相量法

R
W直 =I 2RT
T i 2 ( t ) Rd t R W交 0
例 周期电压如图所示。求其有效值U。 u(t)/V 2 1 0
1 2 3 4 5 6
t/s
解 根据有效值的定义,有
1 U T
T 0
u 2 ( t )dt
2 3 1 1 2 2 2 0 1 dt 1 2 dt 2 0 dt 1.29 V 3
有效值也称均方根值(root-mean-square,简记为 rms。)
正弦电压有效值与最大值的关系: 1 U Um 或 U m 2U 2
工程上说的正弦电压、电流一般指有效值,如设备铭牌 额定值、电网的电压等级等。但绝缘水平、耐压值指的是 最大值。 测量中,电磁式交流电压、电流表读数均为有效值。 * 注意区分电压、电流的瞬时值、有效值、最大值的符号。
频率f : 每秒钟完成循环的次数,单位:Hz(赫兹) 。
关系 : f 1 T
2f
2 T
小常识
* 电网频率: 中国 50 Hz
美国 、日本 60 Hz * 有线通讯频率:300 - 5000 Hz
* 无线通讯频率: 30 kHz - 3×104 MHz
i(t)=Imcos( t + φ)
例 + u + u1
U1 U2 U3
u1 (t ) 3 2 cos 314t V
-
u2 (t ) 4 2 cos (314t 90o ) V 求u。 + u2 u(t ) u (t ) u (t ) 5 2 cos (314t 53.1o ) V 1 2 U2 490 V U1 30o V
u, i u i O
天津理工电路习题及答案 第八章 相量法

第八章 相量法8.1 学习指导8.1.1 学习要点(1)正弦量及其三要素。
(2)相位差的概念。
(3)相量的概念及其性质。
(4)KCL 、KVL 的相量形式。
(5)R 、L 、C 元件VAR 的相量形式。
8.1.2内容概述1.正弦量1)正弦量的时域表达式(以i 为例):)t cos(I i m ψω+= ①2)正弦量的三要素、有效值的定义 (1)角频率、频率、周期(要素之一) 角频率:dt)t (d ψωω+=,即正弦量单位时间内变化的电角度,单位:rad /s(弧度/秒)。
频率:f —单位时间内正弦量变化的周波数,单位:Z H周期:T —正弦波变化一次所需要的时间,即一个完整周波在时间轴上的宽度,单位:s 、ms 、s μω、f 、T 之间的关系:f 2πω=T1f = 或 f 1T =(2)最大值、有效值(要素之二)式①中:m I —最大值;I —有效值。
有效值的定义:若i 为周期性电流函数(不一定是正弦量),则i 有效值的定义式为 ⎰=T2dt i T1I上式可写成:含义是:对同一电阻R ,在周期T 内,i 通过R 时产生的热量与恒定电流I 通过R 时产生的热量相等。
正弦量:I 2I m =对电压等量有效值的定义式在形式上与电流i 的定义式相同。
(3)相位角、初相角(要素之三)相位角: ψω+t ,单位:rad 或(o )(弧度或度)。
初相角:ψ,单位:rad 或(o )(弧度或度)。
注意:正弦量的一个周期对应的相位角为2πrad 或360o 3)相位差相位差是正弦稳态电路中的一个重要概念,设两个正弦量分别为 )t cos(f f 1m 11ψω+= )t cos(f f 2m 22ψω+= 则1f 与2f 之间的相位差定义为)t (112ψωϕ+=-)t (2ψω+=21ψψ- ② 设πϕπ≤≤-12则:(1)当12ϕ>0时,称1f 越前(超前) 2f (12ϕ角),或2f 滞后1f (12ϕ角)。
西安交大版电路第8章_相量法

9
二、相量和正弦量的比较: 相量和正弦量的比较:
①联系: 联系: 实数范围的正弦时间函数和复数范围的复指数常数一一对应。 实数范围的正弦时间函数和复数范围的复指数常数一一对应。 欧拉公式:e jθ = cos θ + j sin θ, 欧拉公式:
θ
a
b
b b = F sin θ θ = arctan a 请注意:上式与教材 请注意:上式与教材P202倒数第二行的差别。 倒数第二行的差别。 倒数第二行的差别
为正确判定θ所在的象限,我们将 、 的正负号分别 为正确判定 所在的象限,我们将a、b的正负号分别 所在的象限 保留在分母分子中,而不用小括号。 保留在分母分子中,而不用小括号。
2π ω = 2πf = T
额定值为有效值, 额定值为有效值, 耐压值为最大值。 耐压值为最大值。
热效应上与一个周期内的平均效应相等的直流值。 热效应上与一个周期内的平均效应相等的直流值。 ③有效值: 有效值: 周期电流的有效值: 周期电流的有效值: = I 正弦电流的有效值: 正弦电流的有效值:I =
2 2 2
sin ωt +ψu − ar ( ctg
i(t)
ωL
R
)
R L
& & 取相量: & 取相量:U = RI + jωLI
& I= & U R + jωL
+R 2 + ω 2 L2 ∠arctg
ωL
R
=
U R 2 + ω 2 L2
8相量法

-b
4 . 极坐标式
F | F |
共轭复数: F * | F | e j ( ) a jb
5
二、复数的四则运算及其几何表示
1.加减法 设F1、F2为复数:
F1 a1 jb1 | F1 | e j1
F2 a2 jb2 | F2 | e j 2
+j
F1 F2 (a1 a2 ) j(b1 b2 )
设电流的结构如下:
i
R
L
+
+ + uR - + uL C uS -
uC
-
i 2I cos( t i ) w
代入上式,得:
24
1 R 2 I cos( t i ) wL 2 I sin( t i ) w w 2 I sin( t i ) 2U S cos( t u ) w w wC
14
同频余弦量的相位差
设两同频率的余弦量: u Umcos(ω t u )
i Imcos(ω t i )
两同频率的余弦量相位差: =初相位之差。与时间起点无关。
1. u i 0
(w t u ) (w t i ) u i u
有效值和相位差。
正弦电流(压):随时间按余弦规律变动的电流(压)。 如图表示一条支路流过正弦电流。 指定电流参考方向和时间原点,余弦电流及其波形如图所示。 i Im i 最大值
i I m cos( t i ) w
初相位
O
i
wt
12
一、余弦量的三要素
振幅或幅值 (取正值)
角频率w
w 瞬时值表达式: i I m cos( t i )
第八章+相量法

I i(t ) 2 Icos(ω t ) I
I
U θ u (t ) 2Ucos(wt θ ) U
不同频率的相量不能画在一张相量图上。
二、相量运算
同频的正弦量相加减运算就变成对应的相量相加减运算。 i1 i2 = i 3
u1 u2 = u3
上式表明:流入某一节点的所有电流用相量表示时 仍满足KCL;而任一回路所有支路电压用用相量表示时 仍满足KVL。
二、电阻 i(t) + uR(t) R 1、 u, i 关系 已知 i (t ) 2 I cos(wt Ψ i )
则 uR (t ) Ri(t ) 2 RI cos(wt Ψ i )
490 V U 2
U U 553.1o V U 1 2
例
+
+
u
-
+ u2 -
u1
30o V U 1
490 V U 2
同频正弦量的加、减运算可借助相量图进行。
Im
U2
U1 U 2
U U 553.1o V U 1 2
0 则 i I mcoswt
2
0 =0 =/2 =-/2
wt
则 i I mcos(wt ) 2
一般规定:| | 。
三、 相位差 :两个同频率正弦量相位角之差。 设 u(t)=Umcos(w t+ u), i(t)=Imcos(w t+ i) 则 相位差 j = (w t+ u)- (w t+ i)= u- i 初相位之差 j >0, u 超前i j 角,或i 滞后 u j 角(u 比 i 先到达最大值); u, i u i j <0, i 超前 u j 角, u, i i u
电路原理(邱关源)习题答案第八章相量法

第八章相量法求解电路的正弦稳态响应,在数学上是求非齐次微分方程的特解.引用相量法使求解微分方程特解的运算变为复数的代数运运算,从儿大大简化了正弦稳态响应的数学运算.所谓相量法,就是电压、电流用相量表示, RLC元件用阻抗或导纳表示,画出电路的相量模型,利用KCL,KVL和欧姆定律的相量形式列写出未知电压、电流相量的代数方程加以求解,因此,应用相量法应熟练掌握:(1)正弦信号的相量表示;(2) KCL,KVL的相量表示;(3) RLC元件伏安关系式的相量形式;(4) 复数的运算.这就是用相量分析电路的理论根据.8-1将以下复数化为极坐标形式:(1) Fi=-5-j5;⑵ F2 =-4+ j3;⑶ F3 =20+j40;(4) F4=j10; (5) F5=-3; (6) F6=2.78 +j9.20o解:(1) F1 =-5-j5 = a Z0a = (-5)2 (-5)2 =5.2-5 v1-arctan ——=-135 -5 (因F1在第三象限)故F1的极坐标形式为F1=5%'2/ -135-(2) F2 =—4 + j3=C(Y)2+32/arctan⑶—4)=52143.13:(F2在第二象限)(3)F3 =20+ j40 = J202 +402N arctan(40/20) =44.72/63.43二(4) F4 =10j =10/90 二⑸ F5=-3 = 3/180 二(6)F6 =2.78 + j 9.20 = 32.782+9.202/arctan(9.20/2.78) = 9.61,73.19 :注:一个复数可以用代数型表示,也可以用极坐标型或指数型表示,即F=a1+ j a2 =a/e =ae ja它们相互转换的关系为:2 2 1-arctan—a〞0 a2 a i和a1 = acosi a2= asin?需要指出的,在转换过程中要注意F在复平面上所在的象限,它关系到日的取值及实部a i和虚部a2的正负.8-2将以下复数化为代数形式:〔1〕F i=10/—73;〔2〕F2 =15/112.6:;〔3〕F3 =1.2/152;〔4〕F4=10/-90 :〔5〕F i =5Z-180=;〔6〕 F i =10/ -1351解:〔1〕 F i =10/— 73°=10xcos〔—73二〕十j10xsin〔—73〕= 2.92 —j9.56⑵ F2=15/112.6〞 = 15cos112.6、15sin112.6' = -5.76+j13.85〔3〕 F3 =1.2/152 口=1.2cos152' + 1.2sin152 0 = —1.O6 + jO.56〔4〕F4 =10=-90*=-jIO〔5〕F1 =5/-180口= -5〔6〕 F i =10/-135,0cos〔-135:〕+10sin〔-135二〕=-7.07-j7.078 —3假设IO./.“十A260 °= 175/中.求A和中.解:原式=100+ Acos600+ ja sin600=175c o s9 + j175s in中根据复数相等的定义,应有实部和实部相等,即Acos60 100 =175cos虚部和虚部相等Asin60 =175sin「把以上两式相加,得等式A2 100 A -20625 -0-100主,1002+4乂20625 1 102.07A = ---------------------------------- 二+解得 2 「202.069.3102.07 ——Asin602sin =-------------- = --------------- — 175 175=30.348-4求8—1题中的F ,F6和F 2/F6.解:F 2 F6=(—4 j3) (2.78 j9.20) =5 143.13 9.61 73.19= 48.05. 216.32 =48.05. -143.684 j3 5. 143.13F 2 F6 = ------------ --- = ----------------- = 0.52 69.942.78 j9.20 9.61 73.198 — 5求8 —2题中的F 1 +巳和E/F 5 o解:F 1 F 5 - 10. - 73 5. - 180= 10cos(-73 ) j10sin(-73 ) -5 =-2.08 - j9.56 =9.78 -102.2710. -73F 1 F 5= ---------------------------- = 2 -73180 =2 1075/-1808 —6 假设.i 1 = -5cos(314t +60)Ai 2 = 10sin(314t + 60)A,i 3 =4cos(314t 60 )A(1)写出上述电流的相量,并绘出它们的相量图; (2)1与心和i1与)的相位差;(3)绘出3的波形图;(4)假设将3表达式中的负号去掉将意味着什么? (5)求的周期T 和频率f .解:(1) i 1 二 一5cos(314t+601 =5cos(314t+60 = —180=) =5cos(314t —120bi 2 =10sin(314t 60 ) = 10cos(314t - 30 )=0.505 所以故i 1 , i 2和i 3的相量表达式为(4)假设将i i (t)中的负号去掉,意味着i i 的初相位超前了 180二.即i i 的 参考方向反向.(5) i i (t)的周期和频率分别为2 二 2 二T =——= ------ =0.02s = 20ms314 .1■ ■1f =一 =——= ---- =50 HzT 2 二 0.02注:定义两个同频率的正弦信号的相位差等于它们的初相之差,因此在 比拟相位差时,两个正弦量必须满足(1)同频率;(2)同函数,即都是正 弦或都是余弦;(3)同符合,即都为正号或都为负号,才能进行比拟.8-7 假设两个同频正弦电压的相量分别为U i =50/30 V ,5 =T00/-150 V ,其频率 f=100Hz .求:5I i : 一 120 A,1210 4:——30 A,13 :——60 A2 2(3) i i (t)的波形图见题解图(b)所示.13 =1 - 3 - -120 -60 - -180其相量图如题解图(a)所示.(1)写出u i,出的时域形式;(2) 3与弘的相位差.(1)u1(t) = 50.. 2 cos(2 ft 30 ) = 50 .. 2 cos(628t 30 )Vu2(t) =-100.2cos(2二ft-150 ) =100..2cos(628t-150 =180 )V 二100,2cos(628t 30 )V(2)由于U1=50. 30 V ,U2=-100/-150 V =100. 30 V故相位差为中=30<30' = 0:即u1与u2同相位.8-8 :3(t) =22072cos(314t—120 1Vu2(t) =220,2 cos(314t 30 )V(1)画出它们的波形图,求出它们的有效值、频率f和周期T;(2)写出它们的相量和画出其相量图,求出它们的相位差;(3)如果把电压电的参考方向反向,重新答复(1), (2).解:(1)波形如题解8—8图(a)所示.有效值为u1 =u2 = 220V u2314f1 = f2 =——= ---------------------- =50Hz频率2二2二1 1T1 = T2 0.02 s周期 f 50(2) 5和弘的相量形式为U1 =220 -120 V U2=220 30 V故相位差为 =i - :2 =-120 -30 <-150 相量图见题解图(b)所示.(3)U2的参考方向反向,u2 (t)变为一u2 (t),有效值、频率和周期均 不变,—U 2(t )的相量为 U'2 =220/30—180口=200/—150V故U1和U2的相位差为*=91-中2=-120 -(-150)=30 波形图和向量图见题解图(a)和(b).8 — 9一段电路的电压、电流为:3,u =10sin(10 t - 20 )V i =2cos(103t -50 )A(1)画出它们的波形图和向量图;(2)求出它们的相量差.33解:(1) u =10s lM10 t—20 )=10cos10 t —110 )V ,故 u 和 i 的相量分别为U a =22072cos 侬t +10)V , U b =22045cosgt -110 =)V , U c = 220 2 cos( t 130 )V求:(1) 3个电压的和;(2) U ab ,U bc ; (3)画出它们的相量图--------- ------------- 0 .2 I =-50 A210U =-110 V60 o8-10图示三个电压源的电压分别为:u(a) +1 -------处+e ; c ~ +题解8—10图解:“,u b, U c的相量为U a = 220 10 VU b=220. -110VU c =220. 130 V(1)应用相量法有U a U b U c=220 10 220/ -110 220 130a c=0即三个电压的和u a⑴u b(t) u c⑴=0⑵ U ab =U a -U b =220/10 220/-110 := 220 3 40 VU bc =U b -U c =220 -110 -220 130= 220.3 -80 V(3)相量图如题解8—10图所示u c(a)中电压表读数为V 1:30V ; V 2:60V ;图(b)中的V 1 :15V ; 100V .(电压表的读数为正弦电压的有效值.)求图中电压U s .题8—11图解法一:(a)图:设回路中电流「=1/0:根据元件的电压、电流相量关系,可得题8-11图U R = RI = RI 0 =3.0 V U L = jX L l = X L I 90 =6.90 V那么总电压 U S =U R -U L =30 • j60V所以U s 的有效值为US =痴2 +602 = 67.08V(b)图:设回路中电流相量I =1/0二A,由于U R = RI = RI 0 =15 0 VU L —X L I =X L I 90 =80 90 V8-11 图 V 2 :80V . V 3 :题解8—10图元件相量关系后效值关系相位关系相量图电阻R UR = RI R U R =RI R仇=%U C=-jX C I =X C I -90 =100 -90 V所以总电压U S =U R U L U C =15 j80 -100j =15-j 20V故U s的有效值为U S=J132+202=25V解法二:利用相量图求解.设电流「=1/0 '为参考相量,电阻电压U R与「同相位,电感电压U L超前I'90 :电容电压U c要滞后「90[总电压U s与各元件电压向量构成一直角三角形.题解8-11图〔a〕和〔b〕为对应原图〔a〕和〔b〕的相量图.由题解图〔a〕可得U S = . U R U L = 302 602 = 67.08V由题解图〔b〕可得U S = ,U R 〔U C-U L〕2 = 152〔100 -80〕2 = 258V题解8—11图注:这一题的求解说明,R, L, C元件上电压与电流之间的相量关系、有效值和相位关系〔如下表所示〕是我们分析正弦稳态电路的根底,必须很好地理解和掌握.电感LU L = jX L I LU L = jX L 「 仇=仇+90二电容CU C = - jX C I C U C = X C I C仇=d -90二1 -----------------------------8—12图示正弦电流电路中,电流表的读数分别为 A :5A ; A 2:2°A;A 3 :25A o 求:〔1〕图中电流表A 的读数;〔2〕如果维持A 的读数不变,而把电 源的频率提升一倍,再求电流表 A 的读数.解法一:〔1〕 R, L, C 并联,设元件的电压为U R 二二U L 二U C 二U 二U 0根据元件电压、电流的相量关系,可得U U I R5/0 AR RU UI L =——=——-90 A - - j20A jXL X L应用KLC 的相量形式,总电流相量为I = I R I L I C =5-j20 j25 = 5 j5 =5' 2 45 A故总电流表的读数.・' =I =5、.2 =7.07A(2)设U R ==U L =U C =U -U — 0U U,,…—『一 ,、一 , I R =- =— =5,0 A. 当电流的频率提图一倍后,由于 R R不变,所以UR -U不I CU- jX C90 = 25 90 = j 25A题8—12图U UIc == = 2 25. 90 =50. 90 A一jX C _j ; 2 cI =I R I L 1c =5-j10 j50 =5 j40即,电流表的读数解法二: 利用相量图求解.设U =U /00=U R =U L =Uc 为参考向量,根据元件电压、电流的相位关系知,I R 和U 同相位,1c 超前90: I L 滞后U 901 ■ ■ ■ 相量图如题解8—12图所示,总电流「与I R, I c 和I L 组成一个直角三角形.故 电流表的读数为... =\IR(I c -I L )2A即 (1)@ =,52 +(25 -20)2 =7.07A⑵ @ =,52 +(25 -10)2 =40.31A注:从8—11题的解法二,可以体会到应用向量图分析电路的要点,那就是 首先要选好一个参考相量,这个参考相量的选择,必须能方便地将电路中其它电变,而X L =2^L 增大一倍,26C 减小一倍,因此,有U 1 ——=—20.jX L j2 L 2所以A - -52 402 -40.31A题解8—12图压、电流相量,根据电路的具体结构及参数特点逐一画出,把所给的条件转化成 相量图中的几何关系.最后根据相量图中的相量关系,使问题得到解决.一般对 串联电路,选电流作参考方向较方便,如 8-11题.对并联电路,那么选电压作参 考相量较方便,如8-12题.有些问题通过相量图分析将很直观和简便.8-13 对RL 串联电路作如下两次测量:(1)端口加90V 直流电压=0)时, 输入电流为3A; (2)端口加f =50H z 的正弦电压90V 时,输入电流为1.8A .求R 和L 的值.题解8—13图解:由题意画电路如题解8—13图所示.(1)当u s 为90V 直流电压时,电感L 看作短路,那么电阻RU-(2)当u s 为90V 交流电压时,设电流「=1/0口=1.8/0二A,根据相量法,U S = RI jX L I =30 1.8 jX L 1.8 U S =90 = 1.8 , 302 X i 2X L= (90)2 -302 =40 】1.8, X L X L 40L = ----- = ------- = -------- 解得 • 2开 100二8-14某一元件的电压、电流(关联方向)分别为下述 4种情况时,它可能是U0.127H 庆什么元件?'u =10cos(10t 十 45 1V (D i =2sin(10t +135)AU = 10. 45 V2即电压、电流同相位,根据元件电压、电流相位关系可知这是一个 5建的电阻元件.(1)把电压变为余弦形式有u=cos(100t - j 90 )V102 U 45 I =0 A(2) u 和i 的相量为J 2V 2U5一二5 45 (1 j); R jX L 那么I.. 255R : ---- :. iX L :--- :. i即这是一个 「2 的电阻和v 2 的电感的串联组合.3,、.,8—15电路由电压源u s n 00 cos(10 t)V 及R 和L= 0.025H 串联组成.电感端电 压的有效值为25V .求R 值和电流的表达式.解:由题意画电路的相量模型如题解 8—15图(a)所示,相量图如题解图 (b)所示.由于100U.2 0X L = L=103 0.025= 25」u =10sin(100t)V(2) i =2cos(100t)AU = -10costV (3) 、i=-sintA;u = 10cos(314t+451V (4)、 i =2cos(314t)A解:(1)把电流变为余弦形式有= 2cos(10t +135、901=2cos(10t + 45°)A,u和i 的相量为题解8—15图由图〔b〕知电阻电压的有效值为U R 66.144R = —R = -------- =66.144' 1所以电阻为I 1「滞后U S的角度(由于是感性电路)为.U L . 25Z= arcsin——=arcsin -------- -- - 20.70U S100 2因此电流的瞬时表达式为i(t) = 2cos(103t -20.70 )A100■ _________I U S— = ------------------------ 2—— =1 -20.70 A也可根据R jX L 66.144 j25得i(t) = 2cos(103t -20.70 )A8-16图示电路I1 =I2 =10A.求I和U S.■ ■ ■ ■ ■解:设U S为参考相量.I1与U S同相位,I2超前U S901相量图如题解8-题解8—16图题解8—16图I = J l2-12 = J102・ 102 =10、,2 A12Z= arctan = arctanl = 4511由电路图知U S = RI1 =10 10 = 100V故U s和「分别为U S -100. 0 VI = I. :Z =10,2 45 A8-17图示电路中1s=2/0 A.求电压u o■■' u u1s = I R ' I L =二 '解:R jX Lu - I S -2 0= 2 45V1 .2 —451即j题8—17图。
电路理论课后习题解答08

电路理论课后习题解答08第八章相量法8-1如果已知I1??5秒?314t?60?? a、 i2?10罪?314t?60?? a、 i3?4cos?314t?60?? a、(1)写出上述电流的相量并绘制相量图;(2) I1和I2之间以及I1和I3之间的相位差;(3)绘制I1的波形图;(4)若将i1表达式中的负号去掉将意味着什么?(5)求i1的周期t和频率f。
解决方案:(1)I1??5秒?314t?60 5秒?314t?60?? 180度?A.5秒?314t?120度?i2?10si?n3t1?4.因此,I1、I2和I3的相量表达式为.??6?041ts?3?1?0coo30i1?52??120a,i2?o.102??30a,i3?o.42?60aO其相量图如图(a)所示5+ji1?t?060?120??0??30+1-2.5-5t(a)题解8-1图(b)(2)? 12?? 1.2.90度?13?? 1.3.有关180o(3)波形图,请参见图(b)(4)意味着i1的初相位超前了180o,即i1的参考方向反向。
(5)t?220ms,f?1t?50hz8-2如果已知具有相同频率的两个正弦电压的相量为U1?50? 30,u2??100?? 150伏o..其频率f?100hz。
求:(1)写出u1,u2的时域形式;(2)u1与u2的相位差。
解决方案:(1)OU1?T502cos?2.英尺?30度??502cos?628t?30点?五、u2?t1002cos?2?ft?150.o.o??1002cos?628t?150?180oo??1002cos?628t?30o?v(2) u1?50? 30岁,u2?100? 30ov,所以相位差是??0,即它们是同相的。
8-3已知三个电压源的电压分别为:ua?2202cos??t?10??v,乌布?2202cos??T110? 五、加州大学?2202cos??T130?? v、求:(1)三个电压之和;(2)uab,ubc;(3)画出它们的相量图。
chapter08相量法电路原理

N
线性
w1
w2
N
线性
w非
线性
不适用 ③ 相量法可以用来求强制分量是正弦量的任意常系数线
性微分方程的特解,即可用来分析正弦稳态电路。
8.3 电阻、电感和电容元件上电压 和电流的相量关系
一. 电阻
i(t)
+ uR(t) -
已i知 (t)2Isiw n ty ()
wy 则 u R (t) R (t) i2 R sI itn )(
L
iR
jw L
+ iL
iC
uS
C
-
+ IL
R
US
-
IR
IC
1/jw C R
时域电路
iL iC iR
LdiL1
dt C
iCdt uS
1
RiR C iCdt
时域列写微分方程
相量模型
IL I C IR
jwLILjw1CI C US
RIR
1
jwC
IC
相量形式代数方程
相量模型:电压、电流用相量;元件用复数阻抗或导纳。
画相量图:选电流为参考向量(w L > 1/w C )
ULUUCj来自URIU
j
UX
UR
电压三角形
U UR 2 UX 2
.
IR
+
.
+ UR-
请看演示
三. 相量图
ωy y i(t)2 I sitn i() I I i
wy y u (t)2 U sitn u ( ) U U u
•
U
•
I
yu yi
四. 相量运算
(1) 同频率正弦量相加减
邱关源《电路》笔记及课后习题(相量法)【圣才出品】

第8章相量法8.1 复习笔记一、复数相关知识点1.复数的表示形式如图8-1-1所示,在复平面内有一个向量F,可以用以下几种方式表示:(1)代数形式(2)三角函数形式F=|F|(cosθ+jsinθ)(3)指数形式F=|F|e jθe jθ=cosθ+jsinθ(欧拉公式)(4)极坐标形式F=|F|∠θ图8-1-12.复数运算设有两个复数分别为F1=a1+jb1,F2=a2+jb2。
(1)加减运算F1±F2=(a1+jb1)±(a2+jb2)=(a1±a2)+j(b1±b2)复数的加减运算在复平面上符合平行四边形求和法则,如图8-1-2所示。
图8-1-2 复数的加减运算(2)乘法运算所以|F1F2|=|F1||F2|arg(F1F2)=arg(F1)+arg(F2)(3)除法运算所以(4)旋转因子①e jθ=1∠θ,若则②e jπ/2=j,e-jπ/2=-j,e jπ=-1,e j2π=1。
二、相量法基础(1)正弦量的表达式:u(t)=U m cos(ωt+φ)。
式中,U m为振幅,ω为角频率,φ为初相,三者称为正弦量的三要素。
有效值即其均方根值相量:表征正弦时间函数的复值常数。
(2)有效值相量:U▪=U∠φu,复值常数的模表示有效值,由此可知(3)正弦量的相量表示法:分为有效值相量和最大值相量。
例如,正弦量其有效值相量I▪=10∠50°A。
其对应的最大值相量三、电路定律的相量形式(1)KCL、KVL定律的相量形式∑I▪=0∑U▪=0(2)电路元件VCR的相量形式①电阻元件:U▪=R I▪。
即电阻上的电压和电流同相位,相量图如图8-1-3所示。
图8-1-3②电感元件:U▪=jωL I▪。
即电感上的电压超前电流90°,相量图如图8-1-4所示。
图8-1-4③电容元件:U▪=I▪/(jωC)即电容上的电压滞后电流90°,相量图如图8-1-5所示。
