最新数学建模第三次作业
经济数学建模作业及答案

2、如果连续复利时,以什么利率才能使本金在8年内变成3倍?1、在每半年复利一次的情况下,以8%的利率,需要经过多长时间才能使现值增到2.5倍?3、连续收益流量每年按80万元持续5年,若以年利率5%贴现,其现值应是多少?T=11.68年r=13.73%55%00S 80353.92t e dt -==⎰8003S S re =4、某汽车使用寿命为10年,若购买此车需35000元,若租用此车每年租金为7200元,若资金的年利率为14%,按连续复利计算,问买车与租车哪一种方式合算。
计算租车资金流量总值的现值,然后与购买费相比。
租车租金流量总值的现值为所以买车比租车合算。
002.5S S +=2T0.08(1)2101014141172003875635000i i i i i S e e -%-%==≈>=∑∑5、一商家销售某种商品的价格满足关系x p 2.07-=(万元/吨),x 为销售量(单位:吨);商品的成本函数是C =3x +1(万元)。
(1) 若每销售一吨商品,政府要征税t (万元),求该商家获最大利润时商品的销售量;(2) t 为何值时,政府税收总额最大。
6、已知某企业生产的商品的需求弹性为1.2,如果该企业准备明年将价格降低15%,问这种商品的销量预期会增长多少?总收益会增长多少?2'5(2) 10 0 22T tx t t T t ==-=⇒=R18%,3%R Q Q∆∆==令2(70.2)31(4)0.21Px C Tx x x tx t x x --=----=---'''5()0,()0102L x L x x t=<⇒=-(1)利润L(x)=7、某消费者打算购买两种商品q 1和q 2,他的预算约束是240元,两种商品的单价分别是10元和2元,其效用函数为U=q 1q 2,消费者的最优商品组合是什么?一元钱的边际效用是多少?8、效用函数U (q 1,q 2) 应满足的条件是以下的A,B 之一:A. U (q 1,q 2) =c 所确定的函数q 2=q 2(q 1)单调减、下凸;0,0,0,0,0.B 21222221221>∂∂∂<∂∂<∂∂>∂∂>∂∂q q Uq U q U q U q U AB ⇒证明:对U (q ,q 2) =c 两端求q 1的一阶导和二阶导12102240q q +=1212MU MU P P =1212,60q q ==解建立方程组得解出一元钱边际效用为610、在确定性存贮模型中,在费用中增加购买货物本身的费用,确定不允许缺货的最优订货周期和订货批量。
第十组数学建模第三次作业

易拉罐形状和尺寸的最优设计我们只需略加留神就会发现销量很大的饮料(比如饮料量为355 毫升的爽口可乐、青岛啤酒等 ) 的饮料罐 (即易拉罐 )的形状和尺寸几乎都是相同的。
看来,这并不是有时,这应当是某种意义下的最优设计。
自然,对于单个的易拉罐来说,这类最优设计能够节俭的钱可能是很有限的,可是假如是生产几亿,甚至几十亿个易拉罐的话,能够节俭的钱就很可观了。
此刻来研究易拉罐的形状和尺寸的最优设计问题。
详细说,达成以下的任务:1.取一个饮料量为 355 毫升的易拉罐,比如 355 毫升的爽口可乐饮料罐,丈量考证模型所需要的数据,比如易拉罐各部分的直径、高度,厚度等,并把数据列表加以说明。
2.设易拉罐是一个正圆柱体。
什么是它的最优设计其结果能否能够合理地说明所丈量的易拉罐的形状和尺寸,比如说,半径和高之比,等等。
3.设易拉罐的中心纵断面以下列图所示,即上边部分是一个正圆台,下边部分是一个正圆柱体。
什么是它的最优设计其结果能否能够合理地说明所丈量的易拉罐的形状和尺寸。
4.利用对所丈量的易拉罐的洞察和想象力,做出对于易拉罐形状和尺寸的最优设计。
易拉罐形状和尺寸的最优设计此题在成立数学模型的基础上,用LINGO实证剖析了各样标准下易拉罐的优化设计问题,并将实测数据和模型摸拟结果进行了对照剖析。
结论表示,易拉罐的设计不只需考虑资料成本(造价 ),还要知足构造稳定、雅观、方便使用等方面的要求。
在第二个问题中,易拉罐被假定为圆柱体,针对资料最省的标准,获得了不一样顶部、底部与侧面资料厚度比时的最优设计方案。
针对资料厚度的不一样,成立两个模型:模型一,设易拉罐各个部分厚度和资料单价完整相同,最优设计方案为半径与高的比R : H1: 2 ( H 为圆柱的高, R 为圆柱的半径 );模型二,设易拉罐顶盖、底部厚度是罐身的 3 倍,经过计算获得半径与高R : H 1:6 时,表面积最小。
一般状况下,当顶盖、底部厚度是罐身的 b 倍时,最优设计方案为R : H2b 。
最新数学建模第三次作业.docx

精品文档院系:数学学院专业:信息与计算科学年级:2014 级学生姓名:王继禹学号:201401050335教师姓名:徐霞6.6 习题3.一个慢跑者在平面上沿着他喜欢的路径跑步,突然一只狗攻击他,这只狗以恒定速率跑向慢跑者,狗的运动方向始终指向慢跑者,计算并画出狗的轨迹。
解:(1)模型分析建立:狗的轨迹:在任意时刻,狗的速度向量都指向它的目标慢跑者。
假设 1:慢跑者在某路径上跑步,他的运动由两个函数 X(t)和 Y(t)描述。
假设 2:当 t=0 时,狗是在点 (x0,y0)处,在时刻 t 时,它的位置是 (x(t),y(t)) 那么下列方程成立:222(1)狗以恒定速率跑:X’+y’=w(2)狗的速度向量平行于慢跑者与狗的位置的差向量:将上述方程带入等式:,可得:再将λ代入第二个方程,可得狗的轨迹的微分方程:(2)程序及结果dog 函数[dog.m]function[zs,isterminal,direction] = dog(t,z,flag)global w; % w=speed of the dogX=jogger(t);h = X-z;nh=norm(h);if nargin<3 || isempty(flag)zs=(w/nh)*h;elseswitch (flag)case 'events'zs = nh-1e-3;isterminal = 1;direction = 0;otherwiseerror(['Unknow flag:'flag]);endend慢跑者的运动轨迹方程,水平向右[jogger.m]function s = jogger(t);s = [8*t;0];标记的函数[cross.m]function cross(Cx,Cy,v)Kx = [Cx Cx Cx Cx-v Cx+v];Ky = [Cy Cy+2.5*v Cy+1.5*v Cy+1.5*v Cy+1.5*v]plot(Kx,Ky);plot(Cx,Cy,'o' );主程序:静态显示[main1.m]global wy0 = [60;70];w=10;options = odeset('RelTol',1e-5,'Events', 'on' ); [t,Y] = ode23('dog' ,[0,20],y0,options);clf;hold on ;axis([-10,100,-10,70]);plot(Y(:,1),Y(:,2));J=[];for h=1:length(t),w = jogger(t(h));J=[J;w'];endplot(J(:,1),J(:,2),':');p = max(size(Y));cross(Y(p,1),Y(p,2),2)hold off ;动态显示[main2.m]global w;y0=[60;70];w=10;options = odeset('RelTol',1e-5,'Events', 'on' ); [t,Y]=ode23('dog' ,[0,20],y0,options); J=[];for h=1:length(t);w= jogger(t(h));J=[J;w'];endxmin = min(min(Y(:,1)),min(J(:,1)));xmax = max(max(Y(:,1)),max(J(:,1)));ymin = min(min(Y(:,2)),min(J(:,2)));ymax = max(max(Y(:,2)),max(J(:,2)));clf;hold on ;axis([xmin-10 xmax ymin-10 ymax]);title('The jogger and the Dog');for h = 1:length(t)-1,plot([Y(h,1),Y(h+1,1)],[Y(h,2),Y(h+1,2)],'-', 'Color', 'red', 'EraseMode ' , 'none');plot([J(h,1),J(h+1,1)],[J(h,2),J(h+1,2)],'-', 'Color', 'green', 'EraseMo de', 'none');drawnow;pause(0.1);endplot(J(:,1),J(:,2),':' );p = max(size(Y));cross(Y(p,1),Y(p,2),2)hold off;结果t=12.2761812635281,在 12.27 秒后狗追上慢跑者。
数学建模作业及答案

数学建模作业姓名:叶勃学号:班级:024121一:层次分析法1、 分别用和法、根法、特征根法编程求判断矩阵1261/2141/61/41A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦11/2433217551/41/711/21/31/31/52111/31/5311A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦的特征根和特征向量(1)冪法求该矩阵的特征根和特征向量 程序为:#include<iostream> #include<math.h> using namespace std;#define n 3 //三阶矩阵#define N 20 #define err 0.0001 //幂法求特征值特征向量 void main(){cout<<"**********幂法求矩阵最大特征值及特征向量***********"<<endl; int i,j,k;double A[n][n],X[n],u,y[n],max;cout<<"请输入矩阵:\n"; for(i=0;i<n;i++) for(j=0;j<n;j++)cin>>A[i][j]; //输入矩阵 cout<<"请输入初始向量:\n"; for(i=0;i<n;i++)cin>>X[i]; //输入初始向量 k=1; u=0;while(1){ max=X[0]; for(i=0;i<n;i++) {if(max<X[i]) max=X[i]; //选择最大值 }for(i=0;i<n;i++)y[i]=X[i]/max; for(i=0;i<n;i++)X[i]=0;for(j=0;j<n;j++)X[i]+=A[i][j]*y[j]; //矩阵相乘}if(fabs(max-u)<err){cout<<"A的特征值是 :"<<endl; cout<<max<<endl; cout<<"A的特征向量为:"<<endl; for(i=0;i<n;i++) cout<<X[i]/(X[0]+X[1]+X[2])<<" ";cout<<endl;break;}else{if(k<N) {k=k+1;u=max;} else {cout<<"运行错误\n";break;}}} }程序结果为:(2)和法求矩阵最大特征值及特征向量程序为:#include<stdio.h>#include<iostream>#include<math.h> using namespace std;#define n 3 //三阶矩阵#define N 20void main(){int i,j,k;double A[n][n],w[n],M[n],u[n],W[n][n],max;cout<<"********和法求矩阵的特征根及特征向量*******"<<endl;cout<<"请输入矩阵:\n";for(i=0;i<n;i++)for(j=0;j<n;j++)cin>>A[i][j]; //输入矩阵 //计算每一列的元素和M[0]=0;M[1]=0;M[2]=0;for(i=0;i<n;i++)for(j=0;j<n;j++){M[i]+=A[j][i];}//将每一列向量归一化for(i=0;i<n;i++)for(j=0;j<n;j++){W[j][i]=A[j][i]/M[i];}//输出按列归一化之后的矩阵Wcout<<"按列归一化后的矩阵为:"<<endl;for(i=0;i<n;i++)for(j=0;j<n;j++){cout<<W[i][j]<<" ";if(j==2)cout<<endl;} //求特征向量w[0]=0;w[1]=0;w[2]=0;for(i=0;i<n;i++)for(j=0;j<n;j++){w[i]+=W[i][j];}cout<<"特征向量为:"<<endl; for(i=0;i<n;i++){u[i]=w[i]/(w[0]+w[1]+w[2]);cout<<u[i]<<" "<<endl;}//求最大特征值max=0;for(i=0;i<n;i++){w[i] = 0;for(j=0;j<n;j++){w[i] += A[i][j]*u[j];}}for(i = 0;i < n;i++){max += w[i]/u[i];}cout<<"最大特征根为:"<<endl;cout<<max/n<<endl; }运行结果为:(3)根法求矩阵最大特征值及特征向量:程序为:#include<stdio.h>#include<iostream>#include<math.h>using namespace std;#define n 3 //三阶矩阵#define N 20void main(){int i,j;double A[n][n],w[n],M[n],u[n],W[n][n],max;cout<<"********根法求矩阵的特征根及特征向量*******"<<endl; cout<<"请输入矩阵:\n";for(i=0;i<n;i++)for(j=0;j<n;j++)cin>>A[i][j]; //输入矩阵//计算每一列的元素和M[0]=0;M[1]=0;M[2]=0;for(i=0;i<n;i++)for(j=0;j<n;j++){M[i]+=A[j][i];}//将每一列向量归一化for(i=0;i<n;i++)for(j=0;j<n;j++){W[j][i]=A[j][i]/M[i];}//输出按列归一化之后的矩阵Wcout<<"按列归一化后的矩阵为:"<<endl;for(i=0;i<n;i++)for(j=0;j<n;j++){cout<<W[i][j]<<" ";if(j==2)cout<<endl;}//求特征向量//w[0]=A[0][0];w[1]=A[0][1];w[2]=A[0][2];w[0]=1;w[1]=1;w[2]=1;for(i=0;i<n;i++){for(j=0;j<n;j++){w[i]=w[i]*W[i][j];}w[i]=pow(w[i], 1.0/3);}cout<<"特征向量为:"<<endl;for(i=0;i<n;i++){u[i]=w[i]/(w[0]+w[1]+w[2]);cout<<u[i]<<" "<<endl;}//求最大特征值max=0;for(i=0;i<n;i++){w[i] = 0;for(j=0;j<n;j++){w[i] += A[i][j]*u[j];}}for(i = 0;i < n;i++){max += w[i]/u[i];}cout<<"最大特征值为:"<<endl; cout<<max/n;}运行结果为:2、编程验证n阶随机性一致性指标RI:运行结果:3、考虑景色、费用、居住、饮食、旅途五项准则,从桂林、黄山、北戴河三个旅游景点选择最佳的旅游地。
全国卷2021年高考第三次联考三模数学试题(理)含答案

姓名 准考证号 绝密★启用前2022届高中毕业班联考理科数学注意事项:1.本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分。
时量120分钟,满分150分。
2.答卷前,考生务必将自己的性名、准考证号填写在答题卡相应位置上。
3.全部答案在答题卡上完成,答在本试题卷上无效。
4.考试结束后.将本试题卷和答题卡一并交回。
第I 卷一、选择题:本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.欧拉公式x i x e ix sin cos +=(i 是虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数之间的关系,被誉为“数学中的天桥。
根据欧拉公式.则复数i e41π在复平面内对应的点所在的象限为A.第一象限B.第二象限C.第三象限D.第四象限2.已知集合:A = {0)2)(2(|≤+-x x x },B= {16|22=+y x y },则=B A A.[-3, -3] B.[-2,2]C.[-4,4]D. 03.等差数列{n a }的公差不为0, 210282624a a a a +=+},则S 13 =A. -1B.OC.-2D.-34.如图正方体AC 1,点M 为线段BB 1的中点,现用一个过点M,C,D 的平面去截正方体,得到上下两部分,用如图的角度去观察上半部分几何体,所得的侧视图为5.已知两个随机变量y x ,之间的相关关系如下表所示:根据上述数据得到的回归方程为a x b yˆˆˆ+=,则大致可以判断 A.a ˆ>0,b ˆ<0 B.a ˆ<0,b ˆ<0 C. aˆ>0,b ˆ>0 D.a ˆ<0,b ˆ>0 6.已知椭圆12222=+b y a x (a>b>0)的左右焦点分别为F 1、F 2,A 为椭圆上一动点(异于左右顶点),若21F AF ∆的周长为6且面积的最大值为12222=-by a x ,则椭圆的标准方程为A.13422=+y xB.12322=+y xC.1222=+y x D.1422=+y x7.执行如图所示的程序框图,则输出的S 为 A. 55 B. 45 C. 66 D. 408.《中国诗词大会》(第二季)亮点颇多。
数学建模课后习题作业

选修课——数学建模部分习题详细解答【陈文滨】1、在稳定的椅子问题中,如设椅子的四脚连线呈长方形,结论如何?【模型假设】(1)椅子四条腿一样长,椅脚与地面接触处视为一点,四脚的连线呈长方形.(2)地面高度是连续变化的,沿任何方向都不会出现间断 (没有像台阶那样的情况),即从数学的角度看,地面是连续曲面.这个假设相当于给出了椅子能放稳的必要条件.(3)椅子在任何位置至少有三只脚同时着地.为保证这一点,要求对于椅脚的间距和椅腿的长度而言,地面是相对平坦的.因为在地面上与椅脚间距和椅腿长度的尺寸大小相当的范围内,如果出现深沟或凸峰(即使是连续变化的),此时三只脚是无法同时着地的。
【模型建立】在上述假设下,解决问题的关键在于选择合适的变量,把椅子四只脚同时着地表示出来.首先,引入合适的变量来表示椅子位置的挪动.生活经验告诉我们,要把椅子通过挪动放稳,通常有拖动或转动椅子两种办法,也就是数学上所说的平移与旋转变换.然而,平移椅子后问题的条件没有发生本质变化,所以用平移的办法是不能解决问题的.于是可尝试将椅子就地旋转,并试图在旋转过程中找到一种椅子能放稳的情形.注意到椅脚连线呈长方形,长方形是中心对称图形,绕它的对称中心旋转180度后,椅子仍在原地.把长方形绕它的对称中心O旋转,这可以表示椅子位置的改变。
于是,旋转角度θ这一变量就表示了椅子的位置.为此,在平面上建立直角坐标系来解决问题.如下图所示,设椅脚连线为长方形ABCD,以对角线AC所在的直线为x轴,对称中心O为原点,建立平面直角坐标系.椅子绕O点沿逆时针方向旋转角度θ后,长方形ABCD转至A1B1C1D1 的位置,这样就可以用旋转角θ(0≤θ≤π)表示出椅子绕点O旋转θ后的位置.其次,把椅脚是否着地用数学形式表示出来.我们知道,当椅脚与地面的竖直距离为零时,椅脚就着地了,而当这个距离大于零时,椅脚不着地.由于椅子在不同的位置是θ的函数,因此,椅脚与地面的竖直距离也是θ的函数.由于椅子有四只脚,因而椅脚与地面的竖直距离有四个,它们都是θ的函数.而由假设(3)可知,椅子在任何位置至少有三只脚同时着地,即这四个函数对于任意的θ,其函数值至少有三个同时为0.因此,只需引入两个距离函数即可.考虑到长方形ABCD是中心对称图形,绕其对称中心 O沿逆时针方向旋转180°后,长方形位置不变,但A,C和B,D对换了.因此,记A、B两脚与地面竖直距离之和为f(θ),C、D两脚与地面竖直距离之和为g(θ),其中θ∈[0,π],从而将原问题数学化。
数学建模第三次作业题答案
答: 程序代码截图:
运行结果截图:
(4)给出一系列的 a 值,用函数 答: 程序代码截图:
x2 a2
y2 25 a2
1
画一组椭圆。
运行结果贴图:
(5)设 y=cos[0.5+((3sinx)/(1+x^2))] 把 x=0~2π间分为 101 点,画出以 x 为横坐标,y 为纵 坐标的曲线。 答: 程序代码截图:
运行结果贴图:
(6)绘制连续调制波形 y sin(t) sin(9t) 在[-2pi,2pi]的图像。 (两种以上方法)
答: 程序代码截图: 运行结果贴图:
程序代码截图:
运行结果贴图:
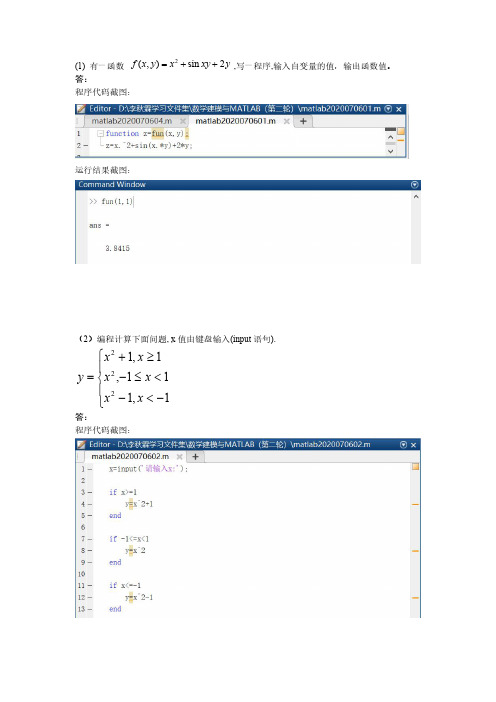
(1) 有一函数 f (x, y) x2 sin xy 2 y ,写一程序,输入自变量的值,输出函数值。
答: 程序代码截图:
运行结果截图:
(2)编程计算下面问题, x 值由键盘输入(input 语句).
x2 1, x 1
y
x
2
,1
x
1
x
2
1,
x
1
答:
程序代码截图:
运行结果截图:
(3)分析下面程序运行后 s1,n1,s2,n2,m 的值. s1=0;s2=0;n1=0;n2=0 x=[1,-4,-8,3,10,-9,7,-3,10, 8,-5,-2,2,0 ]; m=length(x); for i=1:m if x(i)<0 s1=s1+x(i); n1=n1+1; else
(0349)《数学建模》网上作业题及答案

(0349)《数学建模》网上作业题及答案1:第一批次2:第二批次3:第三批次4:第四批次5:第五批次6:第六批次1:[填空题]名词解释13.符号模型14.直观模型15.物理模型16.计算机模拟17.蛛网模型18.群体决策参考答案:13.符号模型:是在一定约束条件或假设下借助于专门的符号、线条等,按一定形式组合起来描述原型。
14.直观模型:指那些供展览用的实物模型以及玩具、照片等,通常是把原型的尺寸按比例缩小或放大,主要追求外观上的逼真。
15.物理模型:主要指科技工作者为一定的目的根据相似原理构造的模型,它不仅可以显示原型的外形或某些特征,而且可以用来进行模拟实验,间接地研究原型的某些规律。
16.计算机模拟:根据实际系统或过程的特性,按照一定的数学规律用计算机程序语言模拟实际运行情况,并依据大量模拟结构对系统或过程进行定量分析。
17.蛛网模型:用需求曲线和供应曲线分析市场经济稳定性的图示法在经济学中称为蛛网模型。
18.群体决策:根据若干人对某些对象的决策结果,综合出这个群体的决策结果的过程称为群体决策。
2:[填空题]名词解释7.直觉8.灵感9.想象力10.洞察力11.类比法12.思维模型参考答案:13.符号模型:是在一定约束条件或假设下借助于专门的符号、线条等,按一定形式组合起来描述原型。
14.直观模型:指那些供展览用的实物模型以及玩具、照片等,通常是把原型的尺寸按比例缩小或放大,主要追求外观上的逼真。
15.物理模型:主要指科技工作者为一定的目的根据相似原理构造的模型,它不仅可以显示原型的外形或某些特征,而且可以用来进行模拟实验,间接地研究原型的某些规律。
16.计算机模拟:根据实际系统或过程的特性,按照一定的数学规律用计算机程序语言模拟实际运行情况,并依据大量模拟结构对系统或过程进行定量分析。
17.蛛网模型:用需求曲线和供应曲线分析市场经济稳定性的图示法在经济学中称为蛛网模型。
18.群体决策:根据若干人对某些对象的决策结果,综合出这个群体的决策结果的过程称为群体决策。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
院系:数学学院专业:信息与计算科学年级:2014级学生姓名:王继禹学号:201401050335 教师姓名:徐霞6.6 习题3.一个慢跑者在平面上沿着他喜欢的路径跑步,突然一只狗攻击他,这只狗以恒定速率跑向慢跑者,狗的运动方向始终指向慢跑者,计算并画出狗的轨迹。
解:(1)模型分析建立:狗的轨迹:在任意时刻,狗的速度向量都指向它的目标慢跑者。
假设1:慢跑者在某路径上跑步,他的运动由两个函数X(t)和Y(t)描述。
假设2:当t=0时,狗是在点(x0,y0)处,在时刻t时,它的位置是(x(t),y(t))那么下列方程成立:(1)狗以恒定速率跑: X’2+y’2=w2(2) 狗的速度向量平行于慢跑者与狗的位置的差向量:将上述方程带入等式:,可得:再将λ代入第二个方程,可得狗的轨迹的微分方程:(2)程序及结果dog函数[dog.m]function [zs,isterminal,direction] = dog(t,z,flag)global w;% w=speed of the dogX=jogger(t);h = X-z;nh=norm(h);if nargin<3 || isempty(flag)zs=(w/nh)*h;elseswitch(flag)case'events'zs = nh-1e-3;isterminal = 1;direction = 0;otherwiseerror(['Unknow flag:' flag]);end慢跑者的运动轨迹方程,水平向右[jogger.m]function s = jogger(t);s = [8*t;0];标记的函数[cross.m]function cross(Cx,Cy,v)Kx = [Cx Cx Cx Cx-v Cx+v];Ky = [Cy Cy+2.5*v Cy+1.5*v Cy+1.5*v Cy+1.5*v] plot(Kx,Ky);plot(Cx,Cy,'o');主程序:静态显示[main1.m]global wy0 = [60;70];w=10;options = odeset('RelTol',1e-5,'Events','on'); [t,Y] = ode23('dog',[0,20],y0,options);clf;hold on;axis([-10,100,-10,70]);plot(Y(:,1),Y(:,2));J=[];for h=1:length(t),w = jogger(t(h));J=[J;w'];endplot(J(:,1),J(:,2),':');p = max(size(Y));cross(Y(p,1),Y(p,2),2)hold off;动态显示[main2.m]global w;y0=[60;70];w=10;options = odeset('RelTol',1e-5,'Events','on'); [t,Y]=ode23('dog',[0,20],y0,options); J=[]; for h=1:length(t);w= jogger(t(h));J=[J;w'];xmin = min(min(Y(:,1)),min(J(:,1)));xmax = max(max(Y(:,1)),max(J(:,1)));ymin = min(min(Y(:,2)),min(J(:,2)));ymax = max(max(Y(:,2)),max(J(:,2)));clf;hold on;axis([xmin-10 xmax ymin-10 ymax]);title('The jogger and the Dog');for h = 1:length(t)-1,plot([Y(h,1),Y(h+1,1)],[Y(h,2),Y(h+1,2)],'-','Color','red','EraseMode ','none');plot([J(h,1),J(h+1,1)],[J(h,2),J(h+1,2)],'-','Color','green','EraseMo de','none');drawnow;pause(0.1);endplot(J(:,1),J(:,2),':');p = max(size(Y));cross(Y(p,1),Y(p,2),2)hold off;结果t=12.2761812635281,在12.27秒后狗追上慢跑者。
慢跑者轨迹是椭圆轨迹[jogger2.m]function s=jogger2(t)s=[10+20*cos(t) 20+15*sin(t)];狗的微分方程[dog.m]function [zs,isterminal,direction] = dog(t,z,flag) global w;% w=speed of the dogX=jogger2(t);h = X-z;nh=norm(h);if nargin<3 || isempty(flag)zs=(w/nh)*h;elseswitch(flag)case'events'zs = nh-1e-3;isterminal = 1;direction = 0;otherwiseerror(['Unknow flag:' flag]);endend主程序[main3.m]global w;y0=[60;70];w=10;options = odeset('RelTol',1e-5,'Events','on');[t,Y]=ode23('dog',[0,20],y0,options); J=[];for h=1:length(t);w= jogger2(t(h));J=[J;w'];endxmin = min(min(Y(:,1)),min(J(:,1)));xmax = max(max(Y(:,1)),max(J(:,1)));ymin = min(min(Y(:,2)),min(J(:,2)));ymax = max(max(Y(:,2)),max(J(:,2)));clf;hold on;axis([xmin-10 xmax ymin-10 ymax]);title('The jogger and the Dog');for h = 1:length(t)-1,plot([Y(h,1),Y(h+1,1)],[Y(h,2),Y(h+1,2)],'-','Color','red','EraseMode ','none');plot([J(h,1),J(h+1,1)],[J(h,2),J(h+1,2)],'-','Color','green','EraseMo de','none');drawnow;pause(0.1);endplot(J(:,1),J(:,2),':');p = max(size(Y));cross(Y(p,1),Y(p,2),2)hold off;结果取w=25有t=4.017776368842910,经过4秒左右狗追上慢跑者。
8.平面上有n(n>=2)个圆,任何两个圆都相交但无3个圆共点。
试问n个圆把平面划分成多少个不连通的区域?解:∵一个圆将平面分为2份两个圆相交将平面分为4=2+2份,三个圆相交将平面分为8=2+2+4份,四个圆相交将平面分为14=2+2+4+6份,…平面内n个圆,其中每两个圆都相交于两点,且任意三个圆不相交于同一点,则该n个圆分平面区域数f(n)=2+(n-1)n=n2-n+2证明:(1)当n=1时,一个圆把平面分成两个区域,而12-1+2=2,命题成立.(2)假设n=k(k≥1)时,命题成立,即k个圆把平面分成k2-k+2个区域.当n=k+1时,第k+1个圆与原有的k个圆有2k个交点,这些交点把第k+1个圆分成了2k段弧,而其中的每一段弧都把它所在的区域分成了两部分,因此增加了2k个区域,共有k2-k+2+2k=(k+1)2-(k+1)+2个区域.∴n=k+1时,命题也成立.由(1)、(2)知,对任意的n∈N*,命题都成立.9.某人有n元钱,他每天买一次物品,每次买物品的品种很单调,或者买一元钱的甲物品,或者买二元钱的乙物品,问他花完这n元钱有多少不同的方式?解:设an表示花完这n元钱的方案种数,若n=1,则只能买甲,有一种方法,故a1=1,若n=2,则可以买2个甲,或者1个乙或1个丙,即a2=3,当n≥3时,花钱的方式由购买甲和购买乙购买丙的种数之和构成,即a n=a n-1+a n-2+a n-2=a n-1+2a n-2则当n≥3时,a n+a n-1=2(a n-1+a n-2),即{a n+1+a n}是公比q=2的等比数列,首项为a2+a1=1+3=4,则a n+1+a n=4•2n-1=2n+1,∴a n+a n-1=2n,两式相减得a n+1-a n-1=2n+1-2-=2-,(n≥2),若n是奇数,a n=2n-1+2n-3+…+22+a1=(2n+1-1)/3若n是偶数,a n=2n-1+2n-3+…+23+a2=(2n+1+1)/3.7.6 习题1.在化工生产中常常需要知道丙烷在各种温度T和压力P下的导热系数K。
下面是实验得到的一组数据:10KPa下的K。
试求T=99C︒和P=10.3x3解:找出温度T相等时,导热系数K与压力P的关系。
由于在不同温度时,仅给出两个K、P的值,因此采用线性近似,把K、P看作是线性关系。
建立M文件:function y=y_lagr1(x0,y0,x)n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;end主程序:p1=[9.7981,13.324]; k1=[0.0848,0.0897]; %T=68℃p2=[9.0078,13.355]; k2=[0.0762,0.0807]; %T=87℃p3=[9.7918,14.277]; k3=[0.0696,0.0753]; %T=106℃p4=[9.6563,12.463]; k4=[0.0611,0.0651]; %T=140℃a2=polyfit(p2,k2,1); a3=polyfit(p3,k3,1);x1=polyval(a2,10.3); x2=polyval(a3,10.3);%x1,x2分别是P=10.3*10^3kPa下87℃和106℃的K值plot(10.3,x1,'k+',10.3,x2,'k+',p1,k1,p2,k2,p3,k3,p4,k4)xlabel('丙烷压力P')ylabel('丙烷导热系数K')title('在不同温度下丙烷导热系数与压力的关系图')gtext('T=68℃'),gtext('T=87℃'),gtext('T=106℃'),gtext('T=140℃')运行后图中所标点为P=10.3*10^3kPa时,T=87℃和T=106℃对应的导热系数K值。
