第四章化学反应速率
化学反应速率

活化分子
活化能:指将lmol具有平均能量的分子变成活化分子所要的 最低能量,单位为kJ· –1 mol Ea = NA *(E0-E平)
• 活化能的决定因素--• 由反应的本性决定,与反应物浓度无关,受温度影响很 小,在温度变化幅度较小时,通常不考虑温度对其影响, 活化能受催化剂影响很大;
• 不同的反应体系,活化能的大小不同。 • 化学反应的活化能:40400 kJ· –1 mol • Ea<40 kJ· –1时,反应快速,如酸碱反应 ; mol • Ea>400 kJ· –1时,反应速率非常小,几乎觉察不到 mol
3
3
(2)I H 2 IO I 2O 2 H 2O(慢)
3 k2
(3)I I 2 O 2 I 2 IO (快) 2
k 3 /k 3 '
(4)I I 2 I (快)
3
k 4 /k 4 '
(5)3IO I 2IO (快)
2 3
k 5 /k 5 '
试根据该机理,写出总反应速率表达式。
反应速率的影响因素:
反应速率方程: v=kcAmcBn , 影响分为两方面,即浓度项cAmcBn 和速率常数k。
(1)浓度的影响:反应物的浓度大,反应速率 大,影响频率因子;
(2)温度的影响: • 定性:温度每上升10C,v增加2~4倍(经验公式) Ea • 定量(阿伦尼乌斯公式 ) :
• 即:基元反应 aA + bB C
速率常数
反应速率方程:v = k cAacBb
(无须考虑产物)
复杂反应:aA+bB C 反应速率方程:v=k cAm c Bn (无须考虑产物) (m,n由实验得出或反应机理推导出)
化学反应速率及其表示方法反应速率理论简介

二、质量作用定律
当其他条件一定时,反应物浓度越大,化学 反应的速率越快。
对有气体参加的化学反应,增大压力,反 应速率也会随之增大。
质量作用定律指出: 在一定温度下,元反应 的反应速率与反应物浓度以其化学计量数的绝 对值为幂指数的乘积成正比。
(3) 温和的催化条件:酶在常温常压下即可发 挥催化作用,温度过高会引起酶变性,失去催化 活性。
(4) 特殊的 pH:酶只能在一定的 pH 范围内发 挥催化作用,如果 pH 偏离这个范围,酶的活性就 会降低,甚至完全丧失。
对于酶的催化作用机理,一般认为是通过生成 某种中间化合物进行的。酶 E 先与底物 S 形成中间 化合物 ES,然后 ES 再进一步分解为产物 P,并释 放出酶 E。此过程可表示为:
E + S 噲垐kk1?1? ES k2 E + P
r Hm rUm=Em,2-Em,1 = (E-Em,1)(E-Em,2)
r H m=Ea-Ea'
第三节 浓度对化学反应速率的影响
一、元反应和复合反应 二、质量作用定律 三、反应级数和反应分子数
一、元反应和复合反应
反应物的微粒间直接碰撞而一步实现的化 学反应,称为元反应。
大多数化学反应要经过若干个元反应才能完 成,这类反应称为复合反应。
反应级数通常是利用实验测定的。
(二)反应分子数
反应分子数是指元反应中参加反应的微粒 的数目。元反应分为单分子反应、双分子反应 和三分子反应。
反应级数与反应分子数是两个不同的概念。 反应级数是指速率方程中浓度项的幂指数之和, 可利用实验测定,它体现了反应物浓度对反应 速率的影响,其数值可能是整数、分数或零, 也可能是负数。反应分子数是对元反应而言的, 它是由反应机理所决定的,其数值只可能是 1、 2、3 。在元反应中,反应级数和反应分子数通 常是一致的。
化学课件第四章、化学反应速率
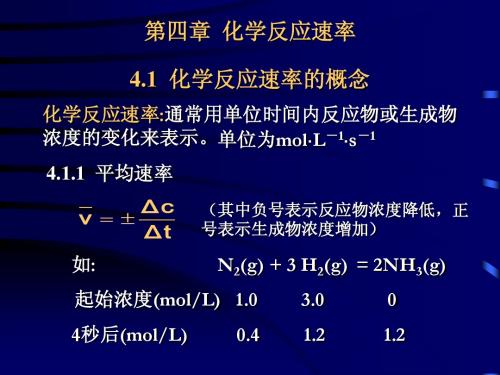
1 1 v = vNH3 = vH2 = vN2 = 0.15mol⋅L−1 ⋅ S−1 2 3
4.1.2 瞬时速率(即时速率) 瞬时速率(即时速率) 瞬时速率: 化学反应进行到某一时刻的速率. 瞬时速率: 化学反应进行到某一时刻的速率.
ν = κ ⋅ c (A)⋅ c (B)
a b
k称为速率常数,其数值为在一定条件(温度、 称为速率常数,其数值为在一定条件(温度、 催化剂) 当各反应物浓度均为1mol· 催化剂)下,当各反应物浓度均为1mol·L-1时的化 学反应速率。 值决定于反应的本性和反应温度, 学反应速率。k值决定于反应的本性和反应温度, 与反应物浓度无关。 值一般都由实验测定。 与反应物浓度无关。k值一般都由实验测定。 (a+b)称为反应总级数 (a+b)称为反应总级数
说明: (1)速率常数 的单位与反应总级数有关: 说明: (1)速率常数k的单位与反应总级数有关: 速率常数k a+b 0 1 2 反应总级数 0级 一级 二级 k的单位 mol·L mol·L-1 · S-1 S -1 L · mol-1 · S-1
(2) a+b称为反应总级数, a为反应物A的级数,b a+b称为反应总级数 a为反应物 的级数,b 称为反应总级数, 为反应物A 为反应物B的级数. 为反应物B的级数.
∆c dc v = ±lim = ± t dt ∆t→ ∆ 0
对任一化学反应: 对任一化学反应:
−ν A ⋅ A−νB ⋅ B = + Y ⋅Y +νΖ ⋅ Z ν 1 dc(A) 1 dc(B) 1 dc(Y) 1 dc(Z) v= = = = ν A dt νB dt νY dt νZ dt
化学反应速率

化学热力学的研究局限性
化学热力学:只预测变化的可能性,不说明变
化的现实性
反应速率
Rate of reaction
✓变化能否发生 如何才能发生
✓变化的方向 ✓变化的结果
速率 进行细节
本质
化学热力学的研究局限性
rGm / kJ mol1
动力学研究表明
1 2
N2
3 2
H2
NH3
H2
• 转化速率定义为:
B
• •
SI单位:mol s1
.
def
d 1 dnB
dt vB dt
转化速率与物质的选择无关,但与化学反 应方程式的写法有关。
二、反应速率 常用单位:
对等容反应,反应速率定义为:
mol·L-1·s-1
反 化学应反速应率方与v程物de式质f V的的 写选 法择v1B有无d关关(n,dBt但/V与)
单分子反应: SO2Cl2 SO2 +Cl2 双分子反应: NO2 CO NO CO2 三分子反应: 2NO+H2 N2O+H2O
三、反应级数和反应分子数
反应级数与反应分子数的区别
• 反应级数
✓速率方程中反应物浓度的指数之
和
✓体现反应物浓度对反应速率的影
响
✓数值可以是整数、分数或零,可
以是负数
k
CH2
C2 Cl2
k 为反应速率系数
1
H2 + Br2 = 2HBr
v
k
CH2
C2 Br2
1 k CHBr
CBr2
H2 + I2 = 2HI
v k CH2 CI2
反应速率系数 k
第四章 化学反应速率和化学平衡1

第三节
浓度对化学反应速率的影响
一、 基元反应与复合反应 基元反应(elementary reaction):由反应物微粒(分子、 原子、离子或自由基等)一步直接生成产物的反应。 复合反应(overall reaction):由多个元反应组成的反应 例如H2和I2的气相反应:
H2+I2 2HI
这是一个复合反应, 由以下基元反应组成:
为1/cA,0; ③当cA,0=cD,0时,二级反应的半衰期: t1 / 2
1 k A c A,0
例3
乙酸乙酯皂化为二级反应:
CH2COOC2H5+NaOH CH3COONa+C2H5OH
设NaOH与CH3COOC2H5的初浓度均为cA,0=0.0100
mol/L,反应20min后,NaOH的浓度降低了0.00566 mol/L。求速率常数k与此反应的半衰期。
值可是整数、分数或负数。反应分子数是对基元反应而言 的,由反应机理决定,数值只可能是1、2或3.
简单级数反应的速率方程小结
一些典型简单级数反应的微分及积分速率方程及其特征见下表。 表中 n 级反应只列出了其微分速率方程为 dcA/dt=kAcAn 的一种 简单形式。
n 0 1 微分速率方程
dcA kA dt
dcA k A cA dt dcA 2 k A cA dt
积分速率方程 cA,0cA=kAt
t1/2 cA,0/(2kA) (ln 2)/kA
线性关系 cA~t ln cA~t
k的单位 molm3s1 s1
cA,0 ln kAt cA
1 1 kA t cA c A,0
800 代入数据,得: ln 30 k 600
第四章化学反应速率

(二) Arrhenius方程的应用: *测定反应的活化能 lgk = -Ea/2.303RT + lgA 1.作图法:测定不同温度下的反应速率常 数,以lgk对1/T作图,得到一条直线,直线斜率 = -Ea/2.303R 故Ea=-2.303R×(斜率)
2.计算法求Ea 因为 lgk1 = -Ea/2.303RT1 + lgA (1) lgk2 =-Ea/2.303RT2 + lgA (2) 故(2) – (1)得: lg(k2 / k1) = Ea(T2-T1) /2.303RT2T1 *求速率常数或温度 1.若已知Ea、T1、T2和k1,可求得T2温度下 的速率常数k2; 2.若已知Ea、k1、k2和T1 ,可求得另一温度 T2。
一、范托夫规则:温度每升高10K,化学反应速
率约增加到原来的2~4倍。
二、Arrhenius方程
活化能 速率系数 热力学温度
Hale Waihona Puke k = A e -Ea / RT
摩尔气体常数
指数前参量
Arrhenius方程的对数形式: lnk = -Ea / RT + lnA lgk = -Ea / 2.303RT + lgA
反应级数的确定: *首先写出该反应的速率方程式,反应级数待定; *然后固定其他反应物的浓度,只改变某一反应物 的浓度,以确定该反应物的反应级数。 序 号 1 2 3 4 起始浓度(mol⋅L-1) ⋅ 起始浓度 A 1.0×10-2 × 1.0×10-2 × 1.0×10-2 × 2.0×10-2 × B 0.5×10-3 × 1.0×10-3 × 1.5×10-3 × 0.5×10-3 × 反应速率v 反应速率 mol⋅L-1⋅min-1 ⋅ 2.5×10-7 × 5.0×10-7 × 7.5×10-7 × 1.0×10-6 ×
4反应速率

对同一反应,A和Ea一定,当温度升高时,
k 值增大,使反应速率加快。
END 上页 下页
(3).根据 ln k2 Ea T2 T1 对同一反应,升 k1 R T1T2
高一定温度,在高温区k增加较少,在低温区k增
加较多,因此对于原本反应温度不高的反应 ,可
采用升温的方法提高反应速率;
(4).对不同反应,升高相同温度, Ea大的反应 k 增大的倍数大, Ea小的反应 k 增大的倍数小, 因此升高温度对反应慢的反应有明显的加速作用。
END
上页 下页
Arrhenius方程式的应用
◆已知T1 — k1, T2 — k2,求 Ea
T T1时,ln k1 ln A Ea / RT1 T T2时,ln k2 ln A Ea / RT2
两式相减,整理得到:
ln
k2 k1
Ea R
1 T1
1 T2
lg
k2 k1
Ea 2.303R
导出的速率方程为 υ = k [H2 ] [I2 ]
定速步骤,平衡态法。
13
5.速率常数rate constant
(1)定义:k为给定温度下,反应物浓度皆为1mol/L时的 反应速率,也称比速常数。 (2)k不随反应物浓度的变化而改变,即k与浓度无关。 (3)k取决于反应物本性。快反应k大,慢反应k小,且k 与T有关:T↑,k↑. (4)同一反应中不同的速率常数之比等于反应方程式中 各物质的计量系数之比。 (5)k的单位与反应级数有关,可从V=k·[A]m[B]n进行求 算。零级反应 mol·dm-3 ·s-1 ;一级反应 s-1
时的速率常数k。
解:根据阿仑尼乌斯公式
lg k Ea lg A 2.303RT
第第4章 化学反应的速度

2021/3/2 29
三、催化剂对化学反应速率的影响
1.催化剂的定义 能改变化学反应速率,其本身在反应前
后质量和化学组成均不改变的物质。 正催化剂:能加快反应速率 负催化剂:减慢反应速率
2021/3/2 13
υ=k2[H2][I]2
因①始终保持着正逆反应速率相等的平衡状态。
① I2
I+I (快)
υ+= υ- 即 k+[I2]=k-[I]2
[I]2=(k+/k- )[I2] 代入总式
∴ υ=k2(k+/k- )[H2][I2]=k[H2][I2]
虽然该式与质量作用定律形式一致,但H2与I2 化合生成HI的反应并非基元反应。
浓度:mol·dm-3 ; 时间:s or min or h 速率: mol·dm-3·s-1
2021/3/2 4
例 :2N 2O5 4NO 2 O2
(N2O5 )
[N2O5 ]2 t2
[N 2O5 ]1 t1
[N 2O5 ] 100s 1.5 103 t
(NO 2 )
[NO 2 ]2 t2
2021/3/2 2
化学动力学的基本任务:研究各种因 素对反应速率的影响;揭示化学反应进行 的机理;研究物质结构与反应性能之间的 关系。
化学动力学的研究目的:能控制化学 反应的进行;使反应按人们所希望的速率 进行,并得到人们所希望的产品。
2021/3/2 3
§4-1 反应速率的定义及表示方法
1.反应速率的定义:指在一定条件下,由反应 物转变为生成物的快慢程度。 2.反应速率的表示方法:用单位时间内反应物 浓度的减少或生成物浓度的增加来表示。
第四章 化学反应动力学基础—反应速率与反应机理反应速率与反应机理

第四章化学反应动力学基础——反应速率与反应机理4.1 什么是化学动力学?4.2 化学反应速率的含义及其表示法4.3 浓度与反应速率:微分速率方程与反应级数4.4 温度与反应速率:活化能与反应速率理论4.5 反应机理4.6 催化作用4.7 化学动力学前沿话题Ahmed Zewail (Caltech, USA) 1999 年度诺贝尔化学奖获得者"for his studies of the transition states of chemical reactions usingfemtosecond spectroscopy ”http://nobelprize .org/4.1 什么是化学动力学瞬间完成的炸药爆炸反应大西洋底泰坦尼克号船首的腐蚀过程1/2N2(g) + CO2 (g)?●化学动力学的任务:1) 化学反应的速率问题2) 化学反应的机理问题●净反应速率和初速率化学反应有可逆性,所以实验测定的反应速率实际上是正向速率和逆向速率之差,即净反应速率。
有些化学反应逆速率非常小,可看作是单向反应。
可逆反应到达平衡状态时,正向反应速率和逆向反应速率相等,此时净反应速率等于零,平衡浓度不再随时间变化。
我们把反应刚开始一霎那的瞬时速率称为初速率,记作v(2) 基元反应和非基元反应化学反应速率与路径有关。
有些反应的历程很简单,反应物分子相互碰撞,一步就起反应变成生成物。
这种反应叫基元反应。
多数反应的历程较为复杂,反应物分子要经过几步,才能转化为生成物,叫非基元反应。
化学平衡常数式中平衡浓度的方次和化学方程式里的计量系数总是一致的,按化学方程式即可写出平衡常数式,因为化学平衡只取决于反应的始态和终态而与路径无关。
但化学反应速率与路径密切相关,速率式中浓度的方次一般要由实验确定,不能直接按化学方程式的计量系数写出。
k = 6.23 ×10−4 s −1N 2O5分解反应的lg(N2O5)−t图N2O5分解反应的(N2O5)−t图)●半衰期(t1/2将一级反应速率方程改写为:lg[(A)/(A)0] = −kt/ 2.303/2时,此刻的反应时间t= t1/2,也就是反应进行一半当(A) = (A))。
基础化学 第四章 化学反应速率

v k c c
a A
b B
速率方程
k称为速率系数,大小由反应的本 性所决定,与反应物的浓度无关,但受 温度和催化剂的影响。
复合反应的速率方程,可根据组成复合反 应的基元反应的速率方程导出。例如:
C2H4Br2 3KI C2H4 2KBr KI3
分成如下三步进行:
C2H4Br2 KI C2H4 KBr I Br (慢反应) (快反应) KI Br I KBr (快反应) KI 2I KI3
该复合反应的速率方程为:
例题
v k c(C2 H4 Br2 ) c(KI)
在 298.15 K 时,发 生下列反应: aA(aq) bB(aq) Z(aq) 同浓度的 A,B 两种溶液混合,得到下 列实验数据:
实验编号 1 2 3 4 5 cA/mol·L-1 1.0 2.0 4.0 1.0 1.0 cB/mol·L-1 v /mol L1 s1 1.0 1.2×10-2 1.0 2.4×10-2 1.0 4.9×10-2 2.0 4.8×10-2 4.0 0.19
难点:碰撞理论;过渡态理论
新进展:磷酸二甲啡烷片在中国健康
志愿者中的药物代谢动力学研究 • 目的: 研究磷酸二甲啡烷片在中国健康 志愿者中单次和连续多次给药药动学特 征。方法: 12例受试者随机开放3×3拉 丁方试验设计,研究单次给药和连续多次 给药药动学特征。采用HPLC-MS/MS法 测定血浆中二甲啡烷的药物浓度。药动 学参数采用WinNonLin软件计算。结论: 单次给药二甲啡烷的体内过程符合一级 线性动力学过程;多次给药二甲啡烷的蓄 积因子接近3,符合线性累加。
r H m rU m E2 E1
《普通化学》--4化学反应速率

4次碰撞 次碰撞
6次碰撞 次碰撞
8次碰撞 次碰撞
16次碰撞 次碰撞
质量作用定律指出: 在一定温度下, 质量作用定律指出: 在一定温度下,反应速 率与反应物浓度的乘积成正比。 率与反应物浓度的乘积成正比。
表明反应物浓度与反应速率之间定量关 系的数学表达式称为速率方程。 速率方程。 系的数学表达式称为速率方程
介绍一种速率方程的确定方法 — 初始速率法
对反应 NH4+(aq) + NO2-(aq)
实
1 2 3
N2(g) + 2H2O(l)
初始速率(mol dm–3·s–1)
1.35×10-7 × 2.70×10-7 × 5.40×10-7 ×
验
初始c (NH4+)
0.100 mol dm–3 0.100 mol dm–3 0.200 mol dm–3
单位时间内反应物浓度的减少或者产物浓度的 增加来表示. 增加来表示. 浓度常用mol·l-1,时间常用 ,min,h 时间常用s, 浓度常用 , 反应速率又分为平均速率(average rate)和 反应速率又分为平均速率( ) 瞬时速率(instaneous rate)两种表示方法. 瞬时速率( )两种表示方法 平均速率: 平均速率:v = △c / △t +dc(N2O 5) 瞬时速率只能用作图的方法得到: = 瞬时速率只能用作图的方法得到:v = − lim v ∆ t → t0 d
应用Arrhenius方程时,还应注意到下列问题: 方程时,还应注意到下列问题: 应用 方程时 处于方程的指数项中, 有显著影响 在室温下, 有显著影响, ● Ea处于方程的指数项中,对k有显著影响,在室温下, 值降低约80% 。 每增 加 4kJ·mol-1, k值降低约 值降低约 温度升高, 增大 一般反应温度每升高10℃ 增大, ● 温度升高,k增大,一般反应温度每升高 ℃,k将增大 将增大 2~4倍。 倍 ●根据 ln
第四章化学反应速率

反应分子数
研究化学反应速率,确定反应速率方程,可以为研 究化学反应机理提供重要线索。
4-2-1、浓度对化学反应的影响
4、速率常数k 速率常数是在给定的温度下反应物浓度皆为1 mol.dm-3时的反应速率。 速率常数在速率方程中是其比例常数。它在速 率方程中不随反应物浓度的变化而改变。速率常数 是温度的函数。
4-2-1、浓度对化学反应的影响
反应中用不同物质浓度表示速率时,反应方程 式中各物质计量系数不同,则速率方程中速率常数 的数值不同。 如:a A + b B → g G + h H 存在下列关系:
4-2-1、浓度对化学反应的影响
− dC A = r ( A ) = k A [ A ] a [ B ]b dt − dC B = r ( B ) = k B [ A ] a [ B ]b dt dC G a b = r (G ) = k G [ A ] [ B ] ⇒ dt dC H a b = r ( H ) = k H [ A] [ B ] dt
4-2-1、浓度对化学反应的影响
反应级数:是反应速率方程中各反应物浓度 项的幂指数之和。可见,基元反应的反应分子数 和反应级数是相同的。 注意:即使由实验测得的反应级数与反应式 中反应物的计量数之和相等,该反应不一定是基 元反应。
4-2-1、浓度对化学反应的影响
H 2 ( g ) + I 2 ( g ) → 2 HI ( g ) r = k[ H 2 ][ I 2 ] ( )I 2 ⇔ I + I(快) 1 (2)H 2 + 2 I → 2 HI(慢) r = k1[ H 2 ][ I ]2 对反应( )r+ = r−即k + [ I 2 ] = k − [ I ][ I ] 1 k+ [I ] = [I2 ] k−
反应速率的测定

§4–1 化学反应速率 第四章 化学反应速率和化学平衡
(2)物理方法
该方法是测定反应混合物的某些与浓度有关的物理 量随时间的变化,间接得到不同时刻的浓度。此法较化 学方法迅速而方便,既易于跟踪反应,又可制成能自动 记录的装置。通常测定的物理量有:压力、体积、旋光 度、吸光度、电导率等。对于不同反应可以选择不同的 物理量。所选取的物理量不仅要满足灵敏度高、测量方 便的条件,而且要满足在变化范围内物理量同各有关物 质的浓度近似成线性关系的条件,从而可得物理量与浓 度的变换式。
上页 下页 返回 帮助
Δt0 Δt
dt
(D) lim Δc(D) dc(D)
Δt0 Δt
dt
上页 下页 返回 帮助
§4–1 化学反应速率 第四章 化学反应速率和化学平衡
瞬时反应速率也可以用作图的方法求得。如图中曲线
上某点a 或b的斜率,即为时间t1和t2时的反应瞬时
速率。
图4-1 N2O5浓度随时间的变化
= 0.2mol/(L·s)
上页 下页 返回 帮助
§4–1 化学反应速率 第四章 化学反应速率和化学平衡
应用实例中,同一化学反应用不同物质的浓度变化 表示的反应速率为何不同,若要得到一个反应速率值,
则反应速率如何表示?
答:
(N2
)
13(H 2 ) Nhomakorabea
1 2
(NH3
)
瞬时速率是指某一反应在某一时刻的化学反应速率, 可用时间间隔Δ t趋于无限小时的平均速率的极限值或微分 求得。
上页 下页 返回 帮助
§4–1 化学反应速率 第四章 化学反应速率和化学平衡
反应 aA + bB → cC + dD 瞬时速率可表示为
基础化学 第四章 化学反应速率

活化能
活化过程:由反应物过渡到活化体的 过程
活化能(Ea):活化过程中能量的升 高值,是活化体平均能量与反应物平 均能量之差。
要使反应进行,先决条件是反应物分 子必须具有足够能量爬越这个能垒才 能实现。
在过渡状态理论中,活化能为活化配合物 的平均能量与反应物分子的平均能量的差值。
系统的摩尔热力学能变 rUm等于产物的 平均能量(E2)与反应物的平均能量(E1)的差值:
第四节 温度对化学反应速率的影响
一、 van´t Hoff 近似规则
二、Arrhenius 方程
一、 van´t Hoff 近似规则
温度每升高 10 K,化学反应速率大约增 加到原来的2 ~ 4 倍。这一规则称为van´t Hoff 近似规则。
温度对化学反应速率的影响,其实质是温 度对速率系数的影响。 若以 k( T ) 和 k(T+10 K) 分别表示温度为 T 和 T+10 K 时的速率系 数,则有如下关系:
第一节 化学反应速率及其表示方法
一、转化速率 二、反应速率 三、消耗速率和生成速率
一、转化速率
. 转化速率定义为: def d dt
. 根据反应进度的定义有: = d 1 dnB dt vB dt
转化速率与 B 的选择无关,但与化学反应 方程式的写法有关。
二、反应速率
化学反对应于的等快容慢反,应并,通称常之用为单反位应体速积率的。转化速率描述
例
1
H2 + Cl2 = 2HCl
v
k
cH2
c2 Cl2
H2 + Br2 = 2HBr H2 + I2 = 2HI
1
v
k
第四章 化学反应及平衡

2.
3.
4.
5.
2.酶 enzyme 酶作为一种特殊的生物催化剂,除上述特点外,还具有以 下特异性:
1)催化效率高; 2)反应条件温和; 3)高度选择性
用活化分子解释各种因素对反应速率的影响: 活化分子数 = 分子总数×活化分子百分数 活化分子数越多,反应速率越大。
(1) 浓度的影响 当温度一定时,活化分子百分数一定,增大反应物浓度, 使分子总数增加,从而使活化分子数增大,反应速率增大。 (2) 温度的影响 浓度一定,温度升高,活化分子百分数增大,从而使活化 分子数增大,反应速率增大。 (3) 催化剂的影响 浓度和温度都一定,催化剂降低了反应的活化能,活化分 子百分数增大,从而使活化分子数增大,反应速率增大。
若已知反应机理,可根据定速步骤 书写速率方程式。 如 2NO(g)+Br2(g)=2NOBr(g)的反应机
理为: (1) NO+Br2=NOBr2 (慢)(定速步骤) (2) NOBr2 + NO =2NOBr (快) 则速率反程为u = kc(NO)c(Br2)
例如反应:2N2O5 == 4NO2 + O2 是三步反应: N2O5 慢 N2O3 O2 (1) (2) N2O3 快 NO2 NO 最慢 (3) N2O5 NO 3NO2
[C(C)] p×[C(D)] q Qc = [C(A)] m×[C(B)] n Qc ,叫做该反应的浓度商。
Qc < K,反应向正反应方向进行 Qc = K,反应处于平衡状态 Qc > K,反应向逆方向进行
(3)计算反应物或生成物的平衡浓度及反应 物的转化率。
有关化学平衡的计算: 起始量、变化量、平衡量的计算关系
u =k
第四章化学反应速率

分子总数 开始 100 c↑ 200 活化分子的数目 5 10
不变
活化分子的百分数 5%
5%
(二)质量作用定律
一定温度下,元反应的反应速率与各 个反应物浓度幂的乘积成正比 元反应 aA+bB→eE+fF C AaC Bb = kCAaCBb 速率方程式
速率方程式: 反应物浓度与反应速率 间定量关系的数学表达式
2
= -2
dc N 2 dt
dc NH dc H 2 == dt 3 dt
2
3
3)的量纲是: 浓度时间 -1 (mol L-1 ,s min h d a)
第二节
反应速率理论简介
两种理论 碰撞理论 过渡状态理论 一、碰撞理论 (一)碰撞理论要点:
1 、在一定温度下,反应物分子间相互碰撞是 发生化学反应的必要条件; 2、分子间要发生有效碰撞,才能发生反应。
第四章 化学反应速率
第一节 化学反应速率及表示方法
一、化学反应速率
化学反应的快慢是用化学反应速率来衡量的。 指反应体系中各物质的数量随时间的变化率。
二、化学反应速率的表示方法
用单位时间内反应物浓度的减少或生成 物浓度的增加来表示 某一有限时间间隔内浓度的变化量。 1、平均速率: 1 c生成物 1 c反应物 B t B t
(二)反应分子数
--- 元反应方程式中反应物系数之和
元反应中参与反应的微粒(原子、分 子、离子、自由基等)数
化学反应时需要同时碰撞才能反应的分 子总数(微粒总数) 如: H2C — CH | || → CH2=CH—CH=CH2 H2C — CH 单分子反应 2N2O(g) = 2N2(g) + O2(g) 双分子反应 H2(g) + 2I(g)= 2HI(g) 三分子反应 (很少)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E E
浓度、温度、催化剂
对反应速率影响的解释 浓度的影响
温度一定时,反应物浓度越大, 反应物分子总 数越多,活化分子数随之增多,反应速率增大。
温度的影响
浓度一定时,温度越高,活化分子分率的影响示意图
气体分子的能量分布图
催化剂的影响
当反应的浓度和温度一定时,加催化剂能 大大加快反应的速率,原因在于加催化剂 后反应沿着活化能较低的途径进行反应, 活化能降低会大大增加活化分子的分数, 因而大大加快反应速率。
k.c .c
m A
n D
其中, k , m和n值由实验测出。即对非基元反应,反应速率 方程式应由实验测出。 m或n可以为正整数,也可以为分数和零。 m+n为反应级数,常见的反应有一级反应和二级反应。
由实验确定速率方程的简单方法 —初始速率法 1073 k 例 2NOg 2H2 g N2 g 2H2Og
编 号
1
初始浓度/mol.L-1 c(NO)
6.0010-3
V/mol.L-1s-1
c(H2) 1.0010-3 3.1910-3
2 3 4 5 6
6.0010-3 6.0010-3 1.0010-3 2.0010-3 3.0010-3
2.0010-3 3.0010-3 6.0010-3 6.0010-3 6.0010-3
6.3610-3 9.5610-3 0.4810-3 1.9210-3 4.3010-3
试根据表中数据,推出该反应的速率方程式。
解 设反应速率方程式为
=k [c(NO)]m [c(H2)]n
根据表中数据1和2,推出n=1。
根据表中数据4和5,推出m=2。
因此该反应的速率方程式为:
= k[c(NO)] c(H2 )
反应分子数
只可能 是一、 二、三
• 4.3.2 温度对反应速率的影响 温度对反应速率的影响示意图
气体分子的能量分布图
阿仑尼乌斯(Arrhenius)方程 在大量实验事实的基础上,1889年,阿仑尼乌斯证明, 当lnk对1/T作图时可得一直线,很多反应的速率常数 与温度之间都具有这样的关系。这个关系可写作:
= k c a (A) c b (B) ‥·
反应级数
是对宏观 化学反应 包括简单 反应和复 杂反应而 言
是对元步 骤或简单 反应所对 应的微观 化学变化 而言的
反应速率 与浓度的 几次方成 正比,就 是几级反 应 参加反应 的反应物 微粒数目
可为零 、简单 正、负 整数和 分数
形式的复杂 反应,级数 无意义 任何元步骤 或简单反应 所对应的微 观变化,肯 定存在反应 分子数
• 速率常数之间的关系:k=1/aka=-----• 速率之间的关系:例如反应:2A + B → 2C • Va=-dA/ dt • Vb= -dB/ dt • Vc = dC/ dt • V=1/2Va= Vb= 1/2Vc
3、反应级数与反应分子数的差别
概念所属 范围 各个不同 定义或意义 反应中的 允许值 是否肯定存在 对速率方程 不能纳入
一、反应物浓度与化学反应速率的关系
浓度的影响----质量作用定律(用碰撞理论解释) 基元反应:aA + dB == gC + hD a d 则: (速率方程式:含义?)
k.cA .cD
其中:
——反应速率;
k——反应速率常数,由实验测出; α——反应物A的系数,也称为反应物A的级数; d——反应物D的系数,也称为反应物D的级数; α+d ——称为反应级数,相应的反应称为一级反应,二级反应 或三级反应,一级反应和二级反应是常见的,目前还未发现有 四级反应。
• 有的瞬间完成例如爆炸反应、紫外光固化反应; • 有的天长地久例如钟乳石的形成、高分子老化、 高分子自然降解等。
4.2 化学反应速度理论
4.2.1碰撞理论 碰撞.html(旧键断裂、新键生成)
1918年 Lewis(路易斯)以气体分子运动论为基础提出了双分 子反应速率的碰撞理论,对反应速率做了较为正确的解释。 基本论点:气体分子间经过碰撞形成新的分子。反应分子碰 撞的频率越高,反应速率越快,即反应速率大小与反应物分 子碰撞的频率成正比。但理论计算气体分子碰撞频率为 3.5x1028次/升.秒,相当于反应速度5.8x104mol/l.s,即瞬间完成。 实际上气体反应速度千差万别,有的很慢,有的很快。
O3(g)+NO(g)NO2(g)+O2(g)
2NO22NO+O2
SO2Cl2 SO2+Cl2
• 非基元反应 • 由两个或两个以上基元反应组合而成的反应。 • 特点:实验可检测到中间产物,但中间产物被 后面的一步或几步基元反应消耗掉,不出现在 总反应方程式中。
例如:反应 NO2(g)+CO(g) NO(g)+CO2(g)
General formula
对于一般的化学反应: aA + bB yY + zZ
dcA dcB dcY dcZ adt bdt ydt zdt
▲ 实际工作中如何选择,往往取决于哪一种物质更易 通过实验监测其浓度变化。
反应的瞬时速率
c(N2O5)/mol· dm-3
1.00
v=5.4×10-4 mol · dm-3 · s-1
2
为三级反应
• 三、反应级数和速率常数
• 1、反应级数:0、1、2、3,可以是非 整数。
对反应 H2(g)+I2(g)=2HI(g) 反应速率方程式为 = k c(H2) c(I2) 过去很长一段时间都认为该反应是基元反应, 后来实验检出自由基I,证实该反应为非 基元反应,并提出反应机理为: (1) I2(g)=2I(g)(快速平衡) (2) H2(g)+2I(g)=2HI(g)(慢反应) ★由质量作用定律推导其反应速率方程式。
2、速率常数k
• 不随浓度而变。 • 受温度影响。通常温度升高, k 增大。 • 与催化剂有关。通常加催化剂, k 急剧 增大。 • 反应级数不同,k的量纲不同。
– 零级反应 k的量纲为mol.L-1.s-1 – 一级反应 k的量纲为s-1; – 二级反应 k的量纲为(mol· L -1)-1 · s-1;
中间产物NO3可被光谱检测到,但是没有从混合物中 分离出来。因此上述反应可视为由下列两个基元反应 组合而成,或反应历程(机理)为: NO2+NO2 NO3+NO(慢)
NO3+CO NO2+CO2(快)
• 结论:
– 非基元反应是由两个或两个以上基元反应 组合而成的;
– 一个反应是否基元反应只能由实验决定。
反应历程势能图
A
B A B (非催化配合物)
势能
Ea+
Ea_
A 反应进程
B
过渡状态理论认为:
从反应物到生成物之间会形成一种势能较 高的活化配合物(或活化中间体),活化配合 物所处的状态称为过渡状态。 活化配合物的势能Ec较高,不稳定,会很 快分解为产物或反应物。
活化配合物的最低势能与反应物的平均势 量之差为反应的活化能。即 Ea =Ec- E平均
Ea ln k ln A RT Ea / RT 或 k Ae
其中,
A——指数前因子,与碰撞方位因素有关。 Ea——活化能,单位为J.mol-1,对某一给定反应来说,Ea为一 定值,当反应的温度区间变化不大时,Ea和A不随温度而改变。 R=8.314 J.mol-1.K-1。 k——与温度有关,且温度越高, k值越大,反应速率越大。
问题: 反应 2W+X
Y+Z 哪种速率表达式是正确的?
a. b. c. d.
dc (X) dc (Y) dt dt dc (X) dc (W ) dt dt dc (Z) dc (Y) dt dt dc (Z) dc (W ) dt dt
(同学们自己回答)
• 为什么化学反应速率千差万别?
对非基元反应
NO 2 g CO g NOg CO 2 g
T 500K
反应机理为
①NO2 NO2 NO3 NO (慢,速率控制步骤)
②NO3 CO NO2 CO2
(快)
速率控制步骤(慢)的速率=非基元反应的速率 速率方程式为
k c( NO 2 )
加催化剂后 活化分子数大 大增加。 未加催化剂时反应 活化分子的分数。
二、过渡态理论 过渡态.html (有机化学) 要点:任何化学反应,都要经过一个过渡状态 (中间态、过渡态、活性配合物: 旧键部分断 裂、新键部分生成的高能量亚稳态),才能生 成产物。 过渡态特点:①高能量 ②可以分解生成产物,也可以分解 回到反应物。 活化能:反应物的势能与过渡态的能量差。 (活化能越小,则反应越容易进行)。
文物是不可再生的资源
随着空气中二氧化硫浓度的增加,使 得酸雨的“浓度” 也在增加。结果文物被 腐蚀的速度也在加快。
化学动力学 ( 化学的动力学 ) 研究的是反应进行的速
率, 并根据研究反应速率提供的信息探讨反应机理,即研 究反应的快慢和反应进行的途径。
H2与O2具有生成H2O的强烈趋势, 但室温下气体混 合物放置1万年仍看不出生成H2O的迹象。为了利用这个 反应释放的巨大能量 , 就必须提供适当的动力学条件。 因此,化学动力学研究还在于其实用意义。
为什么?
有效碰撞的概念:不一定每次碰撞都能发生反应。能发生 反应的碰撞叫有效碰撞。能发生有效碰撞的分子首先必 须具有足够的能量,以克服分子无限接近时电子云之间 的斥力,导致分子中的原子重排,即发生化学反应。
活化分子:能发生有效碰撞的分子叫活化分子。 活化分子在整个体系中所占的比例称为活化分子百分数。 不同化学反应活化分子百分数不同,因此化学反应速 率也不同。(活化分子与非活化分子的区别在于:能量 不同)。 讨论:①活化分子百分数越大,反应速率越大。 ②由非活化分子变为活化分子:能量升高
