初中数学竞赛立体图形(含答案)
初三数学几何竞赛试题及答案

初三数学几何竞赛试题及答案一、选择题(每题3分,共15分)1. 在直角三角形ABC中,∠C=90°,若a=6,c=10,则b的长度为多少?A. 8B. 9C. 10D. 112. 圆的半径为5,圆心到直线的距离为3,那么直线与圆的位置关系是?A. 相切B. 相交C. 相离D. 内切3. 一个正六边形的边长为a,其外接圆半径为多少?A. aB. √3aC. 2aD. a√34. 已知点P在圆O的内部,PA和PB是点P到圆O的两条切线,PA=PB,圆的半径为r,那么PA的长度为?A. rB. 2rC. √2rD. √3r5. 在三角形ABC中,若∠A=30°,∠B=45°,AB=1,求BC的长度。
A. √2B. √3C. 2D. 3√2二、填空题(每题2分,共10分)6. 已知三角形ABC的三边长分别为a, b, c,且a^2 + b^2 = c^2,那么三角形ABC是_________三角形。
7. 一个圆的直径为10cm,那么它的面积是_________平方厘米。
8. 一个正方体的体积为27立方厘米,它的边长是_________厘米。
9. 如果一个多边形的内角和为900°,那么这个多边形的边数是_________。
10. 在一个直角三角形中,如果一个锐角的度数是另一个锐角的两倍,那么较小的锐角的度数是_________。
三、解答题(每题5分,共20分)11. 在三角形ABC中,已知∠A=60°,∠B=45°,AB=2,求AC的长度。
12. 已知圆O的半径为r,点P在圆O上,PA是点P到圆心O的半径,求点P到圆O的切线长度。
13. 一个正五边形的外接圆半径为R,求正五边形的边长。
14. 已知点M在圆O的直径AB上,且OM=1/3AB,求点M到圆O的切线长度。
四、综合题(每题10分,共20分)15. 已知正方形ABCD的边长为1,E是CD边上的一点,F是BC边上的一点,且CE=CF=1/3。
初中培优竞赛含详细解析 第14讲 三角形

证明:∵ , ∴∠BDE=∠BFC
又∵∠ADC=∠BDE ∴∠BFC=∠ADC
在△BFC和△ADC中
∴
∴ , ,所以、正确
∵AE是∠BAF的角平分线,AE⊥BF,所以△BAF是等腰三角形,AB=AF
易错点:因为蚂蚁爬行必须经过盒面,所以不能凭空理解为连接2点的距离就是最短距离.
8. (2、3) (数学、初中、竞赛、初中竞赛、数学竞赛、初中数学竞赛、三角形、解答题)
如图所示,在Rt△ABC中, ,D是AB的中点, 交BC于E,连结CD.求 的值.
分析:我们根据直角三角形斜边上的中线等于斜边的一半,得到2个等腰三角形,可以分别求出两个角,即可解题.
证明:过K作KM∥BC交AB于M,如图.
∵KM∥BC∴
∵ ,∴ ,
又∵ , ∴
∴ 又∵ KA公用
∴ ,
∴
∵ ,
∴ , 又∵
∴
详解:在Rt△ABC中,D为AB的中点,所以 所以 因为 所以
所以
因为DE上AB,所以 所以 所以
答: 的值为
技巧:在直角三角形中,已知中线,用定理可以迅速解题.
9. (2、3) (数学、初中、竞赛、初中竞赛、数学竞赛、初中数学竞赛、三角形、解答题)
如图所示,在 中, 于D,AE平分 ,交CD于K,交BC于E,F是BE上的一点,且 求证:
分析:设直角三角形两直角边长分别为a,b,则有
求得 所以三角形的面积是24.
详解:24
技巧:因为直角三角形的面积就等于两条直角边乘积一半,所以我们求出ab即可解题.
2019年精选初中数学七年级上册[3.3 从不同方向观察立体图形]北京课改版课后练习[含答案解析]八十一
![2019年精选初中数学七年级上册[3.3 从不同方向观察立体图形]北京课改版课后练习[含答案解析]八十一](https://img.taocdn.com/s3/m/4c9a953e03d8ce2f00662355.png)
2019年精选初中数学七年级上册[3.3 从不同方向观察立体图形]北京课改版课后练习[含答案解析]八十一第1题【单选题】如图,观察这个立体图形,它的左视图是( )A、B、C、D、【答案】:【解析】:第2题【单选题】一个几何体由一些大小相同的小正方体组成,如图是它的主视图和俯视图,那么组成该几何体所需小正方体的个数最少为( )A、3B、4C、5D、6【答案】:【解析】:第3题【单选题】如图是由6个相同的小正方体组成的几何体,那么这个几何体的俯视图是( )A、B、C、D、【答案】:【解析】:第4题【单选题】如图是由5个相同的小立方块组成的立体图形,则它的俯视图是( )A、B、C、D、【答案】:【解析】:第5题【单选题】如图所示的几何体是由若干大小相同的小立方块搭成,则这个几何体的左视图是( )A、B、C、D、【答案】:【解析】:第6题【单选题】如图所示的三视图对应的几何体是( )A、长方体B、三棱锥C、圆锥D、三棱柱【答案】:【解析】:第7题【单选题】如图,是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数是(*)A、3个或4个B、4个或5个C、5个或6个D、6个或7个【答案】:【解析】:第8题【单选题】由若干个相同的小立方体搭成的几何体三视图如图所示,则搭成这个几何体的小立方体的个数是( )A、3B、4C、5D、6【答案】:【解析】:第9题【单选题】下列四个立体图形中,它们各自的三视图有两个相同,而另一个不同的是( )?A、①②B、②③C、②④D、③④【答案】:【解析】:第10题【单选题】有6个相同的立方体搭成的几何体如图所示,则它的主视图是( )A、B、C、D、【答案】:【解析】:第11题【单选题】如图,是由若干个同样大小的小立方体搭成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是( )A、B、C、D、【答案】:【解析】:第12题【填空题】如图,是一个长方体的主视图、左视图与俯视图(单位:cm),根据图中数据计算这个长方体的体积是______cm^3 .【答案】:【解析】:。
初一数学立体图形竞赛教程含例题练习及答案(可编辑)

初一数学立体图形竞赛教程含例题练习及答案初一数学竞赛讲座立体图形空间形体的想象能力是小学生的一种重要的数学能力,而立体图形的学习对培养这种能力十分有效。
我们虽然在课本上已经学习了一些简单的立体图形,如正方体、长方体、圆柱体、圆锥体,但有关立体图形的概念还需要深化,空间想象能力还需要提高。
将空间的位置关系转化成平面的位置关系来处理,是解决立体图形问题的一种常用思路。
一、立体图形的表面积和体积计算例 1 一个圆柱形的玻璃杯中盛有水,水面高 2.5cm,玻璃杯内侧的底面积是72cm2,在这个杯中放进棱长6cm的正方体铁块后,水面没有淹没铁块,这时水面高多少厘米?解:水的体积为72×2.5180(cm3),放入铁块后可以将水看做是底面积为72-6×632(cm2)的柱体,所以它的高为180÷325(cm)。
例2 下图表示一个正方体,它的棱长为4cm,在它的上下、前后、左右的正中位置各挖去一个棱长为1cm的正方体,问:此图的表面积是多少?分析:正方体有6个面,而每个面中间有一个正方形的孔,在计算时要减去小正方形的面积。
各面又挖去一个小正方体,这时要考虑两头小正方体是否接通,这与表面积有关系。
由于大正方体的棱长为4cm,而小正方体的棱长为1cm,所以没有接通。
每个小正方体孔共有5个面,在计算表面积时都要考虑。
解:大正方体每个面的面积为4×4-1×115(cm2),6个面的面积和为15×690(cm2)。
小正方体的每个面的面积为1×11(cm2),5个面的面积和为1×55(cm2),6个小正方体孔的表面积之和为5×630(cm2),因此所求的表面积为90+30120(cm2)。
想一想,当挖去的小正方体的棱长是2cm时,表面积是多少?请同学们把它计算出来。
例 3 正方体的每一条棱长是一个一位数,表面的每个正方形面积是一个两位数,整个表面积是一个三位数。
立体图形的表面展开图测试卷(含答案)初中数学

立体图形的表面展开图测试卷一、选择题(共10小题,每小题3分,满分30分)1.下列物体的形状类似于球的是()A.茶杯B.羽毛球C.乒乓球D.白炽灯泡2.如图把一个圆绕虚线旋转一周,得到的几何体是()A.B.C.D.3.如图,四个几何体分别为长方体、圆柱体、球体和三棱柱,这四个几何体中有三个的某一种视图都是同一种几何图形,则另一个几何体是()A.长方体B.圆柱体C.球体D.三棱柱4.如图是一个正四面体,它的四个面都是正三角形,现沿它的三条棱AC、BC、CD剪开展成平面图形,则所得的展开图是()A.B.C.D.5.如图1,是一个正方体的侧面展开图,小正方体从图2的位置依次翻到第1格、第2格、第3格、这时小正方体朝上面的字是()A.和B.谐C.社D.会6.如图,用一个平面去截长方体,则截面形状为()A.B.C.D.7.如下图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是()A.B.C.D.8.一个几何体是由若干个相同的正方体组成的,其主视图和左视图如图所示,则这个几何体最多可由多少个这样的正方体组成()A.12个B.13个C.14个D.18个9.如图是由几个小立方块所搭成的几何体的俯视图,小正方形体的数字表示该位置小立方块的个数,则该几何体的主视图是()A.B.C.D.10.一个几何体的三视图如图所示,则这个几何体是()A.B.C.D.二、填空题(共10小题,每小题3分,满分30分)11.一个棱柱有12个顶点,所有侧棱长的和是48cm ,则每条侧棱长是_________cm .12.如图所示,是一个立体图形的展开图,请写出这个立体图形的名称:_________.13.展览厅内要用相同的正方体木块搭成一个三视图如图的展台,则此展台共需这样的正方体_________块.14.如图是一个几何体的三视图,根据图中标注的数据可求出这个几何体的体积为_________.15.如图,一个立体图形由四个相同的小立方体组成.图1是分别从正面看和从左面看这个立体图形得到的平面图形,那么原立体图形可能是图2中的_________.(把下图中正确的立体图形的序号都填在横线上)16.下面4个图形均由6个相同的小正方形组成,折叠能围成一个正方体的是_________.17.图1是一个一面靠墙水平摆放的小正方体木块,图2、图3是由这样的小正方体木块靠墙叠放而成,按照这样的规律叠放下去,第5个叠放的图形中,小方体木块的个数是_________个.18.立方体木块的六个面分别标有数字1、2、3、4、5、6,如图,是从不同方向观察这个立方体木块看到的数字情况,数字1和5对面的数字的和是_________.19.如图,是一个直三棱柱的表面展开图,其中,黄色和绿色的部分都是边长等于1的正方形.问这个直三棱柱的体积是_________.20.一只蚂蚁从如图所示的正方体的一顶点A沿着棱爬向B,只能经过三条棱,共有_________种走法.三、解答题(共8小题,满分60分)21.下列三个图形都是由其中一个半圆经过变化而得到的,请分别说出每个图形最简单的变化过程.22.请画出下列几何体的主视图、左视图、俯视图.23.如图所示,是一个由小立方块搭成的几何体的俯视图,小正方体中的数字表示在该位置的小立方块的个数,试画出它的主视图与左视图.24.用白萝卜等材料做一个正方体,并把正方体表面涂上颜色.(1)把正方体的棱二等分,然后沿等分线把正方体切开,得到8个小正方体.观察其中三面被涂色的有a 个,如图①,那么a等于_________;(2)把正方体的棱三等分,然后沿等分线把正方体切开,得到27个小正方体.观察其中三面被涂色的有a个,各面都没有涂色的b个,如图②,那么a+b=_________;(3)把正方体的棱四等分,然后沿等分线把正方体切开,得到64个小正方体.观察其中两面被涂成红色有c个,各面都没有涂色的b个,如图③,那么b+c=_________.25.用一个平面去截一个几何体,截得的多边形可能有哪几种?请把结果画出来.26.如图(1)、(2)都是几何体的平面展开图,先想一想,再折一折,然后说出图(1)、(2)折叠后的几何体名称、底面形状、侧面形状、棱数、侧棱数与顶点数.27.如图,可用一个正方形制作成一副“七巧板”,利用“七巧板”能拼出各种各样的图案,根据“七巧板”的制作过程,请你解答下列问题.(1)“七巧板”的七个图形,可以归纳为三种不同形状的平面图形,即一块正方形,一块_________和五块_________.(2)请按要求将七巧板的七块图形重新拼接(不重叠,并且图形中间不留缝隙),在下面空白处画出示意图.①拼成一个等腰直角三角形;②拼成一个长与宽不等的长方形;③拼成一个六边形.(3)发挥你的想象力,用七巧板拼成一个图案,在下面空白处画出示意图,并在图案旁边写出简明的解说词.28.仔细观察下面的正四面体、正六面体、正八面体,解决下列问题:(1)填空:①正四面体的顶点数V=_________,面数F=_________,棱数E=_________.②正六面体的顶点数V=_________,面数F=_________,棱数E=_________.③正八面体的顶点数V=_________,面数F=_________,棱数E=_________.(2)若将多面体的顶点数用V表示,面数用F表示,棱数用E表示,则V、F、E之间的数量关系可用一个公式来表示,这就是著名的欧拉公式,请写出欧拉公式:_________.(3)如果一个多面体的棱数为30,顶点数为20,那么它有多少个面?参考答案与试题解析一、1-5.CBCBD 6-10.BBBAC二、11. 8 12. 圆锥13. 10 14. 24π15. ①②④16. ①②17.35 18. 719.20. 6三、21.22.(6分)请画出下列几何体的主视图、左视图、俯视图.23.解:如图所示:24.8 9 3225.解:截面的形状可能是三角形、四边形、五边形、六边形,如图所示.26.解:图(1)折叠后是长方体,底面是正方形,侧面是长方形,有12条棱,4条侧棱,8个顶点.图(2)折叠后是六棱柱,底面是六边形,侧面是长方形,有18条棱,6条侧棱,12个顶点.27.解:(1)平行四边形、等腰直角三角形;(2)如图所示:(3)如图所示:让我们舞起来吧!28.解:(1)①4,4,6;②8,6,12;③6,8,12;(2)V、F、E之间的数量关系是:V+F﹣E=2;(3)设面数为F,则20+F﹣30=2,解得F=12,答:它有12个面.。
初中数学竞赛《不规则立体图形的表面积和体积(二)》配套练习题

《不规则立体图形的表面积和体积(二)》配套练习题一、解答题1、有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?2、一个圆柱体底面周长和高相等.如果高缩短4cm,表面积就减少50.24cm2.求这个圆柱体的表面积是多少?3、如图,厚度为0.25毫米的铜版纸被卷成一个空心圆柱(纸卷得很紧,没有空隙),它的外直径是180cm,内直径是50cm.这卷铜版纸的总长是多少米?4、如图,有一卷紧紧缠绕在一起的塑料薄膜,薄膜的直径为20cm,中间有一直径为8cm的卷轴,已知薄膜的厚度为0.04cm,则薄膜展开后的面积是多少平方米?5、一个盖着瓶盖的瓶子里面装着一些水,瓶底面积为10平方厘米,(如下图所示),请你根据图中标明的数据,计算瓶子的容积是多少立方厘米?6、一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如图.已知它的容积为26.4π立方厘米.当瓶子正放时,瓶内的酒精的液面高为6厘米.瓶子倒放时,空余部分的高为2厘米.问:瓶内酒精的体积是多少立方厘米?合多少升?7、铁路油罐车由两个半球面和一个圆柱面钢板焊接而成,尺寸如图所示.问:该油罐车的容积是多少立方米?(π=3.14)8、如图所示,一个5×5×5的立方体,在一个方向上开有1×1×5的孔,在另一个方向上开有2×1×5的孔,在第三个方向上开有3×1×5的孔,剩余部分的体积是多少?表面积为多少?9、如图,原来的大正方体是由125个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?10、如图,ABCD是矩形,BC=6cm,AB=10cm,对角线AC、BD相交O.E、F分别是AD与BC的中点,图中的阴影部分以EF为轴旋转一周,则白色部分扫出的立体图形的体积是多少立方厘米?(π取3)答案部分一、解答题1、【正确答案】307.72【答案解析】涂漆的面积等于大圆柱表面积与小圆柱侧面积之和,为6π×10+π×(6÷2)2×2+4π×5=60π+18π+20π=98π=307.72(平方厘米).【答疑编号10299065】2、【正确答案】182.8736【答案解析】圆柱体底面周长和高相等,说明圆柱体侧面展开是一个正方形.高缩短4cm,表面积就减少50.24cm2.阴影部分的面积为圆柱体表面积减少部分,值是50.24cm2,所以底面周长是50.24÷4=12.56(cm),侧面积是:12.56×12.56=157.7536(cm2),两个底面积是:3.14×(12.56÷3.14÷2)2×2=25.12(cm2).所以表面积为:157.7536+25.12=182.8736(cm2).【答疑编号10299073】3、【正确答案】9388.6【答案解析】卷在一起时铜版纸的横截面的面积为(cm2),如果将其展开,展开后横截面的面积不变,形状为一个长方形,宽为0.25mm(即0.025cm),所以长为7475π÷0.025=938860cm=9388.6m.所以这卷铜版纸的总长是9388.6米.【答疑编号10299080】4、【正确答案】65.94【答案解析】缠绕在一起时塑料薄膜的体积为:[π×(20÷2)2-π×(8÷2)2]×100=8400π(cm3)薄膜展开后为一个长方体,体积保持不变,而厚度为0.04cm,所以薄膜展开后的面积为:8400π÷0.04=659400cm2=65.94平方米【答疑编号10299082】5、【正确答案】60【答案解析】由已知条件知,第二个图上部空白部分的高为7-5=2cm,从而水与空着的部分的比为4∶2=2∶1,由左图知水的体积为10×4,所以总的容积为40÷2×(2+1)=60立方厘米.【答疑编号10299088】6、【正确答案】62.172;0.062172【答案解析】6÷2=326.4π÷(3+1)×3=62.172(立方厘米)62.172立方厘米=62.172毫升=0.062172升.答:酒精的体积是62.172立方厘米,合0.062172升.【答疑编号10299090】7、【正确答案】41.9【答案解析】(立方米)【答疑编号10299093】8、【正确答案】100;204【答案解析】求体积:开了3×1×5的孔,挖去3×1×5=15,开了1×1×5的孔,挖去1×1×5-1=4;开了2×1×5的孔,挖去2×1×5-(2+2)=6,剩余部分的体积是:5×5×5-(15+4+6)=100.(另解)将整个图形切片,如果切面平行于纸面,那么五个切片分别如图:得到总体积为:22×4+12=100.求表面积:表面积可以看成外部和内部两部分.外部的表面积为5×5×6-12=138,内部的面积可以分为前后、左右、上下三个方向,面积分别为2×(2×5+1×5-1×2-1×3)=202×(1×5+3×5-1×3-1)=322×(1×5+1×5-1×1-2)=14所以总的表面积为:138+20+32+14=204.【答疑编号10299104】9、【正确答案】72【答案解析】对于这一类从立体图形中间挖掉一部分后再求体积(或小正方体数目)的题目一般可以采用“切片法”来做,所谓“切片法”,就是把整个立体图形切成一片一片的(或一层一层的),然后分别计算每一片或每一层的体积或小正方体数目,最后再把它们相加.采用切片法,俯视第一层到第五层的图形依次如下,其中黑色部分表示挖除掉的部分.从图中可以看出,第1、2、3、4、5层剩下的小正方体分别有22个、11个、11个、6个、22个,所以总共还剩下22+11+11+6+22=72(个)小正方体.【答疑编号10299107】10、【正确答案】180【答案解析】扫出的图形如图所示,白色部分实际上是一个圆柱减去两个圆锥后所形成的图形.两个圆锥的体积之和为(立方厘米);圆柱的体积为π×32×10=270(立方厘米),所以白色部分扫出的体积为270-90=180(立方厘米).【答疑编号10299110】。
四川省成都市龙泉驿区第一中学校立体几何多选题试题含答案

四川省成都市龙泉驿区第一中学校立体几何多选题试题含答案一、立体几何多选题1.在正方体1111ABCD A B C D -中,M 、N 分别是棱AB 、1CC 的中点,1MB P 的顶点P 在棱1CC 与棱11C D 上运动,有以下四个命题正确命题的序号是( )A .平面1MB P 1ND ⊥B .平面1MB P ⊥平面11ND AC .1MB P 在底面ABCD 上的射影图形的面积为定值D .1MB P 在侧面11D C CD 上射影图形是三角形【答案】BC【分析】取N 与P 重合,结合勾股定理可判断A 选项的正误;利用面面垂直的判定定理可判断B 选项的正误;分点P 在棱1CC 、11C D 上运动两种情况讨论,利用三角形的面积公式可判断C 选项的正误;取点P 与点1C 重合,判断1MB P 在侧面11D C CD 上射影图形形状,可判断D 选项的正误.【详解】对于A 选项,设正方体1111ABCD A B C D -的棱长为2,如下图所示:当点P 与点N 重合时,若1ND ⊥平面1MB P ,1B N ⊂平面1MB P ,则11ND B N ⊥, 由勾股定理可得2211115D N C N C D =+=,同理可得15B N =1122B D = 2221111B N D N B D ∴+≠,则1ND 与1B N 不垂直,假设不成立,A 选项错误; 对于B 选项,取1BB 的中点E ,连接1A E 、EN ,在正方体1111ABCD A B C D -中,11//BB CC ,且E 、N 分别为1BB 、1CC 的中点, 则11//B E C N 且11B E C N =,所以,四边形11B ENC 为平行四边形,则11//EN B C 且11EN B C =,1111//A D B C 且1111A D B C =,所以,11//A D EN 且11A D EN =,所以,四边形11A END 为平行四边形,所以,11//A E D N ,111A B BB =,1B E BM =,11190A B E B BM ∠=∠=,所以,111Rt A B E Rt B BM ≅△△,所以,111B A E BB M ∠=∠,所以,111111190A EB BB M A EB B A E ∠+∠=∠+∠=, 190B FE ∴∠=,所以,11B M A E ⊥,11A D ⊥平面11AA B B ,1B M ⊂平面11AA B B ,111B M A D ∴⊥,1111A D A E A =,11A D 、1A E ⊂平面11ND A ,1MB ∴⊥平面11ND A ,1MB ⊂平面1MB P ,所以,平面1MB P ⊥平面11ND A ,B 选项正确;对于C 选项,设正方体1111ABCD A B C D -的棱长为a .若点P 在棱1CC 上运动时,1MB P 在底面ABCD 上的射影为MBC △, 此时,射影图形的面积为21224MBC a a S a =⋅=△; 若点P 在棱11C D 上运动时,设点P 在底面ABCD 上的射影点为G ,则G CD ∈, 且点G 到AB 的距离为a ,1MB 在底面ABCD 内的射影为MB ,则1MB P 在底面ABCD 内的射影为MBG △, 且21224MBG a a S a =⋅⋅=△.综上所述,1MB P 在底面ABCD 内的射影图形的面积为定值,C 选项正确; 对于D 选项,当点P 与1C 重合时,P 、1B 两点在平面11D C CD 上的射影重合, 此时,1MB P 在侧面11D C CD 上的射影不构成三角形,D 选项错误.故选:BC.【点睛】方法点睛:证明面面垂直常用的方法:(1)面面垂直的定义;(2)面面垂直的判定定理.在证明面面垂直时,一般假设面面垂直成立,然后利用面面垂直转化为线面垂直,即为所证的线面垂直,组织论据证明即可.2.如图,正方体1111ABCD A B C D -的棱长为3,点E ,F 分别在1CC ,1BB 上,12C E EC →→=,12BF FB →→=.动点M 在侧面11ADD A 内(包含边界)运动,且满足直线//BM 平面1D EF ,则( )A .过1D ,E ,F 的平面截正方体所得截面为等腰梯形B .三棱锥1D EFM -的体积为定值C .动点M 10D .过B ,E ,M 的平面截正方体所得截面面积的最小值为【答案】BCD【分析】由题做出过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,进而计算即可排除A 选项;根据//BM 平面1D EF ,由等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===即可得B 选项正确;取1AA 靠近1A 点的三等分点H , 1DD 靠近D 点的三等分点I ,易知M 的轨迹为线段HI ,故C 选项正确;过M 点做BE 的平行线交1AA 于P ,交1DD 于O ,连接,BP OE ,易知过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,进而得当H 位于点I 时,截面面积最小,为四边形ABEI 的面积,且面积为S AB BE =⋅=【详解】解:对于A 选项,如图,取BF 中点G ,连接1A G ,由点E ,F 分别在1CC ,1BB 上,12C E EC →→=,12BF FB →→=,故四边形11A D EG 为平行四边形,故11//AG D E ,由于在11A B G △,F 为1B G 中点,当N 为11A B 中点时,有11////NF A G D E ,故过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,此时12D N ==,EF ==1D EFN 不是等腰梯形,故A 选项错误;对于B 选项,三棱锥1D EFM -的体积等于三棱锥1M D EF -的体积,由于//BM 平面1D EF ,故三棱锥1M D EF -的体积等于三棱锥1B D EF -的体积,三棱锥1B D EF -的体积等于三棱锥1D BEF -的体积,而三棱锥1D BEF -的体积为定值,故B 选项正确; 对于C 选项,取1AA 靠近1A 点的三等分点H , 1DD 靠近D 点的三等分点I ,易知1////HB AG NF ,1//BI D F ,由于1,HI BI I NF D F F ==,故平面//BHI 平面1D EF ,故M 的轨迹为线段HI ,故C 选项正确;对于D 选项,过M 点做BE 的平行线交1AA 于P ,交1DD 于O ,连接,BP OE ,则过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,易知当H 位于点I 时,平行四边形BPOE 边BP 最小,且为AB ,此时截面平行四边形BPOE 的面积最小,为四边形ABEI 的面积,且面积为S AB BE =⋅=D 选项正确;故选:BCD【点睛】本题解题的关键在于根据题意,依次做出过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,进而讨论AD 选项,通过//BM 平面1D EF ,并结合等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===知B 选项正确,通过构造面面平行得M 的轨迹为线段HI ,进而讨论C 选项,考查回归转化思想和空间思维能力,是中档题.3.正方体1111ABCD A B C D -中,E 是棱1DD 的中点,F 在侧面11CDD C 上运动,且满足1//B F 平面1A BE .以下命题正确的有( )A .侧面11CDD C 上存在点F ,使得11B F CD ⊥B .直线1B F 与直线BC 所成角可能为30︒C .平面1A BE 与平面11CDD C 所成锐二面角的正切值为2D .设正方体棱长为1,则过点E ,F ,A 5 【答案】AC【分析】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,易证得平面1//B MN 平面1A BE ,可得点F 的运动轨迹为线段MN .取MN 的中点F ,根据等腰三角形的性质得1B F MN ⊥,即有11B F CD ⊥,A 正确;当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,可判断B 错误;根据平面1//B MN 平面1A BE ,11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,计算可知C 正确;【详解】取11C D 中点M ,1CC 中点N ,连接11,,B M B N MN ,则易证得11//B N A E ,1//MN A B ,从而平面1//B MN 平面1A BE ,所以点F 的运动轨迹为线段MN . 取MN 的中点F ,因为1B MN △是等腰三角形,所以1B F MN ⊥,又因为1//MN CD ,所以11B F CD ⊥,故A 正确;设正方体的棱长为a ,当点F 与点M 或点N 重合时,直线1B F 与直线BC 所成角最大,此时11tan C B F ∠=1tan 3023︒<=,所以B 错误; 平面1//B MN 平面1A BE ,取F 为MN 的中点,则1MN C F ⊥,1MN B F ⊥,∴11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角,11111tan B C B FC C F ∠==22,所以C 正确;因为当F 为1C E 与MN 的交点时,截面为菱形1AGC E (G 为1BB 的交点),面积为62,故D 错误. 故选:AC.【点睛】本题主要考查线面角,二面角,截面面积的求解,空间几何中的轨迹问题,意在考查学生的直观想象能力和数学运算能力,综合性较强,属于较难题.4.已知正方体1111ABCD A B C D -的棱长为2,点O 为11A D 的中点,若以O 6为半径的球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,则下列结论正确的是( )A .11//A D 平面EFGHB .1AC ⊥平面EFGHC .11A B 与平面EFGH 所成的角的大小为45°D .平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7【答案】ACD【分析】如图,计算可得,,,E F G H 分别为所在棱的中点,利用空间中点线面的位置关系的判断方法可判断A 、B 的正确与否,计算出直线AB 与平面EFGH 所成的角为45︒后可得C 正确,而几何体BHE CGF -为三棱柱,利用公式可求其体积,从而可判断D 正确与否.【详解】如图,连接OA ,则2115OA AA =+=,故棱1111,,,A A A D D D AD 与球面没有交点. 同理,棱111111,,A B B C C D 与球面没有交点.因为棱11A D 与棱BC 之间的距离为26>BC 与球面没有交点. 因为正方体的棱长为2,而26<球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,所以棱11,,,AB CD C C B B 与球面各有一个交点, 如图各记为,,,E F G H .因为OAE △为直角三角形,故22651AE OE OA -=-=,故E 为棱AB 的中点. 同理,,F G H 分别为棱11,,CD C C B B 的中点.由正方形ABCD 、,E F 为所在棱的中点可得//EF BC ,同理//GH BC ,故//EF GH ,故,,,E F G H 共面.由正方体1111ABCD A B C D -可得11//A D BC ,故11//A D EF因为11A D ⊄平面EFGH ,EF ⊂平面EFGH ,故11//A D 平面EFGH ,故A 正确.因为在直角三角1BA C 中,122A B =2BC = ,190A BC ∠=︒,1A C 与BC 不垂直,故1A C 与GH 不垂直,故1A C ⊥平面EFGH 不成立,故B 错误. 由正方体1111ABCD A B C D -可得BC ⊥平面11AA B B ,而1A B ⊂平面11AA B B , 所以1BC A B ⊥,所以1EF A B ⊥在正方形11AA B B 中,因为,E H 分别为1,AB BB 的中点,故1EH A B ⊥,因为EF EH E =,故1A B ⊥平面EFGH ,所以BEH ∠为直线AB 与平面EFGH 所成的角,而45BEH ∠=︒,故直线AB 与平面EFGH 所成的角为45︒,因为11//AB A B ,故11A B 与平面EFGH 所成的角的大小为45°.故C 正确.因为,,,E F G H 分别为所在棱的中点,故几何体BHE CGF -为三棱柱, 其体积为111212⨯⨯⨯=,而正方体的体积为8, 故平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7,故D 正确. 故选:ACD.【点睛】本题考查空间中线面位置的判断、空间角的计算和体积的计算,注意根据球的半径确定哪些棱与球面有交点,本题属于中档题.5.如图,正方体1111ABCD A B C D -的棱长为1,线段11B D 上有两个动点E ,F ,且2EF =.则下列结论正确的是( )A .三棱锥A BEF -的体积为定值B .当E 向1D 运动时,二面角A EF B --逐渐变小C .EF 在平面11ABB A 内的射影长为12D .当E 与1D 重合时,异面直线AE 与BF 所成的角为π4【答案】AC【分析】对选项分别作图,研究计算可得.【详解】选项A:连接BD ,由正方体性质知11BDD B 是矩形,1112212224BEF S EF BB ∆∴=⋅=⨯⨯= 连接AO 交BD 于点O由正方体性质知AO ⊥平面11BDD B ,所以,AO 是点A 到平面11BDD B 的距离,即22AO = 112213312A BEF BEF V S AO -∆∴=⨯=⨯⨯= A BEF V -∴是定值.选项B:连接11A C 与11B D 交于点M ,连接11,AD AB ,由正方体性质知11AD AB =,M 是11B D 中点,AM EF ∴⊥ ,又1BB EF ⊥,11//BB AAA EFB ∴--的大小即为AM 与1AA 所成的角,在直角三角形1AA M 中,12tan MAA ∠=为定值. 选项C:如图,作1111,,,FH A B EG A B ET EG ⊥⊥⊥在直角三角形EFT 中,221cos 45222FT EF =⨯=⨯= 12HG FT ∴== 选项D:当E 与1D 重合时,F 与M 重合,连接AC 与BD 交于点R ,连接1D R ,1//D R BM 异面直线AE 与BF 所成的角,即为异面直线1AD 与1D R 所成的角,在三角形1AD R 中,22111132,2AD D R MB BB M B ===+=22AR = 由余弦定理得13cos 6AD R ∠=故选:AC【点睛】本题考查空间几何体性质问题.求解思路:关键是弄清(1)点的变化,点与点的重合及点的位置变化;(2)线的变化,应注意其位置关系的变化;(3)长度、角度等几何度量的变化.求空间几何体体积的思路:若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解.其中,求三棱锥的体积常用等体积转换法;若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.6.如图,已知矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE ∆沿直线DE 翻折成1A DE ∆,若M 为线段1A C 的中点,则ADE ∆在翻折过程中,下列说法正确的是( )A .线段BM 的长是定值B .存在某个位置,使1DE AC ⊥ C .点M 的运动轨迹是一个圆D .存在某个位置,使MB ⊥平面1A DE 【答案】AC 【分析】取CD 中点F ,连接BF ,MF ,根据面面平行的判定定理可得平面//BMF 平面1A DE ,由面面平行的性质定理可知//BM 平面1A DE ,可判断D ;在BFM ∆中,利用余弦定理可求得BM a =为定值,可判断A 和C ;假设1DE A C ⊥,由线面垂直的判定定理可得DE ⊥平面1A CE ,由线面垂直的性质定理可知1DE A E ⊥,与11DA A E ⊥矛盾,可判断B . 【详解】解:取CD 的中点F ,连接BF ,MF ,∵M ,F 分别为1A C 、CD 中点, ∴1MF A D ∥,∵1A D ⊂平面1A DE ,MF ⊄平面1A DE , ∴MF 平面1A DE , ∵DF BE ∥且DF BE =, ∴四边形BEDF 为平行四边形, ∴BFDE ,∵DE ⊂平面1A DE ,BF ⊄平面1A DE , ∴BF ∥平面1A DE , 又BFMF F =,BF 、MF ⊂平面BMF ,∴平面//BMF 平面1A DE , ∵BM ⊂平面BMF , ∴BM ∥平面1A DE ,即D 错误,设22AB AD a ==, 则112MF A D a ==,2BF DE a ==,145A DE MFB ︒∠=∠=, ∴222cos45BM MF BF MF BF a ︒=+-⋅⋅=,即BM 为定值,所以A 正确,∴点M 的轨迹是以B 为圆心,a 为半径的圆,即C 正确, ∵2DE CE a ==,2CD AB a ==,∴222DE CE CD +=,∴DE CE ⊥, 设1DE A C ⊥,∵1A C 、CE ⊂平面1A CE ,1AC CE C =,∴DE ⊥平面1A CE , ∵1A E ⊂平面1A CE ,∴1DE A E ⊥,与11DA A E ⊥矛盾, 所以假设不成立,即B 错误. 故选:AC . 【点睛】本题考查立体几何中的翻折问题,涉及到线段长度的求解、直线与平面位置关系的判定、点的轨迹的求解、反证法的应用等知识点,考查学生的空间立体感和推理论证能力.7.在正方体1111ABCD A B C D -中,如图,,M N 分别是正方形ABCD ,11BCC B 的中心.则下列结论正确的是( )A .平面1D MN 与11BC 的交点是11B C 的中点 B .平面1D MN 与BC 的交点是BC 的三点分点 C .平面1D MN 与AD 的交点是AD 的三等分点 D .平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ,延长DE ,1D N ,并交于点F ,连FM 并延长分别交,BC AD 于,P Q ,连1,D Q PN 并延长交11B C 与H ,平面四边形1D HPQ 为所求的截面,进而求出,,P Q H 在各边的位置,利用割补法求出多面体11QPHD C CD 的体积,即可求出结论.【详解】如图,取BC 的中点E ,延长DE ,1D N ,并交于点F , 连接FM 并延长,设FM BC P ⋂=,FM AD Q ⋂=, 连接PN 并延长交11B C 于点H .连接1D Q ,1D H ,则平面四边形1D HPQ 就是平面1D MN 与正方体的截面,如图所示.111111////,22NE CC DD NE CC DD ==,NE ∴为1DD F ∆的中位线,E ∴为DF 中点,连BF , ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒, ,,A B F ∴三点共线,取AB 中点S ,连MS ,则12//,,23BP FB MS BP MS BC MS FS =∴==, 22111,33236BP MS BC BC PE BC ∴==⨯=∴=, E 为DF 中点,11//,233PE DQ DQ PE BC AD ∴===N 分别是正方形11BCC B 的中心,11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点, 点Q 是线段AD 靠近点D 的三等分点, 点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P ', 做出线段11A D 靠近1D 的三等分点G ,连接QP ',HP ',QG ,GH ,1H QPP Q GHD V V '--=, 所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体 从而平面1D MN 将正方体分成两部分体积比为2∶1. 故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积,确定出平面与正方体的交线是解题的关键,考查直观想象、逻辑推理能力,属于较难题.8.如图,正三棱柱11ABC A B C -中,11BC AB ⊥、点D 为AC 中点,点E 为四边形11BCC B 内(包含边界)的动点则以下结论正确的是( )A .()1112DA A A B A BC =-+ B .若//DE 平面11ABB A ,则动点E 的轨迹的长度等于22AC C .异面直线AD 与1BC ,所成角的余弦值为66D .若点E 到平面11ACC A 的距离等于32EB ,则动点E 的轨迹为抛物线的一部分 【答案】BCD 【分析】根据空间向量的加减法运算以及通过建立空间直角坐标系求解,逐项判断,进而可得到本题答案. 【详解】解析:对于选项A ,()1112AD A A B A BC =-+,选项A 错误; 对于选项B ,过点D 作1AA 的平行线交11A C 于点1D .以D 为坐标原点,1DA DB DD ,,分别为,,x y z 轴的正方向建立空间直角坐标系Oxyz .设棱柱底面边长为a ,侧棱长为b ,则002aA ⎛⎫ ⎪⎝⎭,,,300B ⎛⎫ ⎪ ⎪⎝⎭,,,130B b ⎛⎫ ⎪ ⎪⎝⎭,,,102a C b ⎛⎫- ⎪⎝⎭,,,所以132a BC a b ⎛⎫=-- ⎪ ⎪⎝⎭,,,132a AB a b ⎛⎫=- ⎪ ⎪⎝⎭,,. ∵11BC AB ⊥,∴110BC AB ⋅=,即2223022a a b ⎛⎫⎛⎫--+= ⎪ ⎪ ⎪⎝⎭⎝⎭,解得22b a =. 因为//DE 平面11ABB A ,则动点E 的轨迹的长度等于122BB AC =.选项B 正确. 对于选项C ,在选项A 的基础上,002a A ⎛⎫⎪⎝⎭,,,300B a ⎛⎫ ⎪ ⎪⎝⎭,,,()0,0,0D ,12022a C a ⎛⎫- ⎪ ⎪⎝⎭,,,所以002a DA ⎛⎫= ⎪⎝⎭,,,132222a BC a a ⎛⎫=- ⎪ ⎪⎝⎭,-,, 因为211162cos ,||||622a BC DA BC DA BC DA a a ⎛⎫- ⎪⋅⎝⎭<>===-,所以异面直线1,BC DA 所成角的余弦值为66,选项C 正确. 对于选项D ,设点E 在底面ABC 的射影为1E ,作1E F 垂直于AC ,垂足为F ,若点E 到平面11ACC A 的距离等于3EB ,即有31E F EB =,又因为在1CE F ∆中,311E F E C =,得1EB E C =,其中1E C 等于点E 到直线1CC 的距离,故点E 满足抛物线的定义,另外点E 为四边形11BCC B 内(包含边界)的动点,所以动点E 的轨迹为抛物线的一部分,故D 正确.故选:BCD 【点睛】本题主要考查立体几何与空间向量的综合应用问题,其中涉及到抛物线定义的应用.。
2023-2024学年部编版初中数学七年级上册课时练《4.1.1 立体图形和平面图形》03(含答案)
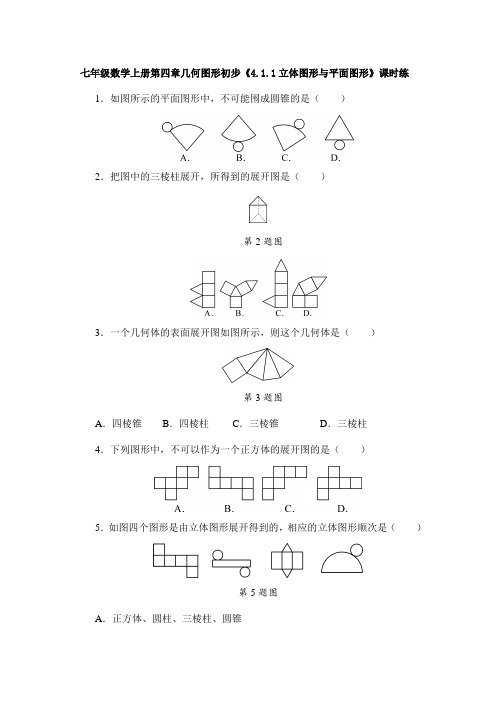
七年级数学上册第四章几何图形初步《4.1.1立体图形与平面图形》课时练1.如图所示的平面图形中,不可能围成圆锥的是()2.把图中的三棱柱展开,所得到的展开图是()第2题图3.一个几何体的表面展开图如图所示,则这个几何体是()第3题图A.四棱锥B.四棱柱C.三棱锥D.三棱柱4.下列图形中,不可以作为一个正方体的展开图的是()5.如图四个图形是由立体图形展开得到的,相应的立体图形顺次是()第5题图A.正方体、圆柱、三棱柱、圆锥B.正方体、圆锥、三棱柱、圆柱C.正方体、圆柱、三棱锥、圆锥D.正方体、圆柱、四棱柱、圆锥6.一个几何体的展开图如图所示,这个几何体是()A.三棱柱B.三棱锥C.四棱柱D.四棱锥第6题图7.如图是一个长方体形状包装盒的表面展开图,折叠制作完成后得到长方体的容积是(包装材料厚度不计)()A.40×40×70B.70×70×80C.80×80×40D.40×70×80第7题图8.如图是一个正方体展开图,把展开图折叠成正方体后,“你”字一面相对面上的字是()A.我B.中C.国D.梦第8题图9.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)()A.1或2或3B.3或4或5C.4或5或6D.1或2或6 第9题图10.下列图形是一些立体图形的平面展开图,请将这些立体图形的名称填在对应的横线上.11.如图是正方体的展开图,则原正方体相对两个面上的数字积的最小值是____________.第11题图12.如图是一个正方体的平面展开图,标注了A字母的是正方体的正面,如果正方体的左面与右面标注的式子相等,求x的值.第12题图13.将一张长与宽的比为2∶1的长方形纸片按图1、图2所示的方式对折,然后沿图3中的虚线裁剪,得到图4,最后将图4的纸片再展开铺平,则所得到的图案是()第13题图14.如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图形可以是()第14题图15.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子,共有____________种添加方法.第15题图16.如图所示,在正方体各面上写上数1,2,3,而在展开图中也分别写上了两个或一个指定的数.请你在展开图的其他各面上写上适当的数,使得相对的面上两数的和等于7.第16题图17.如图所示,有分别写着a,b,c,d,e,f的六个小正方形.(1)这6个小正方形能否围成一个小正方体?(2)若把写有a的正方形分别移到c,d,e上面,其余不变,能否围成正方体?(3)如果把写有a的正方形分别移到b,c,d下面,其余不变,能否围成一个正方体?第17题图18.如图所示,有一放在桌面上的正方体的盒子ABCD-A1B1C1D1,在盒子外的顶点A处有一只蚂蚁,而在对角的顶点C1处有一滴蜜糖,蚂蚁应沿着什么路径爬,才能最快吃到蜜糖.请画出蚂蚁爬行的路线,共有几条路线并简要说明理由.第18题图参考答案1—5.DBACA6—9.CDDD10.四棱锥圆柱三棱柱11.-812.x=113—14.AC15.416.由正方体图形知1,2,3共用一个顶点,可在展开图中确定出这三个数,再找它们的相对面.如图(图2答案不唯一).第16题图17.(1)能(2)能(3)不能18.如图,共有6条路线.理由略第18题图。
初中数学几何图形专题训练50题含答案

初中数学几何图形专题训练50题含答案(单选、填空、解答题)一、单选题1.如图,已知∠AOC=∠BOD=90º,∠AOD=150º,则∠BOC 的度数为( )A .30ºB .45ºC .50ºD .60º 2.下列图形属于立体图形的是( )A .正方形B .三角形C .球D .梯形 3.已知∠AOB =75°,以O 为端点作射线OC ,使∠AOC =48°,则∠BOC 的度数为( )A .123°B .123°和27°C .23°D .27°4.如图,已知点C 是线段AB 的中点,2AC cm =, 1.5DC cm =,则BD =( )A .0.5cmB .1cmC .1.5cmD .2cm 5.已知A ,B ,C ,D 四点,任意三点都不在同一直线上,以其中的任意两点为端点的线段的数量是( )A .5B .6C .7D .8 6.如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若2110∠=︒,那么1∠的度数是( )A .10°B .20°C .30°D .40° 7.如图,已知∠ACB=90°,CD∠AB ,垂足是D ,则图中与∠A 相等的角是( )A.∠1B.∠2C.∠B D.∠1、∠2和∠B 8.在地理课堂上,老师组织学生进行寻找北极星的探究活动时,李佳同学使用了如图所示的半圆仪,则下列四个角中,最可能和互补的角为()A.B.C.D.9.下列说法正确的是()A.连接两点的线段,叫做两点间的距离B.射线OA与射线AO表示的是同一条射线C.经过两点有一条直线,并且只有一条直线D.从一点引出的两条直线所形成的图形叫做角10.我军在海南举行了建国以来海上最大的军事演习,位于点O处的军演指挥部观测到军舰A位于点O的北偏东65︒方向(如图),同时观测到军舰B位于点O处的南偏西20︒方向,则AOB∠=()A .85︒B .105︒C .125︒D .135︒ 11.如图,小玮从A 处沿北偏东40°方向行走到点B 处,又从点B 处沿东偏南23°方向行走到点C 处,则∠ABC 的度数为( )A .99°B .107°C .127°D .129° 12.如图,CE 是ABC 的外角ACD ∠的平分线,且CE 交BA 的延长线于点E ,30B ∠=︒,100ACD ∠=︒,则E ∠的度数为( )A .10°B .15°C .20°D .25° 13.如图所示,正方体的展开图为( )A .B .C .D .14.如图方格纸中每个小正方形的边长均为1,线段AC 的两个端点均在小正方形的顶点上,点P 也在小正方形的顶点上.某人从点P 出发,沿图中已有的格点所连线段走一周(即不能直接走线段AC 且要回到P ),则这个人所走的路程最少是( )A .7B .14C .10D .不确定 15.如图,等边∠ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是边AC 上一点,若AE =2,则EM +CM 的最小值为( )AB .C .D .16.已知A ,B ,C 三点在同一条直线上,M ,N 分别为线段AB ,BC 的中点,且AB =60,BC =40,则MN 的长为( )A .10B .50C .10或50D .无法确定 17.如图,从4点钟开始,过了40分钟后,分针与时针所夹角的度数是( )A .090B .0100C .0110D .0120 18.一副三角板按如图方式摆放,且1∠的度数比2∠的度数小20︒,则2∠的度数为( )A .35︒B .40︒C .45︒D .55︒ 19.一把直尺和一块三角板ABC (含30°,60°角)的摆放位置如图,直尺一边与三角板的两直角边分别交于点D 、点E ,另一边与三角板的两直角边分别交于点F 、点A ,且∠CED=50°,那么∠BAF=()A.10°B.50°C.45°D.40°20.如图,直线AB MN∥,点C为直线MN上一点,连接AC、BC,∠CAB=40°,∠ACB=90°,∠BAC的角平分线交MN于点D,点E是射线AD上的一个动点,连接CE、BE,∠CED的角平分线交MN于点F.当∠BEF=70°时,令ECMα∠=,用含α的式子表示∠EBC为().A.52αB.10α︒-C.1102α︒-D.1102α-︒二、填空题21.如图,将∠AOB 绕点O 按逆时针方向旋转40°后得到∠COD,若∠AOB=15°,则∠AOD 的度数是______°.22.若∠A与∠B互余,则∠A+∠B=_____;若∠A与∠B互补,则∠A+∠B=_____. 23.如图,点A、O、B在一条直线上,且∠AOD=35°,OD平分∠AOC,则图中∠BOC=______度.24.如图,在直线AB 上有一点O ,OC ∠OD ,OE 是∠DOB 的角平分线,当∠DOE =20°时,∠AOC =___°.25.一个直棱柱有12条棱,则它是__棱柱.26.如图,EF 是ABC 的中位线,BD 平分ABC ∠交EF 于D ,若6,10AB BC ==,则DF =______.27.已知5526α∠=︒',则α∠的余角为____________28.在墙上钉一根细木条至少要钉2根钉才稳,根据是_________________________; 29.在棱柱中,任何相邻的两个面的交线都叫做______,相邻的两个侧面的交线叫做_______.30.如图所示,//AB CD ,CE 平分ACD ∠,并且交AB 于E ,118A ∠=︒,则AEC ∠等于______.31.如图,AOB 与COB △关于边OB 所在的直线成轴对称,AO 的延长线交BC 于点D .若45BOD ∠=︒,20C ∠=︒,则ADC ∠=___________.32.一副三角板按如图放置,则下列结论:∠如果230∠=︒,则有AC DE ∥;∠如果BC AD ∥,则有245∠=︒;∠如果445∠=︒,那么160∠=︒;∠ BAE CAD ∠+∠ 随着2∠的变化而变化,其中正确的是____.33.已知C 是线段AB 的中点,AB=10,若E 是直线AB 上的一点,且BE=3,则CE=_____34.如图,C ,D 是线段AB 上两点,已知AC :CD :DB=1:2:3,M 、N 分别为AC 、DB 的中点,且AB=8cm ,求线段MN 的长_____.35.已知OC 为一条射线,OM 平分AOC ∠,ON 平分BOC ∠.(1)如图1,当60AOB ∠=︒,OC 为AOB ∠内部任意一条射线时,MON ∠=_____; (2)如图2,当60AOB ∠=︒,OC 旋转到AOB ∠的外部时,MON ∠=_____; (3)如图3,当AOB α∠=,OC 旋转到AOB ∠(120BOC ∠<︒)的外部时,求MON ∠,请借助图3填空.解:因为OM 平分AOC ∠,ON 平分BOC ∠ 所以1122COM AOC CON BOC ∠=∠∠=∠,(依据是____________) 所以MON COM ∠=∠-_________12AOC =∠-_______12=________. 36.如图,已知60BAC ∠=︒,AD 是角平分线且20AD =,作AD 的垂直平分线交AC 于点F ,作DE AC ⊥,则DEF 的周长为 ______.37.平面内,已知AOB 90∠=,20,BOC OE ∠=平分,AOB OF ∠平分BOC ∠,则EOF ∠=______.38.如图所示,设L AB AD CD =++,M BE CE =+,N BC =.试比较M 、N 、L 的大小:________.39.已知点C 在线段AB 上,2AC BC =,点D 、E 在直线AB 上,点D 在点E 的左侧.(1)若18AB =,点D 与点A 重合,8DE =,则EC =_________;(2)若2AB DE =,线段DE 在直线AB 上移动,且满足关系式32AD EC BE +=,则CD AB =_______.三、解答题40.如图所示,在长方形ABCD 中,6cm BC ,8cm CD =,现绕这个长方形的一边所在直线旋转一周得到一个几何体.请解决以下问题:(1)说出旋转得到的几何体的名称?(2)如果用一个平面去截旋转得到的几何体,那么截面有哪些形状(至少写出3种)?(3)求旋转得到的几何体的表面积?(结果保留π)41.将一个正方体的表面沿某些棱剪开,展成一个平面图形,你能得到哪些形状的平面图形?42.如图,OB 为AOC ∠的平分线,OD 是COE ∠的平分线.(1)如果40AOB ∠=︒,30DOE ∠=︒,那么BOD ∠为多少度?(2)如果140AOE ∠=︒,30COD ∠=︒,那么AOB ∠为多少度?(3)如果AOC α∠=︒,COE β∠=︒,则BOD ∠=______°,如果AOE θ∠=︒,则BOD ∠=______︒.43.如图,点C 是线段AB 上的一点,点M 是线段AC 的中点,点N 是线段BC 的中点.(1)如果12,5AB cm AM cm ==,求BC 的长;(2)如果8MN cm =,求AB 的长.44.如图,一只蚂蚁沿长方体的表面从顶点A 爬到另一顶点M ,已知AB =3,AD = 4,BF = 5.求这只蚂蚁爬行的最短距离.45.已知AB CD ∥,点M 、N 分别在直线AB 、CD 上,AME ∠与CNE ∠的平分线所在的直线相交于点F .(1)如图1,点E 、F 都在直线AB 、CD 之间且70MEN ∠=︒时,MFN ∠的度数为___________;(2)如图2,当点E在直线AB、CD之间,F在直线CD下方时,写出MEN∠与MFN∠之间的数量关系,并证明;∠与(3)如图3,当点E在直线AB上方,F在直线AB与CD之间时,直接写出MEN∠之间的数量关系.MFN46.O为直线AB上的一点,OC∠OD,射线OE平分∠AOD.(1)如图∠,判断∠COE和∠BOD之间的数量关系,并说明理由;(2)若将∠COD绕点O旋转至图∠的位置,试问(1)中∠COE和∠BOD之间的数量关系是否发生变化?并说明理由;(3)若将∠COD绕点O旋转至图∠的位置,探究∠COE和∠BOD之间的数量关系,并说明理由.47.已知,P是线段AB的中点,点C是线段AB的三等分点,线段CP的长为4 cm.(1)求线段AB的长;(2)若点D是线段AC的中点,求线段DP的长.48.【提出问题】如图1,在直角ABC中,∠BAC=90°,点A正好落在直线l上,则∠1、∠2的关系为【探究问题】如图2,在直角ABC中,∠BAC=90°,AB=AC,点A正好落在直线l 上,分别作BD∠l于点D,CE∠l于点E,试探究线段BD、CE、DE之间的数量关系,并说明理由.【解决问题】如图3,在ABC中,∠CAB、∠CBA均为锐角,点A、B正好落在直线l 上,分别以A、B为直角顶点,向ABC外作等腰直角三角形ACE和等腰直角三角形BCF,分别过点E、F作直线l的垂线,垂足为M、N.∠试探究线段EM、AB、FN之间的数量关系,并说明理由;∠若AC=3,BC=4,五边形EMNFC面积的最大值为49.如图,两个形状、大小完全相同的含有3060︒︒、的三角板如图∠放置,PA PB 、与直线MN 重合,且三角板PAC ,三角板PBD 均可以绕点P 逆时针旋转.(1)求DPC ∠;(2)如图∠,若三角板PBD 保持不动,三角板PAC 的边PA 从PN 绕点P 逆时针旋转一定角度,PF 平分,APD PE ∠平分CPD ∠,求EPF ∠.(3)如图∠,在图∠基础上,若三角板PAC 的边PA 从PN 开始绕点P 逆时针旋转,转速为3︒/秒,同时三角板PBD 的边PB 从PM 绕点P 逆时针旋转,转速为2︒/秒,(当PC 转到与PM 重合时,两三角板都停止转动),求CPD BPN∠∠的值. (4)如图∠,在图∠基础上,若三角板PAC 开始绕点P 逆时针旋转,转速为5︒/秒,同时三角板PBD 绕点P 逆时针旋转,转速为1︒/秒,(当PA 转到与PM 重合时,两三角板都停止转动),在旋转过程中,PC PB PD 、、三条射线中,当其中一条射线平分另两条射线的夹角时,直接写出旋转的时间.参考答案:1.A【详解】试题分析:根据∠AOC=∠BOD=90º,∠AOD=150º,可得∠COD的度数,从而求得结果.∠∠AOC=∠BOD=90º,∠AOD=150º∠∠COD=∠AOD-∠AOC=60°∠∠BOC=∠BOD-∠COD=30°故选A.考点:本题考查的是角的计算点评:本题是基础应用题,只需学生熟练掌握角的大小关系,即可完成.2.C【分析】依据立体图形的定义回答即可.【详解】解:正方形、三角形、梯形是平面图形,球是立体图形.故选:C.【点睛】本题主要考查的是立体图形的认识,掌握相关概念是解题的关键.3.B【分析】讨论:当OC在∠AOB的内部,如图1,则∠BOC=∠AOB-∠AOC;OC在∠AOB的外部,如图2,则∠BOC=∠AOB+∠AOC.【详解】解:当OC在∠AOB的内部,如图1,∠∠AOB=75°,∠AOC=48°,∠∠BOC=∠AOB-∠AOC=75°-48°=27°;当OC在∠AOB的外部,如图2,∠∠AOB=75°,∠AOC=48°,∠∠BOC=∠AOB+∠AOC=75°+48°=123°,综上所述,∠BOC的度数为27°或123°.【点睛】本题考查的是角的计算,在解答此题时要注意进行分类讨论,不要漏解.4.A【分析】根据线段中点和线段之间的关系计算即可.【详解】解:点C是线段AB的中点,∴2==,BC AC cm∴2 1.50.5=-=-=.BD BC CD cm故选:A.【点睛】本题考查线段中点和线段的长度关系,掌握线段中点的性质是解答关键.5.B【分析】根据题意画出示意图,即可得答案.【详解】解:如图所示,有四个点,且每三点都不在同一直线上,每两点连一条线段,则可以连6条线段,故选:B.【点睛】本题主要考查了直线、线段、射线数量问题,能正确根据题意画出图形是解决问题的关键.6.D【分析】利用平行线的性质和平角的性质可以求得结果得出答案.【详解】解:如图示∠=︒,将一块含有30︒的直角三角板的顶点放在直尺的一边上,2110∠32110∠=∠=︒,∠11802301801103040∠=︒-∠-︒=︒-︒-︒=︒【点睛】本题主要考查了平行线的性质,正确得出3∠的度数是解题关键.7.B【分析】【详解】∠∠ACB= 90°,即∠1+∠2= 90°又∠在Rt∠ACD 中,∠A+∠1=90°∠∠A=∠2故选:B.8.D【详解】析:根据图形估计∠AOB 的大致度数,然后根据互为补角的和等于180°进行解答即可.解答:解:根据图形可得∠AOB 大约为135°,∠与∠AOB 互补的角大约为45°,综合各选项D 符合.故选D .9.C【分析】根据线段、射线、直线的定义即可解题.【详解】解:A. 连接两点的线段长度,叫做两点间的距离B. 射线OA 与射线AO 表示的是同一条射线,错误,射线具有方向性,C. 经过两点有一条直线,并且只有一条直线,正确,D. 错误,应该是从一点引出的两条射线所形成的图形叫做角,故选C.【点睛】本题考查了线段、射线、直线的性质,属于简单题,熟悉定义是解题关键. 10.D【分析】根据方向角的定义以及角的和差关系进行计算即可.【详解】解:由方向角的定义可知,65NOA ∠=︒,20SOB ∠=︒,∠906525AOE ∠=︒-︒=︒,∠AOB AOE EOS SOB ∠=∠+∠+∠,259020=︒+︒+︒故选:D .【点睛】本题考查方向角,理解方向角的定义是解决问题的前提.11.B【分析】根据方位角的概念,画图正确表示出方位角,即可求解.【详解】如图:∠小明从A 处沿北偏东40︒方向行走至点B 处,又从点B 处沿东偏南23︒方向行走至点C 处,∠40DAB ∠=︒,23CBF ∠=︒,∠向北方向线是平行的,即AD BE ∥,∠40ABE DAB ∠=∠=︒,∠90EBF ∠=︒,∠902367EBC ∠=︒-︒=︒,∠4067107ABC ABE EBC ∠=∠+∠=︒+︒=︒,故选B .【点睛】本题考查方位角,解题的关键是画图正确表示出方位角.12.C 【分析】先根据角平分线的定义求出1502ECD ACD ∠=∠=︒,再由三角形外角的性质求解【详解】解:∠CE平分∠ACD,∠ACD=100°,∠1502ECD ACD∠=∠=︒,∠∠B=30°,∠∠E=∠ECD-∠B=20°,故选C.【点睛】本题主要考查了角平分线的定义,三角形外角的性质,熟知角平分线的定义和三角形外角的性质是解题的关键.13.A【分析】根据正方体的展开图的性质判断即可;【详解】A中展开图正确;B中对号面和等号面是对面,与题意不符;C中对号的方向不正确,故不正确;D中三个符号的方位不相符,故不正确;故答案选A.【点睛】本题主要考查了正方体的展开图考查,准确判断符号方向是解题的关键.14.B【分析】根据题意作图得到运动的轨迹,根据矩形的周长特点即可求解.【详解】如图,这个人所走的路程是图中的矩形,周长为2(3+4)=14故选B.【点睛】此题主要考查网格的作图,解题的关键是根据题意作出图形求解.15.C【分析】连接BE,交AD于点M,过点E作EF∠BC交于点F,此时EM+CM的值最小,求出BE即可.【详解】解:连接BE,交AD于点M,过点E作EF∠BC交于点F,∠∠ABC是等边三角形,AD是BC边上的中线,∠B点与C点关于AD对称,∠BM=CM,∠EM+CM=EM+BM=BE,此时EM+CM的值最小,∠AC=6,AE=2,∠EC=4,在Rt∠EFC中,∠ECF=60°,∠FC=2,EF=在Rt∠BEF中,BF=4,∠BE=故选:C.【点睛】本题考查轴对称求最短距离,熟练掌握轴对称求最短距离的方法,灵活运用勾股定理是解题的关键.16.C【分析】根据题意画出图形,再根据图形求解即可.【详解】解:(1)当C在线段AB延长线上时,如图1,∠M、N分别为AB、BC的中点,∠BM=12AB=30,BN=12BC=20;∠MN=50.(2)当C在AB上时,如图2,同理可知BM =30,BN =20,∠MN =10;所以MN =50或10,故选C .【点睛】本题考查线段中点的定义,比较简单,注意有两种可能的情况;解答这类题目,应考虑周全,避免漏掉其中一种情况.17.B【分析】4点时,分针与时针相差四大格,即120°,根据分针每分钟转6°,时针每分钟转0.5°,则40分钟后它们的夹角为40×6°﹣4×30°﹣40×0.5°.【详解】4点40分钟时,钟表的时针与分针形成的夹角的度数=40×6°﹣4×30°﹣40×0.5°=100°.故选B .【点睛】本题考查了钟面角:钟面被分成12大格,每大格30°;分针每分钟转6°,时针每分钟转0.5°.18.D【分析】根据题意结合图形列出方程组,解方程组即可.【详解】解:由题意得,1290,2120∠+∠︒⎧⎨∠-∠︒⎩==,解得135,255.∠︒⎧⎨∠︒⎩==. 故选:D .【点睛】本题考查的是余角和补角的概念和性质,两个角的和为90°,则这两个角互余;若两个角的和等于180°,则这两个角互补.19.A【分析】先根据∠CED =50°,DE ∠AF ,即可得到∠CAF =50°,最后根据∠BAC =60°,即可得出∠BAF 的大小.【详解】∠DE ∠AF ,∠CED =50°,∠∠CAF =∠CED =50°,∠∠BAC =60°,∠∠BAF=60°﹣50°=10°,故选:A.【点睛】此题考查平行线的性质,几何图形中角的和差关系,掌握平行线的性质是解题的关键.20.D【分析】先求出∠ABC,再延长CE,交AB于点G,结合平行线的性质表示出∠BCE,然后根据三角形内角和定理表示∠CED,再根据角平分线得定义表示出∠CEB,最后根据三角形内角和定理得出答案.【详解】在∠ABC中,∠CAB=40°,∠ACB=90°,∠∠ABC=50°.延长CE,交AB于点G,∠MN BA∥,∠EGBα∠=,∠ACM=∠BAC=40°,∠∠ACE=α-40°,∠∠BCE=90°-(α-40°)=130°-α.∠∠CEA=180°-∠CAE-∠ACE,∠∠CED=180°-∠CEA=∠CAE+∠ACE=20°+(α-40°)=α-20°.∠EF平分∠CED,∠∠CEF=111022CEDα∠=-︒,∠∠CEB=1110706022αα-︒+︒=+︒,∠∠EBC=11180(60)(130)10 22ααα︒-+︒-︒-=-︒.故选:D.【点睛】本题主要考查了角平分线的定义,三角形内角和定理,平行线的性质,将待求角转化到适合的三角形是解题的关键.21.55°##55度【分析】根据将∠AOB 绕点O 按逆时针方向旋转40°后得到∠COD ,可得∠BOD = 40° 即可得∠AOD =∠BOD +∠AOB = 55°.【详解】∠将∠AOB 绕点O 按逆时针方向旋转40°后得到∠COD .∠∠BOD = 40°,∠∠AOB = 15°∠∠AOD =∠BOD +∠AOB = 40°+ 15°= 55°,故答案为:55°.【点睛】本题考查三角形的旋转变换,解题的关键是掌握旋转的性质.22. 90°##90度 180°##180度【分析】根据互余,互补的定义即可得到结果.【详解】若∠A 与∠B 互余,则∠A +∠B =90°;若∠A 与∠B 互补,则∠A +∠B =180°.故答案为:90°,180°【点睛】解答本题的关键是熟记和为90°的两个角互余,和为180°的两个角互补. 23.110【分析】根据角平分线可得270AOC AOD ∠=∠=︒,再利用补角的性质求解即可得.【详解】解:∵OD 平分AOC ∠,35AOD ∠=︒,∴223570AOC AOD ∠=∠=⨯︒=︒,∵AOC ∠与BOC ∠是邻补角,∴180AOC BOC ∠+∠=︒,∴18070110BOC ∠=︒-︒=︒.故答案为:110.【点睛】题目主要考查角平分线的计算及补角的性质,理解题意,结合图形求角度是解题关键.24.50【分析】先求出∠BOD ,根据平角的性质即可求出∠AOC .【详解】∠OE 是∠DOB 的角平分线,当∠DOE =20°∠∠BOD =2∠DOE =40°∠OC ∠OD ,∠∠AOC =180°-90°-∠BOD =50°故答案为:50.【点睛】此题主要考查角度求解,解题的关键是熟知角平分线的性质、直角的性质. 25.四【详解】试题解析:设该棱柱为n 棱柱,根据题意得:3n =12.解得:n =4.所以该棱柱为四棱柱,故答案是:四.26.2【分析】根据中位线的性质可得EF BC ∥,EF =12BC =5,则有∠CBD =∠BDE ,AE =BE =12AB =3,再根据BD 平分∠ABC ,有∠ABD =∠CBD ,即有∠ABD =∠BDE ,则可得DE =BE =3,问题得解.【详解】∠EF 是∠ABC 的中位线,∠EF BC ∥,EF =12BC =5,E 点为AB 中点, ∠∠CBD =∠BDE ,AE =BE =12AB =3. ∠BD 平分∠ABC ,∠∠ABD =∠CBD ,∠∠ABD =∠BDE ,∠DE =BE =3.∠DF =EF −DE =EF −BE =5−3=2.故答案为:2.【点睛】本题考了三角形中位线的性质、角平分线的性质以及等角对等边的知识,求出DE =BE 是解答本题的关键.27.3434'︒【分析】直接利用互余两角的关系,结合度分秒的换算得出答案.【详解】解:∠5526α∠=︒',∠α∠的余角为:9055263434'=︒'︒-︒.故答案为:3434'︒.【点睛】此题主要考查了余角的定义和度分秒的转换,正确把握相关定义是解题关键. 28.两点确定一条直线【分析】由于两点确定一条直线,所以在墙上固定一根木条至少需要两根钉子.【详解】在墙上固定一根木条至少需要两根钉子,依据的数学道理是两点确定一条直线. 故答案为两点确定一条直线.【点睛】当木工师傅锯木板时,他会用墨盒在木板上弹出墨线,这样会使木板沿直线锯下;在正常情况下,射击时只要保证瞄准的一只眼在两个准星确定在直线上,才能射中目标等等;它们都是运用了“两点确定一条直线”的直线的性质.29. 棱, 侧棱;【分析】由棱柱的组成部分的定义直接填空即可.【详解】在棱柱中,任何相邻的两个面的交线都叫做棱,相邻的两个侧面的交线叫做侧棱. 故答案为棱;侧棱.【点睛】熟记面与面相交成线,在棱柱中,任何相邻的两个面的交线都叫做棱. 30.31°【分析】要求AEC ∠的度数,根据平行线的性质,只需求得2∠的度数.显然结合平行线的性质以及角平分线的定义就可解决.【详解】解://AB CD ,CE 平分ACD ∠交AB 于E ,118A ∠=︒,1112(180)(180118)3122A ∴∠=∠=︒-∠=︒-︒=︒, 231AEC ∴∠=∠=︒,故答案为:31°.【点睛】本题考查的是角平分线的性质及平行线的性质,比较简单,需同学们熟练掌握.31.70︒##70度【分析】根据三角形外角的定义和性质可知ADC A ABD ∠=∠+∠,利用轴对称的性质求出A ∠与ABD ∠的大小并进行计算即可. 【详解】解:AOB 与COB △关于边OB 所在的直线成轴对称∴20A C ∠=∠=︒,2ABD ABO ∠=∠,根据三角形外角的性质可知:在AOB 中,452025ABO BOD A ∠=∠-∠=︒-︒=︒222550ABD ABO ∴∠=∠=⨯︒=︒∴ 在ABD △中,205070ADC A ABD ∠=∠+∠=︒+︒=︒.故答案为:70︒.【点睛】本题考查轴对称的性质和三角形外角的性质,熟练运用三角形的外角性质进行计算是本题的解题关键.32.∠∠∠【分析】根据平行线的判定与性质即可逐一进行证明.【详解】解:∠∠230∠=︒,∠190260∠=︒-∠=︒,∠60AED ∠=︒,∠1AED ∠=∠,∠AC DE ∥;所以∠正确;∠∠BC AD ∥,∠345B ∠=∠=︒,∠290345∠=︒-∠=︒;所以∠正确;∠如图,∠445,60EGF GEF ∠=∠=︒∠=︒,∠4560105GFA ∠=︒+︒=︒,∠1GFA C ∠=∠+∠,∠45C ∠=︒,∠160∠=︒.所以∠正确.∠∠123290∠+∠=∠+∠=︒,∠21239090180BAE CAD ∠+∠=∠+∠+∠+∠=︒+︒=︒,∠BAE CAD ∠+∠随着2∠的变化不会发生变化;所以∠错误;所以其中正确的是∠∠∠.故答案为:∠∠∠.【点睛】本题考查了平行线的判定与性质,解决本题的关键是准确区分平行线的判定与性质,并熟练运用.33.2或8【分析】由已知C 是线段AB 中点,AB=10,求得BC'= 5,进一步分类探讨:E 在BC 内;E 在BC 的延长线上;由此画图得出答案即可.【详解】C 是线段AB 的中点, AB= 10,BC= AB= 5,如图,当E 在BC 内,CE= BC- BE= 5- 3=2;∠如图,E 在BC 的延长线上,CE= BC+ BE= 5+3=8 ;所以CE= 2或8;故本题答案为:2或8.【点睛】解决本题的关键突破口是分类讨论,本题考查了学生综合分析的能力,要求学生掌握线段中点的意义,线段的和与差.34.153cm 【分析】根据线段的比例,可得线段的长度,根据线段的和差,可得答案.【详解】∠AC :CD :DB=1:2:3,设AC=a ,CD=2a ,DB=3a ,∠AB=AC+CD+DB=a+2a+3a=6a=8,解得:a=43, ∠AC=43,DB=3×43=4, ∠M 、N 分别为AC 、DB 的中点, ∠AM=12AC=23,BN=12DB=2, ∠MN=AB-AM-BN=8-23-2=513(cm ). 故答案为:153cm 【点睛】本题考查了与线段中点有关的计算,根据比例关系列出方程求出各线段的长是关键.35. 30° 30° 角平分线定义 ∠CON 12BOC ∠ α 【分析】对于(1),根据角平分线定义得12COM AOC ∠=∠,12CON BOC ∠=∠,再结合12MON COM CON AOB ∠=∠+∠=∠,可得答案; 对于(2),仿照(1),根据12MON COM CON AOB ∠=∠-∠=∠求解; 对于(3),仿照(2)解答即可.(1)因为OM 平分∠AOC ,ON 平分∠BOC , 所以12COM AOC ∠=∠,12CON BOC ∠=∠, 所以11603022MON COM CON AOB ∠=∠+∠=∠=⨯︒=︒. 故答案为:30°.(2) 因为OM 平分∠AOC ,ON 平分∠BOC , 所以12COM AOC ∠=∠,12CON BOC ∠=∠, 所以11603022MON COM CON AOB ∠=∠-∠=∠=⨯︒=︒. 故答案为:30°.(3)因为OM 平分∠AOC ,ON 平分∠BOC , 所以12COM AOC ∠=∠,12CON BOC ∠=∠(依据的角平分线定义), 所以111222MON COM CON AOC BOC α∠=∠-∠=∠-∠=. 故答案为:角平分线定义,∠CON ,12BOC ∠,α. 【点睛】本题主要考查了角的和差的计算,角平分线定义,掌握角平分线定义是解题的关键.36.10+【分析】根据含30°角的直角三角形的性质求出DE 、根据勾股定理求出AE ,根据线段垂直平分线的性质、三角形的周长公式计算,得到答案.【详解】解:∠60BAC ∠=︒,AD 是角平分线,∠30DAE ∠=︒,在Rt DAE 中,20,30AD DAE =∠=︒, ∠1102DE AD ==,由勾股定理得:AE =∠AD 的垂直平分线交AC 于点F ,∠FA FD =,∠DEF 的垂直10DE EF FD DE EF FA DE AE =++=++=+=+故答案为:10+【点睛】本题考查的是直角三角形的性质、勾股定理、线段垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.37.35︒或55︒【分析】分OC 在AOB ∠的内部和外部进行讨论,运用角平分线性质及角的和差进行运算即可.【详解】解:∠AOB 90∠=,OE 平分,AOB ∠ ∠∠BOE=12∠AOB=45°∠20,BOC ∠=OF 平分BOC ∠ ∠∠FOC=∠FOB =12∠BOC=10°当OC 在AOB ∠的内部时,如图∠∠EOF=∠BOE-∠BOF=45-10=35︒︒︒当OC 在AOB ∠的外部时,如图∠∠EOF=∠BOE+∠BOF=45+10=55︒︒︒故答案为:35︒或55︒【点睛】本题考查了角平分线的定义,先求出∠BOC 的度数,再求出∠FOC 的度数,最后求出答案,有两种情况,以防漏掉.38.L M N >>【分析】根据连接两点的所有线中,线段最短的性质解答.【详解】∠AB+AE >BE ,CD+DE >CE ,∠AB+AE+CD+DE >BE+CE ,即l >m ,又BE+CE >BC ,即m >n ,∠L M N >>.【点睛】本题考查了知识点两点之间线段最短,解题的关键是熟记性质.39. (1)4 (2)116或1742. 【分析】(1)画出符合题意的图形,由18,2AB AC BC ==,求解BC ,再利用线段的和差关系求解EC 即可得到答案;(2)根据AC=2BC ,AB=2DE ,线段DE 在直线AB 上移动,满足关系式32AD EC BE +=,再分六种情况讨论,∠当DE 在点A 左侧时,∠当A 在DE 之间时,∠当DE 在线段AC 上时,∠当C 在DE 之间时,∠当D 在CB 之间时,∠当D 在B 的右边时,可以设CE=x ,DC=y ,用含x 和y 的式子表示,,AD EC BE 的长,从而得出x 与y 的等量关系,即可求出 CD AB的值. 【详解】解:(1)如图,18AB DB ==,2,AC BC = 163BC AB ∴==, 8DE =,1886 4.EC AB DE BC ∴=--=--=(2)∠AC=2BC ,AB=2DE ,满足关系式32AD EC BE +=, ∠当DE 在点A 左侧时,如图,设CE=x ,DC=y , 则DE y x =-,∠()()242,33AB y x AC AB y x =-==-,()12222,333BC y x y x =-=-∠41,33AD DC AC x y =-=- ∠2133BE BC CE y x =+=+ ∠7133AD EC x y +=- ∠32AD EC BE +=, ∴ ()23,AD EC BE += ∠7121233333x y y x ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭, 解得,811x y =, ∠ ()11.826211CD y y AB y x y y ===-⎛⎫- ⎪⎝⎭ ∠当A 在DE 之间时,如图,设,,CE x CD y == 则DE y x =-, 同理可得:11.6CD AB = ∠当DE 在线段AC 上时,设,,CE x CD y == 则DE y x =-,,222,DE y x AB DE y x ∴=-==-24422,,33333AC AB y x BC y x ∴==-=- 1411,,3333AD AC CD y x AD CE y x ∴=-=-+=- 21+,33BE BC CE y x ==+ AD CE ∴+<,BE32AD EC BE +=, AD CE ∴+>,BE∴ 不合题意舍去;∠当C 在DE 之间时,如图,设CE=x ,DC=y , 则DE=x+y ,∠()()242,,33AB x y AC AB x y =+==+ ()()112333BC AB x y x y ==+=+, ∠41,33AD AC DC x y =-=+ ∠7133AD EC x y +=+ ∠21,33BE BC CE y x =-=- ∠32AD EC BE += ∴ ()23,AD EC BE += ∠7121233333x y y x ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭, 解得,417x y =, ∠ ()174242217CD y y AB x y y y ===+⎛⎫+ ⎪⎝⎭. ∠当D 在CB 之间时,设,,CD y CE x == 则,222,DE x y AB DE x y =-==- 4422,,3333AC x y BC x y ∴=-=- 4112,,3333AD AC CD x y BE CE BC x y ∴=+=-=-=+ 71,33AD CE x y ∴+=- ∠32AD EC BE += ∴ ()23,AD EC BE += 同理可得:8,11x y = 与图形条件x >y 不符舍去, ∠当D 在B 的右边时,设,,CD y CE x == 则,222,DE x y AB DE x y =-==-4422,,3333AC x y BC x y ∴=-=- 4112,,3333AD AC CD x y BE CE BC x y ∴=+=-=-=+ 71,33AD CE x y ∴+=- ∠32AD EC BE += ∴ ()23,AD EC BE += 同理可得:8,11x y =与图形条件x >y 不符,舍去, 综上:CD AB 的值为:116或1742. 故答案为116或1742. 【点睛】本题考查的是线段的和差关系,二元一次方程思想,与线段相关的动态问题,分类讨论的思想,掌握以上知识是解题的关键.40.(1)圆柱(2)长方形、圆形或梯形(3)168π平方厘米或224π平方厘米【分析】(1)由图形旋转性质可知旋转后得到的几何体是圆柱;(2)用一个平面截圆柱,从不同角度截取的形状不同;(3)分情况讨论,找出圆柱的底面半径和高,即可求解.【详解】(1)解:由图形旋转性质可知,绕长方形的一边所在直线旋转一周后所得立方体为柱体、底面为圆,因此得到的几何体是圆柱.故答案为圆柱.(2)解:用一个平面截圆柱,截面形状可能为长方形、圆形或梯形.(3)解:分情况讨论,若绕BC 边旋转,则所得圆柱的表面积为:228286=224S S S 侧底平方厘米;若绕CD 边旋转,则所得圆柱的表面积为:226268=168S S S 侧底平方厘米.故旋转得到的几何体的表面积为168π平方厘米或224π平方厘米.【点睛】本题考查了点、线、面、体,截几何体,圆柱的表面积计算等知识点,解题关键是理解点动成线、线动成面、面动成体.41.【解析】略42.(1)70BOD ∠=︒(2)40AOB ∠=︒ (3)()12αβ+;12θ【分析】(1)根据角平分线的定义得出40BOC AOB ∠=∠=︒,30DOC DOE ∠=∠=︒,再根据角度之间的关系求出BOD ∠的度数即可;(2)先根据角平分线的定义,30COD ∠=︒,得出260COE COD ∠=∠=︒,根据140AOE ∠=︒,求出80AOC ∠=︒,根据角平分线的定义即可得出答案; (3)根据角平分线的定义得出1122BOC AOC ∠=∠=︒,1122COD COE ∠=∠=︒,根据角度之间的关系得出()12BOD ∠=+︒;根据角平分线的定义得出12BOD AOE ∠=∠. 【详解】(1)解:∠OB 为AOC ∠的平分线,OD 是COE ∠的平分线,∠40BOC AOB ∠=∠=︒,30DOC DOE ∠=∠=︒,∠403070BOD BOC DOC ∠=∠+∠=︒+︒=︒.(2)解:∠OD 是COE ∠的平分线,30COD ∠=︒,∠260COE COD ∠=∠=︒,∠140AOE ∠=︒,∠80AOC AOE COE ∠=∠-∠=︒,∠OB 为AOC ∠的平分线,∠4120AOB AOC ∠=∠=︒. (3)解:∠OB 为AOC ∠的平分线,OD 是COE ∠的平分线,AOC α∠=︒,COE β∠=︒,∠1122BOC AOC ∠=∠=︒,1122COD COE ∠=∠=︒, ∠()111222BOD BOC COD ∠=∠+∠=︒+︒=+︒; ∠OB 为AOC ∠的平分线,OD 是COE ∠的平分线,∠1BOC AOB 2∠=∠,12COD COE ∠=∠, ∠BOD BOC COD ∠=∠+∠1122AOC COE =∠+∠ ()12AOC COE =∠+∠ 12AOE =∠ 12=. 故答案为:()12αβ+;12θ. 【点睛】本题主要考查了角平分线的定义,几何图形中的角度计算,解题的关键是熟练掌握角平分线的定义,数形结合.43.(1)2BC cm =;(2)16AB cm =【分析】(1)先求出AC ,根据BC=AB-AC ,即可求出BC ;(2)求出BC=2CN, AC=2CM,把MN=CN+MC=8cm 代入求出即可.【详解】解: (1) ∠点M 是线段AC 的中点,∠AC=2AM,∠AM=5cm,∠AC=10cm,∠AB=12cm ,∠BC=AB-AC=12-10=2cm,(2)∠点M 是线段AC 的中点,点N 是线段BC 的中点.∠BC=2NC ,AC=2MC,∠MN=NC+MC=8cm ,∠AB=BC+AC=2NC+2MC==2(NC+MC)=2MN=28⨯cm=16cm .【点睛】本题考查了两点之间的距离的应用,主要考查学生的观察图形的能力和计算能力.44【分析】由AB=3,AD=4,BF=5长宽高三种长度不同,蚂蚁走的折面不同,距离也不同,要按不同的棱展开两个面,(1)长方形沿着棱ND展开,(2)长方形沿着棱DC展开,(3)长方形沿着棱BC展开,用勾股定理求出对角线的长度,再比较取最短者.【详解】∠AB=3,AD=4,BF=5∠MC =BF=AE=5,BC=AD=MF=4,MN= CD=AB=3(1)长方形沿着棱ND展开如图∠所示时,在Rt∆AEM中AM2=AE2+EM2= AE2+(NE+MN)2=52+(3+4)2=25+49=74,(2)长方形沿着棱DC展开如图∠所示时,AM2=AB2+( BC+CM)2=32+(4+5)2=9+81=90,(3)长方形沿着棱BC展开如图∠所示时,AM2=MF2+( AB+BF)2=42+(3+5)2=16+64=80,∠ AM=∠【点睛】本题考查蚂蚁所走最短路径问题,涉及长方体的侧面展开问题,要会分析最短路径涉及几个面展开,展开后走的哪条路径为最短,分别求出经比较才能解决问题.45.(1)145°(2)∠MEN=2∠MFN,证明见解析(3)1∠MEN+∠MFN=180°,证明见解析2【分析】分析:(1)过E作EH∠AB,FG∠AB,根据平行线的性质得到结论;(2)根据三角形的外角的性质得,平行线的性质,角平分线的定义即可得到结论;(3)根据平行线的性质得到∠MGE∠∠ENC,根据角平分线的定义得到∠MGE∠∠ENC∠2∠FNG∠∠AME∠2∠1∠∠E∠∠MGE∠∠E∠2∠FNG,根据三角形的外角的性质和四边形的内角和即可得到结论.(1)解:如图1,过E作EH∠AB,FG∠AB。
全国初中数学竞赛真题及答案大全

全国初中数学竞赛真题及答案大全(总72页)--本页仅作预览文档封面,使用时请删除本页--2007年全国初中数学竞赛(海南赛区)初赛试卷(本试卷共6页,满分120分,考试时间:3月18日8:30——10:30)一、选择题(本大题满分50分,每小题5分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母代号填写在下表相应题号下的方格内1. 若m 为实数,则代数式m+m 的值一定是A. 正数 C.负数 D.非负数2.如图1所示,是两架处在平衡状态的天平,那么,对于a、b、c三种物体的重量,下列判断正确的是A.c>a B.a<b C.a<c D. b<c3. 如图2,点C是∠PAQ的平分线上一点,点B、B′分别在边AP、AQ 上,如果再添加一个条件,即可推出AB=AB′,那么该条件不可以是A. BB′⊥ACB. CB=CB′C. ∠ACB=∠ACB′D. ∠ABC=AB′C4.图3是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是13,小正方形的面积是1,直角三角形的两条直角边长分别为a、b,则(a+b)2的值是A.13 B.19 C.25 D.169 图3图2图15.已知m 是方程01x -x 2=+2006的一个根,则代数式3+1++22m 20062005m -m 的值等于6.将一段72cm 长的绳子,从一端开始每3cm 作一记号,每4cm 也作一记号,然后从有记号的地方剪断,则这段绳子共被剪成的段数为A .37B .36C .35D .347. 某旅游团92人在快餐店就餐,该店备有9种菜,每份菜单单价分别为1、2、3、4、5、6、7、8、9(元),旅游团领队交代:每人可选不同的菜,但金额都须正好10元,且每一种菜最多只能买一份,这样,该团成员在购菜完全符合要求的所有方案中,至少有一个方案的人数不少于A .9人B .10人C .11人D .12人8.如图4是由几块相同的小正方体搭成的立体图形的三视图,则这立体图形中小正方体共有( )块A .9B .10C .11D .129.如图5,将△ABC 沿着它的中位线DE 折叠后,点A 落到点A ′,若∠C=120 ,∠A=26,则∠A ′DB 的度数是A .120B .112C .110D .10810. 方程xx -x 22=2的正根的个数是 A .0个 B .1个 C .2个 D .3个 二、填空题(本大题共8小题,每小题5分,满分40分)11.若[]x 表示不超过x 的最大整数,如[][][]0==3=2.30.7-43.7-,,等,则[][]=3+5π-_________12.在直径为4cm 的⊙O 中,长度为32cm 的弦BC 所对的圆周角的度数为 .13.如图6,电路图上有四个开关A 、B 、C 、D 和一个小灯泡,闭合开关D 或同时闭合开关A 、B 、C 都可以使小灯泡放光,那么随机闭合其中两个开关,能使小灯泡发光的概率为 ____________°.14.如图7,在△ABC 中,AB=5,AC=3,D 为BC 的中点,AD=2,则tan ∠BAD= __________.15.若干个 装卸一批货物,每个工人的装卸速度相同,如果这些工人同时工作,则需10小时装卸完毕;现改变装卸方式,开始一个人干,以后每隔t (整数)小时增加一个人干,每个参加装卸的人都一直干到装卸完毕,且最后参加的一个人装卸的时间是第一个人的41,则按改变的方式装卸,自始至终共需时间 小时.16.在一次自行车越野赛中,甲、乙两名选手所走的路程y (千米)随时间x (分钟)变化的图象(全程)分别用图8中的实线(O →A →B →C )与虚线(OD )表示,那么,在本次比赛过程中,乙领先甲时的x 的取值范围是 .17.已知a <3,b >3,且1-k b a =+,ab=3,则k 的最小整数值是_____________.18.若50z -y x 30z y x =+3=++,,且x 、y 、z 均为非负数,则z y 5x M 2+4+=的最大值为_________________.三、解答题(本大题共2小题,每小题15分,满分30分)19. 已知在△ABC 中,∠ACB=90,AC=BC=4,现将一块边长足够大的直角三角板的直角顶点置于AB 的中点O ,两直角边分别经过点B 、C ,然后将三角板绕点O 按顺时针方向旋转一个角度 0(α<α<90),旋转后,直角三角板的直角边分别与AC 、BC 相交于点K 、H ,四边形CHOK 是旋转过程中三角板与△ABC 的重叠部分(如图所示)。
初中数学-立体图形与平面图形(练习题)

word格式-可编辑-感谢下载支持4.1.1立体图形与平面图形(一)基础练习1.下列图形不是立体图形的是()A.球B.圆柱C.圆锥D .圆2.圆柱的侧面是面,上、下两个底面都是。
3.有一个面是曲面的立体图形有(列举出三个)。
4.三棱柱的侧面有个长方形,上、下两个底面是两个都一样的三角形。
5.由点动成,由线动成,由动成体。
6.长方体ABCD-A′B′C′D′有个面,条棱,个顶点。
与棱AB垂直相交的棱有条,与棱AB平行的棱有条。
7.若一个棱柱的底面是一个七边形,则它的侧面必须有个长方形,它一共有个面。
拓展提高8.苏轼的诗句“横看成岭侧成峰,远近高低各不同”说明的现象是____________________________________________。
9.长方体属于()A.棱锥B.棱柱C.圆柱D.以上都不对10.下列几何体中(如图1)属于棱锥的是()(1) (2) (3) (4) (5) (6)①②③④⑤⑥图1A.①⑤B.①C.①⑤⑥D.⑤⑥11.月球、西瓜、易拉罐、篮球、热水瓶胆、书本等物体中,形状类似圆柱的有()A.1个B.2个C.3个D.4个12.用一个平面去截一个长方体.截面的边数可能会出现的情况有()A.3种B.4种C.5种D.6种13.在下列立体图形中,不属于多面体的是()A.四棱台B.圆锥体C.五棱柱D.长方体14.下图中是四棱台的侧面展开图的是()15.如图所示,该物体的俯视图是()16.直角三角形绕它最长边(即斜边)旋转一周得到的几何体为()。
湖北武汉市第六中学立体几何多选题试题含答案
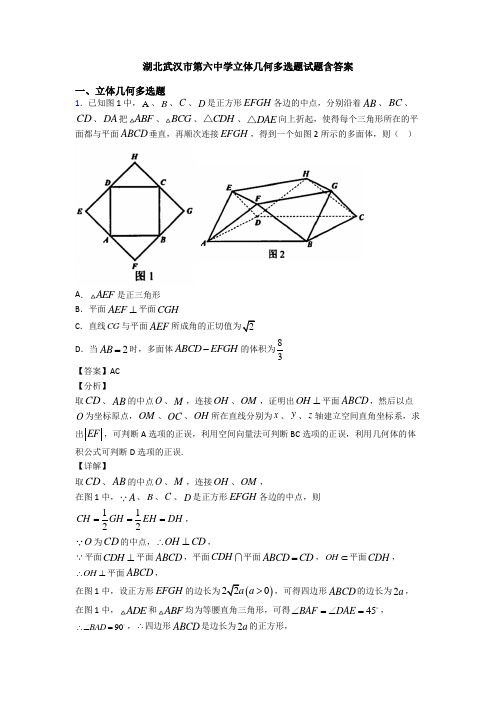
湖北武汉市第六中学立体几何多选题试题含答案一、立体几何多选题1.已知图1中,A 、B 、C 、D 是正方形EFGH 各边的中点,分别沿着AB 、BC 、CD 、DA 把ABF 、BCG 、CDH △、DAE △向上折起,使得每个三角形所在的平面都与平面ABCD 垂直,再顺次连接EFGH ,得到一个如图2所示的多面体,则( )A .AEF 是正三角形B .平面AEF ⊥平面CGHC .直线CG 与平面AEF 2D .当2AB =时,多面体ABCD EFGH -的体积为83【答案】AC 【分析】取CD 、AB 的中点O 、M ,连接OH 、OM ,证明出OH ⊥平面ABCD ,然后以点O 为坐标原点,OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系,求出EF ,可判断A 选项的正误,利用空间向量法可判断BC 选项的正误,利用几何体的体积公式可判断D 选项的正误. 【详解】取CD 、AB 的中点O 、M ,连接OH 、OM , 在图1中,A 、B 、C 、D 是正方形EFGH 各边的中点,则1122CH GH EH DH ===,O 为CD 的中点,OH CD ∴⊥,平面CDH ⊥平面ABCD ,平面CDH 平面ABCD CD =,OH ⊂平面CDH ,OH ∴⊥平面ABCD ,在图1中,设正方形EFGH 的边长为()220a a >,可得四边形ABCD 的边长为2a , 在图1中,ADE 和ABF 均为等腰直角三角形,可得45BAF DAE ∠=∠=, 90BAD ∴∠=,∴四边形ABCD 是边长为2a 的正方形,O 、M 分别为CD 、AB 的中点,则//OC BM 且OC BM =,且90OCB ∠=,所以,四边形OCBM 为矩形,所以,OM CD ⊥,以点O 为坐标原点,OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系,则()2,,0A a a -、()2,,0B a a 、()0,,0C a 、()0,,0D a -、(),,E a a a -、()2,0,F a a 、(),,G a a a 、()0,0,H a .对于A 选项,由空间中两点间的距离公式可得2AE AF EF a ===,所以,AEF 是正三角形,A 选项正确;对于B 选项,设平面AEF 的法向量为()111,,m x y z =,(),0,AE a a =-,()0,,AF a a =,由11110m AE ax az m AF ay az ⎧⋅=-+=⎪⎨⋅=+=⎪⎩,取11z =,则11x =,11y =-,则()1,1,1m =-,设平面CGH 的法向量为()222,,n x y z =,(),0,CG a a =,()0,,CH a a =-, 由222200n CG ax az n CH ay az ⎧⋅=+=⎪⎨⋅=-+=⎪⎩,取21z =-,可得21x =,21y =-,则()1,1,1n =--,()22111110m n ⋅=+--⨯=≠,所以,平面AEF 与平面CGH 不垂直,B 选项错误;对于C 选项,6cos ,23CG m CG m a CG m⋅<>===⨯⋅, 设直线CG 与平面AEF 所成角为θ,则sin 6θ=,23cos 1sin θθ=-=,所以,sin tan 2cos θθθ==,C 选项正确; 对于D 选项,以ABCD 为底面,以OH 为高将几何体ABCD EFGH -补成长方体1111ABCD A B C D -,则E 、F 、G 、H 分别为11A D 、11A B 、11B C 、11C D 的中点,因为2AB =,即1a =,则1OH =,长方体1111ABCD A B C D -的体积为2214V =⨯=,11211111113326A A EF A EF V S AA -=⋅=⨯⨯⨯=△,因此,多面体ABCD EFGH -的体积为111044463ABCD EFGH A A EF V V V --=-=-⨯=, D 选项错误. 故选:AC. 【点睛】方法点睛:计算线面角,一般有如下几种方法:(1)利用面面垂直的性质定理,得到线面垂直,进而确定线面角的垂足,明确斜线在平面内的射影,即可确定线面角;(2)在构成线面角的直角三角形中,可利用等体积法求解垂线段的长度h ,从而不必作出线面角,则线面角θ满足sin hlθ=(l 为斜线段长),进而可求得线面角; (3)建立空间直角坐标系,利用向量法求解,设a 为直线l 的方向向量,n 为平面的法向量,则线面角θ的正弦值为sin cos ,a n θ=<>.2.已知三棱锥A BCD -的三条侧棱AB ,AC ,AD 两两垂直,其长度分别为a ,b ,c .点A 在底面BCD 内的射影为O ,点A ,B ,C ,D 所对面的面积分别为A S ,B S ,C S ,D S .在下列所给的命题中,正确的有( ) A .2A BCO D S SS ⋅=; B .3333A B C D S S S S <++;C .若三条侧棱与底面所成的角分别为1α,1β,1γ,则222111sin sin sin 1αβγ++=;D .若点M 是面BCD 内一个动点,且AM 与三条侧棱所成的角分别为2α,2β,2γ,则22cos α+2222cos cos 1βγ+=.【答案】ACD 【分析】由Rt O OA '与Rt O AD '相似,得边长关系,进而判断A 正确;当M 与O 重合时,注意线面角与线线角的关系,即可得C 正确;构造长方体,建立直角坐标系,代入夹角公式计算可得D 正确;代入特殊值,可得B 错误. 【详解】由三棱锥A BCD -的三条侧棱AB ,AC ,AD 两两垂直,则将三棱锥A BCD -补成长方体ABFC DGHE -,连接DO 并延长交BC 于O ', 则AO BC ⊥.对A :由Rt O OA '与Rt O AD '相似,则2O A O O O D '''=⨯又12A S BC O D '=⋅,12BCOS BC O O '=⋅, 22221124DS BC O A BC O A ⎛⎫''=⋅=⋅ ⎪⎝⎭所以2A BCOD S SS ⋅=,故A 正确.对B :当1a b c ===时,33318B C D S S S ===,则33338B C D S S S ++=,而332333322288A S ⎛⎫=⨯⨯=> ⎪ ⎪⎝⎭,此时3333A B C D S S S S >++,故B 不正确. 对D :分别以AB ,AC ,AD 为x ,y ,z 轴,建立空间直角坐标系. 设(),,M x y z ,则(),,AM x y z =,222AM x y z =++,(),0,0AB a =,()0,,0AC b =,()0,0,AD c =所以222222222cos cos cos AM AB AM AC AM AD AM ABAM ACAM ADαβγ⎛⎫⎛⎫⎛⎫⋅⋅⋅++=++ ⎪ ⎪ ⎪ ⎪⎪⎪⋅⋅⋅⎝⎭⎝⎭⎝⎭2222221x y z AMAMAM=++=,所以D 正确.对C :当M 与O 重合时,AO ⊥面BCD ,由D 有222222cos cos cos 1αβγ++=,由各侧棱与底面所成角与侧棱与所AO 成角互为余角,可得C 正确. 故选:ACD.【点睛】关键点睛:本题考查空间线面角、线线角、面积关系的问题,计算角的问题关键是建立空间直角坐标系,写出点的坐标,利用数量积的公式代入计算,解决这道题目还要结合线面角与线线角的关系判断.3.已知球O 为正方体1111ABCD A B C D -的内切球,平面11A C B 截球O 的面积为24π,下列命题中正确的有( )A .异面直线AC 与1BC 所成的角为60°B .1BD ⊥平面11AC B C .球O 的表面积为36πD .三棱锥111B AC B -的体积为288 【答案】AD 【分析】连接11A C ,1A B ,通过平移将AC 与1BC 所成角转化为11A C 与1BC 所成角可判断A ;通过反证法证明B ;由已知平面11A C B 截球O 的面积为24π求出正方体棱长,进而求出内切球的表面积可判断C ;利用等体积法可求得三棱锥111B AC B -的体积可判断D. 【详解】对于A ,连接11A C ,1A B ,由正方体1111ABCD A B C D -,可知11//A C AC ,11AC B ∴∠为异面直线AC 与1BC 所成的角,设正方体边长为a,则1111AC A B BC ==,由等边三角形知1160A C B ∠=,即异面直线AC 与1BC 所成的角为60,故A 正确; 对于B ,假设1BD ⊥平面11A C B ,又1A B ⊂平面11A C B ,则11BD B A ⊥,设正方体边长为a ,则11A D a =,1A B =,1BD =,由勾股定理知111A D B A ⊥,与假设矛盾,假设不成立,故1BD 不垂直于平面11A C B ,故B 错误; 对于C ,设正方体边长为a,则11AC =,内切球半径为2a,设内切球的球心O 在面11A C B 上的投影为O ',由等边三角形性质可知O '为等边11A C B △的重心,则11123233O A AC a ='=⨯=,又12OA a =,∴球心O 到面11A C B 的距离==,又球心与截面圆心的连线垂直于截面,∴6a =,又截面圆的面积224S ππ⎫=⎪⎪⎝⎭=,解得12a =,则内切球半径为6,内切球表面积214644S ππ==⨯,故C 错误;对于D ,由等体积法知111111111111212122812383B A C B B A C B A C B V V S a --==⨯⨯=⨯⨯=,故D 正确; 故选:AD【点睛】关键点点睛:本题考查了正方体和它的内切球的几何结构特征,关键是想象出截面图的形状,从而求出正方体的棱长,进而求出内切球的表面积及三棱锥的体积,考查了空间想象能力,数形结合的思想,属于较难题.4.如图,矩形ABCD 中, 22AB AD ==,E 为边AB 的中点.将ADE 沿直线DE 翻折成1A DE △(点1A 不落在底面BCDE 内),若M 在线段1A C 上(点M 与1A ,C 不重合),则在ADE 翻转过程中,以下命题正确的是( )A .存在某个位置,使1DE A C ⊥B .存在点M ,使得BM ⊥平面1A DC 成立 C .存在点M ,使得//MB 平面1A DE 成立D .四棱锥1A BCDE -体积最大值为24【答案】CD【分析】利用反证法可得A 、B 错误,取M 为1A C 的中点,取1A D 的中点为I ,连接,MI IE ,可证明//MB 平面1A DE ,当平面1A DE ⊥平面BCDE 时,四棱锥1A BCDE -体积最大值,利用公式可求得此时体积为2. 【详解】如图(1),取DE 的中点为F ,连接1,A F CF , 则45CDF ∠=︒,22DF =,故212254222222CF =+-⨯⨯=, 故222DC DF CF ≠+即2CFD π∠≠.若1CA DE ⊥,因为11,A D A E DF FE ==,故1A F DE ⊥,而111A F A C A ⋂=, 故DE ⊥平面1A FC ,因为CF ⊂平面1A FC ,故DE CF ⊥,矛盾,故A 错. 若BM ⊥平面1A DC ,因为DC ⊂平面1A DC ,故BM DC ⊥, 因为DC CB ⊥,BM CB B ⋂=,故CD ⊥平面1A CB ,因为1AC ⊂平面1A CB ,故1CD A C ⊥,但1A D CD <,矛盾,故B 错. 当平面1A DE ⊥平面BCDE 时,四棱锥1A BCDE -体积最大值, 由前述证明可知1A F DE ⊥,而平面1A DE平面BCDE DE =,1A F ⊂平面1A DE ,故1A F ⊥平面BCDE ,因为1A DE △为等腰直角三角形,111A D A E ==,故12A F = 又四边形BCDE 的面积为13211122⨯-⨯⨯=, 故此时体积为132232⨯=D 正确.对于C ,如图(2),取M 为1A C 的中点,取1A D 的中点为I ,连接,MI IE ,则1//,2IM CD IM CD =,而1//,2BE CD BE CD =, 故//,IM BE IM BE =即四边形IEBM 为平行四边形,故//IE BM ,因为IE ⊂平面1A DE ,BM ⊄平面1A DE ,故//MB 平面1A DE , 故C 正确. 故选:CD.【点睛】本题考查立体几何中的折叠问题,注意对于折叠后点线面的位置的判断,若命题的不成立,往往需要利用反证法来处理,本题属于难题.5.(多选题)如图所示,正方体1111ABCD A B C D -中,1AB =,点P 在侧面11BCC B 及其边界上运动,并且总是保持1AP BD ⊥,则以下四个结论正确的是( )A .113P AA D V -=B .点P 必在线段1BC 上 C .1AP BC ⊥D .AP ∥平面11AC D【答案】BD 【分析】 对于A ,1111111113326P AA D AA DV S CD -=⋅=⨯⨯⨯⨯=,对于B,C,D ,如图以D 为坐标原点可建立空间直角坐标系,利用空间向量判即可. 【详解】对于A ,因为点P 在平面11BCC B ,平面11BCC B ∥平面1AA D , 所以点P 到平面1AA D 即为C 到平面1AA D 的距离,即为正方体棱长, 所以1111111113326P AA D AA DV S CD -=⋅=⨯⨯⨯⨯=,A 错误; 对于B ,以D 为坐标原点可建立如下图所示的空间直角坐标系:则11(1,0,0),(,1,),(1,1,0),(0,0,1),(1,1,1),(0,1,0)A P x z B D B C 所以11(1,1,),(1,1,1),(1,0,1)AP x z BD BC =-=--=--, 因为1AP BD ⊥,所以1110AP BD x z ⋅=--+=,所以x z =,即(,1,)P x x , 所以(,0,)CP x x =,所以1CP xBC =-,即1,,B C P 三点共线, 所以点P 必在线段1B C 上,B 正确;对于C ,因为1(1,1,),(1,0,1)AP x x BC =-=-, 所以111AP BC x x ⋅=-+=, 所以1AP BC ⊥不成立,C 错误;对于D ,因为11(1,0,1),(0,1,1),(0,0,0)A C D , 所以11(1,0,1),(0,1,1)DA DC ==, 设平面11AC D 的法向量为(,,)n x y z =,则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩,令1x =,则1,1z y =-=,所以(1,1,1)n =-, 所以110AP n x x ⋅=-+-=,所以AP n ⊥, 所以AP ∥平面11AC D ,D 正确, 故选:BD 【点睛】此题考查了空间线线垂直的判定,线面平行的判定,三棱锥的体积,考查空间想象能力,考查计算能力,属于较难题.6.已知正方体1111ABCD A B C D -棱长为2,如图,M 为1CC 上的动点,AM ⊥平面α.下面说法正确的是()A .直线AB 与平面α所成角的正弦值范围为322⎣⎦B .点M 与点1C 重合时,平面α截正方体所得的截面,其面积越大,周长就越大 C .点M 为1CC 的中点时,若平面α经过点B ,则平面α截正方体所得截面图形是等腰梯形D .已知N 为1DD 中点,当AM MN +的和最小时,M 为1CC 的中点 【答案】AC 【分析】以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系D xyz -,利用空间向量法可判断A 选项的正误;证明出1AC ⊥平面1A BD ,分别取棱11A D 、11A B 、1BB 、BC 、CD 、1DD 的中点E 、F 、Q 、N 、G 、H ,比较1A BD 和六边形EFQNGH 的周长和面积的大小,可判断B 选项的正误;利用空间向量法找出平面α与棱11A D 、11A B 的交点E 、F ,判断四边形BDEF 的形状可判断C 选项的正误;将矩形11ACC A 与矩形11CC D D 延展为一个平面,利用A 、M 、N 三点共线得知AM MN +最短,利用平行线分线段成比例定理求得MC ,可判断D 选项的正误. 【详解】对于A 选项,以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系D xyz -,则点()2,0,0A 、()2,2,0B 、设点()()0,2,02M a a ≤≤,AM ⊥平面α,则AM 为平面α的一个法向量,且()2,2,AM a =-,()0,2,0AB =,2232cos ,,32288AB AMAB AM AB AM a a ⋅<>===⎢⋅⨯++⎣⎦, 所以,直线AB 与平面α所成角的正弦值范围为32⎣⎦,A 选项正确;对于B 选项,当M 与1CC 重合时,连接1A D 、BD 、1A B 、AC ,在正方体1111ABCD A B C D -中,1CC ⊥平面ABCD ,BD ⊂平面ABCD ,1BD CC ∴⊥,四边形ABCD 是正方形,则BD AC ⊥,1CC AC C =,BD ∴⊥平面1ACC , 1AC ⊂平面1ACC ,1AC BD ∴⊥,同理可证11AC A D ⊥,1A D BD D ⋂=,1AC ∴⊥平面1A BD ,易知1A BD 是边长为22(12322234A BD S =⨯=△为22362=.设E 、F 、Q 、N 、G 、H 分别为棱11A D 、11A B 、1BB 、BC 、CD 、1DD 的中点,易知六边形EFQNGH 是边长为2的正六边形,且平面//EFQNGH 平面1A BD , 正六边形EFQNGH 的周长为62,面积为()236233⨯⨯=,则1A BD 的面积小于正六边形EFQNGH 的面积,它们的周长相等,B 选项错误; 对于C 选项,设平面α交棱11A D 于点(),0,2E b ,点()0,2,1M ,()2,2,1AM =-,AM ⊥平面α,DE ⊂平面α,AM DE ∴⊥,即220AM DE b ⋅=-+=,得1b =,()1,0,2E ∴,所以,点E 为棱11A D 的中点,同理可知,点F 为棱11A B 的中点,则()2,1,2F ,()1,1,0EF =,而()2,2,0DB =,12EF DB ∴=,//EF DB ∴且EF DB ≠, 由空间中两点间的距离公式可得2222015DE =++=()()()2222212205BF =-+-+-=,DE BF ∴=,所以,四边形BDEF 为等腰梯形,C 选项正确;对于D 选项,将矩形11ACC A 与矩形11CC D D 延展为一个平面,如下图所示:若AM MN +最短,则A 、M 、N 三点共线,11//CC DD ,2222222MC AC DN AD ∴===+, 11222MC CC =≠,所以,点M 不是棱1CC 的中点,D 选项错误. 故选:AC.【点睛】本题考查线面角正弦值的取值范围,同时也考查了平面截正方体的截面问题以及折线段长的最小值问题,考查空间想象能力与计算能力,属于难题.7.在长方体1111ABCD A B C D -中,23AB =12AD AA ==,,,P Q R 分别是11,,AB BB AC 上的动点,下列结论正确的是( ) A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥C .当1AR A C ⊥时,1ARD R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABD【分析】如图所示建立空间直角坐标系,计算142D P CQ b ⋅=-,()12222D R CQ b λλ⋅=--,134AR D R ⋅=-,10D R n ⋅=,得到答案. 【详解】如图所示,建立空间直角坐标系,设()2,,0P a ,0,23a ⎡∈⎣,()2,23,Q b ,[]0,2b ∈,设11A R AC λ=,得到()22,23,22R λλλ--,[]0,1λ∈.()12,,2P a D -=,()2,0,CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;()122,23,2D R λλλ=--,()12222D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确;1AR A C ⊥,则()()12,23,222,23,2212440AR AC λλλλλλ⋅=--⋅--=-+-+=, 14λ=,此时11333313,,,,02222224AR D R ⎛⎫⎛⎫⋅=-⋅-=-≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,C 错误; 113AC A R =,则4234,,33R ⎛⎫ ⎪ ⎪⎝⎭,14232,,33D R ⎛⎫=- ⎪ ⎪⎝⎭,设平面1BDC 的法向量为(),,n x y z =,则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得()3,1,3n =-, 故10D R n ⋅=,故1//D R 平面1BDC ,D 正确.故选:ABD .【点睛】本题考查了空间中的线线垂直,线面平行,意在考查学生的计算能力和空间想象能力,推断能力.8.如图,已知矩形ABCD 中,2AB AD =,E 为边AB 的中点,将ADE ∆沿直线DE 翻折成1A DE ∆,若M 为线段1A C 的中点,则ADE ∆在翻折过程中,下列说法正确的是( )A .线段BM 的长是定值B .存在某个位置,使1DE AC ⊥C .点M 的运动轨迹是一个圆D .存在某个位置,使MB ⊥平面1A DE【答案】AC【分析】取CD 中点F ,连接BF ,MF ,根据面面平行的判定定理可得平面//BMF 平面1A DE ,由面面平行的性质定理可知//BM 平面1A DE ,可判断D ;在BFM ∆中,利用余弦定理可求得BM a =为定值,可判断A 和C ;假设1DE A C ⊥,由线面垂直的判定定理可得DE ⊥平面1A CE ,由线面垂直的性质定理可知1DE A E ⊥,与11DA A E ⊥矛盾,可判断B .【详解】解:取CD 的中点F ,连接BF ,MF ,∵M ,F 分别为1A C 、CD 中点,∴1MF A D ∥,∵1A D ⊂平面1A DE ,MF ⊄平面1A DE ,∴MF 平面1A DE ,∵DF BE ∥且DF BE =,∴四边形BEDF 为平行四边形,∴BF DE ,∵DE ⊂平面1A DE ,BF ⊄平面1A DE ,∴BF ∥平面1A DE ,又BF MF F =,BF 、MF ⊂平面BMF ,∴平面//BMF 平面1A DE ,∵BM ⊂平面BMF ,∴BM ∥平面1A DE ,即D 错误,设22AB AD a ==,则112MF A D a ==,BF DE ==,145A DE MFB ︒∠=∠=,∴BM a ==,即BM 为定值,所以A 正确,∴点M 的轨迹是以B 为圆心,a 为半径的圆,即C 正确, ∵DE CE ==,2CD AB a ==, ∴222DE CE CD +=, ∴DE CE ⊥,设1DE A C ⊥,∵1A C 、CE ⊂平面1A CE ,1AC CE C =, ∴DE ⊥平面1A CE ,∵1A E ⊂平面1A CE ,∴1DE A E ⊥,与11DA A E ⊥矛盾,所以假设不成立,即B 错误.故选:AC .【点睛】本题考查立体几何中的翻折问题,涉及到线段长度的求解、直线与平面位置关系的判定、点的轨迹的求解、反证法的应用等知识点,考查学生的空间立体感和推理论证能力.。
初三数学立体图形试题答案及解析
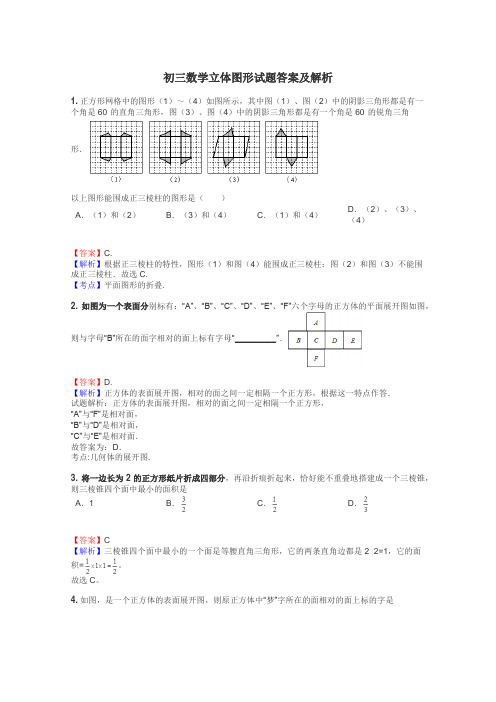
初三数学立体图形试题答案及解析1.正方形网格中的图形(1)~(4)如图所示,其中图(1)、图(2)中的阴影三角形都是有一个角是60°的直角三角形,图(3)、图(4)中的阴影三角形都是有一个角是60°的锐角三角形.以上图形能围成正三棱柱的图形是()A.(1)和(2)B.(3)和(4)C.(1)和(4)D.(2)、(3)、(4)【答案】C.【解析】根据正三棱柱的特性,图形(1)和图(4)能围成正三棱柱;图(2)和图(3)不能围成正三棱柱.故选C.【考点】平面图形的折叠.2.如图为一个表面分别标有:“A”、“B”、“C”、“D”、“E”、“F”六个字母的正方体的平面展开图如图,则与字母“B”所在的面字相对的面上标有字母“_________”.【答案】D.【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.试题解析:正方体的表面展开图,相对的面之间一定相隔一个正方形,“A”与“F”是相对面,“B”与“D”是相对面,“C”与“E”是相对面.故答案为:D.考点:几何体的展开图.3.将一边长为2的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地搭建成一个三棱锥,则三棱锥四个面中最小的面积是A.1B.C.D.【答案】C【解析】三棱锥四个面中最小的一个面是等腰直角三角形,它的两条直角边都是2÷2=1,它的面积=。
故选C。
4.如图,是一个正方体的表面展开图,则原正方体中“梦”字所在的面相对的面上标的字是A.大B.伟C.国D.的【答案】D。
【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点,所以,面“伟”与面“国”相对,面“大”与面“中”相对,“的”与面“梦”相对。
故选D。
5.如图是某一立方体的侧面展开图,则该立方体是()A B C D【答案】D【解析】从立方体的侧面展开图来看,两个有圆的面是隔开的,不相邻,所以排除A、B;观察立方体的侧面展开图,立方体中小正方形中含有三角形的两个面是相邻的,且其两面都与含有深色的一个圆的那个面相邻,所以选D【考点】正方体点评:本题考查正方体,解答本题需要掌握正方体的图形结构,本题考查考生的观察能力和空间想象能力6.如图所示为一个无盖长方体盒子的展开图(重叠部分不计),根据图中数据,可知该无盖长方体的容积为.【答案】6【解析】作图分析无盖长方体可根据阴影部分位置不同来展开,所以一直底面宽为3-1=2cm;长为5-2=3cm。
初三数学立体图形试题答案及解析

初三数学立体图形试题答案及解析1.一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“成”相对的字是()A.中B.功C.考D.祝【答案】B.【解析】这是一个正方体的平面展开图,共有六个面,相对两个面之间隔一个正方形.因此,其中面“成”与面“功”相对,“中”与面“考”相对,面“预”与面“祝”相对.故选B.【考点】正方体及其表面展开图.2.如果一个多面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥。
如图是一个四棱柱和一个六棱锥,它们各有12条棱,下列棱柱中和九棱锥的棱数相等的是A.五棱柱B.六棱柱C.七棱柱D.八棱柱【答案】B【解析】九棱锥侧面有9条棱,底面是九边形,也有9条棱,共9+9=18条棱,A、五棱柱共15条棱,故此选项错误;B、六棱柱共18条棱,故此选项正确;C、七棱柱共21条棱,故此选项错误;D、九棱柱共27条棱,故此选项错误;故选:B.【考点】棱柱与棱锥3.如图所示的是某几何体的三视图,则该几何体的形状是()A.三棱锥B.正方体C.三棱柱D.长方体【答案】C.【解析】根据三视图可以想象出该物体由三条棱组成,底面是三角形,此只有三棱柱的三视图与题目中的图形相符.故选C.【考点】由三视图判断几何体.4.下面给出的正多边形的边长都是20cm,请分别按下列要求设计一种剪拼方法(用虚线表示你的设计方案,把剪拼线段用粗黑实线,在图中标注出必要的符号和数据,并作简要说明.(1)将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型,使它的表面积与原正方形面积相等;(2)将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型,使它的表面积与原正三角形的面积相等;(3)将图3中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型,使它的表面积与原正五边形的面积相等.【答案】(1)作图见解析(2)作图见解析(3)作图见解析【解析】思路分析:(1)在正方形四个角上分别剪下一个边长为5的小正方形,拼成一个正方形作为直四棱柱的底面即可;(2)在正三角形的每一角上找出到顶点距离是5的点,然后作边的垂线,剪下后拼成一个正三角形,作为直三棱柱的一个底面即可;(3)在正五边形的每一角上找出到顶点距离是5的点,然后作边的垂线,剪下后拼成一个正五边形,作为直五棱柱的一个底面即可.解:(1)如图1,沿黑线剪开,把剪下的四个小正方形拼成一个正方形,再沿虚线折叠即可;(2)如图,2,沿黑线剪开,把剪下的三部分拼成一个正三角形,再沿虚线折叠即可;(3)如图3,沿黑线剪开,把剪下的五部分拼成一个正五边形,再沿虚线折叠即可.点评:本题考查了图形的剪拼,解题的关键在于根据拼成棱柱的表面积与原图形的面积相等,从而判断出剪下的部分拼成的图形应该是棱柱的一个底面.5.如图是一个几何体的三视图,根据图中提供的数据(单位:cm)可求得这个几何体的体积为A.2cm3B.3cm3C.6cm3D.8cm3【答案】B【解析】该几何体的主视图以及左视图都是相同的矩形,俯视图也为一个矩形,可确定这个几何体是一个长方体,此长方体的长与宽都是1,高为3,所以该几何体的体积为1×1×3=3cm3。
奥林匹克数学竞赛初赛七年级考试卷(B)含答案

16.如图4是由几块相同的小正方体搭成的立体图形的三视图,则这立体图形中小正方体共有()块.
A、9B、10C、11D、12
Part 3计算:
17. 18.
Part 4列方程解应用题。
19、一队学生从甲地到乙地,速度为每小时8千米,当行进2千米路后,通讯员奉命回甲地取东西,他以每小时10千米的速度回甲地取了东西后,立即以同样速度追赶队伍,结果在距乙地3千米处追上队伍,求甲、乙两地的距离(取东西的时间不计)。
世界少年奥林匹克数学竞赛(中国区)选拔赛
2020-2021初赛试卷 七年级(B卷)
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄
考生须知:本卷共120分,考试时间90分钟。第1至20题,每题6分。
考试期间,不得使用计算工具或手机
Part 1填空题
1.计算: + + +……+ =。
A、37B、36C、35D、34
15.某旅游团92人在快餐店就餐,该店备有9种菜,每份菜单单价分别为1、2、3、4、5、6、7、8、9(元),旅游团领队交代:每人可选不同的菜,但金额都须正好10元,且每一种菜最多只能买一份,这样,该团成员在购菜完全符合要求的所有方案中,至少有一个方案的人数不少于(C).
A.52 B.55 C.58 D.62
12.适合 的整数x的值的个数有(D)
A.5B.4C.3D.2
13.已知m是方程 的一个根,则 的值等于(D).
A、2005B、2006C、2007D、.2008
14.将一段72cm长的绳子,从一端开始每3cm作一记号,每4cm也作一记号,然后从有记号的地方剪断,则这段绳子共被剪成的段数为(B).
高中数学竞赛讲义 立体图形、空间向量(练习题) 新人教A版

ABCDE FCDFABOCD EOA§19立体图形,空间向量课后练习1.甲烷分子由一个碳原子和四个氢原子组成,其空间构型为一正四面体,碳原子位于该正四 面体的中心,四个氢原子分别位于该正四面体的四个顶点上.若将碳原子和氢原子均视为一 个点(体积忽略不计),且已知碳原子与每个氢原子间的距离都为a ,则以四个氢原子为顶点 的这个正四面体的体积为( )A,3827aB,327a C,313a D,389a 2.夹在两个平行平面之间的球,圆柱,圆锥在这两个平面上的射影都是圆,则它们的体积之比为( )A,3:2:1 B,2:3:1 C,3:6:2 D,6:8:33.设二面角a αβ--的大小是060,P 是二面角内的一点,P 点到,αβ的距离分别为1cm, 2cm,则点P 到棱a 的距离是( )A,3cmB,3cm C,23cmD,3cm 4.如图,E,F 分别是正三棱锥A -BCD 的棱AB,BC的中点,且DE ⊥EF.若BC=a ,则此正三棱锥的体积是( )A,324aB,324a335.棱长为的正八面体的外接球的体积是( )A,6πB,27C,3D,3 6.若线段AB 的两端点到平面α的距离都等于2,则线段AB 所在的直线和平面α的位置关系是 .7.若异面直线,a b 所原角为060,AB 是公垂线,E,F 分别是异面直线,a b 上到A,B 距离为 2和平共处的两点,当3EF =时,线段AB 的长为 .8.如图(1),在直四棱柱1111A B C D ABCD -中,当底面四边形ABCD 满足条件 时,有1A C ⊥1B 1D (注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)9.如图(2),是一个正方体的展开图,在原正方体中,有下列命题:①AB 与EF 所连直线平行; ②AB 与CD 所在直线异面; ③MN 与BF 所在直线成060; ④MN 与CD 所在直线互相垂直.其中正确命题的序号为 .(将所有正确的都写出)10.如图,在ABC ∆中,AB=AC=13,BC=10,DE//BC 分别交AB,AC 于D,E.将ADE ∆沿 DE 折起来使得A 到1A ,且1A DE B --为060的二面角,求1A 到直线BC 的最小距离.11.如图,已知矩形ABCD 中,AB=1,BC=a (0)a >,PA ⊥平面ABCD,且PA=1. A BCDA BC D图(1)ABENM 图(2)A B CDP Q(1)问BC 边上是否存在点Q 使得PQ ⊥QD?并说明理由;(2)若边上有且只有一个点Q,使得PQ ⊥QD,求这时二面角Q PD A --的正切.课后习题答案1.过顶点A,V 与高作一截面交BC 于点M,点O 为正四面体的中心,1O 为底面ABC 的中心, 设正四面体VABC 的棱长为m ,则AM=2m =VM,1O M=136AM m =, 1233O A AM m ==,13VO m ==,得113OO VO VO a =-=-在1Rt AOO ∆中,22211AO OO AO =+,即222()()33a m a m =-+,得3m a =. 则1VO =43a ,有203111(sin 60)32V ABC V m VO -=⋅⋅⋅⋅=.选B. 温馨提示:正四面体外接球的半径VO :内切球的半径1OO =1:3:13a a =.2. 32212341::():(2):(2)2:3:133V V V R R R R R πππ=⋅⋅⋅=,选B.3.设PA ⊥棱a 于点A,PM ⊥平面α于点M,PN ⊥平面β于点N,PA=t ,PAM θ∠=,则sin 1sin(60)2t t αα=⎧⎨-=⎩,5sin αα=,有sin α=或(舍去),所以1sin 3t α==cm ,选B. 4.由DE ⊥EF,EF//AC,有DE ⊥AC,又AC ⊥BD,DE BD=D,得AC ⊥平面ABD.由对称性得090BAC CAD BAD ∠=∠=∠=,于是2AB AC AD a ===. 311()3222224B ACD V a a -=⋅⋅⋅⋅=,选B.5.可由两个相同的四棱锥底面重合而成,有2r =得r =外接球的体积3433V r π==,选D. 6.当2AB <时,AB//α;当2AB =时,AB//α或AB ⊥α;当2AB >时,AB//α或与α斜交. 7.由EF EA AB BF =++,得22222cos EFEA AB BF EA BF θ=+++⋅⋅(1)当060θ=时,有219412212AB =+++⋅⋅⋅,得2AB =(2)当0120θ=时,有219412212AB=++-⋅⋅⋅,得6AB =8. AC ⊥BD.(或ABCD 是正方形或菱形等)9.将展开的平面图形还原为正方体NACF EMBD -,可得只②,④正确.10.解:设ABC ∆的高AO 交DE 于点1O ,令1AO x =, 由12=,有112OO x =-,在11A OO ∆中,01160A O O ∠=,有222011111112cos 60A O A O O O A O O O =+-⋅⋅⋅得1AO =当6x =时,1A 到直线BC 的最小距离为6.11.解:(1)(如图)以A 为原点建立空间直角坐标系,设BQ x =,则 Q (1,,0)x ,P(0,0,1),D (0,,0)a 得(1,,1)PQ x =-,(1,,0)QD a x =--由PQ QD ⊥,有(1,,1)(1,,0)0x a x -⋅--=,得210x ax -+= ①若方程①有解,必为正数解,且小于a .由2()40a ∆=--≥,0a >,得2a ≥. (i)当2a ≥时,BC 上存在点Q,使PQ ⊥QD;(ii)当02a <<时, BC 上不存在点Q,使PQ ⊥QD.(2)要使BC 边上有且只有一个点Q,使PQ ⊥QD,则方程①有两个相等的实根,这时,2()40a ∆=--=,得2a =,有1x =.又平面APD 的法向量1(1,0,0)n =,设平面PQD 的法向量为2(,,)n x y z = 而(1,1,0)QD =-,(0,2,0)(0,0,1)(0,2,1)PD =-=-,由2200n QD n PD ⎧⋅=⎪⎨⋅=⎪⎩,得(,,)(1,1,0)0(,,)(0,2,1)0x y z x y z ⋅-=⎧⎨⋅-=⎩,解得,2x y z y ==有2(1,1,2)n =,则121212cos ,n n n n n n ⋅<>===⋅,则12tan ,n n <>=Q PD A --的正切为。
世界少年奥林匹克数学竞赛初赛七年级考试卷(A)含答案

世界少年奥林匹克数学竞赛(中国区)选拔赛 2012-2013 初赛试卷 七年级(A 卷) ┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 考生须知:本卷共120分,考试时间90分钟。
第1至20题,每题6分。
考试期间,不得使用计算工具或手机Part 1 填空题1. 计算: 211⨯+321⨯+431⨯+……+100991⨯= 。
2. 当1±≠x 时,方程20111133=--+++x x x x 的解是 。
3. 计算:3001×2999= 。
4. 计算: 97×103×10009= 。
5. 计算:1234712345-1234620122⨯= 。
6. 计算:当3-=x ,31=y 时,5y 3-2+x 的值是 。
7. 计算:=2-2-2--2-2-223201********* 。
8. 计算:有两个质数的平方和是125,这两质数的和是 。
9.当=x 时,分式 32+x x的值为0。
10. 732012÷的余数是 。
Part 2 单项选择题(把字母填在空格处)11. 如果4a-3b=7,并且3a+2b=19,14a-2b 的值是 。
A.52B.55C.58D.62 12.若m 为实数,则代数式m +m 的值一定是( ).A 、正数B 、0C 、负数D 、非负数 _______学校 姓名_________辅导教师__________年级____考场____考号手机电话 ---------------------------------------装-----------------------------订---------------------------线----------------------------------13.已知m 是方程01x -x 2=+2006的一个根,则3+1++22m 20062005m -m 的值等于( ). A 、2005 B 、2006 C 、2007 D 、.200814.将一段72cm 长的绳子,从一端开始每3cm 作一记号,每4cm 也作一记号,然后从有记号的地方剪断,则这段绳子共被剪成的段数为( ).A 、37B 、36C 、35D 、3415.某旅游团92人在快餐店就餐,该店备有9种菜,每份菜单单价分别为1、2、3、4、5、6、7、8、9(元),旅游团领队交代:每人可选不同的菜,但金额都须正好10元,且每一种菜最多只能买一份,这样,该团成员在购菜完全符合要求的所有方案中,至少有一个方案的人数不少于( ).A 、9人B 、10人C 、11人D 、12人16.如图4是由几块相同的小正方体搭成的立体图形的三视图,则这立体图形中小正方体共有( )块.A 、9B 、10C 、11D 、12Part 3 计算:17. 20022003)2()2(-+-; 18. 5.702.04.01.05.201.03.02.0-+=--x xPart 4 列方程解应用题。
【初中数学】人教版七年级上册第3课时 立体图形的展开图(练习题)

人教版七年级上册第3课时立体图形的展开图(270)1.如图是一个正方体的表面展开图,如果把它重新折成正方体,那么与点G重合的是哪两点?并用字母表示三对相对的面.2.如图,有一个外观为圆柱形的物体,它的内部构造看不到,当分别用一组平面沿水平方向(自上而下)和竖直方向(自左而右)截这个物体时,得到了如图所示的(1)(2)两组形状不同的截面,请你试着说出这个物体的内部构造.3.下列图形中可以作为一个三棱柱的展开图的是()A. B. C. D.4.一个几何体的展开图如图所示,这个几何体是()A.圆锥B.圆柱C.四棱柱D.四棱锥5.如图是某几何体的展开图,那么这个几何体是.6.如图,剪去一个正方形,使剩余部分恰好能折成一个正方体,那么应剪去哪个小正方形?写出所有可能的情况.7.下列四个图形中,是三棱锥的表面展开图的是()A. B. C. D.8.将如图所示的长方体的表面展开,下列选项中错误的是()A. B. C. D.9.如图是一个几何体的展开图,则这个几何体是.10.如图是一个几何体(字母朝外)的表面展开图,每个面上都标有字母,请回答下列问题:(1)如果B在几何体的前面,那么哪一个字母在后面?(2)如果E在几何体的下面,那么哪一个字母在上面?(3)如果D在前面,F在左面,那么哪一个字母在上面?哪一个字母在右面?哪一个字母在下面?11.将一个正方体沿某些棱展开后,能够得到的平面图形是()A. B. C. D.12.如图是一个正方体的表面展开图,把展开图折叠成正方体后,“美”字一面的相对面上的字是()A.丽B.连C.云D.港13.如图是正方体的展开图,若约定用字母S表示正方体的侧面,用T表示上面,用A表示底面,则字母A在展开图中的位置是()A.①B.②C.③D.④14.在如图②所示的正方体表面展开图中,确定图①中正方体上的点P,Q,S,T的位置,并标出来.15.如图①,正方体的下半部分涂上了黑色油漆,在如图②的正方体表面展开图中把刷油漆的部分涂黑(图②中涂黑部分是正方体的下底面).16.如图,图(1)和图(2)中所有的正方形都全等,将图(1)中的正方形放在图(2)中的①②③④某一位置,所组成的图形不能围成正方体的位置是()A.①B.②C.③D.④17.如图给定的是纸盒的外表面展开图,则能由它折叠而成的是()A. B. C. D.18.如图,将图①围成如图②所示的正方体,则图①中的红心“”标志所在的正方形是正方体中的()A.面CDHEB.面BCEFC.面ABFGD.面ADHG参考答案1.【答案】:解:结合图形可知,围成正方体后点A,点C和点G重合.四边形ABMN 与四边形FEJI,四边形LMJK与四边形CBED,四边形MJEB与四边形HIFG分别是相对面【解析】:解:结合图形可知,围成正方体后点A,点C和点G重合.四边形ABMN 与四边形FEJI,四边形LMJK与四边形CBED,四边形MJEB与四边形HIFG分别是相对面2.【答案】:这个圆柱的内部构造为:圆柱中间有一球状空洞,即空心球【解析】:这个圆柱的内部构造为:圆柱中间有一球状空洞,即空心球3.【答案】:A【解析】:三棱柱展开后,侧面是三个长方形,上、下底面各是一个三角形.由此可得只有A是三棱柱的展开图.故选 A4.【答案】:A5.【答案】:圆柱6.【答案】:解:应剪去标有1或2或3的小正方形【解析】:根据有“田”字格的展开图都不是正方体的表面展开图可知7.【答案】:B【解析】:三棱锥的四个面都是三角形,还要能围成一个立体图形,可排除C,D;而A不能围成立体图形.故选 B.8.【答案】:C9.【答案】:五棱柱10(1)【答案】解:如果B在几何体的前面,那么字母D在后面(2)【答案】解:如果E在几何体的下面,那么字母C在上面(3)【答案】解:如果D在前面,F在左面,那么字母C在上面,字母A在右面,字母E在下面11.【答案】:C12.【答案】:D13.【答案】:D【解析】:正方体的表面展开图,相对的面之间一定相隔一个正方形,∵用S表示正方体的侧面,用T表示上面,用A表示底面,∴S与②是相对面,T与④是相对面14.【答案】:解:如图所示:15.【答案】:解:如图所示.16.【答案】:A【解析】:将图(1)的正方形放在图(2)中的①的位置将会出现重叠的面,所以不能围成正方体.故选A17.【答案】:B【解析】:A.展开得到,不能和原图相对应,故本选项错误;B.展开得到,能和原图相对应,故本选项正确;C.展开得到,不能和原图相对应,故本选项错误;D.展开得到,不能和原图相对应,故本选项错误.故选B18.【答案】:A。
【数学竞赛】七年级数学思维探究(20)丰富的图形世界(含答案)

空间与图形欧拉1707 1783 ,是18世纪最优秀的数学家之一,他不只在数学上作出了伟大贡献,并且把数学成功地应用到其余领域,在数论中,欧拉首选引进了欧拉函数n ,用多种方法证了然花费小定理,对著名的哥尼斯堡大桥问题的解答创始了图论的研究,别的,欧拉还在物理、天文、建筑以及音乐、哲学等方面获得了绚烂的成就.20.丰富的图形世界解读课标20 世纪初,伟大的法国建筑家列·柯尔伯齐曾说:“我想,到当前为止,我们从没有生活在这样的几何时期,四周的全部都是几何学.”生活中包含着丰富的几何图形,圆的月亮,平的湖面,直的树干,造型奇异的建筑,不停挪动、反转、放大减小的电视画面,, 图形有的是立体的,有的是平面的,立体图形与平面图形之间的联系,从以方面得以表现:1.立体图形的睁开与折叠;2.从各个角度察看立体图形;3.用平面去截立体图形.察看概括、操作实验、睁开想象、推理论证是探究图形世界的基本方法.问题解决例 1如图是一个正方体表面睁开图,假如正方体相对的面上标明的值相等那么x y_____.试一试睁开与折叠是两个步骤相反的过程,从折叠复原成正方体人手.82x y88 10例 2 如图,是由一些完整相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是()主视图左视图俯视图A.5个 B 6个C.7个D.8个试一试依据三视图和几何体的关系。
分别确立该几何体的列数和每一列的层数.例 3由一些大小相同的小正方体构成的简单几何体的主视图和俯视图如图.( 1)请你画出这个几何体的一种左视图;( 2)若构成这个几何体的小正方体的块数为n ,求n 的值.俯视图主视图试一试本例能够在“脑子”中想象达成,也能够用实物摆一摆,从操作实验人手,从俯视图可推测左视图只好有两列,由主视图剖析出俯视图每一列小正方形的块数状况是解本例的重点,而有序思虑、分类议论,则可防止重复与遗漏.例 4 如图是由若干个正方体形状木块堆成的,平放于桌面上,此中,上边正方体的下底面四个极点正是下边相邻正方体的上底面各边的中点,假如最下边的正方体的棱长为 1,且这些正方体露在外面的面积和超出8 ,那么正方体的个数起码是多少?按此规律堆下去,这些正方体露在外面的面积和的最大值是多少?试一试全部正方体侧面面积和再加上全部正方体上边露出的面积和,就是需求的面积.从简单人手,归纳规律.例 5 要把一个正方体切割成 49 个小正方体(小正方体大小能够不等) ,绘图表示. 剖析与解本例是一道图形切割问题, 解答本例需要较强的空间想象能力和推理论证能力, 需要把图形性 质与计算适合联合.为方便起见, 设正方体的棱长为 6 个单位, 第一不可以切出棱长为 5 的立方体, 不然不行能切割成49 个小 正方体. 设切出棱长为 1的正方体有 a 个,棱长为 2的正方体有 b 个,假如能切出 1个棱长为 4 的正方体,则有 a 8b 64 216 6 4 的正方体.a b 49 ,解之得 b 14 ,不合题意,因此切不出棱长为1 7设切出棱长为 1的正方体有 a个,棱长为 2的正方体有 b 个,棱长为 3 的正方体有 c个,a 8b 27c 216, c 4 ,故可切割棱长分别为1、 2 、 3 的正方体各有 36个、9a b,解得 a 36 , b 9 c 49 个、 4 个,分法如下图.欧拉公式例 6 成立模型18 世纪瑞士数学家欧拉证了然简单多面体中极点数(V )、面数(F)、棱数(E )之间存在的一个有趣的关系式,被称为欧拉公式,请你察看以下几种简单多面体模型,解答以下问题.四周体 长方体 正八面体 正十二面体( 1)依据上边多面体模型,达成表格中的空格多面体 极点数( V ) 面数( F ) 棱数( E )四周体 44长方体 8 6 12 正八面体812正十二面体201230你发现极点数( V )、面数( F )、棱数( E )之间存在的关系式是 _____. ( 2)一个多面体的面数比极点数大 8 ,且有 30 条棱,则这个多面体的面数是_____. ( 3)某个玻璃饰品的外形是简单多面体, 它的表面面是由三角形和八边形两种多边形拼接而成, 且有 24 个极点,每个极点处都有 3 条棱,设该多面体表面面三角形的个数为 x 个,八边形的个数为 y 个,求 x y 的值.解(1)6;6;V FE 2( 2) 20( 3)这个多面体的面数为x y,棱数为24 3 36 (条)2依据 V F E 2,可得24 x y 36 2 ,∴ x y 14 .模型应用如图,有一种足球是由数块黑白相间的牛皮缝制而成,黑皮为正五边形,白皮为正六边形,且边长都相等,求正五边形、正六边形个数.解设足球表面的正五边形有x 个,正六边形有y个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体图形空间形体的想象能力是小学生的一种重要的数学能力,而立体图形的学习对培养这种能力十分有效。
我们虽然在课本上已经学习了一些简单的立体图形,如正方体、长方体、圆柱体、圆锥体,但有关立体图形的概念还需要深化,空间想象能力还需要提高。
将空间的位置关系转化成平面的位置关系来处理,是解决立体图形问题的一种常用思路。
一、立体图形的表面积和体积计算例1一个圆柱形的玻璃杯中盛有水,水面高2.5cm,玻璃杯内侧的底面积是72cm2,在这个杯中放进棱长6cm的正方体铁块后,水面没有淹没铁块,这时水面高多少厘米?解:水的体积为72×2.5=180(cm3),放入铁块后可以将水看做是底面积为72-6×6=32(cm2)的柱体,所以它的高为180÷32=5(cm)。
例2下图表示一个正方体,它的棱长为4cm,在它的上下、前后、左右的正中位置各挖去一个棱长为1cm的正方体,问:此图的表面积是多少?分析:正方体有6个面,而每个面中间有一个正方形的孔,在计算时要减去小正方形的面积。
各面又挖去一个小正方体,这时要考虑两头小正方体是否接通,这与表面积有关系。
由于大正方体的棱长为4cm,而小正方体的棱长为1cm,所以没有接通。
每个小正方体孔共有5个面,在计算表面积时都要考虑。
解:大正方体每个面的面积为4×4-1×1=15(cm2),6个面的面积和为15×6=90(cm2)。
小正方体的每个面的面积为1×1=1(cm2),5个面的面积和为1×5=5(cm2),6个小正方体孔的表面积之和为5×6=30(cm2),因此所求的表面积为90+30=120(cm2)。
想一想,当挖去的小正方体的棱长是2cm时,表面积是多少?请同学们把它计算出来。
例3正方体的每一条棱长是一个一位数,表面的每个正方形面积是一个两位数,整个表面积是一个三位数。
而且若将正方形面积的两位数中两个数码调过来则恰好是三位数的十位与个位上的数码。
求这个正方体的体积。
解:根据“正方体的每一条棱长是一个一位数,表面的每个正方形面积是一个两位数,整个表面积是一个三位数”的条件,可知正方体的棱长有5,6,7,8,9这五种可能性。
根据“将正方形面积的两位数中两个数码调过来恰好是三位数的十位上与个位上的数码”,可知这个正方体的棱长是7。
如下表:因此这个正方体的体积是7×7×7=343。
例4一个长、宽和高分别为21cm,15cm和12cm的长方体,现从它的上面尽可能大地切下一个正方体,然后从剩余的部分再尽可能大地切下一个正方体,最后再从第二次剩余的部分尽可能大地切下一个正方体,剩下的体积是多少立方厘米?解:根据长方体的长、宽和高分别为21cm,15cm和12cm的条件,可知第一次切下尽可能大的正方体的棱长是12cm,其体积是12×12×12=1728(cm3)。
这时剩余立体图形的底面形状如图1,其高是12cm。
这样,第二次切下尽可能大的正方体的棱长是9cm,其体积是9×9×9=729(cm3)。
这时剩余立体图形可分割为两部分:一部分的底面形状如图2,高是12cm;另一部分的底面形状如图3,高是3cm。
这样,第三次切下尽可能大的正方体的棱长是6cm,其体积是6×6×6=216(cm3)。
因此,剩下的体积是21×15×12-(123+93+63)=3780-2673=1107(cm3)。
说明:如果手头有一个泥塑的长方体和小刀,那么做出这道题并不难。
但实际上,我们并没有依赖于具体的模型和工具,这就是想象力的作用。
我们正是在原有感性经验的基础上,想象出切割后立体的形状,并通过它们各个侧面的形状和大小表示出来。
因此,对一个立体图形,应该尽可能地想到它的原型。
例5下图是一个长27cm,宽8cm,高8cm的长方体。
现将它分为4部分,然后将这4部分重新组拼,能重组为一个棱长为12cm的正方体。
请问应该怎么分?解:重组成的正方体的棱长是12cm,而已知长方体的宽是8cm,所以要把宽增加4cm,为此可按下图1中的粗线分开,分开后重组成图2的形状;图2的高是8cm,也应增加4cm,为此可按图2中的虚线分开,分开后重组成图3的形状。
图3就是所组成的棱长为12cm的正方体。
说明:这里有一个朴素的思想,就是设法把不足12cm的宽和高补成12cm的棱长,同时按照某种对称的方式分割。
在解关于立体图形的问题时,需要有较丰富的想象力,要能把平面图形在头脑中“立”起来,另外还应有一定的作图本领和看图能力。
例6雨哗哗地不停地下着,如在雨地里放一个如右图那样的长方体的容器(单位:厘米),雨水将它下满要用1时。
有下列(1)~(5)不同的容器,雨水下满各需多长时间?解:根据题意知雨均匀地下,即单位面积内的降雨量相同。
所以雨水下满某容器所需的时间与该容器的容积和接水面(敞开部分)的面积之比有关。
因为在例图所示容器中:需1时接满,所以二、立体图形的侧面展开图例7 左下图是一个立体图形的侧面展开图(单位:cm),求这个立体图形的表面积和体积。
解:这个立体图形是一个圆柱的四分之一(如右上图),圆柱的底面半径为10cm,高为8cm。
它的表面积为例8左下图是一个正方体,四边形APQC表示用平面截正方体的截面。
请在右下方的展开图中画出四边形APQC的四条边。
解:把空间图形表面的线条画在平面展开图上,只要抓住四边形APQC四个顶点所在的位置这个关键,再进一步确定四边形的四条边所在的平面就可容易地画出。
(1)考虑到展开图上有六个顶点没有标出,可想象将展开图折成立体形,并在顶点上标出对应的符号,见左下图。
(2)根据四边形所在立体图形上的位置,确定其顶点所在的点和棱,以及四条边所在的平面:顶点:A—A,C—C,P在EF边上,Q在GF边上。
边AC在ABCD面上,AP在ABFE 面上,QC在BCGF面上,PQ在EFGH面上。
(3)将上面确定的位置标在展开图上,并在对应平面上连线。
需要注意的是,立体图上的A,C点在展开图上有三个,B,D点在展开图上有二个,所以在标点连线时必须注意连线所在的平面。
连好线的图形如右上图。
例9如右图所示,剪一块硬纸片可以做成一个多面体的纸模型(沿虚线折,沿实线粘)。
这个多面体的面数、顶点数和棱数的总和是多少?解:从展开图可以看出,粘合后的多面体有12个正方形和8个三角形,共20个面。
这个多面体上部的中间是一个正三角形,这个正三角形的三边与三个正方形相连,这样上部共有9个顶点,下部也一样。
因此,多面体的顶点总数为 9×2=18(个)。
在20个面的边中,虚线有19条,实线有34条。
因为每条虚线表示一条棱,两条实线表示一条棱,所以多面体的总棱数为19+34÷2=36(条)。
综上所述,多面体的面数、顶点数和棱数之和为20+18+36=74。
说明:数学家欧拉曾给出一个公式:V+F-E=2。
公式中的V表示顶点数,E表示棱数,F表示面数。
根据欧拉公式,知道上例多面体的面数和顶点数之后,棱数便可求得:E=V+F-2=20+18-2=36(条)。
三、立体图形的截面与投影例10用一个平面去截一个正方体,可以得到几边形?解:如下图,可得到三角形、四边形、五边形和六边形。
例11一个棱长为6cm的正方体,把它切开成49个小正方体。
小正方体的大小不必都相同,而小正方体的棱长以厘米作单位必须是整数。
问:可切出几种不同尺寸的正方体?每种正方体的个数各是多少?解:13=1,23=8,33=27,43=64,53=125,63=216。
如果能切出1个棱长为5cm的正方体,那么其余的只能是棱长为1cm的正体体,共切出小正方体1+(63-53)÷1=92(个)。
因为92>49,所以不可能切出棱长为5cm的正方体。
如果能切出1个棱长为4cm的正方体,那么其余的只能是棱长为1cm或2cm的正方体。
设切出棱长为1cm的正方体有a个,切出棱长为2cm的正方体有b个,则有设切出棱长为1cm的正方体有a个,棱长为2cm的正方体有b个,棱长为3cm 的正方体有c个,则解之得a=36,b=9,c=4。
所以可切出棱长分别为1cm,2cm和3cm的正方体,其个数依次为36,9和4。
例12现有一个棱长为1cm的正方体,一个长宽为1cm高为2cm的长方体,三个长宽为1cm高为3cm的长方体。
下列图形是把这五个图形合并成某一立体图形时,从上面、前面、侧面所看到的图形。
试利用下面三个图形把合并成的立体图形(如例)的样子画出来,并求出其表面积。
例:解:立体图形的形状如下图所示。
从上面和下面看到的形状面积都为9cm2,共18cm2;从两个侧面看到的形状面积都为7cm2,共14cm2;从前面和后面看到的形状面积都为6cm2,共12cm2;隐藏着的面积有2cm2。
一共有18+16+12+2=46(cm2)。
练习81.一个长方体水箱,从里面量得长40cm,宽30cm,深35cm,里面的水深10cm。
放进一个棱长20cm的正方体铁块后,水面高多少厘米?2.王师傅将木块刨成横截面如下图(单位:cm)那样的高40cm的一个棱柱。
虚线把横截面分成大小两部分,较大的那部分的面积占整个底面的60%。
这个棱柱的体积是多少立方厘米?3.在底面为边长60cm的正方形的一个长方体的容器里,直立着一根高1m,底面为边长15cm的正方形的四棱柱铁棍。
这时容器里的水半米深。
现在把铁棍轻轻地向正上方提起24cm,露出水面的四棱柱铁棍浸湿部分长多少厘米?4.下列各图形中,有的是正方体的展开图,写出这些图形的编号。
5.小玲有两种不同形状的纸板,一种是正方形,一种是长方形。
正方形纸板的总数与长方形纸板的总数之比是1∶2。
她用这些纸板做成一些竖式和横式的无盖纸盒(如下图),正好将纸板用完。
在小玲所做的纸盒中,竖式纸盒的总数与横式纸盒的总数之比是多少?6.请你在下面图(2)中画出3种和图(1)不一样的设计图,使它们折起来后都成为右图所示的长方形盒子(直线段与各棱交于棱的中点)。
7.在桌面上摆有一些大小一样的正方体木块,从正南方向看如下左上图,从正东方向看如下右上图,要摆出这样的图形至多用多少块正方体木块?至少需要多少块正方体木块?8.有一个正方体,它的6个面被分别涂上了不同的颜色,并且在每个面上至少贴有一张纸条。
用不同的方法来摆放这个正方体,并从不同的角度拍下照片。
(1)洗出照片后,把所拍摄的面的颜色种类不同的照片全部挑选出来,最多可以选出多少张照片?(2)观察(1)中选出的照片,发现各张照片里的纸条数各不相同。
问:整个正方体最少贴有多少张纸条?练习8 答案:1.15cm。
