薄板方孔的有限元分析资料
开孔模板有限元分析

如图所示,一个长300 mm,宽80 mm,厚5 mm的平板,上边缘有一个半径为10 mm的半孔,板的两端受50N1、在DM模块建立如图所示的面向有限元分析的的实体模型;2、将实体模型导入DS模块中进行静力学求解,给出其总体的位移图、应力图、开孔截面上的正应力分布图等;将理论值与实际值相比较;3、,分析两个模型求解结果的不同,并将理论值与实际值相比较;4、要求熟悉仿真分析的基本步骤,学会结合力学知识对有限元计算结果进行分析。
解题步骤(模型1):1、启动ANSYS Workbench;2、在Toolbox下打开Component Systems,拖动Geometry至到右侧空白区域内;3、双击A2项,打开Design Modern界面,选择Millimeter单位,单击OK按钮;图1 选择单位制4、在XY平面创建模型,尺寸如图2所示,拉伸厚度为5mm;图2 模型的基本尺寸5、如图3所示,选中板的一个端面,单击新建平面Plane4,在明细窗口中设置如图4所示,单击Generate即生成平板的中心面;图3 中心面图4 明细窗口6、如图5所示,冻结模型(tools>freeze),在中心面处生成切片(create>slice),基准面选择Plane4;图5 冻结模型7、用鼠标直接拖住toolbox中的static structural至A2栏中,如图6所示,双击B4栏;图6 打开static structural模块8、设置单位制,选择units>metric(mm,kg,N,s,mV,mA);9、定义材料属性,点击左侧结构树中的geometry,在出现的2个solid中单击其中的一个,添加新材料:返回到project schematic窗口,再双击B2栏,如图7所示;图7 workbench材料库10、设置材料属性,相关设置如图8所示;图8 编辑材料属性11、返回到project,然后用鼠标左键选中B4栏并在右键弹出的快捷菜单中选中refresh;12、确定材料,点击左侧结构树中的geometry中的第一个solid,然后执行如图9所示步骤(material >assignment >steel);图9 确定材料13、划分网格,在mesh的明细栏窗口中设定element size为5mm,单击Generate生成如图10所示的网格;图10 网格划分14、施加约束和载荷,单击static structural,选择长方体的左侧面,用鼠标右键选择insert>fixed support,选择长方体右侧面,用鼠标右键选择insert>force,大小设定为50N,方向如图11所示;图11 约束和载荷15、求解,单击solution,在弹出的工具条deformation下选择totall查看总变形,stress下选择equivalent stress查看Von Mises等效应力;选择normal查看该面的正应力,单击Generate。
基于MARC的含圆孔正方形薄板四周受力性能的有限元分析报告

基于MARC的含圆孔正方形薄板四周受标题:针对含圆孔的正方形板四周受力性能的有限元分析摘要:采用通用的有限元程序MARC研究含圆孔的正方形板四周受力问题。
在工件工作时,小孔的边缘会产生应力集中的现象,极端情况下甚至会发生破坏,导致失效。
通过对该模型的分析,计算出其最大应力、最大位移及所发生的位置,得出其承载能力和变形特征,使该力学模型更好服务于建造等工程方面。
关键词:圆孔、正方形板、受均布力、最大应力、最大位移、位置、四分之一Title: hole for a square plate with four weeks of the force Finite Element AnalysisAbstract: In view of daily life, building structure, mechanical steel structure of the existence of multi-shaped plate with a circularhole is the mechanical model, its bearing capacity and designstudies and calculations of concern. In this paper, generalfinite element program MARC square hole of the plate four weekswith the force the issue. Through analysis of the model tocalculate the maximum stress, maximum displacement and thelocation of occurrence, reached its carrying capacity anddeformation characteristics. So that the mechanical model tobetter serve the construction and other projects.Keywords: round hole, square plate, force, maximum stress, maximum displacement, position, deformationcharacteristics,horizontal direction, vertical direction, aquarter正文1.引言:鉴于日常生活中建筑结构,机械钢架等结构中多存在含圆孔的正形板的力学模型,其承载性能和设计方法的研究和计算值得关注。
薄板弯曲问题有限元法

T
wl xl yl
Fzl M zl M yl T
j
xj
yj
wj
7
第8页/共24页
薄板弯曲时,只有w(x,y)是薄板变形的未知基本函数,而其它量,如u,v 等都是w(x,y)的函数,故薄板矩形单元的位移函数的选择实际就是w(x,y) 的选取。注意单元有12个自由度,则
w(x, y) 1 2x 3 y 4x2 5xy 6 y2
1 2
(w,
Ljj
w, Ljm
),
a5
1 2
(w,Lii
w, Lim
),
6
1 2
(w,Lii
w, Lij
w, Lji
w,Ljj
),
7
wj
wm
1 2 (w,Ljj
w, Ljm
)
8
wi
wm
1 2
(w,Lii
w, Lim
)
w,Lij 表示w对Li的 偏导数在j点的值。
9
wi
wj
1 2
(w,Lii
角形和矩形。为了使相邻单元间同时可传递力和力矩,节点当作刚性节点
,即节点处同时有节点力和节点力矩作用。每个节点有三个自由度,即一
个扰度和分别绕x,y轴的转角。 1.设位移函数
l
xl
yl wl
m
xm ym wm
节点位移分量和节点力分量
i
xi
yi
wi
q e wi xi yi F e Fzi M xi M yi
w(x, y) c1 c2 x c3x2 c4 x3
四个系数刚好通过i,j两个端点的扰度值和绕y轴的两个转角值唯一确定 ;同时,相邻单元在此边界上也能通过i,j的值唯一确定,故连续。
实验四薄板圆孔的有限元分析

(2) 生成一个圆孔 Main Menu>Preprocessor>Modeling>Create>Areas>Circle>Solid Circle,弹出如图所示的 【Solid Circular Area】对话框。分别在【WP X】、【WP Y】和【Radius】文本框中输入“0”、 “0”、“5”。单击 OK 按钮,生成结果如下左图所示。 (3) 执行面相减操作 Main Menu>Preprocessor>Modeling>Operate>Booleans>Subtract>Areas,弹出一个拾取 框。拾取编号为 A1 的面,单击 OK 按钮。然后拾取编号为 A2 的圆面,单击 OK 按钮。生 成结果如下右图所示。
泊松比=0.3 拉伸载荷:
P=1000Pa 几何参数:
平板厚度 t=0.1m。 单元类型:
Structural Solid Quad 8node 82 1. 定义工作文件名和工作标题 (1) 定义工作文件名 Utility Menu>File>Change Jobname,输入文件名,选择【New log and error files】复选框, 单击 OK 按钮。 (2) 定义工作标题 Utility Menu>File>Change Title,输入工作标题,单击 OK。 (3) 重新显示 Utility Menu>Plot>Replot (4) 关闭三角坐标符号 Utility Menu>PlotCtrls>Window Controls>Window Options,弹出【Windows Options】对
单击 Add 按钮,弹出如图所示的【Library of Element Types】对话框。选择“Structural Solid” 和“Quad 8node 82”选项,单击 OK 按钮,然后单击 Close 按钮。
薄板方孔的有限元分析.
2012 级系专业学号学生姓名指导教师完成日期2014年7月16日摘要ANSYS是目前在工业上常使用的计算机辅助分析软件包。
当物体的模型在软件中建立完成并网格化后,只需附加适当的条件,即可直接利用有限元素法来计算,进而了解所建立的模型或产品的特性。
本课题以含一个方孔的薄板为研究对象,利用ANSYS软件,对其内力分布进行了研究与分析[2]。
首先,设置单元类型、材料性质等,并建立薄板的实体模型,然后建立出相应的三维模型,对薄板进行划分网格,再对该模型设置边界条件、施加约束,最后进行求解,就可以得到薄板分布图、变形图、应力云图。
设计工程师可在计算机上模拟物体在收到外力影响后所产生的应力及应变情形,从所分析出来的特性数据中,可判断出此产品设计的可行性[1]。
本文结果在将来的工程中也具有一定的参考价值。
关键词:ANSYS 薄板应力图均布力有限元目录第1章绪论 (1)1.1课题研究的背景和意义 (1)1.2ANSYS软件的初步了解 (1)1.2.1前处理模块PREP7 (1)1.2.2 分析计算模块SOLUTION (1)1.2.3 后处理模块POST1和POST26 (2)ANSYS软件的后处理过程包括两个部分:通用后处理模块POST1和时间历程后处理模块POST26。
通过有好的用户界面,可以很容易获得求解过程的计算结果并对其进行显示。
这些结果可能包括位移、温度、应力、应变、速度以及热流等,输出形式可以有图形显示和数据列表两种[5]。
(2)第2章论文研究的内容和过程 (3)2.1主要研究内容 (3)2.2ANSYS内力分析过程 (3)2.2.1 建立薄板的有限元 (3)2.2.2 ANSYS求解器:施加荷载并执行求解 (4)第3章创新扩展 (5)第4章心得体会 (11)参考文献 (12)第1章绪论1.1课题研究的背景和意义简支T字梁是比较基础也是比较常见的模型,因此,对其在承受各种荷载的情形下,进行正确的应力和应变分析都是十分有必要和有意义的,在实际工程更为复杂的情况下,也可以简化成熟悉的模型,便于工程师分析该工程的实用性。
ANSYS 有限元分析 平面薄板

v1.0 可编辑可修改《有限元基础教程》作业二:平面薄板的有限元分析班级:机自101202班 姓名:韩晓峰 学号:0210一.问题描述:P Ph1mm R1mm10m m 10mm条件:上图所示为一个承受拉伸的正方形板,长度和宽度均为10mm ,厚度为h 为1mm ,中心圆的半径R 为1mm 。
已知材料属性为弹性模量E=1MPa ,泊松比为,拉伸的均布载荷q =1N/mm 2。
根据平板结构的对称性,只需分析其中的二分之一即可,简化模型如上右图所示。
二.求解过程:1 进入ANSYS程序 →ANSYS →ANSYS Product Launcher →File management →input job name: ZY2→Run2设置计算类型ANSYS Main Menu: Preferences →select Structural → OK3选择单元类型ANSYS Main Menu: Preprocessor →Element Type →Add/Edit/Delete →Add →selectSolid Quad 4node 42 →OK → Options… →select K3: Plane Strs w/thk →OK →Close 4定义材料参数ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural→Linear →Elastic →Isotropic →input EX: 1e6, PRXY: → OK5定义实常数以及确定平面问题的厚度ANSYS Main Menu: Preprocessor →Real Constants …→Add/Edit/Delete →Add →Type 1→OK →Real Constant Set ,THK:1→OK →Close6生成几何模型a 生成平面方板ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Rectangle →By 2 Corners →WP X:0,WP Y:0,Width:5,Height:5→OKb 生成圆孔平面ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Circle →Solid Circle→WPX=0,WPY=0,RADIUS=1→OKb 生成带孔板ANSYS Main Menu: Preprocessor →Modeling→Operate →Booleans → Subtract →Areas →点击area1→OK→点击area2→OK7 网格划分ANSYS Main Menu: Preprocessor →Meshing →Mesh Tool→(Size Controls) Global: Set →SIZE: →OK →iMesh →Pick All → Close8 模型施加约束a 分别给左边施加x和y方向的约束ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Displacement → On lines →拾取左侧边→OK →select UX,UY→ OKb 给斜边施加x方向均布载荷Main Menu: Solution →Define Loads →Apply →Structural →Pressure →On Lines →拾取右侧边;OK →VALUE:-10→OK9 分析计算ANSYS Main Menu: Solution →Solve →Current LS →OK→Close10 结果显示ANSYS Main Menu: General Postproc →Plot Results →Deformed Shape…→ select Def + Undeformed →OK→Contour Plot →Nodal Solu…→select: DOF solution, Displacement vector sum, Def + Undeformed , Stress ,von Mises stress, Def +v1.0 可编辑可修改Undeformed→OK11显示整体效果Utility Menu→PlotCtrls→Style>Symmetry Expansion>Periodic/Cyclic Symmetry Expansion→1/4Dihedral Sym→OK10 退出系统ANSYS Utility Menu: File→Exit…→ Save Everything→OK三.结果分析:图1 建模、网格划分、加载图图2 变形图图3 整体应力。
薄板有限元分析-FEM 作业
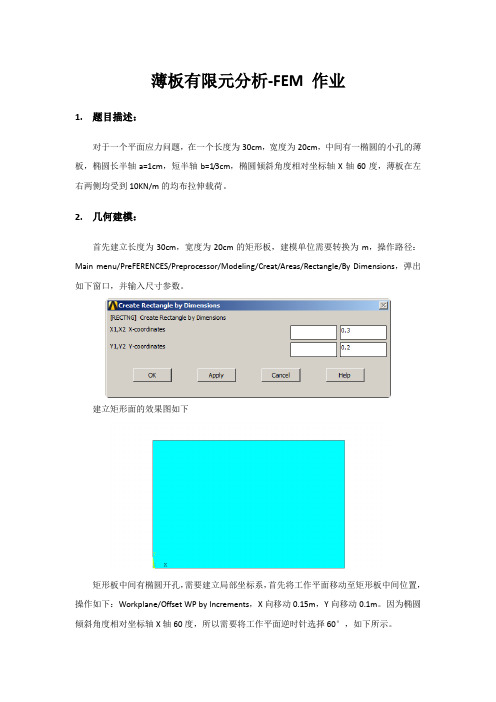
薄板有限元分析-FEM 作业1.题目描述:对于一个平面应力问题,在一个长度为30cm,宽度为20cm,中间有一椭圆的小孔的薄板,椭圆长半轴a=1cm,短半轴b=1/3cm,椭圆倾斜角度相对坐标轴X轴60度,薄板在左右两侧均受到10KN/m的均布拉伸载荷。
2.几何建模:首先建立长度为30cm,宽度为20cm的矩形板,建模单位需要转换为m,操作路径:Main menu/PreFERENCES/Preprocessor/Modeling/Creat/Areas/Rectangle/By Dimensions,弹出如下窗口,并输入尺寸参数。
建立矩形面的效果图如下矩形板中间有椭圆开孔,需要建立局部坐标系,首先将工作平面移动至矩形板中间位置,操作如下:Workplane/Offset WP by Increments,X向移动0.15m,Y向移动0.1m。
因为椭圆倾斜角度相对坐标轴X轴60度,所以需要将工作平面逆时针选择60°,如下所示。
在平面中间建立柱坐标系。
操作如下:Workplane/Local Coordinate System/Create Local CS/At WP Origin。
弹出如下菜单,设置坐标系类型为Cylindrical 1,点击OK。
其中Par1输入1/3,表示b=1/3分别通过关键点建立,建立椭圆的两个端点,坐标分别为(0.1,0,0)、(-0.01,0,0),关键点建立的操作路径如下:Main menu/PreFERENCES/Preprocessor/Modeling/Creat/ Keypoints/In Actice CS。
然后在当前坐标系下连接这两个关键点。
操作路径:Main menu/PreFERENCES/Preprocessor/Modeling/Creat/lines/In Active Coord,弹出对话框,分别拾取上述两个节点,点击OK完成建模,如下所示。
有限元分析薄板挠度(附C程序)

1问题描述某周边简支非均匀的矩形(或圆形)板在均布载荷作用下挠度过大。
结合实际,提出集中改进设计方案,并进行对比分析。
2.问题分析不均匀板有两种主要的情况,结构不均匀和材料不均匀,结构不均匀是指板的厚度不是常量,材料不均匀体现在板的弹性模量和泊松比是变化的。
另外,有的板可以是以上两种情况的混合情形。
不均匀板与均匀板的有限元问题有哪些差别呢?下面从均匀板问题推导出非均匀板有限元问题的解决方法。
2.1应力应变先以结构不均匀板为例来讨论。
假设一矩形板长为2,宽为2,厚度沿x ,y 不均匀,由一函数()h ,h x y =描述,但仍然符合薄板假设。
对于均匀板,显然h 是一个常数。
设挠度为()=x,y ωω,则板内应变向量可以表示为{}2222211==z 12x x y y xy xy x z y x y ρεεεωεγγ⎧⎫⎧⎫∂⎪⎪⎪⎪∂⎪⎪⎪⎪⎧⎫⎪⎪⎪⎪∂⎪⎪⎪⎪⎪⎪=-⎨⎬⎨⎬⎨⎬∂⎪⎪⎪⎪⎪⎪⎩⎭⎪⎪⎪⎪∂⎪⎪⎪⎪∂∂⎪⎪⎪⎪⎩⎭⎩⎭应力应变关系为{}1p z D σρ⎧⎫⎡⎤=⎨⎬⎣⎦⎩⎭弯矩扭矩矩阵{}{}()()h ,2h ,2x y x y M zdz σ-=⎰这里就体现出不均匀板和均匀板的区别了。
积分完毕后,可以得到{}[]1M D ρ⎧⎫=⎨⎬⎩⎭其中薄板的弯曲系数矩阵[]()()()321,1012101/2Eh x y D μμμμ⎡⎤⎢⎥=⎢⎥-⎢⎥-⎣⎦是关于薄板总体坐标的函数,所以对各个分单元都是不同的。
各单元的弯曲系数矩阵可以采用单元中心处的代替。
那么就可以得出一系列的弯曲系数矩阵[]D ei 。
如果单元划分得足够细,是可以代替真实解的。
2.2单元分析可以将板分为边长为0.25的矩形小单元,每一个单元都是一样的。
对于任何一个单元的节点,都有3项独立的位移{}i i i xi i yi i w w w y w x δθθ⎧⎫⎪⎪⎪⎪⎧⎫⎪⎪⎛⎫∂⎪⎪⎪⎪==⎨⎬⎨⎬⎪∂⎝⎭⎪⎪⎪⎪⎩⎭⎪⎪∂⎛⎫⎪⎪- ⎪∂⎪⎪⎝⎭⎩⎭位移模式()22312345672233389101112,w x y x y x xy y x x y xy y x y xy αααααααααααα=+++++++++++形状函数矩阵是一个112⨯的行向量()[],kl mn N x y N N N N =⎡⎤⎣⎦其中222222222222222211128111111i i i i i i i i i i i i i x x y y x x y y x y N a b a b a b x x y y y y x x y y x x y x a b b a b a ⎛⎫⎡⎛⎫⎛⎫=++++--⎡⎤ ⎪⎪⎪⎣⎦⎢⎝⎭⎝⎭⎣⎝⎭⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++--++-⎥ ⎪⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎥⎦(),,,i k l m n =单元刚度矩阵[][][][]1212ee TS k B D B dxdy ⨯=⎰很明显,积分式中包含了弹性系数矩阵,而不同单元的弹性系数矩阵是不同的,所以,即便单元划分相同,得到的单元刚度矩阵也不同。
四边固支矩形薄板固有振动的理论计算和有限元分析

四边固支矩形薄板固有振动的理论计算和有限元分析四边固支矩形薄板是一种典型的结构,其固有振动特性的计算对于结构的稳定性以及对外载荷的响应有着重要的影响。
本文将从理论计算和有限元分析两个方面来探讨四边固支矩形薄板的固有振动特性。
一、理论计算在理论计算中,四边固支矩形薄板的固有振动频率可以通过以下公式进行计算:f_n = (C_n^2 + D_n^2)^0.5 / (2πt)^0.5 * (EH^3/12ρ(1-μ^2)),其中,f_n为第n阶固有频率;C_n和D_n分别为第n阶水平和竖直模态振型的振幅比;t为薄板厚度;E为材料的弹性模量;H为矩形薄板的一侧长度;ρ为材料的密度;μ为材料的泊松比。
根据上述公式,我们可以对四边固支矩形薄板进行理论计算,得出其固有振动频率,并根据振动模型分析结构的稳定性以及响应能力。
二、有限元分析在有限元分析中,我们可以通过建立合适的有限元模型,利用求解振型特征值和振型模态来得出四边固支矩形薄板的固有振动特性。
有限元分析的主要步骤包括:1.建立有限元模型:根据实际结构情况,选择合适的有限元支撑和单元类型,对结构进行离散化网格化处理,建立结构有限元模型。
2.确定边界条件:对于固支矩形薄板,边界条件为四边界固定支撑。
3.求解特征值和振型:对于固有振动频率,我们可以通过求解振型特征值和振型模态来得出。
4.分析特征值和振型:得出固有振动频率,我们可以进一步分析与理论计算结果的一致性,同时还可以分析振型特征值与振型模态,进一步了解结构的稳定性和响应能力。
通过有限元分析,我们可以更加精确地了解四边固支矩形薄板的固有振动特性,为结构设计和应用提供更加实际的参考依据。
总之,四边固支矩形薄板的固有振动特性对于结构稳定性和响应能力有着重要的影响。
通过理论计算和有限元分析两个方面的探讨,我们可以更好地理解并应用这一结构特性。
为了更加深入地了解四边固支矩形薄板的固有振动特性,我们可以从以下几个方面进行数据的收集和分析:1. 材料弹性模量与密度:材料的弹性模量和密度直接影响到四边固支矩形薄板的固有振动频率。
薄板有限元分析

板中圆孔的应力集中问题:如图所示为一个承受单向拉伸的无限大板,在其中心位置有一个小圆孔。
材料属性为弹性模量E= Pa泊松比为0.3,拉伸载荷q=1000Pa平板厚度t=0.1.201、定义工作名和工作标题(1)定义工作文件名:在弹出的Cha nge Job name对话框中输入Plate。
选择New log and error files复选框,单击OK按钮。
(2)定义工作标题:在弹出的的Change Title对话框中输入The analysis of plate stress with small circle单击OK按钮。
(3)重新显示:执行replot命令。
2、定义单元类型和材料属性(1)选择单元类型:在弹出的Element Type中,单击Add按钮,弹出所示对话框,选择Structural Solid 和Quad 8node 82选项,单击OK ,然后 单击close 。
(2) 设置材料属性:在弹出的 defi ne material models behavior 窗口中,双 击 structural/linear/elastic/isotropic 选项,弹出 linear isotropic material properties for material number 1 对话框,EX 和 PRXY 分别输入 2e11 和0.3,单击OK,执行exit 命令Lintar Isotropic f^lattrial Proptrtits for f^lattrial Numbtr 1Add Temperature Delete Temperature□K(3)保存数据:单击SAVE_DB 按钮。
3、创建几何模型PRXYCancel Linejr Isotropic Properties for Material Nuinbcr 1T1Help(1)生成一个矩形面:执行相应操作弹出create recta ngle by dime nsio ns对话框,输入数据,单击OK,显示一个矩形。
开孔薄板有限元分析报告

开孔薄板有限元分析报告一、有限元分析的目的通过对两种模型(一个上边开口的和另一个上下两边开口的模型)的静力分析,比较与其对应的理论解的不同,了解有限元仿真软件与理论计算存在的,进一步熟悉workbench求解有限元问题的一般步骤。
二、实体建模(两个模型)建立如下所示的模型,其中,边长300mm,宽80mm,厚5mm,边缘为半径是10mm的半孔。
上边开口的实体模型(模型A)上下两边开口的模型(模型B)模型A模型B模型采用的单元类型模型A:1 3862 LID186 (20 Node Quadratic Hexahedron)2 3858 SOLID186 (20 Node Quadratic Wedge)3 112 CONTA174 (Quadratic Quadrilateral Contact)4 112 TARGE170 (Quadratic Quadrilateral Target)5 64 SURF154 (3D Quadratic Quadrilateral)模型B:1 3856 SOLID186 (20 Node Quadratic Hexahedron)2 3866 SOLID186 (20 Node Quadratic Wedge)3 100 CONTA174 (Quadratic Quadrilateral Contact)4 100 TARGE170 (Quadratic Quadrilateral Target)5 64 SURF154 (3D Quadratic Quadrilateral)2.载荷与约束的施加方法(绘图表示并说明);两模型施加的载荷与约束相同约束:单击static structural,选择长方体的左侧面,鼠标右键选择“insert>fixed support”载荷:选择长方体的左侧面,鼠标右键选择“insert>force”,大小为50N。
10.2 薄板问题的有限元法

薄板拟协调元与广义协 调元 ∂ w ∂ w ∂ w
(ε) =
w2
2 2 2
∂x
2
∂y
2
( q ) = w1
w3
∂w ∂n 12
∂x∂y T ∂w ∂w ∂n 23 ∂n 31 2
3 ∂w
薄板拟协调元与广义协 调元 同样为了解决协调性问题, 同样为了解决协调性问题,龙驭球院士提出了广义协
调元,在其《新型有限元论》中介绍了大量广义协调单 调元,在其《新型有限元论》 元, 下面就其基本思想作一介绍 。
广义协调元与常规位移元的作法差别很小, 广义协调元与常规位移元的作法差别很小, 以广义坐标法建立单元位移模式为例, 以广义坐标法建立单元位移模式为例,仅是在 确定广义坐标上有所不同。 确定广义坐标上有所不同。 薄板常规位移元的作法: 1) 薄板常规位移元的作法: ) 第一步,选定单元结点位移向量, 第一步,选定单元结点位移向量,并构造单元位 移场(挠度)的多项式: 移场(挠度)的多项式: 位移模式 2 2 w = a1 + a2 x + a3 y + a4 x + a5 xy + a6 y + L = Fa
y
θy1
x 3
1、直角坐标系下的位移模式方案
z
w1 2
三角形单元有9个结点位移, 三角形单元有9个结点位移, 由帕斯卡三角形 可知,要达到完整三次多项式要10 10项 可知,要达到完整三次多项式要10项,而舍去 任意一三次项将无法保证坐标不变性。 任意一三次项将无法保证坐标不变性。 监克维奇) 2、 Zienkiewicz(监克维奇)提出了面积坐标位 移模式
薄板弯曲问题的有限元分析

变分原理与有限元素法课程报告报告名称:薄板弯曲问题的有限元分析姓名:学号:导师:专业:2015.5.15目录1.问题描述 (3)2.理论基础 (3)2.1矩形薄板弯曲单元 (3)2.1.1挠度函数 (3)2.1.2单元刚度矩阵 (5)2.2四边简支矩形板的纳维叶解法 (5)3.有限元模型 (6)4.结果与分析 (7)4.1均布载荷作用下四边简支板 (7)4.2集中载荷作用下四边简支板 (8)4.2均布载荷作用下四边固支板 (9)4.2集中载荷作用下四边固支板 (10)4.5总结 (11)1.问题描述一块方板,边长为L,厚度为t(51/801≤≤t L ),材料为铝,分别用不同密度的四节点12个自由度的矩形单元来划分网格。
要求:考虑四边简支和四边固支两种边界情况,分别计算受均匀载荷q 和在板中心处受集中载荷P 两种载荷情况下,板的中心挠度max ω(不超过板厚t 的1/5),进而计算出不同情况下的方板的中心挠度系数;将计算出的系数与精确解进行比较,通过比较发现不同有限元网格密度对薄板弯曲问题计算结果的影响。
本例中,方板边长L=40mm,厚度t=1mm,铝的弹性模量E=70GPa,泊松比3.0=μ,粗略计算当q=0.1MPa 或者P=50N 时,板中心挠度小于板厚的1/5,属于小挠度弯曲,因此载荷可取这两个值。
2.理论基础2.1矩形薄板弯曲单元2.1.1挠度函数薄板弯曲单元中比较简单的是四节点12个自由度的矩形单元,将矩形薄板沿坐标方向划分为若干矩形单元,如图1所示,每个单元设有四个节点,每个节点位移有三个分量:挠度w,绕x 轴的转角y w x ∂∂=/θ,绕y 轴的转角x w y ∂-∂=/θ,即)4,3,2,1()/()/(}{=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∂∂-∂∂=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=i x w y w w w i i i yi xi i i ϕϕδ图1单元的节点位移为TT T T Te ]}{}{}{}{[}{4321δδδδδ=节点荷载为)4,3,2,1(}{=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=i M M V F yi xi i i 单元的节点荷载为TT T T Te F F F F F ]}{}{}{}{[}{4321=取位移函数为31231131029283726524321xy y x y xy y x x y xy x y x w αααααααααααα+++++++++++=在位移函数中,前三项包含了单元的刚体位移状态,二次项代表了单元的均匀应变状态。
带孔平板的有限元分析

二、带孔平板的有限元分析1:问题描述图所示为一个有中心圆孔的薄板,薄板厚度t=0.01m,薄板弹性模量E=210000N/cm2,泊松比μ=0.3,p=100N/cm,ρ=2.7g/cm3此问题为平面应力问题,用有限元求解出带孔平板的应力集中问题,并与弹性力学的精确解进行比较。
2:求解步骤第一步:建立工作文件名和工作标题(1)选择Utility Menu—File—Change Jobname命令,出现Change Jobname对话框。
在Enter new jobname 输入栏中输入工作文件名plate,单击Ok按钮关闭该对话框。
(2)选择Utility Menu—File—Change Tile命令,出现Change Tile对话框,在输入栏中输入Stress analysis in a sheet,单击Ok按钮关闭该对话框。
第二步:设置计算类型选择Main Menu—Preference—Structural-Ok命令.第三步:选择单元类型选择Main Menu—Preprocessor—Element Type—Add/Edit/Delete命令,出现Element Type对话框,选择Solid-Quad 4node 42—Ok命令,再在Element Type对话框中选择Options—K3:Plane Strs w/thk/—Ok—Close命令.第四步:定义材料参数选择Main Menu—Preprocessor—Material Props—Material Models—双击Structural—双击Linear—双击Elastic—双击Isotropic命令,出现如下对话框填写Ex:2.1e5,PRXY:0.3;选择Ok命令。
第五步:定义实常数以确定平面问题的厚度选择Main Menu—Preprocessor—Real condtants—Add/Edit/Delete—Add—Type1—Ok命令,出现以下对话框,在Real condtant Set No中填写1,在THK中填写1,选择Ok—Close命令.第六步:创建几何模型1:生成平面方板选择Main Menu—Preprocessor—Modeling—Creating—Areas—Rectangle—By 2 Corners—Wp X:0, Wp Y:0,Width:100,Height:100—Ok1:生成圆孔平面选择Main Menu—Preprocessor—Modeling—Creating—Areas—Circle—Solid Circle—Wp X:50, Wp Y:50,Radis:5—Ok2:生成带孔方板选择Main Menu—Preprocessor—Modeling—Operate—Booleana—Subtract—Areas,鼠标点击方板1—Ok,在Multi-Entities窗口点击Ok,在Subtract Areas窗口点击Ok.. 鼠标点击圆孔2—Ok, 在Multi-Entities窗口点击Ok,在Subtract Areas窗口点击Ok.出现如下图1:第七步:网格划分选择Main Menu—Preprocessor—Meshing—MeshTool命令,在MeshTool窗口点击Size Controls下的Globle:Set—NDIV:29—Ok, 在MeshTool窗口点击Mesh—Pick all—Close命令。
有限元分析及理论上机报告

有限元分析及理论上机报告报告(一)Demo7 stress一、问题描述一个承受拉力的平板,在其中心位置有一个小圆孔,其结构尺寸如下图所示,要求分析其结构圆孔处的Mises应力分布。
材料特性:弹性模量E = 210000 MPa,泊松比 =0.3拉伸载荷:P=100MPa平板厚度:d=1mm二、方法概述,建模思路和分析策略1由于薄板只在边缘上受到了平行于板面的并沿厚度均匀分布的力,所以平板处于平面应力状态。
在创建部件(Part)时,薄板的模型所在空间(Space)设置为(2D Planer),绘制图形。
2由于该平板受力模型的结构和载荷是对称的,所以,可以取用模型的1/4进行分析。
其图形如下所示。
3材料为线弹性材料,其材料属性设置为Elasticity中的Elastic,设置其弹性模量(E=210000MPa)和泊松比( =0.3)。
薄板属于实体,其截面属性种类为实体(Solid),然后赋予其截面属性。
4由薄板的受力情况和分析要求可知,薄板的应力分析为线性/非线性的静力学分析,所以其分析步的类型为Static、General,不用考虑几何非线性(NLgeom>off)。
5模型所受的载荷为均布压力,使用载荷类型为(pressure)。
由于模型的对称,所以对模型的左侧和底部的边界线设置边界条件,固定边界。
由受力分析结果可得:左侧边界为XSYMM,底部边界为YSYMM。
6中心圆孔处为应力集中区域,且为分析结果要求重点,应局部网格加密。
划分网格,然后提交分析。
三、分析过程中遇到的问题及解决方法分析过程中没有遇到什么问题,但是需要注意几个方面。
1、在定义截面属性时,应注意的是平面应力分析问题的截面属性不是shell,而应该是solide(实体)。
其次注意平面的厚度。
一会吧其次,边界条件应该在分析步的第一步(initial)里添加,否则会导致有限元分析的失败。
载荷的添加应该是在第二步,注意载荷的方向为由里向外—100 三,由于取用的是板子的1/4作为分析的模型,所以将边界条件固定来模仿相应的应力情况,即固定相应边的XY方向上的坐标。
ANSYS有限元分析平面薄板

ANSYS有限元分析平面薄板ANSYS是全球领先的工程仿真软件公司,提供一系列强大的有限元分析工具,用于解决各种工程问题。
在工程设计中,平面薄板的有限元分析是一项非常重要的工作,可以帮助工程师了解结构的强度和稳定性,优化设计方案,提高产品性能和安全性。
平面薄板是一种常见的结构,广泛应用于建筑、航空航天、汽车、船舶等领域。
在设计和分析平面薄板时,工程师通常需要考虑多个因素,如外载荷、边界条件、材料性能等。
有限元分析可以有效地模拟这些复杂情况,帮助工程师预测结构的行为和性能。
在使用ANSYS进行平面薄板的有限元分析时,通常需要按照以下步骤进行:1.几何建模:首先需要使用ANSYS的几何建模工具创建平面薄板的几何模型。
可以选择不同的几何形状和尺寸,以满足设计要求。
2.网格划分:接下来需要对几何模型进行网格划分,将其分割成小的单元,以便进行有限元分析。
网格的划分对分析结果的准确性和计算效率有着重要影响,需要进行适当的网格优化。
3.材料定义:在进行有限元分析之前,需要定义平面薄板的材料性能,如弹性模量、屈服强度、密度等。
在ANSYS中可以选择不同的材料模型,如线弹性、非线性弹性等。
4.加载和边界条件:根据设计要求和实际工况,设定平面薄板的外载荷和边界条件。
可以对板材施加不同的力、压力、温度等载荷,以模拟实际工作环境。
5.分析求解:进行有限元分析求解,计算平面薄板在给定载荷下的应力、应变、变形等物理量。
可以通过不同的分析类型,如静力分析、动力分析、热力分析等,获取不同的结构响应。
6.结果后处理:分析求解完成后,需要对结果进行后处理,查看和分析平面薄板的应力分布、变形情况、破坏状态等。
通过可视化工具和图表,可以直观地了解结构的性能和问题。
通过以上步骤,工程师可以利用ANSYS进行平面薄板的有限元分析,评估结构的稳定性和安全性,优化设计方案,提高产品性能和寿命。
有限元分析是一种强大的工程设计工具,可以为工程师提供准确、可靠的数值模拟结果,帮助他们做出更好的决策。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012 级系
专业
学号
学生姓名
指导教师
完成日期2014年7月16日
摘要
ANSYS是目前在工业上常使用的计算机辅助分析软件包。
当物体的模型在软件中建立完成并网格化后,只需附加适当的条件,即可直接利用有限元素法来计算,进而了解所建立的模型或产品的特性。
本课题以含一个方孔的薄板为研究对象,利用ANSYS软件,对其内力分布进行了研究与分析[2]。
首先,设置单元类型、材料性质等,并建立薄板的实体模型,然后建立出相应的三维模型,对薄板进行划分网格,再对该模型设置边界条件、施加约束,最后进行求解,就可以得到薄板分布图、变形图、应力云图。
设计工程师可在计算机上模拟物体在收到外力影响后所产生的应力及应变情形,从所分析出来的特性数据中,可判断出此产品设计的可行性[1]。
本文结果在将来的工程中也具有一定的参考价值。
关键词:ANSYS 薄板应力图均布力有限元
目录
第1章绪论 (1)
1.1课题研究的背景和意义 (1)
1.2ANSYS软件的初步了解 (1)
1.2.1前处理模块PREP7 (1)
1.2.2 分析计算模块SOLUTION (1)
1.2.3 后处理模块POST1和POST26 (2)
ANSYS软件的后处理过程包括两个部分:通用后处理模块POST1和时间历程后处理模块POST26。
通过有好的用户界面,可以很容易获得求解过程的计算结果并对其进行显示。
这些结果可能包括位移、温度、应力、应变、速度以及热流等,输出形式可以有图形显示和数据列表两种[5]。
(2)
第2章论文研究的内容和过程 (3)
2.1主要研究内容 (3)
2.2ANSYS内力分析过程 (3)
2.2.1 建立薄板的有限元 (3)
2.2.2 ANSYS求解器:施加荷载并执行求解 (4)
第3章创新扩展 (5)
第4章心得体会 (11)
参考文献 (12)
第1章绪论
1.1课题研究的背景和意义
简支T字梁是比较基础也是比较常见的模型,因此,对其在承受各种荷载的情形下,进行正确的应力和应变分析都是十分有必要和有意义的,在实际工程更为复杂的情况下,也可以简化成熟悉的模型,便于工程师分析该工程的实用性。
但是随着现在长大桥梁或其他大规模工程的发展,梁施工质量的进一步要求,单纯的依靠理论计算不仅计算强度大,而且观察其变形、受力等情况不太明显[3]。
在这种情况下如迈达斯、ANSYS等一些数值模拟软件相应的发展了起来。
根据前人对梁模型受力情况的研究以及梁数值建模时的简化方法和参数选取,综合分析,本课题采用ANSYS有限元数值模拟来进行研究。
通过ANSYS 可以很直观的看出并读出梁结构各处的应变、应力分布,确定危险段,以及读出危险段数值是否满足设计要求。
方便、直观、简单、快捷、准确,对于实际施工时预先处理,防止不必要损失,提前预防,保证施工过程及使用过程的安全性具有重要意义[4]。
1.2 ANSYS软件的初步了解
ANSYS软件主要包括前处理模块、分析计算模块和后处理模块三个部分。
1.2.1前处理模块PREPROCESSOR
前处理模块主要有两部分内容:实体建模和网格划分。
1.2.2 分析计算模块SOLUTION
前处理完成后,用户可以在求解阶段获得分析结果。
在此阶段,可以定义分析类型、分析选项、荷载数据和荷载步选项,然后进行求解。
1.2.3 后处理模块GENERAL POSTPROC
ANSYS软件的后处理过程:通过用户界面,可以很容易获得求解过程的计算结果并对其进行显示。
这些结果可能包括位移、温度、应力、应变、速度以及热流等,输出形式可以有图形显示和数据列表两种[5]。
第2章论文研究的内容和过程
2.1 主要研究内容
本章以含一个方孔的薄板为工程实例进行应力分析,主要参数如下:板长2mm,宽0.6mm,厚0.02mm,弹性模量2E+10MPa,泊松比0.3。
2.2ANSYS内力分析过程
2.2.1 建立薄板的有限元
1. 设置工作名称和图形标题
Utility Menu>File>Change Jobname,制定分析的工作名称为Banfangkong;
Utility Menu>File>Change Title,指定图形显示区域的标题为BFK。
2.设置计算类型
ANSYS Main Menu: Preferences →select Structural →ok
3.选择计算类型
ANSYS Main Menu: Preprocessor →Element Type→Add/Edit/Delete… →Add… →select solid 2 node65 →OK (back to Element Types window) →Close (the Element Type window)
4.定义材料参数
ANSYS Main Menu:Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →input EX:2 e11, PRXY:0.3 →OK
5.创建薄板
ANSYS Main Menu: Preprocessor →Sections →Modeling→Create→V olumes →Block→By Dimensions 输入坐标(0,0,0),(2,0.6,0.02)
ANSYS Main Menu: Preprocessor →Sections →Modeling→Create→V olumes →Block→By Dimensions 输入坐标(0.975,0.275,0),(1.025,0.325,0.02)(方孔宽0.05)ANSYS Main Menu: Preprocessor →Sections →Modeling→Opreate→Booleans →Subtract→V olumes→pick v1→OK→pick v2→OK
6.划分网格调
SIZE,0.06
MSHAPE,1,3D
MSHKEY,0
vmesh,all
DA,5,ALL,
2.2.2 ANSYS求解器:施加荷载并执行求解
7.模型施加约束
✓最左端加约束
ANSYS Main Menu:Solution →Define Loads →Apply →Structural →Displacement →On Area →pick →OK
✓施加y方向的载荷
ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Pressure →On Area →Pick All →V ALI:100 →OK
8.分析计算
ANSYS Main Menu: Solution →Solve →Current LS →OK(to close the solve Current Load Step window) →OK
9.结果显示
ANSYS Main Menu: General Postproc →Plot Results →Deformed Shape…
→select Def + Undeformed →OK得变形图
Solu →Nodal Solution>Stress>von Mises stress点击OK得应力云图
ANSYS Main Menu: General Postproc→Plot Results →Contour Plot →Nodal Solu
MN MX X
Y
Z SMX =.606E-06
第3章创新扩展
不同大小方孔比较
方孔边长为0.1
网格划分图
应力图
变形图
应力云图
方孔边长为0.2 网格划分图
应力图
变形图
应力云图
第4章心得体会
参考文献
[1] 张向东. 隧道力学[M]. 江苏: 中国矿业大学出版社, 2010
[2] 谭上俞, 肖盛燮, 陶庆东. 城市下穿式矩形框架隧道的力学分析[J]. 西部交通科技, 2011,
(11): 35-37
[3] 李建平. 盾构隧道混凝土管片受力分析[J]. 山西建筑, 2012, 38(24): 189-190
[4] Mroueh H, Shahrour I. A simplified 3D model for tunnel construction using tunnel boring
machines[J]. Tunnelling and Underground Space, 2008, (23): 38-45
[5] Youakim S A S. Nonlinear analysis of tunnels in clayey/sandy soil with a concrete lining[J].
Engineering Structures, 2000, (22): 701-722。
