组合截面惯性矩
截面的几何性质面积矩惯性矩惯性积平行移轴公式

注意平方问题
第十六次课结束处
§A-3 惯性矩和惯性积的平行移轴公式
一、平行移轴公式
O
z
Iz=∫ A y2dA =∫ A(a+yC)2dA =∫ Aa2dA + 2a∫ A yCdA +∫ A yC2dA
y
C
dA
a zc
yc
∫ A yCdA 对形心轴的面积矩=0
b zc z
∫ A yC2dA 对形心轴的惯性矩
y yc
故 Iz=∫ A a2dA + IzC
同理
Iy=∫ A b2dA + IyC Iyz=∫ A abdA + IyCzC
二、组合截面惯性矩的计算式
Iy=∫ A z2dA
=∫ A1z2dA +… +∫ Anz2dA
n
= ∑ Iyi
i=1
同理
n
Iz = ∑ Izi
i=1
n
Iyz = ∑ Iyzi
i=1
例5 图示矩形中,挖去两个直径为d 的圆形,求余 下图形对z轴的惯性矩。
b/2 b/2
z
Iz
1 12
bh3
5 d 4
32
y
例6 由两个20a号槽钢截面图形组成的组合平面图形,设 a =100mm,设求此组合平面图形对y,z两根对称轴的惯性矩。
a
z0
z
zC
y
yC
A=28.83×102mm2, Iyc=128×104mm4 Izc=1780.4×104mm4 ,z0=20.1mm
附录A 截面的几何性质
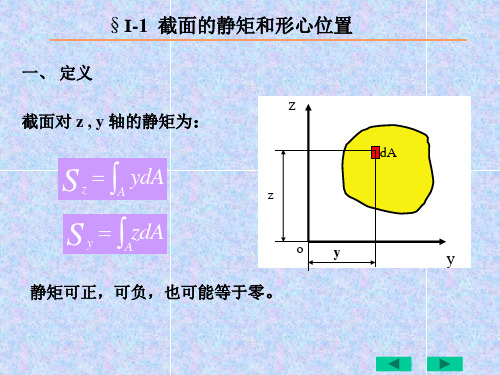
§A-1 截面的面积矩和形心位置
一、面积矩的定义
Sy=∫ zdA A
截面的静矩和形心位及惯性矩的计算
y
dA
x
x 0
截面对 x , y 轴的惯性积为
Ixy A xydA
惯性矩的数值恒为正,惯性积则可能为正值,负值,
也可能等于零。
y
若 x , y 两坐标轴中有一个为
dA y
截面的对称轴,则截面对 x , y 轴的 惯性积一定等于零 。
dx dx x
截面对 x , y 轴的惯性半俓为
iy
Z1 80 Z2 0
所以截面的形心坐标为
ZC
A1 Z1 A1
A2 Z2 A2
46.7mm
20 140
zc
20
1
yc
ZC
2
y
100
I1yC
1 12
20 1403
20 140
(8046.7)2
I
2 yC
1 12
100
203
100
20
(46.7)2
zc
120 103 152 120 10
1 12
703
10
(25)2
70
10
100.4 104 mm 4
Iy 278.4 104 mm4
70 20 10
120
y
80
c
x
10
y
I xy 0 15 20 120 10 0 (25) (35) 70 10
x2
10
70 2
45mm
y2 5mm
y 10
1 x1
y1
组合截面惯性矩求解方法研究

中图 分 类 号 : T U 3 1 1 . 4
文献标识码 : A
在众多的力学概念中, 惯性矩极为重要, 因为构件的许 多受力指标都与之相关。作为工程技术人员, 应该熟悉惯 性矩的求解方法, 至少应该知道如何求解常见构件截面的 惯性矩。工作中, 经常需要用到截面惯性矩, 此时, 在现有
第1 5卷 第 1 1 期 2 0 1 5年 1 1月
鸡 西 大 学 学 报
J OURNA L 0F J I XI UN I VER S I T Y
Vo 1 . 1 5 No .1 1
NO Y . 2 Ol 5
文章编号 : 1 6 7 2— 6 7 5 8 ( 2 0 1 5 ) 1 1 — 0 0 5 8— 3
作 者简 介 : 吴 三元 , 硕 士, 贵 州大 学 ; 二级注册建造师 , 凯 里 碧 桂 园物 业 发 展 有 限公 司 。 基 金项 目 : 国 家 自然 科 学 基 金 ( 编号 : 5 1 4 6 8 0 0 8 ) ; 贵州大学研究生创新基金 ( 研理工 2 0 1 4 0 6 2) 。
详 细 介 绍 了如 何 运 用 A u t o C A D, P K P M, A B A Q U S等 软 件 求 解 组 合 截 面 的惯 性 矩 以及 各 自的优 缺 点 , 对 工 程 技 术 人
员而言 , 有一定的参考价值。
关键词 : 组合截面 ; 惯性 矩; P K P M; A u t o C A D
组 合 截 面 惯 性 矩 求解 方 法研 究
吴 三元 , 庄锦 亮 , 赵 玉
( 贵 州 大 学 土木 工程 学 院 , 贵州 贵阳 5 5 0 0 2 5 )
摘
要: 惯性矩是一 个重要 的截 面几何 参数 , 构件 的许 多力 学指标都 与之 相关。拟 以组合截 面 为研 究对 象 ,
材料力学惯性矩

y'c
0.6 2.52 (1.26 1.2) 0.6 2.52 2 0.2 2.4
0.16m;
返回 下一张 上一张 小结
第二节 惯性矩和惯性积
一、极惯性矩:
定义:平面图形中任一微面积dA与它到坐 标原点O旳距离ρ平方旳乘积ρ2dA,称为该面积 dA对于坐标原点o旳极惯性矩。
500 500
(2)计算形心主惯性矩:
(z、y轴即形心主轴)
z1
z1
a12 1
50 103 12
20
52
500
1.17
105
cm 4 ;
z2
z2
a22 2
10 503 12
35
202
500
2.17 105 cm4 ;
z z1 z2 117 2 17105 3.34105 cm4;
I zy
z y dA;
A
特点:①惯性积是截面对某两个正交
坐标轴而言。不同截面对同一对轴或同一截面对不同轴旳惯性积
均不同。惯性积是代数值。
②若截面有一根为对称轴,则该截面对涉及此对称轴在 内旳一对正交坐标轴旳惯性积必为零。
单位: m4 , mm4;
返回 下一张 上一张 小结
例5-2 求矩形截面对其对称轴旳惯性矩和惯性积。
Sy
z
A
dA
A
zc ;
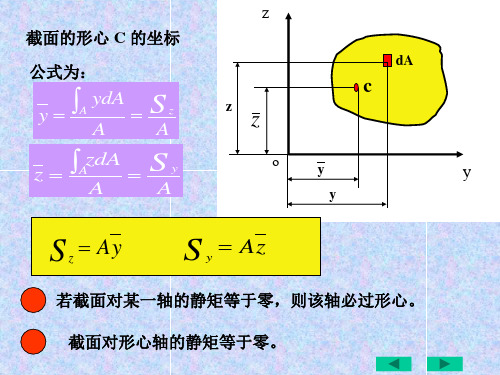
当Sz=0或Sy=0时,必有yc=0或zc=0,可知截面对某轴旳
静矩为零时,该轴必经过截面形心;反之,若某轴经过形心,
则截面对该轴旳静矩为零。
截面的几何性质面积矩惯性矩惯性积平行移轴公式

1
HOHAI UNIVERSITY
2
HOHAI UNIVERSITY
例1 求如图矩形Sz和Sy
解:Sz
ydA
A
ah
ybdy
a
bh(a h) 2
A yC
同样地
Sy
bh(d
b) 2
A
zC
z b/2 b/2 a
y h/2
h/2
dy
y
d
3
HOHAI UNIVERSITY
解: A1 15050mm 2 A2 18050mm 2
150
A3 250 50mm 2
50
C1
yC1 255mm yC2 140mm
5c0
C2
yC3 25mm zC1 zC2 zC3 0
50
C3
z
yC
A1
yC1 A2 yC2 A1 A2 A3
A3
yC 3
250
y
15050 255 18050140 25050 25 mm 15050 18050 25050
i=1
同理
n
Iz =∑ Izi
i=1
n
Iyz =∑ Iyzi
i=1
12
HOHAI UNIVERSITY
例5 图示矩形中,挖去两个直径为d 的圆形,求余下 图形对z轴的惯性矩。
b/2 b/2
z
Iz
1 bh3 12
5 d 4
32y13HOHAI UNIVERSITY
14
HOHAI UNIVERSITY
作业题 求图示工字形截面对z轴的惯性矩。
b d
z
15
惯性矩、静矩、截面抵抗矩计算

惯性矩和对Y轴的惯性矩。
y
解:
100
1)求出A1和A2分别对自身形心 2
轴的惯性矩
0
I x1
b1h13 12
100 203 12
66.67 103
100
A1 •Ⅱ•ຫໍສະໝຸດ A2Ⅰx1
xc a2 30 x
Ix2
b2h23 12
20 100 3 12
16.67 105
2 0
2)求对整个截面形心X轴的惯性矩
截面对x轴的惯性矩:
I x y2dA
量纲:L4 y
A
截面对y轴的惯性矩: I y x2dA
A
注意:
1)同一截面对不同的轴惯性 矩不同;
2)惯性矩永远为正值;
x
dA
y r
x
3)惯性矩的单位为m4;
2、惯性半径(回转半径)
截面对x轴的惯性半径: ix I x / A 截面对y轴的惯性半径: iy I y / A
二、常见截面的惯性矩和惯性半径
形心轴:通过截面形心的坐标轴 ➢ 矩形截面对于其对称轴(即形心轴)x,y的惯性矩。
y
对x轴的惯性矩
x
Ix
1 12
bh3
h 对y轴的惯性矩:
b
Iy
1 12
hb3
➢ 矩形截面对于其对称轴(即形心轴)x,y的惯性半径。
y
对x轴的惯性半径
x
h
ix
Ix A
1/12bh3 h
截面的几何性质
知识点:截面惯性矩和静矩的计算 一、截面惯性矩的定义及计算 二、常见截面的惯性矩和惯性半径 三、组合截面的概念 四、惯性矩的平行移轴公式 五、静矩的概念及公式 六、常见截面的静矩
截面的静矩和形心位置及惯性矩的计算

x 0
截面对 x , y 轴的惯性积为
Ixy A xydA
惯性矩的数值恒为正,惯性积则可能为正值,负值,
也可能等于零。
y
若 x , y 两坐标轴中有一个为
dA y
截面的对称轴,则截面对 x , y 轴的 惯性积一定等于零 。
dx dx x
截面对 x , y 轴的惯性半俓为
iy
Iy , A
二 、 截面的主惯性轴和主惯性矩
I x1y1
Ix
2
Iy
sin 2α
I xy cos 2α
主惯性轴 —— 总可以找到一个特定的角 0 , 使截面对新坐标 轴 x0 , y0 的惯性积等于 0 , 则称 x0 , y0 为主惯轴。
主惯性矩——截面对主惯性轴的惯性矩。
形心主惯性轴 ——当一对主惯性轴的交点与截面的形心 重合时,则称为形心主惯性轴。
x
80
§ І -2 极惯性矩 惯性矩 惯性积
定义:
z dA
z
截面对 o 点的极惯性矩为
y
Ip Aρ2dA
y 0
截面对 y ,z 轴的惯性矩分别为
Iy A z2dA Iz A y2dA
因为 ρ2 y2 z2
I p Aρ2 dA
所以 Ip = Ix + Iy
y
y
dA
ix
Ix A
例 2 _ 1 求矩形截面对其对称轴 x , y 轴的惯性矩。
解:
dA = b dy
Ix
A y2dA
h
2h
by2dy
2
bh3 12
Ix A y2dA
截面的静矩和形心位置及惯性矩的计算
y1 60mm
矩形 2
A2 10 70 700mm2
x2
10
70 2
45mm
y2 5mm
y 10
1 x1
y1
o
2 y2
10
x2
x
80
所以
x
A1 x1 A 2 x2 A1 A2
37500 1900
20mm
y
A1 y1 A1
A2 y2 A2
75500 1900
40mm
y 10
1 x1
求形心主惯性矩的步骤
确定形心 的位置
x
Ai x i
,
y
Ai
yi
Ai
Ai
选择一对通过形心且便于计算惯性矩(积)的坐 标轴 x ,y, 计算 Ix , Iy , Ixy
I x I xi I y I yi
I xy I xyi
确定主惯性轴的位置
I 1 2 xy
2 0
tg
(
)
Ix Iy
y
80
c
x
10
y
Ix
1 12
120 103 152 120 10
1 12
703
10
(25)2
70
10
100.4 104 mm 4
Iy 278.4 104 mm4
70 20 10
120
y
80
c
x
10
y
I xy 0 15 20 120 10 0 (25) (35) 70 10
yc
C(a,b)
xc
b
x
Ix , Iy , Ixy _____ 截面对 x , y 轴的惯性矩和惯性积。
3.4截面惯性矩和抗弯截面模量详解

d 3
32
2.空心圆截面
p D4 IZ = (1- a 4 ) 64 d a= D
WZ
D 3
32
(1 4 )
2
3.对薄壁圆环截面 4.矩形截面
I 0.4d s z
3
W 0.8d s z
bh 3 IZ 12
化工设备设计基础
bh 2 WZ 63源自3.4.3 组合截面惯性矩
6
例1续
3.4 截面惯性矩和抗弯截面模量
解: 静矩定理(求组合截面的形心位置):
140 20 70 100 20 (140 10) a 140 20 100 20 100 103mm
y
20
I
C1 C C2
a1=47
z1 z
140
20
化工设备设计基础
图3-24
a2=33
103
1.平行移轴定理:
I 1 y dA ( y a) dA
2 2 z 1 A A
( y 2ay a )dA
2 2 A
y dA 2a ydA a dA
2 2 A A A
I z1 I Z 2aAyc a 2 A
若 yc 0
则 I z1 I Z a 2 A
n Z 1 Z 2 Z n Z i 1 i
同理:
I (I ) (I ) (I ) (I )
n y y 1 y 2 y n y i 1
i
化工设备设计基础
5
例1
3.4 截面惯性矩和抗弯截面模量
求图示T字形截面对通过其形心C的z轴之 惯性矩(图中尺寸单位为mm)。
化工设备设计基础
组合截面计算相对于中性轴的惯性矩I

4.梁的剪应力 (1)掌握矩心截面的剪应力计算公式 及静矩的概念; (2)了解工字形及T形截面梁的剪应 力计算公式。
5.梁的强度条件 (1)掌握梁的正应力强度条件及抗弯截面模量; (2)能够利用强度条件公式解决三种不同类型的强 度计算问题:强度校核,选择截面,确定容许荷 载; (3)掌握梁的剪应力强度条件并能利用该公式进行 剪应力的强度校核。 6.提高梁弯曲强度的主要途径 (1)掌握提高梁弯曲强度的三种途径:选择合理的 截面形状,变截面梁,合理安排梁的受力。
• (二)梁的强度条件 • 1.正应力强度条件 M max • max =
WZ
IZ WZ • WZ-抗弯截面模量。 y max
; • 矩形截面ymax=h/2;圆形截面 ymax=d/2 2 bh ; • 代入公式即得:矩心截面 WZ 2 6 • 圆形截面 W d
Z
三、基本内容
• (一)基本概念及公式 • 1.弯曲变形――构件基本变形之一 • 弯曲内力弯矩、剪力对应正应力、剪应力。 • 2.正应力公式 M = y IZ • (1)公式由纯弯推导,但对非纯弯曲也适用。 • 其中M—横截面上的弯矩; • IZ-截面对中性轴的惯性矩; • y-所求应力点至中性轴的距离,Z轴为通过形心 的轴。
1确定t形截面的形心o通过二个面积对z1轴的面积矩去除二个面积的和可得yc确定e轴??11120120120zy20201202ycy33ozy20201201ycy3?2计算截面对形心轴e的惯性矩根据矩形惯性矩通过平行移轴公式计算出t形截面对形心轴e的惯性矩
工 程 力 学
直播课堂11
安徽电大:姚志刚
五、例题分析
9-3(P150) 9-4(P151) 9-6(P153)
截面形心和惯性矩的计算

工程构件典型截面几何性质的计算2.1面积矩1.面积矩的定义图2-2.1任意截面的几何图形如图2-31所示为一任意截面的几何图形(以下简称图形)。
定义:积分和分别定义为该图形对z轴和y轴的面积矩或静矩,用符号S z和S y,来表示,如式(2—2.1)(2—2.1)面积矩的数值可正、可负,也可为零。
面积矩的量纲是长度的三次方,其常用单位为m3或mm3。
2.面积矩与形心平面图形的形心坐标公式如式(2—2.2)(2—2.2)或改写成,如式(2—2.3)(2—2.3)面积矩的几何意义:图形的形心相对于指定的坐标轴之间距离的远近程度。
图形形心相对于某一坐标距离愈远,对该轴的面积矩绝对值愈大。
图形对通过其形心的轴的面积矩等于零;反之,图形对某一轴的面积矩等于零,该轴一定通过图形形心。
3.组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。
如式(2—2.4)(2—2.4)式中,A和y i、z i分别代表各简单图形的面积和形心坐标。
组合平面图形的形心位置由式(2—2.5)确定。
(2—2.5)2.2极惯性矩、惯性矩和惯性积1.极惯性矩任意平面图形如图2-31所示,其面积为A。
定义:积分称为图形对O点的极惯性矩,用符号I P,表示,如式(2—2.6)(2—2.6)极惯性矩是相对于指定的点而言的,即同一图形对不同的点的极惯性矩一般是不同的。
极惯性矩恒为正,其量纲是长度的4次方,常用单位为m4或mm4。
(1)圆截面对其圆心的极惯性矩,如式(2—7)(2—2.7)(2)对于外径为D、内径为d的空心圆截面对圆心的极惯性矩,如式(2—2.8)(2—2.8)式中,d/D为空心圆截面内、外径的比值。
2.惯性矩在如图6-1所示中,定义积分,如式(2—2.9)(2—2.9)称为图形对z轴和y轴的惯性矩。
惯性矩是对一定的轴而言的,同一图形对不同的轴的惯性矩一般不同。
惯性矩恒为正值,其量纲和单位与极惯性矩相同。
组合截面计算相对于中性轴的惯性矩I

矩形组合截面惯性矩计算
矩形组合截面的惯性矩计算公式为:$I = frac{b times h^{3}}{12}$,其中b为矩形 截面的宽度,h为矩形截面的高度。
该公式适用于矩形组合截面,当需要计算矩形组合截面相对于中性轴的惯性矩时 ,可以先分别计算各个矩形截面的惯性矩,然后根据中性轴的位置进行相应的调 整。
04 组合截面相对于中性轴的 惯性矩计算
中性轴上的惯性矩
定义
中性轴是组合截面中所有材料点 到中性面的距离都是相等的轴线 。
特性
惯性矩是描述截面抵抗弯曲变形 能力的量,而中性轴上的惯性矩 是组合截面惯性矩的代表值。
相对于中性轴的惯性矩计算公式
公式
相对于中性轴的惯性矩计算公式为 $I = frac{1}{A}int_{A}y^2dA$,其中 $y$ 是材料点到中性轴的距离,$A$ 是 截面面积。
结构稳定性分析
结构稳定性分析是组合截面惯性矩的另一个重要应用。通过计算组合截面的惯性矩,可以确定结构在 承受外力作用时的稳定性,从而评估结构是否能够保持其形状和功能。
在进行结构稳定性分析时,需要考虑不同方向的惯性矩对结构稳定性的影响。例如,在承受侧向压力 的结构中,需要考虑平行于中性轴的惯性矩对结构抗侧向变形能力的影响。
组合截面计算相对于中性轴的惯性 矩i
contents
目录
• 引言 • 引言 • 组合截面的几何特性 • 组合截面惯性矩的计算方法 • 组合截面相对于中性轴的惯性矩计算 • 组合截面惯性矩的应用 • 结论
01 引言
引言
组合截面相对于中性轴的惯性矩计算 是工程中常见的需求。
掌握组合截面相对于中性轴的惯性矩 计算方法对于结构设计、强度分析和 优化等具有重要意义。
惯性矩计算方法及常用截面惯性矩计算公式

惯性矩计算方法及常用截面惯性矩计算公式惯性矩(也称为惯性矩、二阶矩)是描述物体抵抗绕轴旋转的特性的物理量。
在工程中,惯性矩常用于计算和设计梁、轴等结构的强度和稳定性。
本文将介绍惯性矩的计算方法以及常用的截面惯性矩计算公式。
惯性矩的计算方法主要有几何法、积分法和转动倾斜坐标等方法。
1.几何法:几何法是一种通用的计算惯性矩的方法,适用于简单的几何形状,如矩形、圆形等。
几何法的思想是将复杂的截面分解为简单的几何形状,并使用其相关的公式计算每个部分的惯性矩,然后将它们相加。
2.积分法:积分法是一种基于微积分的方法,适用于复杂的截面形状。
该方法基于将截面分割为无穷小的面积元,然后使用积分计算每个面积元的惯性矩,并将它们相加得到整个截面的惯性矩。
3.转动倾斜坐标:转动倾斜坐标是一种特殊的坐标系选择方法,适用于具有对称轴的截面。
在该方法中,坐标轴被选择为与截面的对称轴对齐,这样会使得部分惯性矩相消,从而简化惯性矩的计算。
下面介绍几个常见截面形状的惯性矩计算公式:1.矩形截面:- 矩形的惯性矩计算公式:I = (bh^3)/12,其中b为矩形的宽度,h为矩形的高度。
2.圆形截面:-圆形的惯性矩计算公式:I=πr^4/4,其中r为圆的半径。
3.圆环截面:-圆环的惯性矩计算公式:I=π(R^4-r^4)/4,其中R为外圆半径,r 为内圆半径。
4.T形截面:-T形的惯性矩计算公式:I=(b1h1^3)/12+b1h1(y1-y)^2+(b2h2^3)/12,其中b1和b2为宽度,h1和h2为高度,y为距离底边的垂直距离。
这些是一些常见的截面形状的惯性矩计算公式,对于其他复杂的截面形状,可以使用几何法、积分法或转动倾斜坐标方法来计算惯性矩。
总结起来,惯性矩是描述物体抵抗绕轴旋转的特性的物理量。
惯性矩的计算方法主要有几何法、积分法和转动倾斜坐标等方法。
常见截面的惯性矩计算公式包括矩形截面、圆形截面、圆环截面和T形截面。
这些公式在结构工程中广泛应用,可以帮助工程师设计和计算各种结构的强度和稳定性。
惯性矩的计算方法及常用截面惯性矩计算公式

惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一.重点及难点:(一).截面静矩和形心1.静矩的定义式如图1所示任意有限平面图形,取其单元如面积dA ,定义它对任意轴的一次矩为它对该轴的静矩,即ydAdSx xdAdS y == 整个图形对y 、z 轴的静矩分别为⎰⎰==AAy ydASx xdAS (I-1) 2.形心与静矩关系 图I-1设平面图形形心C 的坐标为C C z y , 则 0A S y x=, AS x y = (I-2) 推论1 如果y 轴通过形心(即0=x ),则静矩0=y S ;同理,如果x 轴通过形心(即0=y ),则静矩0=Sx ;反之也成立。
推论2 如果x 、y 轴均为图形的对称轴,则其交点即为图形形心;如果y 轴为图形对称轴,则图形形心必在此轴上。
3.组合图形的静矩和形心设截面图形由几个面积分别为n A A A A ⋯⋯321,,的简单图形组成,且一直各族图形的形心坐标分别为⋯⋯332211,,,y x y x y x ;;,则图形对y 轴和x 轴的静矩分别为∑∑∑∑========ni ni ii xi x ni ii n i yi y y A S S x A S 1111S (I-3)截面图形的形心坐标为∑∑===ni ini ii AxA x 11 , ∑∑===ni ini ii AyA y 11 (I-4)4.静矩的特征(1) 界面图形的静矩是对某一坐标轴所定义的,故静矩与坐标轴有关。
(2) 静矩有的单位为3m 。
(3) 静矩的数值可正可负,也可为零。
图形对任意形心轴的静矩必定为零,反之,若图形对某一轴的静矩为零,则该轴必通过图形的形心。
(4) 若已知图形的形心坐标。
则可由式(I-1)求图形对坐标轴的静矩。
若已知图形对坐标轴的静矩,则可由式(I-2)求图形的形心坐标。
组合图形的形心位置,通常是先由式(I-3)求出图形对某一坐标系的静矩,然后由式(I-4)求出其形心坐标。
材料力学-截面几何特性

I 0 xC 2 yC 2
IxC IxC1 A1 yc21 IxC2 A2 yc22 1104 mm4 1200mm2 (15mm)2 28.58mm4 700mm2 (25mm)2 100.33mm4
64
9 /2
Ix2 Ix2C A2 (a xc2 )2 28mm 4 (80mm )2 (100 17)2 8 3467mm4
组合截面对x轴的惯性矩为
I x I x1 2I x2 5333mm4 23467mm4 12270mm4
§I-4 惯性矩和惯性积的转轴公式 ·截面 的主惯性轴和主惯性矩
A
A ( yC b)2 dA
A ( yC2 2byC b2 )dA
I xC 2bSxC b2 A
Ix IxC 2bSxC b2 A
因为C为形心
SxC AyC 0
y
yC
x
dA
a
r
bC y
xC
x
I x I xC b2 A 同理:
I y I yC a2 A I xy I xC yC abA I p I pC (a2 b2 ) A
C1
80
x
图(b)
x
xi
Ai
x 1
A1x
2
A2
A
A1A2
409600 45 7700 19.7mm 9600 7700
y
yi Ai
y 1
A1
y
2
A2
A
A1 A2
609600 65 7700 39.7mm 9600 7700
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
瑞典空军部队参谋长比约克格伦说,地区军事活动已回复到“冷战时期水平”。“我们大致已回到上世纪80年代后期和90年代初期的水平。”
=0.18mm
< ,满足。
7. 自振频率计算
仅考虑恒载作用下组合板的挠度:
=0.145mm
自振频率
Hz>15Hz,满足。
另外,在压型钢板的顶面必须焊接横向短钢筋以保证压型钢板与混凝土层共同工作。圆头焊钉应穿过压型钢板焊于钢梁上,只作为压型钢板与混凝土层的抗剪储备,满足构造,本设计选用M16的焊钉。
中跨组合板的计算此处从略。
欧洲航空安全局说,去年在公海上特别是波罗的海上空,涉及民航机和“不合作”军机的安全事件大幅增加。北约官员说,今年1月至3月,北约军机在欧洲各地
=53.63mm
组合截面惯性矩:
=26.282×
荷载标准组合下的挠度计算:
=0.21mm
< ,满足。
荷载准永久组合下的挠度计算:
4. 斜截面抗剪验算
× =16.77kN>1.87kN,满足。
5. 支座负弯矩配筋计算
=80-25=55mm
=
<51.73 ,满足。
实配 :
6. 挠度计算
由变形相等原则,将混凝土材料等效为钢材:
中新网5月6日电 综合报道,瑞典官员日前表示,俄罗斯战斗机频频在波罗的海出没,且瑞典和芬兰海域出现疑似俄罗斯潜水艇,已使得波罗的海出现20多年来最严重的军事对峙状态。
