理论力学第二章讲解
合集下载
理论力学第二章(2)
合力FR 的大小等于原力系的主矢
合力FR 的作用线位置
MO FR
小结：平面任意力系简化结果讨论
主矢
FR 0
FR 0
主矩
MO 0
MO 0 MO 0
MO 0
最后结果
说明
合力 合力作用线过简化中心
合力 合力偶
合力作用线距简化中心M O FR
与简化中心的位置无关
平衡
与简化中心的位置无关
21
简化为一个力：
c os (FR
,
i)
Fx FR
,
cos(FR ,
j)
Fy FR
原力系的主矢与简化中心O的位置无关
主矩： 原力系中各力对简化中心O之矩的代数和称为原力
系对点O的主矩。
n
M O M O (F1) M O (F2 ) ...... M O (Fn ) M o (Fi ) i 1
主矩与简化中心的选择有关
称点O为简化中心 F1’、F2’、….Fn’平面汇交力系，合力为FR’
M1、M2、….Mn平面力偶系，合力偶矩为MO
10
1、主矢和主矩
FR’=F1’+F2’+….+Fn’=F ’= F
主矢：量（简平称面为力主系矢中）所有各力的矢量和FR′称为该力系的主矢
主矢FR′的大小和方向余弦为：
FR (Fx )2 (Fy )2
11
平面任意力系向作用面内一点简化
一般力系（任意力系）向一点简化汇交力系+力偶系
（复杂力系）
（两个简单力系）
汇交力系 力偶系
力，FR‘(主矢) ， (作用在简化中心)
力偶 ，MO (主矩) ， (作用在该平面上)
理论力学第2章平面任意力系
空载时轨道A 、 B的约束反力，并问此起重机在使用过程中有无翻
倒的危险。
解：
（1）起重机受力图如图
（2）列平衡方程 ：
MA 0:
Q
Q(6 2) RB 4 W 2 P(12 2) 0
MB 0:
Q(6 2) W 2 P(12 2) RA 4 0
6m
解方程得:
W
P
12m
RA 170 2.5P
FR' Fi Fxi Fy j
MO MO (Fi )
3. 平面任意力系的简化结果
（1）FR´= 0，Mo ≠ 0, （2）FR´ ≠ 0，Mo = 0, （3）FR´≠ 0，Mo ≠ 0, （4）FR´= 0，Mo = 0,
合力偶，合力偶矩，MO MO (Fi )
合力，合力作用线通过简化中心O。
3
F2
j
F3
x
(437.6)2 (161.6)2
F1
1 1
100
Oi
1 2
466.5N
200
MO 21.44N m
y
合力及其与原点O的距离如图(c) 。 MO
x
y
d
x
O
FR FR′ 466.5N FR´
FR
O
d MO 45.96mm
(b)
(c)
FR
10
例11 水平梁AB受按三角形分布的载荷作用，如图示。载荷的
M
l
l
30
B
D
° F
3l
P
q
A
21
解：T字形刚架ABD的受力如图所示。
M
l
l
Fx 0
30
B
FAx 1 • q • 3a Fcos30 0
理论力学 第二章 刚体的基本运动
0
nπ 式中n为转速 单位：转/ 分(r/min) 。 山东大学 土建与水利学院工程力学系 THEORETICAL MECHANICS 30
§ 2.2 刚体绕定轴的转动
3.角加速度
描述角速度变化的快慢程度
2
d d lim 2 t 0 t dt dt
单位：弧度/秒2 (rad/s2 ) α与同号，刚体加速转动；
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
§2.4 轮系的传动比
1 n1 r2 Z2 i1,2 2 n2 r1 Z1
此结论对于锥齿轮传动和带 轮传动同样适用。 在一些复杂轮系（如变速器） 中包含有几对齿轮。可将每一对 齿轮的传动算出后，将它们连乘 起来，变为可得总的传动比。
392.8 62.5 转 2π
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
例 题
例2- 3 轮子绕O点作定轴转动，其加速度方向和轮的半径
成60度角，求轮的转动方程，以及角速度和转角之间的关系。
00, 0.
M
O
a
60
THEORETICAL MECHANICS
解 ： AB 杆 为 平 移 ， O1A 为 定 轴 转 动 。 根 据 平移的特点，在同一瞬 时，M、A两点具有相同 的速度和加速度。
THEORETICAL MECHANICS
山东大学 土建与水利学院工程力学系
例 题
A点作圆周运动，其运动方程为
s O1 A 3π t
ds dv vA 3π （m/s) a A t 0 dt dt
§ 2.1 刚体的平行移动
理论力学课件第2章PPT教学课件
2020/12/10
8
• 4.平面汇交力系平衡的解析条件
F Fx2 Fy2 0 Fx F1x F2x Fnx0 Fy F1y F2y Fny0
2020/12/10
9
• 例2-3 重量P=20kN的重物用钢丝绳挂 在滑轮B并固定在绞车D上。A,B,C为 光滑铰接。杆和滑轮自重不计。求杆 AB和 BC所受的力。
• 解：画工件的受力图。 • 螺栓A给工件的力FA向左。螺栓B给工
件的力FB向右。
MB0:FAlM1M2M30
1 FAl(M1M2M3)20N0 FBFA20N0
2020/12/10
19
PPT教学课件
谢谢观看
Thank You For Watching
2020/12/10
20
考虑方向BC的静力 平衡：
F B CP co 3s 0P si3n 0 0 F BC P co 3s 0P si3n 0 2.3 7k2N
2020/12/10
12
§2-2 平面力对点力矩 的概念及计算
• 1.力对点的矩 • 作用在物体上的力矩是使物体绕点转动状
态发生改变的一种量度。 • 钳工用扳手拧紧螺丝、司机扳动方向盘，
• (2) 分析AB的受力：AB杆在,B,C受到约束 力，3个约束力组成平面汇交力系，并相交 于点E。
2020/12/10
5
2020/12/10
6
tan 0.5, 26.565
FA sin45
F sin(45
)
FC sin(90
)
sin45
F A F sin(45 ) 2.236F 22.36k N
都用到力矩。
2020/12/10
理论力学课件 第二章质点组力学讲解
心重合。
重心：质点系所受重力的合力的作用点。
（3）对于只有两个质点所组成的质点组 而言，其质心位置在质点1与质点2这两点连 线上，质心与质点1、2的距离反比于质点1、 2的质量。
例1 一凹底的圆锥体，由高为h、底面半径为 R的匀质正圆锥体自底面挖去高为d（d<h）的 共轴圆锥而成。求此凹底圆锥体的质心位置。
v
2 y
V
1 m(2M m) cos2
(M m)2
tan vy (1 m ) tan
vx
M
故由于炮车反冲 v V 而 。
例3 一个重量为P的人,手拿一个重为Q的物
体到最,以高与时水，平将线物成体α以角相的对速于度他v自0向己前的跳速。度当他u跳
水平向后抛出。问由于物体的后抛使人的跳远 的距离增加了多少？
m m
4 V v 4
zc
h
s
(3h d ) 4
§2.2 动量定理与动量守恒律
一、动量定理
假设由n个质点所组成的质点组，其中某一
个O的质位点矢的为质r量i ，为作m用i，其对上某的惯诸性力参的考合系力坐为标原点
Fi Fi(i) Fi(e)
质点pi的运mi 动dd2t微r2i 分F方i(i) 程Fi(e)
本章重点研究内容
〈一〉质心及质心运动定理 〈二〉动量定理及其守恒律 〈三〉动量矩定理及其守恒律 〈四〉动能定理、机械能守恒律 〈五〉两体问题、变质量问题
§2.1 质点组的基本概念
一、质点组的内力和外力 质点组：由许多（有限或无限）相互联系
着的质点所组成的系统。
内 力：质点组内质点间的相互作用力。
外 力：质点组外的物体对质点组内质点
理论力学第2章质点组力学ppt课件
最新版整理ppt
25
最新版整理ppt
26
和
最新版整理ppt
27
举例
最新版整理ppt
28
§2.4 动能定理与机械能守恒定 律
1 质点组的动能定理
最新版整理ppt
30
刚体情形
最新版整理ppt
31
2 机械能守恒定律
▪ 对质点组来讲，内力所作的功之和一般并不 为零，所以，若只有外力是保守力而内力并 不是保守力，质点组的机械能并不守恒；
54
最新版整理ppt
55
举例
最新版整理ppt
56
最新版整理ppt
57
最新版整理ppt
58
2 火箭原理
时间关系不讲， 若有兴趣请自己看书
最新版整理ppt
59
作业8讲解
最新版整理ppt
60
第15讲到此结束
最
最新版整理ppt
10
§2.2 动量定理与动量守恒定律
1 质点组动量定理
最新版整理ppt
12
最新版整理ppt
13
最新版整理ppt
14
2 质心运动定理
最新版整理ppt
15
最新版整理ppt
16
3 动量守恒定律
（3）由于 pmvC
，所以质心作惯性运动。
（4）如果合外力在某轴投影为零，则动量投影为常量。
i 1
i 1
i 1
最新版整理ppt
35
小结
▪ 质点组的三个动力学基本定理在分量形式下 一共有七个方程，和它们相关的守恒律成立 时也是这样。
▪ 但由于质点组的独立变量通常都大于七，所 以这些方程并不能用来确定质点组中每一质 点的运动，而只能由它们得出运动总的趋向 和某些特征，特别是与质心有关的总的特征。
理论力学第二章-PPT精品
第二章：有心运动
• §2.1 有心力和有心运动
– 如果运动质点受到的力及其作用先总是通过 惯性系中的某一固定点，这样的力(场)叫做 有心力（场），力所指向或背向的固定点叫 做力心，指向力心的有心力叫做引力，背向 力心的是斥力。
– 有心力的量值，一般只是力心与质点间距离 r 的函数，在有心力作用下质点的运动叫做 有心运动。
有心力是保守力，质点在运动过程中，其总的机械
能守恒
ETV12m(rm)2krm 2
rm2h
p rm1e
m2h pk2
r p
1ecos
E2m k42(h e21)
2m2h e1k4 E
质点的总 机械能与 轨道偏心 率的关系
e<1, 则 E<0, 则轨道为椭圆 e=1, 则 E=0, 则轨道为抛物线 e>1, 则 E>0, 则轨道为双曲线
进行变换 u 1 r
将
r h du
d hu 2
代入 r r 2 F(r)
m
r
h
d 2u
d 2
h 2u 2
d 2u
d 2
mh2u2(d2uu)F(u)
d2
有心运动的轨道微分方程 --- Binet （比内)公式
p
mh2
p
u2
mh2
p
1 r2
§2.2 距离平方反比引力下的质点运动
•
距离平方反比引力形式
k2 GMm
F
k2 r2
er
er
作变量代换 u 1 r
F(r)F(u)k2u2
d2u u k2
• §2.1 有心力和有心运动
– 如果运动质点受到的力及其作用先总是通过 惯性系中的某一固定点，这样的力(场)叫做 有心力（场），力所指向或背向的固定点叫 做力心，指向力心的有心力叫做引力，背向 力心的是斥力。
– 有心力的量值，一般只是力心与质点间距离 r 的函数，在有心力作用下质点的运动叫做 有心运动。
有心力是保守力，质点在运动过程中，其总的机械
能守恒
ETV12m(rm)2krm 2
rm2h
p rm1e
m2h pk2
r p
1ecos
E2m k42(h e21)
2m2h e1k4 E
质点的总 机械能与 轨道偏心 率的关系
e<1, 则 E<0, 则轨道为椭圆 e=1, 则 E=0, 则轨道为抛物线 e>1, 则 E>0, 则轨道为双曲线
进行变换 u 1 r
将
r h du
d hu 2
代入 r r 2 F(r)
m
r
h
d 2u
d 2
h 2u 2
d 2u
d 2
mh2u2(d2uu)F(u)
d2
有心运动的轨道微分方程 --- Binet （比内)公式
p
mh2
p
u2
mh2
p
1 r2
§2.2 距离平方反比引力下的质点运动
•
距离平方反比引力形式
k2 GMm
F
k2 r2
er
er
作变量代换 u 1 r
F(r)F(u)k2u2
d2u u k2
理 论 力 学 教学 课程第2章
上一页 下一页 返回
第二节 平面力偶系的简化与平衡
• 在国际单位制中，力矩的单位是 N·m（牛顿·米）或 kN·m（千牛 顿·米）。
• 在计算力系的合力对某点 O 的矩时，常用到合力矩定理：平面汇交 力系的合力对某点 O的矩等于各分力对 O 点矩的代数和，即
• 该定理建立了合力对点的矩与分力对同一点的矩的关系，其也可运用 于有合力的其他力系。它提供了计算力对点的矩的另一种方法，此外 它还可以用于确定力系合力作用线的位置。
于零的合力。平面汇交力系平衡的必要和充分条件是，力系的合力等 于零。其矢量表达式为 • 力系平衡的几何条件是，力系的力多边形自行封闭，如图 2-2 所示。
上一页 下一页 返回
第一节 平面汇交力系的简化与平衡
• 二、平面汇交力系合成与平衡的解析法
• 1．力在坐标轴上的投影 • 设力 F 作用于 A 点，如图 2-4 所示。在力 F 作用线所在的平面内任
• 设力 F 作用于刚体上的 A 点，为了将力 F 平行移动到刚体内另外一 点 O ［图 2-17 （ a ）］，又不改变其作用效应，可以进行如下等效 变换：先在 O 点施加平行于力 F 的一对平衡力 F ‘ 和 F ’‘ ，且令 F ’= - F ‘’= F ［图 2-17 （ b ）］。根据加减平衡力系公理，所加的 一对力并不改变原来的力 F 对刚体的作用效应，即力 F ［图 2-17 （ a ）］与力系 ( F ‘, F ’‘, F ) ［图 2-17 （ b ）］等效。图 2-17 （ b ）中力 F 与 F ’‘ 构成力偶，力系又可看作由作用于 O 点的力 F ’ 和力偶 ( F , F ‘’) 组成，可用图 2-17 （ c ）中所示力系表示，即为力 F 向 O点平移的最终结果。力偶 ( F , F ‘’) 称为附加力偶，其力偶矩 M= Fd ，而力 F 对 O 点的矩MO（F） =Fd ，附加力偶 ( F , F '') 的 力偶矩 M 为
第二节 平面力偶系的简化与平衡
• 在国际单位制中，力矩的单位是 N·m（牛顿·米）或 kN·m（千牛 顿·米）。
• 在计算力系的合力对某点 O 的矩时，常用到合力矩定理：平面汇交 力系的合力对某点 O的矩等于各分力对 O 点矩的代数和，即
• 该定理建立了合力对点的矩与分力对同一点的矩的关系，其也可运用 于有合力的其他力系。它提供了计算力对点的矩的另一种方法，此外 它还可以用于确定力系合力作用线的位置。
于零的合力。平面汇交力系平衡的必要和充分条件是，力系的合力等 于零。其矢量表达式为 • 力系平衡的几何条件是，力系的力多边形自行封闭，如图 2-2 所示。
上一页 下一页 返回
第一节 平面汇交力系的简化与平衡
• 二、平面汇交力系合成与平衡的解析法
• 1．力在坐标轴上的投影 • 设力 F 作用于 A 点，如图 2-4 所示。在力 F 作用线所在的平面内任
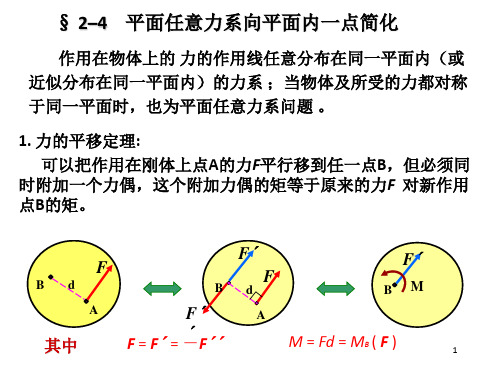
• 设力 F 作用于刚体上的 A 点，为了将力 F 平行移动到刚体内另外一 点 O ［图 2-17 （ a ）］，又不改变其作用效应，可以进行如下等效 变换：先在 O 点施加平行于力 F 的一对平衡力 F ‘ 和 F ’‘ ，且令 F ’= - F ‘’= F ［图 2-17 （ b ）］。根据加减平衡力系公理，所加的 一对力并不改变原来的力 F 对刚体的作用效应，即力 F ［图 2-17 （ a ）］与力系 ( F ‘, F ’‘, F ) ［图 2-17 （ b ）］等效。图 2-17 （ b ）中力 F 与 F ’‘ 构成力偶，力系又可看作由作用于 O 点的力 F ’ 和力偶 ( F , F ‘’) 组成，可用图 2-17 （ c ）中所示力系表示，即为力 F 向 O点平移的最终结果。力偶 ( F , F ‘’) 称为附加力偶，其力偶矩 M= Fd ，而力 F 对 O 点的矩MO（F） =Fd ，附加力偶 ( F , F '') 的 力偶矩 M 为
理论力学 第二章
平面任意力系1第二章平面力系第二部分平面任意力系平面任意力系：各力的作用线在同一平面内，既不汇交于一点，又不相互平行的力系。
[例]第二章平面力系第二部分平面任意力系§2–5 力的平移定理§2–6 平面任意力系向一点简化§2–7 平面任意力系的简化结果• 合力矩定理§2–8 平面任意力系的平衡条件和平衡方程§2–9 平面平行力系的平衡方程§2–10 静定与超静定问题的概念•物体系统的平衡§2–11 平面简单桁架的内力分析平面任意力系习题课§2-5 力的平移定理力的平移定理：作用在刚体上点A的力可以平行移到任一点B，但必须同时附加一个力偶。
这个力偶的矩等于原来的力对新作用点B的矩。
FF[证] 力力系），力偶（力FFF''+'FFF''',,F说明：①力的平移定理揭示了力与力偶的关系：力力+力偶（例断丝锥）②力平移的条件是附加一个力偶M，且M与d有关，M=F•d③力的平移定理是力系简化的理论基础。
任意力系向一点简化汇交力系+力偶系未知力系）（已知力系）汇交力系力，F R '(主矢) ，(作用在简化中心)力偶系力偶，M O (主矩) ，(作用在该平面上)§2-6平面任意力系向一点简化大小：主矢方向：与简化中心的关系：'R F 123'R iF F F F F =+++=∑ 主矢12312 ()()()O O O O i M M M M M F M F M F =+++=++=∑主矩2222'''()()R Rx Ry x y F F F F F =+=+∑∑11tg tg xRyRx yF F F F α--==∑∑（移动效应）(与简化中心位置无关)[因主矢等于各力的矢量和]大小：主矩M O 方向：与简化中心的关系：()O O i M M F =∑（转动效应）固定端（插入端）约束在工程中常见的雨搭车刀方向规定+ —(与简化中心有关)[因主矩等于各力对简化中心取矩的代数和]固定端（插入端）约束说明①认为F i 这群力在同一平面内;②将F i 向A 点简化得一力和一力偶;③F RA 方向不定可用正交分力F Ay ,F Ax 表示;④F Ay ,F Ax , M A 为固定端约束力;⑤F Ay , F Ax 限制物体平动, M A 限制转动。
理论力学-课件第2章
三、简化结果的进一步讨论 合力矩定理的证明
对平面力系向作用面内一点简化后得到的主矢和主矩做进一步分析后，
可能出现以下四种情况：
分别讨论这些情况
（1） FR 0，MO 0 （2） FR 0，MO 0 （3） FR 0，MO 0 （4） FR 0，MO 0
情况（1）FR 0，MO 0，说明该力系无主矢，而最终简化为一个力偶， 其力偶矩就等于力系的主矩。 值得指出，当力系简化为一个力偶时，主矩与简化中心的选取无关。
MO (F) Fh
其中，点O称为矩心；h称为力臂；Fh表示力使物体绕点O转动效果的大小； MO (F) 是一个代数量。
规定：使物体逆时针方向转动的力矩为正，反之为负。
根据定义
图2-3所示的力 F1 对点O的矩为
MO (F1) F1h1 F1hsin
由定义知：力对点的矩与矩心的位置有关， 同一个力对不同点的矩是不同的。因此，对力矩要指明矩心。
方程式（2-19）也完全表达了力系的平衡条件：由 M A 0 知，
该力系不能与力偶等效，只能简化为一个作用线过矩心A的合力，
或者为平衡力系；
由 M B 0 知，若该力系有合力，则合力必通过A，B连线
最后，由 Fx 0 知，若有合力，则它必垂直于x轴；而据限制条件，
A，B连线不垂直于x轴，故该力系不可能简化为一个合力，
三、简化结果的进一步讨论 合力矩定理的证明
情况（4）FR 0，MO 0 ，表明该力系对刚体总的作用效果为零。 根据牛顿惯性定律， 此时物体将处于静止或匀速直线运动状态，即物体处于平衡状态。
第四节 平面力系的平衡条件与平衡 方程式
平面力系平衡的充分和必要条件是 力系的主矢及作用面内任意一点的主矩同时为零。
理论力学课件 第二章 质点运动2
1）许多重要运动，例如天体运动，并没有明显的施力者 2）摒弃感性认识，通过运动形式，理性推断力的存在
解释二：第一定律和第二定律所关注的力，并不相同
牛顿之前，人们认为天使 在推动星体运动
牛顿通过第一定律告诉人们如何发现和理解“隐藏”的力。
2.2.1牛顿三大运动定律
二、牛顿运动定律（动力学基础） （2）牛顿第二定律
新的科学和技术的出现都是渐进式的，有迹可循。
1）累积“离散” 脉冲力，解决连续力的作用问题； 2）微积分的基本思想诞生了！
[1]牛顿《自然哲学的数学原理》
脉冲力与连续轨道运动[1]
2.2.1牛顿三大运动定律
二、牛顿运动定律（动力学基础）
（3）牛顿第三定律
To any action there is always an opposite and equal reaction; in other words, the actions of two bodies upon each other are always equal and always opposite in direction.[1] 对任意作用总是存在着方向相反大小相等的反作用；换句话说，两个物体彼此的相 互作用总是相等的，并且指向对方。
量化描述：翻译成数学语言
[1]牛顿《自然哲学的数学原理》
2.2.1 牛顿三大运动定律
二、牛顿运动定律（动力学基础） （1）牛顿第一定律
Every body perseveres in its state of being at rest or of moving uniformly straight forward except insofar as it is compelled to change its state by forces impressed.[1] 每一个物体都保持静止或者一直向前均匀地运动的状态，除非有外加的力迫使它 改变它自身的状态为止。
解释二：第一定律和第二定律所关注的力，并不相同
牛顿之前，人们认为天使 在推动星体运动
牛顿通过第一定律告诉人们如何发现和理解“隐藏”的力。
2.2.1牛顿三大运动定律
二、牛顿运动定律（动力学基础） （2）牛顿第二定律
新的科学和技术的出现都是渐进式的，有迹可循。
1）累积“离散” 脉冲力，解决连续力的作用问题； 2）微积分的基本思想诞生了！
[1]牛顿《自然哲学的数学原理》
脉冲力与连续轨道运动[1]
2.2.1牛顿三大运动定律
二、牛顿运动定律（动力学基础）
（3）牛顿第三定律
To any action there is always an opposite and equal reaction; in other words, the actions of two bodies upon each other are always equal and always opposite in direction.[1] 对任意作用总是存在着方向相反大小相等的反作用；换句话说，两个物体彼此的相 互作用总是相等的，并且指向对方。
量化描述：翻译成数学语言
[1]牛顿《自然哲学的数学原理》
2.2.1 牛顿三大运动定律
二、牛顿运动定律（动力学基础） （1）牛顿第一定律
Every body perseveres in its state of being at rest or of moving uniformly straight forward except insofar as it is compelled to change its state by forces impressed.[1] 每一个物体都保持静止或者一直向前均匀地运动的状态，除非有外加的力迫使它 改变它自身的状态为止。
理论力学课件-第二篇 第二章 基本力系(基本知识点)
i =1 i =1 i =1 → n → n → n →
即合力的大小和方向分别为
n 2 i =1 n 2 i =1 n i =1
F合=(∑ Fix ) +(∑ Fiy) ( ∑ Fiz ) 2 +
n → →
∑F
i =1
n
n iy
ix
F , , (2)汇交力系平衡的充要条件是该力系的合力为零 (2)汇交力系平衡的充要条件是该力系的合力为零 ① 汇交力系平衡的几何条件是力多边形自行封闭 ② 汇交力系平衡的几何条件是力系中各力在三个坐标轴上 投影的代数和分别等于零, 投影的代数和分别等于零,即
M 合 =∑ M i
i =1
→
n
→
(4)力偶不可能与一个力相平衡,换句话说力偶中的两个力不可能合成为 力偶不可能与一个力相平衡, 一个力,即力偶无合力或力偶不可能与一个力等效.因此, 一个力,即力偶无合力或力偶不可能与一个力等效.因此,一个力偶是最简 单的力系之一. 单的力系之一. 力偶系平衡的充要条件是该力偶系的合力偶矩等于零, (5)力偶系平衡的充要条件是该力偶系的合力偶矩等于零,即力偶系中各 力偶矩的矢量和等于零,以式表示为: 力偶矩的矢量和等于零,以式表示为:
第二章 基本力系-基本知识点 基本力系-
一,基本知识点
1.任意力系总可分解为两个基本力系——汇 任意力系总可分解为两个基本力系——汇 交力系和力偶系 1.1, 1.1,汇交力系的合成与平衡 1.2, 1.2,力偶系的合成与平衡
1.1汇交力系的合成与平衡 1.1汇交力系的合成与平衡
(1)汇交力系是指力系中各力作用线汇交于一共同点的力系,它总可 汇交力系是指力系中各力作用线汇交于一共同点的力系, 以合成为一个作用线通过汇交点的合力, 以合成为一个作用线通过汇交点的合力,合力的力矢可由以下方法确 定: 合力的力矢由力多边形(从任一点开始, ① 几何法 合力的力矢由力多边形(从任一点开始,按一定的比 依次作出力系中各力矢的首尾相接的开口多边形,称为力多边形) 例,依次作出力系中各力矢的首尾相接的开口多边形,称为力多边形) 的封闭边决定,其指向由力多边形的起点指向终点, 的封闭边决定,其指向由力多边形的起点指向终点,即
即合力的大小和方向分别为
n 2 i =1 n 2 i =1 n i =1
F合=(∑ Fix ) +(∑ Fiy) ( ∑ Fiz ) 2 +
n → →
∑F
i =1
n
n iy
ix
F , , (2)汇交力系平衡的充要条件是该力系的合力为零 (2)汇交力系平衡的充要条件是该力系的合力为零 ① 汇交力系平衡的几何条件是力多边形自行封闭 ② 汇交力系平衡的几何条件是力系中各力在三个坐标轴上 投影的代数和分别等于零, 投影的代数和分别等于零,即
M 合 =∑ M i
i =1
→
n
→
(4)力偶不可能与一个力相平衡,换句话说力偶中的两个力不可能合成为 力偶不可能与一个力相平衡, 一个力,即力偶无合力或力偶不可能与一个力等效.因此, 一个力,即力偶无合力或力偶不可能与一个力等效.因此,一个力偶是最简 单的力系之一. 单的力系之一. 力偶系平衡的充要条件是该力偶系的合力偶矩等于零, (5)力偶系平衡的充要条件是该力偶系的合力偶矩等于零,即力偶系中各 力偶矩的矢量和等于零,以式表示为: 力偶矩的矢量和等于零,以式表示为:
第二章 基本力系-基本知识点 基本力系-
一,基本知识点
1.任意力系总可分解为两个基本力系——汇 任意力系总可分解为两个基本力系——汇 交力系和力偶系 1.1, 1.1,汇交力系的合成与平衡 1.2, 1.2,力偶系的合成与平衡
1.1汇交力系的合成与平衡 1.1汇交力系的合成与平衡
(1)汇交力系是指力系中各力作用线汇交于一共同点的力系,它总可 汇交力系是指力系中各力作用线汇交于一共同点的力系, 以合成为一个作用线通过汇交点的合力, 以合成为一个作用线通过汇交点的合力,合力的力矢可由以下方法确 定: 合力的力矢由力多边形(从任一点开始, ① 几何法 合力的力矢由力多边形(从任一点开始,按一定的比 依次作出力系中各力矢的首尾相接的开口多边形,称为力多边形) 例,依次作出力系中各力矢的首尾相接的开口多边形,称为力多边形) 的封闭边决定,其指向由力多边形的起点指向终点, 的封闭边决定,其指向由力多边形的起点指向终点,即
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例2-5
已知:啮合力F = 1400 N, 压力角 θ 20 ，半径 r 60mm 求: MO (F)
解:直接按定义
MO (F) F h F r cos θ 78.93 N m
按合力矩定理
MO (F ) MO (Ft ) MO (Fr ) F cos θ r 78.93 N m
Fx
F x
F1 cos30
F2 cos 60
F3 cos 45
F4 cos 45
129.3N
Fy F y F1 sin 30 F2 sin 60 F3 sin 45 F4 sin 45 112.3N
FR Fx2 Fy2 171.3N
Fy 0
F F cos30 F cos60 0
BC
1
2
解得： F 27.32kN BC
例2-4 已知：液压夹紧机构，F = 3 kN，l = 1500 mm， h = 200 mm。忽略自重；
求：平衡时，压块 C 对工件的水平压力，以及AB 杆受力。
解：AB、BC 杆为二力杆。
i 1
N个力的情况：
力多边形 首尾相连
FF11
FR1 F1 F2
3
FR2 FR1 FR3 Fi
i 1
.
.
.
.
.
.
.
.
.
n
FR FRn1 Fn Fi Fi i1
F1 F2 F3 F4 F2 F4 F3 F1
第二章 平面力系
平面力系——力系中各力都处于同一平面
可分为：
平面汇交力系 平面力偶系 平面平行力系 平面任意力系
§2-1 平面汇交力系
1.平面汇交力系合成的几何法 ——力多边形法则
两个力的情况：
力平行四边形
力三角形
三个力的情况：
FR1 F1 F2 3
FR2 FR1 FR3 Fi
求：系统平衡时，杆AB、BC所受的力。
解：AB、BC杆为二力杆，
取滑轮B（或点B），画受力图
用解析法，建图示坐标系
Fx 0
F F cos 60 F cos 30 0
BA
1
2
坐标轴应尽F 量F选取P与未知力作用线相垂直
1
2
解（得可：简化F平衡方7程.32）1kN BA
cos Fx 0.7548
FR cos β Fy 0.6556
FR
40.99 , β 49.01
4.平面汇交力系的平衡方程
平衡条件 FR 0 即 FR ( Fx )2 ( Fy )2
平衡方程
Fx 0
Fy 0
例2-3 已知： 系统如图，不计杆、轮自重，忽略滑轮大小， P = 20 kN；
由合矢量投影定理，得合力投影定理
FRx Fx FRy Fy
根据合矢量投影定理：合矢量在某一轴上的投影，等于各 分矢量在该轴上投影的代数和。
Fx F1x F2x ...... Fnx Fx Fy F1y F2 y ...... Fny Fy
2.方向：转动方向
力的作用线通过矩心时， 力矩为零
MO (F) F h 2A MO(F) r F
力对点之矩是一个代数量，它的绝对值等于力的大小与力臂的乘
积，它的正负：力使物体绕矩心逆时针转向时为正，反之为负。
常用单位 N m 或 kN m。
二、汇交力系的合力矩定理
首尾相连
2.平面汇交力系平衡的几何条件
平衡条件 Fi 0
平面汇交力系平衡的必要和充分条件是： 该力系的力多边形自行封闭。（即起点和终点重合）
例2-1 已知：AC=CB，F =10kN，各杆自重不计； 求：CD杆及铰链 A 的受力。
解：CD为二力杆，取 AB 杆，画受力图。
用几何法，画封闭力三角形。
力矩与合力矩的解析表达式
MO (F) MO (Fy ) MO (Fx )
x Fy y Fx x F sin y F cos
汇交力系的合力矩定理
MO (FR ) MO (Fi )
代入，得
MO (FR ) (xi Fiy yi Fix )
FR F1 F2 Fn
r
FR
r
F1
r
F2
r
Fn
MO (FR ) MO (F1) MO (F2 ) MO (Fn )
即 MO (FR ) MO (Fi )
平面汇交力系
MO (FR ) MO (Fi )
平面汇交力系的合力对于平面内一点的矩，等于所有各分 力对该点的矩的代数和。（合力矩定理）
取销钉 B
用解析法
Fx 0
FBA cosθ FBC cosθ 0
得 F F
BA
BC
例2-4 已知： F = 3 kN, l = 1500 mm, h = 200 mm.忽略自重；
求ቤተ መጻሕፍቲ ባይዱ平衡时，压块 C 对工件的水 平压力，AB 杆受力。
Fy 0 2FBA sin θ F 0
合力矢大小、方向的确定：
FR Fx2 Fy2 ( Fx )2 ( Fy )2
cos(FR , i)
Fx FR
cos(FR ,
j)
Fy FR
例2-2 已知: 图示平面共点力系, F1 = 200N, F2 = 300N,
F3 = 100N, F4 = 250N。求:力系的合力。 解：用解析法
按比例量得 FC 28.3kN, FA 22.4kN
F
或利用三角公式计算 FC 2 2F, FA 5F
3、平面汇交力系合成的解析法 合力 FR在坐标轴上的投影为 Fx FR cos Fy FR cos
合力等于各力矢量和，即
FR F1 F2 .... Fn Fi
得
FBA
F
2 sin
11.35
kN
压块 C 对工件的水平压力为
FCB
cos
F
2 sin
cos
F
2 tan
11.25
kN
§2-2 平面力对点之矩 平面力偶
一、平面力对点之矩（力矩）
力矩作用面，O称为矩心，O 到力的作用线的垂直距离h称 为力臂。
两个要素：
1.大小：力F与力臂h的乘积