理论力学第二章
理论力学第二章

M F d F d
2 2 2 4
F F F
3
4
F F F
3 4
3 4 3 4 1 2
M Fd F F d F d F d M M
平面内任意力偶可以合成一个合力偶,该合力偶系的平衡条件
尾相接,合力沿反方向构成封闭边。
二.平面汇交力系平衡的几何条件
平面汇交力系平衡的充要条件:
Fi 0
平面汇交力系平衡的几何条件:该力系各分力组成的力多边形自行封闭
例2.1 已知AC=CB,P=10kN,求铰链A的约束力和杆DC所受的力。支架
的横梁AB与斜杆DC以铰链C相连,并以铰链A、D连接于铅直墙上。杆DC
三.平面汇交力系合成的解析法
1.力在坐标轴上的投影与力沿轴的分解
FR=FRx+FRy=FRxi+FRy j
2.合矢量投影定理
合矢量投影定理:合力在某一轴上的投影,等于各分力在
同一轴上投影的代数和。
即:FRx=Fx1+Fx2+…+Fxn =∑Fx FRy=Fy1+Fy2+…+Fyn =∑Fy
3.平面汇交力系合成的解析法
2、力偶矩
力偶中两力所在平面称为力偶作用面. 力偶两力之间的垂直距离称为力偶臂.
两个要素 a.大小:力与力偶臂乘积
b.方向:转动方向
力偶矩:M=±Fd=±2A△ABC,代数量, 逆为正,顺为负。单位:N· m,或kN· m
力偶不能合成为一个力,或用一个力来等效替换; 力偶也不能用一个力来平衡。
四.同平面内力偶的等效定理
ix
例2.4 图示踏板,各杆自重不计,已知:F、α、l、B点坐标 (xB、yB)。求(1)力F对A点之矩;(2)平衡时杆CD的拉力。
理论力学第二章.

(a)
(b) 图2.1 力多边形
(c)
3
从图2—1b可见,在合成该平面汇交力的合力时,也可不必将中间力矢量
FR1 、 FR 2 一一求出。只需从力 F1 的终点B作出与力 F2 相等的矢量 BC ,再从
BC 的终点C作出一个与力 F3相等的矢量 CD ,最后从CD 的终点D作出一个与 F4 力相等的矢量力相等的矢量 DE 。连接 F1 的始点A与最后一个矢量的终点
FR F1 F2 Fn Fi
(2-1)
三、平面汇交力学平衡的几何条件
当力多边形自行闭合,即合力 FR 0,于是平面汇交力系平衡;反之,若平面汇 交力系平衡,即合力 FR 0。所以,平面汇交力系平衡的充分必要条件是:力多边形 自行闭合,或平面汇交力系的合力等于0,即
例2.1 AC和BC两杆用铰链C连接,两杆的另一端分别铰支在墙上,如 图2-2(a)示。在点C悬挂重10kN的物体,已知AB=AC=2m,BC=1m,如杆重 不计,求两杆所受的力。 解(1)取销钉C为研究对象; (2)画销钉C的受力图,如图2-2(b)示; (3)作封闭力三角形,如图2-2(c)示。 由于封闭的力三角形与三角形ABC相似,故
所以
F=11.5kN , NB=23.1kN
由作用力和反作用力的关系,碾子对障碍物的压力等于 23.1kN。
此题也可用力多边形方法用比例尺去量。
例2-3 已知: AC CB, F 10 kN ,各杆自重不计; 求:CD 杆及铰链 A 的受力.
解:CD 为二力杆,取 AB杆,画受力图. 用几何法,画封闭力三角形.
求:在中心作用的水平力F的大小和碾子对障碍物的压力。
解: ①选碾子为研究对象 ②取分离体画受力图
理论力学第二章

Ph
l
q dx x
0
l
0
x2 l
q dx
§2-4 平面力偶理论
一.力偶和力偶矩 1.力偶
由两个等值、反向、不共线的(平行)力组
成的力系称为力偶,记作 F, F
2.力偶矩 力偶中两力所在平面称为力偶作用面 力偶两力之间的垂直距离称为力偶臂 两个要素 a.大小:力与力偶臂乘积 b.方向:转动方向 力偶矩
力对点之矩是一个代数量,它的绝对值等于力的 大小与力臂的乘积,它的正负:力使物体绕矩心逆时 针转向时为正,反之为负.常用单位N·m或kN·m
二、合力矩定理 平面汇交力系
MO FR MO Fi
该结论适用于任何合力存在的力系
三、力矩与合力矩的解析表达式
MO F MO Fy MO Fx
求: 光滑螺柱AB所受水平力. 解:由力偶只能由力偶平衡的性 质,其受力图为
M 0
FAl M1 M2 M3 0
解得
FA
FB
M1 M2 l
M3
200N
例2-10 已知 M 2kN m,OA r 0.5m,θ 30 ;
1
求:平衡时的 M 2及铰链O,B处的约束力. 解:取轮,由力偶只能由力偶平衡的性质,画受力图.
例2-1
已知: P=20kN,R=0.6m, h=0.08m 求:
1.水平拉力F=5kN时,碾子对地面及障碍物的压力? 2.欲将碾子拉过障碍物,水平拉力F至少多大?
3.力F沿什么方向拉动碾子最省力,及此时力F多大??
解: 1.取碾子,画受力图. 用几何法,按比例画封闭力四边形
理论力学第2章

则: (0.2785 FR F )i (0.1691 F ) j (0.9463 F )k ;
求力系的主矩:即求各力对 在坐标轴上的矩 M xi , M yi , M zi 方法一:利用分力计算力矩:
x 3F
z
F3 y
3F
M x ( F3 ) M x ( F3 x ) M x ( F3 y ) M x ( F3z ) 6 6 0( F )(2b) 0 Fb; F3 z 6 3 M y ( F3 ) 0;
2 2
m
y
12420 3420
FR
o
x
对A、D点的主矩分别为:
M A M Ai 0.3F2 0.2F3 25N m M D M Di 0.4F1 sin 60 0.3F2 0.2F3 4.282N m
m
A
O M O
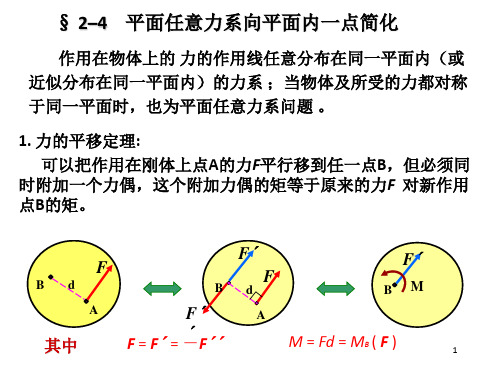
d
M d F
一个力不仅可以分解为几个力, 还可以分解为力和力偶。
2.2.2 力系等效定理
充要条件:两力系的主矢相等, 对同一点的主矩相等. 1 2 FR FR 1 2 Mo Mo
矩心O是任意选择的
1 1 1 M o M o OO FR 2 2 2 M o M o OO FR 1 2 Mo Mo
1. 几何法(力多边形法) 注意:主矢没有 作用点!
F3
F2
F4
F 1
F3
F4
F1
' FR F22 解析法力系的主矢
' FR 的三个投影为:
Fi Fxii Fyi j Fzi k
理论力学第二章

(1)
(2)
0
60
T2
T1 α
由(2)式解得:
N D Q - T2 sin
Q
Q 2 P sin 60
0
Q
3P
ND
END
(b)
[习题2-1] B
600
A
SAB SAC
A
B SAB
300
W (a)
W
200 700
C
∑X=0:
2.1 平面汇交力系合成与平衡的几何法 一、合成的几何法 1. 两个共点力的合成 公理3:作如右图所示。
A
F1
R α φ
F2
也可用力的三角形法则来作, 如右下图所示R : 合力R大小和方向可直接由图上
按比例尺寸量取,此法叫图解法。
除了上面介绍的图解法之外,也可用三角函数来计算 合力R的大小和方向: 由余弦定理求合力R的大小:
C
解: 2)用解析法求解
a. 取AC杆为分离体: b.画其受力图:
600
(二力体)
c.选择坐标系:
(1)
B y A RA
W = 5kN (三力体)
d.列平衡方程: ΣX=0: SBC = RA
ΣY=0: SBC· sin30o+RA· sin30o= W C x 将(1)代入得: SBC = RA 0 30 = W/(2· sin30o) SBC = W = 5 kN
第一篇
静力学
Statics
第2章
平面汇交力系 与平面力偶理论
引 言
力系的概念:
平面力系 ------ ? ...... 在同一平面上。 空间力系 ------ ???
理论力学 第二章

扭矩扳手
2-3 平面力对点之矩的概念及计算
一、力对点的矩(力矩) 力对点的矩(力矩)
M O ( F ) = ± F ⋅ d ,单位N•m或KN•m 单位N KN•
→
→
① ②
是代数量。 M O ( F ) 是代数量。
M O ( F ) 正负判定: 正负判定:
→
→
M O (F ) (F
+
→ →
-
③ 当F=0或d=0时, O (F ) =0。 =0或 =0时 M =0。 点O为矩心,d为力臂。 为矩心, 为力臂。 角 形面积,或是矢量积的模。 面积,或是矢量积的模。 ④ M O (F ) = ± 2⊿AOB= r × F 2⊿AOB= 力对点0矩的大小等于2 力对点0矩的大小等于2倍三
Fx = X i , F y = Y j
F = X +Y
2 2
→
→ →
→
X cos α = F
Y cos β = F
2-2 平面汇交力系合成与平衡的解析法
区分力沿轴的分力和力在两轴上的投影: 区分力沿轴的分力和力在两轴上的投影: 力沿轴的分力和力在两轴上的投影 • 分力是矢量,投影是代 分力是矢量, 数量,二者性质不同。 数量,二者性质不同。 • 在直角坐标系中,投影 在直角坐标系中, 的大小与分力的大小相 但在斜角坐标系中, 同,但在斜角坐标系中, 二者不等。 二者不等。
∑F = 0 ix
− FBA + F cos60 − F2 cos30 = 0 1
o o
∑F =0 iy
FBC − F cos30 − F cos60 = 0 1 2
o o
F = F2 = P 1
解得: FC = 27 32kN 解得: B .
理论力学第2章平面任意力系
空载时轨道A 、 B的约束反力,并问此起重机在使用过程中有无翻
倒的危险。
解:
(1)起重机受力图如图
(2)列平衡方程 :
MA 0:
Q
Q(6 2) RB 4 W 2 P(12 2) 0
MB 0:
Q(6 2) W 2 P(12 2) RA 4 0
6m
解方程得:
W
P
12m
RA 170 2.5P
FR' Fi Fxi Fy j
MO MO (Fi )
3. 平面任意力系的简化结果
(1)FR´= 0,Mo ≠ 0, (2)FR´ ≠ 0,Mo = 0, (3)FR´≠ 0,Mo ≠ 0, (4)FR´= 0,Mo = 0,
合力偶,合力偶矩,MO MO (Fi )
合力,合力作用线通过简化中心O。
3
F2
j
F3
x
(437.6)2 (161.6)2
F1
1 1
100
Oi
1 2
466.5N
200
MO 21.44N m
y
合力及其与原点O的距离如图(c) 。 MO
x
y
d
x
O
FR FR′ 466.5N FR´
FR
O
d MO 45.96mm
(b)
(c)
FR
10
例11 水平梁AB受按三角形分布的载荷作用,如图示。载荷的
M
l
l
30
B
D
° F
3l
P
q
A
21
解:T字形刚架ABD的受力如图所示。
M
l
l
Fx 0
30
B
FAx 1 • q • 3a Fcos30 0
理论力学第二章汇交力系与平面力偶系

FBC= 224.23 kN 代入(3)、(4)解得
tan θ = 1.631 , θ = 58.5°
FA= 303.29 kN
y
FBC
FD
C
45°
30°
x
W2
y
FA
θB
x
45°
W1 F'BC
第二章 汇交力系与平面力偶系
§2–1 平面汇交力系的合成与平衡
投影法的符号法则: 当由平衡方程求得某一未知力的值
y
FBC
B 30°
x
FAB
FD 30° W
b
联立求解,得
FAB= -54.5kN , FBC= 74.5kN
反力FAB为负值,说明该力实际指向与图上假定指向相反。 即杆AB实际上受拉力。
第二章 汇交力系与平面力偶系
§2–1 平面汇交力系的合成与平衡
例2–5 如图已知W1=100 kN, W2=250 kN。不计各
Fx F cos
Fy
Fy F cos
O 2、力在空间直角坐标轴上的投影:
F
Fx x
一次投影法:
Z
Fx F cos Fy F cos
F
O
y
FZ F cos
第二章 汇交力系与平面力偶系
x
★§2–2 空间汇交力系的合成与平衡 二次投影法:
已知力F 和某一平面(oxy)的夹
角为θ,又已知力F 在该平面
杆自重,A,B,C,D各点均为光滑铰链。试求平衡状
态下杆AB内力及与水平的夹角。
A
θB
D
W1
45° C
30°
W2 第二章 汇交力系与平面力偶系
§2–1 平面汇交力系的合成与平衡
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章 力系的等效与简化2-1试求图示中力F 对O 点的矩。
解:(a )l F F M F M F M M y O y O x O O ⋅==+=αsin )()()()(F (b )l F M O ⋅=αsin )(F(c ))(sin cos )()()(312l l Fl F F M F M M y O x O O +--=+=ααF (d )2221sin )()()()(l l F F M F M F M M y O y O x O O +==+=αF2-2 图示正方体的边长a =0.5m ,其上作用的力F =100N ,求力F 对O 点的矩及对x 轴的力矩。
解:)(2)()(j i k i Fr F M +-⨯+=⨯=Fa A O m kN )(36.35)(2⋅+--=+--=k j i k j i Fam kN 36.35)(⋅-=F x M2-3 曲拐手柄如图所示,已知作用于手柄上的力F =100N ,AB =100mm ,BC =400mm ,CD =200mm ,α = 30°。
试求力F 对x 、y 、z 轴之矩。
解:)cos cos sin (sin )4.03.0()(2k j i k j F r F M αααα--⨯-=⨯=F D Ak j i αααα22sin 30sin 40)sin 4.03.0(cos 100--+-=力F 对x 、y 、z 轴之矩为:m N 3.43)2.03.0(350)sin 4.03.0(cos 100)(⋅-=+-=+-=ααF x M m N 10sin 40)(2⋅-=-=αF y Mm N 5.7sin 30)(2⋅-=-=αF z M2—4 正三棱柱的底面为等腰三角形,已知OA=OB =a ,在平面ABED 内沿对角线AE 有一个力F , 图中θ =30°,试求此力对各坐标轴之矩。
习题2-1图A r A习题2-2图(a )习题2-3图(a)ABr 解:)sin 45sin cos 45cos cos ()(k j i i F r F M θθθ+︒+︒-⨯=⨯=F a A O )45sin cos sin (k j ︒+-=θθaF 力F 对x 、y 、z 轴之矩为:0)(=F x M230sin )(aF aF M y -=︒-==F Fa aF M z 4645sin 30cos )(=︒︒=F2-5 如图所示,试求力F 对A 点之矩及对x 、y 、z 轴之矩。
解:F r F M ⨯=AB A )(5354F F d d d-k j i = =)743(51k j i -+-Fd)34(5)(j i j F M +⨯=Fd O力F 对x 、y 、z 轴之矩为:0)(=F x M ;0)(=F y M ;Fd M z 54)(-=F2—6 面。
求这四个力偶的合力偶。
解:4321M M M M M+++=k j i )53()54(43241M M M M M +--+-=m N 8.1284.14⋅---=k j i2-7 已知一平面力系对A (3,0),B A B = 0,M C =–10kN ·m 。
试求该力系合力的大小、方向和作用线。
解:由已知M B = 0知合力F R 过B 点; 由M A = 20kN ·m ,M C = -10kN ·m 知F R 位于A 、C 间,且CD AG 2=(图a )在图(a )中,设 OF = d ,则 θcot 4=dCD AG d 2)sin 3(==+θ (1)θθsin )25.4(sin dCE CD -== (2)即 θθsin )25.4(2sin )3(dd -=+d d -=+93, 3=d F 点的坐标为(-3, 0) 合力方向如图(a ),作用线如图过B 、F 点;习题2-4图习题2-5图习题2-6图 (a ) 43 M 1M 2 M 3M 4习题2-7图34tan =θ 8.4546sin 6=⨯==θAG8.4R R ⨯=⨯=F AG F M AkN 6258.420R ==F 即 )kN 310,25(R =F作用线方程:434+=x y讨论:本题由于已知数值的特殊性,实际G 点与E 点重合。
2-8 已知F 1 = 150N ,F 2 = 200N ,F 3 = 300N ,F =F '= 200N 。
求力系向点O 的简化结果,并求力系合力的大小及其与原点O 的距d 。
80200100131121FFF'1yRF 'o2.7xoM yRF oxd解:N .64375210145cos 321-=--︒-=∑F F F F xN .61615110345sin 321-=+-︒-=∑F F F F ym N 44.2108.02.0511.045sin )(31⋅=-⨯+⨯︒=∑F F F M O F向O 点简化的结果如图(b );合力如图(c ),图中N 5.466)()(22'R =∑+∑=y x F F F ,m N 44.21⋅=O M合力N 5.466'R R ==F F ,mm 96.45R==F M d O2-9 图示平面任意力系中F 1 = 402N ,F 2 = 80N ,F 3 = 40N ,F 4 = 110M ,M = 2000 N ·mm 。
各力作用位置如图所示,图中尺寸的单位为mm 。
求(1)力系向O 点简化的结果;(2)力系的合力的大小、方向及合力作用线方程。
FFFF (0,30)(20,20)(20,-30)(-50,0)45yxRF 'ooM yxoRF (0,-6)解:N 15045cos 421R -=--︒=∑=F F F F F x x045sin 31R =-︒=∑=F F F F y y(a)yxRF O θθCG ADEF423d5.4-习题2-8图习题2-9图N 150)()(22'R =∑+∑=y x F F Fm m N 900305030)(432⋅-=--+=∑=M F F F M M O O F向O 点简化结果如图(b );合力如图(c ),其大小与方向为N 150'R R i F F -==设合力作用线上一点坐标为(y x ,),则x y O O yF xF M M R R R )(-==F将O M 、'R y F 和'R x F 值代入此式,即得合力作用线方程为:mm 6-=y2-10 图示等边三角形板ABC ,边长a ,今沿其边缘作用大小均为F P 的力,方向如图(a )所示,求三力的合成结果。
若三力的方向改变成如图(b )所示,其合成结果如何?解(a )0'R =∑=i F Fa F a F M A P P 2323=⋅=(逆) 合成结果为一合力偶a F M P 23=(逆) (b )向A 点简化i F P 'R 2F -=(←)a F M A P 23=(逆) 再向'A 点简化,a F M d A 43'R==合力i F P R 2F A -=(←)2-11 图示力系F 1 = 25kN ,F 2 = 35kN ,F 3 = 20kN ,力偶矩m = 50kN ·m 。
各力作用点坐标如图。
试计算(1)力系向O 点简化的结果;(2)力系的合力。
解(1)向O 点简化 kN 10'R k F F =∑=i)(F M M O O ∑=mkN )10580(200 002 3- 35- 0 00 2 2 250 00 2- 3 50⋅+-=+++=j i kj i k j i k j i j(2)合力kN 10R k F =设合力作用线过点)0,,(y x ,则F F FF F F 习题2-10图 F F F A 'A d R F F 'A M 习题2-11图z xoM M a)0,0,(a A RF 'RFj i M kj i 10580100 00 +-==O x y 5.10-=x ,0.8-=y ,0=z合力作用线过点(-10.5,-8.0,0)。
2-12 图示载荷F P =1002N , F Q =2002N ,分别作用在正方形的顶点A 和B 处。
试将此力系向O 点简化,并求其简化的最后结果。
解:N )(100P k i F +-=N )(200Q k j i F +--=mN )300200(200200- 20001 1 1000 1000 0 1 )(⋅-=-+-=j i kj i k j i F O MN )300200300('R k j i F F +--=∑=iQ P F F F r M ⨯+⨯=B A O合力 N )300200300('R R k j i F F +--== 设合力过点(0,,y x ),则j i M kj i 300200300200- 3000 -==-O y x得 1=x ,32=y ,0=z 即合力作用线过点(0,32,1)。
2-13 图示三力F 1、 F 2和 F 3的大小均等于F ,作用在正方体的棱边上,边长为a 。
求力系简化的最后结果。
解:先向O 点简化,得k F F ='R , k j M Fa Fa O +=因0'R ≠⋅O M F ,故最后简化结果为一力螺旋。
该力螺旋k F F ='R ,k M Fa = 设力螺旋中心轴过)0,,(y x O ',则 j M F r Fa O ==⨯'1R即j k j i Fa Fy x = 0 00 得 a x -=,0=y ,0=z即合成最后结果的力螺旋中心轴上一点坐标为(0,0,a -)。
习题2-12图习题2-13图2-14 某平面力系如图所示,且F 1=F 2=F 3=F 4= F ,问力系向点A 和B 简化的结果是什麽?二者是否等效?解:(1)先向A 点简化,得)(2Rj i F -='F ;Fa M A 2= (2)再向B 点简化,得)(2Rj i F -='F ;0=B M 二者等效,若将点B 处的主矢向点A 平移,其结果与(1)通。
2-15 某平面力系向两点简化的主矩皆为零,此力系简化的最终结果可能是一个力吗?可能是一个力偶吗?可能平衡吗?解:可能是一个力,也可能平衡,但不可能是一个力偶。
因为(1),平面力系向一点简化的结果为一主矢和一主矩,而由已知是:向两点简化的主矩皆为零,即简化结果可能为(0,R ='A M F ),(0,R ='B M F )(主矢与简化中心无关),若0R≠'F ,此时已是简化的最后结果:一合力'R R F F =经过A 点,又过B 点。
