胡汉才编著《理论力学》课后习题答案第2章力系的简化
《理论力学》第二章力系的简化习题解

第二章力系的简化习题解[习题2-1] 一钢结构节点,在沿OA,OB,OC的方向上受到三个力的作用,已知,,,试求这三个力的合力.解:作用点在O点,方向水平向右.[习题2-2] 计算图中已知,,三个力分别在轴上的投影并求合力. 已知,,.解:合力的大小:方向余弦:作用点:在三力的汇交点A.[习题2-3] 已知,,,,求五个力合成的结果(提示:不必开根号,可使计算简化).解:合力的大小: 方向余弦:作用点:在三力的汇交点A.[习题2-4] 沿正六面体的三棱边作用着三个力,在平面OABC内作用一个力偶. 已知,,,.求力偶与三个力合成的结果.解:把,,向平移,得到:主矢量:的方向由E指向D.主矩:方向余弦:[习题2-5] 一矩形体上作用着三个力偶,,.已知,,,,求三个力偶合成的结果.解:先把在正X面上平行移动到x轴.则应附加力偶矩:把沿轴上分解:主矩:方向余弦:[习题2-6] 试求图诸力合成的结果.解:主矢量:竖向力产生的矩顶面底面斜面-0.76 0.2 0.75 主矩:方向余弦:[习题2-7] 柱子上作有着,,三个铅直力, 已知,,,三力位置如图所示.图中长度单位为,求将该力系向点简化的结果.解:主矢量:竖向力产生的矩3.5 1.7 0主矩:方向余弦:[习题2-8] 求图示平行力系合成的结果(小方格边长为)解:主矢量:ABCD8.4 -4.35主矩:方向余弦:[习题2-9] 平板OABD上作用空间平行力系如图所示,问应等于多少才能使该力系合力作用线通过板中心C.解:主矢量:由合力矩定理可列出如下方程:[习题2-10] 一力系由四个力组成。
已知F1=60N,F2=400N,F3=500N,F4=200N,试将该力系向A点简化(图中长度单位为mm)。
解:主矢量计算表0 0 600 200 0300 546.41 -140方向余弦:-110.564 120 0 主矩大小:方向余弦:[习题2-11]一力系由三力组成,各力大小、作用线位置和方向见图。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
华科理论力学教材(第2版2020年7月第4次印刷)课后习题解答(z2)

1.4.2. 构架整体、AB 部分、弯杆 BC。 P A
B
C
解:2.
1.4.3. 三铰拱整体、AB 部分、BC 部分。 P
F
B
A
C
解:3.
F A
B
F' CBy
FCBy
P
F' CBx
FA
FCBx
FCy
C FCx
目录
1.4.4. A 形构架整体、AB 杆、BC 杆、DE 杆及销钉 B(力 P 作用在销钉 B 上)。
的大小。
FR
F2 60
F1
60
F3
题 2.3 图
目录
解:(1) R F1 F2 F3 上式向 F2 所在方向投影得:
1 2
R
F2
F1
cos
30
∴ R 2F2 2F1
3 100 2173 2
3 200N 2
∴ R 的大小为 200N,指向与假设相反。
( 2 ) Z 0 , ( 设 Z ' 为 F2 的 正 方 向 ) F2 F1 cos 30 0
上的 G 通过三力汇交法得到 O 处的合力为 45 度,则本次作业也认为是正确的
1.4.9.上题中,若销钉 A、C 均与 AC 杆固连,画出 AC 杆受力图。又若销钉 A、B 均与 AB 杆固连,画出 AB 力图。 解:[9.1]若销钉 A、C 均与 AC 杆固连,画出 AC 杆受力图
F
' A
A
F地
题第一步,只要求真解在受力图的可能范围内,通过以后计算可知,销钉 B 对构件 BA 的作
用力为 0,故可假设为任何方向。 1.4.11. 机构整体、连杆 AB、圆盘 O、滑块 B。
理论力学课后的习题及答案解析...doc
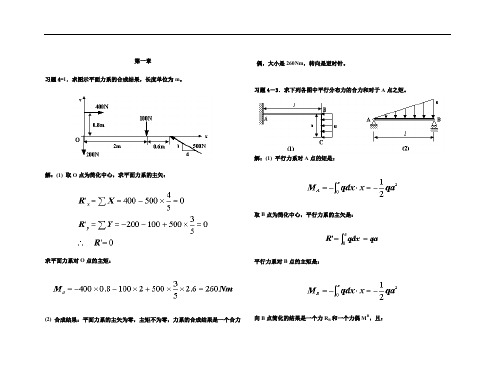
第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
理论力学课后答案

C(a-2)DR(a-3)(b-1)DR第1篇 工程静力学基础第1章 受力分析概述1-1 图a 、b 所示,Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影,并比较分力与力的投影。
习题1-1图解:(a )图(c ):11 s i n c o s j i F ααF F +=分力:11 cos i F αF x = , 11 s i n j F αF y =投影:αcos 1F F x = , αs i n 1F F y =讨论:ϕ= 90°时,投影与分力的模相等;分力是矢量,投影是代数量。
(b )图(d ): 分力:22)cot sin cos (i F ϕααF F x -= ,22sin sin j F ϕαF y = 投影:αcos 2F F x = , )cos(2αϕ-=F F y讨论:ϕ≠90°时,投影与分量的模不等。
1-2 试画出图a 和b习题1-2图比较:图(a-1)与图(b-1)不同,因两者之F R D 值大小也不同。
(c ) 22x(d )1-3 试画出图示各物体的受力图。
习题1-3图B或(a-2)B(a-1)(b-1)F(c-1) 或(b-2)(e-1)F(a)1-4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重,杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图,并加以讨论。
习题1-4图1-5 图示刚性构件ABC 由销钉A 和拉杆D 支撑,在构件C 点作用有一水平力F 。
试问如果将力F 沿其作用线移至D 或E (如图示),是否会改为销钉A 的受力状况。
解:由受力图1-5a ,1-5b 和1-5c 分析可知,F 从C 移至E ,A 端受力不变,这是因为力F 在自身刚体ABC 上滑移;而F 从C 移至D,则A 端受力改变,因为HG 与ABC 为不同的刚体。
1(f-1)'A(f-2)1O(f-3)F F'F 1(d-2)F yB 21(c-1)F A B1B FDx y(b-2)1(b-3)F yB 2 A A B1B F习题1-5图AxF(b-3)E D(a-3)B(b-2)(b-1)F 'CBC(c)AxF1-6 试画出图示连续梁中的AC 和CD 梁的受力图。
胡汉才编著理论力学课后习题答案第2章力系的简化

力系的简化第二章,的力F,5)两点(长度单位为米),且由A指向B.通过A(3,0,0),B(0,42-1 。
,对z轴的矩的大小为在z轴上投影为22 /5。
答:F / ;6 F上和y,c,则力F在轴z2-2.已知力F的大小,角度φ和θ,以及长方体的边长a,b的矩x ;F对轴;Fy= 的投影:Fz=F 。
)= M ( x)··()(··;-··;cos=FFz=F答:φsinφbFy=θFsincosφφcosφ+cMxFcos41-图2 图2-40F,则该力,若F=100N,4)两点(长度单位为米)),B(0,2-3.力4通过A(3,4、0 。
,对x轴的矩为在x轴上的投影为320N.m;答:-60NAE内有沿对角线,在平面ABED2-4.正三棱柱的底面为等腰三角形,已知OA=OB=a °,则此力对各坐标轴之矩为:α=30的一个力F,图中。
)= );M(F= ((MF)= ;MF zYx6Fa/4 =(F);M)=0,(F)=-Fa/2MF答:M(zxy2-5.已知力F的大小为60(N),则力F对x轴的矩为;对z轴的矩为。
答:M(F)=160 N·cm;M(F)=100 N·cmzx43-图2 2图-42O2-6.试求图示中力F对点的矩。
M(F)=Flsinα解:a: O M(F)=Flsinαb: Oα+ Flcos)sinc: M(F)=F(l+lα2O13??22?lM?Fl?Fsin d: 2o1。
轴的力矩M1000N2-7.图示力F=,求对于z z图题2-8 7题2-图。
试求=40N,M=30N·m=40N2-8.在图示平面力系中,已知:F=10N,F,F321其合力,并画在图上(图中长度单位为米)。
解:将力系向O点简化=30N F=F-R12X40N -=R=-F3V R=50N ∴m )··3+M=300N+FF主矩:Mo=(+F312d=Mo/R=6mO合力的作用线至点的矩离iiRR0.8-=),(cos,=0.6),(cos合力的方向:iR )=-53,°08'(iR ,')(=143°08,内作用一力偶,其矩M=50KNGA转向如图;又沿·m,2-9.在图示正方体的表面ABFE2RR =50。
第2章—力系的简化—工程力学(静力学和材料力学)课后习题答案

工程力学(静力学与材料力学)习题详细解答(第2章)习题2-2图第2章 力系的简化2-1 由作用线处于同一平面内的两个力F 和2F 所组成平行力系如图所示。
二力作用线之间的距离为d 。
试问:这一力系向哪一点简化,所得结果只有合力,而没有合力偶;确定这一合力的大小和方向;说明这一合力矢量属于哪一类矢量。
解:由习题2-1解图,假设力系向C 点简化所得结果只有合力,而没有合力偶,于是,有∑=0)(F C M ,02)(=⋅++−x F x d F ,dx =∴,F F F F =−=∴2R ,方向如图示。
合力矢量属于滑动矢量。
2-2 已知一平面力系对A (3,0),B (0,4)和C (-4.5,2)三点的主矩分别为:M A 、M B 和M C 。
若已知:M A =20 kN·m 、M B =0和M C =-10kN·m ,求:这一力系最后简化所得合力的大小、方向和作用线。
解:由已知M B = 0知合力F R 过B 点;由M A = 20kN ·m ,M C = -10kN ·m 知F R 位于A 、C 间,且CD AG 2=(习题2-2解图)在图中设OF = d ,则θcot 4=dCD AG d 2)sin 3(==+θ (1) θθsin )25.4(sin d CE CD −== (2)即θθsin )25.4(2sin )3(dd −=+ d d −=+93 3=d习题2-1图习题2-1解图R∴ F 点的坐标为(-3, 0)合力方向如图所示,作用线过B 、F 点; 34tan =θ 8.4546sin 6=×==θAG 8.4R R ×=×=F AG F M A kN 6258.420R ==F 即 )kN 310,25(R=F 作用线方程:434+=x y 讨论:本题由于已知数值的特殊性,实际G 点与E 点重合。
2-3三个小拖船拖着一条大船,如图所示。
理论力学课后习题及答案解析..

第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
胡汉才编著《理论力学》课后习题答案 第1章静力学基本概念

第一章 静力学基本概念
1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量
B.自由矢量
C.定位矢量
1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相
反,则其合力可表为( C )。
A.1F –2F
B.2F - 1F
C.1F +2F
图1-18 图1-19 1-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小 x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6
B. 70.0
C. 136.6
D.25.9
1-4 力的可传性只适用于 A 。
A. 刚体
B. 变形体
1-5 加减平衡力系公理适用于 C 。
A. 刚体;
B. 变形体;
C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0
B. F/2
C. F/6
D.-F/3
1-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为: Fx = -402N ,Fy = 302N ,Fz = 502 N 。
图1-20 图1-21。
理论力学课后习题答案Word版

理论力学
第二章:
友情提示:本资料代表个人观点,如有帮助请下载,谢谢您的浏览!
理论力学第二版第二章答案 罗特军

w.
kh
da
w.
三角形 EAB
1 aymax 2
co
正方形 ABCD
a2
静力学习题及解答—力系的简化
2.12 求图示均质混凝土基础重心的位置(图中长度单位为 m )
魏
体积 Si mm3 图形 1 图形 2 图形 3 图形形心:xC 10.08 2.40 1.89
泳
形心坐标 x mm 1.8 4.6 0.9 1.0 1.0 2.5
静力学习题及解答—力系的简化
2.6 底面为正方形的长方体棱边上作用有 8 个大小均等于 FP 的力,如图所示。试 求该力系的简化结果。
魏
泳
涛
m
因此,原力系合力为 4 FP k ,作用线过正方形中点。
课
后
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
案
网
ww
w.
kh
子力系 3: F7 和 F8 构成的力偶,力偶矩矢量为 FP ak 。
S 0
魏
π
y sin x
0
dy sin xdx 2
0
泳
π
涛
da w. co m
yC
π y sin x 1 1 π 2 π y d x d y d x y d y sin xdx 0 0 0 S S 2S 8
由对称性, xC
π 2
课
后
答
四川大学 建筑与环境学院 力学科学与工程系 魏泳涛
w.
co
静力学习题及解答—力系的简化
2.11 在图示变长为 a 的均质正方形薄板 ABCD 中挖去等腰三角形 EAB , 试求 E 点 y 坐标的最大值 ymax ,使剩余薄板的重心仍在板内。
理论力学第二章 力系的简化习题解

1F 2F 3F 0135090O第二章 力系的简化习题解[习题2-1] 一钢结构节点,在沿OA,OB,OC 的方向上受到三个力的作用,已知kN F 11=,kN F 41.12=,kN F 23=,试求这三个力的合力.解:01=x F kN F y 11-=)(145cos 41.102kN F x -=-= )(145sin 41.102kN F y ==kN F x 23= 03=y F)(121030kN F F i xi Rx =+-==∑=00113=++-==∑=i yi Ry F F122=+=Ry Rx R R F F 作用点在O 点,方向水平向右.[习题2-2] 计算图中已知1F ,2F ,3F 三个力分别在z y x ,,轴上的投影并求合力. 已知kN F 21=,kN F 12=,kN F 33=.解:kN F x 21= 01=y F 01=z F)(424.0537071.01cos 45sin 022kN F F x =⨯⨯==θ)(567.0547071.01sin 45sin 022kN F F y =⨯⨯==θ)(707.0707.0145sin 022kN F F z =⨯== 03=x F 03=y F kN F z 33= )(424.20424.0230kN F F i xi Rx =++==∑=)(567.00567.0030kN F F i yi Ry =++==∑=)(707.33707.003kN F F i zi Rz =++==∑=合力的大小:)(465.4707.3567.0424.2222222kN F F F F Rz Ry Rx R =++=++=方向余弦:4429.0465.4424.2cos ===R Rx F F α 1270.0465.4567.0cos ===R Ry F F βy8302.0465.4707.3cos ===R Rz F F γ 作用点:在三力的汇交点A.[习题2-3] 已知N F 621=,N F 322=,N F 13=N F 244=,N F 75=,求五个力合成的结果(提示:不必开根号,可使计算简化).解:01=x F 01=y F N F z 621-=02=x F N F y 322= 02=z F N F x 13-= 03=y F 03=z F)(221222460cos 45cos 0044N F F x =⨯⨯==)(3223222460sin 45cos 0044N F F y -=⨯⨯-=-=)(4222445sin 044N F F z =⨯==)(353)62(3457cos sin 22255N F F x =⨯++⨯==θγ)(454)62(3457sin sin 22255N F F y =⨯++⨯==θγ )(62)62(34627cos 22255N F F z =++⨯==γ)(43210050N F F i xi Rx =++-+==∑=)(4432032050N F F i yi Ry =++-++==∑=)(462400625N F F i zi Rz =++++-==∑=合力的大小:)(93.634444222222N F F F F Rz Ry Rx R ==++=++=方向余弦:33344cos ===R Rx F F α33344cos ===RRy F F β 33344cos ===R Rz F F γ "'08445433arccos====γβα 作用点:在三力的汇交点A.[习题2-4] 沿正六面体的三棱边作用着三个力,在平面OABC 内作用一个力偶. 已知N F 201=,N F 302=,N F 503=,m N M ⋅=1.求力偶与三个力合成的结果.解:把1F ,2F ,3F 向1O 平移,得到:主矢量: 0302050213---=--=F F F F R)(42.0202.0)(11m N F F M x ⋅-=⨯-=⨯-= 0)(1=F M y0)(1=F M z)(62.0302.0)(22m N F F M x ⋅-=⨯-=⨯-= )(5.415.03015.0)(22m N F F M y ⋅=⨯=⨯=0)(2=F M z 0)(3=F M x)(5.715.05015.0)(33m N F F M y ⋅-=⨯-=⨯-=0)(3=F M zM 的方向由E 指向D.)(25.825.65.2)()(3111m N F M F M M O O OC ⋅=+=+=∑)(8.01502002001sin 22m N M M x ⋅=+⨯==θ)(6.01502001501cos 22m N M M y ⋅-=+⨯-=-=θA 3F mm图题42-D图题52-xya0=z M)(2.98.0064)(31m N M F M Mx i i x x⋅-=++--=+=∑∑=)(6.36.05.75.40)(31m N M F M M y i i y y⋅-=--+=+=∑∑=00000)(31=+++=+=∑∑=z i i z zM F M M主矩:)(88.90)6.3()2.9()()()(222222m N M M M M z y x O ⋅=+-+-=++=∑∑∑方向余弦:9312.088.92.9cos 0-=-==∑M M xα 3644.088.96.3cos 0-=-==∑M M yβ 088.90cos 0===∑M Mzγ [习题2-5] 一矩形体上作用着三个力偶),('11F F ,),('22F F ,),('33F F .已知N F F 10'11==,N F F 16'22==,N F F 20'33==,m a 1.0=,求三个力偶合成的结果.解:先把1F 在正X 面上平行移动到x 轴. 则应附加力偶矩:)(11.010)(11m N a F F M x ⋅=⨯==)(1)(11m N F M M x x ⋅==)(22.010211m N a F M y ⋅-=⨯-=⋅-=01=z M把2F 沿z y ,轴上分解:)(314.117071.01645cos 022N F F y =⨯==)(314.117071.01645sin 022N F F z =⨯== 02=x M)(263.22.0314.11222m N a F M z y ⋅-=⨯-=⋅-= )(263.22.0314.11222m N a F M y z ⋅=⨯=⋅=03=x M 03=y M)(21.02033m N a F M z ⋅-=⨯-=⋅-=100131=++==∑∑=i xi xM M)(263.40263.2231m N M M i yi y⋅-=+--==∑∑=)(263.02263.2031m N M Mi zi z⋅=-+==∑∑=主矩:)(387.4263.0)263.4(1)()()(222222m N M M M M z y x O ⋅=+-+=++=∑∑∑方向余弦:2280.0387.41cos 0===∑M Mxα 9717.0387.4263.4cos 0=-==∑M M y β 0599.0387.4263.0cos 0===∑M M zγ [习题2-6] 试求图诸力合成的结果. 解: 主矢量:0725=-+=R F)(086.175.02.0)76.0()()()(222222m N M M M M z y x O ⋅=++-=++=∑∑∑方向余弦:6996.0086.176.0cos 0-=-==∑M M xα1842.0086.12.0cos 0===∑M M yβ 6906.0086.175.0cos 0===∑M M zγ[习题2-7] 柱子上作有着1F ,2F ,3F 三个铅直力, 已知kN F 801=,kN F 602=, kN F 503=,三力位置如图所示.图中长度单位为mm ,求将该力系向O 点简化的结果.解:)(190506080kN F -=----= 主矢量: )(891.307.15.3)()()(222222m N M M M M z y x O ⋅=++=++=∑∑∑方向余弦:8995.0891.35.3cos 0===∑M Mxα 4369.0891.37.1cos 0===∑M Myβ 0891.30cos 0===∑M Mzγ [习题2-8] 求图示平行力系合成的结果(小方格边长为mm 100)图习题82-题2—9图解: 0937712=---+=F主矢量:主矩:)(46.9)35.4(4.8)()(2222m kN M M M y x O ⋅=-+=+=∑∑方向余弦:8879.046.94.8cos 0===∑M M xα 4598.046.935.4cos 0=-==∑M M yβ [习题2-9] 平板OABD 上作用空间平行力系如图所示,问y x ,应等于多少才能使该力系合力作用线通过板中心C. 解: 主矢量:)(3046587kN F R -=-----= 由合力矩定理可列出如下方程: 43088854⨯-=⨯-⨯--y12064404=++y )(4m y =33066654⨯=⨯+⨯+x )(6m x =[习题2-10] 一力系由四个力组成。
理论力学 第2章力系的简化习题解答

第二章 力系的简化 习题解答2-1在立方体的顶点A 、H 、B 、D 上分别作用四个力,大小均为F ,其中1F 沿AC ,2F 沿IG ,3F 沿BE ,4F 沿DH 。
试将此力系简化成最简形式。
解:各力均在与坐标平面平行的面内,且与所在平面的棱边成45°角。
将力系向A 点简化,主矢'R F 在坐标轴上的投影为045cos 45cos '21=-=F F F Rx ,FF F F F F Ry 245cos 45cos 45cos 45cos '4321=+-+=,F F F F Rz 245cos 45cos '43=+= 。
用解析式表示为: ()k j F +=F R 2'设立方体的边长为a ,主矩A M 在坐标轴上的投影为 045cos 45cos 32=⋅+⋅-=a F a F M Ax , Fa a F a F M Ay 245cos 45cos 42-=⋅-⋅-= ,Fa a F a F M Az 245cos 45cos 42=⋅+⋅= 。
用解析式表示为:()k j M +-=Fa A 2。
因为,0'=⋅A R M F ,所以,主矢和主矩可以进一步简化为一个力,即力系的合力。
合力的大小和方向与主矢相同,'R R F F =;合力作用点的矢径为()i MF r a F R R =⨯=2'',所以,合力大小为2F ,方向沿对角线DH 。
2-2三力321,F F ,F 分别在三个坐标平面内,并分别与三坐标轴平行,但指向可正可负。
距离c b a ,,为已知。
问:这三个力的大小满足什么关系时力系能简化为合力?又满足什么关系时能简化为力螺旋?解:这力系的主矢为k j i 321'F F F F R ++=; 对O 点的主矩为k j i a F c F b F M O 213++=。
当主矢与主矩垂直时,力系能简化为合力。
(完整版)理论力学课后答案第二章

解 册究対繼*晦矍*曲:/」平衛ii 殳宦廉,交廉”的钓痕力耳欝珊谊寸c 乃向如I 用 b 陌示.収啪杯爺Cy*血平胡那论鬥式⑴* (?)峡立・解紂佔2…已暂 F 兰5 am N .棗与撑祎自虫不计匚求 BC'ffK 内力及铁员 的反力。
解该系统曼力如图(訂, 三力匸交于艰0・苴封訥的力 三角膠如图冷人祥得 屉二5OOON 』仏 二疔000 W2-2在铰链A 、B 处有力F i , F 2作用,如图所示。
该机 F i 与F 2的关系。
2-3铰链4杆机构CABD 的CD 边固定, 构在图示位置平衡,不计杆自重。
求力 30T >◎60°检(b)B解⑴柠点掐坐WAS 力如囲 归所示"H3平祈刖论咼节点瓦腿标歴覺力如国 所小*血丫轉理论得2S -F^ ccs 30fr -f ; cosW )0 =0^=-^=—^— = 1.553^F 、: - 0.644已扣两伦备車P A ^P L •处于T册状态,杆電不比求I )若片=丹=巴 角e -?2)若 P A - 300 B = 0血=?ffi 八5两轮受力分别 如图示■对A 辂育SX = 0* F 刚 cEjedO* — F\g oos$ = 0SY 二 0a F sx tin60T - F 屈 sinfl - P A = tj对 B 轮育 SX ■ 0, Fn ooa? - F,\&8^3(/ = 0 IV = 0. F rw sinff 下 F 斶 anJO* - P n =(1) 四牛封程嬴立求AL 爾<3-30*(2) 把拧-0\F A - 300 M 代入方社,联立解筹P fl = 100 N2-5如图2-10所示,刚架上作用力F 。
试分别计算力F解 M A (F) = -FbcoseM s [F) - -Fb cos0 + FosinB二F(osiii0-bcos0)2-6已知梁AB 上作用1力偶,力偶矩为M ,梁长为I ,梁重不计。
理论力学第二章课后习题答案

理论力学第二章课后习题答案·12·理论力系第2章平面汇交力系与平面力偶系一、是非题(恰当的在括号内踢“√”、错误的踢“×”)1.力在两同向平行轴上投影一定相等,两平行相等的力在同一轴上的投影一定相等。
2.用解析法求平面呈报力系的合力时,若挑选出相同的直角坐标轴,其税金的合力一定相同。
(√)3.在平面汇交力系的平衡方程中,两个投影轴一定要互相垂直。
(×)4.在维持力偶矩大小、转为维持不变的条件下,可以将例如图2.18(a)右图d处为平面力偶m移至例如图2.18(b)所示e处,而不改变整个结构的受力状态。
(×)(a)图2.185.如图2.19所示四连杆机构在力偶m1m2的作用下系统能保持平衡。
6.例如图2.20右图皮带传动,若仅就是包角发生变化,而其他条件均维持维持不变时,并使拎轮旋转的力矩不能发生改变。
(√图2.19图2.201.平面呈报力系的均衡的充要条件就是利用它们可以解言的约束反力。
2.三个力汇交于一点,但不共面,这三个力3.例如图2.21右图,杆ab蔡国用数等,在五个力促进作用下处在平衡状态。
则促进作用于点b的四个力的合力fr=f,方向沿4.如图2.22所示结构中,力p对点o的矩为plsin。
5.平面呈报力系中作力多边形的矢量规则为:各分力的矢量沿着环绕着力多边形边界的某一方向首尾相接,而合力矢量沿力多边形半封闭边的方向,由第一个分力的起点指向最后一个分力的终第面汇交力系与平面力偶图2.21图2.226.在直角坐标系中,力对坐标轴的投影与力沿坐标轴分解的分力的大小但在非直角坐标系中,力对坐标轴的投影与力沿坐标轴分解的分力的大小不相等。
1.例如图2.23右图的各图为平面呈报力系所作的力多边形,下面观点恰当的就是(c)。
(a)图(a)和图(b)就是平衡力系则(b)图(b)和图(c)就是平衡力系则(c)图(a)和图(c)就是平衡力系则(d)图(c)和图(d)就是平衡力系则f2f2f1(a)(b)(c)2.关于某一个力、分力与投影下面说法正确的是(b)。
理论力学习题答案(修改6月19日)

⃗rc
=
m1⃗r1
+
m2⃗r2 M
+ m3⃗r3
=
1 3
( 2ˆi + ˆj +
) 3kˆ ,
⃗vc
=
⃗r˙c
=
ˆj
+
1 kˆ, 3
p⃗c = M⃗vc = 3ˆj + kˆ,
∑3 J⃗ = mi⃗ri × ⃗vi = −3ˆi + 3kˆ,
i=1
T
=
∑3
1 2
mi
vi2
=
4.
i=1
4. 证明:两质点系的角动量为,J⃗ = R⃗ c × M V⃗c + ⃗r × µ⃗v,其中,M = m1 + m2, µ 为折合质量,⃗r 为相对位矢,c 表示质心。
6
6. 半径为 r 的均质圆球在半径为 R 的固定圆柱的内表面滚动,试求圆球绕平
衡位置做微振动的运动方程及周期。
解:
vc
=
(R
−
r)θ˙, ω
=
(R
− r
r)θ˙ , Ic
=
2 mr2 5
T
=
1 2
mvc2
+
1 2
Icω2
= 7 m(R − r)2θ˙2 10
V = mg (R − (R − r) cos θ)
l
2± 2 g
7
8. 如果上题的双摆系统不是系在固定点上,而是系在一个可以在光滑水平杆 上自由运动的质量为 2m 的小环上,继续令 m1 = m2 = m,l1 = l2 = l,试 求系统的运动方程及周期。
解:
L=T −V
=
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章力系的简化
2-1.通过A(3,0,0),B(0,4,5)两点(长度单位为米),且由A指向B的力F,在z轴上投影为,对z轴的矩的大小为。
答:F/2;62F/5。
2-2.已知力F的大小,角度φ和θ,以及长方体的边长a,b,c,则力F在轴z和y上的投影:Fz= ;Fy= ;F对轴x的矩
M x(F)= 。
答:Fz=F·sinφ;Fy=-F·cosφ·cosφ;Mx(F)=F(b·sinφ+c·cosφ·cosθ)
图2-40 图2-41
2-3.力F通过A(3,4、0),B(0,4,4)两点(长度单位为米),若F=100N,则该力
在x轴上的投影为,对x轴的矩为。
答:-60N;
2-4.正三棱柱的底面为等腰三角形,已知OA=OB=a,在平面ABED内有沿对角线AE的一个力F,图中α=30°,则此力对各坐标轴之矩为:
M x(F)= ;M Y(F)= ;M z(F)= 。
答:M x(F)=0,M y(F)=-Fa/2;M z(F)=6Fa/4
2-5.已知力F的大小为60(N),则力F对x轴的矩为;对z轴的矩为。
答:M x(F)=160 N·cm;M z(F)=100 N·cm
图2-42 图2-43
2-6.试求图示中力F 对O 点的矩。
解:a: M O (F)=F l sin α
b: M O (F)=F l sin α
c: M O (F)=F(l 1+l 3)sin α+ F l 2cos α
d: ()22
21l l F F M o +=αsin 2-7.图示力F=1000N ,求对于z 轴的力矩M z 。
题2-7图 题2-8图
2-8.在图示平面力系中,已知:F 1=10N ,F 2=40N ,F 3=40N ,M=30N ·m 。
试求其合力,并画在图上(图中长度单位为米)。
解:将力系向O 点简化
R X =F 2-F 1=30N
R V =-F 3=-40N ∴R=50N 主矩:Mo=(F 1+F 2+F 3)·3+M=300N ·m
合力的作用线至O 点的矩离 d=Mo/R=6m
合力的方向:cos (R ,)=,cos (R ,)=-
(R,i)=-53°08’
(R,i)=143°08’
2-9.在图示正方体的表面ABFE内作用一力偶,其矩M=50KN·m,转向如图;又沿GA,BH作用两力R、R?,R=R?=502KN;α=1m。
试求该力系向C点简化结果。
解:主矢:
'
R=ΣF i=0
主矩:M c=M+m(R,R?)
又由M cx=-m(R,R?)·cos45°=-50KN·m
M cY=0
M cz=M-m(R,R?)·sin45°=0
∴M c的大小为
Mc=(M cx2+M cY2+M cz2)1/2
=50KN·m
M c方向:
Cos(M c,i)=cosα=M cx/Mc=-1,α=180°
Cos(M c,j)=cosβ=M cY/Mc=0,β=90°
Cos(M c,k)=cosγ=M cZ/Mc=0,γ=90°
即M c沿X轴负向
题2-9图题2-10图
2-10.一个力系如图示,已知:F1=F2=F3,M=F·a,OA=OD=OE=a,OB=OC=2a。
试求此力系的简化结果。
解:向O点简化,主矢R?投影
Rx?=-F·
2
1
R Y ?=-F ·21 R Z ?=F ·2 R ?=-F ·21i -F ·2
1j +F ·2j 主矩M o 的投影:
M ox =2
13Fa ,M oY =0,M oz =0 M o ?=2
13Fa i R ?·M o =-213aF 2≠0,R ?不垂直M o 所以简化后的结果为力螺旋。
2-11.沿长方体的不相交且不平行的棱边作用三个大小相等的力,问边长a ,b ,c 满足什么条件,这力系才能简化为一个力。
解:向O 点简化 R ?投影:Rx?=P ,R Y ?=P ,Rz?=P
R ?=P i +P j +P j
主矩M o 投影:M ox =bP -cP ,M oY =-aP ,M oz =0
M o=(bP -cP )i -aP j
仅当R ?·M o=0时才合成为力。
(P +P j +P )[(bP -cP )-ap j =0
应有 P (bP -cP )=0,PaP=0,
所以 b=c ,a=0
2-12.曲杆OABCD 的OB 段与Y 轴重合,BC 段与X 轴平行,CD 段与Z 轴平行,已知:P 1=50N ,P 2=50N ;P 3=100N ,P 4=100N ,L 1=100mm ,L 2=75mm 。
试求以B 点为简化中心将此四个力简化成最简单的形式,并确定其位置。
图2-49
解:向B 简化
Rx?=50N R Y ?=0 R Z ?=50N R?=502 R?方向: cos α=21
cos β=0 cos γ=21
主矩M B M xB =·m M YB =m zB =0 M B =·m
主矩方向 cos α=1 cos β=0 cos γ=0 M B 不垂直R ?
Mn B =·m M iB =·m
d=M B /R?=0.025m
2-13.结构如图所示,求支座B 的约束力。
题2-13图 (a) P F B 23= (b) P F B 223= (c) P .F B 821=
2-14.图示曲柄摇杆机构,在摇杆的B 端作用一水平阻力R ,已知:OC=r ,AB=L ,各部分自重及摩擦均忽略不计,欲使机构在图示位置(OC 水平)保持平衡,试求在曲柄OC 上所施加的力偶的力偶矩M 。
图2-51
解:一)取OC ΣMo (F )=0
Nsin45°·r -M=0,N=M/(r sin45°)
取AB Σm A (F )=0
RLsin45°-N?2rsin45°=0,N?=
21RL/r M=4
12RL 二)取OC ΣX=0 Xo -Ncos45°=0,Xo=4
12LR/r ΣY=0 Yo+Nsin45°=0,Yo=-412LR/r 取AB ΣX=0 X A +N ’cos 45°-R=0,
X A =(1-41
2L/r )R
ΣY=0 Y A -N ’sin 45°=0,Y A =
412RL/r。
