高一数学向量课件
合集下载
“高一数学必修2-向量课件”

向量的模和单位向量可以用于计 算距离和方向。
参数方程
参数方程是用参数来表示向量的方程。
向量方程的应用
平面的解析式
可以用向量方程来表示平面。
代数方程的转化
向量方程可以将代数方程转 化为几何问题。
其他应用
向量方程在物理、工程和计 算机图形学中有广泛应用。
向量的模、单位向量及其应用
向量模
向量的模等于向量的长度。
单位向量
单位向量是模为1的向量。
应用举例
高一数学必修2——向量 课件
本课件介绍高一数学必修2的向量部分内容,包括向量的定义及基本概念,表 示和运算,共线和共面的判定,数量积和夹角的性质,向量在平面内的投影 及应用,叉乘的运算规则和几何意义,以及向量空间的基本概念。
向量的表示和运算
向量表示
向量加法
向量可以用有向线段或坐标表示。 向量加法满足交换律和结合律。
应用举例
向量投影可以用来计算物体 在斜面上的重力分量。
向量叉乘及其运算规则
叉乘定义
叉乘是两个向量的积的向量。
叉乘运算规则
叉乘满足右手法则和分配律。
向量叉乘的几何意义以及应用
1
几何意义
叉乘的模等于由两个向量所确定的平行
应用举例
2
四边形的面积。
叉乘可以用来计算平行四边形的面积和
判定三个向量共面。
3
补充知识
可以通过叉乘来计算向量的混合积。
平面向量和向量组的线性运算
线性组合
线性组合是指多个向量与对应的系数相乘再求和的 过程。
向量组的线性相关和线性无关
线性相关和线性无关描述向量组中向量之间的关系。
向量空间的基本概念和性质
1 向量空间定义
参数方程
参数方程是用参数来表示向量的方程。
向量方程的应用
平面的解析式
可以用向量方程来表示平面。
代数方程的转化
向量方程可以将代数方程转 化为几何问题。
其他应用
向量方程在物理、工程和计 算机图形学中有广泛应用。
向量的模、单位向量及其应用
向量模
向量的模等于向量的长度。
单位向量
单位向量是模为1的向量。
应用举例
高一数学必修2——向量 课件
本课件介绍高一数学必修2的向量部分内容,包括向量的定义及基本概念,表 示和运算,共线和共面的判定,数量积和夹角的性质,向量在平面内的投影 及应用,叉乘的运算规则和几何意义,以及向量空间的基本概念。
向量的表示和运算
向量表示
向量加法
向量可以用有向线段或坐标表示。 向量加法满足交换律和结合律。
应用举例
向量投影可以用来计算物体 在斜面上的重力分量。
向量叉乘及其运算规则
叉乘定义
叉乘是两个向量的积的向量。
叉乘运算规则
叉乘满足右手法则和分配律。
向量叉乘的几何意义以及应用
1
几何意义
叉乘的模等于由两个向量所确定的平行
应用举例
2
四边形的面积。
叉乘可以用来计算平行四边形的面积和
判定三个向量共面。
3
补充知识
可以通过叉乘来计算向量的混合积。
平面向量和向量组的线性运算
线性组合
线性组合是指多个向量与对应的系数相乘再求和的 过程。
向量组的线性相关和线性无关
线性相关和线性无关描述向量组中向量之间的关系。
向量空间的基本概念和性质
1 向量空间定义
6.2.3 向量的数乘运算(课件)高一数学(人教A版2019必修第二册)

(1) a 2e,b 2e; (2) a e1 e2,b 2e1 2e2; (3) a e1 e2,b e1 2e2 。
(1)共线 (2)共线 (3) 不共线
向量的数乘运算
例练结合
例1:计算 (1) (3) 4a; 解:(1)原式= (-3 4) a 12a;
(2) 3(a b) 2(a b) a;
(2)原式= 3a 3b 2a 2b a 5b;
(3) (2a 3b c) (3a 2b c).
(3)原式= 2a 3b c 3a 2b c a 5b 2c.
向量的数乘运算
方法小结
3:6
向量的数乘运算
例练结合
例2:□ABCD的两条对角线相交于点M,且 AB a, AD b, 试用 a, b
解析:因为A→B∥C→D,|A→B|=2|C→D|,所以A→B=2D→C,D→C=1A→B. 2
(1)A→C=A→D+D→C=e2+12e1.
(2)M→N=M→D+D→A+A→N=-1D→C-A→D+1A→B=-1e1-e2+1e1=1e1-e2.
2
2
4
24
向量的数乘运算
例练结合
在本例中,若条件改为B→C=e1,A→D=e2,试用 e1,e2 表示向量M→N.
B.-1A→B-1A→D 22
C.-1A→B+1A→D D.1A→B-1A→D
22
22
4.已知 e1,e2 是两个不共线的向量,a=2e1-e2,b=ke1+e2,若 a 与 b 是共线向量,则实数
k=________.
1.B 2.C 3.D 4.-2
向量的数乘运算
课堂小结
思考:
(1)通过这节课,你学到了什么知识? (2)在解决问题时,用到了哪些数学思想?
6.1平面向量的概念(同步课件)高一数学课件

[答案] 的模为0,方向任意.
情境设置
新知生成
1.具有______的线段叫作有向线段.通常在有向线段的终点画上箭头表示它的方向.它包含三个要素:______、______、______.
2.向量 的大小称为向量 的______(或称模),记作_____.长度为0的向量叫作零向量,记作 .长度等于___个单位的向量叫作单位向量.向量也可以用字母 , , , 表示.
5.(1)平行向量是否一定方向相同?
[答案] 不一定;
(2)不相等的向量是否一定不平行?
[答案] 不一定;
(3)与任意向量都平行的向量是什么向量?
[答案] 零向量;
(4)若两个向量在同一直线上,则这两个向量一定是什么向量?
[答案] 平行(共线)向量.
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
D
A.相等向量 B.平行向量 C.有相同起点的向量 D.模相等的向量
[解析] 如图, , , , 既不全是相等向量,也不全是平行向量,起点也不全是相同,故A,B,C错误;
而 ,故D正确.故选D.
3.(多选题)下列说法错误的有( ).
A.共线的两个单位向量相等B.相等向量的起点相同C.若 ,则一定有直线 D.若向量 , 共线,则点 , , , 可能不在同一直线上
问题3:若 , ,则一定有 吗?
[答案] 不一定.因为当 时, , 可以是任意向量.
新知生成
1.平行向量:方向____________的非零向量叫作平行向量(也叫作共线向量).向量 , 平行,记作 .
2.相等向量:长度______且方向______的向量叫作相等向量.用有向线段表示的向量 与 相等,记作_______.
[解析] 作出向量如图所示.
情境设置
新知生成
1.具有______的线段叫作有向线段.通常在有向线段的终点画上箭头表示它的方向.它包含三个要素:______、______、______.
2.向量 的大小称为向量 的______(或称模),记作_____.长度为0的向量叫作零向量,记作 .长度等于___个单位的向量叫作单位向量.向量也可以用字母 , , , 表示.
5.(1)平行向量是否一定方向相同?
[答案] 不一定;
(2)不相等的向量是否一定不平行?
[答案] 不一定;
(3)与任意向量都平行的向量是什么向量?
[答案] 零向量;
(4)若两个向量在同一直线上,则这两个向量一定是什么向量?
[答案] 平行(共线)向量.
1.判断下列结论是否正确.(正确的打“√”,错误的打“×”)
D
A.相等向量 B.平行向量 C.有相同起点的向量 D.模相等的向量
[解析] 如图, , , , 既不全是相等向量,也不全是平行向量,起点也不全是相同,故A,B,C错误;
而 ,故D正确.故选D.
3.(多选题)下列说法错误的有( ).
A.共线的两个单位向量相等B.相等向量的起点相同C.若 ,则一定有直线 D.若向量 , 共线,则点 , , , 可能不在同一直线上
问题3:若 , ,则一定有 吗?
[答案] 不一定.因为当 时, , 可以是任意向量.
新知生成
1.平行向量:方向____________的非零向量叫作平行向量(也叫作共线向量).向量 , 平行,记作 .
2.相等向量:长度______且方向______的向量叫作相等向量.用有向线段表示的向量 与 相等,记作_______.
[解析] 作出向量如图所示.
高一人教A版高中数学必修第二册《6.2.3向量共线定理》课件

高一人教A版高中数学必修第二册课件
6.2.3向量共线定理
学习目标:
1.学习并掌握向量共线定理 2.能够灵活应用向量共线定理:能用向量的共线定理证明三点共线,
能用向量共线定理构建方程组求参数
复习回顾
向量的数乘:
实数与向量a的积是一个向量,这种运算 叫做向量的数乘,记为 a
其方向和长度规定如下:
(1) a a ;
2
2
(1 3 )
a
2 t
b (3)
2
由于a和b是两个不共线向量,可知
t 0
2
1 3 0
2
解得t= 1 3
例题反思:
向量共线定理的应用,体现向量线性 运算和方程组的综合应用。解题的关键是 依据向量共线的充要条件,先列出向量的 关系式,再转化为解方程组求参数问题, 这是向量共线定理的一个常规解题思路。
定理应用
例2.已知 a、b 是两个不共线向量,向量b-ta , 1 a 3 b 共线,求实数t的值。 22
解:由于 a 和 b是两个不共线向量,所以 1 a 3 b 为非零向量, 22
向量b-ta , 1 a 3 b 共线,则b-ta (1 a 3 b) (1)
22
22
即(t )a (1 3 )b (2)
学法指导
新课程标准有以下几项变化,一是理念变化:确立核心素养导向的课 程目标;二是结构变化:明确学业要求与学业质量标准;三是内容变化: 调整教学要求和增加教学内容。最终是要结合学生认知水平和生活经验, 设计合理的生活情境、数学情境、科学情境。关注情境的真实性,适当引 入数学文化,真正让学生感受数学与生活的密切关系和对生活的影响以及 作用。培养学生的核心素养目标,从本质上提升教学质量。
6.2.3向量共线定理
学习目标:
1.学习并掌握向量共线定理 2.能够灵活应用向量共线定理:能用向量的共线定理证明三点共线,
能用向量共线定理构建方程组求参数
复习回顾
向量的数乘:
实数与向量a的积是一个向量,这种运算 叫做向量的数乘,记为 a
其方向和长度规定如下:
(1) a a ;
2
2
(1 3 )
a
2 t
b (3)
2
由于a和b是两个不共线向量,可知
t 0
2
1 3 0
2
解得t= 1 3
例题反思:
向量共线定理的应用,体现向量线性 运算和方程组的综合应用。解题的关键是 依据向量共线的充要条件,先列出向量的 关系式,再转化为解方程组求参数问题, 这是向量共线定理的一个常规解题思路。
定理应用
例2.已知 a、b 是两个不共线向量,向量b-ta , 1 a 3 b 共线,求实数t的值。 22
解:由于 a 和 b是两个不共线向量,所以 1 a 3 b 为非零向量, 22
向量b-ta , 1 a 3 b 共线,则b-ta (1 a 3 b) (1)
22
22
即(t )a (1 3 )b (2)
学法指导
新课程标准有以下几项变化,一是理念变化:确立核心素养导向的课 程目标;二是结构变化:明确学业要求与学业质量标准;三是内容变化: 调整教学要求和增加教学内容。最终是要结合学生认知水平和生活经验, 设计合理的生活情境、数学情境、科学情境。关注情境的真实性,适当引 入数学文化,真正让学生感受数学与生活的密切关系和对生活的影响以及 作用。培养学生的核心素养目标,从本质上提升教学质量。
6.2.2向量的减法运算(课件)高一数学下学期课件(人教A版必修第二册)

AC
AO AD
CA
BC BA
DO
PA R T · 2
向量减法的应用
• 向量减法的应用
例题解析:如图,已知向量 a,b, c, d, 求作向量a b,c d.
D
b
d
ab
A
B
cd
a
c
C
O
• 向量减法的应用
例题解析:如图,平行四边形ABCD,AB a, AD b ,你能
用a,b AC, DB.
表示
解:由题意,
AC a b DB a b
• 向量减法的应用
课堂练习:试用几何的方式证明: (a b) a b
b
b
a (a b)
a
ab
• 向量减法的应用
课堂练习:如图所示,四边形ACDE是平行四边形,点B是该
平行四边形外一点,且 AB a,AC b,AE c 试用向量 a,b, c 表
同向共线
反向共线
a
a
b
b
a-b
a-b
• 向量减法的定义
向量的减法 自然语言:减去一个向量等于加上这个向量的相反向量。
符号语言: 图形语言:
a b a (b)
B
a-b
b
A
Oa
向量减法共起点,减号后指减号前
• 向量减法的定义
挑战活动 将下列向量运算与相应结几果何进含行义匹配
BA BC
AD
OD AO
习题6.2 4,6,7
课后作业
进阶挑战
习题6.2 17,22,23
祝各位同学学习愉快
— End —
示向量CD,BC, BD. 解:由题意,
CD AE c
BC AC AB b a BD BC CD b a c
高一下学期数学人教A版必修第二册6.2.3向量共线定理课件

数学运算、逻辑推理——破解向量的数乘运算
设点 O 在△ABC 内部,且有Ԧ+2Ԧ+3Ԧ =0,则△ABC 的面积与△AOC 的面积之比
为(
C ).
A.2∶1
B.3∶2
C.3∶1
D.5∶3
解析 如图,延长 OB 至点 B1,使 BB1=OB,延长 OC 至点 C1,使 CC1=2OC,连接 AB1,AC1,B1C1,则
C.垂心
D.外心
如图,在△ABC 中,O 为外心,可得 OA=OB=OC,
∵Ԧ+Ԧ+Ԧ =Ԧ,∴Ԧ+Ԧ=Ԧ-Ԧ =Ԧ.
设 AB 的中点为 D,则 OD⊥AB,Ԧ=2Ԧ ,
∴CM⊥AB,可得 CM 在 AB 边的高线上.
同理可证,AM 在 BC 边的高线上.
A,B,D
的三个点是___________.
2.已知 A,B,P 三点共线,O 为直线外任意一点,若 Ԧ=xԦ+yԦ,求 x+y 的值.
解析 因为 A,B,P 三点共线,所以 Ԧ=λԦ,
即 Ԧ-Ԧ=λ(Ԧ-Ԧ),所以 Ԧ=(1-λ)Ԧ+λԦ,故 x=1-λ,y=λ,即 x+y=1.
故 M 是△ABC 两高线的交点,可得 M 是△ABC 的垂心.
故选 C.
C
).
课前预学
已知 O 是平面上一定点,A,B,C 是平面上不共线的三个点,动点 P
满足 Ԧ=Ԧ+λ
Ԧ
Ԧ
+ Ԧ
|Ԧ|
| |
A.内心
解析
,λ∈[0,+∞),则点 P 的轨迹一定通过△ABC 的(
B.垂心
C.重心
1՜ 3՜
՜
高一数学平面向量 PPT课件 图文

解: ka+b=k(1, 2)+(-3, 2)= (k-3,2k+2)
a-3b=(1, 2)-3(-3, 2)= (10, -4)
(ka+b)∥(a-3b)
-4(k-3)-10(2k+2)=0
K=- 1
3
∵
ka+b=
10 3
,
4 3
=-
1 3
(a-3b)
∴它们反向
例2
思考:
此题还有没有其它解法?
分析 要证A、B、D三点共线,可证 AB=λBD关键是找到λ
解: ∵BD=BC+CD= 2a + 8b+ 3(a b)=a+5b
∴AB=2 BD
AB∥ BD
且AB与BD有公共点B
∴ A、B、D 三点共线
例3
知识结构
平面向量小 复习
知识要点 例题解析 巩固练习
课外作业
练习5 已知a=(1,0),b=(1,1),c =(-1,0) 求λ和μ,使 c =λa +μb.
新课标人教版课件系列
《高中数学》
必修4
2.6《平面向量-复习》
平面向量复习
知识结构 要点复习 例题解析
巩固练习
制作:曾毅 审校:王伟
知识结构
平面向量 复习
知识要点 例题解析 巩固练习
课外作业
表示 向量的三种表示
平
三角形法则
面
向量加法与减法
向
平行四边形法则
量
向量平行的充要条件
运算 实数与向量的积
知识Байду номын сангаас点 例题解析 巩固练习
课外作业
a-3b=(1, 2)-3(-3, 2)= (10, -4)
(ka+b)∥(a-3b)
-4(k-3)-10(2k+2)=0
K=- 1
3
∵
ka+b=
10 3
,
4 3
=-
1 3
(a-3b)
∴它们反向
例2
思考:
此题还有没有其它解法?
分析 要证A、B、D三点共线,可证 AB=λBD关键是找到λ
解: ∵BD=BC+CD= 2a + 8b+ 3(a b)=a+5b
∴AB=2 BD
AB∥ BD
且AB与BD有公共点B
∴ A、B、D 三点共线
例3
知识结构
平面向量小 复习
知识要点 例题解析 巩固练习
课外作业
练习5 已知a=(1,0),b=(1,1),c =(-1,0) 求λ和μ,使 c =λa +μb.
新课标人教版课件系列
《高中数学》
必修4
2.6《平面向量-复习》
平面向量复习
知识结构 要点复习 例题解析
巩固练习
制作:曾毅 审校:王伟
知识结构
平面向量 复习
知识要点 例题解析 巩固练习
课外作业
表示 向量的三种表示
平
三角形法则
面
向量加法与减法
向
平行四边形法则
量
向量平行的充要条件
运算 实数与向量的积
知识Байду номын сангаас点 例题解析 巩固练习
课外作业
高一下学期数学人教A版必修第二册6.2.3向量的数乘运算课件(2)
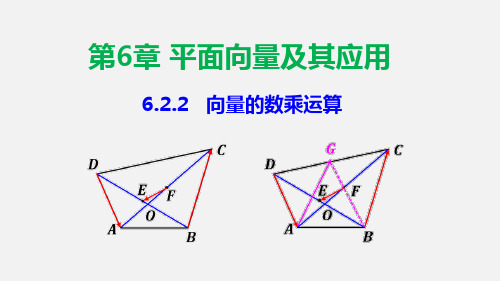
Ԧ
2
向量的线性运算
线性运算
难点点拨
【1】向量的线性运算类似于代数多项式的运算,主要是“合并同类项”“提取
公因式”,只不过这里的“同类项”“公因式”都是向量,实数可以看做是
向量的系数.
【2】对于向量的线性运算,关键是把握运算顺序,即先根据运算律去括号,再
进行数乘运算,最后进行向量的加减,即“先乘除,后加减”.
已知ΔABC的边BC上有一点D满足BD=3DC,则AD可以怎么表示?
A. AD=-2AB+3AC
B. AD= AB+
C.
√ AD= AB+
D. AD= AB+
AC
AC几何性质运用不准确
如图,E、F分别是四边形ABCD对角线AC、BD的中点,
设BC= ,DA= ,试用 , 表示EF.
, = 试用, 表示向量、 、和.
解: = − = − ( + ) = − −
=
= ( − ) = −
= = +
= − = − = − ( − ) = − +
第6章 平面向量及其应用
6.2.2 向量的数乘运算
0
学习目标
1.了解向量数乘的概念并理解数乘运算的几何意义
2.理解并掌握向量数乘的运算律
3.会进行向量的数乘运算
2
向量的线性运算
线性运算
难点点拨
【1】向量的线性运算类似于代数多项式的运算,主要是“合并同类项”“提取
公因式”,只不过这里的“同类项”“公因式”都是向量,实数可以看做是
向量的系数.
【2】对于向量的线性运算,关键是把握运算顺序,即先根据运算律去括号,再
进行数乘运算,最后进行向量的加减,即“先乘除,后加减”.
已知ΔABC的边BC上有一点D满足BD=3DC,则AD可以怎么表示?
A. AD=-2AB+3AC
B. AD= AB+
C.
√ AD= AB+
D. AD= AB+
AC
AC几何性质运用不准确
如图,E、F分别是四边形ABCD对角线AC、BD的中点,
设BC= ,DA= ,试用 , 表示EF.
, = 试用, 表示向量、 、和.
解: = − = − ( + ) = − −
=
= ( − ) = −
= = +
= − = − = − ( − ) = − +
第6章 平面向量及其应用
6.2.2 向量的数乘运算
0
学习目标
1.了解向量数乘的概念并理解数乘运算的几何意义
2.理解并掌握向量数乘的运算律
3.会进行向量的数乘运算
高一数学人必修课件向量共线的条件与轴上向量坐标运算

计算分子间的相互作用力
03
利用向量的点积等运算,可以计算分子间的相互作用力,如范
德华力、氢键等。
向量在经济学中应用
描述经济变量的变化趋势
向量可以表示经济变量的变化趋势,如价格、产量等的变化方向 和幅度。
进行经济预测和决策分析
利用向量的运算和分析方法,可以对经济变量进行预测和决策分析 ,如回归分析、时间序列分析等。
轴的正方向。
03
标记坐标
空间中的任意一点P可以用一个有序实数组(x, y, z)来表示,其中x、y、
z分别称为点P的横坐标、纵坐标和竖坐标。
空间向量在坐标系中表示方法
确定向量的起点和终点
在空间直角坐标系中,向量可以用起点和终点两个点来确定。起点为向量的始点 ,终点为向量的终点。
向量的表示方法
向量可以用有向线段来表示,有向线段的长度表示向量的大小,有向线段的方向 表示向量的方向。同时,向量也可以用坐标形式来表示,即向量的坐标等于终点 坐标减去起点坐标。
案例二
已知向量a=(2, 1, -1)和向量b=(1, -2, 3),求向量a与向量b的和。根据空间向量的加法运算规则,可 得a+b=(2+1, 1+(-2), (-1)+3)=(3, -1, 2)。
04
向量共线与坐标运算综合 应用
平面向量与空间向量关系
平面向量是二维空间中的向量,可以 用有序数对表示,而空间向量是三维 空间中的向量,可以用有序三元组表 示。
高一数学人必修课件
向量共线的条件与轴
上向量坐标运算 汇报人:XX
20XX-01-21
目录
• 向量共线条件及性质 • 轴上向量坐标运算方法 • 空间向量在坐标系中表示方法 • 向量共线与坐标运算综合应用
向量的概念 高一数学课件(人教B版2019必修第二册)

6向量的长度: 向量 AB 的大小也就是向量的
长度(或叫做模),记做| AB |,|a| 平面直角坐
7零向量、单位向量概念:
标系内有多
①长度为0的向量叫零向量,记作
少个单位向
0 量?
②长度为1个单位长度的向量,叫单位向量.
8.平行向量定义: ①方向相同或相反的非零
向量叫平行向量; ②规定0与任一向量平行.
变式三:与向量OA长度相等的共线向量有哪些? CB、DO、FE
例5:D、E、F依次是等边△ABC的边AB、
BC、CA的中点,在以A、B、C、D、E、F
为起点或终点的向量中,
(1)找出与向量 DE
A
相等的向量; AF和FC
D
F
(2)找出与向量 DF
共线的向量.
B
E
C
BE,EB,EC,CE,BC,CB,FD
向量a、b、c平行,记作a∥b∥c.
9.相等向量定义
长度相等且方向相同的向量叫相 等向量.
(1)向量a与b相等,记作a=b;
(2)零向量与零向量相等; (3)任意两个相等的非零向量,都可用同一条有向 线段来表示,并且与有向线段的起点无关
10共线向量 : 任一组平行向量都可移到同一 直线上.因此平行向量 也叫共线向量
北京 O )50o
天津 A
巩固概念.下面几个命题:
(1)若a = b,b = c,则a = c。 (2)若|a|=0,则a = 0 (3)若|a|=|b|,则a = b
(4)两个向量a、b相等的充要条件是
|a|=|b| a ∥b
(5)若A、B、C、D是不共线的四点,则AB=DC是
四边形ABCD是平形四边形的充要条件。
6.1.1 向量的概念
6.3.1平面向量基本定理课件-高一下学期数学人教A版必修第二册

巩固新知
ⅹ
ⅹ
ⅹ
ⅹ
√
平面向量基本定理
(存在性)
(唯一性)
平面向量相等的充要条件
巩固新知
【练习】(1)(多选)设{,}是平面内所有向量的一个基底,则下列四组向量中,能作为基底的是( ) A.+和- B.3-4和6-8 C+2和2+ D.和+(2)已知向量{,}是一个基底,实数x,y满足 (3x-4y)+(2x-3y)=6+3,则x-y=_____.
典型例题
解题反思:将不共线的向量作为基底表示其他向量的一种方法:是运用向量的线性运算法则对所求向量不断转化,直至能用基底表示为止
例1.已知 ,C为线段AO上距离A较近的一个三等分点,D为线段CB上距C较近的一个三等分点,则用 表示 的表达式为( )
C
D
B
典型例题
2.向量的数量积是否为零,是判断相应的两条线段(或直线)是否垂直的重要方法之一.
A
解题反思:1.直径所对的圆周角为直角
练习2
已知正方形ABCD中,E,F分别为AB,BC的中点,求证:AF⊥DE.
巩固新知
【练习】课本P27 练习3
典型例题
P、A、B三点共线
C
练习3:
拓展训练
例4.
解题反思:将不共线的向量作为基底表示其他向量的方法:1.运用向量的线性运算法则对所求向量不断转化,直至能用基底表示为止2.通过列向量方程或方程组,利用基底表示向量的唯一性求解。
A
拓展训练
探究新知
平面向量基本定理
(存在性)
(唯一性)
说明:若共线,则当与共线时可用表示,且表示方法不唯一;
当不共线时不可用表示
判断正误:如果是平面α内两个不共线的向量 1.一个平面内只有一对不共线的向量可作为表示该平面内所有 向量的基底 ( ) 2.一个平面内任意两个向量都可作为两个基底( ) 3.基底向量可以是零向量( ) 4.使一确定向量的实数对(无数多个( ) 5.若λ+μ=,则λ =μ=0( )
ⅹ
ⅹ
ⅹ
ⅹ
√
平面向量基本定理
(存在性)
(唯一性)
平面向量相等的充要条件
巩固新知
【练习】(1)(多选)设{,}是平面内所有向量的一个基底,则下列四组向量中,能作为基底的是( ) A.+和- B.3-4和6-8 C+2和2+ D.和+(2)已知向量{,}是一个基底,实数x,y满足 (3x-4y)+(2x-3y)=6+3,则x-y=_____.
典型例题
解题反思:将不共线的向量作为基底表示其他向量的一种方法:是运用向量的线性运算法则对所求向量不断转化,直至能用基底表示为止
例1.已知 ,C为线段AO上距离A较近的一个三等分点,D为线段CB上距C较近的一个三等分点,则用 表示 的表达式为( )
C
D
B
典型例题
2.向量的数量积是否为零,是判断相应的两条线段(或直线)是否垂直的重要方法之一.
A
解题反思:1.直径所对的圆周角为直角
练习2
已知正方形ABCD中,E,F分别为AB,BC的中点,求证:AF⊥DE.
巩固新知
【练习】课本P27 练习3
典型例题
P、A、B三点共线
C
练习3:
拓展训练
例4.
解题反思:将不共线的向量作为基底表示其他向量的方法:1.运用向量的线性运算法则对所求向量不断转化,直至能用基底表示为止2.通过列向量方程或方程组,利用基底表示向量的唯一性求解。
A
拓展训练
探究新知
平面向量基本定理
(存在性)
(唯一性)
说明:若共线,则当与共线时可用表示,且表示方法不唯一;
当不共线时不可用表示
判断正误:如果是平面α内两个不共线的向量 1.一个平面内只有一对不共线的向量可作为表示该平面内所有 向量的基底 ( ) 2.一个平面内任意两个向量都可作为两个基底( ) 3.基底向量可以是零向量( ) 4.使一确定向量的实数对(无数多个( ) 5.若λ+μ=,则λ =μ=0( )
平面几何中的向量方法 高一数学课件(人教A版2019必修第二册)

向量具有“几何”与“代数”的双重身份
1、我们学了向量的线性运算与数量积运算,你能说出它们的 几何意义吗?这与平面几何哪些内容可以相互联系与转化?
B A
O D
A
B C
O B
A B
)
O
A
数量积性质?
求模 求夹角 证垂直
2、向量的代数身份是通过什么来实现的?坐标表示
当向量与平面坐标系结合以后,向量的运算就可以完全转化为“代数” 的计算
又有公共点 P,则 A,C, P 三点共线.所以 B 正确.
故选:B
5.(多选)点 P 是ABC 所在平面内一点,满足
PB PC PB PC 2PA 0 ,则ABC 的形状不可能是
A.钝角三角形
B.直角三角形
C.等腰三角形
D.等边三角形
【详解】∵P 是 ABC 所在平面内一点,且
,∴ , | PB PC | | PB PC 2PA | 0
例 7.如图,已知正方形 ABCD 的边长为 1, 点 E 是 AB 边上的动点,求:
(1) DE CB 的值;(2) DE DC 的最大值.
(2)因为 DE 1, x, DC 0,1 ,所以 DE CB 1 0 x 1 x , 因为0 x 1, 所以 DE DC 的最大值是 1.
例 8.如图,在
(1)当 a , b 满足什么条件时,a b a b ? (2)当 a ,b 满足什么条件时, a b a b ?
(2)由(1)可得, a b AC, a b BD a b a b ,即 AC BD ,此时四边形 ABCD 为矩 形从而可得 AB AD a b 时, a b a b .
(5)、两向量垂直的充要条件:向量 a b a •b 0
6.2.1向量的加法运算课件-2024-2025学年高一下学期数学人教A版必修第二册

我们知道:数能进行运算,因为有了运算而使数的威力无穷。向量 是否也能进行运算呢?
位移、力是向量,它们可以合成,能否从位移、力的合成中得到启 示,引进向量的加法呢?
下面先学习向量的加法。
新课引入 探究新知识
问题1:如图,某质点从点A经过点B到点C,这个质点的位移如何表示?
位移 可以看作位移 与 的合成
新课引入 探究新知识
例1: 如图,已知向量
,求作向量 A
。
B 口诀:
首尾相接,首 指向尾
C
新课引入 探究新知识 一、向量的加法三角形法则
二、向量加法的平行四边形法则
新课引入 探究新知识
三、向量加法的性质
问题4
新课引入
问题5
探究新知识
新课引入
问题6
探究新知识
新课引入 探究新知识
三、向量加法的性质
(1)分别写出图中与向量 FD 相等的向量。 (2)分别写出图中与向量 FD 共线的向量。
A
D
F
B
E
C
新课引入 结束语
谢谢观看!
b+c+d=c,表示向西走了2 km. 【答案】 西 2
新课引入 课堂小结
本节课我们学习了哪些内容?
1.结合物理知识,理解与掌握了向量加法的三角形法则,平行 四边形法则,性质及其运算律;
2.能熟练地运用向量的加法法则及其运算律解决相关的实际问 题.
新课引入 布置作业
如图,D,E ,F分别是△ABC的各边中点:
(1) a+d 表示向________走了________km;
(2) b+c 表示向________走了________km;
新课引入 探究新知识
(3) a+c+d表示向________走了________km;
位移、力是向量,它们可以合成,能否从位移、力的合成中得到启 示,引进向量的加法呢?
下面先学习向量的加法。
新课引入 探究新知识
问题1:如图,某质点从点A经过点B到点C,这个质点的位移如何表示?
位移 可以看作位移 与 的合成
新课引入 探究新知识
例1: 如图,已知向量
,求作向量 A
。
B 口诀:
首尾相接,首 指向尾
C
新课引入 探究新知识 一、向量的加法三角形法则
二、向量加法的平行四边形法则
新课引入 探究新知识
三、向量加法的性质
问题4
新课引入
问题5
探究新知识
新课引入
问题6
探究新知识
新课引入 探究新知识
三、向量加法的性质
(1)分别写出图中与向量 FD 相等的向量。 (2)分别写出图中与向量 FD 共线的向量。
A
D
F
B
E
C
新课引入 结束语
谢谢观看!
b+c+d=c,表示向西走了2 km. 【答案】 西 2
新课引入 课堂小结
本节课我们学习了哪些内容?
1.结合物理知识,理解与掌握了向量加法的三角形法则,平行 四边形法则,性质及其运算律;
2.能熟练地运用向量的加法法则及其运算律解决相关的实际问 题.
新课引入 布置作业
如图,D,E ,F分别是△ABC的各边中点:
(1) a+d 表示向________走了________km;
(2) b+c 表示向________走了________km;
新课引入 探究新知识
(3) a+c+d表示向________走了________km;
6.1平面向量的概念-高一数学同步教学课件(人教A版必修第二册)
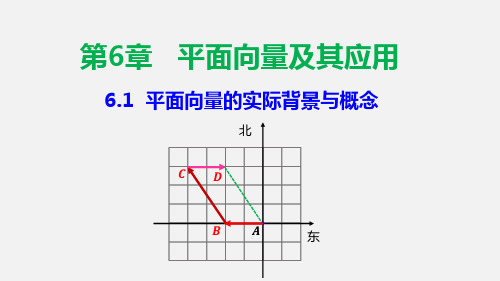
②要注意0和
的区分及联系:0是一个实数, 是一个向量,并
且| |=0,书写时 0 表示零向量,一定不能忘记上面的箭头.
③单位向量有无数个,它们大小相等,但是方向不一定相同.
④在平面内,将表示所有单位向量的有向线段的起点平移到
同一点,则它们的终点就会构成一个半径为1的圆.
3
相等向量与共线向量
【3】向量可以用有向线段来表示,但是向量不是有向线段,也不能说有向线段
是向量.
咱俩差不多,
我还可以表示你
有向线段
向量
但是你不是我,
我是不一样的烟火
2
向量的几何表示
印刷体
两种特殊的向量
【1】零向量——长度为0的向量叫做零向量,记作
【2】单位向量——长度等于1个单位长度的向量,叫做单位向量
①若用有向线段表示零向量,则其终点和起点重合.
那么终点的位置就确定了.
向量
的模
向量AB的大小称为向量AB的长度,也叫做向量
AB的模,记作 |AB|
向量的模
2
向量的几何表示
概念辨析
——向量和有向线段是一回事吗?
【1】从定义上看,向量有大小和方向两个要素,而有向线段有起点、方向、长
度三个要素,因此这是两个不同的量;
【2】在平面内,向量可以自由平移,而有向线段是固定的线段;
方向两个要素,这也
是判断一个量是否为
向量的重要方法.
1
向量的概念
例①
有人说:由于海平面以上的高度(海拔)用正数表示,
海平面以下的高度用负数表示,所以海拔也是向量.
你同意吗?温度、角度是向量吗?为什么?
【解】海拔不是向量,它只有大小没有方向.
海拔的正负不表示方向,只表示在海平面的上方还是下方.
的区分及联系:0是一个实数, 是一个向量,并
且| |=0,书写时 0 表示零向量,一定不能忘记上面的箭头.
③单位向量有无数个,它们大小相等,但是方向不一定相同.
④在平面内,将表示所有单位向量的有向线段的起点平移到
同一点,则它们的终点就会构成一个半径为1的圆.
3
相等向量与共线向量
【3】向量可以用有向线段来表示,但是向量不是有向线段,也不能说有向线段
是向量.
咱俩差不多,
我还可以表示你
有向线段
向量
但是你不是我,
我是不一样的烟火
2
向量的几何表示
印刷体
两种特殊的向量
【1】零向量——长度为0的向量叫做零向量,记作
【2】单位向量——长度等于1个单位长度的向量,叫做单位向量
①若用有向线段表示零向量,则其终点和起点重合.
那么终点的位置就确定了.
向量
的模
向量AB的大小称为向量AB的长度,也叫做向量
AB的模,记作 |AB|
向量的模
2
向量的几何表示
概念辨析
——向量和有向线段是一回事吗?
【1】从定义上看,向量有大小和方向两个要素,而有向线段有起点、方向、长
度三个要素,因此这是两个不同的量;
【2】在平面内,向量可以自由平移,而有向线段是固定的线段;
方向两个要素,这也
是判断一个量是否为
向量的重要方法.
1
向量的概念
例①
有人说:由于海平面以上的高度(海拔)用正数表示,
海平面以下的高度用负数表示,所以海拔也是向量.
你同意吗?温度、角度是向量吗?为什么?
【解】海拔不是向量,它只有大小没有方向.
海拔的正负不表示方向,只表示在海平面的上方还是下方.
6.1.1向量的概念课件-高一上学期数学人教B版【精美】

单位向量有 AB ,a ,b ,CD .
e是单位向量的充要条件是| e | 1
新知探究
同学们发生的位移方向相同吗?大小相同吗? 位移的大小、方向都相同
向前三步走,向右看齐
相等向量:大小相等、方向相同的向量
B
a
A
b
F
D
cd
C
E
a EF, AB CD,b c
新知探究
思考:(1)| a | = | b | 是 a = b 的充要条件吗?
新知探究
例3 如图所示,找出其中共线的向量,并写出共 线向量模之间的关系
b
e
a
c
d
f
a // c,| a | 1 | c |; 2
b // d,| b | 1 | d |; 3
e // f,| e | 5 | f |. 2
巩固练习
练习1 下列四个命题中:
①路程、速度都是向量; ②向量的模是一个正实数; ③共线向量一定是方向相同的向量 ④相等的非零向量方向一定相同 真命题的个数为( B ).
目标检测
测试4
如图所示,四边形ABCD和ABDE都是平行四边形.
A
B
(1)与ED 向量相等的向量为__A_B_,__D__C__; NhomakorabeaE
D
C
(2)若| AB |=3,则向量 EC 的模等于____6____.
解析:(1)在平行四边形ABCD和ABDE中, ∵ AB= ED, AB=DC, ∴ ED= DC. (2)由(1)知 ED= DC, ∴E,D,C三点共线, | EC|=|ED |+|DC|=2| AB |=6.
向量的表示
表示方法 两个大写字母 一个小写字母
6.1.5 向量的线性运算(课件)高一数学(人教B版2019必修第二册)

高一数学课件
第六章 平面向量初步
6.1.5 向量的线性运算
高一必修第二册(2019人教B版)
学习目标
1.理解向量线性运算的定义及运算法则.(重点) 2.能利用向量的线性运算解决简单问题.(难点)
新知导入
情 景 一 : 向量的加法运算、数乘向量运算,它们的结果都是向量,这就是说,
这两者可以进行混合运算.例如,对于任意向量 ,式子
用已知向量表示未知向量的技巧: ①由已知向量表示未知向量时,要善于利用三角形法则、平行四边形法则以及 向量线性运算. ②当直接表示较困难时,应考虑利用方程(组)求解.
6
【 解 析 】 (1)原式=6a-4b+3a+15b-20b+5a=14a-9b;
(2)原式=1(4a+16b-16a+8b)=1(-12a+24b)=-2a+4b.
6
6
课堂练习
【训练 4】已知向量 a,b.
(1)计算:6a-[4a-b-5(2a-3b)]+(a+7b);
(2)把满足 3x-2y=a,-4x+3y=b 的向量 x,y 用 a,b 表示出来.
课堂总结
向量的线性运算: 向量的加法、减法和数乘向量以及它们的混合运算,通常叫作向量的线性运算.
向量共线: 一般地,如果存在实数λ,使得=λ,则与平行且有公共点 A,从而 A,B,C 三 点一定共线.
课堂总结
向量线性运算的方法: 向量的线性运算类似于代数多项式的运算,主要是“合并同类项”“提取公因式”, 但这里的“同类项”“公因式”指向量,实数看做是向量的系数.
A.a=2e,b=-2e;
B.a=e1-e2,b=-2e1+2e2
C.a=4e1-25e2,b=e1-110e2 D.a=e1+e2,b=2e1-2e2.
第六章 平面向量初步
6.1.5 向量的线性运算
高一必修第二册(2019人教B版)
学习目标
1.理解向量线性运算的定义及运算法则.(重点) 2.能利用向量的线性运算解决简单问题.(难点)
新知导入
情 景 一 : 向量的加法运算、数乘向量运算,它们的结果都是向量,这就是说,
这两者可以进行混合运算.例如,对于任意向量 ,式子
用已知向量表示未知向量的技巧: ①由已知向量表示未知向量时,要善于利用三角形法则、平行四边形法则以及 向量线性运算. ②当直接表示较困难时,应考虑利用方程(组)求解.
6
【 解 析 】 (1)原式=6a-4b+3a+15b-20b+5a=14a-9b;
(2)原式=1(4a+16b-16a+8b)=1(-12a+24b)=-2a+4b.
6
6
课堂练习
【训练 4】已知向量 a,b.
(1)计算:6a-[4a-b-5(2a-3b)]+(a+7b);
(2)把满足 3x-2y=a,-4x+3y=b 的向量 x,y 用 a,b 表示出来.
课堂总结
向量的线性运算: 向量的加法、减法和数乘向量以及它们的混合运算,通常叫作向量的线性运算.
向量共线: 一般地,如果存在实数λ,使得=λ,则与平行且有公共点 A,从而 A,B,C 三 点一定共线.
课堂总结
向量线性运算的方法: 向量的线性运算类似于代数多项式的运算,主要是“合并同类项”“提取公因式”, 但这里的“同类项”“公因式”指向量,实数看做是向量的系数.
A.a=2e,b=-2e;
B.a=e1-e2,b=-2e1+2e2
C.a=4e1-25e2,b=e1-110e2 D.a=e1+e2,b=2e1-2e2.
人教版必修4高一上册数学课件《2.2.2向量的加法与减法》

由a 唯一确定
2.点A的坐标与向量a
的坐标的关系?
y
若a以为起点,两者相同
a
A(x, y)
向量a 一 一 对 应 坐标(x ,y)
a j
Oi
x
3.两个向量相等的条件,利用坐标如何表示?
a b x1 x2且y1 y2
变形:如图分别用基底 i,j 表示向量 a、b、 c、d,
并求出它们的坐标。
-3
探索2:
在平面直角坐标系内,起点不在坐标
原点O的向量如何用坐标来表示?
解决方案:
可通过向量的 平移,将向量的起点 移到坐标的原点O处.
yA a
a
ox
y
a xi +y j y
a
A
OA xi +y j
j
O
i
x
x
平面向量的坐标表示
y
D
如图,i, j 是分别与x轴、y轴方向相同
a C
的单位向量,若以 i, j 为基底,则 A
2.2.2向量的坐标表示与运算
复
习
1、平面向量基本定理的内容是什么?
2、什么是平面向量的基底?
平面向量的基本定理:
如果 e1 , e2是同一平面内的两个不共 线的向量,那么对于这一平面内的任一 向量 a ,有且只有一对实数 λ1 , λ2 使 得a= λ1 e1+ λ2 e2 向量的基底:
不共线的平面向量 e1 , e2 叫做这 一平面内所有向量的一组基底.
向量的坐标运算法则
a (x1, y1),b (x2 , y2 ) 则:a b (x1 x2 , y1 y2 ) a b (x1 x2 , y1 y2 )
a (x1, y1)
高一下学期数学人教A版必修第二册6.1平面向量的概念 课件

相对地,把只有大小没有方向的量称 为数量。如年龄、身高、长度、面积、 体积、质量等都是数量。
6.1.2 向量的几何表示
温故知新
对于长度,我们可以用线段表示,比如 一个直角三角形的边长可以表示为
BC=3, AB=4, AC=5
问题3:我们应该用什么 4
5
图形去表示向量呢?
有向线段
3
新课讲授
通常,在线段AB中,规定一个顺序,
a
a
b
b
定义:方向相同或相反的非零向量叫做平行 向量,记作a//b.
规定:零向量与任何一个向量都平行
问题6:你能根据向量的定义给相等向量 下一个定义吗?
长度相等且方向相同的向量,叫做相等
向量。
a
记作a=b
b
例2、辨析正误 (1)任意两个相等的非零向量,都可以用同一条
有向线段表示,并且与有向线段的起点无关。( √ )
因此,平行向量也称为共线向量
l
C
OB A
例3 如图,设O是正六边形ABCDEF的中心。 (1)写出图中的共线向量; (2)分别写出图中与 OA,OB,OC 相等的向量。
解:
B
A
(1)OA,CB,DO,FE是共线向量;
O
C
F
OB,DC,EO,AF是共线向量;
OC,AB,ED,FO是共线向量。
D
E
(2)OA=CB=DO;
假设A为起点,B为终点,我们就说线
段AB具有方向,具有方向的线段叫做
有向线段。ຫໍສະໝຸດ B(终点)有向线段 三要素:
起点、方
A(起点)
向和长度
线段AB的长度就是对应有向线段 AB 的长 度,可以记作AB或者 AB .
6.1.2 向量的几何表示
温故知新
对于长度,我们可以用线段表示,比如 一个直角三角形的边长可以表示为
BC=3, AB=4, AC=5
问题3:我们应该用什么 4
5
图形去表示向量呢?
有向线段
3
新课讲授
通常,在线段AB中,规定一个顺序,
a
a
b
b
定义:方向相同或相反的非零向量叫做平行 向量,记作a//b.
规定:零向量与任何一个向量都平行
问题6:你能根据向量的定义给相等向量 下一个定义吗?
长度相等且方向相同的向量,叫做相等
向量。
a
记作a=b
b
例2、辨析正误 (1)任意两个相等的非零向量,都可以用同一条
有向线段表示,并且与有向线段的起点无关。( √ )
因此,平行向量也称为共线向量
l
C
OB A
例3 如图,设O是正六边形ABCDEF的中心。 (1)写出图中的共线向量; (2)分别写出图中与 OA,OB,OC 相等的向量。
解:
B
A
(1)OA,CB,DO,FE是共线向量;
O
C
F
OB,DC,EO,AF是共线向量;
OC,AB,ED,FO是共线向量。
D
E
(2)OA=CB=DO;
假设A为起点,B为终点,我们就说线
段AB具有方向,具有方向的线段叫做
有向线段。ຫໍສະໝຸດ B(终点)有向线段 三要素:
起点、方
A(起点)
向和长度
线段AB的长度就是对应有向线段 AB 的长 度,可以记作AB或者 AB .
高一数学平面向量的概念及线性运算PPT优秀课件

a+b=λLeabharlann a-b),即(λ-1)a=(1+λ)b,
∴ λ-1=0 1+λ=0
,λ 无解,故假设不成立,即 a+b 与 a-b 不平行,故选 D.
错源二:向量有关概念理解不当
【例2】 如图,由一个正方体的12条棱构成的向量组成了一个集合M,则集合M的元 素个数为________.
错解:正方体共有12条棱,每条棱可以表示两个向量,一共有24个向量.答案是24. 错解分析:方向相同长度相等的向量是相等向量,故AA1―→=BB1―→=CC1―→ = DD1―→ , AB―→ = DC―→ = D1C1―→ = A1B1―→ , AD―→ = BC―→ = B1C1―→=A1D1―→.错解的原因是把相等的向量都当成不同的向量了. 正解:12条棱可以分为三组,共可组成6个不同的向量,答案是6. 答案:6
错解分析:错解一,忽视了 a≠0 这一条件.错解二,忽视了 0 与 0 的区别,AB―→+
BC―→+CA―→=0;错解三,忽视了零向量的特殊性,当 a=0 或 b=0 时,两个等号同时
成立.
正解:∵向量 a 与 b 不共线,
∴a,b,a+b 与 a-b 均不为零向量.
若 a+b 与 a-b 平行,则存在实数 λ,使
∴|AM―→|=12|AD―→|=12|BC―→|=2.故选 C.
【例2】 (2010年安徽师大附中二模)设O在△ABC的内部,且OA―→+OB―→+ 2OC―→=0,则△ABC的面积与△AOC的面积之比为( ) (A)3 (B)4 (C)5 (D)6
解析:由 OC―→=-12(OA―→+OB―→),设 D 为 AB 的中点, 则 OD―→=12(OA―→+OB―→), ∴OD―→=-OC―→,∴O 为 CD 的中点, ∴S△AOC=12S△ADC=14S△ABC,∴SS△△AAOBCC=4.故选 B.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
是指显像剂引入体内后几小时以内的显像()A.1小时B.2小时C.4小时D.6小时E.8小时 [多选]左房室瓣口血流频谱的影响因素包括()。A.性别B.年龄C.心率D.呼吸E.前负荷 [单选,A1型题]关于麻黄药理作用叙述错误的是()A.兴奋中枢B.升高血压C.抗炎D.镇咳E.保肝 [单选]老年人有反复发作的霰粒肿时,首先应考虑()A.继发感染的可能B.鳞状细胞癌的可能C.基底细胞癌的可能D.眼睑皮脂腺癌的可能E.以上均不是 [单选]下列关于动脉弹性的说法哪项是正确的().A.一氧化氮是内皮细胞产生的重要缩血管物质B.大动脉弹性和外周血管压力反射波是脉压的主要决定因素C.大动脉弹性减退,脉搏波传导速度减慢D.阻力小动脉的弹性和功能影响脉搏波传导速度E.以上均不正确 [单选]在实际建筑工程中,按绝缘方式一般应优先选用的电缆为()。A.橡皮绝缘电缆B.聚氯乙烯绝缘电缆C.油浸纸绝缘电缆D.交联聚乙烯绝缘电缆 [单选,A4型题,A3/A4型题]男,50岁,因躯干、双下肢汽油火焰烧伤3小时入院,烧伤面积为60%,其中深Ⅱ度20%,Ⅲ度40%,入院后立即给予补液及应用广谱抗生素预防感染治疗。入院第3天行手术切痂自体微粒皮加大张异体皮移植术。术后因患者发热,给予持续大剂量广谱抗生素以控制感染,术 [单选]女性,45岁。间歇性无痛性肉眼血尿2个月,伴蚯蚓状血块。膀胱镜检查:膀胱内未见肿瘤。左输尿管口喷血。为尽快明确诊断,最有价值的检查是()A.CTB超C.MRID.左肾穿刺顺行造影E.左肾盂输尿管逆行造影 [单选]在海上拖运超大型沉箱施工应当在启拖开始之日()天前向启拖地所在海区的区域主管机关递交发布海上航行警告、航行通告的书面申请。A.3B.5C.7D.10 [问答题,简答题]皮肤接触氢氧化钠如何急救? [单选]Afullyloadedmotor-propelledlifeboatmustbecapableofattainingaspeedofatleast().A.3knotsinsmoothwaterB.6knotsinsmoothwaterC.3knotsinroughwaterD.6knotsinroughwater [单选]()不是水路运输的优点。A.建设投资少B.管理复杂C.运输成本低D.劳动生产率高 [单选]在软土地基上建斜坡结构防波堤,堤心抛石有挤淤要求、抛石顺序应()。A.沿堤横断面从一端向另一端抛B.沿堤纵断面从一段的一端向另一端抛C.沿堤的横断面从中间向两侧抛D.沿堤断面全面平抛 [名词解释]两囊幼虫 [填空题]A,B两组分等摩尔扩散的代表单元操作是(),A在B中单向扩散的代表单元操作是()。 [单选]冬天走进橙色的房间里有一种温暖的感觉,这是()现象。A.感觉适应B.感觉对比C.联觉D.视觉 [单选,A2型题,A1/A2型题]《实验室认可管理办法》规定的中国实验室认可原则,不包括()。A.自愿申请原则B.非歧视原则C.国家强制原则D.专家评审原则E.国家认可原则 [单选]锅炉分气缸的主要作用是()。A、储存蒸汽B、蒸汽的汽水分离C、分配蒸汽D、多台锅炉蒸汽并用 [单选,A型题]超品种配药指在一个科室门诊就医的处方上,西药处方大于()。A.5个B.4个C.6个D.3个E.7个 [单选,A1型题]结核病时发生的变态反应属于几型()A.Ⅰ型B.Ⅱ型C.Ⅲ型D.Ⅳ型E.Ⅴ型 [单选]下列关于隧道衬砌裂缝病害防治的说法错误的是()。A.设计时应根据围岩级别选取衬砌形式及衬砌厚度B.钢筋保护层必须保证不小于3cmC.混凝土宜采用较大的水灰比,降低骨灰比D.混凝土温度的变化速度不宜大于5°C/h [单选]外板以()为理论线。A.板的内缘B.板厚C.板的中心线 [多选]应当实施检验检疫的出入境快件包括()。A.有关国际条约、双边协议规定应当实施动植物检验检疫和卫生检疫的B.列入《法检商品目录》内的C.属于实施强制性认证制度、卫生注册登记制度管理的D.其他有关法律法规规定应该实施检验检疫的 [名词解释]保险备用信用证 [单选]中国人民银行实行()负责制。A.个人B.集体C.法人D.行长 [单选,A1型题]在血吸虫发育各阶段,引起人体主要病理变化的是()。A.尾蚴B.成虫C.虫卵D.幼虫E.毛蚴 [单选]当遇到深度访谈或对问题所知不多时常用()A.专题调查B.定量调查C.半定量调查D.定性调查E.以上都不是 [问答题,简答题]请标出下图中的形位公差附加符号的意思: [单选,A1型题]马的初情期年龄是()A.10~15月龄B.6~12月龄C.8~15月龄D.12月龄E.8~10月龄 [问答题,简答题]货运检查主要内容有那些? [填空题]当变压器保护动作跳闸时,应先投入备用变压器,再查找(),记录(),同时()。 [单选]Inmarsat通信系统中,提供用户电传用于公共通信与遇险报警的低速数据业务是()。A、标准F移动站B、标准B移动站C、标准C移动站D、标准M移动站 [单选,A2型题,A1/A2型题]关于退行性主动脉瓣病变下列描述不正确的是()A.病理改变可为钙化、黏液样变B.多为轻度狭窄C.一般左冠瓣重于右冠瓣和无冠瓣D.可累及心脏传导系统E.与性别有关,一般男性多于女性 [单选]治疗十二指肠球部溃疡的重点是()A.根除幽门螺杆菌与制酸B.保护黏膜C.少食多餐D.应用镇静剂E.早期手术 [单选]下列各项中,不应计入营业外收人的是()。A.债务重组利得B.处置固定资产净收益C.收发差错造成存货盘盈D.确实无法支付的应付账款 [单选]大型运输机的最大使用负过载大约为()。A.0.5-2.5B.1.5-2.5C.0.5-1.5D.2-3 [多选]桥梁拆除施工应根据拆除工程施工现场作业环境,制定相应的消防安全措施,施工现场应设置()等设施和器材。A.消防车通道B.消火栓C.报警器D.应急救援车E.灭火器材 [问答题,简答题]型车钩缓冲装置由哪些部件组成? [名词解释]适熟蚕 [填空题]黑色金属表面一般都存在氧化皮,俗称()。
