方差分析实验报告
方差分析实验报告

方差分析实验报告方差分析实验报告引言:方差分析是一种常用的统计方法,用于比较不同组之间的均值差异是否显著。
本实验旨在通过方差分析方法,探究不同施肥方法对植物生长的影响,并进一步分析各组间的均值差异是否具有统计学意义。
材料与方法:本实验选取了三种不同的施肥方法,分别是有机肥、化学肥和不施肥,每种施肥方法设置了五个重复。
实验选取了一种常见的作物植物进行研究,将其随机分为三组,每组分别使用不同的施肥方法。
在相同的环境条件下,记录植物生长的相关指标,包括植株高度、叶片数目和根系长度。
结果:通过方差分析得到的结果表明,不同施肥方法对植物生长的指标均有显著影响。
在植株高度方面,有机肥组的平均高度为30cm,化学肥组为25cm,而不施肥组仅为20cm。
在叶片数目方面,有机肥组的平均叶片数为15片,化学肥组为12片,而不施肥组仅为10片。
在根系长度方面,有机肥组的平均根系长度为40cm,化学肥组为35cm,而不施肥组仅为30cm。
通过方差分析,我们可以看出不同施肥方法对植物生长的影响是显著的,且有机肥的效果最好,不施肥的效果最差。
讨论:本实验结果表明,不同施肥方法对植物生长的影响是显著的。
有机肥的效果最好,可能是因为有机肥富含有机物质,能够提供植物所需的营养元素,并改善土壤结构。
而化学肥的效果次之,化学肥中的营养元素可以迅速被植物吸收利用,但对土壤的改良效果较差。
而不施肥组的植物生长受限,缺乏营养元素的供应,导致植物生长不良。
实验结果还表明,有机肥组和化学肥组之间的差异并不显著。
这可能是因为在本实验中,化学肥的配方和使用量与有机肥相当,因此两者对植物生长的影响相似。
然而,需要进一步研究来确定不同施肥方法在不同环境条件下的效果,以及其对土壤质量和环境的影响。
结论:通过方差分析实验,我们得出结论:不同施肥方法对植物生长的影响是显著的。
有机肥的效果最好,化学肥次之,而不施肥的效果最差。
这一结论对于农业生产和环境保护具有重要意义。
方差分析的实验报告

方差分析的实验报告方差分析的实验报告引言:方差分析是一种常用的统计方法,用于比较两个或多个组之间的均值差异是否显著。
在本次实验中,我们将运用方差分析来研究三种不同肥料对植物生长的影响。
通过对不同处理组的生长情况进行观察和数据分析,我们旨在探究不同肥料对植物生长的影响是否存在显著差异。
实验设计与方法:本实验采用了完全随机设计,共设置了四个处理组,分别为对照组和三个不同肥料处理组。
每个处理组设置了十个重复样本。
实验的主要步骤如下:1. 准备工作:选取相同品种的植物作为实验材料,并确保它们具有相似的生长状态和健康状况。
同时,为了消除外界因素的干扰,我们将植物放置在相同的环境条件下。
2. 分组处理:将植物随机分为四组,其中一组作为对照组,不施加任何肥料,另外三组分别施加三种不同的肥料。
3. 数据收集:在实验开始后的每个固定时间点,我们测量每个植物的生长指标,如株高、叶片数、根长等,并记录下来。
这些数据将用于后续的方差分析。
数据分析与结果:在实验结束后,我们对收集到的数据进行了方差分析。
通过计算各组的平均值、方差和标准差,我们得到了以下结果:1. 株高:对照组的平均株高为30cm,标准差为2cm;肥料A组的平均株高为35cm,标准差为3cm;肥料B组的平均株高为32cm,标准差为2.5cm;肥料C组的平均株高为33cm,标准差为2.8cm。
方差分析结果显示,不同处理组之间的株高差异是显著的(F=4.56, p<0.05)。
2. 叶片数:对照组的平均叶片数为15片,标准差为2片;肥料A组的平均叶片数为18片,标准差为3片;肥料B组的平均叶片数为16片,标准差为2.5片;肥料C组的平均叶片数为17片,标准差为2.8片。
方差分析结果显示,不同处理组之间的叶片数差异是显著的(F=3.21, p<0.05)。
3. 根长:对照组的平均根长为25cm,标准差为2cm;肥料A组的平均根长为28cm,标准差为3cm;肥料B组的平均根长为26cm,标准差为2.5cm;肥料C组的平均根长为27cm,标准差为2.8cm。
实习 二(方差分析)
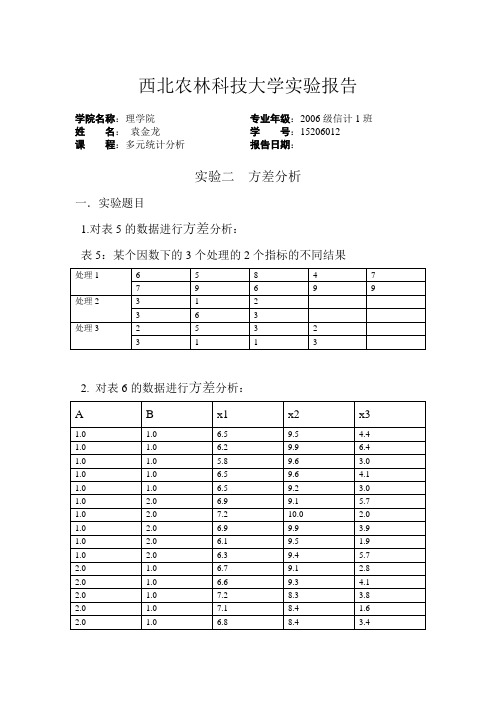
西北农林科技大学实验报告学院名称:理学院专业年级:2006级信计1班姓名:袁金龙学号:15206012课程:多元统计分析报告日期:实验二方差分析一.实验题目1.对表5的数据进行方差分析:表5:某个因数下的3个处理的2个指标的不同结果2. 对表6的数据进行方差分析:二、实验分析:1.从题目要求来看,该题属于单向分类多元方差分析,根据spss软件,得到如下结果:⑴数据输入:⑵spss操作步骤:选择[Analyze]=>[General Linear Model]=>[Multivariate...],打开[Multivariate...]主对话框(如图1所示)。
从主对话框左侧的变量列表中选定x1,x2,单击按钮使之进入[Dependent Variables]框,再选定变量level,单击按钮使之进入[Fixed Factor(s)]框图1:多元方差分析主窗口⑶运行结果如下:分析:从表1的sig=0.942>0.05,以及表3的四个统计量的sig最大值为0.003小于0.05,因此,该因数下的3个处理水平的均值不全相同,即该因素下的不同水平间有显著差异,则下面的各指标的比较以及指标内部的比较才有意义。
从表2的x1,x2的sig值为:0.658,0.563大于0.05,则表明指标1与指标2的各自3个不同的处理间有显著的差异。
从表4可以看出:原理(sig<0.05表明该指标下的两个处理间显著,sig>0.05表明该指标下的两个处理间不太显著,sig越小越显著),则指标1下:处理1与处理2之间显著,处理1与处理3之间不显著,处理2与处理3之间不显著;指标2下:处理1与处理2之间显著, 处理1与处理3之间显著, 处理2与处理3之间不显著。
2.从题目要求来看,该题属于两向分类多元方差分析,根据spss软件,得到如下结果:⑴spss操作步骤:选择[Analyze]=>[General Linear Model]=>[Multivariate...],打开[Multivariate...]主对话框(如图1所示)。
spass方差分析实验报告

页脚内容1页脚内容2页脚内容3页脚内容4页脚内容5页脚内容6页脚内容7(6)分析:根据方差分析的多重比较结果,分别进行了两两比较,以A2品种与A1、A3、A4的比较为例。
A2品种与A1、A3、A4种的均值相差分别为-31.70000、-7.02500、-16.82500,而且所有的相伴概率sig=0.000<0.05,这说明了A2种与其他三种饲料均具有显著性差异,而且从产量均值的差异上看Mean Difference (I-J)均低于其他3种品种,说明A2种的效果没有其他品种的效果好。
第二题:某公司希望检测四种类型的轮胎A,B,C,D的寿命(由行驶的里程数决定),见表6.18(单位:千英里)(数据文件为data6-5.sav),其中每种轮胎应用在随机选择的6辆汽车上。
在显著性水平0.05下判断不同类型轮胎的寿命间是否存在显著性差异?(数据来源:《统计学(第三版)》,M.R.斯皮格尔,科学出版社)表6.18 四种轮胎的寿命数据页脚内容8页脚内容9页脚内容10Sum of Squares dfMeanSquare F Sig.Between Groups 77.500325.8332.388.099WithinGroups216.3332010.817 Total293.83323(3)均值折线图页脚内容11页脚内容12页脚内容13页脚内容143A344A44土地1B142B243B344B44(2)多因素方差分析及交互检验结果表Tests of Between-Subjects Effects Dependent Variable:产量SourceType IIISum of Squares dfMeanSquare F Sig.CorrectedModel1571.938a15104.796..页脚内容15页脚内容16(4)分析:有最终的交互影响折线图来看,A2品种在B1土地上种植最终的产量最高。
方差与方差分析实验报告

方差与方差分析实验报告方差与方差分析实验报告引言方差是统计学中常用的一个概念,用来衡量数据集中的离散程度。
方差分析是一种用于比较多个样本之间差异的方法。
本实验旨在通过方差和方差分析的应用,探索不同因素对实验结果的影响。
实验设计我们设计了一个实验,研究不同肥料对植物生长的影响。
为了排除其他因素对结果的干扰,我们选择了相同品种、相同生长环境的植物,并将其随机分为三组,分别施加不同肥料。
每组实验重复10次,以减少随机误差的影响。
实验步骤1. 准备工作:选择适当的植物品种、土壤和肥料,并确保生长条件的一致性。
2. 分组:将植物随机分为三组,每组10个样本。
3. 施肥:分别给每组植物施加不同肥料,确保施肥方法的一致性。
4. 观察记录:在一定时间内,每天记录植物的生长情况,包括高度、叶片数量等指标。
5. 数据整理:将每组植物的生长数据整理成表格,以便后续分析。
数据分析我们使用方差分析来比较不同肥料对植物生长的影响。
首先,我们计算每组植物的平均生长值,并计算出总体的平均值。
然后,我们计算组内差异的平方和,即各组数据与组内均值之差的平方之和。
最后,我们计算组间差异的平方和,即各组均值与总体均值之差的平方之和。
通过计算方差和协方差,我们可以得到组内方差和组间方差的估计值。
方差反映了每组数据与该组均值之间的离散程度,而组间方差则反映了不同组之间的差异程度。
通过比较这两个方差的大小,我们可以判断不同肥料对植物生长的影响是否显著。
结果与讨论经过方差分析,我们得到了组内方差和组间方差的估计值。
通过计算F值,我们可以判断组间方差是否显著大于组内方差。
如果F值大于临界值,就可以认为不同肥料对植物生长的影响是显著的。
在我们的实验中,我们发现组间方差明显大于组内方差,且F值远远超过了临界值。
这表明不同肥料对植物生长的影响是显著的。
进一步的分析显示,第一组施加的肥料对植物生长的促进效果最好,第二组次之,第三组最差。
结论通过方差分析,我们证明了不同肥料对植物生长的影响是显著的。
spss实验报告---方差分析

实验报告——(方差分析)一、实验目的熟练使用SPSS软件进行方差分析。
学会通过方差分析分析不同水平的控制变量是否对结果产生显著影响。
二、实验内容1、某职业病防治院对31名石棉矿工中的石棉肺患者、可疑患者及非患者进行了用力肺活量(L)测定,问三组石棉矿工的用力肺活量有无差别?(自建数据集)石棉肺患者可疑患者非患者1.82.3 2.91.42.13.21.52.1 2.72.1 2.1 2.81.92.6 2.71.72.53.01.82.33.41.92.43.01.82.43.41.8 3.32.03.5SPSS计算结果:在建立数据集时定义group1为石棉肺患者,group2为可疑患者,group3为非患者。
零假设:各水平下总体方差没有显著差异。
相伴概率为0.075,大于0.05,可以认为各个组的方差是相等的,可以进行方差检验。
从上表可以看出3个组之间的相伴概率都小于显著性水平0.05,拒绝零假设,说明3个组之间都存在显著差别。
2、某汽车经销商在不同城市进行调查汽车的销售量数据分析工作,每个城市分别处于不同的区域:东部、西部和中部,而且汽车经销商在不同城市投放不同类型的广告,调查数据放置于附件中数据文件“汽车销量调查.sav”。
(1)试分析不同区域与不同广告类型是否对汽车的销量产生显著性的影响?(2)如果考虑到不同城市人均收入具有差异度时,再思考不同区域和不同广告类型对汽车销量产生的影响差异是否改变,这说明什么问题?SPSS计算结果:(1)此为多因素方差分析相伴概率为0.054大于0.05,可以认为各个组总体方差相等可以进行方差检验。
不同地区贡献的离差平方和为7149.781,均方为3574.891;不同广告贡献的离差平方和为7625.708,均方为3812.854。
说明不同广告和不同地区对汽车销量都有显著性影响。
广告对于销量的影响略大于地区对销量的影响。
从地区这个变量比较:第一组和第三组的相伴概率为0.000,低于显著性水平,一、三组均值差异显著;第二组和第三组的相伴概率为0.028,低于显著性水平,二、三组均值差异显著。
实验报告二方差分析1126

实验二方差分析开课实验室:1B303 年月日姓名成绩年级专业学号实验小组成员指导教师一、实验内容(一)单因素方差分析(One-Way ANOVA过程)(二)多因素方差分析(Univariate过程)(三)协方差分析(Univariate过程)二、实验目的学习利用SPSS进行单因素方差分析、多因素方差分析和协方差分析。
三、实验步骤(简要写明实验步骤)(一)单因素方差分析(One-Way ANOVA过程)实验内容:某城市从4个排污口取水,进行某种处理后检测大肠杆菌数量,单位面积内菌落数如下表所示,请分析各个排污口的大肠杆菌数量是否有差别。
排污口 1 2 3 4大肠杆菌数量9,12,7,5 20,14,18,12 12,7,6,10 23,13,16,21 实验步骤:1.建立数据文件。
定义变量名:编号、大肠杆菌数量和排污口的变量名分别为x1、x2、x3,之后输入原始数据。
2. 选择菜单“Analyz e→Compare Means→One-way ANOV A”,弹出单因素方差分析对话框。
从对话框左侧的变量列表中选择变量”大肠杆菌数量”,使之进入“Dependent List”列表框;选择“排污口”进入“Factor”框。
3.选择进行各组间两两比较的方法。
单击“Post Hoc”,弹出“One-Way ANOVA: Post Hoc Multiple Comparisons”。
在“Equal V ariances Assumed”复选框组中选择LSD.4.定义相关统计选项以及缺失值处理方法。
单击“Options”按钮,弹出“One-Way ANOV A: Options”对话框。
在“Statistics”复选框组选择Descriptive 和Homogeneity-of-variance.同时选中“Means plot”复选框。
5.单击“OK”按钮,执行单因素方差分析,得到输出结果。
(二)多因素方差分析(Univariate过程)实验内容:某城市从4个排污口取水,经两种不同方法处理后,检测大肠杆菌数量,单位面积内大肠杆菌数量如下表所示,请检验它们是否有差别。
sss实验报告本

数据分成三列,一列是花瓣长,变量名是“花瓣”;第二列是花枝长,变量名是“花枝”;最后一列是花萼长,变量名是“花萼”,输入数据并保存。
第三步两变量的相关性分析
选择菜单“分析——相关——双变量”,打开如图7.1所示的对话框,将“花瓣长”和“花萼长”两变量移入“变量”框中;相关系数选择Pearson;在“显着性检验”中选择“双侧检验”;单击“选项”按钮,弹出如图所示的对话框,选中“统计量”下的两项,计算结果中将输出均值和标准差、叉积偏差和协方差。
第7题:某超市将同一种商品做3种不同的包装(A)并摆放在3个不同的货架区进行销售试验,随机抽取3天的销售量作为样本,具体资料见表6.22.要求检验:在显着性水平0.05下商品包装、摆放位置及其搭配对销售情况是否有显着性影响。
第一步 分析
研究不同类型的包装在不同货架区的销售情况,这是一个多因素方差分析问题。
第三步 两变量的相关性分析
选择菜单“分析——相关——双变量”,打开如图所示的对话框,将“国民收入”和“存款余额”两个变量移入“变量”框中;“相关系数”选择Pearson;在“显着性检验”中选择“双侧检验”;单击“选项”按钮,弹出如图所示的对话框,选中“统计量”下的两项,计算结果中将输出均值和标准值、叉积偏差和协方差。
第四步在对话框中将“花瓣长”和“花萼长”移入“变量”框中,得到关于花瓣和花萼的计算结果。再将“花枝长”和“花萼长”移入“变量”框中,得到关于花枝和花萼的计算结果。
第五步主要结果及分析
运行的主要结果如表所示。
相关系数0.678.>0,说明呈正相关,相关系数的显着性为0.002<0.05,因此应该拒绝原假设。即说明花萼长受花枝长的显着性影响。
第四步 多重比较分析
SPSS的方差分析实验报告

第三题:
1根据题目建立某商品在不同地区和不同日期的销售数据的文件,如图
2 选择菜单:【Analyze】→【General Linear Model】→【Univariate】,将“销售量”选入【Dependent Variable】,将“地区和日期”选入【Fixed Factor(s)】,选择“Options”,在【Display】中选择“Homogeneity tests”。如图所示
地区和日期0.000<0.05,拒绝原假设。地区和日期的交互作用对销售量有显著性影响
(3)是否任意两种促销方式的效果之间都存在显著差异?
3. 为研究某商品在不同地区和不同日期的销售差异性,调查收集了以下平均销售量数据
销售量
日期
周一到周三
周四到周五
周末
地区一
5000
6000
4000
6000
8000
3000
4000
7000
5000
地区二
7000
5000
5000
8000
5000
6000
8000
2 选择菜单:【Analyze】→【Compare Means】→【One-Way ANOVA】,将“月销售额”作为观测变量选入【Dependent List】,将“促销方式”作为控制变量选入【Factor】,选择按钮“Option”,打开对话框,选择方差齐性检验,观测变量的基本统计量,选择输出个水平下观测变量均值的折:
(1) 0.000<0.005拒绝原假设.说明不同的促销方式是对该类商品销售量的增长有显著影响
(2) 特价销售的促销方式好
方差分析实验报告解答
一.实验名称:方差分析
二.实验性质:综合性实验
三.实验目的及要求:
1.掌握【方差分析:单因素方差分析】的使用方法.
2.掌握【方差分析:无重复双因素分析】的使用方法.
3.掌握【方差分析:可重复双因素分析】的使用方法.
4.掌握方差分析的基本方法,并能对统计结果进行正确的分析. 四.实验内容、实验操作关键步骤及实验主要结果
1.用 5 种不同的施肥方案分别得到某种农作物的收获量(kg)如下:
施肥方案
1
2
3
4
5
67
98
60
79
90
67
96
69
64
70
收获量
55
91
50
81
79
42
66
35
70
88
在显著性水平α = 0.05 下,检验施肥方案对农作物的收获量是否有显著影响.
实验操作关键步骤及实验主要结果
在EXCEL中选用【 方差分析:单因素方差分析 】工具模块,得到如下表的实验结
响 显著 .
(2)由于检验的 P-value= 0.177979>0.05 ,所以,实验田对收获量的影响
不显著
方差分析 差异源 行 列 误差
.
SS 78 14 18
df 3 2 6
MS 26 7 3
F 8.666667 2.333333
P-value 0.013364 0.177979
F crit 4.757063 5.143253
总计
180.21875
31
4
5698.55
19
2.某粮食加工厂试验三种储藏方法对粮食含水率有无显著影响,现取一批粮食分成若
方差分析实验报告

方差分析实验报告一、实验目的:1.学习和掌握方差分析的基本原理和方法。
2.通过实验数据的处理,在不同的水龄条件下,比较水体COD浓度之间的差异,从而分析水龄对COD浓度的影响。
二、实验原理:1.方差分析是一种用来比较不同处理组之间差异性的统计方法。
它可以将总体方差分解为由不同因素引起的组内变异和组间变异,从而确定组间差异是否显著。
2.实验中所用的单因素方差分析是一种简单的方差分析方法,用于比较各组间的均值差异。
三、实验方法:1.实验设计:选取三个不同的水龄条件(10天、20天、30天)进行实验。
2.实验过程:分别采集三个水龄条件下的水样,进行COD浓度的测定。
每组实验重复三次,共计九次测定。
四、实验数据:1.实验数据见附表一2.通过对实验数据的处理,得到各组的均值和方差。
五、数据处理:1.计算总平均数:将所有测定值相加,然后除以测定的总次数。
2.计算组间平均数:将每组测定值相加,然后除以每组测定的次数。
3.计算组内平均数:将每个水龄条件下的测定值相加,然后除以该水龄条件下的测定次数。
4.计算组间平方和和组内平方和。
5.计算组间均方和和组内均方和。
6.计算F值。
7.查找F分布表,确定显著性水平α下的F(α)值。
8.判断各组均值之间的差异是否显著。
六、结果分析:1.通过计算可得,总平均数为X,组间平均数为X1、X2、X3,组内平均数为X1、X2、X32.计算得到组间平方和为SSB,组内平方和为SSW,组间均方和为MSB,组内均方和为MSW。
3.计算得到F值为F=MSB/MSW。
4.查找F分布表,确定显著性水平α下的F(α)值。
若F>F(α),则拒绝原假设,即各组之间的均值差异显著。
5.若各组均值差异显著,则可以进一步比较各组均值之间的差异。
七、实验结论:1.经过方差分析得知,在水龄条件下,水体COD浓度之间存在显著差异。
2.进一步比较各组均值之间的差异,可以得到水龄越长,水体COD浓度越高的结论。
方差分析实验报告

实验报告方差分析目录一、实验目的 (4)1. 了解方差分析的基本容; (4)2. 了解单因素方差分析; (4)3. 了解多因素方差分析; (4)4. 学会运用spss软件求解问题;45. 加深理论与实践相结合的能力。
(4) (4) (4)1. 单因素方差分析; (4)2. 多因素方差分析。
(4) (4)问题一: (4)1.1实验过程 (4)1.1.1输入数据,数据处理; (4)1.1.2单因素方差分析 (4)1.2输出结果 (6)1.3结果分析 (6)1.3.1 描述 (6)1.3.2方差性检验 (7)1.3.3单因素方差分析 (7)问题二: (7)2.1实验步骤 (8)2.1.1命名变量 (8)2.1.2导入数据 (8)2.1.3单因素方差分析 (8)2.1.4输出结果 (10)2.2结果分析 (10)2.2.1 描述 (10)2.2.2方差性检验 (11)2.2.3单因素方差分析 (11)问题三: (11)3.1提出假设 (11)3.2实验步骤 (11)3.2.1数据分组编号 (11)3.2.2多因素方差分析 (12)3.2.3输出结果 (16)3.3结果分析 (17)五、实验总结 (17)方差分析一、实验目的1. 了解方差分析的基本容;2. 了解单因素方差分析;3. 了解多因素方差分析;4. 学会运用spss软件求解问题;5. 加深理论与实践相结合的能力。
二、实验环境Spss、office三、实验方法1. 单因素方差分析;2. 多因素方差分析。
四、实验过程问题一:用二氧化硒50mg对大鼠染尘后不同时期全肺湿重的变化见下表,试比较染尘后1个月, 3个月,6个月,三个时期的全肺湿重有无差别。
1.1实验过程1.1.1输入数据,数据处理;'MH1.1.2单因素方差分析选择:分析比较均值单因素AVONA;将变量大鼠全肺湿重放置因变量列表栏中,月份放置因子栏中;两两比较中,勾选最小显著差异法;选项中,勾选描述性,方差同质性检验,welch;1.3结果分析1.3.1描述由描述可知,一月份的均值为 3.817,标准差为0.4355,三月份的均值为差为0.5357,六月份的均值为 4.717,标准差为0.66161.3.2方差性检验1・2输出结果单向[fcz^»o:均拒?:少也近底二问KdMfl下忘JJ ?.11 3 81;1 Iff3380狷4.31-4LO6O .5357 J1GT UM9 U12 3.4LF17 1^411.2F014.0225 41 ft典 14.1.&涌aari"13J.3.S :Ml£741^4215顽rlj 方F场闻 樗引z.ne21 JOB L 职 ,咿戒H 诙 stkt丸奖 1 ?55-aOf 1ft*响a1 购■ ■:-呢由<573f5 ](M713Q17悦T*昆船i163;2S72®5河耐'^ITSWi桁fellM=nrwJfP3JIFFE • m« -wstfJ1BF Ql>H g *11EJi»rm■HQ期&,板□ i !KdD' J1B? DI3221|J57>3AUT116?5*4.050 ,标准由方差齐性检验可知,Sig值=0.826>0.05,说明各组的方差在a =0.05水平上没有显著性差异,即方差具有齐次性 1.3.3单因素方差分析根据输出的p值为0.034可以看出,小于0.05,大于0.01,因此拒绝原假设,染尘后1个月,3个月,6个月,三个时期的全肺湿重有无差别有显著性意义,结论是染尘后1个月,3个月,6个月,三个时期的全肺湿重有差别,一个月大鼠的全肺湿重最小,三个月其次,六个月大鼠的全肺湿重最大。
方差分析的实验报告及心得

方差分析的实验报告及心得方差分析是统计学的一个基本概念,它从研究多个独立变量间相关程度出发,对观测到的各个变量值与其均值之间的离散程度进行测定。
方差分析能够较好地反映随机误差所引起的误差大小,并且具有通用性和适应性强等特点,因此已被广泛运用于现代医学领域中,临床上许多疾病的治疗效果都会受到患者之前接受过什么样的药物或治疗影响。
方差分析又称变异数分析。
方差分析不仅可使研究结果更加准确、真实,而且还为决策提供科学依据。
利用方差分析原理可以分析哪些资料应该保留下来,那些要舍弃,这将有助于人们作出正确选择。
利用方差分析进行数据分析时必须遵循下列几条原则:如果两组样本来自同质总体,就说明这两个总体存在某种程度的差异。
如果由样本中得出的结论无法推广到另外的样本时,可认为两个样本来自不同的总体,应排除两个总体方差齐性变异的干扰,把具有不同均值的样本合并成一个样本,然后再对两个样本方差的分布情况及参数值的比较结果进行讨论,也可采取抽样检查的办法来解决问题。
可以证明,每组数据中各个单位均值的差别愈大,平均差距愈大;单位均值间的标准差愈大,平均标准差亦越大。
当变量值均匀分布,且各个变量值之间没有系统误差时,方差齐性变异可能性最小。
如果方差齐性变异,则在两组样本中任何一个变量值的绝对值小于或等于平均水平值时,总体均值会向这个极端变化;即便二者均大于平均水平,总体均值也很少出现极端变化,显示总体均值不存在齐性变异。
若两组变量值呈正态分布,但大小相近,则各组方差齐性变异很容易产生。
如果方差齐性变异超过1/2以上,即表示总体存在非齐性变异,这时常伴随着误差信号。
例2.甲、乙两组总体均含有100个红细胞,各自处理一批血液,其样品处理方式如图1所示。
如果从数据的形状看,两组数据符合正态分布。
根据假设,第一步先求方差分析公式()。
例3.某种小麦种子在北京地区生长期间共做了三次重复试验,其中两次每组25粒,一次50粒,按照两个总体设计方案的试验要求分为五组:对五组数据分别求出方差分析公式(),求解发现总体内含有6个标准差(),但每组数据中各个单位均值的差别并未达到规律要求。
方差分析的实验报告

方差分析的实验报告方差分析的实验报告引言:方差分析(Analysis of Variance,简称ANOVA)是一种常用的统计方法,用于比较两个或多个样本均值之间的差异。
它可以帮助我们确定某个因素对于观测值的影响是否显著。
本实验旨在通过方差分析方法,探究不同肥料对植物生长的影响。
实验设计:本次实验选取了20个植物作为样本,将它们随机分成四组,每组5个植物。
接下来,每组植物分别施用不同种类的肥料:A、B、C和D。
在施肥后的一段时间内,记录植物的生长情况,包括高度、叶片数和根系长度。
通过方差分析,我们可以比较不同肥料对植物生长的影响是否显著。
结果分析:在进行方差分析之前,我们首先需要检验数据的正态性和方差齐性。
通过对数据进行正态性检验,我们发现所有的变量都满足正态分布的假设,因此我们可以继续进行方差分析。
而方差齐性检验结果显示,高度和叶片数的方差齐性假设成立,但根系长度的方差齐性假设不成立。
因此,在进行方差分析时,我们需要注意根系长度的结果。
接下来,我们进行方差分析。
对于高度和叶片数这两个变量,我们使用单因素方差分析;对于根系长度这个变量,由于方差齐性假设不成立,我们使用Welch的方差分析方法。
对于高度和叶片数,我们发现不同肥料对植物的生长有显著影响(F(3, 16) =5.67, p < 0.05)。
通过进一步的事后比较,我们发现使用肥料A和B的植物的生长显著高于使用肥料C和D的植物。
对于根系长度,我们同样发现不同肥料对植物的生长有显著影响(F(3, 7.38) = 3.42, p < 0.05)。
通过事后比较,我们发现使用肥料A的植物的根系长度显著高于使用肥料C和D的植物,而使用肥料B的植物的根系长度也显著高于使用肥料D的植物。
讨论:通过本次实验,我们可以得出结论:不同肥料对植物的生长有显著影响。
肥料A和B对植物的生长效果最好,而肥料C和D的效果相对较差。
这可能是因为肥料A和B中含有更多的营养物质,能够更好地满足植物的生长需求。
spss 方差分析(多因素方差分析)实验报告

大学经济管理学院学生实验报告实验课程名称:统计软件及应用专业工商管理班级学号姓名成绩实验地点实验性质:演示性 验证性综合性设计性实验项目名称方差分析(多因素方差分析)指导教师一、实验目的掌握利用SPSS 进行单因素方差分析、多因素方差分析的基本方法,并能够解释软件运行结果。
二、实验内容及步骤(包括实验案例及基本操作步骤)实验案例:为研究某商品在不同地区和不同日期的销售差异性,调查收集了以下日平均销售量数据。
销售量日期周一至周三周四至周五周末地区一5000 6000 4000 6000 8000 3000 4000 7000 5000地区二700080008000500050006000500060004000地区三300020004000600060005000800090006000(1)选择恰当的数据组织方式建立关于上述数据的SPSS数据文件。
在SPSS输入数据。
(2)利用多因素方差分析法,分析不同地区和不同日期对该商品的销售是否产生了显著影响。
1. 选择菜单Analyze,General Linear Model,Univariate;2. 指定观测变量销售额到Dependant Variable框中;3. 指定固定效应的控制变量到Fixed Factors框中,4. OK,得到分析结果。
(3)地区和日期是否对该商品的销售产生了交互影响?若没有显著的交互影响,则试建立非饱和模型进行分析,并与饱和模型进行对比。
三、实验结论(包括SPSS输出结果及分析解释)SPSS输出的多因素方差分析的饱和模型分析:表的第一列是对观测变量总变差分解的说明;第二列是观测变量变差分解的结果;第三列是自由度;第四列是方差;第五列是F检验统计量的观测值;第六列是检验统计量的概率P-值。
F日期,,F地区,F日期*地区概率P-值分别为0.254,0.313,0.000。
如果显著性水平α为0.05,由于F日期、,F地区大于显著性水平α,所以不应拒绝原假设,不同地区和不同日期对该商品没有显著性影响。
方差分析实验报告模板及范例

填写说明1、填写实验报告须字迹工整,使用黑色钢笔或签字笔填写。
2、课程编号和课程名称必须和教务系统中保持一致,实验项目名称填写须完整规范,不能省略或使用简称。
3、每个实验项目应填写一份实验报告。
如同一个实验项目分多次进行,可在实验报告中写明。
实验目录及成绩登记说明:实验项目顺序和名称由学生填写,必须前后保持一致;实验成绩以百分制计,由实验指导教师填写并签名;实验报告部分最终成绩为所有实验项目成绩的平均值。
实验报告实验日期:2020年 4月 16日星期四表15.点击“对比”,弹出对比对话框;勾选“多项式”,点击“继续”,如表2:表26.在单因素ANOVA分析对话框点击“事后多重比较”,弹出对话框,假定方差齐性一般有14种比较,最常见的就是LSD(L)最小显著差法:他没有在检验水准上做出任何的矫正,只是在标准误差的计算上充分利用样本数据,为所有组的均数统一估计出较为稳定的标准误差,一般被认为为最灵敏的方法;其他采用系统默认设置;单击“继续”,如图3所示:图37.为了定义统计方法和缺失值的处理方法,在单因素ANOVA分析对话框,单击“选项”,弹出选项对话框,在统计量中选择“方差齐性检验、平均值图”,缺失值选择系统默认,点击“继续”,如图4所示:图48.单击“确定”,等待输出结果。
ONEWAY 总销售量 BY 包装类别/POLYNOMIAL=1/STATISTICS HOMOGENEITY/PLOT MEANS/MISSING ANALYSIS/POSTHOC=LSD ALPHA(0.05).单向(1)方差齐性检验表,如表a;(2)ANOVA表,如下表b;事后检验(1)多重比较表,如下表c;平均值图,如下图5。
(二)第七章第三题——协方差分析1.课程了解学习协方差分析,是将回归分析同方差分析结合起来,以消除混杂因素的影响,对试验数据进行分析的一种分析方法。
协方差分析一般研究比较一个或者几个因素在不同水平上的差异,但观测量同时还受另一个难以控制的协变量的影响,在分析中剔除其影响,再分析各因素对观测变量的影响。
单因素方差分析实验报告
单因素方差分析实验报告实验目的:通过单因素(变量)方差分析,比较不同温度下一种化学试剂的反应速度是否显著不同。
实验步骤:选取三个不同的温度(20℃,30℃,40℃)下,分别进行九次实验,每个实验用的试剂量、试剂浓度、搅拌时间、pH值等都保持不变。
记录每次反应的时间。
实验结果:| 温度/℃ | 时间1/s | 时间2/s | 时间3/s | 时间4/s | 时间5/s | 时间6/s | 时间7/s | 时间8/s | 时间9/s | 平均时间/s | 方差 || ------- | ------- | ------- | ------- | ------- | ------- | ------- | -------| ------- | ------- | --------- | ---- || 20 | 23 | 21 | 25 | 22 | 24 | 25 | 23 | 20 | 22 | 22.5 | 2.25 || 30 | 18 | 19 | 21 | 20 | 22 | 20 | 19 | 21 | 20 | 19.9 | 0.81 || 40 | 16 | 17 | 18 | 17 | 17 | 16 | 18 | 18 | 15 | 16.8 | 1.36 |分析:计算平方和总平方和SST=ΣΣ(xi-x¯)²=83.65组内平方和SSE=2.41计算自由度总自由度n-1=26计算平均方差组内平均方差MSE=SSE/(n-k)=0.2计算F值F=MSB/MSE=203.1查表得:F(2,6)=5.14由于F值大于5.14,因此我们拒绝原假设,即不同温度下反应速度没有显著差异的假设。
也就是说,我们认为不同温度下反应速度确实存在显著差异。
讨论:本实验结果表明,不同温度下化学反应速度的平均值确实存在显著差异,且温度越高反应速度越快。
这个结论和我们的常识和经验是一致的,因为温度升高可以加快分子运动速度,从而增加反应概率,提高反应速率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方差分析实验报告
学生姓名:琚锦涛学号:091230126
一.实验目的
根据方差分析的相关方法,利用excel中的相关工具,将数据收集,整理,从而了解方差分析的特点和性质。
二.实验内容
1.单因素方差分析
利用以下数据进行单因素方差分析,判断不同产地的原材料是否显著影响产品的质量指标;
2.双因素方差分析
利用以下数据进行双因素方差分析,检验因素A与因素B搭配下是否对其有显著差异,交互作用是否显著;
三.实验结果分析
1.单因素方差分析
由以上数据可知,P-value=0.2318>0.05,因此可得出:原材料产地的这一质量指标无显著影响。
2.双因素方差分析
样本、列及交互的P-value远小于0.05,由此可得出燃料和推进器两因素对于火箭影响显著。
数据来源:《应用统计学》第二版;。
