有限元网格剖分方法概述
有限元网格划分和收敛性
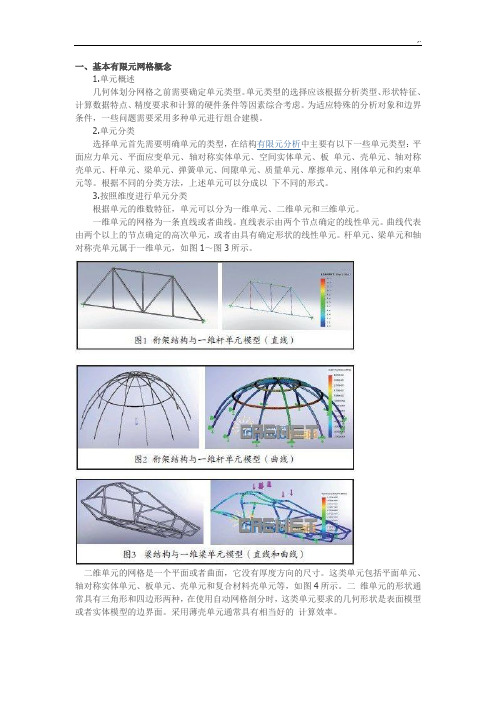
一、基本有限元网格概念1.单元概述几何体划分网格之前需要确定单元类型。
单元类型的选择应该根据分析类型、形状特征、计算数据特点、精度要求和计算的硬件条件等因素综合考虑。
为适应特殊的分析对象和边界条件,一些问题需要采用多种单元进行组合建模。
2.单元分类选择单元首先需要明确单元的类型,在结构有限元分析中主要有以下一些单元类型:平面应力单元、平面应变单元、轴对称实体单元、空间实体单元、板单元、壳单元、轴对称壳单元、杆单元、梁单元、弹簧单元、间隙单元、质量单元、摩擦单元、刚体单元和约束单元等。
根据不同的分类方法,上述单元可以分成以下不同的形式。
3.按照维度进行单元分类根据单元的维数特征,单元可以分为一维单元、二维单元和三维单元。
一维单元的网格为一条直线或者曲线。
直线表示由两个节点确定的线性单元。
曲线代表由两个以上的节点确定的高次单元,或者由具有确定形状的线性单元。
杆单元、梁单元和轴对称壳单元属于一维单元,如图1~图3所示。
二维单元的网格是一个平面或者曲面,它没有厚度方向的尺寸。
这类单元包括平面单元、轴对称实体单元、板单元、壳单元和复合材料壳单元等,如图4所示。
二维单元的形状通常具有三角形和四边形两种,在使用自动网格剖分时,这类单元要求的几何形状是表面模型或者实体模型的边界面。
采用薄壳单元通常具有相当好的计算效率。
三维单元的网格具有空间三个方向的尺寸,其形状具有四面体、五面体和六面体,这类单元包括空间实体单元和厚壳单元,如图5所示。
在自动网格划分时,它要求的是几何模型是实体模型(厚壳单元是曲面也可以)。
4.按照插值函数进行单元分类根据单元插值函数多项式的最高阶数多少,单元可以分为线性单元、二次单元、三次单元和更高次的单元。
线性单元具有线性形式的插值函数,其网格通常只具有角节点而无边节点,网格边界为直线或者平面。
这类单元的优点是节点数量少,在精度要求不高或者结果数据梯度不太大的情况下,采用线性单元可以得到较小的模型规模。
有限元网格划分的基本原则与通用方法!

有限元网格划分的基本原则与通用方法!本文首先研究和分析有限元网格划分的基本原则,再对当前典型网格划分方法进行科学地分类,结合实例系统地分析各种网格划分方法的机理、特点及其适用范围,如映射法、基于栅格法、节点连元法、拓扑分解法、几何分解法和扫描法等。
最后阐述当前网格划分的研究热点,综述六面体网格和曲面网格划分技术,展望有限元网格划分的发展趋势。
引言有限元网格划分是进行有限元数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素,在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss) 积分,而壳、板、梁单元的厚度方向采用辛普生 (Simpson) 积分。
有限元网格划分基本原则有限元方法的基本思想是将结构离散化,即对连续体进行离散化,利用简化几何单元来近似逼近连续体,然后根据变形协调条件综合求解。
所以有限元网格的划分一方面要考虑对各物体几何形状的准确描述,另一方面也要考虑变形梯度的准确描述。
为正确、合理地建立有限元模型,这里介绍划分网格时应考虑的一些基本原则。
1. 网格数量网格数量直接影响计算精度和计算时耗,网格数量增加会提高计算精度,但同时计算时耗也会增加。
当网格数量较少时增加网格,计算精度可明显提高,但计算时耗不会有明显增加;当网格数量增加到一定程度后,再继续增加网格时精度提高就很小,而计算时耗却大幅度增加。
所以在确定网格数量时应权衡这两个因素综合考虑。
2. 网格密度为了适应应力等计算数据的分布特点,在结构不同部位需要采用大小不同的网格。
在孔的附近有集中应力,因此网格需要加密;周边应力梯度相对较小,网格划分较稀。
由此反映了疏密不同的网格划分原则:在计算数据变化梯度较大的部位,为了较好地反映数据变化规律,需要采用比较密集的网格;而在计算数据变化梯度较小的部位,为减小模型规模,网格则应相对稀疏。
有限元分析网格划分的关键技巧

网格规模和分辨率的选择是有限元分析网格划分中的重要环节。以下是选择 合理的网格规模和分辨率时需要考虑的几个因素:
1、分析精度:网格规模和分辨率越大,分析精度越高,但同时也会增加计 算成本。因此,需要在精度和成本之间找到平衡点。
2、计算资源:网格规模和分辨率越大,需要的计算资源越多,需要考虑计 算机硬件的性能和应用场景的需求。
4、三角形单元:适用于不规则区域和复杂结构的模拟,如表面模型等。
5、四边形单元:适用于规则区域和简单结构的模拟,如立方体、圆柱等。
6、高阶单元:高阶单元具有更高的计算精度,但同时也需要更多的计算资 源。
在选择合适的单元类型和阶次时,需要考虑以下因素:
1、分析精度:根据分析目标和实际需求,选择能够满足精度要求的单元类 型和阶次。
4、施加边界条件和载荷:对计算域的边界和加载条件进行定义,以模拟实 际工况。
5、进行有限元分析和求解:利用有限元分析软件进行计算,得到各节点处 的响应和位移等结果。
6、结果后处理:对分析结果进行可视化处理,如云图、动画等,以便更好 地理解和评估仿真结果。
技巧2:如何选择合适的单元类 型和阶次
5、经验准则:根据类似问题的经验和网格划分准则,可以指导网格规模和 分辨率的选择。例如,对于结构分析,通常建议最大单元尺寸不大于最小特征尺 寸的1/10。
技巧4:如何使用有限元分析软件自动划分网格
随着有限元分析软件的发展,越来越多的软件提供了自动划分网格的功能。 使用这些功能可以大大简化网格划分的过程,提高分析效率。下面介绍两种常见 的自动划分网格方法:
2、计算效率:在保证精度的前提下,尽量选择计算效率较高的单元类型和 阶次。
3、单元特性:了解各种单元类型的适用范围和局限性,以便在分析过程中 更好地满足实际需求。
有限元的网格划分技术

有限元的网格划分技术对于有限元分析来说,网格划分是其中最关键的一个步骤,网格划分的好坏直接影响到解算的精度和速度。
网格化有三个步骤:定义单元属性(包括实常数)、在几何模型上定义网格属性、划分网格。
定义网格的属性主要是定义单元的外形、大小。
单元大小基本上在线段上定义,可以用线段数目或长度大小来划分,可以在线段建立后立即声明,或整个实体模型完成后逐一声明。
采纳BottOm-UP方式建立模型时,采纳线段建立后立即声明比较便利且不易出错。
例如声明线段数目和大小后,叁制对象时其属性将会一•起夏制,完成上述操作后便可进行网格化命令。
网格化过程也可以逐步进行,即实体模型对象完成到某个阶段就进行网格话,如所得结果满足,则连续建立其他对象并网格化。
网格的划分可以分为自由网格(free meshing)、映射网格(mapped meshing)和扫略网格(SWeeP meshing)等。
一、自由网格划分自由网格划分是自动化程度最高的网格划分技术之一,它在面上可以自动生成三角形或四边形网格,在体上自动生成四周体网格。
通常状况下,可采用ANSYS的智能尺寸掌握技术(SMARTSIZE命令)来自动掌握网格的大小和疏密分布,也可进行人工设置网格的大小(AESIZE、LESIZE、KESIZE、ESIZE等系列命令)并掌握疏密分布以及选择分网算法等( MOPT 命令)。
对于简单几何模型而言,这种分网方法省时省力,但缺点是单元数量通常会很大,计算效率降低。
同时,由于这种方法对于三维简单模型只能生成四周体单元,为了获得较好的计算精度,建议采纳二次四周体单元(92号单元)。
假如选用的是六面体单元,则此方法自动将六面体单元退化为阶次全都的四周体单元,因此,最好不要选用线性(•阶次)的六面体单元(没有中间节点,比如45号单元),由于该单元退化后为线性的四周体单元,具有过大的刚度,计算精度较差;假如选用二次的六面体单元(比如95 号单元),由于其是退化形式,节点数与其六面体原型单元全都,只是有多个节点在同一位置而己,因此,可以采用TCHG命令将模型中的退化形式的四周体单元变化为非退化的四周体单元(如92号单元),削减每个单元的节点数量,提高求解效率。
有限元网格剖分

有限元网格剖分有限元计算的本质在于可以将连续的场域问题转变为离散的场域问题进行求解,而在这个由连续场域向离散场域转变的过程的核心在于有限元模型的网格划分。
进行有限元计算的主要过程体现在:首先确定出能和边值问题相对应的泛函数及可以相互等价的变分问题,进行有限元网格划分,将连续的场域离散成离散场域,在有限单元上利用一个已知的函数,例如线性的或者二次的,将有限单元上的未知连续函数近似的表示出来,求解泛函数的极值,得到一系列的方程组,进行方程组的求解,求解结束后将计算的结果进行显示,如果需要其它的一些场量时需要进行后处理等。
在上述的有限元求解的过程中,有限元模型的网格划分其中最为关键的一个环节,有限元模型的网格划分直接决定了有限元法在解决实际问题中所体现的能力,更是直接决定了有限元计算软件的计算精度。
一个有限元计算软件如果前处理的程序性能不够强大,则它的通用性就不会太强。
有限元模型的网格划分模块时有限元计算软件的前处理部分的主要模块。
有限元模型单元的大小和疏密度的合理设置,是保证计算精确性的重要保障,而有限元网格的合理性是建立在网格自动剖分程序所形成的初步网格的基础之上的,需要进一步的细分网格环节来实现合理的网格划分。
而有限元软件的自适应网格细分不需要依靠计算机用户的网格划分经验,仅仅凭借着有限元软件自带的功能就可以实现有限元网格的合理细化。
当前随着计算机的快速发展,网格剖分的算法已经得到了更大程度上的完善和发展,一些更为发展的求解域都可以进行网格的合理剖分。
有限元网格的自适应剖分软件能够利用软件自身的功能属性自动决定出网格在哪一个地方需要进行网格的进一步细化,细化的具体程度是多少,进而得到一个较为合理的网格划分,并且在该模型上可以获得较为准确的计算结果。
有限元网格的进一步细分的目的在于能够使得软件根据计算场域的特征和计算场量的分布情况合理的设置网格,使得模型中的每一个单元的计算精确性基本相同。
网格剖分的自适应软件彻底的改变了以往网格划分计算人员剖分经验的依赖性,而且还能够在数量较小的节点单元的情况下获取较高的计算求解精度。
有限元网格剖分与网格质量判定指标

有限元网格剖分与网格质量判定指标有限元网格剖分与网格质量判定指标一、引言有限元法是一种常用的数值分析方法,广泛应用于工程、力学等领域。
在有限元方法中,对于复杂的几何体,需要将其分割成多个简单的几何单元,称为有限元。
而有限元的形状和尺寸对计算结果的精度和稳定性有重要影响。
因此,有限元网格剖分和网格质量判定指标的选择和优化是提高有限元方法计算精度和效率的关键。
二、有限元网格剖分的基本原则和方法有限元网格剖分的基本原则是要确保网格足够细密,以捕捉几何体的细节和特征。
一般来说,有限元网格剖分可以分为以下几个步骤:1. 几何体建模:根据实际问题建立几何体模型,可以使用CAD软件进行建模。
2. 离散化:将几何体分割成简单的几何单元,如三角形、四边形或六面体等。
3. 网格生成:根据几何单元的尺寸和形状要求生成网格。
一般可采用三角形剖分算法或四边形剖分算法进行网格生成。
4. 网格平滑:对生成的网格进行平滑处理,以提高网格的质量。
三、网格质量判定指标网格质量判定指标是用来评价和衡量网格质量好坏的指标。
一个好的网格是指网格单元形状较正、网格单元之间大小相近、网格单元的边界规则等。
常用的网格质量判定指标包括:1. 网格单元形状度:用于评价网格单元的形状正交性和变形。
常用的形状度指标有内角度、调和平均内角度和狄利克雷三角形剖分等。
2. 网格单元尺寸误差:用于评价网格单元尺寸与理想尺寸之间的差异。
常用的尺寸误差指标有网格单元长度标准差、最大和最小网格单元尺寸比等。
3. 网格单元的四边形度:用于评价四边形网格的形状规则性。
常用的四边形度指标有圆度、直角度和Skewness等。
四、网格质量优化方法为了改善有限元网格质量,可以采用以下方法:1. 网格加密:通过将大尺寸网格单元划分为小尺寸网格单元,提高网格的细密度。
2. 网格平滑:通过对矩阵约束或拉普拉斯平滑等方法对网格进行平滑处理,改善网格单元的形状。
3. 网格优化:通过对网格单元的拓扑结构和形状进行优化,提高网格的质量。
基于数字图像的复合材料有限元网格剖分算法

me a n s me t h o d d e t e c t e d g e s i n t h e i ma g e . Nu me ic r l a e x p e i r me n t s s h o w t h e e f f e c t i v e n e s s f o t h e lg a o r i t h m.
张 兰 , 许 磊 , 张 阳
( 1 . 西安航空职业技术学院基础部 , 陕西 西安 7 1 0 0 8 9 ; 2 . 西安航空职业技术学院航 空材料工程学院, 陕西 西安 7 1 0 0 8 9 ;
3 . 西北工业大 学理 学院, 陕西 西安 7 1 0 1 2 9 )
摘要 : 在 对 复合 材料 的 S E M( S c a n n i n g E l e c t r o n i c Mi c r o s c o p e , 扫 描 电子 显 微 镜 ) 图像 进 行 边 缘检 测 的 基 础 上 , 对 二 值 图采 用
2 0 1 3年第 1 O期 文章编 号 : 1 0 0 6 - 2 4 7 5 ( 2 0 1 3 ) 1 0 - 0 0 3 5 - 0 3
计 算 机 与 现 代 化 J I S U A N J I Y U X I A N D A I H U A
《2024年有限元网格剖分与网格质量判定指标》范文

《有限元网格剖分与网格质量判定指标》篇一一、引言有限元法是一种广泛应用于工程分析中的数值计算方法。
其核心步骤之一就是网格剖分,即将求解域离散化为有限个相互连接的子域,即有限元。
网格的质量直接影响到有限元分析的精度和效率。
因此,有限元网格剖分与网格质量判定指标的研究具有重要意义。
本文将详细介绍有限元网格剖分的过程及网格质量判定指标。
二、有限元网格剖分1. 初始准备在进行有限元网格剖分前,需要对求解域进行合理的预处理,包括几何模型的建立、边界条件的设定等。
此外,还需根据问题的性质选择合适的网格类型,如二维平面网格、三维立体网格等。
2. 网格剖分方法有限元网格剖分的方法主要有自动剖分和手动剖分两种。
自动剖分方法基于计算机算法,能够快速生成网格,但可能无法满足特定的精度要求。
手动剖分方法则更加灵活,可以根据问题需求进行精细的调整。
在实际应用中,常将两种方法结合使用,以达到更好的效果。
3. 网格剖分步骤(1)确定网格的规模和密度:根据问题的性质和求解精度要求,确定网格的规模和密度。
(2)生成基础网格:利用计算机算法或手动操作生成基础网格。
(3)优化网格:对基础网格进行优化,包括调整节点位置、修改单元形状等,以提高网格的质量。
(4)输出网格:将优化后的网格导出,供有限元分析软件使用。
三、网格质量判定指标网格质量是影响有限元分析结果的重要因素。
为了评估网格的质量,需要采用一系列的判定指标。
以下是常用的几个指标:1. 雅可比(Jacobian)值:雅可比值反映了单元的形状和大小是否合理。
其值接近1时,表示单元形状接近于等边形状;其值偏离1过大时,表示单元形状发生了畸变。
2. 纵横比:纵横比是指单元最长边与最短边之比。
纵横比越小,表示单元形状越接近正方形或等边形状;反之,则表示单元形状发生了较大的拉伸或压缩。
3. 翘曲度(Warpage):翘曲度用于衡量单元角点的偏离程度。
翘曲度越大,表示单元形状越不规则。
翘曲度可以作为评估单元形状优劣的指标之一。
ANSYS有限元网格划分浅析

ANSYS有限元网格划分浅析有限元分析作为现代工程设计领域中不行或缺的工具,旨在通过对复杂结构进行数值模拟,猜测其力学行为和性能。
而有限元网格划分作为有限元分析的前提条件,直接影响着分析结果的准确性和计算效率。
本文将对ANSYS有限元网格划分的原理和技巧进行浅析,并探讨其在工程设计中的应用。
一、有限元网格划分的基本原理有限元网格划分是将连续物体离散化成有限个离散单元,构建有限元模型的过程。
其原理主要涉及两个方面:几何划分和节点生成。
1.1 几何划分几何划分是将实际结构划分为有限单元的过程,主要包括自动划分和手动划分两种方式。
自动几何划分是ANSYS通过对实际结构进行自动网格划分的功能,依据用户指定的几何参数进行自适应划分,最大程度地保持结构的准确外形。
这种划分方法具有快速、高效的优点,特殊适用于复杂结构的网格划分。
手动几何划分是由用户通过手动操作构建网格划分,使用ANSYS提供的几何划分工具进行几何实体的划分和组合,依据结构外形和特点进行网格划分的方式。
这种划分方法需要用户具备一定的几何划分技巧和阅历,能够对结构进行合理的划分。
1.2 节点生成节点生成是指依据坐标系和几何划分,自动生成有限元网格中的节点坐标。
在划分完成后,节点将依据有限元单元的外形和尺寸进行生成。
节点生成过程中主要包括节点编号、坐标值和自由度的定义。
节点编号是为每个节点赐予唯一的标识,便利在后续分析中进行节点相关的计算;坐标值是节点在几何坐标系中的坐标值,用于描述节点在空间中的详尽位置;自由度的定义是为节点定义相应的位移或位移的导数,用于后续求解分析中的节点位移计算。
二、ANSYS有限元网格划分的技巧2.1 网格密度的控制网格密度是指网格单元数目与结构体积之比,其决定了有限元模型对结构细部行为的描述能力。
合理控制网格密度能够提高分析结果的准确性和计算效率。
一般来说,细节丰富的区域应接受较小的网格单元,而结构较简易的区域可以接受较大的网格单元。
(完整版)有限元网格剖分方法概述

有限元网格剖分方法概述在采用有限元法进行结构分析时,首先必须对结构进行离散,形成有限元网格,并给出与此网格相应的各种信息,如单元信息、节点坐标、材料信息、约束信息和荷载信息等等,是一项十分复杂、艰巨的工作。
如果采用人工方法离散对象和处理计算结果,势必费力、费时且极易出错,尤其当分析模型复杂时,采用人工方法甚至很难进行,这将严重影响高级有限元分析程序的推广和使用。
因此,开展自动离散对象及结果的计算机可视化显示的研究是一项重要而紧迫的任务。
有限元网格生成技术发展到现在, 已经出现了大量的不同实现方法,列举如下:1.映射法映射法是一种半自动网格生成方法,根据映射函数的不同,主要可分为超限映射和等参映射。
因前一种映射在几何逼近精度上比后一种高,故被广泛采用。
映射法的基本思想是:在简单区域内采用某种映射函数构造简单区域的边界点和内点,并按某种规则连接结点构成网格单元。
也就是根据形体边界的参数方程,利用映射函数,把参数空间内单元正方形或单元三角形(对于三维问题是单元立方体或单元四面体)的网格映射到欧氏空间,从而生成实际的网格。
这种方法的主要步骤是,首先人为地把分析域分成一个个简单可映射的子域,每个子域为三角形或四边形,然后根据网格密度的需要,定义每个子域边界上的节点数,再根据这些信息,利用映射函数划分网格。
这种网格控制机理有以下几个缺点:(1)它不是完全面向几何特征的,很难完成自动化,尤其是对于3D区域。
(2)它是通过低维点来生成高维单元。
例如,在2D问题中,先定义映射边界上的点数,然后形成平面单元。
这对于单元的定位,尤其是对于远离映射边界的单元的定位,是十分困难的,使得对局部的控制能力下降。
(3)各映射块之间的网格密度相互影响程度很大。
也就是说,改变某一映射块的网格密度,其它各映射块的网格都要做相应的调整。
其优点是:由于概念明确,方法简单,单元性能较好,对规则均一的区域,适用性很强,因此得到了较大的发展,并在一些商用软件如ANSYS等得到应用。
有限元网格划分方法与基本原理

结构有限元分析中的网格划分技术及其应用实例结构有限元分析中的网格划分是否直接关系到解算的效果。
本文简述了网格划分应用的基本理论,并以空间自由曲面覆盖件和大型整体网络钢筋壳体产品的有限元分析中的网格划分为实例对象,详细讲述了空间自由和三维实体的网格划分基本理论及其在工程中的实际应用,非常具有现实意义和借鉴价值。
一、前言有限元网格划分是进行有限元数值模拟分析至关重要的一步,它直接影响着后续数值计算分析结果的精确性。
网格划分涉及单元的形状及其拓扑类型、单元类型、网格生成器的选择、网格的密度、单元的编号以及几何体素。
从几何表达上讲,梁和杆是相同的,从物理和数值求解上讲则是有区别的。
同理,平面应力和平面应变情况设计的单元求解方程也不相同。
在有限元数值求解中,单元的等效节点力、刚度矩阵、质量矩阵等均用数值积分生成,连续体单元以及壳、板、梁单元的面内均采用高斯(Gauss)积分,而壳、板、梁单元的厚度方向采用辛普生(Simpson)积分。
辛普生积分点的间隔是一定的,沿厚度分成奇数积分点。
由于不同单元的刚度矩阵不同,采用数值积分的求解方式不同,因此实际应用中,一定要采用合理的单元来模拟求解。
CAD软件中流行的实体建模包括基于特征的参数化建模和空间自由曲面混合造型两种方法。
Pro/E和S oildWorks是特征参数化造型的代表,而 CATIA与Unigraphics等则将特征参数化和空间自由曲面混合造型有机的结合起来。
现有CAD软件对表面形态的表示法已经大大超过了CAE软件,因此,在将CAD实体模型导入CAE软件的过程中,必须将CAD模型中其他表示法的表面形态转换到CAE软件的表示法上,转换精度的高低取决于接口程序的好坏。
在转换过程中,程序需要解决好几何图形(曲线与曲面的空间位置)和拓扑关系(各图形数据的逻辑关系)两个关键问题。
其中几何图形的传递相对容易实现,而图形间的拓扑关系容易出现传递失败的情况。
数据传递面临的一个重大挑战是,将导入CAE程序的CAD模型改造成适合有限元分析的网格模型。
有限元网格划分原理

有限元网格划分原理
有限元网格划分原理是一种用于计算领域离散化的数值方法。
它将连续的领域划分为有限数量的小单元,每个小单元称为有限元。
这些有限元可被视为数学模型中的局部区域,其内部的物理过程可以被近似为线性或非线性的形式。
有限元网格划分原理的目标是将整个领域划分为足够多的有限元,以便能够准确地描述所研究的问题。
划分时需要考虑几何形状、边界条件、计算资源等因素,以获取一个高效且准确的离散模型。
通常,将整个领域划分为小单元可以更好地逼近真实物理过程,并提供对系统行为的详细理解。
在有限元网格划分过程中,首先确定领域的几何形状和边界条件。
然后,选择适当的离散化方法,将领域划分为小单元,如三角形、四边形、六边形或四面体。
每个小单元内的变量以形函数的形式进行逼近,形函数可根据问题的特点进行选择。
一旦完成网格划分,就可以在每个有限元中设置数学方程,在整个领域上建立一个代数系统。
该系统由一系列线性或非线性方程组组成,其中每个方程对应于一个小单元。
通过求解这些方程,可以获得在整个领域中变量的近似解。
有限元网格划分原理的核心思想是将复杂问题转化为简单的局部问题,并通过将领域划分为小单元来近似描述整个系统。
通过调整网格大小和形状,可以调整计算精度和效率。
因此,有限元网格划分原理是计算力学、结构力学、流体力学等领域中常用的数值方法之一。
适用于电磁场有限元计算的网格剖分算法

第38卷第6期 计算机应用与软件Vol 38No.62021年6月 ComputerApplicationsandSoftwareJun.2021适用于电磁场有限元计算的网格剖分算法章春锋 汪 伟 吴天纬 安斯光(中国计量大学机电工程学院 浙江杭州310016)收稿日期:2019-10-18。
浙江省自然科学基金项目(LY19E070003);国家自然科学基金项目(61701467)。
章春锋,硕士生,主研领域:电磁场有限元剖分与数值计算。
汪伟,教授。
吴天纬,硕士生。
安斯光,副教授。
摘 要 网格剖分是有限元法的关键,其剖分得到的网格质量决定了有限元法计算结果的准确性。
提出基于Persson Strang算法生成非结构化三角形网格的新算法。
通过分析Laplacian平滑函数作用原理,提出新的平滑函数来减少迭代次数;提出一种在优化设计过程中无重构变形方法,通过定义边界网格框架利用坐标映射技术可以快速推导出网格;通过设置质量评估来解决不可终止性的可能和过度迭代,加入边界节点筛选功能,并对剖分得到的三角元进行有限元逆序编号处理。
将该算法与Persson Strang算法进行剖分效果对比,验证该算法应用于电磁场领域的有效性。
关键词 网格剖分 平滑函数 坐标映射 有限元 电磁场中图分类号 TP3 文献标志码 A DOI:10.3969/j.issn.1000 386x.2021.06.035MESHGENERATIONALGORITHMFORFINITEELEMENTCALCULATIONOFELECTROMAGNETICFIELDZhangChunfeng WangWei WuTianwei AnSiguang(CollegeofMechanicalandElectricalEngineering,ChinaJiliangUniversity,Hangzhou310016,Zhejiang,China)Abstract Meshgenerationisthekeyofthefiniteelementmethod.Thequalityofthemeshgeneratedbythemeshgenerationdeterminestheaccuracyoftheresultsofthefiniteelementmethod.AnewunstructuredtrianglemeshgenerationalgorithmbasedonPersson Strangalgorithmisproposed.ByanalyzingtheprincipleofLaplaciansmoothingfunction,anewsmoothingfunctionwasproposedtoreducethenumberofiterations;anonreconstructiondeformationmethodwasproposedintheprocessofoptimizationdesign,whichcanquicklydeducethegridbydefiningtheboundarygridframeworkandusingthecoordinatemappingtechnology;thepossibilityofnonterminationandoveriterationcanbesolvedbysettingthequalityevaluation,andnodefilteringfunctionwasaddedtotheboundary,andthetrigonometricelementsobtainedbysubdivisionwerenumberedinreverseorderbyfiniteelementmethod.ComparedwiththePersson Strangalgorithm,thisalgorithmisprovedtobemoreeffectiveinelectromagneticfield.Keywords Meshgeneration Smoothingfunction Coordinatemapping Finiteelement Electromagneticfield0 引 言优异的适应场域边界几何形状以及媒介物理性质变异的能力,使有限元法成为各类电磁场、电磁波工程问题定量分析和优化设计的主导数值计算方法之一[1]。
有限元网格划分方法

早期采用人工网格划分,速度慢、工作量大、出错率高,对复杂 空间结构划分困难。 对平面问题和较规则空间问题,为了对网格形式进行人为控制, 半自动网格划分也可取。 对复杂空间结构宜自动网格划分,显著提高划分速度,减轻工作 强度。
一、半自动划分方法 人机交互进行,分析人员确定结点位置和形成单元,但结点坐 标、节点和单元编号等由计算机自动完成。 1.设置定义坐标系 根据局部结构特点,建立和选取适当坐标系描述节点坐标:直 角坐标、柱坐标、球坐标? 2.定义节点 指定结点位置或由已有结点生成新结点。 3.定义单元 由节点或已有单元生成新单元。
二、网格疏密 网格疏密又称相对网格密度,指不同部位网格大小不同。 应力集中区(梯度变化较大处)应较密网格 计算精度不随网格数绝对增加,网格数应增加到关键部位。
132单元←→84单元 精度相当
网络有疏密时,要注意疏密之间的过渡。一般原则是网格尺 寸突变最少,以免畸形或质量较差的网络。
常见过渡方式: 1.单元过渡。用三角形过渡四边形、用四面体和五面体过渡六面 体。 2.强制过渡。用约束条件保持大小网格间的位移连续。这时大小 网格节点不可能完全重合,网格间有明显界面。 u u3 v v3 (1)多点约束等式 u2 1 , v2 1 2 2 (2)约束单元 3.自然过渡。大小网格间平滑过渡。其中网格会变形,质量降 低;网格尺寸越悬殊,过渡距离越近,网格质量影响越严重。
2.几何模型的建立与处理 (1)为使曲线某内点成为单元节点,曲线剪断。 (2)为使曲面某内线成为单元边,曲面剪断。 (3)为使实体某内面成为单元面,实体剪断
3.网格大小和疏密控制 (1)总体尺寸 (2)局部尺寸 设置离散偏差 设置曲线网格数 设置点附近网格尺寸
实体模型 曲面模型
有限元计算单元网格划分

有限元语言及编译器(Finite Element Language And it’s Compiler,以下简称FELAC) 是中国科学院数学与系统科学研究院梁国平研究院于1983年开始研发的通用有限元软件平 台,是具有国际独创性的有限元计算软件,是PFEPG系列软件三十年成果(1983年—2013 年)的总结与提升,有限元语言语法比PFEPG更加简练,更加灵活,功能更加强大。目前 已发展到2.0版本。其核心采用元件化思想来实现有限元计算的基本工序,采用有限元语 言来书写程序的代码,为各领域,各类型的有限元问题求解提供了一个极其有力的工具。 FELAC可以在数天甚至数小时内完成通常需要一个月甚至数月才能完成的编程面或体单元过渡
1)从小单元到大单元过渡时,应使同一节点所连接的单元不致相差太大,避免突然过渡现象。 通常用计算结果调整,保证同一节点所连接的单元精度值至少在0.1以下。单元精度值根据单元内节 点应力与节点平均应力的误差计算。
2)难于过度处最好使用过渡单元,过渡单元的使用要比用同一单元勉强过渡的计算结果要好。 例如:对于复杂体结构间的过渡,最好使用“金子塔”单元过渡。 (5)面或体转接部位的单元 几何模型圆角过渡处的单元划分,根据弧长对应的圆心角和半径确定,对于半径为3mm左右、 圆心角大于90度的转接弧长,通常至少要划分3~4个单元。 (6)高应力区的单元 对高应力区,要进行网格细分应力稳定性计算。即采用多次局部网格细分并进行计算,当前、 后两次计算结果满足所需的精度要求时(通常要求小于0.03)确定网格。 总之,几何模型网格划分时,要在单元类型、单元形态、单元大小、单元过渡和局部应力稳定 等方面下功夫,才能满足工程上的精度要求,达到预期的结果。
有限元网格体绘制中的剖切算法

第7卷(A 版) 第1期2002年1月中国图象图形学报Jou rnal of I m age and Grap h icsV o l .7(A ),N o.1Jan .2002基金项目:国家杰出青年科学基金项目(19525206);国家重点基础研究专项经费(G 1999032805)收稿日期:2000206209;改回日期:2000211220有限元网格体绘制中的剖切算法杨晓松 顾元宪 李云鹏 关振群(工业装备结构分析国家重点实验室;大连理工大学工程力学系,大连 116024)摘 要 为了解决体绘制中的遮挡问题和加快复杂剖切体的剖切操作,在M S 体绘制算法的基础上,研究和提出了一种体绘制中任意封闭多面体的剖切和多种变换函数,并进一步展现了数据场内部的数据分布情况.另外,由于通过二叉树对多剖切体情况下Stencil 参照值的合并,使得算法在每一切层上的绘制次数达到最少,同时还统一了剖切体前后表面Stencil 操作,并减少了不必要的法线运算,从而大大加快了复杂剖切体的剖切操作.关键词 可视化 体绘制 剖切 有限元网格中图法分类号:T P 391.72 文献标识码:A 文章编号:100628961(2002)0120055208Cutti ng A lgor ithm i n the Volu m e Render i ng of FE MYAN G X iao 2song ,GU Yuan 2x ian ,L I Yun 2p eng ,GU AN Zhen 2qun(S tate K ey L aboratory of S tructu re A naly sis f or Ind ustry E qu ipm ent ,D ep t .ofE ng ineering M echanics ,D alian U niversity of T echnology ,D alian 116024)Abstract V o lum e rendering is a very effectived m ethod to help u ser to find p rob lem s in side a very comp licated structu re .Compared w ith su rface based visualizati on m ethods ,it keep s mo re detail info rm ati on in the final 2D i m age .T h is advan tage ju st b rings up ano ther b ig p rob lem .U sually som e i m po rtan t info rm ati on is ob scu red o r overw hel m ed by the data standing clo ser to the ob server .To so lve th is p rob lem ,tw o algo rithm s are pu t fo rw ard in th is paper .Cu tting the structu re w ith an arb itrary convex po lyhedron to b ring fo rw ard the focu sed part .By u sing the hardw are suppo rted stencil functi on in OpenGL ,the cu tting operati on becom e very fast and easy .A no ther m ethod is the defin iti on of m u lti p le tran sfer functi on s.T he in tegrati on of these tw o m ethods m akes the u ser’s in specti on mo re flex ib le .To ach ieve nearly real ti m e respon se ,several op ti m izati on m ethods are taken in th is paper .T he rendering ti m e in each slice is decreased to the m in i m um due to the com b inati on of stencil reference values by u sing b inary tree .T he in tegrati on of the stencil operati on s betw een the fron t and back faces ofpo lyhedron speed the algo rithm greatly by saving lo ts of comp licate no rm al compu tati on s .Keywords V isualizati on ,V o lum e rendering ,Cu tting ,F in ite elem en t m eshes0 引 言体绘制与其他三维有限元数据场的可视化方法相比,其主要优点是能够在一个二维图中展现出更多的数据信息,但信息的增多,则不可避免地会造成图象信息之间的互相遮挡,为了解决该问题,虽然设置了透明度,但位于结构后面的单元往往在最终图中的贡献量非常低,甚至完全无法辨认,因此如何解决体绘制中遮挡问题,是近年来,体绘制研究中的一个重要问题.通常有两种解决此问题方法,其中一种是用剖切方法(即通过剖切将前面的遮挡部分完全去掉)来展现结构后面的部分,如今体绘制中的剖切方法,依据剖切面的不同一般分为平面剖切[1]和任意封闭多面体剖切两类,其中,平面剖切由于计算比较简单,因此对体绘制的绘制速度基本上不构成任何影响,而任意封闭多面体的剖切则比较复杂,如今提高体绘制效率的措施,通常都是采用硬件加速的策略,以提高体绘制的响应速度,例如W esterm ann利用O p enGL的三维纹理硬件加速技术实现了任意封闭多面体对体数据的剖切[2];另一种方法是通过对数据场定义多个变换函数[3]来进行体数据剖切.由于在体绘制中,变换函数直接影响着单元的色彩与透明度,因此通过定义多个变换函数,在不影响正常体光照模型的情况下,再通过降低数据集中某一部分单元的透明度,同样也可以达到展现数据场内部情况的效果.本文综合利用了上述两类方法的优点,在M S 体绘制方法[4]的基础上,利用任意封闭的剖切体与有限元模型进行相交的方法,来对数据场中的单元进行分类,并通过对不同的子集定义不同的映射变换函数,来为用户提供一种非常灵活的展现结构内部数据分布的方法.由于采用硬件直接支持的O p enGL的Stencil功能来实现单元的剖切,其算法效率和响应速度很高,因此通过算法分析,本文在如下几个方面对算法进行了改进,从而使算法效率得到大幅度提高:(1)通过二叉树来合并多个剖切体情况的Stencil参照值,以使每一切层上的绘制次数达到最少;(2)利用包围盒技术来对Stencil测试和深度测试进行优化,以减少不必要的象素填充操作;(3)利用O p enGL的Scisso r和包围盒技术,来减少外表面面片与剖切体的求交操作;(4)通过对剖切体前后表面Stencil操作的统一,从而节省了复杂剖切体绘制中繁琐的面片求法线运算.1 体绘制中的剖切算法本文算法是在M S算法的基础上,利用Stencil 功能来实现三维有限元数据场体绘制的剖切操作,其算法的流程如下:(1)定义封闭多面体以及相应映射变换函数;(2)fo r each slice do;(3)采用由封闭多面体与当前切面相切的方法来设置Stencil缓冲区的值;(4)处理边、单元、外表面的活性表;(5)绘制相邻剖切面之间的外表面;(6)形成剖切多边形;(7)绘制剖切面多边形,并累加.1.1 任意封闭多面体与变换函数的定义这里,多种变换函数与剖切,实际上就是在单元上定义了一种集合关系,若每一个封闭多面体都意味着对三维空间的一个二值划分,即将多面体划分为内外两个部分,则集合P j的定义如下P j={E i,E i+1,…}(1)式中,P代表封闭多面体,E代表单元.由该式可见,一个单元可以同时属于多个封闭多面体.由于每一个集合都对应着一个变换函数,所以当一个单元属于多个集合时,该单元所采用的变换函数将取决于各集合之间的并、交、差操作.变换函数的定义要根据数据场的物理意义和剖切多面体的用途而定.其中对物理意义的数据结构,如应力场等,通常采用如下所示的二值函数:F(s)=Θhigh=0193if s>TΘl ow=0107if s<T(2)式中,s为应力值,Θhigh为高阻光度,Θl ow为低阻光度, T为阈值.对于剖切掉的部分则无需定义变换函数,在设置Stencil时,这类单元将不参加绘制操作.1.2 OpenG L中stenc il功能Stencil是O p enGL中的一个重要功能,因为Stencil测试通常与深度测试共同来控制图形的绘制,且这种测试主要由Stencil-Func和Stencil-O p 两个函数来完成,其中,Stencil-Func用于决定通过stencil测试的区域是否进行绘制,而Stencil-O p则用于决定stencil测试的结果对stencil缓冲区本身的影响.Stencil测试可以采取的操作有GL-KEEP、GL-ZERO、GL-R EPLA CE、GL-I N CR、GL-D ECR、GL-I NV ER T等.本文算法则利用GL-I N CR和GL-D ECR来实现体绘制的剖切.在Stencil操作中,由于Stencil缓冲区中的值起着至关重要的作用,因此本文利用Stencil缓冲区中的值对单元进行分类.目前微机显卡大都支持8b it的Stencil缓冲区,即可以实现最多8个剖切多面体的定义.如表1所示,若某象素(某一单元与当前切面相切所得的切面多边形中的象素)位于第3、4和7剖切多面体内部,则在绘制该象素时,就可以依据第3、4和7集合之间的集合操作,并采用相应的变换函数来将数据映射为颜色和透明度,以便参与体绘制的积分运算.65中国图象图形学报第7卷(A版)表1象素所对应的Stencil 缓冲区内的值按位表示50001100101.3 利用stenc il 功能实现体绘制中的剖切算法M S算法是通过一组平行于投影面的平面与结构相切的方法,将各剖切面多边形依次累加来实现体绘制的.图1给出了单元与当前切面相切时形成的切面多边形的示例,而体绘制的剖切,关键就是在填充切面多边形时,对填充象素进行分类,即判断哪些象素是位于剖切多面体内部的象素.这样,三维体绘制中的剖切就转换成一个两维点集的分类问题.图1 单元与切面相切形成的切面多边形这里,首先以一个剖切多面体的情况为例,来讨论如何实现体绘制.图2(a )给出了一个简单的剖切体——球体.在实现体绘制时,算法的目的就是要判断在当前切面上,哪些象素位于球体的内部,即对切面中的所有象素定义一个集合;图2(b )给出了球体与当前切面的相交圆,这一相交圆实际上就定义了象素集合的划分方法,其中位于圆内的象素就是属于剖切多面体应该剖切掉的部分.这样只要将Stencil 缓冲区中相应的象素设置为1,然后在绘制单元的切面多边形时,就可禁止相交圆内的象素绘制,这也就实现了体绘制的剖切.图2 任意封闭多面体与切面相切这里,相交圆的求法虽可以采用软件的方法,但由于每一个切面都要进行这种求交操作,因此运算量不是很高.本文通过硬件支持的Stencil 测试来求得相交圆,具体方法如下:11311 体绘制前的准备工作(1)封闭多面体前后面的划分,如图3(a )所示.首先将剖切多面体的各顶点坐标映射到屏幕坐标系,然后在屏幕坐标系内,求得剖切多面体各面片的法线方向,其法线方向向外,再求该矢量与单位向量(0,0,1)的点积,如果结果为正,则说明该面片方向向前,为前表面,否则为后表面.(2)打开Stencil 测试开关,允许对Stencil 缓冲区进行修改,然后关掉深度测试.图3 Stencil 缓冲区内容的设置11312 在体绘制循环内部对每一个切层进行以下操作:(1)清除Stencil 缓冲区中的内容,将深度缓冲区中的内容置成当前切面的Z 坐标值,然后打开深度测试开关,并关掉深度缓冲区与颜色缓冲区的写开关,即在设置Stencil 缓冲区时,不允许修改已有的体绘制图象.(2)Stencil -Func 中,测试函数将设置为GL -ALW A YS ,将R efV al 置为1,即Stencil 测试的比较结果为通过,且在Stencil -O p 中,与Stencil 测试和深度测试都通过对应的操作,均采用GL -I N CR ,即增1操作,然后绘制剖切多面体的所有后表面,如图3(b )所示,这时由于后表面完全位于当前切面的后面,故深度测试通过.另外,由于Stencil 测试为通过,所以在所有后表面所覆盖的象素上(相交圆的内部)Stencil 缓冲区的内容由0增加为1,其余皆为0.75第1期杨晓松等:有限元网格体绘制中的剖切算法(3)不改变Stencil -Func 的设置,即Stencil 测试为永远通过,并且在Stencil -O p 中,与深度测试和Stencil 测试都通过对应的操作均采用GL -D ECR ,即减1操作,然后绘制剖切多面体的所有前表面,如图3(c )所示,这时通过深度测试的部分,在切面上即形成一个圆环,而且其圆环内部的象素在Stencil 缓冲区中的值由1减为0,小圆内部仍为1.其实这一部分为1的象素正是剖切多面体与当前切面的相交圆,也正是本文算法需要求得的.(4)关闭深度测试,打开颜色缓冲区写开关,Stencil -O p 将设置为GL -KEEP ,即不对Stencil 缓冲区进行任何改变,同时将Stencil -Func 中的R efV al 置为0x 01,然后比较函数,若为不等于,则允许剖切多面体外面的部分参加绘制,并开始绘制单元的切面多边形、小单元与外表面.1.4 多个剖切多面体的结合无论采用多少个剖切多面体,其关键问题仍然是如何进行2维切面上象素集的划分问题.如图4所示,n 个剖切多面体即意味着将象素集分为2n 个子集,且每个子集对应一个变换函数.在一般情况下,有3个剖切多面体已经足够了,因为若定义8个以上变换函数,对于应用来说,实际上是非常不方便的.本文将这种集合划分为如下两类:其中一类是进行纯粹的剖切,即位于剖切多面体内部的部分将完全剖切掉,而不参加体绘制的积分运算;另一类集合划分则是要为每一个剖切多面体定义一个变换函数.这种变换函数由用户指定,通常采用的是如式2所示的高通函数.由于阈值T 的选取将决定该连通域的用途,因此T =1可视为为了展现结构内部为透明的特殊情况,同时,高阻光度ΘH igh 、低阻光度ΘLow 和T 3个参数的灵活选取,为用户提供了探索结构内部数据分布的十分有效的方法.由于每一个剖切体可以用Stencil 缓冲区中的一个位来表示,因此对于一般的硬件配置来讲,最多可以支持8个剖切体.由于不同的变换函数需要对单元顶点的颜色和透明度重新计算,且每增加一个变换函数就需要增加至少一次绘制操作,所以变换函数越少,绘制次数也就越少,算法的响应速度也就相应地越快.由于每一次绘制将只对应一个固定的Stencil 参照值,所以绘制次数直接等于Stencil 参照值的数目.图5给出了图4中各部分的Stencil 参照值,如果3个剖切体都是纯粹剖切,那么是否需要按照7个参照值绘制7次呢?在这种情况下,实际上,只需要按照7个参照值合并的结果000绘制一次就可以了.这样,减少参照值就成了提高算法效率的关键.参照值的合并算法是一种按位的操作,如设A和B 为要合并的参照值,则可将A 和B 按位进行异或操作,设结果为C .如果C 中只有一位为1,则A 和B 可以合并;如果全为0,则A 和B 相同.绘制时将Stencil 比较的M ask 设为C 的反,参照值可以选择为A 或B .以010和011为例来说明,其异或结果为001,此时如果采用110作为掩码,那么只需要比较前两位,即只需比较01就可以了.如果合并的参照值比较多,则需要将掩码和参照值一起传递下去.此时被掩码遮掉的位可以用X 表示.现以010、011、110和111的合并为例,若前两个合并为01X ,后两个为11X ,再次合并为X 1X ,则最终的掩码为010.但并不是所有的参照值都可以合并,例如010和001就无法进行合并,它们要进行两次绘制才能完成.最终的合并结果实际上是取决于合并次序,如在合并010、011、001、110、111和101时,如果010和011合并为01X ,而111和101合并为1X 1,那么剩下的就无法合并下去了,最终的绘制次数为4.如果合并次序为010+011=01X ,110+111=11X ,11X +01X =X 1X ,001+101=X 01,则最终的绘制次数为2,且时间将是前面的一半,所以合并次序对于提高算法效率是十分重要的.解决的方法是利用二叉树来对参照值进行合并,且二叉树的每一层代表着一个剖切体的集合划分,但在建立二叉树之前,需要确定3个剖切体的顺序,即首先对所有要合并的参照值进行分析,统计每一个位上相同值的个数,然后哪一位的数目越高,其在树上的位置也就越高.以上面的6个参照值为例进行分析可见,由于中间位有4个1、2个0,最后一85中国图象图形学报第7卷(A 版)位也有4个1和2个0,只有第1位有3个1和3个0,所以可以取中间位为树的第1层,最后一位为第2层,第1位为第3层.这样6个参照值中,中间位为1的4个值就可以合并到一起,而不会因为位于不同的树的分支,而无法合并.图6以上面的3个剖切体为例,给出了一个二叉树的结构,其叶节点为未合并前的参照值,中间的节点为合并后的参照值,树的深度为剖切体数目加一,每一个节点仅记录一个布尔数,即只记录该节点是否有值.图6还给出了上面所述的6个参照值合并的例子,合并的最终结果为两个X 01和X 1X ,这是最优解.1.5 利用包围盒加速剖切操作本文算法是建立在M S 体绘制算法之上的,由于体绘制算法的关键问题是响应速度,所以必须对剖切操作的系统开销进行分析,以便在原算法的时间开销之外,实现最小的时间增长.据分析,剖切操作涉及到以下几部分操作:(1)预处理.这里仅涉及到剖切多面体的坐标变换等一次性操作,由于一般剖切多面体都比较简单,且顶点与面数都不是很多,因此这部分操作所消耗的时间基本上可以忽略不计.(2)在体绘制循环内部的操作.由于对于每一个切面来讲,所有操作都要进行一遍,所以这里所消耗的时间就至关重要.这里有两项比较消耗时间的操作,其一是清除Stencil 缓冲区和深度缓冲区,另一个是剖切多面体前后表面的绘制.同时这两项操作所消耗的时间将直接与显卡的象素填充速度相关,即如果填充速度比较慢,则这部分操作将成为剖切操作的瓶颈.为了提高剖切操作的效率,本文采用包围盒的方法来减少填充象素的数目,即对于所有剖切多面体,首先在屏幕坐标系内,求其外包围盒(三维),然后为每个多面体记录Z 轴方向的两个值Z m ax 、Z m in .通常情况下,由于多面体都是对结构的某一部分进行裁减,因此在Z 轴方向贯穿的情况比较少,这样就避免了在Z <Z m in 和Z >Z m ax 时,无谓的多面体前后表面的填充操作,若在Z 轴方向多面体贯穿的层数越少,则求取包围盒节省的时间也就越多.这样在每一个剖切面上,采用两维的包围盒技术,并利用O p enGL 的Scisso r 函数在A lp ha 和Stencil 测试之前,对填充区域进行裁减,就避免不必要的清Stencil 缓冲区和深度缓冲区的操作,而且多面体在X 2Y 平面内覆盖的面积越少,算法效率提高得也就越大.2 外表面面片的剖切外表面的绘制作为M S 算法的一部分,必须在剖切时加以考虑.由于位于相邻切面之间的外表面面片不像切面那样具有统一的深度,因此处理将比较复杂.如今进行外表面面片剖切所采用的方法可以有如下两种:(1)假设切面间的外表面面片具有统一的深度,这时可以采用与切面多边形绘制时,同样的Stencil 缓冲区,且原有体绘制算法不变,但这是一种近似方法,其误差主要集中于剖切多面体与相邻切面的相交多边形的边缘处.这样如果在体绘制中切面数越多,即相邻切面之间的间距越小,那么由此产生的误差也就越小,所以这种方法比较适合于切面数在200以上的情况.(2)当切面数比较少时,若采用第1种方法,由于在剖切多面体的边缘处,将出现明显的锯齿状的面片,因此这时应该采用比较精确的绘制方法,其需要改变的步骤主要是深度缓冲区的统一赋值,而且对于每一个外表面面片,应作如下操作:步骤1 清Stencil 缓冲区,关闭颜色缓冲区的写开关;步骤2 绘制外表面面片,用于将面片的深度写入深度缓冲区;步骤3 同前面算法:分别绘制剖切多面体的前后表面,设置Stencil 缓冲区;步骤4 关闭深度测试和深度缓冲区写开关,打开颜色缓冲区写开关,绘制外表面面片.由于每一个面片都需要对Stencil 缓冲区进行单独设置,因此算法所需要的时间要增长很多.对此,本文主要采用下面的两种方法来提高算法的效率:95第1期杨晓松等:有限元网格体绘制中的剖切算法(1)将面片的包围盒与多面体的包围盒进行简单的相交比较,如果面片位于多面体包围盒之外,则不必进行Stencil设置,而直接进行绘制即可,而且这种测试将去除掉大部分的面片.(2)如果第1种测试失败,则将采用前述的方法进行绘制,但由于面片一般都比较小,涉及的象素不是很多,这时若采用O p enGL的Scisso r功能,就可以避免很多无谓的象素填充,而只影响到面片涉及的很小一部分区域.实践证明,采用这两种方法可以节省很多时间.另外,由于切面数较少时,体绘制消耗的时间也比较少,所以从整体的时间消耗来讲,外表面面片的绘制对体绘制算法的影响不是很大.3 实例分析图7给出了一个由6300个节点组成的实体结构,在一个长方体剖切情况下的体绘制图象.为了清晰地观察到剖切面的情况,这里若采用纯粹剖切方法,结构其他部分的透明度则比较低,为3%.图8给出了该剖切结果图象,其剖切部分采用93%的透明度进行绘制.图9给出了该结构在两个剖切长方体剖切情况下的图象,其两个长方体都采用纯粹剖切方法.图10在同样剖切情况下,其中一长方体采用纯粹的剖切,另一个采用比较高的透明度.从图11中可以看出,两个长方体将结构中所有单元分成4个集合,其中,(2)和(4)其各部分如图11所示,同属一个集合.如果一长方体采用Stencil 缓冲区中最右边一位,另一个长方体采用第2位,则(1)~(5)各部分的Stencil参照值分别为0X11、0X10、0X01、0X10、0X00;如果两者都采用纯粹剖切(图9),则可以将Stencil参照值设为0X00.图10的绘制则需要两步操作,即首先如图9一样,绘制第(5)部分,然后将Stencil参照值设为0X10,透明度设为93%,再对(2)(4)部分进行绘制即可.图7 单一长方体的纯粹剖切结果图8 单一长方体的剖切结果(透明度93%)图9 两个长方体对结构的纯粹剖切结果图10 两个长方体剖切的透明度控制图11 两个长方体的剖切示意图06中国图象图形学报第7卷(A版)4 复杂剖切体的实现大家知道,长方体是比较常用的剖切体,由于其结构比较简单,因此往往无法满足用户的要求.除了长方体外,通常采用的剖切体还有球体、圆柱以及圆锥等等,但构成这类剖切体的表面已经不是平面,而是曲面.为了处理方便和提高算法效率,通常是采用小面片来进行逼近.为了达到比较好的效果,面片数量可以选取得比较多,因而这就为剖切带来了一定的难度,因为当视角改变时,由于剖切体的前后表面需要重新判定,因而这也就涉及到所有面片法线方向的求解,由于运算量相当大,所以必须对算法进行改进,以便进一步减少前后表面的判定运算.通过对算法的分析可以发现,之所以要进行剖切体前后表面的判定,其主要原因是绘制过程不一致,因为在绘制后表面时,Stencil 操作是增1,而绘制前表面时,Stencil 操作是减1.如果能够将两者统一起来,就不需要进行前后表面的判定,也就可以节省掉剖切中繁重的法线计算,但问题是如何选择合适的Stencil 操作,以使得对每个剖切体所对应的位来讲,两次同样操作数据不变,即该操作的二值运算如下:O p (0)=1,O p (1)=0此时,可以采用的操作虽然有GL -I N CR 、GL -D ECR 和GL -I NV ER T 3种.然而由于GL -I N CR 和GL -D ECR 在进位和借位时,将改变其他位的值,这将影响到其他剖切体的集合定义,所以只有GL -I NV ER T 能够正确实现这一操作.这样由于前后表面绘制操作的统一,因此在预处理时,就不需要进行前后表面的判定,而只要将剖切体的各个面片依次绘制即可,而且即使对于比较复杂的封闭剖切体,其算法效率仍然比较高.图12和13给出了将球体和圆台作为剖切体的情况.图12 球的剖切图13 圆台的剖切5 结 论本文在有限元网格M S 体绘制算法的基础上,提出了一种多个封闭多面体的剖切算法,并给出了多种变换函数的定义,从而为用户提供了一个十分灵活的观察数据场内部情况的方法.由于本文通过二叉树方法对Stencil 参照值进行了合并,因而大大减少了在每一切层上绘制的次数,并使得算法效率得到了很大的提高.下表给出了图11中合并后的参照值的数目与绘制时间的对比(300切层).表2 图11合并后的参照值数目与绘制时间对照表参照值数1234绘制时间(s )11.37413.60915.1616.47对于复杂的剖切体,通过对其前后面的合并,使得算法在设置Stencil 操作上,效率提高了近10%,以图12为例,在原算法中,是利用O p enGL 的glCu llFace 功能来判断剖切球的前后表面,其Stencil 缓冲区的设置时间为3123s (300切层),而采用GL -I NV ER T 合并操作后的时间为2181s .另外,由于可利用包围盒和O p enGL 的裁减功能来减少不必要的Stencil 测试,从而可以大幅度地提高算法的效率,因为Stencil 测试所消耗时间往往比较大,如图12所示结构,在无剖切时,其绘制的时间为31645s (300切层),利用球体剖切的绘制时间为91934s ,而采用包围盒技术后的绘制时间为41998s .另外,算法效率提高的程度还和剖切体与结构的相交程度有关,即相交的部分越小,算法效率提高得也就越大.参考文献1 M ark W .Jones ,M in Chen .Fast cutting operati ons on th ree16第1期杨晓松等:有限元网格体绘制中的剖切算法。
有限元网格剖分

有限元网格剖分 (转自中科大有限元论坛)有限元网格剖分1. 引言有限元法是求解复杂工程问题的一种近似数值解法,现已广泛应用到力学、热学、电磁学等各个学科,主要分析工作环境下物体的线性和非线性静动态特性等性能。
有限元法求解问题的基本过程主要包括:分析对象的离散化-有限元求解-计算结果的处理三部分。
曾经有人做过统计:三个阶段所用的时间分别占总时间的40%~50%、5%及50%~55%。
也就是说,当利用有限元分析对象时,主要时间是用于对象的离散及结果的处理。
如果采用人工方法离散对象和处理计算结果,势必费力、费时且极易出错,尤其当分析模型复杂时,采用人工方法甚至很难进行,这将严重影响高级有限元分析程序的推广和使用。
因此,开展自动离散对象及结果的计算机可视化显示的研究是一项重要而紧迫的任务。
可喜的是,随着计算机及计算技术的飞速发展,出现了开发对象的自动离散及有限元分析结果的计算机可视化显示的热潮,使有限元分析的“瓶颈”现象得以逐步解决,对象的离散从手工到半自动到全自动,从简单对象的单维单一网格到复杂对象的多维多种网格单元,从单材料到多种材料,从单纯的离散到自适应离散,从对象的性能校核到自动自适应动态设计/分析,这些重大发展使有限元分析摆脱了仅为性能校核工具的原始阶段,计算结果的计算机可视化显示从简单的应力、位移和温度等场的静动态显示、彩色调色显示一跃成为对受载对象可能出现缺陷(裂纹等)的位置、形状、大小及其可能波及区域的显示等,这种从抽象数据到计算机形象化显示的飞跃是现在甚至将来计算机集成设计/分析的重要组成部分。
2. 有限元分析对网格剖分的要求有限元网格生成就是将工作环境下的物体离散成简单单元的过程,常用的简单单元包括:一维杆元及集中质量元、二维三角形、四边形元和三维四面体元、五面体元和六面体元。
他们的边界形状主要有直线型、曲线型和曲面型。
对于边界为曲线(面)型的单元,有限元分析要求各边或面上有若干点,这样,既可保证单元的形状,同时,又可提高求解精度、准确性及加快收敛速度。
《2024年有限元网格剖分与网格质量判定指标》范文

《有限元网格剖分与网格质量判定指标》篇一一、引言有限元法是一种广泛应用于工程分析中的数值计算方法。
其核心步骤之一就是网格剖分,即将求解域离散化为有限个相互连接的子域,即有限元。
网格的质量直接影响到有限元法求解的精度和效率。
因此,合理有效的网格剖分及网格质量判定是进行有限元分析的重要环节。
本文将重点探讨有限元网格剖分的方法以及网格质量判定指标。
二、有限元网格剖分1. 网格剖分原则有限元网格剖分应遵循以下原则:(1)贴体性:网格应尽可能贴合求解域的形状,以减少边界处的近似误差。
(2)适度性:网格的疏密程度应适中,既要保证足够的计算精度,又要避免过细的网格导致计算量过大。
(3)连续性:网格的连接应保持连续性,避免出现断点或重叠现象。
2. 网格剖分方法常见的有限元网格剖分方法包括:(1)映射法:适用于规则的求解域,通过映射函数将规则域的网格映射到实际求解域上。
(2)插值法:根据边界条件或已知的物理量分布,通过插值函数生成网格。
(3)Delaunay三角剖分法:通过三角化方法将求解域划分为一系列三角形单元,适用于二维和三维求解域。
三、网格质量判定指标网格质量是衡量网格优劣的重要指标,直接影响着有限元法求解的精度和效率。
常见的网格质量判定指标包括:1. 单元形状:包括单元的几何形状、角度等。
单元形状良好的网格能提高计算的精度和稳定性。
通常要求单元的角度尽可能接近于标准角度(如90度)。
2. 扭曲度:指单元形状与其标准形状(如立方体或四边形)之间的相似程度。
扭曲度较小的单元具有更好的计算性能和稳定性。
对于三维问题,可以考察单元的体积扭曲度;对于二维问题,可以考察单元的面积扭曲度。
3. 纵横比:指单元的最大边长与最小边长之比。
纵横比过大的单元可能导致求解过程中的数值不稳定和计算误差增大。
因此,应尽量保持单元的纵横比在合理范围内。
4. 光滑性:指网格中相邻单元之间的过渡是否平滑。
光滑性良好的网格能提高计算的精度和收敛速度。
《2024年有限元网格剖分与网格质量判定指标》范文

《有限元网格剖分与网格质量判定指标》篇一一、引言有限元分析(Finite Element Analysis, FEA)是工程领域中广泛使用的一种数值分析方法,它能够模拟复杂的物理现象和工程问题。
而有限元网格剖分作为有限元分析的基础,其质量和精度直接影响到分析结果的准确性。
因此,本文将重点探讨有限元网格剖分的过程以及网格质量判定指标,旨在为工程技术人员提供有益的参考。
二、有限元网格剖分1. 网格剖分流程有限元网格剖分流程包括以下步骤:问题定义、网格规划、几何模型构建、单元选择、剖分实现及质量控制。
首先,根据问题需求确定求解区域和边界条件;其次,根据问题特性和计算需求进行网格规划,如确定单元类型、尺寸等;然后,根据几何模型进行网格生成;接着,选择合适的单元类型进行剖分;最后,对生成的网格进行质量控制和优化。
2. 网格类型与单元选择有限元网格的类型主要包括结构化网格和非结构化网格。
结构化网格具有较好的规则性和连续性,适用于规则的求解区域;而非结构化网格则具有较强的适应性和灵活性,适用于复杂的几何模型。
在单元选择方面,常用的单元类型包括四边形单元、三角形单元、六面体单元等。
不同类型的单元具有不同的精度和计算效率,需要根据具体问题选择合适的单元类型。
三、网格质量判定指标网格质量是影响有限元分析结果的重要因素。
为了确保分析结果的准确性,需要采用一系列的网格质量判定指标来评估网格的质量。
以下是一些常用的网格质量判定指标:1. 单元形状质量指标单元形状质量指标用于评估单元的形状是否符合要求。
常见的单元形状质量指标包括面积比、角度比等。
这些指标可以反映单元的形状是否过于扭曲或狭长,从而影响计算的精度和稳定性。
2. 光滑性指标光滑性指标用于评估网格的光滑程度。
在剖分过程中,可能会产生一些尖锐的边缘或角落,这些都会影响分析结果的准确性。
光滑性指标可以通过计算单元间的连接性和相邻单元间的连续性来评估。
3. 雅可比矩阵条件数雅可比矩阵条件数用于评估网格的扭曲程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有限元网格剖分方法概述在采用有限元法进行结构分析时,首先必须对结构进行离散,形成有限元网格,并给出与此网格相应的各种信息,如单元信息、节点坐标、材料信息、约束信息和荷载信息等等,是一项十分复杂、艰巨的工作。
如果采用人工方法离散对象和处理计算结果,势必费力、费时且极易出错,尤其当分析模型复杂时,采用人工方法甚至很难进行,这将严重影响高级有限元分析程序的推广和使用。
因此,开展自动离散对象及结果的计算机可视化显示的研究是一项重要而紧迫的任务。
有限元网格生成技术发展到现在, 已经出现了大量的不同实现方法,列举如下:1.映射法映射法是一种半自动网格生成方法,根据映射函数的不同,主要可分为超限映射和等参映射。
因前一种映射在几何逼近精度上比后一种高,故被广泛采用。
映射法的基本思想是:在简单区域内采用某种映射函数构造简单区域的边界点和内点,并按某种规则连接结点构成网格单元。
也就是根据形体边界的参数方程,利用映射函数,把参数空间内单元正方形或单元三角形(对于三维问题是单元立方体或单元四面体)的网格映射到欧氏空间,从而生成实际的网格。
这种方法的主要步骤是,首先人为地把分析域分成一个个简单可映射的子域,每个子域为三角形或四边形,然后根据网格密度的需要,定义每个子域边界上的节点数,再根据这些信息,利用映射函数划分网格。
这种网格控制机理有以下几个缺点:(1)它不是完全面向几何特征的,很难完成自动化,尤其是对于3D区域。
(2)它是通过低维点来生成高维单元。
例如,在2D问题中,先定义映射边界上的点数,然后形成平面单元。
这对于单元的定位,尤其是对于远离映射边界的单元的定位,是十分困难的,使得对局部的控制能力下降。
(3)各映射块之间的网格密度相互影响程度很大。
也就是说,改变某一映射块的网格密度,其它各映射块的网格都要做相应的调整。
其优点是:由于概念明确,方法简单,单元性能较好,对规则均一的区域,适用性很强,因此得到了较大的发展,并在一些商用软件如ANSYS等得到应用。
2 。
拓扑分解法拓扑分解法较其它方法发展较晚, 它首先是由Wordenwaber提出来的。
该方法假设最后网格顶点全部由目标边界顶点组成, 那么可以用一种三角化算法将目标用尽量少的三角形完全分割覆盖。
这些三角形主要是由目标的拓扑结构决定, 这样目标的复杂拓扑结构被分解成简单的三角形拓扑结构。
该方法生成的网格一般相当粗糙, 必须与其它方法相结合, 通过网格加密等过程, 才能生成合适的网格。
该方法后来被发展为普遍使用的目标初始三角化算法, 用来实现从实体表述到初始三角化表述的自动化转换。
单一的拓扑分解法因只依赖于几何体的拓扑结构使网格剖分不理想,有时甚至很差。
3.连接节点法这类方法一般包括二步:区域内布点及其三角化。
早期的方法通常是先在区域内布点, 然后再将它们联成三角形或四面体, 在三角化过程中, 对所生成的单元形状难于控制。
随着Delaunay三角化(简称为DT ) 方法的出现, 该类方法已成为目前三大最流行的全自动网格生成方法之一。
DT法的基本原理:任意给定N个平面点Pi(i=1,2,…,N)构成的点集为S,称满足下列条件的点集Vi为Voronoi多边形。
其中,Vi满足下列条件:Vi ={ X:|X- Pi|(|X- Pj|,X(R2,i(j,j=1,2,…,N }Vi为凸多边形,称{ Vi}mi=1为Dirichlet Tesselation图或对偶的Voronoi图。
连接相邻Voronoi多边形的内核点可构成三角形Tk,称集合{ Tk }为Delaunay三角剖分。
DT法的最大优点是遵循“最小角最大”和“空球”准则。
因此,在各种二维三角剖分中,只有Delaunay三角剖分才同时满足全局和局部最优。
“最小角最大”准则是在不出现奇异性的情况下,Delaunay三角剖分最小角之和均大于任何非Delaunay剖分所形成三角形最小角之和。
“空球”准则是Delaunay三角剖分中任意三角形的外接圆(四面体为外接球)内不包括其他结点。
DT 技术发展到现在, 已经出现了大量的不同算法。
一般可以将其分为以下三大类:以Bower 和Green、Sibsos 为代表的Voronoi方法;以Watson为代表的空外接圆法和以Lawson 为代表的对角线交换算法。
一般来说, 直接计算Voronoi 图的方法比较复杂, 所需内存大, 计算效率低。
随着直接计算DT 方法的出现, 这类方法现已很少采用。
Lawson 算法特别适用于二维Delaunay 三角化, 它不存在象Watson 算法中出现的退化现象, 对约束情况同样适用, 计算效率高。
但在三维情况下, 对角线交换的推广变成了对角面交换, 而对角面交换将可能改变区域体积和外边界, 因此Lawson 算法不能直接推广到三维情况。
Watson 算法概念简单, 易于编程实现, 也能够实现约束三角化, 而且通过一些适当修改, 例如, 增加每一单元的相邻单元数据结构等, 可以将对三角形的搜索局限在新点所在单元的近邻之中, 从而大大提高了原算法效率, 因此该法的应用频度最广。
但该法也有一些不足:即出现所谓退化现象或产生所谓Sliver 单元。
虽然Delaunay 三角化方法在2D 平面区域问题中取得了相当大的成功, 但在3D 情形, 基于最大2最小角判据的对角线交换规则不再成立, 而基于外接圆判据的Delaunay 三角化一般也不再能保证生成的网格质量。
非常遗憾的是, 这是Delaunay 三角化的本质弱点。
另外, 虽然Delaunay 三角化提供了一种较好的方法将空间点集三角化, 但Delaunay判据本身并不能指导怎样在空间布点, 因此, 必须寻找一种较好的布点方法, 既要点的分布满足密度控制的要求, 又要求三角化的结果形状尽可能好。
目前基于Delaunay 三角化理论的3D 网格生成技术仍然是一活跃的研究课题, 许多学者正对此进行深入研究。
Delaunay三角化网格自动生成方法的事前(a-priori)网格控制能力不强。
然而,Delaunay 三角化网格自动生成方法却非常适合于事后(a-postoriori)网格局部加密,因为它的网格控制机理是面向整个分析域的,可以通过在原来网格的任意局部插入新的节点,然后做新的三角剖分,达到局部加密的目的。
4.几何分解法在这种方法中节点与单元同步生成, 与拓扑分解法完全不同的是在实体分解过程中,考虑了所生成的单元形状及大小, 确保生成的单元质量尽量地好(在拓扑分解法中, 并不考虑生成的单元形状, 而且除边界顶点外, 一般不增加新的顶点)。
常用的有两种:递归法和迭代法。
递归法:Tracy、左建政和Chae等先离散二维物体边界,然后沿离散边界向物体内挖掉一个、两个或三个三角形,重复此操作直到区域挖空为止。
Lindhom、Blacker和B.P. Johnston等使用的迭代法不同于前者,首先从物体中挖掉边界层而不是单元,然后三角化边界层。
上述为二维迭代法,Chae在此基础上发展了三维迭代几何分解法,主要分两步:采用二维迭代几何分解法生成表面三角形,然后采用三种算子挖切凸体为四面体。
在挖切时,突出的特点在于采用新方法生成关键点。
关键点的生成分两步考虑:一是考虑新点对周围面和边的影响;二是通过调整比例因子来确定新点位置。
Chae也将所提出的算法成功地应用于自适应网格生成中,但由于被剖分物体形状必须是单连通凸域,因此,不能实现全自动网格生成。
迭代法:Bykat采用该法。
他首先将物体划分为凸体(手工或自动),随后根据网格密度分布,在每个凸体边界上插入结点,然后将物体中间“最长轴”一分为二,在该轴上插入结点,继续对两部分做递归分割直到最后子域均为三角形为止。
商业网格生成软件Triquamesh 仍采用该法,只是分割线的选取与Bykat不同。
几何分解法的最大优点是在离散物体时考虑网格单元的形状和大小,因此,所生成的网格单元形状和分布均较好。
最大缺点是自动化程度低,不利于复杂件网格生成。
5. 栅格法栅格法又分为栅格叠合法和四(八)叉树法。
栅格叠合法最早由Thacker,GonzaleZ和Putland提出,它是将栅格置放于物体之上。
既可在栅格的规则点处布置节点,也可在栅格单元中随机布置结点,容易得到均匀网格,然后对栅格与物体求交,将在物体外的栅格去掉,物体内的栅格保留作为网格。
在边界处的栅格需要变形,也就是要调整节点的位置以满足边界条件的要求,最终产生的网格内部单元完全一样,只是边界单元不同。
栅格越密, 网格质量将越好。
这种方法的不足是所生成的网格与所选择的初始栅格及其取向有关, 网格边界单元质量差。
这种方法在原理上相当简单,也易于扩充到三维, 对于相对规则的问题区域不失为一种简单有效的方法。
叉树法网格生成的过程是完全面向几何特征的,它通过一系列几何操作,同时从几何模型数据库中取得分析物体的几何信息,以及网格控制参数信息等,来完成网格划分。
叉树法主要指四叉树和八叉树编码法。
对于二维问题,一个方形区域用四叉树法分成4个四边形,每个四边形再继续用四叉树法细分,最终形成四边形网格。
三维情况采用类似的八叉树法可得到六面体网格。
概括起来说,该算法主要由以下两个步骤完成,1)首先找到一个能够完全包含分析域的正方形,然后利用四叉树性质离散该正方形至所需要的大小。
同时,把这些离散信息保留在一个四叉树数据结构中,通过这个树状数据结构,把离散的子正方形联系起来。
2)从第一步产生的四叉树数据库中,取出满足终止条件的边界和内部子正方形来形成网格单元,并存储于网格数据库中。
同时,使某些特殊点自动成为网格单元的节点,例如结构的支撑点、集中载荷的作用点等。
大多数实体造型系统都采用树形数据结构进行几何及拓扑描述,在此基础之上,Yerry等提出了“修正的八叉树”法等有限元网格生成算法。
基于“修正的八叉树”法的空间编码法在问题域内部容易生成高质量的单元,但是边界单元需要进一步处理,以免因质量太差而不适合有限元分析。
空间编码法有两个本质属性即阶梯结构和空间可访问性可以实现与实体造型系统的集成,并且客易精整网格质量。
虽然有限四(八)叉树方法已经取得了相当大的成功, 它适用于任何复杂的二维和三维区域问题, 而且算法效率几乎与单元节点数呈线性增长, 其网格生成易于实现密度控制, 易于进行自适应分析, 也易于同实体造型系统相结合, 但其缺点也是明显的, 所生成网格与所选择的初始栅格及其取向有关, 网格边界单元质量差, 程序实现相当复杂, 所需内存较大, 不利于实现并行处理等。
综上所述,在实际过程中,Delaunay法目前应用最广泛,但是不能生成六面体。
栅格法和叉树法内部单元质量好,但不能与边界完全拟合。
随着时间的推移,会不断地有一些新方法出现,原有的算法也会得到进一步完善和发展。
