(新课标)天津市2019年高考数学二轮复习 专题能力训练6 函数与方程及函数的应用 理
(新课标)天津市2019年高考数学二轮复习 题型练8 大题专项(六)函数与导数综合问题 理

题型练8 大题专项(六)函数与导数综合问题1.(2018北京,理18)设函数f(x)=[ax2—(4a+1)x+4a+3]e x.(1)若曲线y=f(x)在点(1,f(1))处的切线与x轴平行,求a;(2)若f(x)在x=2处取得极小值,求a的取值范围。
2。
已知a≥3,函数F(x)=min{2|x—1|,x2-2ax+4a-2},其中min{p,q}=(1)求使得等式F(x)=x2—2ax+4a-2成立的x的取值范围;(2)①求F(x)的最小值m(a);②求F(x)在区间[0,6]上的最大值M(a)。
3.已知函数f(x)=x3+ax2+b(a,b∈R).(1)试讨论f(x)的单调性;(2)若b=c-a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(-∞,—3)∪,求c的值。
4。
已知a>0,函数f(x)=e ax sin x(x∈[0,+∞)).记x n为f(x)的从小到大的第n(n∈N*)个极值点。
证明:(1)数列{f(x n)}是等比数列;(2)若a≥,则对一切n∈N*,x n<|f(x n)|恒成立。
5.(2018天津,理20)已知函数f(x)=a x,g(x)=log a x,其中a>1.(1)求函数h(x)=f(x)-x ln a的单调区间;(2)若曲线y=f(x)在点(x1,f(x1))处的切线与曲线y=g(x)在点(x2,g(x2))处的切线平行,证明x1+g(x2)=-;(3)证明当a≥时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线.6。
设函数f(x)=,g(x)=-x+(a+b)(其中e为自然对数的底数,a,b∈R,且a≠0),曲线y=f(x)在点(1,f(1))处的切线方程为y=a e(x-1).(1)求b的值;(2)若对任意x∈,f(x)与g(x)有且只有两个交点,求a的取值范围。
题型练8大题专项(六)函数与导数综合问题1.解(1)因为f(x)=[ax2-(4a+1)x+4a+3]e x,所以f'(x)=[2ax—(4a+1)]e x+[ax2-(4a+1)x+4a+3]e x=[ax2-(2a+1)x+2]e x(x∈R)。
2019年高考数学(理科,天津课标版)二轮复习专题能力训练 Word版含答案8

专题能力训练8 利用导数解不等式及参数的取值范围一、能力突破训练1.设f (x )=x ln x-ax 2+(2a-1)x ,a ∈R .(1)令g (x )=f'(x ),求g (x )的单调区间;(2)已知f (x )在x=1处取得极大值,求实数a 的取值范围.2.(2018全国Ⅲ,理21)已知函数f (x )=(2+x+ax 2)·ln(1+x )-2x.(1)若a=0,证明:当-1<x<0时,f (x )<0;当x>0时,f (x )>0;(2)若x=0是f (x )的极大值点,求a.3.已知函数f (x )=ax+x ln x 的图象在x=e(e 为自然对数的底数)处的切线的斜率为3.(1)求实数a 的值;(2)若f (x )≤kx 2对任意x>0成立,求实数k 的取值范围;(3)当n>m>1(m ,n ∈N *)时,证明:.nm mn>m n4.设函数f (x )=ax 2-a-ln x ,其中a ∈R .(1)讨论f (x )的单调性;(2)确定a 的所有可能取值,使得f (x )>-e 1-x 在区间(1,+∞)内恒成立(e =2.718…为自然对数的底数).1x 5.设函数f (x )=a ln x ,g (x )=x 2.12(1)记g'(x )为g (x )的导函数,若不等式f (x )+2g'(x )≤(a+3)x-g (x )在x ∈[1,e]内有解,求实数a 的取值范围;(2)若a=1,对任意的x 1>x 2>0,不等式m [g (x 1)-g (x 2)]>x 1f (x 1)-x 2f (x 2)恒成立.求m (m ∈Z ,m ≤1)的值.6.已知函数f (x )=-2(x+a )ln x+x 2-2ax-2a 2+a ,其中a>0.(1)设g (x )是f (x )的导函数,讨论g (x )的单调性;(2)证明:存在a ∈(0,1),使得f (x )≥0在区间(1,+∞)内恒成立,且f (x )=0在区间(1,+∞)内有唯一解.二、思维提升训练7.已知函数f (x )=x 3+x 2+ax+1(a ∈R ).13(1)求函数f (x )的单调区间;(2)当a<0时,试讨论是否存在x 0∈,使得f (x 0)=f .(0,12)∪(12,1)(12)专题能力训练8 利用导数解不等式及参数的取值范围一、能力突破训练1.解 (1)由f'(x )=ln x-2ax+2a ,可得g (x )=ln x-2ax+2a ,x ∈(0,+∞).则g'(x )=-2a=,1x 1-2ax x 当a ≤0时,x ∈(0,+∞)时,g'(x )>0,函数g (x )单调递增;当a>0时,x时,g'(x )>0,函数g (x )单调递增,x 时,函数g (x )单调递减.∈(0,12a)∈(12a ,+∞)所以当a ≤0时,g (x )的单调增区间为(0,+∞);当a>0时,g (x )单调增区间为,单调减区间为(0,12a)(12a,+∞).(2)由(1)知,f'(1)=0.①当a ≤0时,f'(x )单调递增,所以当x ∈(0,1)时,f'(x )<0,f (x )单调递减.当x ∈(1,+∞)时,f'(x )>0,f (x )单调递增.所以f (x )在x=1处取得极小值,不合题意.②当0<a<时,>1,由(1)知f'(x )在区间内单调递增,1212a (0,12a )可得当x ∈(0,1)时,f'(x )<0,x时,f'(x )>0.∈(1,12a)所以f (x )在区间(0,1)内单调递减,在区间内单调递增,所以f (x )在x=1处取得极小值,不合题(1,12a )意.③当a=时,=1,f'(x )在区间(0,1)内单调递增,在区间(1,+∞)内单调递减,1212a 所以当x ∈(0,+∞)时,f'(x )≤0,f (x )单调递减,不合题意.④当a>时,0<<1,当x时,f'(x )>0,f (x )单调递增,1212a ∈(12a,1)当x ∈(1,+∞)时,f'(x )<0,f (x )单调递减,所以f (x )在x=1处取极大值,合题意.综上可知,实数a 的取值范围为a>12.2.解 (1)当a=0时,f (x )=(2+x )ln(1+x )-2x ,f'(x )=ln(1+x )-,x1+x设函数g (x )=f'(x )=ln(1+x )-,则g'(x )=,x1+x x(1+x )2当-1<x<0时,g'(x )<0;当x>0时,g'(x )>0.故当x>-1时,g (x )≥g (0)=0,且仅当x=0时,g (x )=0,从而f'(x )≥0,且仅当x=0时,f'(x )=0.所以f (x )在(-1,+∞)内单调递增.又f (0)=0,故当-1<x<0时,f (x )<0;当x>0时,f (x )>0.(2)①若a ≥0,由(1)知,当x>0时,f (x )≥(2+x )·ln(1+x )-2x>0=f (0),这与x=0是f (x )的极大值点矛盾.②若a<0,设函数h (x )==ln(1+x )-f (x )2+x +ax22x2+x +ax2.由于当|x|<min时,2+x+ax 2>0,故h (x )与f (x )符号相同.{1,1|a |}又h (0)=f (0)=0,故x=0是f (x )的极大值点当且仅当x=0是h (x )的极大值点.h'(x )=11+x ‒2(2+x +ax 2)-2x (1+2ax )(2+x +ax 2)2=x 2(a 2x 2+4ax +6a +1)(x +1)(ax 2+x +2)2.若6a+1>0,则当0<x<-,且|x|<min时,h'(x )>0,故x=0不是h (x )的极大值点.6a +14a {1,1|a |}若6a+1<0,则a 2x 2+4ax+6a+1=0存在根x 1<0,故当x ∈(x 1,0),且|x|<min 时,h'(x )<0,所以{1,1|a |}x=0不是h (x )的极大值点.若6a+1=0,则h'(x )=x 3(x -24)(x +1)(x 2-6x -12)2.则当x ∈(-1,0)时,h'(x )>0;当x ∈(0,1)时,h'(x )<0.所以x=0是h (x )的极大值点,从而x=0是f (x )的极大值点.综上,a=-16.3.解 (1)∵f (x )=ax+x ln x ,∴f'(x )=a+ln x+1.又f (x )的图象在点x=e 处的切线的斜率为3,∴f'(e)=3,即a+ln e +1=3,∴a=1.(2)由(1)知,f (x )=x+x ln x ,若f (x )≤kx 2对任意x>0成立,则k对任意x>0成立.≥1+lnxx 令g (x )=,则问题转化为求g (x )的最大值,g'(x )==-1+lnxx 1x·x -(1+lnx )x 2lnxx2.令g'(x )=0,解得x=1.当0<x<1时,g'(x )>0,∴g (x )在区间(0,1)内是增函数;当x>1时,g'(x )<0,∴g (x )在区间(1,+∞)内是减函数.故g (x )在x=1处取得最大值g (1)=1,∴k ≥1即为所求.(3)证明:令h (x )=,则h'(x )=xlnx x -1x -1-lnx(x -1)2.由(2)知,x ≥1+ln x (x>0),∴h'(x )≥0,∴h (x )是区间(1,+∞)内的增函数.∵n>m>1,∴h (n )>h (m ),即,nlnn n -1>mlnmm -1∴mn ln n-n ln n>mn ln m-m ln m ,即mn ln n+m ln m>mn ln m+n ln n ,∴ln n mn +ln m m >ln m mn +ln n n .整理,得ln(mn n )m >ln(nm m )n .∴(mn n )m >(nm m )n ,∴nm mn>m n.4.解 (1)f'(x )=2ax-(x>0).1x=2ax 2-1x 当a ≤0时,f'(x )<0,f (x )在区间(0,+∞)内单调递减.当a>0时,由f'(x )=0,有x=12a.此时,当x 时,f'(x )<0,f (x )单调递减;∈(0,12a)当x时,f'(x )>0,f (x )单调递增.∈(12a,+∞)(2)令g (x )=,s (x )=e x-1-x.1x ‒1ex -1则s'(x )=e x-1-1.而当x>1时,s'(x )>0,所以s (x )在区间(1,+∞)内单调递增.又由s (1)=0,有s (x )>0,从而当x>1时,g (x )>0.当a ≤0,x>1时,f (x )=a (x 2-1)-ln x<0.故当f (x )>g (x )在区间(1,+∞)内恒成立时,必有a>0.当0<a<时,>1.1212a 由(1)有f <f (1)=0,而g >0,(12a)(12a)所以此时f (x )>g (x )在区间(1,+∞)内不恒成立.当a时,令h (x )=f (x )-g (x )(x ≥1).≥12当x>1时,h'(x )=2ax--e 1-x >x->0.1x +1x 21x +1x 2‒1x =x 3-2x +1x 2>x 2-2x +1x 2因此,h (x )在区间(1,+∞)单调递增.又因为h (1)=0,所以当x>1时,h (x )=f (x )-g (x )>0,即f (x )>g (x )恒成立.综上,a∈[12,+∞).5.解 (1)不等式f (x )+2g'(x )≤(a+3)x-g (x ),即a ln x+2x ≤(a+3)x-x 2,12化简,得a (x-ln x )x 2-x.≥12由x ∈[1,e]知x-ln x>0,因而a 设y=,≥12x 2-xx -lnx .12x 2-xx -lnx 则y'=(x -1)(x -lnx )-(1-1x )(12x 2-x)(x -lnx )2=(x -1)(12x +1-lnx)(x -lnx )2.∵当x ∈(1,e)时,x-1>0,x+1-ln x>0,12∴y'>0在x ∈[1,e]时成立.由不等式有解,可得a ≥y min =-,12即实数a 的取值范围是[-12,+∞).(2)当a=1时,f (x )=ln x.由m [g (x 1)-g (x 2)]>x 1f (x 1)-x 2f (x 2)恒成立,得mg (x 1)-x 1f (x 1)>mg (x 2)-x 2f (x 2)恒成立,设t (x )=x 2-x ln x (x>0).m2由题意知x 1>x 2>0,则当x ∈(0,+∞)时函数t (x )单调递增,∴t'(x )=mx-ln x-1≥0恒成立,即m恒成立.≥lnx +1x 因此,记h (x )=,得h'(x )=lnx +1x -lnxx 2.∵函数在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,∴函数h (x )在x=1处取得极大值,并且这个极大值就是函数h (x )的最大值.由此可得h (x )max =h (1)=1,故m ≥1,结合已知条件m ∈Z ,m ≤1,可得m=1.6.(1)解 由已知,函数f (x )的定义域为(0,+∞),g (x )=f'(x )=2(x-a )-2ln x-2,(1+a x)所以g'(x )=2-2x +2a x 2=2(x -12)2+2(a -14)x 2.当0<a<时,g (x )在区间内单调递增,14(0,1-1-4a2),(1+1-4a2,+∞)在区间内单调递减;(1-1-4a 2,1+1-4a2)当a时,g (x )在区间(0,+∞)内单调递增.≥14(2)证明 由f'(x )=2(x-a )-2ln x-2=0,解得a=(1+a x)x -1-lnx1+x-1.令φ(x )=-2ln x+x 2-2x-2(x +x -1-lnx 1+x -1)(x -1-lnx 1+x -1)(x -1-lnx 1+x -1)2+x -1-lnx 1+x -1.则φ(1)=1>0,φ(e)=--2<0.e (e -2)1+e-1(e -21+e-1)2故存在x 0∈(1,e),使得φ(x 0)=0.令a 0=,u (x )=x-1-ln x (x ≥1).x 0-1-ln x 01+x -10由u'(x )=1-0知,函数u (x )在区间(1,+∞)内单调递增.1x ≥所以0==a 0<<1.u (1)1+1<u (x 0)1+x -1u (e )1+e-1=e -21+e -1即a 0∈(0,1).当a=a 0时,有f'(x 0)=0,f (x 0)=φ(x 0)=0.由(1)知,f'(x )在区间(1,+∞)内单调递增,故当x ∈(1,x 0)时,f'(x )<0,从而f (x )>f (x 0)=0;当x ∈(x 0,+∞)时,f'(x )>0,从而f (x )>f (x 0)=0.所以,当x ∈(1,+∞)时,f (x )≥0.综上所述,存在a ∈(0,1),使得f (x )≥0在区间(1,+∞)内恒成立,且f (x )=0在区间(1,+∞)内有唯一解.二、思维提升训练7.解 (1)f'(x )=x 2+2x+a ,方程x 2+2x+a=0的判别式为Δ=4-4a ,①当a ≥1时,Δ≤0,则f'(x )≥0,此时f (x )在R 上是增函数;②当a<1时,方程x 2+2x+a=0两根分别为x 1=-1-,x 2=-1+,1-a 1-a 解不等式x 2+2x+a>0,解得x<-1-或x>-1+,1-a 1-a 解不等式x 2+2x+a<0,解得-1-<x<-1+,1-a 1-a 此时,函数f (x )的单调递增区间为(-∞,-1-)和(-1+,+∞),1-a 1-a 单调递减区间为(-1-,-1+).1-a 1-a 综上所述,当a ≥1时,函数f (x )的单调递增区间为(-∞,+∞);当a<1时,函数f (x )的单调递增区间为(-∞,-1-)和(-1+,+∞),单调递减区间为(-1-1-a 1-a ,-1+).1-a 1-a (2)f (x 0)-f +ax 0+1--a -1(12)=13x 30+x 2013·(12)3‒(12)2·12=+a 13[x 3-(12)3]+[x 20-(12)2](x 0-12)=13(x 0-12)(x 20+x 02+14)+(x 0-12)·+a +x0+(4+14x 0+7+12a ).(x 0+12)(x 0-12)=(x 0-12)·(x 203+x 06+11212+a )=112(x 0-12)x 20若存在x 0,使得f (x 0)=f ,则4+14x 0+7+12a=0在内有解.∈(0,12)∪(12,1)(12)x 20(0,12)∪(12,1)由a<0,得Δ=142-16(7+12a )=4(21-48a )>0,故方程4+14x 0+7+12a=0的两根为x 1'=x'2=x 20-7-21-48a 4-7+21-48a4.由x 0>0,得x 0=x'2=,-7+21-48a4依题意,0<<1,即7<<11,所以49<21-48a<121,即-<a<-,-7+21-48a421-48a 2512712又由得a=-,-7+21-48a 4=1254故要使满足题意的x 0存在,则a ≠-54.综上,当a 时,存在唯一的x0满足f (x 0)=f ,当a ∈(-2512,-54)∪(-54,-712)∈(0,12)∪(12,1)(12)时,不存在x0满足f (x 0)=f ∈(-∞,-2512]∪(-54)∪[-712,0)∈(0,12)∪(12,1)(12).。
2019年高考数学(理科,天津课标版)二轮复习专题能力训练 Word版含答案22

|AB|= .
{ 6.若直线
l:
������
������ =
= ������, 3+
������������(t
为参数)与圆
C:ρ=2cos
θ
相切,则
k= .
{ 7.已知圆 C1 的参数方程为 ������������==csoins������������,(φ 为参数),以坐标原点 O 为极点,x 轴的非负半轴为极轴建立极 ( )π
坐标系,圆 C2 的极坐标方程为 ρ=2cos ������ + 3 .
(1)圆 C1 的参数方程化为普通方程为 ,圆 C2 的极坐标方程化为直角坐标方程 为 ;
(2)圆 C1,C2 的公共弦长为 .
( ) ( ) π
π
8.在极坐标系中,点 2,6 到直线 ρsin ������ - 6 =1 的距离是 .
高清试卷 下载可打印
专题能力训练 22 坐标系与参数方程(选修 4—4)
能力突破训练Βιβλιοθήκη { 1.在直角坐标系xOy 中,已知曲线
C 的参数方程是
������
������ = sin������, = cos������ +
1(α 为参数),若以
O 为极点,x 轴的非负
半轴为极轴,则曲线 C 的极坐标方程可写为 .
为参数)相切,则此直线的倾斜角
α= .
5.以直角坐标系的原点为极点,x 轴的非负半轴为极轴,并在两种坐标系中取相同的长度单位.已知直
{ 线的极坐标方程为
π
θ=4(ρ∈R),它与曲线
������������==12++22csoins������������,(α 为参数)相交于两点
2019年高考数学(理科,天津课标版)二轮复习专题能力训练 含答案7

专题能力训练7导数与函数的单调性、极值、最值一、能力突破训练1.已知函数f(x)的导函数为f'(x),且满足f(x)=af'(1)x+ln x,若f'=0,则a=()A.-1B.-2C.1D.2w3.若定义在R上的函数f(x)满足f(0)=-1,其导函数f'(x)满足f'(x)>k>1,则下列结论中一定错误的是()A.fB.f-C.f--D.f--4.已知常数a,b,c都是实数,f(x)=ax3+bx2+cx-34的导函数为f'(x),f'(x)≤0的解集为{x|-2≤x≤3}.若f(x)的极小值等于-115,则a的值是()A.-B.C.2D.55.(2018全国Ⅲ,理14)曲线y=(ax+1)e x在点(0,1)处的切线的斜率为-2,则a=.6.在曲线y=x3+3x2+6x-1的切线中,斜率最小的切线方程为.7.设函数f(x)=a e x++b(a>0).(1)求f(x)在[0,+∞)上的最小值;(2)设曲线y=f(x)在点(2,f(2))处的切线方程为y=x,求a,b的值.8.设函数f(x)=x e a-x+bx,曲线y=f(x)在点(2,f(2))处的切线方程为y=(e-1)x+4.(1)求a,b的值;(2)求f(x)的单调区间.9.(2018全国Ⅰ,理21)已知函数f(x)=-x+a ln x.(1)讨论f(x)的单调性;<a-2.(2)若f(x)存在两个极值点x1,x2,证明:--10.已知函数f(x)=x3+-x2-ax-a,x∈R,其中a>0.(1)求函数f(x)的单调区间;(2)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围;(3)当a=1时,设函数f(x)在区间[t,t+3]上的最大值为M(t),最小值为m(t),记g(t)=M(t)-m(t),求函数g(t)在区间[-3,-1]上的最小值.二、思维提升训练11.已知定义在R上的函数f(x)的导函数为f'(x),对任意x∈R满足f(x)+f'(x)<0,则下列结论正确的是() A.e2f(2)>e3f(3) B.e2f(2)<e3f(3)C.e2f(2)≥e3f(3)D.e2f(2)≤e3f(3)12.已知f'(x)为定义在R上的函数f(x)的导函数,对任意实数x,都有f(x)<f'(x),则不等式f(m+1)<e m+1f的解集为.13.已知函数f(x)=.(1)求函数f(x)的单调区间;(2)当x>0时,若f(x)>恒成立,求整数k的最大值.14.已知函数f(x)=ln x-ax2+x,a∈R.(1)若f(1)=0,求函数f(x)的单调递减区间;(2)若关于x的不等式f(x)≤ax-1恒成立,求整数a的最小值;(3)若a=-2,正实数x1,x2满足f(x1)+f(x2)+x1x2=0,求证:x1+x2≥-.15.已知函数f(x)=x2+2cos x,g(x)=e x(cos x-sin x+2x-2),其中e≈2.718 28…是自然对数的底数.(1)求曲线y=f(x)在点(π,f(π))处的切线方程.(2)令h(x)=g(x)-af(x)(a∈R),讨论h(x)的单调性并判断有无极值,有极值时求出极值.专题能力训练7导数与函数的单调性、极值、最值一、能力突破训练1.D解析因为f'(x)=af'(1)+,所以f'(1)=af'(1)+1,易知a≠1,则f'(1)=-,所以f'(x)=-又因为f'=0,所以-+2=0,解得a=2.故选D.2.D解析设导函数y=f'(x)的三个零点分别为x1,x2,x3,且x1<0<x2<x3.所以在区间(-∞,x1)和(x2,x3)上,f'(x)<0,f(x)是减函数,在区间(x1,x2)和(x3,+∞)上,f'(x)>0,f(x)是增函数,所以函数y=f(x)的图象可能为D,故选D.3.C解析构造函数F(x)=f(x)-kx,则F'(x)=f'(x)-k>0,∴函数F(x)在R上为单调递增函数.->0,∴F->F(0).∵F(0)=f(0)=-1,∴f-->-1,即f---1=-,∴f--,故C错误.4.C解析依题意得f'(x)=3ax2+2bx+c≤0的解集是[-2,3],于是有3a>0,-2+3=-,-2×3=,则b=-,c=-18a.函数f(x)在x=3处取得极小值,于是有f(3)=27a+9b+3c-34=-115,则-a=-81,解得a=2.故选C.5.-3解析设f(x)=(ax+1)e x,可得f'(x)=a·e x+(ax+1)e x=(ax+a+1)e x,∴f(x)=(ax+1)e x在(0,1)处的切线斜率k=f'(0)=a+1=-2,∴a=-3.6.3x-y-2=0解析y'=3x2+6x+6=3(x+1)2+3≥3.当x=-1时,y'min=3;当x=-1时,y=-5.故切线方程为y+5=3(x+1),即3x-y-2=0.7.解(1)f'(x)=a e x-当f'(x)>0,即x>-ln a时,f(x)在区间(-ln a,+∞)内单调递增;当f'(x)<0,即x<-ln a时,f(x)在区间(-∞,-ln a)内单调递减.①当0<a<1时,-ln a>0,f(x)在区间(0,-ln a)内单调递减,在区间(-ln a,+∞)内单调递增,从而f(x)在区间[0,+∞)内的最小值为f(-ln a)=2+b;②当a≥1时,-ln a≤0,f(x)在区间[0,+∞)内单调递增,从而f(x)在区间[0,+∞)内的最小值为f(0)=a++b.(2)依题意f'(2)=a e2-,解得a e2=2或a e2=-(舍去).所以a=,代入原函数可得2++b=3,即b=故a=,b=8.解(1)因为f(x)=x e a-x+bx,所以f'(x)=(1-x)e a-x+b.依题设,-即----解得a=2,b=e.(2)由(1)知f(x)=x e2-x+e x.由f'(x)=e2-x(1-x+e x-1)及e2-x>0知,f'(x)与1-x+e x-1同号.令g(x)=1-x+e x-1,则g'(x)=-1+e x-1.所以,当x∈(-∞,1)时,g'(x)<0,g(x)在区间(-∞,1)上单调递减;当x∈(1,+∞)时,g'(x)>0,g(x)在区间(1,+∞)上单调递增.故g(1)=1是g(x)在区间(-∞,+∞)上的最小值,从而g(x)>0,x∈(-∞,+∞).综上可知,f'(x)>0,x∈(-∞,+∞).故f(x)的单调递增区间为(-∞,+∞).9.(1)解f(x)的定义域为(0,+∞),f'(x)=--1+=--①若a≤2,则f'(x)≤0,当且仅当a=2,x=1时,f'(x)=0,所以f(x)在(0,+∞)内单调递减.②若a>2,令f'(x)=0,得x=--或x=-当x ---时,f'(x)<0;当x ---时,f'(x)>0.所以f(x)在---内单调递减,在---内单调递增.(2)证明由(1)知,f(x)存在两个极值点时,当且仅当a>2.因为f(x)的两个极值点x1,x2满足x2-ax+1=0,所以x1x2=1,不妨设x1<x2,则x2>1.由于--=--1+a--=-2+a--=-2+a--,所以--<a-2等价于-x2+2lnx2<0.设函数g(x)=-x+2ln x,由(1)知,g(x)在(0,+∞)内单调递减,又g(1)=0,从而当x∈(1,+∞)时,g(x)<0.所以-x2+2ln x2<0,即--<a-2.10.解(1)f'(x)=x2+(1-a)x-a=(x+1)(x-a).由f'(x)=0,得x1=-1,x2=a>0.当x变化时,f'(x),f(x)的变化情况如下表:故函数f(x)的单调递增区间是(-∞,-1),(a,+∞);单调递减区间是(-1,a).(2)由(1)知f(x)在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减,从而函数f(x)在区间(-2,0)内恰有两个零点当且仅当--解得0<a<所以a的取值范围是(3)当a=1时,f(x)=x3-x-1.由(1)知f(x)在区间[-3,-1]上单调递增,在区间[-1,1]上单调递减,在区间[1,2]上单调递增.①当t∈[-3,-2]时,t+3∈[0,1],-1∈[t,t+3],f(x)在区间[t,-1]上单调递增,在区间[-1,t+3]上单调递减.因此f(x)在区间[t,t+3]上的最大值M(t)=f(-1)=-,最小值m(t)为f(t)与f(t+3)中的较小者.由f(t+3)-f(t)=3(t+1)(t+2)知,当t∈[-3,-2]时,f(t)≤f(t+3),则m(t)=f(t),所以g(t)=f(-1)-f(t).因为f(t)在区间[-3,-2]上单调递增,所以f(t)≤f(-2)=-故g(t)在区间[-3,-2]上的最小值为g(-2)=--②当t∈[-2,-1]时,t+3∈[1,2],且-1,1∈[t,t+3].下面比较f(-1),f(1),f(t),f(t+3)的大小.因为f(x)在区间[-2,-1],[1,2]上单调递增,所以f(-2)≤f(t)≤f(-1),f(1)≤f(t+3)≤f(2).因为f(1)=f(-2)=-,f(-1)=f(2)=-,从而M(t)=f(-1)=-,m(t)=f(1)=-所以g(t)=M(t)-m(t)=综上,函数g(t)在区间[-3,-1]上的最小值为二、思维提升训练11.A解析令g(x)=e x f(x),则g'(x)=e x(f(x)+f'(x))<0,所以g(x)在R上单调递减,所以g(2)>g(3),即e2f(2)>e3f(3).故选A.12.(-∞,-2)解析若g(x)=,则g'(x)=->0,所以g(x)在R上为增函数.又不等式f(m+1)<e m+1f等价于,即g(m+1)<g,所以m+1<,解得m<-2.13.解(1)由f(x)=,知x∈(-1,0)∪(0,+∞).所以f'(x)=-令h(x)=1+(x+1)ln(x+1),则h'(x)=1+ln(x+1).令h'(x)=0,得x=-1,易得h(x)在区间--内单调递减,在区间-内单调递增.所以h(x)min=h-=1->0,∴f'(x)<0.故f(x)的单调递减区间为(-1,0),(0,+∞).(2)当x>0时,f(x)>恒成立,则k<(x+1)f(x).令g(x)=(x+1)f(x)=,则g'(x)=--令φ(x)=1-x+ln(x+1)(x>0)⇒φ'(x)=-<0,所以φ(x)在区间(0,+∞)内单调递减.又φ(2)=ln 3-1>0,φ(3)=2ln 2-2<0,则存在实数t∈(2,3),使φ(t)=0⇒t=1+ln(t+1).所以g(x)在区间(0,t)内单调递减,在区间(t,+∞)内单调递增.所以g(x)min=g(t)==t+1∈(3,4),故k max=3.14.解(1)因为f(1)=1-=0,所以a=2.此时f(x)=ln x-x2+x,x>0.则f'(x)=-2x+1=-(x>0).令f'(x)<0,则2x2-x-1>0.又x>0,所以x>1.所以f(x)的单调递减区间为(1,+∞).(2)(方法一)令g(x)=f(x)-(ax-1)=ln x-ax2+(1-a)x+1,则g'(x)=-ax+(1-a)=--当a≤0时,因为x>0,所以g'(x)>0.所以g(x)在区间(0,+∞)内是增函数,又g(1)=ln 1-a×12+(1-a)+1=-a+2>0,所以关于x的不等式f(x)≤ax-1不能恒成立.当a>0时,g'(x)=--=--(x>0),令g'(x)=0,得x=所以当x时,g'(x)>0;当x时,g'(x)<0,因此函数g(x)在x内是增函数,在x内是减函数.故函数g(x)的最大值为g=ln a+(1-a)+1=-ln a.令h(a)=-ln a,因为h(1)=>0,h(2)=-ln 2<0,又h(a)在a∈(0,+∞)内是减函数,且a为整数, 所以当a≥2时,h(a)<0.所以整数a的最小值为2.(方法二)由f(x)≤ax-1恒成立,得ln x-ax2+x≤ax-1在区间(0,+∞)内恒成立, 问题等价于a在区间(0,+∞)内恒成立.令g(x)=,因为g'(x)=--,令g'(x)=0,得-x-ln x=0.设h(x)=-x-ln x,因为h'(x)=-<0,所以h(x)在区间(0,+∞)上单调递减,不妨设-x-ln x=0的根为x0.当x∈(0,x0)时,g'(x)>0;当x∈(x0,+∞)时,g'(x)<0,所以g(x)在x∈(0,x0)内是增函数;在x∈(x0,+∞)内是减函数.所以g(x)max=g(x0)=因为h=ln 2->0,h(1)=-<0,所以<x0<1,此时1<<2,即g(x)max∈(1,2).所以a≥2,即整数a的最小值为2.(3)证明:当a=-2时,f(x)=ln x+x2+x,x>0.由f(x1)+f(x2)+x1x2=0,得ln x1++x1+ln x2++x2+x1x2=0,从而(x1+x2)2+x1+x2=x1·x2-ln(x1·x2).令t=x1·x2(t>0),φ(t)=t-ln t,则φ'(t)=-可知,φ(t)在区间(0,1)内单调递减,在区间(1,+∞)内单调递增.所以φ(t)≥φ(1)=1,所以(x1+x2)2+x1+x2≥1,因此x1+x2-或x1+x2--(舍去).15.解(1)由题意f(π)=π2-2,又f'(x)=2x-2sin x,所以f'(π)=2π,因此曲线y=f(x)在点(π,f(π))处的切线方程为y-(π2-2)=2π(x-π),即y=2πx-π2-2.(2)由题意得h(x)=e x(cos x-sin x+2x-2)-a(x2+2cos x),因为h'(x)=e x(cos x-sin x+2x-2)+e x(-sin x-cos x+2)-a(2x-2sin x)=2e x(x-sin x)-2a(x-sin x)=2(e x-a)(x-sin x),令m(x)=x-sin x,则m'(x)=1-cos x≥0,所以m(x)在R上单调递增.因为m(0)=0,所以当x>0时,m(x)>0;当x<0时,m(x)<0.①当a≤0时,e x-a>0,当x<0时,h'(x)<0,h(x)单调递减,当x>0时,h'(x)>0,h(x)单调递增,所以当x=0时h(x)取到极小值,极小值是h(0)=-2a-1;②当a>0时,h'(x)=2(e x-e ln a)(x-sin x),由h'(x)=0得x1=ln a,x2=0.(ⅰ)当0<a<1时,ln a<0,当x∈(-∞,ln a)时,e x-e ln a<0,h'(x)>0,h(x)单调递增;当x∈(ln a,0)时,e x-e ln a>0,h'(x)<0,h(x)单调递减;当x∈(0,+∞)时,e x-e ln a>0,h'(x)>0,h(x)单调递增.所以当x=ln a时h(x)取到极大值.极大值为h(ln a)=-a[ln2a-2ln a+sin(ln a)+cos(ln a)+2],当x=0时h(x)取到极小值,极小值是h(0)=-2a-1;(ⅱ)当a=1时,ln a=0,所以当x∈(-∞,+∞)时,h'(x)≥0,函数h(x)在区间(-∞,+∞)上单调递增,无极值;(ⅲ)当a>1时,ln a>0,所以当x∈(-∞,0)时,e x-e ln a<0,h'(x)>0,h(x)单调递增;当x∈(0,ln a)时,e x-e ln a<0,h'(x)<0,h(x)单调递减;当x∈(ln a,+∞)时,e x-e ln a>0,h'(x)>0,h(x)单调递增.所以当x=0时h(x)取到极大值,极大值是h(0)=-2a-1;当x=ln a时h(x)取到极小值,极小值是h(ln a)=-a[ln2a-2ln a+sin(ln a)+cos(ln a)+2].综上所述:当a≤0时,h(x)在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增,函数h(x)有极小值,极小值是h(0)=-2a-1;当0<a<1时,函数h(x)在区间(-∞,ln a)和区间(0,+∞)上单调递增,在区间(ln a,0)上单调递减,函数h(x)有极大值,也有极小值,极大值是h(ln a)=-a[ln2a-2ln a+sin(ln a)+cos(ln a)+2],极小值是h(0)=-2a-1;当a=1时,函数h(x)在区间(-∞,+∞)上单调递增,无极值;当a>1时,函数h(x)在区间(-∞,0)和(ln a,+∞)上单调递增,在区间(0,ln a)上单调递减,函数h(x)有极大值,也有极小值,极大值是h(0)=-2a-1,极小值是h(ln a)=-a[ln2a-2ln a+sin(ln a)+cos(ln a)+2].。
(新课标)天津市2019年高考数学二轮复习 专题能力训练5 基本初等函数、函数的图象和性质 理

专题能力训练5 基本初等函数、函数的图象和性质一、能力突破训练1.下列函数在其定义域上既是奇函数又是减函数的是 ()A.f(x)=-x|x|B.f(x)=x sin xC.f(x)=D.f(x)=2.已知a=21.2,b=,c=2log52,则a,b,c的大小关系为()A.c<b<aB.c<a<bC.b<a<cD.b<c<a3.(2018全国Ⅲ,理7)函数y=-x4+x2+2的图象大致为()4.函数f(x)在区间(-∞,+∞)内单调递减,且为奇函数,若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是()A.[-2,2]B.[-1,1]C.[0,4]D.[1,3]5.已知函数f(x)=且f(a)=-3,则f(6-a)=()A.-B.-C.-D.-6.(2018全国Ⅱ,理11)已知f(x)是定义域为(-∞,+∞)内的奇函数,满足f(1-x)=f(1+x),若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=()A.-50B.0C.2D.507.已知a>b>1,若log a b+log b a=,a b=b a,则a= ,b= .8.若函数f(x)=x ln(x+)为偶函数,则a= .9.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)内单调递增.若实数a满足f(log2a)+f(lo a)≤2f(1),则a的取值范围是.10.设奇函数y=f(x)(x∈R),满足对任意t∈R都有f(t)=f(1-t),且当x∈时,f(x)=-x2,则f(3)+f的值等于.11.设函数f(x)=的最大值为M,最小值为m,则M+m= .12.若不等式3x2-log a x<0在x∈内恒成立,求实数a的取值范围.二、思维提升训练13.函数y=的图象大致为()14.已知f(x)是定义在R上的偶函数,当x>0时,f(x)=若f(-5)<f(2),则a 的取值范围为()A.(-∞,1)B.(-∞,2)C.(-2,+∞)D.(2,+∞)15.已知函数f(x)(x∈R)满足f(-x)=2-f(x),若函数y=与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(x m,y m),则(x i+y i)=()A.0B.mC.2mD.4m16.已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增.若实数a满足f(2|a-1|)>f(-),则a的取值范围是.17.设f(x)是定义在R上且周期为2的函数,在区间[-1,1]上,f(x)=其中a,b∈R.若f=f,则a+3b的值为.18.若函数e x f(x)(e=2.718 28…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质.下列函数中所有具有M性质的函数的序号为.①f(x)=2-x②f(x)=3-x③f(x)=x3④f(x)=x2+219.已知函数f(x)=e x-e-x(x∈R,且e为自然对数的底数).(1)判断函数f(x)的奇偶性与单调性.(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立?若存在,求出t;若不存在,请说明理由.专题能力训练5基本初等函数、函数的图象和性质一、能力突破训练1.A解析函数f(x)=在其定义域上既是奇函数又是减函数,故选A.2.A解析∵b==20.8<21.2=a,且b>1,又c=2log52=log54<1,∴c<b<a.3.D解析当x=0时,y=2>0,排除A,B;当x=时,y=-+2>2.排除C.故选D.4.D解析因为f(x)为奇函数,所以f(-1)=-f(1)=1,于是-1≤f(x-2)≤1等价于f(1)≤f(x-2)≤f(-1).又f(x)在区间(-∞,+∞)单调递减,所以-1≤x-2≤1,即1≤x≤3.所以x的取值范围是[1,3].5.A解析∵f(a)=-3,∴当a≤1时,f(a)=2a-1-2=-3,即2a-1=-1,此等式显然不成立.当a>1时,f(a)=-log2(a+1)=-3,即a+1=23,解得a=7.∴f(6-a)=f(-1)=2-1-1-2=-2=-6.C解析∵f(-x)=f(2+x)=-f(x),∴f(x+4)=f[(x+2)+2]=-f(x+2)=f(x).∴f(x)的周期为4.∵f(x)为R上的奇函数,∴f(0)=0.∵f(2)=f(1+1)=f(1-1)=f(0)=0,f(3)=f(-1)=-f(1)=-2,f(4)=f(0),∴f(1)+f(2)+f(3)+f(4)=0.∴f(1)+f(2)+…+f(50)=f(49)+f(50)=f(1)+f(2)=2.7.42解析设log b a=t,由a>b>1,知t>1.由题意,得t+,解得t=2,则a=b2.由a b=b a,得b2b=,即得2b=b2,即b=2,∴a=4.8.1解析∵f(x)是偶函数,∴f(-1)=f(1).又f(-1)=-ln(-1+)=ln,f(1)=ln(1+),因此ln(+1)-ln a=ln(+1),于是ln a=0,∴a=1.9解析由题意知a>0,又lo a=log2a-1=-log2a.∵f(x)是R上的偶函数,∴f(log2a)=f(-log2a)=f(lo a).∵f(log2a)+f(lo a)≤2f(1),∴2f(log2a)≤2f(1),即f(log2a)≤f(1).又f(x)在[0,+∞)上单调递增,∴|log2a|≤1,-1≤log2a≤1,∴a10.-解析根据对任意t∈R都有f(t)=f(1-t)可得f(-t)=f(1+t),即f(t+1)=-f(t),进而得到f(t+2)=-f(t+1)=-[-f(t)]=f(t),得函数y=f(x)的一个周期为2,则f(3)=f(1)=f(0+1)=-f(0)=0,f=f=-,所以f(3)+f=0+=-11.2解析f(x)==1+,设g(x)=,则g(-x)=-g(x),故g(x)是奇函数.由奇函数图象的对称性知g(x)max+g(x)min=0,则M+m=[g(x)+1]max+[g(x)+1]min=2+g(x)max+g(x)min=2.12.解由题意知3x2<log a x在x内恒成立.在同一平面直角坐标系内,分别作出函数y=3x2和y=log a x的图象.观察两函数图象,当x时,若a>1,函数y=log a x的图象显然在函数y=3x2图象的下方,所以不成立;当0<a<1时,由图可知,y=log a x的图象必须过点或在这个点的上方,则log a,所以a,所以a<1.综上,实数a的取值范围为a<1.二、思维提升训练13.D解析y=为奇函数,排除A项;y=cos 6x有无穷多个零点,排除C项;当x在原点右侧附近时,可保证2x-2-x>0,cos 6x>0,则此时y>0,故选D.14.B解析因为f(x)是定义在R上的偶函数,所以f(-5)=f(5)=5a+log55=1+5a,则不等式f(-5)<f(2)可化为f(5)<f(2).又f(2)=4+4+3=11,所以由5a+1<11可得a<2,故选B.15.B解析由f(-x)=2-f(x),得f(x)的图象关于点(0,1)对称.而y==1+的图象是由y=的图象向上平移一个单位长度得到的,故y=的图象关于点(0,1)对称.则函数y=与y=f(x)图象的交点也关于点(0,1)对称,且每一组对称点(x i,y i),(x'i,y'i)(i=1,2,…,m)满足x i+x'i=0,y i+y'i=2,所以(x i+y i)=x i+y i=0+2=m.16解析由题意知函数f(x)在区间(0,+∞)上单调递减,又f(x)是偶函数,则不等式f(2|a-1|)>f(-)可化为f(2|a-1|)>f(),则2|a-1|<,|a-1|<,解得<a<故答案为17.-10解析∵f=f,∴f=f,=-a+1,易求得3a+2b=-2.又f(1)=f(-1),∴-a+1=,即2a+b=0,∴a=2,b=-4,∴a+3b=-10.18.①④解析对①,设g(x)=e x·2-x,则g'(x)=e x=e x·2-x>0,∴g(x)在R上单调递增,具有M性质;对②,设g(x)=e x·3-x,则g'(x)=e x=e x·3-x<0,∴g(x)在R上单调递减,不具有M性质;对③,设g(x)=e x·x3,则g'(x)=e x·x2(x+3),令g'(x)=0,得x1=-3,x2=0,∴g(x)在区间(-∞,-3)上单调递减,在区间(-3,+∞)上单调递增,不具有M性质;对④,设g(x)=e x(x2+2),则g'(x)=e x(x2+2x+2),∵x2+2x+2=(x+1)2+1>0,∴g'(x)>0,∴g(x)在R上单调递增,具有M性质.故填①④.19.解 (1)∵f(x)=e x-,且y=e x是增函数,y=-是增函数,∴f(x)是增函数.∵f(x)的定义域为R,且f(-x)=e-x-e x=-f(x),∴f(x)是奇函数.(2)由(1)知f(x)是增函数且为奇函数.∵f(x-t)+f(x2-t2)≥0对x∈R恒成立,∴f(x-t)≥f(t2-x2),∴t2-x2≤x-t,∴x2+x≥t2+t对x∈R恒成立.又对一切x∈R恒成立,0,∴t=-即存在实数t=-,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立.。
2019年高考数学(理科,天津课标版)二轮复习专题能力训练 Word版含答案12

专题能力训练12 数列的通项与求和一、能力突破训练1.已知等差数列{a n }的前n 项和为S n ,若a 1=2,a 4+a 10=28,则S 9=( ) A.45B.90C.120D.752.已知数列{a n }是等差数列,满足a 1+2a 2=S 5,下列结论错误的是( ) A.S 9=0B.S 5最小C.S 3=S 6D.a 5=03.已知数列{a n }的前n 项和S n =n 2-2n-1,则a 3+a 17=( ) A.15B.17C.34D.3984.已知函数f (x )满足f (x+1)=32+f (x )(x ∈R ),且f (1)=52,则数列{f (n )}(n ∈N *)前20项的和为( ) A.305B.315C.325D.3355.已知数列{a n },构造一个新数列a 1,a 2-a 1,a 3-a 2,…,a n -a n-1,…,此数列是首项为1,公比为13的等比数列,则数列{a n }的通项公式为( )A.a n =32−32×(13)n,n ∈N *B.a n =32+32×(13)n,n ∈N *C.a n ={1,n =1,32+32×(13)n ,n >2,且n ∈N *D.a n =1,n ∈N *6.已知数列{a n }满足a 1=1,a n -a n+1=na n a n+1(n ∈N *),则a n = .7.(2018全国Ⅰ,理14)记S n 为数列{a n }的前n 项和.若S n =2a n +1,则S 6= .8.已知S n 是等差数列{a n }的前n 项和,若a 1=-2 017,S 2 0142 014−S2 0082 008=6,则S 2 017= . 9.已知在数列{a n }中,a 1=1,a n+1=a n +2n+1,且n ∈N *. (1)求数列{a n }的通项公式;(2)令b n =2n+1a n a n+1,数列{b n }的前n 项和为T n .如果对于任意的n ∈N *,都有T n >m ,求实数m 的取值范围.10.已知数列{a n}的前n项和为S n,且a1=0,对任意n∈N*,都有na n+1=S n+n(n+1).(1)求数列{a n}的通项公式;(2)若数列{b n}满足a n+log2n=log2b n,求数列{b n}的前n项和T n.11.设数列{a n}的前n项和为S n.已知2S n=3n+3.(1)求{a n}的通项公式;(2)若数列{b n}满足a n b n=log3a n,求{b n}的前n项和T n.二、思维提升训练12.给出数列11,12,21,13,22,31,…,1k ,2k -1,…,k1,…,在这个数列中,第50个值等于1的项的序号是( ) A.4 900B.4 901C.5 000D.5 00113.设S n 是数列{a n }的前n 项和,且a 1=-1,a n+1=S n S n+1,则S n = . 14.已知等差数列{a n }的公差为2,其前n 项和S n =pn 2+2n (n ∈N *). (1)求p 的值及a n ;(2)若b n =2(2n -1)a n,记数列{b n }的前n 项和为T n ,求使T n >910成立的最小正整数n 的值.15.已知数列{a n }满足a n+2=qa n (q 为实数,且q ≠1),n ∈N *,a 1=1,a 2=2,且a 2+a 3,a 3+a 4,a 4+a 5成等差数列. (1)求q 的值和{a n }的通项公式;(2)设b n =log 2a2n a 2n -1,n ∈N *,求数列{b n }的前n 项和.16.设数列A:a1,a2,…,a N(N≥2).如果对小于n(2≤n≤N)的每个正整数k都有a k<a n,则称n是数列A的一个“G时刻”.记G(A)是数列A的所有“G时刻”组成的集合.(1)对数列A:-2,2,-1,1,3,写出G(A)的所有元素;(2)证明:若数列A中存在a n使得a n>a1,则G(A)≠⌀;(3)证明:若数列A满足a n-a n-1≤1(n=2,3,…,N),则G(A)的元素个数不小于a N-a1.专题能力训练12 数列的通项与求和一、能力突破训练1.B 解析 因为{a n }是等差数列,设公差为d ,所以a 4+a 10=a 1+3d+a 1+9d=2a 1+12d=4+12d=28,解得d=2.所以S 9=9a 1+9×82d=18+36×2=90.故选B . 2.B 解析 由题设可得3a 1+2d=5a 1+10d ⇒2a 1+8d=0,即a 5=0,所以D 中结论正确.由等差数列的性质可得a 1+a 9=2a 5=0,则S 9=9(a 1+a 9)2=9a 5=0,所以A 中结论正确. S 3-S 6=3a 1+3d-6a 1-15d=-3(a 1+4d )=-3a 5=0,所以C 中结论正确. B 中结论是错误的.故选B . 3.C 解析 ∵S n =n 2-2n-1,∴a 1=S 1=12-2-1=-2.当n ≥2时,a n =S n -S n-1 =n 2-2n-1-[(n-1)2-2(n-1)-1] =n 2-(n-1)2+2(n-1)-2n-1+1 =n 2-n 2+2n-1+2n-2-2n=2n-3.∴a n ={-2,n =1,2n -3,n ≥2.∴a 3+a 17=(2×3-3)+(2×17-3)=3+31=34.4.D 解析 ∵f (1)=52,f (2)=32+52,f (3)=32+32+52,…… f (n )=3+f (n-1),∴{f (n )}是以52为首项,32为公差的等差数列. ∴S 20=20×52+20(20-1)2×32=335. 5.A 解析 因为数列a 1,a 2-a 1,a 3-a 2,…,a n -a n-1,…是首项为1,公比为13的等比数列,所以a n -a n-1=(13)n -1,n ≥2.所以当n ≥2时,a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n-1)=1+13+(13)2+…+(13)n -1=1-(13)n1-13=32−32×(13)n . 又当n=1时,a n =32−32×(13)n=1, 则a n =32−32×(13)n,n ∈N *.6.2n 2-n+2 解析 因为a n -a n+1=na n a n+1,所以a n -an+1a n a n+1=1a n+1−1a n =n ,1a n=(1a n -1a n -1)+(1a n -1-1a n -2)+…+(1a 2-1a 1)+1a 1=(n-1)+(n-2)+…+3+2+1+1a 1=(n -1)(n -1+1)2+1=n 2-n+22(n ≥2). 所以a n =2n 2-n+2(n ≥2).又a 1=1也满足上式,所以a n =2n 2-n+2. 7.-63 解析 ∵S n =2a n +1,①∴S n-1=2a n-1+1(n ≥2).②①-②,得a n =2a n -2a n-1,即a n =2a n-1(n ≥2).又S 1=2a 1+1,∴a 1=-1.∴{a n }是以-1为首项,2为公比的等比数列,则S 6=-1(1-26)1-2=-63.8.-2 017 解析 ∵S n 是等差数列{a n }的前n 项和,∴{S n n}是等差数列,设其公差为d.∵S 2 0142 014−S2 0082 008=6,∴6d=6,d=1. ∵a 1=-2 017,∴S 11=-2 017. ∴S nn=-2 017+(n-1)×1=-2 018+n. ∴S 2 017=(-2 018+2 017)×2 017=-2 017.故答案为-2 017. 9.解 (1)∵a n+1=a n +2n+1,∴a n+1-a n =2n+1,∴a n-a n-1=2n-1,∴a n=a1+(a2-a1)+(a3-a2)+…+(a n-a n-1)=1+3+5+…+(2n-1)=n(1+2n-1)2=n2.(2)由(1)知,b n=2n+1n n+1=2n+1n2(n+1)2=12−1(n+1)2,∴T n=(112-122)+(122-132)+…+[1n2-1(n+1)2]=1-1(n+1)2,∴数列{T n}是递增数列,∴最小值为1-1(1+1)2=34,只需要34>m,∴m的取值范围是(-∞,3).10.解(1)(方法一)∵na n+1=S n+n(n+1),∴当n≥2时,(n-1)a n=S n-1+n(n-1),两式相减,得na n+1-(n-1)a n=S n-S n-1+n(n+1)-n(n-1),即na n+1-(n-1)a n=a n+2n,得a n+1-a n=2.当n=1时,1×a2=S1+1×2,即a2-a1=2.∴数列{a n}是以0为首项,2为公差的等差数列.∴a n=2(n-1)=2n-2.(方法二)由na n+1=S n+n(n+1),得n(S n+1-S n)=S n+n(n+1),整理,得nS n+1=(n+1)S n+n(n+1),两边同除以n(n+1),得S n+1n+1−S nn=1.∴数列{S nn }是以S11=0为首项,1为公差的等差数列,∴S nn=0+n-1=n-1.∴S n=n(n-1).当n≥2时,a n=S n-S n-1=n(n-1)-(n-1)(n-2)=2n-2.又a1=0适合上式,∴数列{a n}的通项公式为a n=2n-2.(2)∵a n +log 2n=log 2b n ,∴b n =n ·2a n =n·22n-2=n·4n-1.∴T n =b 1+b 2+b 3+…+b n-1+b n =40+2×41+3×42+…+(n-1)×4n-2+n×4n-1,① 4T n =41+2×42+3×43+…+(n-1)×4n-1+n×4n , ②由①-②,得-3T n =40+41+42+…+4n-1-n×4n=1-4n 1-4-n×4n =(1-3n )×4n-13. ∴T n =19[(3n-1)×4n +1].11.解 (1)因为2S n =3n +3,所以2a 1=3+3,故a 1=3. 当n>1时,2S n-1=3n-1+3,此时2a n =2S n -2S n-1=3n -3n-1=2×3n-1,即a n =3n-1, 所以a n ={3,n =1,3n -1,n >1.(2)因为a n b n =log 3a n , 所以b 1=13,当n>1时,b n =31-n log 33n-1=(n-1)·31-n . 所以T 1=b 1=13;当n>1时,T n =b 1+b 2+b 3+…+b n =1+(1×3-1+2×3-2+…+(n-1)×31-n ), 所以3T n =1+(1×30+2×3-1+…+(n-1)×32-n ),两式相减,得2T n =23+(30+3-1+3-2+…+32-n )-(n-1)×31-n =23+1-31-n 1-3-1-(n-1)×31-n=136−6n+32×3n, 所以T n =1312−6n+34×3n. 经检验,当n=1时也适合. 综上可得T n =1312−6n+34×3n. 二、思维提升训练12.B 解析 根据条件找规律,第1个1是分子、分母的和为2,第2个1是分子、分母的和为4,第3个1是分子、分母的和为6,……第50个1是分子、分母的和为100,而分子、分母的和为2的有1项,分子、分母的和为3的有2项,分子、分母的和为4的有3项,……分子、分母的和为99的有98项,分子、分母的和为100的项依次是:1,2,3,…,50,51,…,99,第50个1是其中第50项,在数列中的序号为1+2+3+…+98+50=98(1+98)2+50=4 901. 13.-1n解析 由a n+1=S n+1-S n =S n S n+1,得1S n−1S n+1=1,即1S n+1−1S n =-1,则{1S n }为等差数列,首项为1S 1=-1,公差为d=-1,∴1S n =-n ,∴S n =-1n. 14.解 (1)(方法一)∵{a n }是等差数列,∴S n =na 1+n (n -1)2d=na 1+n (n -1)2×2=n 2+(a 1-1)n. 又由已知S n =pn 2+2n ,∴p=1,a 1-1=2,∴a 1=3,∴a n =a 1+(n-1)d=2n+1,∴p=1,a n =2n+1.(方法二)由已知a 1=S 1=p+2,S 2=4p+4, 即a 1+a 2=4p+4,∴a 2=3p+2. 又等差数列的公差为2,∴a 2-a 1=2,∴2p=2,∴p=1,∴a 1=p+2=3,∴a n =a 1+(n-1)d=2n+1,∴p=1,a n =2n+1.(方法三)当n ≥2时,a n =S n -S n-1=pn 2+2n-[p (n-1)2+2(n-1)]=2pn-p+2,∴a 2=3p+2,由已知a 2-a 1=2,∴2p=2,∴p=1, ∴a 1=p+2=3,∴a n =a 1+(n-1)d=2n+1, ∴p=1,a n =2n+1.(2)由(1)知b n =2(2n -1)(2n+1)=12n -1−12n+1,∴T n =b 1+b 2+b 3+…+b n=(11-13)+(13-15)+(15-17)+…+(12n -1-12n+1)=1-12n+1=2n2n+1.∵T n >910,∴2n2n+1>910, ∴20n>18n+9,即n>92. ∵n ∈N *,∴使T n >910成立的最小正整数n 的值为5.15.解 (1)由已知,有(a 3+a 4)-(a 2+a 3)=(a 4+a 5)-(a 3+a 4),即a 4-a 2=a 5-a 3,所以a 2(q-1)=a 3(q-1).又因为q ≠1,故a 3=a 2=2,由a 3=a 1·q ,得q=2. 当n=2k-1(k ∈N *)时,a n =a 2k-1=2k-1=2n -12; 当n=2k (k ∈N *)时,a n =a 2k =2k =2n2.所以,{a n }的通项公式为a n ={2n -12,n 为奇数,2n 2,n 为偶数.(2)由(1)得b n =log 2a 2n a 2n -1=n 2n -1.设{b n }的前n 项和为S n ,则S n =1×120+2×121+3×122+…+(n-1)×12n -2+n ×12n -1,12S n =1×121+2×122+3×123+…+(n-1)×12n -1+n ×12n , 上述两式相减,得12S n =1+12+122+…+12n -1−n2n =1-12n 1-12−n 2n =2-22n −n2n, 整理得,S n =4-n+22n -1.所以,数列{b n }的前n 项和为4-n+22n -1,n ∈N*.16.(1)解 G (A )的元素为2和5. (2)证明 因为存在a n 使得a n >a 1,所以{i ∈N *|2≤i ≤N ,a i >a 1}≠⌀.记m=min{i ∈N *|2≤i ≤N ,a i >a 1}, 则m ≥2,且对任意正整数k<m ,a k ≤a 1<a m . 因此m ∈G (A ).从而G (A )≠⌀. (3)证明 当a N ≤a 1时,结论成立.以下设a N >a 1. 由(2)知G (A )≠⌀.设G (A )={n 1,n 2,…,n p },n 1<n 2<…<n p . 记n 0=1.则a n 0<a n 1<a n 2<…<a n p .对i=0,1,…,p ,记G i ={k ∈N *|n i <k ≤N ,a k >a n i }. 如果G i ≠⌀,取m i =min G i ,则对任何1≤k<m i,a k≤a ni <a mi.从而m i∈G(A)且m i=n i+1,又因为n p是G(A)中的最大元素,所以G p=⌀.从而对任意n p≤k≤N,a k≤a np ,特别地,a N≤a np.对i=0,1,…,p-1,a ni+1-1≤a ni.因此a ni+1=a ni+1-1+(a ni+1−a ni+1-1)≤a ni+1.所以a N-a1≤a np -a1=∑i=1p(a ni−a ni-1)≤p.因此G(A)的元素个数p不小于a N-a1.。
(新课标)天津市2019年高考数学二轮复习 专题能力训练5 基本初等函数、函数的图象和性质 理

专题能力训练5基本初等函数、函数的图象和性质一、能力突破训练1.下列函数在其定义域上既是奇函数又是减函数的是 ()A.f(x)=-x|x|B.f(x)=x sin xC.f(x)=D.f(x)=2.已知a=21.2,b=,c=2log52,则a,b,c的大小关系为()A.c<b<aB.c<a<bC.b<a<cD.b<c<a3.(2018全国Ⅲ,理7)函数y=-x4+x2+2的图象大致为()4.函数f(x)在区间(-∞,+∞)内单调递减,且为奇函数,若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是()A.[-2,2]B.[-1,1]C.[0,4]D.[1,3]5.已知函数f(x)=且f(a)=-3,则f(6-a)=()A.-B.-C.-D.-6.(2018全国Ⅱ,理11)已知f(x)是定义域为(-∞,+∞)内的奇函数,满足f(1-x)=f(1+x),若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=()A.-50B.0C.2D.507.已知a>b>1,若log a b+log b a=,a b=b a,则a= ,b= .8.若函数f(x)=x ln(x+)为偶函数,则a= .9.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)内单调递增.若实数a满足f(log2a)+f(lo a)≤2f(1),则a的取值范围是.10.设奇函数y=f(x)(x∈R),满足对任意t∈R都有f(t)=f(1-t),且当x∈时,f(x)=-x2,则f(3)+f的值等于.11.设函数f(x)=的最大值为M,最小值为m,则M+m= .12.若不等式3x2-log a x<0在x∈内恒成立,求实数a的取值范围.二、思维提升训练13.函数y=的图象大致为()14.已知f(x)是定义在R上的偶函数,当x>0时,f(x)=若f(-5)<f(2),则a 的取值范围为()A.(-∞,1)B.(-∞,2)C.(-2,+∞)D.(2,+∞)15.已知函数f(x)(x∈R)满足f(-x)=2-f(x),若函数y=与y=f(x)图象的交点为(x1,y1),(x2,y2),…,(x m,y m),则(x i+y i)=()A.0B.mC.2mD.4m16.已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增.若实数a满足f(2|a-1|)>f(-),则a的取值范围是.17.设f(x)是定义在R上且周期为2的函数,在区间[-1,1]上,f(x)=其中a,b ∈R.若f=f,则a+3b的值为.18.若函数e x f(x)(e=2.718 28…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质.下列函数中所有具有M性质的函数的序号为.①f(x)=2-x②f(x)=3-x③f(x)=x3④f(x)=x2+219.已知函数f(x)=e x-e-x(x∈R,且e为自然对数的底数).(1)判断函数f(x)的奇偶性与单调性.(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立?若存在,求出t;若不存在,请说明理由.专题能力训练5基本初等函数、函数的图象和性质一、能力突破训练1.A解析函数f(x)=在其定义域上既是奇函数又是减函数,故选A.2.A解析∵b==20.8<21.2=a,且b>1,又c=2log52=log54<1,∴c<b<a.3.D解析当x=0时,y=2>0,排除A,B;当x=时,y=-+2>2.排除C.故选D.4.D解析因为f(x)为奇函数,所以f(-1)=-f(1)=1,于是-1≤f(x-2)≤1等价于f(1)≤f(x-2)≤f(-1).又f(x)在区间(-∞,+∞)单调递减,所以-1≤x-2≤1,即1≤x≤3.所以x的取值范围是[1,3].5.A解析∵f(a)=-3,∴当a≤1时,f(a)=2a-1-2=-3,即2a-1=-1,此等式显然不成立.当a>1时,f(a)=-log2(a+1)=-3,即a+1=23,解得a=7.∴f(6-a)=f(-1)=2-1-1-2=-2=-6.C解析∵f(-x)=f(2+x)=-f(x),∴f(x+4)=f[(x+2)+2]=-f(x+2)=f(x).∴f(x)的周期为4.∵f(x)为R上的奇函数,∴f(0)=0.∵f(2)=f(1+1)=f(1-1)=f(0)=0,f(3)=f(-1)=-f(1)=-2,f(4)=f(0),∴f(1)+f(2)+f(3)+f(4)=0.∴f(1)+f(2)+…+f(50)=f(49)+f(50)=f(1)+f(2)=2.7.42解析设log b a=t,由a>b>1,知t>1.由题意,得t+,解得t=2,则a=b2.由a b=b a,得b2b=,即得2b=b2,即b=2,∴a=4.8.1解析∵f(x)是偶函数,∴f(-1)=f(1).又f(-1)=-ln(-1+)=ln,f(1)=ln(1+),因此ln(+1)-ln a=ln(+1),于是ln a=0,∴a=1.9解析由题意知a>0,又lo a=log2a-1=-log2a.∵f(x)是R上的偶函数,∴f(log2a)=f(-log2a)=f(lo a).∵f(log2a)+f(lo a)≤2f(1),∴2f(log2a)≤2f(1),即f(log2a)≤f(1).又f(x)在[0,+∞)上单调递增,∴|log2a|≤1,-1≤log2a≤1,∴a10.-解析根据对任意t∈R都有f(t)=f(1-t)可得f(-t)=f(1+t),即f(t+1)=-f(t),进而得到f(t+2)=-f(t+1)=-[-f(t)]=f(t),得函数y=f(x)的一个周期为2,则f(3)=f(1)=f(0+1)=-f(0)=0,f=f=-,所以f(3)+f=0+=-11.2解析f(x)==1+,设g(x)=,则g(-x)=-g(x),故g(x)是奇函数.由奇函数图象的对称性知g(x)max+g(x)min=0,则M+m=[g(x)+1]max+[g(x)+1]min=2+g(x)max+g(x)min=2.12.解由题意知3x2<log a x在x内恒成立.在同一平面直角坐标系内,分别作出函数y=3x2和y=log a x的图象.观察两函数图象,当x时,若a>1,函数y=log a x的图象显然在函数y=3x2图象的下方,所以不成立;当0<a<1时,由图可知,y=log a x的图象必须过点或在这个点的上方,则log a,所以a,所以a<1.综上,实数a的取值范围为a<1.二、思维提升训练13.D解析y=为奇函数,排除A项;y=cos 6x有无穷多个零点,排除C项;当x在原点右侧附近时,可保证2x-2-x>0,cos 6x>0,则此时y>0,故选D.14.B解析因为f(x)是定义在R上的偶函数,所以f(-5)=f(5)=5a+log55=1+5a,则不等式f(-5)<f(2)可化为f(5)<f(2).又f(2)=4+4+3=11,所以由5a+1<11可得a<2,故选B.15.B解析由f(-x)=2-f(x),得f(x)的图象关于点(0,1)对称.而y==1+的图象是由y=的图象向上平移一个单位长度得到的,故y=的图象关于点(0,1)对称.则函数y=与y=f(x)图象的交点也关于点(0,1)对称,且每一组对称点(x i,y i),(x'i,y'i)(i=1,2,…,m)满足x i+x'i=0,y i+y'i=2,所以(x i+y i)=x i+y i=0+2=m.16解析由题意知函数f(x)在区间(0,+∞)上单调递减,又f(x)是偶函数,则不等式f(2|a-1|)>f(-)可化为f(2|a-1|)>f(),则2|a-1|<,|a-1|<,解得<a<故答案为17.-10解析∵f=f,∴f=f,=-a+1,易求得3a+2b=-2.又f(1)=f(-1),∴-a+1=,即2a+b=0,∴a=2,b=-4,∴a+3b=-10.18.①④解析对①,设g(x)=e x·2-x,则g'(x)=e x=e x·2-x>0,∴g(x)在R上单调递增,具有M性质;对②,设g(x)=e x·3-x,则g'(x)=e x=e x·3-x<0,∴g(x)在R上单调递减,不具有M性质;对③,设g(x)=e x·x3,则g'(x)=e x·x2(x+3),令g'(x)=0,得x1=-3,x2=0,∴g(x)在区间(-∞,-3)上单调递减,在区间(-3,+∞)上单调递增,不具有M性质;对④,设g(x)=e x(x2+2),则g'(x)=e x(x2+2x+2),∵x2+2x+2=(x+1)2+1>0,∴g'(x)>0,∴g(x)在R上单调递增,具有M性质.故填①④.19.解 (1)∵f(x)=e x-,且y=e x是增函数,y=-是增函数,∴f(x)是增函数.∵f(x)的定义域为R,且f(-x)=e-x-e x=-f(x),∴f(x)是奇函数.(2)由(1)知f(x)是增函数且为奇函数.∵f(x-t)+f(x2-t2)≥0对x∈R恒成立,∴f(x-t)≥f(t2-x2),∴t2-x2≤x-t,∴x2+x≥t2+t对x∈R恒成立.又对一切x∈R恒成立,0,∴t=-即存在实数t=-,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立.。
2019年高考数学(理科)二轮复习(天津课标版)专题能力训练Word版含答案23

专题能力训练23不等式选讲(选修4—5)能力突破训练1.不等式|x-2|+|4-x|<3的解集是()A.3,9B.3,9C.(1,5)D.(3,9)2.已知不等式|x-2|>1的解集与关于x的不等式x2+ax+b>0的解集相同,则a,b的值为()A.a=1,b=3B.a=3,b=1C.a=-4,b=3D.a=3,b=-43.“a>2”是“关于x的不等式|x+1|+|x-1|≤a的解集非空”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件4.不等式x+3>|2x-1|的解集为.5.若关于x的不等式|x+1|+|x-3|≥|m-1|恒成立,则m的取值范围为.6.设函数f(x)=|x-4|+|x-3|,则f(x)的最小值m=.7.若函数f(x)=|x+2|+|x-m|-4的定义域为R,则实数m的取值范围为.8.使关于x的不等式|x+1|+k<x有解的实数k的取值范围是.思维提升训练9.不等式1<|x+1|<3的解集为()A.(0,2)B.(-2,0)∪(2,4)C.(-4,0)D.(-4,-2)∪(0,2) 10.已知不等式|y+4|-|y|≤2x +a 2x 对任意的实数x ,y 成立,则正实数a 的最小值为( )A.1B.2C.3D.4 11.已知关于x 的不等式|2x-m|≤1的整数解有且仅有一个值为2,则整数m= .12.若不等式|x+a|≤2在x ∈[1,2]时恒成立,则实数a 的取值范围是 .13.已知函数f (x )=|x-2|-|x-5|,则不等式f (x )≥x 2-8x+15的解集为 .14.若不等式x 2+25+|x 3-5x 2|≥ax 在[1,12]上恒成立,则实数a 的取值范围是 .15.设函数f (x )=|x-4|+|x-a|(a<4),(1)若f (x )的最小值为3,则a= ;(2)不等式f (x )≥3-x 的解集为 .##专题能力训练23 不等式选讲(选修4—5)能力突破训练1.B 解析 原不等式可化为 x <2,2-x +4-x <3或 2≤x <4,x -2+4-x <3或 x ≥4,x -2+x -4<3,解得32<x<2或2≤x<4或4≤x<92,即3<x<9.故不等式的解集为 x 3<x <9 . 2.C 解析 解不等式|x-2|>1得x<1或x>3,所以x 2+ax+b=0的两个根为1和3,由根与系数的关系知a=-4,b=3.3.A解析∵|x+1|+|x-1|表示在数轴上到-1,1两点距离和大于等于2,∴a>2时,不等式|x+1|+|x-1|≤a 非空.而当a=2时|x+1|+|x-1|≤a也非空.∴必要性不成立,故选A.4. x-2<x<4解析不等式等价于2x-1≥0,x+3>2x-1或2x-1<0,x+3>1-2x,解得1≤x<4或-2<x<1,故不等式解集为 x-23<x<4.5.[-3,5]解析∵|x+1|+|x-3|≥|(x+1)-(x-3)|=4,∴不等式|x+1|+|x-3|≥|m-1|恒成立,只需|m-1|≤4,即-3≤m≤5.6.1解析方法一:f(x)=|x-4|+ x-3≥|(x-4)-(x-3)|=1,故函数f(x)的最小值为1,即m=1.方法二:f(x)=2x-7,x≥4 1,3≤x<4, 7-2x,x<3.当x≥4时,f(x)≥1;当x<3时,f(x)>1;当3≤x<4时,f(x)=1,故函数f(x)的最小值为1.所以m=1.7.(-∞,-6]∪[2,+∞)解析根据题意,不等式|x+2|+|x-m|-4≥0恒成立,所以(|x+2|+|x-m|-4)min≥0.又|x+2|+|x-m|-4≥|m+2|-4,所以|m+2|-4≥0⇒m≤-6或m≥2.8.(-∞,-1)解析∵|x+1|+k<x⇔k<x-|x+1|,又x-|x+1|=2x+1,x<-1, -1,x≥-1,∴x-|x+1|的最大值为-1.∴k<-1.思维提升训练9.D解析由|x+1|>1,|x+1|<3⇒x+1>1或x+1<-1,-3<x+1<3⇒x>0或x<-2,-4<x<2,故-4<x<-2或0<x<2.10.D11.4解析由|2x-m|≤1,得m-12≤x≤m+12.∵不等式的整数解为2,∴m-1≤2≤m+1⇒3≤m≤5.又不等式仅有一个整数解2,∴m=4.12.[-3,0]解析由题意得-2≤x+a≤2,-2-x≤a≤2-x,所以(-2-x)max≤a≤(2-x)min,因为x∈[1,2],所以-3≤a≤0.13.{x|5-3≤x≤6}解析原不等式可化为x<2,2-x-(5-x)≥x2-8x+15或2≤x<5,x-2-(5-x)≥x2-8x+15或x≥5,x-2-(x-5)≥x2-8x+15,解得x∈⌀或5-3≤x<5或5≤x≤6,故5-≤x≤6,即不等式的解集为{x|5-≤x≤6}.14.(-∞,10]15.(1)1(2)R解析(1)因为|x-4|+|x-a|≥|(x-4)-(x-a)|=|a-4|.又因为a<4,所以当且仅当a≤x≤4时等号成立.故|a-4|=3,即a=1.(2)不等式f(x)≥3-x即不等式|x-4|+|x-a|≥3-x(a<4),①当x<a时,原不等式可化为4-x+a-x≥3-x,即x≤a+1.所以,当x<a时,原不等式成立.②当a≤x≤4时,原不等式可化为4-x+x-a≥3-x.即x≥a-1.所以,当a≤x≤4时,原不等式成立.③当x>4时,原不等式可化为x-4+x-a≥3-x.即x≥a+7.由于a<4时4>a+7.所以,当x>4时,原不等式成立.综合①②③可知,不等式f(x)≥3-x的解集为R.。
2019年高考数学(理科,天津课标版)二轮复习思想方法训练 Word版含答案1

1
把 C(2,4)代入抛物线方程得 p=2,所以曲线段 OC 的方程为 y=x2(x∈[0,2]).
设 P(x,x2)(x∈[0,2])在 OC 上,过点 P 作 PQ⊥AB 于点 Q,PN⊥BC 于点 N,
故|PQ|=2+x,|PN|=4-x2,则矩形商业楼区的面积 S=(2+x)(4-x2)(x∈[0,2]).
D.
������
4.已知{an}是等差数列,a1=1,公差 d≠0,Sn 为其前 n 项和,若 a1,a2,a5 成等比数列,则 S8 的值为( )
A.16
B.32
C.64
D.62
5.已知函数 f(x)=ax+b(a>0,a≠1)的定义域和值域都是[-1,0],则 a+b= .
6.已知直线 y=a 交抛物线 y=x2 于 A,B 两点.若该抛物线上存在点 C,使得∠ACB 为直角,则 a 的取值范 围为 .
= (1 + ������2)[(������1 + ������2)2 - 4������1������2]
2 (1 + ������2)(4 + 6������2)
=
1 + 2������2
.
因为点 A(2,0)到直线
y=k(x-1)的距离
d=
|������|
1 + ������2,所以△AMN
������ = - 2.
1
3.
综上,a+b=2+(-2)=-2
6.[1,+∞) 解析 以 AB 为直径的圆的方程为 x2+(y-a)2=a,
{ ������ = ������2,
由 ������2 + (������ - ������)2 = ������,得 y2+(1-2a)y+a2-a=0.
2019年高考数学(理科,天津课标版)二轮复习专题能力训练 Word版含答案22

专题能力训练22 坐标系与参数方程(选修4—4)能力突破训练1.在直角坐标系xOy 中,已知曲线C 的参数方程是(α为参数),若以O 为极点,x 轴的非{x =sinα,y =cosα+1负半轴为极轴,则曲线C 的极坐标方程可写为 .2.已知曲线C 的参数方程为(t 为参数),C 在点(1,1)处的切线为l ,以坐标原点为极点,x 轴{x =2cost ,y =2sint 的正半轴为极轴建立极坐标系,则l 的极坐标方程为 .3.已知两曲线参数方程分别为C 1:(0≤θ<π)和C 2:(t ∈R ),它们的交点坐标为 {x =5cosθ,y =sinθ{x =54t 2,y =t .4.若直线(t 为参数)与圆(φ为参数)相切,则此直线的倾斜角α= {x =tcosα,y =tsinα{x =4+2cosφ,y =2sinφ.5.以直角坐标系的原点为极点,x 轴的非负半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为θ=(ρ∈R ),它与曲线(α为参数)相交于两点A 和B ,则|AB|= π4{x =1+2cosα,y =2+2sinα.6.若直线l :(t 为参数)与圆C :ρ=2cos θ相切,则k= . {x =t ,y =3+kt 7.已知圆C 1的参数方程为(φ为参数),以坐标原点O 为极点,x 轴的非负半轴为极轴建立极{x =cosφ,y =sinφ坐标系,圆C 2的极坐标方程为ρ=2cos.(θ+π3)(1)圆C 1的参数方程化为普通方程为 ,圆C 2的极坐标方程化为直角坐标方程为 ;(2)圆C 1,C 2的公共弦长为 . 8.在极坐标系中,点到直线ρsin =1的距离是 .(2,π6)(θ-π6)思维提升训练9.已知曲线C 1的参数方程是(t为参数).以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲{x =t ,y =3t 线C 2的极坐标方程是ρ=2,则C 1与C 2交点的直角坐标为 .10.在直角坐标系xOy 中,直线l 的参数方程为(t为参数).在极坐标系(与直角坐标系xOy {x =2-22t ,y =3+22t取相同的长度单位,且以原点O 为极点,以x 轴非负半轴为极轴)中,圆C 的方程为ρ=2sin θ.3(1)圆C 的直角坐标方程为 ;(2)设圆C 与直线l 交于点A ,B ,若点P 的坐标为(2,),则|PA|+|PB|= .311.已知曲线C 的极坐标方程是ρ=1,以极点为原点,极轴为x 轴的非负半轴建立平面直角坐标系,直线l 的参数方程为(t为参数).{x =1+t2,y =2+3t (1)直线l 的普通方程与曲线C 的直角坐标方程分别为 ;(2)设曲线C 经过伸缩变换得到曲线C',设曲线C'上任意一点为M (x ,y ),则x+2y 的最小值{x '=3x ,y '=y 3为 .12.已知圆C 的极坐标方程为ρ=2cos θ,直线l 的参数方程为(t为参数),点A 的极坐标为{x =12+32t ,y =12+12t,设直线l 与圆C 交于点P ,Q.(22,π4)(1)圆C 的直角坐标方程为 ; (2)|AP|·|AQ|= .##专题能力训练22 坐标系与参数方程(选修4—4)能力突破训练1.ρ=2sin θ 解析 依题意知,曲线C :x 2+(y-1)2=1,即x 2+y 2-2y=0,所以(ρcos θ)2+(ρsin θ)2-2ρsin θ=0.化简得ρ=2sin θ.2.ρsin 解析 ∵曲线C 的参数方程为(t 为参数),(θ+π4)=2{x =2cost ,y =2sint∴其普通方程为x 2+y 2=2.又∵点(1,1)在曲线C 上,∴切线l 的斜率k=-1.故l 的方程为x+y-2=0,化为极坐标方程为ρcos θ+ρsin θ=2,即ρsin(θ+π4)= 2.3 解析 消去参数θ得曲线方程C 1为+y 2=1(0≤y ≤1),表示椭圆的一部分.消去参数t 得曲.(1,255)x 25线方程C 2为y 2=x ,表示抛物线,可得两曲线有一个交点,联立两方程,解得故交点45{x 25+y 2=1,y 2=45x ,{x =1,y =255,坐标为(1,25).4 解析 由题意得直线y=x tan α,圆:(x-4)2+y 2=4.如图,sin α=,∴α=.π6或5π624=12π6或5π6.5 解析 ∵极坐标方程θ=(ρ∈R )对应的平面直角坐标方程为y=x ,.14π4曲线(α为参数)的平面直角坐标方程为(x-1)2+(y-2)2=4,圆心(1,2),r=2,{x =1+2cosα,y =2+2sinα∴圆心到直线y=x 的距离d=,|AB|=2=2|1-2|2=22r 2-d 24-12=14.6.-337.(1)x 2+y 2=1 =1 (2)(x -12)2+(y +3)23解析 (1)由得x 2+y 2=1.{x =cosφ,y =sinφ,又∵ρ=2cos=cos θ-sin θ,(θ+π3)3∴ρ2=ρcos θ-sin θ.3ρ∴x 2+y 2-x+y=0,3即=1.(x -12)2+(y +3)2(2)由圆心距d==1<2,得两圆相交.(0-12)2+(0+32)2由{x 2+y 2=1,x 2+y 2-x +3y =0,得A (1,0),B(-12,-3).∴|AB|=(1+12)2+(0+32)2= 3.8.1 解析 ρsin==1,(θ-π6)ρ(sinθcos π6-sin π6cosθ)因为在极坐标系中ρcos θ=x ,ρsin θ=y ,所以直线可化为x-y+2=0.3同理点可化为(,1),(2,π6)3所以点到直线距离为d==1.|3-3+2|3+1思维提升训练9.(,1) 解析 由曲线C 1的参数方程3{x =t ,y =3t ,得y=x (x ≥0),①33曲线C 2的极坐标方程为ρ=2,可得方程x 2+y 2=4,②由①②联立解得故C 1与C 2交点的直角坐标为(,1).{x =3,y =1,310.(1)x 2+(y-)2=3 (2)2 解析 (1)由ρ=2sin θ,得x 2+(y-)2=3,3233故圆C 的直角坐标方程为x 2+(y-)2=3.3(2)将l 的参数方程代入圆C 的直角坐标方程,得=3,(2-22t )2+(22t )2即t 2-2t+1=0.由于Δ>0,故可设t 1,t 2是上述方程的两实根.2所以t 1+t 2=2 2.故由上式及t 的几何意义,得|PA|+|PB|=|t 1|+|t 2|=t 1+t 2=2 2.11.(1)y=x-+2,x 2+y 2=1 (2)-3321解析 (1)由题意得直线l 的普通方程为y-2=(x-1),圆C 的直角坐标方程为x 2+y 2=1.3(2)易得曲线C':+y 2=1.令x 29{x =3cosθ,y =sinθ,则x+2y=3cos θ+2sin θ=sin(θ+φ),3321(其中tanφ=3)故x+2y 的最小值为-321.12.(1)(x-1)2+y 2=1 (2) 解析 (1)由ρ=2cos θ,得ρ2=2ρcos θ.12∵ρ2=x 2+y 2,ρcos θ=x ,∴x 2+y 2=2x ,即(x-1)2+y 2=1.∴圆C 的直角坐标方程为(x-1)2+y 2=1.(2)由点A 的极坐标,得点A 的直角坐标为(22,π4)(12,12).将代入(x-1)2+y 2=1,消去x ,y 整理得t 2-t-=0.{x =12+32t ,y =12+12t3-112设t 1,t 2为方程t 2-t-=0的两个根,则t 1t 2=-,所以|AP|·|AQ|=|t 1t 2|=3-12121212.。
2019年高考数学(理科,天津课标版)二轮复习专题能力训练 Word版含答案7
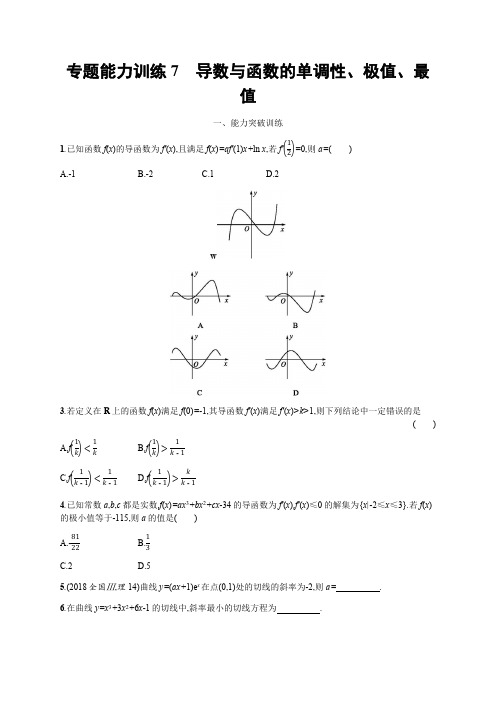
(2)由(1)知 f(x)在区间(-2,-1)内单调递增,在区间(-1,0)内单调递减,从而函数 f(x)在区间(-2,0)内恰
{ ( ) ������( - 2) < 0,
1
1
有两个零点当且仅当
������( - 1) > 0,解得 ������(0) < 0,
0<a<3.所以 a 的取值范围是
0,3
专题能力训练 7 导数与函数的单调性、极值、最值
一、能力突破训练
1
1
������ 1
1.D 解析 因为 f'(x)=af'(1)+������,所以 f'(1)=af'(1)+1,易知 a≠1,则 f'(1)=1 - ������,所以 f'(x)=1 - ������ + ������.又因为 f'
所以 x1x2=1,不妨设 x1<x2,则 x2>1.
������(������1) - ������(������2) 1
ln ������1 - ln ������2
ln ������1 - ln ������2
- 2ln ������2
������(������1) - ������(������2)
( ) ( ) 1
������
1
1
1
即 f ������ - 1 > ������ - 1-1=������ - 1,∴f ������ - 1 > ������ - 1,故 C 错误.
2������
������
3������
4.C 解析 依题意得 f'(x)=3ax2+2bx+c≤0 的解集是[-2,3],于是有 3a>0,-2+3=-3������,-2×3=3������,则 b=- 2
2019年高考数学(理科,天津课标版)大二轮复习:综合能力训练 Word版含答案
综合能力训练第Ⅰ卷(选择题,共40分)一、选择题(本大题共8小题,每小题5分,共40分)1.已知集合A=,B={x|y=lg(4x-x 2)},则A ∩B 等于( ){x ||x -12|≤32}A .(0,2]B .[-1,0)C .[2,4)D .[1,4)2.设直线x+y=1与抛物线y 2=2px (p>0)交于A ,B 两点,若OA ⊥OB ,则△OAB 的面积为( )A .1B .C .D .25253.已知奇函数f (x )在R 上是增函数,g (x )=xf (x ).若a=g (-log 25.1),b=g (20.8),c=g (3),则a ,b ,c 的大小关系为( )A.a<b<cB.c<b<aC.b<a<cD.b<c<a4.(2018浙江,3)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm 3)是( )A .2B .4C .6D .85.执行如图所示的程序框图.若输入n=3,则输出的S=( )A.67B.37C.89D.496.已知双曲线=1(a>0,b>0)被斜率为1的直线截得的弦的中点为(4,1),则该双曲线离心率的值是x 2a 2‒y 2b 2( )A .B .5262C .D .21037.已知函数f (x )=若f (1)+f (a )=2,则a 的所有可能值为( ){sin (πx 2),-1<x <0,e x -1,x ≥0,A .1B .-C .1,-D .1,2222228.已知实数a ,b ,c.( )A .若|a 2+b+c|+|a+b 2+c|≤1,则a 2+b 2+c 2<100B .若|a 2+b+c|+|a 2+b-c|≤1,则a 2+b 2+c 2<100C .若|a+b+c 2|+|a+b-c 2|≤1,则a 2+b 2+c 2<100D .若|a 2+b+c|+|a+b 2-c|≤1,则a 2+b 2+c 2<100第Ⅱ卷(非选择题,共110分)二、填空题(本大题共6小题,每小题5分,共30分)9.已知a ,b ∈R ,i 是虚数单位,若(1+i)(1-b i)=a ,则的值为 . ab 10.在(2x-1)5的展开式中,含x 2的项的系数是 .(用数字填写答案)11.已知两球O 1和O 2在棱长为1的正方体ABCD-A 1B 1C 1D 1的内部,且互相外切,若球O 1与过点A 的正方体的三个面相切,球O 2与过点C 1的正方体的三个面相切,则球O 1和O 2的表面积之和的最小值为 .12.在极坐标系中,直线4ρcos +1=0与圆ρ=2sin θ的公共点的个数为 . (θ-π6)13.设变量x ,y 满足约束条件的最小值是 . {y ≤3x -2,x -2y +1≤0,2x +y ≤8,则yx -114.a ,b 为空间中两条互相垂直的直线,等腰直角三角形ABC 的直角边AC 所在直线与a ,b 都垂直,斜边AB 以直线AC 为旋转轴旋转,有下列结论:①当直线AB 与a 成60°角时,AB 与b 成30°角;②当直线AB 与a 成60°角时,AB 与b 成60°角;③直线AB 与a 所成角的最小值为45°;④直线AB 与a 所成角的最大值为60°.其中正确的是 .(填写所有正确结论的编号) 三、解答题(本大题共6小题,共80分)15.(13分)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c.已知sin(A+C )=8sin 2.B2(1)求cos B ;(2)若a+c=6,△ABC 的面积为2,求b.16.(13分)已知数列{a n }中,a 1=2,且a n =2a n-1-n+2(n ≥2,n ∈N *).(1)求a 2,a 3,并证明{a n -n }是等比数列;(2)设b n =,求数列{b n }的前n 项和S n .a n2n -117.(13分)如图,在棱长为2的正方体ABCD-A 1B 1C 1D 1中,E ,F ,M ,N 分别是棱AB ,AD ,A 1B 1,A 1D 1的中点,点P ,Q 分别在棱DD 1,BB 1上移动,且DP=BQ=λ(0<λ<2).(1)当λ=1时,证明:直线BC 1∥平面EFPQ.(2)是否存在λ,使平面EFPQ 与平面PQMN 所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.18.(13分)某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4,现从这10人中随机选出2人作为该组代表参加座谈会.(1)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;(2)设X为选出的2人参加义工活动次数之差的绝对值,求随机变量X的分布列和数学期望.19.(14分)已知椭圆C :=1(a>b>0)的左、右焦点F 1,F 2与椭圆短轴的一个端点构成边长为4的x 2a 2+y 2b 2正三角形.(1)求椭圆C 的标准方程;(2)过椭圆C 上任意一点P 作椭圆C 的切线与直线F 1P 的垂线F 1M 相交于点M ,求点M 的轨迹方程;(3)若切线MP 与直线x=-2交于点N ,求证:为定值.|NF 1||MF 1|20.(14分)已知函数f (x )=ln(1+x )+x 2-x (a ≥0).a2(1)若f (x )>0对x ∈(0,+∞)都成立,求a 的取值范围;(2)已知e 为自然对数的底数,证明:∀n ∈N *,<e .e <(1+1n 2)(1+2n 2)…(1+nn 2)##综合能力训练1.A 解析 ∵A=[-1,2],B=(0,4),∴A ∩B=(0,2].故选A .2.B 解析 设A (x 1,y 1),B (x 2,y 2),由x+y=1与抛物线y 2=2px ,得y 2+2py-2p=0,解得y 1=-p+,x 1=1+p-,y 2=-p-,x 2=1+p+,p 2+2p p 2+2p p 2+2p p 2+2p 由OA ⊥OB 得,x 1x 2+y 1y 2=0,即[(1+p )2-(p 2+2p )]+[p 2-(p 2+2p )]=0,化简得2p=1,从而A,B ,OA 2==5-2,OB 2==5+2,△OAB 的面积(3-52,-1+52)(3+52,-1-52)x 21+y 215x 22+y 225S=|OA||OB|=故选B .1252.3.C 解析 ∵f (x )是R 上的奇函数,∴g (x )=xf (x )是R 上的偶函数.∴g (-log 25.1)=g (log 25.1).∵奇函数f (x )在R 上是增函数,∴当x>0时,f (x )>0,f'(x )>0.∴当x>0时,g'(x )=f (x )+xf'(x )>0恒成立,∴g (x )在区间(0,+∞)上是增函数.∵2<log 25.1<3,1<20.8<2,∴20.8<log 25.1<3.结合函数g (x )的性质得b<a<c.故选C .4.C 解析 由三视图可知该几何体为直四棱柱.∵S 底=(1+2)×2=3,h=2,12×∴V=Sh=3×2=6.5.B 解析 由题意得,输出的S 为数列的前3项和,而,{1(2n -1)(2n +1)}1(2n -1)(2n +1)=12(12n -1-12n +1)即S n =故当输入n=3时,S 3=,故选B .12(1-12n +1)=n 2n +1.376.A 解析 设直线l 与双曲线交于点A (x 1,y 1),B (x 2,y 2),则=0,即(x 1+x 2)(x 1-x 2)a 2‒(y 1+y 2)(y 1-y 2)b 2y 1-y 2x1-x 2=由弦的中点为(4,1),直线的斜率为1可知,x 1+x 2=8,y 1+y 2=2,=1,b 2(x 1+x 2)a 2(y 1+y 2).y 1-y 2x 1-x 2,e 2=1+e=故选A .∴b 2a 2=14b 2a2=54.∴52.7.C 解析 ∵f (1)=e 1-1=1,∴f (a )=1.若a ∈(-1,0),则sin(πa 2)=1,∴a=-若a ∈[0,+∞),则e a-1=1,22.∴a=1.因此a=1或a=-22.8.D 解析 (举反例排除)选项A 中,令a=b=10,c=-110,则|a 2+b+c|+|a+b 2+c|=|100+10-110|+|10+100-110|=0<1.而a 2+b 2+c 2=100+100+1102=200+1102>100,故选项A 不成立;选项B 中,令a=10,b=-100,c=0,则|a 2+b+c|+|a 2+b-c|=0<1.而a 2+b 2+c 2=100+1002+0>100,故选项B 不成立;选项C 中,令a=100,b=-100,c=0,则|a+b+c 2|+|a+b-c 2|=0<1.而a 2+b 2+c 2=1002+1002+0>100,故选项C 不成立;故选D .9.2 解析 (1+i)(1-b i)=1+b+(1-b )i =a ,则所以=2.故答案为2.{1+b =a ,1-b =0,{a =2,b =1,即ab 10.-40 解析 (2x-1)5的展开式的通项为T r+1=(2x )5-r (-1)r =(-1)r 25-r x 5-r.C r 5C r 5根据题意,得5-r=2,解得r=3.所以含x 2项的系数为(-1)325-3=-22=-40.C 35C 2511.3(2-)π 解析 ∵AO 1=R 1,C 1O 2=R 2,O 1O 2=R 1+R 2,333∴(+1)(R 1+R 2)=,R 1+R 2=,球O 1和O 2的表面积之和为4π()≥4π·23333+1R 21+R 22(R 1+R 22)2=2π(R 1+R 2)2=3(2-)π.312.2 解析 ∵4ρcos +1=0,展开得2cos θ+2ρsin θ+1=0,∴直线的直角坐标方程为2(θ-π6)3ρ3x+2y+1=0.∵ρ=2sin θ两边同乘ρ得ρ2=2ρsin θ,∴圆的直角坐标方程为x 2+y 2-2y=0,圆心为(0,1),半径r=1.∴圆心到直线的距离d=<r=1.|23×0+2×1+1|(23)2+22=34∴直线与圆相交.∴直线与圆公共点的个数为2.13.1 解析 由约束条件作出可行域如图,联立解得A (3,2),{y ≤3x -2,x -2y +1≤0,2x +y ≤8{x -2y +1=0,2x +y =8,的几何意义为可行域内的动点与定点P (1,0)连线的斜率,则其最小值为k PA ==1.y x -12-03-114.②③ 解析 由题意,AB 是以AC 为轴,BC 为底面半径的圆锥的母线,由AC ⊥a ,AC ⊥b ,得AC ⊥圆锥底面,在底面内可以过点B ,作BD ∥a ,交底面圆C 于点D ,如图所示,连接DE ,则DE ⊥BD ,∴DE ∥b.连接AD ,在等腰三角形ABD 中,设AB=AD=,当直线AB 与a 成60°角时,∠ABD=60°,故BD=又22.在Rt △BDE 中,BE=2,∴DE=,过点B 作BF ∥DE ,交圆C 于点F ,连接AF ,由圆的对称性可知2BF=DE=,∴△ABF 为等边三角形,∴∠ABF=60°,即AB 与b 成60°角,②正确,①错误.由最小角定2理可知③正确;很明显,可以满足直线a ⊥平面ABC ,直线AB 与a 所成的最大角为90°,④错误.故正确的说法为②③.15.解 (1)由题设及A+B+C=π,得sin B=8sin 2,B2故sin B=4(1-cos B ).上式两边平方,整理得17cos 2B-32cos B+15=0,解得cos B=1(舍去),cos B=1517.(2)由cos B=得sin B=,1517817故S △ABC =ac sin B=ac.12417又S △ABC =2,则ac=172.由余弦定理及a+c=6得b 2=a 2+c 2-2ac cos B =(a+c )2-2ac (1+cos B )=36-2=4.×172×(1+1517)所以b=2.16.解 (1)由已知a n =2a n-1-n+2(n ≥2,n ∈N *)得a 2=4,a 3=7.a n -n=2a n-1-2n+2,即a n -n=2[a n-1-(n-1)].=2(n ≥2,n ∈N *),且a 1-1=1,∵a n -na n -1-(n -1)∴{a n -n }是以1为首项,2为公比的等比数列.(2)由(1)得a n -n=(a 1-1)·2n-1,即a n=2n-1+n ,∴bn ==1+a n2n -1n2n -1.设c n =,且前n 项和为T n ,n2n -1则T n =+…+,①120+221+322n2n -1T n =+…+,②12121+222+323n2n①-②,得T n =1++…+=2-12(12+122+12312n -1)‒n 2n =1-12n1-12‒n 2n 2+n 2n .故T n =4-,S n =n+4-2+n 2n -12+n 2n -1.17.解法一 (1)证明:如图①,连接AD 1,由ABCD-A 1B 1C 1D 1是正方体,知BC 1∥AD 1.当λ=1时,P 是DD 1的中点,又F 是AD 的中点,所以FP ∥AD 1,所以BC 1∥FP.而FP ⊂平面EFPQ ,且BC 1⊄平面EFPQ ,故直线BC 1∥平面EFPQ.(2)如图②,连接BD.因为E ,F 分别是AB ,AD 的中点,所以EF ∥BD ,且EF=BD.又DP=BQ ,DP ∥12BQ ,所以四边形PQBD 是平行四边形,故PQ ∥BD ,且PQ=BD ,从而EF ∥PQ ,且EF=PQ.12在Rt △EBQ 和Rt △FDP 中,因为BQ=DP=λ,BE=DF=1,所以EQ=FP=,所以四边形EFPQ 也是等腰梯形.1+λ2同理可证四边形PQMN 也是等腰梯形.分别取EF ,PQ ,MN 的中点为H ,O ,G ,连接OH ,OG ,则GO ⊥PQ ,HO ⊥PQ ,而GO ∩HO=O ,故∠GOH 是平面EFPQ 与平面PQMN 所成的二面角的平面角.若存在λ使平面EFPQ 与平面PQMN 所成的二面角为直二面角,则∠GOH=90°.连接EM ,FN ,则由EF ∥MN ,且EF=MN 知四边形EFNM 是平行四边形.连接GH ,因为H ,G 是EF ,MN 的中点,所以GH=ME=2.在△GOH 中,GH 2=4,OH 2=1+λ2-=λ2+,OG 2=1+(2-λ)2-=(2-λ)2+,(22)212(22)212由OG 2+OH 2=GH 2,得(2-λ)2++λ2+=4,解得λ=1±,121222故存在λ=1±,使平面EFPQ 与平面PQMN 所成的二面角为直二面角.22解法二 以D 为原点,射线DA ,DC ,DD 1分别为x ,y ,z 轴的正半轴建立如图③所示的空间直角坐标系.由已知得B (2,2,0),C 1(0,2,2),E (2,1,0),F (1,0,0),P (0,0,λ).=(-2,0,2),=(-1,0,λ),=(1,1,0).BC 1FP FE (1)证明:当λ=1时,=(-1,0,1).FP 因为=(-2,0,2),BC 1所以=2,即BC 1∥FP.BC 1FP 而FP ⊂平面EFPQ ,且BC 1⊄平面EFPQ ,故直线BC 1∥平面EFPQ.(2)设平面EFPQ 的一个法向量为n =(x ,y ,z ),则由可得于是可取n =(λ,-λ,1).{FE ·n =0,FP ·n =0{x +y =0,-x +λz =0.同理可得平面MNPQ 的一个法向量为m =(λ-2,2-λ,1).若存在λ,使平面EFPQ 与平面PQMN 所成的二面角为直二面角,则m ·n =(λ-2,2-λ,1)·(λ,-λ,1)=0,即λ(λ-2)-λ(2-λ)+1=0,解得λ=1±22.故存在λ=1±,使平面EFPQ 与平面PQMN 所成的二面角为直二面角.218.解 (1)由已知,有P (A )=C 13C 14+C 23C 210=13.所以,事件A 发生的概率为13.(2)随机变量X 的所有可能取值为0,1,2.P (X=0)=,C 23+C 23+C 24C 210=415P (X=1)=,C 13C 13+C 13C 14C 210=715P (X=2)=C 13C 14C 210=415.所以,随机变量X 的分布列为X 012P 415715415随机变量X 的数学期望E (X )=0+1+2=1.×415×715×41519.(1)解 依题意,2c=a=4,∴c=2,b=23.∴椭圆C 的标准方程为=1.x 216+y 212(2)解 由(1)知F 1(-2,0),设P (x 0,y 0),M (x ,y ),过椭圆C 上点P 的切线方程为=1,①x 0x16+y 0y12直线F 1P 的斜率,则直线MF 1的斜率=-,k F 1P =y 0x 0+2k MF 1x 0+2y 0直线MF 1的方程为y=-(x+2),x 0+2y 0即yy 0=-(x 0+2)(x+2),②①②联立,解得x=-8,故点M 的轨迹方程为x=-8.(3)证明 依题意及(2),知点M ,N 的坐标可表示为M (-8,y M ),N (-2,y N ),点N 在切线MP 上,由①式得y N =,3(x 0+8)2y 0点M 在直线MF 1上,由②式得y M =,6(x 0+2)y 0|NF 1|2=,|MF 1|2=[(-2)-(-8)]2+,y 2N=9(x 0+8)24y 20y 2M=36[y 20+(x 0+2)2]y 20故|NF 1|2|MF 1|2=9(x 0+8)24y 20·y 2036[y 20+(x 0+2)2]=,③116·(x 0+8)2y 20+(x 0+2)2注意到点P 在椭圆C 上,即=1,x 2016+y 2012于是,代入③式并整理得,故的值为定值y 20=48-3x 204|NF 1|2|MF 1|2=14|NF 1||MF 1|12.20.(1)解 ∵f (x )=ln(1+x )+x 2-x ,其定义域为(-1,+∞),∴f'(x )=+ax-1=a211+x x (ax +a -1)1+x.①当a=0时,f'(x )=-,当x ∈(0,+∞)时,f'(x )<0,x1+x 则f (x )在区间(0,+∞)内单调递减,此时,f (x )<f (0)=0,不符合题意.②当0<a<1时,令f'(x )=0,得x 1=0,x 2=>0,1-aa 当x 时,f'(x )<0,则f (x )在区间内单调递减,∈(0,1-aa)(0,1-aa)此时,f (x )<f (0)=0,不符合题意.③当a=1时,f'(x )=,当x ∈(0,+∞)时,f'(x )>0,x 21+x 则f (x )在区间(0,+∞)内单调递增,此时,f (x )>f (0)=0,符合题意.④当a>1时,令f'(x )=0,得x 1=0,x 2=<0,当x ∈(0,+∞)时,f'(x )>0,1-aa 则f (x )在区间(0,+∞)内单调递增,此时,f (x )>f (0)=0,符合题意.综上所述,a 的取值范围为[1,+∞).(2)证明 由(1)可知,当a=0时,f (x )<0对x ∈(0,+∞)都成立,即ln(1+x )<x 对x ∈(0,+∞)都成立,∴ln +ln +…+ln +…+,即ln …(1+1n 2)(1+2n 2)(1+nn 2)<1n2+2n2nn2[(1+1n 2)(1+2n 2)··(1+nn 2)]<1+2+…+nn 2=n +12n .由于n ∈N *,则=1.n +12n =12+12n ≤12+12×1∴ln <1.[(1+1n 2)(1+2n 2)…(1+nn 2)]<e .∴(1+1n 2)(1+2n 2)…(1+nn 2)由(1)可知,当a=1时,f (x )>0对x ∈(0,+∞)都成立,即x-x 2<ln(1+x )对x ∈(0,+∞)都成立,12+…+<ln +ln +…+ln ,∴(1n 2+2n 2+…+nn 2)‒12(12n 4+22n 4n 2n4)(1+1n 2)(1+2n 2)(1+n n 2)即n (n +1)2n 2‒12[n (n +1)(2n +1)6n 4]<ln ,[(1+1n 2)(1+2n 2) (1)n n 2)]得6n 3+4n 2-3n -112n 3<ln [(1+1n 2)(1+2n 2)…(1+nn 2)].由于n ∈N *,则6n 3+4n 2-3n -112n 3=6n 3+(3n 2-3n )+(n 2-1)12n 3≥6n 312n3=12.<ln ∴12[(1+1n 2)(1+2n 2)…(1+nn 2)].∴e <(1+1n2)(1+2n2) (1)nn2).<e .∴e <(1+1n 2)(1+2n 2)…(1+nn 2)。
2019年高考数学(理科,天津课标版)二轮复习专题能力训练 Word版含答案2

{ { x+2y=-5,由
������
+ ������
2������ - ������
= =
1-,5,解得
������ = ������ =
-
12,,即
A(-1,-2),此时
a=-1,所以要使
x+2y≥-5
恒成立,则-1≤a≤1,
故选 C.
9.9 解析 由题意,作出可行域如图.要使 z=x+y 取得最大值,当且仅当过点(5,4)时,zmax=9.
������ ������
������
14.A 解析 原不等式可化为(a-1)x- ������������+2ay≥0,两边同除以 y,得(a-1)������ ‒ ������+2a≥0,令 t= ������,则(a-
2+ 6
2+ 6
1)t2-t+2a≥0,由不等式恒成立知,a-1>0,Δ=1-4(a-1)·2a≤0,解得 a ≥ 4 ,amin= 4 ,故选 A.
{ ������ + ������ - 2 ≤ 0,
13.已知 x,y 满足约束条件 ������ - 2������ - 2 ≤ 0, 若 z=y-ax 取得最大值的最优解不唯一,则实数 a 的值为 2������ - ������ + 2 ≥ 0,
( )
1
A.2或-1
1
B.2或 2
C.1 或 2
{������ + 2������ - 5 ≥ 0,
9.(2018 全国Ⅱ,理 14)若 x,y 满足约束条件 ������ - 2������ + 3 ≥ 0,则 z=x+y 的最大值为 . ������ - 5 ≤ 0,
2019年高考数学(理科,天津课标版)二轮复习专题能力训练 Word版含答案8

专题能力训练8 利用导数解不等式及参数的取值范围一、能力突破训练1.设f (x )=x ln x-ax 2+(2a-1)x ,a ∈R .(1)令g (x )=f'(x ),求g (x )的单调区间;(2)已知f (x )在x=1处取得极大值,求实数a 的取值范围.2.(2018全国Ⅲ,理21)已知函数f (x )=(2+x+ax 2)·ln(1+x )-2x.(1)若a=0,证明:当-1<x<0时,f (x )<0;当x>0时,f (x )>0;(2)若x=0是f (x )的极大值点,求a.3.已知函数f (x )=ax+x ln x 的图象在x=e(e 为自然对数的底数)处的切线的斜率为3.(1)求实数a 的值;(2)若f (x )≤kx 2对任意x>0成立,求实数k 的取值范围;(3)当n>m>1(m ,n ∈N *)时,证明:.nmmn>mn4.设函数f (x )=ax 2-a-ln x ,其中a ∈R .(1)讨论f (x )的单调性;(2)确定a 的所有可能取值,使得f (x )>-e 1-x 在区间(1,+∞)内恒成立(e =2.718…为自然对数的底数).1x 5.设函数f (x )=a ln x ,g (x )=x 2.12(1)记g'(x )为g (x )的导函数,若不等式f (x )+2g'(x )≤(a+3)x-g (x )在x ∈[1,e]内有解,求实数a 的取值范围;(2)若a=1,对任意的x 1>x 2>0,不等式m [g (x 1)-g (x 2)]>x 1f (x 1)-x 2f (x 2)恒成立.求m (m ∈Z ,m ≤1)的值.6.已知函数f (x )=-2(x+a )ln x+x 2-2ax-2a 2+a ,其中a>0.(1)设g (x )是f (x )的导函数,讨论g (x )的单调性;(2)证明:存在a ∈(0,1),使得f (x )≥0在区间(1,+∞)内恒成立,且f (x )=0在区间(1,+∞)内有唯一解.二、思维提升训练7.已知函数f (x )=x 3+x 2+ax+1(a ∈R ).13(1)求函数f (x )的单调区间;(2)当a<0时,试讨论是否存在x 0∈,使得f (x 0)=f .(0,12)∪(12,1)(12)专题能力训练8 利用导数解不等式及参数的取值范围一、能力突破训练1.解 (1)由f'(x )=ln x-2ax+2a ,可得g (x )=ln x-2ax+2a ,x ∈(0,+∞).则g'(x )=-2a=,1x 1-2ax x 当a ≤0时,x ∈(0,+∞)时,g'(x )>0,函数g (x )单调递增;当a>0时,x 时,g'(x )>0,函数g (x )单调递增,x 时,函数g (x )单调递减.∈(0,12a )∈(12a ,+∞)所以当a ≤0时,g (x )的单调增区间为(0,+∞);当a>0时,g (x )单调增区间为,单调减区间为(0,12a )(12a ,+∞).(2)由(1)知,f'(1)=0.①当a ≤0时,f'(x )单调递增,所以当x ∈(0,1)时,f'(x )<0,f (x )单调递减.当x ∈(1,+∞)时,f'(x )>0,f (x )单调递增.所以f (x )在x=1处取得极小值,不合题意.②当0<a<时,>1,由(1)知f'(x )在区间内单调递增,1212a (0,12a )可得当x ∈(0,1)时,f'(x )<0,x 时,f'(x )>0.∈(1,12a )所以f (x )在区间(0,1)内单调递减,在区间内单调递增,所以f (x )在x=1处取得极小值,不合题(1,12a )意.③当a=时,=1,f'(x )在区间(0,1)内单调递增,在区间(1,+∞)内单调递减,1212a 所以当x ∈(0,+∞)时,f'(x )≤0,f (x )单调递减,不合题意.④当a>时,0<<1,当x 时,f'(x )>0,f (x )单调递增,1212a ∈(12a ,1)当x ∈(1,+∞)时,f'(x )<0,f (x )单调递减,所以f (x )在x=1处取极大值,合题意.综上可知,实数a 的取值范围为a>12.2.解 (1)当a=0时,f (x )=(2+x )ln(1+x )-2x ,f'(x )=ln(1+x )-,x1+x 设函数g (x )=f'(x )=ln(1+x )-,则g'(x )=,x1+x x (1+x )2当-1<x<0时,g'(x )<0;当x>0时,g'(x )>0.故当x>-1时,g (x )≥g (0)=0,且仅当x=0时,g (x )=0,从而f'(x )≥0,且仅当x=0时,f'(x )=0.所以f (x )在(-1,+∞)内单调递增.又f (0)=0,故当-1<x<0时,f (x )<0;当x>0时,f (x )>0.(2)①若a ≥0,由(1)知,当x>0时,f (x )≥(2+x )·ln(1+x )-2x>0=f (0),这与x=0是f (x )的极大值点矛盾.②若a<0,设函数h (x )==ln(1+x )-f (x )2+x +ax22x2+x +ax 2.由于当|x|<min 时,2+x+ax 2>0,故h (x )与f (x )符号相同.{1,1|a |}又h (0)=f (0)=0,故x=0是f (x )的极大值点当且仅当x=0是h (x )的极大值点.h'(x )=11+x ‒2(2+x +ax 2)-2x (1+2ax )(2+x +ax 2)2=x 2(a 2x 2+4ax +6a +1)(x +1)(ax 2+x +2)2.若6a+1>0,则当0<x<-,且|x|<min 时,h'(x )>0,故x=0不是h (x )的极大值点.6a +14a {1,1|a |}若6a+1<0,则a 2x 2+4ax+6a+1=0存在根x 1<0,故当x ∈(x 1,0),且|x|<min 时,h'(x )<0,所以{1,1|a |}x=0不是h (x )的极大值点.若6a+1=0,则h'(x )=x 3(x -24)(x +1)(x 2-6x -12)2.则当x ∈(-1,0)时,h'(x )>0;当x ∈(0,1)时,h'(x )<0.所以x=0是h (x )的极大值点,从而x=0是f (x )的极大值点.综上,a=-16.3.解 (1)∵f (x )=ax+x ln x ,∴f'(x )=a+ln x+1.又f (x )的图象在点x=e 处的切线的斜率为3,∴f'(e)=3,即a+ln e +1=3,∴a=1.(2)由(1)知,f (x )=x+x ln x ,若f (x )≤kx 2对任意x>0成立,则k 对任意x>0成立.≥1+ln xx令g (x )=,则问题转化为求g (x )的最大值,g'(x )==-1+ln xx 1x ·x -(1+ln x )x 2ln x x 2.令g'(x )=0,解得x=1.当0<x<1时,g'(x )>0,∴g (x )在区间(0,1)内是增函数;当x>1时,g'(x )<0,∴g (x )在区间(1,+∞)内是减函数.故g (x )在x=1处取得最大值g (1)=1,∴k ≥1即为所求.(3)证明:令h (x )=,则h'(x )=x ln xx -1x -1-ln x(x -1)2.由(2)知,x ≥1+ln x (x>0),∴h'(x )≥0,∴h (x )是区间(1,+∞)内的增函数.∵n>m>1,∴h (n )>h (m ),即,n ln nn -1>m ln mm -1∴mn ln n-n ln n>mn ln m-m ln m ,即mn ln n+m ln m>mn ln m+n ln n ,∴ln n mn +ln m m >ln m mn +ln n n .整理,得ln(mn n )m >ln(nm m )n .∴(mn n )m >(nm m )n ,∴nm m n >mn .4.解 (1)f'(x )=2ax-(x>0).1x =2ax 2-1x 当a ≤0时,f'(x )<0,f (x )在区间(0,+∞)内单调递减.当a>0时,由f'(x )=0,有x=12a .此时,当x 时,f'(x )<0,f (x )单调递减;∈(0,12a )当x 时,f'(x )>0,f (x )单调递增.∈(12a ,+∞)(2)令g (x )=,s (x )=ex-1-x.1x ‒1ex -1则s'(x )=e x-1-1.而当x>1时,s'(x )>0,所以s (x )在区间(1,+∞)内单调递增.又由s (1)=0,有s (x )>0,从而当x>1时,g (x )>0.当a ≤0,x>1时,f (x )=a (x 2-1)-ln x<0.故当f (x )>g (x )在区间(1,+∞)内恒成立时,必有a>0.当0<a<时,>1.1212a 由(1)有f <f (1)=0,而g >0,(12a )(12a )所以此时f (x )>g (x )在区间(1,+∞)内不恒成立.当a 时,令h (x )=f (x )-g (x )(x ≥1).≥12当x>1时,h'(x )=2ax--e 1-x >x->0.1x +1x 21x +1x 2‒1x =x 3-2x +1x 2>x 2-2x +1x 2因此,h (x )在区间(1,+∞)单调递增.又因为h (1)=0,所以当x>1时,h (x )=f (x )-g (x )>0,即f (x )>g (x )恒成立.综上,a ∈[12,+∞).5.解 (1)不等式f (x )+2g'(x )≤(a+3)x-g (x ),即a ln x+2x ≤(a+3)x-x 2,12化简,得a (x-ln x )x 2-x.≥12由x ∈[1,e]知x-ln x>0,因而a 设y=,≥12x 2-x x -ln x .12x 2-x x -ln x 则y'=(x -1)(x -ln x )-(1-1x )(12x 2-x)(x -ln x )2=(x -1)(12x +1-ln x)(x -ln x )2.∵当x ∈(1,e)时,x-1>0,x+1-ln x>0,12∴y'>0在x ∈[1,e]时成立.由不等式有解,可得a ≥y min =-,12即实数a 的取值范围是[-12,+∞).(2)当a=1时,f (x )=ln x.由m [g (x 1)-g (x 2)]>x 1f (x 1)-x 2f (x 2)恒成立,得mg (x 1)-x 1f (x 1)>mg (x 2)-x 2f (x 2)恒成立,设t (x )=x 2-x ln x (x>0).m2由题意知x 1>x 2>0,则当x ∈(0,+∞)时函数t (x )单调递增,∴t'(x )=mx-ln x-1≥0恒成立,即m 恒成立.≥ln x +1x 因此,记h (x )=,得h'(x )=ln x +1x -ln xx 2.∵函数在区间(0,1)上单调递增,在区间(1,+∞)上单调递减,∴函数h (x )在x=1处取得极大值,并且这个极大值就是函数h (x )的最大值.由此可得h (x )max =h (1)=1,故m ≥1,结合已知条件m ∈Z ,m ≤1,可得m=1.6.(1)解 由已知,函数f (x )的定义域为(0,+∞),g (x )=f'(x )=2(x-a )-2ln x-2,(1+ax )所以g'(x )=2-2x +2ax2=2(x -12)2+2(a -14)x 2.当0<a<时,g (x )在区间内单调递增,14(0,1-1-4a 2),(1+1-4a2,+∞)在区间内单调递减;(1-1-4a 2,1+1-4a2)当a 时,g (x )在区间(0,+∞)内单调递增.≥14(2)证明 由f'(x )=2(x-a )-2ln x-2=0,解得a=(1+ax )x -1-ln x 1+x -1.令φ(x )=-2ln x+x 2-2x-2(x +x -1-ln x 1+x -1)(x -1-ln x 1+x -1)(x -1-ln x 1+x -1)2+x -1-ln x 1+x -1.则φ(1)=1>0,φ(e)=--2<0.e (e -2)1+e -1(e -21+e -1)2故存在x 0∈(1,e),使得φ(x 0)=0.令a 0=,u (x )=x-1-ln x (x ≥1).x 0-1-ln x 01+x -1由u'(x )=1-0知,函数u (x )在区间(1,+∞)内单调递增.1x ≥所以0==a 0<<1.u (1)1+1<u (x 0)1+x -10u (e )1+e -1=e -21+e -1即a 0∈(0,1).当a=a 0时,有f'(x 0)=0,f (x 0)=φ(x 0)=0.由(1)知,f'(x )在区间(1,+∞)内单调递增,故当x ∈(1,x 0)时,f'(x )<0,从而f (x )>f (x 0)=0;当x ∈(x 0,+∞)时,f'(x )>0,从而f (x )>f (x 0)=0.所以,当x ∈(1,+∞)时,f (x )≥0.综上所述,存在a ∈(0,1),使得f (x )≥0在区间(1,+∞)内恒成立,且f (x )=0在区间(1,+∞)内有唯一解.二、思维提升训练7.解 (1)f'(x )=x 2+2x+a ,方程x 2+2x+a=0的判别式为Δ=4-4a ,①当a ≥1时,Δ≤0,则f'(x )≥0,此时f (x )在R 上是增函数;②当a<1时,方程x 2+2x+a=0两根分别为x 1=-1-,x 2=-1+,1-a 1-a 解不等式x 2+2x+a>0,解得x<-1-或x>-1+,1-a 1-a 解不等式x 2+2x+a<0,解得-1-<x<-1+,1-a 1-a 此时,函数f (x )的单调递增区间为(-∞,-1-)和(-1+,+∞),1-a 1-a 单调递减区间为(-1-,-1+).1-a 1-a 综上所述,当a ≥1时,函数f (x )的单调递增区间为(-∞,+∞);当a<1时,函数f (x )的单调递增区间为(-∞,-1-)和(-1+,+∞),单调递减区间为(-1-1-a 1-a 1-a,-1+).1-a (2)f (x 0)-f +ax 0+1--a -1(12)=13x 30+x 2013·(12)3‒(12)2·12=+a 13[x 30-(12)3]+[x 20-(12)2](x 0-12)=13(x 0-12)(x 20+x 02+14)+(x 0-12)·+a +x 0+(4+14x 0+7+12a ).(x 0+12)(x 0-12)=(x 0-12)·(x 203+x 06+11212+a )=112(x 0-12)x 20若存在x 0,使得f (x 0)=f ,则4+14x 0+7+12a=0在内有解.∈(0,12)∪(12,1)(12)x 20(0,12)∪(12,1)由a<0,得Δ=142-16(7+12a )=4(21-48a )>0,故方程4+14x 0+7+12a=0的两根为x 1'=,x'2=x 20-7-21-48a 4-7+21-48a4.由x 0>0,得x 0=x'2=,-7+21-48a4依题意,0<<1,即7<<11,所以49<21-48a<121,即-<a<-,-7+21-48a21-48a 2512712又由得a=-,-7+21-48a 4=1254故要使满足题意的x 0存在,则a ≠-54.综上,当a 时,存在唯一的x 0满足f (x 0)=f ,当a ∈(-2512,-54)∪(-54,-712)∈(0,12)∪(12,1)(12)∈时,不存在x 0满足f (x 0)=f (-∞,-2512]∪(-54)∪[-712,0)∈(0,12)∪(12,1)(12).。
2019年高考数学(理科,天津课标版)二轮复习专题能力训练 Word版含答案10

π
2
������������
������������
������������·sin∠������������������ 3 × sin4 3 × 2 3 10
由正弦定理sin∠������������������ = sin∠������������������,得 sin∠BAC= ������������ = 5 = 5 = 10 .
10.设△ABC 的内角 A,B,C 的对边分别为 a,b,c,a=btan A,且 B 为钝角.
π
(1)证明:B-A=2; (2)求 sin A+sin C 的取值范围.
( )π
11.设 f(x)=sin xcos x-cos2 ������ + 4 . (1)求 f(x)的单调区间;
( )������
1
11.解 (1)由题意知 f(x)= 2 ‒
2
= 2 ‒ 2 =sin 2x-2.
π
π
π
π
由-2+2kπ≤2x ≤ 2+2kπ,k∈Z,可得-4+kπ≤x ≤ 4+kπ,k∈Z;
π
3π
π
3π
由2+2kπ≤2x ≤ 2 +2kπ,k∈Z,可得4+kπ≤x ≤ 4 +kπ,k∈Z.所以 f(x)的单调递增区间是
1 3 22 6 53
=3 × 3 + 3 × 3 = 9 . 13.A 解析 由正弦定理,得 sin Csin A=sin Acos C.
因为 0<A<π,所以 sin A>0,从而 sin C=cos C.
π
又 cos C≠0,所以 tan C=1,则 C=4,
高考数学天津卷函数与方程历年真题解析

高考数学天津卷函数与方程历年真题解析一、函数部分在高考数学中,函数是一个重要的概念。
下面我们将从历年真题中选取一些典型题目,进行详细解析。
1. 【2019天津卷】设函数f(x) = 3x + a, g(x) = 2x - b,则方程f(g(x)) = 7的解为x =2.求a和b的值。
解析:首先,根据函数的复合性质,我们可以得到f(g(x)) = f(2x-b)= 3(2x-b) + a = 6x - 3b + a。
将x = 2代入方程,可以得到6(2) - 3b + a = 7。
进一步化简得到a - 3b = -5。
另外,根据题目给出的条件x = 2,我们可以得到f(g(2)) = f(2) = 7。
代入f(x) = 3x + a可以得到3(2) + a = 7,进一步化简得到a = 1。
将a = 1代入前面得到的方程a - 3b = -5,可以得到1 - 3b = -5,进一步化简得到b = 2。
因此,解为a = 1,b = 2。
2. 【2018天津卷】设函数f(x) = 2x - 1,g(x) = x^2 + a,则方程f(g(x)) = 3有两个相等的实根。
求实数a的取值范围。
解析:首先,根据函数的复合性质,我们可以得到f(g(x)) = f(x^2 + a) = 2(x^2 + a) - 1 = 2x^2 + 2a - 1。
由于方程f(g(x)) = 3有两个相等的实根,说明对于某个实数x,有2x^2 + 2a - 1 = 3成立。
进一步化简得到2x^2 + 2a - 4 = 0,即x^2 + a - 2 = 0。
根据方程有两个相等的实根的条件,可得Δ = a^2 - 4。
当Δ = 0时,方程有两个相等的实根。
因此有a^2 - 4 = 0,即a^2 = 4,解得a = ±2。
因此,实数a的取值范围为a ∈ {-2, 2}。
二、方程部分方程是高考数学中的重要内容之一。
下面我们将从历年真题中选取一些典型题目,进行详细解析。
【配套K12】[学习](新课标)天津市2019年高考数学二轮复习 专题能力训练6 函数与方程及函数的
天津市2019年高考数学二轮复习 专题能力训练6 函数与方程及函数的](https://img.taocdn.com/s3/m/d6e55991960590c69ec376f0.png)
专题能力训练6 函数与方程及函数的应用一、能力突破训练1.f(x)=-+log2x的一个零点落在下列哪个区间()A.(0,1)B.(1,2)C.(2,3)D.(3,4)2.设函数f(x)的零点为x1,函数g(x)=4x+2x-2的零点为x2,若|x1-x2|>,则f(x)可以是()A.f(x)=2x-B.f(x)=-x2+x-C.f(x)=1-10xD.f(x)=ln(8x-2)3.如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4 m和am(0<a<12),不考虑树的粗细.现用16 m长的篱笆,借助墙角围成一个矩形花圃ABCD,设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位:m2)的图象大致是()4.已知M是函数f(x)=e-2|x-1|+2sin在区间[-3,5]上的所有零点之和,则M的值为()A.4B.6C.8D.105.已知函数f(x)是奇函数,且满足f(2-x)=f(x)(x∈R),当0<x≤1时,f(x)=ln x+2,则函数y=f(x)在区间(-2,4]上的零点个数是()A.7B.8C.9D.106.(2018全国Ⅲ,理15)函数f(x)=cos在[0,π]上的零点个数为.7.已知e是自然对数的底数,函数f(x)=e x+x-2的零点为a,函数g(x)=ln x+x-2的零点为b,则f(a),f(1),f(b)的大小关系为.8.某商场对顾客实行购物优惠活动,规定购物付款总额要求如下:①若一次性购物不超过200元,则不给予优惠;②若一次性购物超过200元但不超过500元,则按标价给予9折优惠;③若一次性购物超过500元,则500元按第②条给予优惠,剩余部分给予7折优惠.甲单独购买A商品实际付款100元,乙单独购买B商品实际付款450元,若丙一次性购买A,B两件商品,则应付款元.9.已知函数f(x)=2x,g(x)=+2.(1)求函数g(x)的值域;(2)求满足方程f(x)-g(x)=0的x的值.10.如图,一个长方体形状的物体E在雨中沿面P(面积为S)的垂直方向做匀速移动,速度为v(v>0),雨速沿E移动方向的分速度为c(c∈R).E移动时单位时间内的淋雨量包括两部分:①P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与|v-c|×S成正比,比例系数为;②其他面的淋雨量之和,其值为.记y为E移动过程中的总淋雨量.当移动距离d=100,面积S=时,(1)写出y的表达式;(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度v,使总淋雨量y最少.二、思维提升训练11.如图,偶函数f(x)的图象如字母M,奇函数g(x)的图象如字母N,若方程f(g(x))=0,g(f(x))=0的实根个数分别为m,n,则m+n=()A.18B.16C.14D.1212.已知函数f(x)=函数g(x)=3-f(2-x),则函数y=f(x)-g(x)的零点个数为()A.2B.3C.4D.513.设函数f(x)=(1)若a=1,则f(x)的最小值为;(2)若f(x)恰有2个零点,则实数a的取值范围是.14.已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且R(x)=(1)写出年利润W(单位:万元)关于年产量x(单位:千件)的函数解析式;(2)当年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大.(注:年利润=年销售收入-年总成本)15.甲方是一农场,乙方是一工厂,由于乙方生产须占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付的情况下,乙方的年利润x(单位:元)与年产量q(单位:t)满足函数关系:x=2 000.若乙方每生产一吨产品必须赔付甲方s元(以下称s为赔付价格).(1)将乙方的年利润w(单位:元)表示为年产量q(单位:t)的函数,并求出乙方获得最大利润的年产量;(2)在乙方年产量为q(单位:t)时,甲方每年受乙方生产影响的经济损失金额y=0.002q2(单位:元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格s是多少?专题能力训练6函数与方程及函数的应用一、能力突破训练1.B解析由题意得f(x)单调递增,f(1)=-1<0,f(2)=>0,所以f(x)=-+log2x的零点落在区间(1,2)内.2.C解析依题意得g-2<0,g=1>0,则x2若f(x)=1-10x,则有x1=0,此时|x1-x2|>,因此选C.3.B解析设AD长为x cm,则CD长为(16-x)cm,又因为要将点P围在矩形ABCD内,所以a≤x≤12,则矩形ABCD的面积S=x(16-x).当0<a≤8时,当且仅当x=8时,S=64,当8<a<12时,S=a(16-a),即f(a)=画出分段函数图形可得其形状与选项B接近,故选B.4.C解析因为f(x)=e-2|x-1|+2sin=e-2|x-1|-2cos πx,所以f(x)=f(2-x).因为f(1)≠0,所以函数零点有偶数个,且两两关于直线x=1对称.当x∈[1,5]时,函数y=e-2(x-1)∈(0,1],且单调递减;函数y=2cos πx∈[-2,2],且在[1,5]上有两个周期,因此当x∈[1,5]时,函数y=e-2(x-1)与y=2cos πx 有4个不同的交点;从而所有零点之和为4×2=8,故选C.5.C解析由函数f(x)是奇函数且满足f(2-x)=f(x)知,f(x)是周期为4的周期函数,且关于直线x=1+2k(k∈Z)成轴对称,关于点(2k,0)(k∈Z)成中心对称.当0<x≤1时,令f(x)=ln x+2=0,得x=,由此得y=f(x)在区间(-2,4]上的零点分别为-2+,-,0,,2-,2,2+,-+4,4,共9个零点.故选C.6.3解析令f(x)=cos=0,得3x++kπ,k∈Z,∴x=,k∈Z.则在[0,π]的零点有故有3个.7.f(a)<f(1)<f(b)解析由题意,知f'(x)=e x+1>0恒成立,则函数f(x)在R上是单调递增的,因为f(0)=e0+0-2=-1<0,f(1)=e1+1-2=e-1>0,所以函数f(x)的零点a∈(0,1).由题意,知g'(x)=+1>0,则函数g(x)在区间(0,+∞)上是单调递增的.又g(1)=ln 1+1-2=-1<0,g(2)=ln 2+2-2=ln 2>0,则函数g(x)的零点b∈(1,2).综上,可得0<a<1<b<2.因为f(x)在R上是单调递增的,所以f(a)<f(1)<f(b).8.520解析设商品价格为x元,实际付款为y元,则y=整理,得y=∵0.9×200=180>100,∴A商品的价格为100元.∵0.9×500=450,∴B商品的价格为500元.当x=100+500=600时,y=100+0.7×600=520,即若丙一次性购买A,B 两件商品,则应付款520元.9.解 (1)g(x)=+2=+2,因为|x|≥0,所以0<1,即2<g(x)≤3,故g(x)的值域是(2,3].(2)由f(x)-g(x)=0,得2x--2=0.当x≤0时,显然不满足方程,当x>0时,由2x--2=0整理,得(2x)2-2·2x-1=0,(2x-1)2=2,解得2x=1±因为2x>0,所以2x=1+,即x=log2(1+).10.解 (1)由题意知,E移动时单位时间内的淋雨量为|v-c|+,故y=(3|v-c|+10)(v>0).(2)由(1)知,当0<v≤c时,y=(3c-3v+10)=-15;当c<v≤10时,y=(3v-3c+10)=+15.故y=①当0<c时,y是关于v的减函数.故当v=10时,y min=20-②当<c≤5时,在(0,c]内,y是关于v的减函数;在(c,10]内,y是关于v的增函数.故当v=c时,y min=二、思维提升训练11.A解析由题中图象知,f(x)=0有3个根0,a,b,且a∈(-2,-1),b∈(1,2);g(x)=0有3个根0,c,d,且c∈(-1,0),d∈(0,1).由f(g(x))=0,得g(x)=0或a,b,由图象可知g(x)所对每一个值都能有3个根,因而m=9;由g(f(x))=0,知f(x)=0或c,d,由图象可以看出f(x)=0时对应有3个根,f(x)=d时有4个,f(x)=c时只有2个,加在一起也是9个,即n=9,∴m+n=9+9=18,故选A.12.A解析因为f(x)=所以f(2-x)=f(2-x)=f(x)+f(2-x)=所以函数y=f(x)-g(x)=f(x)-3+f(2-x)=其图象如图所示.显然函数图象与x轴有2个交点,故函数有2个零点.13.(1)-1(2)[2,+∞)解析 (1)当a=1时,f(x)=当x<1时,2x-1∈(-1,1);当x≥1时,4(x-1)(x-2)∈[-1,+∞).故f(x)的最小值为-1.(2)若函数f(x)=2x-a的图象在x<1时与x轴有一个交点,则a>0,并且当x=1时,f(1)=2-a>0,所以0<a<2.同时函数f(x)=4(x-a)(x-2a)的图象在x≥1时与x轴有一个交点,所以a<1.若函数f(x)=2x-a的图象在x<1时与x轴没有交点,则函数f(x)=4(x-a)(x-2a)的图象在x≥1时与x轴有两个不同的交点,当a≤0时,函数f(x)=2x-a的图象与x轴无交点,函数f(x)=4(x-a)(x-2a)的图象在x≥1上与x轴也无交点,不满足题意.当21-a≤0,即a≥2时,函数f(x)=4(x-a)·(x-2a)的图象与x轴的两个交点x1=a,x2=2a都满足题意.综上,a的取值范围为[2,+∞).14.解 (1)当0<x≤10时,W=xR(x)-(10+2.7x)=8.1x--10;当x>10时,W=xR(x)-(10+2.7x)=98--2.7x.故W=(2)①当0<x≤10时,由W'=8.1-=0,得x=9.当x∈(0,9)时,W'>0;当x∈(9,10]时,W'<0.所以当x=9时,W取得最大值,即W max=8.1×9-93-10=38.6.②当x>10时,W=98-98-2=38,当且仅当=2.7x,即x=时,W取得最大值38.综合①②知:当x=9时,W取得最大值38.6,故当年产量为9千件时,该公司在这一品牌服装的生产中所获的年利润最大.15.解 (1)因为赔付价格为s元/吨,所以乙方的实际年利润为w=2 000-sq(q≥0).因为w=2 000-sq=-s,所以当q=时,w取得最大值.所以乙方取得最大利润的年产量q= t.(2)设甲方净收入为v元,则v=sq-0.002q2,将q=代入上式,得到甲方净收入v与赔付价格s之间的函数关系式:v=又v'=-,令v'=0得s=20.当s<20时,v'>0;当s>20时,v'<0.所以当s=20时,v取得最大值.因此甲方向乙方要求赔付价格s为20元/吨时,获最大净收入.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题能力训练6 函数与方程及函数的应用
一、能力突破训练
1.f(x)=-+log2x的一个零点落在下列哪个区间()
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,4)
2.设函数f(x)的零点为x1,函数g(x)=4x+2x-2的零点为x2,若|x1-x2|>,则f(x)可以是()
A.f(x)=2x-
B.f(x)=-x2+x-
C.f(x)=1-10x
D.f(x)=ln(8x-2)
3.如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4 m和a m(0<a<12),不考虑树的粗细.现用16 m长的篱笆,借助墙角围成一个矩形花圃ABCD,设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位:m2)的图象大致是()
4.已知M是函数f(x)=e-2|x-1|+2sin在区间[-3,5]上的所有零点之和,则M的值为()
A.4
B.6
C.8
D.10
5.已知函数f(x)是奇函数,且满足f(2-x)=f(x)(x∈R),当0<x≤1时,f(x)=ln x+2,则函数y=f(x)在区间(-2,4]上的零点个数是()
A.7
B.8
C.9
D.10
6.(2018全国Ⅲ,理15)函数f(x)=cos在[0,π]上的零点个数为.
7.已知e是自然对数的底数,函数f(x)=e x+x-2的零点为a,函数g(x)=ln x+x-2的零点为b,则
f(a),f(1),f(b)的大小关系为.
8.某商场对顾客实行购物优惠活动,规定购物付款总额要求如下:
①若一次性购物不超过200元,则不给予优惠;
②若一次性购物超过200元但不超过500元,则按标价给予9折优惠;
③若一次性购物超过500元,则500元按第②条给予优惠,剩余部分给予7折优惠.
甲单独购买A商品实际付款100元,乙单独购买B商品实际付款450元,若丙一次性购买A,B两件商品,则应付款元.
9.已知函数f(x)=2x,g(x)=+2.
(1)求函数g(x)的值域;
(2)求满足方程f(x)-g(x)=0的x的值.
10.
如图,一个长方体形状的物体E在雨中沿面P(面积为S)的垂直方向做匀速移动,速度为v(v>0),雨速沿E 移动方向的分速度为c(c∈R).E移动时单位时间内的淋雨量包括两部分:①P或P的平行面(只有一个面淋
雨)的淋雨量,假设其值与|v-c|×S成正比,比例系数为;②其他面的淋雨量之和,其值为.记y为E移动过程中的总淋雨量.当移动距离d=100,面积S=时,
(1)写出y的表达式;
(2)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度v,使总淋雨量y最少.
二、思维提升训练
11.如图,偶函数f(x)的图象如字母M,奇函数g(x)的图象如字母N,若方程f(g(x))=0,g(f(x))=0的实根个数分别为m,n,则m+n=()
A.18
B.16
C.14
D.12
12.已知函数f(x)=函数g(x)=3-f(2-x),则函数y=f(x)-g(x)的零点个数为()
A.2
B.3
C.4
D.5
13.设函数f(x)=
(1)若a=1,则f(x)的最小值为;
(2)若f(x)恰有2个零点,则实数a的取值范围是.
14.已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且
R(x)=
(1)写出年利润W(单位:万元)关于年产量x(单位:千件)的函数解析式;
(2)当年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大.(注:年利润=年销售收入-年总成本)。
