数模Logistic曲线模型
逻辑曲线(Logistic回归)

逻辑回归的参数解释
β0
截距,表示当所有解释变量x都为0时, logit P的估计值。
β1, β2, ..., βp
斜率,表示各解释变量对logit P的影 响程度。
逻辑回归的假设条件
线性关系
假设自变量与因变量之间存在线性关系,即因变 量的变化可以被自变量的线性组合所解释。
误差项同分布
假设误差项服从同一分布,通常是正态分布。
评估指标
根据任务类型选择合适的评估指标,如准确率、召回率、F1分数等。
模型比较
将新模型与其他同类模型进行比较,了解其性能优劣。
04 逻辑回归的优缺点
优点
分类性能好
逻辑回归模型在二分类问题上 表现优秀,分类准确率高。
易于理解和实现
逻辑回归模型形式简单,参数 意义明确,方便理解和实现。
无数据分布假设
总结词
在某些情况下,逻辑回归可能不是解决回归问题的最佳选择,此时可以考虑其他替代方 案。
详细描述
当因变量是连续变量,且自变量和因变量之间的关系非线性时,线性回归可能不是最佳 选择。此时可以考虑使用其他回归模型,如多项式回归、岭回归、套索回归等。另外, 当自变量和因变量之间的关系不确定时,可以考虑使用支持向量回归等模型进行预测。
06 总结与展望
总结
应用广泛
逻辑回归模型在许多领域都有广泛的应用,如医学、金融、市场 营销等,用于预测和解释二元分类结果。
理论基础坚实
基于概率和统计理论,逻辑回归模型能够提供可靠的预测和解释, 尤其是在处理小样本数据时。
灵活性和可解释性
模型参数可以解释为对结果概率的影响程度,这使得逻辑回归成为 一种强大且易于理解的工具。
在二分类问题中,逻辑回归通过将线性回归的输出经过逻辑函数转换,将连续的预测值转换为概率形式,从而实 现对因变量的二分类预测。逻辑函数的形式为1 / (1 + e ^ (-z)),其中z为线性回归的输出。
logistic模型 微分方程

logistic模型微分方程logistic模型是一种常用的数学模型,用来描述某一变量随时间变化的规律。
它是基于微分方程建立的,通过对变量的增长速率进行建模,可以预测和解释许多现象和问题。
本文将介绍logistic模型的基本原理和应用。
我们来看看logistic模型的微分方程形式。
logistic模型的微分方程可以表示为:dP/dt = k * P * (1 - P/K)其中,P表示随时间变化的变量,t表示时间,k和K是常数。
这个方程描述了P的变化率与P本身以及时间t的关系。
在这个方程中,P的增长速率是由两个因素决定的:一是P本身的大小,二是P相对于K的距离。
logistic模型的应用非常广泛,特别是在生物学、经济学和社会科学等领域。
在生物学中,logistic模型可以描述种群的增长过程。
当种群数量很小时,增长速率很快;而当种群数量接近环境容量时,增长速率会减慢。
在经济学中,logistic模型可以描述市场的饱和现象。
当市场需求量很小时,增长速率很快;而当市场需求量接近供应量时,增长速率会减慢。
在社会科学中,logistic模型可以描述一种观点或理论的传播过程。
当接受者较少时,传播速度很快;而当接受者接近总人口时,传播速度会减慢。
除了上述应用外,logistic模型还可以用于预测和解释其他现象和问题。
例如,可以用logistic模型来预测疾病的传播过程、预测产品的市场份额、预测人口的增长趋势等等。
通过对logistic模型进行参数估计和模型拟合,可以得到对未来发展的预测和解释。
总结一下,logistic模型是一种基于微分方程的数学模型,用来描述某一变量随时间变化的规律。
它通过对变量的增长速率进行建模,可以预测和解释许多现象和问题。
logistic模型的应用非常广泛,包括生物学、经济学和社会科学等领域。
通过对logistic模型的参数估计和模型拟合,我们可以得到对未来发展的预测和解释。
希望本文对读者能够理解logistic模型的基本原理和应用,并在实际问题中加以运用。
(完整版)数学建模logistic人口增长模型

Logistic 人口发展模型一、题目描述建立Logistic 人口阻滞增长模型 ,利用表1中的数据分别根据从1954年、1963年、1980年到2005年三组总人口数据建立模型,进行预测我国未来50年的人口情况.并把预测结果与《国家人口发展战略研究报告》中提供的预测值进行分析比较。
分析那个时间段数据预测的效果好?并结合中国实情分析原因。
表1 各年份全国总人口数(单位:千万)二、建立模型阻滞增长模型(Logistic 模型)阻滞增长模型的原理:阻滞增长模型是考虑到自然资源、环境条件等因素对人口增长的阻滞作用,对指数增长模型的基本假设进行修改后得到的。
阻滞作用体现在对人口增长率r 的影响上,使得r 随着人口数量x 的增加而下降。
若将r 表示为x 的函数)(x r 。
则它应是减函数。
于是有:0)0(,)(x x x x r dt dx== (1)对)(x r 的一个最简单的假定是,设)(x r 为x 的线性函数,即 )0,0()(>>-=s r sxr x r (2) 设自然资源和环境条件所能容纳的最大人口数量mx ,当mx x =时人口不再增长,即增长率)(=m x r ,代入(2)式得m x rs =,于是(2)式为)1()(mx x r x r -= (3)将(3)代入方程(1)得:⎪⎩⎪⎨⎧=-=0)0()1(x x x x rx dtdxm (4)解得:rt mme x x x t x --+=)1(1)(0(5)三、模型求解用Matlab 求解,程序如下: t=1954:1:2005;x=[60.2,61.5,62.8,64.6,66,67.2,66.2,65.9,67.3,69.1,70.4,72.5,74.5,76.3,78.5,80.7,83,85.2,87.1,89.2,90.9,92.4,93.7,95,96.259,97.5,98.705,100.1,101.654,103.008,104.357,105.851,107.5,109.3,111.026,112.704,114.333,115.823,117.171,118.517,119.85,121.121,122.389,123.626,124.761,125.786,126.743,127.627,128.453,129.227,129.988,130.756];x1=[60.2,61.5,62.8,64.6,66,67.2,66.2,65.9,67.3,69.1,70.4,72.5,74.5,76.3,78.5,80.7,83,85.2,87.1,89.2,90.9,92.4,93.7,95,96.259,97.5,98.705,100.1,101.654,103.008,104.357,105.851,107.5,109.3,111.026,112.704,114.333,115.823,117.171,118.517,119.85,121.121,122.389,123.626,124.761,125.786,126.743,127.627,128.453,129.227,129.988];x2=[61.5,62.8,64.6,66,67.2,66.2,65.9,67.3,69.1,70.4,72.5,74.5,76.3,78.5,80.7,83,85.2,87.1,89.2,90.9,92.4,93.7,95,96.259,97.5,98.705,100.1,101.654,103.008,104.357,105.851,107.5,109.3,111.026,112.704,114.333,115.823,117.171,118.517,119.85,121.121,122.389,123.626,124.761,125.786,126.743,127.627,128.453,129.227,129.988,130.756];dx=(x2-x1)./x2; a=polyfit(x2,dx,1);r=a(2),xm=-r/a(1)%求出xm 和rx0=61.5;f=inline('xm./(1+(xm/x0-1)*exp(-r*(t-1954)))','t','xm','r','x0');%定义函数 plot(t,f(t,xm,r,x0),'-r',t,x,'+b');title('1954-2005年实际人口与理论值的比较') x2010=f(2010,xm,r,x0) x2020=f(2020,xm,r,x0) x2033=f(2033,xm,r,x0)解得:x(m)= 180.9516(千万),r= 0.0327/(年),x(0)=61.5得到1954-2005实际人口与理论值的结果:根据《国家人口发展战略研究报告》我国人口在未来30年还将净增2亿人左右。
logit模型的原理与应用

P( y i x)
1
表示:属于后 k 1个等级的累积概率与前 i 个等级的累积概率的比数之对数,故该模型称 为累积比数模型 。 ......( cumulative odds model )
17
3.Logit 模型----多分类(有序)
在探讨影响智力因素的研究中,调查了 875 名小学一年级学生的智商与母亲的文化 程度,结果见下表。试分析两者间的关系。
1
1
0.8 0.6
0.8 0.6
0.4 0.2 0 -4 -2 0
Pobit模型
0.4 0.2 0
Logit模型 6
2
4
3.Logit 模型---提出
5.2.2 logit 模型 该模型是 McFadden 于 1973 年首次提出。其采用的是 logistic 概率分布函数。 其形式是 pi = F(yi) = F(+ xi) =
这里,儿童智商是多分类定性有序变量,宜建立累积比数 logistic 回归。影响因素母 亲文化程度亦是多分类定性有序变量,可直接进入方程。 回归模型见表。
变量 x 常数项 回归系数
0.6373
标准误差
0.0934 0.1454 0.1358 0.1935
Z
6.824
P
0.00
1 2 3
1.4578 1.2254 3.5630
1.2 Y 1.0 0.8 0.6
1, pi xi , 0,
xi 1 0 xi 1 xi 0
0.4 0.2 0.0 -0.2 0 5 10 15 20 25 X 30
(5)
此模型由 James Tobin 1958 年提出,因此称作 Tobit 模型(James Tobin 1981 年获诺贝尔经济学奖) 。
Logistic模型 ppt课件

2、该方法对样本含量的要求较大,当控制的分层因素较 多时,单元格被划分的越来越细,列联表的格子中频 数可能很小,将导致检验结果的不可靠。
3、卡方检验无法对连续性自变量的影响进行分析, 而这将大大限制其应用范围
和最小二乘法区别
选择 “转换”—“计算变量” 命令
在数字表达式框中,输入公式: rv.bernoulli(0.7)
这意思为:返回概率为0.7的bernoulli分 布随机值如果在0.7的概率下能够成功,
那么就为1,失败的话,就为"0"
步骤三:剔除缺失值
用"missing”函数的时候,如果“违约”变量中,确实存 在缺失值,它的返回值应该为“1”或者 为“true", 为
(1)取值区间:上述模型进行预报的范围为整个实数 集,而模型左边的取值范围为 0≤ P≤ 1,二者并 不 相符。模型本身不能保证在自变量的各种组合下,因 变量的估计值仍限制在0~1内。
(2)曲线关联:根据大量的观察,反应变量P与自变 量的关系通常不是直线关系,而是S型曲线关系。 显 然,线性关联是线性回归中至关重要的一个前提假设, 而在上述模型中这一假设是明显无法满足的。
0.概05率,值由为于0年.0龄0[6的。n概如x率果i (值显y小i著于性y显水)]著平2 性为水 Sco平re,j 所以是i能1 进入方n 程的。 y(1 y)(xi x) i1
步骤十:Hosmer和Lemeshow检验
从 Hosmer 和 Lemeshow 检验表中,可以看出:经过4次 迭代后,最终的卡方统计量为:11.919,而临界值为: Chi-square(0.05,8) = 15.507 卡方统计量< 临界值,从Sig 角度来看:0.155 > 0.05 , 说 明模型能够很好的拟合整体,不存在显著的差异。
logistic曲线特点

1. S 型形状:logistic 曲线呈现出S 型的形状,它由两个部分组成:缓慢增长阶段和快速增长阶段,然后是饱和阶段。
2. 对称性:logistic 曲线是对称的,这意味着它在左右两侧是相同的。
3. 饱和点:logistic 曲线有一个饱和点,即增长速度开始减缓并最终停止的点。
4. 可预测性:logistic 曲线可以通过数学模型进行预测,这使得它在许多领域中得到了广泛的应用,例如生物学、经济学和社会学等。
5. 拐点:logistic 曲线有一个拐点,即增长速度由快变慢的点。
6. 斜率变化:logistic 曲线的斜率在不同阶段是不同的,这反映了增长速度的变化。
7. 初始值:logistic 曲线的初始值是一个重要的参数,它决定了曲线的起始位置和形状。
8. 极限值:logistic 曲线有一个极限值,即饱和点,它代表了系统所能达到的最大值。
9. 增长率:logistic 曲线的增长率在不同阶段是不同的,这反映了系统的内在特性。
10. 时间依赖:logistic 曲线的形状和参数取决于时间,这使得它可以用来描述随时间变化的过程。
logistic曲线拟合

logistic曲线拟合istic曲线拟合(parametriccurvefitting)是一种拟合曲线的数学方法,通常用于在已知有限数据的情况下找到一条可能符合这些数据的曲线。
此类曲线往往包含许多参数,因此其表示式有多种可能,其中一种最可能拟合现有数据的曲线就是istic曲线拟合的结果。
在istic曲线拟合中,数据点拟合的过程以统计模型为基础,使用一种最小二乘法或其他拟合技术,用来拟合有限数据点,提取其更适当的参数以表示拟合曲线。
一般来说,令拟合曲线的总和最小是最小二乘istic曲线拟合的目标。
istic曲线拟合广泛应用于科学和工程领域,其中包括天文学、物理学、化学、生物学等等,是一种重要的数据处理方法。
istic曲线拟合的最常见用例是在数据拟合和特征提取的过程中,计算机图像处理,数据建模等任务中。
以下就是istic曲线拟合的实际应用。
1、主要应用于对特定模型数据拟合和特征提取:例如,在物理学中,istic曲线拟合可以用于拟合曲线或曲面,以提取其特征,如角度、拐点等。
在计算机视觉中,istic曲线拟合可用于拟合曲线或曲面,以提取其表面特征,如角点、旋转点等。
2、测量和分析具有复杂模式的数据:在工程、经济研究中,istic 曲线拟合可用于测量和分析具有复杂曲线模式的数据,如经济活动和政治决策等。
3、拟合统计图:在统计图中,istic曲线拟合可用于拟合数据,找出其有关的统计学特征,如中位数和中值,以及统计分布的均值和方差等。
4、在机器学习中应用:istic曲线拟合也可用于机器学习任务,如分布函数估计或统计建模等。
例如,istic曲线拟合可以用于拟合给定数据的高斯分布,以更好地建模数据。
istic曲线拟合是一种广泛应用于科学和工程领域的重要技术,能够有效拟合数据,提取其特征,实现测量和分析,并用于机器学习任务,为工程设计、科学研究、机器学习等工作大大提高效率,并也带来深远的影响。
因此,istic曲线拟合可以作为一门研究课题,深入研究其原理和应用。
Logistic曲线
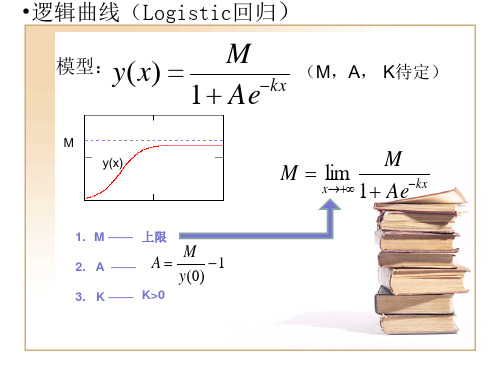
M = − kx 1 + Ae
(M,A,K>0待定)
作对数变换 化为直线型
M ln( − 1) = ln A − kx y
新的因变量P 新的因变量 新的截距 b
A=
M −1 y ( 0)
新的截距 b:lnA :
利用简化公式求斜率
−k =
∑ x P − b∑ x ∑x
i i 2 i
i
•逻辑曲线(Logistic回归)
化为直线型
(A,K待定)
ln y = ln A + k ln x
Line( X,
A= e
b
较好方法: 较好方法
b Y ) = k
y = A ⋅ xk + C
方法一:取定C0,化为直线型
(A,K,C待定)
A0 先给出 V := k 0 猜想值 0 C 0
y = kx + b0
i
(截距 已知,斜率 待定) 唯 一 伴 办 返 法
利用简化公式
∑ x y − b∑ x k= ∑x
i 2 i
i
截距未知:
y = kx + b
Lxy k= Lxx b = y − kx
数
(k,b待定)
繁
伴 返
方法一:利用公式
方法
:计
b = line(X,Y) k
Ex:草履虫在试管培养液中生长观察
T(天 T(天) 0 y(只) 2 1 2 3 4 5 378 6 380 7 381 8 381 20 135 320 374
考虑模型:
M y(t ) = − kt 1 + Ae
•逻辑曲线(Logistic回归)
logistic模型与matlab入门

对应p的分量依次是次数从高 到底各多项式系数
用Richard模拟 水稻叶伸长生长
1
y(t) 47.1(1 98.56e 0.5398t )11.829
关于inline函数
例如: y=inline(‘sin(x)-cos(x)’,’x’) 输入y(0),可得:-1 作图: x=0:0.1:2*pi;plot(x,y(x))
(1)Logistic模型的特点: 模型具有固定的拐点,只能描述一种特定形状的S曲线 。
(2)面临的问题: 生物在一个完整的时间序列里,生物的总生长量最初比
较小,随时间的增加逐渐增长而达到一个快速生长时期,尔 后增长速度趋缓,最终达到稳定的总生长量。此生长过程的 图象描述称为是一种拉长的S形曲线。 (3)更合适的模型描述——Richards模型(1951)
什么是数学建模
把现实世界中的实际问题加以提炼,抽 象为数学模型,求出模型的解,验证模型的 合理性,并用该数学模型所提供的解答来解 释现实问题,我们把数学知识的这一应用过 程称为数学建模。
建模全过程示意图
数学建模的一般步骤
堂上思考题
如何估计一个人体内血液的总量?
示例3、人口预报
一、两个经典模型:
d=eig(A), [v,d]=eig(A): 特征值与特征向量
rand(m,n):
m行n列均匀分布随机数矩阵
randn(m,n):
m行n列正态分布随机数矩阵
Matlab使用
1、matlab使用环境 2、四则运算与一些常用函数 3、关于矩阵提取 4、图形功能 5、M-文件编写
3、关于矩阵的提取,:运算
MATLAB工作区:
可查看所有变量值
logit模型

logit模型Logit模型(Logit model,也译作"评定模型","分类评定模型",又作Logistic regression,"逻辑回归")是离散选择法模型之一,Logit 模型是最早的离散选择模型,也是目前应用最广的模型。
是社会学、生物统计学、临床、数量心理学、计量经济学、市场营销等统计实证分析的常用方法。
Logit模型(Logit模型,也翻译为“评估模型”,“分类评估模型”,也称为Logistic回归,“ logistic回归”)是离散选择方法模型之一,属于多元分析,社会学,生物统计学,临床,定量心理学,计量经济学,市场营销等统计实证分析的常用方法。
物流分配公式P(Y =1│X= x)= exp(x'β)/(1 + exp(x'β))通常通过最大似然来估计参数β。
Logit模型是最早的离散选择模型,也是使用最广泛的模型。
Logit模型首先由Luce(1959)根据IIA特性得出。
Marschark (1960)用最大效用理论证明了Logit模型的一致性。
Marley(1965)研究了模型形式与非确定效用项的分布之间的关系,证明了极值分布可以推导模型的Logit形式。
McFadden(1974)反过来证明,具有Logit形式的模型的非确定性项必须服从极值分布。
从那时起,Logit模型已在心理学,社会学,经济学和交通运输领域得到广泛使用,并且衍生并开发了其他离散选择模型以形成完整的离散选择模型系统,例如Probit模型和NL模型(Nest Logit模型)。
),混合Logit模型等。
该模型假定单个n对选择分支j的效用包括两部分:效用决定因素项和随机项:Logit模型得到广泛应用的原因主要是由于其概率表达式的显着特征,模型的快速求解速度以及便捷的应用。
当模型选择集不发生变化时,仅当每个变量的级别发生变化时(例如行进时间发生变化),就可以轻松解决新环境中每个选择分支的概率。
浅析Logistic数学模型在江西省在岗职工未来十年工资水平预测中的应用

发明与创新
3
Copyright©博看网 . All Rights Reserved.
· 教育探索 ·
年份 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008
一、引言
工资的发展和经济密切相关,我国经济发展的战略目标是
要在21世纪中叶使我国人均国民生产总值达到中等发达国家水
平,所以在未来的几十年内我国工资会增长较快。但经济发展
到一定程度之后,发展速度会减慢,以避免出现经济危机。工
资的增长又与经济增长相关,所以工资达到一定值后工资的增
长率将会减小。据此,本文选定一个S型曲线来反映工资的增
长规律,即建立Logistic数学模型来反映江西省在岗职工年平均
工资的增长情况。 二、建立江西省在岗职工年平均工资预测的Logistic数学
模型
(一)Logistic数学模型表达式的建立
由于工资水平的增长速度是先快后慢,因此建立反映工资
水平变化规律的Logistic数学模型表达式如下:
y
=
a
1 + be−ct
我们把1989年的年平均工资和2018年的年平均工资代入(1)中,
计算出 b, c 的值作为初始值,= 其值为 b0 0= .000732, c0 0.1378.
有了 b, c 的初始值之后,我们对Logistic模型进行回归分析,利
^
^
用MATLAB软件求出 b, c 的估计值为 b = 0.0006, c = 0.1341.
表1 1989年到2028年实际工资与预测工资数据对比表
logistic模型及其matlab算法
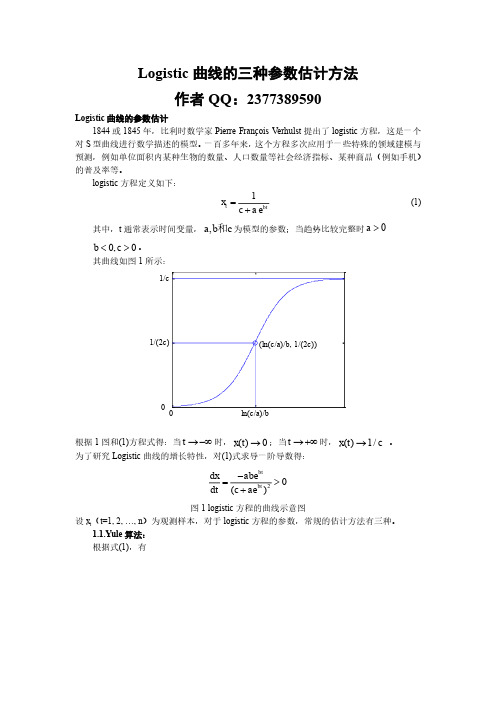
Logistic 曲线的三种参数估计方法作者QQ :2377389590Logistic 曲线的参数估计1844或1845年,比利时数学家Pierre François Verhulst 提出了logistic 方程,这是一个对S 型曲线进行数学描述的模型。
一百多年来,这个方程多次应用于一些特殊的领域建模与预测,例如单位面积内某种生物的数量、人口数量等社会经济指标、某种商品(例如手机)的普及率等。
logistic 方程定义如下:1et btx c a =+ (1) 其中,t 通常表示时间变量,,a b c 和为模型的参数;当趋势比较完整时0a >0,0b c <>。
其曲线如图1所示:0 1/(2c)1/c根据1图和(1)方程式得:当t →-∞时,()0x t →;当t →+∞时,()1/x t c → 。
为了研究Logistic 曲线的增长特性,对(1)式求导一阶导数得:20()btbt dx abe dt c ae -=>+ 图1 logistic 方程的曲线示意图设x t (t =1, 2, …, n )为观测样本,对于logistic 方程的参数,常规的估计方法有三种。
1.1.Yule 算法: 根据式(1),有111(1)=11()(1)(1)(1)t t tt t b t btbt b btb b tx x xx x c ae c ae ae c c e c ae e c e x ++++--+=-++--=+=--- (2) 设11t tt t x x z x ++-=、1b e γ=-以及(1)b c e β=--,则式(2)变形为线性方程t t z x γβ=+,利用普通最小二乘(OLS )方法可以得到这个方程参数的估计值,b 和c 的估计值也可以进一步得到。
为得到a 的估计值,将式(1)变形为:1ˆˆˆln ln t c a bt x ⎛⎫-=+ ⎪⎝⎭t =1. 2.…, n (3) 左右分别对t 求和11(1)ˆˆˆln ln 2nt t n n c n a b x =⎛⎫+-=+ ⎪⎝⎭∑ (4) 因此,a 的估计值为:111(1)ˆˆˆexp ln 2n t t n n a c b n x =⎧⎫⎡⎤⎛⎫+⎪⎪=--⎨⎬⎢⎥ ⎪⎝⎭⎪⎪⎣⎦⎩⎭∑ (5)1.2.Rhodes 算法: 根据式(1),有(1)1(1)1(1)b t t b b b t bbtc ae x c ce ce ae e c e x +++=+=-++=-+(6) 设11t t z x +=、1t t s x =、(1)b c e γ=-以及b e β=,则式(6)变形为t t z s γβ=+。
四参数logistic约束模型

四参数logistic约束模型
首先,让我们来看增长率参数。
这个参数代表了增长的速率,也就是说,它决定了增长曲线的陡峭程度。
增长率参数的值越大,增长曲线就会越陡峭,增长速度越快;反之,增长率参数越小,增长曲线就会越平缓,增长速度越慢。
其次,上限参数是指增长过程的上限值,也就是增长过程最终会趋于的数值。
在实际应用中,这个参数可以用来描述一个系统或者过程的最大容量或者最大承载能力。
当增长过程接近上限值时,增长速度会逐渐减缓,最终趋于稳定状态。
然后,下限参数则是指增长过程的下限值,也就是增长过程的起始值。
这个参数可以用来描述一个系统或者过程的初始状态,或者是增长过程的最小值。
在实际应用中,下限参数通常用来表示某个过程的起始状态或者最小容量。
最后,增长偏移参数用于描述增长曲线的偏移情况。
它可以用来调整增长曲线的位置,使其与实际数据更好地拟合。
增长偏移参数的调节可以帮助我们更准确地预测增长过程的发展趋势。
总的来说,四参数logistic约束模型提供了一种灵活而全面的方法来描述各种增长过程,通过调节这四个参数的值,我们可以更好地理解和预测不同系统和过程的增长趋势。
这种模型在许多领域都有着广泛的应用,对于研究和预测各种增长现象都具有重要的意义。
四参数logistic曲线拟合

四参数logistic曲线拟合
四参数逻辑回归模型(4PLM)是一种非线性回归模型,用于描述因变量和自变量之
间的关系。
它比传统的逻辑回归模型具有更大的灵活性,因为它允许曲线形状更复杂。
四参数逻辑回归模型的公式为:
y=1+(cx)b a−d+d
其中:
•a是曲线的上界(当x趋向于无穷大时,y的值)。
•b是曲线的形状参数。
•c是曲线的中点(当y等于0.5时,x的值)。
•d是曲线的下界(当x趋向于无穷小或等于0时,y的值)。
要拟合四参数逻辑回归模型,您需要使用适当的统计软件或编程语言。
以下是一个使用Python和SciPy库进行四参数逻辑回归拟合的示例代码:
拟合参数为:[2.00195345 0.99999991 5.00000164 0.00000012]
这些参数值对应于四参数逻辑回归模型的公式中的a,b,c,d。
通过拟合,我们可以找到最适合数据的模型参数,并使用它们来描述因变量和自变量之间的关系。
Logistic模型及建模流程概述

Logistic 模型及建模流程概述1. Logistic 模型介绍1.1 问题的提出在商业及金融领域中,存在这么一类问题,问题中需要被解释的目标量通常可以用YES 或者NO 两种取值来表示,如:卖出了商品为YES ,未卖出商品为NO ;顾客对超市的本次宣传活动做了响应为YES ,没有任何响应为NO ;信用卡持卡人本月逾期付款为YES ,按时还款了为NO ; 等等;对于这类问题的分析,我们不可以采用标准的线性回归对其进行建模分析,是因为目标变量的二元分布违背了线性回归的重要假设模型的目标是给出一个(0,1)之间的概率,而标准的线性回归模型产生的值是在这个范围之外 1.2 Logistic 模型对于上述问题,我们提出了logistic 模型:∑+=-iii x P P βα)1ln(∑+=-ii i x e PPβα1∑+∑++=ii i iii x x eeP βαβα1Logistic 模型可以保证:i x 值在- ∞和+ ∞之间;估计出来的概率值在0和1之间;与事件odds ()1/(p p odds -=)直接相关;可以很好地将问题转化为数学问题,并且模型结果容易解释;1.3 Logistics 回归的假设概率是自变量的logistics 函数)exp(1)exp(110110n n n n x x x x p ββββββ+⋅⋅⋅++++⋅⋅⋅++=这样得到的概率似乎没有实际意义,只是反映一种趋势,x x n βββ+⋅⋅⋅++110比较大时p 就会比较大 取log 值得到:logodds这样可以线性化,我们把这模型称为‘linear in the log-odds ’ 模型假设:1) 没有重要变量被忽略,不包含使得系数有偏的相关变量2) 不包含外来变量,包含的不相关变量会增加参数估计的标准误差,但是却不会使得系数有偏。
观测值独立自变量的观测值没有误差 1.4 最大似然准则抛一枚硬币10次,结果如下:T H T T T H T T T H假设结果独立,考虑得到的结果的概率,P(T H T T T H T T T H) =P(T)P(H)P(T)P(T)P(T)P(H)P(T)P(T)P(T)P(H)=P(H)3 [1-P(H)]7,如果我们能计算出参数P(H)的值,就能得到掷硬币结果的概率的数值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
传染病问题中的SIR模型
摘要:
2003年春来历不明的SARS病毒突袭人间,给人们的生命财产带来极大的危害。
长期以来,建立传染病的数学模型来描述传染病的传播过程,分析受感染人数的变化规律,探索制止传染病蔓延的手段等,一直是我国及全世界有关专家和官员关注的课题。
不同类型的传染病的传播过程有其各自不同的特点,我们不是从医学的角度一一分析各种传染病的传播,而是从一般的传播机理分析建立各种模型,如简单模型,SI模型,SIS 模型,SIR模型等。
在这里我采用SIR(Susceptibles,Infectives,Recovered)模型来研究如天花,流感,肝炎,麻疹等治愈后均有很强的免疫力的传染病,它主要沿用由Kermack 与McKendrick在1927年采用动力学方法建立的模型。
应用传染病动力学模型来描述疾病发展变化的过程和传播规律,预测疾病发生的状态,评估各种控制措施的效果,为预防控制疾病提供最优决策依据, 维护人类健康与社会经济发展。
关键字:传染病;动力学;SIR模型。
一﹑模型假设
在疾病传播期内所考察的地区范围不考虑人口的出生、死亡、流动等种群动力因素。
总
人口数N(t)不变,人口始终保持一个常数N。
人群分为以下三类:
易感染者(Susceptibles),
其数量比例记为s(t),表示t时刻未染病但有可能被该类疾病传染的人数占总人数的比例;感染病者(Infectives),
其数量比例记为i(t),表示t时刻已被感染成为病人而且具有传染力的人数占总人数的比例;
恢复者(Recovered),
其数量比例记为r(t),表示t时刻已从染病者中移出的人数(这部分人既非已感染者,也非感染病者,不具有传染性,也不会再次被感染,他们已退出该传染系统。
)占总人数的比例。
病人的日接触率(每个病人每天有效接触的平均人数)为常数λ,日治愈率(每天被治愈的病人占总病人数的比例)为常数μ,
显然平均传染期为1/μ,传染期接触数为σ=λ/μ。
该模型的缺陷是结果常与实际有一定程度差距,这是因为模型中假设有效接触率传染力是不变的。
Logistic曲线模型:
如下为拟合的原始数据点:
选定初始值A=500(至于为何选取A=500,请参阅相关文献资料,有相当多的方法供选取),分别代入x=1,F(x)=3和x=2,F(x)=13到Logistic曲线方程
>>[b,c]=solve('500/(1+b*exp(-c*1))=3','500/(1+b*exp(-c*2))=13','b,c')
解得初始值:A=500, b=732.6,c=1.487
编写Matlab程序LogisticDemo.m如下:%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% x=1:8;
y=[3,13,80,195,332,895,1038,1143];
c0=[500,732.6,1.487];
fun=inline('c(1)./(1+c(2).*exp(-c(3).*x))','c','x');
b=nlinfit(x,y,fun,c0);b
t=0:.01:8;
plot(x,y,'r.',t,fun(b,t)) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Matlab中运行如上程序,结果如下图
红色框内对应的3个值即为A,b,c的参数解。
最终解得:A=1165, b=3109,c=1.5 Logistic曲线方程为:。
