第十六章 实验十五 用双缝干涉测光的波长
高考物理实验-用双缝干涉测光的波长

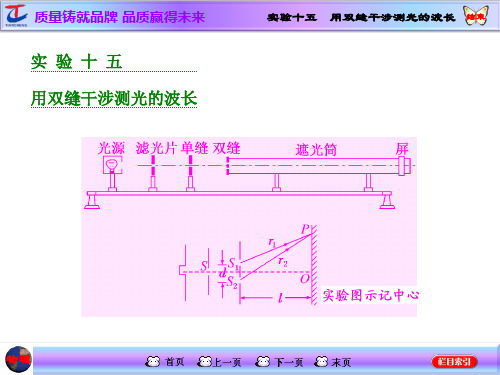
用双缝干涉测光的波长知识元用双缝干涉测光的波长知识讲解一、实验目的观察干涉图样,测定光的波长.二、实验原理双缝干涉中相邻两条明(暗)条纹间的距离△x与波长λ、双缝间距离d及双缝到屏的距离L 满足△x=λ.因此,只要测出△x、d和L,即可求出波长λ.三、实验器材双缝干涉仪(包括光具座、光源、滤光片、单缝、双缝、遮光筒、毛玻璃屏、测量头)、刻度尺.四、实验步骤1.观察双缝干涉图样①将光源、滤光片、单缝、双缝、遮光筒、毛玻璃屏依次安放在光具座上,如图所示.②接好光源,打开开关,使灯丝正常发光.③调节各器件的高度,使光源灯丝发出的光能沿轴线到达光屏.④安装双缝,使双缝与单缝的缝平行,二者间距5~10cm.⑤观察白光的干涉条纹.⑥在单缝和光源间放上滤光片,观察单色光的干涉条纹.2.测定单色光的波长(1)安装测量头,调节至可清晰观察到干涉条纹.(2)使分划板中心刻线对齐某条亮条纹的中央,记下手轮上的读数a1,转动手轮,使分划板中心刻线移动,记下移动的条纹数n和移动后手轮的读数a2,a1与a2之差即n条亮纹的间距.(3)用刻度尺测量双缝到光屏间距离l(d是已知的).(4)重复测量、计算,求出波长的平均值.(5)换用不同滤光片,重复实验测量其他单色光的波长.五、注意事项1.安装器材时,注意调节光源、滤光片、单缝、双缝的中心均在遮光筒的中心轴线上,并使单缝、双缝平行且竖直.2.光源灯丝最好为线状灯丝,并与单缝平行且靠近.3.调节的基本依据是:照在屏上的光很弱,主要原因是灯丝与单缝、双缝、测量头、遮光筒不共轴所致,干涉条纹不清晰的主要原因是单缝与双缝不平行.4.光波波长很短,△x、l的测量对波长λ的影响很大,l用毫米刻度尺测量,△x利用测量头测量.可测多条亮纹间距再求△x,采用多次测量求λ的平均值法,可减小误差.例题精讲用双缝干涉测光的波长例1.在“用双缝干涉测光的波长”实验中,将所用器材按要求安装在如图甲所示的光具座上,然后接通电源使光源正常工作。
实验十五 用双缝干涉实验测量光的波长

例1 [2021·浙江6月选考] 如图所示是“用双缝干涉测量光的波长”实验的装置.实验中:
(1)观察到较模糊的干涉条纹,要使条纹变得清晰,值得尝试的是____(填选项前的字母).
A.旋转测量头B.增大单缝与双缝间的距离C.调节拨杆使单缝与双缝平行
则所测单色光的波长为_____ .(结果保留3位有效数字)
考向一 实验仪器的创新
例2 [2022·南开中学模拟] 如图所示是用光传感器做双缝干涉的实验装置.激光光源在铁架台的最上端,中间是刻有双缝的挡板,下面是光传感器.光传感器是一个小盒,在图中白色狭长矩形部分,沿矩形的长边分布着许多光敏单元.这个传感器各个光敏单元得到的光照信息经计算机处理后,在荧光屏上显示出来.
第十四单元 光学
实验十五 用双缝干涉实验测量光的波长
教材原型实验
拓展创新实验
教师备用习题
作业手册
一、实验目的
1.观察双缝干涉图样,掌握实验方法.
2.测量单色光的波长.
二、实验原理
相邻两条亮条纹的中心间距 与入射光波长 ,双缝 、 间距 及双缝与屏的距离 满足的关系式为: ,则 .据此可测算出光的波长.
(2)用激光替代普通光源来做本实验,最主要是利用了激光的____(填选项前的字母).
A.相干性高 B.平行度好 C.亮度高
A
[解析] 激光的相干性高,因此可用激光替代普通光源来做实验,故A正确,B、C错误.
光传感器沿矩形的长边分布着许多光敏单元,传感器各个光敏单元得到的光照信息经计算机处理后,可以在显示器上显示出来;然后根据显示器上干涉图像的条纹间距,可以算出光的波长.
(1)若想增加从目镜中观察到的条纹个数,该同学可____(填选项前的字母).
实验十五 用双缝干涉测光的波长
结束
(2)将测量头的分划板中心刻线与某亮纹中心对齐,将该亮纹定为 第 1 条亮纹,此时手轮上的示数如图实1511 甲所示,然后同方 向转动测量头,使分划板中心刻线与第 6 条亮纹中心对齐,记下 此时如图乙所示的手轮上的示数13.870 ______mm,求得相邻亮纹的间 距 Δx 为______mm 。 2.310
物理
质量铸就品牌 品质赢得未来
实验十五
用双缝干涉测光的波长
结束
l 解析:由条纹间距公式 Δx=dλ,d 指双缝间距离,l 指双缝到 屏的距离,可知:A 项中 l 减小,Δx 变小;B 项中 λ 变大,Δx 变大;D 项中 d 变大,Δx 变小。故 A、B、D 正确。
答案:ABD
物理
质量铸就品牌 品质赢得未来
由于激光是相干光源。故可以去掉的部件是②③。 心刻线对准第 10 条亮条纹,读下手轮的读数如图乙所示。则相
1.610 邻两亮条纹的间距是______mm 。
考查实验操作读数及数据处理 甲图读数是 0.045 mm,乙图读数是 14.535 图实152 mm,它们的 差值是 14.490 mm,中间跨越了 10-1=9 个条纹间距, (4)如果已经量得双缝的间距是 0.30 mm、双缝和光屏之间的
图实1511 解析:图甲的读数为 2.320 mm,图乙的读数为 13.870 mm,
13.870-2.320 Δx= mm=2.310 mm。 6-1
物理
质量铸就品牌 品质赢得未来
实验十五
用双缝干涉测光的波长
结束
(3)已知双缝间距 d 为 2.0×10-4 m, 测得双缝到屏的距离 l 为 0.700 m,
实验十五
用双缝干涉测光的波长
结束
用双缝干涉测量光的波长课件

双缝干涉实验介绍
双缝干涉实验装置
光源
提供单色光,如激光。
双缝装置
由两个相距一定距离的狭缝组成,用于产生相干 光束。
屏幕
放置在双缝装置的后面,用于观察干涉条纹。
关领域的发展。
对未来学习的启示
1 2 3
重视实验操作和观察 通过双缝干涉实验,我们了解到实验操作和观察 的重要性,这是理解物理现象和规律的基础。
深入理解光的本质 双缝干涉实验让我们更深入地理解了光的本质, 包括光的波动性和粒子性等方面的知识。
培养探究和创新精神 双缝干涉实验不仅是一个验证理论的实验,也是 一个探究和创新的过程,通过实验可以培养我们 的探究和创新精神。
环境因素误差
环境因素如温度、湿度等的变化也 会对实验结果产生影响。因此,在 实验过程中,需要尽量保持环境因 素的稳定。
实验结论
光的波长与干涉现象的关系
光的波长决定了干涉条纹的间距
光的波长越长,干涉条纹间距越大;波长越短,间距越小。
干涉现象是光波动性的体现
干涉现象是光波动性的直接证据,通过干涉条纹可以直观地了解光波的特性。
双缝干涉实验原理
干涉现象
当两束相干光波相遇时,它们会相互 加强或抵消,形成明暗交替的干涉条 纹。
波长与干涉条纹间距
测量波长
通过测量干涉条纹的间距,结合已知 的光源和双缝间距,可以计算出光的 波长。
光的波长越长,干涉条纹间距越大; 反之,波长越短,间距越小。
测量光的波长
测量光波长的原理
光的干涉现象
用双缝干涉测量光的 波长课件
【课件】用双缝干涉实验测量光的波长(课件)

此时手轮上的示数如图3所示。图2读数x1=__________mm,图3读数
9.200
n=__________mm。
(3)用刻度尺测量双缝到光屏的距离L,已知双缝的间距d。
(4)根据以上实验数据,求得单色光波长的表达式为λ=__________.(用
第(2)(3)中的字母表示)。
感谢观看
但都由分划板、目镜、手轮等构成。转动手
轮,分划板会左右移动。测量时,应使分划
板的中心刻线与条纹的中心对齐(图4.4-3),
记下此时手轮上的读数。然后转动测量头,
使分划板中心刻线与另一条纹的中心对齐,
再次记下手轮上的读数。两次读数之差表示
这两个条纹间的距离∆x。
PART 02
实验仪器及步骤
实验仪器
➢知道获得干涉图样的实验操作要求,理解实验中满足干涉
条件的方法。
➢会用控制变量的方法分别研究光的颜色、双缝距离等与条
纹间距的关系。
➢会设计实验数据记录表并记录数据,会根据给出的波长表
达式计算不同颜色光的波长。
实验原理
➢ 在“用双缝干涉测量光的波长”实验中,让灯泡发出的光先通
过滤光片变成单色光,再通过单缝片把单色光变成线光源,最
会引起干涉条纹移动而使读数无效。
3.测量条纹间距时,测量头中分划板中心线必须与条纹的中央对齐
4.本实验仪器型号不同,则测量头也不同,须掌握正确读数方法。
PART 03
数据分析及处理
数据处理及分析
【数据记录】
数据记录
双缝间距d/m
双缝片到屏的距离 l/m
手轮读数a1/m
手轮读数a2/m
移动条纹数n -1
遮光筒的轴线传播。
《用双缝干涉仪测定光的波长》 知识清单

《用双缝干涉仪测定光的波长》知识清单一、实验目的使用双缝干涉仪精确测定光的波长,加深对光的波动性的理解。
二、实验原理当一束单色光通过双缝时,会在屏幕上形成明暗相间的干涉条纹。
相邻两条亮纹(或暗纹)之间的距离Δx 与双缝间距 d、双缝到屏幕的距离 L 以及光的波长λ 之间存在关系:λ =d·Δx / L。
通过测量Δx、d 和 L,就能够计算出光的波长λ。
三、实验器材双缝干涉仪(包括光源、滤光片、单缝、双缝、遮光筒、光屏等)、测量头(由目镜、手轮、分划板等组成)、米尺。
四、实验步骤1、安装仪器将光源、滤光片、单缝、双缝、遮光筒依次安装在光具座上,调整各部件的高度和位置,使光源发出的光能够顺利通过各部件,在光屏上形成清晰的干涉条纹。
2、观察干涉条纹打开光源,通过目镜观察干涉条纹的形状、间距和清晰度。
若条纹不清晰,可适当调整单缝和双缝的位置。
3、测量条纹间距转动测量头的手轮,使分划板的中心刻线与某一亮纹的中心对齐,记下此时手轮上的读数 a₁。
然后移动分划板,使中心刻线与相邻的另一亮纹的中心对齐,记下此时手轮上的读数 a₂。
则相邻两条亮纹的间距Δx =|a₂ a₁| / n,其中 n 为测量的亮纹间隔数。
4、测量双缝到光屏的距离 L用米尺测量双缝到光屏的距离 L。
5、测量双缝间距 d取下双缝,用显微镜测量双缝的间距 d。
6、计算光的波长将测量得到的Δx、d 和 L 代入公式λ =d·Δx / L,计算出光的波长。
7、重复测量为了减小测量误差,重复进行多次测量,取平均值作为最终结果。
五、注意事项1、单缝和双缝应相互平行,且缝的宽度要适当。
缝太宽,干涉条纹不清晰;缝太窄,光的强度太弱,也不利于观察。
2、测量头的读数要准确,读数时要注意估读。
3、测量双缝间距 d 时,要使用显微镜,并注意正确的测量方法和读数。
4、光源要稳定,且亮度适中,以保证干涉条纹清晰。
5、实验环境要尽量安静,避免振动对实验结果的影响。
实验十五用双缝干涉测光的波长

将白光光源C放在光具座最左端,依次放置其他光学元件,由左至右,表示各光学元件的字母排列顺序应为C、________、A.
本实验的步骤有: 取下遮光筒左侧的元件,调节光源高度,使光束能直接沿遮光筒轴线把屏照亮; 按合理顺序在光具座上放置各光学元件,并使各元件的中心位于遮光筒的轴线上; 用米尺测量双缝到屏的距离;
1
在实验中,若经粗调后透过测量头上的目镜观察,看不到明暗相间的条纹,只看到一片亮区,造成这种情况的最可能的原因是
2
________________________________________________.
3
在“用双缝干涉测光的波长”的实验中,装置如图11所示.双缝间的距离d=3 mm. 图11
用测量头(其读数方法同螺旋测微器)测量数条亮纹间的距离.
在操作步骤②时还应注意______________________________
和__________________________________________________.
03
02
01
图4
将测量头的分划板中心刻线与某亮纹中心对齐,将该亮纹定为第1条亮纹,此时手轮上的示数如图4所示,然后同方向转动测量头,使分划板中心刻线与第6条亮纹中心对齐,记下此时图乙中手轮上的示数________mm.求得相邻亮纹的间距Δx为________mm.
然后再转动手轮,分划板中心刻线向右移动,依次经过2、3……明纹,最终与明纹6中心对齐,分划板中心刻线与明纹1和明纹6对齐时游标卡尺示数分别如图中B、C所示(游标卡尺为10分度),则图B对应的读数为________m,图C对应的读数为________m.用刻度尺量得双缝到屏的距离为60.00 cm.由双缝上标示获知双缝间距为0.2 mm,则发生干涉的光波波长为________m.
实验十五用双缝干涉测光的波长

使用高精度的测量工具,如显微镜、测微器等。
提高操作者的技能水平,确保操作过程中产生的误差最 小化。
05 结论与总结
实验结论
1
成功观察到双缝干涉现象,验证了光的波动性质。
2
通过测量干涉条纹间距,计算得到单色光的波长。
3
实验结果与理论值基本一致,证明了双缝干涉实 验的可靠性。
实验收获与体会
01 掌握了双缝干涉实验的基本原理和操作方 法。
在双缝干涉实验中,单色光通过两条狭缝后形成相干光源,在光屏上产生明暗交 替的干涉条纹。
波长的定义与测量方法
波长是光波的一个基本参数,表 示光波在一个周期内传播的距离。
在双缝干涉实验中,可以通过测 量干涉条纹的间距来间接测量光
的波长。
具体测量方法包括使用测量尺或 显微镜来测量光屏上相邻干涉条 纹之间的距离,并根据干涉公式
THANKS FOR WATCHING
感谢您的观看
误差分析
测量误差
由于实验过程中使用的测量工具可能存在误差, 导致测量结果存在偏差。
环境因素
实验环境中的温度、湿度等变化可能对实验结果 产生影响。
操作误差
实验操作过程中可能存在的误差,如调整显微镜 时产生的误差等。
误差分析
为了获得更准确的实验结果,可以采取以下措施
在稳定的实验环境下进行实验,尽量减少环境因素的影 响。
干涉条纹的清晰度
观察到清晰的干涉条纹,表明实验过程中双缝干涉现象明显。
条纹间距与波长关系
通过观察不同波长的光产生的干涉条纹间距,可以初步判断波长与条纹间距之间的关系。
测量结果计算
测量双缝间距
使用显微镜测量双缝间距,确保 测量结果的准确性。
计算波长
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验十五 用双缝干涉测光的波长 目标要求 1.掌握由Δx =l dλ测量光的波长的原理,并会测单色光波长.2.观察单色光的双缝干涉图样,掌握测量头测量条纹间距的方法.实验技能储备1.实验原理单色光通过单缝后,经双缝产生稳定的干涉图样,图样中相邻两条亮(暗)条纹间距Δx 与双缝间距d 、双缝到屏的距离l 、单色光波长λ之间满足λ=d lΔx . 2.实验步骤(1)观察双缝干涉图样①将光源、遮光筒、毛玻璃依次安放在光具座上,如图所示.②接好光源,打开开关,使灯丝正常发光.③调节各器件的高度和角度,使光源灯丝发出的光能沿遮光筒轴线到达光屏.④安装单缝和双缝,尽量使缝的中点位于遮光筒的轴线上,使单缝与双缝平行,二者间距约为5~10 cm.⑤在单缝和光源间放上滤光片,观察单色光的干涉条纹.(2)测量单色光的波长①安装测量头,调节至可清晰观察到干涉条纹.②使分划板中心刻线对齐某条亮条纹的中心,记下此时手轮上的读数a 1,将该条纹记为第1条亮条纹;转动手轮,使分划板中心刻线移动至第n 条亮条纹的中心,记下此时手轮上的读数a n .③用刻度尺测量双缝与光屏间距离l (d 是已知的).④改变双缝间的距离d ,双缝到屏的距离l ,重复测量.3.数据分析(1)条纹间距Δx =a n -a 1n -1.(2)波长λ=d l Δx . (3)计算多组数据,求λ的平均值.4.注意事项(1)安装时,注意使光源、透镜、滤光片、单缝、双缝的中心均在遮光筒的中心轴线上,并使单缝、双缝平行且间距适当.(2)光源灯丝最好为线状灯丝,并与单缝平行且靠近.(3)调节的基本依据:照在光屏上的光很弱,主要原因是灯丝与单缝、双缝,测量头与遮光筒不共轴;干涉条纹不清晰,一般原因是单缝与双缝不平行.考点一 教材原型实验例1 如图所示,在“用双缝干涉测量光的波长”实验中:(1)在光具座上放置的光学元件依次为:①光源、②滤光片、③________、④________、⑤遮光筒、⑥光屏(含测量头).(2)利用图中装置研究双缝干涉现象时,下列说法中正确的是________.A .将光屏移近双缝,其他条件不变,干涉条纹间距变小B .将滤光片由蓝色的换成红色的,其他条件不变,干涉条纹间距变大C .将单缝向双缝移动一小段距离后,其他条件不变,干涉条纹间距变大D .换一个两缝之间距离更大的双缝,其他条件不变,干涉条纹间距变小E .去掉滤光片,其他条件不变,干涉现象消失(3)在某次测量中,将测量头的分划板中心刻线与某条亮条纹中心对齐,将该亮条纹记为第1条亮条纹,此时手轮上的示数如图甲所示.然后同方向转动测量头,使分划板中心刻线与第6条亮条纹中心对齐,此时手轮上的示数如图乙所示,则此示数为________ mm ,由此可求得相邻亮条纹的间距Δx 为________ mm.(4)已知双缝间距d 为2.0×10-4 m ,测得双缝到屏的距离l 为0.700 m ,由计算式λ=__________,求得所测红光波长为________ nm.答案 (1)单缝 双缝 (2)ABD(3)13.870 2.310 (4)Δxd l 660 解析 (1)由题图可知,③为单缝,④为双缝.(2)将光屏移近双缝,l 减小,则由Δx =l dλ可知,在其他条件不变时,干涉条纹间距变小,故A 正确;将滤光片由蓝色的换成红色的,则波长λ变大,所以其他条件不变时,干涉条纹间距变大,故B 正确;将单缝向双缝移动一小段距离后,其他条件不变时,干涉条纹间距不变,故C 错误;换一个两缝之间距离更大的双缝,则d 变大,在其他条件不变时,干涉条纹间距变小,故D 正确;去掉滤光片,其他条件不变,会形成彩色干涉条纹,故E 错误.(3)由题图乙可得读数为x 2=13.5 mm +37.0×0.01 mm =13.870 mm ,由题图甲可得读数为x 1=2 mm +32.0×0.01 mm =2.320 mm ,则相邻亮条纹的间距Δx =x 2-x 15=13.870-2.3205mm =2.310 mm.(4)由Δx =l d λ可得λ=d l Δx ,代入数据解得,波长为λ=2.310×10-3×2.0×10-40.700m =6.6×10-7 m =660 nm.例2 (2023·浙江省镇海中学模拟)(1)如图所示,小王同学做在“用双缝干涉测量光的波长”实验中发现目镜中干涉条纹与分划板中心刻线始终有一定的角度,下列哪个操作可以使得分划板中心刻线与干涉条纹平行________.A .仅拨动拨杆B .仅旋转单缝C .仅前后移动凸透镜D .仅旋转毛玻璃处的测量头(2)小王同学将分划板中心刻线与干涉条纹调平行后,将测量头的分划板中心刻线与某条亮条纹中心对齐,将该亮条纹定为第1条亮条纹,此时手轮上的示数如图所示,手轮上的示数是________ mm.答案 (1)D (2)50.15解析 (1)若要使得分划板中心刻线与干涉条纹平行,则仅旋转毛玻璃处的测量头即可,故选D.(2)手轮上的示数是50 mm +0.05 mm ×3=50.15 mm.考点二 探索创新实验例3 洛埃德在1834年提出了一种更简单的观察干涉的装置.如图所示,单色光从单缝S 射出,一部分入射到平面镜后反射到屏上,另一部分直接投射到屏上,在屏上两光束交叠区域里将出现干涉条纹.单缝S 通过平面镜成的像是S ′.(1)通过洛埃德镜在屏上可以观察到明暗相间的干涉条纹,这和双缝干涉实验得到的干涉条纹一致.如果S 被视为其中的一个缝,________相当于另一个“缝”.(2)实验中已知单缝S 到平面镜的垂直距离h =0.15 mm ,单缝到光屏的距离D =1.2 m ,观测到第3条亮条纹中心到第12条亮条纹中心的间距为22.78 mm ,则该单色光的波长λ=________ m .(结果保留1位有效数字)(3)以下哪些操作能够增大光屏上相邻两条亮条纹之间的距离________.A .将平面镜稍向上移动一些B .将平面镜稍向右移动一些C .将光屏稍向右移动一些D .将光源由红色光改为绿色光答案 (1) S ′ (2)6×10-7 (3)AC解析 (1)通过洛埃德镜在屏上可以观察到明暗相间的干涉条纹,这和双缝干涉实验得到的干涉条纹一致.如果S 被视为其中的一个缝,S ′相当于另一个“缝”.(2)第3条亮条纹中心到第12条亮条纹中心的间距为22.78 mm ,则相邻亮条纹间距为Δx =22.78×10-312-3m ≈2.53×10-3 m ,等效双缝间的距离为d =2h =0.30 mm =3.0×10-4 m ,根据双缝干涉条纹间距Δx =D d λ,则有λ=d D Δx =3.0×10-4×2.53×10-31.2m ≈6×10-7 m. (3)根据双缝干涉条纹间距Δx =D d λ可知,仅增大D 、仅减小d 或仅增大波长λ都能够增大光屏上相邻两条亮条纹之间的距离,所以A、C正确.课时精练1.(2021·浙江6月选考·17(2))如图所示是“用双缝干涉测量光的波长”实验的装置.实验中:(1)观察到较模糊的干涉条纹,要使条纹变得清晰,值得尝试的是________.(单选)A.旋转测量头B.增大单缝与双缝间的距离C.调节拨杆使单缝与双缝平行(2)要增大观察到的条纹间距,正确的做法是________.(单选)A.减小单缝与光源间的距离B.减小单缝与双缝间的距离C.增大透镜与单缝间的距离D.增大双缝与测量头间的距离答案(1)C(2)D解析(1)若粗调后看到的是模糊不清的条纹,则最可能的原因是单缝与双缝不平行,要使条纹变得清晰,可尝试调节拨杆使单缝与双缝平行,故选C.(2)根据Δx=ldλ,可知要增大条纹间距,可以增大双缝到光屏的距离l或减小双缝的间距d,故选D.2.可发出红、黄、绿三色光的多层警示灯,被广泛应用于数控机床、电子机械自动化生产线等工业领域.某同学想采用如图甲所示的实验装置测定三种色光的波长.(1)打开多层示警灯的绿光灯,将遮光筒对准光源放置.在光源和双缝之间还必须放置一个________(选填“滤光片”或“单缝”),其目的是保证经双缝得到的两列光是________(选填“相干”或“非相干”)光;(2)已知双缝之间的距离为0.6 mm,双缝到屏的距离为1.5 m,绿光的干涉图样如图乙所示,分划板中心刻线在A 位置时螺旋测微器的读数为1.128 mm ,在B 位置时读数如图丙所示,为________ mm ,则该绿光的波长为________ nm(计算结果保留三位有效数字);(3)在不改变其他条件的情况下,该同学又进行了几组实验,通过照相底片记录了干涉图样,分别测量了红光、黄光的波长(红光为625 nm 、黄光为570 nm).图(a)、(b)、(c)是实验中记录下的三种色光的干涉图样,但被不小心弄混了,经判断绿光产生的干涉图样是图________(选填(a)、(b)或(c)).答案 (1)单缝 相干 (2)6.526 540 (3)(c)解析 (1)在光源和双缝之间还必须放置一个单缝,其目的是保证经双缝得到的两列光是相干光.(2)分划板中心刻线在B 位置时读数为6.5 mm +2.6×0.01 mm =6.526 mm条纹间距为Δx =6.526-1.1284mm =1.349 5 mm 由Δx =l d λ解得该绿光的波长λ=d l Δx =0.6×10-31.5×1.349 5×10-3 m =5.398×10-7 m ≈540 nm.(3)由波长关系λ红>λ黄>λ绿,可知在其他条件不变的情况下,干涉图样条纹间距Δx 红>Δx 黄> Δx 绿,所以绿光的条纹间距最小,则绿光产生的干涉图样是题图(c).3.寒假期间小明利用图甲所示的物品,测量了某型号刀片的厚度.实验过程如下:(1)点燃蜡烛,用蜡烛火焰把玻璃片的一面熏黑;(2)并齐捏紧两片刀片,在玻璃片的熏黑面划出两条平直划痕;(3)如图乙所示,将激光光源和玻璃片固定在桌上,并将作为光屏的白纸固定在距离足够远的墙上.(4)打开激光光源,调整光源的高度并使激光沿水平方向射出,恰好能垂直入射在两划痕上.(5)观察白纸上的干涉条纹如图丙所示.用刻度尺测出a 、b 两点间的距离为________ cm ,则两相邻暗纹中心之间的距离Δy =________ cm.(6)测得玻璃片到光屏的距离L =3.00 m ,已知该红色激光的波长λ=700 nm ,利用公式求出双划痕间距d =________ mm ,即为刀片厚度(结果保留两位有效数字).答案 (5)10.50 2.1 (6)0.10解析 (5)用刻度尺测出a 、b 两点间的距离为10.50 cm ,两相邻暗纹中心之间的距离为Δy =10.505cm =2.1 cm. (6)刀片的厚度为Δy =L d λ,解得d =0.10 mm.。
