平行四边形知识结构图1资料讲解
平行四边形复习课件

E A
B
D
C F
综合运用
一.如图,△ABC中,点O是边AC上一个动点,过 O作直线MN∥BC,设MN交∠BCA的平分线 于点E,交∠BCA的外角平分线于点F。
1. 探究:线段OE与OF的数量关系并加以证明; 2. 当点O在边AC上运动时, 四边形AECF是
矩形? 二.证明你的结论。
∴ 四边形BFDE是平行四边形
产品品鉴会活 动方案
汇报人姓名
A
D
O
边 矩形对边平行且相等;B
C
角 矩形的四个角都是直角;
对角线 矩形的对角线相等且互相平分;
对称性 既是中心对称图形又是轴对称图形
直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半.
矩形的判定方法 A
D
O
B
C
1.有一个角是直角的平行四边形是矩形。
A
B
•9
4.△ABC中,D、E分别是AB、AC的中点, BC=10cm,则DE=_5__c_m__.
5. △ABC中,D、E分别是AB、AC的中点,
∠A=50°, ∠B=70°,则∠AED=_____.60°
A
A
D
E
B (4)
C
D
E
B
(5)
C
6. 如图,在周长为20cm的 ABCD中,
AB≠AD,AC,BD相交于点O,OE⊥BD
6.已知正方形ABCD中,对角线AC=10cm, P为AB上任意一点,PE⊥AC,PF⊥BD, E、F为垂足,则PE+PF=5cm 。
综合运用
已知:如图,E、F为 ABCD的对角线AC所在直线 上的两点,AE=CF,求证: BE=DF.
平行四边形思维导图全章

平行四边形与多边形主题单元学习目标知识技能:1、掌握平行四边形、菱形、矩形、正方形的概念,了解他们之间的关系;2、掌握平行四边形及特殊平行四边形的性质与判定;3、掌握多边形的内角和与外角和公式;4、了解基础图形的密铺。
过程与方法:1、经历平行四边形与特殊平行四边形性质与判定的探索过程,丰富学生从事数学活动的经验与体验进一步培养学生的合情推理能力,增强学生的简单逻辑推理意识,使学生掌握说理的基本方法。
2、通过多边形内角和的推导过程,让学生体会并掌握知识转化的思想情感态度与价值观:1、通过实例引入,让学生体验数学在生活中的无处不在,体验数学图形在生活中的重要作用。
2、通过密铺图案设计,让学生体验到数学的美,培养审美意识。
3.通过小组合作学习,培养主动参与、勇于探究的精神.4.通过师生共同活动,在学习活动中培养良好的情感,合作交流,主动参与的意识,在独立思考的同时能够认同他人。
对应课标专题问题设计1. 三角形的三边长有怎样的数量关系?2. 怎样说明三角形的内角和是180°?3. 多边形的内角和有什么性质?4. 三角形、多边形的外角和有什么性质?5. 三角形是否具有稳定性?所需教学材料和资源信息化资源几何画板课件常规资源作图工具(直尺,三角尺,量角器等)教学支撑环境学生每人一台计算机的网络教室或多媒体教室,几何画板软件其他纸笔等学习活动设计第一课时:三角形的内角和定理活动1:探索三角形三边关系【活动步骤】1.任意长度的三条线段都能组成三角形吗?教师组织学生用短木条进行实验.2.组成三角形的三条线段有何关系?学生观察、猜想,教师组织学生交流.3.用文字或式子表述你发现的结论.【技术应用】在几何画板中画三条线段,观察它们的长度满足什么条件是可构成三角形.活动2:探索三角形内角和【活动步骤】1.验证三角形内角和是180°.利用三角形纸片,通过剪拼成平角的方法验证;.利用几何画板软件,通过度量计算的方法验证.2.探索证明方法,用规范的推理步骤表达你的推证过程.3.班内交流证法,思考证明方法的本质和关键.【技术应用】(1)探索结论时,计算验证;(2)探索证明方法时,动态体现转化过程.活动3:探索三角形的外角性质【活动步骤】1.自主学习,探索三角形一个外角与内角的关系;2.组内交流结论和方法;3.学以致用,用刚得到的结论,求出三角形的外角和;4.开阔思路,用不同方法求得三角形的外角和.【技术应用】探索外角和;动态体现三角形的三个外角转化为一个周角的过程.第二课时:多边形的内角和与外角和活动一:探究四边形内角和【活动步骤】1.提出问题:三角形的内角和为180°,那么四边形的内角和是多少?2.指导学生探究,交流。
平行四边形章节重难点思维导图上课讲义

平行四边形章节重难点思维导图
精品文档
Ufi y i ;l!H
过
住质
对怡民轴习
矩形
宵三个和£宜朗的冏边羽是地尉
判走
时爲罐相等的平疔四边晦星矩形
罡义
却塩対边分益年行的四辻羽.
对边孚齐目辑等 性质
两IB 対吊曲刖輻誓 对雷蟻互相平分
曲喟灼讥井角巫行的四囚甲痒▽厅円応那. 两也刘忧分别鉅利:冃辺世JS 平陌四边托” 扎定
-tn 对边平和H 相曙的w 边羽見讦上川边羽 iSlF
S H 】
一组邨边相尊的平存四边能叫變总
、
平行四边形
菱形
1判庠
鼻壽竽打四
A 住:』4和
丫
I 性质
\ 时帝駕虬槽1良,亂母最对箱故T 井飢律鶴
四妹边都生月的四边骸足農花 细兀边杓算的TtfH 边廉足菱聒 对甫舞相耳垂直的YiJPl 边形是菱宠
对肃總兀相平什的四边母是平廿四边形1
茴枳
两曲耐用用等的四辿瞄足平疗西址书 S Al
S = ri h
性虜
—'2 <h, ■:旳F :袅苛用爼的;S
. LI 苒一迥那血oh 的平行E :血母叫皿臣
评卜廟亂艮白用,囚案也邢押算
对柏找抬轩n 耳相畢岂辛片‘毎廉对閑找平曲
正方册
判疋|
有一牛期再宜曲的蔓总是止方世 有ill 邻边rti 才的矩应是兀庁聯
制作人;西平目金刚初级中学 高敬华
收集于网络,如有侵权请联系管理员删除
$=H :-任d 人
面扶
S I UI.2 b 肓对将扎的LL。
平行四边形知识框架
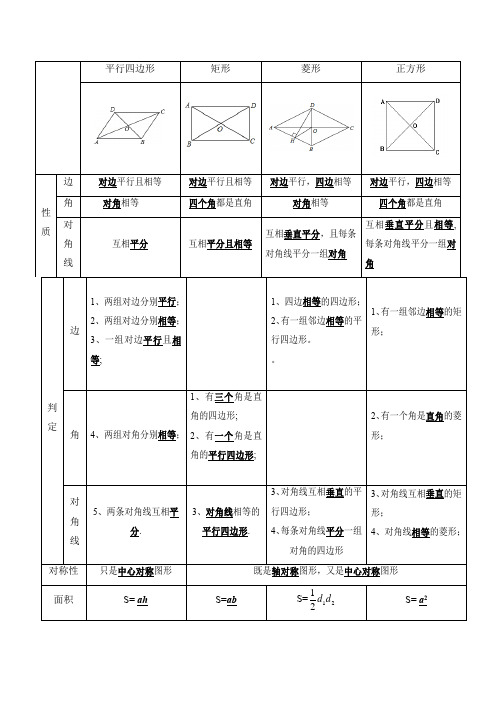
2、有一组邻边相等的平行四边形。
。
1、有一组邻边相等的矩形;
角
4、两组对角分别相等;
1、有三个角是直角的四边形;
2、有一个角是直角的平行四边形;
2、有一个角是直角的菱形;
对角线
5、两条对角线互相平分.
3、对角线相等的平行四边形.
3、对角线互相垂直的平行四边形;
4、每条对角线平分一组对角的四边形
3、对角线互相垂直的矩形;
4、对角线相等的菱形;
对称性
只是中心对称图形
既是轴对称图形,又是中心对称图形
面积
S=ah
S=ab
S=
S=a2
平行四边形
矩形
菱形
正方形
性
质
边
对边平行且相等
对边平行且相等
对边平行,四边相等
对边平行,四边相等
角
对角相等
四个角都是直角
对角相等
四个角都是直角
对角线
互相平分
互相平分且相等
互相垂直平分,且对角线平分一组对角
判定
边
1、两组对边分别平行;
2、两组对边分别相等;
3、一组对边平行且相等;
四边形知识图谱

四边形知识图谱(一)四边形由一般到特殊的演变示意图(二)特殊四边形平行四边形矩形菱形正方形 等腰梯形定 义 有两组对边分别平行的四边形是平行四边形。
有一个角是直角的平行四边形是矩形。
有一组邻边相等的平行四边形是菱形。
有一组邻边相等且有一个角是直角的平行四边形。
两腰相等的梯形是等腰梯形。
性 质1对边平行且相等。
2对角相等,邻角互补。
3对角线互相平分 1四个角都是直角。
2对角线相等。
1四条边都相等。
2两条对角线互相垂直,并且每一条对角线平分一组对角。
具有平行四边形、矩形、菱形的所有特征。
1两腰相等两底平行 2同一底上的两角相等 3两条对角线相等 判 定1定义: 2判定定理:(1)两组对边分别相等的四边形是平行四边形。
(2)两组对角分别相等的四边形是平行四边形。
(不能直接用) (3)一组对边平行且相等的四边形是平行四边形。
(4)对角线互相平分的四边形是平行四边形。
1定义: 2判定定理: (1)对角线相等的平行四边形是矩形。
(2)有三个角是直角的四边形是矩形。
1定义: 2判定定理: (1)一组邻边相等的平行四边形是菱形。
(2)对角线互相垂直的四边形是菱形。
(1)先证明是矩形再证明一组邻边相等。
(2)先证明是菱形再证一个角是直角。
1定义:先判断是梯形在证明两腰相等。
2同一底上的两个角相等的梯形是等腰梯形。
3对角线相等的梯形是等腰梯形。
对称性轴对称图形轴对称图形 轴对称图形 轴对称图形。
平行四边形的性质ppt课件
相交于点O.
A
D
求证:OA=OC,OB=OD.
1O 3
42
B
C
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
方法提示:
1.有关四边形的问题常常转化为三角形问题解决;
D
2、证明线段相等常 用全等
A
C B
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
复习旧知
1.定义:
有两组对边分别平行的四边形
叫做平行四边形。
A
2.记作: ABCD
3.读作:平行四边形ABCDB
D C
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
情景引入
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到 晚年的时候,终于拥有了一块平行四边形的土地,由于年 迈体弱,他决定把这块土地分给他的四个孩子,他是这样
分的:
老大
老二
老四
老三
当四个孩子看到时,争论不休,都认为自己的地 少,同学们,你认为老人这样分合理吗?为什么?
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
课堂小结
1、今天,你学到了什么知识? 2、你能总结以下平行四边形有哪些性质吗?
平行四边形性质及定理PPT课件

的平衡和美感。
图案设计
02
平行四边形在图案设计中也有广泛应用,如纺织品、壁纸、地
毯等的设计。
舞台布景和道具设计
03
在舞台布景和道具设计中,平行四边形也常被用于创造视觉效
果和空间感。
THANKS FOR WATCHING
感谢您的观看
一组对边平行
总结词
如果一个四边形中有一组对边平 行,则该四边形是平行四边形。
详细描述
这是平行四边形的一个基本判定 定理。如果一个四边形的对边平 行,则这个四边形必然是平行四 边形。
一组对边相等
总结词
如果一个四边形中有一组对边相等, 则该四边形是平行四边形。
详细描述
这也是平行四边形的一个基本判定定 理。如果一个四边形的对边相等,则 这个四边形必然是平行四边形。
窗户和门的形状设计
平行四边形因其独特的对边平行和相 对边相等的特性,常被用于创造空间 感和视觉效果。
窗户和门的形状设计经常采用平行四 边形,以实现采光和通风的最佳效果。
建筑结构的稳定性
平行四边形的对角线互相平分,这使 得它在建筑结构设计中具有稳定性, 如桥梁、房屋的支撑结构等。
机械设计中的应用
机械零件的形状设计
平行四边形性质及定理ppt课件
contents
目录
• 平行四边形的基本性质 • 平行四边形的判定定理 • 特殊平行四边形 • 平行四边形在实际生活中的应用
01 平行四边形的基本性质
对边平行
总结词
平行四边形的对边是平行的。
详细描述
这是平行四边形的基本性质之一,即相对的两条边是平行的,不会相交于一点。
直角三角形斜边中线定 理,矩形的对角线相等
且互相平分。
平行四边形知识结构及知识点

1、知识结构
2、对称性:
①平行四边形是中心对称图形,其对称中心是两条对角线的交点;
②等腰梯形是轴对称图形,其对称轴是过上、下两底的中点的直线;
③矩形、菱形、正方形既是轴对称图形,又是中心对称图形。
3、相关定理:
①直角三角形斜边上的中线等于斜边的一半;
②如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
3、对角线相等的梯形是等腰梯形
③平行四边形的面积公式:S =底 高;菱形的面积公式:S =两条对角线积的一半。
④梯形的面积公式:S =(上底+下底) 高 2 =中位线长 高
4、注意:
⑴四边形中常见的基本图形
⑵梯形问题中辅助线的常用方法(目的:转化为三角形和平行四边形或构造全等三角形)
特殊
四边形
性质
判定
边
角
对角线
边
角
对角线
平行
四边形
1、有一组邻边相等且有一个角是直角的平行四边形是正方形。
2、有一组邻边相等的矩形是正方形。
3、有一个角是直角的菱形是正方形。
4、对角线相等的菱形是正方形。
5、对角线互相垂直的矩形是正方形。
等腰
梯形
两底
平行
两腰
相等
同一底
上的两个底角相等腰梯形。
2、在同一底上的两个底角相等的梯形是等腰梯形。
1、有一个角是直角的平行四边形是矩形
2、三个角是直角的四边形是矩形
3、对角线相等的平行四边形是矩形
菱形
四边
相等
对角相等
邻角互补
对角线互相垂直平分,且每条对角线平分一组对角
1、一组邻边相等的平行四边形是菱形
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、知识结构图:
二、平行四边形的性质
边角对角线平行四边形对边平行且相等对角相等,邻角互补对角线互相平分矩形对边平行且相等四个角都是直角对角线相等且互相平分
菱形对边平行,四边相等对角相等,邻角互补对角线互相垂直平分,每条对角线平分一组对角
正方形对边平行,四边相等四个角都是直角对角线互相垂直平分且相等,每条对角线平分一组
对角
三、平行四边形的常用判定方法
平行四边形1) 两组对边分别平行的四边形是平行四边形; 2) 两组对边分别相等的四边形;
3) 一组对边平行且相等的;4)两组对角分别相等的四边形 5) 对角线互相平分的四边形;
矩形1)有一个角是直角的平行四边形是矩形; 2)有三个角是直角的四边形是矩形;3)对角线相等的平行四边形是矩形。
4)对角线平分且相等的四边形是矩形
菱形1)有一组邻边相等的平行四边形是菱形; 2)四条边都相等的四边形是菱形;3)对角线互相垂直的平行四边形是菱形。
4)对角线平分且垂直的四边形是菱形
正方形1)有一个角是直角且有一组邻边相等的平行四边形是正方形;
2)有一组邻边相等的矩形是正方形; 3)有一个角是直角的菱形是正方形。
1.三角形的中位线平行且等于第三边的一半
2.直角三角形斜边上的中线等于斜边的一半
3.菱形的面积公式:对角线乘积的一半
练习题:
1.不能判定四边形ABCD 为平行四边形的题设是( ) (A )AB 平行且等于CD 。
(B )∠A=∠C ,∠B=∠D 。
(C )AB=AD ,BC=CD 。
(D )AB=CD ,AD=BC 。
2.下面性质中菱形有而矩形没有的是( )
(A )邻角互补(B )内角和为360°(C )对角线相等 (D )对角线互相垂直 3.正方形具有而菱形不一定具有的性质是( ) (A )四条边相等 (B )对角线互相垂直平分 (C )对角线平分一组对角 (D )对角线相等
4、顺次连结任意四边形四边中点所得的四边形一定是( ) A 、平行四边形 B 、矩形 C 、菱形 D 、正方形
5.如图,□ABCD 中,∠C=108°,BE 平分∠ABC,则∠ABE 等于( ) A.18° B.36° C.72° D.108° 6.下列命题中,真命题是( )
A 、有两边相等的平行四边形是菱形
B 、对角线垂直的四边形是菱形
C 、四个角相等的菱形是正方形
D 、两条对角线相等的四边形是矩形 7、□ABCD 中,∠A =50°,则∠B =__________,∠C =__________。
8.已知菱形两条对角线的长分别为5cm 和8cm ,则这个菱形的面积是______cm .
9、菱形ABCD 的周长为36,其相邻两内角的度数比为1:5,则 此菱形的面积为_________。
10、对角线长为22的正方形的周长为___________,面积为__________。
11.如图,过矩形ABCD 的对角线BD 上一点K 分别作矩形两边的平行线MN 与PQ ,那么图中矩形AMKP 的面积
S 1与矩形QCNK 的面积S 2的关系是S 1 S 2(填“>”或“<”或“=” )
A
第11题图 第12题图
12.如图,在矩形ABCD 中,点E 、F 分别在AB 、DC 上,BF ∥DE ,若AD=12cm ,AB=7cm ,
•且AE :EB=5:2,则阴影部分的面积为_______cm
N
M
Q
C
B
E
D
C
B A
例1:
(1)如图,已知四边形ABCD 为平行四边形,∠A +∠C =80°,平行
四边形ABCD 的周长为46 cm ,且AB -BC =3 cm ,求平行四边形ABCD 的各边长和各内角的度数.
例2(1)如图,矩形ABCD 的对角线AC 、BD 相交于点O ,∠AOB=2∠BOC ,若对角线AC=6cm ,
则该矩形的周长和面积各是多少?
(2):如图,菱形ABCD 的边长为8㎝,∠BAD=120°,则菱形ABCD 的面积为
例3:如图,矩形ABCD 的对角线AC 、BD 交于点O ,过点D 作DP ∥OC ,且 DP=OC ,连结CP 。
(1)试判断四边形CODP 的形状;
(2)如果条件“矩形ABCD ”变为“正方形ABCD ”呢?
例4:如图,已知四边形ABCD 中,AC=BD ,E 、F 、G 、H 分别是AB 、BC 、
CD 、DA 边上的中点。
(1)求证:四边形EFGH 是菱形;
(2)添加一个条件,使四边形ABCD 是正方形,并说明理由。
D A B
C
O A B C D
O
发现:(1)顺次连接对角线既不相等也不垂直的四边形各边中点得;
(2)顺次连接对角线相等但不垂直的四边形各边中点得;
(3)顺次连接对角线互相垂直但不相等的四边形各边中点得;
(4)顺次连接对角线相等且互相垂直的四边形各边中点得
例5. 如右下图,把AD=12cm,AB=8cm的矩形沿着AE为折痕对折使点D落在BC上点F处,则DE= cm。
例6.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA 的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
