相平衡与相图原理
合集下载
第六章相平衡与相图(5)-三元系统-2012中南大学无机材料科学基础课件
资源加工与生物工程学院
（二）相图特点
1．液相互溶
2．固相完全不互溶
3．不生成化合物
4．只有一个三元低共熔点
（三）投影图
投影图是将无变量点及界
线向浓度三角形投影而成。
第六章 相平衡相图——6.5 三元系统
资源加工与生物工程学院
立体图与平面投影图的关系
(1) 立体图的空间曲面（液相面）
→平面上的初晶区
资源加工与生物工程学院
第六章
6.1 概 述
相平衡与相图
6.2 相平衡及其研究方法 6.3 单元系统 6.4 二元系统 6.5 三元系统
第六章 相平衡相图——6.5 三元系统
资源加工与生物工程学院
6.5
一 、基本原理
三元系统
二、基本类型
1、具有一个低共熔点的三元相图 2、具有一个一致熔融二元化合物的三元相图 3、具有一个一致熔融三元化合物的三元相图 4、具有一个不一致熔融二元化合物的三元相图
第六章 相平衡相图——6.5 三元系统
资源加工与生物工程学院
一 基本原理
（一）三元系统组成表示方法和浓度三角形性质
1．组成表示法 （1）浓度三角形 ——等边三角形：表示 三元系统的组成
第六章 相平衡相图——6.5 三元系统
资源加工与生物工程学院
三个顶点 ——三个纯组分A、B、C； 三条边（AB、BC、AC） ——三个二元系统组成；
无论在哪种三角形中，任何一点的组成都可采用
作双线法求得，反过来已知组成也可在图中找到 相应的点。
第六章 相平衡相图——6.5 三元系统
资源加工与生物工程学院
2．浓度三角形性质 （1）等含量规则：平行于三角形 一边的直线，线上任意一个组成 点所含对面顶点组分的含量不变， 如MN线上，C%=常数 （2）定比例规则：三角形一顶点
相平衡和相图
单元系相图
Hale Waihona Puke 相图的建立相图的建立方法：实验法和计算法。 建立过程：配制－测冷却曲线－确定转变温度 －填入坐标－绘出曲线。
杠杆定律
低共熔体系相图
形成部分互溶固溶体相图
课上作业：写出合金Ⅳ由0经12-3的变化过程
相平衡和相图
一 几个基本概念 相：体系内部物理性质和化学性质完全均匀的部 分称为“相” 相图：对于多相体系，各相间的相互转化，新相 的形成，旧相的消失与温度，压力，组成有关。 根据实验数据给出的表示相变规律的各种几何 图形称为相图。从这种几何图形上，可以直观 看出多相体系中各种聚集状态和它们所处的条 件（温度，压力，组成）。
• 相平衡：在一个热力学体系内，当不同相之间相互接 触时，若发生物质从一相迁至另一相的过程，则此过 程称为相变过程。在相变过程中，当宏观物质的迁移 停止时，称为相平衡。 • 相律:描述平衡体系中独立组元数，相数和自由度数之 间的关系 自由度是指平衡系统中保持平衡相数不变的条件下独立 可变的因素（如温度、压力、浓度等）的数目 F=C-P+2 （1） 凝聚系统，相律可写成 F=C-P+1 （2） 式中： F是自由度数； C是组成材料系统的独立组元 数； P是平衡相的数目。
相图与相平衡全解
相图的作用：
? 预示不同条件下可能出现的各种组态以及条件 改变时, 各种组态可能发生转变的方向和限度；
? 了解体系在不同条件下的相转变及相平衡存在 的状态；
? 为提高已有材料的性能及设计、开发和研制新 材料提供重要依据；
? 预测材料的性能，为制定材料的制备、合成和 加工工艺提供参考依据。
§1 相图中的点、线、面
F ? C? P?n
ⅰ）相
相：指物质系统中具有稳定和相同的
化学组成、晶体结构、聚集状态以及相同 物理、化学性质的 完全均匀 一致的所有部 分的总和。相可以是单质，也可以是由几 种物质组成的均匀液相或化合物。
“完全均匀”是指物质在分子或离子 水平上的均匀混合状态。
特点：不同相之间有明显界面；机械
方法可分开；通过不同相的宏观界面性质 发生突变；与数量多少无关；与是否连续 无关。
无论溶质原子是以何种方式进入晶格，总会 对溶剂晶格造成一定程度的畸变。这种点阵畸变 会使晶体能量升高，即晶格畸变能。
畸变能越高，晶格越不稳定。单位体积畸变 能的大小与溶质原子溶入的数量以及溶质、溶剂 原子的相对尺寸差别有关。
此外，溶解度还与晶体结构类型、电负性和 电子浓度等因素有关。
§3 平衡态与平衡凝固
在没有外界影响的条件下，系统各部分的宏 观性质长时间内不发生变化的状态。没有外界影 响，是指系统与外界之间不通过作功或传热的方 式交换能量，否则系统就不能达到并保持平衡态。
实际中并不存在完全不受外界影响、宏观性 质绝对保持不变的系统，所以平衡态只是一个理 想化的概念，它是在一定条件下对实际情况的抽 象和概括。只要系统状态的变化很小而可以忽略， 就可以近似看成平衡态。
? 从一种结构转变为另一种结构； ? 化学成分的不连续变化； ? 更深层次序结构的变化并引起物理性质的突变。
材料科学基础第四张相平衡与相图(1)
化学位： 当温度、压力不变因组元增加一个摩尔， 引起吉布斯自由能的变化，就是组元的化 学位或偏摩尔自由能。它代表了系统内物 质传递的驱动力。
组元2在β相 中化学位等于其 在α相中的化学位 推演如下：
多元系统的吉布斯自由能是温度、压力及各组元摩尔 数n1、n2…….函数，即可写成 G＝f（T、P、n1、n2……….)
二元系中,三相平衡的热力学条件是每个组元在各相中的化学位相等,即 μα1＝μβ1＝μγ1 μα2＝μβ2＝μγ2 多元复相平衡的普遍条件是每个组元在各相中的化学势都必须彼此相等,即 μαi＝μβi＝μγ i ＝…＝μPi
其中,α、β、γ…P表示合金中存在的相,i代表合金中的第i个组元 。 μPi则表示P相中i组元的化学位，即上标表示平衡相，下标表示组元。
温度与压力都能变动的情况
二、 SiO2系统相图 •也有晶型变化：
（＜573℃）低温型α－SiO2 （α－石英） （573℃－870℃） 高温型β－SiO2 （β－石英） （870℃－1470℃） 磷石英β2－SiO2 （β2－磷石英） （1470℃－1713℃） 方石英β－方SiO2 这四种不同晶体结构的SiO2存在 的温度、压力范围不同
•确定两平衡相的相对量: •将成分坐标当作杠杆，以合金的成分点为 •支点，Wα和WL看成作用于a、b两点的力， •则与力学上的杠杆定律一样，即 • WL／Wα＝0b／a0 •上式表明合金在两相区内，两平衡相的相 •对量之比与合金成分点两边的线段长度呈 •反比关系。
•合金中两平衡相的含量也可用下式表达： Wα％＝（C－CL）／（Cα－CL） ＝a0 ／abχ100％ WL％＝（Cα－C）／（Cα－CL） ＝ 0b ／ab χ100％ 在两相区内，温度一定时，两相的质量比 是一定的。
《材料科学基础》课件——第五章相平衡与相图第一节第二节第三节第四节
相和相平衡
Байду номын сангаас四、自由度与相律
1、自由度：平衡系统中独立可变的因素
自由度数：独立可变的强度变量的最大数目
(强度变量与广度变量的区别）
2、相律：自然规律
在平衡系统中由于受平衡条件的制约，系统内
存在的相数有一定限制。 组元数 相数P≥1
吉布斯相律：不可为负数
f=c-p+n
外界影 响因素
通常外界影响因素只考虑T、P，所以f=c-p+2
• 掌握匀晶，包晶，共晶相图的特点，进而了解二元合金的一些平衡凝固，固 相转变的规律。
• 重点难点： • 二元系相图的建立，杠杆定律 • 包晶相图，共晶相图，共晶合金 • 相图分析，各种液固，固相转变的判断
材料的性能决定于内部的组织结构，而组织结构
又由基本的相所组成。
相：均匀而具有物理特性的部分，并和体系的其他 部分有明显界面。
晶型转变过程都是在恒温下进行，并伴随有体 积、密度的变化。 2、SiO2系统相图 α-石英与β-石英相变相当慢， β-石英常因冷却过快而被保留 到室温，在常压下，低于573℃
单元系相图
β-石英很稳定，所以自然界或低温时最常见的是 β-石英。晶型转变时，体积效应特别显著。 Al2O3、ZrO2也具有多晶型转变。 3、聚合物相图 （1）状态由分子间作用力决定，分子间约束力弱
共晶相图，平衡凝固，共晶合金，包晶相图，形成化合物的相图，含有双液 共存区的相图，熔晶相图等 ，二元相图的几何规律 ，单相，双相及三相共 存区，相图特征 ，二元系相图的分析，分析的方法与步骤，分析举例。
• 教学目的： • 学习相平衡与相图的基本知识，了解相图在材料科学学习中的重要性，学会
相图的使用。
相平衡与相图
液相线 B的熔点
A的熔点
A和B的二元低共熔点
4个相区： 固相线 L、L+A、 L+B、A+B
特点： 两个组分在液态时能以任何比例互溶，形成单相溶液；但在 固态时则完全不互溶，二个组分各自从液相中分别结晶。 组分间无化学作用，不生成新的化合物
杠杆规则
如果一个相分解为2个相，则生成的2个相的数量与原始
65
35
35
1450
725
铁碳平衡图
铁碳平衡图 （iron-carbon equilibrium diagram ）， 又称铁碳相图或铁碳状态图。它以温度为纵坐标，碳含量 为横坐标,表示在接近平衡条件（铁-石墨）和亚稳条件
（铁－碳化铁）下（或极缓慢的冷却条件下）以铁、碳为
组元的二元合金在不同温度下所呈现的相和这些相之间的 平衡关系。
4
二元系统
C=2，一般情况下，凝聚系统中的相律：
一、二元相图表示方法
F=C+P+1=3-P
当P=1时，F=2
当P=2时，F=1
当γ =3时，F=0 相数最大为3，自由度最大为2，对于浓度：A+B=A'%+B'%=100% 任意确定一个，则另一个确定相图为T组成图
二 具有一个低共熔点的简单二元相图
相平衡与相图
主要内容
发展历史 相图基础知识 单元系相图 二元系相图 三元系相图
1 相图发展历史
一 理论基础
平衡图的理论基础是吉布斯（J W Gibbs）的相律 ，他于1876年创建相律。
二 发展历程 1990年：罗泽朋（Bakhuis Roozeboom）发表了《用相律的观点来
看复相平衡》巨著的第一部分。
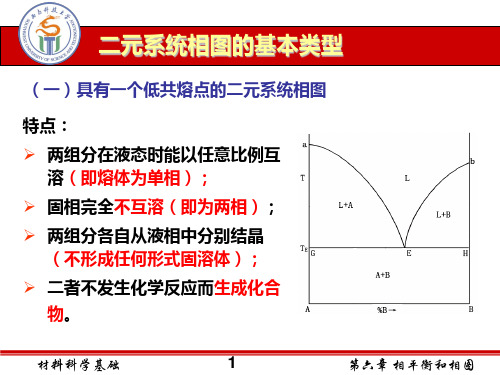
A的熔点
A和B的二元低共熔点
4个相区： 固相线 L、L+A、 L+B、A+B
特点： 两个组分在液态时能以任何比例互溶，形成单相溶液；但在 固态时则完全不互溶，二个组分各自从液相中分别结晶。 组分间无化学作用，不生成新的化合物
杠杆规则
如果一个相分解为2个相，则生成的2个相的数量与原始
65
35
35
1450
725
铁碳平衡图
铁碳平衡图 （iron-carbon equilibrium diagram ）， 又称铁碳相图或铁碳状态图。它以温度为纵坐标，碳含量 为横坐标,表示在接近平衡条件（铁-石墨）和亚稳条件
（铁－碳化铁）下（或极缓慢的冷却条件下）以铁、碳为
组元的二元合金在不同温度下所呈现的相和这些相之间的 平衡关系。
4
二元系统
C=2，一般情况下，凝聚系统中的相律：
一、二元相图表示方法
F=C+P+1=3-P
当P=1时，F=2
当P=2时，F=1
当γ =3时，F=0 相数最大为3，自由度最大为2，对于浓度：A+B=A'%+B'%=100% 任意确定一个，则另一个确定相图为T组成图
二 具有一个低共熔点的简单二元相图
相平衡与相图
主要内容
发展历史 相图基础知识 单元系相图 二元系相图 三元系相图
1 相图发展历史
一 理论基础
平衡图的理论基础是吉布斯（J W Gibbs）的相律 ，他于1876年创建相律。
二 发展历程 1990年：罗泽朋（Bakhuis Roozeboom）发表了《用相律的观点来
看复相平衡》巨著的第一部分。
8.1 相平衡与相图原理之二元相图
18 相平衡与相图原理8.1 相、相平衡与相律8.2 二元相图8.3 铁碳相图28.1 相、相平衡与相律吉布斯（Gibbs）相律f=C-Φ+2f=C-Φ+1压力一定P =C+1f=03一、二元相图的表示与建立方法4一、二元相图的表示与建立方法热分析法Ð配制系列成分的合金（以Cu-Ni合金为例）Ð测定上述合金的冷却曲线Ð找出冷却曲线上的转折点，即合金的临界点Ð将各临界点标在以温度为纵坐标，以成分为横坐标的图中，将同类临界点连接起来即可得到合金相图二、杠杆定律6三、二元相图（binary alloy diagram)的基本类型（一）匀晶(uniform grain)相图L L+ αα两组元在液态和固态时都能以任何比例完全互溶的的相系所组成的相图，如Cu-Ni、Au-Ag、Au-Pt等7结晶过程的分析Ø组织变化：h L →L+α→αØ成分变化:h L相：b →a 1→a 2→a沿液相线变化h α相：b →c 1→c 2 →a沿固相线变化8具有极值的匀晶相图9（二）共晶(eutectic)相图两组元在液态中无限互溶，在固态时有限互溶且发生共晶反应的一种相图，如Pb-Sn、Pb-Sn、Ag-Cu、Al-Si等10（二）共晶相图（1）固溶体型合金（W Sn <19%)的结晶过程 结晶过程：L →L+α→α→α+βⅡ 室温组织：α+βⅡ11（二）共晶相图（2）共晶合金（W Sn =61.9%)的结晶过程结晶过程：L →（α+β）恒温12（二）共晶相图（3）亚共晶合金hypoeutectic （19%<W Sn <61.9%)的结晶过程Ø结晶过程：L →L+α→α+（α+β）→α+βⅡ+（α+β）Ø室温组织组成物：α+（α+ β）+ βⅡ恒温13（二）共晶相图（3）亚共晶合金的结晶过程过共晶合金（61.9%<W Sn <97.5%)的室温组织是什么？141516（2）合金Ⅱ（10.5%<W Ag <42.4%）的结晶过程17（3）合金Ⅲ（42.4%<W Ag <66.3%）的结晶过程181.形成化合物的相图:稳定化合物192.形成化合物的相图:不稳定化合物202.偏晶相图由一定成分的液相L 1恒温转变为一定成分的固相和另一成分的液相L2的过程称为偏晶反应，具有偏晶反应的主要有：Cu-S、Mn-Pb、Fe-O、Bi-Zn等213.熔晶相图由一个固相转变为一个液相和另一个固相的过程称为熔晶反应，具有熔晶反应的主要有Fe-S、Cu-Sb、Ca-Mn等224.合晶相图由成分不同的两个液相L1和L2相互作用形成一个固相的过程称为合晶反应，具有合晶转变的有Na-Zn、K-Zn、Cr-Pr等235.共析相图由一个固相转变为另外两个固相的过程称为共析反应24(四）其它类型的相图6.包析反应由两个成分不同的固相相互作用转变成另一个固相的过程25（一）二元相图的几何规律Ð1）平衡相的成分必定沿相界线随温度而变化Ð2）相区接触法则：相邻相区的相数差为1，即两个单相区之间必定有一个由这两相组成的两相区，两个两相区必须以单相区或三相水平线隔开。
第8章 相平衡与相图原理(Fe-C合金平衡结晶过程)-1精品PPT课件
F+ Fe3CⅢ。
室温下Fe3CⅢ
最大量为:
0 . 0 2 1 8 0 . 0 0 0 8 Q F e 3 C I I I 6 . 6 9 0 . 0 0 0 8 1 0 0 % 0 . 3 %
㈡ 共析钢的结晶过程
合金液体在 1-2点间转变
为g。到S点
发生共析转 变：
gS→aP+Fe3C, g 全部转变
共晶转变结束时，两相的相对重量百分比为:
Qg
6 .6 9 4 .3 1 0 0 % 6 .6 9 2 .1 1
5 2 .2 % ，
Q F e3C
4 7 .8 %
C点以下, g 成分沿ES线变化，共晶g 将析出Fe3CⅡ。
Fe3CⅡ与共晶Fe3C 结合，不易分辨。
1’
g
Fe3C
2
温度降到2点, g 成分达到0.77%, 此时, 相的相对重量:
过共晶白口铁 共晶白口铁 亚共晶白口铁
过共析钢 共析钢 亚共析钢
工业纯铁
⑶ 白口铸铁 (2.11~6.69%C) 铸造性能好, 硬而脆
① 亚共晶白口铸铁 (2.11~4.3%C)
② 共晶白口铸铁 (4.3%C)
③ 过共晶白口铸铁 (4.3~6.69%C)
㈠工业纯铁的 结晶过程
合金液体在1-2
冷却时发生包晶反应.
Ⅲ
A
H
B
J
以0.45%C的钢为例 合金在4点以前通过匀
晶—包晶—匀晶反应全
G S
P
a+Fe3C
部转变为g。到4点，由
g 中析出a 。到5点, g 成分沿GS线变到S点，g 发生
共析反应转变为珠光体。温度继续下降，a 中析出
第八章-相平衡与相图原理
f 1 单变量体系
F 3 三相共存
f 0 无变量体系
单组分体系的自由度最多为2，双变量体系 的相图可用平面图表示。
2024/7/17
单组分体系的相图
相点 表示某个相状态（如相态、组成、温度 等）的点称为相点。 物系点 相图中表示体系总状态的点称为物系点。 在T-x图上，物系点可以沿着与温度坐标平行的垂线 上、下移动；在水盐体系图上，随着含水量的变化， 物系点可沿着与组成坐标平行的直线左右移动。
2024/7/17
照片为亚共晶Pb-Sn合金的显微组织照片， 图中块状深色组织为先共晶相，其余黑白相间的基体为共晶组织。
2024/7/17
气体，不论有多少种气体混合，只有一个气相。 液体，按其互溶程度可以组成一相、两相或三 相共存。 固体，一般有一种固体便有一个相。两种固体粉 末无论混合得多么均匀，仍是两个相（固体溶液 除外，它是单相）。
2024/7/17
三相点与冰点的区别
三相点是物质自身的特性，不能加以改变，如H2O 的三相点。 T 273.16 K , p 610.62 Pa . 冰点是在大气压力下，水、冰、气三相共存。当大 气压力为105 Pa时，冰点温度为 273.15 K ，改变外 压，冰点也随之改变。
2024/7/17
2024/7/17
• 二组元在液态和固态都能够完全相互溶解，所 有成分(Ni: 0~100%)的合金在固态只有一种晶 体结构，相图中只有一个固相区。
• 因此，能够形成匀晶合金系的两种组元必须具 有相同的晶体结构，相同的原子价，原子半径 接近(相差不超过15％)，相互不形成化合物。
2024/7/17
设合金的平均成分为x，合金的总量为Q，在温度T1时液、 固 质两量相为平QS衡。，则液有相：的成分为xL、质量为QL，固相的成分为xS、
相平衡与相图原理
室温组织:
F + P，500×
(4)过共析钢 ( C % = 1.2 % )结晶过程
各组织组成物的相对量：
Fe3CII % = ( 1.2 – 0.77 ) / ( 6.69 – 0.77 )
≈7% P % ≈ 1 – 7 % = 93 % 各相的相对量：
Fe3CII % ≈ 1.2 / 6.69 = 18 % F % ≈ 1 – 18 % = 82 %
室温组织:
P + Fe3CII 400×
(5)共晶白口铁 ( C % = 4.3 % )结晶过程
室温组织: （低温）莱氏体 Le′ （P + Fe3CII + 共晶 Fe3C ）, 500×
莱氏体 Le′的性能：硬而脆
(６)亚共晶白口铁 ( C % = 3 % )结晶过程
室温组织:
Le′+ P + Fe3CII
亚共晶白口铁 ＜ 4.3 % 共晶白口铁 ＝ 4.3 % 过共晶白口铁 ＞ 4.3 %
几种 常见 碳钢
类型 钢号 碳质量分数／％
亚共析钢 20 45 60 0.20 0.45 0.60
共析钢 T8 0.80
过共析钢
T10
T12
1.00 1.20
(1)工业纯铁 ( C % ≤ 0.0218 % )结晶过程
20
液固两相区
40 60 Ni%
Ni 80 100
匀晶合金的结晶过程
L
T,C
T,C
L
1500
1455
L
1400 1300
c
a
L+
匀晶转变 L
1200d
1100 1000 1083
第五章 相平衡
二元凝聚系统相图表示法：T－x图
一、二元凝聚系统相图的基本类型
1.具有一个低共熔点的简单二元系统相图
特点：两组分在液态时完全互溶，形成单相溶液； 固态时完全不互溶，二组分各自从液相中分别结 晶，组分间无化学作用，不生成新化合物。
⑴
相
图
分
析
G
H
相区：
aEb : 高温熔体的单相区 (液相区)
bEH : L B 两相平衡共存区
熔体(1600℃) 熔体 (1670℃)
α－石英
870℃
1470℃
α－鳞石英
α－方石英
1723℃ 熔融石英
573℃
163℃
180～270℃
急
冷
β－石英
β－鳞石英
β－方石英
石英玻璃
117℃ γ－鳞石英 同 级 转 变(慢)
同
类 转
(快)
变
SiO2相图
1、在573℃以下的低温，SiO2的稳定晶型为－石英，加热至573℃转变为高温型 的－石英，这种转变较快；冷却时在同一温度下以同样的速度发生逆转变。如 果加热速度过快，则－石英过热而在1600℃时熔融。如果加热速度很慢，则在 870℃转变为－鳞石英。
以 忽略压强的影响，相律中的“2”应为“1”。
3. 必须正确判断独立组分数、独立化学反应式、相数以及限 制条件数，才能正确应用相律。
4. 自由度只取“0”以上的正值。如果出现负值，则说明体系可 能处于非平衡态。
第二节 单元系统相图
单元系统中， c = 1
f=c–p+2=3–p
pmin=1 pmax=3
2. 介稳态 即热力学非平衡态，经常出现于硅酸盐系统中。
如： α－石英 870α℃－鳞石英 1470℃α－方石英
相平衡与相图
17
5.5 -6 80 327 271 451 657 1412
-26 -71 60 246 144 306 578 1090
50 24 64 88 55 69 89 32
合金体系"热分析"原理
热分析法研究固液平衡体系相图主要是依据体系发生相变时伴随着相变潜热的吸 收或放出，导致体系冷却速度的变化，来研究相变过程的规律。由实验数据所绘 制的温度(T)与时间(t)的曲线，称为“步冷曲线”，由步冷曲线斜率的变化可提 供相的产生、消失、和达成相平衡的信息。
4
610.62
273.16
水的相图
2.2 单组分体系的两相平衡- 克拉贝龙(Clapeyron)方程式
可适用于任何纯物质体系的各类两相平衡，如气～液、气～固、液～固或固～固 晶型转变等。
如气～液、气～固、液～固或固～固晶型转变等。如果 α、β 两相中有一相是气相（设 β 为气相），则因气体体积远大于液体和固体的体积，即 Vm(g)》Vm(l) 或 Vm(s) 。对比之 下可略去液相或固相的体积，而
可得 Φ = 1 ，f = 3 Φ = 2 ，f = 2 Φ = 3 ，f = 1 Φ = 4 ，f = 0
即"三变量体系" 即"二变量体系" 即"单变量体系" 即"无变量体系"
通常情况下，描述体系状态时以温度（T）、压力（p）和组成 （浓度 x1 或 x2 ）三个变量为坐标构成的立体模型图。
固定 T 就得 p～x 图，固定 p 就得 T～x 图对工业上的提纯、分离、精馏、分馏 分面很有实用价值
6
三、二级相变
一类相变称之为一级相变（first order phase transition），特点是，如果改变体系的独 立强度变量（例如 pVT 系统的 t，p，x1，x2，……，xr ），一旦这些变量或其中之一 达到相变能发生的值时，从宏观上看相变将突然发生。它是一种不连续的突变现象，表 现出在确定的强度变量值时发生，同时体积、熵、焓等热力学量发生不连续的但有限的 突变。我们通常所见的气、液、固态的相变都属于这类相变。
5.5 -6 80 327 271 451 657 1412
-26 -71 60 246 144 306 578 1090
50 24 64 88 55 69 89 32
合金体系"热分析"原理
热分析法研究固液平衡体系相图主要是依据体系发生相变时伴随着相变潜热的吸 收或放出，导致体系冷却速度的变化，来研究相变过程的规律。由实验数据所绘 制的温度(T)与时间(t)的曲线，称为“步冷曲线”，由步冷曲线斜率的变化可提 供相的产生、消失、和达成相平衡的信息。
4
610.62
273.16
水的相图
2.2 单组分体系的两相平衡- 克拉贝龙(Clapeyron)方程式
可适用于任何纯物质体系的各类两相平衡，如气～液、气～固、液～固或固～固 晶型转变等。
如气～液、气～固、液～固或固～固晶型转变等。如果 α、β 两相中有一相是气相（设 β 为气相），则因气体体积远大于液体和固体的体积，即 Vm(g)》Vm(l) 或 Vm(s) 。对比之 下可略去液相或固相的体积，而
可得 Φ = 1 ，f = 3 Φ = 2 ，f = 2 Φ = 3 ，f = 1 Φ = 4 ，f = 0
即"三变量体系" 即"二变量体系" 即"单变量体系" 即"无变量体系"
通常情况下，描述体系状态时以温度（T）、压力（p）和组成 （浓度 x1 或 x2 ）三个变量为坐标构成的立体模型图。
固定 T 就得 p～x 图，固定 p 就得 T～x 图对工业上的提纯、分离、精馏、分馏 分面很有实用价值
6
三、二级相变
一类相变称之为一级相变（first order phase transition），特点是，如果改变体系的独 立强度变量（例如 pVT 系统的 t，p，x1，x2，……，xr ），一旦这些变量或其中之一 达到相变能发生的值时，从宏观上看相变将突然发生。它是一种不连续的突变现象，表 现出在确定的强度变量值时发生，同时体积、熵、焓等热力学量发生不连续的但有限的 突变。我们通常所见的气、液、固态的相变都属于这类相变。
相平衡和相图
材料科学基础
30
第六章 相平衡和相图
C 例：根据下列相图 (1) 用连线规则划分副三角形。 (2) 用箭头标出界线上温度变化方向及界线性质。 C (3) 判断S、S1、S2化合物的性质。 (4) 写出各无变量点的性质及反应式。 (5)在相图下侧画出A－B二元系统相图。 u v (6) 分析熔体M1、M2的析晶路程。 S (M1在SO连线上)
第六章 相平衡和相图
13
3、背向线规则
在浓度三角形中，一个三元系统的组成点愈靠近某个顶点，
该顶点所代表的组分的含量就愈高；反之，愈少。
C 若熔体在冷却时析出某一
顶点所代表的组元，则液
相中组成点必定沿着该顶 点与熔体组成点的连线向 背离该顶点的方向 A
材料科学基础
D
B
第六章 相平衡和相图
14
4、杠杆规则
C C
b L .2 N
a
e2
K
1
.
B
x B
z y
熔体1
L LB 1[B，(B)] a[B，B+(A)] f=3 f=2
L B+N f=1
L B＋A K[x，B+A+(N)] f=1
e1
L＋AB＋N f=0
K[y(A消失),N＋B]
LN＋B＋C L[z,N+B+(C)] f=0
L(液相消失)[1,N+B+C]
所谓一致熔融化合物是一种稳定 的化合物。它与正常的纯物质一 样具有固定的熔点，融化时，所
产生的液相与固相的化合物组成 相同，故称一致熔融
材料科学基础
2
第六章 相平衡和相图
2、不一致熔融化合物： 一种不稳定的化合物，加热这种 化合物到某一温度便发生分解， 分解产物是一种液相和一种晶相， 二者组成与原来化合物组成完全 不同。 点：纯物质熔点；低共熔点； 转熔点等 线：液相线（3条）固相线等；
30
第六章 相平衡和相图
C 例：根据下列相图 (1) 用连线规则划分副三角形。 (2) 用箭头标出界线上温度变化方向及界线性质。 C (3) 判断S、S1、S2化合物的性质。 (4) 写出各无变量点的性质及反应式。 (5)在相图下侧画出A－B二元系统相图。 u v (6) 分析熔体M1、M2的析晶路程。 S (M1在SO连线上)
第六章 相平衡和相图
13
3、背向线规则
在浓度三角形中，一个三元系统的组成点愈靠近某个顶点，
该顶点所代表的组分的含量就愈高；反之，愈少。
C 若熔体在冷却时析出某一
顶点所代表的组元，则液
相中组成点必定沿着该顶 点与熔体组成点的连线向 背离该顶点的方向 A
材料科学基础
D
B
第六章 相平衡和相图
14
4、杠杆规则
C C
b L .2 N
a
e2
K
1
.
B
x B
z y
熔体1
L LB 1[B，(B)] a[B，B+(A)] f=3 f=2
L B+N f=1
L B＋A K[x，B+A+(N)] f=1
e1
L＋AB＋N f=0
K[y(A消失),N＋B]
LN＋B＋C L[z,N+B+(C)] f=0
L(液相消失)[1,N+B+C]
所谓一致熔融化合物是一种稳定 的化合物。它与正常的纯物质一 样具有固定的熔点，融化时，所
产生的液相与固相的化合物组成 相同，故称一致熔融
材料科学基础
2
第六章 相平衡和相图
2、不一致熔融化合物： 一种不稳定的化合物，加热这种 化合物到某一温度便发生分解， 分解产物是一种液相和一种晶相， 二者组成与原来化合物组成完全 不同。 点：纯物质熔点；低共熔点； 转熔点等 线：液相线（3条）固相线等；
第六章 相平衡和相图
•如果加热速度很慢，则在870℃转变为－鳞石英。
如果加热速度过快，则－石英过热而在1600℃时熔融。
鳞石英
117 163 230
573
870
1200～1350
1470 1600 1670 1713 ℃
•－鳞石英缓慢加热，在1470℃时转变为－方石英，继续加热 到1713℃熔融。 •－鳞石英在加热较快时，过热到1670℃时熔融。 •当缓慢冷却时，在870℃仍可逆地转变为－石英；当迅速冷却 时，沿虚线变化
p=3 , f=0 ,无变量系统
冰的饱和蒸汽压曲线（升华曲线）
三相点与冰点是一 回事吗
二、具有多晶转变的单元系统相图
E F
β型
α型
实线部分： 四个单相区：1相 五条界线：2相共存
两个三相点：B,C
晶体的升华曲线（或延长线）与液体的蒸发曲线（或延长线） 的交点是该晶体的熔点。如C点，实际是三相点。 两种晶型的升华曲线（或延长线）的交点是两种晶型的晶型转 变点。如B点，实际是三相点。
化合物
固溶体 同质多晶
二、相律 根据Gibbs相律 F= C－P＋2
平衡时最多 有几个相
F－ 自由度数
C－ 独立组元数
P－ 相数
2 － 温度和压力外界因素
盐水系统
建立多相系统中自由度数、独立组元数、相数之间的关系
二、相律
假设一系统中有S种化学物质，在平衡条件下形成P种物相， 每种相中都有S种化学物质。 则总变量数：P（S-1）+2
120 163 230
573
870
1200～1350
1470 1600 1670 1713 ℃
采 取 的 措 施
① 在870℃适当保温，促使鳞石英生成； ② 在1200～1350℃加快升温速度避免生成α- 方石英; ③ 在配方中加入Fe2O3或CaO等矿化剂。在1000℃左右产生一定 量的液相，石英、方石英在此液相中的溶解度大，而鳞石英的溶 解度小，因而石英、方石英不断溶入液相，而鳞石英则不断从液 相中析出。
材料科学基础课件第六章--相平衡与相图
F = C－P＋n
自由 度数
独立组 元数
F = C－P＋2
对凝聚态体系， 压力恒定或影响 较小，其相律为:
F = C－P＋1
组元数C多，自 由度F大；相数P 多，自由度小
6.1.3 相平 衡研究方法
动态法
静态法 (淬冷法)
热分 析法
差热分 析法
T/℃
(1ቤተ መጻሕፍቲ ባይዱ 热分析法
1
2
3
原理：根据系统在冷却
ab c
100 80Bi 60Bi 20Bi 100 Bi 20Cd 40Cd 80Cd Cd
T/℃
ab c d e
t/s
Bi-Cd合金冷却曲线
546.15K
596.15K
L
L+Bi(s) ●
L+Cd(s)
20 40 Bi(s)+Cd(s) 80
0 Bi
WCd/%
100 Cd
Bi-Cd系统相图
液相线：由凝固开始温度连接起来的相界线 固相线：由凝固终结温度连接起来的相界线
元系统相图
P ●：熔点
■：转变点
2
L
●
Ⅱ
3
■
1
●
Ⅰ
O T0 T2 T1 T3
T
图 6-7 具有不可逆多晶转变的
单元系统相图
晶体I T3 晶体II
晶体Ⅰ 晶体Ⅱ 液相
(1) 晶体I、Ⅱ有稳定区 (2) 转变温度T3<T1 、T2(熔点)
T1 液 相 T2
（1）晶体Ⅱ无稳定区 （2）T3>T1、T2
6.2.2 单元系统专业相图
G
E
H
A+B
A
相平衡和相图(共294张PPT)
C＝1，称为单元系统； C＝2，称为二元系统； C＝3，称为三元系统学反响，那么： 独立组元数＝物种数〔即组元数〕
〔2〕如果系统中存在化学反响并建立了平衡，
那么： 独立组元数＝物种数一独立化学反响数
〔指独立化学平衡关系式数〕
例如，由CaCO3、CaO、CO2组成 的系统，在高温下存在下述反响：
〔1〕稳定相平衡局部〔即实线局部〕 相区： FCD是液相区； ABE是β-晶型的相区； EBCF是α-晶型的相区， 在ABCD以下是气相区。
相界线：
CD线：是液相和气相两相平衡共存线，即液相
的蒸发曲线； BC线：是α-晶型和气相两相平衡共存线，即α-
晶型的升华曲线；
AB线：是β-晶型和气相两相平衡共存线，即β晶型的升华曲线；
〔或延长线〕的交点是该晶体的熔点。
②两种晶型的升华曲线的交点是两种晶型的多晶转 变点。
③在同一温度下，蒸气压低的相更加稳定。所以， 介稳平衡的虚线，总是在稳定平衡的实线上方 。
④交汇于三相点的三条平衡曲线互相之间 的位置遵循下面两条准那么：
a、每条曲线越过三相点的延长线必定在另 外两条曲线之间。
b、同一温度时，在三相点附近比容差最大 的两相之间的单变量曲线或其介稳延长 线居中间位置。
假设该反响能够到达平衡，那么有 一个独立的化学反响平衡常数。
此时，虽然组元数＝3，但独立组元 数C＝3－1＝2。
4、自由度 在一定范围内，可以任意改变而不
引起旧相消失或新相产生的独立变量称 为自由度，平衡系统的自由度数用F表示。
这些变量主要指组成〔即组分的浓 度〕、温度和压力等。
5、外界影响因素 影响系统平衡状态的外界因素包括：温度、压力、电
主要区别在于固-液平衡的熔融曲线OC线倾斜
〔2〕如果系统中存在化学反响并建立了平衡，
那么： 独立组元数＝物种数一独立化学反响数
〔指独立化学平衡关系式数〕
例如，由CaCO3、CaO、CO2组成 的系统，在高温下存在下述反响：
〔1〕稳定相平衡局部〔即实线局部〕 相区： FCD是液相区； ABE是β-晶型的相区； EBCF是α-晶型的相区， 在ABCD以下是气相区。
相界线：
CD线：是液相和气相两相平衡共存线，即液相
的蒸发曲线； BC线：是α-晶型和气相两相平衡共存线，即α-
晶型的升华曲线；
AB线：是β-晶型和气相两相平衡共存线，即β晶型的升华曲线；
〔或延长线〕的交点是该晶体的熔点。
②两种晶型的升华曲线的交点是两种晶型的多晶转 变点。
③在同一温度下，蒸气压低的相更加稳定。所以， 介稳平衡的虚线，总是在稳定平衡的实线上方 。
④交汇于三相点的三条平衡曲线互相之间 的位置遵循下面两条准那么：
a、每条曲线越过三相点的延长线必定在另 外两条曲线之间。
b、同一温度时，在三相点附近比容差最大 的两相之间的单变量曲线或其介稳延长 线居中间位置。
假设该反响能够到达平衡，那么有 一个独立的化学反响平衡常数。
此时，虽然组元数＝3，但独立组元 数C＝3－1＝2。
4、自由度 在一定范围内，可以任意改变而不
引起旧相消失或新相产生的独立变量称 为自由度，平衡系统的自由度数用F表示。
这些变量主要指组成〔即组分的浓 度〕、温度和压力等。
5、外界影响因素 影响系统平衡状态的外界因素包括：温度、压力、电
主要区别在于固-液平衡的熔融曲线OC线倾斜
第七章相平衡与相图A
研制开发新材料确定材料成分制订材料生产加工和热处理工艺分析平衡态的组织和可能的非平衡态组织变化预测材料的性能进行材料失效分析一相平衡概念和相律一个结构的相转变为另一种结构相的过程称为相变相变
第7章 相平衡与相图
教学内容
1.相、相平衡、相图等基本概念 2.单元系相图 3.二元系中的相平衡 4.共晶相图 5.包晶相图 6.偏晶相图 7.复杂相图 8.包含固-固反应的相平衡 9.三元系中的相平衡
体系为单相 相点落在线上: f = 1 自由度为1
两相平衡 相点落在交点: f = 0 自由度为0
三相共存
举例：
举例：
7.3 二元系中的相平衡
一、成分的描述 质量分数和摩尔分数。 如A组元的质量分数为wA、摩尔分数为xA， 其相对原子量为MA；B组元的质量分数为wB、 摩尔分数为xB，其相对原子量为MB，则： xA=(wA/MA)/(wA/MA + wB/MB) xB=(wB/MB)/(wA/MA + wB/MB)
相组成物是指组成合金 显微组织的基本相。
组织组成物是指合金在 结晶过程中，形成的具
有特定形态特征的独立 组成部分。
α
β
19
61.9
97.5
M
%
97.5 61.9 97.5 19
100%
45.4%
亚共晶合金 19%＜Sn% ＜61.9 % 过共晶合金 61.9 %＜Sn% ＜97.5%
L 匀 晶 转变 L多 共晶转变 脱溶转变 ( ) II ( )
相界线
在相图上将各相区分隔开的线叫相界线， 由于相界线的特性不同，可区分为： ①液相线：其上全为液相，线下有固相出现， 可以表示为L/L+。 ②固相线：其下全为固相，可表示为L+/L。
第7章 相平衡与相图
教学内容
1.相、相平衡、相图等基本概念 2.单元系相图 3.二元系中的相平衡 4.共晶相图 5.包晶相图 6.偏晶相图 7.复杂相图 8.包含固-固反应的相平衡 9.三元系中的相平衡
体系为单相 相点落在线上: f = 1 自由度为1
两相平衡 相点落在交点: f = 0 自由度为0
三相共存
举例：
举例：
7.3 二元系中的相平衡
一、成分的描述 质量分数和摩尔分数。 如A组元的质量分数为wA、摩尔分数为xA， 其相对原子量为MA；B组元的质量分数为wB、 摩尔分数为xB，其相对原子量为MB，则： xA=(wA/MA)/(wA/MA + wB/MB) xB=(wB/MB)/(wA/MA + wB/MB)
相组成物是指组成合金 显微组织的基本相。
组织组成物是指合金在 结晶过程中，形成的具
有特定形态特征的独立 组成部分。
α
β
19
61.9
97.5
M
%
97.5 61.9 97.5 19
100%
45.4%
亚共晶合金 19%＜Sn% ＜61.9 % 过共晶合金 61.9 %＜Sn% ＜97.5%
L 匀 晶 转变 L多 共晶转变 脱溶转变 ( ) II ( )
相界线
在相图上将各相区分隔开的线叫相界线， 由于相界线的特性不同，可区分为： ①液相线：其上全为液相，线下有固相出现， 可以表示为L/L+。 ②固相线：其下全为固相，可表示为L+/L。
.相平衡与相图原理
湖
北
汽
车
工
业
学
院
40
三、相图规律－相区接触法则；
1. 平衡相的成分必定沿相界线随温度而变化
2.单相区与单相区只能有一个点接触，而不应有一 条边界线。 3.相邻相区的相数相差为1，单相区与双相区相 邻；邻近的两个单相区被一个两相区隔开，两相 区与三相区相邻。 4.一个三相反应的水平线和三个两相区相遇
学
院
15
二、二元相图的基本类型 1.匀晶相图 两组元在液态和固态 时都能以任何比例完全 互溶的相系，所形成的 相图为匀晶相图
湖
北
汽
车
工
业
学
院
16
具有极值的匀晶相图
湖
北
汽
车
工
业
学
院
17
2.共晶相图(binary eutectic systems）
两组元在液态中无限互溶，在固态时有限互溶且发生共晶反 应(eutectic reaction)的一种相图，如Pb-Sn、Ag-Cu、Al-Si 等
湖 北 汽 车 工 业 学 院 42
湖
北
汽
车
工
业
学
院
43
湖
北
汽
车
工
业
学
院
44
湖
北
汽
车
工
业
学
院
45
湖
北
汽
车
工
业
学
院
46
湖
北
汽
车
工
业
学
院
47
湖
北
汽
车
工
业
学
院
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Au-Cu，Fe-Co等在相图 上具有极小点
Pb-Ti等相图上具有极大点
2、固溶体的平衡凝固
（1）结晶过程及组织
（2）固溶体成分的变化和相平衡
（3）固溶体的结晶规律
• a. 固溶体的结晶与纯金属不同， 它不在恒温下进行，而是在一个 温度范围内不断降温条件下完成 的
• b. 固溶体的凝固过程与纯金属一 样，也包括形核与长大两个阶段
是表示在平衡条件下，系统的自由度、组元和平衡相数之 间的关系，它是系统平衡条件的数学表达式。
f=c-p+n f=c-p+2
对于凝聚态系统，有：f=c-p+1
注意： f=C-P+2
•（1）平衡状态下f不可能为负数，相数p必须大于 等于1，即在系统中至少有一个相存在，否则将不 可能构成系统。 •（2）相律给出了平衡状态下体系中存在的相数与 组元数及温度、压力之间的关系，对分析和研究相 图有重要的指导作用。 •（3）相律只能表示体系中组元和相的数目，不能 指明组元或相的类型和含量 •（4）相律不能预告反应动力学（速度）
8、凝固：材料由液态转变成固态的过程称为凝固。
结晶：若凝固后的物质为晶体，则这种凝固称为结晶。 一般金属及其合金皆为晶体，故称为金属结晶。
二、相平衡条件和相律
1、平衡
（平衡状态：系统吉布斯自由能处于最低所对 应的状态。）
当合力为零时，系统处于机械平衡；
当温差消失时，系统处于热平衡；
当系统中各相的化学势相等，各组元的浓度不再变化 时，系统就达到了化学平衡
二、杠杆定律
设合金的总重量为1，则有
杠杆定律的说明：
两相平衡共存（两相区） 确定相的含量
三、二元相图的基本类型
（一）匀晶相图 1、匀晶相图 • 匀晶转变：由液相直接结晶
出单相固溶体的过程。
• 匀晶相图：完全具有匀晶转 变的相图。如 Cu-Ni、AuAg、Ag-Pt等相图。
• 组元特征：两个组元化学性 质相近，晶体结构相同，晶 格参数相差不大，在液态和 固态都能完全互溶。
补充：单元系相图 特征：C=1， f=C-P+2=3-P
一、相图的建立
二、相图分析
• 1. 三个单相区：
f＝1-1+2＝2
2. 三个两相线： oa代表水汽二相图共存 (蒸发曲线)； ob代表冰汽二相的平衡共存 (升华曲线)； oc线则代表冰水二相图共存（冰的熔融曲线）
f＝1-2+2＝1
3.一个三相点：系统中的冰、水、汽三相共存的状态。 （f=1-3+2=0)
第二节 二元相图
• 二元系相图是研究二元体系在热力学平衡条件下，相 与温度、成分之间关系
一、二元相图的表示与建立方法
1、成分的表示 常用质量百分数
A
MAxA
100%
MAxA MBxB
B
MBxB 100% MAxA MBxB
xA
A / MA
100%
A / MA B / MB
xB
B / MB
一个固相的过程。 • 二次相（次生相）：二次结晶析出的相。 • 组织组成物：在结晶的各个阶段中形成清晰
3、组织：人们用肉所观察到的材料形貌。
4、组织组成物：组织中形貌相同的组成部分。
5、相：体系中具有相同物理与化学性质的，且与其他部分 以界面分开的均匀部分称为相。
相的理解： （1）一个相中可以包含几种物质，即几种物质可以形成
一个相； （2）一种物质可以有几个相； （3）固体机械混合物中有几种物质就有几个相。
第八章 相平衡与相图原理
第一节 相、相平衡与相律
一、基本概念
1、合金：由两种或两种以上的元素组成，其中至少有 一种为金属，组成具有金属性的材料称为合金。
2、组元：构成材料的最简单、最基本、可以独立存在的 物质。它可以是纯元素也可以是稳定化合物。
C=1，单元系统，如纯铁 C=2，二元系统，如Pb－Sn合金 C=3，三元系统，如Fe－C－Si合金 C>3，多元系统
• 共晶转变：是指从一个液相中 同时结晶出两个成分不同的固 相的过程。
• 共晶体（共晶组织）：共晶转 变的产物（两相机械混合物）。
• 共晶温度：发生共晶转变时的 液相的温度。
• 共晶相图：两个组元在液态无 限互溶，而在固态有限互溶或 互不相溶并发生共晶转变形成 共晶组织的相图。
常用术语：
• 先共晶相：共晶转变形成前的相。 • 二次结晶（脱溶）：从一个固溶体中析出另
100%
A / MA B / MB
2、相图的测定方法 实验法：热分析、膨胀法、磁性法、硬度测定法等 理论计算法 热分析法建立相图示意：
补充：多相平衡的公切线原理
1、公切线法则
（1）对于二元系统， 若在等温恒压条件下处 于两相平衡共存，则可 对两相的吉布斯自由能 曲线作公切线，公切线 在两曲线上切点对应的 成分为其平衡成分。
• c. 合金结晶形核时需要能量起伏 和成分起伏
• d. 固溶体的凝固依赖于两组元原 子的扩散
• e. 平衡凝固得到的固溶体显微组 织和纯金属相同，除了晶界外， 晶粒之间和晶粒内部的成分却是 相同的。
固溶体平衡结晶示例
合金全部凝固完毕，得到与原液相成分相同的单相均匀固 溶体
（二）共晶相图
1、共晶相图
如果同时达到三种平衡，那么系统就达到了化学热力学 平衡
2、相平衡：各相的化学热力学平衡。
具体指合金系中，参与结晶或相变过程的各相之间的相 对量和相的浓度不再改变时所达到的一种动态平衡。
3、自由度：在平衡系统中独立可变的因素。 4、自由度数：指在平衡系统中可以独立改变的变量的最 大数目。
5、相律（吉布斯相律）：
注意：不同的相之间必然有界面将其分开，但由 界面分开的并不一定就是两个不同的相
6、相图 表示合金系中合金状态、压力、温度及成分之间关
系的图解。是研究不同成分合金平衡关系的图形。又 称为平衡图或状态图。
对单元系采用T~P图，两元系采用T~P~X。
7、相变：从一种相到另一种相的转变 固态相变: 由不同固相之间的转变
（2）在两切点之间成分范围内的二元合金，具有 切点成分的相平衡共存时系统的吉布斯自由能最低
2、二元系两相平衡
在这两条曲线的公切线上得到两个公切点 a 和 b 。 这两个切点就是合金处于 α + β 两相平衡时，两个 平衡相的成分。
三相呈两个两相平衡时的自由能曲线
3、二元系统的三相平衡
自由能-成分曲线与共晶相图的关系