matlab曲线拟合函数的具体步骤
matlab数学公式拟合 曲线

matlab数学公式拟合曲线
在MATLAB中,可以使用拟合函数来拟合数学公式的曲线。
拟合函数是一种通过给定的数据点,计算出最佳拟合曲线的方法。
首先,我们需要导入要拟合的数据点。
假设我们的数据点包括n 个(x,y)对,其中x是自变量的值,y是因变量的值。
可以使用MATLAB中的数组来存储这些数据点。
例如,我们可以定义一个x数组和一个y数组,分别存储自变量和因变量的值。
接下来,我们可以使用polyfit函数进行拟合。
polyfit函数可以根据给定的数据点,计算出多项式的系数,从而构建拟合曲线。
例如,我们可以使用一次多项式(直线)进行拟合:
```matlab
p = polyfit(x, y, 1);
```
这将返回一个包含两个元素的数组p,其中p(1)是一次项的系数,p(2)是常数项的系数。
然后,我们可以使用polyval函数利用拟合的结果来计算拟合曲线上的点的值。
例如,我们可以使用以下代码计算拟合曲线上的点的y 值:
```matlab
y_fit = polyval(p, x);
```
最后,我们可以使用plot函数将原始数据点和拟合曲线绘制在同一个图形上:
```matlab
plot(x, y, 'o', x, y_fit, '-');
```
以上代码将在图形窗口中绘制出原始数据点(用圆圈表示)和拟合曲线(用直线表示)。
通过调整拟合函数的阶数,我们可以尝试不同次数的拟合(例如二次、三次等),以找到最适合数据的拟合曲线。
希望以上介绍对你有所帮助!。
matlab曲线曲面拟合讲解及实例

例如:
x1=[1.0500 1.0520 1.0530 1.0900 1.0990 1.1020 1.1240 1.1420...
1.1490 1.0500 1.0520 1.0530 1.0900 1.0990 1.1020 1.1240 1.1420 1.1490];
x2=[3.8500 1.6500 2.7500 5.5000 7.7000 3.3000 4.9500 8.2500 11.5500...
52.5000 62.0000];
data=[x1;x2]; ห้องสมุดไป่ตู้ %类似于将x1 x2整合成一个2维数组。
a0= [-0.0014,0.07];
option=optimset('MaxFunEvals',5000);
format long;
同理用Symbolic Math Toolbox可以直接执行
>> ezmesh('X.^2 - Y.^2', [-2 2], [-2 2])
surf函数
在函数不能表示成z = f(x, y)时,需要用surf函数。比如x2+y2+z2=1.
先需要用柱面坐标或者球坐标来表示。这里用柱面坐标表示为 r2+z2=1
x = sqrt(1-z2)cosθ, x = sqrt(1-z2)sinθ;
执行matlab指令:
>> [theta, Z] = meshgrid((0:0.1:2)*pi, (-1:0.1:1));
>> X =sqrt(1 - Z.^2).*cos(theta);
>> Y =sqrt(1 - Z.^2).*sin(theta);
曲线拟合法的Matlab实现

曲线拟合法的Matlab实现曲线拟合在许多科学和工程领域中都有广泛应用,包括机器学习,数据科学,信号处理,控制工程等。
在Matlab中实现曲线拟合的方法有多种,其中最常用的是使用fit()函数。
以下是一个基本的示例,演示如何在Matlab中使用fit()函数进行曲线拟合。
我们需要一些数据。
假设我们有一组x和y数据点,我们想要在这些点上拟合一条曲线。
y = 3*x.^2 + 2*x + 1 + randn(size(x));fitresult = fit(x, y, 'poly1');在这里,'poly1'表示我们想要拟合一个一次多项式。
你可以使用'poly2','poly3'等来拟合更高次的多项式。
同样,你也可以使用其他类型的模型,如指数、对数、自定义函数等。
然后,我们可以使用plot()函数将原始数据和拟合曲线一起绘制出来。
在这里,'hold on'命令用于保持当前图像,这样我们就可以在同一个图形上绘制多条线了。
我们可以使用fitresult来获取拟合曲线的参数和其他信息。
例如:以上就是在Matlab中进行曲线拟合的基本步骤。
需要注意的是,对于复杂的实际问题,可能需要进行更复杂的模型选择和参数优化。
也可以使用其他工具如curve fitting toolbox进行更详细的分析和拟合。
最小二乘曲线拟合是一种数学统计方法,用于根据给定数据点拟合出一条曲线或曲面,使得该曲线或曲面最小化每个数据点到拟合曲线或曲面的平方误差之和。
这种方法广泛应用于数据分析和科学计算等领域。
本文将介绍最小二乘曲线拟合的基本原理和在Matlab中的实现方法。
假设有一组数据点 (x_i, y_i),i=1,2,...,n,需要拟合出一条曲线y=f(x)。
最小二乘法要求曲线 f(x)最小化每个数据点到曲线的平方误差之和,即E = sum (f(x_i)-y_i)^2对曲线 f(x)进行求导,得到一元一次方程:f'(x)=sum(f(x)-y)*x-sum(f(x)-y)E = sum [(f'(x))^2] * x^2 - 2 * sum [f(x) * f'(x) * x] + 2 * sum [f(x)^2]令 E对 f'(x)的导数为零,可得到最小二乘曲线拟合的方程:sum [f'(x)^2] * x^2 - 2 * sum [f(x) * f'(x) * x] + 2 * n * f(x)^2 = 0在Matlab中,可以使用polyfit函数实现最小二乘曲线拟合。
7.4 用Matlab求解曲线拟合问题

2 [ f ( x ) y ] i i i 1 11
最小
12
1)输入以下命令: x=0:0.1:1;
10 8 6 4
y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];
问题归结为,求 a1,a2, …am 使 J(a1,a2, …am) 最小。
线性最小二乘拟合 f(x)=a1r1(x)+ …+amrm(x)中 函数{r1(x), …rm(x)}的选取 1. 通过机理分析建立数学模型来确定 f(x); 2. 将数据 (xi,yi) i=1, …n 作图,通过直观判断确定 f(x): f=a1+a2x + + + + + f=a1+a2x+a3x2 + + + + + f=a1+a2x+a3x2 + + + + +
f=a1+a2/x + + +
f=aebx +
+
-bx f=ae + +
+ +
+ + +
+
+ +
一、用Matlab进行多项式曲线拟合
1. Matlab中提供函数polyfit作多项式f(x)=a1xm+ …+amx+am+1 曲线拟合,具体的调用格式如下: a=polyfit(x,y,m)
拟合多项式次数 已知数据点向量(长度相同) 输出拟合多项式系数 a=[a1, …am , am+1] (数组)
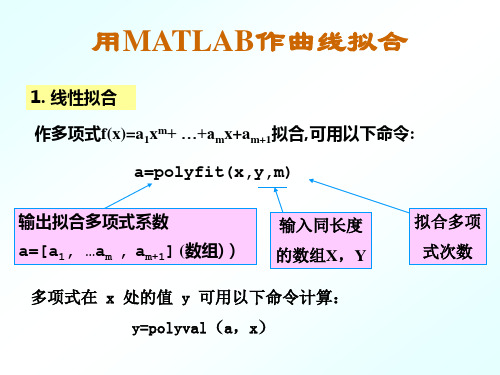
用MATLAB作曲线拟合
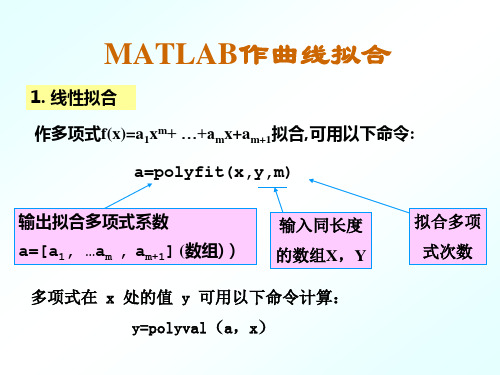
1. 线性拟合 作多项式f(x)=a1xm+ …+amx+am+1拟合,可用以下命令:
a=polyfit(x,y,m)
输出拟合多项式系数 a=[a1, …am , am+1] (数组))
输入同长度 的数组X,Y
多项式在 x 处的值 y 可用以下命令计算: y=polyval(a,x)
0.0062 0.0062 x = 0.0063 -0.0034
0.0056 0.0063 0.2542
0.0059 0.0063
4)拟合得a=0.0063 b=-0.0034 k=0.2542
0.0061 0.0063
可以看出,两个命令的计算结果是相同的.
例. 由数据 温度t(0C) 20.5 32.7 51.0 73.0 95.7
6.50,6.59];
x0=[0.2,0.05,0.05];
x=lsqcurvefit ('curvefun1',x0,tdata,cdata)
f= curvefun1(x,tdata)
解法2: 用命令 lsqnonlin f(x)=F(x,tdata,ctada)= (a be0.02kt1 c1,, a be0.02kt10 c1)T x=(a,b,k)
function f=curvefun1(x,tdata)
f=x(1)+x(2)*exp(-0.02*x(3)*tdata)
2)输入命令
%其中 x(1)=a; x(2)=b;x(3)=k;
tdata=100:100:1000
cdata=1e-03*[4.54,4.99,5.35,5.65,5.90,6.10,6.26,6.39,
matlabcftool做拟合教程

matlabcftool做拟合教程cftool做拟合教程一、单一变量的曲线逼近Matlab有一个功能强大的曲线拟合工具箱 cftool ,使用方便,能实现多种类型的线性、非线性曲线拟合。
下面结合我使用的Matlab R2007b 来简单介绍如何使用这个工具箱。
假设我们要拟合的函数形式是 y=A*x*x + B*x, 且A>0,B>0 。
1、在命令行输入数据:》x=[110.3323 148.7328 178.064 202.8258033 224.7105 244.5711 262.908 280.0447 296.204 311.5475];》y=[5 10 15 20 25 30 35 40 45 50];2、启动曲线拟合工具箱》cftool3、进入曲线拟合工具箱界面“Curve Fitting tool”(1)点击“Data”按钮,弹出“Data”窗口;(2)利用X data和Y data的下拉菜单读入数据x,y,可修改数据集名“Data set name”,然后点击“Create data set”按钮,退出“Data”窗口,返回工具箱界面,这时会自动画出数据集的曲线图;(3)点击“Fitting”按钮,弹出“Fitting”窗口;(4)点击“New fit”按钮,可修改拟合项目名称“Fit name”,通过“Data set”下拉菜单选择数据集,然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:· Custom Equations:用户自定义的函数类型· Exponentia l:指数逼近,有2种类型, a*exp(b*x) 、a*exp(b*x) + c*exp(d*x)· Fourier:傅立叶逼近,有7种类型,基础型是 a0 +a1*cos(x*w) + b1*sin(x*w)· Gaussian:高斯逼近,有8种类型,基础型是a1*exp(-((x-b1)/c1)^2)· Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving· Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~· Power:幂逼近,有2种类型,a*x^b 、a*x^b + c· Rational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型· Smoothing Spline:平滑逼近(翻译的不大恰当,不好意思)· Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是a1*sin(b1*x + c1)· Weibull:只有一种,a*b*x^(b-1)*exp(-a*x^b)选择好所需的拟合曲线类型及其子类型,并进行相关设置:第 1 页——如果是非自定义的类型,根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数;——如果选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口,有“Linear Equations线性等式”和“General Equations构造等式”两种标签。
matlab输入数据拟合曲线

一、引言Matlab是一种强大的数学计算软件,广泛用于工程、科学和金融等领域。
在实际工作中,经常需要对输入数据进行曲线拟合,以找到数据之间的潜在关系或者预测未来的变化趋势。
本文将介绍如何使用Matlab对输入数据进行曲线拟合的方法和步骤。
二、数据准备在进行曲线拟合之前,首先需要准备好输入数据。
可以是实验数据、观测数据或者模拟数据,数据的形式可以是一维数组、二维矩阵或者多维数组。
确保数据的准确性和完整性是进行曲线拟合的第一步。
三、选择合适的拟合函数根据输入数据的特点和需要拟合的曲线形式,需要选择合适的拟合函数。
Matlab提供了丰富的内置拟合函数,如polyfit、lsqcurvefit、fit 等,也可以根据需要编写自定义的拟合函数。
不同的拟合函数表达了不同的数学关系,选择合适的拟合函数是进行曲线拟合的关键一步。
四、进行曲线拟合在选择了合适的拟合函数之后,可以利用Matlab的拟合工具对输入数据进行曲线拟合。
具体步骤包括:加载数据、选择拟合函数、设置拟合参数、调用拟合函数进行拟合、获取拟合结果和评估拟合效果等。
在拟合过程中,需要考虑拟合的精度、稳定性和适用性,并进行适当的参数调节和优化。
五、评估拟合效果完成曲线拟合之后,需要对拟合效果进行评估。
常用的评估指标包括拟合曲线和原始数据的拟合度、残差分布和拟合参数的可靠性等。
Matlab提供了丰富的工具和函数,如polyval、residuals、confint 等,可以方便地进行拟合效果的评估和分析。
六、进一步分析和应用基于曲线拟合的结果,可以进行进一步的分析和应用。
可以利用拟合曲线进行数据预测、趋势预测、参数优化、模型比较等。
Matlab提供了丰富的工具和函数,如forecast、polyderpare等,可以方便地进行进一步分析和应用。
七、总结与展望本文介绍了使用Matlab进行曲线拟合的方法和步骤,包括数据准备、拟合函数选择、曲线拟合、拟合效果评估和进一步分析。
曲线拟合 matlab

曲线拟合 matlab
在MATLAB中进行曲线拟合可以使用多种方法,其中最常见的是使用fit 函数,它是Curve Fitting Toolbox 中的一个函数。
以下是一个基本的示例:
matlab
% 生成一些数据
x = linspace(0,10,100);
y = 3*x.^2 + 2*x + randn(size(x));
% 使用fit函数进行拟合
f = fit(x', y', 'poly1');
% 绘制原始数据和拟合曲线
plot(f, x, y);
在这个例子中,我们首先生成了一些数据,然后使用fit 函数对数据进行拟合。
在这个例子中,我们使用的是一次多项式('poly1'),但你可以选择其他多项式或非多项式函数。
拟合完成后,你可以使用 f 这个拟合对象来绘制原始数据和拟合曲线。
注意:在使用Curve Fitting Toolbox之前,你需要先安装它。
你可以在MATLAB的Add-Ons Explorer中找到并安装它。
matlab曲线拟合函数的具体步骤

matlab曲线拟合函数的具体步骤编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(matlab曲线拟合函数的具体步骤)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为matlab曲线拟合函数的具体步骤的全部内容。
matlab曲线拟合函数的具体步骤是什么1、在命令行输入数据:2、启动曲线拟合工具箱》cftool3、进入曲线拟合工具箱界面“Curve Fitting tool"(1)点击“Data”按钮,弹出“Data”窗口;(2)利用X data和Y data的下拉菜单读入数据x,y,可修改数据集名“Data set name”,然后点击“Create data set”按钮,退出“Data”窗口,返回工具箱界面,这时会自动画出数据集的曲线图;(3)点击“Fitting”按钮,弹出“Fitting"窗口;(4)点击“New fit”按钮,可修改拟合项目名称“Fit name”,通过“Data set"下拉菜单选择数据集,然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:Custom Equations:用户自定义的函数类型Exponential:指数逼近,有2种类型, a*exp(b*x)、 a*exp(b*x) + c*exp(d*x)Fourier:傅立叶逼近,有7种类型,基础型是 a0 + a1*cos(x*w) + b1*sin(x*w)Gaussian:高斯逼近,有8种类型,基础型是 a1*exp(—((x—b1)/c1)^2) Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape—preservingPolynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~Power:幂逼近,有2种类型,a*x^b 、a*x^b + cRational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4—5th degree ~;此外,分子还包括constant型Smoothing Spline:平滑逼近(翻译的不大恰当,不好意思)Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是 a1*sin(b1*x+ c1)Weibull:只有一种,a*b*x^(b-1)*exp(—a*x^b)选择好所需的拟合曲线类型及其子类型,并进行相关设置:——如果是非自定义的类型,根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数;——如果选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口。
matlab中拟合曲线的算法

一、引言在科学和工程领域中,拟合曲线是一种重要的数学工具,它用于寻找一条曲线,使得该曲线最好地描述已知的数据点或者模拟实验结果。
MATLAB作为一种强大的数学计算软件,拥有丰富的拟合曲线的算法和工具。
本文将介绍MATLAB中拟合曲线的算法,包括常见的线性拟合、多项式拟合、非线性拟合等。
二、线性拟合1. 线性拟合是指采用线性方程来拟合已知数据点的方法。
在MATLAB 中,可以使用polyfit函数来实现线性拟合。
该函数的基本语法如下: p = polyfit(x, y, n),其中x和y分别代表已知数据点的横坐标和纵坐标,n代表拟合多项式的阶数。
函数返回一个长度为n+1的向量p,其中p(1)、p(2)分别代表拟合多项式的系数。
2. 通过polyfit函数可以实现对数据点的线性拟合,得到拟合曲线的系数,并且可以使用polyval函数来计算拟合曲线在指定点的取值。
该函数的基本语法如下:yfit = polyval(p, x),其中p代表拟合曲线的系数向量,x代表待求取值的点,yfit代表拟合曲线在该点的取值。
三、多项式拟合1. 多项式拟合是指采用多项式方程来拟合已知数据点的方法。
在MATLAB中,可以使用polyfit函数来实现多项式拟合,和线性拟合类似。
不同之处在于,可以通过调整多项式的阶数来适应不同的数据特性。
2. 除了使用polyfit函数进行多项式拟合外,MATLAB还提供了Polytool工具箱,它是一个方便的图形用户界面,可以用于拟合已知数据点并可视化拟合曲线。
使用Polytool工具箱,用户可以直观地调整多项式的阶数和观察拟合效果,非常适合初学者和快速验证拟合效果。
四、非线性拟合1. 非线性拟合是指采用非线性方程来拟合已知数据点的方法。
MATLAB中提供了curvefitting工具箱,其中包含了众多非线性拟合的工具和算法,例如最小二乘法、最大似然法、拟合优度计算等。
通过该工具箱,用户可以方便地进行各种复杂数据的非线性拟合。
matlab b样条曲线拟合

标题:MATLAB中B样条曲线拟合一、介绍B样条曲线是一种常用的曲线拟合方法,广泛应用于工程、数学、经济等领域。
MATLAB作为一种强大的数学软件工具,具有丰富的函数库和绘图功能,能够很好地支持B样条曲线的拟合和可视化。
本文将介绍MATLAB中B样条曲线的拟合方法及其实现过程。
二、B样条曲线的基本原理B样条曲线是一种参数化曲线,由基函数和控制点共同确定。
其基本原理包括:1. 基函数的选择:B样条曲线的形状由基函数决定,常用的基函数包括均匀B样条、非均匀B样条等。
2. 控制点的作用:控制点是B样条曲线形状的关键参数,通过调整控制点的位置可以改变曲线的形状。
3. 参数化表示:B样条曲线是通过参数t来表示的,调整参数t的取值可以在曲线上取得不同的点。
三、MATLAB中的B样条曲线拟合方法MATLAB提供了丰富的函数库和工具箱,其中包括了B样条曲线的拟合函数。
一般而言,拟合B样条曲线的基本步骤包括:1. 导入数据:首先需要导入需要拟合的数据点,通常是二维平面上的点集。
2. 调用拟合函数:MATLAB提供了基于B样条曲线的拟合函数,例如spline和interp1等。
3. 可视化结果:拟合完成后,可以使用MATLAB的绘图工具对拟合结果进行可视化,观察拟合效果。
四、B样条曲线拟合案例为了更好地理解MATLAB中B样条曲线的拟合方法,我们以一个实际的案例进行说明。
假设有一个二维数据点集P={(P1,P1),(P2,P2),…,(PP,PP)},我们希望利用B样条曲线对这些数据点进行拟合。
1. 数据导入:我们需要将数据点集导入MATLAB环境中,可以通过数组的形式或者直接从外部文件读取。
2. 调用拟合函数:利用MATLAB提供的拟合函数,例如spline或interp1,对数据点集进行B样条曲线的拟合。
3. 可视化结果:我们可以使用MATLAB的绘图工具对拟合结果进行可视化,观察拟合效果,进一步调整参数以获得更好的拟合结果。
matlab曲线拟合输出拟合函数在其他文件调用

Matlab曲线拟合输出拟合函数在其他文件调用在使用Matlab进行曲线拟合时,我们通常会得到一个拟合函数,用于描述实验数据的趋势和规律。
然而,有时候我们需要在其他文件中调用这个拟合函数,以便进行进一步的分析和处理。
本文将介绍如何在Matlab中输出拟合函数,并在其他文件中调用这个函数。
让我们来看一下如何在Matlab中进行曲线拟合,并输出拟合函数。
假设我们已经有了一组实验数据x和对应的y,我们可以使用Matlab 中的polyfit函数来进行多项式拟合。
我们可以使用二次多项式来拟合数据:```matlabp = polyfit(x, y, 2);```这将得到一个二次多项式拟合的系数p。
接下来,我们可以使用polyval函数来计算拟合后的y值,并且将拟合结果绘制成图表:```matlaby_fit = polyval(p, x);plot(x, y, 'o', x, y_fit, '-');```通过这样的步骤,我们就可以在Matlab中完成曲线拟合,并且得到拟合函数的系数。
接下来,我们需要将这个拟合函数输出到其他文件中,以便在其他程序中进行调用。
为了实现这一点,我们可以将拟合函数写入到一个独立的文件中。
我们可以创建一个名为"fitting_function.m"的文件,将拟合函数写入其中:```matlabfunction y_fit = fitting_function(x, p)y_fit = polyval(p, x);end```在这个文件中,我们定义了一个名为"fitting_function"的函数,用于计算拟合后的y值。
这个函数需要输入实验数据x和拟合函数的系数p,然后返回拟合后的y值。
现在,我们可以在其他文件中调用这个函数了。
假设我们需要在一个名为"main_program.m"的文件中调用拟合函数。
matlab二次拟合曲线

matlab二次拟合曲线
在Matlab中进行二次拟合曲线的方法如下:
1. 准备数据:假设有n个数据点,其中x为自变量,y为因变量。
将数据按照自变量x的顺序排列。
2. 使用polyfit函数进行二次拟合:使用polyfit函数可以拟合
出二次多项式的系数。
函数的输入参数为自变量x和因变量y,以及拟合的次数,这里为2。
```matlab
coefficients = polyfit(x, y, 2);
```
3. 绘制拟合曲线:利用polyval函数可以根据拟合的系数绘制
拟合曲线。
函数的输入参数为自变量x、拟合的系数coefficients以及拟合的次数。
```matlab
x_fit = linspace(min(x), max(x), 100); % 生成用于绘制拟合曲线
的自变量
y_fit = polyval(coefficients, x_fit); % 根据拟合的系数获取对应
的因变量值
plot(x, y, 'o'); % 绘制原始数据点
hold on;
plot(x_fit, y_fit); % 绘制拟合曲线
hold off;
```
以上代码可以将原始数据点以圆点的形式绘制出来,同时绘制出二次拟合曲线。
调整自变量x_fit的范围和数量,可以控制拟合曲线的平滑程度。
用MATLAB作曲线拟合
2. lsqnonlin 已知数据点: 已知数据点: xdata=(xdata1,xdata2,…,xdatan) ydata=(ydata1,ydata2,…,ydatan) lsqnonlin用以求含参量x(向量)的向量值函数 用以求含参量x 向量) 用以求含参量 f(x)=(f (x),…,f f(x)=(f1(x),f2(x), ,fn(x))T
T 2 2
中的参量x 中的参量x,使得
2
f ( x) f ( x) = f1 ( x) + f 2 ( x) + ⋯ + f n ( x)
最小。 最小。 其中 fi(x)=f(x,xdatai,ydatai) ) ( , =F(x,xdatai)-ydatai
输入格式为: 输入格式为: 1) x=lsqnonlin(‘fun’,x0); 2) x= lsqnonlin (‘fun’,x0,options); 3) x= lsqnonlin (‘fun’,x0,options,‘grad’); 4) [x,options]= lsqnonlin (‘fun’,x0,…); 5) [x,options,funval]= lsqnonlin (‘fun’, 说明:x= , , ); x0,…); lsqnonlin (‘fun’,x0,options); fun是一个事先建立的 是一个事先建立的 定义函数f(x)的M-文件, 文件, 定义函数 的 文件 自变量为x 自变量为 选项见无 迭代初值 约束优化
n 2 i i
∑ ( F ( x, xdata ) − ydata )
i =1
最小
输入格式为: 输入格式为: (1) x = lsqcurvefit (‘fun’,x0,xdata,ydata); (2) x =lsqcurvefit (‘fun’,x0,xdata,ydata,options); (3) x = lsqcurvefit (‘fun’,x0,xdata,ydata,options,’grad’); (4) [x, options] = lsqcurvefit (‘fun’,x0,xdata,ydata,…); (5) [x, options,funval] = lsqcurvefit (‘fun’,x0,xdata,ydata,…); (6) [x, options,funval, Jacob] = lsqcurvefit (‘fun’,x0,xdata,ydata,…); 说明:x = lsqcurvefit (‘fun’,x0,xdata,ydata,options); fun是一个事先建立的 是一个事先建立的 定义函数F(x,xdata) 的 定义函数 M-文件 自变量为 和 文件 文件 自变量为x和 xdata 选项见无 迭代初值 已知数据点 约束优化
使用Matlab进行曲线拟合

使用Matlab进行曲线拟合引言在科学研究和工程应用中,曲线拟合是一个非常常见和重要的问题。
通过拟合实验数据或者观测数据,我们可以找到一条曲线,以最佳地描述数据的趋势。
Matlab是一个功能强大的数值计算软件,提供了丰富的工具和函数,可以帮助我们对数据进行曲线拟合。
本文将介绍如何使用Matlab进行曲线拟合,并给出一些实际案例。
一、简单线性回归简单线性回归是曲线拟合中最基础的一种方法。
它假设数据可以用一条直线来表示。
在Matlab中,使用"polyfit"函数可以很方便地进行简单线性回归。
该函数可以从数据中拟合出一个多项式,我们可以选择线性多项式来进行简单线性回归。
下面是一个例子:```matlabx = [1, 2, 3, 4, 5];y = [2, 3, 4, 5, 6];p = polyfit(x, y, 1);f = polyval(p, x);plot(x, y, 'o'); % 绘制原始数据点hold on;plot(x, f, 'r-'); % 绘制拟合曲线```在这个例子中,我们有一个包含5个数据点的数据集,分别存储在向量"x"和"y"中。
通过polyfit函数,我们可以拟合出一个线性多项式的系数"p",然后使用polyval函数来计算拟合曲线上各个x点对应的y值。
最后,使用plot函数将原始数据点和拟合曲线绘制在同一张图上。
这样我们就可以直观地看到拟合效果。
二、非线性曲线拟合除了简单线性回归,Matlab还提供了许多其他方法来进行非线性曲线拟合。
这些方法通常需要指定一个函数形式,然后通过调整函数的参数来拟合数据。
其中最常用的方法之一是最小二乘法。
在Matlab中,可以使用lsqcurvefit函数来进行非线性曲线拟合。
下面是一个例子:```matlabx = [1, 2, 3, 4, 5];y = [5.1, 6.2, 7.1, 8.5, 9.9];f = @(c,x) c(1) * exp(-c(2)*x) + c(3); % 定义拟合函数c0 = [1, 1, 1]; % 初始参数猜测c = lsqcurvefit(f, c0, x, y); % 进行曲线拟合plot(x, y, 'o'); % 绘制原始数据点hold on;plot(x, f(c, x), 'r-'); % 绘制拟合曲线```在这个例子中,我们有一个包含5个数据点的数据集,存储在向量"x"和"y"中。
matlab拟合正态分布曲线

正态分布曲线是统计学中常用的一种分布模型,也叫高斯分布曲线,它是以高斯函数为基础的一种连续分布函数。
在实际的统计分析中,经常需要对数据进行拟合,使得数据分布符合正态分布曲线。
而MATLAB作为一个强大的数学计算工具,提供了丰富的函数和工具箱,可以用来进行正态分布曲线的拟合。
本文将介绍MATLAB中拟合正态分布曲线的方法和步骤,以及一些实际案例的应用。
一、MATLAB拟合正态分布曲线的方法1. 数据准备在进行正态分布曲线拟合之前,首先需要准备好数据。
这些数据可以是实验测量得到的,也可以是从其他来源获取的。
在MATLAB中,可以将这些数据存储在一个向量或矩阵中,以便后续进行处理。
2. 正态分布曲线拟合函数MATLAB提供了normfit函数来进行正态分布曲线的拟合。
normfit函数的基本语法是:[mu, sigma] = normfit(X)其中,X是输入的数据向量,mu和sigma分别是拟合得到的正态分布曲线的均值和标准差。
利用这些参数,可以画出拟合得到的正态分布曲线。
3. 绘制正态分布曲线一旦得到了拟合的参数mu和sigma,就可以利用normpdf函数绘制出拟合得到的正态分布曲线。
normpdf函数的基本语法是:Y = normpdf(X, mu, sigma)其中,X是自变量的取值,mu和sigma是拟合得到的均值和标准差,Y是对应的概率密度函数值。
将X和Y绘制在图上,就可以得到拟合的正态分布曲线了。
4. 拟合效果评估拟合得到的正态分布曲线与原始数据的分布进行比较,一般采用残差分析、拟合优度检验等方法来评估拟合的效果。
MATLAB提供了相应的函数和工具,可以进行这些评估。
二、实际案例应用以下是一个简单的实际案例,演示了如何利用MATLAB进行正态分布曲线的拟合。
假设有一组实验测量数据X,需要对其进行正态分布曲线的拟合。
% 生成实验数据X = randn(1, 1000);% 进行正态分布曲线的拟合[mu, sigma] = normfit(X);% 绘制拟合得到的正态分布曲线x = -4:0.1:4;y = normpdf(x, mu, sigma);plot(x, y, 'r', X, zeros(1, 1000), 'o');在这个案例中,首先生成了一组标准正态分布的随机数据X。
matlab曲线拟合方法

曲线拟合方法在MATLAB中的应用本篇文章主要介绍了曲线拟合方法在MATLAB中的应用,包括曲线拟合的基本原理、MATLAB中的曲线拟合工具箱、曲线拟合的步骤以及应用实例。
通过本篇文章的学习,读者可以掌握曲线拟合方法在MATLAB中的应用,为解决实际问题提供有力支持。
曲线拟合方法在MATLAB中的应用曲线拟合是数学中常见的一种数据处理方法,通过拟合曲线可以更好地描述数据之间的关系。
在科学研究和工程实践中,曲线拟合方法的应用非常广泛。
MATLAB作为一种常用的数学软件,提供了强大的曲线拟合工具箱,使得曲线拟合变得更加方便和简单。
一、曲线拟合的基本原理曲线拟合是指通过寻找一条曲线,使得这条曲线尽可能地贴近原始数据点。
在数学上,曲线拟合可以表示为一个方程组,即要求解一个多元非线性方程组。
通过最小二乘法等方法,可以求得最优解,即拟合曲线。
二、MATLAB中的曲线拟合工具箱MATLAB中的曲线拟合工具箱提供了多种拟合方法,包括线性回归、非线性回归、多项式拟合等。
用户可以根据需要选择不同的拟合方法,并进行参数调整和优化。
通过工具箱提供的可视化工具,可以直观地观察拟合结果,并进行相应的调整。
三、曲线拟合的步骤1. 准备数据:将原始数据导入MATLAB中,并进行必要的预处理,如去除异常值、标准化等。
2. 选择拟合方法:根据数据的特点和需求选择合适的拟合方法,如线性回归、非线性回归、多项式拟合等。
3. 拟合曲线:使用所选的拟合方法进行曲线拟合,得到拟合曲线和参数。
4. 可视化结果:使用MATLAB中的可视化工具,将原始数据和拟合曲线可视化展示出来。
5. 结果分析:根据可视化结果和拟合参数进行分析,得出结论。
四、应用实例1. 股票价格预测:通过收集股票历史价格数据,使用曲线拟合方法预测未来价格趋势。
2. 气象数据分析:通过收集气象数据,使用曲线拟合方法分析气温、湿度等因素之间的关系。
3. 生物医学研究:通过曲线拟合方法分析基因序列与蛋白质结构之间的关系。
matlab 散点 构建拟合曲线

在MATLAB中构建散点的拟合曲线,可以按照以下步骤进行:
输入数据:首先,需要在MATLAB中输入你的数据。
这可以通过创建一个矩阵或者直接从文件中导入数据来完成。
例如,你可以创建一个包含x和y值的矩阵:
matlab
x = [1, 2, 3, 4, 5];
y = [2, 3, 4, 5, 6];
绘制散点图:使用scatter函数来绘制散点图。
matlab
scatter(x, y);
拟合曲线:使用polyfit函数进行线性拟合。
例如,进行一阶线性拟合:
matlab
p = polyfit(x, y, 1);
在这里,1表示拟合的阶数,也就是线性拟合。
polyfit函数将返回一个向量,包含了拟合多项式的系数。
绘制拟合曲线:使用polyval函数在给定的x值上计算多项式的值,然后可以用plot函数绘制拟合曲线:
matlab
yfit = polyval(p, x);
hold on;
plot(x, yfit, 'r');
在这里,'r'表示曲线的颜色为红色,hold on命令用于在同一图像窗口中绘制多条曲线。
显示图像:最后,可以使用title,xlabel,和ylabel函数来添加图像的标题,x轴标签,和y 轴标签:
matlab
title('我的拟合曲线');
xlabel('x值');
ylabel('y值');
保存图像:通过点击MATLAB工具栏上的保存按钮,或者选择“File > Save As”来保存生成的图像。
matlab批量拟合曲线

在MATLAB中批量拟合曲线可以使用多种方法,其中一种常用的方法是使用`cftool`工具箱进行操作。
以下是使用`cftool`进行批量拟合的步骤:
1. 输入`cftool`打开工具箱,只选取一组数据拟合。
2. 点击生成代码。
3. 查看代码并做修改。
另外,还可以使用多项式拟合(`polyfit`和`polyval`)方法进行批量拟合。
这种方法可以对数据进行拟合(自定义用几次多项式),返回相应的参数,然后用`polyval`生成拟合后的数据点。
例如,以下代码对抛物线`y=3x^2+6x+5`进行拟合:
```matlab
x = -5:0.1:5; % 自变量范围
y = 3*x.^2+6*x + 5 + randn(size(x)); % 因变量,添加随机噪声
p = polyfit(x,y,2); % 用二次曲线(抛物线)进行拟合
yy = polyval(p,x); % 生成拟合后的数据点
plot(x,y,'.'); % 原始数据点
hold on; % 保持当前图像
plot(x,yy,'r','LineWidth',2) % 拟合后的曲线
```
在`polyfit(x,y,2)`中,`x`表示自变量,`y`表示因变量,`2`表示用二次曲线(抛物线)进行拟合,得到的`p`其实是对应的参数估计值,`yy`为拟合数据点。
另外在实验中还加了一个随机噪声。
以上是两种常用的MATLAB批量拟合曲线的方法,根据具体需求选择适合的方法进行操作。
matlab谐振曲线拟合

matlab谐振曲线拟合
在MATLAB中进行谐振曲线拟合,你可以使用内置的函数,如`polyfit`和`polyval`,来进行多项式拟合。
以下是一个基本的步骤:
1.生成或获取你的谐振数据。
这可能是一个x和y的向量,其中x是频率,y是响应。
2.使用`polyfit`函数来拟合你的数据。
例如,如果你想要一个二次拟合,你可以这样做:
```matlab
p=polyfit(x,y,2);
```
这会返回一个二次多项式的系数。
3.使用`polyval`函数来评估拟合的曲线。
例如:
```matlab
y_fit=polyval(p,x);
```
4.绘制原始数据和拟合的曲线。
例如:
```matlab
plot(x,y,'o',x,y_fit,'-');
legend('原始数据','拟合曲线');
```
以上是一个基本的步骤。
你可能需要根据你的具体需求进行调整。
例如,你可能需要调整`polyfit`中的度数以获得更好的拟合,或者使用其他的优化方法来找到最佳的拟合参数。
你也可能需要处理异常值或缺失数据,这可能需要额外的步骤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab曲线拟合函数的具体步骤是什么
1、在命令行输入数据:
2、启动曲线拟合工具箱
》cftool
3、进入曲线拟合工具箱界面“Curve Fitting tool”
(1)点击“Data”按钮,弹出“Data”窗口;
(2)利用X data和Y data的下拉菜单读入数据x,y,可修改数据集名“Data set name”,然后点击“Create data set”按钮,退出“Data”窗口,返回工具箱界面,这时会自动画出数据集的曲线图;
(3)点击“Fitting”按钮,弹出“Fitting”窗口;
(4)点击“New fit”按钮,可修改拟合项目名称“Fit name”,通过“Data set”下拉菜单选择数据集,然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:
Custom Equations:用户自定义的函数类型
Exponential:指数逼近,有2种类型, a*exp(b*x) 、 a*exp(b*x) + c*exp(d*x) Fourier:傅立叶逼近,有7种类型,基础型是 a0 + a1*cos(x*w) + b1*sin(x*w) Gaussian:高斯逼近,有8种类型,基础型是 a1*exp(-((x-b1)/c1)^2) Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving
Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~
Power:幂逼近,有2种类型,a*x^b 、a*x^b + c
Rational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型
Smoothing Spline:平滑逼近(翻译的不大恰当,不好意思)
Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是 a1*sin(b1*x + c1)
Weibull:只有一种,a*b*x^(b-1)*exp(-a*x^b)
选择好所需的拟合曲线类型及其子类型,并进行相关设置:
——如果是非自定义的类型,根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数;
——如果选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口。
(5)类型设置完成后,点击“Apply”按钮,就可以在Results框中得到拟合结果。
