球柱透镜的联合与转换.
球柱面透镜光学技术--圆柱透镜与环曲面透镜

+3.00D
+5.00D -2.00D
+3.00DS/+2.00DCx170
+5.00DS/-2.00DCx80
例:请将-1.25DCx60/+2.75DCx150转换成球
柱镜形式。
解:-1.25DS/+4.00DCx150
+2.75DS/-4.00DCx60
球柱面透镜的联合最方便直观的方法是用光 学十字图,或者也可分别联合球面镜、柱面镜,使
另一新柱镜屈光力等于原球镜与柱镜屈光力之和, 其轴与原柱镜轴的方向相同
例:将+4.00DS/+1.00DCx90转换为正交柱镜 解一: 一个新柱镜: +4.00DCx180 另一新柱镜: (+4.00+1.00)x90 = +5.00DCx90 正交柱镜形式:+4.00DCx180/+5.00DCx90
45
-3.00D +2.50D +2.75D +2.50D -1.00D +1.25D -3.00D +2.50D +2.75D -1.50D
+0.75D +1.75D
135
+2.50D +0.75D -1.75D
+2.50DS/-1.75DCx45
+0.75DS/+1.75DCx135
解2:(2)/(3)联合结果为
(+2.50+2.75)DS/(-1.00+1.25)DCx135
+5.25DS/+0.25DCx135
球柱镜转换三种公式

球柱镜转换三种公式
球面镜和球柱镜是眼镜中较为常见的两种镜片类型,它们常常用
于矫正人们的视力问题。
在某些情况下,我们需要将球面镜转换为球
柱镜或者将球柱镜转换为球面镜,此时需要用到以下三种公式:
1. 球面镜转换为球柱镜公式:
Cylinder = S × tan(Axis)
式中,Cylinder表示所需的柱镜度数,S表示原始的球面度数,Axis表示原始的度数方向。
2. 球柱镜转换为球面镜公式:
Spherical = (Cylinder × cos(Axis))^2 + (Sphere)^2
式中,Spherical表示所需的球面度数,Cylinder表示原始
的柱镜度数,Axis表示原始的度数方向,Sphere表示原始的球面度数。
3. 度数方向转换公式:
NewAxis = OldAxis + 90°
式中,NewAxis表示转换后的度数方向,OldAxis表示原始
的度数方向。
使用这些公式可以方便地将球面镜和球柱镜互相转换,但是这仅
适用于简单的度数转换,对于复杂的眼镜度数问题,建议咨询专业的
眼科医生或验光师。
镜片联合

即 -4.00≈ -0.25*90
五、透镜的光学恒等变换
从上述各个例题中不难找出透镜联合的结果 于原联合透镜之间的规律性的关系,对于这 种关系可以总结概括为三句话:即透镜的光 学恒等变换:
这三句话为:
新球面透镜的顶焦度为原球面透镜的顶角度与柱面透 镜的顶焦度之代数和; 新柱面透镜的顶焦度为原柱面透镜顶焦度的相反数; 新轴位:若原轴位小于、等于90°的加90°,大于 90°的减90°。 应用这三句话——光学恒等变换的规则,就可以不用 光学十字线图而直接迅速写出透镜的联合结果。
例:
+1.00-1.00*150≈-1.00*60≈-1.00+1.50*60≈-0.75*150
解:=>-1.75+2.25*60
=>+0.50-2.25*150
谢谢
三、柱面透镜的联合
1、同轴位柱面透镜的联合,
起结果也是用求代数和的方法获得。
2、轴位互相垂直的柱面透镜的联合
(1)光学十字线 ) 轴位互相垂直的柱面透镜的联合就不能用简 单的求代数和的方法获得其联合效果,必须 借助于光学十字线,所谓光学十字线就是在 一个以垂直和水平相交的十字线区域内标出 各个子午线方向上的柱面(或球面)透镜的 屈光力。
球柱透镜的联合与转换
一、透镜的联合
透镜的联合就是: 两块或两块以上的各种眼用透镜叠合、密接, 透镜的联合用符号“≈”来表示。
例:
透镜-3.00联合透镜+4.00可以写作: -3.00≈+4.00 透镜-2.00联合透镜-5.00可以写作: -2.00≈-5.00等等。
二、球面透镜联合
球面透镜之间的联合结果, 可用求代数和的方法来获得。 如:-3.00≈+4.00=> +1.00
球柱透镜的联合与转换

球柱透镜的联合与转换(闫海泉)一联合:什么是联合就是符号相加在一起。
在两条主子午线上具有相同的屈光度和符号能力相等(球面透)在镜片同心圆上的屈光度相等90180例如:×180视力达到加上×180视力达到轴位相同可以直接相加减最后结果:×180(单散形式)(×180)应该写在90度上作用力在180度屈光度不相同说明有散光存在例如:-2..00DC×××180|×90(这种形式称为正交柱镜形式)那么咱们要把它转换成球柱形式(口诀)1.小做球:2.差做柱:3.轴为大:180最后结果:|×180例如:×180|+×901.小做球:+2.差做柱:3.轴为大:180例如:+×45|×1351.小做球:2.差做柱:+3.轴为大:45咱们计算一下++最后结果:+|+×90有的医院还会开出这样的处方:-1.00 L右眼度数:|×90左眼度数:|×180注:(两个眼睛的散光轴位不一样容易带镜不舒适)例如:×35|+×145(也是由正交柱镜的形式转换成球柱的形式)结果:+|×35(这种柱大于球的形式叫混合散光不用在转换)下面是把球柱形式转换成正交柱镜的形式例如:|×90咱们的转换成正交柱镜形式的口诀:一柱.球直转:轴与.原轴相垂直:180另柱.两相加:轴同.原轴相同:90最后结果:×180|×90 (一般用于隐形眼镜带散光的镜片眼配时需要了解各方象上的屈光度所用的)例如(1):隐形眼镜超过就要降多数。
咱们在看:×180|×90一般要降:×180|×90最后佩戴散光隐形眼镜转换的度数结果是|×90(我们在用裂隙片检查个方向上的屈光度时也要用到的)例如(2):|+×35转换结果:×125|×35(那么35度轴在转换时小于或等于90时加90大于90减90)我们在验光经常能运用到的例如(1):远用.×45老花.+近用等于两个相加在一起:+|×45原则我们要符号相同:转换口诀:代数合.+変符号.+转轴.135最后转换结果:+|+×135(处方结果)例如(2):远用.|×180老花.+近用等于两个相加在一起:+|×180原则我们要符号相同:转换口诀:代数合.+変符号.+转轴.90最后转换结果:+|+×90例如(3):|+×90转换:代数合.変符号.转轴.180最后转换结果:|×180例如(4):|+×60转换:代数合.+変符号.转轴.150最后转换结果:+|×150(象这种还是不能转换成同符号的咱们称它为混合性散光最后一定要保持柱为负号的形式)(为什么柱要转成负的因为负柱的镜片相对要薄一些还有咱们接受负散光比正的要快一些)例如:|+×90(象这种我们就要把它转换成柱为负的形式)转换结果:+|×180练习题(1):×90|+×180结果:+|×90练习题(2):+|×30结果:+×120|+×30我们还可以用另一种方式换算例如:它们两个之间共有的度数是多少我们就可以把它做为球的形式:|×180我们在用十字线方法来表示一下下面的屈光度例如(1)结果:例如(2)×90结果:练习题:某患者配镜处方为+|+×135,若再加上一镜片+|×45,视力效果更佳,问此患者实际所需之进度应为什么球柱面透镜结果:+|+×135。
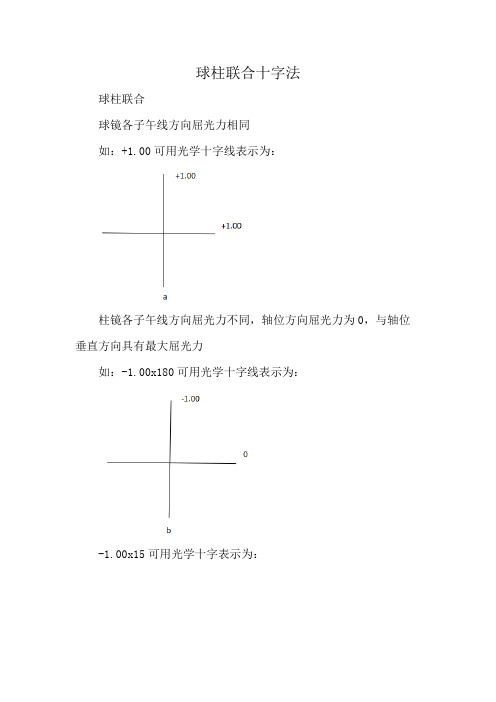
球柱联合十字法
球柱联合十字法
球柱联合
球镜各子午线方向屈光力相同
如:+1.00可用光学十字线表示为:
柱镜各子午线方向屈光力不同,轴位方向屈光力为0,与轴位垂直方向具有最大屈光力
如:-1.00x180可用光学十字线表示为:
-1.00x15可用光学十字表示为:
处方-1.00/-1.00X180,可以看成是-1.00DS的球镜和-
1.00x180的柱镜联合
将两个十字水平和垂直方向分别相加,则
在水平方向为-1.00+0=-1.00,
垂直方向-1.00+-1.00=-2.00,
这个球柱面透镜两条互相垂直的子午线方向上的屈光力就计算出来了。
球柱分解
同样,我们还可以用十字分解的方法来进行处方换算
分解1:
分解后可以表示为:-2.00+1.00x90
分解2:
分解后可以表示为:-1.00-1.00x180
即:-1.00-1.00x180<=>-2.00+1.00x90,与公式等效换算后的处方一致。
球柱镜的联合与转换

柱面镜转换为球面镜的原理
逆向思维
与球面镜转换为柱面镜相反,我们可以将柱面镜看作是无数个小的球面镜的组合 。当光线通过柱面镜折射后,每个小球面镜都会对光线进行汇聚或发散作用。
球面镜的形成
通过调整柱面镜的截面形状和大小,可以使得经过折射后的光线汇聚或发散到一 个点上,从而形成一个球面镜的效果。
球柱镜转换的应用实例
联合成像质量评价
对球柱镜联合使用时的成像质量进行评价,包括清晰度、畸变等 方面。
06 球柱镜的应用领域与发展趋势
CHAPTER
球柱镜在光学领域的应用
光学成像
01
球柱镜可用于光学成像系统中,如望远镜、显微镜等,以校正
像差、提高成仪器中,如干涉仪、椭偏仪等,以实现
CHAPTER
球面镜的光学性质
01
02
03
反射成像
球面镜通过反射光线形成 虚像或实像,遵循光的反 射定律。
焦距
球面镜的焦距取决于其曲 率半径,焦距越短,成像 越清晰。
像差
球面镜存在像差,如球差 、彗差等,影响成像质量 。
柱面镜的光学性质
折射成像
柱面镜通过折射光线形成 虚像或实像,遵循光的折 射定律。
光电显示
球柱镜在光电显示技术中可用于提高显示器的分辨率、色彩还原度和 观看舒适度。
球柱镜的发展趋势与挑战
微型化与集成化
高性能化
随着光电子器件的不断微型化,球柱镜也 需向微型化、集成化方向发展,以适应微 型光电子系统的需求。
球柱镜的性能需不断提高,包括光学性能 、机械性能、热稳定性等,以满足高端光 电子应用的要求。
眼镜行业
在眼镜行业中,球柱镜的转换被广泛应用于近视、远视、 散光等视觉问题的矫正。通过精确计算和设计,可以制作 出符合个体视觉需求的眼镜片。
客观验光检影,,,,,

3 / 24
-3.00
0
认真看书,主动思考
5
四、课堂小结
本节课我们主要学习了透镜的光
学力量分析图,其特点是柱面透镜各 认真听讲
子午线上的屈光力不等,且按规律周
10
期变化着,这是视光学中一个非常重
要的知识内容,希望大家好好掌握。
五、布置作业
梳理本课知识要点
• 透镜力量水平和水平相加,垂直
和垂直相加
[讲述]上节课我们还有一个课后思考 题还未解决
如顾客配镜光度为-1.50DS/-1.00DC×
90,戴镜不适应,经复查后验光度数调
整为-1.75DS/-0.50DC×90,次度数应为
验光失误还是工作失误。请大家思考为
5
什么?
[过渡]这节课呢,我们要学习透镜的联
• 透镜力量水平和水平相加,垂直
和垂直相加
10
认真听讲,并仔细做笔记。
-3.0
1.0
-4.
05 / 24
+ -3.0
=
0
-3.0
5 认真看书,找出问题答案并 积极举手回答问题。
透镜的光学力量图
1.
2,
-1.50 -5.0
-2.50
-2.00
10
认真听讲并根据书中相应 解释做相应理解。
认真听讲 [设问]接下来请同学们认真看书,找
认真看书,主动思考 认真听讲
1.-1.00DC×180/+2.00DC×180
9 / 24
+
=
0
0
0
认真听讲,努力回忆学过的 知识点。
2.-1.00DC×180/+1.00DC×180
球柱镜片光学技术—柱镜片联合(眼镜光学技术课件)

=
-2.00 -1.00X90
-2.00
+ 0
0
= -3.00
-3.00 +
-3.00
+1.00 0
-2.00X180 / -3.00X90
=
-3.00 +1.00X180
2.00 180 / 3.00 90 2.00 1.00 90或 3.00 1.00 180
可见,两个柱镜正交联合后,形成的球柱透镜 有表达式两种,这两种球柱镜的表达形式在屈光能 力上是一样的。
2.两柱镜片轴向垂直联合
两柱面透镜轴向相互垂直而密贴联合,也称为垂轴 联合或正交联合。正交联合的两柱面透镜,其光学效应相 当于一个新球柱透镜;同样,一个球柱透镜也可以用两个 正交透镜的形式来表达。
-2.00
0
-2.00
0
+ 0
= -3.00
+ -2.00
-1.00
-2.00X180 / -3.00X90
三、球柱镜片的表达形式及转换
从前面用光学十字线法进行柱镜片的联合 可以看出,一个球柱镜片可以有三种表达方式, 分别是: 正交柱镜 球柱镜(负散表达式) 球柱镜(正散表达式)
• 课堂练习
– 将下列球柱镜片处方转换成其它两种形式:
+1.00 X 180 / +3.00 X 90 +3.50 +0.50 X 180 +0.75 -0.50 X 90 -1.25 +0.75 X 180 -4.00 -2.00 X 90 +6.50 -3.00 X 180 +3.75 X 90 / +1.25 X 180 +5.00 -1.25 X 180
眼的屈光系统及球柱转换

举例: -2.00/-0.50*180=-2.50/+0.50*90
-3.50/+1.00*180=-2.50/-1.00*90
习题
1.+0.50/-0.50*90 2.+0.50*90/-0.50*180 3.-6.00/-1.00*20 4.-2.00/-2.00*180 5.-1.50/-0.50*90/+1.00 6.+6.00/-3.00*180
谢谢!!!
初级培训 眼的屈光系统及球柱转换
济宁市明俊眼镜有限公司
一、眼的结构
眼球是视觉器官的主体部分,是感受 光刺激的部位,近似于球形。眼球前后直 径平均为24mm,水平横径(宽度)为 23.5mm,垂直直径(高度)为23mm。
眼的屈光系统包括角膜、房水、晶状体 (睫状肌)、玻璃体、视网膜、黄斑区。
视网膜分布位部
系统细胞间联系方式 功能特点
中央凹处无 愈近周边愈多
聚合式联系
中央凹处密集 愈向周边部愈少
单线联系
光敏度高,司暗觉,无色 光敏度低,司昼觉,有色觉, 觉,细微结构分辨力差 细微结构分辨力高
眼球的光学常数如下: 角膜前面曲率半径 7.8mm 角膜后面曲率半径 6.8mm 角膜屈光指数 1.376 角膜系统屈光力 43.05D 晶体前面曲率半径 10mm 晶体后面曲率半径 6.0mm 晶体皮质屈光指数 1.386 晶体核屈光指数 1.406 晶体系统屈光力 19.11D 房水、玻璃体的屈光指数 1.336 眼球总屈光力 58.64D
睫状肌
在自动调节过程中活动的两种作用力是: 玻璃体运动和睫状肌收缩。 两种力都可以在自由调节的过程中使光学 面向前和向后移动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
球柱透镜的联合与转换(闫海泉)
一联合:什么是联合就是符号相加在一起。
-2.00DS
在两条主子午线上具有相同的屈光度和符号能力相等-2.00DS
(球面透)
在镜片同心圆上的屈光度相等
90
180
例如:-2.00D C×180 视力达到0.9
加上 -0.50DC×180 视力达到1.0
轴位相同可以直接相加减最后结果:-2.50DC×180 (单散形式)
(-2.00D C×180)应该写在90度上作用力在180度
-3.00
-2.00 屈光度不相同说明有散光存在
例如:-2..00D C×90-3.00D C×180 -3.00DC×180|-2.00×90
(这种形式称为正交柱镜形式)
那么咱们要把它转换成球柱形式(口诀)1.小做球:-2.00DS
2.差做柱:-1.00DC
3.轴为大:180
最后结果:-2.00DS|-1.00DC×180
例如:-3.00DC×180|+2.00DC×90
1.小做球:+
2.00DS
2.差做柱:-5.00DC
3.轴为大:180
例如:+3.00DC×45|-2.00DC×135
1.小做球:-
2.00DS
2.差做柱:+5.00DC
3.轴为大:45
咱们计算一下
+3.00
+5.00
最后结果:+3.00|+2.00×90
有的医院还会开出这样的处方:
R -1.00 L _3.00
-2.00 -1.00
右眼度数:-1.00DS|-1.00DC×90 左眼度数:-1.00DS|-2.00DC×180 注:(两个眼睛的散光轴位不一样容易带镜不舒适)
例如: -4.00DC×35|+2.00DC×145(也是由正交柱镜的形式转换成球柱的形式)
结果:+2.00DS|-6.00DC×35(这种柱大于球的形式叫混合散光不用在转换)
下面是把球柱形式转换成正交柱镜的形式
例如:-4.50DS|-1.00DC×90
咱们的转换成正交柱镜形式的口诀:一柱.球直转:-4.50DC
轴与.原轴相垂直:180
另柱.两相加:-5.50DC
轴同.原轴相同:90
最后结果:-4.50DC×180|-5.50DC×90
(一般用于隐形眼镜带散光的镜片眼配时需要了解各方象上的屈光度所用的)
例如(1):隐形眼镜超过-4.00D就要降多数。
咱们在看:-4.50DC×180|-5.50DC×90
一般要降:-4.25DC×180|-5.00DC×90
最后佩戴散光隐形眼镜转换的度数结果是 -4.25DS|-0.75DC×90
(我们在用裂隙片检查个方向上的屈光度时也要用到的)
例如(2):-4.50DS|+1.00DC×35
转换结果:-4.50DS×125|-3.50DC×35
(那么35度轴在转换时小于或等于90时加90 大于90减90)
我们在验光经常能运用到的
例如(1):远用.-1.50DC×45
老花.+2.50D
近用等于两个相加在一起:+2.50DS|-1.50DC×45
原则我们要符号相同:转换口诀:代数合.+1.00DS
変符号.+1.50DC
转轴.135
最后转换结果:+1.00DS|+1.50DC×135(处方结果)
例如(2):远用.-1.00DS|-1.00DC×180
老花.+2.50D
近用等于两个相加在一起:+1.50DS|-1.00DC×180
原则我们要符号相同:转换口诀:代数合.+0.50DS
変符号.+1.00DC
转轴.90
最后转换结果:+0.50DS|+1.00DC×90
例如(3):-3.50DS|+1.00DC×90
转换:代数合.-2.50DS
変符号.-1.00DC
转轴.180
最后转换结果:-2.50DS|-1.00DC×180
例如(4):-2.00DS|+3.00DC×60
转换:代数合.+1.00DS
変符号.-3.00DC
转轴.150
最后转换结果:+1.00DS|-3.00DC×150
(象这种还是不能转换成同符号的咱们称它为混合性散光最后一定要保持柱为负号的形式) (为什么柱要转成负的因为负柱的镜片相对要薄一些还有咱们接受负散光比正的要快一些) 例如:-1.00DS|+2.00DC×90(象这种我们就要把它转换成柱为负的形式)
转换结果:+1.00DS|-2.00DC×180
练习题(1):-3.00DC×90|+2.00DC×180
结果: +2.00DS|-5.00DC×90
练习题(2):+6.00DS|-1.00DC×30
结果:+6.00DC×120|+5.00DC×30
我们还可以用另一种方式换算
例如:
-3.00D 它们两个之间共有的度数是多少-2.00D我们就可
以把它做为球的形式:-2.00DS|-1.00×180
-2.00D
我们在用十字线方法来表示一下下面的屈光度
例如(1)-4.00DS
-4.00DS
结果:
-4.00DS
例如(2)-4.00DC×90
结果: -4.00DC
练习题:
某患者配镜处方为+10.00DS|+3.00DC×135,若再加上一镜片+5.00DS|-1.00DC×45,视力效果更佳,问此患者实际所需之进度应为什么球柱面透镜?
结果:+14.00DS|+4.00DC×135。
