球柱镜的联合与转
球柱镜转换三种公式

球柱镜转换三种公式
球面镜和球柱镜是眼镜中较为常见的两种镜片类型,它们常常用
于矫正人们的视力问题。
在某些情况下,我们需要将球面镜转换为球
柱镜或者将球柱镜转换为球面镜,此时需要用到以下三种公式:
1. 球面镜转换为球柱镜公式:
Cylinder = S × tan(Axis)
式中,Cylinder表示所需的柱镜度数,S表示原始的球面度数,Axis表示原始的度数方向。
2. 球柱镜转换为球面镜公式:
Spherical = (Cylinder × cos(Axis))^2 + (Sphere)^2
式中,Spherical表示所需的球面度数,Cylinder表示原始
的柱镜度数,Axis表示原始的度数方向,Sphere表示原始的球面度数。
3. 度数方向转换公式:
NewAxis = OldAxis + 90°
式中,NewAxis表示转换后的度数方向,OldAxis表示原始
的度数方向。
使用这些公式可以方便地将球面镜和球柱镜互相转换,但是这仅
适用于简单的度数转换,对于复杂的眼镜度数问题,建议咨询专业的
眼科医生或验光师。
镜片联合

即 -4.00≈ -0.25*90
五、透镜的光学恒等变换
从上述各个例题中不难找出透镜联合的结果 于原联合透镜之间的规律性的关系,对于这 种关系可以总结概括为三句话:即透镜的光 学恒等变换:
这三句话为:
新球面透镜的顶焦度为原球面透镜的顶角度与柱面透 镜的顶焦度之代数和; 新柱面透镜的顶焦度为原柱面透镜顶焦度的相反数; 新轴位:若原轴位小于、等于90°的加90°,大于 90°的减90°。 应用这三句话——光学恒等变换的规则,就可以不用 光学十字线图而直接迅速写出透镜的联合结果。
例:
+1.00-1.00*150≈-1.00*60≈-1.00+1.50*60≈-0.75*150
解:=>-1.75+2.25*60
=>+0.50-2.25*150
谢谢
三、柱面透镜的联合
1、同轴位柱面透镜的联合,
起结果也是用求代数和的方法获得。
2、轴位互相垂直的柱面透镜的联合
(1)光学十字线 ) 轴位互相垂直的柱面透镜的联合就不能用简 单的求代数和的方法获得其联合效果,必须 借助于光学十字线,所谓光学十字线就是在 一个以垂直和水平相交的十字线区域内标出 各个子午线方向上的柱面(或球面)透镜的 屈光力。
球柱透镜的联合与转换
一、透镜的联合
透镜的联合就是: 两块或两块以上的各种眼用透镜叠合、密接, 透镜的联合用符号“≈”来表示。
例:
透镜-3.00联合透镜+4.00可以写作: -3.00≈+4.00 透镜-2.00联合透镜-5.00可以写作: -2.00≈-5.00等等。
二、球面透镜联合
球面透镜之间的联合结果, 可用求代数和的方法来获得。 如:-3.00≈+4.00=> +1.00
球柱镜的联合与转换

球面透镜的联合
• 球面透镜之间的联合结果,可用求代数和 的方法来获得。即球镜与球镜的直接相互 加减 • 如-3.00DS/-2.00DS=-5.00DS • -3.00DS/+4.00DS=+1.00DS
9
柱面透镜的联合
• 柱镜与柱镜的联合 • 1.轴位相同时,柱镜与柱镜的联合,度数可 直接加减,但轴位不变。 • 如1】-1.00DC×180/+2.00DC×180 • 等于+1.00DC×180 • 如2】-1.00DC×180/+1.00DC×180 • 等于0
32
• 4.将下列处方转变为其他两种形式 • (1)+5.00×180/+5.75×90; (2) 0.75/+0.50×180 • (3)+2.25/-3.75×90; (4)1.12×90/+0.37×180
• 5.下列四片薄球透镜相互密叠,求组合之焦距 (cm) • +1.25/+0.50×90 -2.00×180/-l.50×90 • +0.25×90/-l.25×180 +0.50/-2.5×90
33
• 6.将下列透镜用正交柱面形式表示 • (1)+0.50/-0.25×180; (2) -1.75/-1.50×90 • (3)+4.25/+1.75×180; (4)-2.00/+4.00×90 • 7.球柱面组合+2.00+200×90系由两个平柱 透镜正交合并而成,若将镜度较低之柱面旋转 90°,则组合之新镜度是什么? • 8.两平柱面透镜以两轴平行合并一起所得合 成镜度为+4.00×90,当一柱面旋转 90°,则 新镜度含有一柱面+9.00×180,求合成之球 面镜度,以及原有平柱透镜之镜度。
球柱镜的联合与转换

柱面镜转换为球面镜的原理
逆向思维
与球面镜转换为柱面镜相反,我们可以将柱面镜看作是无数个小的球面镜的组合 。当光线通过柱面镜折射后,每个小球面镜都会对光线进行汇聚或发散作用。
球面镜的形成
通过调整柱面镜的截面形状和大小,可以使得经过折射后的光线汇聚或发散到一 个点上,从而形成一个球面镜的效果。
球柱镜转换的应用实例
联合成像质量评价
对球柱镜联合使用时的成像质量进行评价,包括清晰度、畸变等 方面。
06 球柱镜的应用领域与发展趋势
CHAPTER
球柱镜在光学领域的应用
光学成像
01
球柱镜可用于光学成像系统中,如望远镜、显微镜等,以校正
像差、提高成仪器中,如干涉仪、椭偏仪等,以实现
CHAPTER
球面镜的光学性质
01
02
03
反射成像
球面镜通过反射光线形成 虚像或实像,遵循光的反 射定律。
焦距
球面镜的焦距取决于其曲 率半径,焦距越短,成像 越清晰。
像差
球面镜存在像差,如球差 、彗差等,影响成像质量 。
柱面镜的光学性质
折射成像
柱面镜通过折射光线形成 虚像或实像,遵循光的折 射定律。
光电显示
球柱镜在光电显示技术中可用于提高显示器的分辨率、色彩还原度和 观看舒适度。
球柱镜的发展趋势与挑战
微型化与集成化
高性能化
随着光电子器件的不断微型化,球柱镜也 需向微型化、集成化方向发展,以适应微 型光电子系统的需求。
球柱镜的性能需不断提高,包括光学性能 、机械性能、热稳定性等,以满足高端光 电子应用的要求。
眼镜行业
在眼镜行业中,球柱镜的转换被广泛应用于近视、远视、 散光等视觉问题的矫正。通过精确计算和设计,可以制作 出符合个体视觉需求的眼镜片。
球柱镜的联合与转换

15
柱面透镜的联合
• • • • • 柱镜联合口诀 以小为球,两差为柱,轴对大数。 如-2.00DC×180/-1.00DC×90 等于-1.00DS/-1.00DC×180 可以力量图予以论证
-2.00
-1.00
16
柱面透镜的联合
• • • • 柱镜与柱镜的联合 如-2.00DC×180/+1.00DC×90 以小为球,两差为柱,轴对大数。 可不分正负,以绝对值小的为球镜。
3
透镜的光学力量图
• 球柱透镜的光学力量 • 如-3.00DS/-1.00DC×180 • 透镜力量水平和水平相加,垂直和垂直相 加
-3.00 -1.00 -4.00
+
0 -3.00
=
-3.00
4
透镜ቤተ መጻሕፍቲ ባይዱ光学力量图
• 1.
-1.50
2.
5.00
-2.50 -2.50
-1.50
-2.00
5
透镜的光学力量图
透镜的联合
•
• • • •
透镜的联合就是两块或两块以上的各种 眼用透镜叠合、密接,透镜的联合用符号 “/”来表示。 如:透镜-3.00DS.联合透镜+4.00DS.可以 写作: -3.00DS./+4.00DS. 透镜-2.00D.S.联合透镜-5.00D.S.可以写 作: -2.00DS./-5.00DS.等等。
33
• 6.将下列透镜用正交柱面形式表示 • (1)+0.50/-0.25×180; (2) -1.75/-1.50×90 • (3)+4.25/+1.75×180; (4)-2.00/+4.00×90 • 7.球柱面组合+2.00+200×90系由两个平柱 透镜正交合并而成,若将镜度较低之柱面旋转 90°,则组合之新镜度是什么? • 8.两平柱面透镜以两轴平行合并一起所得合 成镜度为+4.00×90,当一柱面旋转 90°,则 新镜度含有一柱面+9.00×180,求合成之球 面镜度,以及原有平柱透镜之镜度。
球柱镜的联合和转换课件
7
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
球面透镜的联合
• 球面透镜之间的联合结果,可用求代数和 的方法来获得。即球镜与球镜的直接相互 加减
• 如-3.00DS/-2.00DS=-5.00DS • -3.00DS/+4.00DS=+1.00DS
-3.00
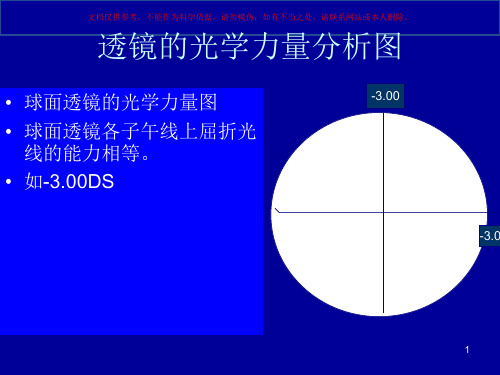
• 柱面透镜的光学力量图 • 柱面透镜各子午线上的
屈光力不等,且按规律 周期变化着。 • 如-3.00DC×180
2
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
透镜的光学力量图
• 球柱透镜的光学力量
• 如-3.00DS/-1.00DC×180
• 透镜力量水平和水平相加,垂直和垂直相 加
ቤተ መጻሕፍቲ ባይዱ14
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
柱面透镜的联合
• 柱镜联合口诀
• 以小为球,两差为柱,轴对大数。
• 如-2.00DC×180/-1.00DC×90
• 等于-1.00DS/-1.00DC×180
-2.00
• 可以力量图予以论证
-1.00
15
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
18
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
球柱面透镜的联合
• 1.同轴位球柱面透镜的联合: • 也可用求代数和的方法获得联合结果。 • 如: • +1.00DS/+0.50DC×90/-l.50DS/-
球柱镜片光学技术—柱镜片联合(眼镜光学技术课件)

=
-2.00 -1.00X90
-2.00
+ 0
0
= -3.00
-3.00 +
-3.00
+1.00 0
-2.00X180 / -3.00X90
=
-3.00 +1.00X180
2.00 180 / 3.00 90 2.00 1.00 90或 3.00 1.00 180
可见,两个柱镜正交联合后,形成的球柱透镜 有表达式两种,这两种球柱镜的表达形式在屈光能 力上是一样的。
2.两柱镜片轴向垂直联合
两柱面透镜轴向相互垂直而密贴联合,也称为垂轴 联合或正交联合。正交联合的两柱面透镜,其光学效应相 当于一个新球柱透镜;同样,一个球柱透镜也可以用两个 正交透镜的形式来表达。
-2.00
0
-2.00
0
+ 0
= -3.00
+ -2.00
-1.00
-2.00X180 / -3.00X90
三、球柱镜片的表达形式及转换
从前面用光学十字线法进行柱镜片的联合 可以看出,一个球柱镜片可以有三种表达方式, 分别是: 正交柱镜 球柱镜(负散表达式) 球柱镜(正散表达式)
• 课堂练习
– 将下列球柱镜片处方转换成其它两种形式:
+1.00 X 180 / +3.00 X 90 +3.50 +0.50 X 180 +0.75 -0.50 X 90 -1.25 +0.75 X 180 -4.00 -2.00 X 90 +6.50 -3.00 X 180 +3.75 X 90 / +1.25 X 180 +5.00 -1.25 X 180
球柱镜转换算

球柱镜转换算
球柱镜转换算
近视、远视和散光同属于屈光不正,都可以导致视力下降,单纯近视/远视镜片周边光度范围都是同样(或接近)的近视/远视度数,而散光则是有轴向的,只是在某一个轴向上有度数,散光因经线的表示方式不同,有正散和负散,综合验光仪上的散光片都为负散,符号“-”,此时需要进行换算
换算原则:
1、相加(球柱镜带+-符号相加);
2、变符号(散光前符号变化+变-、-变+)
3、转轴(≥90减90,<90加90)
举例:-2.00DS+1.00DC*150
-1.00DS-1.00DC*60
隐形眼镜换算方法
公式换算法
验光出来的度数是框架眼镜的度数。
镜片后表面顶点距离与角膜的距离,亚洲人大约是12毫米。
配隐形眼镜度数有一换算公式:Fe=F/1-dF
公式中Fe是隐形眼镜的配戴度数;F是框架眼镜的度数;d是镜眼距12mm。
举例:验配光度-4.00 D
-4/(1-0.012×-4)=-3.82D,可选择-3.75D。
球柱透镜联合与转换

最后结果:-2.00DS|-1.00DC×180
例如:-3.00DC×180|+2.00DC×90
1.小做球:+2.00DS
2.差做柱:-5.00DC
3.轴为大:180
例如:+3.00DC×45|-2.00DC×135
1.小做球:-2.00DS
2.差做柱:+5.00DC
3.轴为大:45
球柱透镜的联合与转换(闫海泉)
一联合:什么是联合就是符号相加在一起。
-2.00DS
在两条主子午线上具有相同的屈光度和符号能力相等
-2.00DS
(球面透)
在镜片同心圆上的屈光度相等
90
180
例如:-2.00DC×180 视力达到0.9
加上 -0.50DC×180 视力达到1.0
轴位相同可以直接相加减 最后结果:-2.50DC×180 (单散形式)
原则我们要符号相同:转换口诀:代数合.ǂDC
转轴.135
最后转换结果:+1.00DS|+1.50DC×135(处方结果)
例如(2):远用.-1.00DS|-1.00DC×180
老花.+2.50D
近用等于两个相加在一起:+1.50DS|-1.00DC×180
原则我们要符号相同:转换口诀:代数合.+0.50DS
结果:+2.00DS|-6.00DC×35(这种柱大于球的形式叫混合散光不用在转换)
下面是把球柱形式转换成正交柱镜的形式
例如:-4.50DS|-1.00DC×90
咱们的转换成正交柱镜形式的口诀:一柱.球直转:-4.50DC
轴与.原轴相垂直:180
另柱.两相加:-5.50DC
