离中趋势测量法word版
描述离中趋势的测定内容

描述离中趋势的测定内容离中趋势是指一个数据集或样本中的数据点偏离中心或均值的趋势。
在统计学和机器学习中,离中趋势的测定是非常重要的,可以用于评估数据集中的数据分布、检测异常值、预测趋势等。
以下是几种常见的离中趋势测定方法:1. 中心度测定 (Centrality Determination):中心度是指一个数据点在网络中的重要性。
在社交网络分析中,中心度可以用于测定一个节点在网络中的中心地位。
在图论中,节点的中心度是指该节点在网络中的度数总和。
在统计学中,中心度可以用于测定数据的中心度。
2. 分布测定 (Distribution Determination):分布是指数据集或样本的分布情况。
在统计学中,分布测定可以用于评估数据的分布形状、对称程度、峰度等。
常用的分布测定方法包括正态分布测定 (Normal Distribution Determination)、偏态分布测定 (Unimodal Distribution Determination)、双态分布测定 (Bimodal Distribution Determination) 等。
3. 异常值检测 (Outlier Detection):异常值是指数据集或样本中偏离正常范围的数据点。
在统计学和机器学习中,异常值检测可以用于检测数据集中的异常值、预测趋势等。
常用的异常值检测方法包括离群值检测 (Outlier Detection)、异常点检测 (Outlier Detection)、离中趋势测定 (Centrality Determination) 等。
4. 趋势测定 (Trend Determination):趋势是指数据集或样本在一定时间内的变化趋势。
在统计学和机器学习中,趋势测定可以用于评估数据的变化情况、预测未来趋势等。
常用的趋势测定方法包括时间序列分析 (Time SeriesAnalysis)、回归分析 (Regression Analysis) 等。
第四章 集中趋势和离中趋势

四分位数的位置确定方法: 四分位数的位置确定方法:
方法1: 方法 :定义算法
n QL 位置 = 4 Q 位置 = 3n U 4
方法2:以中位数为中心,从两端再计算中位数,公式: 方法 :以中位数为中心,从两端再计算中位数,公式:
n + 1 2 +1 = 2
在偏斜不大时,中位数大约位于均值与众数的 处 在偏斜不大时,中位数大约位于均值与众数的1/3处。
x − Mo = 3( x − Me)
3 Me − Mo x= 2
Mo − 2 x Me = 3
算术平均数适用于定距变量(或数值变量、 算术平均数适用于定距变量(或数值变量、 定量变量),中位数适用于定序变量, ),中位数适用于定序变量 定量变量),中位数适用于定序变量,众数则适用 于定类变量(或定性变量) 于定类变量(或定性变量)
K i = Li + iN / K − Fi −1 × di fi
表示第i 分位数; 表示第i Ki表示第i个K分位数; Li表示第i个K分位数所在组的下 限;N表示数据总个数;Fi-1表示第i个K分位数所在组的前一组 表示数据总个数; 表示第i 的累积次数; 是第i 分位数所在组的次数。 是第i 的累积次数;fi是第i个K分位数所在组的次数。di= Ui-Li是第i 分位数所在组的组距。 个K分位数所在组的组距。
中位数是位置平均数,不受极端值的影响。 中位数是位置平均数,不受极端值的影响。各个数值 相对其中位数的绝对离差之和为最小。 相对其中位数的绝对离差之和为最小。 不足:中位数确定时只与中间位置的相关数据有关, 不足:中位数确定时只与中间位置的相关数据有关, 而不考虑其它数值的大小,缺乏敏感性;计算复杂。 而不考虑其它数值的大小,缺乏敏感性;计算复杂。
第五章离中趋势测量法-资料

组距
f
150~154
1
154~158
2
158~162
7
162~166
10
166~170
16
170~174
12
174~178
7
178~182
5
合计
60
计算
左边数 列的标 准差
2019/9/29
13
[解] 因为是分组资料,计算标准差运用加权式,并
参见下表
S f(XX)2 24 96.9 5(cm )
A组:60 ,60,60,60,60 B组:58,59,60,61,62 C组:40,50,60,70,80 D组:80,80,80,80,80 数据显示,平均数相同,离势可能不同;平均
数不同,离势可能相同。
2019/9/29
2
变异指标用以反映总体各单位标志值的变动范围或参 差程度,与平均指标相对应,从另一个侧面反映了总体的 特征。
Z分数的算术平均数等于0
Z分数的标准差等于1,方差也等于1
2019/9/29
17
第四节 相对离势
上述各种反映离中趋势的变异指标,都具有和原 资料相同的计算单位,称绝对离势。但欲比较具有不 同单位的资料的参差程度,或比较单位虽相同而均值 不相同的资料的参差程度,离势的绝对指标则很可能 导致某些错误结论。所以,我们还得了解和学习相对 离势。
组距
f
150~156
3
156~162
9
162~168
25
168~174
34
174~180
20
180~186
7
186~192
1
192~198
1
合计
MBA应用统计学课件 第四章 集中趋势和离中趋势的度量

4.2.2 相对数的种类
2. 结构相对数
例如: 1999年我国的出口贸易总额为212亿
元,其中农副产品出口为49亿元,轻纺产品出口为
95.4 亿 元 , 重 工 业 产 品 ( 包 括 矿 产品)的出口为
67.6亿元,则结构相对数的计算方法:
1999年农副产品出口所占比重
482 480 480 / 360
=1.5(天)
所以,该厂提前了一个月零一天来完成全年计
4.2 统计相对数
4.2.1 相对数的概念和作用 4.2.2 相对数的种类 4.2.3 计算和应用相对数应注意的
问题
4.2.1 相对数的概念和作 用
1. 概念: 相对数是两个有联系的指标数值之比
2. 作用 a. 可以说明事物发生和发展的程度相互关联
b、计划完成相对数的计算方法
(4)计划执行进度情况的检查
计算公式如下:
计划执行进度指标
自期初至检查之日累计实际完成数 全期计划数
100%
4.2.2 相对数的种类
b、计划完成相对数的计算方法
例如,某企业2007年工业总产值为2400万 元,1-6月份实际完成1440万元,则计划完成程度指 标=1440/2400*100%=60%。说明该企业2007年1-6月份 完成全年计划的60%,完成了进度计划。
决。
4.2.2 相对数的种类
b、计划完成相对数的计算方法
(1)当计划指标为绝对数时,计划完成 相对数的计算则采用以 上公式即可。
如某工业企业2006年计划总产值为500万 元,实际实现产值525万元,则该企业产值计划完成 相对数=525/500×100%=105%,表明该企业超额5%完 成产值计划。
第5章离中趋势度量法

四分位差
(quartile deviation)
1. 对顺序数据离散程度的测度
2. 也称为内距或四分间距
3. 上四分位数与下四分位数之差
Qd = QU – QL 4. 反映了中间50%数据的离散程度
5. 不受极端值的影响
6. 用于衡量中位数的代表性
4 - 20
西北工业大学管理学院
为什么称作标准差
Mary Smith 和Jason Jones都在申请奖学金,Mary 参加的是the Academic College Testing Service (ACT)test , 成 绩 为 26 ; Jason 参 加 的 是 the Stanford Admission Test (SAT),成绩是1100。两 类 考 试 的 分 数 范 围 分 别 是 0-36 、 200-1600 , 那 么 谁将获得奖学金?
M d i1 n
k
组距分组数据
Mi x fi
M d i1 n
4 - 24
西北工业大学管理学院
统计学
STATISTICS
平均差
(例题分析)
某电脑公司销售量数据平均差计算表
按销售量分组
140~150 150 ~ 160 160 ~ 170 170 ~ 180 180 ~ 190 190 ~ 200 200 ~ 210 210 ~ 220 220 ~ 230 230 ~ 240
2040
统计学
STATISTICS
平均差
(例题分析)
k
M d
i 1
Mi x n
fi
2040 120
17(台)
含义:每一天的销售量平均数相比,
第四章 离中趋势的测量

第二节 方差和标准差
平均差AD:差异量数的指标。
方差(variance):指离差平方的算术平均数 定义公式:
2
2 ( X ) i i 1
N
N
分组数据的样本方差
f (M
i
分组数据
s
2
i
x)
2
n 1
2 i
一般数据
s
2
(x x ) n 1
0.25 Q1
0.25
0.25 Q2
0.25 Q3
计算第p百分位步骤
第一步:从小到大排列原始数据 第二步:计算指数i i=(p/100)×n, n为项数,p为所求的百分位的位置 第三步:若i不是整数,将i向上取整;若i是整数,则第p百分位数是第i项 与第 i+1 项数据的平均值 例:有12个职员薪金的数据,求第85和第50百分位数。 解:(1)将12个数据从小到大排序如下: 2210 2225 2350 2380 2380 2390 2420 2440 2450 2550 2630 2825 (2) i=(p/100)×n=(85/100)×12=10.2 (3) 由于i=10.2不是整数, 向上取整,所以第85百分位数对应的是 第11项, 其值为2630。 同理,计算第50百分位(中位数)。i=(50/100) ×12=6,是整数, 第50百分位数是第6项和第7项的平均值,即(2390+2420)/2=2405。
0 1 1 4 0 4
N=6
x 0
x
2
10
X
2 i
226
X
2
i
36
10 S 2 5
10 S 1.414 5
第五讲 集中趋势和离中趋势的度量 PPT课件
xH 1
1 1
x1 m1 x2 m2
m1 m2 mn
m
1 xn mn
1
1
1
1
x1 m1 x2 m2 xn mn
m x
m1 m2 mn
第二节 数值平均数
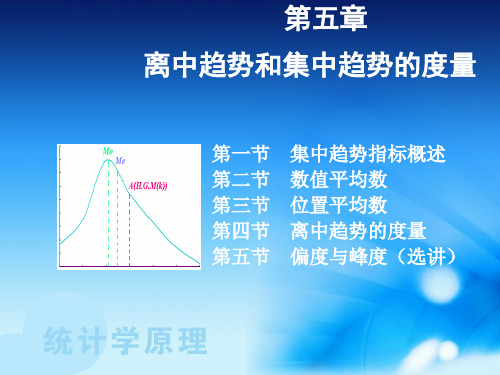
调和平均数
上述公式是加权调和平均数的公式。若各变量值 的权数都相等时,加权调和平均数简化为简单调和 平均数。即:
xG
f
x f1 1
x2 f2
xn fn f
xf
第二节 数值平均数
本节小结
本节主要讨论了算术平均数、调和平 均数、几何平均数三种数值平均数的应用条 件和计算方法,其中最常用的是算术平均数。
第三节 位置平均数
本节重点 众数、中位数的概念与计算方法
本节难点 众数、中位数的的定义
x
100%
第四节 离中趋势的度量
本节小结
标志变异指标的意义与测定既是本 章的重点,也是整个统计学中的重要问 题。特别要弄清楚标准差的计算原理、 计算方法和离散系数的应用条件。
(x x) 0或(x x) f 0
第二节 数值平均数
(五)算术平均数的数学性质 ⒉各变量值与算术平均数的离差平方和
为最小。
(x x)2 min 或(x x)2 f min
第二节 数值平均数
二、调和平均数
又叫倒数平均数,即各变量值的倒数的算术平均 数的倒数。调和平均数用 xH 表示。
第一节 集中趋势指标概述
集中趋势是指一组数据向某一中心值靠拢 的倾向,测度集中趋势即要寻找数据一般水平 的代表值或中心值。
集中趋势指标即统计平均数,是反 映若干统计数据一般水平或集中趋势的 综合指标。它可能表现为总体内各单位 某一数量标志的一般水平,也可能表现 为总体在某一段时期内的数量一般水平。
离中趋势的测定

离中趋势的测定
离中趋势是统计学中用于描述数据集中趋势的一种指标。
常见的离中趋势测定方法包括以下几种:
1. 平均值:计算数据集的算术平均值,即将所有数据相加后除以数据的个数。
2. 中位数:将数据集按照大小的顺序排列,然后找出中间位置的数值。
如果数据个数为奇数,则中位数是中间的数值;如果数据个数为偶数,则中位数是中间两个数值的平均值。
3. 四分位数:将数据集按照大小的顺序排列,然后将数据集分成四个等分,每个等分包含25%的数据。
第一个四分位数(Q1)是数据集的25%位置处的数值,第二个四分位数是数据集的50%位置处的数值(即中位数),第三个四分位数(Q3)是数据集的75%位置处的数值。
4. 极差:计算数据集的最大值与最小值之间的差值。
5. 方差:计算数据集中每个数据与平均值的差值的平方的平均值。
6. 标准差:方差的平方根。
这些测定方法可以帮助我们了解数据集的离散程度和分布情况,从而揭示出数据集的离中趋势。
选择合适的测定方法取决于数据集的特点以及我们希望得到的信息。
第五章-离中趋势测量法

⑴简单标准差 对于未分组资料计算标准差时可 采用简单法,其计算公式为:
(x x ) n
2
例,求26,45,88,62,74这些数字的标准差
⑵加权标准差 按照分组资料(变量数列)计算标准差时可采 用加权法。由组距数列计算标准差时,还应先 求出组中值(开口组的组中值以邻近组的组距 确定),再按加权法计算。其计算公式为:
AD x x n
…………(5.1)
例1,有两个参赛篮球队队员身高(单位:cm)如下: 甲队:185 191 195 202 217 乙队:190 197 199 200 204 以上述资料为例,计算简单平均差。
⑵加权平均差 在资料已经分组时,平均差采用加 权平均法计算,其计算公式为:
AD
第五章 离中趋势测量法 离中趋势测量法
离中趋势是指变量数列中变量值 之间的差异程度或离散程度。
本章重点: 1、平均差 2、方差与标准差 3、离散系数 本章难点: 1、方差与标准差 2、是非标志的方差
变异指标的概念和作用
一、变异指标的概念 变异指标又称标志变动度,是反映总体各单位标志值之间差异程度的 综合指标。 二、变异指标的作用 1、是衡量平均指标代表性的尺度 2、可用来研究现象的稳定性和均衡性 3、在抽样调查和相关分析中有着重要作用 变异指标用以反映总体各单位标志值的变动范围或参差程度,与平 均指标相对应,从另一个侧面反映了总体的特征。变异指标不仅可以 综合地显示变量值的离中趋势,还可以用来判别平均数的代表性。
(1)当 x M
e
M 0时 , 对 称 分 布 ;
,右偏分布; <Me < Mo时,左偏分布。
(三) 偏态系数
我们在前面讨论统计图时已经对频数分布的正态和 偏态有所认识。我们又看到了算术平均数与中位数、众 数之间存在的关系:当总体呈对称分布时,X 、 M 、 M 三者完全相等;当总体呈不对称的偏态分布时,它们之 间存在着数量(位置)的差异。因此,偏态可由 X 与 M o 的差来表示,即
离中趋势的测度

2552.8(7 元)
i1
k
(xi x)2 fi
电话费用的标准差为: s
i1 k
2552.87 50.53(元)
( fi) 1
i1
第二十五页,共56页。
平均差
(mean deviation)
1. 各变量值与其均值(jūn zhí)离差绝对值的平均数 2. 能全面反映一组数据的离散程度 3. 数学性质较差,实际中应用较少
合计
200 1 100
解:
Vr
200 112 112
1 112 200
0.44 44%
在所调查的200人当中,关注非 别克的人数占44%,异众比率还是 比较大。因此,用“别克”来反映 城市居民对汽车品牌的一般趋势, 其代表性不是很好
第八页,共56页。
四分(sì fēn)位差(quartile deviation)
4. 计算公式为
未分组数据 (shùjù)
组距分组数据 (shùjù)
n
xi x
M d i1 n k Mi x fi
M d i1 n
第二十六页,共56页。
平均差 (例题(lìtí)分析)
某电脑公司销售量数据平均差计算表
按销售量分组
140—150 150—160 160—170 170—180 180—190 190—200 200—210 210—220 220—230 230—240
只有n-1个数据可以自由取值,其中必有一个数据则 不能自由取值 3. 例如,样本有3个数值,即x1=2,x2=4,x3=9,则
x = 5。当 x = 5 确定后,x1,x2和x3有两个数据 可以自由取值,另一个则不能自由取值,比如x1=6, x2=7,那么x3则必然取2,而不能取其他(qítā)值 4. 样本方差用自由度去除,其原因可从多方面来解释, 从实际应用角度看,在抽样估计中,当用样本方差去 估计总体方差σ2时,它是σ2的无偏估计量
社会统计学课件:第4章 离中趋势的测量

f
190
1090750 5740.79 190
2 x2 x 2
5740 .79 74.47 2 195 .01
13.96
成绩
x
人数 f
50 以下 45
10
50—60 55
20
60—70 65
40
70—80 75
50
80—90 85
40
90 以上 95
30
合计
190
标准差的作用
用来比较分析两个或两个以上同类现象平均数相等时平均 数的代表性:即
第四章 离中趋势测量法
二、标志变异指标的作用
1、用标志变异指标衡量和比较平均指标 的代表性。
2、用标志变异指标反映经济活动过程的 均衡性、稳定性和节奏性。
3、标志变异指标在相关分析和抽样调查 中的应用。
甲乙丙三车间都有7个工人,生产的零件 数如下:
甲:72 73 74 75 76 77 78 乙:30 50 65 75 90 100 115 丙:75 75 75 75 75 75 75 平均数都为75件。但代表性谁好。
R =Xmax– Xmin
[例] 求74,84,69,91,87,74,69这些数字 的全距。
[解] 把数字按顺序重新排列:69,69,74, 74,84,87,91,显然有
R =Xmax– Xmin =91—69=22
对分组资料,不能确知最大值和最小值,求全距: (1)用组值最大组的组中值减去最小组的组中值 (2)用组值最大组的上限减去最小组的下限 (3)用组值最大组的组中值减去最小组的下限;
集中趋势和离中趋势的度量
例释
这 是 一 个 印 度 男 孩
a
14
二、平均数:定义与类型
大数定律
nl im Px1x2 n
xn
0
a
15
二、平均数:定义与类型
特点:代表值,抽象差异 作用:比较,评价,推算 类型 ✓ 静态与动态
✓ 位置(众数,中位数)与数值 (算术,调和,几何)
a
16
本节小结
当我们欲估计总体的种种性质时,其 中一类即总体的“同质性”。这种 “同质性”真义何在?它的确是存在 的吗?此即本次讨论的主要问题。
第五章 集中趋势和离中趋势的度量
a
1
教学目的要求 本章重点 本章难点 教学时数 教学方法 本章小结
a
2
第五章 集中趋势和离中趋势的度量
第一节 第二节 第三节 第四节 第五节
集中趋势指标概述 数值平均数 位置平均数 离中趋势的度量 偏度与峰度(选讲)
a
3
教学目的要求
通过本章的学习,要求达到:①明确平均 数和标志变异指标的概念和作用;②熟练 掌握数值平均数和标准差的特点及其计算 方法;③了解众数、中位数的概念、特点 及其计算方法;④能正确区分数值平均数 和位置平均数,了解几种平均数之间的关 系;⑤了解计算平均数和离中趋势指标应 注意的问题。
300
23660 1920100
算术平均 78.8667 6219.95
6400.33
方差(总体) 180.38 方差(样本) 180.99
a
62
五、偏度与峰度
K-阶原点矩与K-阶中心矩:总体 参数与样本估计量
偏度的度量:Pearson经验公式 偏度(峰度)的度量:3-阶(4-阶)
中心矩
第五章离中趋势测量法

第五章 离中趋势测量法第一节 全距与四分位差 全矩与全矩的性质·四分位差第二节 平均差对于未分组资料·对于分组资料·平均差的性质 第三节 标准差对于未分组资料·对于分组资料·标准差的性质及方差·标准分(Z 分数) 第四节 相对离势变异系数(全矩系数·平均差系数·标准差系数)·异众比率一、填空1.对收集来的数据,数值最大者和最小者之差叫作( ),又称之为( )。
2.各变量值对其算术平均数(或中位数)离差绝对值的算术平均数,称之为( )。
3.全距由于没有度量( )之间的变异性,所以数据资料的利用率很低。
4.用绝对离势除以均值得到的相对指标,即为( )。
5.所谓( ),是指非众数的频数与总体单位数的比值。
6.偏斜系数是以标准差为单位的算术平均数与众数的离差,其取值一般在( )之间。
偏斜系数为0表示( ),偏斜系数为3+或3-则表示极右或极左偏态。
二、单项选择1.下面资料中哪个厂子的平均工资代表性意义最大( ),哪个厂子最小( )。
平均工资(元) 职工人数 工资标准差(元)A 甲厂 108 346 9.80B 乙厂 96 530 11.40C 丙厂 128 210 12.10D 丁厂 84 175 9.60 2.变异指标中,以两数之差为计算基准的是( )。
A 全距B 平均差C 标准差D 方差3.比较两个性质不同的变量数列的平均数的代表性大小,必须计算( )。
A 标准差B 平均差C 全距D 标准差系数4.设有甲乙两个变量数列,甲数列的平均数和标准差分别为20和2.5,乙数列的平均数和标准差分别为50和5.2 ,这些数据说明( )。
A 甲数列的稳定性高于乙数列B 甲数列的稳定性低于乙数列C 甲乙两数列的稳定性相同D 甲乙两数列的稳定性无法比较5.某企业1994年职工平均工资为5200元,标准差为110元,1998年职工平均工资增长了40%,标准差扩大到150元。
第五章 离中趋势测量法_社会统计学

2014-6-16
10
求72、81、86、69、57这些数字的标准差。
X
72 81 86 69 57 365
(X X )
( X X )2
1 64 169 16 256 506
X2
5184 6561 7395 4761 3249 27151
-1 8 13 -4 -16 0
2014-6-16
11
8
2014-6-16
[例1] 试分别以算术平均数为基准,求85,69, 69,74,87,91,74这些数字的平均差。 [例2] 试以算术平均数为基准,求下表所示数据 的平均差。
计算左 边数列的 平均差
2014-6-16
9
第三节 标准差(standard deviation)
各变量值对其算术平均数的离差平方 的算术平均数的平方根,均方差,又称 用S表示。 即克服平均差带有绝对值的缺点, 又保留其综合平均的优点。 1. 对于未分组资科
2014-6-16 19
2.
异众比率
所谓异众比率,是指非众数的频数与总体单位数 的比值,用V· R来表示
其中:
为众数的频数;
是总体单位数
异众比率能表明众数所不能代表的那 一部分变量值在总体中的比重。
2014-6-16
20
例1:某项调查发现,现今三口之家的家庭最多 (32%),求异众比率。某开发商根据这一报导,将房 屋的户型大部分都设计为适合三口之家居住的样式和面 积,你认为如何呢? 例2:设为测体重,得到成人组和婴儿组各100人的 两个抽样总体。成人组平均体重为65千克,全距为10千 克;婴儿组平均体重为4千克,全距为2.5千克。能否认 为成人组体重的离势比婴儿组体重的离势大?
离中趋势的度量

1、未分组数据求方差和标准差
S2= (X-Xm)2/n
S=√ S2=√(X-Xm)2/n
或者
S2=(X2-(X)2/n)/n
S=√(X2-(X)2/n)/n
现在你正浏览到当前第十八页,共三十页。
例:
Xi 6 5 7 4 6 8 N=6, X=36
Xi-Xm=x 0 -1 1 -2 0 2
x=0
X2
72
71
99
50
76
75
66
94
85
85
75
67
38
81
83
83
94
69
82
54
92
84
86
78
66
72
71
99
50
85
75
67
38
81
现在你正浏览到当前第二十九页,共三十页。
作业二:计算下列次数分布表的方差和标准差
表1
分组区间 f
39-41
4
36-38
8
33-35
14
30-32
19
27-29
8
24-26
0 1 1 4 0 4 x2 =10
Xi2 36 25 49 16 36 64 Xi2 =226
现在你正浏览到当前第十九页,共三十页。
2、已分组数据求方差和标准差
S2= (fd2/N-(fd/N)2)·i2 S=√ (fd2/N-(fd/N)2)·i
其中:d=(Xc-AM)/i, (Xc-为各分组区间的组中值,f为 各分组区间的次数,AM为估计平均数,N=f,I 为组距。
现在你正浏览到当前第二十四页,共三十页。
第三章集中趋势和离中趋势
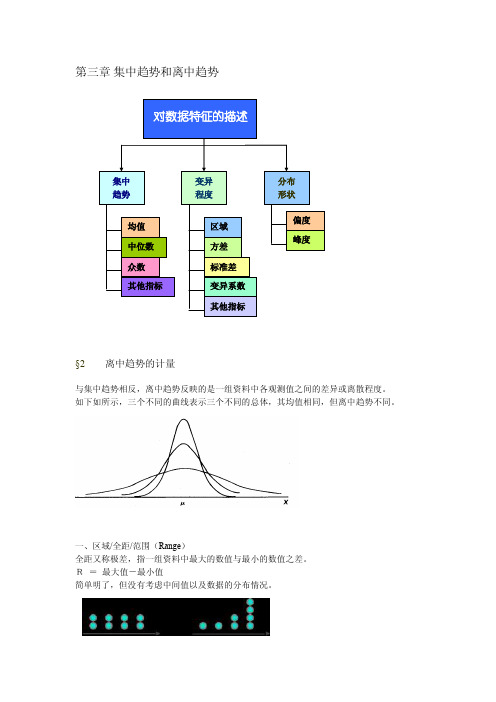
第三章集中趋势和离中趋势§2离中趋势的计量与集中趋势相反,离中趋势反映的是一组资料中各观测值之间的差异或离散程度。
如下如所示,三个不同的曲线表示三个不同的总体,其均值相同,但离中趋势不同。
一、区域/全距/范围(Range)全距又称极差,指一组资料中最大的数值与最小的数值之差。
R=最大值-最小值简单明了,但没有考虑中间值以及数据的分布情况。
二、平均差(A verage Deviation )1、一组数据值与其均值之差的绝对值的平均数称为平均差。
以A.D.表示,其计算公式为: nXX D A ni i ∑=-=1..平均差充分考虑了每一个数值离中的情况,完整地反映了全部数值的分散程度,在反映离中趋势方面比较灵敏,计算方法也比较简单。
它的缺陷在于,由于它的敏感性,使得它易受极端值影响,特别是绝对值运算给数学处理带来很多不便。
2、在ECXCEL 中计算平均差 函数A VEDEV三、四分位距 (Interquartile Range) Q = Q 3 - Q 1四、方差(V ariance )与标准差(Standard Deviation ) 方差与标准差是测度离中趋势的最重要、最常用的量。
1、总体方差是一组总体资料中各数值与其算术平均数离差平方和的平均数。
通常用2σ表示。
总体标准差则是总体方差的平方根,用σ表示。
nxni i∑=-=122)(μσ,nxni i∑=-=12)(μσ请注意:在这里,我们是用μ来表示总体均值的。
从方差与标准差的定义和计算公式,我们看到它与平均差同样,都是以离差来反映一组数据的差异程度的,所不同在于对离差的处理方式不同,方差和标准差是通过对离差进行平方来避免正负离差的互相抵消,这使得它不仅能够考虑所有数据的情况来可以反映数据离散程度的大小,而且避免了绝对值计算,使得数学上的处理更加方便,此外,方差在统计推断上具有较佳的统计与数学性质,这就使得方差成为最重要的离中趋势测度量。
第四章离中趋势

例4-4 在三个班级进行某项能力研究,三个班测查结果的平均数和 标准差分别如下:求三个班的总标准差。
班级
n
x
s
1
42
103
16
2
36
110
12
3
50
98
17
总平均数=(42*103+36*110+50*98)/(42+36+50)=103.02
NiSi2 42162 36122 50172 30386
常用的差异量数有全距四分位差平均差方差与标准差变异系33第一节全距与百分位差第二节平均差方差与标准差第三节标准差的应用第四节差异量数的选用第四章差异量数44第一节全距与百分位差range也称极差polesdeviation是一组数据中最大值与最小值的差是反映离中趋势的一种最简单的变异指标用r表示
第四章 差异量数
19
第三节 标准差的应用
一、差异系数(coefficient of variation) 差异系数又称变异系数、相对标准差等,它是一种相对差异量,
用 CV 来表示,为标准差对平均数的百分比,其计算公式如下:
CV s 100% X
式中:S 为样本标准差;
X 为样本平均数。
20
[例4-5] 已知某小学一年级学生的平均体重为25千克,体重的标 准差3.7千克;平均身高110厘米,标准差为6.2厘米,问体重与身高的 离散程度那个大?
在心理学研究中,经常合成各实验点的资料,也会牵涉方差或标准差 合成。
计算总方差和总标准差的公式如下:
ST 2
NiSi2 Nidi2 Ni
ST
NiSi2 Nidi2 Ni
式中:ST 2 为总方差;ST 为总标准差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章离中趋势测量法平均指标对总体的共性和一般水平作了概括,以此来说明总体标志值分布的集中趋势。
但是总体作为统计对象,还有其变异性的一面。
变异指标用以反映总体各单位标志值的变动范围或参差程度,与平均指标相对应,从另一个侧面反映了总体的特征。
变异指标不仅可以综合地显示变量值的离中趋势,还可以用来判别平均数的代表性。
所谓离中趋势,是指数列中各变量值之间的差距和离散程度。
离势小,平均数的代表性高;离势大,平均数代表性低。
例如有A、B、C、D四组学生各5人的成绩如下:A组:60,60,60,60,60 B组:58,59,60,61,62C组:40,50,60,70,80 D组:80,80,80,80,80A组、B组、C组的平均成绩均为60分,D组的平均成绩为80分。
就平均数而言,A、B、C三组相同,D组的平均数高于前三组。
就离势而言,A,D两组一样,都为0;C组的离势最大,B组次之。
所以,平均数不同,离势可能相同;平均数相同.离势可能不同;平均数不同,当然离势也可能不同。
可见,要掌握总体资料中各标志值的离散、参差或分布情况,测定离中趋势也是必不可少的。
变异指标的种类较多,如按计算的基准来分有以下两类:(1)以两数之差来表达的有全距和四分位差等。
(2)以对平均数偏差来表达的有平均差、标准差等。
变异指标如按数量关系来分有以下两类;(1)凡用绝对数来表达的变异指标,统称绝对离势,主要有极差、平均差、四分位差、标准差等。
(2)凡用相对数来表达的变异指标,统称相对离势,主要有异众比率、标准差系数、平均差系数和一些常用的偏态系数。
第一节全距与四分位差关于变异指标,前面其实我们已有所接触,第三章讨论统计分组时谈到的全距便是。
全距是测定离中趋势最简单的一种指标。
它和四分位差一样,是以两数之差来表达的。
1.全距全矩是最大变量值与最小变量值之差,用R来表示。
对未分组资料,计算全距用原始式。
由于全距是一组数据中两个极端值之差,所以它又称极差。
R=X N—X1 (5.1)其中:X N是全部数据中最大的标志值,X1是最小的标志值。
[例5.1.1] 求74,84,69,91,87,74,69这些数字的全距。
[解] 把数字按顺序重新排列:69,69,74,74,84,87,91,显然有R =X N —X 1=91—69=22对于分组资料,在第三章我们已经知道,由于不能确知变量实际的最大值和最小值,因而求全距有以下三种方法:(1)用组值最大组的组中值减去组值最小组的组中值,此法求出的全距一般比实际上的全距要小些。
(2)用组值最大组的上限减去组值最小组的下限,此法求出的全距一般比实际上的全距要大些。
(3)用组值最大组的组中值减去组值最小组下限;或用组值最大组上限减去组值最小组的组中值。
此法求出的全距多接近于实际上的全距。
全距的最大优点是:计算简单,便于直观。
缺点是;①受极端值影响大,遇含开口组的资料时将无法计算;②由于没有量度中间各个单位间的差异性,所以数据利用率很低,信息丧失严重;③受抽样变动影响很大。
一般说来,大样本全距要比小样本全距大些,因为大样本有较多的机会包含最极端的变量值。
2.四分位差在第四章,我们已经了解了四分位数的计算。
它的一个用途就是,用第三四分位数和第一四分位数的半距作为测定离中趋势的一种变异指标,以避免全距测量离中趋势受极端值影响大这个缺点。
四分位差就是第三四分位数和第一四分位数的半距,用Q ·D 表示Q ·D =213Q Q - (5.2) 四分位差优点是避免了极端值变动的影响,但由于它仅以两数之差为基准,全距的另两个缺点依然无法避免。
第二节 平均差要测定变量值的离中趋势,尤其是要测定各变量值相对于平均数的差异情况,一个很自然的想法就是计算各变量值与算术平均数的离差。
但由于算术平均数的性质,各变量值与其算术平均数离差的代数和恒为零,所以用这个性质无法构造出能够测定离中趋势的变异指标。
为此,我们采取处理离差绝对值的办法,如此构造出来的变异指标,称为平均差,用A ·D 表示。
1.对于未分组资料平均差被定义为各变量值对其算术平均数(或中位数)离差绝对值的算术平均数。
对于未分组资料,求平均差用原始式,即A ·D =NX X ∑- (5.3)[例5.2.1] 试分别以算术平均数为基准,求85,69,69.74,87,91,74这些数字的平均差。
[解] 先用求平均指标的公式求出这些数字的算术平均数,得X = 78.4再利用表5.1,以算术平均数为基准求出A ·D =NX X ∑- =74.55 = 7.91 表5.12.对于分组资料对于分组资料,计算平均差需用加权式A ·D =∑∑-fXX f (5.4)[例5.2.2] 试以算术平均数为基准,求表3.10所示数据的平均差。
[解] 先算出算术平均数X =∑∑f fX =32119829=3.06(人) = 再利用表5.2算出A ·D =∑∑-fXX f =322738.2418 = 0.75(人)由此可见,2002年天津市家庭以户均人口3.06人为基准,家庭人口的平均差是0.75人。
表5.23.平均差的性质平均差以及接下来要讨论的标准差,虽都是变异指标,但就其计算的数学方法来看,仍属于算术平均数。
所以平均差在受抽样变动影响、受极端值影响和处理不确定组距这三方面,它的性质均同于算术平均数。
与此同时,平均差由于计算时采用了取绝对值来消除正负号的影响的方法,它不便于代数运算,而且平均差的意义在理论上也不容易作出阐述,所以平均差作为变异指标,其运用比下面的标准差要少得多。
另外,根据中位数的性质可知,各变量值对中位数之差的绝对值总和为最小。
因而,有时以中位数为基准来计算平均差反倒比以算术平均数为基准来计算平均差更合理。
第三节标准差为了克服平均差带有绝对值计算的缺点,同时保留平均差的优点(即它已将总体中各个单位标志值的差异全部包括在内),故将各离差平方后求算术平均,再求平方根,来构造变异指标,这样就得到一个常用的而且也是最重要的变异指标——标准差,用S表示。
1.对于未分组资科标准差被定义为各变量值对其算术平均数的离差平方的算术平均数的平方根,又称均方差。
对于末分组资料,求标准差用原始式,即S =()NXX∑-2(5.5)①①计算样本资料的标准差,应以(N―1)作为分母更合适,因为在通常的情况下,分母应为自由度数,在这里取N是近似,在N大的情况下没有多少差别。
这将在“参数估计”一章得到说明。
[例5.3.1] 求72、8l 、86、69、57这些数的标准差。
[解] 先求出算本平均数 X = NX ∑ = 5365 = 73.0再利用表5.3求出标准差S = ()NX X ∑-2=5506= 10.06 表5.3在大多数情况下,由于作为基准的X 不是简单的数值,所以求标难差用原始式(5.5)运算起来数字很繁,容易发生错误。
为此,我们可以利用标准差便于代数运算的特点,把(5.5)式变形为S = 22⎪⎪⎭⎫⎝⎛-∑∑N X N X (5.6)① [例5.3.2] 应用(5.6)式求上例的标准差。
[解]仍利用表5.3,各项数字已列于表中S = 22⎪⎪⎭⎫ ⎝⎛-∑∑N X N X = 25365527151⎪⎭⎫ ⎝⎛-= 10.06①证明:()NX X ∑-2=NXX X X∑∑∑+-222 =2222XX NX+-∑=22⎪⎪⎭⎫ ⎝⎛-∑∑N X NX2. 对于分组资料对分组资料,计算标准差要用加权式,即S =()NX X f ∑-2(5.7)①[例5.3.4] 求表3.12的标准差〔参见表5.4〕 [解] 先求出算术平均数 X =NfX∑=10017028= 170.28(厘米) 再利用(5.7)式求出标准差,各项数字已列于表5.4中S =()NX X f ∑-2=10016.5672= 7.53 (厘米)由此可见,100个男性青年的身高,以平均身高170.28厘米为基准,标准差是7.53厘米。
表5.4对于标准差的加权式,我们也可以通过代数运算,将(5.7)式变形为①(5.7)式可以写成 S =()∑-2XX PS = 22⎪⎪⎭⎫⎝⎛-∑∑N fX N fX (5.8)② [例5.3.5] 利用(5.8)式求上例的标准差〔参见表5.4〕。
[解] S =22⎪⎪⎭⎫⎝⎛-∑∑N fX NfX =2100170281002905200⎪⎭⎫ ⎝⎛-= 7.53 (厘米) 3. 标准差的性质标准差是测定总体各单位标志值的离散状况和差异程度的最佳指标,这是因为它在数学上便于代数运算,并且具有许多特有的性质:(1)以算术平均数为基准计算的标准差,较之以任何其他数值为基准计算的标准差要小。
这是因为算术平均数的“最小平方”性质:各变量值对算术平均数的离差的平方和,必定小于它们对任何其他数(X ’)偏差的平方和,即()NX X ∑-2≤()NX X ∑-2' (未加权式) (5.9a )或()NX X f ∑-2≤()NX X f ∑-2' (加权式) (5.9b )(2) 标准差同平均差一样,虽都是变异指标,但就其计算的数学方法来看,仍属于算术平均数。
因为它已将总体中各单位标志值的差异全部包括在内了,所以它受抽样变动的影响小。
但是,标准差在受极端值影响和处理不确定组距这两方面,缺点均与算术平均数相同。
值得注意的是,在推论统计中我们将发现,方差是比标准差更有理论价值的概念。
所谓方差,即标准差的平方,它直接写成S 2。
从第十章开始,我们将逐渐频繁地使用方差,但目前我们仍然集中讨论标准差。
这两个概念是很容易互换的,可以直接从一个转换到另一个。
4.标准分运用标准差.还可将原来不能直接比较的离差标准化,使之可以相加、相减、平均或者相互比较。
为此我们引入一个新的变量,用符号Z 表示,它被定义为变量X 的标准分Z =SXX - (5.10)②(5.8)式可以写成 S =∑∑-22)(PX PX由公式可以看到,Z分数是以离差与标准差的比值来测定变量X与X的相对位置的,它有三个特性:(1)对于给定资料,由于算术平均数和标准差都是确定值,所以Z是和X一一对应的变量;(2) Z分数没有单位,是一个不受原资料单位影响的相对数,因而也适用于不同单位资料的比较;(3) Z分数实际表达了变量值距算术平均数X有几个标准差。
比如Z=2,表示该变量值离X有2个S的距离;Z=1.3,表示变量值离X有1.3个S的距离。
因为Z分数和正态分布有密切关系,所以在第七章求Z分数的过程,也称为变量标准化的过程。
以后我们将看到,均值不同和方差不同的正态分布经Z 分数标准化后,成为标准正态分布,所以Z也有标准正态变量之称。
