midas截面几何性质计算
midas截面几何性质计算

下面我们来讲一下预制梁的横向力分布系数计算从上面我能看出常见的预制梁包括板梁、小箱梁、T梁跨中横向力分布系数:对于板梁和小箱梁由于横向联系比较薄弱,所以采用铰接板梁法对于T梁有横隔板比较多,认为是刚接,所以采用刚接板梁法梁端横向力分布系数:通常采用杠杆法下面就讲一下30米简支转连续T梁横向力分布系数计算:主梁横断面见附件桥博计算横向力分布系数计算需要输入的数据见附件包括主梁宽、抗弯、抗扭、左板长、左板惯矩、右板长、右板惯矩、主梁跨度G/E等首先计算主梁的抗弯抗扭惯矩(中梁、边梁断面尺寸见附件,梁高200cm)中梁:===================================================== MIDAS SPC TEXT OUTPUT FILE == (Tue Jun 17 20:45:16 2008) == - - =========================================================================================================UNIT: KN . M========================================================================================================* Section-P1 (PLANE)====================================================* A :* Asx :* Asy :* Ixx : 抗弯惯矩* Iyy : 0.* Ixy :* J : 抗扭惯矩----------------------------------------------------* (+)Cx :* (-)Cx :* (+)Cy :* (-)Cy :----------------------------------------------------* (+)1/Sx :* (-)1/Sx :* (+)1/Sy :* (-)1/Sy : 9.====================================================边梁:===================================================== MIDAS SPC TEXT OUTPUT FILE == (Tue Jun 17 20:48:08 2008) == - - =========================================================================================================UNIT: KN . M========================================================================================================* Section-P1 (PLANE)====================================================* A :* Asx :* Asy :* Ixx : 抗弯惯矩* Iyy : 0.* Ixy :* J : 抗扭惯矩----------------------------------------------------* (+)Cx :* (-)Cx :* (+)Cy :* (-)Cy :----------------------------------------------------* (+)1/Sx :* (-)1/Sx :* (+)1/Sy :* (-)1/Sy :====================================================由于结构是多跨连续梁(本文假定是3x30简支转连续T梁),所以应该考虑抗弯刚度修正系数根据中跨:边跨=30 :30= : 1查《梁桥下册》P204页等截面连续梁等效简支梁刚度修正系数表:跨度比二跨连续梁三跨连续梁四跨连续梁L21 边跨L1 中跨L2 边跨L1 中跨L2 边跨L1 中跨L22内插得项目边跨中跨K则在计算边跨横向力分布系数,边跨的中梁和边梁的抗弯惯矩需要乘以中梁:边梁:而在计算中跨横向力分布系数,中跨的中梁和边梁的抗弯惯矩需要乘以中梁:边梁:对于计算抗扭惯矩在上次课程中我们给除了箱梁断面的简化计算公式,在这里我也给出T 梁断面的简化计算公式见《公路桥梁荷载横向分布计算》李国豪石洞编第21页,粘贴在附件中,供大家学习!左板惯矩右板惯矩就是等刚度桥面板抗弯惯矩,他是考虑相邻两篇主梁间桥面板的连接作用,其宽度取相邻横梁间距,翼板厚度取靠近主梁梁肋d1/3处的厚度,详细说明请参照《公路桥梁荷载横向分布计算》李国豪石洞编第22页桥面中线距首梁距离:对于杠杆法和刚性横梁法为桥面的中线到首梁的梁位线处的距离;对于刚接板梁法则为桥面中线到首梁左侧悬臂板外端的距离,用于确定各种活载在影响线上移动的位置。
midas课件1

1.截面几何特性计算画cad图→保存为dxf格式(2004)按毫米单位1:1画图→导入cad文件→生成截面文件(类型plane)→(section面→generate 生产→plane→name→calulate properties now→框选截面→apply→截面变成黄色→可以查看(properties list)→保存(特性保存text格式(可以转到Excel中(数据→分列));截面保存section(数据→分列)export→midas section file(一个一个的截面保存)2.使用截面文件建模设计材料设计截面(设计用数值截面)→导入刚才生成截面→从SPC导入(填写数据不能为0,能自动的点自动生成→建立一个节点然后扩展,3.変高粱方法一:建立变截面→变截面组(所有变截面按一定规律变化)截面简单→截面特性→变截面(注意偏心只能中上部)→建立单元→形成模型→特性→变截面组→名称→全选→截面形状变化(多项式)方法二:使用数值截面10月13号课组使用不当分析之前先定义施工阶段分析控制、移动荷载分析控制,点默认,但必须点。
先分析再psc设计预混梁,钢混梁不用10块空心板,计算跨径16米公路等级二级。
结构重要性系数(跨径确定桥的类型、安全等级)空心板截面,荷载(温度荷载桥合拢时温度,梯度温度铺装类型)A类预应力构架10月27号课堂建模规划→建模类型(单位)→材料(混凝土c50和钢绞线及有可能有没有质量的混凝土,一般钢筋不算材料)和截面(软件里面的数据填写、从cad中导入(单位一致)、冲击系数的计算(计算表格)公式(公路(基频计算方式)及城市(计算跨径的公式))横向分布计算(桥梁博士计算(3.2及以下)、xcp文件、Word (计算书)、Excel、AutoCAD(导入civil,导出civil))横向分布系数:支点处→杠杆法跨中处→铰、刚接板(梁)法刚性横梁法(忽略抗扭)→修正的刚性横梁法G-M法横向分布计算→桥博(工具)手算法(Excel表格)Madis civil →梁格体系在单位(作用于边梁)荷载作用下各片量的挠度f→梁格体系和单梁体系,梁格体系在单位(作用于边梁)荷载作用下各片量的挠度f,单梁体系下单位荷载作用下的挠度f2,两者相除。
MIDAS截面特性计算器使用说明

MIDAS/SPC(SectionalPropertyCalculator)
并连
复
线。
<图9>建立直线对话框 建立直线对话框
<图1010-(1)> 移动复制点的对话框
<图1010-(2)> 移动复制指定的点
在所有可以建立线的对话框中,都提供可以指定线的厚度和线的对齐方向的功能(Width和Alignment)功 能。构成Line截面的线必须有厚度,而构成Plane截面的线不需要有厚度(用户即使指定了线的厚度,在 生成Plane截面之后也会自动忽略线的厚度)。现在是Plane截面,线不需要有厚度,所以其相关的功能无 法使用。
截面列表 换算的基准材料(联合截面时)
截面的形状、形心位置、基准材料部分
表示联合截面 单位体系 截面特性 -面积(Area:联合截面时为有效面积) -截面惯性矩(Ixx,Iyy) -截面惯性积(Ixy) -抗扭刚度(J) -从形心到各方向最外端的距离 显示截面排序的方法
<图3>输出截面特性对话框
在SPC里建立的截面可以通过以下文件形式输出。 MIDAS/Civil[Gen]的MCT[MGT]文件 此时无法导出具体的截面形状,而是按MIDAS/Civil[Gen]截面数据库中的“数值”形式建 立一个正方形,其边长为截面有效面积的平方根。另外,SPC不提供截面的周长、剪切 面积、剪切系数的计算结果,这些值均按0处理。 AutoCADDXF文件 在SPC里建立的截面形状可以输出DXF格式的文件。在截面的形心位置会自动生成点。 文本文件 各种截面特性值在文本文件里以表格形式输出。除输出SPC所计算的截面特性以外,还 输出截面抵抗拒(SectionModulus:Z=I/c)。
midas简支梁计算PPT课件

1
一、简支梁
桥梁长度:L = 14 m,混凝土结构 (C40) 截面形式: H=2 m ,B=1 m 实腹式矩形截面 荷载:集中荷载50tonf 求解全桥剪力、弯矩和给定点位移
2
1、节点的建立
3
2、节点输入
4
4、单元的建立(点选或扩展建立)
5
5、定义材料和截面
定义材料
模型 / 材料和截面特性 / 材料 类型>混凝土 ; 规范> JTG04(RC) 数据库> C40 名称〉主梁↵
19
1、节点的建立
20
2、单元的建立(用扩展单元 建立)
21
3、材料、截面和边界条件定义同前,模型建立如下
22
4、定义荷载(均布荷载)
23
24
5、点击运行进行分析求解 6、查看内力 (结果/内力/ 梁单元内力图 )
25
剪力图
26
弯矩图
27
7、查看位移
28
8、移动荷载分析 荷载规范选择
定义截面
模型 /材料和截面特性 / 截面/添加 截面类型>数据库/用户> 实腹长方形 截面 截面号 ( 1 ) ; 名称 (梁截面)
6
6、定义材料
7
7、定义截面
8
定义好材料和截面后利用拖放定义到所要定 义的单元 注:也可在建立单元前先定义材料和截面, 在建立单元时赋予
9
8、定义边界条件
10
11
You Know, The More Powerful You Will Be
42
结束语
感谢聆听
不足之处请大家批评指导
Please Criticize And Guide The Shortcomings
02-Midas Civil截面特性计算器SPC

01Midas Civil截面特性计算器SPC1、截面特性计算器①截面特性计算器的功能使用截面特性计算器的目的是为了导入在midas中无法直接建立的截面。
②截面特性计算器的使用标准流程1)首先在CAD中画好所要导入的截面,并另存为dxf格式的文件。
2)打开截面特性计算器,导入dxf文件。
3)使用”Model>Section>Generate”功能形成截面,在”Name”中输入截面的名称(方便后面导入时截面的识别),并勾选其中的”Calculate Properties Now”,同时完成截面特性的计算。
4)使用”Model>Section>Export”功能导出sec文件,勾选其中的”MIDAS Sectin File”,命名后即可导出需要的sec文件。
5)然后在”File>Save”中保存spc文件,以便以后查询,或直接退出,程序会提示是否保存。
③在midas中导入上面形成的截面。
打开midas的“模型-材料和截面特性-截面”,点击“添加”,点击PSC选项,在下拉框中选择“PSC-数值”,点击“从SPC中导入截面”,选择相应的sec文件即可。
(若sec中含有多个截面,会弹出对话框,选择所需要的截面即可。
)2、利用截面特性计算器绘制特殊截面双拼45a工字钢①在CAD绘制双拼45a工字钢截面图形,另存为dxf格式文件。
②打开截面特性计算器,导入双拼45a工字钢dxf文件。
File>Import>AutoCAD DXF>OK③使用”Model>Section>Generate ”功能形成截面,在”Name ”中输入截面的名称,Type:Plane,Angle:2,Apply 。
④计算截面特性及导出sec 文件,Property>Calculate Section Property,MeshSize:10mm,Pause after Each Calc(打开),Apply。
迈达斯截面特性简介

. sax对x轴的面积矩
say对y轴的面积矩
ixx,iyy,ixy分别是对x轴的惯性矩,y轴惯性矩,xy的截面惯性积,对应于材料力学
帮助文件说明如下:
Asy:单元局部坐标系y轴方向的有效抗剪面积(Effective Shear Area)。
Asz:单元局部坐标系z轴方向的有效抗剪面积(Effective Shear Area)。
Ixx:对单元局部坐标系x轴的扭转惯性距(Torsional Resistance)。
Iyy:对单元局部坐标系y轴的惯性距(Moment of Inertia)。
Izz:对单元局部坐标系z轴的惯性距(Moment of Inertia)。
Cyp:沿单元局部坐标系+y轴方向,单元截面中和轴到边缘纤维的距离。
Cym:沿单元局部坐标系-y轴方向,单元截面中和轴到边缘纤维的距离。
Czp:沿单元局部坐标系+z轴方向,单元截面中和轴到边缘纤维的距离。
Czm:沿单元局部坐标系-z轴方向,单元截面中和轴到边缘纤维的距离。
Qyb:沿单元局部坐标系z轴方向的剪切系数。
Qzb:沿单元局部坐标系y轴方向的剪切系数。
Peri:O :截面外轮廓周长。
Peri:I :箱型或管型截面的内轮廓周长。
Cent:y :从截面最左侧到形心轴的距离。
Cent:z :从截面最下端到形心轴的距离。
y1、z1:截面左上方最边缘点的y、z坐标。
y2、z2:截面右上方最边缘点的y、z坐标。
y3、z3:截面右下方最边缘点的y、z坐标。
y4、z4:截面左下方最边缘点的y、z坐标。
'.。
MIDAS截面特性计算器使用说明

例题的截面大小为125×250,可以点击工具里的(GridSetting)图标,
将GridSize设为10。
由于SPC的GridSetting里以所指定的栅格间距为基准进行相关的画图、视图功能,所以即使不直接使用 栅格捕捉功能,适当地指定其栅格间距会更方便一些。
下面绘制Plane截面: 调出Model>Curve>Create>Line菜单,在生成直线对话框 ( 参见图 9) 里的 Point1 处输入 –3.75,0, 选择 Dx,Dy选项,输入0,75之后点击Apply按钮。
的DeltaX,Y的Dx栏输入0,Dy栏输入12.5之后点击Apply按钮。 用同样的方法选择最新建立的点之后,在<图10-(1)>的点移动复制对话框里的DeltaX,Y的 Dx栏输入62.5,Dy栏输入0后点击Apply按钮就会生成像<图11>一样的轮廓线。
9
MIDASIT()
目录菜单
<图11>进行点的移动复制
<图1212-(1)> 线移动复制对话框
<图1212-(2)>移动复制完的线
通过将<图11>所示的线向左侧复制来完成需要加厚的部分。 调出Model>Curve>Translate菜单,选择<图11>里所示的线作为对象。在<图12-(1)>所示的线移动复 制对话框里选择Mode里的Copy。在DeltaX,Y的Dx栏里输入-10,Dy栏里输入0。然后,选定CopyO ption里的ConnectEndsbyLine选项之后点击Apply按钮。如<图12-(2)>所示,将选定的线通过移动复 制生成新的线,然后将两线的末端用直线连接。
Midas Civil建模设计用数值截面-截面参数设置

midas Civil 技术资料----设计用数值截面-截面参数设置目录midas Civil 技术资料1 ----设计用数值截面-截面参数设置 1 1问题提出2 2设计截面定义及参数设置 2 2.1设计用数值截面定义 2 2.2设计用数值截面-参数设置 4 3箱形截面-受扭塑性抵抗矩W t 计算示例 7 参考文献8北京迈达斯技术有限公司 桥梁部2013/04/271问题提出设计用数值截面,矩形、T形、I形截面参数如何设置是非常重要的,关系到设计容许值的结果。
大家可结合如下所述,对照规范公式进行理解。
2设计截面定义及参数设置2.1设计用数值截面定义1.在CAD中绘制设计截面,如图2-1所示,并存为*.dxf文件,分别为矩形、箱形、T形、I形。
单位:m图2-1 截面参数设置-设计截面图2-2 创建截面2.Civil—工具—截面特性值计算器,计算各截面特性并存为midas section file文件,如图2-2、2-3、2-4所示。
图2-3 计算截面特性图2-4 导入sec类型文件在Civil中定义截面时,设计用数值截面可直接导入,具体操作略。
2.2设计用数值截面-参数设置1.矩形截面图2-5 矩形数值截面参数输入矩形可看做只有中腹板,无翼缘厚度的箱形截面来理解设计截面参数的输入。
(1)“设计参数”中:T1(上翼缘厚度),填入一个可忽略的较小值,;T2(下翼缘厚度),填写0;BT(箱形截面外腹板中心距离),填写0;矩形截面该值不起作用;HT(箱形截面上、下翼缘的中心距离),截面高度,对应D62-04式5.5.2-1中的h值。
(2)验算扭转用厚度(最小):实际截面宽度值,对应D62-04式5.5.2-1中的b值,用于计算Wt,可见,该值的准确输入直接关系到抗扭验算的结果。
剪切验算:验算截面对剪切较薄弱的部位的剪力。
(3)Z1, Z3:确定剪力计算位置,以截面底边为基准线沿截面Z轴方向的距离,注意,由材料力学切应力(τmax)计算公式可知,矩形截面,切应力最大值发生在截面形心处,故,一般情况下对于矩形截面Z1, Z3的位置可设置成与Z2重合。
Midas截面特性计算器的使用详细说明

midas允许用户自定义截面形式,不管那种形式的截面,都要先绘制然后在section的generate 里面用plane形式或line形式进行截面特性的计算。
绘制截面前事先根据单位和截面大小设置grid size大小,auto fit选择开,这点非常重要,有时需要关闭坐标系和线宽的显示。
方式一1. point绘制,在point设定起始点,让后tanslate里面的copy,connect by line这样可以实现线的绘制. 2. 绘制完成截面后使用而且必须使用section的generate里面用plane形式完成截面网格划分和特性的计算.注意:此时线宽width是无效的方式二:1.curve方式绘制在line里绘制,用线宽选项生成有宽度的线条,程序根据这个宽度计算截面特性,对于薄壁截面几乎可以准确计算其抗扭刚度,所以不是薄壁界面的闭合截面,应尽量不使用line 方式计算其特性.2. 绘制完成截面后使用而且必须使用section的generate里面用plane形式完成截面网格划分和特性的计算.注意:此时线宽width是必须的.使用镜像功能时,可能要指定其对齐方式,此时需要用到model,curve里面的change width。
curve方式绘制的截面必须闭合,(model---curve--closed loop--regester),选择要闭合的线条(此时可能要关闭线宽显示以方便选中该线)之后才能进行section--line方式生成截面。
注:1. SPC可以在一个窗口里任意的建立很多个截面,使用钝化、和激活可以分别绘制不同截面,并分别进行分析,且可根据名称、位置、截面特性值等可以很方便地对截面进行搜索及排列。
2. AutoCAD DXF 文件在SPC里建立的截面形状可以输出DXF格式的文件。
在截面的形心位置会自动生成点。
3. 欲将AutoCAD DXF 文件正常的导入(Import),DXF的截面必须是在x-y平面内,也就是说所有点的坐标在z轴上的值必须都为0。
Midas Civil建模设计用数值截面 截面参数设置

midas Civil 技术资料----设计用数值截面-截面参数设置目录midas Civil 技术资料1 ----设计用数值截面-截面参数设置 1 1问题提出2 2设计截面定义及参数设置 2 2.1设计用数值截面定义 2 2.2设计用数值截面-参数设置 4 3箱形截面-受扭塑性抵抗矩W t 计算示例 7 参考文献8北京迈达斯技术有限公司 桥梁部2013/04/271问题提出设计用数值截面,矩形、T形、I形截面参数如何设置是非常重要的,关系到设计容许值的结果。
大家可结合如下所述,对照规范公式进行理解。
2设计截面定义及参数设置2.1设计用数值截面定义1.在CAD中绘制设计截面,如图2-1所示,并存为*.dxf文件,分别为矩形、箱形、T形、I形。
单位:m图2-1 截面参数设置-设计截面图2-2 创建截面2.Civil—工具—截面特性值计算器,计算各截面特性并存为midas section file文件,如图2-2、2-3、2-4所示。
图2-3 计算截面特性图2-4 导入sec类型文件在Civil中定义截面时,设计用数值截面可直接导入,具体操作略。
2.2设计用数值截面-参数设置1.矩形截面图2-5 矩形数值截面参数输入矩形可看做只有中腹板,无翼缘厚度的箱形截面来理解设计截面参数的输入。
(1)“设计参数”中:T1(上翼缘厚度),填入一个可忽略的较小值,;T2(下翼缘厚度),填写0;BT(箱形截面外腹板中心距离),填写0;矩形截面该值不起作用;HT(箱形截面上、下翼缘的中心距离),截面高度,对应D62-04式5.5.2-1中的h值。
(2)验算扭转用厚度(最小):实际截面宽度值,对应D62-04式5.5.2-1中的b值,用于计算Wt,可见,该值的准确输入直接关系到抗扭验算的结果。
剪切验算:验算截面对剪切较薄弱的部位的剪力。
(3)Z1, Z3:确定剪力计算位置,以截面底边为基准线沿截面Z轴方向的距离,注意,由材料力学切应力(τmax)计算公式可知,矩形截面,切应力最大值发生在截面形心处,故,一般情况下对于矩形截面Z1, Z3的位置可设置成与Z2重合。
钢管混凝土组合截面计算方法及其在midas中的实现

钢管混凝土组合截面计算方法及其在midas中的实现
5. 结果评估:分析完成后,midas会提供截面的弯曲和剪切强度、应力分布等结果,以评 估截面的性能和安全性。
请注意,具体的计算方法和midas软件的使用可能会根据不同的版本和功能有所不同。建 议您参考midas软件的用户手册、技术文档或咨询midas软件的官方支持,以获取更详细和 准确的信息。
钢管混凝土组合截面计算方法及其在midas中的实现
3. 计算钢管的弯曲和剪切强度。这可以使用钢管的弯曲和剪切设计公式,考虑钢管的抗弯 和抗剪强度、截面形状等。
4. 考虑钢管和混凝土的相互作用,计算截面的整体弯曲和剪切强度。这可以使用相互作用 设计公式,考虑钢管和混凝土的刚度、界面摩擦等。
在midas中,可以使用其提供的组合截面设计功能来进行钢管混凝土组合截面的计算和分 析。具体步骤可能包括:
钢管混凝土组合截面计算方法及其在midas中的实现
钢管混凝土组合截面是一种结构截面形式,由钢管和混凝土组成。在设计和计算中,需要 考虑钢管和混凝土的相互作用,以确定截面的强度和刚度。
钢管混凝土组合截面的计算方法通常包括以下步骤:
1. 确定截面的几何形状和尺寸,包括钢管和混凝土的厚度、直径或宽度等。
2. 根据截面的几何形状和材料特性,计算混凝土的弯曲和剪切强度。这可以使用混凝土的 弯曲和剪切设计公式,考虑混凝土的抗压和抗拉强度、应力分布等。
钢管混凝土组合截面计算方法及其在midas中的实现
1. 创建截面模型:在midas中创建钢管混凝土组合截面的几何模型,包括钢管和混凝土的 尺寸和位置。
2. 材料属性定义:定义钢管和混凝土的材料特性,包括弯曲和剪切强度、弹性模量等。
3. 荷载定义:定义应用在截面上的荷载,包括弯矩、剪力等。
MIDAS-预应力箱梁截面特性值及扭转剪应力的计算验证

② ③
图1. 预应力箱梁截面特性值 MIDAS/Civil中提供的截面特性值有下列四种。
用户自定义截面的特性值 标准截面的特性值 任意截面的特性值 桥梁结构中的预应力箱型截面的特性值
1) 用户自定义截面的特性值
图2显示的是有加劲肋的箱型截面的截面特性值,如图所示用户只需输入基本的几何数据,程 序就会自动计算其特性值,其中有效剪切面积(Asy、Asz)和抗扭惯性矩(Ixx)是按图6~图11中的公 式计算的。
3) 任意截面的特性值
对 于 MIDAS/Civil的截面数据中未提供的截面 , 程序提供了截面特性值计算器SPC(Section Property Calculator)。图4显示的是使用SPC计算的钢混叠合梁的截面特性。目前SPC仅提供截面 的面积、抗弯惯性矩、抗扭惯性矩、中和轴位置、有效抗剪面积等特性值参数。
Ix
=
T φ
,
Ix
=
GIxx L
(1)
在此 Ix : 抗扭刚度(Torsional Resistance) Ixx : 抗扭惯性矩(Torsional Constant) T : 扭矩(Torsional Moment or Torque)
φ : 扭转角度(Angle of Twist)
如上面公式所示,抗扭惯性矩是抵抗扭转的刚度参数,与计算由扭矩引起的剪切应力所使用 的极惯性弯矩(Polar Moment of Inertia)是不同的概念。但是圆形截面或壁厚较大的圆管截面二 者的数值相等。
3.1 有效剪切面积(Asy、Asz : Effective Shear Area)
有效剪切面积用于抵抗计算截面剪力引起剪切变形,所以当不输入该值时,则程序不计算相 应方向的剪切变形。图6为标准形式截面的有效剪切面积计算公式。
midas_civil简支梁模型计算
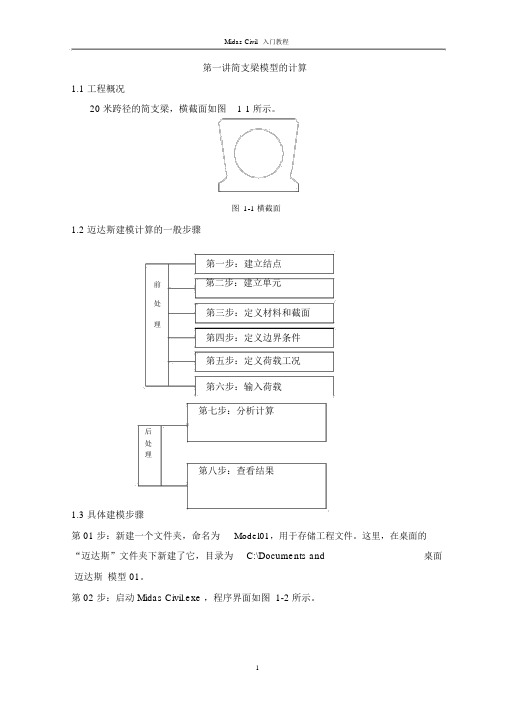
第一讲简支梁模型的计算1.1 工程概况20 米跨径的简支梁,横截面如图1-1 所示。
图1-1 横截面1.2 迈达斯建模计算的一般步骤第一步:建立结点前第二步:建立单元处第三步:定义材料和截面理第四步:定义边界条件第五步:定义荷载工况第六步:输入荷载第七步:分析计算后处理第八步:查看结果1.3 具体建模步骤第 01 步:新建一个文件夹,命名为Model01,用于存储工程文件。
这里,在桌面的“迈达斯”文件夹下新建了它,目录为C:\Documents and桌面迈达斯模型 01。
第 02 步:启动 Midas Civil.exe ,程序界面如图 1-2 所示。
图1-2 程序界面第03 步:选择菜单“文件 (F)->新项目 (N) ”新建一个工程,如图 1-3 所示。
图1-3 新建工程第04 步:选择菜单“文件 (F)->保存 (S) ”,选择目录 C:\Documents and桌面迈达斯模型 01,输入工程名“简支梁 .mcb”。
如图 1-4 所示。
图1-4 保存工程第 05 步:打开工程目录C:\Documents and桌面迈达斯模型01,新建一个 excel 文件,命名为“结点坐标”。
在excel 里面输入结点的x, y, z 坐标值。
如图 1-5 所示。
图1-5 结点数据第06 步:选择树形菜单表格按钮“表格 ->结构表格 ->节点”,将 excel 里面的数据拷贝到节点表格,并“ ctrl+s”保存。
如图 1-6 所示。
图 1-6 建立节点第 07 步:打开工程目录桌面迈达斯模型01,再新建一个 excel 文件,命名为“单元”。
在 excel 里面输入单元结点号。
如图1-6 所示。
图1-6 单元节点第08 步:选择树形菜单表格按钮“表格 ->结构表格 ->单元”,将 excel 里面的数据拷贝到单元表格的“节点1、节点 2”列,并“ ctrl+s”保存。
midas变截面组对称平面距离

中文文章示例:在几何学中,midas变截面组对称平面距离是一个十分有趣的概念。
它涉及了对称几何、平面距离和截面组的深入理解,是几何学中的一个重要概念。
下面我将从简单到复杂,逐步解释这个概念,帮助大家更全面地理解。
1. midas变截面组对称平面距离的含义让我们来了解一下midas变截面组对称平面距离的含义。
在几何学中,midas变是指一种特殊的对称变换,可以将几何图形沿着一条特定的中轴线进行对称。
而截面组是指由若干个平行平面构成的几何图形。
而对称平面距离则是指一个点到其对称平面的距离。
将这三个概念结合起来,midas变截面组对称平面距离即是指在midas变的作用下,截面组中任意一点到其对称平面的距离。
2. midas变截面组对称平面距离的应用midas变截面组对称平面距离在实际应用中具有广泛的意义。
在工程学中,通过对称平面距离的计算可以准确地确定材料的对称性,从而指导工程设计和制造过程。
在现代艺术中,midas变截面组对称平面距离也被广泛应用,艺术家们可以通过对称平面距离的变化来创作出更加富有对称美感的作品。
3. 个人观点和理解对于我个人而言,midas变截面组对称平面距离是一种十分美妙的几何概念。
它不仅具有重要的理论意义,而且在现实生活和艺术创作中也有着丰富的应用。
通过深入理解这个概念,我对几何学的美感有了更深入的体会,也加深了对对称几何的兴趣和研究。
总结随着人们对几何学的深入研究和应用,midas变截面组对称平面距离这一概念必将得到更加广泛的关注和发展。
我深信,通过对这一概念的深入理解和研究,将会为科学技术和艺术创作带来更多的灵感和启发。
以上是关于midas变截面组对称平面距离的一些深入探讨,希望对大家有所启发和帮助。
感谢阅读!midas变截面组对称平面距离是一个非常有趣和复杂的几何概念,它涉及到对称几何、平面距离和截面组的理解,具有重要的理论意义和实际应用价值。
在接下来的内容中,我将对这一概念进行更深入的探讨和应用,并从几何学、工程学和艺术创作的角度来分析和阐述其重要性。
截面几何特性与midas中将荷载转化成质量及收缩徐变计算

在平面弯曲和斜弯曲情形下,横截面与应力平面的交线上各点的正应力值均为零,这条交线称为中性轴。
变形时,横截面将绕中性轴转动。
所有截面中性轴组成的平面称为中性面。
对于平面弯曲,截面的一对形心主轴之一必为某一平面弯曲的中性轴(中心轴只针对纯弯曲而言)。
面的形心就是截面图形的几何中心,质心是针对实物体而言的,而形心是针对抽象几何体而言的,对于密度均匀的实物体,质心和形心重合。
Xc=[∫a(ρxdA)]/ρA=[∫a(xdA)]/A=Sy/A^3表示3次1. 关于截面几何特性与midas 中将荷载转化成质量的研究 毛截面几何特性的计算桥梁中的T 形、工字形截面、箱形截面都可分成许多梯形,设任意梯形如图1所示,上底、下底、高分别为 a 、b 、h ,他的几何特性为:面积:()1A 2a b h =+⨯形心轴位置:()23c b ay h a b +=+对形心轴的惯性矩:()()332436c h a ab b I a b ++=+为了能够清楚理解形心轴、和惯性矩的概念,下面推导一下公式的由来加入有一根简支梁,截面为上述梯形截面材料为钢材或者拉压本构关系(*E σε=)相同的材料(混凝土未开裂前可近似认为此种材料)为了求的这个截面的抗弯承载能力,那么进行截面分析,认为截面符合平截面假设。
截面上受拉区与受压区的边界线为中性轴 为了使截面保持平衡,必须使得受压区合力=受拉区合力h h 0*()c cy y c F dA E x dA σφ--==⎰⎰合力t *()ccy y F dA E x dA σφ--==⎰⎰合力从表达式子可以看出,两者都是面积矩。
就是小面积元对中性轴取矩的求和。
其中*dA dx x =处梯形的宽度。
那么形心轴就是两边对该轴面积矩相等的轴,如果把E φ移到等式左边,右边剩下的就是截面面积矩。
即x dA ⎰那么为了求得该截面的弯矩承载力,那么就得全截面上每小段的合力对中性轴取矩,相当于h h 0**()*c ccy y y M xdA E x xdA σφ---==⎰⎰即2x dA ⎰如果把E φ移到等式左边,那么得h 2c cy c y Mx dA I E φ--==⎰ 从上面可以看出,形心轴和惯性矩的概念了。
迈达斯-截面特性值计算器

。状形面截拟模来面截的式形eniL或面截的式形enalP定 选意任要需据根以可户用中CPS在�状形面截拟模来式形种一ena lP或en iL以能只序程的往以
�
。写缩的”rotaluclaC ytreporP lanoitceS—器算计值性特面截“是CPSΒιβλιοθήκη 明 说 用 使 的 C PS
)rotaluclaC ytreporP lanoitceS( CPS/SADIM
�
。定设行进 gnitteS>slooT 在 者或 � ) g n i t t e S ( 击点里条具工在可等色颜定设、息信型模藏隐/示显、系体位单定设
。算计和模建行进来能功项各出调地便方 很以 可 户 用 � 能 功 的 关 相 算 计 面 截及 模 建 的 C P S 与 有 所 了 供 提 里 单 菜联 关 、 条 具 工 、 单 菜 形 树 在
)rotaluclaC ytreporP lanoitceS( CPS/SADIM
6
。面截的算计行进未和面截的算计面截行进已别区的然了目一以可色颜此过通 。色颜的线的成构所后算计面截成完定指 noitceS detaluclaC 。色颜的分部度厚的线的度厚有定指 :htdiW 。色颜的廓轮外线是的定指线的度厚有于对。色颜的线定指 :lamroN evruC 。色颜的线曲闭封定指 pooL desolC 。色颜景背的口窗作操定指 :dnuorgkcaB 。色颜的体个择选被定指 :ytitnE detceleS weiV � � �
yalpsiD
�
。改更、算换行进的动自而系体位单的定指照按会据数的有所�”)Y(是“ 击点如 ,框话对的下如现出会�系体位单改更果如。系体位单定指里这在 metsyS tinU 。整调的理合行进动自系体位单的定设据根会序程�下况情般一。差误许容定指里这在 ecnareloT
MIDAS截面特性值计算器

问: 在SPC(截面特性值计算器)中DXF文件的应用
答: 步骤如下:
1.先在Tools>Setting中选择相应的单位体系。
如果在CAD中按米画的则选择米。
2. 然后导入DXF
3. 然后在model>curve>intersect中进行交叉计算,以避免在CAD中有没有被分割的线段。
4. 在Section>Generate中定义截面名称。
5. 然后计算特性值。
(也可直接在第4项中计算)
当截面中有内部空心时,可在进行4项后进行下列操作。
a. 在Section>Domain State中选择各部分是否为“空”,当区域中有红色亮显时,按左键为实心,按右键为空心(请看程序中信息窗口的说明提示)。
当截面有不同材料组成时(可超过2种),在进行完上面a操作后,进行下列操作。
b. 在Section>Domain Material中选择各区域材料。
需先定义材料名称和特性值。
在赋予各区域材料特性时,应选择某个材料为基本材料,一般选择混凝土。
在计算不同材料组成的截面的特性值时,应选择相应的单元尺寸。
一般来说划分越细越好,但划分的太细计算时间会很长。
一般在钢骨混凝土中选择钢板厚度的一半即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
看大家对横向力分布系数计算疑惑颇多,特在这里做一期横向力分布系数计算教程(本教程讲的比较粗浅,适用于新手)。
总的来说,横向力分布系数计算归结为两大类(对于新手能够遇到的):1、预制梁(板梁、T梁、箱梁)这一类也可分为简支梁和简支转连续2、现浇梁(主要是箱梁)首先我们来讲一下现浇箱梁(上次lee_2007兄弟问了,所以先讲这个吧)在计算之前,请大家先看一下截面这是一个单箱三室跨径27+34+27米的连续梁,梁高1.55米,桥宽12.95米!!支点采用计算方法为为偏压法(刚性横梁法)mi=P/n±P×e×ai/(∑ai x ai)跨中采用计算方法为修正偏压法(大家注意两者的公式,只不过多了一个β)mi=P/n±P×e×ai×β/(∑ai x ai)β---抗扭修正系数β=1/(1+L^2×G×∑It/(12×E×∑ai^2 Ii)其中:∑It---全截面抗扭惯距Ii ---主梁抗弯惯距 Ii=K Ii` K 为抗弯刚度修正系数,见后L---计算跨径G---剪切模量 G= 旧规范为P---外荷载之合力e---P对桥轴线的偏心距ai--主梁I至桥轴线的距离在计算β值的时候,用到了上次课程我们讲到的计算截面几何性质中的抗弯惯矩和抗扭惯矩,可以采用midas计算抗弯和抗扭,也可以采用桥博计算抗弯,或者采用简化截面计算界面的抗扭,下面就介绍一下这种大箱梁是如何简化截面的:简化后箱梁高度按边肋中线处截面高度(1.55m)计算,悬臂比拟为等厚度板。
①矩形部分(不计中肋):计算公式:It1=4×b^2×h1^2/(2×h/t+b/t1+b/t2)其中:t,t1,t2为各板厚度h,b为板沿中心线长度h为上下板中心线距离It1= 4×(+/2)^2×^2/(2×++=5.454 m4②悬臂部分计算公式: It2=∑Cibiti3其中:ti,bi为单个矩形截面宽度、厚度Ci为矩形截面抗扭刚度系数,按下式计算:Ci=1/3××ti/bi + ×(ti/bi)^5)=1/3××+×^5)=It2=2×××^3=0.0239 m4③截面总的抗扭惯距It= It1+ It2=+=5.4779 m4大家可以用midas计算对比一下看看简化计算和实际能差多少?先计算一下全截面的抗弯和中性轴,下面拆分主梁需要用的到采用<<桥梁博士>>版中的截面设计模块计算全截面抗弯惯距,输出结果如下:<<桥梁博士>>---截面设计系统输出文档文件: D: \27+34+文档描述: 桥梁博士截面设计调试任务标识: 组合截面几何特征任务类型: 截面几何特征计算------------------------------------------------------------ 截面高度: 1.55 m------------------------------------------------------------ 计算结果:基准材料: JTJ023-85: 50号混凝土基准弹性模量: +04 MPa换算面积: 7.37 m2换算惯矩: 2.24 m4中性轴高度: 0.913 m沿截面高度方向 5 点换算静矩(自上而下):主截面:点号: 高度(m): 静矩(m××3):12345------------------------------------------------------------计算成功完成结果:I全= 2.24 m4 中性轴高度H=0.913m下面来讲一下主梁拆分的原则:将截面划分为τ梁和I梁,保持将两截面中性轴与全截面中性轴位置一致。
τ梁和I梁顶板尺寸在两肋间平均划分。
由于中性轴位置不变,可计算底板尺寸,具体尺寸见附件I梁和T梁对于I梁×22×+45×15×+^2/2×40=(2x+40)×20×+20×15×+^2/2×40解的x=49.9cm对于T梁x=785/2-2×=252.7cm采用<<桥梁博士>>版中的截面设计模块计算τ梁和I梁抗弯惯距输出结果如下:I梁:<<桥梁博士>>---截面设计系统输出文档文件: C:\Program Files\DBStudio\DrBridge\Tool\文档描述: 桥梁博士截面设计调试任务标识: 组合构件应力验算任务类型: 截面几何特征计算------------------------------------------------------------ 截面高度: 1.55 m------------------------------------------------------------ 计算结果:基准材料: JTJ023-85: 50号混凝土基准弹性模量: +04 MPa换算面积: 1.43 m**2换算惯矩: 0.446 m**4中性轴高度: 0.897 m沿截面高度方向 5 点换算静矩(自上而下):主截面:点号: 高度(m): 静矩(m**3):12345------------------------------------------------------------ 计算成功完成τ梁:<<桥梁博士>>---截面设计系统输出文档文件: C:\Program Files\DBStudio\DrBridge\Tool\文档描述: 桥梁博士截面设计调试任务标识: 组合构件应力验算任务类型: 截面几何特征计算------------------------------------------------------------ 截面高度: 1.55 m------------------------------------------------------------ 计算结果:基准材料: JTJ023-85: 50号混凝土基准弹性模量: +04 MPa换算面积: 2.31 m**2换算惯矩: 0.713 m**4中性轴高度: 0.908 m沿截面高度方向 5 点换算静矩(自上而下):主截面:点号: 高度(m): 静矩(m**3):12345------------------------------------------------------------计算成功完成算得I型梁 = 0.446 m4 T梁 = 0.713 m4在计算拆分后的I梁或者T梁的抗弯惯矩时,由于结构是多跨连续梁,所以应该考虑抗弯刚度修正系数根据中跨:边跨=34 :27= : 1查《梁桥下册》P204页等截面连续梁等效简支梁刚度修正系数表:跨度比二跨连续梁三跨连续梁四跨连L2 1 边跨L1 中跨L2 边跨L1 中跨L2 边跨L1 中跨L22内插得项目边跨中跨K求取β值中跨:β=1/(1+L^2×G×∑It/(12×E×∑ai^2 Ii)=1/(1+34^2×× E /( 12×E×2×^2×+^2× ×)=边跨:β=1/(1+L^2×G×∑It/(12×E×∑ai^2 Ii)=1/(1+27^2×× E /( 12×E×2×^2×+^2× ×)这样通过上面计算出的结果就可以利用偏压法公式和修正偏压法公式计算横向力分布系数了,在这里就不再多多的描述,大家可以看附件中的word文档,那里面有详细的过程!教程写的有点乱,不知道大家看的怎么样,希望大家有什么问题跟帖,欢迎大家批评指正!!:)下面我们来讲一下预制梁的横向力分布系数计算从上面我能看出常见的预制梁包括板梁、小箱梁、T梁跨中横向力分布系数:对于板梁和小箱梁由于横向联系比较薄弱,所以采用铰接板梁法对于T梁有横隔板比较多,认为是刚接,所以采用刚接板梁法梁端横向力分布系数:通常采用杠杆法下面就讲一下30米简支转连续T梁横向力分布系数计算:主梁横断面见附件桥博计算横向力分布系数计算需要输入的数据见附件包括主梁宽、抗弯、抗扭、左板长、左板惯矩、右板长、右板惯矩、主梁跨度G/E等首先计算主梁的抗弯抗扭惯矩(中梁、边梁断面尺寸见附件,梁高200cm)中梁:===================================================== MIDAS SPC TEXT OUTPUT FILE = = (Tue Jun 17 20:45:16 2008) = = - - =========================================================================================================UNIT: KN . M========================================================================================================* Section-P1 (PLANE)====================================================* A :* Asx :* Asy :* Ixx : 抗弯惯矩* Iyy : 0.* Ixy :* J : 抗扭惯矩----------------------------------------------------* (+)Cx :* (-)Cx :* (+)Cy :* (-)Cy :----------------------------------------------------* (+)1/Sx :* (-)1/Sx :* (+)1/Sy :* (-)1/Sy : 9.====================================================边梁:===================================================== MIDAS SPC TEXT OUTPUT FILE == (Tue Jun 17 20:48:08 2008) == - - =========================================================================================================UNIT: KN . M========================================================================================================* Section-P1 (PLANE)====================================================* A :* Asx :* Asy :* Ixx : 抗弯惯矩* Iyy : 0.* Ixy :* J : 抗扭惯矩----------------------------------------------------* (+)Cx :* (-)Cx :* (+)Cy :* (-)Cy :----------------------------------------------------* (+)1/Sx :* (-)1/Sx :* (+)1/Sy :* (-)1/Sy :====================================================由于结构是多跨连续梁(本文假定是3x30简支转连续T梁),所以应该考虑抗弯刚度修正系数根据中跨:边跨=30 :30= : 1查《梁桥下册》P204页等截面连续梁等效简支梁刚度修正系数表:跨度比二跨连续梁三跨连续梁四跨连续梁L2 1 边跨L1 中跨L2 边跨L1 中跨L2 边跨L1 中跨L22内插得项目边跨中跨K则在计算边跨横向力分布系数,边跨的中梁和边梁的抗弯惯矩需要乘以中梁:边梁:而在计算中跨横向力分布系数,中跨的中梁和边梁的抗弯惯矩需要乘以中梁:边梁:对于计算抗扭惯矩在上次课程中我们给除了箱梁断面的简化计算公式,在这里我也给出T 梁断面的简化计算公式见《公路桥梁荷载横向分布计算》李国豪石洞编第21页,粘贴在附件中,供大家学习!左板惯矩右板惯矩就是等刚度桥面板抗弯惯矩,他是考虑相邻两篇主梁间桥面板的连接作用,其宽度取相邻横梁间距,翼板厚度取靠近主梁梁肋d1/3处的厚度,详细说明请参照《公路桥梁荷载横向分布计算》李国豪石洞编第22页桥面中线距首梁距离:对于杠杆法和刚性横梁法为桥面的中线到首梁的梁位线处的距离;对于刚接板梁法则为桥面中线到首梁左侧悬臂板外端的距离,用于确定各种活载在影响线上移动的位置。
