隧道沉降槽参数
隧道开挖引起的路面沉降预测及数值分析

收稿日期:2009-05-05作者简介:贾晓云(1977-),女,山东菏泽人。
讲师,博士研究生,主要从事隧道衬砌安全度检算与围岩稳定性等方面的教学和科研工作。
E m ai:l jiaxiaoyun @to 。
隧道开挖引起的路面沉降预测及数值分析贾晓云1,2,林宝龙3(1.西南交通大学土木工程学院,成都 610031;2.石家庄铁道学院土木工程分院,石家庄 050043;3.石家庄铁路职业技术学院,石家庄 050041)摘 要:采用Pec k 公式对南水北调中线下穿高速公路段暗涵施工所允许的地表沉降进行预测,确定65mm 为工程允许的地表沉降标准。
提出了双中洞、多分部的暗挖施工方法,并用FLAC-3D 进行数值模拟。
实测表明该法可将路面沉降控制在60mm 以下,能够满足隧道施工安全和环境控制要求。
关键词:南水北调;水工隧洞;暗挖施工;路面沉降;数值分析中图分类号:U 455;P642 26文献标志码:A 文章编号:1003-8825(2010)03-0108-030 引言随着我国交通基础设施的飞速发展,下穿既有建筑物的隧道工程越来越多,如在建的温福铁路的琯头岭隧道、北京地铁天坛东站,以及穿越既有车站的长春南北火车站的南北地下通道等。
下穿高速公路隧洞施工不可避免地会引起地表沉降,高速公路路基及路面不均匀沉降要求严格,若施工控制不当,将造成既有路面不平整度的超限,降低公路的使用功能,严重时还会引起路面结构损伤,造成部分路面功能丧失。
为减少隧道施工对既有高速公路的不良影响,必须对地表沉降变形进行预测及控制。
目前国内外已有较多的关于预测地表沉降的方法,但在下穿高速公路大跨三连拱水工隧洞施工过程中,影响地表沉降的因素很多,任何简单的计算方法均无法反应众多因素的综合影响。
由于数值分析可较为全面地考虑影响地表沉降的各种因素,较为准确地预测隧道施工引起的地表沉降变形。
因此,对大跨水工隧洞施工引起的地表沉降进行数值分析研究具有重要的理论和现实意义。
地铁隧道施工引起沉降槽宽度的影响因素

地铁隧道施工引起沉降槽宽度的影响因素摘要:城市隧道施工引起的地面变形会对环境造成不可避免的负面影响,因此沉降控制是隧道的设计和施工过程中质量管理方面非常重要的一个方面。
在对沉降风险进行控制和管理过程中,沉降槽的宽度又是其中的关键问题之一,它是确定变形影响范围的主要依据。
基于此,本文主要对地铁隧道施工引起沉降槽宽度的影响因素进行分析探讨。
关键词:地铁隧道施工;沉降槽宽度;影响因素1、前言隧道施工引起的地层位移预测与相关风险管理中,地表沉降槽的延伸宽度是一个重要的课题,也是进行沉降预测的主要参数之一。
但是目前一些常见的沉降槽宽度计算公式在很多情况下并不适用,同时国内与国外的应用情况也有很大的差别。
2、沉降槽宽度的影响因素当采用暗挖方法(包括各种盾构法或浅埋暗挖方法等)进行隧道施工时,不可避免地会引起地层的移动,并在地表形成沉降槽。
沉降槽在与隧道走向垂直方向一般呈如图1所示的形态,它的水平延伸范围称为沉降槽宽度。
理论上沉降槽的延伸范围是无限的,但从工程实用的角度,一般将可能对环境或各类结构造成不利影响的距离称为沉降槽宽度。
2.1现有成果的总结与归纳长期以来,很多学者都对沉降槽宽度i的变化规律进行了很多研究,提出了各种不同的计算公式。
在研究者Tan,Ranjith工作的基础上,本文进一步补充了相关的研究成果。
并在此基础上,将上述关于地表沉降槽宽度的公式划分为4类,见表1。
从中可以看出对沉降槽宽度规律的认识发展过程。
(1)第一类公式:i与隧道绝对埋深有关,同时表达式中直接引入了土的强度参数ψ。
即与土层条件直接相关,这符合大多数人的基本概念。
(2)第二类公式:i与相对埋深(即绝对埋深和隧道直径2R之比)之间为幂函数关系;(3)第三类公式:i为绝对埋深和隧道半径的线性函数;(4)第四类公式:i仅仅是隧道绝对埋深的线性函数。
i的表达式从第一类,逐渐演变为第二、第三、第四类公式,有不断简化的趋势。
在北京地区地铁隧道工程的实践当中,需要对上述各类公式的适用性进行探讨。
Peck计算公式

(1)经验公式法
1969年,美国的Peck 在对大量隧道开挖地表沉降的实测数据进行分析的基础上,系统地提出了地层损失的概念和估算隧道开挖地表下沉的实用方法,即著名的Peek 公式[23]。
此后,Peck 本人及其他学者和工程技术人员作了大量工作,使之成为目前应用最为广泛的预计隧道施工地表沉降的方法。
()2max 2exp 2x S x S i ⎛⎫=- ⎪⎝⎭
max 2.52s s V V S i
i π=≈
图8 隧道上部沉降槽断面形状(Peck)
Peck 公式有s V 和i 两个参数,合理确定这两个参数对于正确预测地面沉降的
量值和分布情况起着至关重要的作用,其表达式为:
()
2tan 452i kz ϕπ==︒- 2s l V V R π=
式中:S(x)为距离隧道中心轴线为x 处的地表沉降(mm);S max 为隧道中心线处的地表最大沉降(mm);i 为地表沉降槽宽度系数(m),也即隧道中心至沉降曲线反弯点的距离;k 为沉降槽宽度系数;z 为隧道中心埋深;φ为土体内摩擦角;V s 为施工引起的隧道单位长度的地层损失量(m 3/m),也即隧道施工中实际开挖的岩土体的体积与竣工隧道的体积之差;V l 为地层体积损失率,即单位单位长度地层损失占单位长度盾构体积的百分比;R 为盾构机半径。
传统沉降槽参数及注意事宜

一、从工艺的物料特性及当地的环境考虑:1.由于蒙古地区处于寒冷地带,加上是露天条件,减速机应考虑润滑油容易凝固的问题,不知道投标厂家考虑没有?2.搅拌轴选用问题,不宜因为成本问题而忽视;最好是采用无缝钢管,这样对耙轴的寿命有保障;钢板卷制的有焊缝,容易引起碱脆现象;3.由于底流固含高的原因及底流的影响,在保证耙臂考虑抗弯性能的前提下,不宜采用框架结构(容易引起底流紊乱,对工艺有影响);4.减速机采用形式为传统的蜗轮蜗杆和现在的多点驱动,首要考虑传动的平稳性,这样对减速机的寿命有很大的影响;5.蒙古地区的气温状况,应考虑停机及运行时可能的极端情况,所以还应考虑减速机的输出扭矩比常规设计的安全系数要更大一些;二、耙机装置的部分参数1.φ15×3.5M熟料溶出沉降槽功率考虑2~3KW;转速考虑~0.3r/min;管径采用φ273×14~162.φ22×5M一段脱硅槽功率考虑6KW以上;转速考虑0.25~0.3r/min;管径采用φ273×14~163.φ15×4M二段脱硅槽功率考虑2~3KW;转速考虑~0.3r/min;管径采用φ219×12~144.φ20×6M碳分槽种子沉降槽功率考虑6KW以上;转速考虑0.25~0.3r/min;管径采用φ273×14~165.φ15×3.5M盐沉降槽功率考虑2~3KW;转速考虑~0.3r/min;管径采用φ219×12~146.φ12×5.5m苛化沉降槽功率考虑2~3KW;转速考虑~0.3r/min;管径采用φ219×12~147.φ18×4.5m分离沉降槽功率考虑6KW以上;转速考虑0.25~0.3r/min;管径采用φ273×14~168.φ18×4.5m中和分离沉降槽功率考虑6KW以上;转速考虑0.25~0.3r/min;管径采用φ273×14~16。
最新Peck法计算的盾构隧道地面沉降量及沉陷槽计算公式教学提纲
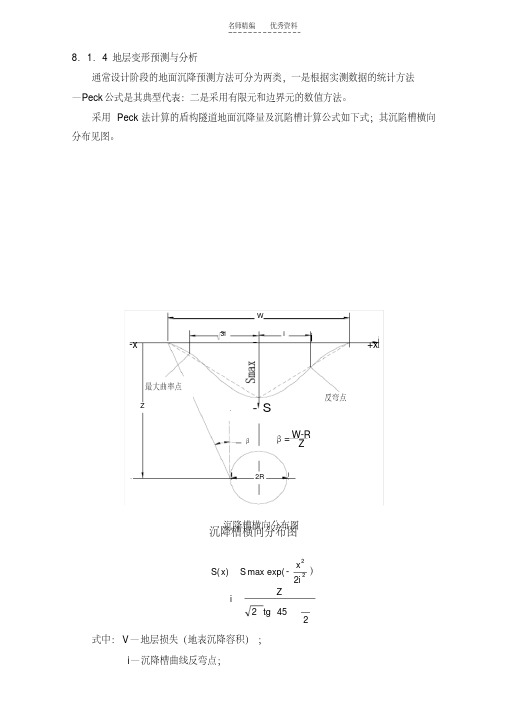
8.1.4 地层变形预测与分析通常设计阶段的地面沉降预测方法可分为两类,一是根据实测数据的统计方法—Peck 公式是其典型代表:二是采用有限元和边界元的数值方法。
采用Peck 法计算的盾构隧道地面沉降量及沉陷槽计算公式如下式;其沉陷槽横向分布见图。
沉降槽横向分布图exp(max )(S x S -222i x )2452tg Z i 式中:V —地层损失(地表沉降容积);i —沉降槽曲线反弯点;W-R β=—— 沉降槽横向分布图i W Z β2R 最大曲率点-x S 3i Z 反弯点+xz—隧道中心埋深根据本标段的地质条件和埋深等,得i=6.9m,由此根据以往的工程实践及经验公式,沉陷槽宽度B≈5i,可得单个隧道盾构推进引起的地表横向沉陷槽宽度约为35m,两座隧道盾构推进引起的地表横向沉陷曲线叠加后其沉陷槽宽度约为50m,并且沉陷槽的主要范围在隧道轴线两侧6m范围内,离轴线3m的沉降量约为最大沉降量的60%~70%,离轴线6m的沉降量约为最大沉降量的25%。
地层损失V值主要是由盾尾空隙引起的土体损失量,它与盾构机盾壳厚度、盾构推进时粘附在盾构上的土体厚度及注浆量等有关,即V=V尾+V粘-V浆盾构推进时粘附在盾构钢板上的土体厚度约为20~40mm,盾壳厚度为70mm,则:V=V尾+V粘-V浆=1.36+0.58α-(1.36+0.58)βα为折减系数,β为同步注浆的充填系数。
取α=0.6 β=0.5 得V=0.73m2由此可得地表最大沉陷值:Smax=23.4mm最大斜率:Qmax=0.0013以上分析值主要是在以往工程经验基础上结合本地铁盾构标段的实际情况,隧道埋深16m左右情况下得出的,最大沉降量满足规范和标书要求。
虽然地表沉降形态是大体相同或相似的,但其最大沉降量总是随着施工工况和地质条件的改变而千差万别,目前控制沉降的主要手段是同步注浆和二次注浆,而注浆的环节常有各种各样的问题发生,如缺量、过量、滞后、漏浆等等,不同的沉降情况常是施工工况和工作状态的反映,同时不同的地质条件沉降亦有所不同,如粉砂土较粘土隆降起量要少,沉降速率要快,淤泥质粘土后期固结沉降则要大点。
盾构隧道沉降分析0730

沉降分析报告1工程概况1.1工程概述本工程为广州地铁3号线北延段龙归~人和区间第一段盾构区间(左线里程ZDK18+015.8~ZDK19+816.092,右线里程YDK18+015.80~YDK19+821.86),盾构机从南端风井始发,向南掘进,经过柏塘桥、北二环高速公路、沙坑涌行至龙归站吊出。
本区间线路最小转弯半径为800m,路线纵向最大坡度为3.5‰,隧道平均埋深8~12m,最大覆土厚度为25.4m1.2地质情况本标段地形主要为农田、果园、鱼塘、厂房、农房以及新修106国道。
隧道洞身主要穿越的地层为粉细砂层<3-1>、中粗砂层<3-2>、冲积~洪积土层<4-1>、岩石全风化带<6>、岩石强风化带<7>、岩石中等风化带<8>,局部有少量硬塑~坚硬状残积土层<5-2>、岩石微风化带<9>。
1.3水文情况(1)地下水位根据地质勘查报告,本标段地下水位埋藏变化比较大,初见水位埋深为0.00~9.50m,平均埋深为2.39m,标高为3.34~15.12m,平均标高为9.24m;稳定水位埋深为0.00~8.50m,平均埋深为2.88m,标高为3.34~15.80m,平均标高为8.86m。
地下水位的变化与地下水的赋存、补给及排泄关系密切,每年5~10月为雨季,大气降雨充沛,水位会明显上升,而在冬季因降水减少,地下水位随之下降。
(2)地下水类型地下水主要赋存在冲积~洪积砂层<3-1>、<3-2>中,根据抽水试验,冲积~洪积砂层水量特别丰富,渗透强。
(3)地下水补给与排泄地下水主要补给为大气降水,部位钻孔受河流影响补给;其排泄主要为大气蒸发,部位钻孔受河流枯竭时向河流排泄影响。
2左线施工沉降概况2.1总体沉降概况本标段隧道施工无重大事故发生,在过北二环高速公路、泥坑涌、品立皮革厂等建(构)筑物时沉降控制良好,保障了建(构)筑物结构安全。
沉降计算和分析

沉降计算和分析1.地面沉降横向分布计算地表沉降横向分布曲线的形状可用Peck[3]公式合理地表达, 这一概念已被人们所接受, 上海地区的许多盾构施工实例也充分证明了它的实际使用效果[4-5]。
Peck 假定施工引起的地面沉降是在不排水情况下发生的, 沉降槽的体积等于地层损失的体积。
地层损失在隧道长度上是均匀分布的,隧道施工产生的地表沉降横向分布近似为一正态分布曲线:式中: S(x)为距离隧道中心线处的地表沉降( m) ;Smax 为隧道中心线处最大地面沉降( m) ; x 为距隧道中心线的距离( m) ; i 为沉降槽宽度系数( m) ;VS 为盾构隧道单位长度地层损失( m3/m) 。
Peck 公式中的VS ( 地层损失) 与盾构种类、操作方法、地层条件、地面环境、施工管理等因素有关, 目前尚难给出确定的解析式。
根据统计,在采用适当技术和良好操作的正常施工条件下,地层损失VS 可表示为:VS=VlπR2 ( 3) 式中: Vl 为地层体积损失率, 即单位长度地层损失占单位长度盾构体积的百分比; R 为盾构机外径( m) 。
沉降槽宽度系数i 决定了盾构施工对周围土体的影响范围, 一般而言, 沉降槽半宽为2.5i。
研究表明, i 取决于接近地表的地层的强度、隧道埋深和隧道半径, 其计算式如下:式中: Z 为地面至隧道中心的深度; Ф为土的内摩擦角。
杭州地铁1 号线隧道外径为6.2 m, 土内摩擦角取为23.2°, 隧道顶部覆土厚度有18.8 m,运用Peck 公式计算可得沉降槽半宽W/2=33.0 m,计算结果见表1, 地面沉降横向分布见图1。
2. 地面沉降纵向分布计算刘建航[6]院士在Peck 法的基础上, 提出了负地层损失概念, 并将地层损失分成开挖面和盾尾后的地层损失两部分, 得出了地面沉降量的纵向分布预测公式:式中: S(y)为距原点距离y 的地面沉降量, 负值为隆起量, 正值为沉降量( m) ; Vl1为盾构开挖面引起的地层损失, 欠挖时为负值( m3/m) ; Vl2为盾构开挖后, 以盾尾空隙压浆不足及盾构改变推进方向为主的所有施工因素引起的地层损失( m3/m) ;y 为沉降点至坐标原点的距离( m) ; yi 为盾构推进点处盾构开挖面至坐标原点的距离, yf 为盾构开挖面至坐标原点距离( m) :yi′=yi- L; yf′=yf – LL 为盾构长度( m) ; Φ( y) 为正态分布函数的积分形式。
透水条件的地铁隧道长期沉降数值计算

广东省江门市初三上学期期末物理试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2019九上·哈尔滨期中) 我国将停止销售40W和60W等种类的白炽灯,而改用节能的荧光灯、LED灯等“能效比”更高的节能灯.改用节能灯的原因是()A . 相同功率的白炽灯和节能灯使用相同的时间,白炽灯消耗的电能多B . 相同功率的白炽灯和节能灯使用相同的时间,白炽灯消耗的电能少C . 相同功率的白炽灯和节能灯消耗相同的电能,节能灯发出的光更亮D . 相同功率的白炽灯和节能灯消耗相同的电能,节能灯发出的光更暗2. (2分)(2012·扬州) 下列现象中,能说明分子在做无规则运动的是()A . 春天柳枝摇曳B . 夏天荷花飘香C . 秋天落叶纷飞D . 冬天瑞雪飘飘3. (2分) (2018九上·河源月考) 如图所示实验,玻璃瓶口的胶塞从瓶口冲出时()A . 玻璃瓶内和瓶口出现的白雾是小水珠B . 胶塞冲出前,气筒需要不断从瓶内抽气C . 胶塞从瓶口冲出瞬间,瓶内水蒸气温度升高D . 胶塞从瓶口冲出过程的能量转化情况与内燃机的压缩冲程相同4. (2分)电磁炉利用高频电流在电磁炉内部线圈产生磁场,磁化铁质铁锅从而形成无数个小涡流(即电流),加速锅底分子运动使锅底自身发热达到加热食物的目的,它具有安全可靠,节能环保等优点,下列正确的是()A . 它在使用中利用了电流的磁效应和化学效应B . 它在使用过程中会产生烟尘和废气C . 加热食物时把电能转化为内能D . 铁、铝、铜锅均可在电磁炉上使用5. (2分)下列关于能源和能量说法中正确的是()A . 汽车散失的热量不能收集起来再次开动汽车,说明能量的转化或转移具有方向性B . 核电站是利用核裂变释放的能量发电,核能是可再生的一次能源C . 加油机给受油机加油的过程中一起水平匀速飞行,受油机的动能不变D . 小孩从滑梯上滑下,感觉臀部很热,他的动能增大,重力势能减少,机械能不变6. (2分)有甲、乙、丙三个轻质小球,甲球带正电,将甲与乙、丙靠近时,它们相互作用的情况如图所示,则下列判断正确的是()A . 乙球一定带负电,丙球可能带正电B . 乙球一定不带电,丙球可能带负电C . 乙球可能带负电,丙球一定带正电D . 乙球可能不带电,丙球一定带负电7. (2分)用蓄电池给用电器供电, 电流强度为5 安时, 电流可持续流动150 秒, 若将电流改为2 安, 则电流可持续流动()A . 150秒;B . 300秒;C . 375秒;D . 425秒8. (2分)给你两根长度相同但横截面积不同的镍铬合金线、一个电源、一只电流表、一只滑动变阻器、一个开关、若干根导线,现需要研究的课题有:(1)导体的电阻跟它的横截面积的关系;(2)导体的电阻跟它的长度的关系;(3)导体的电阻跟它的材料关系。
Peck公式

Peck 公式1969年,Peck在分析了大量地表沉降数据后,提出了地表沉降槽符合高斯分布的概念。
他认为地层变形由地层损失引起,施工引起的地面沉降是在不排水的条件下发生的,从而假定地表沉降槽体积等于地层损失体积。
如今这个公式在世界上广泛应用,成为预估沉降槽的经典公式。
s为地面任一点的沉降值,单位为mm;s为地面沉降的最大值,位于沉降曲线的对称中心上(对应于隧洞轴线位置),单位为mm;m axx为从沉降曲线中心到所计算点的距离,单位为m;i为从沉降曲线对称中心到曲线拐点(反弯点)的距离,一般称为“沉降槽宽度”,单位为m;i3通过对正态分布函数二次求导,令其等于0求得;m/3;V为隧道单位长度地层损失,单位为mV为地层体积损失率,即单位长度地层损失占单位长度盾构体积的百分比;这个参数的取值依赖地方经验。
l其中,i一般由查图表或者经验公式得来,以下列举了一些关于沉降槽宽度系数i的公式(一)Peck通过对大量地表沉降数据和有关工程资料的分析后,得出i为沉降槽宽度系数,单位为m;Z为隧道深度,单位为m;β为隧道周围地层内摩擦角(二)O’Reilly和New提出一种简便的定义i值的方法,即i和隧道深度Z之间存在以下简单的线性关系i为沉降槽宽度系数,单位为m;K为沉降槽宽度参数,这要取决于土性;Z为隧道深度,单位为mClou gh和Schimidt在其关于软黏土隧道的着作中,提出饱和含水塑性粘土中的地面沉降槽宽度系数i由如下公式求得i为沉降槽宽度系数,单位为m;R为隧道半径,单位为m;Z为隧道深度,单位为m(四)Attwell假定沉降槽曲线正态分布,给出估算地表沉降的经验公式i为沉降槽宽度系数,单位为m;R为隧道半径,单位为m;Z为隧道深度,单位为mK和z为统计系数(五)藤田收集了大量的,涉及多种盾构形式的统计资料后,给出以下公式i为沉降槽宽度系数,单位为m;R为隧道半径,单位为m;s为地面沉降的最大值,单位为mm;m axA为沉降槽断面积,单位为2m;mA为隧道断面积,单位为2。
北京地铁隧道地表横向沉降槽参数分析

引用格式:吴锋波,金淮,杨歧焱,等.北京地铁隧道地表横向沉降槽参数分析[J].隧道建设(中英文),2020,40(5):660.WU Fengbo,JIN Huai,YANG Qiyan,et al.Analysis of ground transverse settlement groove parameters of Beijing Metro tunnel[J].Tunnel Construction,2020,40(5):660.收稿日期:2019-12-24;修回日期:2020-03-27基金项目:河北省青年拔尖人才项目资助;河北地质大学博士科研启动基金(BQ2017024)第一作者简介:吴锋波(1982 ),男,河北邢台人,2011年毕业于中国科学院地质与地球物理研究所,地质工程专业,博士,高级工程师,现从事岩土工程风险评估㊁监测方面的研究工作㊂E-mail:wufengbo820424@㊂北京地铁隧道地表横向沉降槽参数分析吴锋波1,金㊀淮2,杨歧焱1,郑卫强1(1.河北地质大学勘查技术与工程学院,河北石家庄㊀050031;2.北京市轨道交通设计研究院有限公司,北京㊀100068)摘要:为解决北京地铁隧道施工不同影响区划分和影响范围确定的不准确问题,对北京地区13条地铁线路㊁903份隧道工程的地表横向沉降槽资料进行分析,根据施工方法和地层条件的不同,分别对盾构法和矿山法施工隧道在黏性土地层㊁砂卵石地层等区域的沉降槽Peck 公式拟合参数进行统计分析,得出地层损失率和宽度参数的分布形态㊁相关统计值以及与隧道相对埋深的相关性㊂研究结果表明:1)地层损失率和宽度参数的数理统计结果可以很好地指导北京及类似地层条件的城市地铁隧道工程影响区划分和影响范围的确定;2)施工方法和地层条件是影响地铁隧道周围地层变形的重要因素,工程地表变形控制应注重相关研究;3)建议各地深入开展地铁隧道沉降槽的拟合分析研究,为隧道工程影响区划分和影响范围确定提供科学依据㊂关键词:地铁隧道;地表横向变形;沉降槽;预测参数DOI :10.3973/j.issn.2096-4498.2020.05.007文章编号:2096-4498(2020)05-0660-12中图分类号:U 45㊀㊀㊀㊀㊀文献标志码:A开放科学(资源服务)标识码(OSID ):Analysis of Ground Transverse Settlement Groove Parametersof Beijing Metro TunnelWU Fengbo 1,JIN Huai 2,YANG Qiyan 1,ZHENG Weiqiang 1(1.School of Prospecting Technology &Engineering ,Hebei GEO University ,Shijiazhuang 050031,Hebei ,China ;2.Beijing Rail and Transit Design &Research Institute Co.,Ltd.,Beijing 100068,China )Abstract :The construction influence zone of Beijing metro tunnel and the influence range are difficult to be distributed.As a result,the ground transverse settlement groove data of 903tunnel projects of 13metro lines in Beijing area are analyzed.The fitting parameters of Peck formula of settlement groove of clay stratum and sandy-cobble strata induced byshield tunneling and mining excavation are statistically analyzed,and the distribution shape,related statistics and correlation with tunnel buried depth of ground loss rate and width parameter are obtained.The research results showthat:(1)The mathematical statistical results of ground loss rate and width parameter can guide the division of metro tunnel influence zone and determination of influence range in Beijing and other cities with similar ground conditions.(2)The construction method and stratum conditions are the important factors affecting the stratum deformation around the metro tunnel,and the relevant researches should be paid attention to in surface deformation control.(3)It is suggested to carry out in-depth analysis and research on the fitting of settlement groove in various regions,so as toprovide scientific reference for the division and determination of metro tunnel influence zone.Keywords :metro tunnel;ground transverse deformation;settlement groove;prediction parameter0㊀引言伴随着我国城市地铁建设的迅猛发展,北京地铁已进入了网络化运营时代,大量新工程仍在积极建设中㊂地铁隧道工程建设一般采用矿山法或盾构法施㊀第5期吴锋波,等:㊀北京地铁隧道地表横向沉降槽参数分析㊀工,其引发地层位移和上方地表的纵横向变形,横向形成 沉降槽 ㊂地表沉降槽的研究方法主要包括经验公式法㊁解析计算法㊁模型试验法和数值模拟法等[1-7],经验公式法是研究隧道开挖引起地表沉降的重要方法之一㊂Peck公式是预测隧道施工引发地表变形的重要经验公式[8],具有模型简单㊁实用有效的特点,可以很好地指导施工㊂由于不同地区地质条件差异较大,经验公式具有一定的地区性[9]㊂M.P.O Reilly 等[10]统计了不同地层中盾构隧道的地层损失率取值范围;R.J.Mair等[11]给出了英国不同地层㊁不同开挖方法下隧道的地层损失率数值;S.Suwansawat 等[12]研究了双线隧道开挖土体损失率与沉降槽宽度的取值㊂GB50911 2013‘城市轨道交通工程监测技术规范“将Peck公式作为土质隧道影响分区的重要依据,规定其影响范围一般包括主要影响区和次要影响区,主要影响区为隧道正上方及沉降曲线反弯点范围内,次要影响区为隧道沉降曲线反弯点至沉降曲线边缘2.5i处(i为沉降槽宽度)[13]㊂各地针对地铁隧道地表沉降槽的预测参数开展了相关研究,多基于一定数量的实测数据对Peck公式的相关参数进行拟合分析㊂魏纲[14]统计分析了我国71个盾构法隧道的土体损失率实测值;郭玉海[15]拟合得出了北京地铁14号线大直径土压平衡盾构的沉降槽参数;陈春来等[16]研究了双线水平平行盾构隧道施工中的土体损失;王鹏等[17]㊁段绍伟等[18]㊁蒋彪等[19]㊁麻凤海等[20]分别研究了武汉㊁长沙㊁长春等地的地铁隧道沉降槽参数;朱才辉等[21-22]整体分析了我国地铁沉降槽相关参数的变化规律;吴昌胜等[23]研究了我国不同直径盾构隧道的地层损失率情况;吴红博等[24]㊁丁智等[25]研究了双线地铁盾构隧道的地层变形特征及土体损失率取值㊂相关研究取得了一定的成果,然而由于基础数据有限,沉降槽参数的统计分析结果在新建隧道工程地表变形预测方面有一定的局限性,不能准确地确定隧道工程的不同影响区域和影响范围㊂本文基于北京地铁丰富的沉降槽资料,针对某一城市开展全面㊁系统的沉降槽拟合参数的数理统计分析研究,相关成果可以很好地揭示其横向沉降槽的变形特性,以期为今后该地区或类似地层城市中隧道工程影响区域划分㊁影响范围确定等提供参考㊂1㊀Peck公式及相关预测参数1969年美国R.B.Peck[8]借鉴采矿学中地面沉降位移的估算方法,在总结大量实测资料的基础上,提出地层损失的概念和估算隧道开挖地表沉降的方法 Peck公式,沉降槽横断面曲线图见图1㊂假定地层损失在整个隧道长度上均匀分布,隧道施工所产生的地表沉降横向分布近似为正态分布,则地表沉降公式为:S(x)=S max exp(-x22i2);(1)S max=V l2π㊃iʈV l2.5㊃i㊂(2)式(1) (2)中:S(x)为隧道两侧横向上距隧道中心x 处的地面沉降量,m;S max为隧道中心处的最大沉降量, m;x为隧道两侧横向上距隧道中心的距离,m;i为沉降槽宽度,曲线反弯点距隧道中心的距离,m;V l为隧道单位长度的地层损失,m3/m㊂其中:i=H+R2π㊃tan45ʎ-φ2()=Z02π㊃tan45ʎ-φ2()㊂(3)式中:H为隧道覆土厚度,m;R为隧道计算半径,m; Z0为隧道中心埋深,m;φ为隧道周围地层内摩擦角, (ʎ)㊂地面沉降槽总宽度Wʈ2.5i㊂图1㊀沉降槽横断面曲线图Fig.1㊀Cross-section curve of settlement groove㊀㊀根据隧道工程地表横向变形形态和Peck公式可以看出,隧道地表横向变形数值与地层损失率V l㊁沉降槽宽度i密切相关㊂已有研究表明,隧道地表沉降槽地层损失率V l决定了沉降量的大小,沉降槽宽度i 决定了沉降槽曲线的形状(如宽而浅或窄而深)㊂为更简单地描述沉降槽宽度,一般取沉降槽宽度系数k= i/Z0[9]㊂以Peck公式为基础,对统计的实测数据进行线性回归,具体拟合方法见文献[26],典型工程拟合结果见图2㊂166隧道建设(中英文)第40卷㊀图2㊀典型工程拟合结果(5号线某车站)Fig.2㊀Typical fitting results(a station on Line5)㊀㊀本文主要选取地表沉降槽的最大沉降值拟合参数作为统计分析的基础数据,以合理预测隧道工程地表的最大变形和影响范围㊂2㊀资料收集及分析本研究采用监测单位资料收集㊁期刊文献整理摘录㊁相关书籍资料摘录等方式对我国北京地区地铁隧道工程地表横向变形资料进行全面㊁系统的收集,共收集到约13条地铁线路㊁903份隧道工程地表横向沉降槽资料㊂具体资料收集结果见表1和图3 (图3中地铁线路加粗部分为资料包含的车站和区间)㊂表1㊀沉降槽资料收集情况Table1㊀Data collection of settlement groove㊀㊀线路名称地表监测断面数量/个北京地铁4号线25北京地铁5号线68北京地铁6号线19北京地铁7号线56北京地铁8号线8北京地铁9号线18北京地铁10号线251北京地铁13号线8北京地铁14号线412北京地铁15号线12北京地铁亦庄线20北京地铁机场线3北京地铁复兴门折返线3总计903㊀注:主要参考文献[27-33]㊂图3㊀沉降槽资料范围示意图Fig.3㊀Scope diagram of settlement groove data㊀㊀根据地铁隧道工程建设特点,将其分为车站㊁标准断面双线区间㊁大断面单线区间分别进行研究㊂双线区间隧道一般为左右线2条标准断面隧道,断面为马蹄形或圆形,直径在6m左右㊂单线区间一般为大断面隧道,直径在10m及以上㊂根据隧道施工方法,分为盾构法和矿山法2类进行研究㊂根据北京地区地层特点,将隧道穿越地层分为黏性土地层(粉土㊁黏性土为主,一般位于城市中东部)和砂卵石地层(砂土㊁圆砾㊁卵石为主,一般位于城市中西部)2类进行研究[34-38]㊂3㊀地铁车站地表横向变形特性北京地铁车站的修建方法主要为矿山法,车站开挖区域内的地层主要为黏性土地层和砂卵石地层㊂3.1㊀沉降槽最大沉降值地表沉降槽的最大沉降值统计结果见图4㊂㊀㊀由统计结果可知:黏性土地层开挖的63个地表沉降槽中沉降最大值为166.60mm,最小值为16.27 mm,平均值为79.57mm,标准差为39.28mm;最大沉降值分布形态近似为正态分布(图4中拟合曲线为正态分布曲线,下同),其主要分布在40~60mm 区段;偏态系数SK=0.505,为中等右偏分布;峰态系数K=-0.665,为扁平分布㊂砂卵石地层开挖的32个地表沉降槽中沉降最大值为148.14mm,最小值为11.84mm,平均值为61.01 mm,标准差为34.45mm;分布形态近似为正态分布,最大沉降值主要分布在20~60mm;偏态系数SK= 0.530,为中等右偏分布;峰态系数K=-0.354,为扁平分布㊂266㊀第5期吴锋波,等:㊀北京地铁隧道地表横向沉降槽参数分析㊀(a)黏性土地层(b)砂卵石地层图4㊀最大沉降值分布频率直方图Fig.4㊀Frequency histogram of maximum settlement distribution ㊀㊀地铁车站开挖断面较大,埋深一般较浅,受地层条件影响较大,同时,对车站上方城市道路交通㊁地下管线也有一定影响,供水㊁雨污水等地下管线的渗漏引发的地层空洞致使车站上方地表变形不易控制㊂由于大粒径卵石的自稳性相对较好,砂卵石地层变形相对小一些㊂矿山法车站施工应注意地层条件和环境条件的影响,加强对地层变形的控制㊂3.2㊀地层损失率地表沉降槽的地层损失率统计结果见图5㊂由统计结果可知:剔除5个拟合异常值后,黏性土地层开挖的32个地表沉降槽中地层损失率数值最大值为6.90%,最小值为0.40%,平均值为1.85%,标准差为1.92%,中位数为1.00%;其分布形态近似为半正态分布,数值主要分布在0%~1.5%,约占总数量的78.1%㊂砂卵石地层开挖的26个地表沉降槽中地层损失率数值最大值为3.75%,最小值为0.40%,平均值为1.41%,标准差为0.88%,中位数为1.35%;分布形态近似为正态分布,数值主要分布在1.0%~1.5%,约占总数量的50.0%;偏态系数SK=1.712,为高度右偏分布;峰态系数K=2.172,为尖峰分布;砂卵石地层具有一定的自稳性,对地层变形影响较大,隧道开挖的地层损失率数值相对较小㊂(a)黏性土地层(b)砂卵石地层图5㊀地层损失率分布频率直方图Fig.5㊀Frequency histogram of ground loss rate distribution 3.3㊀宽度参数地表沉降槽的宽度参数统计结果见图6㊂(a)黏性土地层(b)砂卵石地层图6㊀宽度参数分布频率直方图Fig.6㊀Frequency histogram of width parameter distribution366隧道建设(中英文)第40卷㊀㊀㊀由统计结果可知:黏性土地层中开挖的58个地表沉降槽宽度参数最大值为1.18,最小值为0.22,平均值为0.58,标准差为0.24,中位数为0.54;近似为正态分布,主要分布在0.3~0.4;偏态系数SK=0.648,为中等右偏分布;峰态系数K=-0.463,为扁平分布㊂砂卵石地层中开挖的30个地表沉降槽宽度参数最大值为1.00,最小值为0.46,平均值为0.67,标准差为0.14,中位数为0.63;近似为正态分布,数值主要分布在0.6~0.7;偏态系数SK=1.175,为高度右偏分布;峰态系数K=0.826,为尖峰分布㊂3.4㊀相关性分析地层损失率和宽度参数与隧道相对埋深(隧道中心轴线埋深/隧道直径或等效直径,下同)的相关性统计结果见图7㊂㊀㊀㊀(a)地层损失率(黏性土)(b)宽度参数(黏性土)㊀㊀㊀(c)地层损失率(砂卵石)(d)宽度参数(砂卵石)图7㊀相关性分布图Fig.7㊀Relevance distribution㊀㊀由统计结果可知:隧道相对埋深的数值范围主要为0.6~1.3,黏性土地区沉降槽的地层损失率与宽度参数㊁砂卵石地区沉降槽的地层损失率等分布相对分散,随着隧道相对埋深的增加,没有明显的对应关系;砂卵石地区沉降槽的宽度参数随着该量纲一的量数值的增加近似有线性减小的趋势㊂4㊀双线区间地表横向变形特性北京地铁标准断面双线区间的修建方法主要为盾构法和矿山法,根据区间隧道开挖区域内的地层性质不同进行统计㊂双线隧道的沉降槽形态主要为双峰值型,沉降最大值一般出现在左右两隧道的中心轴线上方附近㊂左右线中心间距较大㊁2个沉降槽的形态较为完整时,分别进行拟合研究;左右线中心间距较小㊁2个沉降槽的形态不完整时,重点对变形值较大的沉降槽进行拟合研究㊂4.1㊀盾构法施工隧道4.1.1㊀沉降槽最大沉降值地表沉降槽的最大沉降值统计结果见图8㊂由统计结果可知,剔除由于涌水涌沙造成的3个地面沉降异常值,黏性土地层中盾构开挖的54个地表沉降槽中沉降最大值为32.60mm,最小值为2.61mm,平均值为11.39mm,标准差为6.62mm;近似为正态分布,主要分布在8~10mm;偏态系数SK=1.245,为高度右偏分布;峰态系数K=1.552,为尖峰分布㊂砂卵石地层中盾构法隧道的变形控制效果较好,19个地表沉降槽中沉降最大值为20.81mm,最小值为2.99mm,平均值为8.60mm,标准差为4.58mm;分布形态为多峰值分布,主要分布在4~6mm和10~12mm㊂466㊀第5期吴锋波,等:㊀北京地铁隧道地表横向沉降槽参数分析㊀(a)黏性土地层(b)砂卵石地层图8㊀最大沉降值分布频率直方图Fig.8㊀Frequency histogram of maximum settlement distribution4.1.2㊀地层损失率地表沉降槽的地层损失率统计结果见图9㊂(a)黏性土地层(b)砂卵石地层图9㊀地层损失率分布频率直方图Fig.9㊀Frequency histogram of ground loss rate distribution㊀㊀剔除7个拟合异常值后,黏性土地层盾构开挖的46个地表沉降槽中地层损失率最大值为8.40%,最小值为0.24%,平均值为3.80%,标准差为2.54%,中位数为3.73%;近似为多峰值分布,主要分布在0%~1%和3%~4%㊂剔除5号线试验段的2个异常值后,砂卵石地层中盾构开挖的18个地表沉降槽地层损失率最大值为8.86%,最小值为0.51%,平均值为3.78%,标准差为2.28%,中位数为3.25%;近似为正态分布,主要分布在3%~4%;偏态系数SK =0.699,为中等右偏分布;峰态系数K =-0.158,为扁平分布㊂双线盾构隧道施工过程中,先行隧道对周围地层具有扰动作用;后行隧道施工对周围地层形成二次扰动,造成地层损失率有一定的增加,出现了一些相对较大的数值,对地层损失率的整体分布形态有较大的影响㊂双线隧道的二次扰动效应与隧道埋深㊁隧道水平间距㊁地层特性㊁盾构施工参数(排土量和注浆压力等)等因素密切相关,施工过程中应予以重视,需深入开展相关研究㊂4.1.3㊀宽度参数地表沉降槽的宽度参数统计结果见图10㊂(a)黏性土地层(b)砂卵石地层图10㊀宽度参数分布频率直方图Fig.10㊀Frequency histogram of width parameter distribution㊀㊀黏性土地层中盾构开挖的57个地表沉降槽宽度参数最大值为0.98,最小值为0.26,平均值为0.53,标准差为0.21,中位数为0.48;近似为正态分布,主要分布在0.3~0.4;偏态系数SK =0.880,为中等右偏分566隧道建设(中英文)第40卷㊀布;峰态系数K=-0.323,为扁平分布㊂砂卵石地层中18个地表沉降槽宽度参数最大值为1.14,最小值为0.22,平均值为0.66,标准差为0.29,中位数为0.67;近似为多峰值分布,主要分布在0.4~0.5和0.6~0.7㊂4.1.4㊀相关性分析地层损失率和宽度参数与隧道相对埋深的相关性统计结果见图11㊂㊀㊀㊀(a)地层损失率(黏性土)(b)宽度参数(黏性土)㊀㊀㊀(c)地层损失率(砂卵石)(d)宽度参数(砂卵石)图11㊀相关性分布图Fig.11㊀Relevance distribution㊀㊀黏性土地区隧道相对埋深的数值范围主要为1.5~3.8,沉降槽的地层损失率随着该量纲一的量参数的增大有近似减小的趋势,近似呈负乘幂的变化趋势;宽度参数随着该量纲一的量参数的增大没有明显的变化趋势㊂砂卵石地区隧道相对埋深的数值范围主要为0.9~4.3,沉降槽的地层损失率随着该量纲一的量参数的增大有近似减小的趋势,近似呈负指数的变化趋势;宽度参数随着该参数的增大有逐渐减小然后增大的趋势,近似为二次多项式的变化趋势㊂4.2㊀矿山法施工隧道4.2.1㊀沉降槽最大沉降值地表沉降槽的最大沉降值统计结果见图12㊂㊀㊀剔除最终地表变形为单沉降槽的数值后,黏性土地层中矿山法开挖的59个地表沉降槽沉降最大值为43.00mm,最小值为4.87mm,平均值为24.55mm,标准差为9.70mm;近似为正态分布,主要分布在20~25 mm;偏态系数SK=-0.170,为左偏分布;峰态系数K=-0.513,为扁平分布㊂区间隧道局部为黏性土㊁砂土互层,存在潜水或承压水时,造成地表变形较大㊂(a)黏性土地层(b)砂卵石地层图12㊀最大沉降值分布频率直方图Fig.12㊀Frequency histogram of maximum settlement distribution666㊀第5期吴锋波,等:㊀北京地铁隧道地表横向沉降槽参数分析㊀㊀㊀砂卵石地层中58个地表沉降槽沉降最大值为32.69mm,最小值为1.69mm,平均值为15.49mm,标准差为7.86mm;近似为正态分布,主要分布在20~25mm;偏态系数SK =0.079,峰态系数K =-0.788,为扁平分布㊂4.2.2㊀地层损失率地表沉降槽的地层损失率统计结果见图13㊂(a)黏性土地层(b)砂卵石地层图13㊀地层损失率分布频率直方图Fig.13㊀Frequency histogram of ground loss rate distribution㊀㊀剔除拟合异常值后,黏性土地层47个地表沉降槽的地层损失率最大值为9.80%,最小值为0.90%,平均值为2.56%,标准差为2.17%,中位数为1.70%;近似为半正态分布,主要分布在1.0%~1.5%,约占总数量的34.05%㊂砂卵石地层48个地表沉降槽中地层损失率最大值为9.96%,最小值为0.25%,平均值为2.66%,标准差为2.54%,中位数为1.53%;近似为正态分布,主要分布在1.0%~2.0%,约占总数量的29.17%㊂黏性土与砂土的互层结构容易导致地表的较大变形,卵石地层可造成管棚施作困难㊁小导管注浆效果不良㊁注浆压力上不去等问题㊂地层存在空洞㊁上层滞水㊁地下管线渗漏等对地层变形控制也有很大影响㊂城市地层条件㊁环境条件对矿山法地表变形影响较大,同时,矿山法施工隧道也有一定的地层二次扰动效应问题㊂4.2.3㊀宽度参数地表沉降槽的宽度参数统计结果见图14㊂(a)黏性土地层(b)砂卵石地层图14㊀宽度参数分布频率直方图Fig.14㊀Frequency histogram of width parameter distribution㊀㊀剔除拟合异常值后,黏性土地层中55个地表沉降槽的宽度参数最大值为1.16,最小值为0.23,平均值为0.49,标准差为0.21,中位数为0.43;近似为正态分布,主要分布在0.3~0.4;偏态系数SK =1.380,为高度右偏分布;峰态系数K =1.643,为尖峰分布㊂砂卵石地层中69个地表沉降槽的宽度参数最大值为1.18,最小值为0.12,平均值为0.62,标准差为0.27,中位数为0.57;近似为多峰值分布,主要分布在0.4~0.5和0.8~0.9㊂4.2.4㊀相关性分析地层损失率和宽度参数与隧道相对埋深的相关性统计结果见图15㊂黏性土地区隧道相对埋深的数值范围主要为1.2~4.3,该区段内地层损失率和宽度参数随着该参数的增大有逐渐减小然后增大的趋势,近似为二次多项式的变化趋势㊂砂卵石地区隧道相对埋深的数值范围主要为1.2~3.3,该区段内地层损失率和宽度参数随着该参数的增大没有明显的变化趋势㊂5㊀单线区间地表横向变形特性北京地铁大断面单线区间的修建方法主要为盾构766隧道建设(中英文)第40卷㊀法和矿山法,单线隧道的沉降槽形态为单峰值型,沉降最大值一般出现在隧道的中心轴线上方附近㊂根据区间隧道开挖区域内的地层性质不同分别进行统计,统计结果见表2㊂㊀㊀㊀(a)地层损失率(黏性土)(b)宽度参数(黏性土)㊀㊀㊀(c)地层损失率(砂卵石)(d)宽度参数(砂卵石)图15㊀相关性分布图Fig.15㊀Relevance distribution表2㊀单线区间沉降槽参数统计Table2㊀Settlement groove parameter statistics of single-track section㊀㊀参数施工方法主要地层样本数量/个最大值最小值平均值标准差最大沉降值/mm 盾构法矿山法黏性土2636.1012.0021.51 5.71黏性土1456.608.4322.6714.16砂卵石942.7015.3327.8410.54地层损失率/%盾构法矿山法黏性土45 5.370.100.90 1.22黏性土67.34 1.68 3.51 2.24砂卵石78.59 4.90 6.90 1.16宽度参数盾构法矿山法黏性土450.480.180.300.07黏性土140.740.230.480.15砂卵石90.860.370.620.13㊀㊀由统计结果可知,北京地铁单线区间隧道的地表变形与施工方法和开挖地层密切相关,黏性土地层中采用盾构法施工的最大沉降值相对较小,平均值为21.51mm,地层损失率和宽度参数的平均值也较小㊂采用矿山法施工时,黏性土地层中隧道开挖可引起相对较大的地表沉降㊂受样本数量的影响,黏性土地层的地表沉降槽最大沉降值㊁地层损失率和宽度参数的平均值相对较小,但其标准差较大,整体数值分布较为离散㊂砂卵石地层较好的自稳性对减小矿山法施工对周围地层的扰动有一定的作用㊂6㊀结论与讨论1)根据隧道功能㊁地层性质㊁施工方法等分类研究了北京地铁隧道地表沉降槽的最大沉降值㊁地层损失率和宽度参数的分布形态,给出了相关统计结果及与隧道相对埋深的相关性㊂相关成果有助于北京地区或类似地层中地铁隧道工程的影响区㊁影响范围等的科学确定㊂866㊀第5期吴锋波,等:㊀北京地铁隧道地表横向沉降槽参数分析㊀统计结果表明,矿山法车站在黏性土地层中的地层损失率平均值为1.85%,标准差为1.92%,宽度参数平均值为0.58,标准差为0.24;砂卵石地层中的地层损失率平均值为1.41%,标准差为0.88%,宽度参数平均值为0.67,标准差为0.14㊂双线盾构法区间在黏性土地层中的地层损失率平均值为3.80%,标准差为2.54%,宽度参数平均值为0.53,标准差为0.21;砂卵石地层中的地层损失率平均值为3.78%,标准差为2.28%,宽度参数平均值为0.66,标准差为0.29㊂双线矿山法区间在黏性土地层中的地层损失率平均值为2.56%,标准差为2.17%,宽度参数平均值为0.49,标准差为0.21;砂卵石地层中的地层损失率平均值2.66%,标准差为2.54%,宽度参数平均值为0.62,标准差为0.27㊂2)城市地铁隧道施工引起的地表变形受城市环境条件㊁地层性质㊁施工方法㊁隧道埋深㊁隧道断面尺寸㊁双线水平间距等因素影响,应深入开展相关影响因素的研究㊂3)随着我国城市地铁建设的不断开展,各地积累了大量的隧道工程地表变形资料,有必要对地表横向变形特性进行深入研究,以针对不同的城市地质条件提出适宜的地表横向沉降槽预测参数㊂参考文献(References):[1]㊀BOBET A.Analytical solutions for shallow tunnels in saturatedground[J].Journal of Engineering Mechanics,2001, 127(12):1258.[2]㊀LOGANATHAN N,POULOS H G.Analytical prediction fortunneling-induced ground movement in clays[J].Journal ofGeotechnical and Geoenvironmental Engineering,1998,124(9):846.[3]㊀GONZA`L EZ C,SAGASETA C.Patterns of soil deformationsaround tunnels:application to the extension of Madrid Metro[J].Computers and Geotechnics,2001,28(6/7):445.[4]VERRUIJT A,BOOKER J R.Surface settlements due todeformation of a tunnel in an elastic half plane[J].Geotechnique,1996,46(4):753.[5]㊀CHOU W,BOBET A.Predictions of ground deformations inshallow tunnels in clay[J].Tunnelling and UndergroundSpace Technology,2002,17(1):3.[6]㊀PARK K H.Analytical solution for tunneling-induced groundmovement in clays[J].Tunnelling and Underground SpaceTechnology,2005,20(3):249.[7]㊀PARK K H.Elastic solution for tunneling-induced groundmovements in clays[J].International Journal ofGeomechanics,2004,4(4):310.[8]㊀PECK R B.Deep excavations and tunneling in softground[C]//Proceedings of the7th International Conference onSoil Mechanics and Foundation Engineering.Mexico City:[s.n.],1969:225.[9]㊀韩煊,李宁,Standing J R.Peck公式在我国隧道施工地面变形预测中的适用性分析[J].岩土力学,2007,28(1):23.HAN Xuan,LI Ning,STANDING J R.An adaptabilitystudy of gaussian equation applied to predicting groundsettlements induced by tunneling in China[J].Rock andSoil Mechanics,2007,28(1):23.[10]㊀OᶄREILLY M P,NEW B M.Settlements above tunnels inthe United Kingdom-their magnitude and prediction[C]//Proceedings of the Tunnelling82.[S.l.]:[s.n.],1982:173.[11]㊀MAIR R J,TAYLOR R N.Theme lecture:bored tunnellingin the urban environment[C]//Proceedings of the FourteenthInternational Conference on Soil Mechanics and FoundationEngineering.Hamburg:Publications Committee ofⅪⅤICSMFE Balkema,1997:2353.[12]㊀SUWANSAWAT S,EINSTEIN H H.Describing settlementtroughs over twin tunnels using a superposition technique[J].Journal of Geotechnical and GeoenvironmentalEngineering,2007,133(4):445.[13]㊀城市轨道交通工程监测技术规范:GB50911 2013[S].北京:中国建筑工业出版社,2013.Code for monitoring measurement of urban rail transitengineering:GB50911-2013[S].Beijing:ChinaArchitecture&Building Press,2013.[14]㊀魏纲.盾构隧道施工引起的土体损失率取值及分布研究[J].岩土工程学报,2010,32(9):1354.WEI Gang.Selection and distribution of ground loss ratioinduced by shield tunnel construction[J].Chinese Journalof Geotechnical Engineering,2010,32(9):1354. [15]㊀郭玉海.大直径土压平衡盾构引起的地表变形规律研究[J].土木工程学报,2013,46(11):128.GUO Yuhai.Study on ground surface movement induced bylarge-diameter earth pressure balance shield tunneling[J].China Civil Engineering Journal,2013,46(11):128.[16]㊀陈春来,赵城丽,魏纲,等.基于Peck公式的双线盾构引起的土体沉降预测[J].岩土力学,2014,35(8):2212.CHEN Chunlai,ZHAO Chengli,WEI Gang,et al.Prediction of soil settlement induced by double-line shieldtunnel based on Peck formula[J].Rock and Soil966。
(整理)Peck法计算的盾构隧道地面沉降量及沉陷槽计算公式.
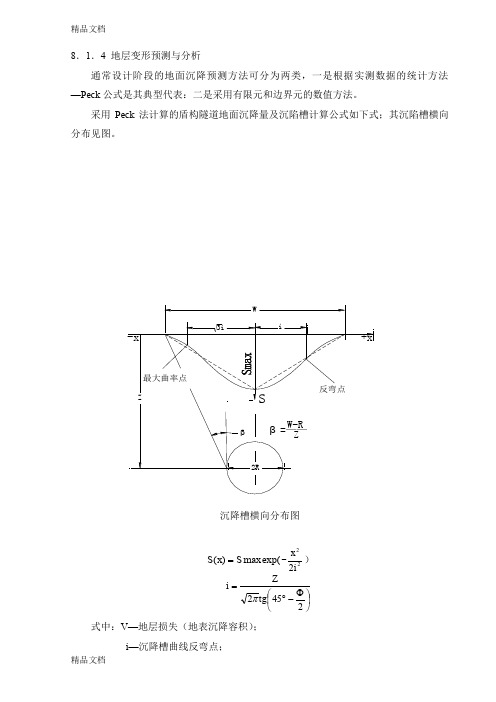
8.1.4 地层变形预测与分析通常设计阶段的地面沉降预测方法可分为两类,一是根据实测数据的统计方法—Peck 公式是其典型代表:二是采用有限元和边界元的数值方法。
采用Peck 法计算的盾构隧道地面沉降量及沉陷槽计算公式如下式;其沉陷槽横向分布见图。
exp(max )(S x S =-222i x )⎪⎭⎫ ⎝⎛Φ-︒=2452tg Zi π式中:V —地层损失(地表沉降容积);i —沉降槽曲线反弯点;z—隧道中心埋深根据本标段的地质条件和埋深等,得i=6.9m,由此根据以往的工程实践及经验公式,沉陷槽宽度B≈5i,可得单个隧道盾构推进引起的地表横向沉陷槽宽度约为35m,两座隧道盾构推进引起的地表横向沉陷曲线叠加后其沉陷槽宽度约为50m,并且沉陷槽的主要范围在隧道轴线两侧6m范围内,离轴线3m的沉降量约为最大沉降量的60%~70%,离轴线6m的沉降量约为最大沉降量的25%。
地层损失V值主要是由盾尾空隙引起的土体损失量,它与盾构机盾壳厚度、盾构推进时粘附在盾构上的土体厚度及注浆量等有关,即V=V尾+V粘-V浆盾构推进时粘附在盾构钢板上的土体厚度约为20~40mm,盾壳厚度为70mm,则:V=V尾+V粘-V浆=1.36+0.58α-(1.36+0.58)βα为折减系数,β为同步注浆的充填系数。
取α=0.6 β=0.5 得V=0.73m2由此可得地表最大沉陷值:Smax=23.4mm最大斜率:Qmax=0.0013以上分析值主要是在以往工程经验基础上结合本地铁盾构标段的实际情况,隧道埋深16m左右情况下得出的,最大沉降量满足规范和标书要求。
虽然地表沉降形态是大体相同或相似的,但其最大沉降量总是随着施工工况和地质条件的改变而千差万别,目前控制沉降的主要手段是同步注浆和二次注浆,而注浆的环节常有各种各样的问题发生,如缺量、过量、滞后、漏浆等等,不同的沉降情况常是施工工况和工作状态的反映,同时不同的地质条件沉降亦有所不同,如粉砂土较粘土隆降起量要少,沉降速率要快,淤泥质粘土后期固结沉降则要大点。
盾构隧道施工引起铁路路基沉降槽宽度系数计算方法

第 14卷 第 3期 2016年 6月
福 建工 程学 院学 报
Journal of Fujian University o f Technology
doi:10.3969/j.issn.1672—4348.2016.03.002
Vo1.14 No.3 Jun.2O16
盾 构 隧道 施 工 引起 铁 路 路 基 沉 降槽 宽度 系数 计 算 方 法
王 鸣 涛 ,吴 波 ,张 鹏 辉
(1.福 建工程 学院 土木工程学 院,福 建 福州 350118; 2.福 建 省 土 木 工程 新技 术 与 信 息 化 重 点 实验 室 ,福 建 福 州 350118)
第 3期
王 鸣涛 ,等 :盾 构 隧道施 工 引起 铁路 路基 沉 降槽宽 度 系数计 算方 法
213
沉 降 的经 验 公 式 中 ,Peck公 式 最 简 便 ,也应 用 最 普 遍 。但 由于 Peck公 式 只是 基 于 有 限 地 区的 实 测 数据 提 出的经 验 公 式 ,其 预测 地 表 沉 降 的 机 理 尚不 明确 ,适用 性 与 适 用 范 围也 需 要 进 一 步 分 析 探 讨 ;其 次 ,以 Peck法 为 代 表 的 经 验 公 式 法并 没 有 考虑 地 下 建 (构 )筑 物 与 土 体 的相 互 作 用 以 及 地 表静 动 荷 载 的影 响 。Peck公 式 中 的参 数 沉 降 槽 宽度 系数 i和地 层 损 失 率 较 难 精 确 确 定 ,对 计 算结 果 影 响 较 大 [9],这 两 个 参 数 与 隧 道 埋 深 、
法计算的盾构隧道地面沉降量及沉陷槽计算公式

8.1.4 地层变形预测与分析通常设计阶段的地面沉降预测方法可分为两类,一是根据实测数据的统计方法—Peck公式是其典型代表:二是采用有限元和边界元的数值方法。
采用Peck法计算的盾构隧道地面沉降量及沉陷槽计算公式如下式;其沉陷槽横向离轴线6m的沉降量约为最大沉降量的25%。
地层损失V值主要是由盾尾空隙引起的土体损失量,它与盾构机盾壳厚度、盾构推进时粘附在盾构上的土体厚度及注浆量等有关,即V=V尾+V粘-V浆盾构推进时粘附在盾构钢板上的土体厚度约为20~40mm,盾壳厚度为70mm,则:V=V尾+V粘-V浆=1.36+0.58α-(1.36+0.58)βα为折减系数,β为同步注浆的充填系数。
取α=0.6 β=0.5 得V=0.73m2由此可得地表最大沉陷值:Smax=23.4mm最大斜率:Qmax=0.0013以上分析值主要是在以往工程经验基础上结合本地铁盾构标段的实际情况,隧道埋深16m左右情况下得出的,最大沉降量满足规范和标书要求。
虽然地表沉降形态是大体相同或相似的,但其最大沉降量总是随着施工工况和地质条件的改变而千差万别,目前控制沉降的主要手段是同步注浆和二次注浆,而注浆的环节常有各种各样的问题发生,如缺量、过量、滞后、漏浆等等,不同的沉降情况常是施工工况和工作状态的反映,同时不同的地质条件沉降亦有所不同,如粉砂土较粘土隆降起量要少,沉降速率要快,淤泥质粘土后期固结沉降则要大点。
以上这些都要求盾构施工时要加强监测工作,以随时了解地面沉降信息,以便及时采取有效措施,以达到控制沉降和减少损失的目的。
8.2 理论分析施工引起的地面沉降和围岩变形,理论分析通过地层—结构模型模拟计算,本次计算采用有限元单元法,利用2D -σ计算程序模拟计算。
8.2.1 计算模型因隧道是一个狭长的建筑物,纵向很长,横向相对尺寸较小。
隧道计算可以取中间每延米隧道,作为平面应变问题来近似处理。
隧道模拟计算模型采用平面应变模型,计算范围上取至地面,下部和横向取隧道洞径的5倍左右为计算域。
Peck-公式

Peck 公式1969年,Peck在分析了大量地表沉降数据后,提出了地表沉降槽符合高斯分布的概念。
他认为地层变形由地层损失引起,施工引起的地面沉降是在不排水的条件下发生的,从而假定地表沉降槽体积等于地层损失体积。
如今这个公式在世界上广泛应用,成为预估沉降槽的经典公式。
s为地面任一点的沉降值,单位为mm;s为地面沉降的最大值,位于沉降曲线的对称中心上(对应于隧洞轴线位置),单位为mm;m axx为从沉降曲线中心到所计算点的距离,单位为m;i为从沉降曲线对称中心到曲线拐点(反弯点)的距离,一般称为“沉降槽宽度”,单位为m;i3通过对正态分布函数二次求导,令其等于0求得;m/3;V为隧道单位长度地层损失,单位为mV为地层体积损失率,即单位长度地层损失占单位长度盾构体积的百分比;这个参数的取值依赖地方经验。
l其中,i一般由查图表或者经验公式得来,以下列举了一些关于沉降槽宽度系数i的公式(一)Peck通过对大量地表沉降数据和有关工程资料的分析后,得出i为沉降槽宽度系数,单位为m;Z为隧道深度,单位为m;β为隧道周围地层内摩擦角(二)O’Reilly和New提出一种简便的定义i值的方法,即i和隧道深度Z之间存在以下简单的线性关系i为沉降槽宽度系数,单位为m;K为沉降槽宽度参数,这要取决于土性;Z为隧道深度,单位为m(三)Clough Array和Schimidt在其关于软黏土隧道的著作中,提出饱和含水塑性粘土中的地面沉降槽宽度系数i由如下公式求得i为沉降槽宽度系数,单位为m;R为隧道半径,单位为m;Z为隧道深度,单位为m(四)Attwell假定沉降槽曲线正态分布,给出估算地表沉降的经验公式i为沉降槽宽度系数,单位为m;R为隧道半径,单位为m;Z为隧道深度,单位为mK和z为统计系数(五)藤田收集了大量的,涉及多种盾构形式的统计资料后,给出以下公式i为沉降槽宽度系数,单位为m;R为隧道半径,单位为m;s为地面沉降的最大值,单位为mm;m ax为沉降槽断面积,单位为2m;AmA为隧道断面积,单位为2。
北京地铁暗挖隧道地表沉降特性分析

2019年第9期(中交基础设施养护集团有限公司,北京 100029)摘 要:文章基于北京地铁16号线某区间隧道地表沉降数据,研究隧道断面初期支护跨度以及施工方法对地表沉降槽宽度系数和地层损失率的影响。
研究结果显示,隧道各断面开挖引起的地表沉降满足Peck 曲线所描述的正态分布规律。
施工场地内地层损失率为0.428%~1.34%,沉降槽宽度系数为0.24~1.08。
双侧壁导坑法和CRD 法引起的地层损失率要远小于上下台阶法,初支的快速封闭成环有利于减小沉降槽宽度系数以及地层损失率。
地表沉降槽宽度系数以及地层损失率与断面初期支护跨度之间存在着指数关系,且随开挖宽度的增大而增大。
关键词:测量数据;施工方法;初支跨度;沉降槽宽度系数;地层损失率中图分类号:P642.2 文献标志码:A 文章编号:2096-2789(2019)09-0026-02作者简介:孙玮泽(1987—),男,硕士,工程师,研究方向:桥梁与隧道工程。
Peck 公式是分析隧道开挖引起地层变形特点的经典公式,其认为隧道开挖引起地表沉降槽体积等于地层损失体积,横向地表沉降分布近似满足以隧道轴线为中心向两侧一定范围内的高斯正态分布。
公式以沉降槽宽度以及地层损失率描述不同地层中隧道开挖所引起的地表沉降趋势的差异。
韩煊等通过国内8个地区的30组数据,对Peck 公式在各地的适用性进行了分析,对不同地区的沉降槽宽度给出了建议值,其中北京的建议值为0.3~0.6。
当隧道埋深以及断面直径确定后,地表沉降槽横向沉降曲线与地层损失率V l 以及沉降槽宽度系数K 有关。
文章基于北京地铁16号线某区间地表沉降数据,分析断面形式、施工方法等对地表沉降曲线的影响,以期为北京地区隧道开挖施工提供参考。
1 工程概况1.1 线路概况北京地铁16号线某区间左线总长约1535m ,右线总长约1514m ,在区间中间位置设置横通道进行开挖。
1.2 工程地质与水文地质依照沉积年代、成因类型、地层岩性及其物理性质,建设场地地层包含人工堆积层、新近沉积层、第四纪沉积层和新近纪沉积岩层,可细分为7个大层。
Peck法计算的盾构隧道地面沉降量及沉陷槽计算公式
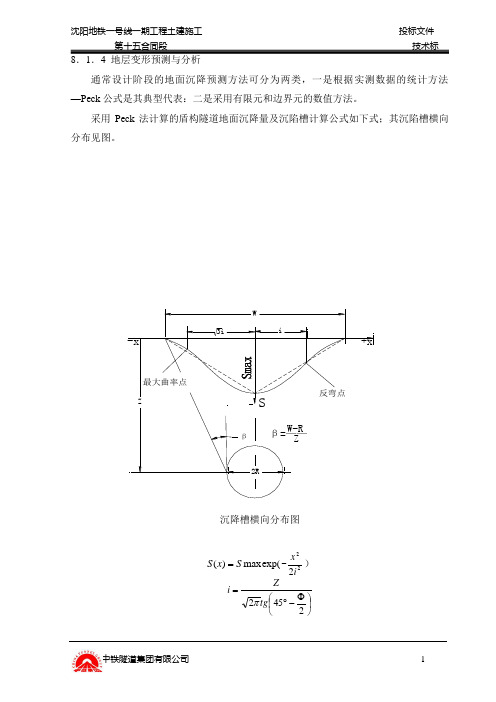
8.1.4 地层变形预测与分析通常设计阶段的地面沉降预测方法可分为两类,一是根据实测数据的统计方法—Peck 公式是其典型代表:二是采用有限元和边界元的数值方法。
采用Peck 法计算的盾构隧道地面沉降量及沉陷槽计算公式如下式;其沉陷槽横向分布见图。
exp(max )(S x S =-222ix ) ⎪⎭⎫ ⎝⎛Φ-︒=2452tg Z i π式中:V—地层损失(地表沉降容积);i—沉降槽曲线反弯点;z—隧道中心埋深根据本标段的地质条件和埋深等,得i=6.9m,由此根据以往的工程实践及经验公式,沉陷槽宽度B≈5i,可得单个隧道盾构推进引起的地表横向沉陷槽宽度约为35m,两座隧道盾构推进引起的地表横向沉陷曲线叠加后其沉陷槽宽度约为50m,并且沉陷槽的主要范围在隧道轴线两侧6m范围内,离轴线3m的沉降量约为最大沉降量的60%~70%,离轴线6m的沉降量约为最大沉降量的25%。
地层损失V值主要是由盾尾空隙引起的土体损失量,它与盾构机盾壳厚度、盾构推进时粘附在盾构上的土体厚度及注浆量等有关,即V=V尾+V粘-V浆盾构推进时粘附在盾构钢板上的土体厚度约为20~40mm,盾壳厚度为70mm,则:V=V尾+V粘-V浆=1.36+0.58α-(1.36+0.58)βα为折减系数,β为同步注浆的充填系数。
取α=0.6 β=0.5 得V=0.73m2由此可得地表最大沉陷值:Smax=23.4mm最大斜率:Qmax=0.0013以上分析值主要是在以往工程经验基础上结合本地铁盾构标段的实际情况,隧道埋深16m左右情况下得出的,最大沉降量满足规范和标书要求。
虽然地表沉降形态是大体相同或相似的,但其最大沉降量总是随着施工工况和地质条件的改变而千差万别,目前控制沉降的主要手段是同步注浆和二次注浆,而注浆的环节常有各种各样的问题发生,如缺量、过量、滞后、漏浆等等,不同的沉降情况常是施工工况和工作状态的反映,同时不同的地质条件沉降亦有所不同,如粉砂土较粘土隆降起量要少,沉降速率要快,淤泥质粘土后期固结沉降则要大点。
隧道沉降槽参数
其中 v为隧道轴水平的竖向总应力, 为 内t 部支承压力, 为粘cu土的不排
水剪切强度。
Macl(1999)和Devriendt(2010)提供了从各种实验研究中选择Ntc的经验 指导,这些研究在组合时,跨度范围很广,可能覆盖直径和不受支 撑的预直径比。
都可能导致Smax的高值和容量的损失,这是难以准确预测的。
现在十八页,总共十八页。
的规i (律z ),这是分析地表以下土体沉降的关
键。由于测量地表以下 土层沉降槽曲线宽
度系数 的试验较为繁琐,所以实测数据很
少,而对于 的测量较为简单, 其实测i( z)
数据相对较多
和 成反比,所以
可以通过 化的规律。Sຫໍສະໝຸດ 的数值来研究max
沿深度变
Smax z i(z)
Smax z
i(z)
-----------隧道开挖引起土层沉降槽曲线形态的分析与计算
现在九页,总共十八页。
-----------砂土地层隧道开挖对地层位移影响的模型试验研究
现在十页,总共十八页。
现在十一页,总共十八页。
最近的研究(Jones 2010)已经表明,Zo值超过35m时,i和Zo之间的关系不是线 性的,这比本文中考虑的隧道深度要大。 比例常数k被称为槽宽参数,并被认 为在很大程度上与建造方法无关(Mair and Taylor,1997)。
Mair和Taylor(1997)总结了大量的现场数据,并得出结论认为0.4 <k <0.6的粘土,k对粘 土的刚度没有依赖性。 相应的数据显示,砂土和砾石中的陨石呈现出更大的分散性,大 部分数据的界限为0.25 <k <0.45。
浅埋暗挖隧道地面沉降槽宽度系数取值的研究

浅埋暗挖隧道地面沉降槽宽度系数取值的研究王哲;姚王晶;周阳敏;曾理彬;魏纲【期刊名称】《浙江工业大学学报》【年(卷),期】2018(46)2【摘要】浅埋暗挖法隧道施工引起的沉降槽宽度系数i值与隧道的半径R、隧道的埋深z和土质有关.采用Attwell分析公式,通过有限元数值模拟得到不同埋深 z下的i值,从而求解出公式中的待定系数K与N,得出新的i值计算公式.在进行待定系数求解时,发现lni与lnz的关系存在线性分段性,对i值的公式进行了分段讨论,结论如下:隧道埋深较浅时,半径 R变化对i值影响大,对应z/D为1.24~1.80时,K=1.73,N=0.17,i/R=1.73 [z/(2R)]0.17;隧道埋深较深时,埋深z变化对i值影响大,对应 z/D为1.80~3.28时,K=1.35,N=0.55,i/R=1.35[z/(2 R)]0.55.通过实测数据分析并与前人公式对比,结果表明上述公式在杭州软土地区浅埋隧道沉降槽宽度系数的取值更加精确.%The width coefficients of settlement troughs caused by the shallow-buried tunneling method are related to the radius R and depth z of tunnels and soil conditions.In this paper,finite element numerical modeling with the Attwell formula is used to obtain the values of i under differentz.The coefficients(K and N)involved in this formula is then determined and the value of i is formulated.In determining the coefficients,it is found that the relationship between ln i and lnz is piecewise linear.Through analyzing the value of i in each phase,the following conclusions are made.When the depth of tunnels is smaller,the variation of R has great influence on the value of i,i.e.,w henz/D=1.24~1.80,K=1.73,N=0.17,and i/R=1.73 [z/(2 R)]0.17. When the depth of tunnels is larger,the variation ofzhas great influence on the value ofi,i.e., w hen z/D=1.80 ~ 3.28,K = 1.35,N = 0.55,and i/R= 1.35 [z/(2 R)]0.55.T hrough the analysis of measured data and comparison with the previous formula,it is confirmed that the proposed formula is more accurate in determining the width coefficients pf settlement troughs in the Hangzhou soft soil area.【总页数】5页(P204-208)【作者】王哲;姚王晶;周阳敏;曾理彬;魏纲【作者单位】浙江工业大学岩土工程研究所,浙江杭州310023;浙江工业大学岩土工程研究所,浙江杭州310023;浙江工业大学岩土工程研究所,浙江杭州310023;浙江工业大学岩土工程研究所,浙江杭州310023;浙江大学城市学院土木工程系,浙江杭州310015【正文语种】中文【中图分类】TU433【相关文献】1.盾构隧道施工引起铁路路基沉降槽宽度系数计算方法2.盾构掘进引起的地层沉降槽宽度系数研究3.盾构法施工地表沉降槽宽度系数i的探讨4.砂-黏复合地层盾构地表沉降分析及沉降槽宽度系数修正5.砂卵石地层盾构隧道施工地表沉降槽宽度系数分析因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的砂砾石数据库的最低值。 ③ 细土的k值在0.4-0.6范围内,与Mair和Taylor(1997)的clays数据库一致。 在软、硬粘土隧道中获得的k值之间没有明显的区别。
④ 随着时间的推移,在马林加地区的土壤中的Smax与膨润土流体的耗散有关, 膨润土流体是用来支持超长管道的。这些土壤中没有随时间的系统变化。所有的
-----------隧道开挖引起土层沉降槽曲线形态的分析与计 算
A
6
Peck 公式如 下:
S x 为距离隧道中心线为x 处的地表沉降值;
S m a x 为隧道中心线处地表最大沉降值; x 为距隧道中心线的水平距离;
i 为地表沉降槽宽度系数, 即沉降槽曲线反弯点至隧道中心线的水平距离。
A -----------隧道开挖引起土层沉降槽曲线形态的分7析与计算
而测数对据于相对的较S m测多a x 量较为S m简和ax 单 z,
其实
成i ( 反z )
比,所以可以通过 S m的ax 数z 值来
研究 沿i (深z ) 度变化的规律。
-----------隧道开挖引起土层沉降槽曲线形态的分析与计算
Hale Waihona Puke A10-----------砂土地层隧道开挖对地层位移影响的模型试验研究
A
13
A
14
在过度固结的粘土中,Vi通常用Macklin(1999)的方法估计:
V取决于现在的稳定数N与崩溃时的稳定数Ntc之比,稳定数N被定 义为:
其中 v 为隧道轴水平的竖向总应力, t 为内部支承压力,c u 为粘土 的不排水剪切强度。 Macl(1999)和Devriendt(2010)提供了从各种实验研究中选择Ntc的经 验指导,这些研究在组合时,跨度范围很广,可能覆盖直径和不 受支撑的预直径比。
A
8
地表以下土层沉降槽断面
对于地表以下至隧道以上土层,地层损失的体积假设依然成立,就 是说地表以下任一土层的沉降槽的体积等于地层损失,而且, 沉降槽仍 为一正态分布曲线,随着土层深度z 的增大,该土层距隧道顶部的垂直 距离减小,土层的沉降槽曲线宽度系数将会减小(图2),于是,Smax和 i两个参数的取值会随深度变化而不同,它们均可表示为深度z的函数。
和范围,这可以减少隧道的收缩效应。从这项研究中可以得出一下结论:
① 对于冰川土壤,重要的是要确定控制沉降槽主要因素的覆盖层是否具有细 或粗材料的特征,因为每种材料的k值已经显示出很大的差异。 正确的选择对于
获得可靠的体积损失预测非常重要。 ② 粗粒土的沉降槽槽宽度系数k值在0.2-0.3范围内,这是Mair和Taylor(1997)
A
4
研 究 目的
①沉降槽宽参数 ②最大槽沉降和体积损失的保守设计估算 ③泥砾土的影响
A
5
地表沉降槽断面
隧道施工时沿与隧道纵向轴线垂直的方向上会出现沉降槽。1969 年在当时大量隧道开挖施工引起的地表沉降实测资料的基础上, Peck 系 统地提出了 地层损失的概念和估算隧道开挖地表下沉的实用方法,即 Peck 公式,它已成为目前应用最为广泛地 预计隧道施工地表沉降的方 法。所谓地层损失,是指隧道施工中实际开挖的土体的体积与竣工体 积之 差。Peck 认为,在不排水情况下隧道开挖所形成的地表沉降槽的 体积应等于地层损失。
A
11
A
12
最近的研究(Jones 2010)已经表明,Zo值超过35m时,i和Zo之间的关系不 是线性的,这比本文中考虑的隧道深度要大。 比例常数k被称为槽宽参数, 并被认为在很大程度上与建造方法无关(Mair and Taylor,1997)。
Mair和Taylor(1997)总结了大量的现场数据,并得出结论认为0.4 <k <0.6的 粘土,k对粘土的刚度没有依赖性。 相应的数据显示,砂土和砾石中的陨石 呈现出更大的分散性,大部分数据的界限为0.25 <k <0.45。
地表沉降横向分布近似为一正态分布曲线,如图 1 所示。公式需要确定
S m a x 和 i 两个参数。因为地表沉降槽的体积应等于地层损失 V 的体积,
地表 沉降槽的体积可以通过积分得到:
求得 i 后,就可以得到S m a x ,然后得到地表任一点的竖向沉降值。
-----------隧道开挖引起土层沉降槽曲线形态的分析与计算
Settlement trough parameters for
tunnels in Irish glacial tills
爱尔兰冰川隧道的沉降槽参数 导师 王海涛 道路与铁道工程 苏鹏
A
1
B.A. McCabe,T.L.L. Orr , C.C. Reilly , B.G. Curran
A
2
A
A
15
A
16
A
17
当方程 (8)和(9)与其他任何经验公式一样,应谨慎使用, 它们可以提供第一次估计,即由于在爱尔兰地形条件下采用当 前的隧道方法进行隧道掘进而可能造成的体积损失。如果遇到 泥砾土,这些数值可能会增加。
A
18
结
论
这篇论文整理爱尔兰各类冰川隧道的经验,以期提供初步的地表沉降的大小
3
关键词:
横向沉降曲线 冰碛 沉降槽宽度 隧道 体积损失 泥砾土
摘要
冰碛(或泥砾)是爱尔兰岛上最普遍的沉积物。 在过去10年的东部 地区,由于对重大建设项目进行实地调查和相关测试,这些冰 碛的行为,尤其是都柏林泥砾土,现在被人们更好地理解了。 尽管同一时期内该国隧道活动增加,但在冰川下的隧道化作业 所引起的沉降方面有非常少的记录。本文介绍了两处冰碛区域 的横向地表沉降数据。在都柏林港口隧道中,有4个剖面被认为 是“软土地”的一部分。 据报道,在中部地区的马林加,一个 用于污水处理建造的管顶式微型隧道有九个剖面;其中一个是在 铁路路基的顶部测量的。用标准的高斯误差函数来解释被测量 的集合,槽宽参数受细颗粒或粗颗粒的比例的影响。此外,还 提供了最大槽沉降和体积损失的保守设计估算,并讨论了泥砾 土的影响。本文首次提供了预测爱尔兰土壤隧道上方地表沉降 的一个经验指导。
-----------隧道开挖引起土层沉降槽曲线形态的分析与计算
A
9
i ( z ) 地表以下沉降槽宽度系数
若要分析地表以下土层沉降槽曲线,
首先需要 了解沉降槽宽度系数沿深
度 i ( z ) 变化的规律,这是分析地表以
下土体沉降的关键。由于测量地表
以下 土层沉降槽曲线宽度系数 的i ( z )
试验较为繁琐,所以实测数据很少,
