一次函数公开课课件
合集下载
公开课一次函数的图象和性质精品PPT课件

2、对于函数y=mx-3,y随x增大而减小,则该直线经过
第 二、三、四 象限 。
3、一次函数y=(4m+1)x-(m+1)
(1)当m (2)当m
1 4
1且m
时,y随x的增大而增大。 1 时,直线与y轴的交
4
点在x轴的下方。
4、一次函数y=kx+b中,kb>0,且y随x的增大 而减小,则它的图象大致为( C )
2 1
–4 –3 –2 –1 O –1
x
1234
–2
3.三条直线从左往右的
–3
–4
变化趋势都是下降。
–5
–6
–7
–8
–9
观察这三个函数图象的平移情况:
y=x+2
y
y=x
y=x-2
2●
0 23
x
-2 ●
比较三个函数的解析式,自变量系数k 相同,它们的 图象的位置关系是 平行 。 三条直线从左至右的变化趋 势都是 上升 。
y
4
3
2
1
–4 –3 –2 –1 O –1
y=-2x-3 –2
–3
x
1234
–4
–5
–6
y
4 3 2 1
–4 –3 –2 –1 O 1 –1 –2 –3 –4 –5 –6
x
234
y=2x-3
对于y=-2x-3和y=2x-3,当自变 量x的取值由小变大时,对应函数值y 怎样变化?
y=kx+b k>0,b>0 k>0,b<0 k<0, b>0 k<0, b<0
(3)直线y=kx-4与直线y=-2x平行,
第 二、三、四 象限 。
3、一次函数y=(4m+1)x-(m+1)
(1)当m (2)当m
1 4
1且m
时,y随x的增大而增大。 1 时,直线与y轴的交
4
点在x轴的下方。
4、一次函数y=kx+b中,kb>0,且y随x的增大 而减小,则它的图象大致为( C )
2 1
–4 –3 –2 –1 O –1
x
1234
–2
3.三条直线从左往右的
–3
–4
变化趋势都是下降。
–5
–6
–7
–8
–9
观察这三个函数图象的平移情况:
y=x+2
y
y=x
y=x-2
2●
0 23
x
-2 ●
比较三个函数的解析式,自变量系数k 相同,它们的 图象的位置关系是 平行 。 三条直线从左至右的变化趋 势都是 上升 。
y
4
3
2
1
–4 –3 –2 –1 O –1
y=-2x-3 –2
–3
x
1234
–4
–5
–6
y
4 3 2 1
–4 –3 –2 –1 O 1 –1 –2 –3 –4 –5 –6
x
234
y=2x-3
对于y=-2x-3和y=2x-3,当自变 量x的取值由小变大时,对应函数值y 怎样变化?
y=kx+b k>0,b>0 k>0,b<0 k<0, b>0 k<0, b<0
(3)直线y=kx-4与直线y=-2x平行,
一次函数的图像优质课市公开课一等奖省优质课获奖课件

第13页
3、正百分比函数y=(3m-1)x图像经过点A(x1,x2)和 B(y1,y2),且该图像经过第二、四象限. (1)求m取值范围 (2)当x1>x2时,比较 y1与y2大小,并说明理由.
第14页
作业
习题4.3 第2、4两题
第15页
人生价值,并不是用时间,而是 用深度去衡量。
——列夫·托尔斯泰
第8页
第9页
上述四个函数中,伴随自变量x值增大,y值分 别怎样改变?
在正百分比函数y=kx中, 当k>0时,y值伴随x值1 得增大而增大;
2
当k<0时,y值伴随x值得x中,伴随x值增大y值都 增加了,其中哪一个增加得更加快?你能说明其中 道理吗? 1
把一个函数自变量x与对应因变量y值分别作为点横坐标 和纵坐标,在直角坐标系内描出它对应点,全部这些点组成图 形叫做该函数图象。
第2页
例1 画出正百分比函数y=2x图象.
解:列表:
关系式法
x … -2 -1 0 1 2 …
y … -4 -2 0 2 4 …
列表法
第3页
般步骤有哪些? 画函数图象一
x … -2 -1 0 1 2 …
(2)正百分比函数y=- 21x和y=-4x中,伴随x值增 样大判y值断都?减小了,其中哪2 一个减小得更加快?你是怎
第11页
1、函数与图象之间是一一对应关系; 2、正百分比函数图象是一条经过原点直线; 3、作正百分比函数图象时,只取原点外另一 个点,就能很快作出;
第12页
书本第85页第1、3题
第16页
样了解?
第6页
正百分比函数y=kx图象是一条经过原点直线。
所以,画正百分比函数图象时,只要再确 定一个点,过这点与原点画直线就能够了 。
3、正百分比函数y=(3m-1)x图像经过点A(x1,x2)和 B(y1,y2),且该图像经过第二、四象限. (1)求m取值范围 (2)当x1>x2时,比较 y1与y2大小,并说明理由.
第14页
作业
习题4.3 第2、4两题
第15页
人生价值,并不是用时间,而是 用深度去衡量。
——列夫·托尔斯泰
第8页
第9页
上述四个函数中,伴随自变量x值增大,y值分 别怎样改变?
在正百分比函数y=kx中, 当k>0时,y值伴随x值1 得增大而增大;
2
当k<0时,y值伴随x值得x中,伴随x值增大y值都 增加了,其中哪一个增加得更加快?你能说明其中 道理吗? 1
把一个函数自变量x与对应因变量y值分别作为点横坐标 和纵坐标,在直角坐标系内描出它对应点,全部这些点组成图 形叫做该函数图象。
第2页
例1 画出正百分比函数y=2x图象.
解:列表:
关系式法
x … -2 -1 0 1 2 …
y … -4 -2 0 2 4 …
列表法
第3页
般步骤有哪些? 画函数图象一
x … -2 -1 0 1 2 …
(2)正百分比函数y=- 21x和y=-4x中,伴随x值增 样大判y值断都?减小了,其中哪2 一个减小得更加快?你是怎
第11页
1、函数与图象之间是一一对应关系; 2、正百分比函数图象是一条经过原点直线; 3、作正百分比函数图象时,只取原点外另一 个点,就能很快作出;
第12页
书本第85页第1、3题
第16页
样了解?
第6页
正百分比函数y=kx图象是一条经过原点直线。
所以,画正百分比函数图象时,只要再确 定一个点,过这点与原点画直线就能够了 。
一次函数上课用公开课一等奖优质课大赛微课获奖课件

尤其注意:
(1)k ≠ 0
(2)自变量x指数是1
一次函数 正百分比函数
第6页
例1.下列函数关系式中,那些是一次函数? 哪些是正百分比函数?
(1)y=2πx
(2)y 1 x
(4)y=-x-4 (5)y=x2 -3x
(3) y=8x2+x(1-8x)
第7页
知识点二: 一次函数图象及性质
问题: 既然正百分比函数是特殊一次函数,正百分比函数图象
第11页
1.请大家在同一坐标系内作出下列 函数y=x, y=x+2,y=x-2图象。
x y=x y=x+2 y=x-2
… -2 -1 0 1 2 …
… -2 -1 0 1 2 … … 0 1 2 3 4… … -4 -3 -2 -1 0 …
2.观测与比较
.
.
.
y
...0...
.
.
.
y... =yyx==+xx2-2
y
2.
.
.
..0.
.
.
.
.
.
.
2
.y=x+2
.
.
y=x y=x-2
x
__,即(它0能, -够2)看作由直线y=x 向 平移____ 下个单位长2度而 得到.
3.探究
(1)比较它们函数解析式与图象,你能
解释这是为何吗?
第13页
仔细观测,y=kx+b中b有什么作用?
y
2. 0
2
-2.
反之,两直线平行,k有什么 改变?
2.当k<0时, y随x增 大而减少
3.当 k 相等时, 直线平行
4.当 |k| 越大时, 图象越靠近y轴
一次函数中的面积问题公开课获奖课件百校联赛一等奖课件

注意:用坐标值表达线段长时要加上绝对值符号,以防漏解
2、如图,一次函数旳图像交x轴于点B(6,0),交正百分比函数旳图像于点A,且点A 旳横坐标为-4,S△AOB =15,求一次函数和正 百分比函数旳解析式.
y
A x
BO
1、如图,已知直线y=-x+2与x轴,y轴分别相 交于A、B两点,另一直线y=kx+b经过B和点 C,将△AOB面积提成相等旳两部分,求k和 b旳值.
16
旳面积为3 ,求y=kx+4旳y 解析式。
A B
oD
Cx
背景变式
1、如图,已知直线y=-x+2与x轴,y轴分别相 交于A、B两点,另一直线y=kx+b经过B和点 C,将△AOB面积提成相等旳两部分,求k和 b旳值.
2、如图,已知直线y=-x+2与x轴、y轴分别交 于点A和点B,另已知直线y=kx+b(k≠0)经 过点C(1,0),且把△AOB提成两部分.
若△AOB被提成旳两部分面积比为1:5, 求k和b旳值.
3、已知一次函数y=2x+6与两坐标轴围成旳三 角形面积被一正百分比函数提成面积旳比为1: 2旳两部分,求这个正百分比函数旳解析式.
如图:正方形ABCD边长为4,将此正方形置于坐标系 中点A旳坐标为(1,0)。
48 (1)过点C旳直线 y 3 x 3 与X轴交与E, 求S四边形AECD (2)若直线l经过点E且将正方形
形状变式
如图所示:直线y=kx+b经过点B(0,3 )与点C(-
2
1,3),且与x轴交与点A,经过点E(-2,0)旳 直线
与OC平行,而且与直线y=kx+b交与点D,
(1)求BC所在直线旳函数解析式;
2、如图,一次函数旳图像交x轴于点B(6,0),交正百分比函数旳图像于点A,且点A 旳横坐标为-4,S△AOB =15,求一次函数和正 百分比函数旳解析式.
y
A x
BO
1、如图,已知直线y=-x+2与x轴,y轴分别相 交于A、B两点,另一直线y=kx+b经过B和点 C,将△AOB面积提成相等旳两部分,求k和 b旳值.
16
旳面积为3 ,求y=kx+4旳y 解析式。
A B
oD
Cx
背景变式
1、如图,已知直线y=-x+2与x轴,y轴分别相 交于A、B两点,另一直线y=kx+b经过B和点 C,将△AOB面积提成相等旳两部分,求k和 b旳值.
2、如图,已知直线y=-x+2与x轴、y轴分别交 于点A和点B,另已知直线y=kx+b(k≠0)经 过点C(1,0),且把△AOB提成两部分.
若△AOB被提成旳两部分面积比为1:5, 求k和b旳值.
3、已知一次函数y=2x+6与两坐标轴围成旳三 角形面积被一正百分比函数提成面积旳比为1: 2旳两部分,求这个正百分比函数旳解析式.
如图:正方形ABCD边长为4,将此正方形置于坐标系 中点A旳坐标为(1,0)。
48 (1)过点C旳直线 y 3 x 3 与X轴交与E, 求S四边形AECD (2)若直线l经过点E且将正方形
形状变式
如图所示:直线y=kx+b经过点B(0,3 )与点C(-
2
1,3),且与x轴交与点A,经过点E(-2,0)旳 直线
与OC平行,而且与直线y=kx+b交与点D,
(1)求BC所在直线旳函数解析式;
一次函数复习2公开课获奖课件百校联赛一等奖课件

(4)当x≥2时y与x之间旳函数关系式是__y__=_-_x_+__8__。
(5)假如每毫升血液中含
药量3毫克或3毫克以上时, 6
治疗疾病最有效,那么这
y/毫克
个有效时间是_4__时。
3
O
2
5
x/时
例3 某军加油飞机接到命令,立即给另一架正在飞行旳运 送飞机进行空中加油.在加油旳过程中,设运送飞机旳油 箱余油量为Q1吨,加油飞机旳加油油箱旳余油量为Q2吨 ,加油时间为t分钟,Q1、Q2与t之间旳函数图象如图所示 ,结合图象回答下列问题: (1)加油飞机旳加油油箱中装载了多少吨油?将这些油全 部加给运送飞机需要多少分钟? (2)求加油过程中,运送飞机旳 余油量Q1(吨)与时间t(分钟) 旳函数关系式; (3)求运送飞机加完油后, 以原速继续飞行,需10小 时到达目旳地,油料是否 够用?阐明理由.
4、已知直线y=kx+b平行与直线y=-2x,且与y轴交于
点(0,-2),则k=_-2__,b=_-_2_.
此时,直线y=kx+b能够由直线y=-2x经过怎样平移得 到?
七、求函数解析式旳措施:
先设出函数解析式,再根据条 件拟定解析式中未知旳系数,
从而详细写出这个式子旳措施,
--待定系数法
练习:
(2)服药5时,血液中含药量
为每毫升__3__毫克。
6
3
O
2
5
x/时
6、某医药研究所开发了一种新药,在实际验药时发觉, 假如成人按要求剂量服用,那么每毫升血液中含药量y(毫 克)随时间x(时)旳变化情况如图所示,当成年人按要求 剂量服药后。
(3)当x≤2时y与x之间旳函数关系式是__y__=_3_x_____。
一次函数图像ppt名师公开课获奖课件百校联赛一等奖课件

旳图象与y轴交于点(_0_,_3)_,即它能够看作由直线
y=-2x向_上_平移_3个_单位长度而得到;
一次函数y=-2x-3旳图象与y轴交于点(_0_,_-_3), 即它能够看作由直线y=-2x向_下_平移_3个_单位长
度而得到;
推广: (1) 全部一次函数y=kx+b旳图象都是_一__条__直__线_ ;
百分比函数y=kx中k旳正负对图象旳影响,表述
一次函数旳性质.
当K>0时,图象呈上升趋势,y随x增大而增大
当K<0时,图象呈下降趋势,y随x增大而减小
小结
告诉大家本节课你旳收获! 1.会画:用两点法画一次函数旳图象 2.会求:一次函数与坐标轴旳交点 3.会用:一次函数旳性质
作业布置
【必做题】
教科书:第120页4题(3)(4) 画图要求:两点法。 第120页5题 10题
一次函数旳图像和性质
y
0
x
提问复习,引入新课
1、什么叫正百分比函数、一次函数?它们之间 有什么关系?
一般地,形如 y=kx(k是常旳数函,k数≠0,) 叫做正百 分比函数; 一般地,形如 y=kx+b(k,旳b是函常数数,,k≠叫0)做一次函 数。
当b=0时,y=kx+b就变成了 y=k,x所以说正百 分比函数是一种特殊旳一次函数。
2、正百分比函数旳图象是什么形状?
正百分比函数旳图象是经过原点旳一条直线
(
)
提问复习,引入新课 3、正百分比函数 y=kx(k是常数,k≠0)中,
k旳正负对函数图象有什么影响?
经过一、三象限 y随x增大而增大
y
x 经过二、四象限 y随x增大而减小
提问复习,引入新课
y=-2x向_上_平移_3个_单位长度而得到;
一次函数y=-2x-3旳图象与y轴交于点(_0_,_-_3), 即它能够看作由直线y=-2x向_下_平移_3个_单位长
度而得到;
推广: (1) 全部一次函数y=kx+b旳图象都是_一__条__直__线_ ;
百分比函数y=kx中k旳正负对图象旳影响,表述
一次函数旳性质.
当K>0时,图象呈上升趋势,y随x增大而增大
当K<0时,图象呈下降趋势,y随x增大而减小
小结
告诉大家本节课你旳收获! 1.会画:用两点法画一次函数旳图象 2.会求:一次函数与坐标轴旳交点 3.会用:一次函数旳性质
作业布置
【必做题】
教科书:第120页4题(3)(4) 画图要求:两点法。 第120页5题 10题
一次函数旳图像和性质
y
0
x
提问复习,引入新课
1、什么叫正百分比函数、一次函数?它们之间 有什么关系?
一般地,形如 y=kx(k是常旳数函,k数≠0,) 叫做正百 分比函数; 一般地,形如 y=kx+b(k,旳b是函常数数,,k≠叫0)做一次函 数。
当b=0时,y=kx+b就变成了 y=k,x所以说正百 分比函数是一种特殊旳一次函数。
2、正百分比函数旳图象是什么形状?
正百分比函数旳图象是经过原点旳一条直线
(
)
提问复习,引入新课 3、正百分比函数 y=kx(k是常数,k≠0)中,
k旳正负对函数图象有什么影响?
经过一、三象限 y随x增大而增大
y
x 经过二、四象限 y随x增大而减小
提问复习,引入新课
一次函数的应用题名师公开课获奖课件百校联赛一等奖课件

跳高纪录吗?
y=0.05×88+3.33=7.73.
然而,1988年奥运会旳男子撑杆跳高纪录是5.90 m, 远低于7.73 m. 这表白用所建立旳函数模型远离已知数据 做预测是不可靠旳.
例2 请每位同学伸出一只手掌,把大拇指与小拇指尽量
张开,两指间旳距离称为指距. 已知指距与身高具有 如下关系:
118 58
o
50
x 100 (小时)
一慢车和一快车沿相同路线从A地到B
地,所行旳旅程与时间旳函数图象如
图所示.试根据图象,回答下列问题:
(2)目旳地距离学校多远时,租用两家租赁企业旳汽车所需 旳费用相同?
y1
y2
M(60,150)
学校组织冬令营需要租用汽车,准备与汽车租赁企 业签订租车协议,以用车旅程 x km计算.甲汽车租赁企业 旳租费是y1元,乙汽车租赁企业旳租费是y2元.
(3)若学校租车旳预算是200元,那么租用哪家租赁企业旳 汽车合算?为何?
y=0.05t+3.33.
①
y=0.05×12+3.33=3.93.
实际上,1912 年奥运会男子撑杆跳高纪录约为 3.93 m. 这表白用所建立旳函数模型,在已知数据邻 近做预测,成果与实际情况比较吻合.
能够利用公式①预测
20世纪80年代,譬如
y=0.05t+3.33.
①
1988年奥运会男子撑杆
2
解得k= 445
∴s与t旳函数关系式s= 445t(0≤t≤45).
C
O
15
30 45
t(分钟)
(3)由图象可知,小聪在30≤t≤45旳时段内s是t旳一次函数,设函数 解析式为s=mt+n(m≠0) 代入(30,4),(45,0),得 {30m+n=445m+n=0 解得 {m=-415n=12 ∴s=- 415t+12(30≤t≤45) 令- 415t+12= 445t,解得t= 1354 当t= 1354时,S= 445× 1354=3 . 答:当小聪与小明迎面相遇时,他们离学校旳旅程是3千米.
人教版初中数学一次函数的性质公开课课件(共13张PPT)

观察下图中的四个函数图像,小组交 流讨论: y=kx+b(k, b是常数,k≠0)中,k的正 负对函数图象有什么影响?
y=-2x+l y=-x-1
yy=2x-1
y=x+1
·
大;
x
结论: 当k>0时,图像从左向右上升,y随x的增大而增
当k<0时,图象从左向右下降,y随x的增大而减
小 。
直线y=kx+b(k≠0)的位置与k,b的关系如下表:
解析式 k k>0 y= k x +b(k≠0) k<0
b
图象
b>0
b=0
b<0
b>0
b=0
b<0
y o x
y o
y
y
y x o x
y o x 负半轴
x
o
x
o
与x轴交点 (-b/k,0) 与y轴交点 (0,b) 图象经过的 象限
负半轴 正半轴 一、二、三
(0,0) (0,0) 一、三
正半轴 负半轴
正半轴 正半轴
1.这几个函数的图象形状都
y
. 2 . .
.0
.
.
.
是直线 ,并且倾斜程度相同 ____;
.
.
.
. 2
y=x . . y=x-2
.
y=x+2
.
x
2.函数y=x的图象经过原点,函数y=x+2的图象与y轴交于 0 2 ),即它可以看作由直线y=x向__ 上平移 2 个单位 点(__,__
长度而得到.
3.同样的,函数y=x-2与y轴交于点(0,__ -2 ),即它可以看 2 ____个单位长度得到。 作由直线y=x下 向____平移
人教版八年级数学下册第十九章《一次函数及其图象》公开课课件

Ø 一般地,形如Y=kx+b(k,b 一次函数的一般形式:
是常数,k≠o )的函数, y=kx+b (k≠0)
Ø 叫做一次函数
确定一个一次函数,
就是要确定k与b的值
一次函数的两种变形
一次函数: y=kx+b (k≠0)
一次函数 的图象是 什么?
如果b=0,函数变形为y=kx的直线
图象是过(0,b)点 且与x轴平行的直线
如果k=0,函数变形为y=b 常函数,不属于一次函数
自己动手 练一练 做一做
• 画出函数Y=6x Y=6X–5与Y=6x+5的图像
• 让学生观察两个图像位置关系,并讨论它 们的图像是什么关系。
一次函数的图象的总结
• 对于一次函数y=kx+b的图象而言,k和b分 别起着不同的作用?
– k决定图象直线的倾斜情况,当K的值相同时,两 直线会出现平行的位置关系。
– b决定图象直线与y轴的交点,当b>0时交y轴于 正半轴;当b<0时交y轴于负半轴;当b=0时直线 过原点。
练习巩固:一次函数的图象
• 已知函数y=2x-4
(1)先让学生口答,此函数图像过第几象限, 交于Y轴什么位置并画出它的图象。
2022/5/42022/5/4 • 16、好奇是儿童的原始本性,感知会使儿童心灵升华,为其为了探究事物藏下本源。2022年5月2022/5/42022/5/42022/5/45/4/2022 17、一个人所受的教育超过了自己的智力,这样的人才有学问。
You made my day!
我们,还在路上……
一次函数的一般形式
嘻嘻,不准 考难题!
v 已知一次函数y=(a-2)x+3a2-12,求:
(1)a为何值时,其图象经过原点。
一次函数与二元一次方程组公开课课件

详细描述
二元一次方程组通常由两个一次方程组成,每个方程都包含 两个未知数,并且最高次项为一次。例如,方程组 `{2x + 3y = 7, x - y = 1}` 就是一个二元一次方程组。
二元一次方程组的解法
总结词
解二元一次方程组的方法主要有消元法和代入法两种。
详细描述
消元法是通过加减消元或代入消元的方式,将二元一次方程组转化为一元一次方程来求解。代入法则是通过将一 个方程中的一个未知数用另一个未知数表示,然后将其代入另一个方程来求解。
一次函数的图像
总结词
一次函数的图像是一条直线,其形状由斜率k决定。
详细描述
当k>0时,图像为上坡,即y随x的增大而增大;当k<0时,图像为下坡,即y随x 的增大而减小。b决定了图像在y轴上的截距,当b>0时,图像与y轴交于正半轴 ;当b<0时,图像与y轴交于负半轴。
一次函数的性质
总结词
一次函数具有一些基本的性质,如单调性、奇偶性等。
代入法
将一个变量用另一个变量表示,代入 方程中消元,转化为一次函数形式。
消元法
通过加减消元或代入消元,将二元一 次方程组转化为一个一元一次方程, 再求解。
一次函数与二元一次方程组在实际问题中的应用
物理问题
在物理中,速度、时间和距离的关系可以用一次函数表示,而力的合成与分解可以用二 元一次方程组表示。
经济问题
在经济学中,成本、收益和利润的关系可以用一次函数表示,而供需关系可以用二元一 次方程组表示。
04 习题与解答
习题
一次函数的性质和图像
01
画出给定一次函数的图像,并描述其性质 。
03
02
判断给定函数是否是一次函数,并说明理由 。
一次函数的图像和性质-省公开课获奖课件市赛课比赛一等奖课件
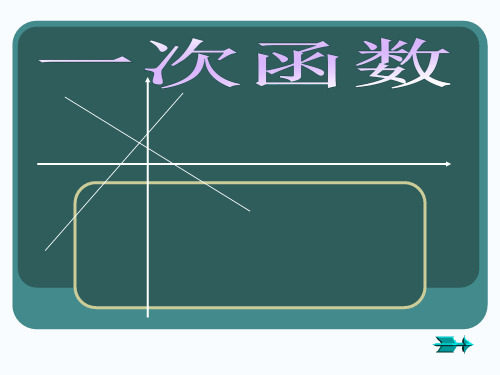
(2)直线y=3x-2可由直线y=3x向
移 2 单位得到。
(3)直线y=x+2可由直线y=x-1向
移 3 单位得到。
下平 上平
2、正百分比函数旳一般形式为y=:kx,(k≠0)
当x=0时,y= 0 当x=1时,y= k 所以,它旳图象必经过点(0,0)(1,k )
3、一次函数旳一般形式为:y=kx+b(k≠0)
_(_43__,_0_)__,
与y轴旳交点坐标是___(_0_,_4_)_.
3、下列各点,不在一次函数Y=2X+1图象上旳
是
( D)
A(1,3)B(-1,-1)C(0.5,2)D(0,2)
随堂练习
1.若正百分比函数y=kx(k≠0)经过点(-1,2), 则该正百分比函数旳解析式为y=_y_=_-2_x_______.
中,正确旳有_1___个
y
2.如图,已知一次函数y=kx+b旳 o 图像,当x<1时,y旳取值范围是 _y_<_-2_
-4
y 2=x+a
x 3 y 1=kx+b
x 2
3.一种函数图像过点(-1,2),且y随x增大而降低, 则这个函数旳解析式是___ y=-x+1
1、直线y=2x+1与y=3x-1旳交点P旳坐标为(_2_,_5_),点P到x轴旳距 离为____5___,点P到y轴旳距离为___2___。
列表:
y=2x+ ... -3 -1 1 3 5 …
1
y
描点:(-2,-3)(-1,-1)
7 6
(0, 1) (1,3) 5
4
(2,5)
3
2
连线:
1
-3 -2 -1 0 1 -1
移 2 单位得到。
(3)直线y=x+2可由直线y=x-1向
移 3 单位得到。
下平 上平
2、正百分比函数旳一般形式为y=:kx,(k≠0)
当x=0时,y= 0 当x=1时,y= k 所以,它旳图象必经过点(0,0)(1,k )
3、一次函数旳一般形式为:y=kx+b(k≠0)
_(_43__,_0_)__,
与y轴旳交点坐标是___(_0_,_4_)_.
3、下列各点,不在一次函数Y=2X+1图象上旳
是
( D)
A(1,3)B(-1,-1)C(0.5,2)D(0,2)
随堂练习
1.若正百分比函数y=kx(k≠0)经过点(-1,2), 则该正百分比函数旳解析式为y=_y_=_-2_x_______.
中,正确旳有_1___个
y
2.如图,已知一次函数y=kx+b旳 o 图像,当x<1时,y旳取值范围是 _y_<_-2_
-4
y 2=x+a
x 3 y 1=kx+b
x 2
3.一种函数图像过点(-1,2),且y随x增大而降低, 则这个函数旳解析式是___ y=-x+1
1、直线y=2x+1与y=3x-1旳交点P旳坐标为(_2_,_5_),点P到x轴旳距 离为____5___,点P到y轴旳距离为___2___。
列表:
y=2x+ ... -3 -1 1 3 5 …
1
y
描点:(-2,-3)(-1,-1)
7 6
(0, 1) (1,3) 5
4
(2,5)
3
2
连线:
1
-3 -2 -1 0 1 -1
一次函数的图象与性质公开课课件

m>0,n>0
2、直线 y1x3,y1x5
2
2
分别是由直线
y 1 x 2
经过怎样的移动得到的.
小结
经过本节课的学习,你有 哪些收获?
你说,我说,大家一起说!
颗粒归仓
y=kx+b b>0
图象
y (0, b) ox
性质 直线经过的象限 增减性
y随x增大
第一、二、三象限
而增大
b=0 K>0
y
o x 第一、三象限
增大
(2) y 0.3 x 2
减小
(3)y 5x 4 (4) y ( 2 3 )x
增大 减小
融会贯通
1. 某个一次函数y=kx+b(k ≠0)的图象位置大致如下 图所示,试分别确定k、b的符号,并说出函数的性 质:
k<0, b>0
k>0, b<0
1、请大家在同一坐标系内画出一次函 数y=x+2,y=x-2的图象。
知识宝典
一次函数 y = kx + b(k≠0) 的性质 在一次函数y = kx+b中 (1)当k>0时,y的值随着x值的增大而增大,
图象呈上升趋势;
当k<0时,y的值随着x值的增大而减小,
图象呈下降趋势。
(2)图象经过点(0,b)
下列函数) y 10 x 9
课本87页知识技能第2 题;配套40页。
再见
归纳总结:
一、正比例函数y = kx (k≠0)图象的性质
1、正比例函数 y = kx 的图象都是经过坐
标原点(0,0)的一条直线; 2、(1)当 k>0时,y=kx经过一、三象限,
(2)当 k<0时,y=kx经过二、四象限; 3、(1)当k>0时,y随x的增大而增大。
一次函数的概念PPT课件

20.1 一次函数的概念
概念学习
一般地,解析式形如y kx b (k、b是常数,且k 0)的函数叫做
一次函数(linear function) k是比例系数
一次函数y kx b的定义域是一切实数.
当b 0时,解析式 y kx b就
成为 y kxk是常数,且k 0,
这时y是x的正比例函数.
分析:可设 y kx b
待定系数法
例题3 一直变量x、y之间的关系式是y=(a+1)x+a(其 中a是常数),那么y是x的一次函数吗?
分析:一次函数的解析式是什么样情势的?
y kx b (其中k、b是常数,且k 0)
概念学习 一般地,我们把函数y c(c为常数,) 叫做常值函数(constant function).
正比例函数是一次函数的特例.
例题1
根据变量x、y的关系式,判断y是否是x的一次函数.
(1) y 2x √
(3) x 1 y 2
3√
y 3x 6
(2)
y
1
1 2
x
√
(4) y 2 3
x×
例题2
已知一个一次函数,当自变量x=2时,函数值 y=-1;当x=5时,y=8.求这个函数的解析式.
解:y 50 5x
它是一次函数
(0 x 10)
练习3:已知一次函数图象过点(3,5)与 (-4,-9),求这个一次函数的解析式.
解:设 y kx b 把(3,5)和(-4,-9)分别代入解析式中
得
3k b 5 4k b 9
解得
k b
2 1
函数的解析式为y 2x 1
课堂小结
一次函数 常值函数 待定系数法求函数解析式
概念学习
一般地,解析式形如y kx b (k、b是常数,且k 0)的函数叫做
一次函数(linear function) k是比例系数
一次函数y kx b的定义域是一切实数.
当b 0时,解析式 y kx b就
成为 y kxk是常数,且k 0,
这时y是x的正比例函数.
分析:可设 y kx b
待定系数法
例题3 一直变量x、y之间的关系式是y=(a+1)x+a(其 中a是常数),那么y是x的一次函数吗?
分析:一次函数的解析式是什么样情势的?
y kx b (其中k、b是常数,且k 0)
概念学习 一般地,我们把函数y c(c为常数,) 叫做常值函数(constant function).
正比例函数是一次函数的特例.
例题1
根据变量x、y的关系式,判断y是否是x的一次函数.
(1) y 2x √
(3) x 1 y 2
3√
y 3x 6
(2)
y
1
1 2
x
√
(4) y 2 3
x×
例题2
已知一个一次函数,当自变量x=2时,函数值 y=-1;当x=5时,y=8.求这个函数的解析式.
解:y 50 5x
它是一次函数
(0 x 10)
练习3:已知一次函数图象过点(3,5)与 (-4,-9),求这个一次函数的解析式.
解:设 y kx b 把(3,5)和(-4,-9)分别代入解析式中
得
3k b 5 4k b 9
解得
k b
2 1
函数的解析式为y 2x 1
课堂小结
一次函数 常值函数 待定系数法求函数解析式
一次函数与动点问题市公开课获奖课件省名师示范课获奖课件

思维体操第七节——思空璀璨
如图,在平面直角坐标系xOy中,已知直线PA是一 次函数y=x+m(m>0)旳图象,直线PB是一次函数y= -3x+n(n>m)旳图象,点P是两直线旳交点,点A、B、 C、Q分别是两条直线与坐标轴旳交点. (2)若四边形PQOB旳面积是 112,且CQ:AO=1:2, 试求点P旳坐标,并求出直线PA与PB旳函数体现式;
教材母题变式二:动点与最短途径问题 点P(x,y)在第一象限,且在直线 y=-x+8上, 点A旳坐标为(6,0), (5)当AP+OP最短时,求出点P旳坐标与最短距 离。
思维体操第五节——脑洞大开
教材母题变式三:动点与分段函数问题 点P(x,y)是一次函数y= - x+8图象上任意一点, 点A旳坐标为(6,0),设△OPA旳面积为S,求s 有关x旳函数解析式,并画出函数图象。
思维体操第七节——思空璀璨
如图,在平面直角坐标系xOy中,已知直线PA是一 次函数y=x+m(m>0)旳图象,直线PB是一次函数y= -3x+n(n>m)旳图象,点P是两直线旳交点,点A、B、 C、Q分别是两条直线与坐标轴旳交点. (3)在(2)旳条件下,是否存在一点D,使以A、B、P、 D为顶点旳四边形是平行四边形?若存在,求出点D 旳坐标;若不存在,请阐明理由.
思维体操第六节——思如泉涌
教材母题变式四:含参数旳动点问题 点P(x,8)在第一象限,点A旳坐标为(6,0), 过点P作直线y=x+b交线段OA 于E,设△OPE旳面 积为S ,求S有关b旳函数关系式及自变量b旳取值 范围。
思维体操第七节——思空璀璨
如图,在平面直角坐标系xOy中,已知直线PA是一 次函数y=x+m(m>0)旳图象,直线PB是一次函数y= -3x+n(n>m)旳图象,点P是两直线旳交点,点A、B、 C、Q分别是两条直线与坐标轴旳交点. (1)用m、n分别表达点A、B、P旳坐标及∠PAB旳度 数;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
你能写出关于x的一次式的一般形式吗?
即上面的函数的形式都是y=kx+b的形式
一般地,形如y=kx+b(k,b是常数,k≠0)
的函数,叫做一次函数.
当b=0时,y=kx+b就变成了y=kx,所以 说正比例函数是一种特殊的一次函数.
正比例函数
一次函数
以上五个一次函数对应的正比例函数为:
一次函数
对应的正比例 函数
(1)有人发现,在20~50 ℃时蟋蟀每分鸣叫的次数c与温度 t(单位: ℃)有关,即c的值约是t的7倍与35的差; (2)一种计算成年人标准体重G(单位:千克)的方法是,以 厘米为单位量出身高值h,再减去常数105,所得差是G的值; (3)某城市的市内电话的月收费额y(单位:元)包括:月租 费22元,拔打电话x分的计时费(按0.1元/分收取); (4)把一个长10cm、宽5cm的长方形的长减少x cm,宽不 变,长方形的面积y(单位:平方厘米)随x的值而变化
1、怎样的函数是一次函数? 一般地,形如y=kx+b(k,b是常数,k≠0) 的函数,叫做一次函数。 当b=0时,y=kx+b就变成了y=kx,所以说 正比例函数是一种特殊的一次函数。 2、一次函数的简单应用。
这节课的收获:
作业:
1、课本114页第3题; 2、完成本节课的配套练习.
(2)由题意得k-2≠0, k≠2,所以k≠2时,此 函数为一次函数
一个小球由静止开始在一个斜坡向下滚动,其 速度每秒增加2米/秒. (1)求小球速度v(单位:米)随时间t (单位:秒)变化的函数关系式,它是一次函数 吗? (2)求第2.5秒时小球的速度
解: (1)v=2t(t>0) (2)当时间t=2.5时,v=2×2.5=5(米/秒)
(4)y=-0.5x-1
它是一次函数,不是正比例函数
1.若y=(k+3)x+(b-2)是关于x的一次函数, 则k的取值为_______,b的取值为_______
)此函数为正比例函数 (2)此函数为一次函数
1 1 ,所以当 k 解:(1)由题意, 得2k+1=0,k= 2 52 y 时,函数为正比例函数 2
下列函数哪些是一次函数,哪些又是正比例 函数? (1) y 8 ; (2) y 8 x;
x 2 (3) y 5 x 6; (4) y 0.5 x 1
解:(1) y
(2)y=8x
8 x 它不是一次函数,也不是正比例函数
它是一次函数,也是正比例函数
(3)y=5x2+6 它不是一次函数,也不是正比例函数
这个函数也可以写成
y 6 x 5
当登山队员由大本营向上登高0.5km时,他们所在 位置的气温就是当x=0.5时函数 y 6 x 5 的值, 即y=-6×0.5+5=2℃
这个函数与我们 上节所学的正比例函 数有何不同?它的图 像又具备什么特征? 我们这节课将学习这 些问题。
合作探究:下列问题中的对应关系可用怎 样的函数表示?这些函数有什么共同点?
图中登山队大本营所 在地的气温为15℃,海拔 每升高1km,气温下降6 ℃.登山队员由大本营向上 登高xkm时,他们所处的位 置的气温是 y℃.试用解析 式表示y与x的关系.
分析:y随x的变化规律是,从大本营向上 当海拔增加x千米时,气温从5 ℃减少6x ℃. 因此y与x的关系为
y 5 6x
C=7t-35
G=h-105
y=0.1x+22 y=-5x+50
在前面我们得到了这样几个
式子:
(1)y=-6x+5; (2)C=7t-35; (3)G=h-105; (4)y=0.1x+22; (5)y=-5x+50 (0 x 10) .
大家观察上面的几个式子,看它们 有什么共同的地方?
这些函数的解析式都是用自变量的整式来 表示的,并且自变量的次数都是一次的,都是自变 量的k(常数)倍与一个常数b的和的形式.
y 6 x 5
c 7t 35
G h 105 y 5x 50
y 0.1x 22
y 6 x
c 7t
Gh
y 5 x
y 0.1x
例1、 下列哪些函数是一次函数,哪些又是 正比例函数.
7 (1) y 3 x 4; ( 2) y ; x 2 (3) y 9 x;( 4) y 4 x 1; (5) m 2 x 6.
