第二节 柱面透镜
球柱面透镜光学技术--圆柱透镜与环曲面透镜

+3.00D
+5.00D -2.00D
+3.00DS/+2.00DCx170
+5.00DS/-2.00DCx80
例:请将-1.25DCx60/+2.75DCx150转换成球
柱镜形式。
解:-1.25DS/+4.00DCx150
+2.75DS/-4.00DCx60
球柱面透镜的联合最方便直观的方法是用光 学十字图,或者也可分别联合球面镜、柱面镜,使
另一新柱镜屈光力等于原球镜与柱镜屈光力之和, 其轴与原柱镜轴的方向相同
例:将+4.00DS/+1.00DCx90转换为正交柱镜 解一: 一个新柱镜: +4.00DCx180 另一新柱镜: (+4.00+1.00)x90 = +5.00DCx90 正交柱镜形式:+4.00DCx180/+5.00DCx90
45
-3.00D +2.50D +2.75D +2.50D -1.00D +1.25D -3.00D +2.50D +2.75D -1.50D
+0.75D +1.75D
135
+2.50D +0.75D -1.75D
+2.50DS/-1.75DCx45
+0.75DS/+1.75DCx135
解2:(2)/(3)联合结果为
(+2.50+2.75)DS/(-1.00+1.25)DCx135
+5.25DS/+0.25DCx135
关于球柱镜的联合与转换课件

作: • -2.00DS./-5.00DS.等等。
8
球面透镜的联合
• 球面透镜之间的联合结果,可用求代数和 的方法来获得。即球镜与球镜的直接相互 加减
• 如-3.00DS/-2.00DS=-5.00DS • -3.00DS/+4.00DS=+1.00DS
• 新轴位:若原轴位小于、等于90º的加90º, 大于90º的减90º。
23
拼
搏
奉 献
• 例:-1.00/+2.00*60
+1.00/-2.00*150
追 求
• +0.50/-0.50*170
卓
越
+0.50*80
24
处方写成光学十字线
拼
搏奉 献Leabharlann • 球镜 +3.00
+3.00
+3.00
追 求
• 柱镜 -2.00*90
关于球柱镜的联合 与转换
1
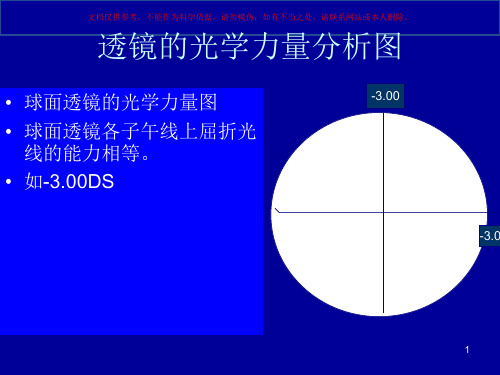
透镜的光学力量分析图
• 球面透镜的光学力量图
-3.00
• 球面透镜各子午线上屈折光 线的能力相等。
• 如-3.00DS
-3.0
2
透镜的光学力量图
-3.00
• 柱面透镜的光学力量图 • 柱面透镜各子午线上的
屈光力不等,且按规律 周期变化着。 • 如-3.00DC×180
3
19
球柱面透镜的联合
• 1.同轴位球柱面透镜的联合: • 也可用求代数和的方法获得联合结果。 • 如: • +1.00DS/+0.50DC×90/-l.50DS/-
柱透镜相位表达式

柱透镜相位表达式:从光的角度解读柱透镜在现代科学中,光学领域一直是一个备受关注的领域。
光学作为一门关于光的传播、反射、折射、干涉、衍射和偏振等现象的学科,其应用范围非常广泛。
在光学领域中,柱透镜相位表达式是一个非常重要的概念。
那么,什么是柱透镜相位表达式呢?柱透镜是一种常见的光学元件,它是一种具有圆柱形或椭圆柱形的透镜。
柱透镜主要用于矫正眼部的散光,同时也被广泛应用于激光加工、光学通讯、生物医学等领域。
柱透镜相位表达式是描述柱透镜的光程差的数学表达式,它是柱透镜的重要性质之一。
柱透镜相位表达式的具体形式为:φ(x,y) = k * x^2 / (2f) + k' * y^2 / (2f)其中,φ(x,y)表示柱透镜在(x,y)处的相位延迟,k和k'分别是柱透镜的两个主要曲率半径,f是柱透镜的等效焦距。
从柱透镜相位表达式中可以看出,柱透镜的相位延迟与柱透镜的曲率半径和等效焦距有关。
其中,曲率半径越大,相位延迟越小;等效焦距越小,相位延迟越大。
通过调节柱透镜的曲率半径和等效焦距,可以控制光线的相位延迟,从而达到矫正眼部散光、调节光路等目的。
除了在眼科医学中的应用外,柱透镜还被广泛应用于激光加工、光学通讯、生物医学等领域。
例如,在激光加工领域,柱透镜可以用于调节激光束的形状和大小,从而实现更精确的加工效果;在光学通讯领域,柱透镜可以用于调节光信号的传输和接收,从而提高光信号的质量和传输距离;在生物医学领域,柱透镜可以用于调节激光束的聚焦和扩散,从而实现更精确的光学成像和治疗效果。
柱透镜相位表达式是描述柱透镜的光程差的数学表达式,它是柱透镜的重要性质之一。
通过调节柱透镜的曲率半径和等效焦距,可以控制光线的相位延迟,从而达到矫正眼部散光、调节光路等目的。
柱透镜在激光加工、光学通讯、生物医学等领域也有广泛的应用。
眼镜学课件 3 球面透镜

第一节 透镜
透镜的概念 由前后两个折射面组成的透明介质称为透镜(lens),这两 个折射面至少有一个是弯曲面
第一节 透镜
透镜的概念 1、球面:各子午线屈光力相同 2、柱面:一条子午线为直线,与之垂直的子午线屈光力最大 3、环曲面:各子午线屈光力不同,最大与最小屈光力子午线
相垂直 4、非球面:整个表面屈光力不一致 5、平面:可看作特殊的球面(曲率半径无穷大)
已知物体距离+1.00D的凸透镜50cm,求像的位置。 解:根据1/u+1/f=1/v
1/(-0.5)+1=1/v v=-1m (成像在透镜左侧1m处)
第二节 球面透镜
概念 球面透镜(spherical lens)(简 称球镜)指前后表面均为球面,或 一面为球面,另一面为平面的透 镜。
球面透镜
凸凹透镜的凹度大于凸度
光学性质
光学作用-遵从折 射定律
当光线通过双凸透 镜的前后两个面, 都分别发生会聚, 因此双凸透镜使光 线会聚
θ1 θ2
n入<n折 θ1>θ2
θ1
θ2
n入>n折 θ1<θ2
球面透镜的光学作用
当光线通过双 凹透镜的前后 两个面,都分别 发生发散,因此 双凹透镜使光 线发散
光轴上成一个点。
薄透镜的焦点
由光轴上的特定点发出的光线,通过球面透镜后出射为 平行光线,这样的点称为球面透镜的第一焦点(F1), 也称为物方焦点。
薄透镜的焦点
第一焦点也可定义为与光轴上正无穷远处的像共轭的光 轴上的物点。
环曲面透镜(toric lens) 指一个面是环曲面(轴向上有 最小屈光力≠0,与最大屈光力方向垂直),另一个面是 球面或平面的透镜。
第二节柱面透镜

– 正柱面透镜
– 负柱面透镜
4
柱面透镜
• 主子午线:
– 轴向子午线:与轴平行 的子午线,在柱面上是 平的,没有弯度。 – 屈光力子午线:与轴垂 直的子午线,在柱面上 的圆形的,弯度最大。
5
光学特性(1)
——光线通过轴向子午线 (图中垂直方向)不会 出现聚散度的改变。 ——光线通过屈光力子 午线(图中水平方 向) 会出现聚散度的改 变。
25
②两柱镜正交密接,若两柱镜屈光 力不等,则联合后等效为一新球柱 透镜。
• [例]求+1.00 DC×90/+3.00 DC×180的等 效屈光力。 • 解: 依题意画光学十字图为:
26
两密接斜交柱镜的联合
• 正切公式法 F1xθ1/F2x θ2 tan2 θ=————
F1+F2cos2 α F2sin2α
20
柱面透镜的正交联合
• 轴位互相垂直,柱镜度相同
– 效果为一个球镜,球镜度为柱镜的度数
• 轴位互相垂直,柱镜度不相同
– 构成一个球柱面透镜
21
两柱镜同轴向的密接联合
• 若两柱镜轴向相同,密接组合后的屈光 力为两柱镜屈光力的代数和,轴向与原 柱镜相同。
22
求+1.75DC×90/-1.75DC×90的等 效屈光力。
n 1 F r
曲率半径 r
• 轴向上屈光力为0
10
柱镜中间方向的屈光力
• 在柱镜轴向与垂轴方向之间任意方向的 屈光力计算公式:
F F sin 2
θ为所求的子午线方向 与柱镜轴的夹角
11
F=-4.00 DC×180,求30°、60° 方向的屈光力。
关于柱面光学透镜在光学成像系统中的运用

关于柱面光学透镜在光学成像系统中的运用作者:朱让甜来源:《中国新技术新产品》2014年第09期摘要:在非球面透镜中柱面镜是最普遍的一种,采用球面系统具有分别描述成像的特点,在一些特殊场合其具有特殊作用。
本文主要分析了柱面光学透镜成像原理,柱面光学透镜反射光线追迹,柱面光学透镜在光学成像系统中的运用。
关键词:柱面光学透镜;光学成像;运用中图分类号:O436 文献标识码:A一、柱面光学透镜成像原理(一)平面镜物体在静止的平面镜中出现的反射,这一结论来自于光学传播的基本定律。
分析虚像原理,可以简单理解为物体对镜平面产生的对称形体。
(二)柱面镜将曲面作为反射面时,入射光线与过曲面形成的成像点法线产生的角便是入射角,是相当于反射光线和同一法线之间产生的反射角,并且在同一平面内产生了入射光线、反射光线和法线,这个平面和过曲面产生的成像点切平面彼此垂直。
但是,在过曲面上由于各点比不是彼此平行的法线方向,例如:柱面法线垂直相交柱轴的很多叉线。
因此,所谓的柱面反射的虚像缺少固定的位置能够寻找,而是随着视点不同位置而出现了差异。
二、柱面光学透镜反射光线追迹将圆柱反射面光线反射作为追迹范例,在圆柱面顶点位置A构建直角右手坐标系,促使AX平行于圆柱面母线,坐标面的子午截面是AXZ。
如此,假如圆柱面设a为曲率半径,与坐标面OYZ平行的任意平面去截圆柱面时,都是在平面AXZ上获得截线,半径是a的圆。
在AXY存在于物面上的点D(X,Y,Z)沿着适量C方向发出一光线,光线在圆柱面上的投射点d1可以通过点d和适量c,促使d成为物面A点到d点的位置向量;圆柱面定A1至投射点a1的位置向量;N则是从A1到垂直于光线的向量,在两表面间线段的光纤通过垂直划分为两部分;分别是从A1向C1产生的辅助向量。
三、柱面光学镜在光学成像系统中的运用(一)单面柱面光学镜在光学系统应用仅在一个方向上柱面镜有曲率,利用柱面反射镜光纤矢量追迹可知,一个截面维度方向对于平行光束来说产生了会聚或者发散功能,但是不会对X轴方向发挥任何作用。
3.2球柱面透镜

•
+4.00DS
6.1环曲面概念
• 弧绕某一直线旋转得到的面叫环曲面.
6.2环曲面的两个弧
① 曲率最小的圆弧称为基弧. ② 曲率最大的圆弧称为正交弧. ③ R基>R正,则F基<F正.
F n 2 n1 r
6.3环曲面透镜的类型
① 内散片(凹环曲面镜片).环曲面在内表面 ② 外散片(凸环曲面镜片).环曲面在外表面
+3.00
• +5.00DS/-2.00DC×90
+5.00
Hale Waihona Puke =+5.00
+5.00 0
+2.00 0
0 -2.00
• 例3-2-2
4.Jackson正交叉柱镜
• 4.1用途
• 检查眼有无散光或散光后是否 完全矫正。
• 4.2规格
• ±0.25D,±0.50D • 4.3使用
5.球柱面透镜的转换
+5.00
+2.00
-6.00
+13.00
+5.00
0
-7.00
+13.00
解:
13.00DS
6.00DC 180/ 8.00DC 90
+6.00 -6.00
+1.00 +1.00
练习
• 例3-2-12 将球柱镜+5.00DS/+2.00DC×180改写为球弧 屈光力为+4.00DS的环曲面镜片形式.
• 例3-2-8请写出图中内散片的处方.
解:
6.00DS
3.00DC 180/ 6.00DC 90
球面屈光力 基弧屈光力 轴向/正交弧屈光力 轴向
球柱镜的联合和转换课件
7
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
球面透镜的联合
• 球面透镜之间的联合结果,可用求代数和 的方法来获得。即球镜与球镜的直接相互 加减
• 如-3.00DS/-2.00DS=-5.00DS • -3.00DS/+4.00DS=+1.00DS
-3.00
• 柱面透镜的光学力量图 • 柱面透镜各子午线上的
屈光力不等,且按规律 周期变化着。 • 如-3.00DC×180
2
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
透镜的光学力量图
• 球柱透镜的光学力量
• 如-3.00DS/-1.00DC×180
• 透镜力量水平和水平相加,垂直和垂直相 加
ቤተ መጻሕፍቲ ባይዱ14
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
柱面透镜的联合
• 柱镜联合口诀
• 以小为球,两差为柱,轴对大数。
• 如-2.00DC×180/-1.00DC×90
• 等于-1.00DS/-1.00DC×180
-2.00
• 可以力量图予以论证
-1.00
15
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
18
文档仅供参考,不能作为科学依据,请勿模仿;如有不当之处,请联系网站或本人删除。
球柱面透镜的联合
• 1.同轴位球柱面透镜的联合: • 也可用求代数和的方法获得联合结果。 • 如: • +1.00DS/+0.50DC×90/-l.50DS/-
眼镜学-教学大纲

《眼镜学》课程教学大纲一、课程简介(一)课程代码: 1221051001(二)课程名称(含英文名称):眼镜学(Ophthalmic Optics)(三)课程类别:专业核心(四)修读对象:眼视光学专业(五)总学时与学分:81学时。
其中理论36学时、实验45学时。
4.5学分。
(六)相关课程:学习本课程前应具备几何光学和眼视光学基础知识。
眼镜学是研究眼镜及其应用的一门科学,它不仅涉及光学、材料学、化学和机械学等传统学科,同时作为一种医疗器具,它还与眼球生理学、眼科学、视光学、双眼视觉学和医学心理学等医学课程有着密不可分的联系。
二、教学目的和教学方法教学目的:眼镜学作为四年制眼视光学专业的一门重要的教学基础必修课程,其学习任务是掌握眼镜学中专业术语的定义和意义,掌握眼镜片的基本理论、基本知识和眼镜的安装工艺等,以及学会将这些知识应用于其他相关专业课程,做到融会贯通和综合运用。
同时,了解眼镜行业的最新动态,例如眼镜片设计和眼镜片材料等的新进展及其应用。
教学方法:1.以大课方式,采用多媒体课件,讲授理论与图片、视频实践相结合为主要教学手段。
2.自学形式,学员利用网络资源进行自学。
3.适当采用临床病例讨论教学。
三、理论与实践教学学时分配四、选用教材和主要教学参考书选用教材:理论课教材:《眼镜学》瞿佳主编人民卫生出版社2011实验课教材:《眼镜学实训指导》瞿佳主编人民卫生出版社2011参考书目:Mo Jalie, The Principles of Ophthalmic Lenses《眼镜技术》瞿佳主编高等教育出版社2005Brooks & Borish, System for Ophthalmic DispensingMo Jalie, Ophthalmic Lenses & Dispensing五、理论教学内容第一章绪论主要讲授内容:第一节:眼镜光学基本原理;第二节:眼镜学的地位与学习意义;学好眼镜学应建立的几个观点;第三节:眼镜的历史和发展。
矫正散光的透镜·

焦线的位置 及 可据 C1C2Ccos2()
22
C1C2CCCco2(s) 2 22
SCsi2n()及
F()SCsi2(n)求出
S C1 C2 C 2
由此可得镜片至最小弥散圆的距离:
ta2nC1sin1C2sin2 C1co1sC2co2s
该距离以屈光度的形式表示为: CC1sin1C2sin2 si2n
C 最小弥散圆的直径S 1 为:
1
1
一散光透镜 S
2
,直径 C2 2 ,求透镜前 SS1S2C1C22C
的物点发出的光经透镜后所成焦线及最小弥散圆的位置及大小。
n
n
解:已知
S, C, (轴向 ), (轴 Ci sin 2i tan 2 i1 n Ci cos 2 i i 1
由扁椭圆过渡为长椭圆的过程中一定会有 一个圆形,称为最小弥散圆
前焦线与后焦线的间隔称为Sturm间隔, 它的大小表示了散光的大小。
2.散光光束中各参数的计算
透镜到前焦线的距离为 ;透
F()F()F() 镜到为度到 最 前 ;后小焦透焦弥线镜线散长直的圆度径距的;为12C121cC21coc离距21oso2C(1ss2is12n)i1CCn2c2c2coo22(2osCs2s22i)s2为离为,ni2n 12c2o(C1c为后s2o1C2cs2o2)s12i(C1ns2i1nC2s22i2)nC焦;为12C22C1c2o(s1)2C2c2o(s2)线透;S2Ct1co2(us1)长镜2C2cro2(s2)m
为任意方向
220 透镜在 0.7 方向的屈光力为多少?
(二) 斜交柱镜的叠加
1.公式法
将两个柱镜片,138 和2 ,合成为一新的镜片,新镜片
柱面镜准直原理

柱面镜准直原理
柱面镜是一种特殊形状的镜子,它的表面是一个圆柱体的侧面。
柱面镜的准直原理是如何实现光线的聚焦和平行化的呢?
我们需要了解光线的传播方式。
光线在空间中传播时,会呈现直线传播的特性,但当光线遇到物体或介质的边界时,会发生折射和反射。
柱面镜利用这一特性,通过其特殊形状将光线进行反射和折射,实现光线的准直。
柱面镜的准直原理可以简单地理解为:当一束光线垂直入射到柱面镜上时,经过反射和折射后,光线会在柱面镜的焦点上聚焦。
同样,当一束光线从柱面镜的焦点射出时,经过反射和折射后,光线会变为平行光。
柱面镜的准直原理可以通过以下实例来说明。
假设我们有一个凸透镜,它的表面是一个圆柱体的侧面。
当一束光线垂直入射到凸透镜上时,光线会经过反射和折射,最终会在凸透镜的焦点处聚焦。
同样,当一束光线从凸透镜的焦点射出时,光线会经过反射和折射,最终变为平行光。
柱面镜的准直原理在许多应用中发挥着重要作用。
例如,在光学仪器中,柱面镜可以用来聚焦和平行化光线,以便进行精确的测量和观察。
在激光器中,柱面镜可以用来调整激光束的形状和方向。
在太阳能集热器中,柱面镜可以用来聚焦太阳光,提高能量的利用效
率。
总结一下,柱面镜的准直原理是通过其特殊形状将光线进行反射和折射,实现光线的聚焦和平行化。
柱面镜在许多领域中都有重要的应用,为光学仪器、激光器和太阳能集热器等提供了有效的光学功能。
通过深入理解柱面镜的准直原理,我们可以更好地应用它们,推动光学技术的发展。
眼镜学课件 3 球面透镜

球镜的面屈光力
例3:水和玻璃之间的界面为凸球面,水的折射率为 1.33,玻璃的折射率为1.53,球面的曲率半径为20cm, 光线从水进入玻璃,则此界面的屈光力为多少?
F = (n2-n1)/r
水
玻璃
= (1.53-1.33)/0.2
概念 球面:由一个圆或一段 弧绕其直径旋转而得
球面透镜的分类
凸透镜(convex lens) 中央厚、周边薄的球镜。凸透 镜对光线有会聚作用,也称为会聚透镜(converging lens)。
凹凸透镜的凸度大于凹度
球面透镜的分类
凹透镜(concav e lens) 中央薄、周边厚的球镜。凹透 镜对光线有发散作用,也发称为发散透镜(diverging lens)
= + 1.00D
球镜的面屈光力
例4:光线从空气经过凹球面进入玻璃,空气折射率为 1.00,玻璃为1.50,界面曲率半径为5cm,则界面的屈光 力为多少?
空气
玻璃 F = (n2-n1)/r
= (1.50-1.00)/(-0.05)
= -10.00D
薄透镜屈光力
如果忽略透镜的中央厚度,透镜的屈光力取决于其前后
透镜的分类
如果中央厚度不能忽略,则称为厚透镜。 对于一般的眼镜片,凹透镜的中央厚度较薄,可以按照薄
透镜的公式计算;而凸透镜,尤其是度数高、中央厚度大、 前后表面较弯的,运用薄透镜的公式则容易造成较大的 偏差。
透镜的成像(薄透镜成像)
相关概念 1.光轴(optical axis) 连接透镜前后表面光学中心的连线 2.焦点(第二焦点,像方焦点,F2)
柱面透镜-文档

柱面透镜20世纪中期,随着科学技术的进步。
电影开始向大画面、大视野、立体感、临场感方向发展,宽银幕电影于1953年问世,它的产生和发展同宽银幕放映镜头(核心部件为柱面透镜)的出现和发展息息相关。
1 变形宽银幕格式制作的两种方式电影发展到今天,尽管产生了各种各样的画幅格式,但是使用最多的画幅格式仍是185:1遮幅和2 40:1宽银幕格式。
1.85:1是最常用的画幅格式,任何35mm摄影机都兼容这种画幅格式。
2.40:1宽银幕结合了视觉效果的因素,增强了身临其境的感觉。
提高了电影艺术的感染力。
2.40:1宽银幕格式的制作方式有两种:一是拍摄时采用变形镜头将影像横向压缩,放映时又用变形镜头将被压缩的影像复原;二是使用普通摄影镜头拍摄的超35mm格式,成像在底片上的画幅尺寸为24.00mm×18.00mm,后期处理时。
将底片面积进行遮挡(将画面垂直向进行裁切),使画面比例达到2.40:1。
然后通过光学变形镜在水平方向以2:1方式的压缩。
将画面放大、转换到中间片上。
2 普通电影的放映物镜最简单的放映物镜由两片透镜组成,其中一个是凸透镜,另一个是凹透镜。
放映物镜除了应使放映像具有良好的像质外,还应有利于像照度的提高,故应有尽可能大的相对孔径。
电影放映物镜的相对孔径一般为1/2~1/2。
在像质要求方面,球差、慧差、色差等宽光束像差应予以特别重视。
对于视场不大的电影放映物镜,常应用匹兹凡型物镜,因它对于小视场范围内的物体有良好的像质。
当视场较大或对像质有更高的要求时,应采用消像散物镜。
柯克物镜、天塞物镜和双高斯物镜都可用作放映物镜。
是一种普通银幕放映的大孔径、较大视场的镜头,相对孔径可达1:1.6。
3 宽银幕电影的放映物镜宽银幕放映物镜与普通银幕放映物镜的成像关系不同。
被它成像的画面是一张“变形”的图片,图片上的景物与实物的比例因方位而异。
在子午方向上有一个固定的比例,在弧矢方向上有一个固定的比例。
通用的宽银幕放映物镜是由普通放映物镜和变形镜组组合起来的,其中变形镜组在子午和弧矢方向上具有不同的放大率,这两种放大率恰恰与电影图片上的子午和弧矢放大率匹配,放映后使银幕上重现原景的正常图样。
3.2柱面透镜

• 课本例1:
3.柱面透镜的屈光力及处方形式
• 3.2斜向镜度
• Fθ=Fsin2θ
• Fθ表示与柱镜轴成θ角方向 的镜度 • F表示垂直于轴的最大镜 度. • θ表示柱镜某一方向与轴的 夹角.
处方示例1(Fmax的方位表示)
• 右眼(OD或RE):+10.00DC ×180
• 左眼(OS或LE):+10.00DC ×180
图中柱镜的轴向用蓝色标示,即是 R120 L60
• 4.1柱面透镜的轴向标 示 • 4.1.1鼻端轴向标示法 • 4.1.2标准标示 法)TABO法) • 4.1.3太阳穴标示法
图中柱镜的轴向用蓝色标示,即是 R60 L60
• 4.1柱面透镜的轴向标 示 • 4.1.1鼻端轴向标示法 180 • 4.1.2标准标示 法)TABO法) • 4.1.3太阳穴标示法 • 例题4 下列轴系以鼻端轴
2.柱面透镜的光学特性
• 2.3柱镜各子午线 上屈光力不等, 且按规律周期性 变化。
• 2.4柱镜的视觉像移。 • 2.4.1平移 • (1)沿柱镜的轴平移 时,像无变化。 • (2)沿最大屈光力方 向(即与轴垂直方向) 平移时: • 正柱镜的逆动; • 负柱镜的顺动。
• 2.4柱镜的视觉像移。 • 2.4.2柱镜的剪动。
(3)R105 L105
75
105
0
180
0
5.1柱面透镜性质的识别
一个方向无像移,其它方向有像移——柱镜; 一个方向无像移,其它方向顺动——凸柱镜; 一个方向无像移,其它方向逆动——凹柱镜
*看镜片边缘厚度,厚度一致时为球镜。厚度不一致时,可能有柱镜成分 或为棱镜。 *旋转镜片,有剪动的就是柱镜或有柱镜成份。
柱面菲涅耳太阳聚光透镜的光学设计和光学效率

柱面菲涅耳太阳聚光透镜的光学设计和光学效率【柱面菲涅耳太阳聚光透镜的光学设计和光学效率】一、引言柱面菲涅耳太阳聚光透镜是太阳能领域中的一项重要技术,它通过聚焦太阳光线来产生高温能量,可用于太阳能发电、热能利用等领域。
本文将以柱面菲涅耳太阳聚光透镜的光学设计和光学效率为主题,深入探讨其原理、设计方法和性能评估。
通过对其光学设计的深入分析,将帮助读者更全面、深入地理解柱面菲涅耳太阳聚光透镜及其在太阳能利用中的应用。
二、柱面菲涅耳太阳聚光透镜的原理柱面菲涅耳太阳聚光透镜的原理基于菲涅耳镜的设计思想,通过曲面微透镜的阵列结构,将太阳光线聚焦到光电转换器上,实现高效地光学聚光。
其核心原理在于利用柱面透镜的曲面结构和菲涅耳透镜的微透镜结构,将太阳光线聚焦到一个小点上,提高光照强度,从而提高光电转换效率。
在设计过程中,需要考虑透镜的表面形貌、阵列的布局和光线的折射、反射等特性,以实现光线的高效聚光和能量的有效利用。
三、柱面菲涅耳太阳聚光透镜的光学设计1. 表面形貌设计柱面菲涅耳太阳聚光透镜的表面形貌设计是关键的一步,它直接影响着光线的聚光效果和光学效率。
通过数值分析和优化算法,可以确定透镜的曲率半径、微透镜的尺寸和间距等参数,以实现近似理想球面或抛物面的形貌,并保证透镜表面的光学质量。
2. 阵列布局设计透镜阵列的布局与间距设计对光学效率有着重要影响,合理设计的阵列布局可有效减小透镜之间的遮挡和光损失。
常见的布局包括方形、六边形等,对于特定的光子通量密度和透镜数量要求,需要进行系统的优化设计,以实现最佳的聚光效果。
3. 光线折射反射模拟在光学设计过程中,需要进行光线的折射和反射模拟,分析光线在透镜表面的传播路径和相互作用,以评估透镜的聚光性能和光学效率。
通过光学仿真软件进行模拟分析,可以对透镜设计参数进行优化,以实现更高的光学性能和能量利用效率。
四、柱面菲涅耳太阳聚光透镜的光学效率评估1. 光学聚光效果评估光学效率的评估主要包括聚光效果、光子集中度等指标,通过实际测试和数值仿真,可以评估透镜的聚光性能和光学聚光效果,验证设计参数的合理性和优化结果的有效性。
第二节柱面透镜

太阳穴标示法
18
柱面透镜的表达式
• 记录柱镜度和轴位
0 +3.00
• 规范记录方法:+3.00DC×90 • 表示+3.00D的柱面透镜,轴在90°方向
19
柱面透镜的正交联合
• 正交柱镜
– 两个柱面透镜轴向相同或互相垂直,并紧密 贴合
• 同轴位的柱面透镜联合
– 效果为一个柱镜,柱镜度为两者的代数和
透镜概述
• 什么是透镜
– 弯曲面
球面
柱面
环曲面
1
柱面透镜 cyl
• 概念:由圆柱体玻 璃的一部分截制而 成
2
柱面透镜
• 柱面
– 柱面的轴 – 柱面的主子午线
• 柱面在与轴平行的方向 上是平面
• 柱面在与轴垂直的方向 上是圆形的,弯度最大
• 这两个方向称为柱面的 两条主子午线方向。
3
柱面透镜
• 一个柱面和一个平面组成
6
光学特性(2)
——凡与柱镜轴成直角 方向的平行投射光 线,其屈折作用视 凸柱镜或凹柱镜而异。
• 光线通过柱面透镜, 将形成一条焦线
– 焦线与轴向平行
7
(3)柱镜各子午线上屈光力不等,且 按规律周期性变化。
(4)通过移动的镜片观 察目标也在移动的 现象。
8
视觉像移与旋转试验
9
屈光力
• 柱面透镜的屈光力
23
两柱镜轴向正交的密接联合
• 两柱镜轴向互相垂直而密接联合,称为 正交联合。 ①两柱镜正交密接,若两柱镜屈光力相 等,则联合后其等效透镜为一球面透镜, 其屈光力与原柱镜屈光力相同。
24
[例]求+0.50 DC×180/+0.50 DC×90的 等效屈光力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正柱面透镜 负柱面透镜
5
柱面透镜
主子午线:
轴向子午线:与轴平行的 子午线,在柱面上是平的 ,没有弯度。
屈光力子午线:与轴垂直 的子午线,在柱面上的圆 形的,弯度最大。
6
光学特性(1)
——光线通过轴向子午线 (图中垂直方向)不会 出现聚散度的改变。 ——光线通过屈光力子 午线(图中水平方 向) 会出现聚散度的改 变。
sin2θ= F2 sin2α C
29
作图法
B O
C A
30
效果为一个球镜,球镜度为柱镜的度数
轴位互相垂直,柱镜度不相同
构成一个球柱面透镜
22
两柱镜同轴向的密接联合
若两柱镜轴向相同,密接组合后的屈光力为两 柱镜屈光力的代数和,轴向与原柱镜相同。
23
求+1.75DC×90/-1.75DC×90的 等效屈光力。
24
两柱镜轴向正交的密接联合
两柱镜轴向互相垂直而密接联合,称为正交联 合。 ①两柱镜正交密接,若两柱镜屈光力相等, 则联合后其等效透镜为一球面透镜,其屈光力 与原柱镜屈光力相同。
25
[例]求+0.50 DC×180/+0.50 DC×90的等效屈光力。
解:
即: +0.50 DC×180/+0.50 DC×90=+0.50 DS。
26
②两柱镜正交密接,若两柱镜屈光 力不等,则联合后等效为一新球柱 透镜。
[例]求+1.00 DC×90/+3.00 DC×180的等 效屈光力。
第二节 柱面透镜
1
透镜概述
什么是透镜
弯曲面
球面
柱面
环曲面
2
柱面透镜 cyl
概念:由圆柱体玻 璃的一部分截制而 成
3
柱面透镜
柱面 柱面的轴 柱面的主子午线
柱面在与轴平行的方向上 是平面
柱面在与轴垂直的方向上 是圆形的,弯度最大
这两个方向称为柱面的两 条主子午线方向。
4
柱面透镜
F n 1 r
曲率半径 r
轴向上屈光力为0
11
柱镜中间方向的屈光力
在柱镜轴向与垂轴方向之间任意方向的屈光力 计算公式:
F F sin 2
θ为所求的子午线方向 与柱镜轴的夹角
12
F=-4.00 DC×180,求30°、 60° 方向的屈光力。
F30=-4× sin2 30°=-4×1/4=-1.OO DC F60=-4×sin2 60°=-4×3/4=-3.00 DC
13
柱面透镜的表示方法
光学十字
14
柱面透镜的表示方法
0 +3.00
表示:
柱面透镜的两条主子午线在水平和垂直方向上 垂直方向为轴向,屈光力为零 水平方向屈光力最大,为+3.00D
15
鼻端轴向标示法
16
标准标示法(TAB0法)
17Biblioteka 轴向标示法国际标准轴向标示法(TABO法)
18
太阳穴标示法
7
光学特性(2)
——凡与柱镜轴成直角 方向的平行投射光 线,其屈折作用视 凸柱镜或凹柱镜而异
。 光线通过柱面透镜,
将形成一条焦线
焦线与轴向平行
8
(3)柱镜各子午线上屈光力不等,且 按规律周期性变化。
(4)通过移动的镜片观 察目标也在移动的 现象。
9
视觉像移与旋转试验
10
屈光力
柱面透镜的屈光力
解: 依题意画光学十字图为:
27
两密接斜交柱镜的联合
正切公式法 F1xθ1/F2x θ2 tan2 θ=——F2—sin2—α
F1+F2cos2 α
S=F1sin2 θ+F2sin2 (α-θ) C=F1+F2-2s
28
汤普森公式法
C= F12 F22 2F1F2cos2
S= F1 F2 C 2
19
柱面透镜的表达式
记录柱镜度和轴位
0 +3.00
规范记录方法:+3.00DC×90 表示+3.00D的柱面透镜,轴在90°方向
20
柱面透镜的正交联合
正交柱镜
两个柱面透镜轴向相同或互相垂直,并紧密贴合
同轴位的柱面透镜联合
效果为一个柱镜,柱镜度为两者的代数和
21
柱面透镜的正交联合
轴位互相垂直,柱镜度相同
