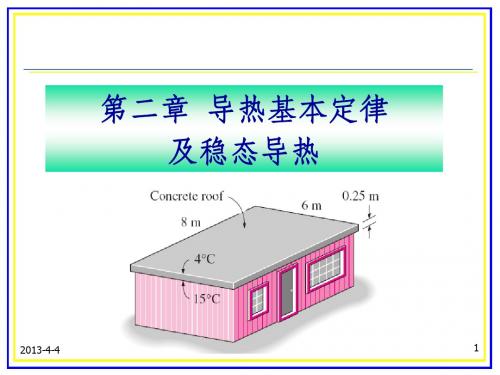
第二章 稳态热传导(导热理论基础)
合集下载
第2章-导热理论基础以及稳态导热2

导热微分方程式
t t t t & c ( ) ( ) ( ) x x y y z z
非稳态项 扩散项 源项
笛卡尔坐标系中三维非稳态导热微分方程的一般表达式。 物理意义:反映了物体的温度随时间和空间的变化关系。
t t t t & c ( ) ( ) ( ) x x y y z z
(1)第一类边界条件:已知导热体边界上的温度值: 稳态导热: tw= const 非稳态导热: tw = f (τ) 例: x=0, t =tw1 x=δ, t =tw2
(2)第二类边界条件: 已知物体边界上热流密度值:
t qw ( ) w 根据傅里叶定律: n t qw ( )w n
t4
r1
r2
r3
推广到n层壁的情况:
q
t 1 t n 1
n
i 1
i i
本章作业
P88
复习题 4,6
2-2,2-7,2-18, 2-22
RA=δ/λ − 单位面积上导热热阻, [m2∙℃/W]
q (t1 t2) t
上式体现了q, λ, δ,Δt 四个变量的关系, 已知其中任意三个,可求另一个
2. 多层平壁 • 多层平壁:由几层不同材料组成 例:房屋的墙壁— 白灰内层、 水泥沙浆层、红砖(青砖)主体层等组成
t ( ) w h(tw tf ) n
是第一类和第二类边界条件的线性组合
2.2.3 导热微分方程的适用范围 1 )适用于 q 不很高,而作用时间长。同 时傅立叶定律也适用该条件。 2 )若时间极短,而且热流密度极大时,则 不适用。 3 )若属极底温度( 0 K)时的导热不适用。
工程热力学与传热学第二章稳态热传导基本概念

0)
2. 常温边界
系统边界温度恒定,即 (T = T_b)
3. 周期性边界
系统边界温度呈周期性变化, 即 (T(x, y, z, t) = T(x + L, y,
z, t))
求解方法
有限差分法
将导热微分方程转化为差 分方程,通过迭代求解温 度分布。
有限元法
将导热微分方程转化为变 分形式,利用有限元离散 化求解温度分布。
在稳态热传导过程中,导热系数和热 阻共同决定了物体内部温度分布的特 性。
当材料的导热系数越大,其对应的热 阻就越小,表示热量传递越容易;反 之,导热系数越小,热阻越大,热量 传递越困难。
04 稳态热传导的实例分析
一维稳态热传导
总结词
一维稳态热传导是热传导在单一方向上的情况,常见于细长物体或薄层材料。
三维稳态热传导
要点一
总结词
三维稳态热传导涉及三个方向的热量传递,常见于球体或 立方体。
要点二
详细描述
在三维稳态热传导中,热量在三个相互垂直的方向上传递 ,常见于球体或立方体等三维物体。三维稳态热传导的温 度分布在不同方向上都是稳定的,其数学模型比一维和二 维情况更为复杂,需要考虑三个方向的热量传递。三维稳 态热传导在解决实际问题时具有重要意义,如地球内部的 热量传递、建筑物的散热分析等。
稳态热传导的重要性
01
02
03
工程应用广泛
稳态热传导在许多工程领 域都有广泛应用,如建筑、 机械、航空航天等。
基础理论支撑
稳态热传导是传热学的基 础理论之一,对于理解更 复杂的传热过程和现象至 关重要。
节能减排
通过掌握稳态热传导规律, 有助于优化能源利用,实 现节能减排。
稳态热传导的应用场景
2. 常温边界
系统边界温度恒定,即 (T = T_b)
3. 周期性边界
系统边界温度呈周期性变化, 即 (T(x, y, z, t) = T(x + L, y,
z, t))
求解方法
有限差分法
将导热微分方程转化为差 分方程,通过迭代求解温 度分布。
有限元法
将导热微分方程转化为变 分形式,利用有限元离散 化求解温度分布。
在稳态热传导过程中,导热系数和热 阻共同决定了物体内部温度分布的特 性。
当材料的导热系数越大,其对应的热 阻就越小,表示热量传递越容易;反 之,导热系数越小,热阻越大,热量 传递越困难。
04 稳态热传导的实例分析
一维稳态热传导
总结词
一维稳态热传导是热传导在单一方向上的情况,常见于细长物体或薄层材料。
三维稳态热传导
要点一
总结词
三维稳态热传导涉及三个方向的热量传递,常见于球体或 立方体。
要点二
详细描述
在三维稳态热传导中,热量在三个相互垂直的方向上传递 ,常见于球体或立方体等三维物体。三维稳态热传导的温 度分布在不同方向上都是稳定的,其数学模型比一维和二 维情况更为复杂,需要考虑三个方向的热量传递。三维稳 态热传导在解决实际问题时具有重要意义,如地球内部的 热量传递、建筑物的散热分析等。
稳态热传导的重要性
01
02
03
工程应用广泛
稳态热传导在许多工程领 域都有广泛应用,如建筑、 机械、航空航天等。
基础理论支撑
稳态热传导是传热学的基 础理论之一,对于理解更 复杂的传热过程和现象至 关重要。
节能减排
通过掌握稳态热传导规律, 有助于优化能源利用,实 现节能减排。
稳态热传导的应用场景
传热学(第四版)第二章:稳态热传导

t t t t ( ) ( ) ( ) Φ x x y y z z
1 单层平壁、第一类边界条件的导热
a 几何条件:单层平板; b 物理条件:、c、 已知;无内热源 c 时间条件: 稳态导热 : t 0 d 边界条件:第一类
2、微元体中内热源的发热量 d 时间内微元体中内热源的发热量:
[2] dxdydz
3、微元体热力学能的增量 内微元体中内能的增量:
t [3] c dxdydz
导热微分方程式、导热过程的能量方程 由 [1]+ [2]= [3]:
t t t t c ( ) ( ) ( ) x x y y z z
§2-2 导热问题的数学描述
根据傅里叶定律: - grad t q [ W m2 ]
要想确定热流密度,应知道物体内的温度场; 因此,确定导热体内的温度分布是导热理论的首要任务
根据热力学第一定律,对于任一微元体:
建立关于t的方程,求解温度分布
假设:(1) 所研究的物体是各向同性的连续介质; (2) 热导率、比热容和密度均为已知; (3) 物体内具有内热源;内热源均匀分布。
1、导入与导出微元体的净热量 沿 x 轴方向、经 x 表面导入的热量:
x qx dydz
沿 x 轴方向、经 x+dx 表面导出的热量:
() x dx qx dx dydz
qx dx qx qx dx x
qx dxdydz x
沿 x 轴方向导入与导出微元体净热量:
20
20
Temperature (C)
15
15
10
10
5
5
0
1 单层平壁、第一类边界条件的导热
a 几何条件:单层平板; b 物理条件:、c、 已知;无内热源 c 时间条件: 稳态导热 : t 0 d 边界条件:第一类
2、微元体中内热源的发热量 d 时间内微元体中内热源的发热量:
[2] dxdydz
3、微元体热力学能的增量 内微元体中内能的增量:
t [3] c dxdydz
导热微分方程式、导热过程的能量方程 由 [1]+ [2]= [3]:
t t t t c ( ) ( ) ( ) x x y y z z
§2-2 导热问题的数学描述
根据傅里叶定律: - grad t q [ W m2 ]
要想确定热流密度,应知道物体内的温度场; 因此,确定导热体内的温度分布是导热理论的首要任务
根据热力学第一定律,对于任一微元体:
建立关于t的方程,求解温度分布
假设:(1) 所研究的物体是各向同性的连续介质; (2) 热导率、比热容和密度均为已知; (3) 物体内具有内热源;内热源均匀分布。
1、导入与导出微元体的净热量 沿 x 轴方向、经 x 表面导入的热量:
x qx dydz
沿 x 轴方向、经 x+dx 表面导出的热量:
() x dx qx dx dydz
qx dx qx qx dx x
qx dxdydz x
沿 x 轴方向导入与导出微元体净热量:
20
20
Temperature (C)
15
15
10
10
5
5
0
传热学课件第 二 章 稳 态 热传导

d2t d x2
m 2 t t f
1
通过肋壁的导热
一、等截面直肋的导热
4.求解:
4>.引入过余温度:<1>式变为 <4> 5>.解微分方程得温度场 <4>式为一个二阶线性齐次常微分方程,它的通解为: =C1emx+C2e-mx <5> 将边界条件<2>、<3>代入<5>即得肋片沿H方向的温度分布:
通过圆筒壁的导热
一、已知第一类边界条件
据傳里叶定律并整理后可得热流量的表达式: 1 ln d2 2l d1 式中的分母即为长度为l的圆筒壁的导热热阻。 单位为:℃/W 实际工程多采用单位管长的热流量ql来计算热流量:
t w1 t w 2
ql
Q l
t w1 t w 2
d ln d2 2 1 1
通过平壁的导热
二、已知第三类边界条件:
q
q
t f 1 t f 2
1 1 h1 h2
也可写作:q=k(tf1-tf2) (请牢记K的物理意义!) 对于冷热流体通过多层平壁的导热,可写作:
t f 1 t f 2
1 h1
i 1
n
i 1 i h2
若已知传热面积A,则热流量为:
e m x H e m x H 0 e mH e mH
d 2 m 2 d x2
or :
0
或写作:
0
ch mx H ch mH
expmx H exp mx H expmH exp mH
1
h21d x 0
传热学

等温线
华北电力大学
传热学 Heat Transfer
2、温度梯度
• 定义:沿等温面法线方向上的温度增量与法向 距离比值的极限。温度梯度表示为:
t t grad t n lim n n 0 n n
式中,n
是等温面法线方向上的单位矢量。
华北电力大学
传热学 Heat Transfer
华北电力大学
传热学 Heat Transfer
沿x 轴方向导入与导出微元体净热量
Φx Φx dx
同理可得:
t dxdydz x x
沿 y 轴方向导入与导出微元体净热量
Φy Φy dy
t dxdydz y y
t ( ) Φ 0 x x
华北电力大学
传热学 Heat Transfer
三、其它坐标系中的导热微分方程式
1. 圆柱坐标系(r, , z)
x r cos ; y r sin ; z z
t 1 t 1 t t c (r ) 2 ( ) ( ) r r r r z z
(3)微元体内热源生成的热量
ΦV Φdxdydz
5. 导热微分方程的基本形式
t t t t c ( ) ( ) ( ) Φ x x y y z z
非稳态项
华北电力大学
三个坐标方向净导入的热量
内热源项
传热学 Heat Transfer
传热学 Heat Transfer
利用两个边界条件
t
x 0, t t1 x , t t2
c2 t1 t 2 t1 c1
t1 t 2
华北电力大学
传热学 Heat Transfer
2、温度梯度
• 定义:沿等温面法线方向上的温度增量与法向 距离比值的极限。温度梯度表示为:
t t grad t n lim n n 0 n n
式中,n
是等温面法线方向上的单位矢量。
华北电力大学
传热学 Heat Transfer
华北电力大学
传热学 Heat Transfer
沿x 轴方向导入与导出微元体净热量
Φx Φx dx
同理可得:
t dxdydz x x
沿 y 轴方向导入与导出微元体净热量
Φy Φy dy
t dxdydz y y
t ( ) Φ 0 x x
华北电力大学
传热学 Heat Transfer
三、其它坐标系中的导热微分方程式
1. 圆柱坐标系(r, , z)
x r cos ; y r sin ; z z
t 1 t 1 t t c (r ) 2 ( ) ( ) r r r r z z
(3)微元体内热源生成的热量
ΦV Φdxdydz
5. 导热微分方程的基本形式
t t t t c ( ) ( ) ( ) Φ x x y y z z
非稳态项
华北电力大学
三个坐标方向净导入的热量
内热源项
传热学 Heat Transfer
传热学 Heat Transfer
利用两个边界条件
t
x 0, t t1 x , t t2
c2 t1 t 2 t1 c1
t1 t 2
传热学 第2章 稳态导热

t t t t c Φ x x y y z z
3、常物性且稳态:
2t 2t 2t Φ a 2 2 2 0 x y z c
如果边界面上的热流密度保持为常数,则 q | w 常数 当边界上的热流密度为零时,称为绝热边界条件
t t qw 0 0 n w n w
18
(3)第三类边界条件 给出了物体在边界上与和它直接接触的流体之 间的换热状况。 根据能量守恒,有:
返回
2.1.1 各类物体的导热机理
气体:气体分子不规则热运动时相互碰撞的结果,高温的气体分子运 动的动能更大 固体:自由电子和晶格振动 对于导电固体,自由电子的运动在导热中起着重要的作用,电的良导 体也是热的良导体 对于非导电固体,导热是通过晶格结构的振动,即原子、分子在其平 衡位置附近的振动来实现的
返回
2.2.2 定解条件
导热微分方程式是能量守恒定律在导热过程中的应用,是一切导热 过程的共性,是通用表达式。 完整数学描述:导热微分方程 + 定解条件 定解条件包括初始条件和边界条件两大类,稳态问题无初始条件 初始条件:初始时刻的状态表示为: =0,t =f (x,y,z)
边界条件: 给出了物体在边界上与外界环境之间在换热上的联系或相互作用
2、推导基本方法:傅里叶定律 + 能量守恒定律 在导热体中取一微元体
进入微元体的总能量+微元体内热源产生的能量-离开微元体的总能量= 微元体内储存能的增加
11
Ein Eg Eout Es
d 时间段内:
Ein Φx Φy Φz d Eiout Φxdx Φy dy Φz dz d
第二章-导热理论基础-2

∂t 1 ∂ ∂t 1 ∂ ∂t ∂ ∂t & λ ρc = λr + 2 ∂ϕ + ∂z λ ∂z + q v ∂τ r ∂r ∂r r ∂ϕ
对于稳态、一维、无内热源情况, 上式可简化为:
r
或写成 其通解为
1 d dt λr = 0 r dr dr d dt r = 0 dr dr t = c 1 ln r + c 2
稳态条件下: 稳态条件下:
ql
r = r1
= q l = q1
r = r2
于是得:
t f1 − t f 2 ql = r2 1 1 1 + ln + 2π r1 h1 2πλ r1 2π r1 h1 t f1 − t f 2 = k l (t f 1 − t f 2 ) = r2 1 1 1 + ln + π d 1 h1 2πλ r1 π d 1 h1
t w1
t w2
tf2
1 h1
δ λ
1 h2
3)多层平壁导热,第一类边界条件 )多层平壁导热,
t w1
tw4
相当于多电阻串联电路
δ1
δ2
δ3
t w1
t w2
t w3
δ2 λ2 δ3 λ3
δ1 λ1
n
tw4
δi ∑ Rt = ∑ λ i =1 i
t w1 − t w 4 ∆t = q= ∑ Rt ∑ Rt
t2=50℃,求炉墙单位面积、单位时间的热损失。
解:材料的平均温度为:
t = (t1 + t2)/2 = (500 + 50)/2 = 275 ℃
对于稳态、一维、无内热源情况, 上式可简化为:
r
或写成 其通解为
1 d dt λr = 0 r dr dr d dt r = 0 dr dr t = c 1 ln r + c 2
稳态条件下: 稳态条件下:
ql
r = r1
= q l = q1
r = r2
于是得:
t f1 − t f 2 ql = r2 1 1 1 + ln + 2π r1 h1 2πλ r1 2π r1 h1 t f1 − t f 2 = k l (t f 1 − t f 2 ) = r2 1 1 1 + ln + π d 1 h1 2πλ r1 π d 1 h1
t w1
t w2
tf2
1 h1
δ λ
1 h2
3)多层平壁导热,第一类边界条件 )多层平壁导热,
t w1
tw4
相当于多电阻串联电路
δ1
δ2
δ3
t w1
t w2
t w3
δ2 λ2 δ3 λ3
δ1 λ1
n
tw4
δi ∑ Rt = ∑ λ i =1 i
t w1 − t w 4 ∆t = q= ∑ Rt ∑ Rt
t2=50℃,求炉墙单位面积、单位时间的热损失。
解:材料的平均温度为:
t = (t1 + t2)/2 = (500 + 50)/2 = 275 ℃
5第2章 稳态热传导

由于处于热平衡状态,于是存在 dt |x h(tw t f ) dx 对这一问题的阐述,在对流传热部分还要详细 介绍!!
于是可求得
2 2 t ( x ) tf 2 h
于是由
dt x dx
dt q x dx
可得:
q |x 0 0
tmax=118º C
2.5.2具有内热源的圆柱体导热
与考虑大平板的思路相似,也分两种情况讨论。 情况一:不考虑圆柱体与流体的对流传热。 如图,一半径为r1的圆柱体, 具有均匀分布的内热源 ,导 热系数λ为常数,外表面恒定温 度为t1,求圆柱体内温度分布。 解:根据前面所学的导热 微分方程,圆柱坐标中的导热 图3 具有均匀内热源的 圆柱体导热 微分方程可简化为:
1 d dt (r ) 0 r dr dr
其边界条件很容易得到: dt ( ) |r 0 0, t |r r1 t1 dr 于是可得圆柱体内的温度分布:
2 dt r t1 0 ,即r=0, tmax 令 1 4 dr
2 2 t (r1 r ) t1 4
传热学基础
主讲教师:王能为
第2章 稳态热传导
复习:上一堂课学习了单层及多层圆筒壁的热 流、热流密度、热阻的公式表达。
单层圆筒壁: 热流密度:
q
t1 t2
r ln(r2 / r1 )
1 2 l t1 t2 ln(r2 / r1 )
热流: qA 多层圆筒壁: 线热流密度: ql 热流:
d 2t 0 2 dx
(1)
边界条件为:
t |x 0 t1 ; t |x t2
于是可求得
2 2 t ( x ) tf 2 h
于是由
dt x dx
dt q x dx
可得:
q |x 0 0
tmax=118º C
2.5.2具有内热源的圆柱体导热
与考虑大平板的思路相似,也分两种情况讨论。 情况一:不考虑圆柱体与流体的对流传热。 如图,一半径为r1的圆柱体, 具有均匀分布的内热源 ,导 热系数λ为常数,外表面恒定温 度为t1,求圆柱体内温度分布。 解:根据前面所学的导热 微分方程,圆柱坐标中的导热 图3 具有均匀内热源的 圆柱体导热 微分方程可简化为:
1 d dt (r ) 0 r dr dr
其边界条件很容易得到: dt ( ) |r 0 0, t |r r1 t1 dr 于是可得圆柱体内的温度分布:
2 dt r t1 0 ,即r=0, tmax 令 1 4 dr
2 2 t (r1 r ) t1 4
传热学基础
主讲教师:王能为
第2章 稳态热传导
复习:上一堂课学习了单层及多层圆筒壁的热 流、热流密度、热阻的公式表达。
单层圆筒壁: 热流密度:
q
t1 t2
r ln(r2 / r1 )
1 2 l t1 t2 ln(r2 / r1 )
热流: qA 多层圆筒壁: 线热流密度: ql 热流:
d 2t 0 2 dx
(1)
边界条件为:
t |x 0 t1 ; t |x t2
稳态热传导导热理论基础

2>.温度梯度是引起物体内热量传递的根本原因。
3>.适用范围:傅里叶定律是一个实验定律,是导热现象经验的规律 性总结,普遍适用各种导热现象。即不论是否变物性(λ=a+bt), 有无内热源,是否非稳态,不论物体几何形状如何,也不论物质 的形态(固﹑液、气),其都适用。
4>.现实意义:只要已知温度场,则可由傅里叶定律求出
第二章 稳态热传导(导热理论 基础)
一、概述 二、傅里叶(J.Fourier)定律 三、导热系数 四、导热微分方程 五、导热微分方程的单值性条件 六、解决一具体导热问题的一般步骤
整理课件
1
导热理论基础
一、概述:
一般我们认为:导热是发生在物体中的宏观现象,故将物质看作是 连续介质。
导热基础理论的主要任务:
1.找出物体内温度与时间、空间的关系式,即求解温度场; 2.找出物体内温度分布与换热量的普遍联系式,即傅里叶定律。 二、傅里叶(J.Fourier)定律: 1.基本概念: 1>.温度场:物体某一时刻其内各点的温度分布:
t=f(x、y、z、) 上式为三维非稳态温度场;当t/=0时,称为三维稳态温度场,即: t=f(x、y、z);若温度场仅和二个或一个坐标有关时则为二维或一 维稳态温度场:即t=f(x、y) 或:t=f(x)。 具有稳态温度场的导热过程我们常称之为稳态导热;具有非稳态温 度场的导热过程我们常称之为非稳态导热。
7. 20 ℃时典型材料的λ(W/m·℃) 铜 399 碳钢 40 水 0.599 干空气 0.0259
一般,金属材料的λ最大,非金属固体材料次之,液体更 次之,而气体最小。
整理课件
6
导热理论基础
四、导热微分方程
1.目的:建立物体内温度
3>.适用范围:傅里叶定律是一个实验定律,是导热现象经验的规律 性总结,普遍适用各种导热现象。即不论是否变物性(λ=a+bt), 有无内热源,是否非稳态,不论物体几何形状如何,也不论物质 的形态(固﹑液、气),其都适用。
4>.现实意义:只要已知温度场,则可由傅里叶定律求出
第二章 稳态热传导(导热理论 基础)
一、概述 二、傅里叶(J.Fourier)定律 三、导热系数 四、导热微分方程 五、导热微分方程的单值性条件 六、解决一具体导热问题的一般步骤
整理课件
1
导热理论基础
一、概述:
一般我们认为:导热是发生在物体中的宏观现象,故将物质看作是 连续介质。
导热基础理论的主要任务:
1.找出物体内温度与时间、空间的关系式,即求解温度场; 2.找出物体内温度分布与换热量的普遍联系式,即傅里叶定律。 二、傅里叶(J.Fourier)定律: 1.基本概念: 1>.温度场:物体某一时刻其内各点的温度分布:
t=f(x、y、z、) 上式为三维非稳态温度场;当t/=0时,称为三维稳态温度场,即: t=f(x、y、z);若温度场仅和二个或一个坐标有关时则为二维或一 维稳态温度场:即t=f(x、y) 或:t=f(x)。 具有稳态温度场的导热过程我们常称之为稳态导热;具有非稳态温 度场的导热过程我们常称之为非稳态导热。
7. 20 ℃时典型材料的λ(W/m·℃) 铜 399 碳钢 40 水 0.599 干空气 0.0259
一般,金属材料的λ最大,非金属固体材料次之,液体更 次之,而气体最小。
整理课件
6
导热理论基础
四、导热微分方程
1.目的:建立物体内温度
第二章 稳态热传导2

环节的热流量相同,则串联过程的总热阻等于各串联环节的分热阻 之和。
典型一维稳态导热问题的分析解
通过平壁的导热
多层平壁
由热阻分析法:q
t1 tn1
n
ri
i 1
t1 tn1
n i
i1 i
问:现在已经知道了q,如何计算其中第 i 层的右侧壁温?
第一层:
q
1 1
r2 d 0 50mm
40mm
r3
45mm
典型一维稳态导热问题的分析解
例题
21 tw1 tw 2 2 tw tw2
t 先假定界面温度为
而 2 0.099
w ,则由题意
0.0002
tw
tw2 2
ln
r2 r1
ln
dx dx
3
tw1
所以对情形3 有 dt dt >
dx dx
x
为什么东北的窗玻璃都采用双层玻璃?
讨论
导热环节越多,串联的热阻就越多,总热阻相对来说就 越大,相同温差下传递的热量越少,越有利于隔热。
典型一维稳态导热问题的分析解
通过圆筒壁的导热
第一次积分
第二次积分
r
dt dr
c1
t c1 ln r c2
典型一维稳态导热问题的分析解
通过圆筒壁的导热
单层圆筒壁
应用边界条件
t1 c1 ln r1 c2 ; t2 c1 ln r2 c2
获得两个系数
c1
典型一维稳态导热问题的分析解
通过平壁的导热
多层平壁
由热阻分析法:q
t1 tn1
n
ri
i 1
t1 tn1
n i
i1 i
问:现在已经知道了q,如何计算其中第 i 层的右侧壁温?
第一层:
q
1 1
r2 d 0 50mm
40mm
r3
45mm
典型一维稳态导热问题的分析解
例题
21 tw1 tw 2 2 tw tw2
t 先假定界面温度为
而 2 0.099
w ,则由题意
0.0002
tw
tw2 2
ln
r2 r1
ln
dx dx
3
tw1
所以对情形3 有 dt dt >
dx dx
x
为什么东北的窗玻璃都采用双层玻璃?
讨论
导热环节越多,串联的热阻就越多,总热阻相对来说就 越大,相同温差下传递的热量越少,越有利于隔热。
典型一维稳态导热问题的分析解
通过圆筒壁的导热
第一次积分
第二次积分
r
dt dr
c1
t c1 ln r c2
典型一维稳态导热问题的分析解
通过圆筒壁的导热
单层圆筒壁
应用边界条件
t1 c1 ln r1 c2 ; t2 c1 ln r2 c2
获得两个系数
c1
传热学考研题库【章节题库】(稳态热传导)【圣才出品】

四、简答题 1.何谓肋片效率?采用加装肋片来强化换热,对肋片的选材、肋片的形状和肋片效率 有何要求? 答:肋片效率是指肋片的实际散热量与假设整个肋片温度都与肋根温度相同时的理想散 热量之比。肋片效率的主要影响因素有: (1)肋片材料的热导率:热导率愈大,肋片效率愈高; (2)肋片高度:肋片愈高,肋片效率愈低;
12.扩展表面中的导热问题可以按一维问题处理的条件是什么?有人认为只要扩展表面 细长,就可按一维问题处理,你同意这种观点吗?
答:(1)扩展表面中的导热问题可以按一维问题处理的条件是扩展表面细长,且导热 系数大。
(2)不同意,表面传热系数相对较小的条件下( hd 0.01 )才可以按一维问题来处
2 / 49
圣才电子书 十万种考研考证电子书、题库视频学习平台
(3)肋片厚度:肋片愈厚,肋片效率愈高; 表面传热系数:出傅里叶导热定律表达式,并说明式中各量和符号的物理意义。
答: q gradt t n 。其中 q 是热流密度矢量; 是导热系数,它表示物质导 n
答:两平壁内的温度分布相同。因为对于常物性、无内热源的无限大平壁的稳态导热, 第一类边界条件下其温度分布仅取决于边界温度,而与材料的导热系数无关。
4.冬天阳光照射的中午晒棉被,试从传热的角度解释晚上睡觉时还会暖和的原因。 答:晚上睡觉时还会暖和的原因:棉被经日晒变得蓬松,空气进入到棉被中,而空气的 导热系数较小,相当于增加了导热热阻,因而睡觉时还觉得暖和。
9.一维无限大平壁的导热问题,两侧给定的均为第二类边界条件,能否求出其温度分
4 / 49
圣才电子书
布?为什么?
十万种考研考证电子书、题库视频学习平台
答:(1)一维无限大平壁的导热问题,两侧给定的均为第二类边界条件,不能求出其
工程热力学与传热学第二章稳态热传导基本概念

实用文档
分析: 假设 1 )肋片在垂直于纸面方向 ( 即深度方向 ) 很长,不考虑温度沿该方向的变化,因此取单位长 度分析;
2 )材料导热系数 λ 及表面传热系数 h 均 为常数,沿肋高方向肋片横截面积 Ac 不变;
3 )表面上的换热热阻 1/h ,远大于肋片的 导热热阻 δ/λ ,即肋片上任意截面上的温度均 匀不变;
一是:确定肋片的温度沿导热热流传递的 方向是如何变化的?
二是:确定通过肋片的散热热流量有多少?
实用文档
1. 通过等截面直肋的导
热
已知:
(1)矩形直肋
(2)肋 根 温 度 为 t0 , 且t0 > t
(3)肋 片 与 环 境 的 表
面传热系数为 h.
(4) , h 和 Ac均 保 持
不变
(5)求:
温度场 t 和热流量
由前面我们已知一维稳态导热的方程式为如下
d 2t dx 2
0
边界条件为:
x 0:t t1 x :t t2
求解步骤: (1)积分求解
dt c1 dx t c1x c2
t t2t1xt1
(2)根据傅里叶定律,得到:
c2 t1 c1 t2 t1
qddxtt2t1t1t2
实用文档
分析:(和电路分析类比)
则有: Φx=-λAc t
x
Φx+dx=-λAc (t t dx)
x x
Φc= hPdxΔt= hPdx(t-t∞)
所以: Φx=-λAc t =Φx+dx+Φc=-λAc (t t dx) +hPdxΔt
x
x x
整理得: d2t hP(t t) dx2 Ac
实用文档
2-1 第二章 导热基本定律及稳态导热

q
q
qx
t x
;
qy
t y
;
qz
t z
q q cos
§2-1 导热基本定律
长江大学机械工程学院
School of Mechanical Engineering
3. 意义: 已知物体内部的温度分布后,由该定律可求
得各点的热流密度或热流量。
例1:已知右图平板中的温度分 布可以表示成如下的形式: t = C1 x2 + C2
冷面
冷面
流体
热面 流体
§2-1 导热基本定律
2. 导热系数的相对大小和典型数据
长江大学机械工程学院
School of Mechanical Engineering
金 属 非 金 属
固 相 液 相 气 相
20℃时: 纯 铜 399 W (m C )
碳 钢 36.7 W (m C )
能准确的计算所研究问题中传递的热流。
要解决的问题:
温度分布如何描述和表示?
温度的分布和导热的热流存在什么关系? 如何得到导热体内部的温度分布?
长江大学机械工程学院
School of Mechanical Engineering
本章内容结构
§2-1 导热基本定律
§2-2 导热问题的数学描述
回答问题1和2 回答问题3 具 体 稳 态 导 热 问 题
§2-1 导热基本定律
长江大学机械工程学院
School of Mechanical Engineering
三、热导率( Thermal conductivity )
1.定义
q grad t
《传热学》第2章_稳态热传导

三三
三三三三三三三三三 三三
三三 三三
三三三三三三三
三三
三三三三三三三三
三三
三三三三三三三三三三三
18
第2章 稳态热传导
2.1 典型一维稳态导热问题的分析解
2.3.1 通过平壁的导热:
一维、稳态、常物性、无内热源情况,考察平板的导热情况。
c t
x
t x
t x
n
中,gradt表示空间某点的温度梯度,
n表示通过该点的等温线上的法向单位矢量,温度升高的方向。
利用等温线和热流线来定量且形 象地表述一个导热过程: 等温线表示热流梯度,而热流线 是与等温线处处垂直的一组曲线, 通过平面上任一点的热流线与该 点的热流密度相切。 相邻两条热流线之间所传递的热 流量处处相等,相当于构成了一 个热流通道。 该方法用于现代工程软件应用。
2.类似于非导电固体;(倾向于此观点)
2
第2章 稳态热传导
等温场(temperature field):
温度场:物体中存在温度的场。 温度分布:各时刻物体中各点温度所组成的集合
分类:
稳态温度场:物体中各点温度不随时间而变。 t f x, y, z 瞬态温度场:物体中各点温度随时间变化。 t f x, y, z,
几何条件: 说明导热体的几何形状(平壁或圆筒壁)和大小(厚度、直径等)
物理条件:
说明导热体的物理特征如:物性参数λ、c 和 r 的数值,是否 随温度变化;有无内热源、大小和分布;是否各向同性 初始(时间)条件: 说明在时间上导热过程进行的特点 稳态导热过程不需要时间条件 — 与时间无关 对非稳态导热过程应给出过程开始时刻导热体内的温度分布
疏密可直观反映出不同区域温度热流密度的相对大小。
第二章-稳态热传导

传热学 Heat Transfer
Shanghai Jiao Tong University
2-2 导热问题的数学描述 温度场
导热微分方程
t f ( x, y, z, )
傅立叶定律
热流量
热流密度
导热微分方程的推导:傅立叶定律 + 能量守恒定律 导入导出微元体的净热流量+ 微元体内热源生成热= 微元体内能的增量 导入热流量 导出热流量 内热源生成热
第一类 第二类 第三类 导热问题的数学描述= 导热微分方程+定解条件
稳态导热:给定边界条件即可。 非稳态导热:给定初始条件和边界条件。
SJTU-OYH
传热学 Heat Transfer
Shanghai Jiao Tong University
2-2 导热问题的数学描述 第一类边界条件(Dirichlet条件):给定边界上的温度值。 稳态导热: 非稳态导热: 第二类边界条件(Neumann条件):给定边界上的热流密度值。 稳态导热: 非稳态导热: 特例:绝热边界
SJTU-OYH
传热学 Heat Transfer
Shanghai Jiao Tong University
2-3 典型一维稳态导热分析解 通过多层平壁的导热
热阻分析法
热流密度
q
t1 t n 1
t1
ri
i 1
n
t1 t n 1
i i 1 i
n
n为层数
t2
t3 t4
温度分布 第一层:
x
y
z
xdx
dxdydz
y dy
z dz
内能增量
t c dxdydz
SJTU-OYH
第二章稳态热传导
向上热流分量Φx在x+dx点的值,其余类推。得到导入微元体 的热流量为:
xx d x xx x xd x xx x x t xd y d z d x yy d y yy y yd y yy y y t yd x d z d y
使微分方程获得适合某一特定问题的解的附加条件,
称为定解条件。
初始条件
非稳态导热
边界条件
稳态导热
边界条件
导热问题的数学描写
二、边界条件分类
1、第一类边界条件:指定边界上的温度分布。
如右图中:
x 0, t tw1 x ,t tw2
对于非稳态导热,这类边界条件还需要给出以下关系式:
0时 ,twf1
zz d z zz zzd z zz z z t zd x d y d z
导热问题的数学描写
微元体热力学能(即内能)的增量= c t dxdydz
微元体内热源的生成热= d x d y d z
式中:ρ——微元体的密度; c ——微元体的比热容; Φ——单位时间内单位体积中内热源的生成热; τ ——时间;
导热问题的数学描写
2、第二类边界条件:指定边界上的热流密度值。 如右图中:
x
,t
x
qw
对于非稳态导热,这类边界条件还需要给出以下关系式:
0时,-nt wf2
导热问题的数学描写
3、第三类边界条件:指定边界上物体与周围流体间的表面传 热系数h及周围流体的温度tf。 如右图中:
x, xtxqwhtwtf
各个时刻物体中各点温度所组成的集合,又称为温 度分布。
t f x,y,z,
稳态温度场(定常温度场)
t f x,y,z
瞬态温度场(非定常温度场)
xx d x xx x xd x xx x x t xd y d z d x yy d y yy y yd y yy y y t yd x d z d y
使微分方程获得适合某一特定问题的解的附加条件,
称为定解条件。
初始条件
非稳态导热
边界条件
稳态导热
边界条件
导热问题的数学描写
二、边界条件分类
1、第一类边界条件:指定边界上的温度分布。
如右图中:
x 0, t tw1 x ,t tw2
对于非稳态导热,这类边界条件还需要给出以下关系式:
0时 ,twf1
zz d z zz zzd z zz z z t zd x d y d z
导热问题的数学描写
微元体热力学能(即内能)的增量= c t dxdydz
微元体内热源的生成热= d x d y d z
式中:ρ——微元体的密度; c ——微元体的比热容; Φ——单位时间内单位体积中内热源的生成热; τ ——时间;
导热问题的数学描写
2、第二类边界条件:指定边界上的热流密度值。 如右图中:
x
,t
x
qw
对于非稳态导热,这类边界条件还需要给出以下关系式:
0时,-nt wf2
导热问题的数学描写
3、第三类边界条件:指定边界上物体与周围流体间的表面传 热系数h及周围流体的温度tf。 如右图中:
x, xtxqwhtwtf
各个时刻物体中各点温度所组成的集合,又称为温 度分布。
t f x,y,z,
稳态温度场(定常温度场)
t f x,y,z
瞬态温度场(非定常温度场)
No.04 0922 2 稳态热传导
h2
2012-2-26
17
通过平壁,圆筒壁和其它变截面物体的导热( §2-3 通过平壁,圆筒壁和其它变截面物体的导热(续)
5 其它变面积或变导热系数问题
求解导热问题的主要途径分两步: 求解导热问题的主要途径分两步: (1) 求解导热微分方程,获得温度场; 求解导热微分方程,获得温度场; (2) 根据 根据Fourier定律和已获得的温度场计算热流量。 定律和已获得的温度场计算热流量。 定律和已获得的温度场计算热流量 对于稳态、无内热源、第一类边条下的一维导热问题,可以不通 对于稳态、无内热源、第一类边条下的一维导热问题, 过温度场而直接获得热流量。此时,一维Fourier定律: 定律: 过温度场而直接获得热流量。此时,一维 定律
2 2 1
t1
t2 − t1
t2 − t1
λ =
∫t λ ( t ) dt
t2
1
t 2 − t1
⇒
Φ =
λ ( t1 − t 2 )
∫x
x2
1
dx A( x)
随温度呈线性分布时, 当 λ 随温度呈线性分布时,即λ = λ0+at,则 λ = λ0 + a , 实际上, 实际上,不论 λ 导热系数。 导热系数。
线性分布
t −t ∆t q = −λ 2 1 = δ δ λ Φ = ∆t δ ( Aλ ) t
δ rλ = λ
δ Rλ = Aλ
t1 t2 o
δ
6
2012-2-26
通过平壁,圆筒壁和其它变截面物体的导热( §2-3 通过平壁,圆筒壁和其它变截面物体的导热(续)
2 多层平壁的导热
显然, 显然,温度呈对数曲线分布
2012-2-26
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导热理论基础
五、导热微分方程的单值性条件(定解条件)
使导热微分方程有唯一解的条件即为单值性条件。 1.时间条件(又称初始条件): ①稳态导热:过程与时间无关,即t/=0,无此条件。 ②非稳态导热:即已知初始时刻物体内温度场,常写作: t|=0=f(x,y,z) 若初始时各点温度相等,则有:t|=0=t0=常数 2.边界条件:反映了导热物体边界上的温度或与边界周围 环境发生热过程的情况。往往是发生导热现象的直接原 因。常被分为第一、二、三等3类条件。
导热理论基础
五、导热微分方程的单值性条件
综上所述,要完整地描述一具体的导热现象, 应有: ①适合该导热问题的导热微分方程式 ②描述该现象特性的单值性条件:a.初始条件 b.边界条件
构成对某一具体导热问题 完整的数学描述
导热理论基础
六、解决一具体导热问题的一般步骤: 1.写出适合于该导热问题的导热微分方程式; 2.写出该导热问题特有的单值性条件; 3.解微分方程,得到物体内的温度场; 4.据傳里叶定律,由温度场求出导热量。
上式即为一般的导热微分方程式。 若材料为常物性,即、、c均为常数,且令=/c有:
t
a
2t x 2
2t y 2
2
2t z 2
q
q c
⑵物性参数为常数且温度场稳态时: t q / 0 2 2t 2t 2t t x 2 y 2 z 2 0 ⑶温度场稳态且无内热源时: 另外可通过坐标变换,将导热微分方程写成圆柱坐标 或球坐标形式。请见式2-12,13。
n
x
导热理论基础
二、傅里叶(J.Fourier)定律:
2.傅里叶(J.Fourier)定律: 在导热现象中,单位时间内通过给定面积的传热量,正比例于该处 垂直导热方向的截面面积及此处的温度梯度,其数学表达式为:
几点问题: 1>.负号表示热量传递指向温度降低的方向,与温度梯度方向相反。 2>.温度梯度是引起物体内热量传递的根本原因。 3>.适用范围:傅里叶定律是一个实验定律,是导热现象经验的规律 性总结,普遍适用各种导热现象。即不论是否变物性(λ=a+bt), 有无内热源,是否非稳态,不论物体几何形状如何,也不论物质 的形态(固﹑液、气),其都适用。
2
t a t 或写成: c 2 式中▽ 为拉普拉斯运算符。上式即常用的导热微分方程。 2 t ⑴物性参数为常数且无内热源时: a t
导热理论基础
四、导热微分方程
5.导温系数(热扩散率) ①定义:物体被加热或冷却时,物体内各部分温度趋向于 均匀一致的能力。 ②表达式: =/c 1 2 ③单位:m /s 3 ④物理意义讲析: 常温常压下: 5 水=0.599w/m· ℃ 空=0.0259w/m· ℃ 水/空≈23 2 4 -7 2 而:水=1.43×10 m /s, 空= 2.14×10-5m2/s, 空/水≈160
y x
y+dy
导热理论基础
四、导热微分方程 对此微元体应用热力学第一定律
[导入微元体的热量-导出微元体的热量]+[内热源发热量] A + B =[热力学能增量] A部: = C ①沿x轴方向:x截面: x=qx· dydz x+dx截面:x+dx=qx+dx· dydz 因qx是x的函数,且在x至x+dx区间内连续可微,据泰勒级数有:
导热理论基础
五、导热微分方程的单值性条件
2.边界条件: ②第二类边界条件:已知任何时刻边界面上的热流密度值, 即已知边界上的温度变化率,但并不已知温度分布,即: q|s=qw or: -t/n|s=qw/ a.稳态时:qw=常数 b.非稳态时:qw = -(t/n)|s=f() 例如:肋片根部的边界情况即x=0处, 其热流通量具有稳定值q0,即: q0=-(t/x)|x=0 -t/x|x=0=q0/ 肋片顶部,当x=l→∞时,可忽略顶端与周围流体的换热 量,而认为此处绝热,即ql=0,此时即相于已知此处第二 类边界条件。 -t/x|x=l=0
n0
n
t+△t t
△ t3 △ t1 △t △ t2
t-△t
写成空间直角坐标系形式有:
gradt i
t x
t j y k
t z
q
4>.温度梯度的方向:法线方向, 指向温度升高的方向。 5>.热流密度向量:与温度梯度 的方向相反,指向温度降低 的方向。垂直于等温面 (线)。
A gradt W q gradt W / m2
4>.现实意义:只要已知温度场,则可由傅里叶定律求出
传热量,故求解导热问题的关键是求解物体中的温度分 布,给求解温度场。
导热理论基础
三、导热系数: 1.定义表达式: = - q/gradt
2.物理意义:表征物质导热能力的大小。数值上等于单位温度降度单 位时间单位面积的导热量。 3.单位:通过量纲分析有:W/m· ℃ 4.由来:一般用实验方法测得。 5.特性:λ是物性参数,它的大小起决于物质的种类和热力状态,一般 工程中仅认为与温度呈线性关系,即: = 0(a+bt) 0为0℃时导热系数 6.隔热保温材料(热绝缘材料):室温条件下(20℃时) 值小于 0.12W/m· ℃的材料。如:岩棉、膨胀珍珠岩等。特点是:a.多为多 孔体或纤维体材料;b.间隙中多充满气体;c.严格讲不能视为连续 介质;d.间隙的无限加大并不能提高保温能力;e.湿度的增加使其 保温能力大大下降。 7. 20 ℃时典型材料的λ(W/m· ℃) 铜 399 碳钢 40 水 0.599 干空气 0.0259
A
dxdydz
x t x y t y z t z
B部:B=qvdxdydz C部:C=c· t/·dxdydz
导热理论基础
四、导热微分方程
据A+B=C,整理消去dxdydz有:
t t t t c x x y y z z q
故沿x轴方向微元体导热的净热流量为: x- x+dx=-qx/x· dxdydz 同理
导热理论基础
四、导热微分方程
②沿y轴方向导入微元体的净热量为: y- y+dy=-qy/y· dxdydz ③沿z轴方向导入微元体的净热量为: z- z+dz=-qz/z· dxdydz 故A部(即微元体导热的净热量)为: A=-(qx/x+qy/y+qz/z)dxdydz 据傳里叶定律有: qx=-· t/x qy=-· t/y qz=-· t/z 代入上式有:
导热理论基础
五、导热微分方程的单值性条件
2.边界条件: ①第一类边界条件:已知物体边界上的温度值。即t|s=tw a.稳态时,tw不随时间改变。 tw=Const or: tw=f(x,y,z) 且 (x,y,z)∈s b.非稳态时,tw随时间改变。 tw=f(x,y,z,) 且 (x,y,z)∈s 例如:一维稳态无限大平壁有: t tw1 t|x=0=tw1 tw2 x t|x==tw2 o 对于二、三维稳态温度场,因其边界面不止两个,此时 应给出各个边界面的温度值。
一般,金属材料的λ最大,非金属固体材料次之,液体 更次之,而气体最小。
导热理论基础
四、导热微分方程
z 1.目的:建立物体内温 度与时间、空间的普遍 y 联系式。 z+dz x 2.原理:热力学第一定 律与傳里叶定律。 3.假定: x+dx a.物质为各向同性的连续 介质; 热源qv dz b.已知:、、c c.有内热源qv:qv为单位 dy 体积单位时间内所产生 dx 的热量,单位为:W/m3 4.推导:如图取任一微 z 元体dv 且 dv=dxdydz, 则有:
二、傅里叶(J.Fourier)定律:
导热理论基础
1.基本概念: 3>.温度梯度gradt:两等温面间的温差△t与其法线方向 的距离△n比值的极限。在单位距离内温度沿法线方 向上的变化值最大、最显著,此时的温度变化率称 t t n 之为温度梯度。即: gradt n
lim n
第二章 稳态热传导(导热理论 基础)
一、概述 二、傅里叶(J.Fourier)定律 三、导热系数 四、导热微分方程 五、导热微分方程的单值性条件 六、解决一具体导热问题的一般步骤
导热理论基础
一、概述: 一般我们认为:导热是发生在物体中的宏观现象,故将物质看作 是连续介质。 导热基础理论的主要任务: 1.找出物体内温度与时间、空间的关系式,即求解温度场; 2.找出物体内温度分布与换热量的普遍联系式,即傅里叶定律。 二、傅里叶(J.Fourier)定律: 1.基本概念: 1>.温度场:物体某一时刻其内各点的温度分布: t=f(x、y、z、) 上式为三维非稳态温度场;当t/=0时,称为三维稳态温度场, 即: t=f(x、y、z);若温度场仅和二个或一个坐标有关时则为二维 或一维稳态温度场:即t=f(x、y) 或:t=f(x)。 具有稳态温度场的导热过程我们常称之为稳态导热;具有非稳态 温度场的导热过程我们常称之为非稳态导热。
导热理论基础
二、傅里叶(J.Fourier)定律: 1.基本概念:
2>.等温面与等温线:(温度场习惯上用等温面图或等温线图来表 示,如图2-1) a.等温面:同一时刻温度场中所有 温度相同的点构成的面。 等温线 b.等温线:不同的等温面与同一平 面相交,在此平面上构成的一簇曲 线。 c.特点:①不同的等温面(线)不 可能相交;②它们或者是完全封闭 的曲面(线),或者终止于物体的 边界上;③沿等温面(线)无热量 传递;④等温面(线)的疏密可直 观反映出不同区域温度梯度(或热 流密度)的相对大小。
q x dx q x
q x x
dx
2qx x 2
