实验·6 时间序列分析的spss应用
SPSS作业关于时间序列分析

欧亚学院金融学院2012~2013学年第二学期实验论文河南省GDP的时间序列研究目录一、摘要二、模型理论知识介绍三、时间序列建模四、结果分析及合理化建议摘要本文采集了近三十年来河南省GDP以及第一、二、三产业和工业增长率等相关数据,运用西方经济学、统计学和计量经济学原理等知识从时间序列的定义出发,通过对GDP、第三产业百分比等部分数据的分析并结合统计软件SPSS,运用ARMA模型建模法对搜集到的数据进行识别、估计、诊断和预测,然后探索河南省GDP及第三个产业经济发展的状况,建立经济模型进行经济预测,并为政府部门和企业的管理决策提供数量化的建议。
[关键词] GDP 计量经济学时间序列分析第三产业 ARMA建模二、模型理论知识介绍GDP:国内生产总值,是核算体系中一个重要的综合性统计指标,也是中国新国民经济核算体系中的核心指标。
它反映一国(或地区)的经济实力和市场规模。
一个国家或地区的经济究竟处于增长抑或衰退阶段,从这个数字的变化便可以观察到。
一般而言,GDP公布的形式不外乎两种,以总额和百分比率为计算单位。
当GDP的增长数字处于正数时,即显示该地区经济处于扩张阶段;反之,如果处于负数,即表示该地区的经济进入衰退时期了。
国内生产总值是指一定时间内所生产的商品与劳务的总量乘以“货币价格”或“市价”而得到的数字,即名义国内生产总值,而名义国内生产总值增长率等于实际国内生产总值增长率与通货膨胀率之和。
因此,即使总产量没有增加,仅价格水平上升,名义国内生产总值仍然是会上升的。
在价格上涨的情况下,国内生产总值的上升只是一种假象,有实质性影响的还是实际国内生产总值变化率,所以使用国内生产总值这个指标时,还必须通过GDP缩减指数,对名义国内生产总值做出调整,从而精确地反映产出的实际变动。
因此,一个季度GDP缩减指数的增加,便足以表明当季的通货膨胀状况。
如果GDP缩减指数大幅度地增加,便会对经济产生负面影响,同时也是货币供给紧缩、利率上升、进而外汇汇率上升的先兆。
SPSS时间序列分析案例

SPSS时间序列分析案例时间序列分析是一种研究时间上连续观测变量的统计方法。
它可以用于预测未来的趋势和模式,帮助企业提前做出调整。
SPSS是一款功能强大的统计分析软件,可以进行各种统计方法的分析。
以下将通过一个时间序列分析案例,介绍SPSS如何进行时间序列分析。
假设家服装零售店想要分析过去几个季度的销售数据,以便预测未来几个季度的销售情况。
该店提供的数据集包含每个季度的销售总额。
首先,我们需要导入数据集到SPSS软件中。
在SPSS软件的主界面,选择“文件”菜单中的“打开”选项,然后选择对应的数据文件。
接下来,我们需要将数据按照时间序列的顺序进行排序。
在数据视图中,点击数据集右上角的“排列数据”按钮,在弹出的菜单中选择时间变量,并按照升序进行排序。
点击“确定”按钮完成排序。
然后,我们可以使用SPSS的时间序列分析工具来执行分析。
在菜单栏选择“分析”选项,然后选择“时间序列”子菜单中的“建模”选项。
在弹出的对话框中选择要分析的变量,即销售总额,并点击“确定”按钮。
SPSS将会输出一个时间序列模型的报告。
报告中包含了多个统计指标,如拟合优度、残差等,以及趋势和季节性的分析结果。
通过这些指标,我们可以判断时间序列的趋势特征和模式,并做出预测。
除了时间序列分析工具,SPSS还提供了其他的时间序列分析方法,如平滑技术、ARIMA模型等。
根据具体的研究目的和数据特点,我们可以选择合适的方法进行分析。
在本案例中,我们可以使用平滑技术来预测未来的销售情况。
平滑技术根据历史数据的平均值来预测未来的值。
在SPSS的时间序列分析工具中,选择“平滑”子菜单中的“simple exponential smoothing”选项,并设置平滑指数和初始预测值。
SPSS将会输出一个平滑结果的报告,包含了预测值和置信区间。
通过以上步骤,我们可以通过SPSS进行时间序列分析,帮助企业做出准确的预测和决策。
当然,在实际应用中,还需要根据具体情况进行参数选择和模型检验,以确保分析结果的可靠性。
SPSS在时间序列预测中的应用

第11章SPSS在时间序列预测中的应用时间序列分析(Time Series Analyze)是概率统计学科中应用性较强的一个分支,在金融经济、气象水文、信号处理、机械振动等众多领域有从所采用的数学工具和理论,时间序列分析分为时域分析和谱分析两大类分析方法预测的流程通常可以用下图来描述11.1 时间序列的预处理11.1.1预处理的基本原理1.使用目的通过预处理,一方面能够使序列的随“时间”变化的、“动态”的特征体现得更加明显,利用模型的选择;另一方面也使得数据满足与模型的要求。
2.基本原理⑴数据采样采样的方法通常有直接采样、累计采样等。
⑵直观分析时间序列的直观分析通常包括离群点的检验和处理、缺损值的补足、指标计算范围是否统一等一些比较简单的,可以采用比较简单手段处理的分析。
⑶特征分析所谓特征分析就是在对数据序列进行建模之前,通过从时间序列中计算出一些有代表性的特征参数,用以浓缩、简化数据信息,以利数据的深入处理,或通过概率直方图和正态性检验分析数据的统计特性。
通常使用的特征参数有样本均值、样本方差、标准偏度系数、标准峰度系数等。
⑷相关分析所谓相关分析就是测定时间序列数据内部的相关程度,给出相应的定量度量,并分析其特征及变化规律。
理论上,自相关系数序列与时间序列具有相同的变化周期.所以,根据样本自相关系数序列随增长而衰减的特点或其周期变化的特点判断序列是否具有平稳性,识别序列的模型,从而建立相应的模型。
3.其他注意事项进行时间序列预处理的时候,常常需要对数据一些变换,例如,取对数,做一阶差分,做季节差分等。
11.1.2 时间序列预处理的SPSS操作详解Step01:数据准备选择菜单栏中的【Data(数据)】→【Define Dates(定义日期)】命令,弹出【Define Dates(定义日期)】对话框。
如果选择月度数据或季度数据,将会出现【Periodicity at higher level (更高级别的周期)】。
课题_第11章 SPSS在时间序列预测中的应用 SPSS19.0软件使用教程

第11章SPSS在时间序列预测中的应用SPSS19.0软件使用教程在进入SPSS后,具体工作流程如下:1.将数据输入SPSS,并存盘以防断电。
2.进行必要的预分析(分布图、均数标准差的描述等),以确定应采用的检验方法。
3.按题目要求进行统计分析。
4.保存和导出分析结果。
下面就按这几步依次讲解。
§1.1 数据的输入和保存1.1.1 SPSS的界面当打开SPSS后,展现在我们面前的界面如下:请将鼠标在上图中的各处停留,很快就会弹出相应部位的名称。
请注意窗口顶部显示为“SPSS for Windows Data Editor”,表明现在所看到的是SPSS的数据管理窗口。
这是一个典型的Windows软件界面,有菜单栏、工具栏。
特别的,工具栏下方的是数据栏,数据栏下方则是数据管理窗口的主界面。
该界面和EXCEL极为相似,由若干行和列组成,每行对应了一条记录,每列则对应了一个变量。
由于现在我们没有输入任何数据,所以行、列的标号都是灰色的。
请注意第一行第一列的单元格边框为深色,表明该数据单元格为当前单元格。
对Windows操作界面不熟悉的朋友可参见SAS入门第一课中的相关内容。
对数据表界面操作不熟悉的朋友可先学习一下EXCEL的操作(因为它的帮助是中文的)。
有的SPSS系统打开时会出现一个导航对话框,请单击右下方的Cancer按钮,即可进入上面的主界面。
1.1.2 定义变量该资料是定量资料,设计为成组设计,因此我们需要建立两个变量,一个变量代表血磷值,习惯上取名为X,另一个变量代表观察对象是健康人还是克山病人,习惯上取名为GROUP。
对数据的统计分析格式不太熟悉的朋友请先学习统计软件第一课。
选择菜单Data==>Define Variable。
系统弹出定义变量对话框如下:该变量定义对话框在SPSS 10.0版中已被取消,这里的操作只适合9.0~7.0版的用户。
对话框最上方为变量名,现在显示为“VAR00001”,这是系统的默认变量名;往下是变量情况描述,可以看到系统默认该变量为数值型,长度为8,有两位小数位,尚无缺失值,显示对齐方式为右对齐;第三部分为四个设置更改按钮,分别可以设定变量类型、标签、缺失值和列显示格式;第四部分实际上是用来定义变量属于数值变量、有序分类变量还是无序分类变量,现在系统默认新变量为数值变量;最下方则依次是确定、取消和帮助按钮。
SPSS时间序列分析spss操作步骤

17 习题
1、 时间序列的基本概念。 时间序列分析过程中有哪几种常用的方法?2、 对数据用时间序列模型进行拟合处理前,应做哪些准备工作?3、 在哪个过程中可进行缺失值的修补?修补缺失值的方法共有几种?4、 在哪个过程中可定义时间变量?5、 时间序列分析是建立在序列的平稳的条件上的,怎样判断序列是否平稳?6、为什么要建一个时间序列的新变量?在SPSS的哪个过程中来建时间序列的新变量?7、光盘中Data17-07.sav(Data17-07a.sav是Data17-07.sav使用中文标签名的同一个文件)记录了一个邮购公司在1989年1月至1998年12月间男、女服装产品的销售量情况以及一些可能影响服装销售的宣传、服务方面的变量。试用学过的时间序列方法对其进行分析,并预测1999年4月的男装的销售量。
返回
时间序列习题参考答案(5)
三、自相关分析
返回
时间序列习题参考答案(6)
表中显示的是自相关计算结果,从左向右,依次列出的是:滞后数、自相关系数值值、标准误差、Box-ljung统计量(值、自由度、原假设成立的概率值)。由于原假设(假设基本过程是独立的,也即假定时间序列所反映的随机过程是白噪声)成立的概率值都小于0.05,所以全部自相关均有显著性意义。
返回
时间序列分析实例输出(2)
模型统计数据
返回
时间序列分析实例输出(3)
预测部分结果
数据编辑器中的新变量
返回
应用时间序列模型
(Applies models对话框
返回
自相关
(Autocorrelations )
返回
Autocorrelations对话框
感谢您的下载观看
返回
时间序列习题参考答案(17)
SPSS软件在“应用时间序列分析”课程教学改革中的应用

SPSS软件在“应用时间序列分析”课程教学改革中的应用吴 迪1 陈 喆2 石晓莉1 朱 迪1(1.白城师范学院数学与统计学院,吉林 白城 137000;2.吉林电力股份有限公司白城发电公司设备部,吉林 白城 137000)摘 要:本文结合“应用时间序列分析”课程特点,在大数据时代背景下,提出了结合SPSS软件辅助教学的教学改革方法。
提高了学生做复杂统计分析的效率,免去了耗时的编程过程,有助于学生更好掌握专业技能,通过所学知识灵活解决实际问题。
关键词:应用时间序列分析;统计软件;课程改革“应用时间序列分析”是高校统计学专业核心课程,该课程内容广泛应用于经济、金融、生物、化学等多门学科中,应用性较强,需要掌握扎实的理论和实践能力。
大数据时代的飞速发展,要求学生具备扎实的统计分析技能和软件的应用能力,实现快速处理数据、图表、分析数据中所含信息。
因此,探讨教学中如何通过SPSS软件辅助课程教学对学生提高运用理论解决实际问题的能力和效率有非常重要的意义。
一、教学中存在的问题目前,我国本科统计学在“应用时间序列分析”课程教学中应用的软件主要有R语言、SAS软件等,这两种软件都是编程软件,教学过程中,编程软件会比较耗时,教学进度变慢,本就不多的实践环节被大量的编程占用了时间,学生能进行的上机实践操作变得有限,课时有限的基础上无法完成大纲内容,教师不得不压缩课上实践比例,这也是导致实践比例下降的原因。
适当引入SPSS软件辅助教学非常有必要。
“应用时间序列分析”课程中,无论是平稳时间序列分析,还是非平稳序列确定性分析,模型复杂程度高,理论难度较大,课堂中理论占比明显高于实践占比,注重公式和模型的推导,忽略实际应用。
学生获得教材附带数据后,根据教师的演示,进行简单的模仿,在数据搜集、处理和分析方面锻炼较少,导致学生理论没有完全掌握的情况下,进行了简单的统计操作,获得的结果和教师一致,产生掌握课程内容的假象,解决实际问题的能力并没有得到锻炼,面对变化的问题情境没有理论的支撑,也没有灵活的应用能力。
SPSS作业关于时间序列分析

SPSS作业关于时间序列分析时间序列分析是一种统计方法,用于研究随时间变化的数据,并从中提取出隐藏在数据背后的模式和趋势。
这种分析方法在经济学、金融学、天气预报、市场调研等领域经常被应用。
SPSS(Statistical Package for the Social Sciences)是一款广泛使用的统计分析软件,它提供了丰富的时间序列分析工具,可以用来处理和分析时间序列数据。
时间序列数据是根据时间顺序排列的一系列观测值,例如每天的股票价格、每月的销售额、每年的气温等等。
通过对这些时间序列数据进行分析,我们可以得到数据的趋势、季节性、周期性等信息,以及对未来数据的预测。
在SPSS中进行时间序列分析的第一步是导入数据。
通常,数据以文本文件的形式存在,我们需要将其导入到SPSS中进行后续操作。
导入数据完成后,我们可以开始对数据进行初步的探索和观察。
SPSS提供了一系列的统计工具,可以用于时间序列数据的分析。
其中最常用的是时间序列图,它可以帮助我们观察数据的趋势和季节性。
通过绘制时间序列图,我们可以更直观地了解数据的波动情况,找出可能的异常值和离群点。
除了时间序列图,SPSS还提供了许多其他的分析工具,如自相关函数、偏自相关函数、移动平均等。
自相关函数可以帮助我们研究数据之间的相关性,了解数据的滞后效应;偏自相关函数则可以帮助我们确定时间序列模型的阶数;移动平均则可以用于平滑时间序列数据,减少数据的随机波动。
时间序列分析的一个重要应用是预测。
通过对过去数据的分析,我们可以建立时间序列模型,并用此模型来预测未来的数据。
SPSS提供了各种预测模型,如ARIMA模型、指数平滑模型等。
通过选择合适的模型和参数,SPSS可以帮助我们进行准确的预测,并提供相应的置信区间和预测误差。
除了基本的时间序列分析工具,SPSS还提供了其他高级功能,如自回归条件异方差模型(ARCH)、广义自回归条件异方差模型(GARCH)等。
【生物数学】时间序列分析及SPSS实现

一、横截面数据与时间序列数据
• 而时间序列的最大特点是观测值并不独立。时间 序列的一个目的是用变量过去的观测值来预测同 一变量的未来值。
• 即时间序列的因变量为变量未来的可能值,而用 来预测的自变量中就包含该变量的一系列历史观 测值。
• 当然时间序列的自变量也可能包含随着时间度量 的独立变量。
例1 某企业从1990年1月到2002年12月到销售数据 (单位:百万元)。该数据共有按时间顺序的月销售 记录156个,数据如下(tssales.sav)。
SPSS操作:时间序列数据绘图
• 早期的SPSS版本,绘制时间序列图可以选择“Graphs→Sequence()”, 对本例选择sales为变量,months为时间轴标签即可。
• 对于SPSS较新的版本,例如SPSS23.0,要选择“分析→时间序列预测→ 序列图”,然后选择sales为变量,months为时间轴标签即可。
SPSS操作:时间序列附加数据的产生
• 当然,根据数据记录的背景不同和不同的需要,我们 也可以选择“Days”、“Weeks” 等其他形式的时间变 量。
• 作为时间序列数据的一个基本要求,其数据都是等间 隔记录的,比如每天或每月记录一个数据。
• 在金融时间序列(比如股票价格),每周的记录时间只 有5天(周一至周五),此时我们也把它当成是等间隔 记录的,此时记录的时间间隔是“每个工作日”。
• Yt = aXt+a(1-a)Xt -1+a(1-a)2Xt -2+ … +a(1-a)t-1X1 (3) • 其中0<a<1为权重指数。a 越大,表示在加权时给予 当前观测值的权重越大,相应地,给予过去观测值的 权重就越小。
• 这里的系数为几何级数。因此称之为“几何平滑”比 使人不解的“指数平滑”似乎更有道理。
SPSS的时间序列分析(共40张PPT)

3、异方差的非平稳时间序列,其各阶自相关函数显著不为零,且呈现
出正负交错,缓慢下降的趋势;偏自相关函数值也呈正负交均值函数、方差函数均为常数,自协方差函数
仅 常数是,时且间对间隔的t,函t数+。h∈如T二都阶使宽协平方稳差随E[机 y过t-程E定(义yt为)]:EE[(yytt+)h=-
E(yt+h)为 E(yt+h)]
存在且与t无关(只依赖于h)。
4.白噪声序列
白噪声序列是一种特殊的平稳序列。它定义为若随机序列{yt}由互不 相关的随机变量构成,即对所有s≠t,Cov(ys,yt)=0,则称其为白噪声序 列。白噪声序列是一种平稳序列,在不同时点上的随机变量的协方差为0。 该特性通常被称为“无记忆性”,意味着人们无法根据其过去的特点推测 其未来的走向,其变化没有规律可循。当模型的残差序列成为白噪声序列 时,可认为模型达到了较好的效果,剩余残差中已经没有可以识别的信息 。因此,白噪声序列对模型检验也是很有用处的。
11.3 时间序列的图形化观察及检验
• 时间序列的图形化及检验目的
通过图形化观察和检验能够把握时间序列的诸 多特征,如时间序列的发展趋势是上升还是下降, 还是没有规律的上下波动;时间序列的变化的周期 性特点;时间序列波动幅度的变化规律;时间序列 中是否存在异常点,时间序列不同时间点上数据的 关系等。
(6)单击Format 按钮定义图形的格式,可选择横向或纵向序列图;对于单变量序
列图,可选择绘制线图或面积图,还可选择在图中绘制序列的均值线;对多变量的 序列图,可选择将不同变量在同一时间点上的点用直线连接起来。
管理统计学SPSS在时间序列预测中的应用.

• 例13-1:已知某企业1986到2005的20年销售额情况,分别 计算3年和7年移动平均趋势值,并作图与原序列比较。
解:3年移动平均趋势值由一系列3个连续观察值平均得 到。第一个3年移动平均趋势值由序列中前3年的观察值相 加再除以3得到:
M ( 3 ) A Y 1 Y 2 Y 3 15 1 85 7 1 5 .7 7 8 1 5 ..6 0 7 23 3 .5 2
移动平均法存在的一些问题:
(1)加大移动平均法的期数(即加大N值)会使平滑波动效果更 好,但会使预测值对时间序列数据的实际变动更不敏感 ;
(2)移动平均值并不总是很好地反映出趋势,由于是平均值, 预测值总是停留在过去的水平上,从而不能预测将来的波 动性;
(3)移动平均法还需要有大量过去数据的记录,如果缺少历史 数据,移动平均法就无法使用。
4. ARIMA模型
(1)基本概念
ARIMA模型全称综合自回归移动平均(AutoRegressive Int egrated Moving Average)模型,简记为ARIMA(p, d, q)模型, 其中AR是自回归,p为自回归阶数;MA为移动平均,q为移动 平均阶数;d为时间序列成为平稳时间序列时所做的差分次数 。ARIMA(p, d, q)模型的实质就是差分运算与ARMA(p, q)模型 的组合,即ARMA(p, q)模型经d次差分后,便为ARIMA(p, d, q )。
10
12
14
10
12
14
k=1 有峰值然后按指数衰减
1.0
0.5
0.0
- 0 .5
2
4
68ຫໍສະໝຸດ (ρ1 > 0,1 > 0)
0.8
0.6
用SPSS软件做时间序列分析
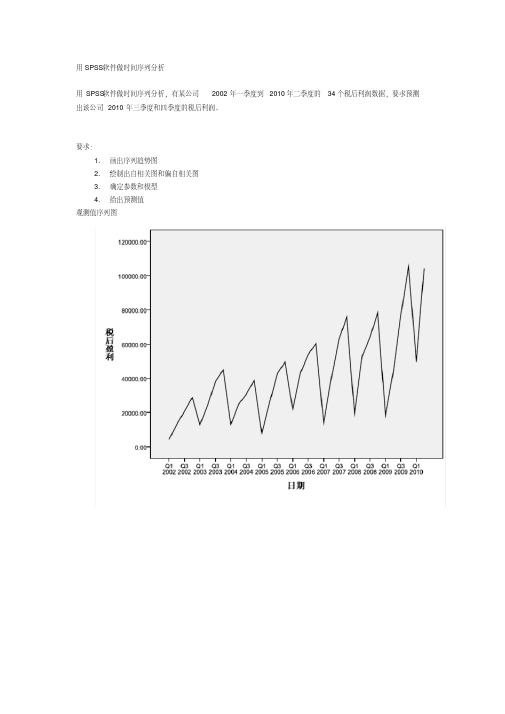
用SPSS软件做时间序列分析用SPSS软件做时间序列分析,有某公司2002年一季度到2010年二季度的34个税后利润数据,要求预测出该公司2010年三季度和四季度的税后利润。
要求:1.画出序列趋势图2.绘制出自相关图和偏自相关图3.确定参数和模型4.给出预测值观测值序列图2税后盈利自相关图序列:税后盈利滞后自相关标准误差aBox-Ljung 统计量值df Sig.b1 .306 .164 3.482 1 .0622 .198 .162 4.987 2 .0833 .185 .159 6.340 3 .0964 .542 .157 18.342 4 .0015 .084 .154 18.641 5 .0026 .067 .151 18.836 6 .0047 .094 .149 19.239 7 .0078 .458 .146 29.093 8 .0009 .041 .143 29.176 9 .00110 .016 .140 29.189 10 .00111 .012 .137 29.197 11 .00212 .236 .134 32.308 12 .00113 -.092 .131 32.806 13 .00214 -.094 .128 33.345 14 .00315 -.079 .125 33.745 15 .00416 .106 .121 34.510 16 .005a. 假定的基础过程是独立性(白噪音)。
b. 基于渐近卡方近似。
偏自相关序列:税后盈利滞后偏自相关标准误差1 .306 .1712 .115 .1713 .107 .1714 .503 .1715 -.279 .1716 -.010 .1717 .046 .1718 .268 .1719 -.130 .17110 -.054 .17111 -.053 .17112 -.081 .17113 -.040 .17114 -.051 .17115 -.027 .17116 -.062 .1713、确定参数和模型时间序列建模程序模型描述模型类型模型 ID 税后利润模型_1 ARIMA(0,1,0)(0,1,0) 模型摘要模型统计量模型预测变量数模型拟合统计量Ljung-Box Q(18)离群值数平稳的 R 方统计量DF Sig.税后利润-模型_1 0 5.502E-17 17.688 18 .476 04、给出预测值2010年第三季度 139621.02万元2010年第四季度170144.55万元剔除季节成分后,平滑处理及剔除循环波动因素的序列图SEASON、MOD_6、MUL、EQU、4 中税后利润的季节性调整序列自相关图序列:SEASON、MOD_6、MUL、EQU、4 中税后利润的季节性调整序列滞后自相关标准误差aBox-Ljung 统计量值df Sig.b1 .728 .164 19.633 1 .0002 .450 .162 27.383 2 .0003 .310 .159 31.169 3 .0004 .207 .157 32.911 4 .0005 .219 .154 34.941 5 .0006 .241 .151 37.484 6 .0007 .243 .149 40.168 7 .0008 .226 .146 42.571 8 .0009 .183 .143 44.213 9 .00010 .162 .140 45.551 10 .00011 .093 .137 46.012 11 .00012 .006 .134 46.015 12 .00013 -.047 .131 46.145 13 .00014 -.021 .128 46.172 14 .00015 -.022 .125 46.204 15 .00016 -.036 .121 46.294 16 .000a. 假定的基础过程是独立性(白噪音)。
spss教程第四章---时间序列分析

第四章时间序列分析由于反映社会经济现象的大多数数据是按照时间顺序记录的,所以时间序列分析是研究社会经济现象的指标随时间变化的统计规律性的统计方法。
.为了研究事物在不同时间的发展状况,就要分析其随时间的推移的发展趋势,预测事物在未来时间的数量变化。
因此学习时间序列分析方法是非常必要的。
本章主要内容:1. 时间序列的线图,自相关图和偏自关系图;2. SPSS 软件的时间序列的分析方法−季节变动分析。
§4.1 实验准备工作§4.1.1 根据时间数据定义时间序列对于一组示定义时间的时间序列数据,可以通过数据窗口的Date菜单操作,得到相应时间的时间序列。
定义时间序列的具体操作方法是:将数据按时间顺序排列,然后单击Date →Define Dates打开Define Dates对话框,如图4.1所示。
从左框中选择合适的时间表示方法,并且在右边时间框内定义起始点后点击OK,可以在数据库中增加时间数列。
图4.1 产生时间序列对话框§4.1.2 绘制时间序列线图和自相关图一、线图线图用来反映时间序列随时间的推移的变化趋势和变化规律。
下面通过例题说明线图的制作。
例题4.1:表4.1中显示的是某地1979至1982年度的汗衫背心的零售量数据。
试根据这些的数据对汗衫背心零售量进行季节分析。
(参考文献[2])解:根据表4.1的数据,建立数据文件SY-11(零售量),并对数据定义相应的时间值,使数据成为时间序列。
为了分析时间序列,需要先绘制线图直观地反映时间序列的变化趋势和变化规律。
具体操作如下:1. 在数据编辑窗口单击Graphs→Line,打开Line Charts对话框如图4.2.。
从中选择Simple单线图,从Date in Chart Are 栏中选择Values of individual cases,即输出的线图中横坐标显示变量中按照时间顺序排列的个体序列号,纵坐标显示时间序列的变量数据。
实验_6时间序列分析的spss应用

实验6 时间序列分析的spss应用6.1实验目的学会运用SPSS统计软件创建时间数列,熟练掌握长期趋势线性模型拟合和季节变动测定的SPSS方法与技能。
6.2相关知识(略)6.3实验内容6.3.1用SPSS统计软件创建时间序列的创建6.3.2用SPSS统计软件处理长期趋势线性模型的拟合(最小二乘法、指数平滑法)及预测。
6.3.3掌握测定季节变动规律的SPSS M定方法。
6.4实验要求6.4.1准备实验数据6.4.2用SPSS统计软件创建彩电出口数量的时间序列6.4.3用最小二乘法测定长期趋势,拟合线性趋势方程,并进行趋势预测。
6.4.4测定彩电出口数量的季节变动规律。
6.4.5用指数平滑法预测2014和2015年的彩电出口数量。
6.5实验步骤6.5.1实验数据为了研究某国彩电出口的情况,某研究机构收集了从2003-2013年某国彩电出口的月度数据,如表6-1所示。
表6-1 我国2003-2013年的我国彩电出口的月度数据(单位:万台)1月2月3月4月5月6月7月8月9月10月11月12月2003 年12.53 13.73 24.45 28.75 32.45 31.11 25.94 32.98 43.49 42.94 63.29 77.28 2004 年30.01 39.63 29.77 42.74 32.25 31.94 32.27 32.59 32.92 30.98 47.44 52.82 2005 年24.08 16.42 31.24 29.33 31.88 30.09 28.08 32.99 44.99 47.57 50.36 75.19 2006 年39.02 25.81 43.38 37.34 39.22 39.87 51.10 50.99 55.16 62.78 57.75 72.20 2007 年28.76 39.38 46.10 39.41 38.74 40.18 45.59 43.31 46.68 54.17 53.65 61.122009 年29.99 37.09 37.70 35.33 29.53 53.64 28.95 25.88 37.61 39.83 28.44 54.85 2010 年55.77 13.96 43.50 32.96 32.91 47.65 39.74 39.48 50.70 60.53 68.22 83.47 2011 年66.35 70.35 86.19 87.50 61.19 93.23 89.31 88.37 90.05 90.06 107.56 101.63 2012 年78.31 91.97 91.73 101.67 77.60 87.64 98.82 79.90 110.86 113.29 125.58 120.24 2013 年101.65 93.53 127.04 133.68 143.76 155.50 170.59 168.96 186.16 181.91 253.78 201.146.5.2创建彩电出口数量时间序列1•先录入数据,录入后的SPSS数据文件如下图6-1所示:妬Q轴回呃眇昶理磁①删i⑥ WW 3B[G)我凫師辿處□也帮前图6-1 录入后的数据文件(部分图)2•定义日期变量。
SPSS在时间序列预测中的应用

(3)相关分析结果
(1)样本自相关系数的值 在SPSS中给出了不同滞后期(Lag列)的样本自相关系数的 值(Autocorrelation列),样本自相关系数的标准误差(Std Error列),以及Box-ljung Statistic的值、自由度(d f列) 和相伴概率(Sig)。通过标准误差值以及Box-ljung Statisti c的相伴概率都可以说该时间序列不是白噪声,是具有自相关 性的时间序列,可以建立ARIMA等模型。Box-ljung Statisti c的相伴概率是在近似认为Box-ljung Statistic服从卡方分布 得到。
2、基本原理
(1)指数平滑法
指数平滑法有助于预测存在趋势和(或)季节的序列。指数平 滑法分为两步来建模,第一步确定模型类型,确定模型是否需 要包含趋势、季节性,创建最适当的指数平滑模型,第二步选 择最适合选定模型的参数。
指数平滑模法一般分为无季节性模型、季节性模型。无季节性 模型包括简单指数平滑法、布朗单参数线性指数平滑法等,季 节性模型包括温特线性和季节性指数平滑法。
理论上,自相关系数序列与时间序列具有相同的变化周期.所 以,根据样本自相关系数序列随增长而衰减的特点或其周期变 化的特点判断序列是否具有平稳性,识别序列的模型,从而建 立相应的模型。
3.其他注意事项
进行时间序列预处理的时候,常常需要对数据一些变换,例如, 取对数,做一阶差分,做季节差分等。
11.1.2 时间序列预处理的SPSS操作详解
Step05 :相关分析
选择菜单栏中的【Analyze(分析)】→【Forecasting(预测)】 →【Autocorrelations(自相关)】命令,弹出【Autocorrelati ons(自相关)】对话框。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验6 时间序列分析的spss应用6.1 实验目的学会运用SPSS统计软件创建时间数列,熟练掌握长期趋势线性模型拟合和季节变动测定的SPSS方法与技能。
6.2 相关知识(略)6.3 实验内容6.3.1 用SPSS统计软件创建时间序列的创建6.3.2用SPSS统计软件处理长期趋势线性模型的拟合(最小二乘法、指数平滑法)及预测。
6.3.3掌握测定季节变动规律的SPSS测定方法。
6.4实验要求6.4.1准备实验数据6.4.2用SPSS统计软件创建彩电出口数量的时间序列6.4.3用最小二乘法测定长期趋势,拟合线性趋势方程,并进行趋势预测。
6.4.4测定彩电出口数量的季节变动规律。
6.4.5用指数平滑法预测2014和2015年的彩电出口数量。
6.5 实验步骤6.5.1 实验数据为了研究某国彩电出口的情况,某研究机构收集了从2003-2013年某国彩电出口的月度数据,如表6-1所示。
表6-1 我国 2003-2013年的我国彩电出口的月度数据(单位:万台)1月2月3月4月5月6月7月8月9月10月11月12月2003年12.53 13.73 24.45 28.75 32.45 31.11 25.94 32.98 43.49 42.94 63.29 77.28 2004年30.01 39.63 29.77 42.74 32.25 31.94 32.27 32.59 32.92 30.98 47.44 52.82 2005年24.08 16.42 31.24 29.33 31.88 30.09 28.08 32.99 44.99 47.57 50.36 75.19 2006年39.02 25.81 43.38 37.34 39.22 39.87 51.10 50.99 55.16 62.78 57.75 72.20 2007年28.76 39.38 46.10 39.41 38.74 40.18 45.59 43.31 46.68 54.17 53.65 61.12 2008年28.87 21.23 35.82 26.97 32.33 24.53 29.39 31.96 38.22 39.24 52.95 68.412009年29.99 37.09 37.70 35.33 29.53 53.64 28.95 25.88 37.61 39.83 28.44 54.85 2010年55.77 13.96 43.50 32.96 32.91 47.65 39.74 39.48 50.70 60.53 68.22 83.47 2011年66.35 70.35 86.19 87.50 61.19 93.23 89.31 88.37 90.05 90.06 107.56 101.63 2012年78.31 91.97 91.73 101.67 77.60 87.64 98.82 79.90 110.86 113.29 125.58 120.24 2013年101.65 93.53 127.04 133.68 143.76 155.50 170.59 168.96 186.16 181.91 253.78 201.146.5.2 创建彩电出口数量时间序列1.先录入数据,录入后的SPSS数据文件如下图6-1所示:图6-1 录入后的数据文件(部分图)2.定义日期变量。
选择“数据-定义日期”,打开“定义日期”主对话框,选择相应的时间设置类型,运行完成后,数据文件中会增加相应的时间变量。
在本案例中,数据是年份和月份数据,且是从2003年1月开始的,所以时间为“年份、月份”类型,且起始年份为2003年,起始月份为1月。
图6-2 “定义日期”对话框运行完成后,在数据文件中增加了3个变量,分别是“YEAR_”“MONTH_”及“DATE_”,如图6-3所示。
图6-3 定义日期变量后的结果(部分图)3.创建时间序列(用移动平均法)选择“转换-创建时间序列”,打开“创建时间序列”对话框,将“出口量”变量移入右侧的“变量-新名称”框中,在“函数”下拉框中选择“中心移动平均”,在“跨度”中输入5表示五项移动平均,然后点击“更改”按钮,设置情况如下图6-4所示:图6-4 创建时间序列对话框设置完毕,单击“确定”按钮,则会在原数据文件中增加一个变量,名称为“出口量_1”的五项移动平均序列。
4.绘制时间序列趋势图选择“分析-预测-序列图”,打开“序列图”对话框,将“出口量”和“出口量_1”移动右侧的“变量”框,并将定义的日期变量设为“时间轴”标签,单击“确定”按钮,系统输出如图6-5所示的时间序列图。
图6-5 序列图设置对话框图6-6 生成的时序图由图6-6中我们可以看出,彩电出口量趋势线变得平滑,随着时间的延长,彩电出口量增加的趋势特征明显。
但是增长并不是单调上升的,而是有涨有落,这种升降不是杂乱无章的,与季节因素有关。
我们知道,影响时间序列的因素有长期趋势变动、季节因素、循环变动和不规则变动,所以案例中彩电出口量的变动除了增长的长期趋势和季节变动的影响外,还受不规则变动和循环变动的影响。
6.5.3用最小二乘法分析彩电出口量变动的长期趋势1.新建一个时间变量,变量名为“时序”,按照时间的顺序设为1,2,3,4,5……选择“分析-回归-线性”,打开“线性回归”对话框,如下图6-7所示。
从左边的待分析变量框中,将变量“出口量”移入“因变量”框中,将变量“时序”移入“自变量”框中。
图6-7 线性回归对话框2.单击“统计量”按钮,弹出如图6-8所示的对话框,依次勾选“估计”、“置信区间”、“协方差矩阵”、“模型拟合度”、“Durbin-Wstson”,单击继续按钮,返回主对话框。
图6-8 线性回归统计量设置子对话框“绘制”、“保存”、“选项”、“Bootstrap”等选项卡的设置可参考回归分析实验的设置。
单击“确定”按钮,提交系统运行。
3.主要运行结果表6-2 回归系数表表6-2是回归系数的估计结果,也是最小二乘法的估计结果。
由表中数据可以看出,常数项和自变量“时序”的t值分别为1.618和11.803。
自变量的显著性概率值为0.000,小于0.05,对因变量有显著性影响,而常数项的显著性概率值为0.108,大于0.05,对因变量的影响不显著。
所以,我们应该去掉常数项,选择“分析-回归-线性回归”,重新打开线性回归主对话框,然后在单击“选项”,打开“线性回归:选项”对话框,不选中“在等式中包含常量”这项,单击“继续”,最后单击“确定”按钮,运行结果如下表6-3所示。
表6-3 不含常数项的回归分析结果由表6-3可以看出,自变量的t值为26.401,显著性概率值为0.000,小于0.05,因此对因变量有显著影响。
即Y=0.879X。
6.5.4 测定彩电出口数量的季节变动规律1.选择“分析-预测-季节性分解”,打开“周期性分解”对话框,按照图6-9进行设置,图6-9 周期性分解对话框2.在周期性分解对话框的右上角有“保存”按钮,点击“保存…”,打开“保存…”对话框,本例选择“添加至文件”。
点击“继续”按钮,返回图6-9所示的主对话框,然后点击“确定”按钮,提交系统运行。
图6-10 “周期:保存…”对话框3.主要运行结果及分析图6-11 模型描述截图图6-11为模型的描述表,显示了模型的名称、类型、季节性期间的长度和移动平均数的计算方法等信息。
图6-12 季节性因素表(截图)图6-12是季节性因素表,由于受季节性的影响,各月份的彩电出口量有很大不同,可看出9,10,11,12月份的季节指数大于1,说明彩电出口在这些月份是旺季,其余月份的季节指数小于1,是淡季,其中2月份的出口情况最差,12月份的彩电出口情况最好。
图6-13 出口量季节变动、循环变动、长期趋势和不规则变动指数计算结果(截图)图6-13是数据文件中显示的数据视图。
从图6-13中可以看出,数据文件中增加了4个序列:ERR_1表示“出口量”序列进行季节性分解后的不规则变动序列;SAS_1表示“出口量”序列进行季节性分解除去季节性因素后的序列;SAF_1表示“出口量”序列进行季节性分解产生的季节性因素序列;STC_1表示“出口量”序列进行季节性分解出来的序列趋势和循环成分。
用数据文件中新增的这4个序列做时序图,按照前面的操作步骤,系统运行结果如下图6-14所示,这些新序列也可以在不同的图上显示。
图6-14 季节性分解后的时序图6.5.5用指数平滑法预测2014和2015年的彩电出口数量1.选择“分析-预测-创建模型”,打开“时间序列建模器”对话框,并按照图6-15进行设置。
首先对“变量”选项卡进行设置,把“出口量”移到右侧的“因变量”栏,“方法”选择指数平滑法。
图6-15 时间序列建模器对话框单击“条件…”按钮,打开“时间序列建模器:指数平滑条件”对话框,本案例中选择“Winters可加性”,这种模型适用于具有线性趋势和不依赖于序列水平的季节性效应序列,如下图6-16所示。
(在图6-16所示的对话框中,依次选择“简单季节性”、“Winters可加性”、“Winters相乘性”,分别建立不同的季节性指数平滑模型。
通过比较发现,“Winters可加性”的拟合最好,“平稳的R方”达到了0.499。
因此,选用“Winters可加性”趋势模型进行预测。
)图6-16 时间序列建模器:指数平滑条件对话框2.“统计量”选项卡设置。
在主对话框中单击“统计量”按钮,打开如图6-17所示的对话框,依次勾选“按模型显示拟合度量、Ljung-Box统计量和离群值的数量”、“平稳的R方”、“拟合优度”、“参数估计”、“显示预测值”选项。
图6-17 输出统计量对话框3.“图表”选项卡设置。
单击“图表”按钮,进入图表输出选择对话框,在选项卡中选择“序列”、“观测值”和“预测值”三项,一般为系统默认。
4.“保存”选项卡的设置。
单击“保存”按钮,进入保存输出选择对话框,如图6-18所示,将“预测值”保存到数据文件中,变量名的前缀“预测值(P)”改为“预测值”,预测期在“选项”中设置。
如果要在输出结果中显示“置信区间的上限”、“置信区间的下限”、“噪声残值”,则可根据数据分析的要求选中。
图6-18 保存选项卡对话框5.“选项”选项卡设置。
单击“选项”,进入“选项”对话框,设置如下图6-19所示。
在预测阶段框中选择第二个选项,并在日期活动框中输入2015年12月,表示预测期到2015年12月,其他为默认设置。
单击“确定”,提交系统运行。
图6-19 “选项”对话框6.主要运行结果表6-5是模型的描述表,表示的对“出口量”变量进行指数平滑法处理,使用的是Winters加法模型。
表6-5 模型描述表表6-6是模型的拟合情况表,包含了八个拟合情况度量指标。
