浙江省高等数学竞赛试题与答案工科类
浙江高三高中数学竞赛测试带答案解析

浙江高三高中数学竞赛测试班级:___________ 姓名:___________ 分数:___________一、选择题1.集合},且,则实数取值范围为()A.B.C.或D.2.若则是的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件3.已知等比数列{}:且第一项至第八项的几何平均数为9,则第三项是()A.B.C.D.4.已知复数为虚数单位),且,则()A.B.C.或D.或5.已知直线与抛物线交于两点,为的中点,为抛物线上一个动点,若满足,则下列一定成立的是()。
A.B.其中是抛物线过的切线C.D.6.某程序框图如下,当E0.96时,则输出的K=()A.20B.22C.D.257.若三位数被7整除,且成公差非零的等差数列,则这样的整数共有()个。
A.4B.6C.7D.88.设函数,则函数的极大值点为()A.B.C.D.9.已知为一次函数,若对实数满足,则的表达式为()。
A.B.C.D.二、填空题1.若,则_________________。
2.已知,若当时恒大于零,则的取值范围为_____________ 。
3.数列,则数列中最大项的值为______________。
4.若,满足,则 ,。
5.设直线与曲线有三个不同的交点,且,则直线的方程为_________________。
6.若则________________________。
7.某动点在平面直角坐标系第一象限的整点上运动(含第一象限轴上的整点),其运动规律为或。
若该动点从原点出发,经过6步运动到(6,2)点,则有__________________种不同的运动轨迹。
三、解答题1.已知抛物线,过轴上一点的直线与抛物线交于点两点。
证明,存在唯一一点,使得为常数,并确定点的坐标。
2.设二次函数在[3,4]上至少有一个零点,求的最小值。
3.设满足数列是公差为,首项的等差数列;数列是公比为首项的等比数列,求证:。
4.设证明。
2010年浙江省高等数学竞赛试题与答案(共4份)

试题共四套:数学类、工科类、经管类、文专类2010浙江省大学生高等数学(微积分)竞赛试题(数学类)一、计算题(每小题14分,满分70分)1.求极限1lim 2n →+∞+⎦2.计算()22222exp 21R x xy y dxdy ρρ⎡⎤-+⎢⎥--⎢⎥⎣⎦⎰⎰. 其中01ρ≤< 3.请用,a b 描述圆 222x y y +≤ 落在椭圆 22221x y a b+= 内的充分必要条件,并求此时椭圆的最小面积。
4.已知分段光滑的简单闭曲线Γ(约当曲线)落在平面π:10ax by cz +++=上,设Γ在π上围成的面积为A ,求()()()bz cy dx cx az dy ay bx dz ax by czΓ-+-+-++⎰其中n Γ与的方向成右手系。
5.设f 连续,满足()()() 22 02exp xf x x x t f t dt =--⎰且()11/f e =,求()()1n f 的值。
二、(满分20)定义数列{}n a 如下:{},,max ,211011dx x a a a n n ⎰-==,4,3,2=n ,求n n a ∞→lim 。
三、(满分20分)设函数)(2R C f ∈,且0)(lim =∞→x f x ,1)(≤''x f ,证明:0)(lim ='∞→x f x 。
四、(满分20分)设非负函数f 在[0,1]上满足)()()(,,y f x f y x f y x +≥+∀且1)1(=f ,证明:(1)]1,0[,2)(∈≤x x x f (2)21)(1≤⎰dx x f 五、(满分20分)设全体正整数集合为+N ,若集合+⊂N G 对加法封闭(即G y x G y x ∈+⇒∈∀,),且G 内所有元素的最大公约数为1,证明:存在正整数N ,当正整数n >N 时,G n ∈(工科类)一、计算题(每小题14分,满分70分)1.求极限1lim 2n →+∞+⎦2.计算()() +22 122dxx x x ∞-∞+-+⎰3.设ABC ∆为锐角三角形,求sin sin sin cos cos cos A B C A B C ++---的最大值和最小值。
浙江省《高等数学》竞赛“连续、导数及其应用专题”历年真题汇总

浙江省《高等数学》竞赛“连续、导数及其应用专题”历年真题汇总第一部分:连续、导数定义,函数导数求解1、 (03 经) xe + y + sin x = 0 ,求 y (0) .x '2、 (04)设 f ( x) = arctan1− x (n ) ,求 f (0) . 1+ x 1 x 3、(04 文)求曲线 y = (1 + ) 在 x = 1 处的切线方程. xf ( x) 求 = 1 , f (0) , f ′(0) 和 f ′′(0) x →0 1 − cos x4、 (05 经) f ( x) 在 x = 0 点二阶可导, lim 设 且的值。
⎧ ln(1 + x) , x>0 ⎪ 5、(05 文)设 f ( x) = ⎨ 可导,求常数 a, b 的值. x ⎪ax + b, x ≤ 0 ⎩6、 (06 文)求曲线 ⎨⎧ x = t 2 − 2t ⎪ 在 t = 0 处的切线方程. ⎪ y arctan t + e y = e 2 ⎩⎧ x = cos(t 2 ) d2y ⎪ 2 7、 (07 经)设 ⎨ ,求 . t −u 2 dx 2 sin udu ⎪y = ∫ 0 e ⎩8、 (07 文)设 f ( x) =3x3 (n) ,求 f ( x) . 2 x − 2x − 3( 2008 )9、 (08)设 f ( x) = x arcsin x ,求 f(0) .10、 (08 经)求曲线 ⎨⎧ x = ln t ⎪ 在 t = 1 处的切线方程. t 2 y = 2t + ∫ e −( ts ) ds ⎪ 1 ⎩2 (2009)11、(09 经) 设 f ( x) = x sin x ,求 f(0) .⎧ x = cot t ⎪ 12、(09 经) 设 ⎨ cos 2t , t ∈ (0,π ) ,求此曲线的拐点. ⎪ y = sin t ⎩13、(10 经) 设 f 连续,满足 f ( x ) = x +2∫x0e x −t f ′(t )dt ,求 f ′(0) 。
高等数学(微积分)竞赛工科类试题整理1

浙江和江苏试题2007浙江省高等数学(微积分)竞赛试题(解答)一.计算题(每小题12分,满分60分) 1、求9⎰.解: 9551155==⎰⎰⎰111111555u t u du=+-==-⎰⎰⎰312222155u u C=-+Cx x ++-+215235)1(52)1(152。
2、求1120(1)(12)limsin xxx x x x→+-+.解:1111220(1)(12)(1)(12)limlimsin x xx xx x x x x x xx→→+-++-+=11022201ln(1)1ln(12)lim (1)(12)(1)(21)2x xx x x x x x x x x x x →⎧⎫⎡⎤⎡⎤++=+--+-⎨⎬⎢⎥⎢⎥++⎣⎦⎣⎦⎩⎭ 0112220(1)ln(1)2(21)ln(12)lim (1)(12)(1)2(21)x xx x x x x x x x x x x x x →⎧⎫⎡⎤⎡⎤-++-++=+-+⎨⎬⎢⎥⎢⎥++⎣⎦⎣⎦⎩⎭ 1122200(1)ln(1)2(21)ln(12)lim (1)lim (12)(1)2(21)x x x x x x x x x x x x x x x x →→⎡⎤⎡⎤-++-++=+-+⎢⎥⎢⎥++⎣⎦⎣⎦22(1)ln(1)2(21)ln(12)limlim2x x x x x x x x e e xx→→-++-++=-00ln(1)2ln(12)lim lim24x x x x e e x x→→-+-+=-22e e e =-+=.3、求p 的值,使22007()()0b x p ax p edx ++=⎰.解: 222007()2007()t x pbb p x p ta a px p e dx te dt =+++++=⎰⎰被积函数是奇函数, 要积分为零, 当且仅当积分区间对称,即:a pb p +=--,解得:2a b p +=-.4、计算2222max{,}00,(0,0)abb x a y dx edy a b >>⎰⎰. 解: 22222222max{,}max{,}00abb xa yb x a y Ddx e dy ed σ=⎰⎰⎰⎰, 其中D 如右图2222222212max{,}max{,}b x a y b x a y D D ed ed σσ=+⎰⎰⎰⎰222212a yb xD D ed ed σσ=+⎰⎰⎰⎰2222ab b ya xa yb xb a dy edx dx edy=+⎰⎰⎰⎰2222b aa yb xa b yedy xedxba=+⎰⎰2222222211()()22b a a yb xed a y ed b x ab ab=+⎰⎰221(1)a beab=-.5、计算2()Sx y dS+⎰⎰,其中S 为圆柱面224,x y +=解: 2221()()2SSSx y dS x y dS ydS +=++⎰⎰⎰⎰⎰⎰142SSdS ydS =+⎰⎰⎰⎰ 8yzD π=+⎰⎰8yzD π=+⎰⎰8π=被积函数关于y 是奇函数,积分区域关于z 对称,二、(20分)设1211211212345632313nun n n=+-++-+++--- ,111123n v n n n=+++++ ,求: (1)1010u v ;(2)lim n n u →∞.解: (1)111232313nn k u k k k=⎛⎫=+- ⎪--⎝⎭∑ 1211211212345632313n n n=+-++-+++--- ,23111111nnnn k k k v n kkk=====-+∑∑∑111111111111123456323132n n n n n ⎛⎫⎛⎫=+++++++++++-+++ ⎪ ⎪--⎝⎭⎝⎭31111121132313nn nn n k k k u v k k k k k ===⎛⎫-=+--- ⎪--⎝⎭∑∑∑11211033nnk k k k k ==⎛⎫=---= ⎪⎝⎭∑∑ 1n vu v ⇒=;(2)111lim lim lim 123n n n n n u v n n n →∞→∞→∞⎛⎫==+++ ⎪++⎝⎭11111lim 1221111n k nn n n n n →∞⎛⎫⎪=+++ ⎪ ⎪++++⎪⎝⎭(图来说明积分上下)2111lim1nn k k nn→∞==+∑201ln 31dx x==+⎰.三、(满分20分)有一张边长为4π的正方形纸(如图),C 、D 分别为A A '、B B '的中点,E为D B '的中点,现将纸卷成圆柱形,使A 与A '重合,B与B '重合,并将圆柱垂直放在xOy 平面上,且B 与原点O 重合,D 若在y 轴正向上,求:(1) 通过C ,E 两点的直线绕z 轴旋转所得的旋转曲面方程; (2) 此旋转曲面、xOy 平面和过A 点垂直于z 轴的平面所围成的立体体积.解:C EL :22224x y z π--==--旋转曲面上任意取一点(,,)M x y z则000(,,)N x y z 的坐标为:0002222z x z y z z ππ-⎧=+⎪⎪⎪=+⎨⎪=⎪⎪⎩,(0,0,)Q zM Q N Q ===化简得:所求的旋转曲面方程为:222282zxy π+-=,(2)(0,0,4)A π,故过(0,0,4)A π垂直z 轴的平面方程为:4z π=BDB 'Ex令0x=,解得在坐标面yo z上的曲线方程为:22282zyπ-=,图中所求的旋转体的体积为:24V dzππ⎛=⎝⎰24282zdzπππ⎛⎫=+⎪⎝⎭⎰242322zdzπππ=+⎰222321283233πππ=+=.四、(20分) 求函数2222(,,)x yzf x y zx y z+=++,在222{(,,)14}D x y z x y z=≤++≤的最大值、最小值.解:222222222222222()2()222(,,)()()xx x y z x x yz xy xz xyzf x y zx y z x y z++-++-'==++++2222232222222222()2()2(,,)()()yz x y z y x yz zx z yx y zf x y zx y z x y z++-++--'==++++2222232222222222()2()2(,,)()()zy x y z z x yz yx y zx z yf x y zx y z x y z++-++--'==++++由于,x y具有轮换对称性,令x y=, 0x=或0y z==解得驻点: (0,,)y y或(,0,0)x对22221(0,,)2x yzf y yx y z+==++, 2222(,0,0)1x yzf xx y z+==++,在圆周2221x y z++=上,由条件极值得:令2222(,,)(1)F x y z x yz x y zλ=++++-(,,)220xF x y z x xλ'=+=8=(,,)20y F x y z z y λ'=+=(,,)20z F x y z y z λ'=+= 222(,,)10F x y z x y z λ'=++-=解得:(0,)22,(0,)22-,(0,22--,(0,22-,(1,0,0),(1,0,0)-1(0,,222f =,1(0,222f -=-,1(0,,222f --=,1(0,)222f -=-,(1,0,0)1f =,(1,0,0)1f -=;在圆周2224x y z ++=上,由条件极值得:令2222(,,)(4)F x y z x yz x y z λ=++++-(,,)220x F x y z x x λ'=+=(,,)20y F x y z z y λ'=+=(,,)20z F x y z y z λ'=+= 222(,,)40F x y z x y z λ'=++-=解得:(0,,(0,,(0,,(0, ,(2,0,0),(2,0,0)-12f =,1(0,2f =-,1(0,2f =,1(0,2f =-,(2,0,0)1f =,(2,0,0)1f -=;2222(,,)x yz f x y z x y z+=++,在222{(,,)14}D x y z x y z =≤++≤的最大值为1,最小值为12-.五、(15分)设幂级数0n n n a x ∞=∑的系数满足02a =,11n n na a n -=+-,1,2,3,n = ,求此幂级数的和函数.证明:0()nn n S x a x∞==∑1111111()(1)n n n nn n n n S x naxaxn x∞∞∞----==='⇒==+-∑∑∑()nnnnn n n ax nxS x nx ∞∞∞====+=+∑∑∑而()1200011(1)nn nn n n n n x nxx nxx xx x x x x ∞∞∞∞-====''⎛⎫⎛⎫'=====⎪ ⎪--⎝⎭⎝⎭∑∑∑∑,即:2()()(1)x S x S x x '-=- 一阶非齐次线性微分方程---常数变易法,求()()0S x S x '-=的通解:()xS x ce=,令()()x S x c x e =代入2()()(1)xS x S x x '-=-得:2()()()(1)xxxx c x e c x e c x e x '+-=-,即:()211()(1)111x x x x xxe c x dx xe dx xe dx x e xx x ---'⎛⎫'==⋅=-⎪----⎝⎭⎰⎰⎰()11xxxxxexee dx ec xx ----=+-=++--⎰故2()()(1)x S x S x x '-=-的通解为:1()11x x x xxe S x e c e ce x x --⎛⎫=++⋅=+ ⎪--⎝⎭,由于(0)0S =,解得1c =-, 故0n n n a x ∞=∑的和函数1()1xS x ex=--.六、(15分)已知()f x 二阶可导,且()0f x >,[]2()()()0f x f x f x '''-≥,x R ∈,(1) 证明:2121212()(),,2x x f x f x f x x R+⎛⎫≥∀∈ ⎪⎝⎭.(2) 若(0)1f =,证明(0)(),f x f x e x R'≥∈.证明: (1) 要证明2121212()(),,2x x f x f x f x x R+⎛⎫≥∀∈ ⎪⎝⎭,只需证明1212121111ln()ln ()ln ,,2222f x f x f x x x x R⎛⎫+≥+∀∈ ⎪⎝⎭,也即说明()ln()F x f x =是凹函数,[]()ln()()f x f x f x ''=,[][]22()()()()ln ()0()()f x f x f x f x f x f x f x ''''-'⎛⎫''==≥ ⎪⎝⎭, 故()ln ()F x f x =是凹函数, 即证.(2)2()()(0)(0)2F F x F F x xξ'''=++[]222()()()(0)ln (0)(0)2()x f x f x f x f f x x f f x ξ='''-'=++(0)f x'≥,即:(0)(),f xf x ex R'≥∈.2008浙江省高等数学(微积分)竞赛试题(解答) *一.计算题1、求xxx x x ee e sin13203lim ⎪⎪⎭⎫ ⎝⎛++→.解:xxxxx xxx x x e e e e e e s i n1320s i n1320331lim 3lim ⎪⎪⎭⎫ ⎝⎛-+++=⎪⎪⎭⎫ ⎝⎛++→→xee e x xeee ee e xxxx xxxxxx xxxee e e sin 13sin 133320323232lim 3lim ⋅++→⋅++⋅++→=⎪⎪⎭⎫ ⎝⎛++=2cos 3320032lim e exeee x xxx==⋅++→。
2012年浙江省高等数学(微积分)竞赛试题及答案 工科类

2012年浙江省高等数学(微积分)竞赛试题 工科类 一:计算题(每小题14分,共70分)1:计算:()+lim log +a ba n x x →∞2设函数f :R R →可导,且,x y R ∀∈,满足:()()+++f x y f x y xy ≥,求()f x 的表达式。
3计算: 0sin ,n x xdx n Z π*∈⎰4计算:{}-min ,2Dx y x y dxdy ⎰⎰,其中D 是2=y x 和2=x y 所围成的封闭区域。
5求曲线{33=cos =sin x a y a θθ()0,>0a θπ≤≤的形心。
二:(本题满分20分)证明:=111+ln <<1+ln ,ni n n n Z n i *∈∑三:(本题满分20分)设2:u RR →,且u 具有二阶连续偏导,求证当u 可以表示成:()()(),=u x y f x f y 的充分必要条件是:2=u u uu x y y y∂∂∂∂∂∂∂ 。
四:(本题满分20分)在空旷的草地上有一个地面半径为3的圆柱体,在墙角栓有一头山羊,其绳长为π,求山羊能吃到草地的面积。
五:(本题满分20分)求证:()-1=1=111-1C =,k nn k nk k n Z k k*∈∑∑参考答案一、计算题1、若a b ≥ l i m l o g(a bx x x x →+∞+l i m l o g(1)l i m l o g (1a b ab ax xx x x x a x a --→+∞→+∞=+=++= 同理,当a b <时,lim log ()a b x x x x →+∞+b =, 所以lim log ()a bx x x x →+∞+max(,)a b =2、解:由假设,0y ∀>,有()()1f x y f x x y+-≥+ f 可导()1f x x +'⇒≥+同理()1()1f x x f x x -''≤+⇒=+ 2()/2f x x x c =++ 3、解:sin d n x x x π⎰()011sin sin nnj j j j x x dx x j xdx ππππππ-====+-∑∑⎰⎰()()201sin d 21212nj n x x x j n n n n n n πππππ==+-=++-=+∑⎰4、解:(){}(){}12,1,,/2,01/2D x y x y x D x y x y x x =≤≤≤≤=≤≤≤≤(){}(){}2234,,1/21,,/2,01/2D x y xy x x D x y xy x x =≤≤≤≤=≤≤≤≤原积分12()d d ()d d D D y x x x y x y x x y =-+-⎰⎰⎰⎰34()d d ()d d D D x y x x y x y y x y +-+-⎰⎰⎰⎰211102d )d d ()d xxxx y x x y x x y x y =-+-⎰⎰⎰21112221002d ()d d ()2d xx xx x y x x y x x y y y +-+-⎰⎰⎰⎰11341456142210021211111()678851232x x x x x x x =-++-++146720112()24621x x x +-+111124724532245=++⨯⨯⨯⨯112533216642117920++=⨯⨯ 5、解:/0c LLx xds ds ==⎰⎰,d /d c LLy y s s =⎰⎰而d 3sin cos d s a θθθθ== 2d 3sin cos d sin cos 3Ls a ba d a ππθθθθθθ/===⎰⎰⎰/2324206d sin 3sin cos d 6sin cos d 5Ly s a x a a a ππθθθθθθθ===⎰⎰⎰0c x ∴= 25c y a =二、证明:显然11111d d j j jj x x x jx +-<<⎰⎰ 2j ≥1 1122111111d 1d 1ln nn n j n j j j j x x n j j x x -===∴=+<+=+=+∑∑∑⎰⎰另一方面111111111111d ln nn n j j j j j x n j jn x n n --+====+>+=+∑∑∑⎰三、证明:()()u f x g y =时,显然有xy x y uu u u = 反之,若xy x y uu u u =成立,即有2()/()0xxy x y y u uu u u u u-== 1/()x u u f x ⇒= 也即1121ln ()d ()()()u f x x g y f x g y =+=+⎰ ()()u f x g y ∴=四、解:(方法一)以圆柱形旁子的圆心为原点,拴羊点在x 轴上3x =点,则羊跑最远的曲线在3x <的区域内是渐开线 即 3(cos (/3)sin )x t t t π=-- 3(sin (/3)cos )y t t t π=+- 记在3x <山羊能吃到草的草地面积为1S3/30213/2/32d 29sin d 2(3sin (3)cos )(3)cos d S y x t t t t t t t t ππππ=-=+--⎰⎰⎰/32029sin d t t π-⎰/32223(3)sin cos (3)cos d t t t t t t πππ⎡⎤=-+-⎣⎦⎰/32029sin d t t π-⎰/322013(3)sin (3)(sin 2)2t t t t t πππ⎡⎤=-+-+⎢⎥⎣⎦/32016(3)(sin 2)9sin d 2t t t t t ππ⎡⎤+-+-⎢⎥⎣⎦⎰()/3/3/322000191133cos 2sin 29cos 2d 2222t t t t t t t t ππππ⎛⎫⎛⎫⎛⎫=----+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎰33/319sin 2349t t ππ⎛⎫=+-=⎪⎝⎭所以山羊能吃到草的草地面积333119218S πππ=+= (方法二) 山羊能吃到草的草地面积S 可表示为一半圆与绳子绕向房子所能到达的面积1S 和 绳子绕向房子时转过θ∆ 其扫过的面积可近似为扇形22r θ∆()2/33103/9S d ππθθπ=-=⎰所以311/18S π=五、证明:111110011111(1)(1)d (1)d nn n k k k k k k k knn n k k k C C t t C t t k t ---===--=-=-∑∑∑⎰⎰ 1100(1)11(1)d d n n t t t t t t ----==⎰⎰101d 1nx x x -=-⎰ 而11100111d d 1nnn k k k t t t t k t -==1-==-∑∑⎰⎰ ∴等式成立。
2012年浙江省高等数学竞赛试题与答案

(试题共 4 套 数学类、工科类、经管类、文专类前面是试题后面是答案)2012 浙江省高等数学(微积分)竞赛试题工科类一计算题:(每小题 14分,满分7 0 分)ab1.求极限 lim lo g x ( x x ) 。
名姓x2.设函数 线达式。
f : RR 可导,且x , yR ,满足f ( x y ) f ( x ) yx y ,求 f ( x ) 的表n3.计算 x sin x d x ( n 为正整数)。
4.计算xy m in x , 2 y d x d y , D为 y2x 与 yx 2 围成的平面有界闭区域。
Dx 35.求曲线 a co s, (0) 的形心,其中 a0 为常数。
号y3a sin证考 二、(满分 20 分)准订证明:1nln nni 111ln n , n 。
i三、(满分 20 分)设 u : R2R 所有二阶偏导连续,证明u 可表示为 u ( x , y )f ( x )g ( y ) 的充分必要条件为业 2u u u 。
u专x y xy装四、(满分 20)在草地中间有一个底面半径为 3 米的圆柱形的房子。
外墙脚拴一只山羊, 已知拴山羊的绳子长为 米,外墙底面半径为 3 米,求山羊能吃到草的草地面积。
五、(满分 20 分)校 学nn证明k 1k1( 1)C nk1kk 11 。
k2012 浙江省高等数学(微积分)竞赛试题经管类一、计算题(每小题 14 分,满分 70 分)1 求极限 limlo g x ( xab) 。
xx名姓 2.设 f ( x )a xb x ( ( n )e sin a , b R 为常数),求 f( 0 ) 。
线n3.计算4.求积分5.设函数x sin x d x ( n 为正整数)。
21x24d x1xx1 2a 0 ,常数 a0 ,试求最小的常数a ,使得 f ( x ) 6 。
f ( x )x, x2x号 二、(满分 20 分)证考准证明:1n订ln n1 1 ln n ,nni 1i三、(满分 20 分)求1 2 n C 2n n 的值。
2007浙江省高等数学竞赛工科类
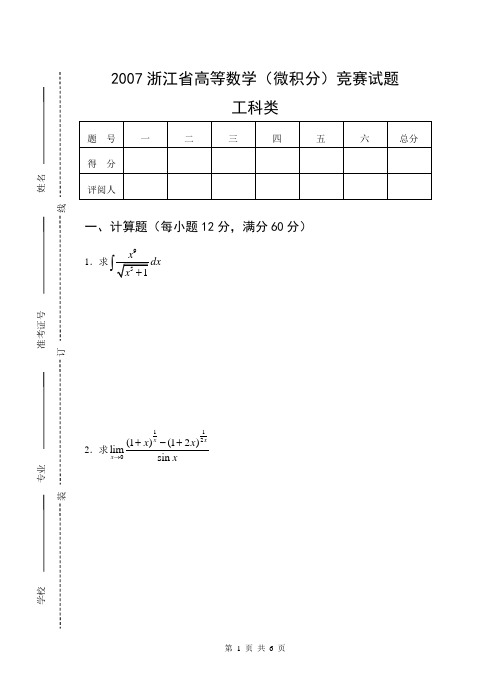
2007浙江省高等数学(微积分)竞赛试题工科类一、计算题(每小题12分,满分60分)1.求92.求1120(1)(12)limsin x xx x x x→+-+装订线3.求p 的值,使22007() ()0bx p ax p e dx ++=⎰4.计算{}2222,max 0ab b x a y dx e dy ⎰⎰,(a>0,b>0)5.计算2()sx y dS +⎰⎰,其中S 为圆柱面224x y +=,(0≤z ≤1)'A'B二、(满分20分)设1211211212345632313nu n n n =+-++-+++---111123n v n n n=+++++求(1)1010u v (2)lim n n u →∞三、(满分20分)有一张边长为4π的正方形纸(如图),C 、D 分别为'AA 、'BB 的中点,E 为'DB 的中点,现将纸卷成圆柱形,使A 与'A 重合, B 与'B 重合,并将圆柱垂直放在xoy 平面上,且B 与原点O 重合,D 落在Y 轴正向上,此时,求:(1)通过C ,E 两点的直线绕Z 轴旋转所得的旋转曲面方程; (2)此旋转曲面、xoy 平面和过A 点垂直于Z 轴的平面所围成的立体体积。
四、(满分20分)求函数2222(,,)x yzf x y zx y z+=++在{}222(,,)|14D x y z x y z=≤++≤的最大值、最小值。
五、(满分15分)设幂级数nn n a x∞=∑的系数满足02a =,11n n na a n -=+-,n=1,2,3…,求此幂级数的和函数()s x 。
六、(满分15分)已知()f x 二阶可导,且()0f x >,[]2''()()'()0f x f x f x -≥,x ∈R(1)证明 21212()()()2x x f x f x f +≥, 12,x x ∀∈R (2)若(0)1f =,证明'(0)(),f x f x e x ≥∈R。
2024年浙江省宁波市高中数学竞赛试题(含答案)

2024年宁波市高中数学竞赛试题一、单选题:本题共4小题,每小题6分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知两圆C 1,C 2,则“C 1,C 2有且仅有三条公切线”是“C 1,C 2相切”的( )A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件2.若α∈{12,1,2},则函数f(x)=x a ln(x 2+1)的图象不可能是( )A. B.C. D.3.已知对任意平面向量AB =(x,y),把AB 绕其起点沿逆时针方向旋转θ角得到向量AP =(x cos θ−y sin θ,x sin θ+y cos θ),叫做把点B 绕点A 沿逆时针方向旋转θ角得到点P.已知圆锥曲线Γ:7x 2+2xy +7y 2=24经过旋转后其方程可以变为标准方程,则此曲线的离心率为( )A. 12B.32C. 1D.24.已知△ABC 的内心为I ,垂心为H ,∠B =π4,若IH//BC ,则∠C 的大小落在区间( )A. (0,π6)B. (π6,π4)C. (π4,π3)D. (π3,π2)二、多选题:本题共3小题,共24分。
在每小题给出的选项中,有多项符合题目要求。
5.设a ,b ,c 是互不相等的正数,若关于x 的不等式a x −b x +c x >0成立.当且仅当x ∈(−∞,1),则( )A. a+c<2bB. 1a +1c>2bC. e a+e c>2e bD. ln a+ln c<2ln b6.数列{a n}是等差数列,周期数列{b n}满足b n=cos(a n).若集合X={x|x=b n,n∈N∗},中恰有三个元素,则数列{b n}的周期T的取值可能是( )A. 4B. 5C. 6D. 77.已知棱长为2的正方体ABCD−A1B1C1D1,点M是线段A1D1上的动点,点N在侧面BCC1B1(包含边界)上且满足B1N⋅C1N=0,下列结论正确的是( )A. 对任意的点M,总存在点N使得MN⊥ACB. 三棱锥M−BCN外接球的球心可以是线段BM的中点C. 三棱锥M−BCN外接球半径的最小值为928D. 二面角M−AC−N的正切的最大值为722三、填空题:本题共6小题,每小题8分,共48分。
2021浙江省高等数学竞赛试题 答案

2021浙江省高等数学竞赛试题答案 2021浙江省高等数学竞赛试题(答案)2021浙江省高等数学竞赛试题答案一、计算题:(每小题14分,满分70分)1-cos x cos 2x1.求极限lim 。
2x →0xsin x cos 2x +2cos x sin 2x解: =limsin x cos 2x +4cos 2x sin xsin x (cos2x +4cos 2x )x →02x 5⎰x 2(x 2+4) dx x +111(2-2) dx 解:=⎰4x x +411x 1=⎰+2--) dx 224x 4x 4(x +4) 4(x +4) ln x 1x 1=-+⎰--) dx44x 4(x 2+4) 4(x 2+4)x arctan 2ln x 1ln(+C =---42.求不定积分3.设f (x ) =ln(t +x ) dt ,求f '(1)的值。
解:令u =t +x f (x ) =⎰ln(t +x ) dt =⎰ln(u ) duf '(x ) =2ln 2x -ln(1+x ) f '(1)=2ln 2-ln 2=ln 24.已知y =y (x ) 由方程e xy +y 3=1确定,求解:e xy (y +xy ') +3y 2y '=0y '=-xyxe +3y 2ye xy e xyy 'x =0=- =-2因为当x =0时y =0 所以y 'x =0=-∞5.求极限 lim。
∑22n →+∞k =1n +kk 1解:lim ∑2 =lim ∑2n →+∞n →+∞n +k n k =1k =1由定积分定义知,极限可以变为⎰dx =ln(1+x ) =ln 201+x 2220lim a 二、(满分20分)设数列{a n }为单调递增的正数列,试讨论极限 n解:当{a n }有界时,lim a n 一定存在,设lim a n =a , 则lim a n当{a n }无界时,lim a n =+∞,lim a n 1/a n =lim eln a n a n'a n 'a n a n三、(满分20分)已知面积为S 的直角三角形绕其斜边旋转一周所得的旋转体体积为V ,求VV =πah 2ah =S =a 2sin θcos θ ⇒h = 222π⇒V =πV =πS 2 所以当θ=时 m a xx sin x⎰01+cos 2x 2πx sin x解:⎰01+cos 2xπ2π-x sin x x sin x =⎰+⎰π1+cos 2x 01+cos 2x 2π-x sin x ⎰π1+cos 2x π-(u +π)sin(u +π) u =x -π−−−→⎰ 201+cos (u +π) π(u +π)sin u =⎰du 01+cos 2uπππsin x 2πx sin x x sin x 2+ 因此⎰=⎰01+cos 2x ⎰01+cos 2x 01+cos 2x πx sin x ⎰01+cos 2x0(π-t )sin(π-t ) t =π-xπ1+cos 2(π-t )(π-t )sin t1+cos 2tππ2x sin x ππsin x=⎰dx =-arctan cos x =241+cos 2x 201+cos 2x 0x sin x 21+cos x+(x >-1) 。
2022年浙江省宁波市高中数学竞赛试题(含答案解析)

2022年浙江省宁波市高中数学竞赛试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知正方形ABCD 的边长为1,则|2|AB BC AC ++=()A .1BC D2.已知,a b R ∈,则“a b >”是“a b >”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.勒洛四面体是一个非常神奇的“四面体”,它是以正四面体的四个顶点为球心,以正四面体的棱长为半径的四个球的公共部分.如图,在勒洛四面体ABCD 中,设弧,AC BD 的中点分别为M ,N ,若线段AB 的长度为a ,则()A .弧AC 的长度为3aπB .线段MN 的长度为aC .勒洛四面体ABCD 能置于一个直径为a 的球内D .勒洛四面体ABCD 的体积大于3124.已知A ,B 分别在两圆222212:1,:4C x y C x y +=+=上运动,且在1C 上存在点P ,使得AP BP ⊥,则线段AB 中点M 轨迹的面积为()A .πB .54πC .2πD .94π二、多选题5.一个装有8个球的口袋中,有标号分别为1,2的2个红球和标号分别为1,2,3,4,5,6的6个蓝球,除颜色和标号外没有其他差异.从中任意摸1个球,设事件A =“摸出的球是红球”,事件B =“摸出的球标号为偶数”,事件C =“摸出的球标号为3的倍数”,则()A .事件A 与事件C 互斥B .事件B 与事件C 互斥C .事件A 与事件B 相互独立D .事件B 与事件C 相互独立6.已知0a >且1a ≠,关于x 的不等式31x a a >-,下列结论正确的是()A .存在a ,使得该不等式的解集是RB .存在a ,使得该不等式的解集是∅C .存在a ,使得该不等式的解集是(,2022)-∞D .存在a ,使得该不等式的解集是2022(,)+∞7.已知函数(),()f x g x 的定义域均为R ,(1)(1)2,()(2)2,(4)()2f x g x g x f x g x f x -++=--=--=,且当(0,1]x ∈时,2()1f x x =+,则()A .(2022)2g =B .()(2)0g x g x ++=C .函数()f x 在(1,3)上单调递减D .方程(2022)f x x +=有且只有1个实根8.设函数()f x 的定义域为I ,区间(,)a b I ⊆,如果对于任意的常数0M >,都存在实数12,,,n x x x ,满足1n a x x b <<<< ,且()()111n i i i f x f x M -+=->∑,那么称()f x 是区间(,)a b 上的“绝对差发散函数”.则下列函数是区间(0,1)上的“绝对差发散函数”的是()A .1()21x f x x =++B .()tan2x f x π=C .2,,(),.x x f x x x ⎧=⎨⎩为无理数为有理数D .()cos2f x x xπ=三、填空题9.设O 为坐标原点,F 是抛物线24y x =的焦点,若P 是该抛物线上一点,且23PFO π∠=,则点P 到y 轴的距离为_____.10.已知实数12,x x 满足()11222ln 3,ln 121x x x x +=--=,则12x x +=_____.11.在44⨯的16个方格中填上实数,使得各行各列都成等差数列.若其中4个方格中所填的数如图所示,则图中打*号的方格填的数是______.*1313133912.已知正三棱柱111ABC A B C -的各棱长均为2,M ,N 分别为棱11,BB CC 上的点.若平面AMN 将三棱柱分为上、下体积相等的两部分,则AMN 的面积的最小值为_____.13.已知n *∈N ,集合{}(,)1|22|1,,n nn A x y x y x y =-+-<∈R ,记1n n A A ∞== ,则集合A中的点组成图形的面积为________.14.已知m ∈R ,关于z 的方程()()2220z z m z z m ++++=有四个复数根1234,,,z z z z .若这四个复数根在复平面内对应的点是一个正方形的四个顶点,则实数m 的值为________.四、解答题15.如图,在ABC 中,2ACB ABC ∠=∠.设点D 是BC 边上一点,满足2BAD ABC ∠=∠.(1)记ABC θ∠=,用θ表示ABBD;(2)若111AB AC+=,求BD .16.已知0a ≥,设函数()|||1|f x x a ax =-+-.(1)判断函数()f x 的奇偶性;(2)若对任意的x ∈R ,不等式()(2)f x x a x ≥-恒成立,求a 的取值范围.17.设点(0,2),(0,2),(0,4)A B F --,过点F 作斜率为k 的直线l 交椭圆221:1164x yΓ+=于C ,D 两点.(1)记直线,,,AC AD BC BD 的斜率分别为1234,,,k k k k .从下列①②③三个式子中任选其一,当k 变化时,判断该式子是否为定值,若是,求出定值;若不是,请说明理由.①12k k ⋅;②14k k ;③23k k .(2)当直线,BC BD 分别交双曲线222:1412y x Γ-=的下支于P ,Q 两点(异于点B )时,求||||PF QF +的取值范围.18.已知无穷正整数数列{}n a 满足()21220222n n n a a n a *+++=∈+N .(1)若21a =,求2022a ;(2)求12022a a +的取值的集合.19.甲、乙两人分别进行投硬币和掷图钉试验,每人各进行100次试验.设k a 为前k 次试验中硬币正面向上的次数,k b 为前k 次试验中图钉针尖朝下的次数,记,(1,2,3,,100)k k k k a bp q k k k=== .(1)若11000,0.5p p ==,问是否存在常数P ,不论试验过程中k p 如何变化,均存在某个()001100k k <<,使得0k p P =?若存在,求出所有P 的可能值;若不存在,请说明理由;(2)若11000,0.7q q ==,问是否存在常数Q ,不论试验过程中k q 如何变化,均存在某个()001100k k <<,使得0k q Q =?若存在,求出所有Q 的可能值;若不存在,请说明理由.参考答案:1.D【分析】利用向量的线性运算和垂直向量的数量积为0可求题设中向量的模.【详解】|2||23|AB BC AC AB BC ++=+= ,故选:D .2.A【分析】判断条件间的推出关系,根据充分必要性的定义判断即可.【详解】当a b >:若,a b 异号,即0a b >>,显然a b >成立;若0a b >≥或0a b ³>,均有a b >成立;所以充分性成立;当a b >:若2a =-,1b =,显然a b >不成立,故必要性不成立.所以“a b >”是“a b >”的充分不必要条件.故选:A 3.D【分析】根据球的对称性可得球心,A C 到弧AC 所在的平面的距离为2a,从而可求弧AC 所在的平面与球的截面圆的半径,故可判断A ;设,AC BD 的中点为分别为,E F ,由球的对称性可得,,,M E F N 共线,连接,BE DE ,计算可得线段MN 的长度,故可得判断BC ,计算出正四面体的体积后可判断D 的正误.【详解】选项A ,弧AC 为两个半径为a 、球心距为a 的球面相交所得的小圆中的弧,根据球的对称性,球心,A C 到弧AC 所在的平面的距离为2a ,因球的半径为a ,故弧AC 所在的平面与球的截面圆的半径为2a ,因为弦AC 的长度为2a a >,故弧AC 所对的圆心角为大于π3,故弧AC 长不为3a π.故A 错误;选项B ,设,AC BD 的中点为分别为,E F ,由球的对称性可得,,,M E F N 共线,连接,BE DE .由A BCD -为正四面体可得AE DE ==,故2EF a ==,而弧AC所在的平面与球的截面圆的半径为2a ,故22222MN a a a a a ⎫=-+=->⎪⎝⎭⎭,故B 错误;选项C ,由MN a >,故C 错误;选项D ,设BCD △的外接圆的圆心为O ,连接AO ,则AO ⊥平面BCD.而12OB =,故AO ==,故由四面体ABCD的体积为2313a ,故D 正确.故选:D.4.C【分析】先考虑//PA x 轴的情形,此时可设(cos ,sin ),(cos ,sin )A P θθθθ-,从而可得M 的轨迹为线段13022x y ⎛⎫=≤≤⎪⎝⎭,当弦AP 在圆上转动时,则可得M 的轨迹为圆环,从而可求其面积,我们也可以作矩形PACB ,利用向量关系可求可得M 的轨迹为圆环,从而可求其面积.【详解】法一:先考虑//PA x 轴时的情形,如图:设(cos ,sin ),(cos ,sin )A P θθθθ-,不妨设,22ππθ⎡⎤∈-⎢⎥⎣⎦,(cos B θ-,所以0,2sin M M x y θ==设sin [1,1]t θ=∈-,则()[1,1]f t t t =+∈-,则()f t 在[]0,1递增,此时()f t ∈;当10t -≤≤时,()f t =因为y y t ==-在[]1,0-上均为减函数,故y t =在[]1,0-上为减函数,且y t =在[]1,0-上的值域为⎤⎦,故()f t =[]1,0-上为增函数,此时()f t ∈,所以()[1,3]f t ∈,此时M 的轨迹为线段13022x y ⎛⎫=≤≤ ⎪⎝⎭.则当弦AP 在圆上转动时,上述线段会扫出一个内径为12,外径为32的圆环,易得面积为2π.法二:如图,作矩形PACB ,其对角线的交点即为M ,连接,,,,OA OB OP OC 取OP 的中点E ,连接EM ,则()()222222||||22OA OB OM MA OM MB OM MB +=+++=+ ,同理222222||||2222OP OC OM MC OM MB +=+=+ ,故2222||||||||OA OB OP OC +=+,即||2OC =,即C 在圆2C 上.则1||||12EM OC ==,则点M 在OP 中点E 为圆心,1为半径的圆上.若记cos sin (cos ,sin ),,22P E θθθθ⎛⎫⎪⎝⎭,则点M 的轨迹方程为22cos sin 122x y θθ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭,即223cos sin 4x y x y θθ+-=+,当θ变化时,x ,y1≤,可得1322≤≤.所以当P 变化时,点M 的轨迹为,内径为12,外径为32的一个圆环,此圆环的面积为2π.故选:C.5.ACD【分析】根据互斥事件的概念可判断AB 的正误,根据独立事件的判断方法可得CD 的正误.【详解】对AB ,若摸得的球为红球,则其标号为1或2,不可能为3的倍数,故事件A 与事件C 互斥,故A 正确;若摸得的球的标号为6,则该标号为3的倍数,故事件B 与事件C 不互斥,故B 错误;对C ,21411(),(),()()()84828P A P B P AB P A P B ======⋅,所以C 正确;对D ,211(),()()()848P C P BC P B P C ====⋅,所以D 正确;故选:ACD .6.ACD【分析】结合指数函数相关知识对选项逐一进行判定.【详解】①1,031,3xa a a x R ≤>≥-∈,故A 正确;②log (31)11,31log (31)3aa xa a a a a x a -><<-=⇒<-,又()log (31)log 2,a a a -∈+∞,故存在a 使得log (31)2022a a -=,不等式解集为(),2022-∞故C 正确;③log (31)1,31log (31)aa xa a a a a x a ->>-=⇒>-,又log (31)(log 2,)a a a -∈+∞,故存在a 使得log (31)2022a a -=,不等式解集为()2022+∞,故D 正确;④结合A 、C 、D 选项,当13a ≤或113a <<或1a >时,不等式都存在解集,故不满足解集为空集,所以B 错误.故选:ACD .7.ACD【分析】由题设中的三个关系式可得()()24g x g x ++=、()()4g x g x =+、(2)(4)0f x f x -+-=、()()f x f x =--,再利用赋值法可判断AB 的正确,最后再结合(0,1]x ∈时2()1f x x =+可得()f x 的图象,从而可判断CD 的正误.【详解】对AB ,由(1)(1)2(4)()2f x g x g x f x -++=⎧⎨--=⎩可得()(2)2(4)()2f x g x g x f x +-=⎧⎨--=⎩,故(2)(4)4g x g x -+-=,所以[][]2(2)4(2)4g x g x --+--=,所以()()24g x g x ++=,故B 错误.故()()244g x g x +++=,故()()4g x g x =+,故()g x 为周期函数,且周期为4,而(1)(1)2()(2)2f x g x g x f x -++=⎧⎨--=⎩可得()(2)2(2)()2f xg x g x f x +-=⎧⎨+-=⎩,故()()224g x g x ++-=,令0x =可得(2)2g =,所以(2022)(2)2g g ==,故A 正确;对C ,由(1)(1)2(4)()2f x g x g x f x -++=⎧⎨--=⎩可得(2)()2()(4)2f xg x g x f x -+=⎧⎨--=⎩故(2)(4)0f x f x -+-=,即(2)(),(4)()f x f x f x f x +=-+=,由(1)(1)2()(2)2f x g x g x f x -++=⎧⎨--=⎩可得(1)(1)2(1)(1)2f xg x g x f x -++=⎧⎨+--=⎩(1)(1)0f x f x -+-=,即()()f x f x =--,故()f x 为奇函数且()f x 为周期函数且周期为4.根据上述性质可得()f x 的图象如下,故()f x 在(1,3)上单调递减,所以C 正确;对D ,又(2022)f x x +=即为(2)f x x +=,此方程即为()2f x x =-的解.结合()f x 的图象可得该方程只有1个解即为2x =,所以D 正确.故选:ACD .8.BCD【分析】对于AB ,可利用导数或基本初等函数的性质研究选项中函数的单调性,从而可判断和的范围,进而判断正误,对于CD ,可取特殊序列,结合放缩法可判断选项的正误.【详解】对A ,()()()222121()21121x f x x x +-'=-=++,当1)x ∈时,()0f x '<,当1,1)x ∈时,()0f x '>,故()f x在1)递减,在1,1)递增,对任意的101n x x <<<< ,存在*N i ∈,使得11011i i n x x x x +<<≤<<<< ,所以()()()()11111()()n i i i n i i f x f x f x f x f x f x -++=-=-+-∑,)()()(){}111max 0,112f f x f f -=-≤<=()112n f x -≤<,故()()1113n i i i f x f x -+=-<-∑A 错误;对B ,因为ππ0,22x ⎛⎫∈ ⎪⎝⎭,故()tan 2x f x π=在()0,1是递增的,对给定的任意的常数0M >,取112x =,考虑()π1tan2,,122x s x M x ⎛⎫=--∈ ⎪⎝⎭,因为1102s M ⎛⎫=--< ⎪⎝⎭,而当1x →时,()s x →+∞,则()πtan 22x s x M =--在1,12⎛⎫⎪⎝⎭上有解,设该解为n x ,故此时()()111πππtantan tan 1242n n n i i i x x f x f x -+=-=-=-∑,则()()1111n i i i f x f x M M -+=-=+>∑,故B 正确;对C ,对给定的任意的常数0M >,设递增数列{}k x 满足:11,,1,2,3,,32k x k n ⎛⎫∈= ⎪⎝⎭,且21k x -为有理数,2k x 为无理数,故221211,,411932k k x x -<<<<则()()1221222112k k k k f f x x x x ++-=>-,()()1221222112k k k k f f x x x x ---=>-,所以()()1111(1)12n i i i f x f x n -+=->-∑,当121n M >+时,必有()()111n i i i f x f x M -+=->∑,故C 正确;对D ,对给定的任意的常数0M >,设1,1,2,,2k x k n k== ,则()()1111111112446222n i i i f x f x n n -+=⎛⎫⎛⎫⎛⎫-=++++++ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭∑ 11123n>+++ ,下证:()()ln 10x x x +<>,设()ln(1),0u x x x x =-+>,则()01xu x x '=>+,故()u x 在()0,∞+上为增函数,故()()00u x u >=,故()()ln 10x x x +<>成立.在上述不等式中令*1,N ,2x n n n =∈≥,则()11ln 1ln ln 1n n n n⎛⎫+-=+< ⎪⎝⎭,故()()111ln 3ln 2ln 4ln 3ln(1)ln ln(1)ln 2n i i i f x f x n n n -+=->-+-+++-=+-∑ ,当2e 1Mn >-时,有()()111(2e 1ln 1)ln 2Mn i i i f x f x M -+=--->+=∑,故D 正确.故选:BCD .9.3【分析】不妨设P 在第一象限,由题设条件可得直线PF 的倾斜角,从而可求其直线方程,联立抛物线方程后可求P 的坐标,从而可求该点到y 轴的距离.【详解】由抛物线的对称性不妨设P 在第一象限,而()1,0F .因为23PFO π∠=,故直线PF 的倾斜角为π3故直线PF的方程为:)1y x =-,即13x y =+,由2413y x x y ⎧=⎪⎨=+⎪⎩可得2403y y --=,故P y =.故3P x =,即P 到y 轴的距离3.故答案为:3.10.1【分析】令()2ln f x x x =+,根据其为增函数可得121x x =+.【详解】设()2ln f x x x =+,则1()20f x x'=+>,故()f x 在()0,∞+上为增函数,而()22ln 121x x --=即为()()2221ln 13x x -+-=,由题可得()()121f x f x =-,所以121x x =-,即121x x =+.故答案为:111.5【分析】设*号的空格上填的实数为x ,由题设可得关于x 的一次方程,求出其解后可得*号的空格上所填之数.【详解】*A131313BC 39如图,设*号的空格上填的实数为x ,第一行第三列所填数为A ,第三行第二列、第三列所填数分别为,B C ,则13,262x A B x +==-.进而有第三列的公差为396536A xd --==,从而16926x C A d +=+=.又13,B ,C 成等差数列,得1692(26)136x x +-=+,解得5x =.故答案为:512.2【分析】根据体积相等可得3BM CN +=,设,3BM t CN t ==-,其中03t <<,利用面积公式和余弦定理可得AMN S = .【详解】由()111111111111BCNM BCNM A BCNM A BCC B ABC A B C A A B C BCC B BCC B S S V V V V S S ----=⋅=⋅-四边形四边形四边形四边形111111112132BCNM ABC A B C ABC A B C BCC B S V V S --=⋅=四边形四边形,故11334344BCNM BCC B S S =⨯==四边形四边形,从而()1232BM CN +⨯=,故3BM CN +=.设,3BM t CN t ==-,其中03t <<.由正三棱柱可得()()22222243,4,432AN t AM t MN t =+-=+=+-,故11sin 22AMN S AM AN MAN AM AN =⨯∠=⨯12AM AN =⨯⨯14=而()2222224AM AN AM AN MN ⨯-+-=故2AMNS ==≥,等号当且仅当32t =时取到,所以()min 2AMN S =△.故答案为:2.13.1【分析】先由特殊情形可得|1|[0,1),|22|[0,1)x y -∈-∈,结合不等式的性质可得结论:“若1(,)x y A ∈,(,)n x y A ∈”,从而可求图形的面积.【详解】若1(,)x y A ∈,则|1||22|1x y -+-<,从而|1|[0,1),|22|[0,1)x y -∈-∈.所以()*1|22|1221N n n x y x y n -+-≤-+-<∈,即得(,)n x y A ∈,故有11n n A A A ∞=== .又1A 中的点组成图形为如图所示的菱形:其中()()312,1,1,,0,1,1,22C D E B ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,该菱形的对角线的交点()1,1M ,故菱形的面积为12112⨯⨯=.所以集合A 中的点组成图形的面积为1.故答案为:1.14.16【分析】先判断判别式中至少有一个为负,若判别式一正一负,则可根据1234z z z z -=-可求16m =,当判别式均为负时,可根据实系数方程的虚数根为共轭复数可判断此时不合题设条件.【详解】设20z z m ++=根为2121,,14,20z z m z z m ∆=-++=的根为342,,18z z m ∆=-,由题意12140,180m m ∆=-≠∆=-≠,即18m ≠且14m ≠.①当18m <时,1234,,,z z z z 均为实数,则四个实数根均在实轴上,矛盾;②当1184m <<时,12,z z 为实数且34,z z 为虚数,且1234z z z z -=-,114816m m m =-=-⇒=;此时22110,063z z z z ++=++=,故12z z ⎧=⎪⎪⎨⎪=⎪⎩或21z z ⎧=⎪⎪⎨⎪=⎪⎩,且342626z z ⎧-+=⎪⎪⎨-⎪=⎪⎩或432626z z ⎧-+=⎪⎪⎨-⎪=⎪⎩,这四个点为以1,03⎛⎫- ⎪⎝⎭为中心,且对角线的方程分别为13x =-,0y =,正方形的顶点.③当14m >时,1234,,,z z z z 均为虚数,因为m 为实数,故12,z z 为共轭复数且121z z +=-,故12,z z 的实部为12-,同理34,z z 的实部为12-,,即四个对应点均在直线12x =-,这与题设矛盾.综上:16m =.故答案为:16m =.15.(1)2cos 1ABBDθ=+(2)1【分析】(1)利用正弦定理可求ABBD;(2)利用正弦定理结合题设条件可得2cos 1AB θ=+,再由(1)中的结论可求BD 的长.【详解】(1)由题,22BAD ACB θθ∠=∠=.在ABD △中,3π2BDA θ∠=-,根据正弦定理可得3sinsin cos cos sin 222sin sin22AB BD θθθθθθθ+==22sincos 2cos sin 222cos 2cos 2cos 12sin 2θθθθθθθθ+==+=+.(2)在ABC 中,根据正弦定理可得sin 2sin AB AC θθ=,所以12cos AC ABθ=,所以1112cos 1AB AC ABθ++==,可得2cos 1AB θ=+.又由(1)知2cos 1ABBDθ=+,所以1BD =..16.(1)当0a =时,()f x 为偶函数;当0a >时,()f x 为非奇非偶函数(2)0a ≤≤【分析】(1)由(1)(1)f f =-可求0a =,结合偶函数定义可得函数为偶函数,而(1)(1)=--f f 不成立,故可判断()f x 的奇偶性;(2)利用赋值法可得02a <≤,再证明当02a <≤时题设中的不等式恒成立,从而可求求a 的取值范围.【详解】(1)易知(1)2|1|,(1)2|1|f a f a =--=+,若(1)(1)f f =-,则2|1|2|1|a a -=+,解得0a =,此时()()||1f x x f x -=-+=,而x ∈R ,故此时()f x 为偶函数;当0a ≠时,(1)(1)f f ≠-,而(1)(1)21210f f a a +-=-++>,故(1)(1)f f ≠--,故此时()f x 为非奇非偶函数.综上,当0a =时,()f x 为偶函数;当0a >时,()f x 为非奇非偶函数.(2)0a =时,2()||1f x x x =+≥-显然成立,所以0a =符合.0a >时,若(,0][2,)x a ∈-∞+∞ ,则(2)0()x a x f x -≤≤恒成立,故只需考虑|||1|(2)x a ax x a x -+-≥-对任意(0,2)x a ∈恒成立.(*),取x a =,有221a a -≥,解得212a ≤,即得02a <≤.而当02a x a <≤<<时,21210ax a -≤-≤,故(*)式可化为2||310x a x ax -+-+≥对任意[0,2]x a ∈恒成立,令2()||31g x x a x ax =-+-+,①当(0,]x a ∈时,2()(31)(1)g x x a x a =-+++恒成立;因为对称轴312a x a +=>,故()2()120g x g a a ≥=-≥.②当[,2)x a a ∈时,2()(31)(1)g x x a x a =--+-,因为对称轴312a x a -=≤,且()2()120g x g a a ≥=-≥.故此时2||310x a x ax -+-+≥对任意[0,2]x a ∈恒成立,因此02a <≤.综上:02a ≤≤.17.(1)均为定值,1212433,3,34k k k k k k ⋅==-=-;(2)28,3⎛⎫+∞ ⎪⎝⎭【分析】(1)设()()1122,,,C x y D x y ,则可用坐标表示1234,k k k k ,联立直线方程和椭圆方程后结合韦达定理化简前者可得它们为定值,从而可得12k k ⋅,14k k ,23k k 均为定值.(2)联立直线PB 的方程和双曲线的方程,求出P x ,再利用公式可求PF ,同理可求PQ ,利用34112k k =可求||||PF QF +的取值范围.【详解】(1)由题可得:4l y kx =-,设()()1122,,,C x y D x y .l 与1Γ联立()2222441324801164y kx k x kx x y=-⎧⎪⇒+-+=⎨+=⎪⎩,则12212232414841k x x k x x k ⎧+=⎪⎪+⎨⎪⋅=⎪+⎩.又()22232448410k k ∆=-⨯⨯+>,故2k >或2k <-.选择①:()()()212121212121212126663622kx kx k x x k x x y y k k x x x x x x ---++--⋅=⋅==222248326363414148441k k k k k k ⨯-⨯+++==+,故12k k ⋅为定值,且1234k k ⋅=,选择②:221111132211112244141614y y y y k k x x x y +---⋅=⨯===-⎛⎫- ⎪⎝⎭即1314k k ⋅=-,而()()()21212121234121212222422112kx kx k x x k x x y y k k x x x x x x ---++++⋅=⋅===.则143414k k k k =-⋅,所以1434134k k k k =-=-⋅,故14kk 为定值,且143k k =-;选择③:同②可得2414k k ⋅=-,则2334134k k k k =-=-⋅,同②可得34112k k ⋅=,故23k k 为定值,且233k k =-.(2)若选择①,则1234k k ⋅=,而221111132211112244141614y y y y k k x x x y +---⋅====-⎛⎫- ⎪⎝⎭,同理2414k k ⋅=-,故3412121111441612k k k k k k ⎛⎫⎛⎫⋅=-⋅-== ⎪ ⎪⋅⎝⎭⎝⎭.若选择②,则143k k =-,而221111132211112244141614y y y y k k x x x y +---⋅====-⎛⎫- ⎪⎝⎭,故34112k k ⋅=.若选择③,则233k k =-,而222222222422222244141614y y y y k k x x x y +---⋅=⨯===-⎛⎫- ⎪⎝⎭,故34112k k ⋅=.综上,无论如何选择,总有34112k k ⋅=.此时34:2,:2PB y k x QB y k x =-=-.PB 与2Γ联立()322322332321231120311412p y k x k k x k x x y x k =-⎧⎪⇒--=⇒=⎨--=⎪⎩,而21P PF y =+,因为P 为双曲线下支上的动点,故2P y ≤-,故22P PF y =--,所以232233248||263131k PF k k =-+=----,同理可得248||631QF k =---.所以()()2234222234343211||||128128173131316k k PF QF k k k k +-⎛⎫+=--=--⨯ ⎪--⎝⎭-++()2234152417316k k =-+-++.因为,BC BD 分别交2Γ下支于P ,Q两点,所以33010123k k ⎧<<⎪⎪⎨⎪<<⎪⎩,且43k k ≠,所以222343231441k k k k ++=,其中2311483k <<且23112k ≠.令()111,,144483g x x x x ⎛⎫=+∈ ⎪⎝⎭,则()222114411144144x x g x x -'=-=,当114812x <<时,()0g x '<,当11123x <<时,()0g x '>,故()g x 在11,4812⎛⎫ ⎪⎝⎭上为减函数,在11,123⎛⎫⎪⎝⎭上为增函数,故22331714448116k k +<<,所以2234117,648k k ⎛⎫+∈ ⎪⎝⎭,故()2234179031616k k <-++<,所以28||||3PF QF +>,故28||||,3PF QF ⎛⎫+∈+∞ ⎪⎝⎭.18.(1)1(2){343,677,1013,2023}.【分析】(1)根据递推关系可得()()()312222n n n n n a a a a a ++++-+=-,根据{}n a 为无穷正整数数列可得310a a -=、420a a -=,从而可求2022a .(2)设212,k k a b a c -==,则可得关于bc 的不定方程,求出解后可得12022a a +的取值的集合.【详解】(1)由条件知:2123231222022,222022n n n n n n n n a a a a a a a a ++++++++=++=+,两式相减得()()()312222n n n n n a a a a a ++++-+=-,因为{}n a 为正整数数列,所以1n a ≥,故312222223n n n n n n n a a a a a a a +++++-=-≤-+,若310a a m -=>,则()*2021,N n n a a n k n +-≠=-∈,则312n n n n a a a a +++-<-,故3121n n n n a a a a +++-≤--,则53311a a a a -≤--,57531a a a a -≤--,79751a a a a -≤--,L ,212321121k k k k a a a a -+---≤--,故()1231121k k a a a a k -+-≤---,当311k a a ->-时,21210k k a a -+-<,这与{}n a 为无穷正整数列矛盾.故310a a -=即310a a -=,同理420a a -=,所以2n n a a +=,所以2022202021a a a ==== .(2)由(1)知2n n a a +=,所以设212,k k a b a c -==,则220222b bc +=+,所以2022bc =.而202223337=⨯⨯,所以{,}{1,2022},{2,1011},{3,674},{6,337}b c =,所以2023,1013,677,343b c +=,所以12022a a +的取值的集合为{343,677,1013,2023}.19.(1)不存在;理由见解析(2)存在,12Q =或23.【分析】(1)取两种特殊情形可判断这样的P 不存在.答案第17页,共17页(2)先由特例判断出,12Q =或23,再证明不论试验过程中k q 如何变化,均存在某个()001100k k <<,使得0k q Q =,故可求Q 的值.【详解】(1)不存在,先考虑最后50次试验硬币正面向上,则对应的(1100)k p k <<均小于0.5.再考虑第2次至第51次试验硬币正面向上,则对应的(1100)k p k <<均大于等于0.5.这与最后50次试验硬币正面向上的情形没有公共的取值,故这样的P 不存在.(2)存在,12Q =或23,先考虑最后70次试验针尖向下,则对应的(1100)k q k <<均小于0.7.再考虑第2次至第71次试验针尖向下,则对应的k q 分别为123707070700,,,,,,,,,234717299100,所以符合要求的Q 只可能取12,23.下证对1,2,3n Q n n-==,必存在01100k <<时,使得0001k k b n q k n -==.设(1)k k S nb n k =--,若第k 次试验针尖朝上,则1k k b b -=,则11(1)(1)(1)(1)(1)k k k k S nb n k nb n k n S n --=--=-----=--;若第k 次试验针尖朝下,则11k k b b -=+,则11(1)(1)(1)11k k k k S nb n k nb n k S --=--=---+=+当2,3n =时,()()()11100110,701001100300S nb n n S n n n =--=--=--=-.所以由介值性定理知,必存在01100k <<,使得00k S =,即0001k k b n q k n-==,得证.。
浙江省高中数学竞赛试卷 参考答案

20XX年浙江省高中数学竞赛试卷参考答案一、选择题(本大题共10小题,每小题5分,共计50分)1. 已知集合,,则=(A )。
A.B.C.D.空集解:由于,所以。
答案为A。
2. 已知椭圆上一点P到点(4, 0)距离等于4,则P点到直线的距离为( C )。
A.4 B.6 C.D.解:因为,则。
于是P到另一个焦点的距离等于。
由于直线为椭圆的左准线方程,则P到直线的距离为。
答案为C。
3. 等差数列中,,,则部分和中最大的是(C )A.B.C.D.解:由题意知,。
所以是单调递减数列。
又。
由此可得当时,最大。
答案为C4. 已知平面上单位向量,则下列关系式正确的是(B )A. B. C. D.解:因为都是非零单位向量,以为边,为对角线构成一个菱形。
所以。
答案为B。
5. 方程有三个不同的实数根,则实数a的取值范围为(A )A. B. C. D.解:令,则。
要使有三个不同的零点,则必须有,即,也即有。
答案为A。
6. 设,则使代数式有意义的动点形成的图形(C )A. 关于x轴对称,B. 关于y轴对称,C. 关于直线对称D.关于直线对称。
解:由题意得,则动点(x,y)形成的图形关于直线y=x对称。
答案为C。
7. 的二项展开式中常数项为(D )。
A.B.C.D.解:由于,则出现常数项,须满足。
答案为D。
8. “函数f(x)在[0, 1]上单调”是“函数f(x)在[0, 1]上有最大值”的(B )A.必要非充分条件B.充分非必要条件C.充分且必要条件D.既非充分也非必要条件解:答案为B。
9.已知立体的三视图如下,问该立体的体积为( C )A . 1B .C .D . 解:答案为 C 。
10. 问下述计算机程序的打印结果为( D ) A .B .C .D .解:答案为 D 。
侧视图(等腰直角三角形,直角边长为1)俯视图(正方形,边长为1)正视图(等腰三角形,底边边长为1,高为1)二、填空题(本大题共7小题,每小题7分,共计49分)11.-8 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012浙江省高等数学(微积分)竞赛试题
工科类
一计算题:(每小题14分,满分70分)
1.求极限lim log ()a
b
x x x x →+∞
+。
2.设函数:f →R R 可导,且,x y ∀∈R ,满足()()f x y f x y xy +≥++,求()f x 的表达式。
3.计算 0
sin d n x x x π
⎰
(n 为正整数)。
4.计算
{}min ,2d d D
x y x y x y -⎰⎰
,D 为2y x =与2y x =围成的平面有界闭区域。
5.求曲线3
3
cos sin x a y a θ
θ
⎧=⎪⎨=⎪⎩,(0)θπ≤≤的形心,其中0a >为常数。
二、(满分20分)
证明:111
ln 1ln
n i n n n i =+<<+∑
,n ¢+∈。
三、(满分20分)
设2
:u →R R 所有二阶偏导连续,证明u 可表示为(,)()()u x y f x g y =的充分必要条件为
2u u u u x y x y
∂∂∂=∂∂∂∂。
四、(满分20)
在草地中间有一个底面半径为3米的圆柱形的房子。
外墙脚拴一只山羊,已知拴山羊的绳子长为π米,外墙底面半径为3米,求山羊能吃到草的草地面积。
五、(满分20分)
证明1
1
111(1)
n
n
k k n
k k C k k -==-=∑∑。
装
订
线
工科类答案
一、计算题
1、若a b ≥ lim log ()a
b
x x x x →+∞
+lim log (1)lim log (1)a
b a
b a x x x x x x
a x a --→+∞→+∞
=+=++=
同理,当a b <时,lim log ()a
b
x x x x →+∞
+b =, 所以lim log ()a
b
x x x x →+∞
+max(,)a b =
2、解:由假设,0y ∀>,有
()()
1f x y f x x y
+-≥+ f Q 可导()1f x x +'⇒≥+
同理()1()1f x x f x x -''≤+⇒=+ 2
()/2f x x x c =++ 3、解:
sin d n x x x π
⎰
()0
1
1
sin sin n
n
j j j j x x dx x j xdx ππ
ππ
ππ-====+-∑∑⎰
⎰
()()20
1
sin d 21212n
j n x x x j n n n n n n π
ππππ==+-=++-=+∑⎰
4、解:(
){}
(){}12,1,,/2,01/2D x y x y x D x y x y x x =≤≤
≤≤=≤≤≤≤
(){}(){}
2
2
34,,1/21,,/2,01/2D x y x
y x x D x y x
y x x =≤≤≤≤=
≤≤≤≤
原积分12
()d d ()d d D D y x x x y x y x x y =
-+-⎰⎰⎰⎰3
4
()d d ()d d D D x y x x y x y y x y +-+-⎰⎰⎰⎰
21
110
2
d )d d ()d x
x
x
x y x x y x x y x y =-+-⎰⎰⎰2
1112221002d ()d d ()2d x
x x
x x y x x y x x y y y +-+-⎰⎰⎰⎰
11
3414561422100
2
1211111()678851232x x x x x x x =-++-++1
46720
112()24621
x x x +-+
111124724532245=
++⨯⨯⨯⨯11253
3216642117920
++=
⨯⨯ 5、解:/0c L
L
x xds ds =
=⎰
⎰,d /d c L
L
y y s s =⎰⎰
而d 3sin cos d s a θθθθ== 2
d 3sin cos d sin cos 3L
s a ba d a ππθθθθθθ/===⎰
⎰⎰
/2
3
2
420
6
d sin 3sin cos d 6sin cos d 5
L
y s a x a a
a π
πθθθθθθθ===⎰
⎰⎰
0c x ∴= 25
c y a =
二、证明:显然
1111
1d d j j j
j x x x j
x +-<<⎰
⎰ 2j ≥
1 1122
11
1111d 1d 1ln n
n n j n j j j j x x n j j x x -===∴=+<+=+=+∑∑∑⎰⎰
另一方面111111111111
d ln n
n n j j j j j x n j j
n x n n --+====+>+=+∑∑∑⎰
三、证明:()()u f x g y =时,显然有xy x y uu u u =
反之,若xy x y uu u u =成立,即有2
()/(
)0x
xy x y y u uu u u u u
-== 1/()x u u f x ⇒= 也即1121ln ()d ()()()u f x x g y f x g y =+=+⎰ ()()u f x g y ∴=
四、解:(方法一)以圆柱形旁子的圆心为原点,拴羊点在x 轴上3x =点,则羊跑最远的曲线在3x <的区域内是渐开线 即 3(cos (/3)sin )x t t t π=-- 3(sin (/3)cos )y t t t π=+- 记在3x <山羊能吃到草的草地面积为1S
3
/3
213/2
/3
2d 29sin d 2(3sin (3)cos )(3)cos d S y x t t t t t t t t ππππ=-=+--⎰
⎰
⎰
/3
20
29sin d t t π-⎰
/322
23(3)sin cos (3)cos d t t t t t t πππ⎡⎤=-+-⎣⎦⎰/320
29sin d t t π-⎰
/3
22
13(3)sin (3)(sin 2)2t t t t t πππ⎡⎤=-+-+⎢⎥⎣⎦/32016(3)(sin 2)9sin d 2t t t t t ππ⎡⎤+-+-⎢⎥⎣⎦⎰ ()/3/3
/322000191133cos 2sin 29cos 2d 2222t t t t t t t t ππππ⎛⎫⎛⎫⎛⎫
=----+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭
⎰
33
/3
19sin 28349
t t ππ⎛⎫=+-=
⎪⎝⎭
所以山羊能吃到草的草地面积33
3
119218
S πππ=+= (方法二) 山羊能吃到草的草地面积S 可表示为一半圆与绳子绕向房子所能到达的面积1S 和 绳子绕向房子时转过θ∆ 其扫过的面积可近似为扇形
2
2
r θ∆
()2
/3
310
3/9S d ππθθπ=-=⎰
所以311/18S π=
五、证明:
111
11001
1111(1)
(1)d (1)d n
n n k k k k k k k k
n
n n k k k C C t t C t t k t ---===--=-=-∑∑∑⎰⎰ 1
100(1)1
1(1)d d n n t t t t t t ----==⎰⎰101d 1n
x x x -=-⎰ 而111
0011
1d d 1n
n
n k k k t t t t k t -==1-==-∑∑⎰⎰ ∴等式成立。
