第二章-6-非线性系统线性化
微分方程的线性化

df ( x) 1 d 2 f ( x) 2 y f ( x) f ( x0 ) ( ) x0 ( x x0 ) ( ) ( x x ) x0 0 2 dx 2! dx
当增量(x- x0)很小时,略去其高次幂项,则
df ( x) y y0 f ( x) f ( x0 ) ( ) x0 ( x x0 ) dx
线性化总结
1) 线性化是相对某一工作点,工作点不同,线
性化方程的系数也不同; 2) 偏差愈小,线性化精度愈高; 3) 线性化适用于连续变化的单值函数。 4) 式中变量是增量,不是绝对量,公式称为增量 方程式 5) 额定工作点若是坐标原点,增量可以写成绝对 量。 6) 当增量并不是很小时,在进行线性化时,为了 验证容许的误差值,需要分析泰勒式中的余项。
df ( x) y ( ) x0 x k x dx
df ( x) k dx x0
是比例系数,它是函数f(x)在工作点 A点的切线斜率。
将线性增量方程代入系统微分方程,便可得系统线性化 方程。
y kx
同理可得,多变量非线性函数
y f ( x1 , x 2 , x n )
微分方程的线性化
然而严格地说,实际物理元件和系统都是非线性 的。 叠加原理不适用于非线性系统,这给求解非线性 系统带来不便,因此需要对所研究的系统作线性 化处理。
非线性系统的线性化
非线性系统进行线性化的条件: 非线性函数是连续函数;系统在预定工作点附近作小偏 差运行,即变量的变化范围很小。
图示为连续变化的非线性 函数 y=f(x) 线性化方法是:把非线性 函数在 工作点x0附近展成 泰勒级数,略 去高次项, 便得一个以增量为变量的 线性函数:
非线性系统

4M sinωt ∴y1(t ) = π π
∫ y(t)sinωtd(ωt) π
1
0
2π
π
2、饱和特性
2 t 当= B1 =为 arcsin a + a ω 时 且( A>a时 输 2kx t = Asin1− a 入 , A> a) , N( A) A πy A Ay 奇函数 A
仅 输 正 信 幅A 函 , N 数, 示。 数 是 入 弦 号 值 的 数 用 ( A)来 示 表 。
二、描述函数的求法
(1)首先由非线性静特性曲 ,画出正弦信号 线 输 下 输 波 , 写 输 波 y(t )的 达 。 入 的 出 形 并出 出 形 表 式
(2)利用傅氏级数求出(t)的基波分量。 y (3)将求得的基波分量代入 义式, 定
()
当 > a时,比例系数总小于。 ∴A = A = 0 A> A k 0 1
ψ1
π
特性 N( A)也是输入 的 A的函数。 即饱和 幅值 的函数。 k ωt x 0 0 a 节, 饱和特性等效 于一ψ1 系数 2π例环 , 个变 π 的比 节
0
B= 1
x1
∫ y(t)sinωtd(ωt) π
0
2π
描述函数
描述函数法是非线性系统的一种近似 分析方法。首先通过描述函数将非线性元 件线性化,然后应用线性系统的频率法对 系统进行分析。分析内容主要是非线性系 统的稳定性和自振荡问题,一般不能给出 时间响应的确切信息。
一、描述函数的定义 1、描述函数的应用条件
,弦 幅作 对的 的 些含 谐分量 将 本 量 中正 来号 相下 大 那包 次流 分。 在环 信 值用 不输 不 高直 波量。 出 构。 闭 结 。 构 弱。 被 大 弱 因 , 以 似 认 在 环 大 削 。 此 可 近 地 为 闭 通 道 只 基 分 在 通 此 应 描 函 内 有 波 量 流 , 时 用 述 数 y 确。 法 得t) = 0 析x 果 比 准 。 于) 际 非 所 r(的 分 结 才 较 确 对 c(t实 的 性 统 -说 由 G 线 系 来 , 于 (s)通 具 低 滤 特 常 有 通 波 性 因 这 条 是 足 。 , 此 个 件 满 的
控制工程基础_第二章(2017)

时,
R F (s) s
18
例 求单位斜坡函数f(t)=t的拉氏变换。 f (t )
单位斜坡函数如图(b) 所示,定义为
0 t 0 f (t ) t t 0
解:利用定义式,可得
O
t
(b)单位斜坡函数
F (s)
0
1 1 st 1 1 st 1 st t e dt t ( e ) e dt 0 e 2 0 0 s s s s 0 s
12
二.举例
1.机械系统的微分方程式
机械系统设备大致分两类:平移的和旋转的。它们之间的区 别在于前者施加的力而产生的是位移,而后者施加的是扭矩产生 的是转角。
牛顿定律和虎克定律等物理定律是建立机械系统数学模型的基础
c1 m c2 xo xi
例1(1)如图所示机械系统。求其微分方程,图中Xi 表示输入位移,Xo 表示输出位移,假设输出端无负 载效应。(c、c1、c2为阻尼系数,k1、k2为弹性系数) 由牛顿定律有: 化为标准式得:
st
例 求单位脉冲函数的拉氏变换。 单位脉冲函数如图(c)所示。定义为
0 t 0 且 (t ) t 0
0
f (t )
(t )
O
0
(t )dt 1
0
t
F ( s) (t )e st dt (t )e st dt (t )e st dt f (0) e st
图c
14
(4)机械旋转系统 图中所示转动惯量为J的转子与弹性系数为k的弹性轴和阻尼 系数为B的阻尼器连接。假设外部施加扭矩m(t),则系统产生一个 偏离平衡位置的角位移(t) 。研究外扭矩m(t)和角位移(t)的关系。
微分方程的线性化

微分方程的线性化
然而严格地说,实际物理元件和系统都是非线性 的。
叠加原理不适用于非线性系统,这给求解非线性 系统带来不便,因此需要对所研究的系统作线性 化处理。
xn
x10, x20, xn0
y k1x1 k2x2 knxn
线性化总结
1) 线性化是相对某一工作点,工作点不同,线 性化方程的系数也不同;
2) 偏差愈小,线性化精度愈高;
3) 线性化适用于连续变化的单值函数。
4) 式中变量是增量,不是绝对量,公式称为增量 方程式
5) 额定工作点若是坐标原点,增量可以写成绝对 量。
1 2!
(
d
2f( dቤተ መጻሕፍቲ ባይዱ2
x)
)
x0
(
x
x0
)
2
当增量(x- x0)很小时,略去其高次幂项,则
df (x) y y0 f (x) f (x0 ) ( dx )x0 (x x0 )
y
(
df (x) dx
)
x0
x
k
x
df (x) k
dx x0
是比例系数,它是函数f(x)在工作点 A点的切线斜率。
6) 当增量并不是很小时,在进行线性化时,为了 验证容许的误差值,需要分析泰勒式中的余项。
非线性系统的线性化
非线性系统进行线性化的条件: 非线性函数是连续函数;系统在预定工作点附近作小偏 差运行,即变量的变化范围很小。
图示为连续变化的非线性 函数
y=f(x)
线性化方法是:把非线性 函数在 工作点x0附近展成 泰勒级数,略 去高次项, 便得一个以增量为变量的 线性函数:
机械控制工程基础(第二章)ppt课件

a0x0t
bm
dmxi t
dtm
bm1
dm1xi t
d tm1
b1
d xi t
dt
b0xi
t
在初始条件为零时,对上式进行拉氏变换
ansnan 1sn 1 a 1sa0X 0s b m smb m 1sm 1 b 1sb 0X i s
故得系统(或环节)的传递函数为
G sX X 0 is sb a m n s sm n a b n m 精 1 1 选s sn Pm P 1 T1 课 件 a b 1 1 s s a b 0 0
x0(t)Txi(t)
精选PPT课件
16
例 下图是简化了的直流发电机组。激磁电压 v恒i 定,磁通不变。
此时电枢电压 与转v速0 成正比•。若 为输入,输出是电压 ,
试v求0此系统的传递函数。
R
•
解:v 0 T
vi i
LM
式中 T——常数
v0 VsT s s 0
GsV 0ssTs
即直流发电机作为测速发电机时,可认为是微分环节。
2
x0
0
精选PPT课件
xi
3
x• 0
0
精选PPT课件
xi
4பைடு நூலகம்
F
0
x?
F
0
x?
精选PPT课件
5
线性化方法:
利用台劳公式 f(x)k n 1 0f(k k )!(a)(xa)kR n(x)
f(a)k n 1 1f(k k )!(a)(x a)kR n(x)
f( x ) f( x 0 ) f( x 0 )x ( x 0 )
物理系统的数学模型
及传递函数
非线性系统线性化课件

详细描述
倒立摆是一种典型的非线性系统,其动态行 为非常复杂。为了更好地分析和设计倒立摆 系统,可以使用线性化方法将其转化为线性 系统。通过这种方法,可以更好地理解倒立 摆系统的动态行为,并设计有效的控制策略 。
实例三:机器人系统线性化
总结词
机器人系统是一种复杂的非线性系统,其动 态行为可以通过使用线性化方法进行近似描 述。
非线性系统线性化的展望是通过不断的研究和发展,提高非 线性系统线性化的精度和稳定性,为实际工程应用提供更好 的理论支持和实践指导。
05
CATALOGUE
非线性系统线性化实例分析
实例一:非线性振荡器系统线性化
总结词
通过使用非线性振荡器系统的线性化方法,可以更好地理解非线性系统的动态行为,并 设计有效的控制策略。
02
解决数值稳定性问题的方法包括 采用高精度计算方法、引入阻尼 项、采用自适应控制策略等,以 提高数值计算的稳定性和精度。
近似误差问题
近似误差问题是指在进行非线性系统 线性化时,由于对非线性系统的近似 处理,导致线性化结果与实际非线性 系统的偏差。
解决近似误差问题的方法包括采用更 精确的近似方法、引入补偿控制策略 等,以减小近似误差对线性化结果的 影响。
泰勒级数展开法的基本思想是将非线性函数在某一参考点处进行幂次展开,形成 无穷级数。通过选取适当的参考点,可以使得级数的前几项近似于非线性函数, 从而得到近似的线性化模型。该方法适用于具有局部特性的非线性系统。
状态空间平均法
总结词
状态空间平均法是一种基于状态空间模型的非线性系统线性化方法,通过将非线性系统在平均状态空间上进行线 性化,可以得到近似的线性模型。
详细描述
描述函数法的基本思想是非线性系统的输入输出关系可以用一个描述函数来描述。描述函数具有一些 特定的特性,如频率响应和相位响应等。通过比较这些特性与线性系统的相应特性,可以得到近似的 线性化模型。该方法适用于具有特定特性的非线性系统。
4、非线性系统的数学模型

2 ( x x ) x10 1 10
当(x1-x10)为微小增量时,可略去二阶以上各项, 写成
df x2 f ( x10 ) dx1
df 其中 K dx1
x10
( x1 x10 )
x20 K ( x1 x10 )
x10
为工作点(x10,x20)处的斜率,
即此时以工作点处的切线代替曲线,得到变量在工 作点的增量方程,经上述处理后,输出与输入之间 就成为线性关系。
输出
输入
液压控制阀中的 圆形窗口;
在不同输入幅值下,元件或环节具有不同的增益。
分段斜面;
阶梯形窗口;
6、滞环特性
输出
输入
铁磁部件的元件
三、单变量非线性系统的线性化
非线性函数的线性化,是指将非线性函数在工 作点附近展开成泰勒级数。 忽略掉高阶无穷小量及余项,得到近似的线性 化方程,来替代原来的非线性函数。
非本质非线性:
能够用小偏差线性化方法进行线性化处理的非线性。
本质非线性 用小偏差线性化方法不能解决的非线性
2、典型非线性特性 (1)饱和特性
输出
输入
k x(t ) y(t ) ka sgn x(t )
x(t ) a x(t ) a
特征:当输入信号超出其线性范围后,输出信号不再随 输入信号变化而保持恒定。
令T1=R1C1,T2=R2C2,T3=R1C2 则得
d 2u0 (t ) du0 (t ) T1T2 (T1 T2 T3 ) u0 (t ) ui (t ) 2 dt dt
一、微分方程的线性化的特点
1、线性控制系统: 由线性元件组成,输入输出问具有叠加性和 齐次性性质。
非线性系统课件

N (A )N (A )ej N (A )Y 1ej1B 1j1 A
A
A
非线性系统
2. 描述函数的求取步骤 (1) 取输入信号为,根据非线性环节的静态特性绘
制出输出非正弦周期信号的曲线形式,根据曲线形式 写出输出y(t)在一周期内的数学表达式。 (2)据非线性环节的静态特性及输出y(t)的数学表达 式,求相关系数A1、B1。 (3)用式(7-8)计算描述函数。
必须指出,长时间大幅度的振荡会造成机械磨损,增加
控制误差,因此在通常情况下,不希望系统产生自振,必
须设法抑制它。
非线性系统
3.频率响应复杂
线性系统的频率响应,即正弦信号作用下系统的稳态输 出是与输入同频率的正弦信号。而非线性系统的频率响应 除了含有与输入同频率的正弦信号分量(基频分量)外, 还含有关于ω的高次谐波分量。
形称为相平面图。
非线性系统
二、绘制相轨迹的方法
解析法
采用解析法绘制相轨迹通常有两种作法。一种方法是通过积分法, 直接由微分方程求解x(t)和的解析关系式。
0
2 Msintdt
1
2M
(c
os 1
c
os2
)
=2M
1- mh2 A
1-
h
2
A
非线性系统
3) 死区滞环继电特性的描述函数为
N (A )= 2 M A1-m A2h1-A h2j2 M A2(m Ah -≥1h )(7-17)
取h=0可得理想继电特性的描述函数为
N(A)=4M
取m=1可得死区继电特性的A描述函数为
足结构要求的一类非线性系统,通过谐波线性化,将非线性特性近似表 示为复变增益环节,分析非线性系统的稳定性或自激振荡 3.李亚普诺夫第二法
第二章 6 非线性系统线性化

(2)
4
线性化
非线性系统 例1:交流伺服电机
Stator(定子)
输入 ec
输出 ω
对于非线性系统(见图2.28 (b)), 转矩-速度平衡方程为
T − Bω = 0
(2)
Stator(定子)
图2.28 (a)
参考磁场 转 矩
伺服电机特性
速度
5
线性化
非线性系统 例1:交流伺服电机
¾ 当出现小变动时,系统平衡方程将变成
T = f (ec ,ω) (1)
从方程 (1)可得
6
线性化
非线性系统 例1:交流伺服电机
显然,交流伺服电机的动态模型是非线性的。
J
dΔω dt
= ΔT
− BΔω =
f (ec ,ω) − BΔω − T0
定子
输入 ec
输出 ω
定子 参考磁场
图2.28 (a)
?
¾ 利用线性化处理来近似描述 系统的非线性特性,也许可 以得到足够的分析精度。
(平衡点)附近的性能,(如
图所示,(if0,ϕ0)为平衡点,受 Δ ϕ 到扰动后,if (t)偏离if0,产生 Δif (t),Δif (t)的变化过程,表 Δ ϕ 征系统在平衡点附近的性能)。
非线性特性的线性化,实质上 就是以平衡点附近的直线代替
Δif
Δif
平衡点附近的曲线。
10
线性化
非线性方程的பைடு நூலகம்性化方法
自动控制理论
第二章 系统方程列写 ——建模
周立芳 徐正国
浙江大学控制科学与工程学系
第二章要点
9 引言 9 电路及组成 9 线性代数与状态的基本概念 9 传递函数及方块图 9 机械传递系统 9 相似电路 9 其他的数学建模实例
第二章-6-非线性系统线性化

(平衡点)附近的性能,(如
图所示,(if0,ϕ0)为平衡点,受 Δ ϕ 到扰动后,if (t)偏离if0,产生 Δif (t),Δif (t)的变化过程,表 Δ ϕ 征系统在平衡点附近的性能)。
非线性特性的线性化,实质上 就是以平衡点附近的直线代替
Δif
Δif
平衡点附近的曲线。
10
线性化
非线性方程的线性化方法
+ dϕ0
dt
= uf0
两式相减激磁回路偏移量微分方程式: Rf Δi f
+ L'f
dΔi f dt
= Δu f
15
线性化
非线性方程的线性化方法:例题
上面得到的激磁回路偏移量微分方程式:
Rf Δif
+ L'f
dΔi f dt
= Δu f
在熟练后通常可直接对原方程式两边取增量求得,从而简化推导过程。
19
小结
线性化
¾ 要建立整个系统的线性化微分方程式, 1. 首先确定系统处于平衡状态时,各元件的工作点; 2. 然后列出各元件在工作点附近的偏移量方程式,消
去中间变量; 3. 最后得到整个系统以偏移量表示的线性化方程式。
20
第二章总结
¾ 首先,介绍了建模的基本概念及重要性 ¾ 为了列写微分方程及状态方程,介绍了一些物
(1) 对激磁电路有:
Rf if
+
dϕ
dt
=u
f
(2) 找出中间变量ϕ与其它变量的关系,同时线性化。
小偏差过程可用以下办法使之线性化。
如前所述,设在平衡点的邻域内, ϕ 对if的各阶导数(直至n+1) 是存在的,它可展成泰勒级数。
14
机械控制工程基础第二章系统的数学模型

机械控制⼯程基础第⼆章系统的数学模型基本要求、重点和难点⼀、基本要求(1)了解数学模型的基本概念。
能够运⽤动⼒学、电学及专业知识,列写机械系统、电⼦⽹络的微分⽅程。
(2)掌握传递函数的概念、特点,会求传递函数的零点、极点及放⼤系数。
(3)能够⽤分析法求系统的传递函数。
(4)掌握各个典型环节的特点,传递函数的基本形式及相关参数的物理意义。
(5)了解传递函数⽅框图的组成及意义;能够根据系统微分⽅程,绘制系统传递函数⽅框图,并实现简化,从⽽求出系统传递函数。
(6)掌握闭环系统中前向通道传递函数、开环传递函数、闭环传递函数的定义及求法。
掌握⼲扰作⽤下,系统的输出及传递函数的求法和特点。
(7)了解相似原理的概念。
(8)了解系统的状态空间表⽰法,了解MATLAB中,数学模型的⼏种表⽰法。
⼆、本章重点(1)系统微分⽅程的列写。
(2)传递函数的概念、特点及求法;典型环节的传递函数。
(3)传递函数⽅框图的绘制及简化。
三、本章难点(1)系统微分⽅程的列写。
(2)传递函数⽅框图的绘制及简化。
概述系统按其微分⽅程是否线性这⼀特性,可以分为线性系统和⾮线性系统。
如果系统的运动状态能⽤线性微分⽅程表⽰,则此系统为线性系统。
线性系统的⼀个最重要的特性就是满⾜叠加原理。
线性系统⼜可分为线性定常系统和线性时变系统。
系统的数学模型是系统动态特性的数学描述。
对于同⼀系统,数学模型可以有多种形式,如微分⽅程、传递函数、单位脉冲响应函数及频率特性等等。
但系统是否线性这⼀特性,不会随模型形式的不同⽽改变。
线性与⾮线性是系统的固有特性,完全由系统的结构与参数确定。
系统建模是经典控制理论和现代控制理论的基础。
建⽴系统数学模型的⽅法有分析法和实验辨识法两种。
前者主要⽤于对系统结构及参数的认识都⽐较清楚的简单系统,⽽后者通常⽤于对系统结构和参数有所了解,⽽需进⼀步精化系统模型的情况。
对于复杂系统的建模往往是⼀个分析法与实验辨识法相结合的多次反复的过程。
非线性系统的线性化处理方法

非线性系统的线性化处理方法,√j}/Z非线性系大连晨光科技开发邮王士和Tp~?/,2.在各种电气设备,自动控制装置,检查与测线段联结,用于分f与”0,则得到分段线性量用仪器仪表中经常碰到线性或近似线性系统.但是,在很多情况下,也会碰到非线性系统问题关于线性系统的理论分析与计算方法在许多文献中已有讨论但是,非线性系统的理论分析与计算方法在近二十年来一直引起人们的关注还有许多线性系统问题尚待讨论.本文试图就非线性系统中一些分支问题,探讨若干处理方法这里讨论的是稳态情况下若干种非线性问题的处理方法:1.线性化法(或分段线性化法);2.函数化法(或分段函数化法),或称经验公式法;3.数字化法等等.‘一,线性化法(或分段线性化法)假设有一含非线性铁心的电路.其磁化曲线具有图1a所示形状.由图可以看出,这是非线性的但是,如果通过原点至急剧弯曲部分画一条斜线oa代替oa弯曲线时,在理论分析与计算上可以得到符合工程实际需要的分析结论与计算结果.这一类处理工程计算的方法.称谓线性化法.H图1如果将磁化曲线画分成若干段.如图1b所……示.将O1,12,23,34,蛎,56各弯曲段甩近似直线n《■气开曩》(199鼍蹄Io-●)化法显然.它比线性化法更逼真一步.在工程分析与计算上将给出更满意的结果.二,函数化法(或分段函数化法)函数化法是将非线性特性曲线近似地用一个经验公式表达,用来分析各种工程技术问题. 显然,它能够给出的计算精确度决定于经验公式与实际曲线逼近程度例如.图l给出的磁化曲线可以用下式表示,即B:,(H)(1)或H一()(2)详见参考文献1中表1—1所示由各作者给出的磁化曲线经验公式.分段函数法是将非线性曲线分割成若干段,然后对各小段分别用某一函数表示.用这些表达式分析与处理各种技术问题.显然,比前一种方法更逼真一步.但是,应用上会带来许多麻烦.计算机的出现,给解决这类工程问题带来了方便.可以看出,分段线性化方法可视作分段函数法的一个特倒.三,数字化方法数字化方法实际上是将一连续变化的非线性特性曲线实施离散化,将其储存在计算机内, 根据计算程序需要随时调用(详见文献2)以上讨论了非线性系统的直接处理方法.主要用于:非线性元件,非线性线路非线性控制,测量与检查等系统的分析与计算.下面讨论若干间接处理方法四,非线性系统的线性变换法图2中的A环节是一个非线性元件或网路,B环节是另一个非线性元件或网络.此方法的基本思想是A环节在系统中无法直接应用其非线性输入一输出特性用B环节具有另一种非线性输入输出特性来补偿.如果B环节设一25—._,●计合理.可使总的输入一输出特性线性化,如图3所示.因此B环节称作对-A环节的整直环节(或元件).设A环节具有非缉眭函数关系X2= f.(x),B环节具有另_非线性爵数关系Xa—f(x).经过综合后.得到总的输入一输出特性为X.一c.X+线性关系.这就是通过整直环节(或元件)B将非线性环节(或元件)A的菲线性系统实现线性化的线性变换法.如果得到图3的直线,再进行技术处理就很方便.例如.如欲得到X一O时.xf一0{在x正向增加时x也正向增加.只需要在B环节后再增设一级移位倒向环节C就可H实现如图4,5趼示,网?I警l3—26I4瞄5五,非线性系统的补偿网路法非线性元件(或装置)采用线性R,L,C或非线性半导体器件等组成元件或网路可以对其非线性逐段地进行朴偿,以l达到更精确的变换, 例如,目前工业上应用的热电偶上采用的各种温度一电压线性变换网路等.六,非线性系统的数字化处理方法此方法与第四章相似,只是将非线性元件(或装置)输出的模拟量用集成电路(模片)交换成数字量,即进行A/D转换.但此数字量尚须经过专用单片机(例如EPROM或EEPR0M)处理之后,才能整直,送给数字显示器或其他控制部件.这时显示器的指示量与非线性元件(或装置)的输入量呈线性关系,关于其它特殊类型的非线性元件(或装胃=)的非线性特性需要根据要求进行线性化,例如, 开关控制元件对发电机进行电压自动调整等需要特殊处理,而不一定要求对其作线性化处理, 关于这些问题,可参考文献3,4.综上所述.在遇到非线性系统问题时.可以参考上面提出的方法进行处理当然.还可根据不同的具体问题提出新的处理方法,对于这方面的具体理论和技术工作,不仅需要对控制系统及其控制的对象有深刻的了解.而且还要有丰富的元器件的理论与实际知识.参考文献[1]王士和缩自动电礁装置,大连铁道学院, 1985[2:张冠生主编电器学,规被】:业m版社】980_l3]扬自厚主编自动控制原理,精金1:业出暖社,198O[4]蔡尚峰主编.自动控制理沧,机被业m版社,198l[5]尤德裴主编数字化酬量技术眨但器.机械】= 业出版社1980[6]常健生缩.捡j羹I与转换技术.机被丁=业m版社,1981[7]王士和郭永波带热电阻捡渊播的解舟折法电杂志】99o3[8]王士和孝章武王常有智艟化湿度控制倥●气开善》(1995N0_4)。
《控制工程基础》课件-第二章

4/21/2023
27
第二章 数学模型
非线性数学模型的线性化
➢ 泰勒级数展开法
函数y=f(x)在其平衡点(x0, y0)附近的泰勒级数 展开式为:
y
f
(x)
f
(x0 )
df (x) dx
x
(x x0 ) x0
4/21/2023
1 2!
d
2 f (x) dx2
x
x0
(
x
x0
)2
1 3!
d
3 f (x) dx3
4/21/2023
20
第二章 数学模型
➢ 线性系统与非线性系统
线性系统 可以用线性微分方程描述的系统。如果方程的 系数为常数,则为线性定常系统;如果方程的
系数是时间t的函数,则为线性时变系统;
线性是指系统满足叠加原理,即:
✓ 可加性: f ( x1 x2 ) f ( x1) f ( x2 )
K
J TC(t)
柔性轴 齿轮
粘性液体 C
J —旋转体转动惯量;K —扭转刚度系数;C —粘性阻尼系数
4/21/2023
12
第二章 数学模型
TK (t) Ki (t) o (t)
TC
(t)
C
d dt
o
(t
)
J
d2 dt 2
o (t)
TK
(t) TC (t)
J
d2 dt 2
o (t)
C
d dt
y
f (x10,
x20
)
f x1
f
x1 x10 x2 x20
( x1
x10 )
x2
( x2
第二章物理系统的数学模型及传递函数

要 消去它们, 就要找出中间变量与其它因素间的关系. 感应 电势 E ( t ) 正比于转速 m ( t ) 和激磁电流 I f 产生的磁通量 由于激磁电流是恒定的, 所以磁通量也恒定, 感应电势仅取 决于转速, 并可表示为:
a
(3) 消去中间变量 从式(1)和式(2)中可见,
i a ( t ), E a ( t ), M m ( t ) 是中间变量,
uC (t ) u (t )
m
d x(t ) dt
2
2
f
dx(t ) dt
Kx(t ) F (t )
相似系统:揭示了不同物理现象之间的相似关系
三、非线性系统的线性化
1)线性系统 线性系统是由线性元件组成的系统,线性微分
方程用来描述线性系统。 若微分方程的系数是常数称线性定常系统,或 线性时不变系统。 这是经典控制论主要研究的对象,因为它可以 方便地进行拉氏变换,并求得传递函数。
4.用解析法建立运动方程的步骤
1)分析系统的工作原理和系统中各变量间的关系,确 定出待研究元件或系统的输入量和输出量; 2)从输入端入手(闭环系统一般从比较环节入手), 依据各元件所遵循的物理,化学,生物等规律,列写 各自方程式,但要注意负载效应。所谓负载效应,就 是考虑后一级对前一级的影响。 3)将所有方程联解,消去中间变量,得出系统输入输 出的标准方程。所谓标准方程包含三方面的内容:① 将与输入量有关的各项放在方程的右边,与输出量有 关的各项放在方程的左边;②各导数项按降幂排列; ③将方程的系数通过元件或系统的参数化成具有一定 物理意义的系数。
§2-1 系统的数学模型
线性系统微分方程的建立
步骤:1.分析系统和元件的工作原理,找出 各物理量之间的关系,确定输出量及输入 量。 2.设中间变量,依据物理、化学等定律忽 略次要因素列写微分方程式。 3. 将所有方程联解,消去中间变量,得出系统
机械控制工程基础第二章的答案及解析
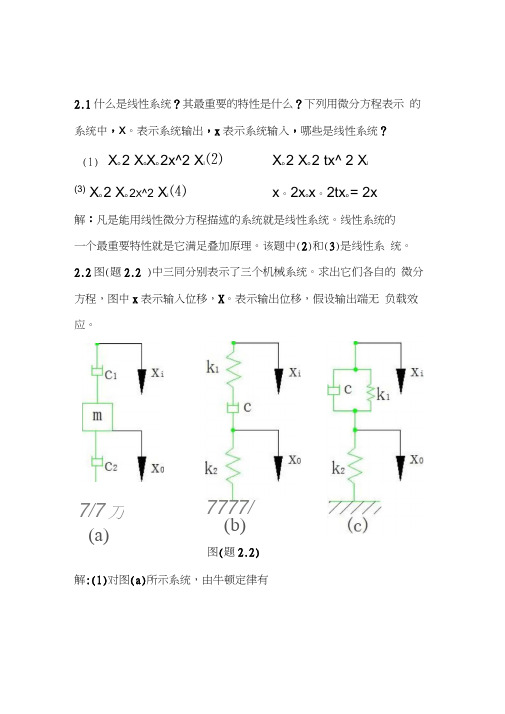
2.1什么是线性系统?其最重要的特性是什么?下列用微分方程表示 的系统中,x 。
表示系统输出,x 表示系统输入,哪些是线性系统? (1)X o2 X oX o2x^2 X i⑵X o2 X o 2 tx^ 2 Xi(3)X o2 X o2X ^2 X i⑷x 。
2x ox 。
2tx o= 2x解:凡是能用线性微分方程描述的系统就是线性系统。
线性系统的 一个最重要特性就是它满足叠加原理。
该题中(2)和(3)是线性系 统。
2.2图(题2.2 )中三同分别表示了三个机械系统。
求出它们各自的 微分方程,图中x 表示输入位移,X 。
表示输出位移,假设输出端无 负载效应。
图(题2.2)解:(1)对图(a)所示系统,由牛顿定律有7/7刀 (a)7777/ (b)c i( x —x 。
) —C 2X 。
二 mx 。
mx 。
( c iC 2)x 。
二 c iXi(X j-x)k i= c(x-x 。
)c(xx °) = k 2x 。
(1) (2)消除中间变量有c (总- k 2)x 。
- k ik zx 。
二 ckix(3) 对图(c)所示系统,由牛顿定律有c ( X - x 。
) k i( X - x 。
)= k zx 。
1c x°+ ( ki+ k 2)x °=cx+ kix2.3 求出图(题2.3)所示电系统的微分方程。
(a)图(题2.3)解:(1)对图⑻ 所示系统,设j 1为流过R 的电流,j 为总电流,则有1 u 厂 R ?iidtC2□ 一 u 。
二 R i j i对图(b)所示系统,引入一中间变量 x,并由牛顿定律有RiCiUiUnR解:设系统输入为M (即),输出二(即),分别对圆盘和质块进行动 力学分析,列写动力学方程如下:1U i-U 。
(i-i i)dtC1消除中间变量,并化简有C 1R 2U(1RC ) U 。
-= 0^+(肯+ C2)⑵ 对图(b )所示系统,设i 为电流,则有1CR 2U 。
控制工程第二章_控制系统的数学基础和数学模型

第二章控制系统的数学基础和数学模型基本要求1.掌握拉氏变换、拉氏反变换的定义、定理。
2.了解数学模型的基本概念。
能够运用动力学、电学及专业知识,列写机械系统、电网络系统的微分方程。
3.掌握传递函数的概念、特点,会求传递函数的零、极点。
4.掌握各个典型环节的特点,传递函数的基本形式及相关参数的物理意义。
5.掌握闭环系统中前向通道传递函数、开环传递函数、闭环传递函数的定义及求法。
掌握干扰作用下,系统传递函数的求法和特点。
6.了解传递函数框图的组成及意义;能够根据系统的微分方程,绘制系统传递函数框图,并实现简化,从而求出系统的传递函数。
7.了解相似原理的概念。
本章重点1.拉氏变换定理。
2.列写系统的微分方程。
3.传递函数的概念、特点及求法。
4.典型环节的传递函数。
5.系统的方框图及其化简。
本章难点1.列写系统微分方程。
2.系统的方框图及其化简。
∞ 2.1 拉普拉斯(L a p l a c e )变换2.1.1 拉氏变换概述1.拉氏变换的定义F (s ) = L [ f (t )] = ⎰0f (t )e -std tf (t ):原函数(实域、时间域) F (s ):象函数(s 域、复数域) s :复变量,s=σ+j ωe - st: 拉氏算子j ω[s]σδ ( t )e -atsin ωtcos ωt2.基本函数的拉氏变换1tkttttu ( t ) r ( t )x i ( t ) k 序号原函数 f (t ) 象函数F (s )1 单位脉冲函数 δ (t ) 12单位阶跃函数 1(t ) 1 s 3 K常数k s4t 单位斜坡函数1 s2 5 tnn ! s n +16 e- at1 s + a7sin ωtω s 2 + ω 28cos ωts s 2 + ω 22.1.2 拉氏变换的主要性质1.线性性质设L [f 1(t )]=F 1(s ),L [f 2(t )]=F 2(s ),k 1,k 2为常数 ,则L [k 1 f 1 (t ) + k 2 f 2 (t )] = k 1L [ f 1 (t )] + k 2 L [ f 2 (t )]= k 1F 1 (s ) + k 2 F 2 (s )2.微分性质若L [f (t )]=F (s ),且f (0)=0,(初始条件为零)则L [ df (t )] =sF (s ) dt3.积分定理若L[f(t)]=F(s),且初始条件为零,则L[⎰ f (t )dt ]= 1 F (s)s4.平移定理若L[[f(t)]=F(s),]则L ⎰e-a t f (t)dt =F (s +a)5.初值定理若L[f(t)]=F(s),则f (0+) = limt →0 f (t) = lim s ⋅F (s)s→∞∞6.终值定理若L [f (t )]=F (s ),则有f (∞) = lim t →∞f (t ) = lim s ⋅ F (s )s →07.延迟定理若L [f (t )]=F (s ),对任一正实数a ,则有L [ f (t - a )]= ⎰0f (t - a )e -st d t = e -as F (s )2.1.2 拉氏变换的主要性质1.线性性质设L [f 1(t )]=F 1(s ),L [f 2(t )]=F 2(s ),k 1,k 2为常数 ,则L [k 1 f 1 (t ) + k 2 f 2 (t )] = k 1L [ f 1 (t )] + k 2 L [ f 2 (t )]= k 1F 1 (s ) + k 2 F 2 (s )2.微分性质若L [f (t )]=F (s ),且f (0)=0,(初始条件为零)则L [ df (t )] =sF (s ) dt3.积分定理若L[f(t)]=F(s),且初始条件为零,则L[⎰ f (t )dt ]= 1 F (s)s4.平移定理若L[[f(t)]=F(s),]则L ⎰e-a t f (t)dt =F (s +a)5.初值定理若L[f(t)]=F(s),则f (0+) = limt →0 f (t) = lim s ⋅F (s)s→∞∞6.终值定理若L [f (t )]=F (s ),则有f (∞) = lim t →∞f (t ) = lim s ⋅ F (s )s →07.延迟定理若L [f (t )]=F (s ),对任一正实数a ,则有L [ f (t - a )]= ⎰0f (t - a )e -st d t = e -as F (s )2.1.3拉氏反变换定义:f(t)=L-1[F(s)],将象函数变换成原函数s:复变量F(s):象函数(s 域、复数域)f(t):原函数(实域、时间域)2.2系统的数学模型数学模型就是描述系统的输出、输入与系统本身结构与参数之间的数学表达式。
非线性系统线性化

化。
令状态偏差为 e x xd ,则有e x xd
由式(1.1)和式(1.2)可得系统的状态偏差方程为:
e x xd f (x,u,t) ( Ad xd Bd v) Ad e [ f (x,u,t) ( Ad x Bdv)] (1.3)
按上述思想,提出如下的基于平衡状态控制原理的非线性控制系统反馈线 性化的直接方法:
(1)按系统的动态性能要求设计一满足希望特性的线性动态系统作为模 型参考系统。
(2)以模型参考系统的状态作为实际被控系统的被控平衡状态。利用李 亚普诺夫直接方法设计控制律使系统对动平衡状态渐进稳定。从而被控系统近 似具有模型参考系统的动态特性,实现非线性系统的反馈线性化。
在非线性系统的模型参考方法中,基于李亚普诺夫直接方法的非线性系统 反馈线性化方法是最重要和最有效的一种设计方法,这类方法称为非线性系统 反馈线性化的直接方法。
运用控制系统动平衡状态的概念,提出一种建立在控制系统动平衡状态渐 近稳定概念上的新的设计方法。本方法认为:控制系统的输入直接控制的是系 统的动平衡状态。系统的输出和状态是在系统结构的约束下运动的。当系统对 其平衡状态大范围渐近稳定时,其状态将在系统结构约束下渐近收敛于系统的 平衡状态。当其平衡状态运动时,系统的状态亦将跟踪其平衡状态运动。因此 控制系统平衡状态的运动,即可实现对系统运动状态及输出的控制。
基于动平衡状态理论的非线性系统反馈 线性化直接方法
按上述方法,基本设计过程如下:
考虑一般的非线性系统
x f (x,u,t)
(1.1)
其中,x Rn 为状态向量,u Rm 为控制向量,f 为向量函数。
设希望的线性系统动态特性为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Stator(定子)
输出 ω ¾ 根据交流伺服电机的平衡方程,有
输入 ec
Stator(定子) 参考磁场
图2.28 (a)
考虑线性关系
T = J d 2θ + b dθ (1‘)
dt 2
dt
T = f (ec ,ω)
(1)
对于非线性系统(见图2.28 (b)),转 矩-速度平衡方程为
T − Bω = 0
∵J
dΔω dt
= ΔT
− BΔω =
f (ec ,ω) − BΔω − T0
T = f (ec ,ω)
泰勒级数展开
T
= T0
ec =ec0 ω=ω0
+
∂f ∂ec
Δec
ec =ec0 ω=ω0
+
∂f
Δω
∂ω ec =ec0
ω=ω0
ec
= T0 + KcΔec + KωΔω
参考磁场
于是
J
dΔω dt
(2)
4
线性化
非线性系统 例1:交流伺服电机
Stator(定子)
输入 ec
输出 ω
对于非线性系统(见图2.28 (b)), 转矩-速度平衡方程为
T − Bω = 0
(2)
Stator(定子)
图2.28 (a)
参考磁场 转 矩
伺服电机特性
速度
5
线性化
非线性系统 例1:交流伺服电机
¾ 当出现小变动时,系统平衡方程将变成
7
线性化
非线性系统 例1:交流伺服电机
¾ 线性化:在工作点(这里是原点)附近,利用泰勒级数展开将非 线性函数 T 进行线性化,并保留线性项,可以得到
定子
输入 ec
输出 ω
定子 参考磁场
图2.28 (a)
8
线性化
非线性系统 例2:钟摆
l mg
¾ 列写钟摆的动态方程
输入 u
u
θ 输出
ml 2 θ = u − mgl sin( θ)
θ=−
g sin(θ) + l
1 ml 2
u
=−g l
f (θ) +
1 ml 2
u
??
9
线性化
非线性方程的线性化
¾ 几乎所有元件或系统的运动方程都是非线性方程。但在比较小 的范围运动来说,把这些关系看作是线性关系,是不会产生很 大误差的。方程式一经线性化,就可以应用线性迭加原理。
¾ 研究非线性系统在某一工作点
(1) 对激磁电路有:
Rf if
+
dϕ
dt
=u
f
(2) 找出中间变量ϕ与其它变量的关系,同时线性化。
小偏差过程可用以下办法使之线性化。
如前所述,设在平衡点的邻域内, ϕ 对if的各阶导数(直至n+1) 是存在的,它可展成泰勒级数。
14
线性化
非线性方程的线性化方法:例题
¾ 经线性化后,得到激磁回路偏移量间的线性关系,动态电感L’f 为常值,但在不同平衡点有不同的值 。
理系统及相应的物理规律,包括:电气、机械、 热力、液位等 ¾ 介绍了矩阵、状态、传递函数、方块图等基本 概念 ¾ 介绍了线性化概念及方法
21
第二章总结
¾ 输入输出变量 ¾ 方程的阶——储能元件 ¾ 输入输出模型的一般形式 ¾ 状态空间方程 ¾ 问题:各种模型之间的关系是如何的?
22
第二章总结
各种模型之间的关系
(反应物)
c(t) = r 2 (t) 2)
Q (t) = αf h(t) ¾ 通常利用一般的非线
性微分方程描述非线 性系统
x = f (x,u)
3
线性化
非线性系统 例1:交流伺服电机
¾ 交流伺服电机如图2.28所示。由图(b)可以看出,转矩-速 度曲线不是直线。因此无法利用线性微分方程来确切地 描述电机特性。
+ dϕ0
dt
= uf0
两式相减激磁回路偏移量微分方程式: Rf Δi f
+ L'f
dΔi f dt
= Δu f
15
线性化
非线性方程的线性化方法:例题
上面得到的激磁回路偏移量微分方程式:
Rf Δif
+ L'f
dΔi f dt
= Δu f
在熟练后通常可直接对原方程式两边取增量求得,从而简化推导过程。
ϕ = ϕ0 + L ' f Δif
或 Δϕ = ϕ − ϕ0 = L ' f Δif
在平衡点附近,经过线性化处理 (忽略偏移量的高次项)后,原方 程的偏移量间已经具有线性关系了。 偏移愈小,这个关系愈准确。
13
线性化
非线性方程的线性化方法:例题
¾ 磁场控制的直流电动机。电枢电压ua为常值,输出为w ,控制 输入为uf 。研究它的小偏差过程,例如控制输入uf改变一个微 量Δuf引起的变化过程。
定子
输入 ec
J
d (ω0 + dt
Δω)
=
(T0
+
ΔT )
−
B(ω0
+
Δω)
(3)
其中,J 是转动惯量
输出 ω
∵ T0 − Bω0 = 0
从方程(3)中消去稳态项,于是可以得到 交流伺服电机的动态模型
定子
参考磁场
图2.28 (a) 注意方程 (1)
J dΔω = ΔT − BΔω dt
= f (ec ,ω) − BΔω − T0
L := 100cm
T1(θ) := M⋅g⋅L⋅sin(θ)
( ) ( ) T2(θ) := M⋅g⋅L⋅cos θ0 ⋅ θ − θ0 + T0
θ0 := 0rad
10
线性化
θ := −π, −15π .. π 16
5 T 1( θ )
0 T 2( θ )
5
10
4
3
2
1
0
1
2
3
4
θ
Students are encouraged to investigate linear approximation accuracy for different values of θ0
T = f (ec ,ω) (1)
从方程 (1)可得
6
线性化
非线性系统 例1:交流伺服电机
显然,交流伺服电机的动态模型是非线性的。
J
dΔω dt
= ΔT
− BΔω =
f (ec ,ω) − BΔω − T0
定子
输入 ec
输出 ω
定子 参考磁场
图2.28 (a)
?
¾ 利用线性化处理来近似描述 系统的非线性特性,也许可 以得到足够的分析精度。
1 ml 2
u
¾ 利用线性化方法,可以得到钟摆动态方程为
f
(θ)
≈
f
(θ0 ) +
df dθ
(θ − θ0 )
θ0 =0
⇔ sin(θ)
≈ 0 + cos(0)θ ⇔
sin(θ) ≈ θ
θ≈−gθ+ 1 u l ml 2
18
非线性系统 例2:钟摆
M := 200gm
g := 9.8 m
s2
( ) T0 := M⋅g⋅L⋅sin θ0
Δϕ
(
dϕ
di f
)0
,(
d2ϕ
di
2 f
)0
,
…
为原平衡点处的一阶、 二阶、…导数.
Δϕ
Δif =if - if 0
Δif
Δif
11
线性化
非线性方程的线性化方法
忽略泰勒级数右端第三项及其以后的各项
ϕ
= ϕ0
+
(
dϕ
di f
)0
Δi
f
+
1 2!(d2ϕFra bibliotekdi2 f
)0
(Δi
f
)2
+
+
1 (dnϕ
n!
Δϕ = ϕ − ϕ0 = L 'f Δif
(3)求以偏移量表示的微分方程式,即线性化方程式。将 uf = u f 0+Δu f , ϕ = ϕ 0+L′fΔif ,if = if 0+Δif 代入原方程
得:
Rf
(i f
0
+
Δi f
)
+
d dt
(ϕ0
+
L' f
Δi f
)
=
uf
0
+
Δu
f
在平衡点
Rf if 0
19
小结
线性化
¾ 要建立整个系统的线性化微分方程式, 1. 首先确定系统处于平衡状态时,各元件的工作点; 2. 然后列出各元件在工作点附近的偏移量方程式,消
去中间变量; 3. 最后得到整个系统以偏移量表示的线性化方程式。
20
第二章总结
¾ 首先,介绍了建模的基本概念及重要性 ¾ 为了列写微分方程及状态方程,介绍了一些物
9 微分方程
LT
(LT)-1
9 传递函数(拉普拉斯形式) ?
9 状态方程
???
23
控制科学与工程学系
(平衡点)附近的性能,(如
图所示,(if0,ϕ0)为平衡点,受 Δ ϕ 到扰动后,if (t)偏离if0,产生 Δif (t),Δif (t)的变化过程,表 Δ ϕ 征系统在平衡点附近的性能)。
非线性特性的线性化,实质上 就是以平衡点附近的直线代替
